Abstract
Human sensory perception is not a faithful reproduction of the sensory environment. For example, at low contrast, objects appear to move slower and flicker faster than veridical. Although these biases have been observed robustly, their neural underpinning is unknown, thus suggesting a possible disconnect of the well established link between motion perception and cortical responses. We used functional imaging to examine the encoding of speed in the human cortex at the scale of neuronal populations and asked where and how these biases are encoded. Decoding, voxel population, and forward-encoding analyses revealed biases toward slow speeds and high temporal frequencies at low contrast in the earliest visual cortical regions, matching perception. These findings thus offer a resolution to the disconnect between cortical responses and motion perception in humans. Moreover, biases in speed perception are considered a leading example of Bayesian inference because they can be interpreted as a prior for slow speeds. Therefore, our data suggest that perceptual priors of this sort can be encoded by neural populations in the same early cortical areas that provide sensory evidence.
Keywords: Bayesian, fMRI, motion, perceptual bias, vision
Introduction
Human perception, in particular motion perception, is known to display consistent biases that are readily apparent when sensory evidence is weak. For example, although the speed of easily visible high-contrast stimuli can be estimated accurately, observers report the speed of less-visible, low-contrast stimuli as slower than their true speed (Thompson, 1982; Stocker and Simoncelli, 2006). Observers are also biased when estimating the rate of temporally flickering stimuli presented at low contrast, but within a certain range they are biased toward high rates (Thompson and Stone, 1997; Hammett and Larsson, 2012). Motion perception (Burr and Thompson, 2011) is a canonical domain of sensory decision-making for which the evidence linking perception to cortical responses has been firmly established (Parker and Newsome, 1998). Indeed, speed perception is thought to be tightly linked with responses in cortical middle temporal area MT because neural contrast thresholds (Seidemann et al., 1999; Wandell et al., 1999) match those of speed perception rather than general visibility (Dougherty et al., 1999). However, single-unit measurements have failed to find neural correlates (Pack et al., 2005; Krekelberg et al., 2006; Livingstone and Conway, 2007) of motion perception biases, suggesting a disconnect in this otherwise well established link.
Motion perception biases are also of particular interest because of their possible relationship to normative theories of perceptual inference. Natural environments rarely provide unequivocal sensory information; a prominent view of motion perception biases (Weiss et al., 2002; Stocker and Simoncelli, 2006) suggests that they are not simply the limitations of imperfect biological systems but instead represent optimal strategies for dealing with ambiguous sensory evidence. This Bayesian view of motion speed perception suggests that weakening sensory evidence by reducing image contrast results in perceptual estimates biased toward a prior for slow speeds. This is appealing because it explains a number of seemingly unrelated motion-related illusions in a single unified framework (Hürlimann et al., 2002; Weiss et al., 2002; Hedges et al., 2011). Thus, understanding the neural basis of motion biases also provides an opportunity to understand the more general question of how putative priors interact with sensory evidence to yield biased percepts.
We hypothesized that an examination at the scale of neural populations would help to resolve the apparent disconnect between cortical responses and motion perception. We used decoding (Kamitani and Tong, 2005), voxel population, and forward-encoding techniques (Serences and Saproo, 2012) to analyze functional magnetic resonance imaging (fMRI) data from human observers, for whom perceptual speed and temporal frequency biases are well established and easily measured. We measured speed and temporal frequency-selective responses using fMRI and found that, at low contrast, the representation in all cortical visual areas studied shifted toward slow speeds and faster temporal frequencies, matching perception rather than the pure sensory evidence. Voxel population, permutation, and forward-encoding analyses confirmed that these were not simple consequences of the reduction in response attributable to reduced contrast, but were a genuine shift in the population response toward perceptual biases. Our results are the first to find a neural representation consistent with perceptual biases for speed and temporal frequency, thus offering a resolution to the disconnect between cortical responses and motion perception in humans. They also suggest that perceptual priors can be incorporated into sensory evidence in the earliest stages of the visual system.
Materials and Methods
Human subjects.
Four healthy adult males were subjects for this study (24–31 years old). Each subject participated in multiple psychophysical experiments to measure sensitivity to speed and temporal frequency as well as four MRI sessions: one for collecting a high-resolution anatomical scan and three functional sessions in which we made structural images and recorded BOLD activity (Ogawa et al., 1990, 1992) in occipital cortex. The RIKEN Functional MRI Safety and Ethics Committee approved all of the procedures before experimentation, and each subject provided written informed consent before each imaging session.
Visual stimuli.
Visual stimuli were programmed using MGL (available from http://justingardner.net/mgl) running on MATLAB (MathWorks). For MRI experiments, stimuli were backprojected onto a screen via an LCD projector (Silent Vision 6011; Avotec) with a resolution of 800 × 600 and a refresh rate of 60 Hz. Subjects viewed the screen at a distance of 38.5 cm, through a mirror. Images were gamma corrected and had a maximum luminance of 4 cd/m2. For psychophysics experiments, stimuli were presented on a CRT monitor (Trinitron 21-inch flat screen; Dell Computer Company) that had a resolution of 1280 × 960 and a refresh rate of 100 Hz. The monitor was gamma corrected and was placed 50.5 cm from the observer.
All of the psychophysics and functional imaging experiments used one-dimensional (1D) broadband stimuli (i.e., with many spatial frequency components; Fig. 1) shown at various contrasts that either moved rigidly at different speeds and directions or flickered at different temporal frequencies. We created these stimuli by first generating a square image that contained 1D white Gaussian noise (i.e., the image was constant in the vertical direction but varied stochastically in the horizontal direction). To produce a stimulus with gray average luminance and avoid aliasing on the display, we then bandpass filtered this noise between 0.33 and 2 cycles/°. Finally, stimuli were windowed with a circular aperture. For speed experiments, these stimuli drifted to the right or to the left at variable speeds. For the temporal frequency experiments, the stimulus was static but underwent sinusoidal contrast modulation in time.
Figure 1.
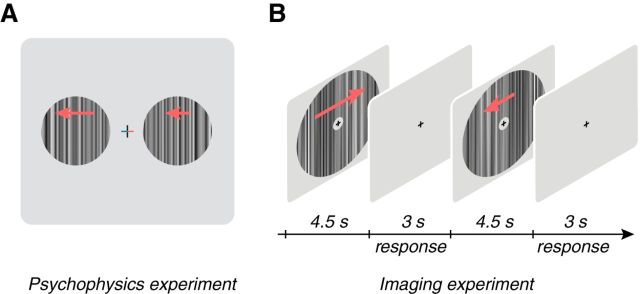
Experimental paradigms. A, Schematic of the methods-of-adjustment psychophysics experiment. Stimuli were broadband 1D textures presented at different contrasts (5, 10, 20, 50, or 100%) and rigidly drifted to the left or the right (indicated by arrows that were not actually presented with the stimulus) at variable speeds (0.25, 1, 2, or 4°/s) or were modulated at different temporal frequencies (1, 3, 6, or 9 Hz). On each trial, the left and right arms of the fixation cross changed color to indicate the location of the reference texture, which was always presented at 100% contrast, and the test texture, which had a variable contrast (red, test; blue, reference). Subjects were instructed to adjust the speed or temporal frequency of the test texture to match the speed or temporal frequency of the reference. B, Schematic diagram of the functional imaging experiment. Subjects fixated a central fixation cross while performing a fixation task. Broadband stimuli moving in different directions (left or right, red arrows that were not actually presented in the stimulus) and speeds (0.25, 1, or 4°/s) or temporal frequencies (1, 3, 6, or 9 Hz) at different contrasts were shown (7.5 or 50%) for 4.5 s with a 3 s intertrial interval in which the screen was gray.
Eye movement analyses.
We made measurements of eye position in two subjects outside of the magnet to ensure that they were able to maintain accurate fixation. Stimuli and task were the same as the speed functional imaging experiment and were conducted while we tracked subject's eye position using an EyeLink 1000 eye tracker (SR Research). A subject's median horizontal and vertical eye position during stimulus presentation did not depend on either the contrast (p > = 0.71, one-way ANOVA) or speed (p > = 0.85) of the stimulus. Moreover, no pairwise comparison of eye position across conditions was found to be significant for speed (p > = 0.67 all pairwise comparisons, Hotelling's T2 test) or contrast (p > = 0.47).
Psychophysical measures of perceptual biases for speed and temporal frequency.
Psychophysical measurements of speed and flicker perception were collected in two separate experiments on the same subjects that participated in the imaging experiments (only three of four subjects were available for the flicker psychophysics experiment). We measured the biases for speed (degrees per seconds) and flicker (hertz) with a method-of-adjustment task. In each experiment, subjects were required to maintain fixation in a central location while two flanking patches were shown 3° from center (3° circular aperture; Fig. 1A). A high-contrast (100%) patch was indicated to be the reference patch by a change in color of one arm of the fixation cross to blue. The second patch was designated as the test patch (indicated by a red fixation cross arm) and had a variable contrast (5, 10, 20, or 50%). In the speed experiment, subjects were instructed to adjust the speed of the test patch until it matched the speed of the reference patch (0.25, 1, 2, or 4°/s) and were given an unlimited time in which to respond. Likewise, for the flicker experiment, subjects had to match the temporal frequency of the reference patch (1, 3, 6, or 9 Hz). The adjusted speed or temporal frequency was reported as the perceptual matching speed or temporal frequency.
Stimuli and task for functional imaging experiments.
For the speed functional imaging experiment, stimuli drifting either to the left or right at varying speeds and contrasts were presented while subjects maintained central fixation. The stimuli were presented in an annular window (3–28° diameter) at three different speeds (0.25, 1, or 4°/s) and two contrasts (7.5 or 50%) in a pseudorandomized order across trials (Fig. 1B). We note that, although the range of speeds chosen are slower than those used for most physiology experiments, we chose them carefully for two reasons. First, we had to ensure that our display was not aliased given the broad range of spatial and temporal frequencies that we chose. Second, the perceptual bias that we sought to study is most apparent at these slow speeds (Thompson, 1982; Stocker and Simoncelli, 2006). For three of four subjects, the stimulus was presented for 4.5 s, followed by a 3 s intertrial interval that consisted of a gray screen. The stimulus presentation interval for the fourth subject was 7.5 s rather than 4.5 s, but the same amount of time data from the imaging time series was used for analysis in every subject, and no qualitative differences were found in the results.
For the temporal frequency experiment, stimuli were identical to the speed experiment in spatial extent and contrast but underwent temporal frequency modulation rather than drifting. That is, images were modulated in time by a sinusoid of frequency of 1, 3, 6, or 9 Hz such that their spatial phase inverted periodically (i.e., flickered). Stimuli were presented for 7.5 s with a 3 s intertrial interval that consisted of a gray screen. The temporal frequency experiment was run on different days than the speed experiment.
For both experiments, subjects fixated a central cross throughout each scan while performing a task intended to keep their behavioral state uniform. For the speed experiment, the fixation cross (composed of two concentric crosses, one light and the other dark; Fig. 1B) matched the contrast of the stimulus annulus and rotated clockwise or counterclockwise as the stimulus drifted to the left or right. During the intertrial interval, a color change of the fixation cross indicated that subjects were to report the speed of the outer edge of the rotating cross as moving either faster or slower than the drifting annulus using a button press. For the flicker experiment, the cross also flickered, and the subject was to report the speed of the cross flicker as faster or slower than the stimulus annulus.
Subjects participated in eight or nine consecutive scans of 36 trials each for the speed and 25 trials each for the temporal frequency experiments. The scans lasted a little over 4 min each, and subjects were allowed to rest between the scans. In each scan, unique stimulus parameter combinations (two contrasts, three speeds, and two direction for the speed experiment and two contrasts and four flicker rates for the temporal frequency experiment) were presented in a pseudorandom order such that each combination of parameters was shown at least three times per scan. This paradigm allowed the collection of 24–27 repetitions for each parameter combination in one scanning session of the speed experiment and 28 repetitions for the temporal frequency experiment.
MRI methods.
All imaging was performed with a Varian Unity Inova 4 tesla whole-body MRI system (now Agilent Technologies) equipped with a head gradient system. In an initial session, a high-resolution 3D anatomical T1-weighted (MPRAGE; TR, 13 ms; TI, 500 ms; TE, 7 ms; flip angle, 11°; voxel size, 1 × 1 × 1 mm; matrix, 256 × 256 × 180) and T2*-weighted (TR, 13 ms; TE, 7 ms; flip angle, 11°; voxel size, 1 × 1 × 1 mm; matrix, 256 × 256 × 180) fast, low-angle shot sequence volumes were collected with a birdcage radio frequency (RF) coil for each subject. To reduce inhomogeneities in image contrast, the T1-weighted volume was divided by the T2*-weighted volume to form the reference high-resolution 3D anatomical volume (Van de Moortele et al., 2009). In three subsequent sessions, a volume RF coil (transmit) and a four-channel receive array (Nova Medical) were used to acquire anatomical (T1-weighted; MPRAGE; TR, 11 ms; TI, 500 ms; TE, 6 ms; flip angle, 11°; voxel size, 1.72 × 1.72 × 1.72 mm; matrix, 128 × 128 × 64) and coregistered functional (T2*-weighted) images. The first of these sessions yielded a retinotopic map and was used to define visual areas. The last two sessions were used to collect functional responses to moving stimuli parameterized by speed and temporal frequency.
Functional scans were collected in 21 slices at an angle approximately perpendicular to the calcarine sulcus. Images had a resolution of 3 × 3 × 3 mm (field of view, 19.2 × 19.2 cm; matrix size, 64 × 64) and were acquired using echo-planar imaging with two shots per image (interleaved across slices), a TR of 1.57 s, a TE of 25 ms, flip angle of 55°, and sensitivity encoding (Pruessmann et al., 1999) with acceleration factor 2. The first five volumes in each scan were discarded to allow longitudinal magnetization to reach steady state, after which an initial volume without phase encoding was collected as a reference for correcting phase errors (Bruder et al., 1992). A navigator echo collected at the beginning of each segment was used to correct intersegment phase and amplitude variations (Kim et al., 1996).
The functional images for each scan were registered to the reference high-resolution 3D anatomical volume of the whole brain. The reference volume was segmented to generate cortical surfaces using Freesurfer (Dale et al., 1999). Subsequently, the anatomy volumes taken at the beginning of each session were registered to the reference volume so that the cortical regions in the functional scans could be identified and aligned with the retinotopy. For data visualization purposes, 2D flattened representations of the visual cortex were created. All analyses were performed in the original (nontransformed) coordinates before being mapped to the cortical surface and specific visual regions.
Various measures were taken to reduce artifacts in functional images. During scanning, respiration was recorded with a pressure sensor, and heartbeat was recorded with a pulse oximeter. These signals were used to attenuate physiological signals in the imaging time series using retrospective estimation and correction in k space (Hu et al., 1995). Head motion was also estimated and corrected (Nestares and Heeger, 2000). We then detrended and high-pass filtered with a cutoff frequency of 0.01 Hz the time series of each voxel.
Visual field definitions.
Retinotopic mapping was used to define visual areas using standard methodology (for details and review, see Gardner et al., 2008; Wandell and Winawer, 2011). Briefly, in a separate scanning session, 10–12 runs of high-contrast sliding radial checkerboard patterns were either shown as rings that expanded and contracted (two runs each) in eccentricity or 90° wedges that rotated clockwise or counterclockwise (three to four runs, each) for 10.5 cycles of 24 s. Time courses were time shifted two to six frames, runs with opposite direction stimuli time reversed and rings and wedges were separately averaged, and the Fourier transform of the averaged responses was taken. The phase of voxel response at the stimulus frequency was displayed on flattened representations of the cortical surface. These projections were used in reference to published criteria to define visual areas V1–V3 and hV4 in all subjects. Area V3A was also defined in three of the four subjects.
Area MT was defined in reference to retinotopic information and a functional localizer (see: Gardner et al., 2008). At the beginning of each experimental session, a functional localizer for visual motion-sensitive responses was run. The localizer consisted of an annulus of dots (0.5–20° radius) that alternated between coherent and incoherent motion in 10 cycles, each cycle lasting for 16 volumes (25.12 s). Coherent motion consisted of an optic flow pattern centered at fixation that alternated between expanding and contracting directions every 2.5 s. Incoherent motion contained the same distribution of dot directions and motions but randomly assigned to different positions. These data were analyzed by computing the coherence of the BOLD response to the stimulus frequency and plotting these on a flattened representation to define motion-selective visual areas according to published criteria.
Finally, we included a control brain region that was not found to be visually responsive by hand drawing a bilateral region of interest in the parietal lobes for each subject. The control brain region was analyzed identically to the retinotopically defined visual areas and was used as one estimate of a null effect. Each brain area had a different number of voxels. V1–V3 averaged 257 voxels each, V3A, hV4, and MT, averaged 96 voxels each, and the control area averaged 206 voxels.
BOLD response instances for decoding, voxel population, and forward-encoding analyses.
For each stimulus presentation, we computed a BOLD “response instance” for each visual area that could be used for decoding and voxel population analyses. Response instances can be thought of as the pattern of BOLD activity in response to each stimulus presentation. Response instances consisted of a scalar value for each voxel within a visual area that represented the stimulus-locked activity that deviated from the mean across the experiment. For each scan, voxel time series were divided by their mean response to convert to percentage signal change. Activity for each voxel was subsequently averaged over time (four volumes; 6.28 s) for each stimulus presentation with a lag of two volumes (3.14 s) from stimulus onset. These scalar responses for each voxel were then converted to be zero mean and unit variance over the entire dataset. That is, for each response, we subtracted the mean and divided by the variance across all responses for that voxel. A collection of these scalar responses for each voxel in a visual area thus formed a response instance: a pattern of cortical activity that was associated with a particular stimulus occurrence. A collection of these response instances were used to build and test decoders for specific stimulus parameters. For the data that was used to determine decoder readout shifts between high and low contrasts, we also removed the mean of each response instance to minimize any potential general effect of contrast.
Decoding the stimulus from BOLD response instances.
Linear stimulus decoders were used to try to predict the speed or temporal frequency of a stimulus occurrence from a response instance. Decoders were always built and tested using fivefold cross-validation. That is, the data were randomly split into five groups, and prediction performance for each group of one-fifth of the trials was evaluated with a decoder built using the remaining four-fifths of the trials. Thus, for each split of the data, four-fifths of the response instances were compiled into a matrix Rbuild, that had one row for each response instance and one column for each voxel. The remaining one-fifth of trials were compiled into an Rtest matrix. Each of these response matrices were associated with column vectors, stest and sbuild, containing the stimulus parameter (either speed or temporal frequency) for each corresponding trial in the response matrices.
A linear decoder is specified by a weight vector, w, whose dot product with each response instance gives a prediction of the stimulus parameter of that trial. That is, each element of w represents a weighting of the corresponding voxel response. A positive weight value indicates that the voxel response tends to linearly increase with the stimulus parameter (e.g., increasing response with increasing speed), and a negative value indicates the opposite (e.g., decreasing response with increasing speed), written in matrix form (matrices are capitalized and vectors are in bold):
where the circumflex over the s indicates that it is the predicted stimulus parameters for the decoder whose weights are specified by w based on the response instance matrix Rbuild. Note that this equation does not include an offset term, which is appropriate for our normalized data (zero mean, unit variance).
We used a regularization method to compute the weight vector w. The ordinary least-squares solution can be used to solve Equation 1 to compute a w that minimizes the squared error of the predicted stimulus parameter from the actual stimulus parameter, sbuild. However, because there are typically many voxels of data with very few repetitions of each response instance, this solution can be underconstrained. So, instead, we used least angle regression with a least absolute shrinkage and selection operator (LARS–lasso; Efron et al., 2004) to compute w. This method includes a term that penalizes the sum of absolute weights (L1 term):
Therefore, this L1 regularization favors solutions to w in which voxels that do not contribute to accurate decoding get weight values of 0 (rather than small idiosyncratic weights distributed around 0 that tend to add noise to the estimates), thus leading to a more robust solution. The LARS method is an incremental algorithm for solving this equation very efficiently, and it also provides a cross-validated fit for the sparsity parameter, λ. That is, λ is not chosen arbitrarily but is fit so that the decoding vector is optimally sparse given the data. This results in a decoding vector, w, that does not suffer heavily from overfitting and therefore generalizes well to holdout data that were not used to fit the decoder.
Decoder performance was evaluated by determining how well the predicted stimulus parameter for each trial in the test set correlated with the actual stimulus parameter. Thus, the correlation coefficient, r, was calculated between the holdout set of stimulus values, stest, and the predicted set, ŝtest. Chance performance for this measure should be 0. We further determined the significance of the performance of each decoder by building decoders 1000 times with different tranches of the data held out for testing, which we refer to as a permutation test. That is, we built 1000 fivefold decoders, each one with a different random subset of the data (on average, each subset should have an equal representation of all stimulus parameters). We calculated empirical confidence intervals on this distribution and compared them with a null hypothesis distribution that was obtained by another 1000 decoders built with randomly permuted data labels.
We found that limiting the number of non-0 weights using the regularized computation of the weight vectors w resulted in better decoding accuracy. Decoding accuracy (measured as r values) for the decoder with the sparse constraint outperformed the decoder calculated with an ordinary least squares solution by an average of 75% across the visual areas and outperformed the simple region-of-interest average by 262%.
To compute how much the prediction of the decoder shifted with reductions in contrast in the proper units (degrees per seconds or temporal frequency), we needed to apply a correction factor to the output of the decoders. One characteristic of sparse decoders is that they shrink the overall range of output toward the mean value of all responses. Although this result is desirable for decoding because this shrinkage actually provides for minimal mean square error between the data and decoded output, we had to correct this shrinkage to report decoder shifts in units of degrees per seconds. This correction factor, c, is calculated as follows:
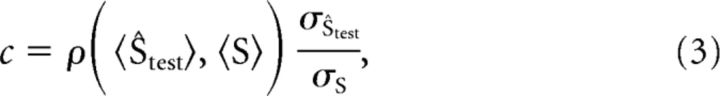 |
where the 〈s〉 is the condition-averaged stimulus speed or decoded speed, σ is the SD of the stimulus speed or the decoded speed, and ρ indicates a correlation operation. Here, the quotient effectively normalizes response range, and the correlation value reapplies the slope of the relationship, approximating the effect of a decoder without shrinkage. Note that the correlation between two univariate variables with unit variance is also the weight, w, calculated with ordinary least squares.
Voxel population analyses.
Population plots of voxel activity (see Figs. 4A, 5A) were used to visualize voxel response as a function of their preferred speed or temporal frequency. To compute the tuning preference of each voxel, we determined whether there was a high-contrast stimulus speed or temporal frequency that drove activity levels significantly higher than any other speed or temporal frequency (one-tailed t test, p < 0.05). Voxels that had significantly high activity for more than one speed or temporal frequency (uncommon) or none at all (more common) were not used in the subsequent analyses. The use of this particular method for defining voxel tuning preference was chosen for clarity but was not critical to the results. We also performed this analysis using methods that forced a continuous-valued tuning preference on every voxel, such as using the sparse-decoder weights w as a measure of tuning preference (a voxel with slow preference would have a negative weight and a voxel with fast preference would have a positive weight) or the normalized voxel-by-voxel correlation of response magnitude with speed or temporal frequency (positive and negative correlation indicate fast and slow preference, respectively) but found no qualitative difference in the results. The tuning preference and activity levels were computed using cross-validation such that four-fifths of the data were used to compute the tuning weight and the remaining one-fifth of the data used to compute the response of the voxel to each stimulus speed or temporal frequency and contrast. Each voxel contributes to six different regions of the plots for a given visual area (eight for temporal frequency data): 2 stimulus contrasts × 3 stimulus speeds. The relationship between the tuning preference and the response was summarized with a linear fit across voxels, and Figures 4B and 5B show the average fit line for all subjects, with error bars depicting the SEM across subjects.
Figure 4.
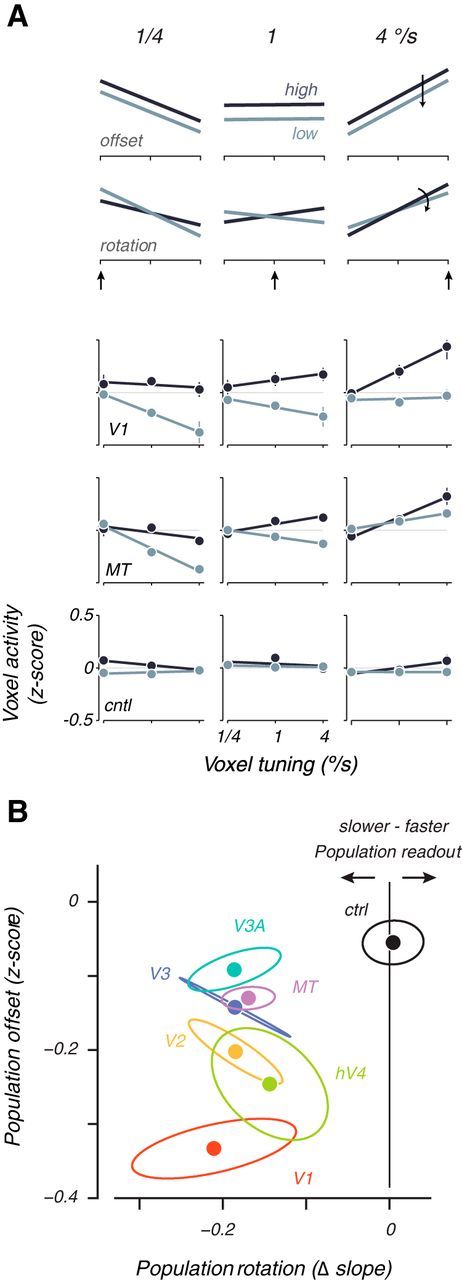
Voxel population analysis of speed shifts. A, Normalized voxel response is plotted as a function of voxel tuning preference for two hypothetical cases (top 2 rows) and three areas averaged across all subjects (bottom 3 rows). Each columns shows activity at one of three different stimulus speeds at high (dark lines) or low (light lines) contrast. The arrow indicates a slow, medium, or fast stimulus speed. Data are cross-validated and averaged across all trials and subjects, reported as z-scores. Error bars are SEM across subjects. A hypothetical general decrease in contrast would shift population activity vertically without changing the slope (first row: “offset”), whereas a hypothetical population shift to slower speeds at low contrasts should result in a rotation of the population response (second row: “rotation”). B, Plot of vertical offset against rotation of population activity lines, averaged across subject for each visual area. Ellipses are SEM across subjects. Clockwise (negative) rotations of the population activity lines as a result of low-contrast stimuli can be interpreted as a shift in the speed representation toward slower speeds. Counterclockwise (positive) rotations can be interpreted as a shift toward higher speeds. cntl, ctrl, Control.
Figure 5.
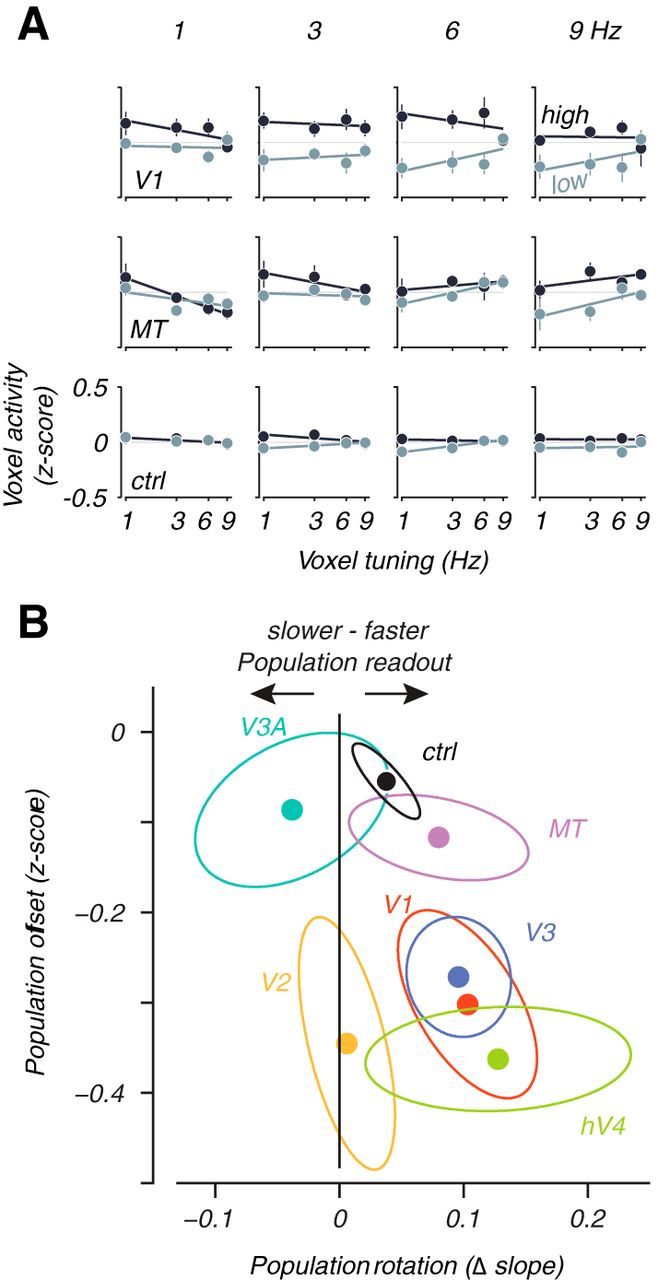
Population plot analysis of temporal frequency shifts. All conventions follow Figure 4. ctrl, Control.
Forward-encoding speed channel model.
We fit a forward-encoding model (Dumoulin and Wandell, 2008; Kay et al., 2008; Brouwer and Heeger, 2009; Serences and Saproo, 2012) to our BOLD data. This allowed us to examine the contrast sensitivity of a hypothetical slow-tuned and fast-tuned input channel to each visual area and to make predictions for how single-unit responses should change with contrast. In the model, we assumed that each voxel represented a population of neurons that weighted and summed hypothetical inputs tuned for slow or fast speeds, which we called speed channels. The specific weighting of inputs from these speed channels determined the speed preference for each voxel. The contrast sensitivity of each channel determined how the modeled voxels will change their response with contrast. We fit the parameters of the channels (speed, contrast sensitivity, and offset) to our measured BOLD responses.
In the model, voxels (or more generically “units”) each received input from two hypothetical stimulus-driven input channels: one channel was linearly tuned to slow speeds and one was tuned to fast speeds. The response of each unit, Ri, was computed according to the following equation:
where αi is a number between 0 and 1 that described the channel weight for voxel i that controlled how much input the unit received from the response of the slow and fast input channels, cslow and cfast. A fast tuned unit having a large αi would get most of its input from the fast input channel by definition. We compute αi for each voxel by regressing its activity with the stimulus speed.
The responses of the slow and fast input channels were modeled as linear functions of the “speed” and “contrast” of the stimulus:
where mslow and mfast are the speed tunings of the channel. A positive value indicated a tuning for fast speed and a negative value tuning for slow speeds. sslow and sfast were the contrast sensitivities of the channels in which a large value indicates a large change in response with a change in contrast. bfast and bslow were offset terms that defined the baseline response of the channel.
The six free speed channel parameters (mslow, mfast, sslow, sfast, bslow, and bfast) were fit for each visual area and subject to best predict the data from all of the voxels (nvoxels) in each visual area for each subject. That is, once the channel weights αi were set for each voxel, for each of the six stimulus types (3 speeds × 2 contrasts), there was a response vector of length nvoxels that contained the mean response to each stimulus type. The six free channel parameters were fit via linear regression to these response vectors using Equations 4 and 5. Thus, for each visual area in total, there were 6 + nvoxels parameters (where the nvoxels parameters correspond to the channel weights, αi) being fit to 6 × nvoxels responses. We determined goodness-of-fit of the model using cross-validation. We first used the fitted model parameters for each area to determine the average response to each of the six stimulus types in the one-fifth validation set for every voxel. We could then calculate the average error for each stimulus condition (3 speeds × 2 contrasts) across every voxel.
Using the model fit, we estimated the size of the shift in speed readout between high and low contrast for both the population and the individual units. For the population readout, we first used the channel outputs to compute a predicted speed. The population readout is
where P is the predicted population readout speed, and pslow and pfast are weights fitted using regression to produce the best estimate of the actual speed of the stimulus for both contrasts. We then computed the difference between the readout speed P between high- and low-contrast stimuli.
To compute the speed tuning shift of individual units, we examined a hypothetical unit tuned to 1°/s that received equal amounts of input from the slow and fast channels at high contrast (i.e., αi = 0.5). We then examined the balance of inputs at low contrast by computing a new tuning weight:
Here, cfast and cslow are the channel inputs computed for a stimulus of 1°/s and contrast of 7.5% using Equation 5. Completely balanced inputs (no change in speed tuning) would result in a tinew value of 0; a complete shift of the input balance toward the faster channel would equal 1, and a complete shift toward the slower channel would equal −1. These values were then mapped back into the log range of speeds and the difference of this value and the original tuning of 1°/s reported as the voxel tuning shifts.
We also estimated tuning shifts for single units by extrapolation from published electrophysiology data by Krekelberg et al. (2006). Their Figure 5A shows the preferred speed for each neuron when contrast was 70% versus the preferred speed at lower contrasts of 20, 10, and 5%. We assumed that decreasing contrast resulted in the same percentage shift in speed preference for all neurons regardless of their speed tuning. This relationship means that the data for each contrast can be fit by a line that passes through the origin of the data and that the slope of that line is the estimate of percentage change in speed preference. Thus, we could calculate the percentage shift in speed preference from 70% contrast to each of the contrast measured in their experiment. With contrast on a log scale, we found that the percentage speed tuning shift to percentage contrast decrement had a linear relationship. When extrapolating this linear relationship to an 85% decrement in contrast for our experiment (reduction in contrast from 50 to 7.5% contrast), we found that the expected speed preference shift was approximately −42%. Thus, a unit tuned to 1°/s at high contrast in our experiment would shift its preference to 0.58°/s at low contrast.
Results
Perceptual biases for speed and temporal frequency
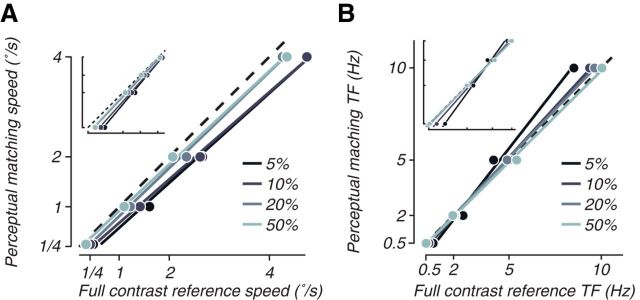
We examined perceptual biases at low contrast for spatially broadband moving and flickering stimuli by using a psychophysical matching procedure and found perceptual biases similar to previous reports (Thompson, 1982; Stone and Thompson, 1992; Müller and Greenlee, 1994; Gegenfurtner and Hawken, 1996; Thompson and Stone, 1997; Snowden et al., 1998; Blakemore and Snowden, 1999; Brooks, 2001; Hürlimann et al., 2002; Anstis, 2003; Stocker and Simoncelli, 2006; Thompson et al., 2006; Hammett and Larsson, 2012; Pretto et al., 2012). Subjects adjusted the speed or temporal frequency of a low-contrast stimulus until it appeared perceptually identical to a simultaneously presented full-contrast reference stimulus (Fig. 1A). For speed, subjects consistently produced perceptual estimates for the low-contrast stimulus (Fig. 2A, ordinate) that were slower than the speed of the full-contrast reference (Fig. 2A, abscissa). On average, we measured a perceptual bias of −0.49°/s (biases at 5% contrast were significantly less than 0 for all subjects; p < 0.05, one tailed t test). For temporal frequency, the bias at low contrast was predominantly in the opposite direction, toward faster temporal frequencies (Thompson and Stone, 1997; Hammett and Larsson, 2012). On average, we measured a perceptual bias of 0.23 Hz (Fig. 2B), although there was some heterogeneity in the perceptual shift across temporal frequencies, in line with previous studies (Hammett and Larsson, 2012). In particular, shifts toward faster temporal frequencies dominated at the higher temporal frequencies for which we ran the fMRI experiment (perceptual biases at 5% contrast were significantly above 0 for all but one subject at 5 and 10 Hz; p < 0.05, one-tailed t test), but, at low temporal frequency, there was an apparent shift toward slower temporal frequencies (Fig. 2B, see in particular the log–log axis inset that highlights changes at lower frequencies; biases at 5% contrast were significantly below 0 at 0.5 Hz and 2 Hz for all subjects; p < 0.05, one-tailed t test). Although this may represent a frequency dependency of the perceptual bias, it could also be attributable to possible changes in strategies of the subjects. At very slow temporal frequencies, subjects can be more sensitive to matching the temporal phase of the control and test stimuli rather than their perception of the frequency. Overall, the bias toward slow for speed and fast for temporal frequency as contrast is lowered replicated previous reports from the psychophysical literature.
Figure 2.
Psychophysics experiments show a perceptual bias for speed and temporal frequency at low contrasts. A, Perceptual estimates of speed versus actual stimulus speed were measured with a method-of-adjustments task, for four speeds and four contrasts (lighter shades are higher contrasts; see legend). The inset shows the same data with a log–log scale. For analysis of statistical significance, see Results. B, Similar diagrams show perceptual biases for contrast flicker. TF, Temporal frequency.
Decoding visual motion speed and temporal frequency from BOLD activity
We used BOLD imaging to ask whether human occipital cortex represents the veridical speed or temporal frequency of stimuli at low contrast or the biased perceptual estimates. We had human subjects view spatially broadband 1D textures similar to the psychophysical experiment (Fig. 1B) as they performed a fixation task and measured BOLD activity from the occipital lobe. The visual stimuli were presented at either high (50%) or low (7.5%) contrast and moved at different speeds and directions or flickered at different rates (speed and temporal frequency measurements were conducted in separate scanning sessions; see Materials and Methods, Stimuli and task for functional imaging experiments). We collected the pattern of voxel activity associated with each stimulus presentation in each retinotopically defined visual area (V1–V3, V3A, hV4, and MT, as well as a control region located in the parietal cortex) and asked whether we could build decoders on one portion of the data that could predict what stimulus was shown on the left out dataset. We began with decoding techniques because they provided a first-order analysis that allowed us to assess both whether there was a representation of speed and temporal frequency that we could measure with BOLD imaging and whether that representation shifted with contrast. We later analyzed voxel populations to determine how the changes in representation could underlie the decoding results.
We reconstructed a continuous estimate of the speed or temporal frequency of stimuli from observed patterns of BOLD response. We used linear decoders, in which each voxel is assigned a tuning weight that correlates with its selectivity for speed (positive weights correspond to fast tuning and negative weights to slow tuning) or temporal frequency. Summing over the weighted response of each voxel produced a continuous readout of speed or temporal frequency. We defined decoder accuracy as the correlation between the actual stimulus speed or temporal frequency and the predicted estimate of the decoder. Note that this is different from a “percentage correct” performance measure that is used for decoders that treat each stimulus type as a separate category and reports how often the category was correctly predicted (Kamitani and Tong, 2005, 2006). This decoding strategy would not have been able to tell us how the represented speed changes with contrast, because it can only predict which one of a set of predetermined categories of presented stimuli was shown and is therefore not sensitive to subtle shifts in representation.
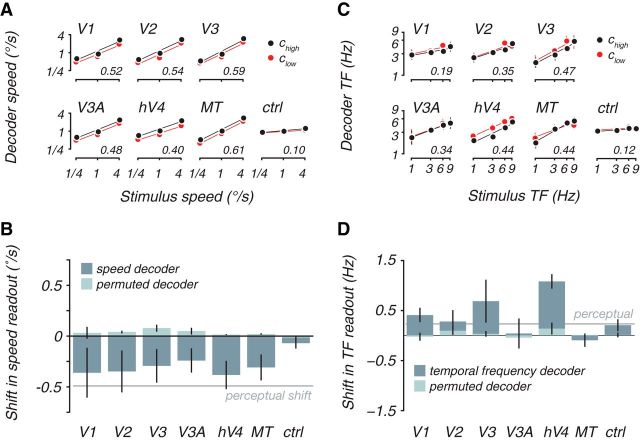
Speed was accurately and significantly decoded from all of the visual areas and shifted toward slower speeds with lower contrast. We built decoders using all data regardless of contrast and found a strong correlation of the cross-validated decoder output and the actual speed presented (r values in axes; 〈r〉 = 0.52 across all visual areas, p < 0.05, except for V3A in one subject, permutation test). Splitting the decoder output for high (Fig. 3A, black) and low (Fig. 3A, red) contrast, we found that the representation shifted toward slower speeds when contrast was lowered. On average, the decoders were biased by −0.32°/s (Fig. 3B, dark bars), which was significantly p < 0.05 over 1000 cross-validated decoders built with unique “build” datasets, except for V1, V2, V3, and hV4 in one subject each) and similar to the perceptual bias (Fig. 3B, gray line).
Figure 3.
Cortical decoders and perception were both biased in the same direction at low contrasts. A, Cross-validated decoder output as a function of stimulus speed, separately for high-contrast (black) and low-contrast (red) test stimuli. Decoder was trained for each subject and visual area, blind to contrast. For this, and all subsequent plots, decoder output is corrected with a scale factor to transform it to stimulus units (degrees per seconds; see Materials and Methods, Decoders). Lines are linear fits. Inset numbers indicate the average cross-validated decoder accuracy across subjects, computed as the correlation between the actual speed and the cross-validated decoder prediction. B, Average decoder and perceptual shift between high and low contrast for speed. Dark bars plot shift in decoder output between high and low contrast computed as the vertical distance between the linear fits in A. Decoder contrast shifts were defined as the mean difference in the decoder speed estimates between trials with high- and low-contrast stimuli for the same stimulus speed, in which negative numbers indicate a shift toward slower speeds at low contrast. No consistent shift was seen using decoders with permuted weight vectors (light bars). Average perceptual shifts from the psychophysical experiment for these two contrasts (−0.49°/s, gray line) was also toward slower speeds at lower contrast. C and D depict analogous measures for temporal frequency, in which the perceptual bias (gray line) was 0.23 Hz. ctrl, Control; TF, temporal frequency.
The decoder shift toward slower speeds was not an artifact of differences in signal/noise ratio between contrast conditions. It might be that, as contrast was lowered, responses become weaker, leading to a drop in decoding accuracy; this would severely compromise our ability to conclude anything about the speed representation at low contrasts. However, we found that speed was decoded equally well regardless of contrast (〈rlow〉 was higher than 〈rhigh〉 for exactly half of the subject areas), indicating similar signal/noise ratios for low-contrasts trials, despite being less visible. We also found that the decoder weights were similar for high- and low-contrast trials (〈r〉 = 0.27; p < 0.05 except for V3 in one subject and V3A for two subjects, Spearman's rank-order correlation; p > 0.1 for the control region), suggesting that the same readout weights could be used to decode speed across both conditions.
Although we built decoders using all of the available data across contrast conditions, the shift toward slower speed was not heavily dependent on this aspect of our analysis. We also built decoders for the high-contrast conditions and tested the output for the low-contrast stimuli and vice versa. This method severely decreased the statistical power of the decoder because it used only 40% of the data to predict a holdout set of 50% (compared with 80/20 build/test sets described above). Nevertheless, we found that the shift in both cases was primarily in the same direction as the more powerful decoder (average bias for both decoders was −0.04°/s for all visual areas and −0.08°/s for only the visual areas with shifts that were significantly different from 0 in either direction; p < 0.05, permutation test). For build-high, test-low decoders, 15 of the 22 subject visual areas showed a significant downward decoding shift. Ten visual areas showed this significant shift for the build-low, test-high decoders. Notably, for the build-high, test-low condition, only V1 in one subject showed a significant shift 0 (p < 0.05) and for the build-low, test-high condition, only V1 in two subjects and V2 in one subject showed this contrary shift (p < 0.05).
The bias toward slow was not a confound with how contrast affects visual cortical responses. Contrast reductions reduce responses in human visual cortex (Tootell et al., 1995; Boynton et al., 1999; Logothetis et al., 2001; Gardner et al., 2005), and if, for example, all voxels decreased their activity with speed, then decoders would necessarily shift toward slower speed as contrast was reduced. However, we found that linear decoders performed 262% better in terms of r value at predicting speed than the simple mean of BOLD activity within each area, indicating that voxels do not all change response in the same way with speed. In particular, we found both positive and negative voxel weights from our analysis (the average distance from 0, μ/σ, of the weight distribution for each area and subject was only 0.086), indicative of tuning for fast and slow speeds, respectively. Thus, decreasing speed does not uniformly decrease BOLD responses, and a reduction in speed readout was not a confound with reduced responses with speed. Moreover, in our analysis, we explicitly removed the mean activity from each cortical activity pattern to avoid artifacts with contrast reduction. Furthermore, had reducing response with contrast artificially reduced the speed readout, we would expect artificial reduction in readout even for decoders with permuted weights (permutation retains the precise balance of positive and negative weights). Instead, this manipulation eliminated the shifts toward slow, yielding average shifts of 0.039°/s (Fig. 3B, light bars) that were not significantly different from 0 (p > 0.05 for all areas and subjects, permutation test).
Temporal frequency could also be decoded from BOLD responses but showed the opposite shift from speed representation toward faster temporal frequencies, thus matching perception and not the veridical stimulus properties. In general, temporal frequency was more difficult to decode than speed (Fig. 3C), although this may have been a partial effect of sample size; for the speed experiment, we collected ∼315 trials over three speeds, but we collected only 225 trials over the four temporal frequencies for the flicker experiment. Decoding was significantly different from 0 for all subjects in hV4 and MT (〈rhV4〉 = 0.42, 〈rMT〉 = 0.43; p < 0.05, permutation test) but significant for only two or three subjects in the other visual areas (〈r〉 = 0.29 in V1, V2, V3, and V3A). As with speed, the decoders performed much better than the simple average of activity for each area, which had no consistent correlation with temporal frequency (exactly half of the subject areas had a positive correlation, whereas half had a negative correlation). Decoder bias was measured as the average difference between the readouts for the high- and low-contrast stimuli for decoders built on both sets of stimuli (Fig. 3D). The magnitude of the bias was largest for areas V3 and hV4 (0.68 and 1.08 Hz, respectively; significantly 0, p < 0.05 except for V3 in one subject, permutation test). The other early visual areas displayed much smaller biases (0.16 Hz on average), and they were not significantly different from 0 (p > 0.05). Despite this lack of significance, we note that the shift is predominantly in the opposite direction to the speed decoder. This shift toward fast (rather than slow) for flickering stimuli also further argues against the possibility that contrast reduction could simply explain the speed effect.
Voxel population activity exhibits both population shifts and general reduction with lowered contrast
The decoding results provide strong first-order evidence that the cortical representation of speed and temporal frequency reliably shifts to match perception rather than the veridical stimulus properties at low contrasts, but it gives little insight into why it shifts. Therefore, we visualized the activity of voxel populations for each visual area to learn how stimulus contrast affects voxel responses as a function of their tuning preference. The population plots display the average activity of each voxel as a function of its preferred speed or temporal frequency, summarized across the whole population of voxels with a linear fit (Figs. 4A, 5A for speed and temporal frequency, respectively). Here, we call a voxel “tuned” for a particular stimulus speed or temporal frequency if its activity at high contrast is significantly higher for that speed or temporal frequency versus all others (however, this particular definition of voxel tuning is not critical for the conclusions obtained; for other ways of identifying selectivity that all gave similar results, see Materials and Methods, Voxel population analyses). Voxel activity is independently computed as the average response to a stimulus of given speed or temporal frequency and contrast. The activity for each voxel is reported as a z-score, normalized across all stimulus presentations to have 0 mean and unit variance (see Materials and Methods, Voxel population analyses). Ideally, population activity tilts upward to the right for a high speed or temporal frequency stimulus (right column) and up to the left for a slow stimulus (left column). Note that this basic effect, apparent in representative data from V1 and MT (Figs. 4A, rows 3 and 4, 5A, rows 1 and 2), is not simply attributable to bias in how voxels were selected for the analysis. Rather, it demonstrates true population selectivity, because the estimates of voxel preference and activity were computed with separate sets of data.
Examination of the population activity plots at each contrast can help to dissociate the effects of a general reduction in response from a speed or temporal frequency-specific shift. A pure general contrast effect that does not change the population readout would cause the population activity to rise or fall uniformly regardless of the preference of each voxel (hypothetical offset; Fig. 4A, top row). A pure speed or temporal frequency-specific contrast effect would shift the population activity toward voxels tuned for slow speeds or fast temporal frequencies and result in a shift of the population readout to match perception. That is, lowering contrast should behave as if the stimulus speed or temporal frequency actually changed, which should tilt the population curve in the appropriate direction. This would be evident as a clockwise rotation (counterclockwise for temporal frequency) of the population curves (hypothetical rotation; Fig. 4A, second row). These two effects are not mutually exclusive; the population response could undergo both a vertical shift and a rotation simultaneously and exhibit both a general reduction in contrast gain and a population shift.
Plotting the contrast-dependent rotation of the population curve against the vertical offset (Figs. 4B, 5B) revealed that a contrast reduction yields speed and temporal frequency-specific population shifts along with a general reduction across all visual areas in all subjects. V1 stood out for the speed data as having the largest general reduction of activity as a function of contrast. All visual areas, including V1, were distinguished from the control area that showed a small general response decrease but no significant population shift (all data to the left of 0; Fig. 4B, black vertical line). Similarly for the temporal frequency data, the majority of the data plotted to the right of 0, indicating a rotation in the population response in the opposite direction to the speed data (Fig. 5B), matching the perceptual effect toward high temporal frequencies. Thus, changes in the representation of speed and temporal frequency showed both general reductions of activity with contrast as expected from previous studies (Albrecht and Hamilton, 1982; Tootell et al., 1995; Boynton et al., 1999; Logothetis et al., 2001; Gardner et al., 2005) and shifts in the population activity that represented the perceptual biases at low contrasts.
Forward-encoding model can reconcile population and single-unit speed shifts
We used a forward-encoding model (Brouwer and Heeger, 2009; Serences and Saproo, 2012) to ask how hypothetical input channels tuned to different speeds with different contrast sensitivities could account for the BOLD measurements from the speed experiment. That is, we modeled the speed selectivity of voxels in our measurements as arising from the difference in input between two hypothetical speed-tuned channels whose speed tuning and contrast sensitivity were fit to best account for the BOLD data (Fig. 6A; cf. Tolhurst et al., 1973; Thompson et al., 2006; for more details, see Materials and Methods, Forward-encoding speed channel model) Thus, a voxel tuned for slow would receive more weight from the slow-tuned channel and a voxel tuned for fast, vice versa. This analysis allowed us to formalize a simple model of speed selectivity and examine how the two channels in the model behave as a function of contrast. It also provided a possible explanation for why single-unit measurements have found tuning preference shifts toward slow with contrast reduction (Pack et al., 2005; Krekelberg et al., 2006; Livingstone and Conway, 2007), which is a result considered to be at odds with perceptual shifts (see Discussion; Krekelberg et al., 2006).
Figure 6.
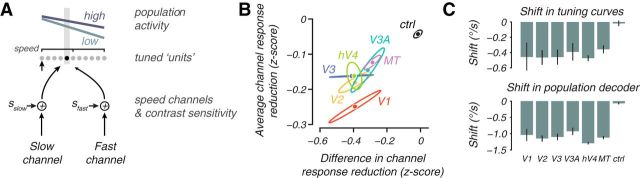
Forward-encoding speed channel model. A, Schematic of a speed channel model fit that explains the population plots. Voxels, or “units,” are arranged according to their speed preference, and their activity in response to a slow stimulus for two contrasts are shown as lines above the units. The units receive weighted input from a slow and a fast channel according to their tuning. Each channel is independently modulated by an additive contrast sensitivity term, s (for details, see Results). B, Plot of average reduction in response of input channels with contrast, (sfast + sslow)/2, versus difference in reduction of response with contrast between high and low speed-tuned input channels, (sfast − sslow)/2. The former is a measure of the general response reduction with contrast, and the latter is a measure of the speed-dependent shift in response with contrast. C, Population shift (bottom row) and individual unit tuning shift (top row, calculated for units tuned 1°/s at high contrast) from the model. Error bars are SEM over models fit to the four subjects. Note difference in vertical scale for the two plots. ctrl, Control.
Examining the fitted parameters of the two speed-tuned channels showed that, although both reduced activity with contrast, the slower channel was more robust to decreased contrast. The model was well fit to the fMRI data for all voxels in each subject and visual area (〈r2〉 = 0.43 on cross-validated data over subjects and visual areas; p < 0.05 for all visual areas, permutation test). Both channels decreased response with contrast (contrast sensitivity parameters: sfast and sslow negative), with the largest average decrease in response across both channels seen in V1 (Fig. 6B, ordinate, which plots the average of sfast and sslow). This is analogous to the vertical shift in the voxel population analysis (Fig. 4B). However, the reduction in response of the two channels with contrast was not equal; the slower channel did not reduce response as much as the fast channel (Fig. 6B, abscissa that plots the difference between sfast and sslow divided by 2). The more robust response at low contrast for the slow speed channel was analogous to the rotation of the voxel population response (Fig. 4B), which indicated more robust responses for slow-tuned voxels (those that get more slow channel input) at low contrast. The general pattern in reduction in response with contrast for the two speed channels was similar for all visual areas and was markedly different from the effect in the control region (Fig. 6B, black). Thus, the forward-encoding channel analysis complemented the voxel population analysis (Fig. 4B) by showing that, although there was a general reduction of response across the two input channels, the slow channel was more robust to contrast reduction.
The channel model predicted both the shift in population representation of speed and shifts in tuning for individual neurons. Reading out the representation of speed from the channel responses showed that, on average, the speed representations shifted by −1.11°/s (Fig. 6C, bottom bar graph; see Materials and Methods, Speed channel model), thus recapitulating the decoding and voxel population analysis of shifts toward slow for the population representation. At the scale of individual units (Fig. 6A, dots), the model displayed the same paradoxical shifts in speed tuning toward slow as has been found in single-unit measurements (Pack et al., 2005; Krekelberg et al., 2006; Livingstone and Conway, 2007). At low contrast, a unit received less input from the fast channel because the slow channel was more robust to contrast reduction. Thus, each individual unit become more influenced by the slow speed channel, and because tuning preference was determined by the balance of the slow and fast channel inputs, the individual units preferred speed tuning shifted to slower speeds. On average, a unit tuned to 1°/s at high contrast would shift its tuning by −0.43°/s at low contrast (Fig. 6C, top row); for similar contrast ranges, we estimate that the single-unit data, adapted from Krekelberg et al. (2006), predicts a tuning shift of nearly the same magnitude −0.42°/s (see Materials and Methods, Speed channel model). Note that the shift in tuning preference is much smaller than that observed at the population level (Fig. 6C, top and bottom histograms have different ordinate scales). Thus, the model demonstrated that a small shift in tuning preference toward slower speeds (which should shift the population readout in a direction opposite of the perceptual shift) can be dominated by an overall population effect in which slower tuned units retain their responses at low contrast, leading to a slower speed readout from the population.
Discussion
We have shown that biases in human motion perception at low contrasts are reflected in BOLD activity in early visual cortex. First, we demonstrated that a distributed representation of speed is accessible with BOLD measurements by building cross-validated decoders that reported the speed of drifting 1D textures at high or low contrast. The decoding results were reliable and significant, in part due to the use of sparse decoders that are well known to be robust to noise and sample size (Kay et al., 2008; Miyawaki et al., 2008). Next we showed that decoder readouts in V1–V3, V3a, hV4, and MT were biased toward slow speeds at low contrasts similarly to perception. Permutation and voxel population analyses showed that this was a genuine effect of contrast on speed representation and not a simple non-speed-specific reduction in overall response. Moreover, decoders built to readout the temporal frequency of a flickering stimulus were biased toward high temporal frequencies at low contrasts, also matching perception. Together, our results resolve a conflict (Pack et al., 2005; Krekelberg et al., 2006; Livingstone and Conway, 2007; Hammett et al., 2013) in the well studied link (Parker and Newsome, 1998) between motion perception and cortical responses by showing that, in humans, cortical visual responses reflect biased perception of speed and temporal frequency rather than veridical stimulus attributes. Prominent theoretical and empirical work has suggested that biases in speed perception represent a prior for slow (Hürlimann et al., 2002; Weiss et al., 2002; Stocker and Simoncelli, 2006; Hedges et al., 2011). If so, our results show that motion perception priors interact with sensory evidence at the earliest stage of cortical processing.
The representation of speed in visual cortex revealed by decoding
The fine spatial scale of distributed cortical speed representations (Liu and Newsome, 2003; Sun et al., 2007) necessitate the use of adaptation (Lingnau et al., 2009) or decoding techniques (Hammett et al., 2013) for their study. Decoding of speed and temporal frequency may be possible because of larger spatial-scale bias in representation, by either biased vasculature signals (Gardner, 2010) or spatial arrangements of tuning preferences (Sasaki et al., 2006; Freeman et al., 2011; Nishimoto et al., 2011). If large-scale biases exist, these signals are potentially inappropriate for high spatial resolution mapping of columnar architecture (Sun et al., 2007) but may still give valid, indirect measures of tuning properties for speed and temporal frequency that can be used to compare how a representation changes across conditions. This is particularly so because there is no evidence that spatial factors like the retinal position of stimuli substantially change perceptual biases for speed (Thompson, 1982; Krekelberg et al., 2006; Stocker and Simoncelli, 2006).
Linking biased motion perception to cortical populations rather than single units
Single-unit studies have generally found responses in apparent conflict with speed perception. Neurons in MT (Pack et al., 2005; Krekelberg et al., 2006) and V1 (Livingstone and Conway, 2007) shift their speed tuning preference to slower speeds at low contrasts. This is paradoxical for a fixed labeled-line readout (Krekelberg et al., 2006) in which each neuron “votes” with its firing rate for its “label,” i.e., preferred speed. The intuition is that, as contrast is lowered, neurons shift their tuning to slower speeds and thus will begin to respond more to stimuli slower than their label. The winning label (i.e., strongest responding neuron) will then be for a faster than veridical speed. This disassociation between MT responses and perception as contrast is lowered (Priebe et al., 2003; Pack et al., 2005; Krekelberg et al., 2006; Livingstone and Conway, 2007) is problematic for the predominant view that neural responses in MT are tightly linked to perception (Parker and Newsome, 1998; Dougherty et al., 1999; Seidemann et al., 1999; Wandell et al., 1999; Priebe and Lisberger, 2004; Liu and Newsome, 2005; Takemura et al., 2012).
It is possible that some experimental factor may account for this disassociation. For example, perceptual speed biases have generally been tested at slow speeds, like the ones used in our study, whereas single-unit physiology has generally used high speeds (Pack et al., 2005; Krekelberg et al., 2006; Livingstone and Conway, 2007). Although more natural, broad-brand stimuli, such as dots (Krekelberg et al., 2006) and textures (Stocker and Simoncelli, 2006) like ones used in our study have universally resulted in slow speed perceptual biases, some reports (Thompson, 1982; Gegenfurtner and Hawken, 1996; Blakemore and Snowden, 1999; Thompson et al., 2006) have suggested little or even opposite biases for sinusoidal gratings moving fast, particularly at 8 Hz. Another experimental factor is the practice of using stimuli optimally matched to the receptive field of each neuron measured at high contrast. At low contrast, receptive fields of MT neurons increase in size and tend to lose their suppressive surrounds (Pack et al., 2005). For example, if neurons tuned for slower speeds increase their receptive field size the most, more slow preferring neurons would be recruited and the population readout would be biased toward slower speeds.
BOLD and extracellular recordings may also reflect different aspects of neural activity. For example, BOLD measurements might be particularly sensitive to synaptic inputs reflecting top-down feedback and neuromodulation (Logothetis, 2008). Top-down modulation might carry information about stimulus biases and adjust sensory representations (Nienborg and Cumming, 2007, 2009), perhaps even as a means to implement hierarchical Bayesian inference (Lee and Mumford, 2003). However, if BOLD is more reflective of top-down biasing, it is puzzling why this modulatory signal we measure would not result in modulated firing rates of individual neurons.
Alternatively, the single-unit measurements may be unified with our BOLD measurements by considering differences in the spatial scale of activity measured. One concrete possibility of this is presented as our forward-encoding model of population data (Fig. 6A) in which hypothetical differences in contrast sensitivity between fast and slow inputs yield both population responses with biases in agreement with perception and individual units with shifts opposite to perception. This model form was chosen for both its simplicity and relationship to previous literature (Tolhurst et al., 1973; Thompson, 1982), but other models that share the negative correlation between contrast sensitivity and speed tuning would behave similarly. Reconciling BOLD and single-unit measurements through considerations of spatial scale is appealing because other apparent disassociations, notably during perceptual suppression (Wilke et al., 2006; Maier et al., 2008), also show close links between perception and large-scale measurements, such as BOLD and local field potentials (Boynton, 2011).
Although this model of speed perception can reconcile our results with single-unit measurements, it still lacks empirical support. However, it does make a number of testable predictions. First, neurons tuned to the fastest speeds should exhibit the largest contrast-induced tuning shift because they receive more input from fast, highly contrast-sensitive speed channels. Indeed, this effect is apparent in three independent reports (Pack et al., 2005; Krekelberg et al., 2006; Majaj et al., 2007). A second, related prediction is that feedforward inputs into speed-tuned cells should have a predictable tradeoff between contrast sensitivity and temporal frequency preference. The motion pathway primarily receives M (magnocellular) inputs from the LGN (Blasdel and Fitzpatrick, 1984; Nakayama and Silverman, 1985; Maunsell et al., 1990). Speed tuning can arise from the combination of M-like responses (Adelson and Bergen, 1985) with different temporal properties (Saul et al., 2005). Whether contrast sensitivity is anticorrelated with temporal frequency within the M-pathway, as required by the model, is not well established because many of the best measurements of these properties were conducted under anesthesia for which temporal frequency tuning is significantly affected (Alitto et al., 2011). We note that contrast-sensitivity differences between P (parvocellular) and M pathways (Shapley et al., 1981; Derrington and Lennie, 1984) are opposite to the expectations for speed (cf. Thompson et al., 2006) but instead could be the basis for biases toward faster temporal frequencies (Thompson and Stone, 1997). Two separate channel mechanisms for speed and flicker perception may be reasonable because neurons that process motion signals do not respond well to transparent motion (Qian and Andersen, 1994), and flickering stimuli are composed of drifting two transparent objects in opposite directions.
Representation of priors for visual perception
Our results suggest that motion perception biases are encoded very early in sensory processing. Why might this be the case? A prevalent normative hypothesis (Knill and Richards, 1996) for motion perception biases suggests that they represent priors for Bayesian inference (Weiss et al., 2002; Stocker and Simoncelli, 2006). In this view, perception becomes biased to a prior for slow motion as sensory signals become weak or ambiguous as when contrast is lowered. Whether temporal frequency biases can also be viewed as a part of optimal inference is an open question. For either case, confirming that biases measured in perception (Stocker and Simoncelli, 2006; Körding, 2007) match likely estimates from environmental statistics would offer strong support. However, measuring these environmental statistics is nontrivial, because self-motion and eye movements as well as the actual distribution of motion statistics need to be accounted for. Thus, current evidence is suggestive but not conclusive about whether the biases reported here are priors that adhere to the expectations of Bayesian computations.
Although many human behaviors can be described as Bayesian inference (Ernst and Banks, 2002; Körding and Wolpert, 2004), little is known about the neural implementation of priors, which are a key component of this theory. One model (Ma et al., 2006) requires two separate populations to encode sensory information and priors, which add to yield a population representing the posterior. However, if biases for slow speed represent a prior, our results suggest that integration of sensory information and priors happens early, in or before V1. Models (Ganguli and Simoncelli, 2010) based on efficient coding that suggest that priors are encoded early through the strategic allocation of neural resources for likely stimuli are more closely aligned with our results. Different neural implementation may be required by priors learned over different timescales. Some priors, including those for motion statistics (Sotiropoulos et al., 2011), may be acquired over a short period of time and require dynamic representation in neural populations (Kok et al., 2012, 2013). Other priors, such as perceptual biases around cardinal orientations (Girshick et al., 2011) that also have early cortical correlates (Furmanski and Engel, 2000) or motion perception biases as studied here, are apparent in most subjects without any training. Thus, they may be neural adaptations to exposure to long-term environmental statistics and therefore reflected in the earliest parts of the sensory processing hierarchy as we have found.
Footnotes
The authors declare no competing financial interests.
This work was supported in part by Grants-in-Aid for Scientific Research 24300146 (J.L.G.) from the Japanese Ministry of Education, Culture, Sports, Science, and Technology. We thank Kenji Haruhana and the Support Unit for Functional Magnetic Resonance Imaging at RIKEN Brain Science Institute for assistance conducting functional imaging experiments and Toshiko Ikari for administrative assistance. We also thank Yuko Hara and Sam Mokhtary for helpful discussions and Andrea Benucci for comments on this manuscript.
References
- Adelson EH, Bergen JR. Spatiotemporal energy models for the perception of motion. J Opt Soc Am A. 1985;2:284–299. doi: 10.1364/JOSAA.2.000284. [DOI] [PubMed] [Google Scholar]
- Albrecht DG, Hamilton DB. Striate cortex of monkey and cat: contrast response function. J Neurophysiol. 1982;48:217–237. doi: 10.1152/jn.1982.48.1.217. [DOI] [PubMed] [Google Scholar]
- Alitto HJ, Moore BD, 4th, Rathbun DL, Usrey WM. A comparison of visual responses in the lateral geniculate nucleus of alert and anaesthetized macaque monkeys. J Physiol. 2011;589:87–99. doi: 10.1113/jphysiol.2010.190538. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Anstis S. Moving objects appear to slow down at low contrasts. Neural Netw. 2003;16:933–938. doi: 10.1016/S0893-6080(03)00111-4. [DOI] [PubMed] [Google Scholar]
- Blakemore MR, Snowden RJ. The effect of contrast upon perceived speed: a general phenomenon? Perception. 1999;28:33–48. doi: 10.1068/p2722. [DOI] [PubMed] [Google Scholar]
- Blasdel GG, Fitzpatrick D. Physiological organization of layer 4 in macaque striate cortex. J Neurosci. 1984;4:880–895. doi: 10.1523/JNEUROSCI.04-03-00880.1984. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Boynton GM. Spikes, BOLD, attention, and awareness: a comparison of electrophysiological and fMRI signals in V1. J Vis. 2011;11:12. doi: 10.1167/11.5.12. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Boynton GM, Demb JB, Glover GH, Heeger DJ. Neuronal basis of contrast discrimination. Vision Res. 1999;39:257–269. doi: 10.1016/S0042-6989(98)00113-8. [DOI] [PubMed] [Google Scholar]
- Brooks K. Stereomotion speed perception is contrast dependent. Perception. 2001;30:725–731. doi: 10.1068/p3143. [DOI] [PubMed] [Google Scholar]
- Brouwer GJ, Heeger DJ. Decoding and reconstructing color from responses in human visual cortex. J Neurosci. 2009;29:13992–14003. doi: 10.1523/JNEUROSCI.3577-09.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bruder H, Fischer H, Reinfelder HE, Schmitt F. Image reconstruction for echo planar imaging with nonequidistant k-space sampling. Magn Reson Med. 1992;23:311–323. doi: 10.1002/mrm.1910230211. [DOI] [PubMed] [Google Scholar]
- Burr D, Thompson P. Motion psychophysics: 1985–2010. Vision Res. 2011;51:1431–1456. doi: 10.1016/j.visres.2011.02.008. [DOI] [PubMed] [Google Scholar]
- Dale AM, Fischl B, Sereno MI. Cortical surface-based analysis. I. Segmentation and surface reconstruction. Neuroimage. 1999;9:179–194. doi: 10.1006/nimg.1998.0395. [DOI] [PubMed] [Google Scholar]
- Derrington AM, Lennie P. Spatial and temporal contrast sensitivities of neurones in lateral geniculate nucleus of macaque. J Physiol. 1984;357:219–240. doi: 10.1113/jphysiol.1984.sp015498. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dougherty RF, Press WA, Wandell BA. Perceived speed of colored stimuli. Neuron. 1999;24:893–899. doi: 10.1016/S0896-6273(00)81036-3. [DOI] [PubMed] [Google Scholar]
- Dumoulin SO, Wandell BA. Population receptive field estimates in human visual cortex. Neuroimage. 2008;39:647–660. doi: 10.1016/j.neuroimage.2007.09.034. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Efron B, Hastie T, Johnstone I, Tibshirani R. Least angle regression. Ann Stat. 2004;32:407–499. doi: 10.1214/009053604000000067. [DOI] [Google Scholar]
- Ernst MO, Banks MS. Humans integrate visual and haptic information in a statistically optimal fashion. Nature. 2002;415:429–433. doi: 10.1038/415429a. [DOI] [PubMed] [Google Scholar]
- Freeman J, Brouwer GJ, Heeger DJ, Merriam EP. Orientation decoding depends on maps, not columns. J Neurosci. 2011;31:4792–4804. doi: 10.1523/JNEUROSCI.5160-10.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Furmanski CS, Engel SA. An oblique effect in human primary visual cortex. Nat Neurosci. 2000;3:535–536. doi: 10.1038/75702. [DOI] [PubMed] [Google Scholar]
- Ganguli D, Simoncelli EP. Implicit encoding of prior probabilities in optimal neural populations. Adv Neural Info Proc Systems. 2010;23:658–666. [PMC free article] [PubMed] [Google Scholar]
- Gardner JL. Is cortical vasculature functionally organized? Neuroimage. 2010;49:1953–1956. doi: 10.1016/j.neuroimage.2009.07.004. [DOI] [PubMed] [Google Scholar]
- Gardner JL, Sun P, Waggoner RA, Ueno K, Tanaka K, Cheng K. Contrast adaptation and representation in human early visual cortex. Neuron. 2005;47:607–620. doi: 10.1016/j.neuron.2005.07.016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gardner JL, Merriam EP, Movshon JA, Heeger DJ. Maps of visual space in human occipital cortex are retinotopic, not spatiotopic. J Neurosci. 2008;28:3988–3999. doi: 10.1523/JNEUROSCI.5476-07.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gegenfurtner KR, Hawken MJ. Perceived velocity of luminance, chromatic and non-fourier stimuli: influence of contrast and temporal frequency. Vision Res. 1996;36:1281–1290. doi: 10.1016/0042-6989(95)00198-0. [DOI] [PubMed] [Google Scholar]
- Girshick AR, Landy MS, Simoncelli EP. Cardinal rules: visual orientation perception reflects knowledge of environmental statistics. Nat Neurosci. 2011;14:926–932. doi: 10.1038/nn.2831. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hammett ST, Larsson J. The effect of contrast on perceived speed and flicker. J Vis. 2012;12:17. doi: 10.1167/12.12.17. [DOI] [PubMed] [Google Scholar]
- Hammett ST, Smith AT, Wall MB, Larsson J. Implicit representations of luminance and the temporal structure of moving stimuli in multiple regions of human visual cortex revealed by multivariate pattern classification analysis. J Neurophysiol. 2013;110:688–699. doi: 10.1152/jn.00359.2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hedges JH, Stocker AA, Simoncelli EP. Optimal inference explains the perceptual coherence of visual motion stimuli. J Vis. 2011;11.pii:14. doi: 10.1167/11.6.14. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hu X, Le TH, Parrish T, Erhard P. Retrospective estimation and correction of physiological fluctuation in functional MRI. Magn Reson Med. 1995;34:201–212. doi: 10.1002/mrm.1910340211. [DOI] [PubMed] [Google Scholar]
- Hürlimann F, Kiper DC, Carandini M. Testing the Bayesian model of perceived speed. Vision Res. 2002;42:2253–2257. doi: 10.1016/S0042-6989(02)00119-0. [DOI] [PubMed] [Google Scholar]
- Kamitani Y, Tong F. Decoding the visual and subjective contents of the human brain. Nat Neurosci. 2005;8:679–685. doi: 10.1038/nn1444. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kamitani Y, Tong F. Decoding seen and attended motion directions from activity in the human visual cortex. Curr Biol. 2006;16:1096–1102. doi: 10.1016/j.cub.2006.04.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kay KN, Naselaris T, Prenger RJ, Gallant JL. Identifying natural images from human brain activity. Nature. 2008;452:352–355. doi: 10.1038/nature06713. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kim SG, Hu X, Adriany G, Uğurbil K. Fast interleaved echo-planar imaging with navigator: high resolution anatomic and functional images at 4 Tesla. Magn Reson Med. 1996;35:895–902. doi: 10.1002/mrm.1910350618. [DOI] [PubMed] [Google Scholar]
- Knill DC, Richards W. Perception as Bayesian inference. Cambridge, UK: Cambridge UP; 1996. [Google Scholar]
- Kok P, Jehee JFM, de Lange FP. Less is more: expectation sharpens representations in the primary visual cortex. Neuron. 2012;75:265–270. doi: 10.1016/j.neuron.2012.04.034. [DOI] [PubMed] [Google Scholar]
- Kok P, Brouwer GJ, van Gerven MAJ, de Lange FP. Prior expectations bias sensory representations in visual cortex. J Neurosci. 2013;33:16275–16284. doi: 10.1523/JNEUROSCI.0742-13.2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Körding K. Decision theory: what “should” the nervous system do? Science. 2007;318:606–610. doi: 10.1126/science.1142998. [DOI] [PubMed] [Google Scholar]
- Körding KP, Wolpert DM. Bayesian integration in sensorimotor learning. Nature. 2004;427:244–247. doi: 10.1038/nature02169. [DOI] [PubMed] [Google Scholar]
- Krekelberg B, van Wezel RJA, Albright TD. Interactions between speed and contrast tuning in the middle temporal area: implications for the neural code for speed. J Neurosci. 2006;26:8988–8998. doi: 10.1523/JNEUROSCI.1983-06.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee TS, Mumford D. Hierarchical Bayesian inference in the visual cortex. J Opt Soc Am A Opt Image Sci Vis. 2003;20:1434–1448. doi: 10.1364/JOSAA.20.001434. [DOI] [PubMed] [Google Scholar]
- Lingnau A, Ashida H, Wall MB, Smith AT. Speed encoding in human visual cortex revealed by fMRI adaptation. J Vis. 2009;9:3.1–14. doi: 10.1167/9.13.3. [DOI] [PubMed] [Google Scholar]
- Liu J, Newsome WT. Functional organization of speed tuned neurons in visual area MT. J Neurophysiol. 2003;89:246–256. doi: 10.1152/jn.00097.2002. [DOI] [PubMed] [Google Scholar]
- Liu J, Newsome WT. Correlation between speed perception and neural activity in the middle temporal visual area. J Neurosci. 2005;25:711–722. doi: 10.1523/JNEUROSCI.4034-04.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Livingstone MS, Conway BR. Contrast affects speed tuning, space-time slant, and receptive-field organization of simple cells in macaque V1. J Neurophysiol. 2007;97:849–857. doi: 10.1152/jn.00762.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Logothetis NK. What we can do and what we cannot do with fMRI. Nature. 2008;453:869–878. doi: 10.1038/nature06976. [DOI] [PubMed] [Google Scholar]
- Logothetis NK, Pauls J, Augath M, Trinath T, Oeltermann A. Neurophysiological investigation of the basis of the fMRI signal. Nature. 2001;412:150–157. doi: 10.1038/35084005. [DOI] [PubMed] [Google Scholar]
- Ma WJ, Beck JM, Latham PE, Pouget A. Bayesian inference with probabilistic population codes. Nat Neurosci. 2006;9:1432–1438. doi: 10.1038/nn1790. [DOI] [PubMed] [Google Scholar]
- Maier A, Wilke M, Aura C, Zhu C, Ye FQ, Leopold DA. Divergence of fMRI and neural signals in V1 during perceptual suppression in the awake monkey. Nat Neurosci. 2008;11:1193–1200. doi: 10.1038/nn.2173. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Majaj N, Stocker A, Tailby C, Movshon JA, Simoncelli EP. The effect of contrast on velocity encoding in macaque area MT. Presented at the 2006 Meeting of Computational and Systems Neuroscience; March 5–8; Salt Lake City, Utah. 2007. [Google Scholar]
- Maunsell JH, Nealey TA, DePriest DD. Magnocellular and parvocellular contributions to responses in the middle temporal visual area (MT) of the macaque monkey. J Neurosci. 1990;10:3323–3334. doi: 10.1523/JNEUROSCI.10-10-03323.1990. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Miyawaki Y, Uchida H, Yamashita O, Sato MA, Morito Y, Tanabe HC, Sadato N, Kamitani Y. Visual image reconstruction from human brain activity using a combination of multiscale local image decoders. Neuron. 2008;60:915–929. doi: 10.1016/j.neuron.2008.11.004. [DOI] [PubMed] [Google Scholar]
- Müller R, Greenlee MW. Effect of contrast and adaptation on the perception of the direction and speed of drifting gratings. Vision Res. 1994;34:2071–2092. doi: 10.1016/0042-6989(94)90318-2. [DOI] [PubMed] [Google Scholar]
- Nakayama K, Silverman GH. Detection and discrimination of sinusoidal grating displacements. J Opt Soc Am A. 1985;2:267–274. doi: 10.1364/JOSAA.2.000267. [DOI] [PubMed] [Google Scholar]
- Nestares O, Heeger DJ. Robust multiresolution alignment of MRI brain volumes. Magn Reson Med. 2000;43:705–715. doi: 10.1002/(SICI)1522-2594(200005)43:5<705::AID-MRM13>3.0.CO;2-R. [DOI] [PubMed] [Google Scholar]
- Nienborg H, Cumming BG. Psychophysically measured task strategy for disparity discrimination is reflected in V2 neurons. Nat Neurosci. 2007;10:1608–1614. doi: 10.1038/nn1991. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nienborg H, Cumming BG. Decision-related activity in sensory neurons reflects more than a neuron's causal effect. Nature. 2009;459:89–92. doi: 10.1038/nature07821. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nishimoto S, Vu AT, Naselaris T, Benjamini Y, Yu B, Gallant JL. Reconstructing visual experiences from brain activity evoked by natural movies. Curr Biol. 2011;21:1641–1646. doi: 10.1016/j.cub.2011.08.031. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ogawa S, Lee TM, Kay AR, Tank DW. Brain magnetic resonance imaging with contrast dependent on blood oxygenation. Proc Natl Acad Sci U S A. 1990;87:9868–9872. doi: 10.1073/pnas.87.24.9868. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ogawa S, Tank DW, Menon R, Ellermann JM, Kim SG, Merkle H, Ugurbil K. Intrinsic signal changes accompanying sensory stimulation: functional brain mapping with magnetic resonance imaging. Proc Natl Acad Sci U S A. 1992;89:5951–5955. doi: 10.1073/pnas.89.13.5951. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pack CC, Hunter JN, Born RT. Contrast dependence of suppressive influences in cortical area MT of alert macaque. J Neurophysiol. 2005;93:1809–1815. doi: 10.1152/jn.00629.2004. [DOI] [PubMed] [Google Scholar]
- Parker AJ, Newsome WT. Sense and the single neuron: probing the physiology of perception. Annu Rev Neurosci. 1998;21:227–277. doi: 10.1146/annurev.neuro.21.1.227. [DOI] [PubMed] [Google Scholar]
- Pretto P, Bresciani JP, Rainer G, Bülthoff HH. Foggy perception slows us down. Elife. 2012;1:e00031. doi: 10.7554/eLife.00031. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Priebe NJ, Lisberger SG. Estimating target speed from the population response in visual area MT. J Neurosci. 2004;24:1907–1916. doi: 10.1523/JNEUROSCI.4233-03.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Priebe NJ, Cassanello CR, Lisberger SG. The neural representation of speed in macaque area MT/V5. J Neurosci. 2003;23:5650–5661. doi: 10.1523/JNEUROSCI.23-13-05650.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pruessmann KP, Weiger M, Scheidegger MB, Boesiger P. SENSE: sensitivity encoding for fast MRI. Magn Reson Med. 1999;42:952–962. doi: 10.1002/(SICI)1522-2594(199911)42:5<952::AID-MRM16>3.0.CO;2-S. [DOI] [PubMed] [Google Scholar]
- Qian N, Andersen RA. Transparent motion perception as detection of unbalanced motion signals. II. Physiology. J Neurosci. 1994;14:7367–7380. doi: 10.1523/JNEUROSCI.14-12-07367.1994. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sasaki Y, Rajimehr R, Kim BW, Ekstrom LB, Vanduffel W, Tootell RBH. The radial bias: a different slant on visual orientation sensitivity in human and nonhuman primates. Neuron. 2006;51:661–670. doi: 10.1016/j.neuron.2006.07.021. [DOI] [PubMed] [Google Scholar]
- Saul AB, Carras PL, Humphrey AL. Temporal properties of inputs to direction-selective neurons in monkey V1. J Neurophysiol. 2005;94:282–294. doi: 10.1152/jn.00868.2004. [DOI] [PubMed] [Google Scholar]
- Seidemann E, Poirson AB, Wandell BA, Newsome WT. Color signals in area MT of the macaque monkey. Neuron. 1999;24:911–917. doi: 10.1016/S0896-6273(00)81038-7. [DOI] [PubMed] [Google Scholar]
- Serences JT, Saproo S. Computational advances towards linking BOLD and behavior. Neuropsychologia. 2012;50:435–446. doi: 10.1016/j.neuropsychologia.2011.07.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shapley R, Kaplan E, Soodak R. Spatial summation and contrast sensitivity of X and Y cells in the lateral geniculate nucleus of the macaque. Nature. 1981;292:543–545. doi: 10.1038/292543a0. [DOI] [PubMed] [Google Scholar]
- Snowden RJ, Stimpson N, Ruddle RA. Speed perception fogs up as visibility drops. Nature. 1998;392:450. doi: 10.1038/33049. [DOI] [PubMed] [Google Scholar]
- Sotiropoulos G, Seitz AR, Seriès P. Changing expectations about speed alters perceived motion direction. Curr Biol. 2011;21:R883–R884. doi: 10.1016/j.cub.2011.09.013. [DOI] [PubMed] [Google Scholar]
- Stocker AA, Simoncelli EP. Noise characteristics and prior expectations in human visual speed perception. Nat Neurosci. 2006;9:578–585. doi: 10.1038/nn1669. [DOI] [PubMed] [Google Scholar]
- Stone LS, Thompson P. Human speed perception is contrast dependent. Vision Res. 1992;32:1535–1549. doi: 10.1016/0042-6989(92)90209-2. [DOI] [PubMed] [Google Scholar]
- Sun P, Ueno K, Waggoner RA, Gardner JL, Tanaka K, Cheng K. A temporal frequency-dependent functional architecture in human V1 revealed by high-resolution fMRI. Nat Neurosci. 2007;10:1404–1406. doi: 10.1038/nn1983. [DOI] [PubMed] [Google Scholar]
- Takemura H, Ashida H, Amano K, Kitaoka A, Murakami I. Neural correlates of induced motion perception in the human brain. J Neurosci. 2012;32:14344–14354. doi: 10.1523/JNEUROSCI.0570-12.2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thompson P. Perceived rate of movement depends on contrast. Vision Res. 1982;22:377–380. doi: 10.1016/0042-6989(82)90153-5. [DOI] [PubMed] [Google Scholar]
- Thompson P, Stone LS. Contrast affects flicker and speed perception differently. Vision Res. 1997;37:1255–1260. doi: 10.1016/S0042-6989(96)00302-1. [DOI] [PubMed] [Google Scholar]
- Thompson P, Brooks K, Hammett ST. Speed can go up as well as down at low contrast: implications for models of motion perception. Vision Res. 2006;46:782–786. doi: 10.1016/j.visres.2005.08.005. [DOI] [PubMed] [Google Scholar]
- Tolhurst DJ, Sharpe CR, Hart G. The analysis of the drift rate of moving sinusoidal gratings. Vision Res. 1973;13:2545–2555. doi: 10.1016/0042-6989(73)90251-4. [DOI] [PubMed] [Google Scholar]
- Tootell RB, Reppas JB, Kwong KK, Malach R, Born RT, Brady TJ, Rosen BR, Belliveau JW. Functional analysis of human MT and related visual cortical areas using magnetic resonance imaging. J Neurosci. 1995;15:3215–3230. doi: 10.1523/JNEUROSCI.15-04-03215.1995. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Van de Moortele PF, Auerbach EJ, Olman C, Yacoub E, Uğurbil K, Moeller S. T1 weighted brain images at 7 Tesla unbiased for proton density, T2* contrast and RF coil receive B1 sensitivity with simultaneous vessel visualization. Neuroimage. 2009;46:432–446. doi: 10.1016/j.neuroimage.2009.02.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wandell BA, Winawer J. Imaging retinotopic maps in the human brain. Vision Res. 2011;51:718–737. doi: 10.1016/j.visres.2010.08.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wandell BA, Poirson AB, Newsome WT, Baseler HA, Boynton GM, Huk A, Gandhi S, Sharpe LT. Color signals in human motion-selective cortex. Neuron. 1999;24:901–909. doi: 10.1016/S0896-6273(00)81037-5. [DOI] [PubMed] [Google Scholar]
- Weiss Y, Simoncelli EP, Adelson EH. Motion illusions as optimal percepts. Nat Neurosci. 2002;5:598–604. doi: 10.1038/nn0602-858. [DOI] [PubMed] [Google Scholar]
- Wilke M, Logothetis NK, Leopold DA. Local field potential reflects perceptual suppression in monkey visual cortex. Proc Natl Acad Sci U S A. 2006;103:17507–17512. doi: 10.1073/pnas.0604673103. [DOI] [PMC free article] [PubMed] [Google Scholar]