Abstract
Claws are the most widespread attachment devices in animals, but comparatively little is known about the mechanics of claw attachment. A key morphological parameter in determining attachment ability is claw sharpness; however, there is a conflict between sharpness and fracture resistance. Sharper claws can interlock on more surfaces but are more likely to break. Body size interacts with this conflict such that larger animals should have much blunter claws and consequently poorer attachment ability than smaller animals. This expected size-induced reduction in attachment performance has not previously been investigated, and it is unclear how animals deal with this effect, and whether it indeed exists. We explored the scaling of claw sharpness with body size using four insect species (Nauphoeta cinerea, Gromphadorhina portentosa, Atta cephalotes and Carausius morosus) each covering a large size range. The scaling of claw sharpness varied significantly between species, suggesting that they face different pressures regarding claw function. Attachment forces were measured for A. cephalotes and G. portentosa (which had different scaling of claw sharpness) on several rough surfaces using a centrifuge setup. As expected, attachment performance was poorer in larger animals. Firstly, larger animals were more likely to slip, although this effect depended on the scaling of claw sharpness. Secondly, when they gripped, they attached with smaller forces relative to their weight. This size-induced reduction in attachment performance has significant implications for the attachment ability of larger animals on rough surfaces.
Keywords: Claw sharpness, Scaling, Attachment performance, Allometry
Introduction
Claws are the most widespread attachment device in the animal kingdom and are found in species ranging from tiny mites (Heethoff and Koerner, 2007) to large cats (Mattheck and Reuss, 1991) and the largest dinosaurs (Lautenschlager, 2014). Claws are an excellent climbing tool, as they can be made from stiff and hard materials (e.g. Bonser, 1996; Schofield et al., 2009; Yang et al., 2014), which reduces wear and allows the generation of large attachment forces (Dai et al., 2002). A key question for understanding claw functioning is, which morphological features are important for claw performance?
Although several studies have correlated various aspects of claw morphology, for example claw curvature, with lifestyle or habitat (D’Amore et al., 2018; Feduccia, 1993; Pike and Maitland, 2004; Tulli et al., 2009, 2011; Zani, 2000), these investigations were conducted exclusively in vertebrates, and the biomechanical principles that link claw morphology to attachment performance were not considered. Correlational studies that have examined both claw morphology and attachment performance (Tulli et al., 2011; Zani, 2000) have not explored the mechanics of attachment and, in particular, did not consider claw tip diameter, a key character influencing attachment ability (Dai et al., 2002; Ditsche-Kuru et al., 2012). Contrastingly, mechanical models of claw function have focused mainly on claw tip diameter (Bullock and Federle, 2011; Dai et al., 2002; Ditsche-Kuru et al., 2012; but see Song et al., 2016); however, these studies have not explored the distribution and ecological relevance of this trait. Hence, there are many unknowns in claw-based attachment.
Claws can provide grip by interlocking with surface asperities (projections from a rough surface). This interaction has been modelled, initially by Dai et al. (2002) and then more comprehensively by Asbeck et al. (2006). An important prediction from both models is that whether or not a claw interlocks is determined by the diameter of the claw tip (DCT) (i.e. claw sharpness) relative to the asperities on the surface it is interacting with. As a rough guide, if DCT is smaller than the diameter of a hemispherical asperity it is engaging with then the claw will interlock. A blunter claw will slip, so that the gripping force will be solely determined by the sliding friction between the body surfaces in contact with the substrate (Asbeck et al., 2006; Dai et al., 2002). Thus, for a given surface of fixed area, sharper claws will have more asperities to interlock with (Fig. 1); for fractal surfaces, the number of usable asperities per unit length should scale with 1/DCT (Asbeck et al., 2006). This simple interlocking model of claw attachment is well supported by studies with live animals (Bullock and Federle, 2011; Dai et al., 2002; Ditsche-Kuru et al., 2012).
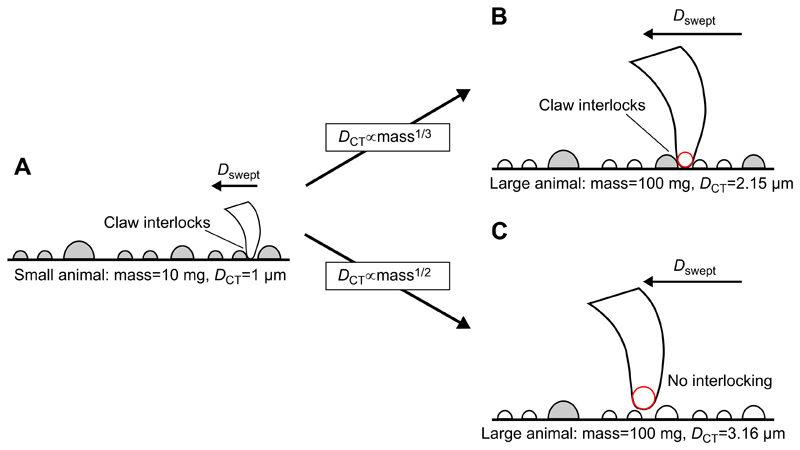
Fig. 1. The effect of different scaling of claw sharpness on attachment performance.
(A) A small animal attempting to grip on a rough surface will easily be able to find a useable asperity (shaded in grey) to interlock its claws with, even if it can only sweep or scan the claw over a short distance (Dswept). For a larger individual, whether or not the claw finds a suitable asperity will depend on the allometry of claw sharpness. (B) For isometric scaling of claw tip diameter (DCT∝mass1/3), although the blunter claw tip has fewer usable asperities per unit length, the animal will probably have longer legs and can thus scan a greater distance (i.e. Dswept is greater). On a fractal surface, this larger claw is thus still likely to find a suitable asperity to interlock with. (C) In contrast, where claw tip diameter shows positive allometry, here scaling to maintain constant stress on claw tips (DCT∝mass1/2), the larger individual will have a much blunter claw tip and will be unlikely to grip. In this case, Dswept will be the same as for the larger animal showing isometric scaling of DCT, but the much blunter claw tip means that over this distance the individual is unlikely to find a usable asperity.
In order for a claw to maximise interlocking ability, it should be as sharp as possible. However, the tips of sharper claws will experience greater stress and therefore face a greater risk of failure than those of blunter claws; consequently, the design of claw tips may be subject to a trade-off (Asbeck et al., 2006; Labonte and Federle, 2015). This trade-off becomes particularly troubling as animals change in body size. Geometric similarity (i.e. DCT∝mass1/3), predicts that larger animals will have blunter claws. This alone may not present a disadvantage for larger animals, as they also have longer legs and hence probably ‘scan’ a larger area to find a usable asperity. Indeed, for surfaces with fractal roughness, isometric growth of leg length would suffice to keep the number of usable asperities constant even for isometrically blunter claws (Fig. 1).
However, isometric claws are predicted to experience increasing stress (force per cross-sectional area) for larger animals, as weight increases faster than claw tip cross-sectional area, which may eventually lead to claw breakage or wear. Therefore, in order to prevent fracture, claw tip diameter should be positively allometric to maintain constant stress. Maintaining constant claw stress would require to be constant, yielding a predicted scaling of DCT∝mass1/2 (Labonte and Federle, 2015). However, such positive allometry would imply that the number of usable asperities would decrease even on fractal surfaces, resulting in poorer attachment performance (Fig. 1). This predicted, size-based reduction in attachment performance has not, to our knowledge, previously been investigated.
Because of the link with body size, scaling studies can be used to explore the dynamics of this trade-off between bluntness and sharpness. Departures from geometric similarity can reveal how mechanical constraints influence trait morphology and performance, although deviations from isometry can also occur for other reasons, and in particular may be constrained by phylogeny (Labonte et al., 2016; Peattie and Full, 2007). Investigating the scaling relationships of claw sharpness across organisms from different groups can therefore reveal the relative importance of the conflicting pressures towards blunt and sharp claws.
Here, we studied the effects of body size on attachment performance through claw morphology by (1) investigating the scaling relationship between body size and claw sharpness for four insect species, each covering a large range of body masses, and (2) testing how attachment performance on rough surfaces is determined by body size.
Materials and Methods
Study animals
Individuals of two cockroach species, Nauphoeta cinerea (Olivier 1789) and Gromphadorhina portentosa (Schaum 1853), and stick insects Carausius morosus (Sinety 1901) were obtained from laboratory colonies. Leafcutter ants Atta cephalotes (L. 1758) were obtained from a laboratory colony with additional individuals obtained from a colony at London Zoo.
Claw morphometry
In order to measure how claw tip diameter changes with body size, we selected individuals from each species (G. portentosa, n=19; N. cinerea, n=20; C. morosus, n=20; A. cephalotes, n=23) to cover the full range of body masses. For G. portentosa, N. cinerea and C. morosus, different-sized individuals were obtained by selecting different instars (hence measuring ontogenetic allometry); whereas for A. cephalotes, the different-sized individuals were all adults of different worker castes (measuring static allometry). NB For holometabolous insect species such as leafcutter ants, it is not possible to obtain an ontogenetic series of claw tip diameters as (in contrast to the hemimetabolous cockroaches and stick insects) the adults are the first stage which have fully developed claws.
Body mass was recorded after collection with a Sartorius MC5 microbalance accurate to 1 µg for smaller insects (ca. <0.5 g, dependent on species) and a Sartorius 1202 MP balance accurate to 10 mg for larger insects. Claws were mounted on carbon tape (Agar Scientific, Stansted, UK) on aluminium stubs (Agar Scientific). As claw orientation could potentially affect the measurement of claw tip diameter, this was standardised by mounting claws laterally (Fig. 2). Claws of some insects were broken, and so to ensure sufficient numbers of unbroken claws, we mounted between two and four claws per individual (dependent on claw damage) to compensate for broken claws. Claws from front, middle and hind legs were used; exploratory statistical tests supported the assumption that there was no difference in claw tip diameter between legs within an individual (likelihood ratio test, P=0.14).
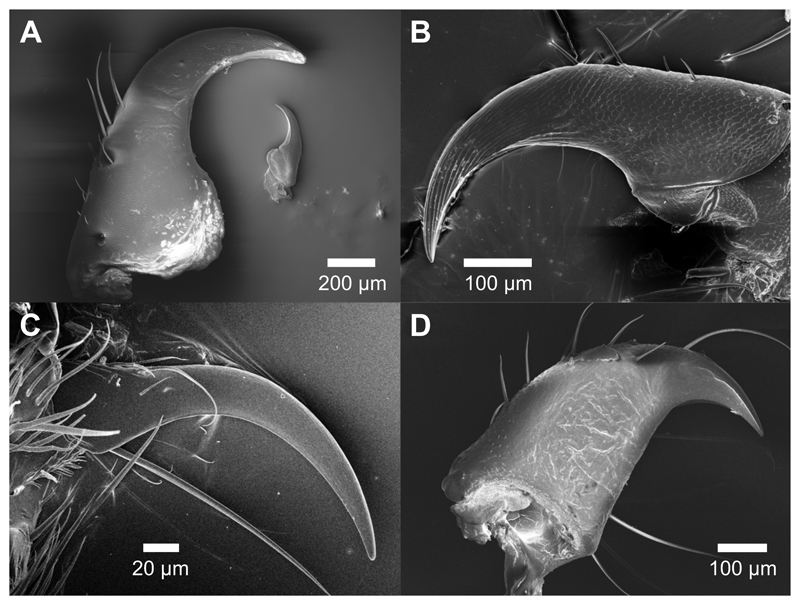
Fig. 2. Scanning electron micrographs of representative claws from the four insect species used, illustrating orientation for measurement of claw tip diameter.
(A) Gromphadorhina portentosa, one claw from both early (small claw) and late (large claw) instars. (B) Nauphoeta cinerea. (C) Atta cephalotes. (D) Carausius morosus.
Claws were imaged either using a Zeiss 1530VP Field Emission SEM or a FEI Verios 460 SEM. As claws were sampled across several years and at different facilities, sputter coating procedures varied slightly, but typically resulted in ca. 50 nm of coating. Claw tip diameter was measured as twice the radius of curvature of the claw tip with ImageJ (Schneider et al., 2012) by fitting a circle into the claw tip as described in Dai et al. (2002).
Attachment performance experiments
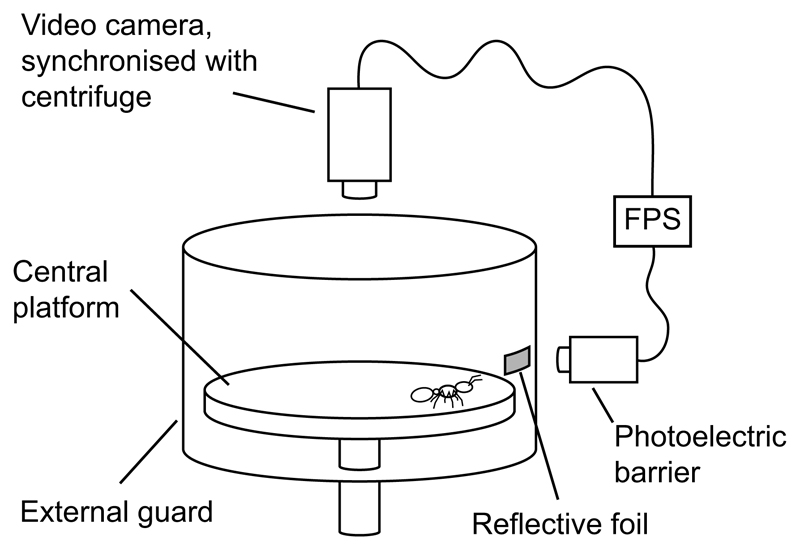
The maximum attachment forces of individuals of a range of masses from A. cephalotes (0.297 to 82.7 mg, n=199) and G. portentosa (47.2 mg to 14.3×103 mg, n=103) were recorded on rough surfaces of several asperity sizes using a centrifuge setup similar to that described in Federle et al. (2000) (Fig. 3). These species were chosen as they were the two species with the largest range of body masses and showed a clear difference in the scaling of claw tip diameter (see Results). The setup consisted of a central horizontal platform attached to the rotor of a centrifuge, and an external guard. As rough substrates, we used aluminium oxide polishing films (Ultra Tec, SantaAna, CA, USA) of varying nominal particle sizes or 80 grit sandpaper (with nominal particle size 190 µm). The nominal particle sizes quoted hereafter are those provided by the manufacturer, which have previously been shown to correspond roughly to the maximum profile height and approximately four times the root mean square roughness (Bullock and Federle, 2011). The substrates were attached to the underside of blank CDs using superglue and the CDs were fixed to the central platform of the centrifuge.
Fig. 3. The centrifuge setup used for attachment performance measurements.
FPS, frames per second.
For a single measurement, insects were placed individually on the substrate. The centrifuge speed was increased until the insect lost grip and fell off. If the insect actively walked off the test surface during a trial, the centrifuge was stopped and the trial restarted. Insects were only used for one trial, and were weighed after testing. Each species was tested on five surfaces of different roughness, chosen to include asperity sizes of a range larger than the range of measured claw tip diameters of each species. Consequently, the surfaces chosen differed between species (see Results).
To identify the rotation speed at which the insects fell off, each trial run was recorded from above using a Basler A602f camera (Basler Vision Technologies, Ahrensburg, Germany). This camera was triggered by a photoelectric sensor detecting a piece of reflective foil attached to the centrifuge, so that the camera took one video frame with each revolution of the centrifuge. Thus, as the centrifuge sped up, the frame rate of the video increased so that a static image of the centrifuge rotor was filmed. This allowed the radial position and rotation speed (frames s−1) at which the insect fell off to be determined. The setup was illuminated, and the video was recorded using StreamPix (versions 3 and 4, NorPix, Montreal, Canada).
Maximum (shear) attachment force was determined by analysing the recorded videos with a custom-written MATLAB script. The distance (r) between the centre of mass of the insect and the centre of rotation, as well as the number of frames per second at the point of detachment were measured to calculate the acceleration, a=r(2π×no. frames s−1)2, experienced by the insect at the moment it detached. Detachment force (F) was then calculated using F=ma, where m is body mass. Forces were standardised by converting to safety factor (S: shear force per body weight, equivalent to the definition of the friction coefficient), using S=F/mg, where g=9.807 N kg−1.
Statistical analyses
The scaling coefficient of allometric relationships between two variables is the slope of the regression line when these variables are plotted on logarithmic axes. Both ordinary least squares (OLS) and standardised major axis (SMA) regression are frequently used in studies of allometry (Labonte and Federle, 2015); however, there is some controversy as to which is the more suitable approach (Egset et al., 2012; Pélabon et al., 2014; Smith, 2009; Warton et al., 2006). We hence report results from both models for all relationships, except for the models of safety factor with body mass where the 95% confidence interval (CI) of some OLS slopes included zero, in which case SMA breaks down. All statistical analyses were performed in R (version 3.4.1, https://www.R-project.org/); SMA regressions and comparisons of slopes and elevations between species were carried out with the package smatr (Warton et al., 2012), using Sidak corrected P-values for pairwise comparisons between species.
For the analyses of the scaling of claw tip diameter with body mass, claw tips that were obviously broken were excluded. Mean claw tip diameter was calculated for each individual. OLS and SMA regression analyses were carried out on log10-transformed variables of body mass and mean claw tip diameter. We also explored analysing the same relationships using minimum claw tip diameter; this yielded slightly higher scaling coefficients but similar results to those for mean claw tip diameter (reported below).
OLS linear regression models were used to analyse the relationship between safety factor, insect mass and surface roughness. Safety factor, mass and surface particle size were log10-transformed for all models. For both G. portentosa and A. cephalotes, inspection of the data and residual plots indicated that safety factors showed a bimodal distribution (Fig. S1). That is, the measured safety factors fell into one of two distinct categories. The insects either produced large safety factors, which we interpreted as reflecting individuals gripping with their claws on the centrifuge surface, or they produced small safety factors, which we interpreted as the insects failing to grip and slipping. In order to comply with the assumptions of the linear model, and to capture this effect and its relationship to body mass in more detail, the results were analysed separately for each category, hereafter termed grip/slip condition.
To separate the two categories of grip/slip condition, we used a cut-off threshold in safety factor, above which the insect was classed as gripping. The cut-off value was determined using an optimisation script, which compared linear models with safety factor as response and insect mass, surface roughness and grip/slip condition as predictors. Safety factor, mass and surface roughness were modelled as continuous variables, and grip/slip condition as a categorical variable. The cut-off value was varied across the range of observed safety factors for each species, and the value that gave the highest adjusted R2 value was chosen as the cut-off. This cut-off safety factor was 2.55 and 8.15 for G. portentosa and A. cephalotes, respectively (Fig. S1).
To assess the suitability of this approach, we compared models with and without this additional categorical predictor. For both A. cephalotes and G. portentosa, inclusion of grip/slip condition resulted in a significant improvement in model fit, as confirmed by a reduction in the Akaike information criterion (AIC) value. To further investigate the relationship between safety factor, mass and surface roughness, we ran separate regression models for the grip and slip conditions for both insect species. Binary logistic regressions were used to test the effect of surface roughness and mass on whether the insects were classed as gripping or slipping.
Results
Allometry of claw tip diameter
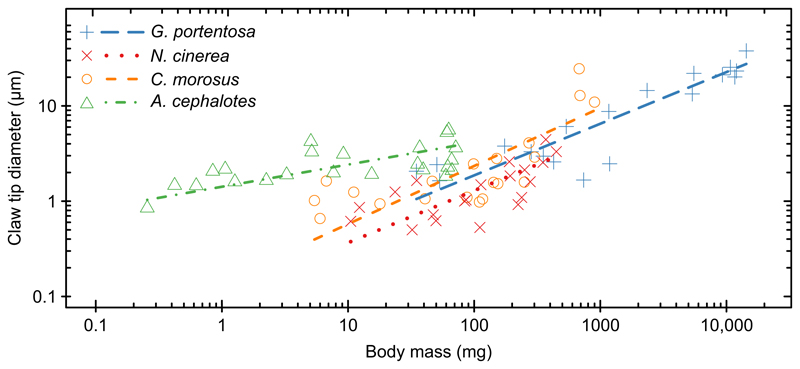
For all four insect species, claw tip diameter increased with body mass (Fig. 4; F-tests, all R2>0.40, P<0.005; note, R2 values are equivalent for OLS and SMA regressions). The scaling of claw tip diameter with body mass differed significantly between species (OLS regression: F3,74=6.76, P=0.0004; SMA regression: P=0.0004). The claw tip diameters of A. cephalotes (measured across the different adult worker castes) increased significantly more slowly with mass than those in the other species (where different instars were measured; pairwise comparisons between A. cephalotes and the other three species, all P<0.01). There were no significant differences in the scaling exponents between the other three species (pairwise comparisons, all P>0.9).
Fig. 4. Scaling relationships [standardised major axis (SMA) regressions] of claw tip diameter with body mass for the four insect species.
Gromphadorhina portentosa (slope=0.542, n=19), N. cinerea (slope=0.547, n=20) and C. morosus (slope=0.609, n=20) showed positive allometry, consistent with a scaling exponent of 1/2, whereas A. cephalotes (slope=0.233, n=23) showed slight negative allometry.
For A. cephalotes, claw tip diameter scaled with body mass with a scaling exponent of 0.233 (SMA, 95% CI: [0.165, 0.328]). Thus, the slope was significantly lower than 1/3, the expected value for isometry. For the other three species, claw tip diameter showed scaling exponents significantly larger than 1/3 (SMA slopes for G. portentosa: 0.542 [95% CI: 0.433, 0.679], N. cinerea: 0.547 [0.383, 0.782] and C. morosus: 0.609 [0.440, 0.843]), indicating positive allometry. For these three species, scaling relationships were consistent with a scaling exponent of 1/2, expected if animals were to maintain a constant tip stress (Fig. 4, Table 1).
Table 1. SMA and OLS regression coefficients of body mass against claw tip diameter for Gromphadorhina portentosa, Nauphoeta cinerea, Carausius morosus and Atta cephalotes.
| Species | Model | Elevation/intercept [log10(μm)] [95% CI−, 95% CI+] |
Slope [95% CI−, 95% CI+] |
R2 |
|---|---|---|---|---|
| G. portentosa | SMA | −0.813 [−1.201, −0.425] | 0.542 [0.433, 0.679] | 0.80 |
| OLS | −0.643 [−1.030, −0.255] | 0.486 [0.363, 0.609] | ||
| N. cinerea | SMA | −0.983 [−1.393, −0.573] | 0.547 [0.383, 0.782] | 0.46 |
| OLS | −0.632 [−1.040, −0.225] | 0.371 [0.171, 0.570] | ||
| C. morosus | SMA | −0.849 [−1.263, −0.436] | 0.609 [0.440, 0.843] | 0.55 |
| OLS | −0.550 [−0.960, −0.140] | 0.454 [0.252, 0.655] | ||
| A. cephalotes | SMA | 0.152 [0.046, 0.257] | 0.233 [0.165, 0.328] | 0.41 |
| OLS | 0.231 [0.130, 0.332] | 0.148 [0.067, 0.229] |
SMA, standardised major axis; OLS, ordinary least squares.
Regression fits for OLS regressions gave lower slopes than those for SMA regressions, but similar conclusions. There were some differences in interpretation of the scaling relationships for individual species, depending on the regression model chosen. For N. cinerea and C. morosus, in contrast to the SMA regression, the scaling exponent from the OLS regressions was not significantly larger than 1/3. Parameters from both models are reported in Table 1.
On fitting an SMA regression model with a common slope to the data from G. portentosa, N. cinerea and C. morosus, the elevations [predicted log10(claw tip diameter) at mass=1 mg (where diameter is in μm)] of the regression fits varied between these species (SMA regression, Wald statistic: W2=9.70, P=0.0078). Thus, although the scaling relationships are similar, for individuals of equal mass the claws differ in sharpness. The claws of N. cinerea were sharper than those of C. morosus (Wald: W1=9.04, P=0.00792), but not significantly different from those of G. portentosa (Wald: W1=3.24, P=0.20) and there was no significant difference in claw sharpness between G. portentosa and C. morosus (Wald: W1=1.32, P=0.58). Notably, the common slope for these three species was still in agreement with a scaling coefficient of 1/2, and this result was consistent between SMA (slope=0.559, 95% CI: [0.476, 0.658]) and OLS (slope=0.493, 95% CI: [0.414, 0.573]) regressions. For A. cephalotes, the scaling exponent was lower than that for the other three species, and hence comparing claw sharpness between this species and the others was only possible for a particular body mass. Nonetheless, in the range of recorded masses for A. cephalotes, claw tip diameters were larger than those for the other three species (Fig. 4).
Attachment performance
The separation of individuals into those that gripped or slipped dramatically and significantly improved the fit of regression models of safety factor against body mass and surface roughness for both G. portentosa (likelihood ratio test, F4,95=62.3, P<0.0001) and A. cephalotes (likelihood ratio test, F4,191=97.1, P<0.0001). For G. portentosa, adding the grip/slip condition into the model increased the adjusted R2 from 0.60 to 0.89 and decreased the AIC from 78.9 to −45.7. For A. cephalotes, adding grip/slip into the model increased the adjusted R2 from 0.41 to 0.80 and decreased the AIC from 258 to 46. Therefore, the analyses of safety factor versus body mass or surface roughness reported below were separated into individuals that gripped and those that slipped.
Gromphadorhina portentosa
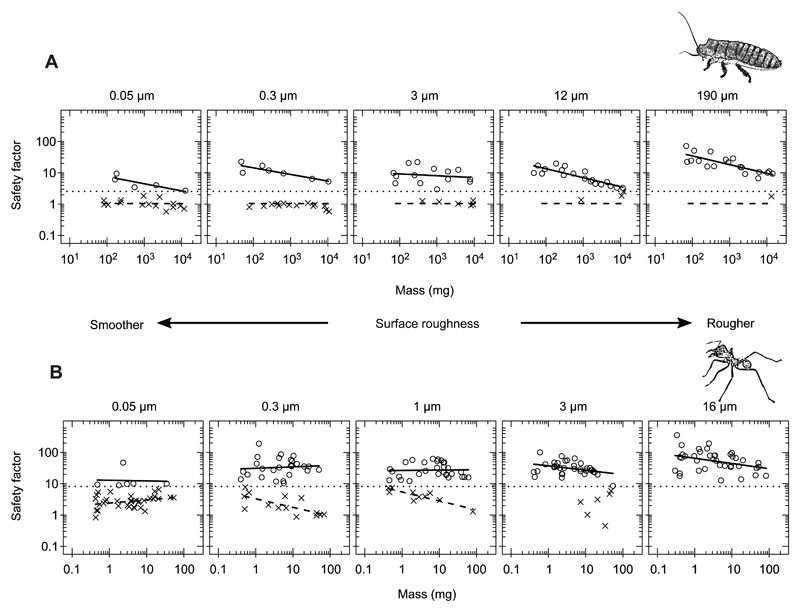
The safety factors attained by G. portentosa on the different surfaces varied from 0.58 to 72 (n=103). Larger individuals had poorer attachment performance in two respects. Firstly, they were less likely to grip on the centrifuge surface than smaller individuals (logistic regression, z=2.815, P=0.0049). Secondly, for those individuals that were able to grip on the surface, safety factor decreased significantly with increasing body mass (slope=−0.211, t60=4.49, P<0.0001; Fig. 5A). Attachment performance improved as surface roughness increased, in terms of both the proportion of individuals that were able to grip (logistic regression, z=2.50, P=0.012) and the safety factor of those individuals (OLS regression, t60=2.156, P=0.035). There were no significant interactions between body mass and surface roughness for models considering either the proportion of individuals that slipped (logistic regression, z=1.62, P=0.10) or safety factor (t60=0.60, P=0.55). Thus, for individuals that gripped on the centrifuge, safety factor scaled with body mass with a scaling exponent of −0.229 (95% CI: [−0.301, −0.157]).
Fig. 5. Scaling relationships between safety factor and body mass for surfaces of different roughness.
(A) Gromphadorhina portentosa cockroaches (n=20, 21, 20, 22 and 20 for 0.05, 0.3, 3, 12 and 190 µm surfaces, respectively). (B) Atta cephalotes ants (n=40 for each surface except 16 µm for which n=39). Points represent individual insects and are categorised by whether the individual gripped (circles) or slipped (crosses), with corresponding (ordinary least squares, OLS) regression lines. A common regression was fitted to the G. portentosa that slipped. The horizontal dotted line indicates the cut-off for the grip/slip condition.
For those individuals that slipped off in the centrifuge, there was no evidence of any effect of surface roughness on safety factor (likelihood ratio test, F2,31=0.68, P=0.51, with data for 12 and 190 µm surfaces excluded because of low sample sizes). We therefore fitted a model of just safety factor versus mass for the G. portentosa that slipped, for which safety factor did not change with mass (t37=0.048, P=0.96), with a scaling exponent of −0.002 (95% CI: [−0.065, 0.062]). The mean safety factor and hence friction coefficient for these individuals was 1.10 (95% CI: [0.97, 1.22]).
Atta cephalotes
There were several relevant differences in the scaling of attachment performance between A. cephalotes and G. portentosa. The safety factors for A. cephalotes covered a larger range than those of G. portentosa (Fig. 5B), varying from 0.45 to 354 (n=199). Additionally, the effects of body mass on attachment performance were less pronounced and more complex in A. cephalotes. Overall, there was no evidence that larger individuals were more likely to slip than smaller individuals (logistic regression, z=1.22, P=0.22), in contrast to G. portentosa. For individuals that gripped, the scaling coefficients of safety factor with body mass became more negative as surface roughness increased (t131=2.25, P=0.026, Fig. 5B). Scaling coefficients of safety factor with body mass were not significantly different from zero on the surfaces with the lowest roughness, but became increasingly negative as surface roughness increased, such that on the roughest (16 µm) surface, safety factor decreased with increasing body mass, with a scaling coefficient of −0.167 (95% CI: [−0.310, −0.025]). There was no interaction between body mass and surface roughness on whether ants gripped or slipped (z=1.22, P=0.22); however, as was the case for G. portentosa, the ants were significantly more likely to grip on rougher surfaces (logistic regression, z=5.20, P<0.0001; Fig. 5B).
For the ants that slipped (only the three substrates with the lowest surface roughness contained enough ants of a wide range of body masses to be included), there was a significant interaction between insect mass and surface roughness (t54=4.80, P<0.0001). For the 0.05 µm surface, there was little change of safety factor with mass, whereas for the 0.3 and 1 µm surfaces, safety factor decreased with mass with scaling exponents of −0.272 (95% CI: [−0.442, −0.103]) and −0.286 (95% CI: [−0.409, −0.163]), respectively (Fig. 5B). The mean safety factor/friction coefficient for individuals that slipped was 3.15 (95% CI: [2.72, 3.57]).
Discussion
Claws are important attachment devices for climbing animals, facilitating grip on a wide range of rough surfaces. Claw function depends on two opposing factors, both related to claw sharpness, here determined by measuring the diameter of the claw tip. Sharper claws can interlock with a larger number of asperities, but are also more likely to break (Labonte and Federle, 2015). Thus, animals face a trade-off, and the relationships between claw sharpness and animal size can reveal the relative importance and influence of these conflicting pressures on claw function.
The scaling relationships of claw sharpness varied between the four insect species studied, indicating that they may be under different pressures regarding claw performance. As predicted, these scaling relationships had significant consequences for the insects’ attachment performance on rough surfaces. Whole-body attachment force measurements of G. portentosa and A. cephalotes revealed that larger individuals attached less well in two respects. Firstly, for G. portentosa, where claw tip diameter showed positive allometry, larger individuals were more likely to slip (as defined in the next paragraph) than smaller individuals. Secondly, for both species, even when gripping onto a surface, larger individuals had mostly smaller safety factors than smaller individuals. The results of this study therefore provide strong evidence that larger animals perform less well on rough surfaces than smaller animals, as a result of the biomechanical constraints of claw design.
We observed a bimodal distribution of safety factors for both G. portentosa and A. cephalotes when gripping on rough surfaces (Fig. S1). This is in perfect agreement with the binary ‘grip and slip’ model proposed by Dai et al. (2002), which states that a claw will either interlock with surface asperities and grip, generating a large attachment force, or fail to interlock and slip, leading to a low attachment force. On exploring models of safety factor and body mass without accounting for this bimodal distribution, the residuals did not comply with model assumptions. When we incorporated the bimodal distribution into our analyses by separating observations using a grip or slip condition, the quality of the models of safety factor and body mass (as determined by AIC and R2) was much improved. Hence, there are good biological and statistical rationale for this data treatment. Our subsequent analyses and discussion of these data follow this categorisation of attachment performance.
Once an individual has gripped onto a surface, the maximum attachment force, and thus safety factor, they can generate will be the force at which the claw–asperity contact fails. Dai et al. (2002) state that this force should be proportional to insect muscle force; however, this is not necessarily the case, as maximum force could alternatively be limited by structural failure of the claw tip or asperity, or elastic rotation of the claw such that it slips off the asperity. In this situation, claw tip diameter may determine maximum force and safety factors (Asbeck et al., 2006).
Hence, attachment performance on rough surfaces can be quantified by recording whether or not an individual grips or slips, and by measuring the safety factor produced when it grips. Exploring how these two measures correlate with claw tip diameter and body size is informative for revealing the determinants of attachment performance.
Determinants of attachment performance
Claw tip diameter
Our results support previous models and experimental work (Asbeck et al., 2006; Bullock and Federle, 2011; Dai et al., 2002; Ditsche-Kuru et al., 2012) which suggested that claw tip diameter is a key determinant of attachment performance on rough surfaces. Moreover, our data also support a key prediction of the consequences of positive allometric growth of claw tip diameter; namely, that if claws become increasingly blunt to maintain stability as body size increases, attachment performance will decrease as the number of usable asperities decreases in relation to the dimensions of the animal (Asbeck et al., 2006; Labonte and Federle, 2015). This can be seen from the differing performances of G. portentosa and A. cephalotes on the centrifuge.
In G. portentosa, claw tip diameter is positively allometric. Correspondingly, for this species, there was a significant reduction in the number of individuals gripping on the centrifuge as body mass increased. Contrastingly, for A. cephalotes, claw tip diameter increased much more slowly with increasing body size, showing slight negative allometry. In A. cephalotes, there was no significant change in the number of individuals gripping or slipping on the centrifuge as body mass increased. Thus, these data suggest that positive allometric scaling of claw tip diameter in species such as G. portentosa constrains the attachment performance of larger animals with respect to their ability to grip on a surface.
For G. portentosa and A. cephalotes, there was variation, even on the same surface and among individuals of the same body size, as to whether they gripped or slipped. This is to be expected given that claw tip diameter between (and within) individuals, and particle size across a surface, will show variability. This is also why G. portentosa, on any given surface, did not show a sharp transition from grip to slip as body size increased (Fig. 5A). For G. portentosa on the 3 µm surface, where there were similar numbers of individuals gripping and slipping, we estimated the body mass at which the probability of slipping was 0.5 as 4.79 g. Using our models of claw tip diameter allometry, this mass would correspond to DCT=15.2 µm (SMA) or DCT=14.0 µm (OLS), in rough agreement with the dimensions of the asperities.
Claw tip diameter could also determine attachment performance in a second way: by influencing the maximum sustainable force (Fmax) once a claw is interlocked with an asperity. If Fmax is the force at which either the asperity fails or the claw/claw tip fails, then the force at failure should scale with (Asbeck et al., 2006). As a consequence of this, failure of the claw–asperity contact through either asperity failure or claw tip failure will depend on how claw tip diameter scales with body mass for the species concerned. Using our data, we can therefore test whether clawtip diameter determines Fmax.
For G. portentosa, DCT∝mass0.542, and so assuming Fmax should scale with mass1.084 for individuals that interlock successfully. Safety factor should therefore remain more or less constant or even increase slightly with body mass, with a predicted coefficient of 0.084 (95% CI: [−0.134, 0.358]). For A. cephalotes DCT∝mass0.233, so Fmax should scale with Hence, safety factor should scale with mass with a coefficient of −0.534 (95% CI: [−0.670, −0.344]). The respective scaling coefficients from the roughest surfaces from neither species agree with these predictions; the coefficient for G. portentosa was −0.280 (95% CI: [−0.390, −0.170]) and for A. cephalotes −0.167 (95% CI: [−0.310, −0.025]). As maximum attachment force is not well explained by either claw or asperity failure, it is likely that a factor other than claw tip diameter determines this aspect of attachment performance.
Muscle force
Maximum sustainable attachment force through interlocking between a claw and an asperity may depend on muscular strength (Dai et al., 2002). Insects can engage their claws with a substrate by a muscular pull on the unguitractor tendon, causing claws to retract (Federle et al., 2001; Snodgrass, 1956). When the insect resists a strong force by gripping onto an asperity with their claws, it is likely that this force will be balanced by a muscular pull (Dai et al., 2002) (assuming the claw is not fully extended). Thus, the claw will move (extend) once the force exceeds the maximum pull the muscle can produce, potentially leading to a loss of grip.
Assuming simple geometric scaling of muscle cross-sectional area, muscle force should scale with mass2/3. If muscular effort determines attachment force, safety factor∝mass2/3/mass∝mass−1/3. This expected coefficient of −1/3 is in good agreement with the observed scaling of safety factor for G. portentosa of −0.280 (95% CI: [−0.390, −0.170]) on the roughest surface. For A. cephalotes, the scaling of safety factor with mass on the roughest surface was −0.167 (95% CI: [−0.310, −0.025]). Hence, our data more broadly support a hypothesis that attachment performance when claws grip is poorer in larger animals because of the decrease of muscle force relative to body mass.
Friction, adhesion and non-claw attachment structures
If an individual fails to grip on the centrifuge, the recorded force as it slips off should just be determined by friction between the insect cuticle and the centrifuge surface. For G. portentosa, safety factor did not change with body mass for these individuals, consistent with the expectation for classic friction (Gao et al., 2004). The safety factor, equivalent to the friction coefficient, for the G. portentosa that slipped was 1.10 (95% CI [0.97, 1.22]). This value is considerably larger than values for rigid solids, including insect cuticle (0.35; unpublished data cited in Dai et al., 2002), suggesting some contribution from soft structures such as the frictional pads (euplantulae) (Clemente and Federle, 2008; Labonte et al., 2014). However, the centrifuge setup may overestimate friction forces for such low angular velocities, potentially explaining the difference in friction coefficient from that determined by Dai et al., (2002).
For the ants that slipped, the situation is more complex. Safety factors were much higher than those for G. portentosa and decreased with increasing body mass for some surfaces. This is not in agreement with a simple friction model and indicates a contribution of adhesion to the observed friction forces. In Hymenoptera, when claws fail to engage, the arolia (adhesive pads) are brought into contact with the surface (Federle et al., 2001) and it may be that these, along with frictional hairs on the ventral surface of the tarsus (Endlein and Federle, 2015), contribute to the higher safety factors observed.
Consequences of the link between claw morphology and attachment performance
We have shown that the scaling of claw sharpness with body size can have a substantial effect on insect attachment performance. The allometry of claw sharpness also has important implications for claw tip stress and the risk of claw breakage (Asbeck et al., 2006; Labonte and Federle, 2015). Thus, the differing scaling relationships observed here imply that the four species may face different constraints relating to surface attachment.
One key difference between the ants and the other three species is that the ants were all adults from worker castes of different size, i.e. we were measuring static allometry, whereas for G. portentosa, N. cinerea and C. morosus, we measured ontogenetic allometry across different instars. Consequently, the observed difference in scaling coefficient between the ants and the other species may reflect constraints relating to the respective types of allometry we observed. For instance, the early instars of G. portentosa, N. cinerea and C. morosus could well risk having very sharp claws, as nymphs are short lived and claws may regenerate through subsequent moults (Brindley, 1897; Maginnis, 2006; O’Farrell and Stock, 1965). However, while static and ontogenetic allometries can differ, the two are linked and often highly conserved (Pélabon et al., 2013). It would be informative to examine ontogenetic versus static allometry of claw sharpness across multiple insect species to test whether, as observed here, a larger scaling coefficient for claw tip diameter is common for ontogenetic scaling.
For G. portentosa, N. cinerea and C. morosus, claw tip diameter showed positive allometry, with scaling coefficients near 1/2, consistent with the hypothesis that claws are designed to maintain constant tip stress and avoid claw breakage (Labonte and Federle 2015). However, the assumption that the maximum force that claws experience scales with mass may not be correct. Our data suggest that maximum attachment force, at least under certain conditions, may be determined by muscle force, i.e. force∝mass2/3. This would change the expected allometry of claw tip diameter; maintaining constant claw tip stress would only require mass2/3/ or DCT∝mass1/3, identical to isometry. The observed positive allometry of claw tip diameter in G. portentosa, N. cinerea and C. morosus speaks against this prediction, and suggests that peak forces experienced by claw tips scale with body mass rather than muscle force.
In marked contrast to that in the other three species, claw tip diameter in A. cephalotes showed negative allometry with a scaling coefficient less than 1/3. This implies that large individuals will experience higher stresses on claws and thus potentially a higher risk of claw damage than small individuals. There are two possible ways in which larger individuals could avoid claw breakage even with a scaling coefficient of less than 1/3. Firstly, claws of larger individuals could be made of progressively stronger materials than claws of smaller individuals (Labonte and Federle, 2015). Secondly, if the claws are relatively blunt, then even with a scaling coefficient <1/3, claw tip stresses will never reach critical levels, even for the largest individuals. For A. cephalotes, the latter hypothesis seems most likely. Given that for individuals of comparable body mass, the claws of A. cephalotes were blunter than those of the other three species, pressure from the risk of claw breakage is relaxed.
Several studies on vertebrates have attempted to correlate variability in claw morphology with ecology (Birn-Jeffery et al., 2012; Crandell et al., 2014; Feduccia, 1993; Lautenschlager, 2014; Pike and Maitland, 2004; Tulli et al., 2009, 2011; Zani, 2000); however, only one study (in Anolis lizards) has examined claw sharpness (Crandell et al., 2014). That study found no significant correlation between claw sharpness and the lizards’ arboreal lifestyle. However, the study used claw tip angle as a proxy for claw sharpness, whereas there is some evidence from penetration-based climbing experiments that claw tip diameter is a much better predictor of attachment force (Provancher et al., 2005).
General implications and future directions
Animals with claws cover an extensive range of body masses. We have shown that as body size increases, claw-based attachment performance decreases as a result of mechanical constraints. Across the animal kingdom, a size-based reduction in attachment performance will have a considerable impact on how claws are used for attachment.
This study focused on the intraspecific allometry of claw sharpness. To improve our understanding of claw morphology and function, future work should explore how claw sharpness varies across species. Firstly, investigating interspecific allometry of claw sharpness would reveal to what extent the scaling of claw sharpness with body size is determined by phylogenetic constraints. Such differences in scaling were found for adhesive pads, where scaling was close to isometry within closely related groups but positively allometric across larger taxonomic units (Labonte et al., 2016). Secondly, comparative studies of claw sharpness, attachment performance and ecology across multiple species would reveal the effects of claw morphology on habitat/niche choice. Finally, a complete picture of claw function will require understanding of how other claw shape parameters interact with claw sharpness to determine attachment performance.
Supplementary Material
Supplementary information available online at http://jeb.biologists.org/lookup/doi/10.1242/jeb.188391.supplemental
Acknowledgements
We gratefully acknowledge Jeremy Skepper, James McMillan, Karin Müller and the Cambridge Advanced Imaging Centre for assistance with SEM, and The ZSL London Zoo for giving us several A. cephalotes ants. We also thank two anonymous reviewers, whose comments helped improve the manuscript. Data presented in this manuscript are included in the PhD thesis of J.G.P. (Pattrick, 2018).
Funding
J.G.P. was funded by a Biotechnology and Biological Sciences Research Council PhD Studentship under grant BB/J014540/1.
List of symbols and abbreviations
- a
acceleration
- AIC
Akaike information criterion
- CI
confidence interval
- DCT
claw tip diameter
- F
force
- Fmax
maximum sustainable attachment force
- FPS
frames per second
- g
acceleration due to gravity
- m
mass
- OLS
ordinary least squares
- r
distance of insect from centre of the centrifuge
- S
safety factor (shear force per body weight)
- SMA
standardised major axis
Footnotes
J.G.P., 0000-0001-6587-5500
Competing interests
The authors declare no competing or financial interests.
Author contributions
Conceptualization: J.G.P., D.L., W.F.; Methodology: J.G.P., D.L., W.F.; Validation: D.L., W.F.; Formal analysis: J.G.P.; Investigation: J.G.P., D.L.; Resources: W.F.; Writing - original draft: J.G.P.; Writing - review & editing: J.G.P., D.L., W.F.; Visualization: J.G.P.; Supervision: D.L., W.F.; Project administration: W.F.
Data availability
The data supporting this manuscript are available from the University of Cambridge data repository: http://doi.org/10.17863/CAM.31453
References
- Asbeck AT, Kim S, Cutkosky MR, Provancher WR, Lanzetta M. Scaling hard vertical surfaces with compliant microspine arrays. Int J Rob Res. 2006;25:1165–1179. [Google Scholar]
- Birn-Jeffery AV, Miller CE, Naish D, Rayfield EJ, Hone DWE. Pedal claw curvature in birds, lizards and mesozoic dinosaurs – complicated categories and compensating for mass-specific and phylogenetic control. PLoS ONE. 2012;7:e50555. doi: 10.1371/journal.pone.0050555. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bonser RHC. Comparative mechanics of bill, claw and feather keratin in the Common Starling Sturnus vulgaris. J Avian Biol. 1996;27:175–177. [Google Scholar]
- Brindley HH. On the regeneration of the legs in the blattidœ. Proc Zool Soc London. 1897;65:903–916. [Google Scholar]
- Bullock JMR, Federle W. The effect of surface roughness on claw and adhesive hair performance in the dock beetle Gastrophysa viridula. Insect Sci. 2011;18:298–304. [Google Scholar]
- Clemente CJ, Federle W. Pushing versus pulling: division of labour between tarsal attachment pads in cockroaches. Proc R Soc B. 2008;275:1329–1336. doi: 10.1098/rspb.2007.1660. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Crandell KE, Herrel A, Sasa M, Losos JB, Autumn K. Stick or grip? Co-evolution of adhesive toepads and claws in Anolis lizards. Zoology. 2014;117:363–369. doi: 10.1016/j.zool.2014.05.001. [DOI] [PubMed] [Google Scholar]
- Dai Z, Gorb SN, Schwarz U. Roughness-dependent friction force of the tarsal claw system in the beetle Pachnoda marginata (Coleoptera, Scarabaeidae) J Exp Biol. 2002;205:2479–2488. doi: 10.1242/jeb.205.16.2479. [DOI] [PubMed] [Google Scholar]
- D’Amore DC, Clulow S, Doody JS, Rhind D, Mchenry CR. Claw morphometrics in monitor lizards: variable substrate and habitat use correlate to shape diversity within a predator guild. Ecol Evol. 2018;8:6766–6778. doi: 10.1002/ece3.4185. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ditsche-Kuru P, Barthlott W, Koop JHE. At which surface roughness do claws cling? Investigations with larvae of the running water mayfly Epeorus assimilis (Heptageniidae, Ephemeroptera) Zoology. 2012;115:379–388. doi: 10.1016/j.zool.2011.11.003. [DOI] [PubMed] [Google Scholar]
- Egset CK, Hansen TF, Le Rouzic A, Bolstad GH, Rosenqvist G, Pélabon C. Artificial selection on allometry: change in elevation but not slope. J Evol Biol. 2012;25:938–948. doi: 10.1111/j.1420-9101.2012.02487.x. [DOI] [PubMed] [Google Scholar]
- Endlein T, Federle W. On heels and toes: How ants climb with adhesive pads and tarsal friction hair arrays. PLoS ONE. 2015;10:e0141269. doi: 10.1371/journal.pone.0141269. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Federle W, Rohrseitz K, Hölldobler B. Attachment forces of ants measured with a centrifuge: better “wax-runners” have a poorer attachment to a smooth surface. J Exp Biol. 2000;203:505–512. doi: 10.1242/jeb.203.3.505. [DOI] [PubMed] [Google Scholar]
- Federle W, Brainerd EL, McMahon TA, Hölldobler B. Biomechanics of the movable pretarsal adhesive organ in ants and bees. Proc Natl Acad Sci. 2001;98:6215–6220. doi: 10.1073/pnas.111139298. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Feduccia A. Evidence from claw geometry indicating arboreal habits of Archaeopteryx. Science. 1993;259:790–793. doi: 10.1126/science.259.5096.790. [DOI] [PubMed] [Google Scholar]
- Gao J, Luedtke WD, Gourdon D, Ruths M, Israelachvili JN, Landman U. Frictional forces and Amontons’ law: from the molecular to the macroscopic scale. J Phys Chem B. 2004;108:3410–3425. [Google Scholar]
- Heethoff M, Koerner L. Small but powerful: the oribatid mite Archegozetes longisetosus Aoki (Acari, Oribatida) produces disproportionately high forces. J Exp Biol. 2007;210:3036–3042. doi: 10.1242/jeb.008276. [DOI] [PubMed] [Google Scholar]
- Labonte D, Federle W. Scaling and biomechanics of surface attachment in climbing animals. Philos Trans R Soc B. 2015;370 doi: 10.1098/rstb.2014.0027. 20140027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Labonte D, Williams JA, Federle W. Surface contact and design of fibrillar “friction pads” in stick insects (Carausius morosus): mechanisms for large friction coefficients and negligible adhesion. J R Soc Interface. 2014;11 doi: 10.1098/rsif.2014.0034. 20140034. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Labonte D, Clemente CJ, Dittrich A, Kuo C-Y, Crosby AJ, Irschick DJ, Federle W. Extreme positive allometry of animal adhesive pads and the size limits of adhesion-based climbing. Proc Natl Acad Sci. 2016;113:1297–1302. doi: 10.1073/pnas.1519459113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lautenschlager S. Morphological and functional diversity in therizinosaur claws and the implications for theropod claw evolution. Proc R Soc B. 2014;281 doi: 10.1098/rspb.2014.0497. 20140497. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maginnis TL. Leg regeneration stunts wing growth and hinders flight performance in a stick insect (Sipyloidea sipylus) Proc R Soc B. 2006;273:1811–1814. doi: 10.1098/rspb.2006.3508. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mattheck C, Reuss S. The claw of the tiger: an assessment of its mechanical shape optimization. J Theor Biol. 1991;150:323–328. [Google Scholar]
- O’Farrell AF, Stock A. Regeneration and the moulting cycle in Blattella germanica L. I. Single regeneration initiated during the first instar. Aust J Biol Sci. 1965;6:485–500. doi: 10.1071/bi9530485. [DOI] [PubMed] [Google Scholar]
- Pattrick JG. Grip, Slip, Petals, and Pollinators: Linking the Biomechanics, Behaviour and Ecology of Interactions Between Bees and Plants. PhD thesis, University of Cambridge; Cambridge, UK: 2018. [Google Scholar]
- Peattie AM, Full RJ. Phylogenetic analysis of the scaling of wet and dry biological fibrillar adhesives. Proc Natl Acad Sci. 2007;104:18595–18600. doi: 10.1073/pnas.0707591104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pélabon C, Bolstad GH, Egset CK, Cheverud JM, Pavlicev M, Rosenqvist G. On the relationship between ontogenetic and static allometry. Am Nat. 2013;181:195–212. doi: 10.1086/668820. [DOI] [PubMed] [Google Scholar]
- Pélabon C, Firmat C, Bolstad GH, Voje KL, Houle D, Cassara J, Rouzic AL, Hansen TF. Evolution of morphological allometry. Ann N Y Acad Sci. 2014;1320:58–75. doi: 10.1111/nyas.12470. [DOI] [PubMed] [Google Scholar]
- Pike AVL, Maitland DP. Scaling of bird claws. J Zool. 2004;262:73–81. [Google Scholar]
- Provancher WR, Clark JE, Geisler B, Cutkosky MR. Towards penetration-based clawed climbing. In: Armada M, González de Santos P, editors. Climbing and Walking Robots: Proceedings of the 7th International Conference CLAWAR 2004; Berlin: Springer; 2005. pp. 961–970. [Google Scholar]
- Schneider CA, Rasband WS, Eliceiri KW. NIH Image to ImageJ: 25 years of image analysis. Nat Methods. 2012;9:671–675. doi: 10.1038/nmeth.2089. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schofield RMS, Niedbala JC, Nesson MH, Tao Y, Shokes JE, Scott RA, Latimer MJ. Br-rich tips of calcified crab claws are less hard but more fracture resistant: a comparison of mineralized and heavy-element biological materials. J Struct Biol. 2009;166:272–287. doi: 10.1016/j.jsb.2009.01.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith RJ. Use and misuse of the reduced major axis for line-fitting. Am J Phys Anthropol. 2009;140:476–486. doi: 10.1002/ajpa.21090. [DOI] [PubMed] [Google Scholar]
- Snodgrass RE. Anatomy of the Honey Bee. Ithaca, NY: Cornell University Press; 1956. [Google Scholar]
- Song Y, Dai Z, Wang Z, Ji A, Gorb SN. The synergy between the insect-inspired claws and adhesive pads increases the attachment ability on various rough surfaces. Sci Rep. 2016;6 doi: 10.1038/srep26219. 26219. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tulli MJ, Cruz FB, Herrel A, Vanhooydonck B, Abdala V. The interplay between claw morphology and microhabitat use in neotropical iguanian lizards. Zoology. 2009;112:379–392. doi: 10.1016/j.zool.2009.02.001. [DOI] [PubMed] [Google Scholar]
- Tulli MJ, Abdala V, Cruz FB. Relationships among morphology, clinging performance and habitat use in Liolaemini lizards. J Evol Biol. 2011;24:843–855. doi: 10.1111/j.1420-9101.2010.02218.x. [DOI] [PubMed] [Google Scholar]
- Warton DI, Wright IJ, Falster DS, Westoby M. Bivariate line-fitting methods for allometry. Biol Rev Camb Philos Soc. 2006;81:259–291. doi: 10.1017/S1464793106007007. [DOI] [PubMed] [Google Scholar]
- Warton DI, Duursma RA, Falster DS, Taskinen S. smatr 3- an R package for estimation and inference about allometric lines. Methods Ecol Evol. 2012;3:257–259. [Google Scholar]
- Yang Z, Liu Z, Dai Z. Surface texture and mechanical behavior of claw material in beetle Dorcus titanus (Coleoptera: Lucanidae) Appl Mech Mater. 2014;461:305–312. [Google Scholar]
- Zani PA. The comparative evolution of lizard claw and toe morphology and clinging performance. J Evol Biol. 2000;13:316–325. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.