Identifying phenological phases in strawberry using multiple change-point models

Phenological phases are a cornerstone of phenology, the study of recurrent biological events over time. We introduce a new statistical modeling approach for identifying phases in phenological series.

Abstract

Plant development studies often generate data in the form of multivariate time series, each variable corresponding to a count of newly emerged organs for a given development process. These phenological data often exhibit highly structured patterns, and the aim of this study was to identify such patterns in cultivated strawberry. Six strawberry genotypes were observed weekly for their course of emergence of flowers, leaves, and stolons during 7 months. We assumed that these phenological series take the form of successive phases, synchronous between individuals. We applied univariate multiple change-point models for the identification of flowering, vegetative development, and runnering phases, and multivariate multiple change-point models for the identification of consensus phases for these three development processes. We showed that the flowering and the runnering processes are the main determinants of the phenological pattern. On this basis, we propose a typology of the six genotypes in the form of a hierarchical classification. This study introduces a new longitudinal data modeling approach for the identification of phenological phases in plant development. The focus was on development variables but the approach can be directly extended to growth variables and to multivariate series combining growth and development variables.

Introduction

Phenology consists of the study of recurrent biological events over time (Rathcke and Lacey, 1985). Recurrent events provide explicit information on the occurrence and duration of phenological phases (Denny et al., 2014), which are of central interest in phenological studies (Rathcke and Lacey, 1985; Wang et al., 2016). Phenological data often take the form of time series with various time indexing (e.g. day, week, and year) and variables of interest. Since temperature is the primary factor determining plant phenology, phenological series are often indexed by thermal time; that is, cumulative degree days above a threshold (Granier and Tardieu, 1998; Tsimba et al., 2013). Temperature responses are often modified by day length, and this influence can be taken into account using photo-thermal time (Craufurd et al., 2001; Li et al., 2018).

The analysis of phenological series falls into the statistical domain of longitudinal data analysis (Diggle et al., 2002) where a relatively large number of individuals are observed repeatedly over time. We here focus on the situation where the time sampling means that count data (i.e. number of newly emerged organs between two successive observation dates) are collected instead of time interval data (i.e. time interval between the emergence of two successive organs) (Denny et al. 2014). Collecting time interval data requires dating a new organ using a morphological stage which may be a source of uncertainty. This uncertainty is minimized in the case of count data since it only concerns a small proportion of the counted organs (often a single one) because of the sequential development of phytomers that helps to determinate in a reliable way the last emerged organ at a given morphological stage. Phenological patterns are often summarized as single traits (e.g. time of first flowering occurrence or flowering duration; see Sønsteby and Heide, 2007; Honjo et al., 2011; Rahman et al., 2014) or studied on the basis of cumulative numbers of organs fitted using sigmoidal functions (Sønsteby and Heide, 2008; Opstad et al., 2011). The shortcoming of this latter approach is that it exclusively focuses on the slowly varying component in phenological series while ignoring the rapidly varying components (e.g. abrupt changes or local fluctuations in the production of organs) (Chatfield, 2003). This approach is thus not appropriate for identifying phenological phases.

Strawberry, the main berry fruit crop (www.fao.org/faostat/en/#home: production data of 2017), is a relevant model to study the occurrence and concomitance of various life cycle events. Vegetative reproduction with stolons or runners (elongated stems) that produce daughter plants (hereafter identified as the runnering process) and sexual reproduction through inflorescences occur successively or jointly depending on genotype, cultural technique, and environment (Costes et al., 2014; Perrotte et al., 2016b). The control of the trade-off between flowering and runnering is crucial for managing the plant production in nurseries and fruit production (Husaini and Neri, 2016). Vegetative propagation could occur at the expense of inflorescences and therefore fruit yield (Tenreira et al., 2017). The molecular basis for this antagonism started to be deciphered with the role of the gibberellin pathway in runnering control (Tenreira et al., 2017; Caruana et al., 2018), which involves the key role of GA20ox and DELLA allowing the trade-off between runnering and non-runnering genotypes. This pathway probably interacts with the flowering pathway involving phosphatidylethanolamine-binding protein (PEBP) family genes (Iwata et al., 2012; Perrotte et al., 2016a) with the hypothesis of the role of SOC (Mouhu et al., 2013). However, despite the fact that several studies (Battey et al., 1998; Darnell et al., 2003; Heide et al., 2013; Kurokura et al., 2013) have been conducted to understand the relationship between flowering and runnering processes, little is known concerning these development processes with time.

The objective of this work was to design a general methodology for identifying phenological phases on the basis of series of count of newly emerged organs. To this end, the approach based on multiple change-point models introduced by Perrotte et al. (2016b) for the identification of flowering phases on the basis of univariate series of counts of inflorescences is here generalized. Multiple change-point models are applied to the identification of phenological phases on the basis of multivariate series combining different types of organs, and new inference capabilities are introduced, in particular (i) the slope heuristic, a criterion that does not require the series to be very ‘long’ for the selection of the number of phases (Guédon, 2015); (ii) credibility intervals for each limit between phases; and (iii) variance decomposition within each phase for assessing the between-plant heterogeneity for a given genotype. These two latter methods coupled with hidden semi-Markov chains, a family of models for the segmentation, asynchronous between individuals, of series previously applied in various settings (Guédon et al., 2007; Dambreville et al., 2015; Lièvre et al., 2016), are used for assessing the assumption of phenological phases synchronous between individuals of a given genotype. Identifying phenological phases synchronous between individuals is particularly relevant to study the influence of environmental conditions (e.g. fluctuating temperatures) on plant development. This new approach is applied for identifying flowering, vegetative development, runnering phases, and consensus phenological phases combining the three development processes in six cultivated strawberry genotypes observed weekly during 7 months. This led us to a new characterization of these genotypes regarding potential agronomical performances.

Materials and methods

Experimental protocol and data sets

Plant material and growth conditions

Six seasonal flowering genotypes (Capriss, Ciflorette, Cir107, Cléry, Darselect, and Gariguette) of the cultivated octoploid strawberry (Fragaria × ananassa) were studied. These genotypes differ by their production of flowers, leaves, crowns, and stolons, and by their chilling requirement and flowering earliness (see Supplementary Table S1 at JXB online). The number of leaves produced and, to a lesser extent, the number of flowers were correlated to the number of crowns produced. Cold-stored plants were obtained from Invenio nursery (Douville, France 0°61'E and 45°02'N, altitude 150 m). In the nursery, these plants received their chilling requirement in autumn 2014 by placing them in a climatic chamber at 2 °C. Afterwards, all the genotypes were planted on 10 December, except Ciflorette (4 December), into a breeding ground bag (ORGAPIN) of 10 liters with drip irrigation and fertilization in a greenhouse at a minimal temperature of 8 °C. The experiment was conducted in randomized blocks with four blocks. Each block consisted of two breeding ground bags per genotype placed side by side, each containing six plants distributed in two rows—12 plants per genotype and block. Only the central plants with the greatest height per block were observed to avoid border effects between neighboring plants belonging to different genotypes. We thus observed a total of 32 replicates per genotype (Supplementary Fig. S1).

Phenological series

For the six seasonal genotypes, 32 plants per genotype were observed during seasonal production. During 27 weeks, from 16 December 2014 to 24 June 2015, the number of newly emerged flowers, leaves, and stolons per plant were counted using morphological criteria (petiole length >0.5 cm for leaves and length >1 cm for stolons). Once counted, the stolons were cut to the base according to production conditions. In addition, the number of crowns (i.e. the number of axes) per plant were counted at the end of the experiment. We checked using ANOVA on ranks (Kruskal–Wallis test) that, for each genotype and development process, there was no block effect on the count distributions pooling all the observation periods. The day of plantation was chosen as the time origin of the phenological series, which were indexed by days. The interval between two successive measurement occasions was between 5 d and 10 d, this interval being a week in more than half of the cases (14 intervals among 26). Because of the unevenly spaced measurement occasions, the data were standardized and each element of a phenological series consisted of the number of weekly emerged organs. A thermal time indexing with base temperature (T_base) at 0 °C (Rosa et al., 2011; Bethere et al., 2016) was defined based on the growing degree day (GDD)

$${\displaystyle \begin{array}{l}{\displaystyle \mathrm{G}\mathrm{D}\mathrm{D}=T_{\mathrm{m}\mathrm{e}\mathrm{a}\mathrm{n}}-T_{\mathrm{b}\mathrm{a}\mathrm{s}\mathrm{e}},}\end{array}}$$

where T_mean is the daily mean temperature computed on the basis of series of temperatures recorded every 10 min, and GDD are cumulated from the planting date.

Statistical models for the identification of phenological phases

We assumed that the phenological pattern of a genotype took the form of a succession of well-differentiated stationary phases where the distribution of the number of weekly emerged organs did not change substantially within each phase, but changed markedly between phases (Perrotte et al., 2016b). These phenological patterns were analyzed using two types of segmentation models applied to each genotype: (i) multiple change-point models for the segmentation, synchronous between individuals, of the phenological series; and (ii) hidden semi-Markov chains for the segmentation, asynchronous between individuals, of the same series. Hidden semi-Markov chains were applied to assess the synchronicity between individuals of the phenological phases.

Segmentation, synchronous between individuals, of phenological series for each genotype using categorical multiple change-point models

We here assume that the phenological phases were common for the different plants measured for a given genotype and used multiple change-point models for the synchronous segmentation of the phenological series of the different plants; see Supplementary Methods S1 for a formal definition of multiple change-point models and associated statistical methods. For each genotype, the data to be segmented thus consisted of a sample of series of length 27 (the number of measurement dates) where each series corresponded to a plant. Univariate series for each type of organ (either flower, leaf, or stolon) and trivariate series combining flowers, leaves, and stolons were considered. The statistical methodology for univariate multiple change-point models directly generalizes to multivariate multiple change-point models since the different observed variables are assumed to be mutually independent within each phase.

Because the number of weekly emerged organs was between 0 and 25 for flowers, 0 and 9 for leaves, and 0 and 11 for stolons, and the frequencies were low for the highest values, we chose to consider these variables as categorical and to group the categories corresponding to the highest values above a given threshold. Furthermore, the frequency distributions for the flowers and the stolons were zero inflated, and standard parametric assumptions for count distributions (e.g. Poisson and negative binomial distributions) were not adapted to our case. The number of categories was seven for the leaves, the last one corresponding to the grouping of the values ≥6 (the frequency of >6 weekly emerged leaves was only 125 to be compared with a sample size of 5184, i.e. the cumulative length of the 192 phenological series) for multiple change-point model estimation. The number of categories was four for the stolons, the last one corresponding to the grouping of the values ≥3 (the frequency of >3 weekly emerged stolons was only 238 to be compared with a sample size of 5184). For the flowers, because the values were more dispersed, we chose to keep alone the value 0 because of its high frequency (between 38% and 46% for the different genotypes), to group by two the following values up to 10, and to group the values ≥11 (the frequency of >11 weekly emerged flowers was only 165 to be compared with a sample size of 5184). We thus directly estimated probability masses for the possible categories within a given phenological phase. The rather large sample sizes (32 plants for each genotype to be multiplied by the length of the phase in observation dates) justified the direct estimation of probability masses for the possible categories.

We adopted a retrospective or off-line inference approach whose objective was to infer the number of phases J, the positions of the J–1 change points, and the within-phase probability masses for each number of organs. For the selection of the number of phases, we used the slope heuristic proposed by Guédon (2015). The principle of this kind of penalized likelihood criterion consists of making a trade-off between an adequate fitting of the model to the data and a reasonable number of parameters to be estimated. Once the number of phases J had been selected for a given genotype, the series were optimally segmented into J phases using the dynamic programming algorithm proposed by Auger and Lawrence (1989). The assessment of multiple change-point models relied on two posterior probabilities (see Supplementary Methods S1 for formal definitions). (i) Posterior probability of the selected J-phase model, namely weight of the J-phase model among all the possible models. This posterior probability is an output of the slope heuristic (see Supplementary Methods S1). (ii) Posterior probability of the optimal segmentation in J phases, namely weight of the optimal segmentation among all the possible segmentations in J phases. This posterior probability should be interpreted with respect to the number of possible segmentations in J phases of a series of length T, which is $\left(\begin{array}{ccc}T& -& 1\\ J& -& 1\end{array}\right)$.

These two posterior probabilities reflect the hierarchical nature of the inference with two successive steps: (i) selection of the number of phases using the slope heuristic considering all the possible segmentations in J phases for J=1,...,J_max; and (ii) computation of the optimal segmentation in the number of phases previously selected.

It is often of interest to quantify the uncertainty concerning change-point positions. To this end, we computed a credibility interval for each change point using the smoothing algorithm proposed by Guédon (2013); see Supplementary Methods S1 for a formal definition. In the multiple change-point models built on the basis of the phenological series, all the estimated parameters (i.e. change points and probability mass functions for the numbers of weekly emerged organs within each phenological phase) are population parameters. It should be noted that because of the rather short length of phenological series and thus of phenological phases, it would be unreliable to estimate probability mass functions for the numbers of weekly emerged organs of each individual within each phenological phase (i.e. individual parameters). Nevertheless, there was some heterogeneity between individuals within each phase, and we thus decomposed the variance within each phase applying first a rank transform following the standard approach of the one-way ANOVA on ranks. The proportion of between-individual variance was used for assessing the commonality of phase definition between individuals.

Segmentation, asynchronous between individuals, of phenological series for each genotype using hidden semi-Markov chains

In order to validate the assumption of phases synchronous between individuals, we built models for the asynchronous segmentation of individuals and then checked the degree of synchronicity of the phases between individuals. These models are hidden semi-Markov chains (HSMCs) which are two-scale segmentation models (for a formal definition of these models and associated statistical methods, see Supplementary Methods S2). In our context, the successive phenological phases and their durations (coarse scale) are represented by a non-observable semi-Markov chain while the number of weekly emerged organs within a phase (fine scale) is represented by categorical observation distributions attached to each state of the semi-Markov chain. Hence, each state of the semi-Markov chain represents a phenological phase. A semi-Markov chain is defined by three subsets of parameters: (i) initial probabilities (π _j; j=0,...,J–1) to model which is the first phase occurring at the beginning of the measurement; (ii) transition probabilities (p_i;i, j=0,...,J–1) to model the succession of phases; and (iii) occupancy distributions attached to non-absorbing states (a state is said to be absorbing if, after entering this state, it is impossible to leave it) to model the phase duration in the number of measurement occasions.

A HSMC adds a fourth subset of parameters to the three subsets of parameters previously defined for the underlying semi-Markov chain: (iv) categorical observation distributions to model the number of weekly emerged organs within a phase.

In order to mimic the deterministic succession of phases of multiple change-point models, we assumed that the semi-Markov chain was composed of successive transient states (a state is said to be transient if, after leaving this state, it is impossible to return to it) followed by a final absorbing state and thus imposed that p_{i i+1}=1 and p_ij=0 for j≠i+1 for each successive transient state i. We also grouped the categories as described for the multiple change-point models for the estimation of the observation distributions. A HSMC was built for each development process and each genotype. The estimated HSMC was used to segment each observed series in phenological phases (Guédon, 2003). The frequency distributions of the limits between phases were extracted from these optimal segmentations and compared with the limits between phases identified using the multiple change-point model estimated on the same phenological series.

Illustration with the identification of flowering phases in Gariguette using categorical multiple change-point models

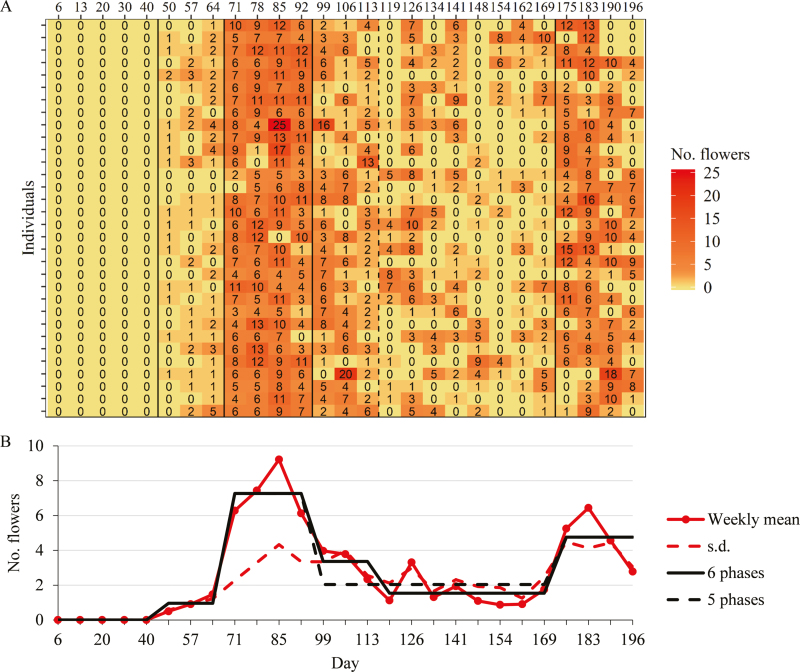
For Gariguette flowering, the slope heuristic favors two multiple change-point models (Fig. 1B): the optimal model with six phases (posterior probability of 0.78) and an alternative model with five phases (posterior probability of 0.22). The optimal segmentations in five and six phases are nested with a supplementary limit between days 113 and 119 in the case of six phases. This can be explained by a not too abrupt decrease of the flower production at the end of the first flowering flush. The segmentations are non-ambiguous with very high associated posterior probabilities (0.99 and 0.91 to be related to 14 950 and 65 780 possible segmentations for five and six phases, respectively). The limits between flowering phases are consistent with abrupt changes of flower production with time for all the individuals (see the heat map in Fig. 1A). The piecewise constant functions corresponding to the successive mean numbers of weekly emerged flowers within each of the six or five phases are consistent with the weekly average numbers of emerged flowers extracted from data (Fig. 1B).

Fig. 1.

Flowering phases identified for Gariguette using univariate categorical multiple change-point models. (A) Heat map of the series of flower production, with the tint scale ranging from light (low intensity) to dark tint (high intensity). Flowering phases are delimited by solid and dashed black lines. Solid black lines represent limits between phases common to the optimal six-phase and alternative five-phase segmentations, and the dashed black line represents the additional limit between phases of the optimal segmentation. (B) The segmentations in phases are represented as piecewise constant functions (solid black lines for the optimal six-phase segmentation and dashed black lines for the alternative five-phase segmentation), with the level of each phase corresponding to the mean number of weekly emerged flowers in the phase. The weekly mean numbers of emerged flowers are represented by red points connected by lines and the associated SDs by dashed red lines. (This figure is available in color at JXB online.)

Results

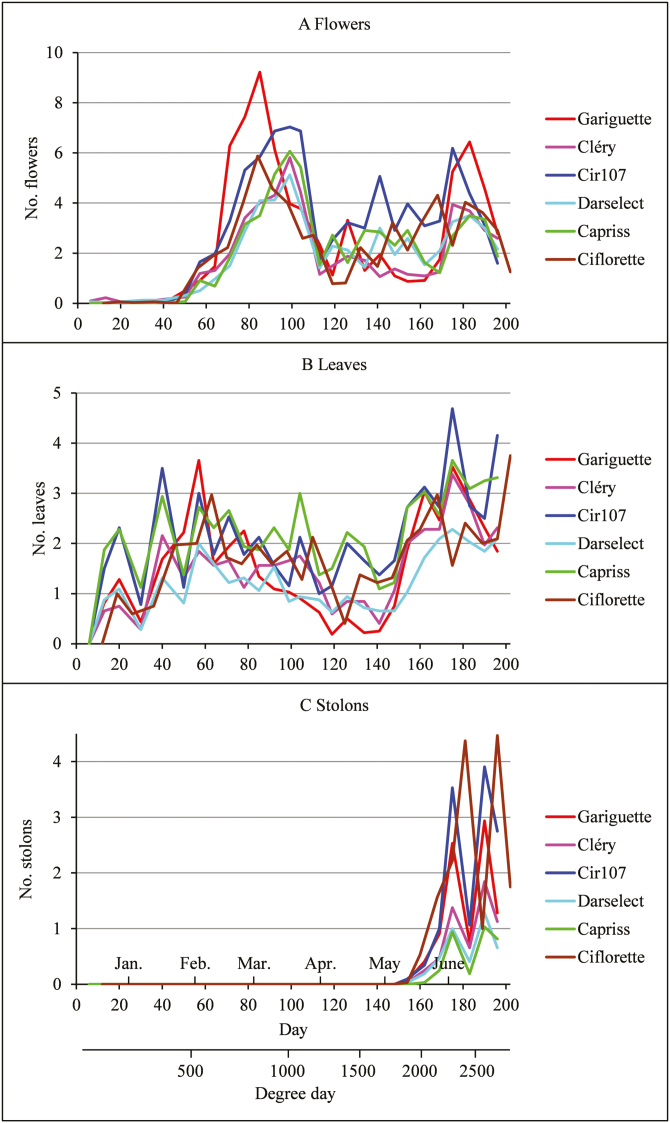
The weekly mean numbers of emerged organs computed for each genotype highlight phenological phases especially for the flowers (see the flowering flush in February–March in Fig. 2A) and stolons (see the runnering flush starting in May in Fig. 2C). We assumed that the flowering, vegetative development (Fig. 2B), and runnering patterns were common to all the 32 individuals of a given genotype and that these patterns took the form of a succession of stationary well-differentiated phases. The analysis of these developmental patterns broke down into two steps. (i) Identification of flowering, vegetative development, or runnering phases, synchronous between individuals, for each genotype; see illustrations in Fig. 1, and Supplementary Figs S2 and S3. We focused in particular on the selection of the number of phases and on the assessment of the synchronous segmentation assumption. (ii) Comparison of the flowering, vegetative development, or runnering patterns between genotypes in order to identify commonalities and differences between genotypes.

Fig. 2.

Weekly mean numbers of emerged (A) flowers, (B) leaves, and (C) stolons for the six genotypes. The time indexing is given both in days after plantation with corresponding months and in cumulative degree-days, these two time indexing being valid for all the genotypes except Ciflorette. (This figure is available in color at JXB online.)

Validation of the assumption of a succession of phenological phases synchronous between individuals

The selection of the number of phenological phases is unambiguous in 11 cases among 18 with high posterior probabilities of the multiple change-point models selected by the slope heuristic (Tables 1–3 for flowering, vegetative development, and runnering, respectively). In the case of a well-supported alternative model (in terms of posterior probability of the multiple change-point model) always with one more or one less phase, the corresponding optimal segmentation is nested (i.e. all the limits except one are common to the two segmentations) or almost nested (i.e. for some limits there is only an overlap between the two credibility intervals). The former case concerns the flowering phases of Gariguette (Table 1), the vegetative development phases of Cléry, Cir107, and Darselect (Table 2), and the runnering phases of Cléry (Table 3), while the latter case only concerns the runnering phases of Darselect and Capriss (Table 3).

Table 1.

Flowering phases identified using univariate categorical multiple change-point models

	Phase	Limit	Phase	Limit	Phase	Limit	Phase	Limit	Phase	Limit	Phase	No. of phases	Posterior probability
													Segment	Model
Gariguette	0, 0	50	0.96, 1.01	71	7.27, 3.57	99			2.04, 2.72	175	4.76, 4.23	5*	0.99	0.22
		(50, 50)	32%	(71, 71)	28%	(99, 99)			7%	(175, 175)	19%
Gariguette	0, 0	50	0.96, 1.01	71	7.27, 3.57	99	3.36, 3.39	119	1.54, 2.24	175	4.76, 4.23	6	0.91	0.78
		(50, 50)	32%	(71, 71)	28%	(99, 99)	23%	(113, 119)	15%	(175, 175)	19%
Cléry	0.14, 0.44	57	1.49, 1.18	78	4.39, 3.24			113	1.35, 2.06	175	3.28, 3.57	5	1	0.9
	34%	(57, 57)	33%	(78, 78)	23%			(113, 113)	11%	(175, 175)	12%
Cir107	0.06, 0.25	57	2.3, 1.83	78	6.39, 3.6			113	3.38, 4.08			4	0.97	0.99
	12%	(57, 57)	32%	(78, 78)	17%			(113, 113)	10%
Darselect	0.17, 0.45	64	1.23, 1.08	78	4.01, 2.74			113	2.33, 2.64			4	0.51	0.99
	28%	(57, 64)	43%	(78, 85)	18%			(113, 113)	7%
Capriss	0.02, 0.14	57	1.14, 1.09	78	4.66, 3.39			113	2.39, 2.98			4	0.99	0.98
	23%	(57, 57)	24%	(78, 78)	16%			(113, 113)	7%
Ciflorette	0.03, 0.24	56	1.83, 1.16	77	4.6, 2.66			105	2.5, 3.26			4	1	1
	58%	(56, 56)	32%	(77, 77)	15%			(105, 105)	5%

For each genotype, the segmentations are presented in two rows as the alternation of phase characteristics (mean and SD of the number of weekly emerged flowers computed from the raw data without grouping in the first row and part of between-individual variance in % in the second row) and limit between phases (limit in the first row and interval with credibility 0.95 for this limit in the second row). The closeness of the limits between phases defines the alignment of this first set of columns describing the segmentations. The number of phases selected by the slope heuristic, the posterior probabilities of the multiple change-point model selected by the slope heuristic, and the optimal segmentation in the corresponding number of phases are given in the last three columns. The ‘*’ indicates a well-supported alternative model in terms of posterior model probability

Table 3.

Runnering phases identified using univariate categorical multiple change-point models

	Phase	Limit	Phase	Limit	Phase	No. of phases	Posterior probability
							Segment	Model
Gariguette	0.003, 0.08			162	1.47 1.78	2	1	0.98
	5%			(162, 162)	19%
Cléry	0.01, 0.27			169	1.09, 1.68	2*	1	0.39
	7%			(169, 169)	44%
Cléry	0, 0	154	0.14, 0.89	169	1.09, 1.68	3	0.32	0.52
		(119, 169)	84%	(169, 175)	44%
Cir107	0.004, 0.09	162	0.67, 1.13	175	2.81, 2.44	3	0.62	0.93
	4%	(154, 162)	65%	(169, 190)	35%
Darselect	0.001, 0.04			162	0.67, 1.24	2	0.99	0.6
	5%			(162, 162)	46%
Darselect	0, 0	154	0.11, 0.44	169	0.76, 1.31	3*	0.64	0.4
		(134, 162)	67%	(162, 190)	53%
Capriss	0.001, 0.04			169	0.64, 1.26	2	0.76	0.82
	4%			(169, 175)	33%
Capriss	0, 0	162	0.14, 0.64	175	0.74, 1.32	3*	0.62	0.18
		(141, 169)	73%	(175, 190)	37%
Ciflorette	0.002, 0.04			160	2.27, 2.43	2	0.97	0.99
	5%			(160, 168)	23%

For each genotype, the segmentations are presented in two rows as the alternation of phase characteristics (mean and SD of the number of weekly emerged stolons computed from the raw data without grouping in the first row and part of between-individual variance in % in the second row) and limit between phases (limit in the first row and interval with credibility 0.95 for this limit in the second row). The closeness of the limits between phases defines the alignment of this first set of columns describing the segmentations. The number of phases selected by the slope heuristic, the posterior probabilities of the multiple change-point model selected by the slope heuristic, and the optimal segmentation in the corresponding number of phases are given in the last three columns. The ‘*’ indicates a well-supported alternative model in terms of posterior model probability

Table 2.

Vegetative development phases identified using univariate categorical multiple change-point models

	Phase	Limit	Phase	Limit	Phase	Limit	Phase	No. of phases	Posterior probability
									Segment	Model
Gariguette	0.63, 1.06	40	2.1, 1.51	92	0.62, 0.79	154	2.56, 1.57	4	0.86	1
	7%	(40, 40)	12%	(92, 99)	10%	(154, 154)	18%
Cléry			1.14, 1.24			154	2.43, 1.79	2*	1	0.17
			6%			(154, 154)	28%
Cléry	0.42, 0.72	40	1.32, 1.27			154	2.43, 1.79	3	1	0.53
	11%	(40, 40)	9%			(154, 154)	28%
Cléry	0.42, 0.72	40	1.62, 1.35	113	0.83, 0.94	154	2.43, 1.79	4*	0.65	0.29
	11%	(40, 40)	12%	(113, 119)	14%	(154, 154)	28%
Cir107			1.71, 1.54			154	3.24, 1.93	2	0.99	0.82
			5%			(154, 154)	24%
Cir107	0, 0	13	1.8, 1.53			154	3.24, 1.93	3*	0.97	0.18
		(13, 13)	6%			(154, 162)	24%
Darselect			0.97, 1.02			162	2.01, 1.45	2*	1	0.24
			5%			(162, 162)	33%
Darselect	0, 0	13	1.02, 1.02			162	2.01, 1.45	3	1	0.76
		(13, 13)	6%			(162, 162)	33%
Capriss			2.19, 1.69					1*	1	0.002
			9%
Capriss	0, 0	13	2.28, 1.67					2	1	0.97
		(13, 13)	10%
Ciflorette			1.7, 1.46					1	1	0.99
			4%

For each genotype, the segmentations are presented in two rows as the alternation of phase characteristics (mean and SD of the number of weekly emerged leaves computed from the raw data without grouping in the first row and part of between-individual variance in % in the second row) and limit between phases (limit in the first row and interval with credibility 0.95 for this limit in the second row). The closeness of the limits between phases defines the alignment of this first set of columns describing the segmentations. The number of phases selected by the slope heuristic, the posterior probabilities of the multiple change-point model selected by the slope heuristic, and the optimal segmentation in the corresponding number of phases are given in the last three columns. The ‘*’ indicates a well-supported alternative model in terms of posterior model probability (except for Capriss for which the optimal segmentation contains a very short first phase consisting of a single date of measurement)

The posterior probabilities of the optimal segmentation are always high (to be related to the number of possible segmentations which is, 26 for two phases, 325 for three phases, 2600 for four phases, 14 950 for five phases, and 65 780 for six phases) and the credibility intervals for the limits between phases are narrow (and often restricted to a single date for 18 limits among 21 for the flowering phases, all the nine limits for the vegetative development phases, and two limits among eight for the runnering phases; Tables 1–3). We will thus only consider the optimal segmentation in the selected number of phases, and expressions such as ‘the optimal/alternative four-phase segmentation’ will be used as a shortcut for ‘the optimal segmentation of the optimal/alternative four-phase model’ in the remainder of this article.

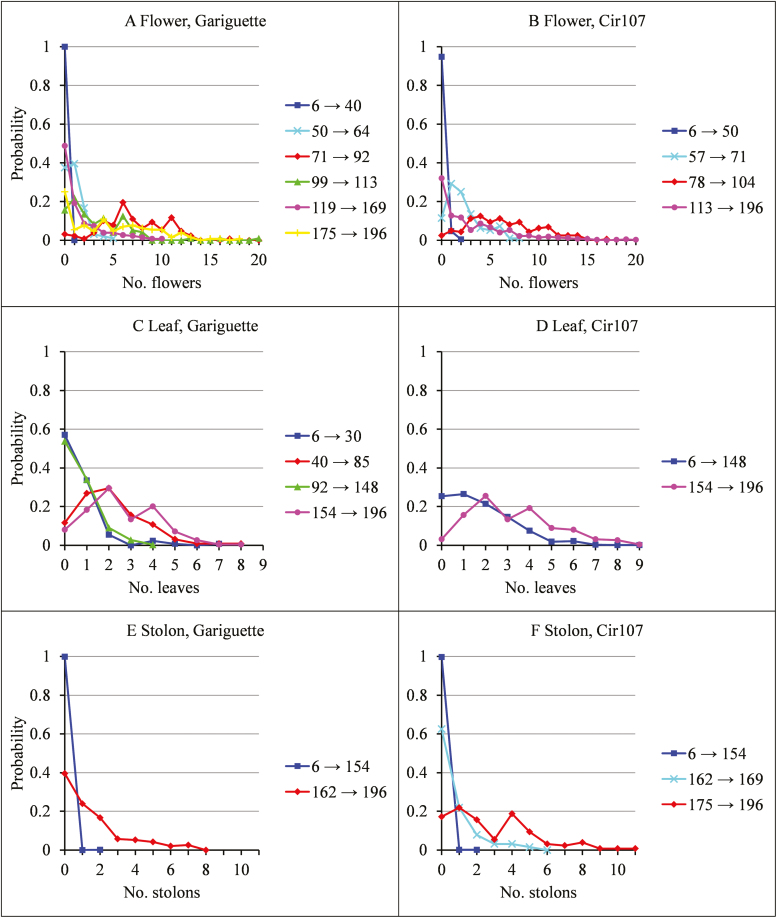
The distributions of the number of weekly emerged flowers, leaves, and stolons for consecutives phases are well differentiated; see summaries in Tables 1–3 and illustrations for two genotypes, Gariguette (Fig. 3A, C, E for flowers, leaves, and stolons, respectively) and Cir107 (Fig. 3B, D, F for flowers, leaves, and stolons, respectively). This is consistent with the segmentation assumption. These distributions are right skewed with various shapes often far from Poisson and negative binomial distribution shapes, some of them being zero inflated. This a posteriori justifies the direct modeling of probability masses for each organ count value appropriately aggregated. The piecewise constant functions deduced from the segmentations often show jumps of high amplitude for the mean number of weekly emerged organs at the limit between phases (Fig. 4A, B, C for flowers, leaves and stolons, respectively). It should be noted that these piecewise constant functions, while illustrative, only constitute a partial summary of the segmentations since the within-phase frequency distributions are always right skewed and often zero inflated and thus far from Gaussian distributions (Fig. 3).

Fig. 3.

Distributions of (A, B) the number of weekly emerged flowers for each successive flowering phase, (C, D) the number of weekly emerged leaves for each successive vegetative development phase, and (E, F) the number of weekly emerged stolons for each successive runnering phase for Gariguette (A, C, E) and Cir107 (B, D, F). The phenological phases are defined by their limits in days after plantation in (A–D). (This figure is available in color at JXB online.)

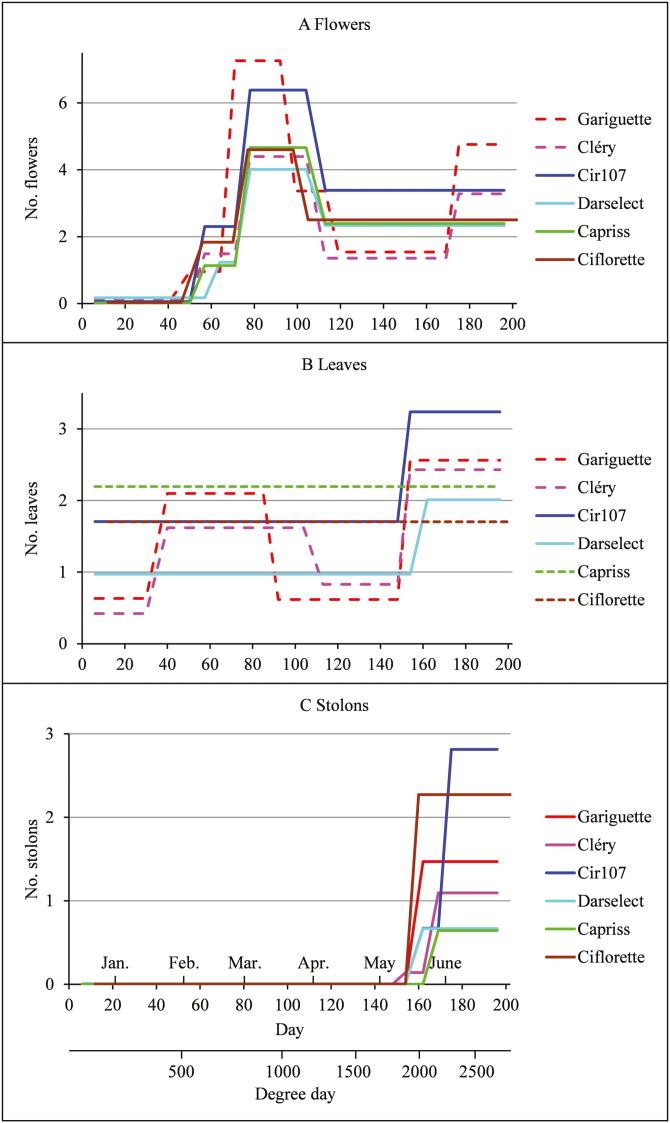
Fig. 4.

(A) Flowering, (B) vegetative development, and (C) runnering phases identified for the six genotypes. The successive phases are represented as piecewise constant functions, with the level of each phase corresponding to the mean number of weekly emerged organs within the corresponding phase. The time indexing is given both in days after plantation with corresponding months and in cumulative degree-days, these two time indexing being valid for all the genotypes except Ciflorette. The piecewise constant functions corresponding to one flush are represented by solid lines, to two flushes by dashed lines, and to no flush by a dotted line. (This figure is available in color at JXB online.)

In order to validate the assumption of phenological phases synchronous between individuals, a HSMC was built for each development process and each genotype. The number of states of the HSMC was the number of phases of the optimal multiple change-point model selected by the slope heuristic. The only exception was the vegetative development for Darselect for which the first phase consisting of a single date could not be modeled using HSMCs and a two-state HSMC corresponding to a well-supported alternative multiple change-point model (Table 2) was thus built. We then assessed the degree of synchronicity of the phenological phases between individuals from the asynchronous segmentation of individuals in phases made using the estimated HSMC. The frequency distributions of the limits between phases are often concentrated on the limit identified with the multiple change-point models and the immediately neighboring measurement dates (Supplementary Tables S2–S4). The mode of the frequency distribution is the limit identified by the multiple change-point models for 20 limits among 21 for the flowering phases, for four limits among eight for the vegetative development phases, but for any of the eight limits for the runnering phases. The differences found for runnering phases can be explained by the asynchronous beginning of stolon production between individuals also reflected in the high percentage (between 65% and 84%) of between-individual heterogeneity in the phase of low stolon production (second phase) preceding the phase of high stolon production (third phase) for Cléry, Cir107, Darselect, and Capriss (Table 3).

Flowering process

Four (Cir107, Darselect, Capriss, and Ciflorette), five (Cléry), or six flowering phases (Gariguette) (Table 1; Fig. 4A) were identified on the basis of the univariate series of flower production. All the genotypes present a common first flush from the end of January to the end of March (between 50 d and 99 d after plantation corresponding to 486 and 1030 GDD, respectively) with a short phase between the end of January and mid-February (71 d after plantation at 789 GDD) between the initial non-flowering phase and the phase corresponding to the peak of flower production of the first flush (Fig. 4A). It is explained in part by the asynchronous increase of flowering for the different individuals of a genotype (percentage of between-individual heterogeneity between 24% and 43% for the different genotypes; see Table 1). The first flush differs between genotypes essentially by the production level of its peak (i.e. third phase), Gariguette having the highest production level, followed by Cir107, and the four other genotypes having relatively similar production levels. Gariguette, which shows the highest peak of flower production for the first flush, also has a short phase intermediate between this peak and the phase of lower flower production. This phase is less well defined since, in the well-supported alternative model with one less phase (posterior probability of 0.22 for the five-phase model instead of 0.78 for the optimal six-phase model), it is merged with the following phase of lower flower production.

The main differences between genotypes concern (i) the occurrence of a second flowering flush from the end of May (175 d after plantation at 2288 GDD) until the end of the experiment for Gariguette and Cléry; (ii) the higher flower production in the flushes for Gariguette and Cir107; and (iii) for the four genotypes without a second flush, the higher flower production for Cir107 (Table 1; Fig. 4A). The six genotypes can thus be grouped according to their flowering pattern in the following way: (i) Gariguette and Cléry with two flowering flushes separated by a phase of lower flower production (Fig. 4A); and (ii) Cir107, Darselect, Capriss, and Ciflorette with a single flowering flush followed by a phase of lower flower production starting in early April (113 d after plantation at 1209 GDD) (Fig. 4A). Within these two patterns, differences of flower production are observed, with a higher flower production within the two flushes for Gariguette compared with Cléry, and a higher flower production for Cir107 compared with Darselect, Capriss, and Ciflorette.

Vegetative development process

One (Ciflorette), two (Cir107 and Capriss), three (Darselect and Cléry), or four vegetative development phases (Gariguette) (Table 2; Fig. 4B) were identified in the univariate series of leaf production. Two alternative models are well supported for Cléry (posterior probabilities of 0.29 for the four-phase model and 0.17 for the two-phase model instead of 0.53 for the optimal three-phase model) and one alternative model for Cir107 (posterior probability of 0.18 for the three-phase model instead of 0.82 for the optimal two-phase model) and Darselect (posterior probability of 0.24 for the two-phase model instead of 0.76 for the optimal three-phase model). The optimal and alternative segmentations are always nested. The optimal segmentation incorporates a very short first phase consisting of a single date of measurement for Darselect and Capriss (Table 2). We did not consider that this first phase represents a biologically meaningful phenomenon and thus chose to merge it with the following phase for further analyses. This corresponds to a well-supported alternative model for Darselect but not for Capriss. For Cléry, we consider both the well-supported alternative two-phase and four-phase models in order to facilitate the comparison between genotypes.

For genotypes without a vegetative flush (Fig. 4B), the leaf production was higher for Capriss than for Ciflorette. For genotypes with at least one vegetative flush (Fig. 4B), all the four genotypes (Gariguette, Cléry, Cir107, and Darselect) show a common flush from early May (154–162 d after plantation at 1903–2039 GDD) until the end of the experiment. This flush differs between genotypes by its leaf production, which is higher for Cir107, intermediate for Gariguette and Cléry, and lower for Darselect. Gariguette and the alternative four-phase segmentation of Cléry are characterized by an additional first vegetative flush starting in mid-January (40 d after plantation at 397 GDD) and ending in mid-March (92 d after plantation at 944 GDD) for Gariguette and early April (113 d after plantation at 1209 GDD) for Cléry, with the leaf production during this flush being higher for Gariguette than for Cléry. In contrast, Cir107, Darselect, and the alternative two-phase segmentation of Cléry are characterized by an initial phase of low leaf production from early December to the end of April, with a higher leaf production for Cir107.

The main differences between genotypes concern (i) the number of vegetative development flushes (zero for Capriss and Ciflorette, one for Cir107, Darselect, and the alternative two-phase model of Cléry, or two flushes for Gariguette and the alternative four-phase model of Cléry); and (ii) the leaf production which is higher for Capriss compared with Ciflorette and for Cir107 compared with Darselect and the alternative two-phase model of Cléry (Fig. 4B). The genotypes can thus be grouped according to their vegetative development pattern in the following way (Fig. 4B): (i) Capriss and Ciflorette without a vegetative development flush; (ii) Darselect and Cir107 with a single flush starting in early May; and (iii) Gariguette with two flushes, Cléry being intermediate between Cir107/Darselect and Gariguette. However, because the alternative four-phase model is better supported than the alternative two-phase model, we chose to group Cléry with Gariguette.

Runnering process

Two (Gariguette, Darselect, Capriss, and Ciflorette) or three runnering phases (Cléry and Cir107) were identified in the univariate series of stolon production (Table 3; Fig. 4C). An alternative three-phase model is well supported for Darselect (posterior probability of 0.4 instead of 0.6 for the optimal two-phase model) and Capriss (posterior probability of 0.18 instead of 0.82 for the optimal two-phase model), and an alternative two-phase model is well supported for Cléry (posterior probability of 0.39 instead 0.52 for the optimal three-phase model). In contrast to the flowering and vegetative development processes, the assumption of phases synchronous between individuals is less well supported in the case of the runnering processes. This is illustrated by (i) the non-nested optimal and alternative segmentations for Darselect and Capriss; (ii) the credibility interval for the limits between phases often not restricted to a single date and sometimes large; (iii) the high between-individual heterogeneity in the phase of low stolon production (second phase) preceding the phase of high stolon production (third phase) for Cléry, Cir107, Darselect, and Capriss (Table 3); and (iv) the difference between the limits obtained by the synchronous and the asynchronous segmentations of individuals (Supplementary Table S4).

All the genotypes present a flush of stolon production from May (162–175 d after plantation at 2039–2288 GDD) until the end of the experiment. The main differences between genotypes concern: (i) the beginning of the flush with a maximum difference of 2 weeks between genotypes (corresponding to 249 GDD); (ii) the presence or not of a short intermediate phase between the phase of non-stolon production and the phase of high stolon production; and (iii) the level of stolon production in the last phase (Table 3; Fig. 4C), with Cir107 having the highest stolon production followed by Ciflorette, Gariguette, and Cléry, and Capriss and Ciflorette having the lowest stolon production. In summary, a single runnering pattern (Fig. 4C) was identified for all the genotypes with a single flush of stolon production which began late in seasonal production. This pattern differs mainly between genotypes by the level of stolon production.

Fluctuations of organ production synchronous between individuals

The production of flowers, leaves, and stolons was affected by marked fluctuations synchronous between individuals during the observation period (Fig. 2). We thus investigated these fluctuations of organ production by first-order differencing the observed series of the number of weekly emerged flowers, leaves, and stolons (Chatfield 2003). The weekly mean first-order differenced series (Supplementary Fig. S4) show numerous deviations from 0, either positive (corresponding to an increase in organ production between two weeks) or negative (corresponding to a decrease in organ production between two weeks). Some of them can be explained by jumps of organ production corresponding to limits between phenological phases (see Tables 1–3), while the others correspond to synchronous fluctuations of organ production between individuals probably due to change in the environmental conditions.

Joint analysis of the flowering, vegetative growth, and runnering processes and typology of the strawberry genotypes

In order to summarize for each genotype the different phases of plant development based on the three development processes, we jointly analyzed the flowering, vegetative development, and runnering processes using trivariate multiple change-points models. These trivariate multiple change-point models highlighted the changes of highest amplitudes for one or several of the three processes (assuming in this latter case that they were synchronous); see Table 4; Fig. 5.

Table 4.

Consensus phases identified using trivariate categorical multiple change point models

	Limits between phases				No. of phases	Posterior probability
						Segment	Model
Gariguette	50, F	71, F	99, F, V	162, R	5	0.98	1
	(50, 50)	(71, 71)	(99, 99)	(162, 162)
Cléry	57, F			169, V, R	3	0.44	0.86
	(57, 57)			(154, 169)
Cléry	57, F		113, F, V	162, R	4*	0.6	0.14
	(57, 57)		(113, 113)	(162, 169)
Cir107	57, F			162, R	3	1	1
	(57, 57)			(162, 162)
Darselect	64, F			162, V, R	3	0.9	1
	(64, 71)			(162, 162)
Capriss	57, F			162, R	3	0.82	1
	(57, 57)			(162, 169)
Ciflorette	56, F			160, R	3	1	1
	(56, 56)			(160, 160)

For each genotype, the limits between phases are presented in two rows [limit in the first row followed by F for flowering, V for vegetative development, and R for runnering if the limit corresponds to a limit identified in the univariate series (the letter is in italics if the limit only falls in the interval with credibility 0.95 or is only identified in a well-supported alternative model) and credibility interval for this limit in the second row]. The closeness of the limits between phases defines the alignment of this first set of columns describing these limits. The number of phases selected by the slope heuristic, the posterior probabilities of the multiple change-point model selected by the slope heuristic, and the optimal segmentation in the corresponding number of phases are given in the last three columns. The ‘*’ indicates a well-supported alternative model in terms of posterior model probability.

Fig. 5.

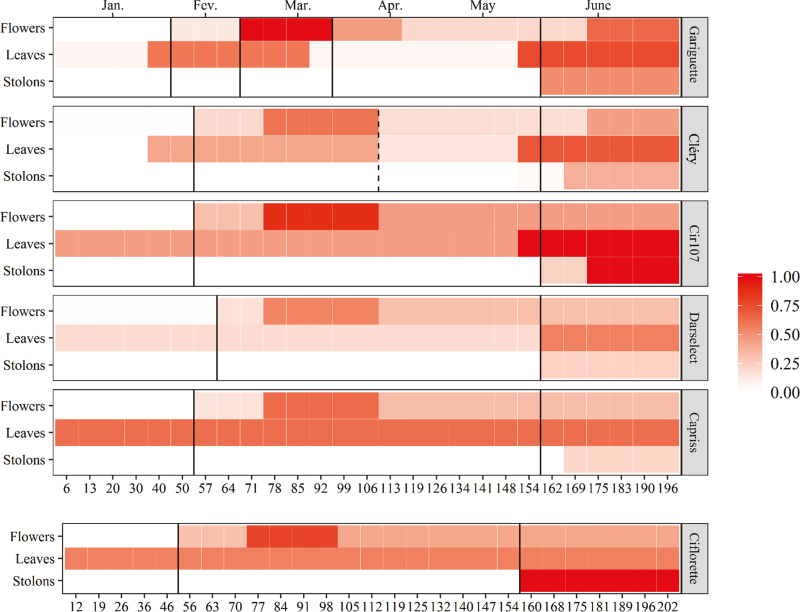
Heat map representation of flowering, vegetative development, and runnering patterns for the six genotypes. The tint scale represents the intensity of each phase normalized by the maximal intensity of each development process (flowering, vegetative development, and runnering processes) for all the genotypes. Vertical black lines represent the consensus limits identified using the optimal trivariate multiple change-point models and the dashed black line represents the supplementary limit between consensus phases identified in the Cléry alternative four-phase segmentation. (This figure is available in color at JXB online.)

For all the genotypes, the first consensus limit between phases corresponds to the beginning of the first flowering flush (i.e. the beginning of the first low flower production phase within this flush), except for Darselect (beginning of the second high flower production phase within this flush) (Table 4; Fig. 5). For Gariguette and Cléry (using the alternative well-supported model in this case), additional consensus limits were identified within the second flowering flush: at the beginning of the second high flower production phase for Gariguette and at the end of this phase for the two genotypes. For all the genotypes, the last consensus limit corresponds to the beginning of the runnering flush. This limit is also explained by the beginning of a vegetative flush for Cléry and Darselect. The non-detection of some limits identified using univariate models (in particular between vegetative phases) can be explained by the lower amplitude of the jumps between successive phases.

Three consensus phases were identified at a macroscopic scale (Fig. 5): a first consensus phase corresponding to a vegetative phase; a second consensus phase beginning with the first flowering flush and ending just before the runnering flush; and a third consensus phase corresponding to the runnering flush. This third phase is roughly concomitant with the vegetative flush at the end of seasonal production for all the genotypes except Capriss and Ciflorette and with the second flowering flush for Gariguette and Cléry (Fig. 5). These results show that the developmental pattern of strawberry is mainly structured by the flowering and runnering processes and suggest different hierarchies between the three development processes during plant development.

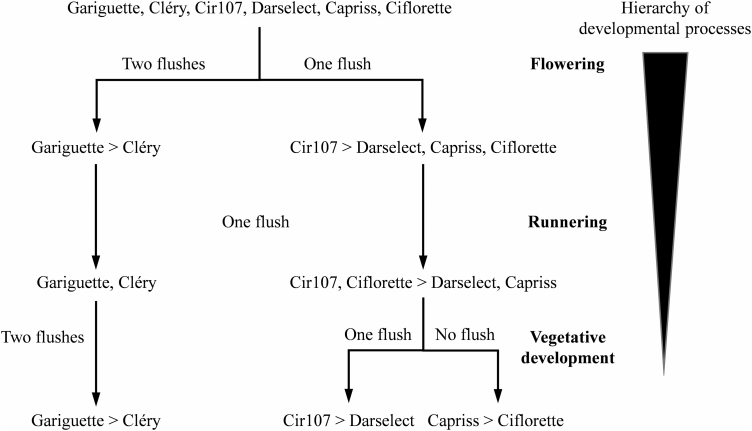
Univariate multiple change-point models highlighted marked differences in flowering, vegetative development, and runnering patterns among the six strawberry genotypes. On this basis, we were able to classify these genotypes hierarchically according to their developmental patterns with primarily one or two flushes of flowering, secondarily a single flush of runnering occurring at the end of the observation period, and zero, one or two flushes of vegetative development, with these flushes being of varying intensity (Fig. 6).

Fig. 6.

Developmental patterns of strawberry genotypes summarized as a hierarchy of development processes. Development processes ordered from the most to the least discriminant; that is, flowering, runnering, then vegetative development are used to hierarchically partition the six genotypes on the basis of the number of flushes for each development process. The genotypes within each group of a partition are ordered according to the number of weekly emerged organs within the phases.

Discussion

Flowering is the main development process for characterizing genotypes

Extension of flowering through neoformation of floral buds

All the genotypes display a first flush of flowering lasting almost 2 months (Fig. 4A). This flush is the consequence of the floral initiation that took place in preformed buds (Barthélémy and Caraglio, 2007) during the previous autumn when temperatures and day length decreased (reviewed in Heide et al., 2013). Usually, this first flowering flush derives from three well-differentiated inflorescences (Bosc et al., 2012; Massetani and Neri, 2016), which each end a primary or a secondary axis. After this first flush, environmental conditions are still favorable for floral initiation, without an intervening dormancy period, and the resulting flower buds are termed neoformed (Puntieri et al., 2002). In our culture conditions of a forced soilless culture system, environmental conditions are still inductive until the beginning of April (in our conditions, 12.7 °C with a 12.45 h photoperiod reported as inducible conditions by Ito and Saito, 1962; Heide, 1977; Heide et al., 2013). To gain a better understanding of the preformation of flower buds (corresponding to organs present in plants at the beginning of the experiment), and neoformation of flower buds, a detailed spatio-temporal architectural analysis (Savini et al., 2005; Massetani et al., 2011) should be conducted.

Flowering intensity

Differences between genotypes in production level of the flowering phases (Table 1; Fig. 4A) could be due to the complexity of inflorescences in terms of number of flowers (Darrow, 1929; Battey et al., 1998). As an illustration, the first inflorescence of Elsanta can produce a maximum of 15 flowers (Battey et al., 1998), while this can reach 30 for Gariguette, well known for its first inflorescence complexity (M.N. Demené, personal communication). Once the apical dominance has been released, development of branch crowns, by sympodial or lateral branching, can occur (Husaini and Neri, 2016). As branch crowns are terminated by inflorescences, the number of branch crowns is intrinsically linked to the number of inflorescences (Hytönen et al., 2004; Tenreira et al., 2017) and consequently is correlated with the number of flowers as shown in our study for most of the genotypes (Supplementary Table S1). This trait could be triggered by the time of the apical dominance release or by the strength of this dominance (Sugiyama et al., 2004).

Flowering earliness

In plants, variations in temperature and light intensity during the floral inductive period for flower bud initiation could explain between-year variations in flowering time (Poethig, 2003). In strawberry, earlier floral initiation in preformed buds in autumn is favored by lower temperatures or lower light intensities than usual but also by a genetic background with genotypes more receptive to environment flowering signals (Opstad et al., 2011). This earliness will lead to a more differentiated terminal inflorescence before dormancy, which will emerge earlier than those issued from late floral initiation (Heide et al., 2013) such as illustrated by Gariguette (Supplementary Table S1) which flowered earlier than the other genotypes (Fig. 4A).

After dormancy, temperature is the main factor for organogenesis of inflorescences and flowers (Massetani et al., 2011), and thermal time could be used to relate flowering occurrence to temperature under a wide range of environmental conditions (e.g. Opstad et al., 2011). In strawberry, constant base temperature for calculation of cumulative GDD for thermal time models differed according to the process (Bethere et al., 2016) and for a single process according to the study (e.g. for flowering Opstad et al., 2011; Bethere et al., 2016). A constant base temperature of 0 °C was used in several analyses for both leaf appearance (Rosa et al., 2011) and flowering (Opstad et al., 2011; Bethere et al., 2016) and we chose to use this base temperature in our study. The use of a thermal time indexing will allow comparison of our results with other experiments regarding the effect of temperature on the duration and production level of the different phenological phases.

In our experiment, differences in timing of floral initiation with consequences on flowering time (Fig. 4A) were due to genotype (Sønsteby, 1997; Opstad et al., 2011) and therefore linked to genetic background. This genetic background could involve allelic differences in the flowering time molecular gene network such as the FT/TFL1 family (Iwata et al., 2012; Koskela et al., 2016). This genetic background can be studied by analyzing simultaneously the temporal expression of these genes and the developmental stages of flower buds (Hyun et al., 2019).

Balance between vegetative development including runnering and flowering

The flowering and runnering processes are the main determinants of the phenological phases observed in this study (Fig. 5). They are also the two reproduction processes (sexual for flowering and vegetative for runnering; Heide et al., 2013). For each crown, leaves are produced sequentially by the terminal meristem while the terminal inflorescence results from the transformation of this meristem (Savini et al., 2005). Stolons are produced by the lateral meristem in specific environmental conditions (high temperatures and long photoperiod; Heide et al., 2013). The production of leaves is thus far less constrained over time than the production of inflorescences or stolons which corresponds to specific organogenesis events or environmental conditions. This could explain why vegetative development appears more regular than flowering and runnering which show changes of higher amplitudes between phases (Fig. 4). A temporal analysis of plant architecture development, namely of the timing and positioning of the vegetative and reproductive development along the axes, would allow identification of the underlying spatio-temporal developmental rules (Massetani et al., 2011).

Multiple change-point models for identifying phases in plant growth and development

HSMCs are more general than multiple change-point models in terms of modeling assumptions, with the capability to represent phases asynchronous between individuals. This is counterbalanced in multiple change-point models by the possibility to model very short phases but also by the availability of methods with a strong mathematical basis for selecting the number of phases. Moreover, discrepancies from the multiple change-point model assumption of phases synchronous between individuals are easily detected using credibility intervals for the limits between phases and parts of between-individual variance within phases.

We introduced multivariate multiple change-point models in order to summarize the flowering, vegetative development, and runnering processes. If the assumption of well-differentiated stationary phases is reasonably valid in the univariate case, it is far less in the multivariate case where the numbers of weekly emerged flowers, leaves, and stolons are integrated in multiple change-point models as three observed variables. We indeed did not expect systematic synchronous changes of these three variables. However, the model behavior is a bit more subtle since a change of high amplitude on a single variable may be sufficient to define a limit between phases. This was illustrated in particular by the stolons for which the well-defined runnering phase was detected for the six genotypes even if we incorporate the flower and leaf variables. We thus exploited this behavior in the meta-analysis combining univariate and multivariate multiple change-point models to help in defining a hierarchy between the different phenological phases identified for each organ using the univariate multiple change-point models. In our study, results of this meta-analysis showed a hierarchy between the three development processes, with first flowering, then runnering, and finally vegetative development.

We here focus on count data corresponding to the number of newly emerged organs which are critical for studying development processes. However, the proposed approach can be directly transposed to interval-scale variables (e.g. change in dimension corresponding to growth variable) as illustrated in Guédon et al. (2007) by the identification of growth phases in forest trees using Gaussian multiple change-point models. Development and growth variables can thus easily be combined in multivariate multiple change-point models, opening up the way for more integrative studies of plant growth and development.

Conclusion

Our results provide evidence that a longitudinal data analysis, based on multiple change-point models, enables the deciphering of complex dynamic developmental traits such as flowering and vegetative development. These results lay the foundation for more efficient breeding of new strawberry varieties by characterizing their developmental patterns. In addition, the identification of phenological phases contributes to advancing our understanding of flowering, vegetative development, and runnering in strawberry.

Supplementary data

Supplementary data are available at JXB online.

Fig. S1. Design of the randomized block experiment.

Fig. S2. Vegetative development phases identified for Gariguette using univariate categorical multiple change-point models.

Fig. S3. Runnering phases identified for Gariguette using univariate categorical multiple change-point models.

Fig. S4. Weekly means with associated confidence intervals computed from the first-order differenced series of the numbers of weekly emerged flowers, leaves, and stolons for all the genotypes except Ciflorette.

Table S1. Cumulative number of flowers, leaves, crowns, and stolons produced per plant during the observation period, Spearman rank correlation coefficient between the cumulative number of flowers and the cumulative number of crowns, chilling requirement, and flowering earlinessfor the six genotypes

Table S2. Frequency distributions of the limits between phases computed from the segmentation, asynchronous between individuals, of the series of flower production using hidden semi-Markov chains.

Table S3. Frequency distributions of the limits between phases computed from the segmentation, asynchronous between individuals, of the series of leaf production using hidden semi-Markov chains.

Table S4. Frequency distributions of the limits between phases computed from the segmentation, asynchronous between individuals, of the series of stolon production using hidden semi-Markov chains.

Methods S1. Definition of categorical multiple change-point models and associated statistical methods.

Methods S2. Definition of hidden semi-Markov chains and associated statistical methods.