Magnesium flux modulates ribosomes to increase bacterial survival

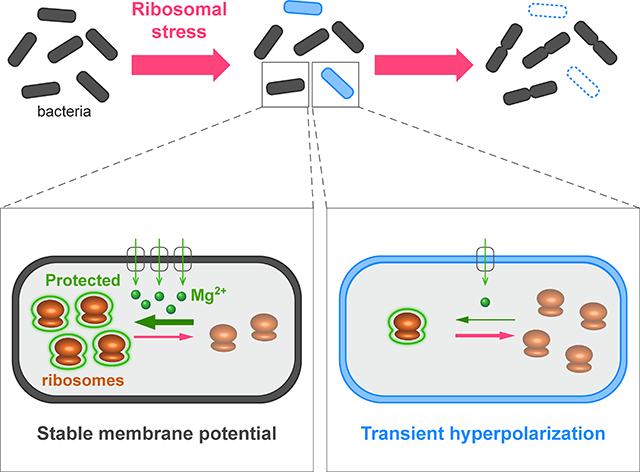
Summary

Bacteria exhibit cell-to-cell variability in their resilience to stress, such as antibiotic exposure. Higher resilience is typically ascribed to “dormant” non-growing cellular states. Here, by measuring membrane potential dynamics of Bacillus subtilis cells, we show that actively growing bacteria can cope with ribosome-targeting antibiotics through an alternative mechanism based on ion flux modulation. Specifically, we observed two types of cellular behavior: Growth defective cells exhibited a mathematically predicted transient increase in membrane potential (hyperpolarization), followed by cell death, while growing cells lacked such hyperpolarization events and showed elevated survival. Using structural perturbations of the ribosome and proteomic analysis, we uncovered that stress resilience arises from magnesium influx, which prevents hyperpolarization. Thus, ion-flux modulation provides a distinct mechanism to cope with ribosomal stress. These results suggest new approaches to increase the effectiveness of ribosome-targeting antibiotics and reveal an intriguing connection between ribosomes and the membrane potential, two fundamental properties of cells.

eTOC blurb

Bacteria cope against ribosome-targeting antibiotics by controlling the influx of intracellular magnesium and controlling their membrane potential.

Graphical Abstract

Introduction

Isogenic bacterial populations can exhibit cell-to-cell variability in their stress response states (Balázsi et al., 2011; Eldar and Elowitz, 2010; Geiler-Samerotte et al., 2013; Reyes and Lahav, 2017; Stecchini et al., 2013). This well-documented heterogeneity has also provided insights into the ability of bacteria to cope with antibiotics. In particular, works by multiple groups have identified a subset of bacterial cells that appear to be in a “dormant” non-growing state, commonly referred to as persister cells, which are more likely to survive exposure to antibiotics (Balaban et al., 2004; Maisonneuve and Gerdes, 2014; Wood et al., 2013). Persisters have since become the focus of many studies aimed at understanding bacterial heterogeneity and its consequences with respect to survival under antibiotic stress (Balaban et al., 2013; Gefen et al., 2008). From these works emerged the understanding that antibiotics targeting active molecular processes in growing cells are less effective against non-growing cells. In other words, if the molecular process affected by the antibiotic is not actively being used by the cell, the antibiotic-mediated inhibition becomes ineffective. The emphasis put on understanding persister cells leaves open the question of whether alternative mechanisms exist through which actively growing cells can cope with antibiotic stress as well.

Various bacterial stress responses have been recently identified through measurement of the cellular membrane potential. For example, monitoring membrane potential dynamics in Escherichia coli cells has shown that the application of mechanical stress (in the form of pressure) increases intracellular calcium levels (Bruni et al., 2017). Furthermore, Bacillus subtilis cells that reside in biofilm communities collectively increase their fitness through potassium ion channel-mediated electrical signaling that enables long-range coordination of metabolic states among cells (Humphries et al., 2017; Larkin et al., 2018; Liu et al., 2015, 2017; Martinez-Corral et al., 2018; Prindle et al., 2015). These studies indicate that bacteria modulate the flux of ions across their cell membrane in response to stress, resulting in changes in the cellular membrane potential. It remains unclear whether bacteria can also modulate ion flux to cope with antibiotic stress.

The regulation of ion flux in bacteria is complicated by the fact that cells discriminate among different inorganic ions that play distinct roles in various intracellular and biochemical processes (Harold, 1977). Inorganic ions can also be toxic at high intracellular concentrations (Banks et al., 2010; Hohle and O’Brian, 2014). For example, while bacterial cells utilize calcium, they maintain a low intracellular concentration of this cation (on the order of 0.1 mM) to avoid toxicity (Gangola and Rosen, 1987). In contrast, diverse biological systems ranging from bacteria to mammalian cells contain around 20 mM magnesium (Romani, 2011), most of which is bound to a variety of physiologically important macromolecular structures such as ribosomes (Klein et al., 2004). Therefore, cells must exert control over their intracellular ion content by modulating ion flux across their membrane. Importantly, cells under conditions of stress may have different requirements for ion content. It is thus not obvious how ion flux, in general, relates to cellular survival under stress conditions. Addressing these fundamental questions requires measurement of ion flux across the cell membrane, which at the single cell-level has remained a technical challenge. Consequently, the single-cell dynamics and cell-to-cell heterogeneity of ion flux is not well characterized in biological systems such as bacteria.

Inorganic ions are also a key determinant of the overall cellular membrane potential, a fundamental physiological feature of all living cells. This electrochemical potential is affected by changes in the net flux of ions across the cellular membrane. The ground-breaking work of Hodgkin and Huxley in the 1950s established a conceptual framework that relates ion flux across the cell membrane to the electrochemical potential of the cell (Hodgkin and Huxley, 1952). Here we utilized such measurement of the cellular membrane potential as a reporter for changes in ion flux across the membrane of undomesticated B. subtilis cells. This approach enabled us to investigate whether individual bacteria differ in their modulation of ion flux, and how the resulting variability in ion content plays a role in the puzzling resilience of bacteria to stress, in particular to stress induced by ribosome-targeting antibiotics.

Results

Single-Cell Level Variability in the Bacterial Membrane Potential

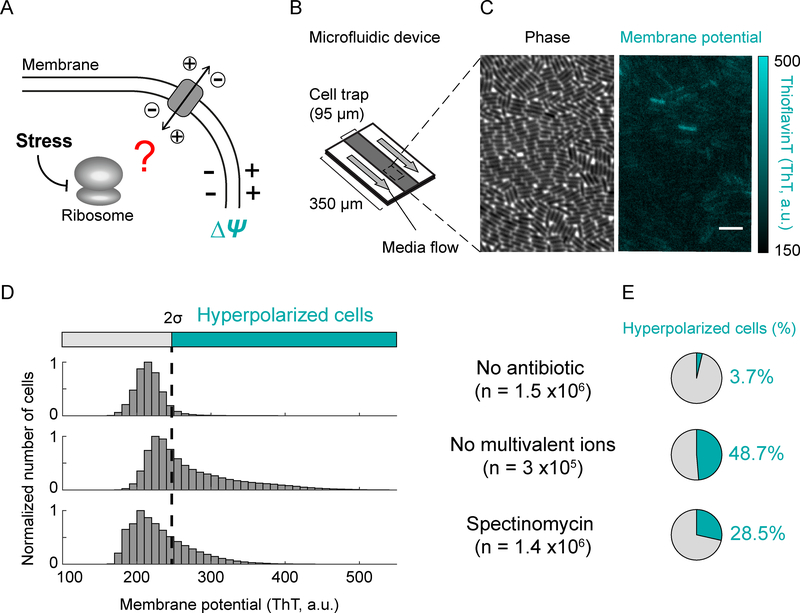
To investigate ion flux in bacteria under ribosomal stress (Figure 1A), we quantitatively measured the membrane potential of individual Bacillus subtilis cells. Specifically, bacteria were grown in minimal defined media (MSgg) inside a microfluidic device (Figure 1B) that provides control over growth media conditions and also enables imaging of individual cells (Figure 1C). We measured membrane potential using a previously characterized fluorescent membrane potential indicator dye, Thioflavin-T (ThT) (Prindle et al., 2015) (Figure 1C). In particular, cells with a more negative (hyperpolarized) membrane potential exhibit a higher fluorescence signal (Figure S1A). We used this experimental approach to first determine the distribution of membrane potential in individual bacteria in the absence of stress. We find that even when no stress is applied, a small percentage of cells (3.68 ± 0.03%, mean ± 95% CI, n= 1.5 × 10⁶) exhibit hyperpolarization (Figures 1D and 1E, top, and S1B–C). Given that the membrane potential directly depends on ion flux, we confirmed that removing extracellular cations in the growth media, which promotes their efflux, increases (thirteen-fold) the fraction of hyperpolarized cells (Figures 1D and 1E, middle). Therefore, perturbing the flux of ions across the cell membrane also quantifiably changes the electrochemical membrane potential in bacteria.

Figure 1.

A fraction of cells exhibits an increase in membrane potential (hyperpolarization).

A) Cartoon illustrating the question of whether the perturbation of ribosomes alters ion flux across the membrane.

B) Schematic of the microfluidic device used in this study. Cells were grown as a single-cell layer under the cell trap with a constant flow of fresh media on both sides of the trap.

C) Phase contrast (left) and corresponding fluorescence (ThT, right) images of cells. The fluorescent dye Thioflavin-T (ThT) reports on the membrane potential. The color bar (right) illustrates the intensity range of ThT-stained cells.

D) Distribution of ThT intensities in a population of cells in the absence of a perturbation (top), in the absence of multivalent ions in the media (middle), or in the presence of sub-lethal doses of spectinomycin (2 mg/L, bottom). The dashed line represents two standard deviations from the mode of the wild-type, which is used as a cutoff to determine the fraction of hyperpolarized cells. ‘n’ represents the number of analyzed cells.

E) Pie charts showing the percentage of hyperpolarized cells from D.

See also Figure S1 and Table S3.

Antibiotic Stress Results in Mathematically Predicted Membrane Potential Hyperpolarization Events

We then focused on the question of whether membrane potential, and thus ion flux, are modulated during stress. Accordingly, we measured the membrane potential in the presence of the antibiotic spectinomycin, which targets the 30S subunit of ribosomes (Carter et al., 2000; Davis, 1987). We used sub-lethal concentrations of spectinomycin (2 mg/L), to minimize off-target effects of antibiotics while still perturbing ribosome function. Our results show that spectinomycin addition increases the fraction of cells that exhibit hyperpolarization by approximately eight-fold (Figures 1D and 1E, bottom, and S1D). Similarly, a four-fold and sixfold increase in the hyperpolarized cell fraction is observed with other ribosome targeting antibiotics, namely kanamycin and chloramphenicol respectively (Figure S1C). Exposing bacteria to sub-lethal concentrations of antibiotics that target ribosomes thus increases the likelihood that bacteria exhibit a more negative membrane potential.

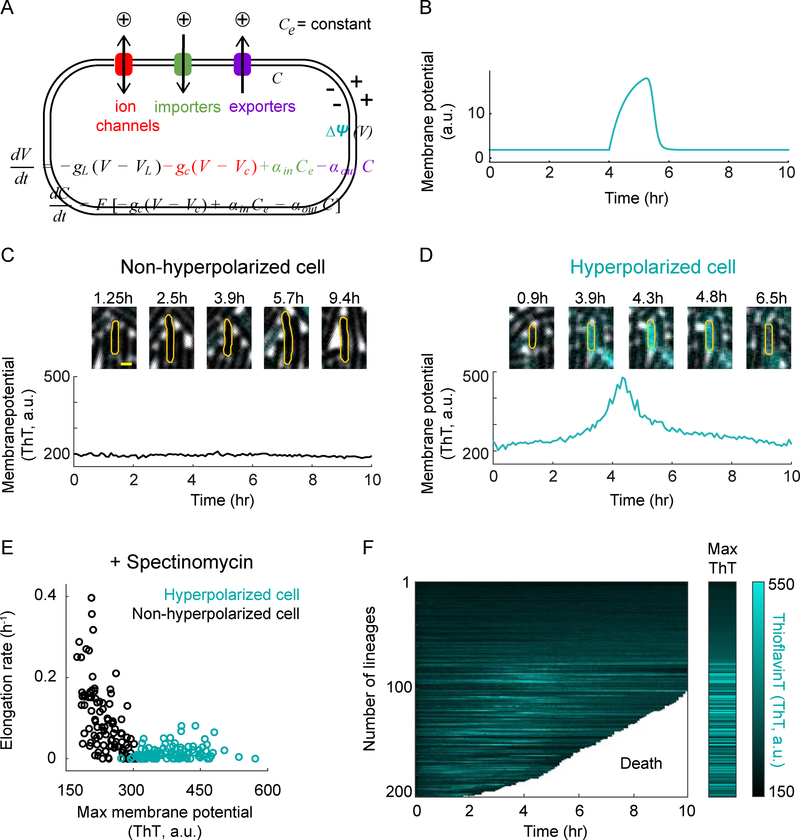
To define the relationship between ion flux modulation and membrane potential dynamics, we constructed a mathematical model inspired by the conceptual framework developed by Hodgkin and Huxley (Figure 2A and see the STAR Methods for details). We used the model to consider cation flux, as the vast majority of inorganic ions in the cell are positively charged and, as shown above, the hyperpolarized cell fraction increases upon removing extracellular cations (Figures 1D and 1E, middle). According to the mathematical model, a change in ion flux that decreases intracellular cation concentration results in a more negative membrane potential. Importantly, the model makes the non-trivial prediction that such hyperpolarization would be transient, rather than permanent (Figure 2B). The transient nature of the hyperpolarization is essentially due to the change in the Nernst potential caused by the modulation of intracellular cation concentration, which over time eliminates the ion flux imbalance that caused the hyperpolarization in the first place. This response takes the form of a perfect adaptation (Ferrell, 2016) to changes in the ion flux (Figure S2A). To test the prediction that hyperpolarization driven by cation flux is temporary, we tracked the membrane potential dynamics of individual bacteria over time (Figures 2C, 2D, S2B and S2C). Indeed, we find that hyperpolarization of bacteria is transient, lasting on average approximately two hours (Figures S2D and S2E). Therefore, the experimentally observed dynamic change in the bacterial membrane potential confirms the model prediction, implicating modulation of cation flux as a probable mechanism for cellular hyperpolarization.

Figure 2.

Membrane potential dynamics can be mathematically predicted and experimentally verified at the single-cell level.

A) Mathematical model describing the relationship between ion flux modulation and membrane potential dynamics.

B) The mathematical model predicts a transient hyperpolarization event in response to a decrease in cation influx.

C) Filmstrip (top) and its corresponding membrane potential as a function of time (bottom) for a representative non-hyperpolarized cell. Yellow scale bar on the most left panel indicates 1 μm.

D) Filmstrip (top) and its corresponding membrane potential as a function of time (bottom) for a representative hyperpolarized cell.

E) Elongation rate as a function of maximum membrane potential (ThT) in the presence of spectinomycin for hyperpolarized (cyan, n = 100) and non-hyperpolarized (black, n = 100) cells.

F) Single-cell ThT time traces showing membrane potential dynamics of the cells in panel E. The white region of the graph marks the death of the tracked cells. The Max ThT stripe shows the maximum projection of each ThT trace. The color bar (right) illustrates the intensity range of ThT-stained cells.

See also Figure S2 and S3.

Single-cell tracking over time also revealed that changes in membrane potential correlate with growth. Using spectinomycin to increase the fraction of hyperpolarized cells, we observe that hyperpolarized cells have a lower elongation (growth) rate compared to cells that do not exhibit such changes in their membrane potential (Figures 2E, and S3A–C). This finding reveals a negative correlation between membrane potential hyperpolarization and bacterial growth rate. Since bacterial growth is typically determined by ribosome activity (Bosdriesz et al., 2015; Schaechter et al., 1958), our results indicate the possibility that hyperpolarization is negatively correlated with ribosome activity. Furthermore, we find that hyperpolarized cells have a higher likelihood of dying compared to cells that do not exhibit transient hyperpolarization events. We determined that only 29% of cells that undergo transient hyperpolarization survive, while 84% of cells that do not exhibit hyperpolarization continue to grow (Figures 2F and S3H). These two types of cellular behavior are also observed for kanamycin and in the absence of antibiotics (Figures S3D–H). These data indicate cellular heterogeneity, where one fraction of cells hyperpolarizes and is very likely to die, while the other fraction of cells lacks large fluctuations in membrane potential and continues to grow and survive under antibiotic-induced ribosomal stress.

Structural Perturbations of the Ribosome Modulate the Fraction of Hyperpolarized Cells

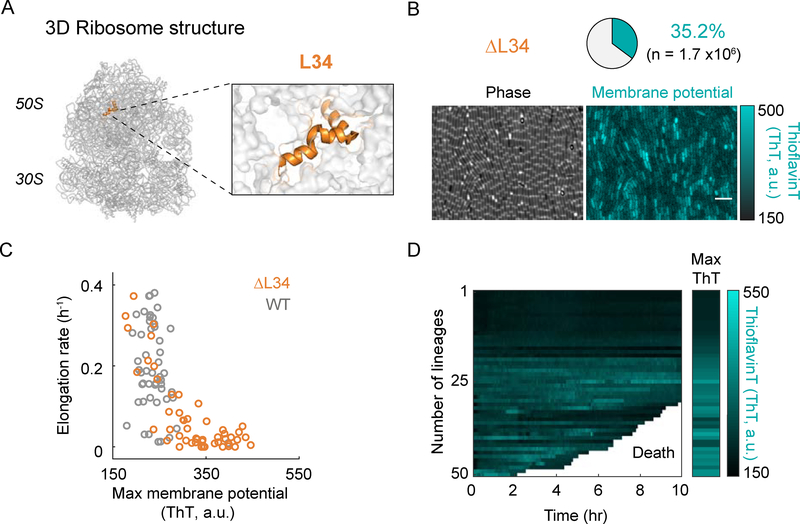
To determine more directly whether ribosomal stress causes changes in the membrane potential and a bias in cell survival, we turned to a structural perturbation of the ribosome complex. Specifically, we deleted the ribosomal L34 protein subunit (ΔrpmH), as this perturbation has been previously shown to destabilize bacterial ribosomes (Akanuma et al., 2014) (Figures 3A and S4A). We find that deletion of L34 (ΔL34) leads to an increase (nearly tenfold) in the fraction of cells that exhibit hyperpolarization (Figures 3B and S1C), even in the absence of antibiotic exposure. This increase in the percentage of hyperpolarized cells upon L34 deletion is similar to the effect of ribosome-targeting antibiotics (Figures 1D and 1E, bottom, and S1C). Consistent with the literature, we also observe a reduced elongation rate in ΔL34 cells compared to wild-type cells (Figure 3C) (Akanuma et al., 2012). These results indicate that a destabilizing structural perturbation of the ribosome complex increases the probability of hyperpolarization in bacterial cells. Furthermore, hyperpolarized ΔL34 cells are more likely to die, similar to what was observed under antibiotic stress (Figures 3D, 2F and S3H). Therefore, not only chemical but also a direct structural perturbation of the ribosome results in transient hyperpolarization and subsequent increase in cell death.

Figure 3.

Deletion of the ribosomal protein L34 increases the fraction of hyperpolarized cells.

A) A schematic of the 3D ribosome structure showing the localization of the ribosomal protein L34 (left). Right panel shows a magnified view of the L34 region. The ribosome structure was obtained from the Protein Data Bank (PDB, ID: 3j9w) and is represented using Pymol.

B) Phase contrast (left) and the corresponding fluorescence (ThT, right) images of the L34 deletion mutant. The pie chart (top) illustrates the percentage of hyperpolarized cells in a population of n = 1.7×10⁶ cells. The color bar (right) illustrates the intensity range of ThT-stained cells.

C) Comparison of elongation rate as a function of maximum membrane potential (ThT) for wild-type (WT, gray, n = 50) and the L34 deletion mutant (ΔL34, orange, n = 50) cells.

D) Single-cell ThT time traces showing membrane potential dynamics of the cells in panel C. The white region of the graph marks the death of the tracked cells. The Max ThT stripe shows the maximum projection of each ThT trace. The color bar (right) illustrates the intensity range of ThT-stained cells.

See also Figure S1C and S4A.

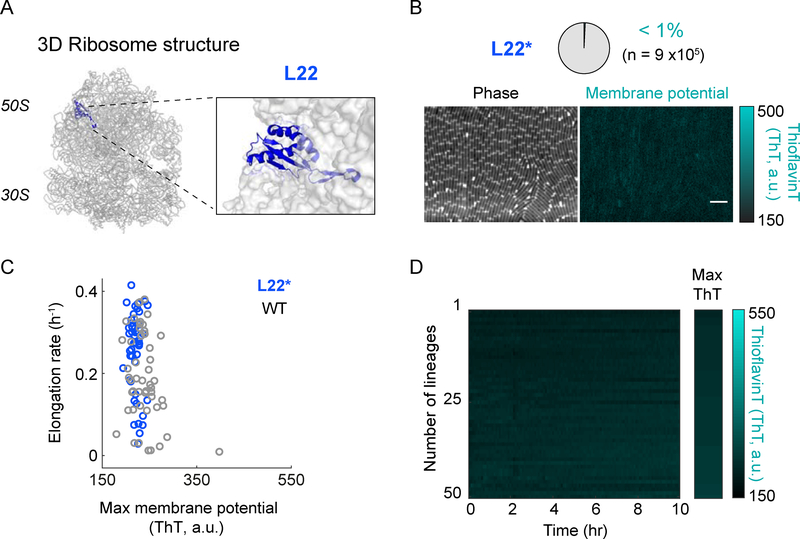
Next, we asked whether a structural perturbation of the ribosomal complex could also generate the opposite phenotype of ΔL34 and reduce hyperpolarization and cell death. To test this hypothesis, we targeted the L22 protein subunit of the ribosome complex (Figures 4A, and S4B–C). Specifically, the L22 subunit has been shown to be important for folding and stabilizing the conformation of the 23S rRNA (Akanuma et al., 2012; Ban et al., 2000). Our quantitative measurements show that L22 loop duplication (L22*) reduces hyperpolarization in bacteria (Figures 4B and S1C). Furthermore, the elongation (growth) rate of L22* mutant cells is overall shifted towards higher values compared to wild-type cells (Figures 4C). Concurrently, we observe less cell death in the L22* mutant strain (Figure 4D). The L22* strain retains these properties even in the presence of spectinomycin (Figure S5). These results indicate that a structural perturbation of the ribosome complex can prevent membrane potential hyperpolarization events in bacterial cells.

Figure 4.

Duplication of a ribosomal protein L22 loop decreases the fraction of hyperpolarized cells.

A) A schematic of the 3D ribosome structure showing the localization of the ribosomal protein L22 (left). Right panel shows a magnified view of the L22 region. The ribosome structure was obtained from the Protein Data Bank (PDB, ID: 3j9w) and is represented using Pymol.

B) Phase contrast (left) and the corresponding fluorescence (ThT, right) images of the L22 loop duplication mutant (L22*). The pie chart (top) illustrates the percentage of hyperpolarized cells in a population of n = 9×10⁵ cells. The color bar (right) illustrates the intensity range of ThT-stained cells.

C) Comparison of elongation rate as a function of maximum membrane potential (ThT) for wild-type (WT, gray, n = 50) and L22* mutant (blue, n = 50).

D) Single-cell ThT time traces showing membrane potential dynamics of the cells in panel C. The Max ThT stripe shows the maximum projection of each ThT trace. The color bar (right) illustrates the intensity range of ThT-stained cells.

See also Figure S4B, S4C, and S5.

Increased Magnesium Flux in the L22* Strain

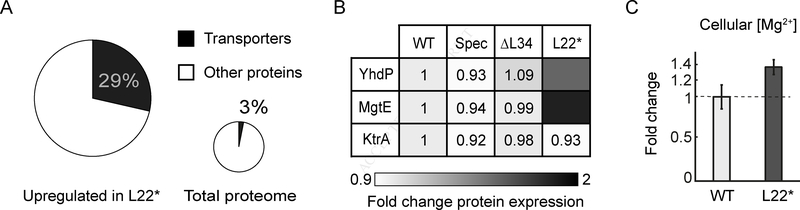
To identify whether the mechanism by which the L22* strain avoids membrane potential hyperpolarization involves ion flux, we turned to mass spectrometry proteomics (Dost et al., 2012). We performed a comparative analysis of the protein levels in the L22* strain relative to wild-type and conditions that cause an increase in the fraction of hyperpolarized cells. The results reveal upregulation of ion transporters in the L22* strain (Figure 5A and Table S2). While ion transporters constitute about 3% of the total measured proteome (~3000 proteins), we find that 28.6% of proteins that are specifically upregulated in the L22* strain are ion transporters. In particular, our analysis shows that the only known magnesium transporters, YhdP (Akanuma et al., 2014; Armitano et al., 2016) and MgtE (Wakeman et al., 2014), are upregulated in the L22* strain (Figure 5B). These data suggest that the L22* has a higher flux of magnesium ions, which is consistent with the higher growth rate of the L22* strain that indicates functional ribosomes (Figure 4C). The L22* strain should thus have a higher intracellular magnesium content relative to wild-type. We turned to Inductively Coupled Optical Emission Spectrometry (ICP-OES), to measure cellular magnesium concentrations. Results show that the L22* strain has on average an approximately 35% higher intracellular magnesium concentration compared to the wild-type strain (Figure 5C). Magnesium flux thus appears to be modulated in the L22* strain through changes in the level of magnesium transporters, resulting in overall higher intracellular magnesium content. These findings provide further evidence for the role of ion flux in membrane potential dynamics and stress resilience in bacteria.

Figure 5.

Proteomics and ICP-OES data showing the enrichment of ion transporters and increased levels of cellular magnesium content in the L22* mutant strain.

A) Pie chart showing the percentage of ion transporters among the upregulated proteins in the L22* strain (left, n = 21). The small pie chart illustrates the percentage of ion transporters among all measured proteins (total proteome, n = 2798).

B) Table comparing the expression of two magnesium transporters (YhdP and MgtE) and one potassium transporter (KtrA) in WT, WT in the presence of spectinomycin, L34 deletion strain (ΔL34), and L22 loop duplication strain (L22*). The color bar (bottom) illustrates the fold change in protein expression.

C) Relative fold change (35 ± 9%) of intracellular magnesium content in the L22* strain compared to wild-type. For details on the ICP-OES measurements, please see the methods section.

See also Table S2.

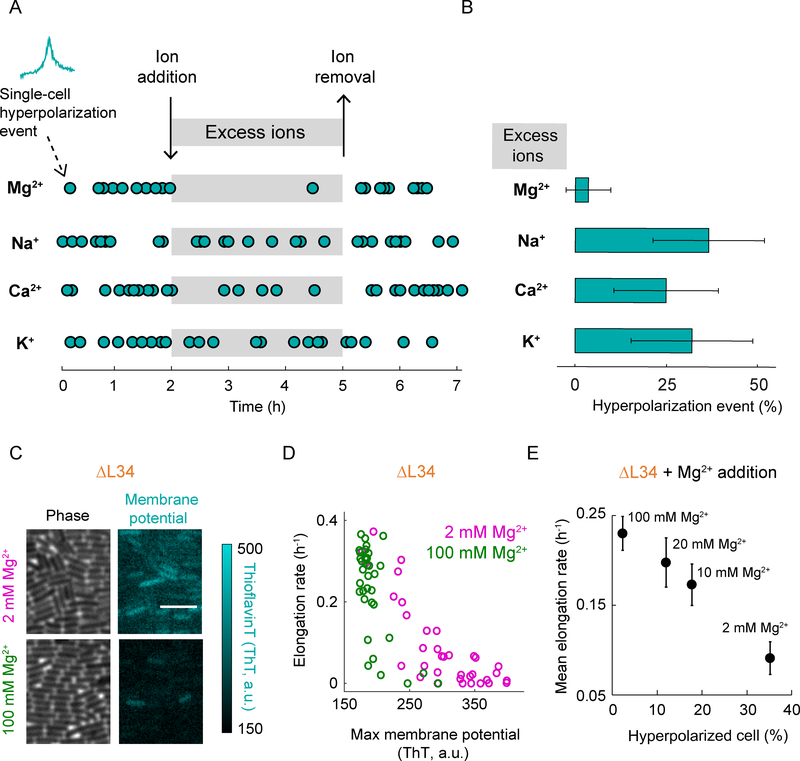
Suppression of Hyperpolarization Events by Extracellular Magnesium

We then tested whether membrane potential hyperpolarization is specifically suppressed by magnesium, or if other cations are equally effective. Experiments show that increasing the extracellular magnesium concentration in the media from 2 mM to 20 mM (which drives magnesium influx) indeed quenches transient hyperpolarization events in wild-type cells that are under antibiotic stress (Figures 6A and 6B, top). Plate assays also show that higher magnesium concentrations in the growth media reduce bacterial death in the presence of antibiotics (Figure S6). In contrast, other cations such as potassium, sodium or calcium are less effective at quenching hyperpolarization (Figures 6A and 6B). These results are consistent with our proteomics data and prior work showing that potassium, sodium or calcium are less effective in stabilizing ribosomes when compared to magnesium (Weiss et al., 1973). As a control, we also show that the quenching of hyperpolarization events by magnesium influx is reversible, as cells once again exhibit hyperpolarization after removal of high extracellular magnesium levels (Figure 6A). Together, these data indicate that increased magnesium flux can prevent hyperpolarization events in bacteria that are subject to ribosomal stress and promote their survival.

Figure 6.

Addition of magnesium decreases the fraction of hyperpolarized cells.

A) Hyperpolarization events as a function of time in the presence (grayed region) and absence of excess ions (Mg²⁺, Na⁺, Ca²⁺, or K⁺). Each dot represents the time point of a hyperpolarization event (n = 28, 30, 32, and 28 for Mg²⁺, Na⁺, Ca²⁺, and K⁺, respectively). Cells were exposed to spectinomycin to increase the occurrence of hyperpolarization events.

B) Bar plot showing the percentage of hyperpolarized cells during the addition of excess ions (Mg²⁺, Na⁺, Ca²⁺, or K⁺). Error bars represent 95% confidence interval (CI).

C) Phase contrast (left column) and the corresponding fluorescence (ThT, right column) images of the L34 deletion strain in the presence of regular (2 mM, top row) and increased (100 mM, bottom row) concentrations of the Mg²⁺ ion. The color bar (right) illustrates the intensity range of ThT-stained cells.

D) Comparison of elongation rate as a function of maximum membrane potential (ThT) for the L34 deletion strain (ΔL34) in the presence of regular (2 mM Mg²⁺, magenta, n = 35) and increased (100 mM Mg²⁺, green, n = 35) concentrations of Mg²⁺ ion. ‘2 mM Mg²⁺’ data is a duplicate of ‘ΔL34’ data in Figure 3C.

E) Mean elongation rate as a function of the percentage of hyperpolarized cells for ΔL34 exposed to various Mg²⁺ ion concentrations (2 mM, 10 mM, 20 mM, and 100 mM). Error bars represent standard error for the y-axis and 95% CI for the x-axis. The x-axis error bars are smaller than the symbol used in this plot.

See also Figure S6 and Figure S7.

Given the above results, we asked whether the addition of excess magnesium ions to the growth media could also reduce hyperpolarization events in the ΔL34 strain and rescue its growth defect. Accordingly, we measured the membrane potential dynamics and growth of the ΔL34 strain under increased magnesium concentrations in the media (Figure 6C). We find that the fraction of hyperpolarizing ΔL34 cells is reduced with increasing magnesium concentration in the media (Figures 6C–E, and S7A). The growth rate defect of the ΔL34 strain is also rescued to wild-type levels with increasing concentrations of excess magnesium, consistent with the literature (Akanuma et al., 2014) (Figures 6D, 6E, and S7B). Together, these results indicate that hyperpolarization events in bacterial cells induced by ribosome destabilization can be counteracted by magnesium-mediated stabilization of the ribosome complex. This effect takes the form of a linear correlation between the growth rate and membrane potential of ΔL34 bacteria (Figure 6E).

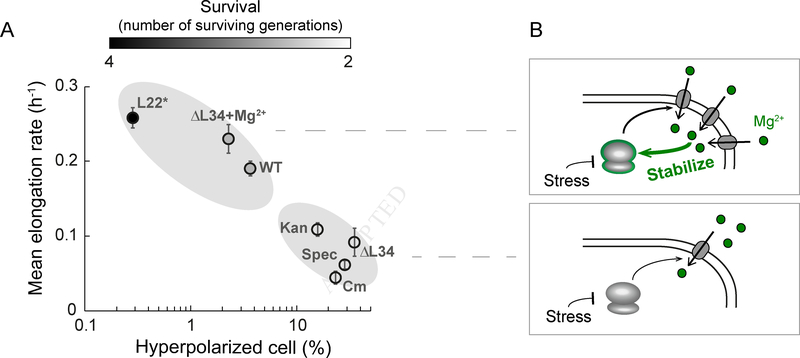
Bacterial Growth and the Probability of Cellular Hyperpolarization Exhibit a Linear Relationship

Finally, we determined whether the multiple perturbations beyond ΔL34 utilized in this study further confirm the linear relationship between the average population growth rate and the fraction of cells that exhibit hyperpolarization events. When we plot the quantitative data obtained from multiple strains and perturbations, we observe that the nature of ribosomal perturbations (stabilizing or destabilizing) and the probability of hyperpolarization are correlated, and indeed fall on an almost linear relationship (Figure 7A, Tables S3 and S4). Modulating magnesium flux enables cells to “move” along this phase space of behaviors, towards higher or lower likelihood of hyperpolarization events. Therefore, the stabilizing role of magnesium on the ribosome complex has a predictable effect on the fraction of cells that hyperpolarize. Furthermore, we tracked the number of generations that survive during the 10 hours of observation and find that populations with a lower percentage of hyperpolarized cells have a higher survival (Figure 7A). Collectively, these results show that the flux of ions, in particular of magnesium, is modulated in bacteria, indicating a mechanism for survival under antibiotic stress (Figure 7B).

Figure 7.

Hyperpolarized cell fraction is correlated with mean growth rate and survival for all ribosomal perturbations tested.

A) Summary of mean elongation rate as a function of hyperpolarized cell percentage (in logarithmic scale) upon ribosomal perturbations used in this study: wild-type (WT), wild-type in the presence of spectinomycin (Spec), wild-type in the presence of kanamycin (Kan), wild-type in the presence of chloramphenicol (Cm), L34 deletion strain (ΔL34), L34 deletion strain in the presence of 100 mM magnesium (ΔL34+Mg²⁺), and L22 loop duplication strain (L22*). Error bars represent standard error for the y-axis and 95% CI for the x-axis. The x-axis error bars are smaller than the symbol used in this plot. Color bar (top) shows the mean surviving generations during the observation period of 10 hours.

B) Cartoon proposing ion flux modulation as a bacterial mechanism to cope with ribosomal stress (surviving cell: top, dying cell: bottom).

See also Tables S3 and S4.

Discussion

Our study reveals an intriguing connection between ion flux in bacterial cells and their ability to cope with antibiotic stress. Specifically, we find that higher magnesium flux promotes growth and survival of bacteria that are exposed to antibiotics targeting ribosomes. It is known that magnesium ions stabilize the structure and function of the ribosome complex, which is comprised of numerous negatively charged rRNA subunits (Nierhaus, 2014). We now show that the ribosome-stabilizing function of magnesium plays an important role in promoting the ability of bacterial cells to cope with ribosome-targeting antibiotics. Consequently, modulation of ion flux becomes a key determinant of bacterial stress resilience.

Our findings also provide a new perspective on the heterogeneous antibiotic response of bacteria that emphasizes the importance of ion flux regulation in bacterial survival. With advances in single-cell measurements, various differences among genetically identical bacterial cells have been identified, such as metabolic states, ability to take up extracellular DNA and formation of spores (Kuchina et al., 2011; Kussell and Leibler, 2005; Pelkmans, 2012; Süel et al., 2007). Here we show that bacteria also differ in their ion flux modulation and that this difference is an important determinant of cellular survival. This finding also identifies future research directions to investigate the molecular mechanisms that are responsible for the observed cell-to-cell variability of ion flux in bacteria.

Uncovering ion flux-based differences in bacterial survival under antibiotic response further suggests means to increase the effectiveness of known antibiotics that target the ribosome complex. Specifically, combining antibiotics with drugs that target bacterial membrane proteins that are responsible for magnesium ion influx could enhance the killing efficiency of ribosome-targeting antibiotics. Since ion flux is critical to all cells, one of the main challenges will be to design drugs that specifically target bacterial ion transporters, in an effort to reduce unwanted side-effects to host cells. However, there are multiple unique properties of bacterial cell walls and membranes, such as their composition and content of membrane proteins, lipids, and polysaccharides (Kwon et al., 2017; Sharma et al., 2012), suggesting possible ways to achieve such specific targeting of bacterial ion transporters.

Concurrently, the bacterial membrane potential appears to be a reliable marker for the sensitivity of bacteria to ribosomal stress and antibiotics. Specifically, membrane potential measurements can determine whether a given bacterial population has a low or high sensitivity to ribosome-targeting antibiotics. New testing methods for bacterial response to antibiotics could thus be developed that do not require measurements of survival or killing efficiency. In other words, the bacterial membrane potential measurement could quickly identify the stress sensitivity of a bacterial population from a single snap shot.

From a more basic science perspective, our findings reveal an intriguing interaction between ribosomes and the membrane potential, suggesting that these ancient and fundamental processes that operate in all living cells have a profound connection. Electrochemical gradients across membranes have been a key element of living systems since the origin of life itself, as is the utilization of ribosome machines for protein synthesis, an essential feature of replication. Our data indicate a bi-directional functional link between ion flux and ribosome function. Ribosomes are necessary to synthesize membrane proteins that govern flux of ions across the membrane, as it is energetically unfavorable for charged molecules to diffuse across the lipid bilayer of a cell. In turn, we now show that ion flux, specifically of magnesium, has a direct impact on ribosome function. The functional interplay between ribosomes and the membrane potential thus offers a new perspective on the link between fundamental cellular processes that are essential for life.

STAR Methods

CONTACT FOR REAGENT AND RESOURCE SHARING

Further information and requests for resources and reagents should be directed to and will be fulfilled by the Lead Contact, Gürol M. Süel (gsuel@ucsd.edu).

EXPERIMENTAL MODEL AND SUBJECT DETAILS

Bacterial Strains

The Bacillus subtilis strains used in this study are listed in Key Resources Table. L34 deletion strain (ΔL34, rpmH::cat) is generated using the pER450-based integration vector (pER450-rpmH) to replace rpmH gene with chloramphenicol resistance gene. It was constructed by Gibson assembly of four PCR products. The 5’ arm and 3’ arm fragments were PCR amplified using the following partial overlapping primers: GS2336 and GS2365 for 5’ arm; GS2364 and GS2339 for 3’ arm, and integrated as recombination arms with pER450 (Cm^R) vector PCR amplified using the following primers: GS2340 and GS2341 for the vector backbone; GS1951 and GS2284 for the CAT gene (overlapping bases in lower case; this region facilitates fusion in Gibson assembly). Please find the DNA sequences of the primers in Key Resources table. The ribosomal protein L22 loop duplication was obtained as a spontaneous Erm^R mutant. The spontaneous Erm^R mutant has a seven amino acid duplication (⁹⁴SQINKRT¹⁰⁰; Figure S4B), which is the same strain as described earlier (Chiba et al., 2009). The strain is confirmed by the whole genome sequencing.

Growth conditions

For time-lapse microscopy, desired B. subtilis strains were streaked on a fresh LB agar plate (with 5 mg/L chloramphenicol or 5 mg/L erythromycin when appropriate) a day before the experiment and incubated at 37 °C overnight. A single colony of the desired strain was used for inoculation of 3 mL LB medium and grown at 37 °C with shaking. The saturated culture was washed with MSgg media [5 mM potassium phosphate (pH 7.0), 100 mM 3-(N-morpholino)propanesulfonic acid (pH 7.0), 2 mM MgCl₂, 700 μM CaCl₂, 50 μM MnCl₂, 100 μM FeCl₃, 1 μM ZnCl₂, 2 μM thiamine, 0.5% glycerol, 0.5% glutamate], and then immediately loaded into a commercial Y04D microfluidic plate (EMD Millipore) and connected to media flow controlling CellAsic Onix2 device. Media flow was kept in 1.5 psi from two inlets throughout the experiment. Cells in the microfluidic chamber were grown in MSgg media at 37 °C for 120 minutes, and then the temperature was kept at 30 °C for the rest of the experiment. Membrane potential dynamics was measured using the 10 μM fluorescent cationic dye Thioflavin-T (ThT, Acros organics, CAS: 2390–54-7) added to the MSgg media 2 hours before the imaging. When required, 2 mg/L spectinomycin, 0.5 mg/L kanamycin, or 5 mg/L chloramphenicol was added 3 hours into the imaging. For the L34 deletion mutant (ΔL34), MSgg media was supplemented with a final concentration of 20 mM MgCl₂ before imaging, to ensure the growth. When appropriate, MgCl₂ concentration was changed 2 hours before the imaging and kept at the desired concentration (2 mM if not stated otherwise).

For proteomics and ICP-OES samples, a single colony of desired strains was grown in 3 mL LB at 37 °C with shaking for 3.5 hours. The saturated culture was washed with MSgg media, diluted 100 times, and further incubated in MSgg at 30 °C with shaking for 16 hours. Cultures were then pelleted at 4000 rpm for 4 minutes. Pellets were resuspended in 6 mL as followed for proteomics experiments: WT with MSgg media, WT with MSgg media supplemented with 2 mg/L spectinomycin, WT with MSgg media supplemented with 100 mg/L spectinomycin, WT with MSgg media supplemented with 0.5 mg/L kanamycin, ΔL34 with MSgg media, ΔyhdP with MSgg media, and L22* with MSgg media. For ICP-OES, pellets were resuspended into the same volume of fresh media and further cultured at 30 °C with shaking for 4 hours before measuring OD600. Later steps of sample preparation for each technique are described later in Proteomic labeling and Mass spectrometry and ICP-OES analysis sections, respectively.

For plating assay to test antibiotic resilience, a single WT colony was inoculated into 2 mL MSgg medium and grown at 37 °C with shaking for 6 hours. The saturated culture was diluted to 0.07 of OD600 into fresh MSgg and MSgg media supplemented with a final concentration of 20 mM or 50 mM MgCl₂, and then further grown at 37 °C with shaking for 2 hours. For the spectinomycin strip test, total 5 × 10⁸ cells were spread on MSgg-agar plate or MSgg-agar plate supplemented with a final concentration of 20 mM MgCl₂ before placing the strip. Plates with three biological replicates were incubated at 37 °C overnight. For the classical plating assay, total of 5 × 10⁵ cells were diluted into 2 mL of MSgg media with conditions described in Figure S6B and S6C. Three biological repeats for each condition were further grown at 37 °C with shaking for 22 hours. Then, 1 mL of culture was used to measure OD600 to determine the dilution and the other 1 mL of culture was used for plating. Spectinomycin results shown in Figure S6B are from 1/10,000 dilution plating. Kanamycin results in Figure S6C are from original culture. Colonies were determined after overnight incubation at 37 °C.

METHOD DETAILS

Time-lapse microscopy

Growth and membrane potential dynamics of B. subtilis cells were monitored with time-lapse fluorescent microscopy at 30 °C using Olympus IX-81 inverted microscope with a motorized stage (ASI). Images were taken with ORCA-Flash4.0 V2 camera (Hamamatsu) and a Lambda XL light source (Sutter Instruments). Single layers of cells were imaged every 5 minutes under 40X objective lens. Before imaging, exposure time was defined based on a calibration using fluorescent beads, in order to ensure the similar light exposure between different experiments.

Modeling the membrane potential dynamics

In order to establish a link between the cation flux through the bacterial membrane and the dynamics of the membrane potential, we consider the following minimal two-dimensional dynamical system:

$$\begin{gathered} \frac{dV}{dt}=-g_L\left(V-V_L\right)-g_C\left(V-V_C\right)+{\alpha }_{in}{C}_e-{\alpha }_{out}, \\ \frac{dC}{dt}=F\left(-g_C\left(V-V_C\right)+{\alpha }_{in}{C}_e-{\alpha }_{out}C\right), \end{gathered}$$

where V(t) is the membrane potential and C(t) is the intracellular concentration of the cation. We consider that the potential across the membrane can change due to three flux processes affecting the cation: passive flow through a channel ( g_C term in the V equation above), active import (α_in term), and active export (α_out term). The rest of factors influencing the dynamics of the membrane potential are represented by the leak term g_L. The dynamics of the cation C(t) is also affected by the three transport terms described above, as shown in its corresponding differential equation. Note that the extracellular cation concentration C_e is assumed constant. The Nernst potential of the cation is given by:

$$V_C=V_0\log \frac{C_e}{C}.$$

When the steady state condition of the cation concentration $\left(\frac{dC}{dt}=0\right)$ is used in the corresponding condition of the membrane potential $\left(\frac{dV}{dt}=0\right)$, we immediately conclude that the steady state value of the latter variable is simply V = V_L, irrespective of the parameters controlling the ion flux dynamics. We can thus expect that ion flux modulation will affect only the transient behavior of the system but not its stationary state, which is the main characteristic of a perfectly adapting system. In agreement with this expectation, we observe that the system responds to a drop in the activity of the channel by producing a hyperpolarization pulse as shown in Figure 2B of the main text. This decrease in activity is modeled by an exponential decay in the parameter g_C at a given time (t = 4 hours in Figure 2B), from an initial value g_C1 to a final value g_C2, with decay constant δ_C:

$$\frac{d{g}_C}{dt}=-{\delta }_c\left(g_C-g_{C2}\right).$$

The values of all model parameters are given in Table S1.

Experimentally, membrane potential is monitored through the fluorescent dye ThT. We model the dynamics of ThT in the following way:

$$\frac{dT}{dt}={\beta }_T-\left({\delta }_{hyp}+{\delta }_{dep}f(V)\right)T,$$

where T(t) represents the concentration of ThT inside the cell. We assume that the ability of the cell to retain the positive dye molecule depends on the membrane potential, in such a way that when the cell hyperpolarizes, it becomes able to retain enough ThT to produce a measurable fluorescence signal. This is modeled by means of the sigmoidal function:

$$f(V)=\frac{1}{2}\left(1+\tanh \left(\frac{V-V_L}{V_S}\right)\right),$$

that ranges from 0 (when V is sufficiently larger than V_L, i.e. when the cell is sufficiently hyperpolarized) to 1 (when the cell is sufficiently depolarized). The steepness of the sigmoidal is controlled by the parameter V_S. We chose biologically reasonable parameter values, and observed that the model predicts hyperpolarization pulses in a wide range of parameter space. The duration of the pulses depends on the model parameters that control the time scale of the system, namely the channel conductances, the cation import rate, and the conductance coefficient, as defined in the supplementary material. The values of these parameters were fitted to the observed duration of the hyperpolarization pulses.

To further validate the model, we experimentally tested a key feature of our minimal model, resulting from the assumption that the dynamics of hyperpolarization events are modulated by the Nernst potential for Mg²⁺ ions, which depends logarithmically on the concentration difference of Mg²⁺ across the membrane. The model consequently predicts that a reduction in the extracellular Mg²⁺ concentration would not result in a noticeable change in either the amplitude or the duration of the hyperpolarization pulses (Figure S2A). We verify this specific prediction experimentally and find that cells growing under a 10-fold reduction in extracellular Mg²⁺ (0.2mM versus 2mM) still undergo hyperpolarization events with similar dynamics (Figures S2D and S2E). This confirms the mathematically predicted robustness of the dynamics to a reduction in extracellular Mg²⁺ ions.

Proteomic labeling and Mass spectrometry

iTRAQ labeling of peptide

Samples prepared as described above were washed three times with 2 mL of Tris-HCl buffer (pH 7.0). Then, cells were pelleted to the volume of about 100 μl. Cell pellets were suspended in 200 μL cold extraction buffer (6 M guanidine hydrochloride (GdnHCl)/100 mM Hepes/10 mM Tris(2- carboxyethyl)phosphine (TCEP), pH 7). 100 μL 0.5mm ZrO₂ beads were added. Cells were lysed by shaking in a Bullet Blender tissue homogenizer (Next Advance, Inc.) at speed 8 for 3 minutes. Proteins were denatured by heating at 94°C for 5 minutes. Samples were diluted 6 times to 1 M GdnHCl with 50 mM Hepes. Proteins were first digested with Lys-C (Wako Chemicals, 125–05061) at 37°C for 15 minutes. Protein solution was further diluted 2 times to 0.5 M GdnHCl with 50 mM Hepes and digested with trypsin (Roche, 03 708 969 001) for 4 hours. Digested peptides were purified on a Waters Sep-Pak C18 cartridges, eluted with 60% acetonitrile. TMT-10 labeling is performed in 50% acetonitrile/ 150 mM Tris, pH7. TMT labeling efficiency is checked by LC-MS/MS to be greater than 99%. Labeled peptides from different samples are polled together for 2D-nanoLC-MS/MS analysis. An Agilent 1100 HPLC system was used to deliver a flow rate of 600 nL/min to a custom 3-phase capillary chromatography column through a splitter. Column phases were a 30 cm long reverse phase (RP1, 5 μm Zorbax SB-C18, Agilent), 8 cm long strong cation exchange (SCX, 3 μm PolySulfoethyl, PolyLC), and 40 cm long reverse phase 2 (RP2, 3.5 μm BEH C18, Waters), with the electrospray tip of the fused silica tubing pulled to a sharp tip (inner diameter <1 μm). Peptide mixtures were loaded onto RP1, and the 3 sections were joined and mounted on a custom electrospray adapter for on-line nested elutions. Peptides were eluted from RP1 section to SCX section using a 0 to 80% acetonitrile gradient for 60 minutes, and then are fractionated by the SCX column section using a series of 15 step salt gradients of ammonium acetate over 20 minutes, followed by high-resolution reverse phase separation on the RP2 section of the column using an acetonitrile gradient of 0 to 80% for 150 minutes.

Data acquisition

Spectra were acquired on a Q-exactive-HF mass spectrometer (Thermo Electron Corporation, San Jose, CA) operated in positive ion mode with a source temperature of 325 °C and spray voltage of 2kV. The automated data-dependent acquisition was employed of the top 20 ions with anisolation window of 1.0 Da and collision energy of 30. The mass resolution is set at 60,000 for MS and 30,000 for MS/MS scans, respectively. Dynamic exclusion was used to improve the duty cycle.

ICP-OES analysis

Samples prepared as described above were pelleted and allowed to dry completely before being weighed and transferred to pre-cleaned 7 mL PTFE vials (Savillex, USA). Samples and (two procedural blanks) were digested (48 hours and 24 hours, both at 145 °C) and dried twice using ultrapure HNO₃, 2 mL. Additionally, H₂O₂ was added and heated to 100 °C for 24 hours, then allowed to dry. Prior to diluting samples 1001x using 2% HNO₃ in pre-cleaned 15 mL centrifuge tubes for analysis, the dried sample residue was brought up to 5 mL using ultrapure HNO₃, 1 mL and MQ H₂O, 4 mL, and allowed to equilibrate in vials overnight at 90 °C. Samples were analyzed on a Perkin Elmer Optima 3000 DV ICP-OES in axial mode, and were quantified by means of external calibration, using a 5 point calibration curve.

QUANTIFICATION AND STATISTICAL ANALYSIS

Analysis of proteomic data

The raw data were extracted and searched using Spectrum Mill vB.06 (Agilent Technologies). MS/MS spectra with a sequence tag length of 1 or less are considered to be poor spectra and were discarded. The remaining MS/MS spectra were searched against UniProt Bacillus subtilis (strain 168) proteome (4,271 protein sequences). A 1:1 concatenated forward-reverse database was constructed to calculate the false discovery rate (FDR). Common contaminant protein sequences were included in the database. There were 8,568 total protein sequences in the database. Search parameters were set to Spectrum Mill’s default settings with the enzyme parameter limited to full tryptic peptides with a maximum mis-cleavage of 1. Cutoff scores were dynamically assigned to each dataset to obtain the false discovery rates (FDR) of 0.1% for peptides, and 1% for proteins. Proteins that share common peptides were grouped using principles of parsimony to address protein database redundancy. Total TMT-10 reporter intensities were used for relative protein quantitation. Peptides shared among different protein groups were removed before quantitation. Isotope impurities of TMT-10 reagents were corrected using correction factors provided by the manufacturer (Thermo). Median normalization was performed to normalize the protein TMT-10 reporter intensities in which the log ratios between different TMT-10 tags are adjusted globally such that the median log ratio is zero.

In order to determine proteins enriched in L22* strain, we first selected proteins being expressed over 1.5 fold in L22* strain compared to WT. Next, we selected proteins being expressed less than 1.1 fold in other conditions compared to WT. These proteins are listed in Table S2.

Protein function assignment was based on Bacillus subtilis databases as followed: Subtiwiki, BsubCyc, UniProt. Membrane proteins with unknown function were classified as putative transporters.

Population analysis: hyperpolarized cell fraction

Trainable Weka segmentation plugin from FIJI (ImageJ) was used to segment cells from each phase contrast image (Arganda-Carreras et al., 2017). Custom-written macro was used to automatically compile the mask and segmentation data from a time-lapse movie. Non-segmented groups of cells, spores, and background noise were eliminated through size filtering. A mask created for each time point was used to extract the mean ThT intensity for each segmented cell (See Figure S1B).

Histograms were generated by compiling ThT intensities from two to four independent time-lapse movies. The fraction of hyperpolarized cells was determined by using a threshold of two standard deviations from the mode of the WT without any antibiotics.

Single cell analysis

Single cell Tracking and death determination

Single-cells were tracked by custom software developed in MATLAB (MathWorks) using time-lapse phase images from two to three independent experiments for each condition. Based on the phase contrast images we define cell death as the time point when the phase contrast inside the cell is fading (being an equivalent of a decrease in intracellular density). All cells were tracked a few time points more to ensure the change in phase contrast is not temporary (Figure S3I).

Elongation rate and max membrane potential

For each lineage’s time trace of cell length, an exponential line was fitted between consecutive divisions (for each generation). A function, f(x) = ae^bx was used for the fitting, where b is the elongation rate of a cell. The ‘elongation rate’ (Figures 2E, 3C, 4C, and 6D) is a mean elongation rate of a single lineage. On the other hand, ‘mean elongation rate’ (Figures 6E and 7A) is the population mean elongation rate under a certain condition. Maximum membrane potential was determined as the maximum value of ThT signal from the corresponding time trace.

Transient-hyperpolarization Determination

Obtained ROIs from a tracked cell were applied to the corresponding CFP images, which report ThT signals. ThT signal of the cell was measured as a function of time (from 30 minutes before any perturbation to the 10 hours into the perturbation unless the cell died before 10 hours). This trace was used to determine whether the cell experienced a transient hyperpolarization. A basal line for each trace was defined as a linear vector extrapolated from the mean of the first 30 minutes to the mean of the last 30 minutes of the time trace. Then, ThT amplitude was calculated as the difference in the intensities between the maximum ThT signal and the basal line. If the amplitude is greater than at least two standard deviation of the WT basal line values, the cell was determined to have a transient hyperpolarization.

Transient-hyperpolarization with excess ions

The addition of excess ions in the media globally decreases ThT signal. For the analysis of single-cell traces with excess ions experiments (Figures 6A and 6B), each ThT time trace was corrected to eliminate the global decrease. The basal line for ThT signal was obtained from the segmentation results of each movie and determined as described earlier. The difference between the basal line before and after the addition of excess ions and the basal line during the addition of excess ions was then added to ThT signal during the ion addition. This corrected time trace was then used to determine the transient hyperpolarization as described earlier. For each condition, five to eight cells with the brightest ThT signal were selected for each hour of the experiment and tracked during the duration of the experiment. We called the timing of the ThT maxima for each time trace as a single-cell hyperpolarization event and plotted it in Figure 6A. Single-cell hyperpolarization events during the addition of excess ions over all hyperpolarization events is presented as a percent with a 95% CI in Figure 6B.

Supplementary Material

1

Figure S1, related to Figure 1.

A) Phase contrast (left column) and the corresponding fluorescence (ThT, right column) images of wild-type Bacillus subtilis cells (top row) and cells exposed to 5 μM of carbonyl cyanide m-chlorophenyl hydrazine (CCCP, bottom row). The color bar (right) illustrates the intensity range of ThT-stained cells.

B) Outline of the segmentation process used to measure hyperpolarized cell fraction of the population. Each phase contrast image (top left) was used to generate a mask (bottom left) which then was applied to the corresponding ThT fluorescence image to measure the mean signal from each cell (right).

C) Distribution of ThT intensities in a population of cells under listed conditions. ‘WT + no antibiotics’ data is a duplicate of Figure 1D. The dashed red line represents two standard deviations from the mean of the wild-type, which is used as a cutoff to determine the fraction of hyperpolarized cells. ‘n’ represents the number of analyzed cells. Segmented cells from three or four independent experiments are used for each condition, except for CCCP addition (two experiments).

D) Bar plot showing the percentage of hyperpolarized cell fraction as a function of spectinomycin concentration (0, 2 and 5 mg/L). Error bars represent 95% confidence interval (CI). The error bars are too small relative to the width of the lines used in the bars and thus not visible.

2

Figure S2, related to Figure 2.

A) The mathematical model predicts a transient hyperpolarization event under regular (2 mM Mg²⁺, black) or 10-fold decreased (0.2 mM Mg²⁺, red) extracellular magnesium concentration.

B) Raw timetraces of membrane potential (ThT) from hyperpolarized cells (n = 119) exposed to sub-lethal concentration (2 mg/L) of spectinomycin.

C) Each time trace is normalized by initial ThT value before antibiotic addition and then aligned by the peak ThT time point (0 hr). Black lines showing mean and standard deviation are overlaid on top.

D) Mean and standard deviation in panel C are re-plotted. Red arrow and the number indicate the half-peak duration (mean ± SD).

E) Mean and standard deviation of hyperpolarization events in 0.2 mM Mg²⁺. Red arrow and the number indicate the half-peak duration (mean ± SD, n = 46).

3

Figure S3, related to Figure 2.

A) ThT signal as a function of time of the representative non-hyperpolarized cell (top, duplicate of figure 2C). Cell length as a function of time for the same cell (bottom).

B) ThT signal as a function of time of the representative hyperpolarized cell (top, duplicate of figure 2D). Cell length as a function of time for the same cell (bottom).

C) Fluorescence intensity of a hyperpolarized cell stained with ThT (cyan, left y-axis) and death marker Sytox Green (red, right y-axis) are measured concurrently over time to test if ThT signal is due to a membrane damage. Sytox Green can enter a cell when the membrane integrity is compromised.

D) Elongation rate as a function of maximum membrane potential (ThT) for hyperpolarized (cyan, n = 50) and non-hyperpolarized (black, n = 50) cells in the absence of antibiotics.

E) Scatter plot showing the distribution of cellular elongation rates (h⁻¹, a color bar on the right) in the absence of antibiotics, as a function of the x and y coordinates (μm) of cells within the observed region of the microfluidic chip (n = 200).

F) Elongation rate as a function of maximum membrane potential (ThT) in the presence of 0.5 mg/L kanamycin for hyperpolarized (cyan, n = 80) and non-hyperpolarized (black, n = 80) cells.

G) Single-cell ThT time traces showing membrane potential dynamics of the cells in panel F. The white region of the graph marks the death of the tracked cells. The Max ThT stripe shows the maximum projection of each ThT trace. The color bar (right) illustrates the intensity range of ThT-stained cells.

H) Conditional death probability for non-hyperpolarized (NH cell, black) and hyperpolarized cells (H cell, cyan) during 10 hours of observation (n = 90, n = 59, n = 107, n = 119, n = 100, and n = 66 from left to right). Error bars represent 95% CI.

I) Phase-contrast images of a dying cell. The yellow contour indicates the location of a representative dying cell. The cell death is defined as the time point when the phase contrast of the cell fades, which typically indicates cell lysis. Yellow scale bar on the most left panel indicates 2 μm.

4

Figure S4, related to Figure 3 and 4.

A) 3D structure and amino acid sequence of Bacillus subtilis L34. Positively charged amino acids are colored in red. The structure was obtained from the Protein Data Bank (PDB, ID: 3J9W) and is represented using Pymol.

B) 3D structure and amino acid sequence of Bacillus subtilis L22. Duplicated amino acids are colored in red and positive amino acids are underlined. The structure was obtained from the Protein Data Bank (PDB, ID: 3J9W) and is represented using Pymol.

C) Lateral and front view of L22 and 23S RNA interface is generated using data from Protein Data Bank (PDB, ID: 3J9W) and represented using Pymol. Different domains of 23S RNA are presented in different colors. The color scheme for L22 protein is the same as in B.

5

Figure S5, related to Figure 4.

A) Phase contrast (top) and the corresponding fluorescence (ThT, bottom) images of L22* strain exposed to 2 mg/L spectinomycin. The color bar (bottom) illustrates the intensity range of ThT-stained cells.

B) Elongation rate as a function of maximum membrane potential (ThT) in the presence of 2mg/L spectinomycin for wild-type (WT, grey, n = 50) and L22* cells (blue, n = 50).

C) Single-cell ThT time traces showing membrane potential dynamics of the cells in panel B. The white region of the graph marks the death of the tracked cells. The Max ThT stripe shows the maximum projection of each ThT trace. The color bar (right) illustrates the intensity range of ThT-stained cells.

6

Figure S6, related to Figure 6.

A) Images of bacteria grown on plates in the presence of antibiotic strips that contain a range of precisely defined spectinomycin concentrations. In the presence of 2 mM Mg²⁺ extracellular concentration (left), the clearing appears at 3 mg/L spectinomycin. In the presence of 20 mM Mg²⁺ extracellular concentration (right), the clearing appears at 6 mg/L spectinomycin. The inserts show a zoomed-in view on the clearing region of 3 biological replicates for each condition.

B) Standard plating assays with cells grown in the presence of varying concentrations of spectinomycin (4 mg/L, 8 mg/L, and 64 mg/L) and extracellular magnesium (2 mM, 20 mM, and 50 mM).

C) Standard plating assays with cells grown in the presence of varying concentrations of kanamycin (0.5 mg/L, 1 mg/L, and 2 mg/L) and extracellular magnesium (2 mM and 20 mM).

7

Figure S7, related to Figure 6.

A) Distribution of ThT intensities in a population of ΔL34 cells exposed to different concentrations of Mg²⁺ in the culture media. ‘2 mM Mg²⁺’ data is a duplicate of Figure S1C (ΔL34). The dashed red line represents two standard deviations from the mode of the wild-type, which is used as a cutoff to determine the fraction of hyperpolarized cells. ‘n’ represents the number of analyzed cells. Segmented cells from three to four independent time-lapse experiments are used for each condition.

B) Elongation rate as a function of maximum membrane potential (ThT) of a ΔL34 cells with different concentration of Mg²⁺ in the culture media as indicated. 2 mM Mg²⁺ is the usual concentration used throughout the paper unless indicated (n = 35, n = 35, n = 31 and n = 35, from left to right).

8

Table S1. List of parameters used in the model, related to Figure 2A.

Table S2. Proteins enriched uniquely in the L22* mutant, related to Figure 5. Proteins marked in bold are ion transporters. The table lists a description of overexpressed proteins and its expression level in wild-type in the presence of spectinomycin (Spec), ΔyhdP, ΔL34, and L22* mutant normalized to wild-type (WT) expression level.

Table S3. Summary values of parameters measured at the population level for the conditions listed, related to Figure 7. The table lists mean ThT level with its standard deviation (ThT std), hyperpolarized cell fraction and its confidence interval (CI), and number of analyzed cells.

Table S4. Summary values of parameters measured at the single-cell level for the conditions listed, related to Figure 7. The table lists the elongation rate with its standard error (SE), mean number of surviving generations with its standard error (SE), and number of analyzed cells.

Highlights.

• Cell-to-cell variability in membrane potential dynamics predicts bacterial survival

• Regulation of magnesium flux increases resilience to ribosome-targeting antibiotics

• Membrane potential and ribosomal activity are functionally linked in bacteria