Recurrent neural networks for early detection of heart failure from longitudinal electronic health record data: Implications for temporal modeling with respect to time before diagnosis, data density, data quantity and data type

Abstract

Background:

We determined the impact of data volume and diversity, and training conditions on recurrent neural network (RNN) methods compared to traditional machine learning methods.

Methods and Results:

Using longitudinal electronic health record (EHR) data, we assessed the relative performance of machine learning models trained to detect a future diagnosis of heart failure (HF) in primary care patients. Model performance was assessed in relation to data parameters defined by: the combination of different data domains (data diversity), the number of patient records in the training data set (data quantity), the number of encounters per patient (data density), the prediction window length and the observation window length (i.e., the time period before the prediction window that is the source of features for prediction). Data on 4,370 incident heart failure (HF) cases and 30,132 group matched controls were used. RNN model performance was superior under a variety of conditions that included: 1) when data were less diverse (e.g., a single data domain like medication or vital signs) given the same training size; 2) as data quantity increased; 3) as density increased; 4) as the observation window length increased; and 5) as the prediction window length decreased. When all data domains were used, the performance of RNN models increased in relation to the quantity of data used (i.e., up to 100% of the data). When data are sparse (i.e. fewer features or low dimension), model performance is lower, but a much smaller training set size is required to achieve optimal performance compared to conditions where data are more diverse and includes more features.

Conclusions:

RNNs are effective for predicting a future diagnosis of heart failure given sufficient training set size. Model performance appears to continue to improve in direct relation to training set size.

Heart failure is a relatively common and costly disease that is strongly associated with mortality. It is estimated that 5.7 million Americans have heart failure, with an annual health care cost of more than $31 billion, and a 50% five-year mortality rate (1). Heart failure is a complex heterogeneous disease (1) with multiple pathophysiologic phenotypes (2) and treatment options (3,4). While post-diagnostic care has been the focus of treatment management, relatively little attention has been devoted to early detection of a future diagnosis (5-7) and intervention before diagnosis.

The rapid growth in volume and diversity of electronic health record (EHR) data opens opportunities to apply machine learning to data on thousands of patients to optimize clinical care for individual patients. We have specifically focused on early detection of heart failure with the expectation that improved model performance will increasingly support early detection and diagnostics and eventually facilitate decision support for preventive care.

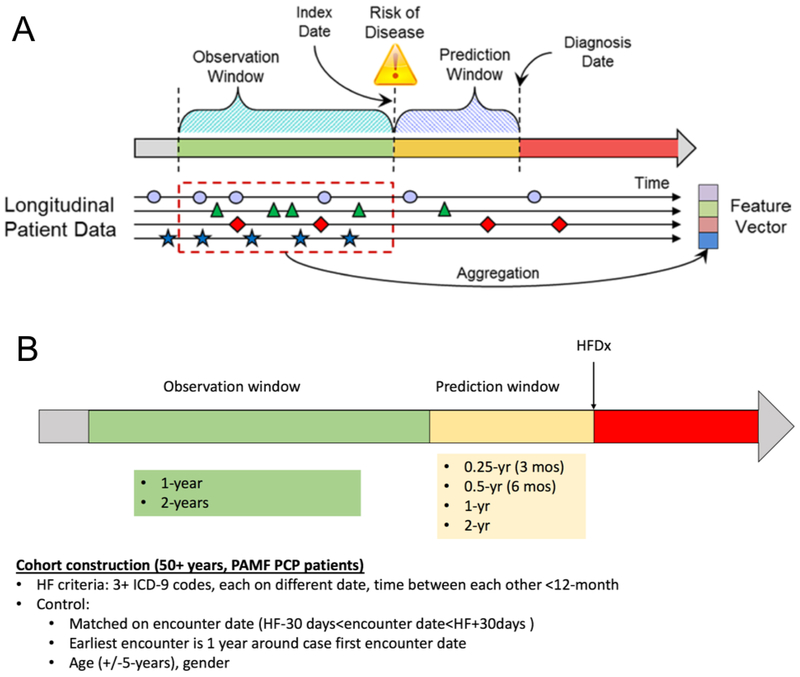
Previously, Ng et al. (6,7) studied early detection of the heart failure using EHR data to understand how model performance varied by modeling parameters. Using comprehensive longitudinal EHR data, Ng et al. (6,7) tested prediction window length (Figure 1A), observation window length (Figure 1A), data diversity, training data size and data density in two traditional machine learning models: L1- regularized logistic regression (LR) and random forest (RF). A limitation of traditional machine learning models for prediction is that temporal information on the relation among features in the observation window is not robustly captured. Instead, typical implementations of traditional machine learning methods represent patient events as aggregated counts or as summary measures (e.g., mean, standard deviation, slope). Some implementations of random forest models have leveraged feature engineering methods via explicit feature construction at separate time periods, but still treat features at different time periods as independent events(8-11). Use of temporal information may enhance model performance and utility for the early detection of disease.

Figure 1:

Relation of prediction window, observation window, and the index and diagnosis (A). Conceptual model for predictive modeling and relative positions of the observation window and prediction window in relation to the heart failure diagnosis (HFDx) data (B).

Recurrent neural networks (RNNs) can encode time-stamped events from EHR data and learn latent representations for use in the classification task. Previously, Choi et al. implemented a recurrent neural network approach (gated recurrent unit) for classification and early detection of heart failure using longitudinal EHR data (12). Choi et al. also implemented RETAIN, an interpretable RNN-based model leveraging attention mechanism (13). It is commonly accepted that RNN models can capture temporal information to outperform traditional models. However, to our knowledge, relatively little is known about the design (e.g., prediction window) and EHR data parameters that influence performance of RNN-based model compared to the traditional machine learning models. We examined this question for the prediction of heart failure.

Ng et al. (6,7) implemented predictive models with LR and RF. We extend the work (Figure 1A) by including temporal RNN modeling. We compare performance of RNN models (gated recurrent unit (GRU)) to traditional machine learning models when considering variation in data density (the number of encounters a patient exhibits), data quantity (the number of patients used in the model), data domains as defined by specific categories of EHR features, and the length of the observation window (i.e., period of time for using EHR data that precedes the HF prediction window) and of the prediction window (i.e., period time before HF clinical diagnosis but following the observation window). Furthermore, we examine the tradeoffs among these parameters, particularly data domain and training set size, and assess the optimal combination of these two parameters.

METHODS

We examined the performance of recurrent neural network (RNN) models compared to L1-regularized logistic regression (LR) and random forest (RF) in early detection of heart failure using longitudinal EHR data. Model performance was evaluated by the area under the curve (AUC). The study was approved by the Sutter Health institutional review committee. Because of the sensitive nature of the data collected for this study, the data will not be made publicy available.

Study design, Population and Source of Data

A nested case-control design was applied to the primary care population from Sutter Palo Alto Medical Foundation (PAMF) Clinics from which longitudinal EHR data were extracted. PAMF has multispecialty group practices, including 497 primary care providers in northern California Bay Area and coastal areas that provide care to 700,000 patients. EpicCare EHR was installed at Sutter-PAMF in 1999. Assignment of patients to a primary care physician (PCP) is documented in an EHR structured field. Incidence heart failure cases and controls were identified from Sutter-PAMF between May 6, 2000 and May 13, 2013 as previously described (12).

Definition of Cases:

Criteria for incident onset of HF were adopted from Gurwitz et al. (14), which relied on qualifying ICD-9 codes for HF with a minimum of three clinical encounters occurring within 12 months of each other. Qualifying cases must have had an assigned PAMF PCP in the appropriate EHR structured field. Qualifying ICD-9 codes included 398.91, 402.01, 402.11, 402.91, 404.01, 404.03, 404.11, 404.13, 404.91, 404.93, 428.0, 428.1, 428.20, 428.21, 428.22, 428.23, 428.30, 428.31, 428.32, 428.33, 428.40, 428.41, 428.42, 428.43,428.9, EP427, EP428, EP429, EP431, EP432, and EP433. The date of diagnosis (HFDx) was assigned to the earliest encounter where HF appeared as a qualifying diagnosis (i.e., as an encounter diagnosis or with a medication order), as long as three such diagnoses occurred within 18 months of each other. Incident cases had to have at least 18 months before the first occurrence of a HF ICD-9 code diagnosis without any indication of previous HF diagnosis or treatment. Analysis was limited to patients who were 40 to 84 years of age at the time of HF diagnosis. A total of 4,370 incident HF cases were identified from Sutter-PAMF over the time period from 2000 to 2013.

Selection of controls:

Controls were selected from the same PAMF clinics as incident HF cases using the following criteria:

1. The first PCP visit occurred within 365 days of the case’s first PCP visit (i.e., to control for secular factors in diagnosis);

2. Control had at least one office encounter within 90 days of the case’s HFDx date (i.e., control was an active primary care patient at the same time as the case);

3. Control did not have a HF diagnosis on or before the HFDx date of the case or within a time window (182 days) after the HFDx date;

4. Control was the same sex/gender as the case;

5. Control’s age (at first PCP visit) was within +/− 5 years of the case’s age

6. The time between the control’s first PCP visit and the case HFDx date ≥ 547 days (to ensure there is enough data for modeling).

We identified all potential controls for each case, and randomly select a maximum of 10 controls per case. We were not able to identify matched controls for 172 cases. These cases were excluded from the study. About 1% (n=42) of cases had 1 to 9 matched controls. The above process resulted in a total of 30,132 controls. Table 1 summarizes characteristics of the cases and controls, using data from the two-year observation window.

Table 1.

Baseline characteristics of the case and control cohorts.

	All patients	Cases	Controls
	N=34,502	N=4,370	N=30,132
Demographics
Gender (% male)	50.3%	51.0%	50.3%
Race (% white)	67.4%	65.7%	67.6%
Race (% black)	1.7%	3.5%	1.5%
Social History
Smoking (% smoker)	3.4%	4.7%	3.3%
Alcohol use (% used)	45.5%	34.7%	46.7%
Vital Signs
Systolic blood pressure (mean)	128.9	128.6	129.0
Diastolic blood pressure (mean)	73.5	71.5	73.8
Pulse (mean)	73.5	74.9	73.3
Respirations (mean, per minute)	16.7	17.3	16.6

Data Extraction and Grouping

Longitudinal EHR encounter data were extracted for all cases and controls from the following five domains: demographic, diagnosis, medication, social history, and vitals (Table 2). Encounters included outpatient office visits and phone visits.

Table 2.

EHR data domain, examples, number of unique variables and number of grouped variables

Data Domain	Examples	Number of Unique Variables	Number of Grouped Variables	Grouping Protocol	Number of input features in RNN model	Number of input features in LF/RF model
Diagnoses*	ICD-9 codes	5739	363	CCS level 3	363	36
Medications†	Beta blockers, loop diuretics, etc.	7189	93	Therapeutic subclass	93	76
Social History	smoking, alcohol use, sexual history, etc.	29	55	Discretized	55	29
Demographics‡	Sex, Race, Hispanic origin, marital status, interpreter needed	5	44	Discretized	44	44
Vitals§	Pulse, systolic blood pressure, diastolic blood pressure, BMI	8	15	Discretized	15	15

For all data types used in the analysis, the number of unique features and number of grouped features is shown. Note that for demographics, social history and vital sign features, the features used in the grouped representation are manually discretized in the following manner: categorical features for demographics and social history are converted to binary features (one for each category), numerical features for demographics and social history are removed. Features for vitals (all numerical) were discretized according to generally understood cutoffs for high, medium and low values.

^*:ICD-9 codes from outpatient visits

^†:Number of unique variables is calculated based on normalized drug names, ignoring the dosing information

^‡:The discretized demographic features are grouped as follows:

Race (prefer not to answer, Black/African American, Hispanic, Guamanian or Chamorro, Asian Indian, Vietnamese, Japanese, American Indian or Alaska Native, White/Caucasian, Unknown, Filipino, Other Pacific Islander, Samoan, Native Hawaiian, Chinese, Korean, Other Asian, Other);

Hispanic origin (Mexian, Peurto Rican, Cuban, other Hispanic/Latino/Spanish origin, Non Hispanic, Prefer not to answer, unknown);

Race line (1,2,3,4,5);

Marital Status (single, separated, life partner, widowed, significant other, married, divorced, unknown, other

Sex: female, male);

Interpreter needed (yes, no);

Social history:

alcohol use (yes, no, not asked);

smoking: cigarettes (yes, no), cigars (yes), pipes (yes, no);

tobacco: chew (yes, no), is tobacco user (yes, passive, quit, never, not asked);

other drugs: is illicit drug user (yes, no, not asked), snuff (yes, no), IV drug user (yes, no);

sexual history: is sexually active (yes, no, not currently, not asked), condom (yes, no), diaphragm (yes, no), intrauterine device (yes, no), pill (yes, no), spermicide (yes, no), male partner (yes, no), female partner (yes, no), abstinence (yes, no);

other: implant (yes, no), injection (yes, no), inserts (yes, no), rhythm (yes, no), sponge (yes, no), surgical (yes, no);

^§.Discretized numerical results of the vitals to three levels:

Pulse: low (below 60), normal (60-100), high (over 100)

Systolic blood pressure: low (below 90), normal (90-140), high (over 140)

Diastolic blood pressure: low (below 60), normal (60-90), high (over 90)

Body mass index: low (below 20), normal (20-30), high (over 30)

For the diagnosis domain, ICD-9 codes from outpatient office visit or phone visits were grouped by the Clinical Classifications Software (CCS) classification, developed the by Agency for Healthcare Research and Quality (AHRQ, https://www.hcup-us.ahrq.gov/toolssoftware/ccs/ccs.jsp). We adopted the CCS level 3 from the multiple-level CCS model to group 5,379 ICD-9 codes into 363 unique groups. Prior work indicated that use of grouped codes improved model performance and parsimony (7). For the same reason, the 7,186 normalized drug names (i.e. combining all branded names and the generic name for a medication) were grouped into 93 unique therapeutic subclasses using the Anatomical Therapeutic Chemical Classification System (https://www.whocc.no/atc_ddd_index/). Dose information was not used. For the demographics domain, sex, race, Hispanic origin, marital status were first categorized (Table 2) and then converted to a boolean variable. Other features included smoking and tobacco type (i.e. cigarette, pipes, cigars, chewable, etc.), alcohol intake status (yes, no, not asked), illicit drug use (snuff, IV drug user), sexual history (sexually active status), and protection method. Numerical values for vital domains were categorized using clinically validated thresholds (i.e. systolic BP is categorized into a categorical variable, “high” if the value is over 140 mmHg and “low” if the value is below 90; body mass index is categorized into a categorical variable, “high” if the value is over 30 and “low” if the value is below 20). Details on all features are described in Table 2.

Feature Construction and Missing data

A feature (e.g., diabetes diagnosis) vector for each patient was created from EHR data specifically extracted from the observation window. The occurrence of one or more feature specific events (e.g., multiple diagnosis of diabetes on different dates) was defined as a boolean variable (1/0) for the logistic regression and RF models. If no associated event (i.e. such as no ICD-9 codes associated with diabetes for a patient) was identified in the observation window the feature value was set to 0. In contrast, for the RNN model, repeated feature specific events were individually defined and date stamped, where the vector was constructed based on each event. For example, if a diabetes diagnosis appeared the first 4 times in 5 total encounters for a patient, then for this patient the diabetes diagnosis feature was represented as (1, 1, 1, 1, 0). Note that for the RNN model, we constructed the vector to encode event specific temporal sequence information that was then evaluated to determine if these representations improved model performance. Table 2 shows the number of grouped features used in the model. The mean of repeated continuous measures (i.e., systolic BP, diastolic BP, BMI), was derived for events within the observation window, and then categorized as previously noted. For lab values, each event was treated as a distinct event and the values were normalized across each feature. Missing values for labs were imputed by the mean lab value for all patients with a record of the lab. Therefore there were no missing values for vitals, age, sex, race, or ethnicity features. If a value was missing for marital status, alcohol use, or tobacco use, a separate category denoted as “missing” was created and represented as a boolean variable.

Predictive Modeling

For LR and RF models, the information gain measure was used to select the top 200 most discriminating features from 570 grouped features (15). Interactions among features were not considered. Internal cross validation was performed to determine the final hyper-parameters defined by the number of features in the logistic regression model and number of trees in the RF model (Table 2). Ten-fold cross-validation was used to train the predictive model and to measure how well the models performed in the independent data sets. The process was repeated 20 times to capture variation of fold splits. Predictive model performance was assessed by the mean of area under receiver operating curve (AUC) measures from repeated cross-validation folds.

For RNN, the data set was repeatedly and randomly split into a 90% training set and a 10% testing set, maintaining case to control ratio in the training set and testing set. To make efficient use of data, five bootstrap iterations were used. Performance was measured as the mean of the AUC computed on predictions made in each testing set.

Experiments were completed on the following design or data parameters to compare performance for machine learning models (RNN, LR, and RF). Unless otherwise specified, the prediction window length was fixed at 1 year and the observation window length was fixed at 2 years. Note that for each patient the length of the prediction window starts at the end of the observation window and extends to the index HF event; there are no events used during this time period to construct features.

• Data diversity was defined by variation in the inclusion of data from the five different domains (diagnosis, medications, social history, demographic, and vitals). Models were developed using each data domain individually, and then together in various combinations including all five data domains as the ultimate model. Analysis was limited to patients with 5 or more encounters in the observation window.

• Data density was defined by the number of patient encounters in the observation window and inclusion criteria varied from a low of 1+ to a high 30+ encounters. Data density was evaluated using data from all five domains.

• Data quantity, defined by the training set size, varied the amount of randomly selected training data from 10% to 100% of all patients (34,502) while keeping the case/control ratio constant. This experiment was limited to selected data domain options that differed by complexity and included: 1) vital signs only (15 features), 2) medications only (93 grouped features). We compared the model performance using a single domain and, separately, all data domains.

• Prediction window length varied from 3 months, 6 months to 2 years in 6-month increments. This experiment was restricted to patients with at least 5 encounters in a 2-year observation window (Figure 1B). The observation window was fixed to be 2 years (Figure 1B).

• Observation window length varied from 3 months, 6 months to 3 years in 6-month increments. This experiment was restricted to patients with at least 5 encounters in a 2-year observation window. The prediction window was fixed to be 1 year (Figure 1B).

Feature selection is part of the LR and RF modeling process, while this is not necessary for RNN modeling. Nonetheless, we performed two sets of experiments in data density and data quantity. We used features selected by LR and RF models as input features to RNN model (i.e. last column in Table 2). Separately, we use all features (i.e. the second to the last column in Table 2) as input features to all three models (i.e., forced LR and RF) to compare model performance. Note that features are not constructed from data in the prediction window, and thus the prediction window excluded data related to HF events (specifically, HF diagnosis codes and medications) that occurred within that window which may have otherwise biased the predictive model.

Modeling Parameters

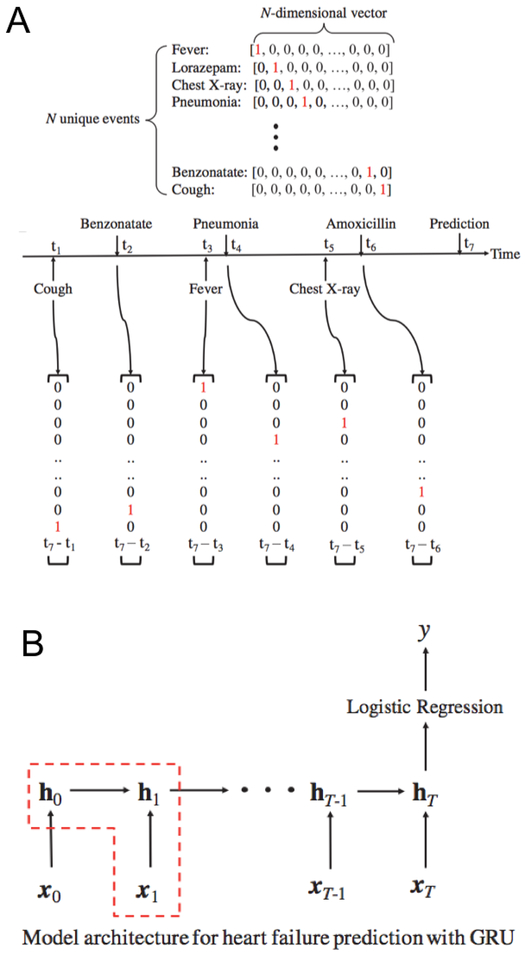
An RNN based model known as a “gated recurrent unit” (GRU), was used to model patient events as one-hot encoded vectors (Figure 2A). For a given patient with a sequence of clinical encounters of length T, the GRU model accepts as input a vector x_t, at each time step t. Information is stored at each time point t = 0, .., T, in a hidden layer with predetermined size. The state of the hidden layer changes over time from 0 to T. After input of all events, logistic regression is used to compute a scalar value y, from the output of the hidden layer at the last time step T. The value of y is transformed into a class label (1 - indicating a heart failure prediction, 0 - indicating a prediction without heart failure; note that values of y less than 0.5 are transformed to class label 0, otherwise to class label 1) (Figure 2B). Using logistic regression to transform the last layer of output is a standard practice for RNN models; usage of logistic regression to transform the output of RF was not used. It is not a standard practice and is not technically meaningful because the output from RF is probabilities for class label predictions.

Figure 2:

One-hot encoding of features included in the RNN model, where all 5 data domains are concatenated into single vector (A). Graphical depiction of model architecture for heart failure prediction with GRU (B).

In all RNN experiments, a single layer of hidden nodes is used. If the entire input feature set contains at least 256 distinct features, then 256 nodes are used in the hidden layer. Otherwise, given an input feature set of size n, then n nodes are used in the hidden layer. L2 regularization of 0.001 was applied. The batch size per model epoch was 10, and the maximum number of epochs was set to 100. The parameters were tuned by picking the combination of regularization factor (0.001, 0.01, 0.1, 1, 10, 100), number of epochs (10, 20, 30, …100), and number of nodes in the hidden layer (16, 32, 64, 128, 256, 512) that resulted in the highest AUC in 10-fold cross validation while using all feature domains.

We used L1-regularized logistic regression (16), implemented using the scikit-learn framework (17). The RF model represents a computationally efficient and robust approach that naturally combines “bagging” and feature selection in the algorithm (18). Internal cross-validation was used to determine the number of trees in the model. The implementation from the scikit-learn framework was utilized (17). All algorithms were implemented using Python.

RESULTS

Performance by data domain

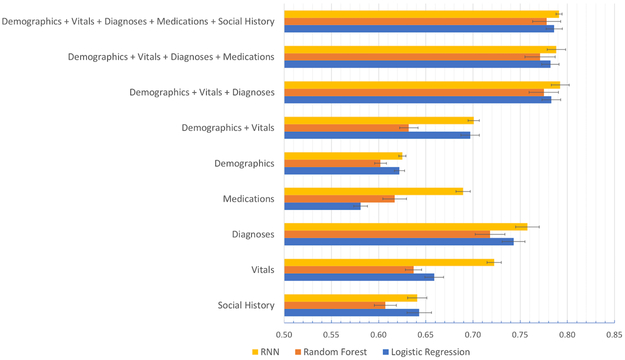
Figure 3 summarizes model performance using grouped features in each individual data domain and, separately, for all data domains combined. For all models and all domain combinations, the performance ranged from an AUC of 0.581 to 0.791. Where appropriate, confidence intervals and P-values computed with the two-tailed t-test are shown.

Figure 3:

Prediction performance of RNN, Random Forest, and Logistic Regression in relation to the use of data domains alone and in combination.

Diagnoses data alone offered the best performance of any single domain, followed by vitals and demographics. More specifically, diagnoses features (i.e., 363 groups) had significantly better performance across all models (AUCs>0.71) compared to other data domains. While the RNN model performance (AUC=0.758 (95% CI 0.733–0.782)) was superior to LR (AUC= 0.743 (95% CI 0.719–0.767), P = 0.497), the LR model performance (AUC= 0.743 (95% CI 0.719–0.767)) was superior to RF (AUC= 0.718 (95% CI 0.687–0.749)) (P = 0.311). The social history data domain (i.e. 55 initial features) had the lowest predictive power across all models (AUCs<0.65), with no significant difference among models. Interestingly, in the medication data domain with its 93 grouped features, the RNN model (AUC = 0.689 (95% CI 0.675–0.702)) substantially outperformed traditional models (i.e., AUCs of 0.581 (95% CI 0.567–0.595) and 0.617 (95% CI 0.592–0.642) for LR (P < 0.0001) and RF (P = 0.001) respectively).

For combinations of data domains, starting with the demographic and vitals domains (e.g. 59 features), the best performance was found for the RNN model (AUC=0.701 (95% CI 0.689–0.712)), which was slightly higher than that of the LR model (AUC= 0.697 (95% CI 0.678–0.716)) (P = 0.798). By adding diagnoses data (e.g. 422 features), the AUC for all models improved significantly (AUCs>0.77); however, model performance did not vary significantly comparing RNN to LR (AUC for RNN = 0.792 (95% CI 0.774–0.811), AUC for LR = 0.783 (95% CI 0.764–0.802); P = 0.606). The addition of other data domains (medication domain first, then social history domain) did not substantially improve model performance. With all data domains, the AUC was greatest for RNN (AUC= 0.791 (95% CI 0.785–0.797)), slightly better than that of the LR model (AUC=0.786 (95% CI 0.769–0.803); P = 0.700).

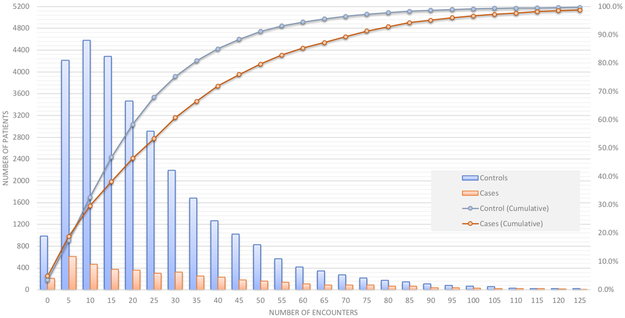
Performance by data density

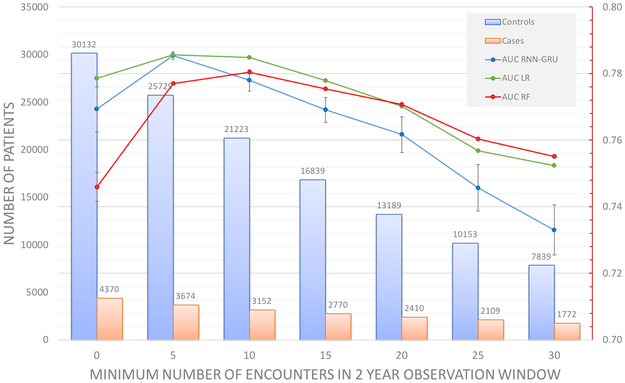
The number of encounters defined by unique dates in the observation window (2 years for this analysis) was first computed for each case and control to determine data density (Figure 4). A total of 4.8% of cases (red line, Figure 4) and 3.5% of controls (blue line, Figure 4) had less than 5 encounters. Half of the controls had less than 20 encounters and half of the cases had less than 25 encounters. As such, there may be potential confounding between the number of encounters, and the quantity of training data.

Figure 4:

Distribution of the number of encounters in the 2-year observation window for cases and controls. Note that the left vertical axis corresponds to number of patients (vertical bars), while the right vertical axis represents cumulative percentage of the total data set (lines).

Figure 5 shows the prediction performance in relation to data density. All models (RNN, RF, LR) were trained on all domains of data (demographics, vital signs, diagnoses, medications, social history). We incrementally increased the minimal number of encounters per patient in units of 5 encounters from 1 to 30. The blue, green and red curves in Figure 5 show the mean of AUCs as a function of the data set density (horizontal axis). Prediction performance peaked between 5+ encounters to 10+ encounters for all models. In order, peak model performance was superior for LR (AUC = 0.786 (95% CI 0.786–0.786)) and RNN (AUC = 0.785 (95% CI 0.783–0.787)), followed by RF (AUC = 0.780 (95% CI 0.786–0.778)), however the differences were not statistically significant. The same trend was observed when training LR and RF on the entire feature space rather than on only the features chosen in the feature selection process (Data Supplement, Figure A1).

Figure 5:

Prediction performance of RNN, Random Forest, and Logistic Regression in relation to data density by minimum number of encounters. Experiments are limited to a 2 year observation window and 1 year prediction window. All data domains were used. Values are recorded as AUC of prediction.

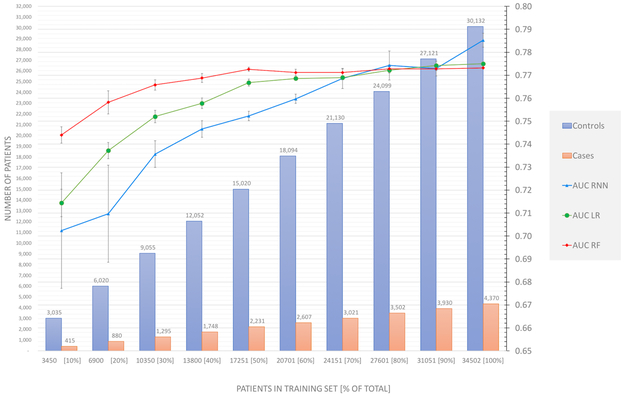
Performance by data quantity (data set size)

Data set size was varied from 10% to 100% of the total dataset (Figure 6), where all patients (4,370 cases and 30,132 controls) and all data domains were included in these experiments.

Figure 6:

Prediction performance as a function of training set size. Experiments are limited to a 2 year observation window and 1 year prediction window. All data domains were used.Values are recorded as AUC of prediction. Note that the left vertical axis correspond to number of patients in the training set (vertical bars), and the right vertical axis corresponds to AUC values (lines).

As the data set size increased (including all data domains: demographics, vital signs, diagnoses, medications, social history), the prediction performance for all models substantially improved, particularly for LR and RNN models. LR performance increased substantially until data on 40% of the cohort (13,800 patients) was used and plateaued when 70% or more of data were used. RF performance plateaued when 40% of data were used. In general, LR performance exceeded that of RF. RNN model performance continually increased even when 100% of the data were used. RNN model performance slightly exceeded that of RF when 70%+ of data were used (P = 0.80) and exceeded that of LR (P = 0.07) when 100% of the data were used (Figure 6). The same trend was observed when training LR and RF on the entire feature space rather than on only the features chosen in the feature selection process (Data Supplement, Figure A2).

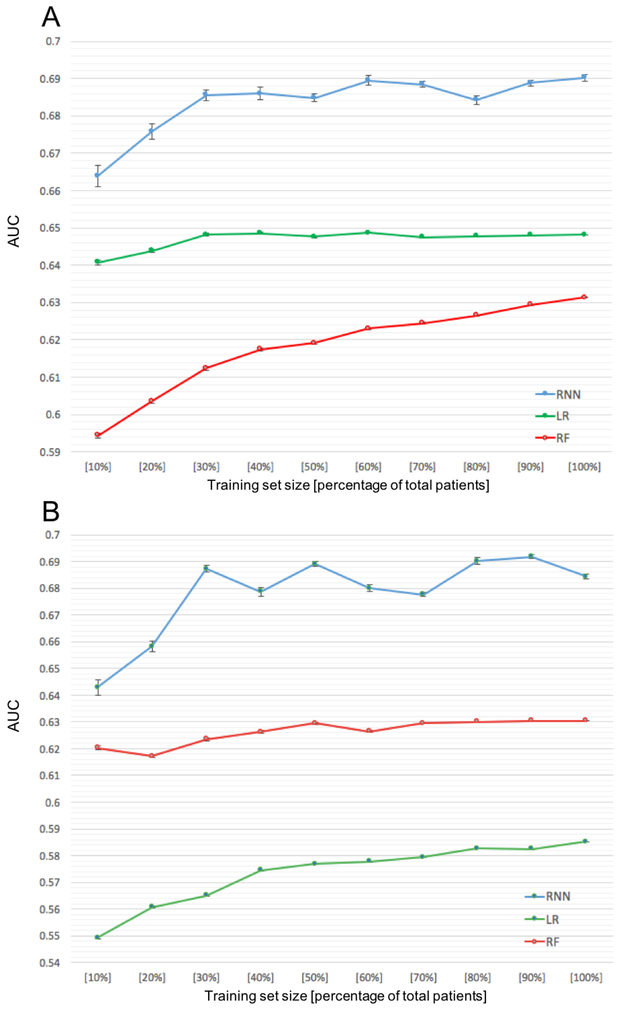
Performance by data diversity and data set size

Using vital sign features (simplest data domain, 15 features) only (Figure 7A), we varied training set size from a 10% random sample to the full sample. In general, model performance increased with increasing training set size. The RNN model (AUC = 0.69 (95% CI 0.683–0.698)) outperformed both the LR (AUC = 0.648 (95% CI 0.6480–0.6481); P<0.0001) and RF models (AUC = 0.631 (95% CI 0.631–0.632); P<0.0001). A similar pattern was observed for medication data (Figure 7B), a more complex data domain, (i.e., 76 features), where the RNN model had superior AUC compared to RF and LR.

Figure 7:

Prediction performance for all models as a function of training set size, using only the vital signs as features (A). Prediction performance as a function of training set size, using only the medications as features (B). Experiments are limited to a 2 year observation window and 1 year prediction window.

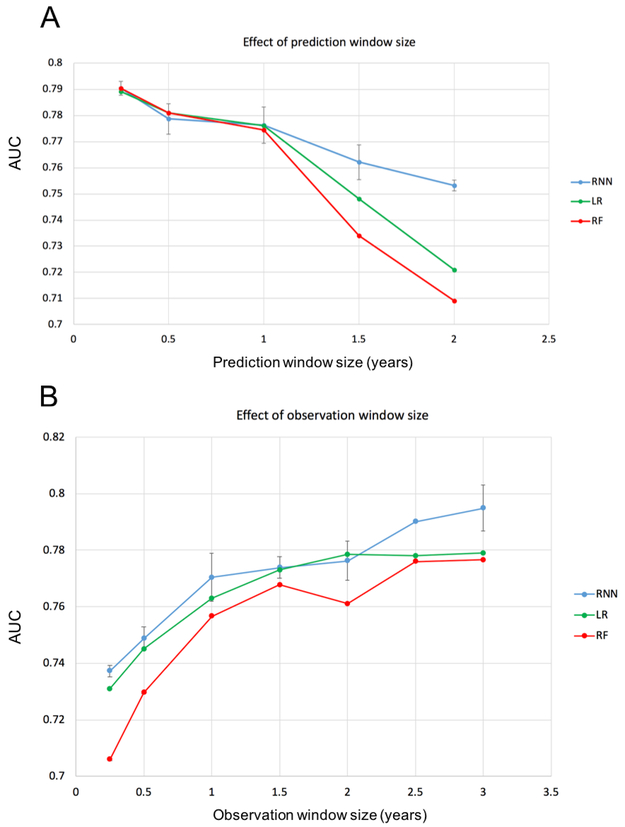
Performance by prediction and observation window length

Performance of RNN, LR and RF classifiers declined in relation to increasing prediction window length (Figure 8A). Model performance for the three models was similar when the prediction window length was one year or less. The RNN model was superior to LR and RF when the prediction window was longer than 1 year. For the RNN model, prediction performance (AUC) was at or above 0.775 for prediction windows less than or equal to 1 year and the AUC declined rapidly in relation to increasing prediction window lengths longer than 1 year; the AUC dropped to 0.753 for a 2 year prediction window (P = 0.012, 2 years vs. 1 year).

Figure 8:

Prediction performance for all models as a function of prediction window size (A) and as a function of observation window size (B). For the analysis of performance as a function of prediction window size, experiments are limited to a 2 year observation window. For the analysis of performance as function of observation window size, experiments are limited to a 1 year prediction window. All data domains were used. Values are recorded as AUC of prediction.

Performance for RNN, LR and RF classifiers increased in relation to increasing observation window length (Figure 8B). The RNN model outperformed both LR and RF models over a range of observational window lengths. Prediction performance was at or above 0.77 AUC for observation windows greater than or equal to 1 year. The AUC did not improve much when we increased the observation window from 1 year to 2 years, but the AUC significantly improved when the observation window was increased to 3 years (AUC=0.795 (95% CI: 0.779–0.817)) (P = 0.0688, 3 years vs. 1 year).

As expected, model performance improved as the observation window increased. This is likely to have occurred because of an increase in the number of encounters available for training models that in turn improves model accuracy. There were 29,403 patients included in all models. The average number of encounters was 16.3 using a 1 year obeservational window, 22.6 for a 1.5 year window, 28.1 for a 2 year window, and 37.2 for a 3 years window. Note that while the number of patients is the same in testing models for each observation window size, larger observation windows yield more encounters per patient. Therefore, a longer observation window means that more events are available for model training, which may contribute to improved accuracy. Similarly, model performance improved as the length of the prediction window decreased (i.e., a shorter time between the index date and diagnosis date) as the events in the observation window were more proximal to the time of diagnosis and thus more medically relevant.

DISCUSSION

Given the growing interest in the use of deep learning in healthcare, we sought to understand how the quantity and diversity of EHR data influences performance (e.g., with respect to AUC) of RNN models compared to traditional models. Because health systems vary substantially in the diversity, quantity and density of EHR data that are available, we explored common data parameters to understand when one machine learning modeling option might be superior to others.

Our results using traditional models for prediction of HF are consistent with previous work (6,7) in demonstrating that data density, diversity and quantity have a substantial impact on model performance. Not surprisingly, the length of the observation window strongly influences model accuracy as it is directly related to data quantity. Model accuracy starts to decline rapidly when the prediction window increases beyond one year, but RNN models perform substantially better than either LR or RF models as the observation window length increases. More generally, RNN models clearly outperform LR and RF models when data were sparse or data diversity was limited (Figures 7A, 7B). On the other hand, as data diversity increased, the performance differences among models decreased, especially when data from all domains were used (Figure 3). Moreover, as data diversity and the number of features were simultaneously increased, RNN models required substantially more training data to compete with LR and RF models. However, we did not have a large enough dataset to discover the performance limits of RNN models.

We focused on comparing performance using different models given the same original input features, and did not consider how features are processed in each model. Theoretically, LR and RF models differ substantially from RNN models in feature management. For LR and RF, feature selection was performed first, and only selected features were used in classification in the respective model (the selected features are usually not of the study interest in evaluating prediction performance). In contrast, feature selection is not an RNN operation. Instead, RNN models use the entire feature space to iteratively construct predictive feature representations. Our experiments on training LR and RF models with the entire feature space showed similar performance trends relative to RNN compared to using only the selected features in the classification steps for LR and RF (Data Supplement, Figure A1, A2).

The superior performance of RNN compared to LR and RF is likely to be explained, in part, by the use of information on temporal sequences of events. That is, given a sequence of clinical visits represented by one-hot encoded feature vectors, the RNN model encodes a state for each time point in the hidden layers. The state is updated as successive clinical visits are encoded. This approach captures temporal information. In contrast, LR and RF, like other traditional models, rely on aggregated measures to represent the experience in an observation window, where temporal information is not robustly captured. Furthermore, an important advantage of the RNN model is that it automatically constructs new predictive feature representations by capturing meaningful non-linear relationships among the original features. By contrast, LR and RF do not offer this feature construction capability.

As expected, RNN model performance is strongly related to data quantity (i.e. training sample size), especially with high dimensional features. This is a potentially significant limitation to the use of RNN models, especially for a health system with limited quantities of data or when there is a need to generalize models to smaller patient subgroups (e.g., minorities). Traditional models achieve optimal performance with considerably less data. Using all data domains (i.e. 570 input features), though, the performance of RNN model increases with increasing training sample size (Figure 6) and eventually outperformed the LR model when all available data are used.

To reliably estimate model parameters in predictive models, it is important to understand the minimum number of samples are required for machine learning models (including RNN) to achieve peak performance. We do not know when the RNN performance reaches a plateau (see Figure 6) as performance appears to continue improving even when 100% of the sample is used for training. The “one-in-ten rule” (19) (i.e. minimum 10 outcome events are needed for one feature in regression model) is a widely-accepted empirical rule of thumb when using traditional machine learning models to avoid overfitting. More recent evidence (20) suggests that the rule of thumb is more likely to be one in at least a 5 to 9 ratio (i.e. 5 to 9 outcome events for one feature in the model) to avoid unreliable modelling. In our study, a total of 200 features (last column in Table 1) were retained in the LR model, where the minimal sample size was expected to be 40% of samples (2,231 cases) (Figure 6). Notably, when using all data domains, the performance of LR (and RF) models plateaued after using 40% of the sample for training. The RNN model requires more training data given the need for estimating hidden layer parameters in addition to estimating weights for input features. To our knowledge, there is no systematic study on minimal training size needed for neural network models and there are few heuristics that address this issue (18, 19). If we use the simplest data domain (vital, 15 features, mean number of encounters is 7.1), a 30% sample (N=13,800) is required for the RNN model to achieve stabilized performance.

The number of training samples required for the RNN model depends on the number of features and the complexity of the network architecture. We applied the simple architecture (a gated recurrent unit model consisting of 1 hidden layer; 256 nodes if input feature set has size n is at least 256, otherwise n nodes if n < 256; one-hot encoding of input dataset of discretized features) in all scenarios. Note that with small training set sizes, the RNN model does not have significantly better performance than the LR model. The full potential of RNN is leveraged with a large enough training set size, yielding more data from which the model can learn temporal representations that are predictive of heart failure. Additional work in the Vapnik-Chervonenkis (VC) dimensionality of recurrent neural network based models has shown that RNN model accuracy can grow with respect to increases in length of inputs (i.e., number of encounters per patient in our study) (21). However, their work is built on the assumption that the event sequence is far greater than the number of parameters in our particular dataset, where the average length of sequences is less than the number of features. Future work should study the effect of these sensitivities on the amount of training data needed for model convergence.

There are several potential limitations to our experiments. First, the latent features derived by our RNN model are not explicit or readily interpretable and thus cannot be extracted and compared with features from the LR or RF models. Second, RNN models may plateau in performance because of dataset size constraints. In our experiments, the RNN model did not appear to plateau given a maximum training dataset size, suggesting that the size of our dataset was insufficient to determine the performance limits of this model. Third, LR and RF were implemented according to standard usage for predictive modeling, under which temporal information is not incorporated into the feature construction. It is possible to construct features that have temporal information for LR and RF models, such as using separate Boolean features for each time point for each existing feature (i.e., if a diagnosis of “Hypertension” appears in three successive time points, then create three Boolean features representing “Hypertension at time 1”, “Hypertension at time 2”, “Hypertension at time 3”). In such a situation, generalized estimating equation (GEE) could be used to control for potential inter-correlation among variables. However, such a strategy deviates from standard practice of aggregating repeated appearance of a feature across time points into a single feature, and also introduces extraneous sparsity into the feature space which increases model training time and impedes interpretability. Fourth, we only used outpatient data for the current analysis, in contrast to previous work (7,12) where both inpatient and outpatient data were used. The study by Ng et al. (6,7) used data from a different health system where such data were available. Ng et al. (6,7) demonstrated that information on even a single hospitalization improves predictive accuracy. As a consequence, the AUCs for LR and RF models described herein where consistently lower than those described by Ng et al.

We recommend five possible areas for future work. 1. Data density in existing data domains could be expanded by including new data resources such as claims data, Epic CareEverywhere data, and feature imputation (22,23) among others. Data from Epic’s CareEverywhere offers a potentially valuable source of data on inpatient care and care that is obtained from providers in other systems; 2. Data could be diversified through access to new data domains (e.g., SureScripts medication dispense data, Geographic Information Systems (GIS) data, etc.) to capture information on patient adherence and elaborate on socioeconomic status and to better understand mediators of access to care (i.e. insurance, provider and clinic information, etc.); 3 Temporal features could be added to the feature set for LR and RF models to improve model performance; 4. Higher-level features could be created as composite feature representations from heterogeneous and high-dimensional concepts to leverage clinical domain knowledge or latent features to improve model generalizability and transfer learning methods (24-27); and 5. Previous work suggests that grouping medical concepts in terms of ontologies can lead to substantial performance gains (6,12). Ng et al. observed that construction of features using ontologies for ICD-9 codes and medication classes can lead to improvement in model AUC, and can lead to reduction in the number of features, thus aiding interpretability. We recommend leveraging existing ontologies to improve performance for RNN models.

Finally, while we have demonstrated the effects of data parameters on AUC performance, these efforts do not necessarily advance the translation of models for use in clinical practice. A predictive score is insufficient for use in clinical practice for a heterogeneous disorder like pre-diagnostic heart failure. Specifically, information needs to be extracted from models to inform a physician on the patient features that may be relevant to care decision-making. To this end, additional work is required to calibrate models and understand how patient subgroups or phenotypes should be formed to account for pathophysiologic heterogeneity and differences in care needs. Retrospective EHR datasets can be used to simulate prospective uses of predictive models and implications of different care scenarios for patient subgroups. Moreover, all predictive models are imperfect. False positive and false negative designations will be the norm and criteria will need to be operationalized to determine if watchful waiting or other actions are warranted. In translating models to clinical practice, other performance metrics will be important, including sensitivity, specificity, precision and area under the precision recall curve (AUPRC), among others. For example, under situations where the feature distribution of the cases are richer (less sparse) compared to controls, then the area under the precision recall curve (AUPRC) may be an informative metric.

What is Known:

• A deeper understanding of best practices for predictive modeling of disease outcomes is required amid rising adoption of machine learning based approaches applied to electronic health record (EHR) data.

• Traditional machine learning models used for early detection of disease do not robustly capture temporal information on relationships between clinical events.

What the Study Adds:

• Modeling of temporal relationships between predictive features is possible via a recurrent neural network based model, which yields improved performance for early detection of disease given sufficient training data size.

• Detailed characterization of performance trade-offs in relation to predictive modeling parameters is possible and shows the value and limitations of using recurrent neural network models on heterogenous EHR data sources comprised of temporal events.