Microenvironmental Modulation of Calcium Wave Propagation Velocity in Engineered Cardiac Tissues

Abstract

Introduction

In the myocardium, rapid propagation of action potentials and subsequent calcium waves is critical for synchronizing the contraction of cardiac myocytes and maximizing cardiac output. In many pathological settings, diverse remodeling of the tissue microenvironment is correlated with arrhythmias and decreased cardiac output, but the precise impact of tissue remodeling on propagation is not completely understood. Our objective was to delineate how multiple features within the cardiac tissue microenvironment modulate propagation velocity.

Methods

To recapitulate diverse myocardial tissue microenvironments, we engineered substrates with tunable elasticity, patterning, composition, and topography using two formulations of polydimethylsiloxane (PDMS) micropatterned with fibronectin and gelatin hydrogels with flat or micromolded features. We cultured neonatal rat ventricular myocytes on these substrates and quantified cell density, tissue alignment, and cell shape. We used a fluorescent calcium indicator, high-speed microscopy, and newly-developed analysis software to record and quantify calcium wave propagation velocity (CPV).

Results

For all substrates, tissue alignment and cell aspect ratio were higher in aligned compared to isotropic tissues. Isotropic CPV and longitudinal CPV were similar across conditions, but transverse CPV was lower on micromolded gelatin hydrogels compared to micropatterned soft and stiff PDMS. In aligned tissues, the anisotropy ratio of CPV (longitudinal CPV/transverse CPV) was lower on micropatterned soft PDMS compared to micropatterned stiff PDMS and micromolded gelatin hydrogels.

Conclusion

Propagation velocity in engineered cardiac tissues is sensitive to features in the tissue microenvironment, such as alignment, matrix elasticity, and matrix topography, which may underlie arrhythmias in conditions with pathological tissue remodeling.

Electronic supplementary material

The online version of this article (10.1007/s12195-018-0522-2) contains supplementary material, which is available to authorized users.

Introduction

Cardiac output is dependent on the precisely synchronized contraction of cardiac myocytes throughout ventricular myocardium. Due to the coupling between excitation and contraction,5 synchronous contraction of the myocardium relies on the rapid and uniform propagation of action potentials and subsequent calcium waves across the tissue. Action potentials are transmitted primarily via low-resistance gap junction channels that electrically couple adjacent cardiac myocytes.25,35 In many pathological settings, declines in cardiac output can be attributed to disrupted action potential propagation, which can lead to arrhythmias. For example, in a myocardial infarction, regions of the myocardium become hypoxic and cardiac myocytes quickly undergo necrosis due to their high metabolic demand. This initiates a wound healing response, culminating in cardiac fibroblasts migrating into affected areas and depositing extracellular matrix (ECM) to form scar tissue. Consequently, myocardial tissue in the neighboring infarct border zone undergoes progressive pathological remodeling, characterized by a loss of alignment, remodeling of gap junctions, and/or changes in ECM composition, elasticity, and organization.4,28,43 Cardiac myocytes in the border zone can also be subjected to higher afterload due to increased ECM rigidity secondary to fibrosis and/or elevated pressure, often inducing myocyte hypertrophy.37 Some combination of these factors can alter the path and/or velocity of propagation, increasing the chance of an arrhythmia.10,25,47 Similarly, in hypertrophic cardiomyopathy, the myocardium undergoes fibrotic remodeling and increases in tissue stiffness13,14 coincident with arrhythmogenesis.11 Thus, pathological remodeling of the tissue microenvironment and arrhythmias are often correlated. However, the impact of many microenvironmental features on propagation are still not fully understood. Clearly establishing microenvironmental regulators of action potential and calcium wave propagation will improve our ability to develop effective therapeutic interventions for many cardiac diseases, and can also guide the engineering of customizable cardiac tissues for implantation.

Because microenvironmental features are nearly impossible to precisely and independently control in vivo, researchers have relied on in vitro and in silico approaches to establish how physical features in the tissue microenvironment impact the electrophysiology of cardiac cells and tissues. By leveraging advances in microfabrication, researchers have shown that providing alignment cues to engineered cardiac tissues via microcontact printing,9,16,19 microtopography,12 or nanotopography24 increases action potential duration and the anisotropy ratio of conduction, identifying tissue alignment as a key regulator of conduction. Micropatterned cell pairs have also demonstrated that myocyte shape and cell–cell junction morphology impacts gap junction density and intercellular conductance,30 further illustrating how tissue architecture can impact electrophysiology. Likewise, computational models have predicted that myocyte size and shape, gap junction distribution and conductivity, and interstitial space each impact conduction.44 Several extrinsic mechanical factors have also been shown to impact cardiac electrophysiology. The elastic modulus of the ECM can alter the morphology of calcium transients22 and action potentials,7 and different regimes of cyclic stretch can affect calcium transient morphology,31 increase connexin 43 expression and polarization,41 and increase conduction velocity.48 Thus, diverse forms of structural and mechanical stimuli have been shown to affect select electrophysiological parameters in cardiac cells and tissues. However, pathological remodeling of cardiac tissue typically entails concurrent remodeling of several features in the microenvironment and we still have limited insight into their independent and combined effects on propagation velocity.

In this study, our goal was to establish how tissue architecture and multiple physical features of the ECM affect propagation velocity in cardiac tissue. To achieve this, we cultured neonatal rat ventricular myocytes on isotropic or microcontact printed soft or stiff PDMS substrates, as well as isotropic or micromolded gelatin hydrogels with elastic moduli similar to soft PDMS. This combination of substrates enabled us to partially de-couple tissue alignment and ECM elasticity, topography, and composition. Next, we compared tissue alignment, cell density, cell shape, and calcium wave propagation velocity (CPV). We found that aligned tissues on stiff PDMS and gelatin hydrogels have higher anisotropy ratios of propagation (longitudinal CPV divided by transverse CPV) compared to those on soft PDMS, likely due in part to distinct substrate-mediated changes in myocyte shape. This suggests that the electrophysiological characteristics of cardiac tissue can be affected by the elasticity and/or topography of the ECM, in addition to tissue alignment. These data reveal novel insight into how remodeling of the tissue microenvironment impacts conduction and potentially arrhythmogenesis in many pathological settings.

Methods

Substrate Fabrication

In a Class 100 cleanroom, silicon wafers were spin-coated with SU-8 2002 negative photoresist (MicroChem, 2 µm thickness), exposed to UV light through custom chrome photomasks, and silanized, as previously described.16,27,38 Photomasks had one of two patterns: 10 µm wide lines separated by 10 µm spaces (referred to as 10 × 10) or 15 µm wide lines separated by 2 µm spaces (15 × 2).1 Featureless wafers (referred to as isotropic) were prepared by silanizing virgin wafers. PDMS Sylgard 184 (Dow Corning) was prepared according to manufacturer instructions and was cast on the master wafers to fabricate stamps.

PDMS-coated coverslips were prepared by spin-coating glass coverslips (25 mm diameter) with one of two varieties of uncured PDMS. For the “stiff PDMS,” Sylgard 184 base was mixed with its curing agent at a weight ratio of 10:1 and degassed with a planetary centrifugal mixer (Thinky, AR-100 Conditioning Mixer). For the “soft PDMS,” Sylgard 527 (Dow Corning) was first prepared by mixing and degassing a pre-polymer solution with equal weights of Parts A and B. Sylgard 184 and 527 were then combined at a weight ratio of 1:20, mixed, and degassed.27,36 PDMS solutions were spread onto glass coverslips using a spin coater (Specialty Coating Systems^TM, G3P-8) set to a max speed of 4000 rpm for 1 min. Coverslips were cured at 65 °C for at least 4 h.

Microcontact printing was used to transfer fibronectin in the 15 × 2 or isotropic pattern onto PDMS-coated coverslips, similar to previous studies.16,27 Briefly, PDMS stamps were sonicated in 95% ethanol, dried, and coated with human fibronectin (Corning) at 50 µg/mL for 1 h in a sterile biosafety cabinet. Stamps were blown dry with sterile air and placed onto UVO-treated (Jelight Company Inc., Model 342) PDMS coverslips. Coverslips were rinsed with sterile PBS, sealed with parafilm, and stored at 4 °C until cell seeding.

To fabricate micromolded gelatin hydrogels on coverslips, we adapted previously published protocols.6,29,46 Briefly, glass coverslips (25 mm diameter) were covered with low-adhesive tape. A 17-mm diameter circle was laser-cut (Epilog Mini 24 Laser Engraver, 30 Watt) into the tape and removed from the center. Coverslips were then chemically activated with NaOH, APTES, and glutaraldehyde to improve gelatin hydrogel attachment, as described previously.2,29 Gelatin pre-polymer solution was prepared by mixing equal volumes of 20% w/v gelatin (Sigma, gelatin from porcine skin, ~ 175 g Bloom, Type A) solution at 65 °C and 8% w/v transglutaminase (Activa^® GS transglutaminase, Ajinomoto) solution at 37°C, both prepared with ultrapure water. Thus, the final concentration was 10% w/v gelatin and 4% w/v transglutaminase. Gelatin solutions were mixed for 20 s and degassed for 20 s in a Thinky mixer, taking care to work quickly as the solution solidifies as it cools to room temperature. Drops (~ 0.5 mL) of gelatin pre-polymer solution were pipetted onto the center of the taped and chemically-activated coverslips. 10 × 10 or isotropic stamps were then gently pressed onto the drop, until all edges of the stamp contacted the taped border. Constructs were incubated at room temperature (22 °C) for 12–24 h. The stamps and remaining tape were then carefully removed, leaving behind a layer of cured gelatin hydrogel with either a flat (isotropic) or micromolded 10 × 10 (anisotropic) surface. The height of the micromolded ridges is approximated as 2 µm, based on the thickness of the photoresist used on the master wafer template and our previous measurements with similar substrates.6 Coverslips were rinsed with PBS, partially dried, and sterilized with 1 min of UVO treatment. Coverslips were then rinsed with sterile PBS, sealed with parafilm, and stored at 4 °C until cell seeding.

Cardiac Myocyte Harvest and Culture

Cardiac myocytes were harvested from 2-day old Sprague–Dawley neonatal rats following procedures previously published and approved by the University of Southern California Animal Care and Use Committee.16,27,31 Immediately following euthanasia, ventricles were extracted, cut into 2–5 mm pieces, and incubated in a trypsin solution (1 mg/mL, Affymetrix) for 11–13 h at 4 °C. Tissue was then further digested to a single-cell suspension with 37 °C collagenase (1 mg/mL, Worthington Biochemical Corp) and trituration in four serial steps. The cell solution was strained to remove large debris and pre-plated twice to reduce the population of non-cardiac myocytes.

Cells were seeded onto microfabricated coverslips at 1100 cells/mm² in 6-well plates. Cells were maintained in M199 supplemented with 10% fetal bovine serum (FBS), 10 mM HEPES, 0.1 mM MEM nonessential amino acids, 2 mM l-glutamine, 20 mM d-glucose, 50 U/mL penicillin, and 1.5 µM vitamin B-12. After 2 days, FBS concentration was lowered to 2% to minimize proliferation of non-myocytes. Cells were maintained in an incubator at 37 °C, 5% CO₂, and > 95% relative humidity.

Staining and Quantification of Cell and Tissue Structure

To quantify cell density and actin alignment, tissues cultured for 3 days were incubated for 10 min with 4% paraformaldehyde (PFA) solution containing 0.05% Triton X-100 to fix and permeabilize cells, respectively. Coverslips were rinsed with PBS and inverted onto drops of PBS with monoclonal mouse anti-sarcomeric α-actinin (Sigma, 1:200). After 1–2 h, coverslips were rinsed and inverted onto drops with: 4′,6-diamidino-2-phenylindole (DAPI, 1:200), Alexa Fluor 488 phalloidin (Life Technologies, 1:200), and Alexa Fluor 546 goat anti-mouse (Life Technologies, 1:200). After 1–2 h, coverslips were rinsed, mounted onto glass slides with ProLong Gold Anti-Fade Reagent (Life Technologies), and sealed with nail polish after curing of the mountant.

Stained tissues were imaged on a Nikon Eclipse Ti inverted fluorescent microscope with an Andor Zyla sCMOS camera. For each coverslip, at least five images were collected at randomly selected locations on the tissue using a 60 × oil immersion objective. Cell density was quantified by counting the number of DAPI-positive nuclei in images using a series of filters and functions in ImageJ, such as Gaussian blur and Watershed transform. To calculate tissue alignment, images of actin stained with Alexa Fluor 488 phalloidin were analyzed using custom MATLAB software for edge detection.16 Global tissue alignment was quantified by calculating the orientational order parameter (OOP) of all edges in a coverslip (combined from all images), which ranges from 0 (completely random) to 1 (completely aligned).19

To quantify myocyte length, width, and aspect ratio, tissues cultured for 3 days were incubated with 1 µg/mL di-8 ANEPPS (Life Technologies), a membrane-staining fluorescent dye, for 10–30 min.31 Tissues were then fixed with 4% PFA for 10 min, without Triton X-100. Coverslips were rinsed and maintained in PBS and imaged with a 60 ×  oil immersion objective on a Nikon C2 point-scanning confocal fluorescent microscope within 6 h. A single z-slice of the tissue was imaged and imported into MATLAB. Several representative cells from each image were manually outlined and matched to ellipses. The length, width, and length:width aspect ratio of the ellipses were averaged for each coverslip and counted as one data point.

Quantification of CPV

To measure CPV, tissues cultured for 3 days were incubated with 1.7 µg/mL Fluo-4 AM calcium-sensitive dye (Life Technologies) in 0.06% Pluronic-127 for 20–40 min, immersed in Tyrode’s solution (5.0 mM HEPES, 1.0 mM magnesium chloride, 5.4 mM potassium chloride, 135.0 mM sodium chloride, 0.33 mM sodium phosphate, 1.8 mM calcium chloride, 5.0 mM d-glucose, pH 7.4 at 37 °C), and moved to the stage of a Nikon Eclipse Ti inverted fluorescent microscope within a 37 °C incubation chamber. After 10 min of acclimation, a platinum point-stimulation electrode was positioned outside of the field of view using a micro-manipulator (Eppendorf, PatchMan NP 2). The electrode was interfaced with a Myopacer (IonOptix, Model MYP100) to deliver 10 V biphasic, charge-balanced pulses at 1 Hz. For aligned tissues, the pacing electrode was positioned such that the calcium wave crossed the tissue in one of two directions: longitudinal (in the direction of tissue alignment) or transverse (perpendicular to tissue alignment). Image sequences (3–4 s) were recorded using a 2 ×  objective lens and an Andor Zyla sCMOS camera at 100 frames per second at 8 binning and a gain of 4.

Custom MATLAB software was developed to calculate CPV from image sequences. First, a Gaussian filter was applied to each frame and the average fluorescence intensity of each frame was calculated. The waveform of fluorescence intensity was periodic at 1 Hz when tissues were captured successfully, which allowed for automatic splitting of each image sequence into individual activation cycles. For each activation cycle, the mean and standard deviation of fluorescence intensity was calculated for every pixel. The activation threshold for each pixel was calculated as the mean plus 0.5 standard deviations. The activation time for each pixel was detected as the time when the fluorescence intensity of the pixel exceeded the activation threshold. Together, the activation times of each pixel were used to form a 2D activation map that displays the wave of calcium release across the tissue.

Due to our large field of view, calcium wave-fronts were typically circular or elliptical, which can confound uniaxial conduction velocity measurements. Thus, to more accurately measure uniaxial conduction velocity, activation maps were manually cropped to the center section of the ellipse of the wave. This removal corrects for parts of the wave travelling in a direction other than the defined direction. To calculate CPV, the x-position (mm) of each pixel of the cropped activation map was plotted against its activation time (s). Robust linear regression was used to automatically remove outlier pixels and to fit a line to the data. CPV was defined as the slope of the regression line (cm/s). If the quality of the fit was low, (robust_s > 13, a measure of the variance from the linear fit), then the measurement was excluded. This unbiased vetting process automatically removes cycles that have abnormal paths of conduction due to gaps in the tissue, etc.

Statistical Analysis

Each condition includes at least five total coverslips (n ≥ 5) from at least three separate cell harvests. All conditions were tested for normality with Lilliefors’ test. If every condition was found to be normally distributed, each subset was tested with one-way ANOVA. Otherwise, the Kruskal–Wallis test was used. p values of pairwise comparisons were calculated with a Fisher’s Least Significant Difference (LSD) Test. If only two conditions were compared, an unpaired, two-tailed Student’s t test was used. Significance was defined as a p-value of 0.05 or less.

Results

Fabrication of Tunable Matrices for Engineering Cardiac Tissues

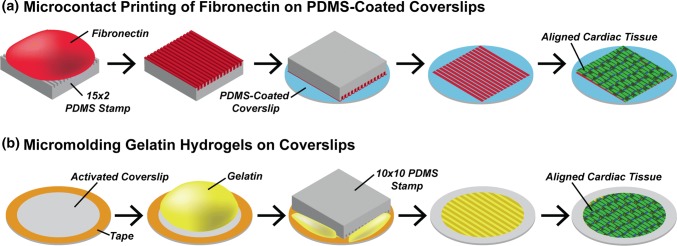
In many pathological settings, cardiac myocytes experience diverse changes in their microenvironment, including variations in tissue alignment, ECM rigidity, and/or ECM topography.4,13,14,28,37 To determine how select features in the microenvironment independently and jointly impact CPV in cardiac tissue, we first fabricated several types of culture substrates with defined alignment, rigidity, and topography, as shown in Fig. 1. To independently modulate tissue alignment and ECM rigidity, we spin-coated coverslips with stiff (elastic modulus: 2.7 MPa) or soft (elastic modulus: 27 kPa) PDMS27 and microcontact printed fibronectin on the surface as either 15 × 2 lines or a uniform coating. The 15 × 2 pattern was chosen because myocytes are known to align longitudinally to the 15 µm-wide lines of fibronectin while also connecting laterally across the relatively narrow 2 µm-separation, inducing the formation of a confluent, aligned tissue without major gaps.1,27 We also fabricated flat and 10 × 10 micromolded gelatin hydrogels. Because cardiac myocytes naturally adhere to gelatin hydrogels without additional surface modifications, cardiac myocytes seeded on flat and micromolded gelatin hydrogels form confluent isotropic and aligned tissues, respectively.29 Previously, we measured the elastic modulus of this gelatin hydrogel formulation as 55 kPa29 and the height of micromolded features as approximately 2 µm.6 In contrast, the height of microcontact printed-fibronectin on PDMS has been reported as approximately 8 nm.17 Thus, micromolded gelatin hydrogels have rigidity similar in magnitude to microcontact printed soft PDMS, but rely on micromolded ridges for cell alignment instead of the presence or absence of fibronectin, which has relatively negligible height.

Figure 1.

Substrate micropatterning and cardiac tissue engineering. (a) Schematic of microcontact printing protocol to transfer FN onto soft and stiff PDMS; (b) schematic of protocol for micromolding gelatin hydrogels. Both micropatterned substrates were seeded with neonatal rat ventricular myocytes, which formed confluent and aligned tissues.

Characterization of Engineered Cardiac Tissue Structure

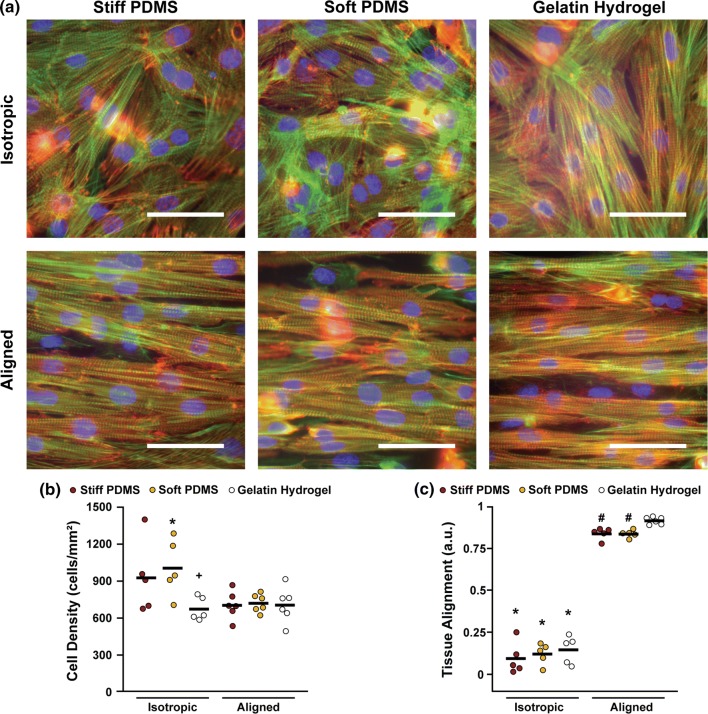
Next, we isolated and cultured neonatal rat ventricular myocytes on all substrates, which self-assembled into tissues after 3 days. Because cell density, tissue alignment, and myocyte shape can impact propagation,44 we quantified these structural parameters by first staining and imaging nuclei, actin, and sarcomeric α-actinin. As shown in Fig. 2a, isotropic and aligned tissues self-assembled on each micropatterned surface with the expected orientation and were relatively confluent in all directions. To measure cell density, we counted the number of nuclei in multiple fields of view for multiple tissues. As shown in Fig. 2b, isotropic tissues on soft PDMS had higher cell density than those on isotropic gelatin hydrogels. Isotropic tissues on soft PDMS were also denser than their aligned counterparts, potentially because of the slight increase in fibronectin coverage on coverslips patterned with featureless stamps compared to 15 × 2 stamps. A similar trend between isotropic and aligned tissues was observed on stiff PDMS, although this was not statistically significant. Although cell density was variable within isotropic tissues, it was similar within aligned tissues across all substrates.

Figure 2.

Tissue density and alignment. (a) Representative images of cardiac tissues engineered on each substrate (blue: nuclei, green: actin, red: sarcomeric α-actinin, scale bars: 50 µm). Cell density (b); and tissue alignment (c) for tissues on each substrate. *p < 0.05 compared to corresponding aligned condition, ⁺p < 0.05 compared to isotropic soft PDMS, ^#p < 0.05 compared to aligned gelatin hydrogel. Statistics details are provided in Supplemental Tables 1–2.

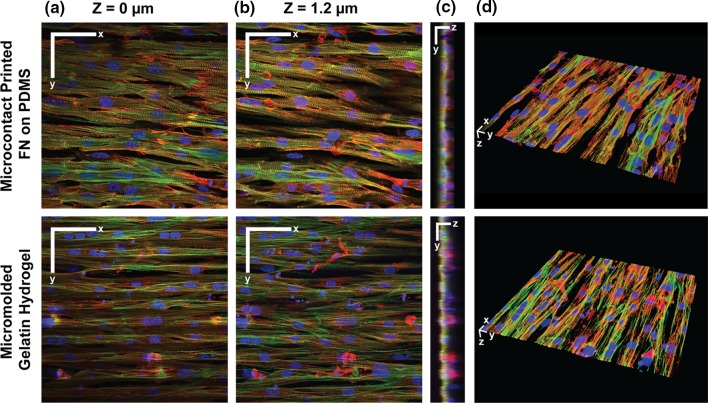
To quantify tissue alignment, we measured the OOP of stained actin filaments in engineered tissues. As shown in Figs. 2a and 2c, all aligned tissues were significantly more aligned than their isotropic counterparts, as expected. When considering only aligned tissues, those on micromolded gelatin hydrogels had a higher OOP than those on either stiff or soft PDMS microcontact printed with 15 × 2 fibronectin. To investigate differences in tissue topography, we collected z-stacks of tissues to visualize their 3D microstructure. Aligned tissues on microcontact printed PDMS were relatively uniform and confluent at lower (Fig. 3a) and higher tissue slices (Fig. 3b), suggesting that the 15 × 2 lines of microcontact printed fibronectin dictated the direction of cell spreading, but did not physically constrain cell morphology in the z-direction. Conversely, aligned tissues on micromolded gelatin hydrogels were relatively confluent at a higher tissue slice (Fig. 3b), but were clearly confined to 10 µm wide lines at a lower tissue slice (Fig. 3a). Similarly, yz-projections (Fig. 3c) and 3D reconstructions (Fig. 3d) of tissues on microcontact printed PDMS were mostly flat, but tissues on micromolded gelatin hydrogels had a near square-wave profile in the z-direction. These distinct tissue topographies correspond to the differences in feature height between micromolded gelatin hydrogels and microcontact printed PDMS, as mentioned above. Together, these data indicate that both microcontact printing and micromolding induced tissue alignment, but for our specific micropatterning parameters, micromolding was a slightly stronger cue that also confined cell spreading and impacted tissue topography.

Figure 3.

3D imaging of engineered tissues. xy-sections at z = 0 µm (a); and z = 1.2 µm (b); yz-projections (c); and 3D reconstructions (d) of tissues engineered on PDMS microcontact printed with fibronectin (FN) (top) and micromolded gelatin hydrogels (bottom). In (a) and (b), scale bars: 50 µm. In (c), y-scale bar: 20 µm, z-scale bar: 4 µm. In (d), scale bars: 10 µm. For all images, blue: nuclei, green: actin, red: sarcomeric α-actinin.

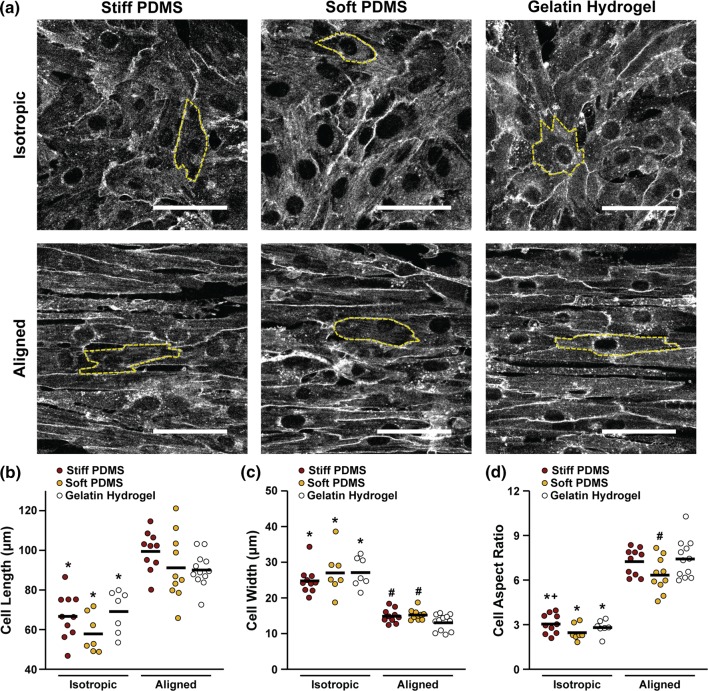
To evaluate myocyte shape differences, we stained engineered tissues with a membrane dye (Fig. 4a) and measured cell length, width, and aspect ratio. As shown in Figs. 4b–4d, cells in aligned tissues were longer and thinner and had a higher aspect ratio than their isotropic counterparts, as expected. Surprisingly, within isotropic tissues, cells on stiff PDMS had a higher aspect ratio than soft PDMS. Within aligned tissues, cells on micromolded gelatin hydrogels were significantly thinner than those on microcontact printed soft and stiff PDMS. Consequently, myocyte aspect ratio was significantly higher on micromolded gelatin hydrogels compared to microcontact printed soft PDMS. Additionally, aligned cells on stiff PDMS were slightly longer and had a slightly higher aspect ratio compared to those on soft PDMS, although these differences were not statistically significant. These results suggest that micromolding and microcontact printing have distinct effects on myocyte shape, while ECM elasticity may also have some subtle effects.

Figure 4.

Cell Shape. (a) Representative images of di-8-ANEPPS membrane staining for cardiac tissues engineered on each substrate. Dotted yellow lines indicate individual cells used to calculate cell shape (scale bars: 50 µm). Cell length (b); width (c); and aspect ratio (d) measured from outlined cells. *p < 0.05 compared to corresponding aligned condition, ⁺p < 0.05 compared to isotropic soft PDMS, ^#p < 0.05 compared to aligned gelatin hydrogel. Statistics details are provided in Supplemental Tables 3–5.

CPV Measurements

To measure CPV, we incubated tissues with Fluo-4 calcium-sensitive dye, transferred tissues to an inverted fluorescent microscope, and paced tissues at 1 Hz with an electrode positioned to the left of the imaging field. While pacing the tissues, we recorded Fluo-4 signal within a relatively large field of view (8.32 × 7.02 mm) at 100 fps to ensure sufficient spatiotemporal sampling for CPV calculations. For aligned tissues, we measured both longitudinal CPV and transverse CPV by adjusting the position of the electrode relative to the orientation of the tissue.

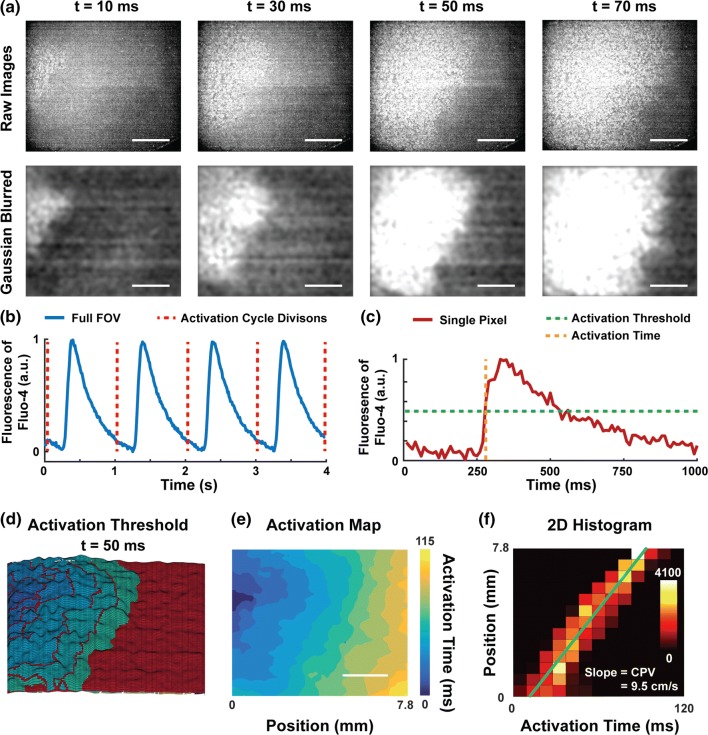
To quantify CPV from Fluo-4 image sequences, we developed and implemented custom MATLAB software. Our software first removes noise with a Gaussian filter (Fig. 5a), then plots the average brightness of each image in each 3–4 s sequence over time (Fig. 5b). The periodicity of the image is then used to automatically detect and separate each activation cycle. Waveforms that do not match 1 Hz are automatically excluded, as this indicates imperfect capture by the pacing electrode. The activation threshold and activation time is then calculated for each pixel in the image sequence based on its mean and standard deviation (Fig. 5c). This per-pixel approach is advantageous because it corrects for brightness differences or optical aberrations across the field of view, which are common in our datasets due to our use of a low-power, 2 ×  objective lens. To demonstrate per-pixel thresholding, we created a surface plot for a representative tissue, with the per-pixel activation threshold represented as a red surface (Fig. 5d and Supplemental Movie 1). Note that the activation threshold varies slightly for each pixel due to local variations in signal-to-noise. As a pixel exceeds its own activation threshold, it is assigned a color that indicates its activation time. Thus, each color represents an isochrone and clearly shows the leading edge of the propagating calcium wave. Our software also creates a 2D activation map, which indicates the activation time for each pixel in the tissue, as shown in Fig. 5e. Next, the distance of every pixel from the left edge of the activation map (closest to the electrode) is plotted against its activation time and a line is matched to these points with robust linear regression. For demonstration purposes, we plotted a 2D histogram with each activation time represented as a separate column (Fig. 5f), which are separated by the sampling period of the camera (10 ms). Note the relatively high number of data points. The slope of that line is then calculated and defined as the CPV. The robust linear regression function within MATLAB provides a metric (robust_s) of the closeness of fit of the data to a line, which we used to automatically remove noisy datasets that typically had tissue defects.

Figure 5.

Flowchart of data processing for CPV. (a) High-speed videos of Fluo-4 calcium transients were Gaussian blurred (scale bars: 2 mm). (b) The average fluorescence signal for the full field of view (FOV) of a tissue over 4 s is shown. Automatic peak detection was used to divide the signal into activation cycles. (c) The fluorescence signal for a single pixel over one activation cycle is shown, with activation threshold and activation time indicated. (d) 3D visualization of activation thresholds and fluorescence 50 ms after initial activation. The z-height of the red surface indicates the activation threshold for each pixel. The other colors are isochrones of activation times, matching the color bar in (e). Within the isochrones, the height represents the fluorescence magnitude of that pixel at the given timepoint. (e) The activation time of each pixel is plotted to generate an activation map (scale bar: 2 mm). (f) The horizontal position of a pixel is plotted against its activation time. The color of each square corresponds to the number of pixels within that square, as indicated by the color bar. Robust linear regression is used to match a line to the data (green), with the slope indicating the CPV.

Because calcium wave fronts are curved or elliptical, with the wave travelling perpendicular to the tangent of that curve, we cropped the activation maps to confine our data to the segment of the wave front travelling parallel to our defined uniaxial measurement direction. Example activation maps are shown in Fig. 6, with cropped areas outlined with dotted lines. The calcium wave is more elliptical on aligned tissues than on isotropic tissues, causing the cropping to typically be narrower on longitudinal measurements and wider on transverse measurements. Without this cropping step, our software calculates artificially high CPV in regions where the wave is not travelling parallel to our measurement direction. Cropping naturally reduces the number of pixels included in each dataset. However, the removed pixels are systematically biased upwards, as shown in Fig. 7a. Thus, the pixels removed by cropping are not an accurate reflection of CPV in the defined direction and would confound our measurements if not eliminated. Cropping the maps also tends to decrease noise and variability in measurements, allowing more cropped samples to pass our automatic vetting process than full FOV samples.

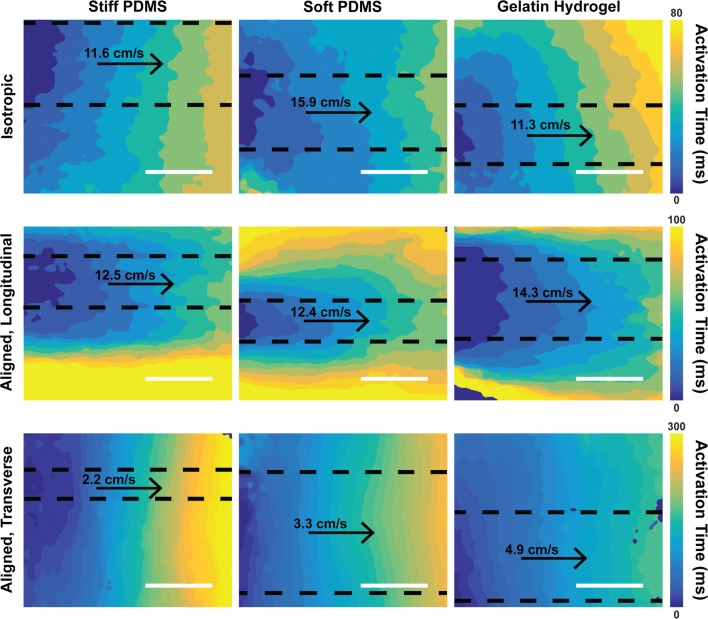
Figure 6.

Activation maps. Representative activation maps for tissues engineered on each substrate. Aligned tissues have both longitudinal and transverse measurements, which correspond to waves travelling parallel and perpendicular to the direction of tissue alignment, respectively. Areas manually chosen for uniaxial CPV measurements are outlined by black dotted lines. The CPV for each activation map is indicated above the arrow indicating the direction of the wave. Each row is scaled to the color bar at the end of that row. Scale bars: 3 mm.

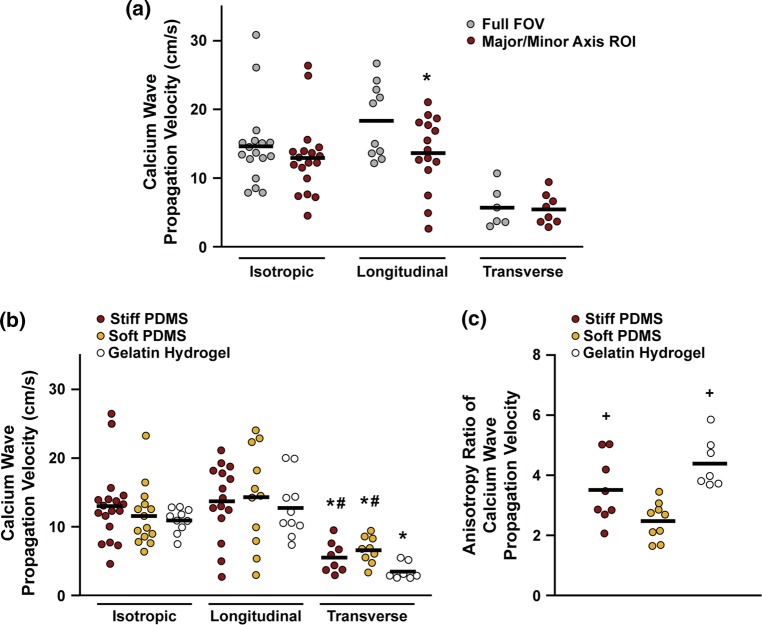
Figure 7.

CPV and anisotropy ratio of CPV. (a) CPV calculated from the full field of view (FOV) of tissues on stiff PDMS compared to those from manually cropped regions of interest (ROI) corresponding to the major/minor axis of the ellipse of the traveling wave. *p < 0.05 compared to corresponding Full FOV CPV. CPV (b) and anisotropy ratio of CPV (c) for tissues on each substrate. In (b), *p < 0.05 compared to corresponding longitudinal and isotropic condition, ^#p < 0.05 compared to transverse, aligned gelatin hydrogel. In (c), ⁺p < 0.05 compared to soft PDMS. Statistics details are provided in Supplemental Tables 6–8.

As shown in Fig. 7b, all isotropic tissues had similar CPV, suggesting that ECM rigidity and substrate composition had minimal impact in isotropic tissues. In aligned tissues, longitudinal CPV was significantly higher than transverse CPV for each substrate, confirming tissue anisotropy and matching results from previous studies that relied on voltage-sensitive dyes.9,12,16 Longitudinal CPV was similar across all conditions, suggesting that microcontact printing and micromolding did not differentially influence longitudinal CPV. However, transverse CPV was significantly lower on micromolded gelatin hydrogels compared to stiff and soft PDMS microcontact printed with fibronectin. This is consistent with some of the changes in cell and tissue architecture that we observed, such as reduced myocyte width on micromolded gelatin hydrogels compared to stiff and soft PDMS microcontact printed with fibronectin.

Next, we compared the anisotropy ratios of CPV (longitudinal CPV divided by transverse CPV) for the aligned tissues. As shown in Fig. 7c, aligned tissues on soft PDMS had a significantly lower anisotropy ratio than those on stiff PDMS and gelatin hydrogels. The higher anisotropy ratio on micromolded gelatin hydrogels is consistent with reduced cell width and decreased transverse CPV, both of which contribute to increases in anisotropy ratio. However, the higher anisotropy ratio on stiff PDMS compared to soft PDMS indicates that the elasticity of the substrate alone also impacts CPV, potentially due to subtle changes in cell shape we also observed. Thus, our data suggests that CPV is sensitive to multiple factors in the cardiac tissue microenvironment.

Discussion

Several features within the tissue microenvironment are known to impact many structural and functional phenotypes in cardiac myocytes, including contractility2,15,32 and metabolism.27,29 However, relationships between the cardiac tissue microenvironment and propagation velocity are less understood. In this study, we investigated how micropatterned PDMS and gelatin hydrogels with distinct geometry, elasticity, topography, and composition affect the structure and CPV in engineered cardiac tissues. Our results indicate that tissue alignment, ECM topography, and ECM rigidity impact CPV in aligned cardiac tissues to different extents, likely due to distinct changes in cell and tissue architecture. These data have important implications for understanding mechanisms of arrhythmogenesis in the many cardiac pathologies associated with diverse remodeling of the tissue microenvironment. Additionally, our data raise important points to consider when engineering scaffolds for cardiac patches intended for implantation and integration with host myocardium after an injury.

For this study, we fabricated substrates designed to mimic characteristics of healthy and diseased cardiac microenvironments. The soft PDMS substrate had an elastic modulus of 27 kPa, similar to healthy myocardium.4 The stiff PDMS substrate had an elastic modulus of 2.7 MPa, which more closely mimics fibrotic tissue after a myocardial infarction or in pathological hypertrophy.4,23 Although the elastic modulus of the stiff PDMS is an order of magnitude greater than passive measurements of pathological cardiac tissue,4,23 many cardiac diseases are also associated with increased pressure, which can increase afterload similar to the high load applied by the stiff substrate. The gelatin hydrogel had an elastic modulus of 55 kPa, which is the same order of magnitude as soft PDMS and slightly higher than passive measurements of healthy cardiac tissue.4 Softer gelatin hydrogels were difficult to fabricate because they often failed to cleanly detach from the stamp, preventing us from testing softer hydrogels. All three materials were either micropatterned uniformly or with parallel lines to cue tissues to become isotropic or aligned and mimic the architecture of diseased or healthy myocardium, respectively. Thus, with these combination of substrates, we independently defined the geometry, elasticity, topography, and composition of the ECM and recapitulated features of healthy and diseased myocardium.

In the myocardium, action potentials must propagate through both the cytoplasm and gap junctions. Cytoplasmic resistance is known to be substantially lower than the resistance of gap junctions.44 For this reason, the propagation of action potentials and subsequent calcium waves is greatly influenced by parameters such as tissue confluence, tissue alignment, and myocyte shape, which we quantified as potential mediators of CPV. Cell density was similar in all aligned tissues, suggesting that cell density and tissue confluence were not root causes of the differences we observed in CPV. Tissue alignment was similar within isotropic tissues, but tissues on micromolded gelatin hydrogels were more aligned than both soft and stiff microcontact printed PDMS. Additionally, cells were thinner on micromolded gelatin hydrogels compared to soft and stiff microcontact printed PDMS. These differences could be due to the slightly different widths of the micropatterns on the two surfaces (10 µm-wide ridges with 10 µm-wide separation on gelatin hydrogels, 15 µm wide lines of fibronectin separated by 2 µm-wide gaps on soft and stiff PDMS). Furthermore, as shown in our 3D image reconstructions, the 2 µm-high micromolded features on gelatin hydrogels imposed physical confinement of cell spreading in the lateral direction. Conversely, PDMS surfaces microcontact printed with fibronectin are relatively flat and thus are less constrictive to cell spreading in the lateral direction. These differences in micropatterned feature height could have also contributed to increased tissue alignment and decreased cell width on micromolded gelatin hydrogels compared to microcontact printed PDMS.

Our results indicate that transverse CPV was lower and anisotropy ratio of CPV was higher on micromolded gelatin hydrogels compared to microcontact printed soft PDMS. Because these substrates have relatively similar elastic moduli, these data suggest that surface topography influences CPV in aligned tissues, likely due in part to the confinement of cell spreading in the lateral direction and subsequent decreases in cell width, as mentioned above. Another consideration is that cells within the grooves are lower in the z-direction, which increases the distance in 3D space that must be travelled by a transverse wave. Additionally, the composition of these substrates in terms of ECM protein and water content are also very different, which could contribute to differences in CPV. However, because CPV was similar in isotropic tissues, substrate composition alone likely did not have a major effect on CPV.

We also found that tissues on microcontact printed stiff PDMS had a higher anisotropy ratio of CPV compared to those on microcontact printed soft PDMS. This functional difference could be explained by some of the geometric changes we observed in these tissues. Cells in aligned tissues on stiff PDMS were slightly longer and had a slightly higher aspect ratio compared to soft PDMS, although neither difference was statistically different. Interestingly, in isotropic tissues, cell aspect ratio on stiff PDMS was significantly higher than on soft PDMS. These results are suggestive of a hypertrophic response of cells on stiff PDMS that is biased towards increasing myocyte length rather than width. Longitudinal CPV was similar on soft and stiff PDMS, while transverse CPV was slightly lower on stiff PDMS (although not statistically significant). These relatively subtle differences in cell length, cell aspect ratio, and transverse CPV potentially had a combinatorial effect, manifesting in a higher anisotropy ratio of CPV in aligned tissues on stiff PDMS compared to soft PDMS. Because these substrates differed primarily in elastic modulus, these data suggest that ECM elasticity can also impact CPV, potentially by promoting growth of myocytes in the longitudinal direction.

Our data have implications for understanding how remodeling of the ECM and tissue microarchitecture contributes to arrhythmogenesis in pathological settings. For example, concentric hypertrophy is associated with increased fibrosis and/or wall stress, decreases in myocyte aspect ratio, and thickening of the ventricular wall.18,20,21,42 This condition commonly progresses to eccentric hypertrophy, associated with increased myocyte aspect ratio, dilation of the ventricle, and ultimately heart failure.18,20 Both of these conditions, and many others characterized by pathological ECM remodeling, such as hypertension,3 are also associated with arrhythmias.8,11 Our findings suggest that the elasticity and/or microscale geometric features in the ECM can alter CPV by mechanisms including, but not limited to, remodeling of myocyte shape. Thus, our data deepens our understanding of how remodeling of multiple features within the tissue microenvironment may increase the risk of arrhythmia for patients with many types of cardiac disease. However, further experiments are required to more precisely delineate relationships between the many complex features of the ECM, tissue microstructure, and arrhythmia.

In our experiments, we measured CPV instead of directly measuring action potential conduction velocity. Our rationale is that, compared to voltage-sensitive dyes, calcium-sensitive dyes are generally less toxic and have greater fluorescent signal compared to voltage-sensitive dyes, allowing for imaging with lower power objectives for longer periods of time. Additionally, several studies have shown that calcium waves immediately follow action potentials26,45 and thus CPV likely approximates action potential propagation velocity. However, this is an unproven assumption for the data presented here and is a limitation of our overall approach.

For our experiments, we recorded movies of Fluo-4 fluorescence in tissues using a standard inverted fluorescent microscope and a high-speed camera. This setup requires relatively standard laboratory imaging equipment that has many uses beyond these specific experiments, in contrast to many expensive and customized optical mapping systems, such as fiber-optic9,16 or microelectrode arrays.33,34 Our approach also affords greater spatial resolution compared to most fiber-optic and microelectrode array systems and thus can be used to more clearly detect the spatial variability of propagation across a tissue. This feature could be useful for characterizing the electrophysiological effects of spatial gradients, such as elastic modulus or cell distribution, across a tissue. The drawback is that our approach has lower temporal sampling frequency, which impedes measuring dynamic, high-resolution features of calcium waves, such as rise time and duration. However, higher temporal sampling frequency is not actually needed to measure CPV. Temporal resolution can be improved by reducing the field of view or measuring only a single line of pixels. However, this comes at the expense of increased noise and decreased spatial resolution, which may or may not be critical for a certain experiment.

To calculate CPV, we developed new data analysis software in MATLAB to automate much of the computation and reduce user intervention. By using a robust linear regression algorithm, our software automatically excluded noisy pixels and non-linear datasets to remove video segments with high amounts of noise and unnatural wave fronts, which could be caused by tissue defects, uneven dye uptake, etc. Additionally, our processing software is easily scalable because there are few manual inputs into the system. Thus, our overall experimental approach and analysis software is relatively streamlined for rapidly measuring and calculating CPV within engineered cardiac tissues.

Due to its scalability, our approach is well-suited for higher-throughput applications, such as drug screening. For example, drugs often fail clinical trials due to off-target effects on the heart, such as increased risk of arrhythmia.40 One common approach for establishing arrhythmia risk pre-clinically is to use cell lines expressing the human ether-a-go-go (hERG) potassium channel, which repolarizes cardiac myocytes at the end of the action potential and is commonly blocked by drugs with pro-arrhythmic side effects.39 The activity of this channel in response to drugs is typically assessed with an automated patch clamp system, which can detect changes in hERG activity that commonly progress to arrhythmias. In vivo tests and in silico simulations are also used to screen for drug toxicity, but in vivo testing is expensive and relatively inefficient and in silico simulations cannot successfully predict all cardiotoxic effects. Unlike these existing platforms, our system can be used to efficiently establish cardiotoxic and/or arrhythmogenic side effects that present at the multi-cellular tissue level, thereby complementing the type of data currently collected with existing hERG screens and in vivo and in silico experiments.

For our system to be adopted for drug screening, one critical improvement is to replace the neonatal rat ventricular myocytes with human induced pluripotent stem cell (hiPSC)-derived cardiac myocytes to increase human relevance and predictive power. Because hiPSC-derived cardiac myocytes can be generated directly from patients, characterizing these cells with our platform will facilitate personalized disease modeling and drug screening. Importantly, because we can also tune the ECM, integrating hiPSC-derived cardiac myocytes with our platforms and software will allow us and others to tease apart the genetic and microenvironmental contributions to conduction velocity and arrhythmias in many different pathological settings. Thus, combining hiPSC-derived cardiac myocytes, our tunable ECM platforms, and our scalable analysis software is one approach to efficiently establish complex, multi-factorial mechanisms of arrhythmogenesis and potential drug targets in a human-relevant system.

The myocardium is a complex tissue consisting of multiple cell types and mechanical stimuli. In this study, we used a simplified model system to identify how the tissue microenvironment impacts CPV in engineered tissues consisting primarily of cardiac myocytes. Future studies will integrate more complex features, such as supporting cell populations and additional forms of mechanical stimuli. Propagation velocity in cardiac tissue is also controlled by many factors beyond tissue architecture, including the expression and localization of gap junctions and ion channels. Future studies will also focus on establishing any molecular mechanisms driving the functional differences we observed here. In summary, our data expands our understanding of the impact of the microenvironment on electrophysiology and arrhythmogenesis in native myocardium and engineered cardiac tissues. Additionally, the workflow and software we established can be extended to many applications in human disease modeling and drug screening.

Electronic supplementary material

Below is the link to the electronic supplementary material.