A Rare Variant Nonparametric Linkage Method for Nuclear and Extended Pedigrees with Application to Late-Onset Alzheimer Disease via WGS Data

Abstract

To analyze family-based whole-genome sequence (WGS) data for complex traits, we developed a rare variant (RV) non-parametric linkage (NPL) analysis method, which has advantages over association methods. The RV-NPL differs from the NPL in that RVs are analyzed, and allele sharing among affected relative-pairs is estimated only for minor alleles. Analyzing families can increase power because causal variants with familial aggregation usually have larger effect sizes than those underlying sporadic diseases. Differing from association analysis, for NPL only affected individuals are analyzed, which can increase power, since unaffected family members can be susceptibility variant carriers. RV-NPL is robust to population substructure and admixture, inclusion of nonpathogenic variants, as well as allelic and locus heterogeneity and can readily be applied outside of coding regions. In contrast to analyzing common variants using NPL, where loci localize to large genomic regions (e.g., >50 Mb), mapped regions are well defined for RV-NPL. Using simulation studies, we demonstrate that RV-NPL is substantially more powerful than applying traditional NPL methods to analyze RVs. The RV-NPL was applied to analyze 107 late-onset Alzheimer disease (LOAD) pedigrees of Caribbean Hispanic and European ancestry with WGS data, and statistically significant linkage (LOD ≥ 3.8) was found with RVs in PSMF1 and PTPN21 which have been shown to be involved in LOAD etiology. Additionally, nominally significant linkage was observed with RVs in ABCA7, ACE, EPHA1, and SORL1, genes that were previously reported to be associated with LOAD. RV-NPL is an ideal method to elucidate the genetic etiology of complex familial diseases.

Introduction

In recent years, there has been a great effort to understand the genetic contribution of rare variants (RVs) to the etiology of complex traits and diseases. The ability to study RVs has been greatly influenced by the availability of massively parallel sequencing, which led to the generation of whole-genome and -exome sequence data for hundreds of thousands of individuals. Most whole-genome and -exome sequence-based complex trait studies are performed using either case-control or population-based data,^{1, 2} but several studies have generated sequence data on families.^{3, 4} Although there are many RV aggregate association methods to analyze case-control and population-based data,^{5, 6, 7, 8, 9, 10, 11} only a few have been developed to analyze families.^{4, 12, 13, 14, 15, 16} In addition to using family-based RV association methods to identify disease loci, linkage analysis can also be performed. Although parametric linkage analysis is inappropriate for complex trait analysis, non-parametric linkage (NPL)¹⁷ (also known as model free or allele sharing methods) is a powerful approach to identify disease loci in families. Although RV parametric linkage methods have been developed,¹⁸ this is not the case for NPL analysis.

Analyzing families segregating complex diseases can increase power to detect association signals compared to analyzing simplex cases, because pathogenic susceptibility variants segregating in pedigrees with multiple affected family members tend to have larger effect sizes.^{19, 20} Additional power can be obtained by analyzing multiple affected family members since frequencies of RVs tend to be increased and their heterogeneity reduced, compared to analyzing samples of unrelated case and control subjects. Therefore, when available, it is highly beneficial to analyze family data for complex traits.

For family-based association analysis, unaffected family members must be included in the analysis, but these unaffected individuals may be asymptomatic carriers of susceptibility variants because for complex traits penetrance can be incomplete.²¹ This is even a greater problem for diseases with late onset age, since many unaffected family members will be below or within the age of onset. Additionally, RV aggregate association methods are generally sensitive to inclusion of non-causal variants.²²

For NPL, the underlying assumption is that affected relatives will share identical by descent (IBD) susceptibility alleles or alleles that are in linkage disequilibrium (LD) with pathogenic variants.²³ Several NPL methods for common variants (minor allele frequency [MAF] > 0.05) have been developed for nuclear and extended families. For nuclear families, allele sharing is compared for affected sibpairs and it is determined if sharing deviates from the expectation under the null using the chi-square goodness-of-fit test,^{24, 25} maximum LOD score test (MLS),^{26, 27, 28} mean test,²⁹ proportion test,^{30, 31}or minmax test.³² Methods for extended pedigrees include the Affected Pedigree Member (APM) method,³³ which is obsolete since it analyzes identical-by-state (IBS) sharing, rather than IBD, and has increased type I and II errors. Kruglyak and colleagues developed an NPL approach,¹⁷ which is based upon IBD sharing between affected family members. For this NPL method, there are several sharing measures, which include the commonly used S_Pairs, which measures IBD sharing within and between relative pairs, and S_All, which estimates the number of alleles from distinct affected pedigree members that are IBD. NPL methods have also been extended to perform multipoint linkage analysis.^{17, 26, 34, 35, 36} These methods, although widely used, had limited success because causal susceptibility variants could not be identified due to disease loci mapping to large genetic intervals, e.g., > 50 Mb. Large intervals occur within families due to long-range LD between common variants. For common variants, locus heterogeneity is an additional problem, because it can dilute the linkage signal and increase the size of the mapped region.^{37, 38, 39} Despite these limitations for the analysis of common variants, applying NPL to analyze RVs can overcome these problems. To further increase the power of analyzing RV using the NPL, an RV-specific method was developed, the RV-NPL, which examines sharing of only RV minor alleles to calculate the test statistic.

For the RV-NPL, an extension of the Kruglyak et al. NPL approach,¹⁷ a regional locus is generated to analyze RVs in aggregate using the collapsed haplotype pattern (CHP) method.¹⁸ IBD sharing is determined using the pedigree-specific regional locus and two IBD methods were developed: CHP-NPL and RV-NPL. As was performed for the NPL method, the CHP-NPL estimates IBD sharing for both major and minor alleles, i.e., haplotypes with at least one RV and haplotypes without any RVs. The RV-NPL estimates IBD sharing only for minor alleles, i.e., haplotypes that carry at least one RV. Using simulation studies and analyzing RVs (MAF < 0.01), the performance of CHP-NPL, RV-NPL, and multipoint NPL was compared. Although the power for the multipoint NPL and CHP-NPL are similar, the RV-NPL is substantially more powerful. When parental genotype data are missing, multipoint NPL analysis can have considerable inflated type I error rates⁴⁰ since the assumption that markers are in linkage equilibrium may be violated. Although markers can be pruned to remove LD, this can lead to a loss in power.⁴¹ Therefore, it is not advisable to use multipoint NPL analysis when there is missing parental genotypes, which often occurs in family-based studies. For CHP-NPL and RV-NPL, type I error rates are well controlled. CHP-NPL and RV-NPL are both robust to population substructure and admixture between and within families, inclusion of nonpathogenic variants, and allelic and locus heterogeneity. In contrast to performing NPL analysis with common variants, the CHP-NPL and RV-NPL usually detect linkage to a small region, e.g., a gene, due to the low levels of LD between RVs. Both methods can also be used to analyze either gene regions or complete genomes using recombination events as boundaries for the regional locus. However, due to the superior power of the RV-NPL, it is recommended to use this method instead of the CHP-NPL.

The RV-NPL was applied to analyze whole-genome sequence (WGS) data generated on 107 nuclear and extended pedigrees with late-onset Alzheimer disease (LOAD) from the Alzheimer disease Sequencing Project (ADSP, dbGaP accession phs000572.v7.p4). Alzheimer disease (AD) is a neurodegenerative disease characterized by dementia that typically begins with subtle or poorly recognized failure of memory and slowly becomes more severe and incapacitating (see GeneReviews in Web Resources). AD is genetically heterogeneous with an estimated heritability of h² = 60%–80%.⁴³ Although genome-wide association studies (GWASs) of common variants have successfully identified LOAD loci, with the exception of APOE, each locus only accounts for a small fraction of disease susceptibility, and a large proportion of LOAD heritability remains unexplained.⁴⁴ Therefore, there is great interest in investigating the role RVs play in the etiology of AD. Application of the RV-NPL to ADSP WGS Caribbean Hispanic and European-ancestry pedigree data found significant evidence of linkage (LOD score > 3.8)⁴⁵ between LOAD and nonsynonymous RVs in PSMF1 (20p13 [MIM: 617858], GenBank: NM_178578.3, LOD = 3.87) and PTPN21 (14q31.3 [MIM: 603271], GenBank: NM_007039, LOD = 3.81). PSMF1 was previously shown to be associated with AD.^{46, 47, 48} PTPN21 was identified as a risk gene for AD in a Bayesian machine learning mediation analysis.⁴⁹ Functional studies suggest that both of these genes are potentially involved in AD etiology neurons.^{50, 51, 52, 53} Additionally, nominally suggestive linkage (p < 0.05) was observed with RVs in ABCA7 (19p13.3 [MIM: 605414], GenBank: NM_019112.3), ACE (17q23.3 [MIM: 106180], GenBank: NM_000789.4), EPHA1 (7q35 [MIM: 179610], GenBank: NM_005232.5), and SORL1 (11q24.1 [MIM: 602005], GenBank: NM_003105.6). These genes were previously reported to be associated at a genome-wide significance level with AD.^{47, 48, 54, 55, 56, 57}

Material and Methods

Rare Variant Extension of NPL

For each pedigree, all variants are phased using an extension of the Lander-Green Algorithm.^{58, 59} After phasing, CHP-based regional loci¹⁸ are constructed using RVs with MAFs below a given threshold criterion, e.g., < 1%. Regional loci can include either all RVs or only those that meet specific annotation specifications, e.g., missense, CADD c-score > 20. When there are missing founder or parental genotypes, regional loci genotypes are reconstructed or inferred based upon CHP genotypes from offspring and their family-specific CHP allele frequencies which are estimated based on MAFs obtained from databases, e.g., gnomAD.⁶⁰ If the analyzed families are from different populations, then ancestry-specific MAFs should be used for each pedigree. Variants not observed in the relevant database population are assigned a MAF of (1 − k)/2N, where N is the number of individuals for the specific population in the database and k is the fraction of singletons observed.⁶¹ If a sufficiently large sample is analyzed, MAFs can be estimated from pedigree founders and reconstructed founders. Only haplotypes that are observed in a pedigree are considered possible haplotypes to impute missing data for that pedigree. Frequencies for CHP alleles are calculated from the M observed RVs in the sample families, i.e., ${\prod }_{i=1}^M\left(1-f_i\right)$ for the wild-type CHP allele where f_i is the MAF for i^th observed RV. For alternative CHP alleles, the occurrence of minor allele in a haplotype with given haplotype pattern [x₁,x₂,…,x_M], x_k∈[0,1] can be approximated by a multivariate Poisson distribution (details on the calculation can be found in Wang et al.¹⁸) and the individual frequency for each of the H observed alternative CHP alleles in a pedigree (i.e., RV-carrying haplotype h_k) is calculated by $\frac{P\left(h_k\right)}{{\sum }_{k=1}^{H}P\left(h_k\right)}\times \left[1-{\prod }_{i=1}^M\left(1-f_i\right)\right]$ where P(h_k) is the probability from Poisson distribution for haplotype h_k such that the cumulative MAF for the alternative CHP alleles is $1-{\prod }_{i=1}^M\left(1-f_i\right)$. Based on the CHP allele frequencies, the missing parental genotypes can be reconstructed.

The alleles of the regional locus are scored to ensure that each haplotype within a pedigree is unique, so there is no loss of linkage information. Additional information on generating regional loci can be found in Wang et al.¹⁸

Each CHP regional locus is used to examine IBD (0, 1, or 2) allele sharing among affected pedigree members. For CHP-NPL, IBD sharing is calculated using both haplotypes with at least one RV and those haplotypes without any RVs. On the other hand, the test statistics for the RV-NPL are calculated only based on sharing of haplotypes that carry at least one RV, i.e., sharing of haplotypes that do not contain a RV does not contribute to linkage signals. Statistics are calculated using two different scoring functions, NPL_All, and NPL_Pairs, for both CHP-NPL and RV-NPL.

For NPL_Pairs, the sum of pairwise IBD sharing for affected pedigree members for the regional CHP locus is obtained for the j^th family with n_j affected relative-pairs by calculating the score,

$$S_{pairs,j}=\sum _{p=1}^{n_j}{\tau }_p,$$

where ${\tau }_p$ is the IBD sharing value for the p^th affected relative-pair, for RV-NPL, ${\tau }_p$ is the sharing of RV carrying haplotypes, with the score measuring the overall pairwise allele-sharing within the j^th family.

When there is no allelic heterogeneity, an increase in power can be obtained for families with more than two affected members using the all score which is implemented in the NPL_All test statistic. The all score was proposed by Whittemore and Halpern.⁶² It can be calculated as follows,

$$S_{all,j}\left(v\right)=2^{-a}\sum _h\left[\prod _{i=1}^{2f}{b}_i\left(h\right)!\right],$$

where a is the number of affected individuals in the j^th family, h is a collection of alleles from the region loci obtained by choosing one allele from each of the affected pedigree members (e.g., h = [A₁₁,A₂₁,…,A_a1] with A₁₁ representing the 1^st allele selected from 1^st affected member and h has a total of 2^a possible combinations), and b_i(h) denotes the number of times that the i^th founder (f) allele appears in h (for i = 1,…,2f). The sum is taken over all 2^a possible ways to choose h. For RV-NPL, b_i(h) will be set to 0 if the i^th founder has a wild-type CHP allele, i.e., haplotype that does not contain any RVs. The score S_all is generated using an inheritance vector v for the j^th family, and the computation details of inheritance vector can be found in Whittemore and Halpern.⁶²

To extend the analysis to the situation where precise IBD sharing values are unknown, the expected values over all possible inheritance patterns can be obtained by

$$S_j=\sum _v{P}_j\left(v_k\right)·S_j\left(v_k\right),$$

where $P_j\left(v_k\right)$ is the posterior probability of inheritance vector v_k for the j^th family. For both approaches, a standardized score

$$Z_j=\frac{\left[S_j-{\mu }_j\right]}{{\sigma }_j}$$

is calculated for the j^th family, where S_j is the score for family j and ${\mu }_j$ and ${\sigma }_j$ represent the mean and standard deviation of S_j under the null hypothesis, respectively. The null distribution of S_j is determined by enumerating every possible inheritance vector under the null for family j. Additionally, for RV-NPL, the null distribution is determined while maintaining the CHP genotypes of founders, since S_j for RV-NPL is dependent on the founder genotypes. The overall Z score is obtained as a linear combination of Z_j scores for a total of all families m,

$$Z=\sum _{j=1}^m{\gamma }_j{Z}_j,$$

where the weight is ${\gamma }_j=1/\sqrt{m}$. Using either the S_All or S_Pairs score, the NPL_All or NPL_Pairs test statistic can be obtained.

When analyzing linkage across multiple RVs, unlike multipoint NPL, which can provide an NPL score at any map positions, CHP-NPL and RV-NPL give a single NPL score for a region. Moreover, in contrast to traditional NPL methods, CHP-NPL and RV-NPL use family-specific CHP allele frequencies enabling the inclusion of correct allele frequencies when joint analysis of families from different populations is performed. For the original version of the NPL,¹⁷ it was demonstrated that the analytical p values were overly conservative when descent information is incomplete, i.e., missing genotype data.⁶³ Therefore, for CHP-NPL the Kong and Cox⁶³ extension was implemented to correct for the conservative nature of the NPL. For RV-NPL, empirical p values are obtained through permutations, by retaining founder haplotypes and then based on Mendelian segregation randomly assigning haplotypes to non-founders. For founders with missing genotypes, their haplotypes are reconstructed using genotype information from offspring and CHP marker allele frequencies obtained as described above. These haplotypes are then assigned to offspring based on Mendelian segregation. For family members with missing sequence data, their simulated genotypes are removed before analysis. Adaptive permutation is used to reduce computational time; p values are evaluated at pre-defined checkpoints, and permutation is terminated for tests that are not significant.

Simulation Framework

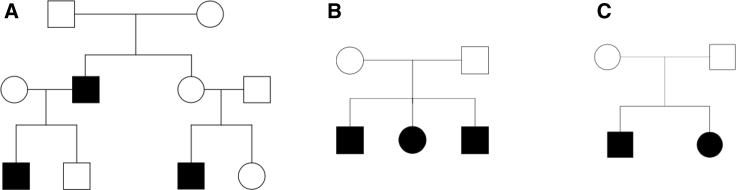
Type I error of RV-NPL and CHP-NPL were evaluated, through simulation studies. Additionally, the power of RV-NPL, CHP-NPL, and multipoint NPL were assessed and compared. Genotypes were simulated for 17,987 autosomal genes across the genome based on the observed variant sites and their corresponding MAFs obtained from 33,370 Non-Finnish Europeans (NFE) recorded in the Exome Aggregation Consortium (ExAC)⁶⁰ database. Genetic maps distances and recombination rates were estimated from the Rutgers Combined Linkage-Physical map⁶⁴ using interpolation. Using RarePedSim,⁶⁵ sequence variant data were generated for three pedigree structures: nuclear families with either two or three affected siblings and an extended pedigree with two branches and three affected family members (Figure 1). Data were generated unconditional on affection status to evaluate type I error and conditional on disease status and phenotype model to evaluate power. Genotype phase information is removed from the simulated data to mimic real-world sample sequences and the data is phased using the Lander-Green Algorithm.^{58, 59} For both the evaluation of type I and II errors, genes with at least one variant with a ExAC NFE MAF ≤ 0.01 were analyzed.

Figure 1.

Pedigree Structures Used in the Simulation Studies

Three different pedigree structures were used for the simulation studies to evaluate type I error and power: Multi-generational pedigree with three affected family members (A), nuclear pedigree with three affected siblings (B), and nuclear pedigree with two affected siblings (C).

Type I Error Evaluation

To evaluate type I error, genotype data were simulated for all autosomal genes across the genome unconditional on the affection status of the family members, i.e., odds ratio (OR) = 1.0. Type I error was evaluated for 100 extended families (Figure 1A); 300 nuclear families with three affected siblings (Figure 1B); and 2,000 nuclear families with two affected siblings (Figure 1C). Data were generated for pedigrees with no missing genotypes, and also for pedigrees with a percentage of founders missing all variant data. One thousand replicates of complete exomes were generated and every gene with one or more RVs was analyzed in each exome. p values were obtained both analytically (CHP-NPL) and empirically (RV-NPL) using one million permutations. Nominal p values were evaluated at 5.0 × 10⁻² (LOD score 0.8), 5.0 × 10⁻³ (LOD score 1.45), and 1.5 × 10⁻⁵ (LOD score 3.8) levels and quantile-quantile (QQ) plots with results from all exome replicates were also generated. Type I error evaluation was performed for RV-NPL_Pairs, RV-NPL_All, CHP-NPL_Pairs, and CHP-NPL_All.

Power Evaluation

Power was evaluated for 100 extended families; 2,000 nuclear families with two affected siblings; and 300 nuclear families with three affected siblings. RV genotypes in each gene were generated conditional on affection status of the pedigree members assuming a multiplicative model for which each causal RV within a gene region has an OR of 5.0 and the disease has a prevalence of 0.01. Although a complex trait is being studied, an OR = 5.0 was selected, since variants for which familial aggregation is observed usually have larger effect sizes than susceptibility variants underlying sporadic disease. For every power evaluation, an exome was generated with 17,987 autosomal genes each linked to the disease, i.e., genotypes generated conditional on the affection status. Every gene with at least one RV was analyzed. It should be noted that since each gene was analyzed individually, genotypes at the other loci do not affect the results. For all analyses the power was determined by the ratio of number of genes with LOD > 3.8 (p value ≤ 1.5 × 10⁻⁵), the genome-wide significance level proposed by Lander and Kruglyak,⁴⁵ to the total number of genes analyzed. Power was evaluated for RV-NPL_Pairs, RV-NPL_All, CHP-NPL_Pairs, and CHP-NPL_All and for comparison purposes RVs in each gene region were also analyzed using multipoint NPL_Pairs and NPL_All as implemented in MERLIN.⁵⁸ p values were obtained analytically for CHP-NPL and multipoint NPL, and empirically using one million permutations for RV-NPL.

Simulations were performed under different scenarios to evaluate and compare the power. To estimate the effect of non-causal variants on power, two different scenarios were used. First, all nonsense, missense, and splice site variants were analyzed where 100%, 75%, and 50% are susceptibility variants (OR = 5.0) and the remaining variants (0%, 25%, and 50%) are neutral (OR = 1). Here the number of variants analyzed was kept constant and as the number of non-causal variants increased the number of susceptibility variants declined. Second, missense, nonsense, and splice site variants were assigned an OR = 5.0 and synonymous variants an OR = 1.0 (non-causal). The data were analyzed including and excluding synonymous variant to evaluate robustness of the methods to including non-causal variants while keeping the number of causal variants consistent. To evaluate the effect of missing data on power, analyses were performed with 10%, 30%, and 50% of the pedigrees having all founders missing their sequence data.

To appraise the effect of locus heterogeneity, data were generated under linkage homogeneity (α = 1.0) and heterogeneity (α = 0.67) and the power was compared. First pedigrees were generated with linkage (all nonsense, missense, and splice site variants have an OR = 5.0) with RVs in every autosomal gene generated conditional on the affection status and then an additional dataset 50% of the sample size of the linked families was generated under the null (all RVs unlinked with an OR = 1.0, i.e., generated unconditional on the pedigree affection status). For the extended pedigrees, 100 were generated with linkage and 50 unlinked. The linked pedigrees were first analyzed separately and then together with the unlinked ones.

Families with intra-familial heterogeneity (inclusion of simplex case subjects) were also simulated to evaluate the performance of RV-NPL_Pairs and RV-NPL_All. Exome data with RVs in every autosomal gene were generated conditional on disease status for extended families with one branch containing two affected siblings and the other branch with an unaffected and affected sibling (Figures S1A). For the analysis, all children had an affected disease status (Figure S1B), to generate data with intra-familial heterogeneity.

Application to Alzheimer Disease Data

The RV-NPL was used to analyze families segregating LOAD. WGS data from 107 LOAD families with 486 members of which 446 have a LOAD diagnosis were available for analysis. The ADSP data were obtained from dbGaP (accession phs000572.v7.p4). WGS data for ADSP were generated at Baylor College of Medicine Human Genome Sequencing Center, Broad Institute Genome Center, and Genome Institute at Washington University. This dataset consists of 112 LOAD pedigrees from different populations: African American (1), Dominican (64), European ancestry (44), and Puerto Rican (3). For the analysis, family members were considered affected if their phenotype was defined as “definite AD,” “probable AD,” “possible AD,” and “family-reported AD.” The mean age of onset for AD was 72.63 years with a standard deviation of 8.46. APOE (MIM: 107741) status was also obtained for all family members and families were selected for WGS sequencing if no more than 75% of affected family members were heterozygous for APOE ε4 allele and none were homozygous. The African American family was excluded from the analysis, due to only a single family being available from this ancestry group. Three additional pedigrees were also excluded due to only one affected family member with available WGS data, making these families incompatible for linkage analysis. An additional pedigree was also excluded due to a high level of missing genotype data. A total of 42 families of European ancestry and 65 Caribbean Hispanic families (62 Dominican and 3 Puerto Rican) were analyzed. The pedigree structures and their ancestries are displayed in Figure S2 and Table S1, respectively.

In addition to the initial quality control (QC) performed by the ADSP QC working group,⁴ genotypes with a genotype quality score (GQ) < 20 were removed. Only variant sites that were flagged as “PASS” for both the Broad and BCM pipelines, had a missing rate ≤ 10%, and had no Mendelian inconsistencies were included in analysis. Gene regions were assigned using RefSeq definitions. MAFs were annotated using the gnomAD database from the NFE and Latino (AMR) populations. For missing genotypes, CHP regional markers were constructed using gnomAD allele frequencies that corresponded to the family’s ancestry, i.e., NFE or AMR. ANNOVAR was used to perform functional annotations.⁶⁶ RV-NPL_All and RV-NPL_Pairs were used to analyze every gene that had at least one RV site. Analysis was performed constructing regional markers within gene regions using frameshift, missense, nonsense, and splice sites variants with a MAF < 0.01 in gnomAD. European and Caribbean Hispanic families were analyzed jointly and separately to elucidate whether there were any association specific to one ancestry.

Results

Type I Error Evaluation

For nuclear (with two or three affected siblings) and extended pedigrees simulated under the null hypothesis of no association, nominal p values were evaluated at 5.0 × 10⁻², 5.0 × 10⁻³, and 1.5 × 10⁻⁵ (Table S2) and quantile-quantile (QQ) plots were also generated (Figures S3–S6). These results suggest that type I error is well controlled for RV-NPL_All, RV-NPL_Pairs, CHP-NPL_All, and CHP-NPL_Pairs. It was also demonstrated that the type I error for CHP-NPL and RV-NPL (all and pairs) is well controlled when founder data were missing (Table S2 and Figures S3–S6).

Power Evaluation

Power was evaluated for nuclear (two and three affected siblings) and extended families analyzing RVs with MAF < 0.01 for RV-NPL_Pairs, RV-NPL_All, CHP-NPL_Pairs, CHP-NPL_All, multipoint NPL_Pairs, and multipoint NPL_All. Performance of the NPL methods was investigated when sequence data were missing for founders, when non-causal variants were included in the analysis, and in the presences of intra- and inter-familial heterogeneity. Since it has been established that multipoint NPL has increased type I error when there are missing parental data and LD is ignored,⁴⁰ analyses were not performed using multipoint-NPL when founders had their genotype data missing. For multipoint NPL and CHP-NPL for both S_all and S_pairs statistics, the power was identical for various scenarios when no data were missing (Table 1 and Figures 2 and S7–S10). For example, when simulated missense, nonsense, frameshift, and splice variants (MAF < 0.01 and all causal) were analyzed for 300 nuclear families with three affected siblings, the power for multipoint NPL_Pairs and CHP-NPL_Pairs are both 0.817. Similarly, for extended families, the power for both multipoint NPL_Pairs and CHP-NPL_Pairs are 0.789. Since NPL_Pairs and NPL_All give identical results for affected sibpairs, the power is only displayed for NPL_Pairs.

Table 1.

Power of CHP-NPL and RV-NPL

	Pairs						All
	Sibpaira		Tripletb		Extendedc		Sibpair		Triplet		Extended
	CHPd	RVe	CHP	RV	CHP	RV	CHP	RV	CHP	RV	CHP	RV
100% causalf	0.801	0.954	0.817	0.932	0.789	0.859	0.801	0.954	0.817	0.930	0.780	0.858
75% causal	0.693	0.918	0.729	0.893	0.711	0.798	0.693	0.918	0.729	0.890	0.703	0.798
50% causal	0.521	0.825	0.588	0.797	0.580	0.672	0.521	0.825	0.588	0.793	0.569	0.671
NS & Sg	0.686	0.890	0.771	0.901	0.761	0.856	0.686	0.890	0.771	0.899	0.756	0.856
Locus Het	0.778	0.947	0.808	0.925	0.787	0.858	0.778	0.947	0.808	0.924	0.778	0.858
10% MFh	0.798	0.953	0.815	0.931	0.788	0.859	0.798	0.953	0.815	0.930	0.779	0.858
30% MF	0.791	0.952	0.813	0.930	0.786	0.858	0.791	0.952	0.813	0.929	0.776	0.858
50% MF	0.784	0.951	0.808	0.929	0.780	0.857	0.784	0.951	0.808	0.928	0.769	0.858

Abbreviations: Het, heterogeneity; MF, missing founders; NS, nonsynonymous; and S, synonymous.

^a2,000 nuclear families with 2 affected siblings

^b300 nuclear families with 3 affected siblings

^c100 extended families

^dCHP-NPL method

^eRV-NPL method

^fPercentage of causal functional variants

^gAnalysis of causal nonsynonymous (NS) and non-causal synonymous (S) RVs

^hPercentage of founders with missing genotypes

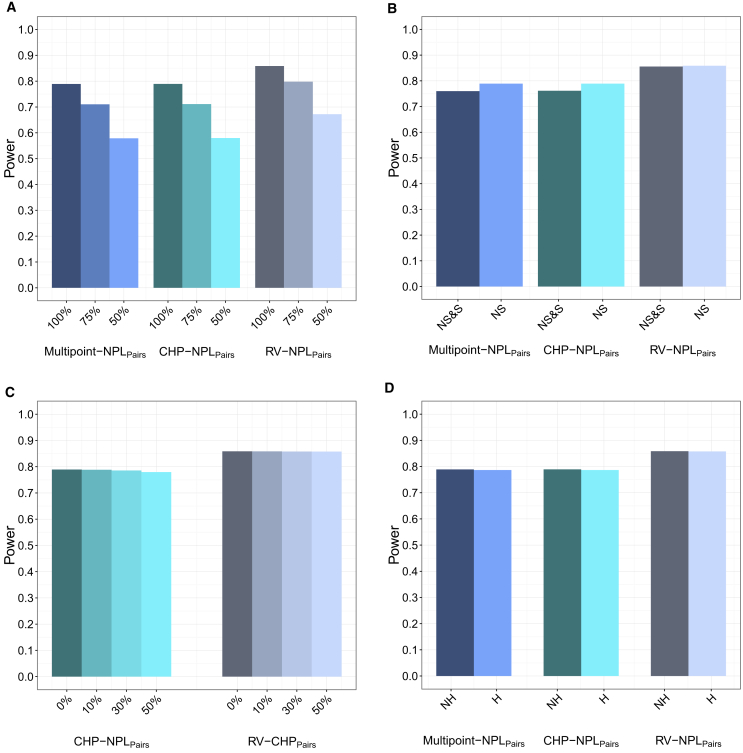
Figure 2.

Exome-wide Power Comparison for RV-NPL_Pairs

Genotypes were generated for 100 extended families, conditional on affection status assuming a multiplicative model in which each causal variant within a gene region has an OR of 5.0. Analysis was performed using RV-NPL_Pairs, CHP-NPL_Pairs, and Multipoint-NPL: with 100%, 75%, and 50% of the variant being causal and the remaining non-causal (OR = 1) (A); with only causal nonsynonymous (NS) variants as well as with causal nonsynonymous (NS) and non-causal synonymous (S) variants (B); with 0%, 10%, 30%, and 50% of the founders missing all genotype data (C); and with no heterogeneity (NH), i.e., 100 linked families as well as with locus heterogeneity (H), i.e., 100 linked and 50 unlinked families (D).

For each scenario, the power for RV-NPL is consistently higher than for CHP-NPL and multipoint NPL for both S_all and S_pairs. The power is displayed for affected sibpairs, nuclear families with three affected siblings, and extended families in Table 1 and Figures 2 and S7–S10. When rare causal missense, nonsense, and splice site variants were analyzed for all autosomal genes for 2,000 affected sibpairs, the power for RV-NPL_Pairs is 19.1% higher than for CHP-NPL_Pairs and multipoint NPL_Pairs. For the same scenario, the power increases by 14.2% (300 nuclear families with three affected siblings) and 8.8% (100 extended pedigrees) when RV-NPL_Pairs instead of CHP-NPL_Pairs or multipoint NPL_Pairs was used to analyze the data (Table 1 and Figures 2, S7, and S8). Similar results are observed for NPL_All (Table 1 and Figures S9 and S10).

For 100 extended pedigrees when 50% of the founders are missing their genotype data and all variants are causal, there is a 10.1% increase in power for RV-NPL_Pairs compared to CHP-NPL_Pairs. Similarly, for 2,000 affected sibpairs when 50% of founders are missing all genotype data and all variants are causal, the power for RV-NPL_Pairs is 21.3% higher than for CHP-NPL_Pairs (Table 1, Figures 2C and S8C).

The impact of non-causal variants on power was also examined. In the first scenario, there is a set number of nonsynonymous variants, but the proportion that are causal was reduced from 100% to 50%. In the second scenario, all nonsynonymous variants are causal and analyzed and then both the causal nonsynonymous and non-causal synonymous variants were analyzed together so that the ratio of nonsynonymous (causal) to synonymous (non-causal) variants is 2:1, to mimic observed ratios of nonsynonymous to synonymous variants.⁶⁰ The first scenario was designed to evaluate a lower-powered yet possibly more realistic etiology for complex traits; the second scenario was designed to assess robustness of the methods to non-causal variants.

In the first scenario, when there is a set number of nonsynonymous variants, for RV-NPL, CHP-NPL, and multipoint NPL, the power decreases with decreasing proportion of causal variants and increasing non-causal variants. For example, compared to 100% causal variants, when only 50% of variants are causal and the rest non-causal, the power of RV-NPL_Pairs decreases by 13.5%, 14.5%, and 21.7% for 2,000 affected sibpairs, 300 nuclear families with three affected siblings, and 100 extended families, respectively. For CHP-NPL_Pairs and multipoint NPL_Pairs, the power for 300 nuclear families with three affected siblings both dropped from 0.817 to 0.588 (by 28.0%) when the proportion of causal variants decreased from 100% to 50% and non-causal variants increased from 0% to 50%. Similarly, for extended families, the power for both CHP-NPL_Pairs and multipoint NPL_Pairs decreased from 0.789 to 0.580 (by 26.5%). Regardless of the proportion of causal variants, RV-NPL consistently displayed higher power than CHP-NPL and multipoint NPL, e.g., when the proportions of causal and non-causal variants are each 50%, the power for RV-NPL_Pairs is 58.2%, 35.5%, and 15.9% higher than for CHP-NPL_Pairs and multipoint NPL_Pairs for affected sibpairs, nuclear families with three affected siblings, and extended families, respectively (Table 1 and Figures 2A, S7A, and S8A). Similar results were observed for NPL_All (Table 1 and Figures S9A and S10A). There is a greater loss of power for CHP-NPL and multipoint NPL compared to RV-NPL as the proportion of causal variants decreases and the non-causal variants increases, e.g., for affected sibpairs when the proportion of causal variants were reduced from 100% to 75%, RV-NPL_Pairs displays a modest 3.7% reduction in power while the power for CHP-NPL_Pairs and multipoint NPL_Pairs is reduced by 13.4%; when the proportion of causal variants was further decreased from 100% to 50%, RV-NPL_Pairs has a 13.5% reduction in power, while the power reduction, 34.9%, for the CHP-NPL_Pairs and multipoint NPL_Pairs is again more severe, which results in an increased power discrepancy between RV-NPL and CHP-NPL from 19.1% to 58.2%. Similarly, for extended pedigrees, when the proportion of causal variants was reduced from 100% to 75%, the power loss for RV-NPL_Pairs is 7.1% compared to a 9.9% for CHP-NPL_Pairs and multipoint NPL_Pairs, and similar results were observed when the proportion of causal variants was reduced from 100% to 50%. This same trend is also observed for affected nuclear families with three affected siblings as well as for NPL_All, suggesting that RV-NPL is more robust to a reduction in causal variants and an inclusion of non-causal variants than CHP-NPL and multipoint NPL (Table 1, Figures 2A, S7A, S8A, S9A, and S10A).

In the second scenario, inclusion of non-causal synonymous variants in the analysis causes substantial reductions in power for CHP-NPL_Pairs and multipoint NPL_Pairs, yet RV-NPL power remains robust to the inclusion of non-causal variants. For example, the initial power for RV-NPL_Pairs was 29.8%, 16.8%, and 12.4% higher than for CHP-NPL_Pairs and multipoint NPL_Pairs for 2,000 affected sibpairs, 300 nuclear families with three affected siblings, and 100 extended families, respectively. The reduction in power for RV-NPL_Pairs when non-causal variants were included in the analysis is 6.6% (2,000 affected sibpairs), 3.4% (300 nuclear families with three affected siblings), and 0.4% (100 extended families) while for both CHP-NPL_Pairs and multipoint NPL_Pairs the drop in power when non-causal variants were included in the analysis is 14.4% (2,000 affected sibpairs), 5.5% (300 nuclear families with three affected siblings), and 3.5% (100 extended families), respectively (Table 1 and Figures 2B, S7B, and S8B) and similar results for NPL_All can be found in Table 1 and Figures S9B and S10B. These results again support that RV-NPL is more robust to non-causal variants than CHP-NPL and multipoint NPL.

Furthermore, the power of RV-NPL is largely maintained when there is missing genotype data. When simulating 10%, 30%, and 50% of families with all founders missing their sequence data, the power of both RV-NPL and CHP-NPL decreases as the proportion of pedigrees missing founder data increases. For all pedigree structures, while the power loss for RV-NPL and CHP-NPL are both very minor, RV-NPL is still more robust to missing genotype data. For example, for each of the three pedigree structures, RV-NPL_Pairs loses 0.1% power on average when 30% of the pedigrees are missing sequence data for all founders compared to when no data is missing, while CHP-NPL_Pairs loses 0.7% power on average. When 50% of the pedigrees with all founders missing all sequence data, RV-NPL_Pairs loses 0.2% power on average compared to when there is no missing data, and on average the power loss for CHP-NPL_Pairs was 1.4% for each of the pedigree structures (Table 1, Figures 2C, S7C, and S8C).

Simulation results for all pedigree structures also demonstrate that RV-NPL is robust to locus heterogeneity, e.g., with only a 0.7% loss in power when 3,000 affected sibpairs were analyzed (1/3 [1,000 pedigrees] unlinked to the disease locus and 2/3 [2,000 pedigrees] linked to all simulated disease loci [α = 0.67]) compared to when only 2,000 affected sibpairs with linkage (α = 1.0) were analyzed. For this same scenario, CHP-NPL and multipoint NPL have < 3% loss of power. Additionally, only very small decreases in power were observed for the analysis of RVs when there was locus heterogeneity for nuclear families with three affected siblings and the extended pedigrees regardless of whether the analysis was performed using RV-NPL, CHP-NPL, or multipoint-NPL (Table 1, Figures 2D, S7D, S8D, S9D, and S10D).

For RV-NPL_All and RV-NPL_Pairs, there is no difference in power for affected sibpairs, since for this family structure the methods are equivalent. For nuclear families with three affected siblings and extended families, the power for S_pairs was slightly higher than for S_all, e.g., when analyzing 100% causal variants for nuclear families with three affected siblings, the power of RV-NPL_Pairs is 0.932 compared to 0.930 for RV-NPL_All. This slight difference is due to intra-familial heterogeneity since there can be simplex case subjects in the families due to the OR and disease prevalence used to generate the RV data conditional on the affection status. The power discrepancy between RV-NPL_Pairs and RV-NPL_All increases when the proportion of causal variants was decreased from 100% to 50% causal, e.g., for 300 nuclear families with three affected siblings, the difference in power changed from 0.2% (0.932 for RV-NPL_Pairs and 0.930 for RV-NPL_All) to 0.5% (0.797 for RV-NPL_Pairs and 0.793 for RV-NPL_All). A similar trend was observed in extended families (Table 1, Figures S7A and S10A). Due to the design of the test, S_all is less robust to intra-familial heterogeneity than S_pairs. However, in the absence of intra-familial heterogeneity, S_all can provide higher test statistics than S_pairs. It was observed that 69.1% of the generated genes have a higher test statistic for S_all than S_pairs (Figure S1 and Table S3). Additionally, we used the proportion of families that have only one type of RV haplotype (i.e., all RV haplotypes observed in a family are the same) as a proxy of allelic homogeneity within a family to further demonstrate its impact on the power of S_all and S_pairs. It was observed that for genes with a higher test statistic for S_all than S_pairs, 79% of the family have only one RV haplotype, while for genes with a higher test statistic for S_pairs than S_all, 66% of families have only one RV haplotype. We also evaluated power for RV-NPL_Pairs and RV-NPL_All when 100 extended pedigrees were generated with intra-familial heterogeneity (changing the affection status to increase the number of simplex cases) were analyzed, and observed that pairs is more powerful than S_all, with the power of RV-NPL_Pairs being 4.4% higher than that of RV-NPL_All when all simulated nonsynonymous RVs are causal.

Analysis of Alzheimer Disease Sequencing Project Data

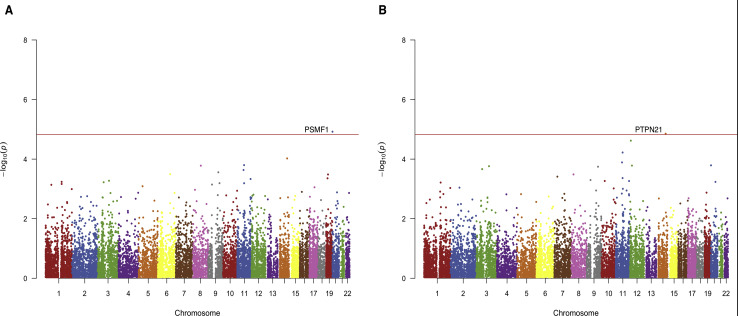
Joint analysis of the Caribbean Hispanics and Europeans identified linkage with two genes, PSMF1 (LOD: 3.87) and PTPN21 (LOD: 3.81), observed reaching the significance threshold of a LOD score ≥ 3.8⁴⁵ (Figure 3). No genes reached a significant LOD score of ≥ 3.8 when analyses were performed separately for Caribbean Hispanics and Europeans.

Figure 3.

Manhattan Plots Displaying the RV-NPL Results for the Analysis of the ADSP Pedigrees

The results from analyzing functional RVs in 107 ADSP pedigrees with European and Hispanic origin for RV-NPL_Pairs (A) and RV-NPL_All (B) are displayed with the red line indicating the significance threshold of LOD = 3.8.

Additionally, nominal significance was observed for several genes that were demonstrated to be associated with LOAD: ABCA7 (RV-NPL_Pairs p = 3.0 × 10⁻², RV-NPL_All p = 6.0 × 10⁻³) and EPHA1 (RV-NPL_Pairs p = 7.0 × 10⁻³, RV-NPL_All p = 6.0 × 10⁻³) display nominal significance in Caribbean Hispanic families while ACE (RV-NPL_Pairs p = 2.8 × 10⁻², RV-NPL_All p = 2.8 × 10⁻²) and SORL1 (RV-NPL_Pairs p = 1.6 × 10⁻², RV-NPL_All p = 1.5 × 10⁻²) are nominally significant in European families.

For PSMF1 (RV-NPL_Pairs p = 1.2 × 10⁻⁵, RV-NPL_All p = 1.6 × 10⁻⁴), seven out of eight missense RVs observed segregate in 14 families with increased RV minor allele sharing, and five RVs are located in conserved nucleotide sites (Table S4). For PTPN21 (RV-NPL_Pairs p = 9.5 × 10⁻⁵, RV-NPL_All p = 1.4 × 10⁻⁵), six missense RVs were observed segregating in eight families with enhanced minor RV allele sharing (Table S5). For ABCA7, 13 missense RVs segregate in 20 pedigrees with RV allele sharing greater than expected under the null hypothesis of no linkage (Table S6). For ACE, three missense RVs were observed in three linked pedigrees, and two of these RVs are conserved and deemed deleterious by at least six bioinformatics tools (Table S7). Two missense RVs in EPHA1 were observed in three pedigrees with linkage, and both RVs are located in conserved sites and deemed deleterious by at least six bioinformatics tools (both have CADD scaled C-scores = 35, Table S8). For SORL1, seven missense RVs were segregating in seven pedigrees with increased sharing. Five of the segregating RVs are conserved and deemed deleterious by at least four of seven bioinformatics tools (Table S9). Pedigrees segregating variants in ABCA7, ACE, EPHA1, PSMF1, PTPN21, and SORL1 are shown in Figure S2 and Table S1.

Discussion

We developed the RV-NPL, to perform aggregated rare-variant NPL analysis, using the CHP method.¹⁸ Based on simulation studies, we demonstrated that RV-NPL has well-controlled type I error. It is a powerful approach to map complex trait loci with familial aggregation and is robust to locus and allelic heterogeneity as well as inclusion of non-causal variants.

Parametric linkage analysis should be used for Mendelian traits, since NPL methods will be less powerful. However, when the genetic model is unknown (which is usually the case for complex traits), NPL is more powerful than parametric linkage analysis,⁶⁷ since for parametric linkage analysis incorrect specification of the disease and penetrance model will lead to a severe loss in power. The power of the NPL is not affected by an unknown underlying genetic model, since it is not specificed.¹⁷ Therefore for the analysis of complex trait family data, NPL and not parametric linkage analysis should be used.

RV-NPL has several major advances over traditional NPL methods. First, it is more powerful than traditional multipoint NPL methods under a variety of simulation scenarios. Additionally, analyzing RVs instead of common ones provides better resolution of the linkage region, usually to within a gene or a small genomic region, which is demonstrated in the analysis of the ADSP pedigrees. Applying NPL methods to analyze common variants led to large genetic intervals, due to their LD structure in families.^{68, 69} In contrast, two factors that aid in fine mapping of loci for RVs are their low levels of LD and the fact that linked variants often differ between families. Moreover, resolution can be further refined when recombination events occur within a gene region, allowing linkage signals to be mapped to sub-units of a gene divided by recombination.

Unlike for parametric linkage analysis where locus heterogeneity can be modeled in the linkage framework, NPL methods do not allow for the incorporation of linkage admixture into the analysis, which for common variant analysis can greatly attenuate power. For RV linkage analysis, there is very little loss in power with the presence of locus heterogeneity because unlinked regions usually do not contain informative variants and thus do not contribute to confounding RV-NPL analysis. This is advantageous for the analysis of complex traits due to extensive locus heterogeneity.

It has previously been demonstrated that NPL methods are robust to population substructure and admixture between and within families.²⁰ For linkage analysis, in the presence of missing data, type I error can be increased when incorrect allele frequencies are used in the analysis.⁴⁰ For each family, population-specific allele frequencies should be used. For example, when the ADSP admixed Caribbean Hispanic families were analyzed, allele frequencies were obtained from the gnomAD AMR population while for the ADSP European-Americans allele frequencies from the NFE were used, to avoid an increase in type I error due to the use of incorrect allele frequencies. No inflation of type I error was observed when mega-analysis was used to analyze families of European and Caribbean Hispanic ancestry. Although for family-based RV aggregate association analysis type I error can be well controlled when there is population admixture and substructure,^{20, 70} an additional problem is that inclusion of non-causal variant can attenuate the signal when the underlying genetic etiology varies by ancestry. Using RV-NPL, families of different ancestries can be analyzed jointly, since linkage is robust to inclusion of families that are not linked to the same loci and non-causal variants.

Though family data can provide several benefits in mapping causal RVs, family-based studies do have drawbacks. The recruitment of probands and their relatives is more time consuming and expensive compared to the ascertainment of unrelated individuals. Pedigrees often have diverse structures and so it is necessary to be able to analyze multiplex pedigrees. The NPL method lends itself well to this situation. Additionally, parental data are often unavailable for families, in particular for late-onset diseases. RV-NPL has only a minimal power loss when founders and parents were missing their genotype data, and for the analysis of the ADSP pedigrees that include complex multi-generational pedigrees that have a large proportion of founders missing all variant data, type I error was well controlled.

As suggested by Lander and Kruglyak,⁴⁵ a LOD score of 3.8 was used as the significance threshold to control the family-wise error rate and provide a genome-wide significance level of 0.05 regardless of the marker loci density. Although Lander and Kruglyak proposed different thresholds depending on the observed pedigree relationships, e.g., sibpairs or uncle-nephew, and then weighting significance levels based on the proportion of each family type, here we apply the most stringent level suggested, a LOD score of 3.8 (p = $1.5\times {10}^{-5}$) regardless of pedigree structure.

Our study observed excess RV sharing for PSMF1 among affected members of fourteen pedigrees and for PTPN21 among affected members of eight pedigrees (Table S1). None of the affected RV carriers in these pedigrees are positive for the APOE ε4 allele. For PSMF1, there are three European families and eleven Caribbean Hispanic families with RV allele with increased minor allele sharing. Among the eight pedigrees with increased minor allele sharing in PTPN21, seven are Caribbean Hispanic and one is European. Different RVs were found in Caribbean Hispanic and European pedigrees: in PSMF1, seven of the eleven Caribbean Hispanic pedigrees and none of the European pedigrees displayed linkage to rs79465651 which is a conserved nucleotide site. For PTPN21, rs150736820 had increased minor allele sharing in the European pedigree, but was not observed in the seven Caribbean Hispanic pedigrees; while rs3825676 had increased minor allele sharing in three out of seven Caribbean Hispanic pedigrees. For both genes, the linkage signals from ancestry specific analyses are weaker than those from the combined pedigrees, suggesting the potential benefit of performing mega-analysis.

LOAD associations with common and rare variants in PSMF1 were previously reported. A small LOAD GWAS study (124 cases) of Israeli Arabs with a low frequency of APOE ε4 carriers reported several common variants associations in the PSMF1 gene region with the most significant SNV having a p = 3.6 × 10⁻⁵.⁴⁶ Associations were also observed in the Alzheimer disease Genetics Consortium (ADGC) and the International Genomics of Alzheimer’s Project (IGAP) datasets. For the ADGC study with 1,968 African- American LOAD cases an association was observed with variant rs35517343 (MAF 0.014 p = 1.9 × 10⁻⁶) which is in the splice region of PSMF1.⁴⁷ Rs35517343 is extremely rare in non-African populations. The discovery stage of the IGAP study in individuals of European ancestry observed a nominal significance of p = 1.6 × 10⁻³ with RV rs202107404 (MAF = 0.00002) which lies in the intronic region of PSMF1.⁴⁸ Functional studies also provide support to PSMF1 potential role in AD etiology. PSMF1 encodes a protein that, through the 11S and 19S regulators, inhibits the activation of the 26S proteasome, which regulates Aβ metabolism and tau degradation. The functional impairment of 26S proteasome, especially in neurons, decreases the activity of α-secretase and leads to the production and accumulation of Aβ,⁵² which is an important feature of AD, therefore suggesting the potential involvement of PSMF1 in AD etiology via inhibiting the function of 26S proteasome. For PTPN21, a previous causal mediation analysis combining large-scale GWAS and brain gene expression data for Europeans, identified this gene as a strong causal mediator for AD.⁴⁹ It has also been found to promote neuron survival through ErbB4/NRG3 pathway and increase neuritic length,⁵³ which is vital for maintaining normal neuronal function, suggesting a potential important role in neural development. A previous GWAS study found PTPN21 significantly associated with schizophrenia,⁵¹ suggesting its involvement in the pathogenesis of neural diseases.

Four known AD-associated genes (ABCA7, ACE, EPHA1, and SORL1) displayed linkage signals with nominal significance in RV-NPL analysis of the ADSP data. A variety of common variants in ABCA7 have been identified as susceptibility loci for LOAD through several GWAS analyses in European and African American populations.^{47, 48, 54, 56} For Europeans, RVs were also reported in several association analyses of LOAD that were performed using targeted sequencing of AD- associated genes.^{71, 72, 73} In a French case-control sample, gene-level RV association analysis identified a significance association between ABCA7 and early-onset AD.⁷⁴ In our study, ABCA7 displayed nominal significance in Caribbean Hispanic, but not in European families. Only weak association with RVs in ABCA7 were previously reported for LOAD in Caribbean Hispanics⁷² and our finding lend support to its involvement in this population. ACE was identified as a risk gene for LOAD with significant association in European population⁴⁸ and an Israeli Arab community,⁷⁵ it could also impact the risk of LOAD by regulating the level of Aβ.⁷⁶ ACE reached nominal significance only in the analysis of the European pedigrees. Previous associations for ACE were only for common variants and this study suggests that functional rare variants may also be involved. EPHA1 was first implicated in LOAD etiology through the association of rs11767557, a common variant in the promoter region, which was reported in two LOAD GWAS meta-analyses of European populations.^{54, 55} Another associated common variant was later found by a GWAS in European population.⁵⁶ Additionally, a targeted sequencing study identified RV rs202178565 to be significantly enriched in Caribbean Hispanics LOAD patients.⁷² In our study, although rs202178565 was not present, EPHA1 still displayed nominal significance in Caribbean Hispanic pedigrees, supporting its involvement in Hispanics. Evidence of linkage in Europeans was not observed for RVs in EPHA1. SORL1 is associated with increased risk of both early- and late-onset AD^{77, 78} and it is involved in the AD etiology through aberrant trafficking and metabolism of the amyloid precursor protein (APP)⁷⁹ that could increase Aβ. Both common variants and RVs have been reported as LOAD risk loci in SORL1. In a family-based joint linkage and association study on targeted sequence data, SORL1 RV rs143571823 showed significant segregation with disease in 87 Caribbean Hispanic LOAD families.⁵⁷ For Europeans, several GWAS meta-analyses identified significant associations between common variants in SORL1 and LOAD.^{56, 77} Although none of the known risk variants were present in ADSP analysis, SORL1 displayed nominal significance in European but not in Caribbean Hispanic pedigrees. For pedigrees that display linkage to ABCA7, ACE, EPHA1, and SORL1 none of the affected pedigree members are positive for the APOE ε4 allele. Considering that the application of RV-NPL in ADSP pedigrees focused on RVs, these findings suggest that genes implicated with AD may harbor both common and rare susceptibility variants.

Although RV-NPL was used to analyze gene regions in genomes, it can also be implemented to analyze complete genomes, using recombination events as boundaries for the regional locus. The ability to use recombination events to aggregate variants is an advantage to RV association methods where prior knowledge or a sliding window are necessary to aggregate RVs outside of gene regions.

RV-NPL is a robust and powerful tool to map RVs for complex disease segregating in families. Results from extensive simulation studies and the analysis of the ADSP data demonstrate the power and robustness of RV-NPL, as well as its ability to fine map loci and to detect linkage to individual genes. These characteristics make RV-NPL an ideal method to elucidate the genetic etiology of complex familial diseases. RV-NPL is implemented primarily in Python with C++ extensions, and the software package is publicly available online.

Declaration of Interests

The authors declare no competing interests.

Published: October 3, 2019

Accession Numbers

The dbGaP accession number for the genome sequences reported in this paper is phs000572.v7.p4.

Web Resources

• ADSP, https://www.niagads.org/adsp/content/home

• ANNOVAR, http://annovar.openbioinformatics.org/en/latest/

• CADD, https://cadd.gs.washington.edu/

• dbGAP, https://www.ncbi.nlm.nih.gov/gap/

• dbSNP, https://www.ncbi.nlm.nih.gov/projects/SNP/

• ExAC Browser, http://exac.broadinstitute.org/

• fathmm, http://fathmm.biocompute.org.uk/

• GenBank, https://www.ncbi.nlm.nih.gov/genbank/

• GeneReviews, Bird, T.D. (1993). Alzheimer disease overview. https://www.ncbi.nlm.nih.gov/books/NBK1161/

• gnomAD, https://gnomad.broadinstitute.org/

• LRT, http://www.genetics.wustl.edu/jflab/lrt_query.html

• Merlin, http://csg.sph.umich.edu/abecasis/merlin/

• Mutation Taster, http://www.mutationtaster.org/

• OMIM, https://www.omim.org/

• PLINK 1.9, https://www.cog-genomics.org/plink2/

• PolyPhen-2, http://genetics.bwh.harvard.edu/pph2/

• PROVEAN, http://provean.jcvi.org/

• RV-NPL, https://github.com/statgenetics/rvnpl

• UCSC Genome Browser, http://genome.ucsc.edu/