Quantitative Studies of an RNA Duplex Electrostatics by Ion Counting

Abstract

RNAs are one of the most charged polyelectrolytes in nature, and understanding their electrostatics is fundamental to their structure and biological functions. An effective way to characterize the electrostatic field generated by nucleic acids is to quantify interactions between nucleic acids and ions that surround the molecules. These ions form a loosely associated cloud referred to as an ion atmosphere. Although theoretical and computational studies can describe the ion atmosphere around RNAs, benchmarks are needed to guide the development of these approaches, and experiments to date that read out RNA-ion interactions are limited. Here, we present ion counting studies to quantify the number of ions surrounding well-defined model systems of RNA and DNA duplexes. We observe that the RNA duplex attracts more cations and expels fewer anions compared to the DNA duplex, and the RNA duplex interacts significantly stronger with the divalent cation Mg²⁺, despite their identical total charge. These experimental results suggest that the RNA duplex generates a stronger electrostatic field than DNA, as is predicted based on the structural differences between their helices. Theoretical calculations using a nonlinear Poisson-Boltzmann equation give excellent agreement with experiments for monovalent ions but underestimate Mg²⁺-DNA and Mg²⁺-RNA interactions by 20%. These studies provide needed stringent benchmarks to use against other all-atom theoretical models of RNA-ion interactions, interactions that likely must be accurately accounted for in structural, dynamic, and energetic terms to confidently model RNA structure, interactions, and function.

Significance

This study presents a quantitative characterization of RNA duplex electrostatics, which is important for a comprehensive understanding of structure and function. We use a powerful “ion counting” method called buffer exchange combined with inductively coupled plasma mass spectroscopy to quantify the number of ions surrounding well-defined model systems of 24-bp RNA and 24-bp DNA. Our results show that double-stranded RNA generates a stronger electrostatic field than a double-stranded DNA of the same length and the same sequence. This work also provides needed stringent benchmarks to test and improve all-atom theoretical models of RNA-ion interactions.

Introduction

RNA performs numerous functions in cells, including the storage and transmittal of genetic information, the regulation of gene expression, and catalysis, and each of these functions is fundamentally affected by the RNA’s high negative charge (1, 2). RNA carries one negatively charged phosphoryl group per residue; hence, biologically relevant RNAs that comprise of hundreds of nucleotides accumulate large charge densities.

Bringing RNA charges in close proximity during folding and function requires overcoming an enormous electrostatic energy barrier (3, 4). Ions, specifically cations, can reduce the electrostatic repulsion, which is referred to as screening (5, 6, 7, 8) and, as importantly, mitigate electrostatic attraction with oppositely charged molecules, such as RNA-binding proteins and aminoglycosides (9, 10, 11, 12). Charge screening by ions is greatly affected by the charge of the cation in addition to its bulk concentration (13, 14), effects that are manifest in the folding of RNAs upon addition of millimolar Mg²⁺ in backgrounds of much higher monovalent cation concentrations (6, 15, 16, 17).

Although there are important examples of specifically bound ions that are required for RNA folding and function (6, 18), the vast majority of interacting ions are dynamically associated in a sheath that surrounds these molecules, referred as the “ion atmosphere” (7, 19, 20, 21, 22, 23). Unlike specifically bound ions that can be investigated by x-ray crystallography and other static structural techniques (18, 24, 25, 26, 27), the dynamic ions present in the ion atmosphere are refractory to most traditional experimental methods (7, 20, 28). However, the ion atmosphere is a critical structural, dynamic, and energetic component of nucleic acids that profoundly affects their folding, compaction, and interactions. Hence, understanding RNA structure and function requires understanding the properties and energetics of its ion atmosphere.

An experimental approach that has been successful for studying the ion atmosphere around double-stranded (ds)DNA and testing theoretical predictions is “ion counting” (20, 21, 22, 23, 29, 30). Ion counting quantifies the number of thermodynamically accumulated cations and thermodynamically excluded anions around a negatively charged macromolecule such as dsDNA. Particularly effective is ion counting through buffer equilibration-inductively coupled plasma mass spectroscopy (BE-ICP-MS) because it allows the study of a large variety of ions over a broad range of ion concentrations, from tens of micromolar to molar (20, 21, 30). Previous studies have shown a strong preferential attraction of cations over the exclusion of anions; for example, a 24-bp DNA attracted 37 ± 1 cations and excluded 9 ± 1 anions (10 mM salt concentration), corresponding to 0.804 ± 0.02 attracted cation and 0.195 ± 0.02 excluded anion per charge unit of the dsDNA (20, 21, 29). Monovalent cation occupancy in the ion atmosphere is insensitive to the cation size across the alkali metal ions Na⁺, K⁺, Rb⁺, and Cs⁺, contrary to several computational predictions (30, 31, 32, 33). Ion counting also revealed preferential association of divalent cations over monovalent cations around the dsDNA; for example, with Na⁺ in fourfold excess of Mg²⁺ (20 vs. 6 mM), the ion atmosphere nevertheless has fourfold more Mg²⁺ than Na⁺ (20, 30).

Over the past decades, experimental and computational studies have considerably advanced our understanding of the ion atmosphere around DNA duplexes. However, our knowledge of the ion atmosphere around RNA helices is limited. There are several computational studies dedicated to quantifying the RNA-ion interactions within the ion atmosphere (34, 35, 36, 37, 38, 39, 40); in particular, Poisson-Boltzmann (PB) calculations have emerged as the approach of choice, in part because it is easily implementable, computationally tractable, and conceptually straightforward (41, 42, 43, 44, 45, 46). However, there are few experimental studies on the RNA electrostatics, and the complex RNAs used typically prevent isolating and dissecting the ion atmosphere and its associated energetics (41, 42, 43, 44, 45, 46, 47, 48). Previous theoretical and computational studies have highlighted a higher linear charge density of the dsRNA compared to the dsDNA that is predicted to result in a stronger electrostatic field around dsRNAs (49, 50, 51, 52) and stronger interactions with ions, particularly with divalent cations like Mg²⁺ (34, 35, 36, 39, 42).

Given the general importance of RNA in biology and the motivation to better understand its electrostatic properties, we carried out ion counting experiments for monovalent and divalent cations around a 24-bp RNA. We compared its ion atmosphere composition to our previous results for a 24-bp DNA having the same sequence. We also compared the experimental results to theoretical PB predictions of the ions within the RNA’s ion atmosphere. Our ion counting results support the predicted stronger electrostatic field of dsRNA than dsDNA and, as was previously observed for dsDNA, results for monovalent cations agree with PB predictions, whereas those for Mg²⁺ do not (20, 21, 23, 53).

Materials and Methods

Reagents

DNA and RNA oligonucleotides were purchased from Integrated DNA Technologies (Coralville, Iowa). The following DNA sequences were used: 24S1: _5′GGT GAC GAG TGA GCT ACT GGG CGG_3′; 24S2: _5′CCG CCC AGT AGC TCA CTC GTC ACC_3′; 23S1: _5′GGT GAC GAG TGA GCT ACT GGG CG_3′; and 23S2: _5′CGC CCA GTA GCT CAC TCG TCA CC_3′. 24 mer RNA sequences were the same as 24S1 and 24S2 except for containing uracil instead of thymine bases. All salts were of the highest purity (TraceSELECT or BioXtra; Sigma-Aldrich, St. Louis, MO). All solutions were prepared in high purity water, ultralow total organic carbon (TOC) biological grade (Aqua Solutions, Deer Park, TX).

Preparation of DNA and RNA samples

DNA and RNA constructs used in this study were duplexes assembled from chemically synthesized oligonucleotides. Before assembly, oligonucleotides were purified by reverse-phase high-performance liquid chromatography (XBridge Oligonucleotide BEH C18; Waters, Milford, MA) and desalted using centrifugal Amicon Ultra-3K filters (Millipore, Burlington, MA). The DNA and RNA constructs were prepared as described previously (20, 21).

BE-ICP-MS

Buffer equilibration for DNA and RNA was carried out using Amicon Ultracel-30K filters (Millipore). Salt samples were prepared in 2 mM sodium 4-(2-hydroxyethyl)piperazine-1-propanesulfonic acid (Na-EPPS) or Mg-EPPS, pH 8.5 and their concentrations were determined by ICP-MS. The initial 500 μL of 0.2–2 mM DNA or RNA samples, with the salt of interest, was spun down to ∼100 μL at 7000 × g in Amicon Ultracel-30K filters at 4°C (to minimize solution evaporation) (54). As shown previously, equilibration between ions associated with nucleic acids and the bulk ions was completed after five rounds of the buffer exchange without any loss of the DNA or RNA; no DNA or RNA was detected in flow-through samples, as determined by ICP-MS (21).

Ion counting

Inductively coupled plasma mass spectrometry (ICP-MS) measurements were carried out using a XSERIES 2 ICP-MS (Thermo Scientific, Waltham, MA). Samples were analyzed as described previously (20, 21, 54). Briefly, aliquots (5–20 μL) of DNA- or RNA-containing sample, the flow-through from the final equilibration, and the equilibration buffer were diluted to 5 mL in 15 mL Falcon tubes with water. Dilution factors, the ratio of diluted to total sample volume, were used to maintain sample concentrations within the linear dynamic range of detection. Calibrations were carried out using standards from SPEX CertiPrep. Quality control samples, containing each element of interest at 50 μM, were assayed every 10 samples to estimate measurement precision (21, 54). A solution of 5% ammonium hydroxide in highly pure, ion-free water (Mili-Q, Millipore) was used as a washout solution between measurements (55).

Ion counting data points reported were collected from two to three independent experiments (i.e., “biological” replicate). Errors are the SD of all biological and technical replicates for a given sample.

The number of associated ions around the DNA and RNA duplex is reported here as a preferential interaction coefficient Γ_i (i = + or −, indicating cation or anion, respectively), where Γ_i is the difference in the ion concentration between the equilibrated nucleic-acid-containing sample $\left({\text{c}}_{\text{ion}}^{\text{NA}}\right)$ and the bulk solution $\left({\text{c}}_{\text{ion}}^{\text{bulk}}\right)$, divided by the DNA or RNA concentration (c_NA; determined by phosphorous measurements using ICP-MS) (Eq. 1) as follows:

$${\mathit{\Gamma }}_{\text{i}}=\frac{{\text{C}}_{\text{ion}}^{\text{NA}}-{\text{C}}_{\text{ion}}^{\text{bulk}}}{{\text{C}}_{\text{NA}}}.$$ (1)

For DNA or RNA, the cation preferential interaction coefficient, Γ₊, is expected to be greater than zero, indicating their accumulation around the negatively charged polyelectrolytes, and Γ₋ for an anion is expected to be less than zero because of repulsive interactions with the DNA or RNA.

Quantification of cation competition

To evaluate differences in the association between Mg²⁺ and monovalent cations (M⁺) with 24-bp RNA, we used the same method as described previously (20). Subsequently, we compared these results to experimental data for the Mg²⁺ versus M⁺ competition around a 24-bp DNA, from the same method and published previously (30). Briefly, the number of competing cations and Mg²⁺ cations around the dsRNA was measured over a range of competing cations concentrations at a fixed Mg²⁺ concentration of 6 mM. The competition constant (CC) was defined as the concentration of competing cation at which the number of the competing cation and Mg²⁺ ions within the ion atmosphere are equal.

PB calculations

The B-form 24-bp DNA and 23-bp DNA and A-form of 24-bp RNA were constructed with the Nucleic Acid Builder package (56). Charges were assigned using the PDB2PQR routine (57) with the CHARMM parameter set. PB calculations were carried out using the Adaptive PB Solver (APBS; version 1.4.1) (58) on a 405 × 405 × 578 Å³ grid with a grid spacing of 1.8 Å and the ion size equal to 2 Å. As ion counting experiments were carried out at 4°C, the simulation temperature was set to 277.15 K and the dielectric constant of the solvent was set to 86 K, characteristic of water at 4°C (59). The internal dielectric of the DNA and the RNA was set to 2 (60, 61, 62, 63). The solvent-excluded volume of the DNA and the RNA molecules was defined with a solvent probe radius of 1.4 Å. Boundary conditions were obtained by Debye-Hückel approximation.

The preferential interaction coefficient of ions i of valence z_i associated with the DNA and the RNA was computed by integrating the excess ion density (3, 20, 64) as follows:

$${\mathit{\Gamma }}_i={\rho }_{b,i}\int \left(\lambda \left(r\right)e^{-z_{i}e\phi \left(r\right)/kT}-1\right)dr,$$ (2)

where ρ_b,i is the bulk ion density; λ(r) defines the region in space that is accessible to ions, where λ(r) = 1, and defines solvent-excluded region (i.e., inside the macromolecule), where λ(r) = 0; e is the elementary charge; $\phi \left(r\right)$is the electrostatic potential; k is the Boltzmann constant; and T is the temperature.

The integration volume was defined as the entire volume of a simulation box including the solvent-excluded region in the DNA and the RNA interior (65). This approach matches the conditions for the experimental measurement because the experiments employ equal total volumes for the nucleic acids and bulk reference samples (21).

Results

An RNA duplex accumulates more Na⁺ ions than a DNA duplex

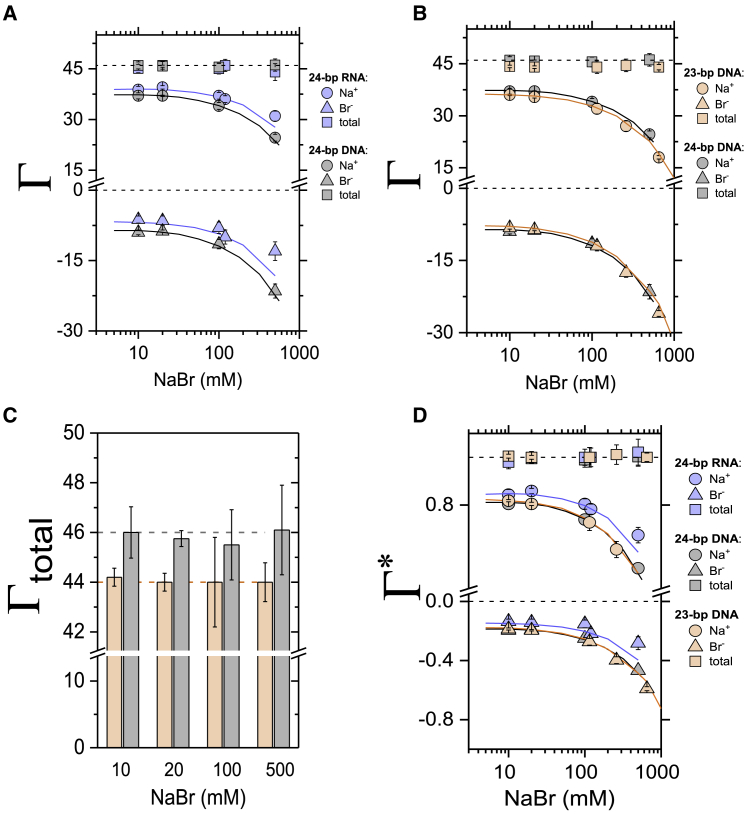
To determine and compare electrostatic properties of DNA and RNA duplexes, we quantified the composition of ion atmospheres around the molecules by carrying out ion counting experiments for NaBr. We chose NaBr for its accuracy of detection by mass spectrometry and because it behaves similarly to the more physiological K⁺ and Cl⁻ ions (21, 30). Measurements revealed that 24-bp RNA attracts on average two more Na⁺ cations and excludes two fewer Br⁻ anions than dsDNA in the concentration range of 10–500 mM (Fig. 1 A; Table S1) despite the same overall charge of −46e and the same sequence. Under all experimental conditions, the sum of ionic charges (e.g., Na⁺ and Br⁻) from the ion atmosphere agrees well with the overall charge of 24-bp DNA and 24-bp RNA (Γ = +46; Fig. 1 A and Table S1, squares versus dashed lines), as expected from the charge neutrality principle (20, 21).

Figure 1.

Quantification of the ion atmosphere around 24-bp RNA, 24-bp DNA, and 23-bp DNA duplexes. (A) The preferential interaction coefficient (Γ, Eq. 1) of attracted Na⁺ cations and excluded Br⁻ anions around 24-bp RNA (blue symbols) and 24-bp DNA (gray symbols) is shown. (B) The preferential interaction coefficient (Γ) of attracted Na⁺ cations and excluded Br⁻ anions around 23-bp (orange symbols) and 24-bp DNA (gray symbols) is shown. In (A) and (B), the total charge of the ion atmosphere summed from the individual ion measurements is shown as squares, and the dashed lines at Γ = +46 and Γ = +44 represent the theoretical charge needed to neutralize the 24-bp DNA and 24-bp RNA charge of −46e and 23-bp DNA charge of −44e. (C) The total number of ions within the ion atmosphere around 23-bp (orange bars) and 24-bp DNA (gray bars) from (B) is shown. Dashed lines are as in (B). (D) The fraction (Γ^∗) of attracted Na⁺ cations and excluded Br⁻ anions per negative charge (phosphorous group) of the molecule, as defined by Eqs. 3, 4, and 5, is shown. Experimental results from BE-ICP-MS ion counting are compared to PB predictions for 24-bp dsRNA (blue line), dsDNA: 24-bp (black line) and 23-bp (orange line). Each data point is the average of two repeats from at least two independent experiments. The reported errors are the SDs of all biological and technical replicates for a given sample. See Tables S1–S3 for data. To see this figure in color, go online.

The difference in the number of ions in the ion atmosphere around the dsRNA and dsDNA is relatively small, yet the two-sample t-test revealed that all data points are significantly different with p-values of <0.02 except the 10 mM data (p = 0.08). To further test whether the ion counting method can detect differences on this scale, we carried out the analogous experiments with 23-bp DNA (Fig. 1 B). The theoretical charge of the 23-bp DNA is −44e (i.e., 2e charge less than the 24-bp DNA), and the experimentally determined charge agreed well with this value (Γ = +44; Fig. 1, B and C, orange squares versus the orange dashed line). We also measured fewer Na⁺ cations attracted to and fewer Br⁻ anions excluded from the 23-bp DNA (t-test: p < 0.03, except the 100 mM data: p = 0.1). These results indicated that ion counting can resolve differences in the molecule charge as small as 2e. Further, results for NaBr association around the 24-bp DNA presented herein are in excellent agreement with previously published data, supporting the robustness of the BE-ICP-MS method (Fig. S1; Tables S1 and S2) (21, 30, 64).

To compare electrostatic properties of RNA and DNA, we represent the fraction of charge neutralization from associated cations $\left({\mathit{\Gamma }}_{+}^{\ast }\right)$ and from excluded anions $\left({\mathit{\Gamma }}_{-}^{\ast }\right)$ per unit charge (Eqs. 3, 4, and 5) as follows:

$${\mathit{\Gamma }}_{+}^{\ast }=\frac{{\mathit{\Gamma }}_{+}}{q_{NA}},$$ (3)

$${\mathit{\Gamma }}_{-}^{\ast }=\frac{{\mathit{\Gamma }}_{-}}{q_{NA}},$$ (4)

and

$${\mathit{\Gamma }}_{+}^{\ast }+{\mathit{\Gamma }}_{-}^{\ast }=1,$$ (5)

where q_NA is the total charge of dsDNA or dsRNA, and Γ₊ and Γ₋ are preferential coefficients for cations and anions, respectively, as defined above (Eq. 1). The sum of ${\mathit{\Gamma }}_{+}^{\ast }$ and ${\mathit{\Gamma }}_{-}^{\ast }$ must equal 1, following the charge neutrality principle.

We observed that the fraction of the associated Na⁺ around 24-bp RNA is larger than for 24-bp DNA (Fig. 1 D)$:{\mathit{\Gamma }}_{Na}^{\ast }$ = 0.86 ± 0.01 vs. 0.80 ± 0.004 for RNA and DNA, respectively (20 mM NaBr). In contrast, we measured no difference in the association of Na⁺ between 24- and 23-bp DNA$:{\Gamma }_{Na}^{\ast }$ = 0.80 ± 0.006 vs. ${\mathit{\Gamma }}_{Na}^{\ast }$ = 0.80 ± 0.004 for 23- and 24-bp DNA, respectively (20 mM NaBr). A greater attraction of cations and the lesser repulsion of anions is indicative of a stronger electrostatic potential around dsRNA than around dsDNA (49, 50, 51, 52), and this stronger electrostatic potential is predicted theoretically by the PB equation (20, 65, 66, 67). Indeed, there is excellent quantitative agreement between the experimental data and the PB predictions (Fig. 1, A, C, and D, points versus lines).

Counting ions around charged molecules can also be achieved by anomalous small-angle x-ray scattering (ASAXS) (22, 29, 41). Our ion counting data give results similar to previous ASAXS data for monovalent ions around 25-bp DNA and 25-bp RNA (29, 34) but provide higher precision (Fig. S2; Table S3). These differences could be experimental or result from sequence differences. The high-throughput and explicit counting of ions via BE-ICP-MS likely render it a preferable tool for broad investigation of ion atmosphere contents as well as for carrying out rigorous error estimates; it also more directly assays ion numbers, but it does not provide information about ion distributions that can be obtained from ASAXS (7, 29, 68).

RNA duplex interacts significantly stronger with Mg²⁺ compared to a DNA duplex

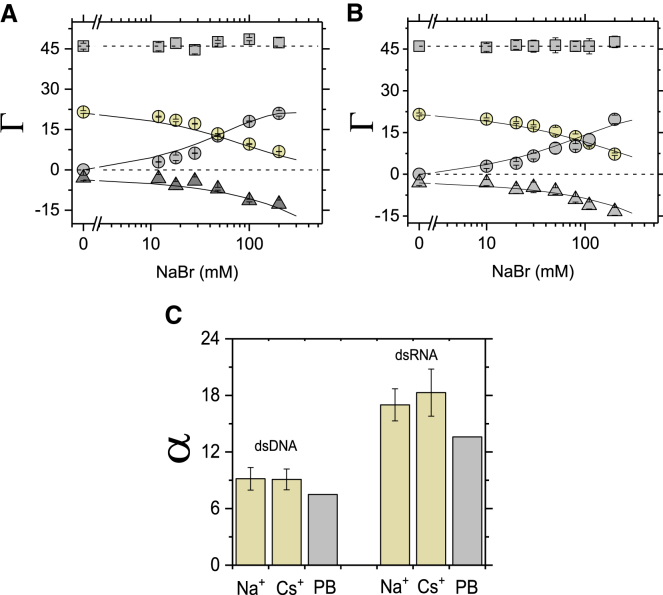
To provide an independent test for the electrostatic differences between the dsDNA and dsRNA, we measured monovalent cation competition for binding to dsDNA and dsRNA against constant concentration of Mg²⁺. DNA and RNA preferentially interact with divalent cations (M²⁺) over monovalent cation (M⁺), and the preference for divalent over monovalent increases as the strength of the molecule’s electrostatic field increases (15, 35, 36, 39, 41, 53, 69).

Our previous ion counting measurements of Mg²⁺ association with the dsDNA revealed 21.5 ± 0.5 divalent cations around the molecule for solutions containing only Mg²⁺ cations (20, 30). We measured the similar number of attracted Mg²⁺ around 24-bp RNA, Γ_Mg = 22.0 ± 0.5. Because total Mg²⁺ association is rather insensitive to differences in charge density for molecules with high charge density like DNA and RNA, we carried out more sensitive (Mg²⁺) versus (M⁺) competition experiments against the two monovalent cations Na⁺ and Cs⁺ to test the effect of charge (i.e., monovalent versus divalent) on energetics of the cation association and to address the effect of the size (Cs⁺ is larger than Na⁺ based on ionic radii). Upon increasing the bulk concentration of Na⁺ or Cs⁺, the number of associated Mg²⁺ decreased, and the number of the competing monovalent cations increased. As expected, charge neutrality was maintained across all concentrations (Fig. 2, A and B). To estimate energetics of monovalent cation interacts with the DNA or the RNA, relative to a Mg²⁺ background, we introduce the unitless parameter α, defined as follows:

$$\mathit{\alpha }=\frac{\text{CC}}{\left[{\text{Mg}}^{2+}\right]},$$ (6)

where CC is the competition constant (i.e., the concentration of competing cation at which the number of the competing cation and Mg²⁺ ions within the ion atmosphere are equal), and [Mg²⁺] is the concentration of the background Mg²⁺, here 6 mM.

Figure 2.

Competitive association of monovalent cations against Mg²⁺ for a 24-bp DNA and RNA duplexes. (A and B) The preferential interaction coefficient (Γ) of associated Na⁺ cations (gray circles), replaced Mg²⁺ cations (yellow circles, [MgBr₂] = 6 mM), and excluded Br⁻ anions (gray triangles) around the 24-bp DNA (A) and around the 24-bp RNA (B) are shown. In (A) and (B), the total charge of the ion atmosphere summed from the individual ion measurements is shown as squares, and the dashed lines at Γ = +46 represent the charge needed to neutralize the total 24-bp DNA and 24-bp RNA charge of −46e. Solid lines are PB calculations. (C) Shown are coefficients for monovalent cations against Mg²⁺$\alpha =\left(CC/\left[M{g}^{2+}\right]\right)$ (Eq. 6), where CC is the concentration of competing cation at which the number of the competing cation and Mg²⁺ ions within the ion atmosphere are equal, [Mg²⁺] is the background concentration (here [Mg²⁺] = 6 mM). Each data point in (B) and (C) with the 24-bp RNA is the average of three independent measurements. Error bars are as in Fig. 1. See Table S4 for data and Tables S5 and S6 for PB calculations. Ion counting data for the 24-bp DNA (A) and (C) are from (30), where the same methodology was used. To see this figure in color, go online.

The relative preferential cation occupancy from the data of Fig. 2, A and B and Table S4 is summarized in Fig. 2 C in terms of α. The cation competition experiments show that Mg²⁺ interacts stronger with the 24-bp RNA compared to the 24-bp DNA, with a measured α value that is twofold higher for the dsRNA (Fig. 2 C; Table S4). Similar values of α for Na⁺ and Cs⁺ against Mg²⁺ suggest that the occupancy of the monovalent cations within the ion atmosphere is insensitive to their size, as shown previously in M⁺ versus M⁺ cation competition experiments (30).

We also carried out PB calculations for the divalent versus monovalent cation competition binding (Fig. 2, A–C). PB predicts that dsRNA interacts stronger with Mg²⁺ than dsDNA (i.e., α_DNA = 7.5 and α_RNA = 13.6; Fig. 2 C) and that twice as much monovalent ion concentration as for the dsDNA is required to reach the equal amount of divalent and monovalent cations within the ion atmosphere around the dsRNA, in accord with the experimental results (Fig. 2 C). However, PB underestimates the strength of the Mg²⁺-DNA and Mg²⁺-RNA interactions, predicting lower monovalent cation concentrations are required to replace Mg²⁺ than is observed experimentally (Fig. 2 C).

In summary, our experimental data showed that dsRNA interacts stronger with Mg²⁺ than dsDNA, consistent with theoretical predictions, but there are nevertheless quantitative differences between experiment and theoretical results.

Discussion

Our ion counting experimental studies allow us to evaluate electrostatic properties of RNA and DNA duplexes. We observed that dsRNA attracts more monovalent cations than dsDNA and interacts more strongly with Mg²⁺. These results indicate that the electrostatic field around the RNA duplex is stronger than that of the DNA duplex, as proposed by numerous computational studies (34, 35, 36, 37, 38, 39, 69).

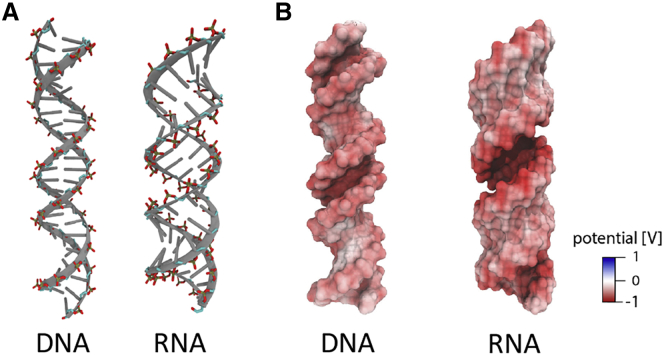
To illustrate the electrostatic differences between RNA and DNA, we carried out PB calculations of the electrostatic surface potentials for the respective canonical helices (Fig. 3 B). PB predicts the electrostatic potential at the phosphate backbone is higher for the dsRNA than for the dsDNA, −830 mV vs. −640 mV (at 10 mM NaCl). This difference is visualized in Fig. 3 B, where the deeper red color indicates the larger negative electrostatic potential around the phosphate groups of the dsRNA.

Figure 3.

Comparison of DNA and RNA duplex shape and electrostatic potential. (A) DNA and RNA duplexes with highlighted phosphate residues are shown. The B-form 24-bp DNA duplex and A-form of 24-bp RNA were constructed with the Nucleic Acid Builder (NAB) package (56). (B) Poisson-Boltzmann (PB) calculations of electrostatic surface potential of the DNA and RNA duplexes from (A) are shown (see also Fig. S3). The electrostatic potential mapped to the molecular surfaces was calculated using Adaptive PB Solver (APBS) (57), and the figures were rendered with visual molecular dynamics (87). To see this figure in color, go online.

Topological differences between DNA and RNA duplexes play the major role in defining the electrostatic properties of the molecules. Phosphoryl groups in dsRNA face inward, along a surface plane of the major groove, whereas those in dsDNA are oriented toward bulk solvent (Fig. 3 A). The shorter P-P distances along dsRNA (5.65 Å vs. 6.62 Å for dsRNA and dsDNA, respectively) and across (9.97 Å vs. 11.69 Å for dsRNA and dsDNA, respectively) the major groove for dsRNA and the minor groove for dsDNA result in the stronger RNA electrostatic field (Fig. 3 B) because Coulombic interactions are distance dependent. The inward facing of the negatively charged phosphate groups may also contribute to enhancing of the electrostatic potential through a phenomenon referred to as electrostatic focusing (70). Indeed, previous crystallographic studies have shown stronger localization of the Mg²⁺ within the deep major groove and at the phosphate groups bridging across the other mouth of the narrow major groove at the most negative electrostatic potential regions of A-form duplex (69).

An important step toward developing quantitative and predictive models of RNA structure, folding, and interactions with binding partners is the quantitative understanding of nucleic acid/ion interaction within the ion atmosphere and at the specific ion binding site. Given the highly complex and dynamic nature of the ion atmosphere, understanding will require synergy between theory and experiment. Experimental methods like ion counting can quantify the overall content of the ion atmosphere and energetics of competitive association of cations, but this method does not provide information about the distribution of ions within the atmosphere. Computational models can in principle provide a thorough and deep understanding of ion/nucleic acid interactions, solvent/nucleic acid interactions, and the dynamic and energetic consequences of these interactions (31, 35, 65, 71, 72, 73, 74, 75, 76, 77, 78). However, such models cannot be assumed to be correct, and even matching to one of previous experimental measurements is insufficient to establish the veracity of models for systems as complex and multivariant as nucleic acid/ion interactions in solution. Instead, robust and deep tests of bona fide blind predictions are needed via ion counting and additional experimental methods.

Here, we tested PB calculations of the preferential interaction coefficients around dsDNA and dsRNA. PB calculations have become the most popular approach to predict and visualize electrostatics of macromolecules, predominantly because it is conceptually straightforward and easily accessible through APBS (web-based server) (58). We observed excellent agreement between PB calculations and experimental results for monovalent ions around dsDNA and dsRNA, except at 500 mM NaBr for the 24-bp RNA (Fig. 1 A, blue symbols), where PB underestimates the number of accumulated Na⁺ cations and overestimates the number of excluded Br⁻ anions compared to experimental results. Our previous systematic studies on monovalent ion accumulation around 24-bp DNA revealed salt activity coefficient effects at high bulk ion concentrations that may be responsible for this deviation because of increased ion-ion correlations and hence the formation of ion pairs within the ion atmosphere (21, 79). Notably, PB theory, because of its mean-field approximation and point-like treatment of ions, does not account for ion-ion correlations and hence underestimates the number of cations and anions for salts that ion-ion correlations have been observed (7, 21, 23, 80, 81, 82). Interestingly, the higher electrostatic field generated by the dsRNA may increase the correlations between Na⁺ and Br⁻ and hence result in the higher ion count at high bulk ion concentration. We also show that PB calculations underestimate energetics of Mg²⁺-dsDNA and Mg²⁺-dsRNA interactions, a result consistently observed in the literature and attributed to the inability of PB and other mean-field theories to account for ion-ion correlations that manifest specifically for higher valence ions (7, 20, 23, 83, 84).

Previous ion counting studies on competitive association of monovalent cations with the dsDNA have proven invaluable in testing all-atom computational models (30). For example, monovalent cation occupancy in the dsDNA and dsRNA ion atmosphere is insensitive to the cation size across the alkali metal ions Na⁺, K⁺, Rb⁺, and Cs⁺, contrary to computational predictions and highlighting the need to reevaluate molecular mechanical force fields for solute-solvent and solvent-solvent interactions. Our new, to our knowledge, experimental results for dsRNA-ion interactions provide the opportunity to test newly developed all-atom models of RNA-Mg²⁺ interactions (73, 75, 77, 85, 86) and initiate a feedback loop between computation and experiment.

Author Contributions

Conceptualization, M.G. and D.H.; Performing experiments, M.G.; Formal analysis, M.G.; Writing, M.G. and D.H.; Funding acquisition, D.H.

Editor: Susan Schroeder.