Replication and generalization in applied neuroimaging

Abstract

There is much interest in translating neuroimaging findings into meaningful clinical diagnostics. The goal of scientific discoveries differs from clinical diagnostics. Scientific discoveries must replicate under a specific set of conditions; to translate to the clinic we must show that findings using purpose-built scientific instruments will be observable in clinical populations and instruments. Here we describe and evaluate data and computational methods designed to translate a scientific observation to a clinical setting. Using diffusion weighted imaging (DWI), Wahl et al., (2010) observed that across subjects the mean fractional anisotropy (FA) of homologous pairs of tracts is highly correlated. We hypothesize that this is a fundamental biological trait that should be present in most healthy participants, and deviations from this assessment may be a useful diagnostic metric. Using this metric as an illustration of our methods, we analyzed six pairs of homologous white matter tracts in nine different DWI datasets with 44 subjects each. Considering the original FA measurement as a baseline, we show that the new metric is between 2 and 4 times more precise when used in a clinical context. Our framework to translate research findings into clinical practice can be applied, in principle, to other neuroimaging results.

1.-. Introduction

We describe methods to translate magnetic resonance imaging (MRI) scientific findings into clinical practice. The goal of scientific discoveries differs from clinical diagnostics. Clinical applications should be based on quantitative measurements that replicate in controlled laboratory conditions. These applications must also be applicable to a clinical environment where data acquisition methods, subject populations, and computational methods can vary substantially.

We base our methods on the ideas of replication and generalization. Because these terms, along with reproducibility, re-execution, and robustness are used in various ways in the literature (Goodman et al., 2016; Kennedy et al., 2019; McNaught and Wilkinson, 1997; Patil et al., 2016; Plesser, 2017), we begin by explaining our usage. Scientific experimentalists typically set out to make a measurement that can be replicated. For example, a team makes a measurement using a specific rig and experimental conditions. Other scientists check the work by following the published instructions that define how to construct the rig and implement the experimental conditions. Scientific replication means repeating the experiment as precisely as possible. This approach is appropriate for investigations that test theories or quantify important phenomena, but replication is not a realistic possibility for extending discoveries into clinical applications. These applications do not have access to the carefully calibrated instruments that have been purpose-built for scientific measurements (for example, the Human Connectome Project scanners). For a scientific discovery to become clinically relevant, the finding must generalize across variations in the population and instruments.

Replication and generalization are contrasted in Figure 1. Panel A emphasizes scientific discovery and replication. An experimental design is chosen and measurements are made with a selected population, data acquisition instruments and methods, and a computational method. We measure the precision of the measurement when the experiment is repeated (test-retest). In this case three replication experiments are illustrated using different data acquisition parameters. If the scientific measurements replicate with sufficient precision, we might carry out generalization measurements (Panel B), to test the extent of applicability of said measurements. The panel illustrates generalization experiments that share the same experimental design, but use different populations (e.g., geographic locales, age and gender), different data acquisition methods, (e.g., pulse sequences and vendors), and different computational methods (e.g., pre-processing software). Translating a scientific measurement into a clinical application is a two step process: beginning with an experiment that replicates, we test how well the experiment generalizes.

Figure 1. Summary of the individual experiments, organized as replication or generalization experiments.

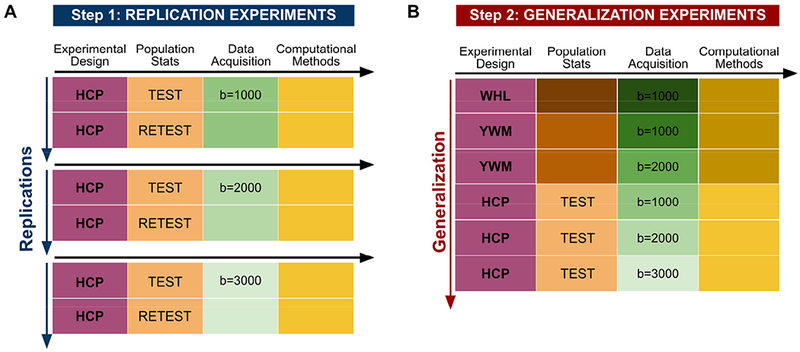
The columns correspond to the experimental pipeline steps; every row corresponds to an experiment. Different colors represent different steps in the experimental pipeline; different shades represent implementation differences within the step. A) Three replication experiments, based on the Human Connectome Project (HCP) test-retest datasets. The difference among the experiments is the b-value used in the acquisition. In a replication experiment, the intention is to repeat the original methods as far as possible, hence the same shades; the test-retest case goes uses the same population and instrumentation at different times. B) The generalization experiment reflects the transition to the clinical environment. The goal is to evaluate whether the measurements are robust to expected variations in the measurement conditions. The generalization is undertaken after validating the results in the replication experiment. The datasets are from Wahl et al (2010) (WHL). Yeatman et al. (2014) (YWM), and (Glasser et al., 2013) (HCP).

This paper applies replication and generalization to a neuroimaging measurement that has the potential to become clinically relevant: identifying lateralized white matter disease in individual subjects. Wahl et al. (2010) used diffusion-weighted imaging (DWI) to measure white matter tracts in healthy adults; they observed that across subjects the mean fractional anisotropy (FA) of homologous pairs of tracts is highly correlated. We hypothesized that this finding might be a fundamental biological trait in healthy participants, that can be measured in research labs and clinical settings. We investigated if the relation between homologous tract pairs is a more useful clinical measure than assessing the measurements from each tract separately. We find that using the relation between homologous left and right tracts does provide a potential clinical measure.

2.-. Materials and methods

To evaluate the replication and generalization of the DWI finding, we obtained data from multiple sources. We use nine datasets that we group into three categories.

• WHL: Original 44 subject dataset used in (Wahl et al., 2010). The authors shared the original DICOM files for this work, and we performed the analysis using our computational methods. We obtain 1 dataset, called WHL1000.

• YWM: We selected a 44 subject subset of the data reported by (Yeatman et al., 2014). The subjects matched the mean age (but not the age range) of the WHL dataset. We obtained two datasets: YWM1000 and YWM2000 that differ in data acquisition parameters (b-values, number of directions).

• HCP: We selected a 44 subjects whose test-retest data are available from the 1200 Human Connectome Project (HCP) release (Glasser et al., 2013). HCP1000, HCP2000 and HCP3000 differ only in data acquisition parameters (b-values). HCP 1000RETEST, HCP2000RETEST and HCP3000RETEST are the corresponding retest data.

Figure 1 represents three replication experiments (panel A) and a generalization experiment (panel B). The replication experiments compare test-retest values of the mean tract FA at three different b-values; the were collected using the same subjects, instruments and computational methods at the HCP. This replication analysis bounds the precision of the estimated mean tract FA: the generalization precision shouldn’t be better than the replication precision.

The generalization experiment compares the mean tract FA across different subjects, instruments and computational methods (Figure 1B). The precision derived from these six experiments assesses generalization. The HCP RETEST experiments are omitted from the generalization experiment to avoid a HCP bias. In addition to subject and instrument differences, the WHL and YWM differ in computational processing. Some unmeasured variability is introduced by non-deterministic aspects of these computations.

In the following sections, we describe three different aspects of the experimental pipeline. The Population statistics section shows that cohorts are similar, but not identical. The Data acquisition section includes MRI pulse sequences and parameter choices that are different between sites and vendors, as is often the case in clinical settings. The Computational methods section describes the infrastructure we used to implement computational reproducibility, as well as a detailed description of the data analysis pipeline and numerical calculations.

2.1.-. Population statistics

The population statistics for the three datasets are similar, but not exactly the same (see Table 1). All the groups include 44 subjects of a similar mean age, ranging from 30.7 to 31.8. The age range of the YWM dataset is the largest, with a standard deviation of 14.4. The HCP dataset age standard deviations is 3.2, which is an approximation: the HCP ages are binned to protect participant privacy. The YMW and WHL datasets are matched in male-female ratio, but the HCP dataset has more females than males. The original publications include more information about the populations (Glasser et al., 2013; Wahl et al., 2010; Yeatman et al., 2014).

Table 1.

Descriptive statistics of the three different populations used across the datasets.

Dataset	Count	Age	Gender	Age
WHL	44	30.8±7.8	20 female	29.5±7.5
			24 male	31.9±7.9
YWM	44	31.8±14.4	24 female	29.5±2.1
			20 male	34.7±3.6
HCP	44	30.7±3.2	31 female	31.9±3.2
			13 male	27.8±3.2

2.2.-. Data acquisition

Table 2 shows the main characteristics of the DWI data acquisition, emphasizing the differences between sites and experiments. As a practical matter, measurements made across multiple sites are very likely to have different MRI scanner models that are calibrated using different tools. The MRI vendors compete on intellectual property concerning the pulse sequences, making a perfect replication either extremely inconvenient or impossible. For example, the scanner used by the HCP site was specially designed and this type of instrument is unlikely to become available to the thousands of clinical sites around the world (Glasser et al., 2016, 2013). The datasets differ with respect to the number of acquisition channels, gradient strength, diffusion directions, b-value and voxel size. Such differences are unavoidable because not all sites can implement the same acquisition parameters. In addition to vendor differences, data are acquired over time, technology evolves, and people make choices.

Table 2.

Main characteristics of the data acquisition parameters across datasets.

Dataset	Scanner Vendor; Model; Location	Magnetic Field; Head Coil Receivers; Max. Gradient Strength	Main Sequence Characteristics	Experiment Codename
WHL	GE Signa EXCITE UCSF	3T 8 channels 40 mT/m	55 dirs., 1.8 mm3 voxels b = 1000 s/mm2	WHL1000
YWM	GE Discovery 750 Stanford CNI	3T 32 channels 40 mT/m	30 dirs., 2 mm3 voxels b = 1000 s/mm2	YMN1000
			96 dirs., 2 mm3 voxels b = 2000 s/mm2	YMN2000
HCP	Siemens Connectom CMRR/WASH WashU	3T 32 channels 100 mT/m	90 dirs., 1.25 mm3 vox b = 1000 s/mm2	HCP1000 & HCP1000RETEST
			90 dirs., 1.25 mm3 vox b = 2000 s/mm2	HCP2000 & HCP2000RETEST
			90 dirs, 1.25 mm3 vox b = 3000 s/mm2	HCP3000 & HCP3000RETEST

2.3.-. Computational methods

The computational methods are divided into two parts: (1) the infrastructure: required for a computationally reproducible system, sometimes called the neuroinformatics platform (Marcus et al., 2011); and, (2) the data analysis pipeline: comprises all the steps starting with the DICOM images generated in the MRI scanner (the acquisition device) to the final published results.

2.3.1.-. Infrastructure for computational reproducibility

The data management and computational infrastructure use a technology (Flywheel.io) that (a) implements reproducible computational methods, (b) tracks provenance of the data, and (c) facilitates data sharing. For reproducibility, all computational methods were performed using containerized methods. These are small virtual machines that include all dependencies and runs the same computation across platforms. The analytical methods implemented in the containers are open-source, and we provide links to the containers in the following sections. To track the provenance, the computational system stores: (a) the input data, (b) the container version that was executed, (c) the container input parameters, and (c) the output files. The analyses are fully reproducible by anyone with IRB authorization to access the system. More details about the infrastructure and implementation can be found at Lerma-Usabiaga et al. (2019).

2.3.2.-. Data analysis pipeline

The diffusion-weighted imaging analysis methods consisted of two main steps, implemented in two containers: preprocessing and tractography. Both were applied to WHL and YWM datasets. The HCP dataset was preprocessed by that consortium (Andersson et al., 2003; Andersson and Sotiropoulos, 2016, 2015) and only the tractography container was applied.

2.3.2.1.-. Preprocessing

The preprocessing consists of the data preparation required to do the tractography and fractional anisotropy (FA) analyses. The preprocessing container comprises the following steps: first, using the tools provided by MRtrix (github.com/MRtrix3/mrtrix3), we perform a principal component analysis (PCA) based denoising of the data; second, additional Rician based denoising and Gibbs ringing corrections were applied (Kellner et al., 2016; Veraart et al., 2016a, 2016b); third, FSL’s eddy current correction was applied (Andersson and Sotiropoulos, 2016); fourth, we performed bias correction using the ANTs package (Tustison et al., 2010); fifth, we applied a Rician background noise removal using MRtrix tools again. The code and parameters are available through GitHub (github.com/vistalab/RTP-preproc) and Docker Hub (hub.docker.com/r/vistalab/RTP-preproc/).

2.3.2.2.-. DWI processing and tractography

The tractography container takes the preprocessed DWI data and an un-preprocessed anatomical T1-weighted file as input. It outputs the FA of the selected 6 homologous tract pairs. The algorithms in the container perform the following steps: first, the diffusion data are aligned and resliced to the anatomical image (https://github.com/vistalab/vistasoft, dtiInit); second, the whole brain white matter streamlines are estimated using the Ensemble Tractography (ET) method (Takemura et al., 2016). ET invokes MRtrix’s constrained spherical deconvolution (CSD) implementation once and the tractography tool 5 times, constructing whole brain tractograms with a range of minimum angle parameters (values 47.2, 23.1, 11.5, 5.7, 2.9). The LiFE (Linear Fascicle Evaluation) method evaluates the tractogram streamlines and retains those that meaningfully contribute to predicting variance in the DWI data (Pestilli et al., 2014). Finally, the Automated Fiber Quantification (AFQ) method (Yeatman et al., 2012) segments streamlines into tracts (Figure 2). The code and parameters are available through GitHub (github.com/vistalab/RTP-pipeline) and the container through Docker Hub (hub.docker.com/r/vistalab/RTP-pipeline).

Figure 2. Six pairs of homologous tracts and their defining ROIs.

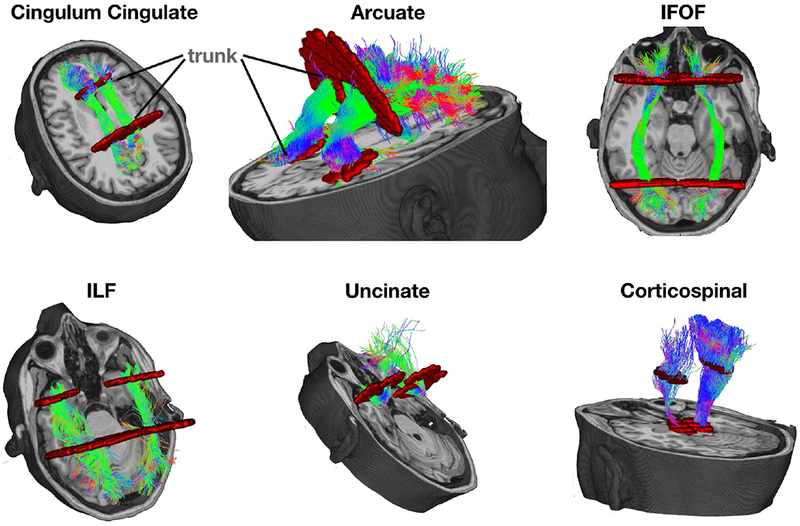
The streamlines serve as a model of white matter tracts; they are selected by fitting to the diffusion weighted imaging (DWI) measurements. The tracts are defined by regions of interest (ROIs, red) that select specific streamlines from the whole brain tractogram. The region between the two ROIs is relatively stable and called the trunk. We estimate a core fiber from the collection of streamlines and sample 100 equally spaced segments. The FA of the core fiber is calculated by combining FA transverse to the core fiber at every sample point, using a Gaussian weighting scheme over distance. The set of sample points is the tract profile; the average of the FA values of the core fiber is the mean tract FA.

2.3.2.3.-. Mean tract FA values

We analyzed the six homologous-tract pairs analyzed in (Wahl et al., 2010) (Figure 2). The ROIs used to identify the streamlines that form the tracts are shown in red. The mean tract FA is calculated in several steps. A core fiber, representing the central tendency of all the streamlines in the tract, is identified. Equally spaced positions along the fiber between the two defining ROIs are sampled (N=100). The FA values of streamlines at locations transverse to each sample position are measured and combined. The value is a Gaussian-weighted sum where the weight depends on the distance from the sample point (Yeatman et al., 2012). The sampling and transverse averaging generates a tract profile of 100 FA values. The mean tract FA is the average of these values.

2.3.3.-. Data preparation and statistical analysis

The data preparation, statistical analysis and plotting scripts read the input data directly from the Flywheel neuroinformatics platform using a software development kit (SDK). To maintain reproducibility and data provenance, these scripts are stored and versioned in a GitHub repository, and the input data are stored and the specific version that was executed is stored in the neuroinformatic platform. The scripts read the files containing the FA values for each subject and each tract, categorize it for the different experiments, create the descriptive plots and calculate the metrics. The scripts to replicate the figures and calculations can be found at https://github.com/garikoitz/paper-reproducibility.

3.-. Results

We first illustrate replication and generalization analyses for the FA measurement of individual tracts and evaluate the usefulness of this measure as a clinical application. Next, we evaluate a metric based on the homologous tract correlation reported by Wahl et al. (2010). The main figures describe one illustrative tract, the inferior fronto-occipital fasciculus (IFOF), and in total we report findings for six pairs of homologous tracts. We selected the mean FA of a tractogram as an example because it is useful to explain our methods, but the analysis can be applied to many other measures. For example, Wahl et al. report four DWI measures (FA, MD, AD, RD).

3.1.-. FA measurement

3.1.1.-. Replication experiment

Figure 3A shows the mean tract FA profiles at three b-values for the streamlines that model the IFOF. The solid and dashed lines show the mean tract profile across subjects for the test (solid) and retest (dashed) acquisitions. The profiles are similar at each b-value; consistent with prior measurements the FA values decrease as b-value increases (Farrell et al., 2007a; Jones and Basser, 2004; Landman et al., 2007; Mukherjee et al., 2008a, 2008b). The shaded regions indicate the range (+/− 1 SD) across the population of participants.

Figure 3. Replication analyses of the tract profile and mean tract FA.

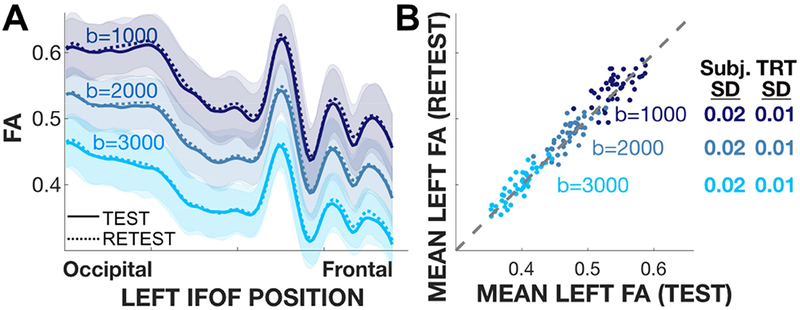
Analyses are shown for a representative tract (left IFOF), and based on the HCP test-retest data. A) Tract profiles of the subject average FA in the test (solid) and retest (dashed) experiments. The mean profile (thin line) and ±1 SD (shaded band) are shown. The profiles at each b-value match very closely; across b-values the profiles have a similar shape but different absolute values. B) Test-retest scatter plot. For all b-values, the SD of the difference between the test-retest pairs of FA values is 0.01 (TRT SD), and the SD of the distribution of FA values is 0.02 (Subj. SD). (Tract profiles and scatter plots for 11 other tracts are similar and reported in Figures S1a, S2).

The test-retest analyses for the mean tract FA of the IFOF are shown in Figure 3B. Each point is a subject, and the three types of symbols show test-retest at three b-values. The test-retest mean tract FA values are distributed near the identity line. For each b-value the mean tract FA varies between subjects (standard deviation, 0.025). The scatter about the identity line is smaller, (standard deviation, 0.01-0.02). The scatter around the identity line is similar for measurements at the three b-values, suggesting that the noise level is similar (Rokem et al., 2015).

The replication analyses for an additional 11 tracts follow the same trends as the IFOF (see Supplemental material, Figures S1a–S2). The FA values decrease with increasing b-value, and the between-subject standard deviation is larger than the within-subject test-retest standard deviation. Considering all tracts, the largest between-subject standard deviation is for the arcuate fasciculus, and the smallest is for the corticospinal tract. In all cases, the shape of the tract profiles remain similar across b-values. This supports the idea that tract profiles are a useful target for further investigation (St-Jean et al., 2019; Yeatman et al., 2014).

3.1.2.-. Generalization experiments

We assess the generalization of the FA measure by comparing the HCP data with those from YWM and WHL. Because of the large differences in FA, we separate the analysis by b-value (Figure 4).

Figure 4. FA Analyses for the generalization experiment and selected tracts.

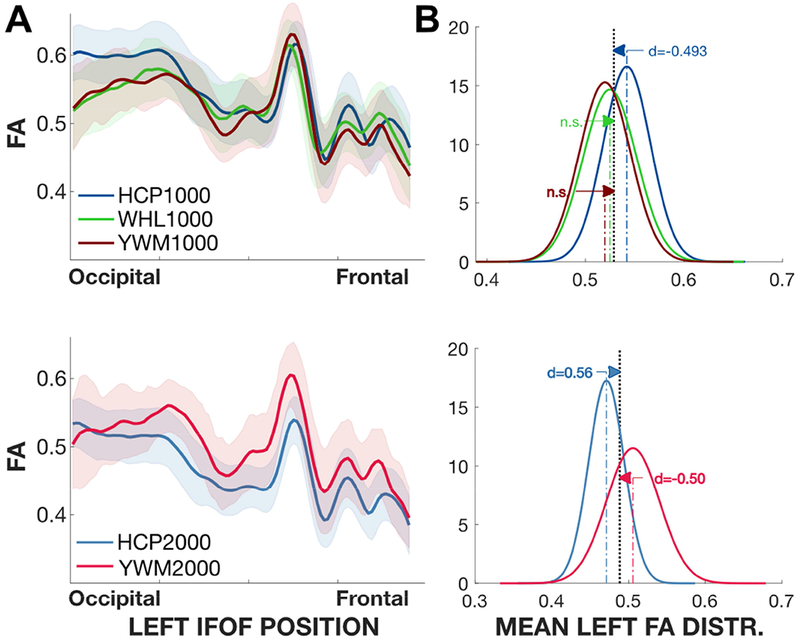
Top: Left Corticospinal. Bottom: Left IFOF. A) The curves show the average FA tract profiles for different experiments. The shaded region is ±1 SD. B) Normal distribution summary of the mean FA values in each experiment. The mean is the average of the FA values of each participant’s profile. The grey plot shows the distribution for all experiments; the curves are scaled so that the sum of the areas of the experiments equals the grey area. The arrows show the difference between each of the means and the group mean, and the numbers express effect size (Cohen’s d). The distributions were estimated using 10,000 bootstrap samples. C) Mean FA values and 90% experimental confidence intervals. n.s.: non-significant. Plots for additional tracts are in the Supplementary Materials (Figure S1b–S1c–S3a–S3b).

The HCP, YWM and WHL data obtained at b=1000 are compared in the top two panels. We use the IFOF tract, but the conclusions are the same for other tracts (see Supplementary material Figures S1b,S1c–S3a–S3b). The tract profile from the HCP dataset is the same as that shown in Figure 2, and the green and red curves are from the WHL and YWM datasets, respectively. Over much of the tract the three data sets agree in the sense that they are closer than the between-subject variance. The HCP tractogram profile diverges from the YWM and WHL on the left side of the graph (occipital end), and this appears to be the largest source of the difference between the three datasets.

The distribution of HCP mean tract FA values are about 1 standard deviation larger than the values in the YWM and WHL data set, and this causes the precision of the generalization to be substantially lower than the precision of the replication (Figure 4B, top). It is notable that at b=1000 the mean FA tract values for the IFOF in the WHL and YWM data sets contain values that are never observed in the HCP data set (FA < 0.47). The expansion of the range of FA values provides an indication of what one would observe in a clinical application compared to measurements obtained at a single site.

The HCP and YWM data obtained at b=2000 are compared in the two bottom panels. In this measurement the HCP FA values are generally lower than the YWM FA values. This difference is seen in the mean FA distributions, which are again separated by about 1 standard deviation. It is notable that at b=2000 the mean FA values for the IFOF include values in the YWM data that are never observed in the HCP data (e.g., FA > 0.55). Again, the generalization analysis shows that combining data from multiple sites extends the range of FA values one would observe from healthy participants.

3.1.3.-. Evaluation

The analyses of replication and generalization do not force a conclusion about whether the technique may have value in practice. Rather, the analyses define the range of values one might observe using a restricted set of instruments and methods (replication), compared to the range of values observed as we measure in clinical applications (generalization). For most tracts, the range of the mean tract FA value increases by about a factor of two as we include data from different, but typical, instruments and sites. Adding more sites, or expanding the population, can only increase this factor.

3.2.-. Homologous tract FA values

The evaluation of mean tract FA motivated us to search for a dependent measure with better generalization. The high positive correlation in FA between pairs of homologous tracts (Wahl et al., 2010), measured across subjects, suggests an alternative measure. The correlation implies that a participant with a relatively high FA value in the left tract will have a relatively high FA in the homologous right tract. Using this type of measure has the potential to improve generalization because measurements of the two tracts depend on common experimental factors. Qualitatively, the measurements of the left tract serve as calibration data to predict the FA measurement of the right tract. This is analogous to the use of image contrast rather than image value.

3.2.1.-. Homologous tracts linear model

The next question we address is how to convert the observed correlations, obtained from multiple participants, into a measurement that can be applied to individual participants. The initial approach is to use the linear model implicit in the correlation. Specifically, the correlation between homologous tracts means that there is an affine transform that predicts the mean tract FA in the right from knowledge of the left.

$${\mathit{PredictedRight}}_{\mathit{FA}}=\alpha {\mathit{MeasuredLeft}}_{\mathit{FA}}+\beta$$

The prediction error (residuals) are the difference between the measured and predicted FA,

$$\mathit{Residuals}={\mathit{MeasuredRight}}_{\mathit{FA}}-{\mathit{PredictedRight}}_{\mathit{FA}},$$

and bootstrapping with replacement from the residuals we estimate the FA range where we expect to find some percentage, say 95%, of the data (Figure 5: the vertical black line represents this range). If we calculate the range of possible PredictedRight_FA values for all MeasuredLeft_FA values, we obtain a band of likely PredictedRight_FA values (green bands). The center of the band is the linear prediction and the dashed (solid) lines represents the 68% (95%) limits. Given a measurement of the left FA, the band defines the range of expected values for the MeasuredRightFA in a healthy participant.

Figure 5. Representation of the relation between homologous tracts.

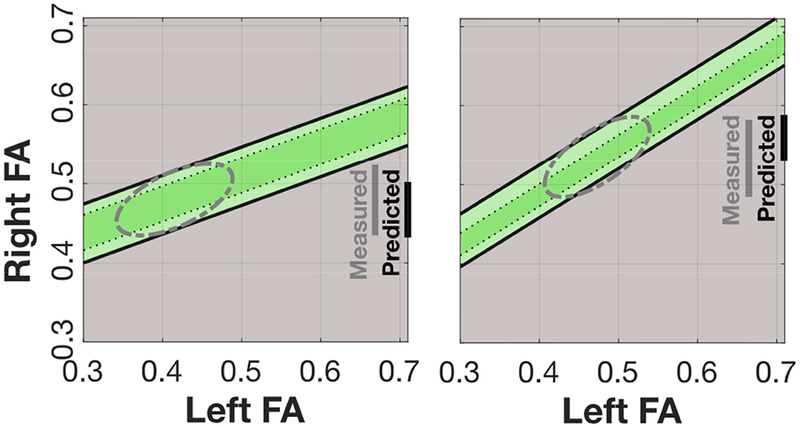
The linear correlation between mean FA in homologous white matter tracts defines a band of predicted right FA values given a left FA value. Measurements across clinically relevant cases, including variations in population, data acquisition, and computational methods, define the correlation and the size and shape of this region. For each tract, a participant’s data may fall inside or outside the green region, and this serves as a diagnostic of their white matter health. Measured: the range of Right FA values. Predicted: the size of the range ofpredicted Right FA values given a Left FA value (vertical height of the green band).

A more general formulation, beyond the linear relation, assesses the distribution of left-right FA values in the plane. These distributions form a cloud of points in the plane that can be reasonably approximated by a bivariate Gaussian. Consequently, the likely locations of the points are circumscribed by an ellipse. The distance of any single point from the center of the ellipse, say measured by the Mahalanobis distance, can serve as a measure of the participant’s health in a clinical application. This formulation has the added benefit incorporating additional information: the absolute value of tract mean FA.

3.2.2.-. Replication of the linear model

A scatterplot of the mean tract FA of the left and right IFOF for six HCP data sets (three b-values, test-retest) is in Figure 6. The different blue colors represent measurements at different b-values, and the different shapes represent test (circles) and retest (crosses) measurements. The slope of the linear relation between the mean tract FA of the left-right IFOF tracts is slightly less than one. Each pair of tracts has its own best-fitting line (see Figure S4a).

Figure 6. Left-Right IFOF FA scatterplots and iso-residual contour lines for HCP.

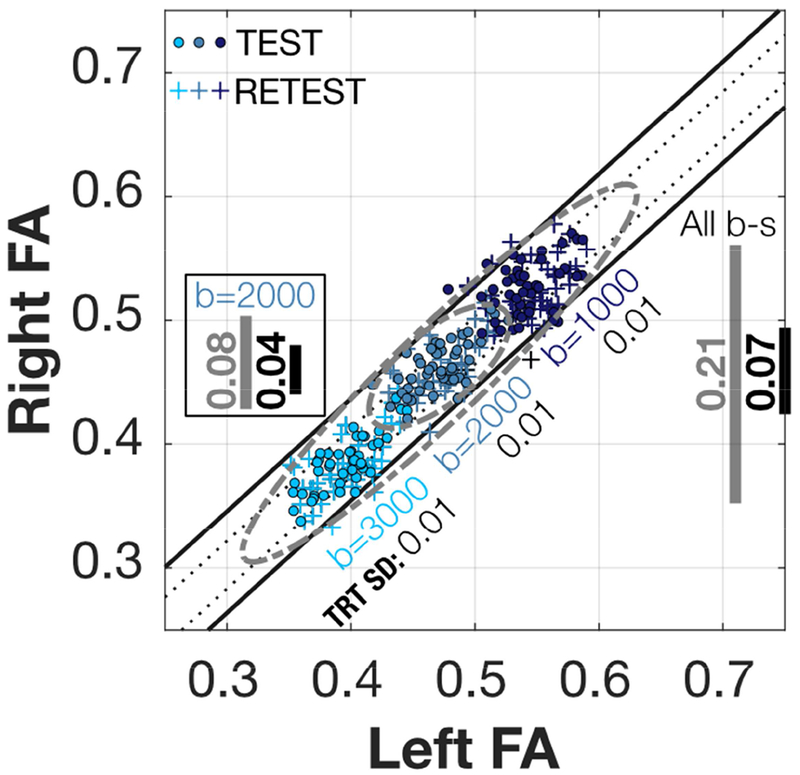
Scatterplot of the Left-Right IFOF HCP mean FA values. Inside the square, the grey line (0.08) shows the 95% range of all Right FA values for b=2000, and the black line (0.04) shows the range of possible values for any given Left FA value. Although not pictured, the values when using the b=2000 test-retest data points increases to 0.09 and 0.05. Outside the square to the right, the grey line (0.21) shows the 95% range of all right FA values for the combined six HCP Test-Retest values. The diagonal bands are the contour lines holding the 68% and 95% of the residuals from the linear model fitted to all the six datasets. See Figure S4a for the rest of the tracts.

The test-retest data points thoroughly intermingle, which is a replication of the left-right linear relation. The mean tract FA of a single tract replicates with a precision of 0.01 s.d. (Figure 3), and the separation in the FA plane for mean tract FA of left-right homologous tracts (corresponding circles and crosses) replicates with the same precision (0.01 s.d.).

The data obtained at the three different b-values fall along roughly the same line. Consequently, this left-right measurement generalizes well across b-values, despite the fact that the mean tract FA values do not (Figure 3). Considering the data from the three b-values, 95% of the FA measurements fall within 0.21 FA (gray line at right). Correspondingly, for the left-right difference 95% of the measurements fall within 0.07 FA (black line at right).

In certain cases, different sites may adopt measurement protocols at a single b-value. In that case, the range of the left-right difference is reduced. For example, in the b=2000 data set the FA range would be reduced to 0.04 FA, which is smaller than the FA range across subjects (0.08 FA).

There are different causes for the range of FA values between subjects. Some of the differences are likely to be the natural variation between subjects. Additional variation may be due to uncontrolled instrumental factors. The co-linear relation between data obtained at the different b-values suggests that some differences arise because the nominal and true gradient (b-value) differs between subjects.

3.2.3.-. Generalization of the linear model

To assess generalization we combined the six datasets at three b-values (b=1000, 2000, 3000) and three sites (WHL,YWM,HCP). The left-right scatterplots, one for each of the six pairs of tracts, are shown in (Figure 7). There are qualitative similarities between data from different tracts, but each has its own parameters and precision.

Figure 7. Homologous tract Left-Right FA scatterplots and iso-residual contour lines.

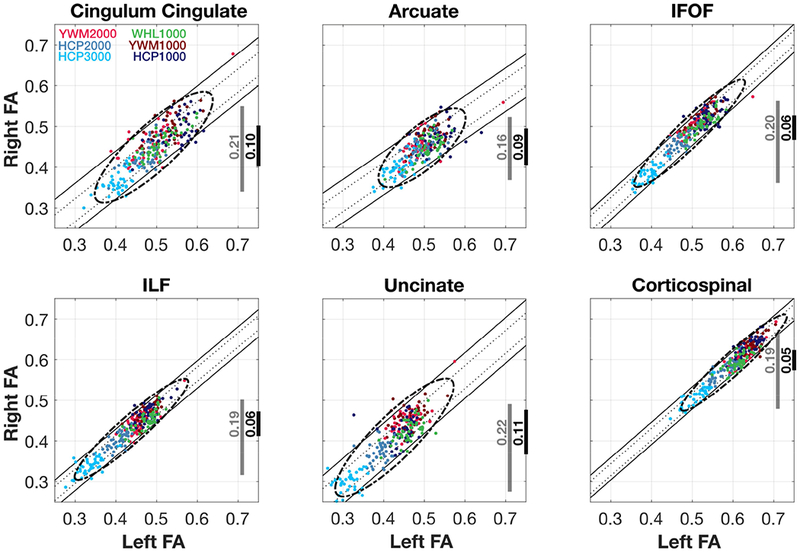
Scatterplot of the Left-Right mean FA for all tracts and all projects. The grey vertical lines shows the 95% range of all Right FA values, and the black line the range of possible values for any given Left FA value. The diagonal bands are the iso-residual contour lines holding the 68% and 95% of the residuals from the linear model fitted to all the six datasets.

The left-right scatterplots of the IFOF, ILF and CST are the most compact. Given a measurement of the left mean tract FA, the right mean tract FA falls within about 0.05 FA. For the Cingulum, Arcuate and Uncinate the left mean tract FA predicts the right mean tract FA within about 0.10 FA. In all cases the slopes of the linear regions (orientation of the principal axis of the ellipse) are near one.

The left-right relation generalizes across the different sites and b-values. For each of the tracts, there is no substantial loss of FA precision when calculating the left-right difference using the data at a single nominal b-value or data from all b-values at all sites.

The scatter plots reveal outliers in the cohort, and one particular sample point stands out. This point arises from a single subject at b=2000 who is an outlier in all of the tracts (YWM2000 data, red dot). In a clinical setting, this subject would be subject to more scrutiny. We can compare this subject’s data to the acquisition at b=1000 (YWM1000). The subject’s FA values in the YWM1000 acquisition are normal, so we assume that something went wrong in the YWM2000 acquisition and/or analyses. Such outliers occur, and it is not unexpected that one of 264 data points might be problematic

Some of the variation in the mean tract FA arises from the tractography algorithms. For example, the Arcuate and Uncinate are more curved than the other tracts, and previously several groups observed that the right Arcuate is not well-recovered from DWI data (Catani et al., 2007; Lebel and Beaulieu, 2009; Wahl et al., 2010; Yeatman et al., 2011). Other differences may arise because of differences in the length of the trunks used to estimate the mean FA of each tract (see Figure 2).

Similar variability was observed in five of the homologous tract pair correlations in the original Wahl et al (2010) experiment (Cingulum Cingulate: 0.57, Arcuate: 0.5, IFOF: 0.88, ILF: 0.73, Uncinate: 0.7), with the one exception of the corticosopinal tract (0.62). The original Wahl et al. result for corticospinal may be due to their method of identifying the corticospinal tract; because using our tractography methods on the original data (WHL1000) the value is higher (0.71).

The correlation values of the data combined across b-values are very high (Cingulum Cingulate: 0.85, Arcuate: 0.76, IFOF: 0.94, ILF: 0.94, Uncinate: 0.87, Corticospinal: 0.95). This suggests that as hoped the same left-right relation is revealed at different b-values and that using the relation rather than absolute FA levels compensates for variations in the data acquisition.

4.-. Discussion

We write in support of the idea that modem neuroimaging is sufficiently mature to develop useful quantitative applications for structural neuroimaging. As an example, we showed how the test-retest MRI scans produce highly reliable diffusion measures, even when accounting for instrumental noise, system calibration between scans, and repeating the probabilistic numerical processing in the computational methods. On the other hand, the experiments confirm prior reports that the compliance range of the data acquisition parameters for FA does not extend to changes in the diffusion gradient b-value (Chou et al., 2013; Farrell et al., 2007b; Hutchinson et al., 2017; Landman et al., 2007). For this reason, we proposed: (i) a two-step assessment system (measure replication, measure generalization) to translate MRI metrics with potential to be useful in the clinic; and, (ii) a simple method for improving the precision of our metrics by using the relationship between two measurements that compensates for the acquisition differences.

4.1.-. Replication-generalization tradeoff

There is a tradeoff between replication and generalization in neuroimaging. Over the past decade, the two extremes have been represented by: (1) the HCP for high-quality highly replicable anatomic, diffusion and functional imaging using custom-designed hardware (the Connectome scanner) and software (e.g., multiband echo planar sequences) that were not generalizable to other platforms (Glasser et al., 2016); and (2) the Enhancing NeuroImaging Genetics through Meta-Analysis (ENIGMA) consortium that began with low quality and low precision imaging metrics that were primarily limited to gross macroscopic features such as total intracranial volume, but were platform-independent and did not require standardized sequences and therefore generalized for worldwide data aggregation.

The tension between these two goals is being addressed by specifying standardized pulse sequences across a broad range of scanners for multicenter studies. This approach is exemplified by the HCP Lifespan protocol (Bookheimer et al., 2019; Harms et al., 2018; Somerville et al., 2018), the ENIGMA protocol (Acheson et al., 2017; Adhikari et al., 2018; Kochunov et al., 2017), and protocols for Precision Medicine studies such as ADNI3 for Alzheimer disease (Reid et al., 2017; Zavaliangos-Petropulu et al., 2019) and TRACK-TBI for traumatic brain injury (Yuh et al., 2013). This approach is applicable to coordinated multi-center studies.

The harmonization of measurements puts a strong emphasis on replication, hoping to limit the problem of generalization. There are economic and technology trademark issues that will prevent the widespread distribution of the most advanced instruments. Because there will be variations in clinical instrumentation and methods, we advocate for investigators to design tools and experiments that directly address generalization. The approach in this paper emphasizes collecting multiple datasets and then evaluating different dependent measures to select the ones that generalize. In this approach, it becomes important to specify the precision and the compliance range when reporting results for potential application, as different pathologies will have different requirements.

4.2.-. Explicit measures of generalization and context of use

Clinical applications should be based on measurements that replicate with confidence intervals that are compact enough to support a meaningful diagnostic. This attribute is crucial for the validation of “biomarkers” that can be widely used for biomedical science and clinical translation. A biomarker is defined by the US National Institutes of Health (NIH) and the US Food & Drug Administration (FDA) as “a defined characteristic that is measured as an indicator of normal biological processes, pathogenic processes, or responses to an exposure or intervention, including therapeutic interventions” (Naylor, 2003). This definition encompasses brain imaging (Mayeux, 2004). Precision Medicine is “an emerging approach for disease treatment and prevention that takes into account individual variability in genes, environment, and lifestyle for each person” (Collins and Varmus, 2015). Objectively quantifying these individual differences in order to tailor treatment and prevention strategies for specific patients requires validated biomarkers. Ensuring the reliability of these biomarkers over time in individual subjects is crucial for adequately testing the efficacy of precision medicine therapies (Senn, 2018). Throughout this work, we provided a valid range of normal values that gives the precision at which departures from normality can be measured. This range, like all the measurements we used in this work, is given in FA units, which is directly interpretable by any researcher or clinical practitioner.

In addition, but less appreciated, is that neuroimaging applications deployed in the field will use a range of instruments, participant populations, and measurement protocols (Goodman et al., 2016); the range of conditions in the field will be wider than that encountered in scientific studies. It is important, therefore, to assess how effectively an applied measurement generalizes across the clinical conditions. For an applied measurement to scale from the lab to the clinic, the result must generalize across these measurement conditions. This range of conditions where the measurement is valid for a proposed application should be specified contained in the “context of use” that the FDA requires as part of the biomarker qualification process (Goodsaid and Mendrick, 2010). After our experiment, we could claim that the context of use of our metric is circumscribed to 3 Tesla MRI magnets and b-values between 1000 and 3000. We think that the symmetry in homologous mean tract FA is a fundamental human biological trait, but we should extend our generalization experiments to extend its context of use.

4.3-. A continuous aggregation platform

The relatively recent increase in complexity of neuroimaging is a major complicating factor that impacts reproducible research. New MR instruments, analysis algorithms and the use of special participants have increased the size and complexity of datasets. In many neuroimaging publications, there is no realistic chance that a reader can repeat the experimental data acquisition or even the computational analyses (Buckheit and Donoho, 1995; Sandve et al., 2013; Wilson et al., 2017). The best we can hope for is to be able to repeat, check, and explore portions of the computational analysis of the published data (Peng, 2011; Stodden et al., 2014).

The increase in computational power has also led to an increase in algorithm complexity and the number of user-defined parameters. Several authors have analyzed the effect of pipeline parameters and reported large impacts on fMRI data; the variations in the result as a function of the parameters can be quite significant. For example, the position of the peak activation may range over a cortical area of 25 cm² (Carp, 2012). (Yarkoni and Westfall, 2017) observe that we are often uncertain about critical parameters that must be in computational models. We can confirm that the general point also applies to DWI methods. It is our experience, too, that scientists find it very difficult to keep track of the specific parameters used in any particular analysis, and even fewer scientists record the combinations of parameters they used during data exploration (Baker, 2016).

To overcome most of these problems, the system we used in this paper encapsulates the software and its dependencies in a container; it also stores the history of which analyses (and with what configuration) were run in the database. This approach overlaps with many of the proposals for scientific reproducibility. For example, (Poldrack et al., 2017) describe desiderata for reproducible research tools that closely align with those we have implemented.

… The entire analysis workflow (including both successful and failed analyses) would be completely automated in a workflow engine and packaged in a software container or virtual machine to ensure computational reproducibility. All data sets and results would be assigned version numbers to enable explicit tracking of provenance … (page 124).

Furthermore, our system is extensible. We can add datasets to our neuroinformatics platform, analyze them with identical computational methods, and check how the compliance range of our measurement changes. Analogously, we can containerize a computational tool from another group, process our data again, and do the same checks. Therefore, new results sets can be continuously aggregated. In the long term, this continuous aggregation will continue to inform the compliance range, and it will naturally work towards the harmonization of measurement protocols: settings that worsen the compliance range will be abandoned. We think that this continuous aggregating and improvement process will provide a useful approach for translating scientific research to the clinic.

4.4.-. Related research

A particularly related recent investigation of DWI generalization considered data from 13 different 3T MRI scanners throughout the USA, representing all three major vendors (GE, Philips and Siemens), found a coefficient of variation (CoV) of 4.2% for the FA of whole-brain white matter, with the FA CoV varying from 2% to 6% for individual major white matter tracts (Palacios et al., 2017). That study was limited to a single subject, to scanners with similar hardware capabilities, and to a harmonized DTI protocol in which all major acquisition parameters are as similar as possible.

This study extends that work by probing generalization across a wider range of acquisition parameters (e.g., spatial resolution, b-value, and the number of diffusion directions) using scanners with different hardware capabilities (e.g., 8 receiver channels vs 32 and 40 mT/m maximum gradient amplitude vs 100 mT/m), and in different participant populations. The scope of our tests is for a very modest set of instruments, data acquisition parameters, and population statistics; but the generalization could have proved much worse. A fundamental difference in our work is the intention to vary the experimental conditions instead of harmonizing them, assessing how the instrumental variations affect the precision range.

Furthermore, the generalization issues in neuroimaging applications are similar to those in other human research fields (He et al., 2015; Shavelson et al., 1989; Shavelson and Webb, 1991; Tipton, 2014); the issues are also closely linked to meta-analysis, which aggregate the outcomes of multiple studies (Evangelou and Ioannidis, 2013; Simpson and Pearson, 1904). The unique features of neuroimaging applications we discuss are that they are motivated by the observation that these applications are likely to arise from experimental measures that are not precisely controlled.

4.5.-. Limitations and opportunities

All the datasets were obtained from research environments. We obtained data from different sites to illustrate our point, but for a real experiment, more datasets with more variability should be included. Further generalization could come from scanners (models, mean field strength), acquisition sequences (e.g. dual-spin echo), population (e.g. age range) or computational methods (e.g. Tracula (Yendiki et al., 2011)). The database system we use is extensible: we can add data and re-evaluate the generalization should new dataset become available.

This work assesses one type of structural data which eliminated the need to analyze the impact of experimental design. Developing a deeper understanding of such factors is important for clinical assessments using task-based functional MRI, say for psychiatric disorders. Such analyses introduce many new parameters including factors ranging from stimulus selection and delivery and subject instructions and compliance.

Some functional experiments quantify characteristics of individual participants (e.g. defining V1). A much larger set of the scientific literature uses group comparisons. In many cases, it will not be clear how to convert a group comparison experiment into a clinical assessment of individual participants.

5.-. Conclusion

This paper illustrates an approach for translating neuroimaging findings from the lab to the clinic. We describe software tools designed for large data sets and computational reproducibility that are helpful calculating the impact of increasing the number of sites, experiments, different subjects, and/or the impact of higher quality instrumentation. We consider a full approach, from the definition of the data set for replication and generalization experiments, to the neuroinformatics platform and computational methods required to define an evaluate metrics with diagnostic value.

• Reproducible white matter diagnostics, generalizable to clinical conditions

• Data collected from multiple scanners into a searchable and computable database

• Data analysis software implemented as platform-independent, reproducible containers

• Strategy to minimize measurement variance across a likely span of clinical scanners