Heterogeneity adjustment with applications to graphical model inference

Abstract

Heterogeneity is an unwanted variation when analyzing aggregated datasets from multiple sources. Though different methods have been proposed for heterogeneity adjustment, no systematic theory exists to justify these methods. In this work, we propose a generic framework named ALPHA (short for Adaptive Low-rank Principal Heterogeneity Adjustment) to model, estimate, and adjust heterogeneity from the original data. Once the heterogeneity is adjusted, we are able to remove the batch effects and to enhance the inferential power by aggregating the homogeneous residuals from multiple sources. Under a pervasive assumption that the latent heterogeneity factors simultaneously affect a fraction of observed variables, we provide a rigorous theory to justify the proposed framework. Our framework also allows the incorporation of informative covariates and appeals to the ‘Bless of Dimensionality’. As an illustrative application of this generic framework, we consider a problem of estimating high-dimensional precision matrix for graphical model inference based on multiple datasets. We also provide thorough numerical studies on both synthetic datasets and a brain imaging dataset to demonstrate the efficacy of the developed theory and methods.

1. Introduction

Aggregating and analyzing heterogeneous data is one of the most fundamental challenges in scientific data analysis. In particular, the intrinsic heterogeneity across multiple data sources violates the ideal ‘independent and identically distributed’ sampling assumption and may produce misleading results if it is ignored. For example, in genomics, data heterogeneity is ubiquitous and referred to as either ‘batch effect’ or ‘lab effect’. As characterized in [29], microarray gene expression data obtained from different labs on different processing dates may contain systematic variability. Furthermore, [30] pointed out that heterogeneity across multiple data sources may be caused by unobserved factors that have confounding effects on the variables of interest, generating spurious signals. In finance, it is also known that asset returns are driven by varying market regimes and economy status, which can be regarded as a temporal batch effect. Therefore, to properly analyze data aggregated from multiple sources, we need to carefully model and adjust the unwanted variations.

Modeling and estimating heterogeneity effect is challenging for two reasons. (i) Typically, we can only access a limited number of samples from an individual group, given the high cost of biological experiments, technological constraint or fast economy regime switching. (ii) The dimensionality can be much larger than the total aggregated number of samples. The past decade has witnessed the development of many methods for adjusting batch effect in high throughput genomics data. See, for example, [43], [2], [30], and [25]. Though progresses have been made, most of the aforementioned papers focus on the practical side and none of them has a systematic theoretical justification. In fact, most of these methods are developed in a case-by-case fashion and are only applicable to certain problem domains. Thus, there is still a gap that exists between practice and theory.

To bridge this gap, we propose a generic theoretical framework to model, estimate, and adjust heterogeneity across multiple datasets. Formally, we assume the data come from m different sources: the i^th data source contributes n_i samples, each having p measurements such as gene expressions of an individual or stock returns of a day. To explicitly model heterogeneity, we assume that the batch-specific latent factor ${\mathbf{f}}_t^i$ influence the observed data $X_{jt}^i$ in batch i (j indexes variables; t indexes samples) as in the approximate factor model:

$$X_{jt}^i={\mathbf{\lambda }}_j^{i^{\prime }}{\mathbf{f}}_t^i+u_{jt}^i,\hspace{0.17em}1\le j\le p,1\le t\le n_i,1\le i\le m,$$ (1.1)

where ${\mathbf{\lambda }}_j^i$ is an unknown factor loading for variable j and $u_{jt}^i$ is a true uncorrupted signal. We consider a random loading ${\mathbf{\lambda }}_j^i.$ The linear term ${{\mathbf{\lambda }}_j^i}^{\prime }{\mathbf{f}}_t^i$ models the heterogeneity effect. We assume that ${\mathbf{f}}_t^i$ is independent of $u_{jt}^i$ and ${\mathbf{u}}_t^i={(u_{1t},\dots ,u_{pt})}^{\prime }$ shares the same common distribution with mean 0 and covariance Σ_p×p across all data sources. In the matrix-form model, (1.1) can be written as

$${\mathbf{X}}^i={\mathbf{\Lambda }}^i{\mathbf{F}}^{i^{\prime }}+{\mathbf{U}}^i,$$ (1.2)

where Xⁱ is a p×n_i data matrix in the i^th batch, Λⁱ is a p×Kⁱ factor loading matrix with ${\mathbf{\lambda }}_j^{i^{\prime }}$ in the j^th row, Fⁱ is an n_i × Kⁱ factor matrix and Uⁱ is a signal matrix of dimension p × n_i. We allow the number of latent factors Kⁱ to depend on batch i. We emphasize here that within one batch, our model is homogeneous. Heterogeneity in this paper refers to that the batch effect terms ${\left\{{\mathbf{\Lambda }}^i{\mathbf{F}}^{i^{\prime }}\right\}}_{i=1}^m$ are different across different groups i = 1,…,m, which are unwanted variations in our study.

To see more clearly on how model (1.2) characterizes the heterogeneity, note that for the t^th sample ${\mathbf{X}}_t^i$, which is the t^th column of Xⁱ,

$$\mathrm{var}({\mathbf{X}}_t^i)={\mathbf{\Lambda }}^i\mathrm{var}({\mathbf{f}}_t^i){\mathbf{\Lambda }}^{i^{\prime }}+\mathbf{\Sigma }.$$ (1.3)

Therefore, the heterogeneity is carried by the low-rank component ${\mathbf{\Lambda }}^i\mathrm{var}({\mathbf{f}}_t^i){\mathbf{\Lambda }}^{i^{\prime }}$ in the population covariance matrix of ${\mathbf{X}}_t^i$. We need to clarify that since we assume both Fⁱ and Uⁱ have mean zero, heterogeneity mentioned in this paper is for covariance structure as shown above instead of mean structure. In addition, our model differs from the random/mixed effect regression model studied in the literature [45, 23, 11] in that our models are factor models without any factors observed, while the mixed/random effect model is a regression model that requires covariate matrices to estimate the batch-specific term.

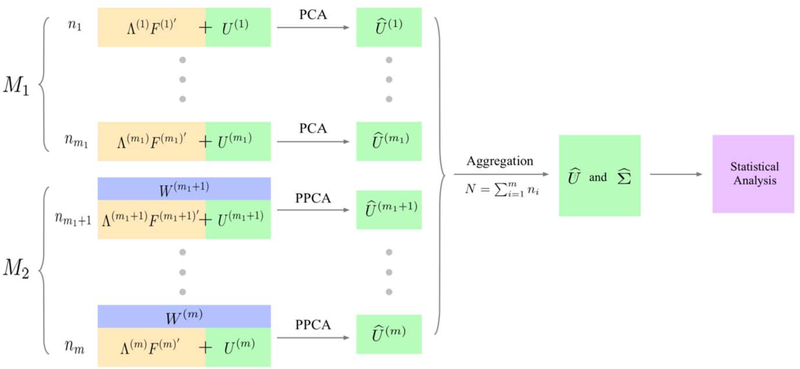
Under a pervasive assumption, the heterogeneity component can be estimated by directly applying principal component analysis (PCA) or Projected-PCA (PPCA), which is more accurate when there are sufficiently informative covariates Wⁱ [18]. Let $\widehat{{\mathbf{\Lambda }}^i}{\widehat{{\mathbf{F}}^i}}^{\prime }$ be the estimated heterogeneity component and $\widehat{{\mathbf{U}}^i}={\mathbf{X}}_t^i-\widehat{{\mathbf{\Lambda }}^i}{\widehat{{\mathbf{F}}^i}}^{\prime }$ the heterogeneity-adjusted signal, which can be treated as homogeneous across different datasets and thus can be combined together for downstream statistical analysis. This whole framework of heterogeneity adjustment is termed ALPHA (short for Adaptive Low-rank Principal Heterogeneity Adjustment) and is schematically shown in Figure 1.

Fig 1.

Schematic illustration of ALPHA: Depending on whether we can find some sufficiently informative covariates W, we implement principal component analysis (PCA) or Projected-PCA (PPCA) methods (labeled respectively M₁ and M₂) to remove the heterogeneity effects ΛF′ for each batch of data. This decision was made adaptively by a heuristic method. After removing the unwanted variations, the homogeneous data ${\left\{{\mathbf{U}}^{(i)}\right\}}_{i=1}^m$ are aggregrated for further analysis.

The proposed ALPHA framework is fully generic and applicable to almost all kinds of multivariate analysis of the combined, heterogeneity adjusted datasets. As an illustrative example, in this paper, we focus on the problem of Gaussian graphical model inference based on multiple datasets. It is a powerful tool to explore complex dependence structure among variables X = (X₁,…,X_p)′. The sparsity pattern of the precision matrix Ω = Σ⁻¹ encodes the information of an undirected graph G = (V,E) where V consists of p vertices corresponding to p variables in X and E describes their dependence relationship. To be specific, V_i and V_j are linked by an edge if and only if ${\Omega }_{ij}\ne 0$ (the (i,j)^th element of Ω), meaning that X_i and X_j are dependent conditioning on the rest of the variables. For heterogeneous data across m data sources, we need to first adjust for heterogeneity using the ALPHA framework. The idea of covariate-adjusted precision matrix estimation has been studied by [7], but they assumed observed factors and no heterogeneity issue, i.e., m = 1.

A significant amount of literature has focused on the estimation of the precision matrix Ω for graphical models for homogeneous data. [49] and [20] developed the Graphical Lasso method using the L₁ penalty and [27] and [42] used a non-convex penalty. Furthermore, [40] and [33] studied the theoretical properties under different assumptions. Estimating Ω can be equivalently reformulated as a set of node-wise sparse linear regression that utilizes Lasso or Danzig selector for each node [35, 48]. To relax the assumption of Gaussian data, [32] and [31] extend the graphical model to the case of semiparametric Gaussian copula and transelliptical family. Via the ALPHA framework, we can combine the adjusted data $\widehat{{\mathbf{U}}^i}$ to construct an estimator for the precision matrix Ω by the above methods. Recent works also focus on joint estimation of multiple Gaussian or discrete graphical models which share some common structure [22, 15, 47, 8, 21]. They are concerned with both the commonality and individual uniqueness of the graphs. In comparison, ALPHA emphasizes more on heterogeneity-adjusted aggregation for one single graph.

The rest of the paper is organized as follows. Section 2 lays out a basic problem setup and necessary assumptions. We model the heterogeneity by a semiparametric factor model. Section 3 introduces the ALPHA methodology for heterogeneity adjustment. Two main methods PCA and PPCA will be introduced for adjusting the factor effects under different regimes. A guiding rule of thumb is also proposed to determine which method is more appropriate. The heterogeneity-adjusted data will be combined to provide valid graph estimation in Section 4. The CLIME method of [9] is applied for precision matrix estimation. Synthetic and real data analyses are carried out to demonstrate the proposed framework in Section 5. Section 6 contains further discussions and all the proofs are relegated to the appendix.

2. Problem setup

To more efficiently use the external covariate information in removing heterogeneity effect, we first present a semiparametric factor model. Then, based on whether the collected external covariates have explaining power on factor loadings, we discuss two different regimes where PCA or PPCA should be used. We will state the conditions under which these methods can be formally justified.

2.1. Semiparametric factor model

We assume that for subgroup i, we have d external covariates ${\mathbf{W}}_j^i={(W_{j1}^i,\dots ,W_{jd}^i)}^{\prime }$ for variable j. In stock returns, these can be attributes of a firm; in brain imaging, these can be the physical locations of voxels. We assume that these covariates have some explanatory power on the loading parameters ${\mathbf{\lambda }}_j^i$ in (1.1) so that it can be further modeled as ${\mathbf{\lambda }}_j^i={\mathbf{g}}^i({\mathbf{W}}_j^i)+{\text{γ}}_j^i$, where gⁱ(·) is the external covariate effects on ${\mathbf{\lambda }}_j^i$ and ${\text{γ}}_j^i$ is the part that can not be explained by the covariates. Thus, model (1.1) can be written as

$$X_{jt}^i={\mathbf{\lambda }}_j^{i^{\prime }}{\mathbf{f}}_t^i+u_{jt}^i={({\text{g}}^i({\mathbf{W}}_j^i)+{\gamma }_j^i)}^{\prime }{\mathbf{f}}_t^i+u_{jt}^i.$$ (2.1)

Model (2.1) does not put much restriction. If ${\mathbf{W}}_j^i$ is not informative at all, i.e., gⁱ(·) = 0, the model reduces to a regular factor model. In a matrix form, model (2.1) can be written as

$${\mathbf{X}}^i={\mathbf{\Lambda }}^i{\mathbf{F}}^{i^{\prime }}+{\mathbf{U}}^i\hspace{0.17em}\text{where}\hspace{0.17em}{\mathbf{\Lambda }}^i={\mathbf{G}}^i({\mathbf{W}}^i)+{\mathbf{\Gamma }}^i,\hspace{0.17em}1\le i\le m.$$ (2.2)

In (2.2), Gⁱ(Wⁱ) and Γⁱ are p×Kⁱ matrices. More specifically, $g_k^i({\mathbf{W}}_j^i)$ and γ_jk are the (j,k)^th element of Gⁱ(Wⁱ) and Γⁱ respectively. Expression (2.2) suggests that the observed data can be decomposed into a low-rank heterogeneity term ${\mathbf{\Lambda }}^i{\mathbf{F}}^{i^{\prime }}$ and a homogeneous signal term Uⁱ. Letting ${\mathbf{u}}_t^i$ be the t^th column of Uⁱ, we assume all ${\mathbf{u}}_t^{i,}\text{s}$ share the same distribution for any t ≤ n_i and for all subgroups i ≤ m with $\mathbb{E}\left[{\mathbf{u}}_t^i\right]=\mathbf{0},\hspace{0.17em}\mathrm{var}({\mathbf{u}}_t^i)=\mathbf{\Sigma }$.

There has been a large literature on factor models in econometrics [3, 5, 17, 44], machine learning [10, 36] and random matrix theories [26, 38, 46]. We refer the interested readers to those relevant papers and the references therein. However, none of these models incorporate the external covariate information. The semiparametric factor model (2.1) was first proposed by [14] and further investigated by [13] and [18]. Using sufficiently informative external covariates, we are able to more accurately estimate the factors and loadings, and hence yield better adjustment for heterogeneity.

Here we collect some notations of eigenvalues and matrix norms used in the paper. For matrix M, we use λ_max(M), λ_min(M) and λ_i(M) to denote the maximum eigenvalue, the minimum eigenvalue and the ith eigenvalue of M respectively. We define the quantities ${\Vert \mathbf{M}\Vert }_{\text{max}}={\text{max}}_{i,j}\left|M_{i,j}\right|$, ${\Vert \mathbf{M}\Vert }_2={\mathbf{\lambda }}_{\text{max}}^{1/2}({\mathbf{M}}^{\prime }\mathbf{M})(\Vert \mathbf{M}\Vert \hspace{0.17em}\text{for short})$, ${\Vert \mathbf{M}\Vert }_F={({\sum }_{i,j}{M}_{ij}^2)}^{1/2}$, ${\Vert \mathbf{M}\Vert }_1={\text{max}}_j{\sum }_i\left|M_{ij}\right|$ and ${\Vert \mathbf{M}\Vert }_{1,1}={\sum }_i{\sum }_j\left|M_{ij}\right|$ to be its entry-wise maximum, spectral, Frobenius, induced ℓ₁ and element-wise ℓ₁ norms.

2.2. Modeling assumptions and general methodology

In this subsection, we explicitly list all the required modeling assumptions. We start with an introduction of the data generating processes.

Assumption 2.1 (Data generating process). (i) $n_i^{-1}{\mathbf{F}}^{i^{\prime }}{\mathbf{F}}^i=\mathbf{I}$.

(ii) ${\left\{{\mathbf{u}}_t^i\right\}}_{t\le n_i,i\le m}$ are independently and identically sub-Gaussian distributed with mean zero and covariance Σ within and between subgroups, and independent of $\left\{{\mathbf{W}}_j^i,{\mathbf{f}}_t^i\right\}$. Let ${\Vert \mathbf{\Sigma }\Vert }_2=C_0<\infty$.

(iii) ${\left\{{\mathbf{f}}_t^i\right\}}_{t\le n_i}$ is a stationary process, with arbitrary temporal dependency. The tail of the factors is sub-Gaussian, i.e., there exist C₁, C₂ > 0 such that for any $\alpha \in {ℝ}^{K^i}$ and $s>0,\hspace{0.17em}\mathbb{P}(\left|{\alpha }^{\prime }{\mathbf{f}}_t^i\right|>s)\le C_1\exp (-C_2{s}^2/{\Vert \alpha \Vert }^2)$.

The above set of assumptions are commonly used in the literature, see [5] and [18]. We omit detailed discussions here.

Based on whether the external covariates are informative, we specify two regimes, each of which requires some additional technical conditions.

2.2.1. Regime 1: External covariates are not informative

For the case that the external covariates do not have enough explanatory power on the factor loadings Λⁱ, we ignore the semiparametric structure and model (2.2) reduces to the traditional factor model, extensively studied in econometrics [3, 44, 37]. PCA will be employed in Section 3.1 to estimate the heterogeneous effect. It requires the following assumptions.

Assumption 2.2. (i) (Pervasiveness) There are two positive constants c_min, c_max > 0 so that

$$c_{\min }<{\text{λ}}_{\min }(p^{-1}{\mathbf{\Lambda }}^{i^{\prime }}{\mathbf{\Lambda }}^i)<{\text{λ}}_{\text{max}}(p^{-1}{\mathbf{\Lambda }}^{i^{\prime }}{\mathbf{\Lambda }}^i)<c_{\text{max}},\hspace{1em}a.s.\hspace{1em}\forall i.$$

(ii) ${\text{max}}_{k\le K^i,j\le p}\left|{\text{λ}}_{jk}^i\right|=O_p(\sqrt{\log \hspace{0.17em}p})$.

The first condition is common and essential in the factor model literature (e.g., [44]). It requires the factors to be strong enough such that the covariance matrix ${\mathbf{\Lambda }}^i\text{cov}({\mathbf{f}}_t^i){\mathbf{\Lambda }}^i+\mathbf{\Sigma }$ has spiked eigenvalues. We emphasize here that this condition is actually not so stringent as it looks. Consider a single-factor model Y_it = b_if_t + u_it, i = 1,…,p, t = 1,…,T. The pervasive assumptions actually imply that $c_{\min }p\le {\sum }_{i=1}^p{b}_i^2\le c_{\text{max}}p$. Note that since c_min can be a small constant, our pervasive assumption just says that the factors ${\left\{f_t\right\}}_{t=1}^T$ have non-negligible effect on a non-vanishing proportion of outcomes. In addition, this condition is trivially true if ${\left\{{\mathbf{\text{λ}}}_j^i\right\}}_{j=1}^p$’s can be regarded as random samples from a population with non-degenerate covariance matrix [17]. Practically, in fMRI data analysis for instance, the lab environment (temperature, air pressure, etc.) or the mental status of the subject being scanned may cause the BOLD (Blood-Oxygen-Level Dependent) level to be uniformly higher at certain time t. This means the brain heterogeneity is globally driven by the factors ${\left\{f_t\right\}}_{t=1}^T$. If the batch effect is only limited to a small number of dimensions, we think it is more appropriate to assume sparsity instead of pervasiveness on top eigenvectors, which is quite different from our problem setups and thus beyond the scope of our paper. The second condition holds if the population has a sub-Gaussian tail.

2.2.2. Regime 2: External covariates are informative

When covariates are informative, we will employ the PPCA [18] to estimate the heterogeneous effect. It requires the following assumptions.

Assumption 2.3. (i) (Pervasiveness) There are two positive constants c_min and c_max so that

$$c_{\min }<{\text{λ}}_{\min }(p^{-1}{\mathbf{G}}^i{({\mathbf{W}}^i)}^{\prime }{\mathbf{G}}^i({\mathbf{W}}^i))<{\text{λ}}_{\text{max}}(p^{-1}{\mathbf{G}}^i{({\mathbf{W}}^i)}^{\prime }{\mathbf{G}}^i({\mathbf{W}}^i))<c_{\text{max}},\hspace{0.17em}a.s.\hspace{0.17em}{\forall }_i.$$

(ii) ${\text{max}}_{k\le K^i,j\le p}E{g}_k{({\mathbf{W}}_j^i)}^2<\infty$.

This assumption is parallel to Assumption 2.2 (i). Pervasiveness is trivially satisfied if ${\left\{{\mathbf{W}}_j^i\right\}}_{j\le p}$ are independent and Gⁱ is sufficiently smooth.

Assumption 2.4. (i) $E{\gamma }_{jk}^i=0,\hspace{0.17em}{\text{max}}_{k\le K^i,j\le p}\left|{\gamma }_{jk}^i\right|=O_P(\sqrt{\log \hspace{0.17em}p})$.

(ii) Write ${\gamma }_j^i={({\gamma }_{j1}^i,\dots ,{\gamma }_{jK}^i)}^{\prime }$. we assume ${\left\{{\gamma }_j^i\right\}}_{j\le p}$ are independent of ${\left\{{\mathbf{W}}_j^i\right\}}_{j\le p}$.

(iii) Define ${\nu }_p={\text{max}}_{i\le m}{\text{max}}_{k\le K^i}{p}^{-1}{\sum }_{j\le p}\mathrm{var}({\gamma }_{jk}^i)<\infty$. We assume

$$\underset{k\le K^i,j\le p}{\text{max}}\sum _{j^{\prime }\le p}|E{\gamma }_{j^{\prime }k}^i{\gamma }_{jk}^i|=O({\nu }_p).$$

Condition (i) is parallel to Assumption 2.2 (ii) whereas Condition (ii) is natural since Γⁱ can not be explained by Wⁱ. Condition (iii) imposes cross-sectional weak dependence of ${\gamma }_j^i$, which is much weaker than assuming independent and identically distributed ${\left\{{\gamma }_j^i\right\}}_{j\le p}$. This condition is mild as main serial dependency has been taken care of by g_k(·)’s.

3. The ALPHA framework

We introduce the ALPHA framework for heterogeneity adjustment. Methodologically, for each sub-dataset we aim to estimate the heterogeneity component and subtract it from the raw data. Theoretically, we aim to obtain the explicit rates of convergence for both the corrected homogeneous signal and its sample covariance matrix. Those rates will be useful when aggregating the homogeneous residuals from multiple sources.

This section covers details for heterogeneity adjustments under the above two regimes: they correspond to estimating Uⁱ by either PCA or PPCA. From now on, we drop the superscript i whenever there is no confusion as we focus on the i^th data source. We use the notation $\widehat{\mathbf{F}}$ if F is estimated by PCA and $\tilde{\mathbf{F}}$ if estimated by PPCA. This convention applies to other related quantities such as $\widehat{\mathbf{U}}$ and $\tilde{\mathbf{U}}$, the heterogeneity-adjusted estimator. In addition, we use notations such as $\check{\mathbf{F}}$ and $\check{\mathbf{U}}$ to denote the final estimators, which are $\widehat{\mathbf{F}}$ and $\widehat{\mathbf{U}}$ if PCA is used, and $\tilde{\mathbf{F}}$ and $\tilde{\mathbf{U}}$ if PPAC is used.

Estimators for latent factors under regimes 1 and 2 satisfy $n^{-1}{\check{\mathbf{F}}}^{\prime }\check{\mathbf{F}}=\mathbf{I}$, which corresponds to normalization in Assumption 2.1 (i). By the principle of least squares, the residual estimator of U then admits the form

$$\check{\mathbf{U}}=\mathbf{X}(\mathbf{I}-\frac{1}{n}\check{\mathbf{F}}{\check{\mathbf{F}}}^{\prime }).$$ (3.1)

3.1. Estimating factors by PCA

In regime 1, we directly use PCA to adjust data heterogeneity. PCA estimates F by $\widehat{\mathbf{F}}$ where the k^th column of $\widehat{\mathbf{F}}/\sqrt{n}$ is the eigenvector of ${\mathbf{X}}^{\prime }\mathbf{X}$ corresponding to the k^th largest eigenvalue. We have the following theoretical results.

Theorem 3.1. Under Assumptions 2.1 and 2.2, we have

$$\begin{array}{l}\widehat{\mathbf{U}}-\mathbf{U}=-\frac{1}{n}\mathbf{U}\mathbf{F}{\mathbf{F}}^{\prime }+\mathbf{\Pi },\\ \widehat{\mathbf{U}}{\widehat{\mathbf{U}}}^{\prime }-\mathbf{U}{\mathbf{U}}^{\prime }=-\frac{1}{n}\mathbf{U}\mathbf{F}{\mathbf{F}}^{\prime }{\mathbf{U}}^{\prime }+\mathbf{\Delta },\end{array}$$

where ${\Vert \mathbf{\Pi }\Vert }_{\text{max}}=O_P(\sqrt{\log \hspace{0.17em}n\log \hspace{0.17em}p}(1/\sqrt{p}+1/n)+\sqrt{\log \hspace{0.17em}n}{\Vert \mathbf{\Sigma }\Vert }_1/p)$ and ${\Vert \mathbf{\Delta }\Vert }_{\text{max}}=O_P((1+n/p)\log \hspace{0.17em}p+n^2{\Vert \mathbf{\Sigma }\Vert }_1^2/p^2)$.

Note that we do not explicitly assume bounded ${\Vert \mathbf{\Sigma }\Vert }_1$. In some applications it might be natural to assume a sparse covariance so that all terms involving ${\Vert \mathbf{\Sigma }\Vert }_1$ can be eliminated, while in other applications such as the graphical model, it is more natural to impose sparsity structure on the precision matrix. In this case, one may want to keep track of the effect of ${\Vert \mathbf{\Sigma }\Vert }_1$ as it can be as large as $O(\sqrt{p})$ as ${\Vert \mathbf{\Sigma }\Vert }_1\le \sqrt{p}{\Vert \mathbf{\Sigma }\Vert }_2=O(\sqrt{p})$.

3.2. Estimating factors by Projected-PCA

In regime 2, we would like to incorporate the external covariates using the Projected-PCA (PPCA) method proposed by [18]. The method applies PCA on the projected data and by projection, covariates information is leveraged to reduce dimensionality. We now briefly introduce the method.

For simplicity, we only consider d = 1, that is, we only have a single covariate. The general case can be found in [18]. To model the unknown function g_k(W_j), we adopt a sieve based idea which approximates g_k(·) by a linear combination of basis functions $\left\{{\varphi }_1(x),{\varphi }_2(x),\cdots \right\}$ (e.g., B-spline, Fourier series, polynomial series, wavelets). Then

$$g_k(W_j)=\sum _{\nu =1}^J{b}_{\nu ,k}{\varphi }_{\nu }(W_j)+R_k(W_j),\hspace{1em}k\le K,j\le p.$$ (3.2)

Here ${\left\{b_{\nu ,k}\right\}}_{\nu =1}^J$ are the sieve coefficients of g_k(W_j), corresponding to the k^th factor loading; R_k is the remainder function representing the approximation error; J denotes the number of sieve bases which may grow slowly as p diverges. We take the same basis functions in (3.2) for all k though they can be different.

Define ${\mathbf{\text{b}}}_k^{\prime }=(b_{1,k},\cdots ,b_{J,k})\in {ℝ}^J$ for each k ≤ K, and correspondingly $\varphi {(W_j)}^{\prime }=({\varphi }_1(W_j),\cdots ,{\varphi }_J(W_j))\in {ℝ}^J$. Then we can write

$$g_k(W_j)=\varphi {(W_j)}^{\prime }{\mathbf{b}}_k+R_k(W_j).$$

Let ${\mathbf{B}}_{J\times K}=({\mathbf{b}}_1,\cdots ,{\mathbf{b}}_K)$, $\mathbf{\Phi }{(\mathbf{W})}_{p\times J}={(\varphi (W_1),\cdots ,\varphi (W_p))}^{\prime }$ and R_k(W_j) be the (j,k)^th element of R(W)p×K. The matrix form (2.2) can be written as

$$\mathbf{X}=\Phi (\mathbf{W})\mathbf{B}{\mathbf{F}}^{\prime }+\mathbf{R}(\mathbf{W}){\mathbf{F}}^{\prime }+\mathbf{\Gamma }{\mathbf{F}}^{\prime }+\mathbf{U},$$ (3.3)

recalling that the data index i is dropped. Thus the residual contains three parts: the sieve approximation error $\mathbf{R}(\mathbf{W}){\mathbf{F}}^{\prime }$, unexplained loading $\mathbf{\Gamma }{\mathbf{F}}^{\prime }$ and true signal U.

The idea of PPCA is simple: since the factor loadings are a function of the covariates in (3.3) and U and Γ are independent of W, if we project (smooth) the observed data onto the space of W, the effect of U and Γ will be significantly reduced and the problem becomes nearly a noiseless one, given that the approximation error R(W) is small.

Define P as the projection onto the space spanned by the basis functions of W:

$$\mathbf{P}=\Phi (\mathbf{W}){(\Phi {(\mathbf{W})}^{\prime }\Phi (\mathbf{W}))}^{-1}\Phi {(\mathbf{W})}^{\prime }.$$ (3.4)

By (3.3), $\mathbf{P}\mathbf{X}\approx \mathbf{P}\Phi (\mathbf{W})\mathbf{B}{\mathbf{F}}^{\prime }\approx \mathbf{G}(\mathbf{W}){\mathbf{F}}^{\prime }$. Thus, F can be estimated from the ‘noiseless projected data’ PX, using the conventional PCA. Let the columns of $\tilde{\mathbf{F}}/\sqrt{n}$ be the eigenvectors corresponding to the top K eigenvalues of the n × n matrix ${\mathbf{X}}^{\prime }\mathbf{P}\mathbf{X}$, which is the sample covariance of the projected data. Then, $\tilde{\mathbf{F}}$ is the PPCA estimator of F. It only differs from PCA in that we use smoothed or projected data PX.

We need the following conditions for basis functions and accuracy of sieve approximation.

Assumption 3.1. (i) There are d_min, d_max > 0 s.t.

$$d_{\min }<{\text{λ}}_{\min }(p^{-1}\Phi {(\mathbf{W})}^{\prime }\Phi (\mathbf{W}))<{\text{λ}}_{\text{max}}(p^{-1}\Phi {(\mathbf{W})}^{\prime }\Phi (\mathbf{W}))<d_{\text{max}}$$

almost surely and max_ν≤_J,j≤p Eϕ_ν(W_j)²< ∞.

(ii) There exists k ≥ 4 s.t. as $J\to \infty ,\hspace{0.17em}{\sup }_{x\in \chi }|g_k(x)-{\sum }_{\nu =1}^J{b}_{\nu ,k}{\varphi }_{\nu }(x){|}^2=O(J^{-k})$ where X is the support of W_j and max_v,k |b_v,k| < ∞.

Condition (ii) is mild; for instance, when {φ_ν} is polynomial basis or Bsplines, it is implied by the condition that smooth curve g_k(·) belongs to a Hölder class $\mathcal{G}=\left\{g:|g^{(r)}(s)-g^{(r)}(t)|\le L{|s-t|}^{\alpha }\right\}$ for some L > 0, with $k=2(r+\alpha )\ge 4$ [34,12].

Recalling the definition of ν_p in Assumption 2.4 (iii), we have the following results.

Theorem 3.2. Choose $J={(p\min \left\{n,p,{\nu }_p^{-1}\right\})}^{1/k}$ and assume $J^2{\varphi }_{\text{max}}^2\log (nJ)=O(p)$ where ${\varphi }_{\text{max}}={\text{max}}_{\nu \le J}{\sup }_{x\in X}{\varphi }_{\nu }(x)$. Under Assumptions 2.1, 2.3, 2.4 and 3.1,

$$\begin{array}{l}\tilde{\mathbf{U}}-\mathbf{U}=-\frac{1}{n}\mathbf{U}\mathbf{F}{\mathbf{F}}^{\prime }+\mathbf{\Pi },\\ \tilde{\mathbf{U}}{\tilde{\mathbf{U}}}^{\prime }-\mathbf{U}{\mathbf{U}}^{\prime }=-\frac{1}{n}\mathbf{U}\mathbf{F}{\mathbf{F}}^{\prime }{\mathbf{U}}^{\prime }+\mathbf{\Delta },\end{array}$$

where ${\Vert \mathbf{\Pi }\Vert }_{\text{max}}=O_P(\sqrt{\log \hspace{0.17em}n/p}(J{\varphi }_{\text{max}}+\sqrt{\log \hspace{0.17em}p})+J{\varphi }_{\text{max}}{\Vert \mathbf{\Sigma }\Vert }_1\sqrt{\log \hspace{0.17em}n}/p)$ and ${\Vert \mathbf{\Delta }\Vert }_{\text{max}}=O_P(n\sqrt{{\nu }_p/p}(J^2{\varphi }_{\text{max}}^2+\log \hspace{0.17em}p)+nJ{\varphi }_{\text{max}}{\Vert \mathbf{\Sigma }\Vert }_1(J{\varphi }_{\text{max}}+\sqrt{\log \hspace{0.17em}p})/p+n^2{J}^2{\varphi }_{\text{max}}^2{\Vert \mathbf{\Sigma }\Vert }_1^2/p^2)$ if there exists C s.t. v_p>C/n.

3.3. A guiding rule for estimating the number of factors, the number of basis functions and determining regimes

We now address the problem of estimating the number of factors for two different regimes. Extensive literature has made contributions to this problem in regime 1, i.e., the regular factor model [4, 1, 28]. [28] and [1] proposed to use ratio of adjacent eigenvalues of ${\mathbf{X}}^{\prime }\mathbf{X}$ to infer the number of factors. They showed the estimator $\widehat{K}=\arg \hspace{0.17em}{\text{max}}_{k\le K_{\text{max}}}{\text{λ}}_k{({\mathbf{X}}^{\prime }\mathbf{X})/\text{λ}}_{k+1}({\mathbf{X}}^{\prime }\mathbf{X})$ correctly identifies K with probability tending to 1, as long as K_max ≥ K and K_max = O(n_i ∧ p).

For the semiparametric factor model, [18] proposed

$$\tilde{K}=\arg \underset{k\le K_{\text{max}}}{\text{max}}{\text{λ}}_k({\mathbf{X}}^{\prime }\mathbf{P}\mathbf{X})/{\text{λ}}_{k+1}({\mathbf{X}}^{\prime }\mathbf{P}\mathbf{X}).$$

Here K_max is of the same order as Jd. It was shown that $\mathbb{P}(\tilde{K}=K)\to 1$ under regular assumptions which we omit here. When we have genuine and pervasive covariates, $\tilde{K}$ typically outperforms $\hat{K}$. More details can be found in [18].

Once we use $\widehat{K}$ and $\tilde{K}$ to estimate the number of factors under the regular factor model and semiparametric factor model respectively, we naturally have an adaptive rule to decide whether the covariates W are informative enough to use PPCA over PCA. We compare two eigen-ratios:

$$\frac{{\text{λ}}_{\widehat{K}}({\mathbf{X}}^{\prime }\mathbf{X})}{{\text{λ}}_{\widehat{K}+1}({\mathbf{X}}^{\prime }\mathbf{X})}\text{vs}\frac{{\text{λ}}_{\tilde{K}}({\mathbf{X}}^{\prime }\mathbf{P}\mathbf{X})}{{\text{λ}}_{\tilde{K}+1}({\mathbf{X}}^{\prime }\mathbf{P}\mathbf{X})}.$$

If the former is larger we identify the dataset as regime 1 and apply regular PCA to get $\widehat{\mathbf{U}}$; otherwise it is regime 2 and PPCA is used to obtain $\tilde{\mathbf{U}}$. The intuition behind this comparison is that the maximal eigen-ratios can be perceived as signal-to-noise ratios in terms of estimating the spiky heterogeneity term. Given that $n^{-1}\mathbf{X}{\mathbf{X}}^{\prime }\approx \mathbf{G}{\mathbf{G}}^{\prime }+\mathbf{\Gamma }{\mathbf{\Gamma }}^{\prime }+\mathbf{\Sigma }$ and $n^{-1}\mathbf{P}\mathbf{X}{\mathbf{X}}^{\prime }\mathbf{P}\approx \mathbf{G}{\mathbf{G}}^{\prime }+\mathbf{P}\mathbf{\Gamma }{\mathbf{\Gamma }}^{\prime }\mathbf{P}+\mathbf{P}\mathbf{\Sigma }\mathbf{P}$, the first ratio measures the eigen-gap between $\mathbf{G}{\mathbf{G}}^{\prime }+\mathbf{\Gamma }{\mathbf{\Gamma }}^{\prime }$ and Σ and the second ratio measures the eigen-gap between $\mathbf{G}{\mathbf{G}}^{\prime }+\mathbf{P}\mathbf{\Gamma }{\mathbf{\Gamma }}^{\prime }\mathbf{P}$ and PΣP. If G(W) is much more important than Γ in explaining the loading structure, projection preserves signal and reduces error to improve the eigen-gap. Conversely, if W is weak in providing useful information, projection reduces both noise and signal. Therefore, if projection enlarges the maximum eigen-gap, we prefer PPCA over PCA to estimate the spiky heterogeneity part. Our proposed guiding rule effectively tells whether projection can further contrast spiky and non-spiky parts of covariance.

The above signal-to-noise ratio comparison can be extended to choose the number of basis functions. Notice that we can regard regular PCA as PPCA with number of basis J = p and hence P = I. In this line of thinking, we can index P by J and maximize ${\text{λ}}_{\tilde{K}(J)}({\mathbf{X}}^{\prime }{\mathbf{P}}^J\mathbf{K})/{\text{λ}}_{\tilde{K}(J)+1}({\mathbf{X}}^{\prime }{\mathbf{P}}^J\mathbf{X})$ over $J\in \left\{1,2,\dots ,J_{\text{max}},p\right\}$, where J = p corresponds to PCA. Here we use notation $\tilde{K}(J)$ and P^J to exhibit their dependency on J. We implement this guiding rule in real data analysis.

In practice, there is still chance of misspecification of the true number of factors K by ALPHA. One might be curious about how this will affect the performance of ALPHA and the subsequent statistical analysis. To clarify this issue, we conduct sensitivity analysis on the number of factors in Section G.3 in the appendix. The take-home message is that the overestimation of K will not hurt, while underestimation of K might mislead subsequent statistical inference.

3.4. Summary of ALPHA

We now summarize the final procedure and convergence rates. We first divide m subgroups into two classes based on whether the collected covariates have significant influence on the loadings.

$${\mathcal{M}}_1=\left\{i\le m|{\mathbf{W}}^i\hspace{0.17em}\text{is not informative}\right\},\hspace{1em}{\mathcal{M}}_2=\left\{i\le m|{\mathbf{W}}^i\hspace{0.17em}\text{is informative}\right\}.$$

ALPHA consists of the following three steps.

Step 1: (Preprocessing) For data source i, determine whether it belongs to ${\mathcal{M}}_1$ or ${\mathcal{M}}_2$ according to the guiding rule given in Section 3.3 and correspondingly estimate K by Ǩ, which equals $\widehat{K}$ or $\tilde{K}$ (and choose J if necessary).

Step 2: (Adjustment) Apply Projected-PCA to estimate if ${\mathbf{\Lambda }}^i{\mathbf{F}}^{i^{\prime }}$ if $i\in {\mathcal{M}}_2$, otherwise use PCA to remove the heterogeneity, resulting in adjusted data ${\check{\mathbf{U}}}^i$, which is either ${\widehat{\mathbf{U}}}^i$ or ${\tilde{\mathbf{U}}}^i$.

Step 3: (Aggregation) Combine adjusted data ${\left\{{\check{\mathbf{U}}}^i\right\}}_{i=1}^m$ to conduct further statistical analysis. For example, estimate sample covariance $\mathbf{\Sigma }$ by $\widehat{\mathbf{\Sigma }}={(N-{\sum }_i{\check{K}}_i)}^{-1}{\sum }_{i=1}^m{\check{\mathbf{U}}}^i{\check{\mathbf{U}}}^{i^{\prime }}$ where $N={\sum }_i{n}_i$ is the aggregated sample size; or estimate sparse precision matrix Ω by existing graphical model methods.

We summarize the ALPHA procedure in Algorithm 1 given in Section A. We also summarize the convergence of ${\widehat{\mathbf{U}}}^i$ and ${\tilde{\mathbf{U}}}^i$ below. To ease presentation, we consider a typical regime in practice: $n_i<C_p,\hspace{0.17em}{\sum }_{i\le m}{K}^i<CN$ for some constant C. We focus on the situation of sufficiently smooth curves k = ∞ so that J diverges very slowly (say with rate $O(\sqrt{\log \hspace{0.17em}p})$) and bounded ϕ_max and ν_p (defined respectively in Theorem 3.2 and Assumption 2.4). Based on discussions of the previous subsections, for estimation of U in ${\Vert \cdot \Vert }_{\text{max}}$, we have

$${\check{\mathbf{U}}}^i-{\mathbf{U}}^i=-{\mathbf{U}}^i{\mathbf{F}}^i{\mathbf{F}}^{i^{\prime }}/n_i+\{\begin{array}{ll}{O}_P(\sqrt{\log n_i\log \hspace{0.17em}p/p}+\sqrt{\log n_i\log \hspace{0.17em}p/n_i})\hfill & \text{if}\hspace{0.17em}i\in {\mathcal{M}}_1,\hfill \\ O_P(\sqrt{\log n_i\log \hspace{0.17em}p/p})\hfill & \text{if}\hspace{0.17em}i\in {\mathcal{M}}_2.\hfill \end{array}$$

Therefore, PPCA dominates PCA as long as the effective covariates are provided However, ${\mathbf{U}}^i{\mathbf{F}}^i{\mathbf{F}}^{i^{\prime }}/n_i$ dominates all the remaining terms so that $||{\check{\mathbf{U}}}^i-{\mathbf{U}}^i|{|}_{\text{max}}=O_P(||{\mathbf{U}}^i{\mathbf{F}}^i{\mathbf{F}}^{i^{\prime }}/n_i|{|}_{\text{max}})O_P(\sqrt{\log n_i\log \hspace{0.17em}p/n_i}).$

In addition, for estimation of $\mathbf{U}{\mathbf{U}}^{\prime }$, we have

$${\check{\mathbf{U}}}^i{\check{\mathbf{U}}}^{i^{\prime }}-{\mathbf{U}}^i{\mathbf{U}}^{i^{\prime }}=-{\mathbf{U}}^i{\mathbf{F}}^i{\mathbf{F}}^{i^{\prime }}{\mathbf{U}}^{i^{\prime }}/n_i+\{\begin{array}{ll}{O}_P(\log \hspace{0.17em}p+\delta )\hfill & \text{if}\hspace{0.17em}i\in {\mathcal{M}}_1,\hfill \\ O_P(n_i\log \hspace{0.17em}p\sqrt{{\nu }_p/p}+\delta )\hfill & \text{if}\hspace{0.17em}i\in {\mathcal{M}}_2,\hfill \end{array}$$ (3.5)

where $\delta =n_i^2{\Vert \mathbf{\Sigma }\Vert }_1^2\log \hspace{0.17em}p/p^2$, depending on ${\Vert \mathbf{\Sigma }\Vert }_1$. If we consider a very sparse covariance matrix so that ${\Vert \mathbf{\Sigma }\Vert }_1$ is bounded, we can simply drop the term δ in both regimes. Then, regime 1 achieves better rate if $p=O(n_i^2{\nu }_p)$ but regime 2 outperforms otherwise.

4. Post-ALPHA inference

We have summarized the order of biases caused by adjusting heterogeneity for each data source in Section 3.4. Now we combine the adjusted data together for further statistical analysis. As an example, we study estimation of the Gaussian graphical model. Assume further ${\mathbf{u}}_t^i~N(\mathbf{0},\mathbf{\Sigma })$ and consider the following class of the precision matrices:

$$\mathcal{F}(s,R)=\left\{\mathbf{\Omega }:\mathbf{\Omega }\succ \mathbf{0},\hspace{0.17em}{\Vert \mathbf{\Omega }\Vert }_1\le R,\hspace{0.17em}\underset{1\le i\le p}{\text{max}}\sum _{j=1}^p\mathrm{𝟙}({\Omega }_{i,j}\ne 0)\le s\right\}.$$ (4.1)

To simplify the analysis, we assume R is fixed, but all the analysis can be easily extended to include growing R.

To estimate Ω = Σ⁻¹ via CLIME, we need a covariance estimator as the input. We assume here the number of factors is known, i.e., the exception probability of recovering Kⁱ has been ignored for ease of discussion. Such an estimator is naturally given by

$$\widehat{\mathbf{\Sigma }}=\frac{1}{N-{\sum }_{i\le m}{K}^i}\sum _{i=1}^m{\check{\mathbf{U}}}^i{\check{\mathbf{U}}}^{i^{\prime }}.$$ (4.2)

Since the number of data sources is huge, we focus on the case of diverging N and p.

4.1. Covariance estimation

Let Σ_N be the oracle sample covariance matrix, i.e., ${\mathbf{\Sigma }}_N=N^{-1}{\sum }_{i=1}^m{\mathbf{U}}^i{\mathbf{U}}^{i^{\prime }}$. We consider the difference between our proposed $\widehat{\mathbf{\Sigma }}$ and ${\mathbf{\Sigma }}_N$ in this subsection. The oracle estimator obviously attains the rate ${\Vert {\mathbf{\Sigma }}_N-\mathbf{\Sigma }\Vert }_{\text{max}}=O_P(\sqrt{\log \hspace{0.17em}p/N})$.

Let ${\mathbf{\xi }}_k^i={\mathbf{U}}^i\overline{{\mathbf{f}}_k^i}/\sqrt{n_i}$ where $\overline{{\mathbf{f}}_k^i}$ is the k^th column of Fⁱ. It is not hard to verify that ${\mathbf{\xi }}_k^i$ is Gaussian distributed with mean zero and variance Σ. Note that ${\left\{{\mathbf{\xi }}_k^i\right\}}_{1\le i\le m,1\le k\le K^i}$ are i.i.d. with respect to k and i, using the assumption ${\mathbf{F}}^{i^{\prime }}{\mathbf{F}}^i/n_i=\mathbf{I}$. By the standard concentration bound (e.g. Lemma 4.2 of [19]),

$$\begin{gathered} {\Vert \sum _{i\le m}(\frac{1}{n_i}{\mathbf{U}}^i{\mathbf{F}}^i{\mathbf{F}}^{i^{\prime }}{\mathbf{U}}^{i^{\prime }}-K^i\mathbf{\Sigma })\Vert }_{\text{max}}={\Vert \sum _{i\le m}\sum _{k\le K^i}({\mathbf{\xi }}_k^i{\mathbf{\xi }}_k^{i^{\prime }}-\mathbf{\Sigma })\Vert }_{\text{max}} \\ =O_P(\sqrt{K^{tot}\log \hspace{0.17em}p}), \end{gathered}$$

where $K^{tot}={\sum }_{i\le m}{K}^i$. Therefore, by (3.5), we have

$$\begin{gathered} {\Vert \widehat{\mathbf{\Sigma }}-{\mathbf{\Sigma }}_N\Vert }_{\text{max}}=\Vert \frac{N}{N-{\sum }_{i\le m}{K}^i}\frac{1}{N}\sum _{i\le m}({\check{\mathbf{U}}}^i{\check{\mathbf{U}}}^{i^{\prime }}-{\mathbf{U}}^i{\mathbf{U}}^{i^{\prime }}+K^i\mathbf{\Sigma }){ \\ +\frac{{\sum }_{i\in \mathcal{M}}{K}^i}{N-{\sum }_{i\in \mathcal{M}}{K}^i}(\frac{1}{N}\sum _{i\le m}{\mathbf{U}}^i{\mathbf{U}}^{i^{\prime }}-\mathbf{\Sigma })\Vert }_{\text{max}}=:O_P(a_{m,N,P}), \end{gathered}$$ (4.3)

where $a_{m,N,P}=\frac{|{\mathcal{M}}_1|\log \hspace{0.17em}p}{N}+\frac{N_2\log \hspace{0.17em}p}{N}\sqrt{\frac{{\nu }_p}{p}}+\frac{\sqrt{K^{tot}\log \hspace{0.17em}p}}{N}+\frac{K^{tot}}{N}\sqrt{\frac{\log \hspace{0.17em}p}{N}}$ and $N_2={\sum }_{i\in {\mathcal{M}}_2}{n}_i$.

We now examine the difference of the ALPHA estimator from the oracle estimator for two specific cases. In the first case, we apply PCA to all data sources, i.e., all $i\in {\mathcal{M}}_1$ and Kⁱ is bounded. We then have a_m,N,p = m log p/N. This rate is dominated by the oracle error rate $\sqrt{\text{log}p/N}$ if and only if $m=O(\sqrt{N/\log \hspace{0.17em}p})$. This means traditional PCA performs optimally for adjusting heterogeneity as long as the number of subgroups grows more slowly than the order of $\sqrt{N/\log \hspace{0.17em}p}$.

If we apply PPCA to all data sources, i.e., $i\in {\mathcal{M}}_2$ and Kⁱ is bounded, then $a_{m,N,p}=\sqrt{{\nu }_p/p}\log \hspace{0.17em}p+\sqrt{m\log \hspace{0.17em}p}/N$. This rate is of smaller order than rate $\sqrt{\log \hspace{0.17em}p/N}$ if p/log p > CN for some constant C > 0. The advantage of using PPCA is that when n_i is bound so that $m\asymp N$, we can still achieve optimal rate of convergence so long as we have a large enough dimensionality at least of the order N.

4.2. Precision matrix estimation

In order to obtain an estimator for the sparse precision matrix from $\widehat{\mathbf{\Sigma }}$, we apply the CLIME estimator proposed by [9]. For a given $\widehat{\mathbf{\Sigma }}$, CLIME solves the following optimization problem:

$$\widehat{\mathbf{\Omega }}=\arg \underset{\mathbf{\Omega }}{\text{min}}{\Vert \mathbf{\Omega }\Vert }_{1,1}\hspace{1em}\text{subject to }{\Vert \widehat{\mathbf{\Sigma }}\mathbf{\Omega }-\mathbf{I}\Vert }_{\text{max}}\le \text{λ,}$$ (4.4)

where ${\Vert \mathbf{\Omega }\Vert }_{1,1}={\sum }_{i,j\le p}|{\mathbf{\Omega }}_{ij}|$ and λ is a tuning parameter. Note that (4.4) can be solved column-wisely by linear programming. However, CLIME does not necessarily generate a symmetric matrix. We can simply symmetrize it by taking the one with minimal magnitude of ${\widehat{\sigma }}_{ij}$ and ${\widehat{\sigma }}_{ji}$. The resulting matrix after symmetrization, still denoted as $\widehat{\mathbf{\Omega }}$ with a little bit abuse of notation, also attains good rate of convergence. In particular, we consider the sparse precision matrix class $\mathcal{F}(s,C_0)$ in (4.1). The following lemma guarantees recovery of any sparse matrix $\mathbf{\Omega }\in \mathcal{F}(s,C_0)$.

Theorem 4.1. Suppose $\mathbf{\Omega }\in \mathcal{F}(s,C_0)$ and let ${\tau }_{m,N,p}=\sqrt{\log \hspace{0.17em}p/N}+a_{m,N.p}$. Choosing $\text{λ}\asymp {\tau }_{m,N,p}$, we have

$${\Vert \widehat{\mathbf{\Omega }}-\mathbf{\Omega }\Vert }_{\text{max}}=O_p({\tau }_{m,N,p}).$$

Furthermore, ${\Vert \widehat{\mathbf{\Omega }}-\mathbf{\Omega }\Vert }_1=O_p(s{\tau }_{m,N,p})$ and ${\Vert \widehat{\mathbf{\Omega }}-\mathbf{\Omega }\Vert }_2=O_p(s{\tau }_{m,N,p})$.

Here we stress that we choose CLIME for the precision matrix estimation because it only relies on the max-norm guarantee ${\Vert \widehat{\mathbf{\Sigma }}-\mathbf{\Sigma }\Vert }_{\text{max}}$. The intuition is that for any true Ω with bounded, ${\Vert \mathbf{\Omega }\Vert }_1$,

$${\Vert \mathbf{I}-\widehat{\mathbf{\Sigma }}\mathbf{\Omega }\Vert }_{\text{max}}={\Vert (\widehat{\mathbf{\Sigma }}-\mathbf{\Sigma })\mathbf{\Omega }\Vert }_{\text{max}}\le {\Vert \widehat{\mathbf{\Sigma }}-\mathbf{\Sigma }\Vert }_{\text{max}}{\Vert \mathbf{\Omega }\Vert }_1=O_{\mathbb{P}}({\Vert \widehat{\mathbf{\Sigma }}-\mathbf{\Sigma }\Vert }_{\text{max}}).$$

One can see from above that fast convergence of ${\Vert \widehat{\mathbf{\Sigma }}-\mathbf{\Sigma }\Vert }_{\text{max}}$ encourages feasibility of Ω, which is a necessary step for establishing consistency of the resulting M-estimator. Interested readers can refer to the proof of Theorem 4.1 for more details. Other possible methods for precision matrix recovery (e.g. graphical Lasso in [20], graphical Dantzig selector in [48] and graphical neighborhood selection in [35]) can be considered for post-ALPHA inference as well, but their convergence rate needs to be studied in a case-by-case fashion.

Theorem 4.1 shows that CLIME has strong theoretical guarantee of convergence under different matrix norms. The rate of convergence has two parts, one corresponding to the minimax optimal rate [48] while the other is due to the error caused by estimating the unknown factors under various situations. The discussions at the end of Section 4.1 suggest that the latter error is often negligible.

In addition, we numerically investigate how misspecification of the number of factors K will affect the precision matrix estimation in Section G.3 in the appendix.

5. Numerical studies

In this section, we first validate the established theoretical results through Monte Carlo simulations. Our purpose is to show that after heterogeneity adjustment, the proposed aggregated covariance estimator $\widehat{\mathbf{\Sigma }}$ approximates well the oracle sample covariance Σ_N, thereby leading to accurate estimation of the true co-variance matrix Σ and precision matrix Ω. We also compare the performance of PPCA and regular PCA on heterogeneity adjustment under different settings.

In addition, we analyze a real brain image data using the proposed procedure. The dataset to be analyzed is the ADHD-200 data [6]. It consists of rs-fMRI images of 608 subjects, of whom 465 are healthy and 143 are diagnosed with ADHD. We dropped subjects with missing values in our analysis. Following [39], we divided the whole brain into 264 regions of interest (ROI, p = 264), which are regarded as nodes in our graphical model. Each brain was scanned for multiple times with sample sizes ranging from 76 to 261 (76 ≤ n_i ≤ 261). In each scan, we acquired the blood-oxygen-level dependent (BOLD) signal within each ROI. Note that subjects have different ages, genders etc., which results in heterogeneity over the covariance structure of the data. We need to remove this unwanted heterogeneity; otherwise it will dilute or corrupt the true biological signal, i.e., the difference in the brain functional network between healthy people and patients due to the disease ADHD.

5.1. Preliminary analysis

To apply our ALPHA framework, we need to first argue the pervasiveness condition Assumption 2.2 holds for the real dataset considered. This is done in Section G.2, together with further discussions on pervasiveness. We also collect the physical locations of the 264 regions as the external covariates. Ideally, we hope these covariates to be pervasive in explaining the batch effect (Assumption 2.3), while bearing no association with the graph structure of u_t. This is reasonably true because: the level of batch effect is non-uniform over different locations of the brain when scanned in fMRI machines; furthermore it has been widely acknowledged in biological studies that spatial adjacency does not necessarily imply brain functional connectivity.

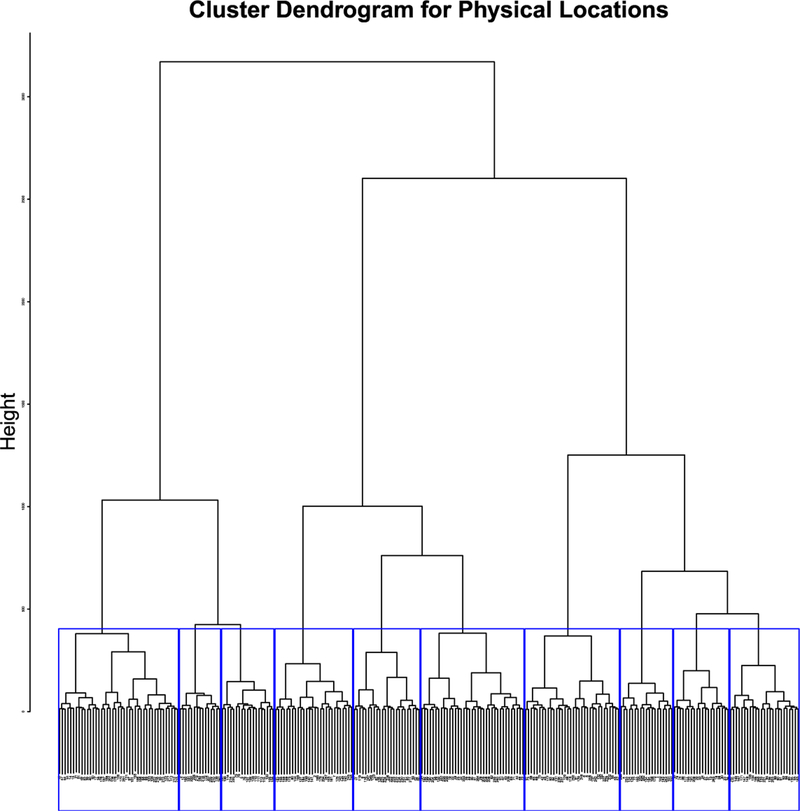
To construct ${\mathbf{W}}_j^i$ from the physical locations, we simply split the 264 regions into 10 clusters (J = 10) by the hierarchy clustering (Ward’s minimum variance method) and use the categorical indices as the covariates of the nodes. The clustering result is shown in Figure 2 and the spatial locations of the 264 regions are shown in Figure 6 in 10 different colors. Black (middle), green (left) and blue (right) represent roughly the region of frontal lobe; gray (middle), pink (left) and magenta (right) occupy the region of parietal lobe; red (left) and orange (right) are in the area of occipital lobe; finally yellow (left) and navy (right) provide information about temporal lobe.

Fig 2.

Cluster Dendrogram for physical locations with J = 10.

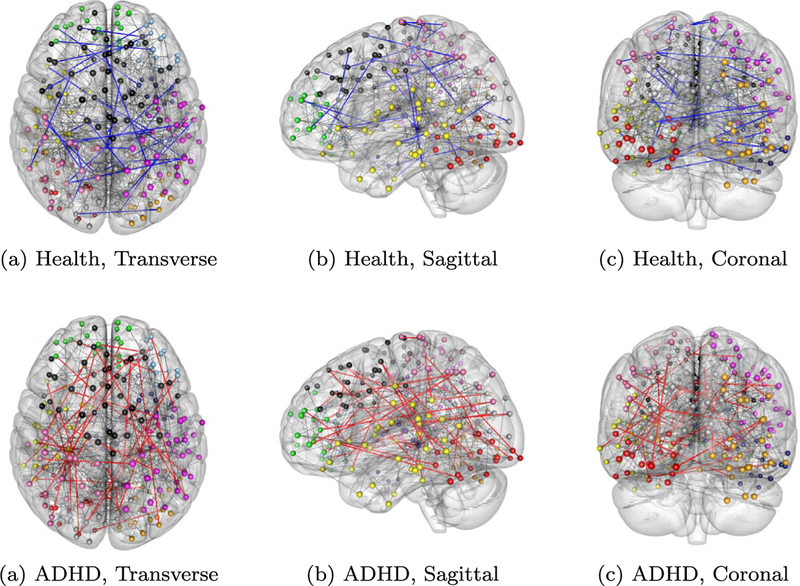
Fig 6.

Estimated brain functional connectivity networks using physical locations as covariates to correct heterogeneity. 10 region clusters are labeled in 10 colors. Black, blue and red edges represent respectively common edges, unshared edges in the healthy group and in the ADHD group.

Here J = 10 is only used to calibrate our synthetic model in the next subsection. In the real data analysis, we will choose J adaptively according to our heuristic guiding rule of the maximal eigen-gap discussed in Section 3.3. Note that here since the covariate W is one-dimensional (d = 1) and discrete, the sieve basis functions are just indicator functions 𝟙(w − 0.5 ≤ W < w + 0.5) for w = 1,…,10. We use the same external covariates for all subjects in both healthy and diseased groups.

The next question is how to divide the subjects into ${\mathcal{M}}_1$ and ${\mathcal{M}}_2$ based on whether the selected covariates explain the loadings effectively. We implemented the method given in Section 3.3 and discovered that 398 healthy (85.6%) and 126 diseased samples (88.1%) prefer PPCA over PCA, meaning that the physical locations indeed have explanatory powers on factor loadings of most subjects. We identified them as subjects in ${\mathcal{M}}_2$ while the others were classified as in ${\mathcal{M}}_1$. Based on the class labels, we employed the corresponding method to estimate the number of factors and adjust the heterogeneity. We used K_max = 3. The estimated number of factors for the two groups are summarized in Table 1.

Table 1.

Distribution of estimated number of factors for healthy and ADHD groups

$\check{K^i}$	1	2	3
Healthy	253	148	64
ADHD	78	40	25

5.2. Synthetic datasets

In this simulation study, for stability, we use the first 15 subjects in the healthy group to calibrate the simulation models. We specify four asymptotic settings for our simulation studies:

1. m = 500, n_i = 10 for i = 1,..,m, p = 100, 200,…,600 and G(W) ≠ 0;

2. m = 100, 200,…,1000, n_i = 10 for i = 1,…,m, p = 264 and G(W) ≠ 0;

3. m = 100, n_i = 10, 20,…,100 for i = 1,…,m, p = 264 and G(W) ≠ 0;

4. m = 20, 40,…,200, n_i = 20, 40,…,200 for i = 1,…,m, p = 264 and G(W) = 0.

Here the last setting represents regime 1, where we should expect PCA to work well when the number of subjects is of order of square root of the total sample size, i.e., $m\asymp \sqrt{N}$. The first three settings represent regime 2 with informative covariates; they present asymptotics with growing p, m and n_i respectively. The details on model calibration and data generation can be found in Section G.1.

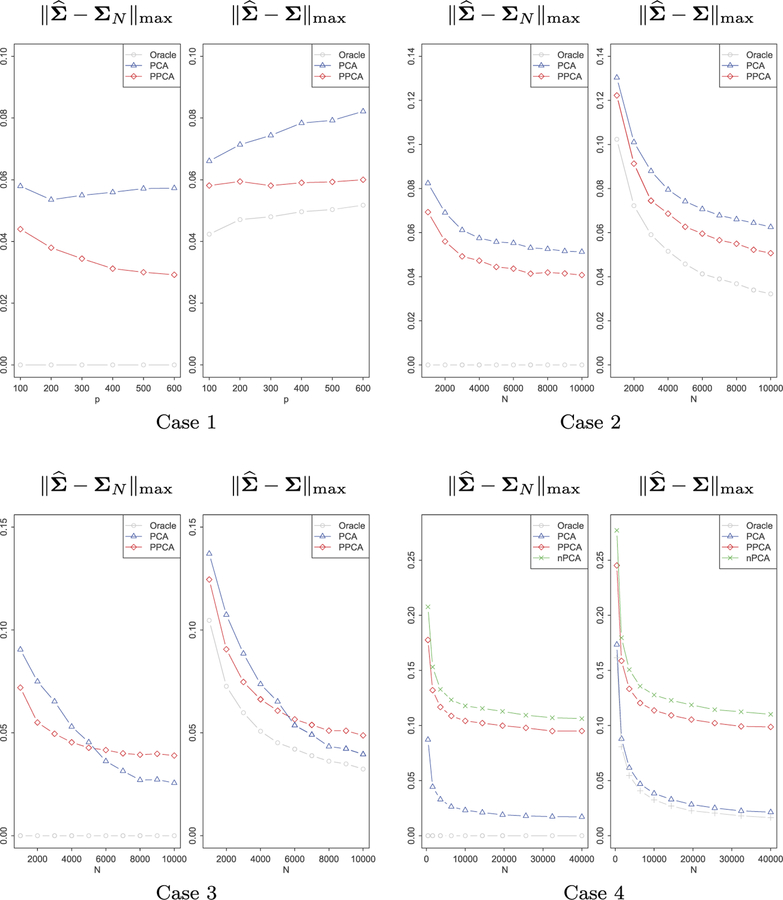
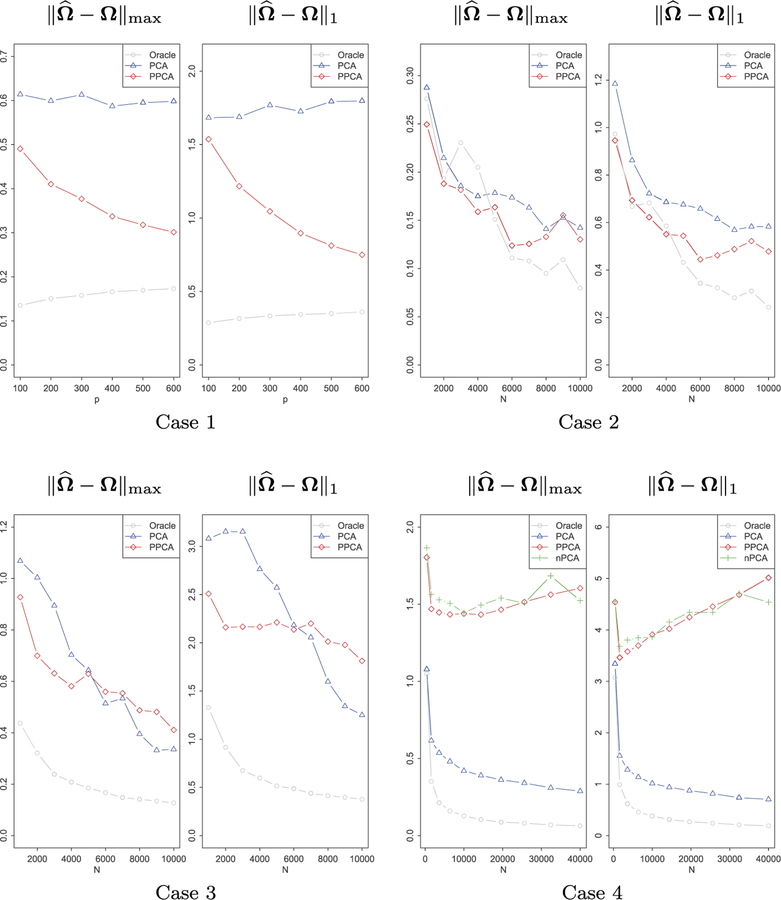
We first investigate the errors of estimating covariance of u_t in max-norm after applying PPCA or PCA for heterogeneity adjustment. We also compare them with the estimation errors if we naively pool all the data together without any heterogeneity adjustment. However, the estimation error of the naively pooled sample covariance is too large to fit in the graph for the first 3 cases, which we thus do not plot. Denote the oracle sample covariance of u_t by Σ_N as before. The estimation errors, based on 100 simulations, under the four settings are presented in Figure 3.

Fig 3.

Estimation of Σ by PCA, PPCA and the oracle sample covariance matrix for 4 different settings. Case 1: m and n_i are fixed while the dimension p increases; case 2: n_i and p are fixed while m increases; case 3: m and p are fixed while n_i increases; case 4: p is fixed, and both m and n_i increase and conditions for PPCA are violated.

In Case 1, m and n_i are fixed while dimension p increases. This setting highlights the advantages of Projected-PCA over regular PCA. From the left panel, we observe that increase of dimensionality improves the performance of Projected-PCA. This is consistent with the rate we derived in theories. In Case 2, n_i and p are fixed while m increases. Both PPCA and PCA benefit from an increasing number of subjects. However, since n_i is small, again PPCA outperforms. In Case 3, m and p are fixed while n_i increases. Both methods achieve better estimation as n_i increases, but more importantly, regular PCA outperforms PPCA when n_i is large enough. This is again consistent with our theories. As illustrated by Section 4.1, when m is fixed, PCA attains the convergence rate ${\Vert \widehat{\mathbf{\Sigma }}-\mathbf{\Sigma }\Vert }_{\text{max}}=O_P(\sqrt{\log \hspace{0.17em}p/N})$, while PPCA only achieves ${\Vert \widehat{\mathbf{\Sigma }}-\mathbf{\Sigma }\Vert }_{\text{max}}=O_P(\log \hspace{0.17em}p/\sqrt{p})$, which is worse than PCA when p/log p = o(N). In Case 4, p is fixed, and both m and n_i increase. Note that the covariates have no explanation power at all, i.e., Condition 2.3 about pervasiveness does not hold so that PPCA is not applicable. Adjusting by PCA behaves much better and PPCA sometimes is as bad as ‘nPCA’, corresponding to no heterogeneity adjustment. This is not unexpected as we utilize a noisy external covariates.

Now we focus on estimation error of the precision matrix. We plug $\widehat{\mathbf{\Sigma }}$, obtained from data after adjusting for heterogeneity, into CLIME to get the estimator $\widehat{\mathbf{\Omega }}$ of $\mathbf{\Omega }$. In Figure 4, ${\Vert \widehat{\mathbf{\Omega }}-\mathbf{\Omega }\Vert }_{\text{max}}$ and ${\Vert \widehat{\mathbf{\Omega }}-\mathbf{\Omega }\Vert }_1$ are depicted under the four asymptotic settings. From the plots we see ${\Vert \widehat{\mathbf{\Omega }}-\mathbf{\Omega }\Vert }_{\text{max}}$ and ${\Vert \widehat{\mathbf{\Omega }}-\mathbf{\Omega }\Vert }_1$ share similar behavior with ${\Vert \widehat{\mathbf{\Sigma }}-\mathbf{\Sigma }\Vert }_{\text{max}}$ shown in Figure 3: in Case 1, n_i is small, so it is advantageous to use PPCA and PPCA behaves better as dimension increases; in Case 2, both PPCA and PCA benefit from an increasing number of subjects and PPCA outperforms PCA; in Case 3, PCA outperforms PPCA when n_i is large enough since m is fixed; in Case 4, the covariates have no explanation power at all so that PPCA does not make sense. In the first three cases, if we do not adjust data heterogeneity, ${\Vert \widehat{\mathbf{\Omega }}-\mathbf{\Omega }\Vert }_{\text{max}}$ and ${\Vert \widehat{\mathbf{\Omega }}-\mathbf{\Omega }\Vert }_1$ will be too large to fit in the current scale.

Fig 4.

Estimation of Ω. Presented are the estimation errors in max-norm and L₁-norm for 4 different settings. In Case 4, nPCA refers to no PCA, i.e., we do not adjust heterogeneity.

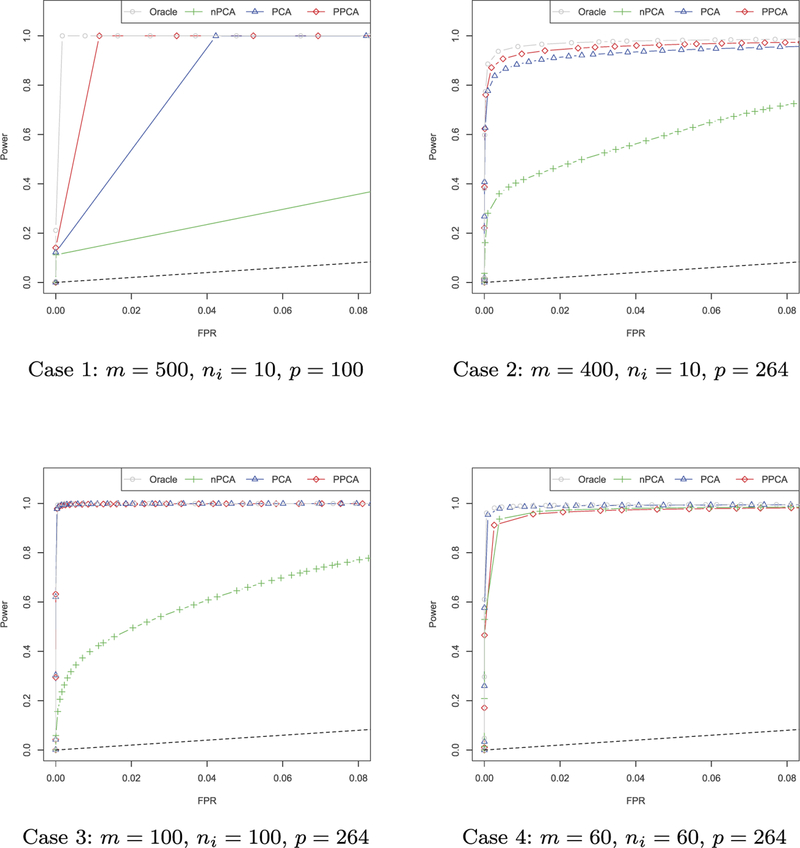
We also present the ROC curves of our proposed methods in Figure 5, which is of interest to readers concerned with sparsity pattern recovery. The black dashed line is the 45 degree line, representing performance of random guess. It is obvious from those plots that heterogeneity adjustment very much improves the sparsity recovery of the precision matrix. When the sample size of each subject is small, genuine pervasive covariates increase the power of PPCA while if the sample size is relatively large, PCA is sufficiently good in recovering graph structures. Also notice that in all cases, the naive method without heterogeneity adjustment can still achieve a certain amount of power, but we can improve the performance dramatically by correcting the batch effects.

Fig 5.

ROC curves for sparsity recovery of Ω for 4 different settings.

5.3. Brain image network data

We report the estimated graphs for both the healthy group and the ADHD patient group with batch effects removed using our ALPHA framework in this subsection. We took various sparsity levels of the networks from 1% to 5% (corresponding to the same set of λ’s for two groups) and selected the common edges, which are stable with respect to tuning, to be depicted.

The brain network produced by our proposed method is presented in Figure 6. It gives 90.7% identical edges for the two networks. However if we ignore heterogeneity and naively pool the data from all subjects together, it generates 10.2% unshared edges, roughly 1% more than ALPHA produces. Therefore, by heterogeneity adjustment, we found less difference in brain functional networks between ADHD patients and healthy people. In addition, we investigate how those unshared edges are distributed across the 10 clusters. We summarized the total degree of unshared edge vertices within each cluster in Table 2. As we can see, in the left occipital lobe (red) and the left parietal lobe (pink), there are significant difference in functional connectivity structure between healthy people and patients, although in general the difference is weak. These are signs that ADHD is a complex disease that affects many regions of the brain. The general methodology we provide here could be valuable for further understanding the mechanism of the disease.

Table 2.

The degree of unshared edge vertices for each cluster

	red	orange	blue	green	yellow	navy	pink	black	magenta	gray
Health	3	4	3	2	7	6	10	12	11	6
ADHD	9	6	7	5	12	5	6	15	9	10

6. Discussions

Heterogeneity is usually informed by the domain knowledge of the dataset. In particular, it occurs with high chance when the data come from different sources or subgroups. In the brain image dataset we used in the numerical study, heterogeneity across patients can stem from difference in age, gender, etc. When it is less clear whether heterogeneity exists, we can calculate multiple summary statistics for all the subgroups and see whether they are significantly different. In the case of pervasive heterogeneity, we can test it by the magnitude of dominating eigenvalues of the covariance matrix in each subgroup. A systematic testing method for heterogeneity is important and we leave it for now as a future research topic. Note that even if all the subgroups are actually homogeneous, ALPHA does not hurt the statistical efficiency under appropriate scaling assumptions. Specifically, for the PCA-based ALPHA, we showed in Section 4.1 that as long as the number of subgroups $m=O(\sqrt{N/\log \hspace{0.17em}p})$, $\check{\mathbf{\Sigma }}$ enjoys the oracle max-norm rate. This means that given homogeneous data, when the number of data splits is not large, ALPHA yields the same statistical rate as the full-sample oracle estimator. For the PPCA-based ALPHA, $\check{\mathbf{\Sigma }}$ enjoys the oracle rate when $p/\log \hspace{0.17em}p=\mathbf{\Omega }(\sqrt{N/\log \hspace{0.17em}p})$.

As we have seen, ALPHA is adaptive to factor structures and is flexible to include external information. However, this advantage of PPCA is accompanied by more assumptions and the practical issue of selecting proper basis functions and the number of them in sieve approximation. One contribution of the paper lies in seamless integration of PCA and PPCA, which leverages effective external covariates. If no valuable covariates exist and the sample size is relatively large for each data source, we have shown conventional PCA is still an effective tool.

Note that our framework is compatible with any statistical procedure that only requires an accurate estimator as the input, like CLIME we illustrate in this work. The ALPHA procedure gives theoretical guarantee for $||\check{\mathbf{U}}-\mathbf{U}|{|}_{\max }$ and $||\widehat{\mathbf{\Sigma }}-\mathbf{\Sigma }|{|}_{\max }$, which serve as foundations for establishing the statistical properties of the subsequent procedure. Besides, ALPHA has potential application and in regression analysis. If the residual terms ${\left\{{\mathbf{U}}^i\right\}}_{i=1}^m$ are true predictors for the response of interest ${\left\{{\mathbf{Y}}^i\right\}}_{i=1}^m$, we can first apply ALPHA to extract the residuals before the regression procedure. For example, the residual BOLD signal we obtained by ALPHA in the brain functional network analysis (Section 5.3) is potentially useful in predicting whether a person has ADHD. This is a typical logistic regression problem based on ALPHA adjustment. We leave the detailed study of combining ALPHA with regression models for future investigation. One recent work [16] has adopted a method similar to ALPHA that extracts residuals for model selection in high dimensional regression.

Finally, we point out two current limitations of ALPHA. The first limitation lies in its pervasiveness assumption of the heterogeneity terms ${\left\{{\mathbf{\Lambda }}^i{\mathbf{F}}^{i^{\prime }}\right\}}_{i=1}^m$. More specifically, for each subgroup i, ALPHA requires the signal strength of the heterogeneous part ${\mathbf{\Lambda }}^i{\mathbf{F}}^{i^{\prime }}$ to overwhelm the homogeneous residual part Uⁱ so that PCA or PPCA can accurately estimate ${\mathbf{\Lambda }}^i{\mathbf{F}}^{i^{\prime }}$ and remove it. Such requirement can be violated in practice when the heterogeneous term has similar signal strength as the homogeneous term. Additionally, statistical methods that require more than the max-norm error guarantee $(||\check{\mathbf{U}}-\mathbf{U}|{|}_{\text{max}},||\check{\mathbf{\Sigma }}-\mathbf{\Sigma }|{|}_{\text{max}})$, say in the general non-sparse situation, may be inappropriate for the post-ALPHA inference for now.

Appendix A: Algorithm for ALPHA

The pseudo code for the algorithm ALPHA is shown as follows.

$$\begin{array}{l}\overline{\underset{\_}{\begin{array}{l}\mathbf{\text{Algorithm}}\hspace{0.17em}\mathbf{1}\hspace{0.17em}\text{Algorithm for adaptive low-rank principal heterogeneity adjustment}\end{array}}}\\ \underset{\_}{\begin{array}{l}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{0.17em}\underset{\_}{\mathbf{Input}:}\hspace{0.17em}\text{Panel }{\mathbf{\text{X}}}_{p\times n_i}^i\text{ and }d\text{-dimensional }{\left\{{\mathbf{\text{W}}}_j^i\right\}}_{j=1}^p\text{ from }m\text{ data sources,}\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}{J}_{\text{max}},\hspace{0.17em}{K}_{\text{max}}(J_{\text{max}}\ge (K_{\text{max}}+1)/d)\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\underset{\_}{\mathbf{Output}:}\hspace{0.17em}\check{{\mathbf{U}}^i},\check{K^i}\text{and}\hspace{0.17em}\widehat{\mathbf{\Sigma }}\\ \hspace{0.17em}\hspace{0.17em}1:\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\mathbf{procedure}\text{ ALPHA}\\ \hspace{0.17em}\hspace{0.17em}2:\hspace{1em}\hspace{1em}\mathbf{for}\hspace{0.17em}\text{each subject }i\le m\hspace{0.17em}\mathbf{d}\mathbf{o}\\ \hspace{0.17em}\hspace{0.17em}3:\hspace{1em}\hspace{1em}\hspace{1em}\widehat{K^i}\leftarrow \arg {\text{max}}_{K\le K_{max}}{\text{λ}}_k({{\mathbf{X}}^i}^{\prime }{\mathbf{X}}^i)/{\text{λ}}_{k+1}({{\mathbf{X}}^i}^{\prime }{\mathbf{X}}^i)\\ \hspace{0.17em}\hspace{0.17em}4:\hspace{1em}\hspace{1em}\hspace{1em}\Delta {\lambda }_0^i\leftarrow {\text{λ}}_{\widehat{K^i}}({{\mathbf{X}}^i}^{\prime }{\mathbf{X}}^i)/{\text{λ}}_{\widehat{K^i}+1}({{\mathbf{X}}^i}^{\prime }{\mathbf{X}}^i)\\ \hspace{0.17em}\hspace{0.17em}5:\hspace{1em}\hspace{1em}\hspace{1em}\mathbf{for}\hspace{0.17em}\text{each }(K_{\text{max}}+1)/d\le J\le J_{\text{max}}\hspace{0.17em}\mathbf{d}\mathbf{o}\\ \hspace{0.17em}\hspace{0.17em}6:\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{0.17em}{\mathbf{P}}_J^i\leftarrow \Phi ({\mathbf{W}}^i){(\Phi {({\mathbf{W}}^i)}^{\prime }\Phi ({\mathbf{W}}^i))}^{-1}\Phi {({\mathbf{W}}^i)}^{\prime }\hspace{0.17em}\text{for}\hspace{0.17em}J\\ \hspace{0.17em}\hspace{0.17em}7:\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{0.17em}\widetilde{K_J^i}\leftarrow \arg {max}_{K\le K_{\text{max}}}{\text{λ}}_k({{\mathbf{X}}^i}^{\prime }{\mathbf{P}}_J^i{\mathbf{X}}^i)/{\text{λ}}_{k+1}({{\mathbf{X}}^i}^{\prime }{\mathbf{P}}_J^i{\mathbf{X}}^i)\\ \hspace{0.17em}\hspace{0.17em}8:\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{0.17em}\Delta {\lambda }_J^i\leftarrow {\text{λ}}_{\widetilde{K_J^i}}({{\mathbf{X}}^i}^{\prime }{\mathbf{P}}_J^i{\mathbf{X}}^i)/{\text{λ}}_{\widetilde{K_J^i}+1}({{\mathbf{X}}^i}^{\prime }{\mathbf{P}}_J^i{\mathbf{X}}^i)\\ \hspace{0.17em}\hspace{0.17em}9:\hspace{1em}\hspace{1em}\hspace{1em}\mathbf{end}\hspace{0.17em}\mathbf{for}\\ 10:\hspace{1em}\hspace{1em}\hspace{1em}{J}_{*}^i\leftarrow \arg {\text{max}}_J\Delta {\text{λ}}_J^i\\ 11:\hspace{1em}\hspace{1em}\hspace{1em}\widetilde{K^i}\leftarrow \widetilde{K_{J_{*}^i}^i}\\ 12:\\ 13:\hspace{1em}\hspace{1em}\hspace{1em}\mathbf{if}\hspace{0.17em}\Delta {\text{λ}}_0^i>\Delta {\text{λ}}_{J_{*}^i}^i(i\in {\mathcal{M}}_1)\hspace{0.17em}\mathbf{then}\\ 14:\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{0.17em}\widehat{{\mathbf{F}}^i}/\sqrt{n_i}\leftarrow \text{eigenvectors of }{{\mathbf{X}}^i}^{\prime }{\mathbf{X}}^i\text{ of the top }\widetilde{K^i}\text{ eigenvalues}\\ 15:\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{0.17em}\widehat{{\mathbf{\Lambda }}^i}\leftarrow {\mathbf{X}}^i\widehat{{\mathbf{F}}^i}/n_i,\hspace{0.17em}\widehat{{\mathbf{U}}^i}\leftarrow {\mathbf{X}}^i-\widehat{{\mathbf{\Lambda }}^i}\widehat{{\mathbf{F}}^i}\\ 16:\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{0.17em}\check{{\mathbf{U}}^i}\leftarrow \widehat{{\mathbf{U}}^i},\check{K^i}\leftarrow \widehat{K^i}\\ 17:\hspace{1em}\hspace{1em}\hspace{1em}\mathbf{else}\\ 18:\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{0.17em}\widetilde{{\mathbf{F}}^i}/\sqrt{n_i}\leftarrow \text{eigenvectors of }{{\mathbf{X}}^i}^{\prime }{\mathbf{P}}_{J_{*}^i}^i\hspace{0.17em}{\mathbf{X}}^i\text{ of the top }\widetilde{K^i}\text{ eigenvalues}\\ 19:\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{0.17em}\widetilde{{\mathbf{\Lambda }}^i}\leftarrow {\mathbf{X}}^i\widetilde{{\mathbf{F}}^i}/n_i,\widetilde{{\mathbf{U}}^i}\leftarrow {\mathbf{X}}^i-\widetilde{{\mathbf{\Lambda }}^i}\widetilde{{\mathbf{F}}^i}\\ 20:\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{0.17em}\check{{\mathbf{U}}^i}\leftarrow \widetilde{{\mathbf{U}}^i},\hspace{0.17em}\check{K^i}\leftarrow \widetilde{K^i}\\ 21:\hspace{1em}\hspace{1em}\hspace{1em}\mathbf{end}\hspace{0.17em}\mathbf{if}\\ 22:\hspace{1em}\hspace{1em}\mathbf{end}\hspace{0.17em}\mathbf{for}\\ 23:\\ 24:\hspace{1em}\hspace{1em}\widehat{\mathbf{\Sigma }}\leftarrow {({\sum }_i{n}_i-{\sum }_i\check{K_i})}^{-1}{\sum }_{i=1}^m\hspace{0.17em}\check{{\mathbf{U}}^i}\stackrel{ˇ}{{{\mathbf{U}}^i}^{\prime }}\\ 25:\hspace{1em}\hspace{1em}\mathbf{return}\hspace{0.17em}{\{\check{{\mathbf{U}}^i}\}}_{i=1}^m,{\{\check{K^i}\}}_{i=1}^m\text{ and }\widehat{\mathbf{\Sigma }}\\ 26:\hspace{0.17em}\mathbf{\text{end procedure}}\end{array}}\end{array}$$

Appendix B: A key lemma

Recall that we defined

$$\check{\mathbf{U}}=\mathbf{X}(\mathbf{I}-\frac{1}{n}\check{\mathbf{F}}{\check{\mathbf{F}}}^{\prime }).$$ (B.1)

where we used notations such as $\check{\mathbf{F}}$ and $\check{\mathbf{U}}$ to denote the final estimators, which are $\widehat{\mathbf{F}}$ and $\widehat{\mathbf{U}}$ if PCA is used, and $\tilde{\mathbf{F}}$ and $\tilde{\mathbf{U}}$ if PPCA is used.

The following lemma holds for $\check{\mathbf{U}}$ no matter whether PCA or PPCA is applied.

Lemma B.1. For any K by K matrix H such that $\Vert \mathbf{H}\Vert =O_P(1),$ if log P = O(n),

$$\check{\mathbf{U}}-\mathbf{U}=-\frac{1}{n}\mathbf{U}\mathbf{F}{\mathbf{F}}^{\prime }+\mathbf{\Pi },$$

where ${\Vert \mathbf{\Pi }\Vert }_{\text{max}}=O_P(\sqrt{\log \hspace{0.17em}n}/n\cdot (||{\mathbf{F}}^{\prime }(\check{\mathbf{F}}-\mathbf{F}\mathbf{H})|{|}_{\text{max}}{\Vert \mathbf{\Lambda }\Vert }_{\text{max}}+||\mathbf{U}(\check{\mathbf{F}}-\mathbf{F}\mathbf{H})|{|}_{\text{max}})+||\check{\mathbf{F}}-\mathbf{F}\mathbf{H}|{|}_{\text{max}}{\Vert \mathbf{\Lambda }\Vert }_{\text{max}}+\sqrt{\log \hspace{0.17em}n}\cdot {\Vert \mathbf{H}{\mathbf{H}}^{\prime }-\mathbf{I}\Vert }_{\text{max}}{\Vert \mathbf{\Lambda }\Vert }_{\text{max}})$; and furthermore

$$\check{\mathbf{U}}{\check{\mathbf{U}}}^{\prime }-\mathbf{U}{\mathbf{U}}^{\prime }=-\frac{1}{n}\mathbf{U}\mathbf{F}{\mathbf{F}}^{\prime }{\mathbf{U}}^{\prime }+\mathbf{\Delta },$$

where ${\Vert \mathbf{\Delta }\Vert }_{\text{max}}=O_P(||\mathbf{U}(\check{\mathbf{F}}-\mathbf{F}\mathbf{H})|{|}_{\text{max}}{\Vert \mathbf{\Lambda }\Vert }_{\text{max}}+||\mathbf{U}(\check{\mathbf{F}}-\mathbf{F}\mathbf{H})|{|}_{\text{max}}^2+||{\mathbf{F}}^{\prime }(\check{\mathbf{F}}-\mathbf{F}\mathbf{H})|{|}_{\text{max}}||\mathbf{\Lambda }|{|}_{\text{max}}^2+n||\mathbf{H}{\mathbf{H}}^{\prime }-\mathbf{I}|{|}_{\text{max}}||\mathbf{\Lambda }|{|}_{\text{max}}^2)$.

The above lemma states that the error of estimating U by $\check{\mathbf{U}}$ (or estimating $\mathbf{U}{\mathbf{U}}^{\prime }$ by $\check{\mathbf{U}}{\check{\mathbf{U}}}^{\prime }$ ) is decomposed into two parts. The first part is inevitable even when the factor matrix F in (3.1) is known in advance. The second part is caused by the uncertainty from estimating F. Since the true F is identifiable up to an orthonormal transformation H, we need to carefully choose H to bound the error Π (or Δ). We will provide explicit rates of convergence for those terms in the following two sections.

Proof. By definition of $\check{\mathbf{U}}$, $\check{\mathbf{U}}=\mathbf{U}(\mathbf{I}-n^{-1}\mathbf{F}{\mathbf{F}}^{\prime })+n^{-1}\mathbf{X}(\check{\mathbf{F}}{\check{\mathbf{F}}}^{\prime }-\mathbf{F}{\mathbf{F}}^{\prime })$. We first look at the converge of $\check{\mathbf{U}}-\mathbf{U}$. Obviously $\mathbf{\Pi }=n^{-1}\mathbf{X}(\check{\mathbf{F}}{\check{\mathbf{F}}}^{\prime }-\mathbf{F}{\mathbf{F}}^{\prime })=I+II$ where

$$I=\frac{1}{n}\mathbf{\Lambda }\mathbf{F}\prime (\check{\mathbf{F}}{\check{\mathbf{F}}}^{\prime }-\mathbf{F}{\mathbf{F}}^{\prime }),\hspace{0.17em}II=\frac{1}{n}\mathbf{U}(\check{\mathbf{F}}{\check{\mathbf{F}}}^{\prime }-\mathbf{F}{\mathbf{F}}^{\prime }).$$

Since ${\mathbf{F}}^{\prime }(\check{\mathbf{F}}{\check{\mathbf{F}}}^{\prime }-\mathbf{F}{\mathbf{F}}^{\prime })={\mathbf{F}}^{\prime }(\check{\mathbf{F}}-\mathbf{F}\mathbf{H}){\check{\mathbf{F}}}^{\prime }+n\mathbf{H}(\check{\mathbf{F}}-\mathbf{F}\mathbf{H}{)}^{\prime }+n(\mathbf{H}{\mathbf{H}}^{\prime }-\mathbf{I}){\mathbf{F}}^{\prime },$ we have

$${\Vert I\Vert }_{\text{max}}=O_P({\Vert \mathbf{\Lambda }\Vert }_{\text{max}}(||{\mathbf{F}}^{\prime }(\check{\mathbf{F}}-\mathbf{F}\mathbf{H})|{|}_{\text{max}}||\check{\mathbf{F}}/n|{|}_{\text{max}}+||\check{\mathbf{F}}-\mathbf{F}\mathbf{H}|{|}_{\text{max}}+||\mathbf{H}{\mathbf{H}}^{\prime }-\mathbf{I}|{|}_{\text{max}}||\mathbf{F}|{|}_{\text{max}})).$$

Similarly $\mathbf{U}(\check{\mathbf{F}}{\check{\mathbf{F}}}^{\prime }-\mathbf{F}{\mathbf{F}}^{\prime })=\mathbf{U}(\check{\mathbf{F}}-\mathbf{F}\mathbf{H}){\check{\mathbf{F}}}^{\prime }+\mathbf{U}\mathbf{F}\mathbf{H}(\check{\mathbf{F}}-\mathbf{F}\mathbf{H}{)}^{\prime }+\mathbf{U}\mathbf{F}(\mathbf{H}{\mathbf{H}}^{\prime }-\mathbf{I}){\mathbf{F}}^{\prime }$, so

$$\left|\right|II|{|}_{\text{max}}=O_P(\left|\right|{\mathbf{U}}^{\prime }(\check{\mathbf{F}}-\mathbf{F}\mathbf{H})\left|{|}_{\text{max}}\right||\check{\mathbf{F}}/n|{|}_{\text{max}}+\left|\right|\mathbf{U}\mathbf{F}/n|{|}_{\text{max}}(\left|\right|\check{\mathbf{F}}-\mathbf{F}\mathbf{H}|{|}_{\text{max}}+||\mathbf{H}{\mathbf{H}}^{\prime }-\mathbf{I}|{|}_{\text{max}}\left|\right|\mathbf{F}|{|}_{\text{max}})).$$

According to Lemma F.4 (i), ||UF/n ||_max = O_P (1) and noting both ||F||_max and $||\check{\mathbf{F}}|{|}_{\text{max}}$ are $O_P(\sqrt{n})$, we conclude the result for ${\Vert \mathbf{\Pi }\Vert }_{\text{max}}$ easily.

Now we consider $\check{\mathbf{U}}{\check{\mathbf{U}}}^{\prime }$ in the following.

$$\begin{gathered} \begin{array}{l}\check{\mathbf{U}}{\check{\mathbf{U}}}^{\prime }=\mathbf{U}(\mathbf{I}-n^{-1}\mathbf{F}{\mathbf{F}}^{\prime }){\mathbf{U}}^{\prime }+n^{-1}\mathbf{U}(\mathbf{I}-n^{-1}\mathbf{F}{\mathbf{F}}^{\prime })(\check{\mathbf{F}}{\check{\mathbf{F}}}^{\prime }-\mathbf{F}{\mathbf{F}}^{\prime }){\mathbf{X}}^{\prime }+n^{-2}\mathbf{X}{(\check{\mathbf{F}}{\check{\mathbf{F}}}^{\prime }-\mathbf{F}{\mathbf{F}}^{\prime })}^2{\mathbf{X}}^{\prime }\\ \\ =:\mathbf{U}{\mathbf{U}}^{\prime }-\frac{1}{n}\mathbf{U}\mathbf{F}{\mathbf{F}}^{\prime }{\mathbf{U}}^{\prime }+III+IV.\end{array} \end{gathered}$$

So $\Delta =III+IV$ and it suffices to bound the two terms.

$$\begin{array}{l}\left|\right|III|{|}_{\text{max}}=O_P(\left|\right|n^{-1}\mathbf{U}(\mathbf{I}-\mathbf{F}{\mathbf{F}}^{\prime }/n)\check{\mathbf{F}}{\check{\mathbf{F}}}^{\prime }\mathbf{F}\left|{|}_{\text{max}}\right|\left|\mathbf{\Lambda }\right|{|}_{\text{max}}+\left|\right|n^{-1}\mathbf{U}(\mathbf{I}-\mathbf{F}{\mathbf{F}}^{\prime }/n)\check{\mathbf{F}}{\check{\mathbf{F}}}^{\prime }{\mathbf{U}}^{\prime }|{|}_{\text{max}})\\ =:O_P(|\left|{\mathbf{J}}_1\right|{|}_{\text{max}}\left|\right|\mathbf{\Lambda }|{|}_{\text{max}}+|\left|{\mathbf{J}}_2\right|{|}_{\text{max}}).\end{array}$$

Decompose J₁ by ${\mathbf{J}}_1=n^{-1}\mathbf{U}(\check{\mathbf{F}}-\mathbf{F}\mathbf{H}){\check{\mathbf{F}}}^{\prime }\mathbf{F}-n^{-2}\mathbf{U}\mathbf{F}\cdot {\mathbf{F}}^{\prime }(\check{\mathbf{F}}-\mathbf{F}\mathbf{H}){\check{\mathbf{F}}}^{\prime }\mathbf{F}$. Therefore,

$$\left|\right|{\mathbf{J}}_1|{|}_{\text{max}}=O_P(\left|\right|\mathbf{U}(\check{\mathbf{F}}-\mathbf{F}\mathbf{H})|{|}_{\text{max}}+n^{-1}|\left|\mathbf{U}\mathbf{F}\right|{|}_{\text{max}}\left|\right|{\mathbf{F}}^{\prime }(\check{\mathbf{F}}-\mathbf{F}\mathbf{H})|{|}_{\text{max}}),$$

since $||{\check{\mathbf{F}}}^{\prime }\mathbf{F}/n|{|}_{\text{max}}\le ||{\check{\mathbf{F}}}^{\prime }\mathbf{F}/n|{|}_F\le ||{\check{\mathbf{F}}}^{\prime }|{|}_F||\mathbf{F}|{|}_F/n=K$. Similar to J₁, we decompose J₂ only replacing ${\check{\mathbf{F}}}^{\prime }\mathbf{F}$ with ${\check{\mathbf{F}}}^{\prime }{\mathbf{U}}^{\prime }$. According to Lemma F.4 (i), $||{\check{\mathbf{F}}}^{\prime }{\mathbf{U}}^{\prime }/n|{|}_{\text{max}}=O_P(||\mathbf{U}\mathbf{F}/n|{|}_{\text{max}}+||\mathbf{U}(\check{\mathbf{F}}-\mathbf{F}\mathbf{H})|{|}_{\text{max}})=O_P(1+||\mathbf{U}(\check{\mathbf{F}}-\mathbf{F}\mathbf{H})|{|}_{\text{max}})$, hence ${\Vert {\mathbf{J}}_2\Vert }_{\text{max}}=O_P((||{\mathbf{J}}_1|{|}_{\text{max}}(1+||\mathbf{U}(\check{\mathbf{F}}-\mathbf{F}\mathbf{H}){||}_{\text{max}}))$. We then conclude that $||III|{|}_{\text{max}}=O_P((||\mathbf{U}(\check{\mathbf{F}}-\mathbf{F}\mathbf{H})|{|}_{\text{max}}+n^{-1}||\mathbf{U}\mathbf{F}|{|}_{\text{max}}||{\mathbf{F}}^{\prime }(\check{\mathbf{F}}-\mathbf{F}\mathbf{H})|{|}_{\text{max}})(||\mathbf{\Lambda }|{|}_{\text{max}}+||\mathbf{U}(\check{\mathbf{F}}-\mathbf{F}\mathbf{H})|{|}_{\text{max}}))$.

Now let us take a look at IV. ${\Vert IV\Vert }_{\text{max}}=||{\mathbf{D}}_1+{\mathbf{D}}_2+{\mathbf{D}}_2^{\prime }+{\mathbf{D}}_3|{|}_{\mathit{\text{max}}}$ where

$$\begin{array}{l}{\mathbf{D}}_1=n^{-2}\mathbf{\Lambda }{\mathbf{F}}^{\prime }{(\check{\mathbf{F}}{\check{\mathbf{F}}}^{\prime }-\text{F}{\mathbf{F}}^{\prime })}^2\mathbf{F}{\mathbf{\Lambda }}^{\prime }=\mathbf{\Lambda }(n\mathbf{I}-n^{-1}{\mathbf{F}}^{\prime }\check{\mathbf{F}}{\check{\mathbf{F}}}^{\prime }\mathbf{F}){\mathbf{\Lambda }}^{\prime },\\ {\mathbf{D}}_2=n^{-2}\mathbf{U}{(\check{\mathbf{F}}{\check{\mathbf{F}}}^{\prime }-\mathbf{F}{\mathbf{F}}^{\prime })}^2\mathbf{F}{\mathbf{\Lambda }}^{\prime }=-n^{-2}\mathbf{U}\mathbf{F}{\mathbf{F}}^{\prime }(\check{\mathbf{F}}{\check{\mathbf{F}}}^{\prime }-\mathbf{F}{\mathbf{F}}^{\prime })\mathbf{F}{\mathbf{\Lambda }}^{\prime }\\ {\mathbf{D}}_3=n^{-2}\mathbf{U}{(\check{\mathbf{F}}{\check{\mathbf{F}}}^{\prime }-\mathbf{F}{\mathbf{F}}^{\prime })}^2{\mathbf{U}}^{\prime }.\end{array}$$

By assumption, ||H||_max ≤ ||H|| = O_P (1). Simple decompositions of D₁ gives

$$\left|\right|{\mathbf{D}}_1|{|}_{\text{max}}=O_P((||{\mathbf{F}}^{\prime }(\check{\mathbf{F}}-\mathbf{F}\mathbf{H})|{|}_{\text{max}}+n\left|\right|\mathbf{H}{\mathbf{H}}^{\prime }-\mathbf{I}|{|}_{\text{max}})\left|\right|\mathbf{\Lambda }|{|}_{\text{max}}^2).$$

Since ${\mathbf{D}}_2=-n^{-2}\mathbf{U}\mathbf{F}{\mathbf{F}}^{\prime }(\check{\mathbf{F}}-\mathbf{F}\mathbf{H}){\check{\mathbf{F}}}^{\prime }\mathbf{F}{\mathbf{\Lambda }}^{\prime }-n^{-1}\mathbf{U}\mathbf{F}\mathbf{H}(\check{\mathbf{F}}-\mathbf{F}\mathbf{H}{)}^{\prime }\mathbf{F}{\mathbf{\Lambda }}^{\prime }-\mathbf{U}\mathbf{F}(\mathbf{H}{\mathbf{H}}^{\prime }-\mathbf{I}){\mathbf{\Lambda }}^{\prime }$, we have

$$\left|\right|{\mathbf{D}}_2|{|}_{\text{max}}=O_P(\left|\right|\mathbf{U}\mathbf{F}/n\left|{|}_{\text{max}}\right|\left|{\mathbf{D}}_1\right|{|}_{\text{max}})=O_P(\left|\right|{\mathbf{D}}_1|{|}_{\text{max}}).$$

It is also not hard to show ${‖{\mathbf{D}}_3‖}_{\max }=O_P\left({‖III‖}_{\max }+{‖{\mathbf{D}}_1‖}_{\max }\right).$ Under both Theorems C.1 and D.1 (replacing $\check{\mathbf{F}}$ by $\widehat{\mathbf{F}}$ for regime 1 and $\tilde{\mathbf{F}}$ for regime 2), we can check the following relationship holds:

$$n^{-1}\left|\right|{\text{UF}\left|\right|}_{\text{max}}\left|\right|\mathbf{U}(\check{\mathbf{F}}-\mathbf{F}\mathbf{H})|{|}_{\text{max}}=O_P(\left|\right|\mathbf{\Lambda }|{|}_{\text{max}}^2).$$

Therefore we have

$$\begin{array}{l}\left|\right|\Delta |{|}_{\text{max}}=||III+IV|{|}_{\text{max}}\\ =O_P(||\mathbf{U}(\check{\mathbf{F}}-\mathbf{F}\mathbf{H})|{|}_{\text{max}}\left|\right|\mathbf{\Lambda }|{|}_{\text{max}}+||\mathbf{U}(\check{\mathbf{F}}-\mathbf{F}\mathbf{H})|{|}_{\text{max}}^2\\ +\left|\right|{\mathbf{F}}^{\prime }(\check{\mathbf{F}}-\mathbf{F}\mathbf{H})\left|{|}_{\text{max}}\right|\left|\mathbf{\Lambda }\right|{|}_{\text{max}}^2+n\left|\right|\mathbf{H}{\mathbf{H}}^{\prime }-\mathbf{I}\left|{|}_{\text{max}}\right|\left|\mathbf{\Lambda }\right|{|}_{\text{max}}^2).\end{array}$$

□

Appendix C: Proof of Theorem 3.1

Recall that PCA estimates F by $\widehat{\mathbf{F}}$ where the k^th column of $\widehat{\mathbf{F}}/\sqrt{n}$ is the eigenvector of ${(pn)}^{-1}{\mathbf{X}}^{\prime }X$ corresponding to the k^th largest eigenvalue. By the definition of $\widehat{\mathbf{F}}$, we have

$$\frac{1}{np}{\mathbf{X}}^{\prime }\mathbf{X}\widehat{\mathbf{F}}=\widehat{\mathbf{F}}\mathbf{K},$$

where K is a K by K diagonal matrix with top K eigenvalues of ${(np)}^{-1}{\mathbf{X}}^{\prime }\mathbf{X}$ in descending order as diagonal elements. Define a K by K matrix H as in [17]:

$$\mathbf{H}=\frac{1}{np}{\mathbf{\Lambda }}^{\prime }\mathbf{\Lambda }{\mathbf{F}}^{\prime }\widehat{\mathbf{F}}{\mathbf{K}}^{-1}.$$

It has been shown that $‖\mathbf{K}‖,\hspace{0.17em}‖{\mathbf{K}}^{-1}‖\hspace{0.17em}\text{and}\hspace{0.17em}‖\mathbf{H}‖,\hspace{0.17em}‖{\mathbf{H}}^{-1}‖$ are all O_P(1).

The following lemma provides all the rates of convergences that are needed for downstream analysis.

Lemma C.1. Under Assumptions 2.1 and 2.2, we have $||\mathbf{\Lambda }|{|}_{\text{max}}=O_P(\sqrt{\log \hspace{0.17em}p})$ and

(i) $||\widehat{\mathbf{F}}-\mathbf{F}\mathbf{H}|{|}_F=O_P(\sqrt{n/p}+1/\sqrt{n})$ and $||\widehat{\mathbf{F}}-\mathbf{F}\mathbf{H}|{|}_{\text{max}}=O_P(\sqrt{\log \hspace{0.17em}n/p}+\sqrt{\log \hspace{0.17em}n}/n)$;

(ii) $||{\mathbf{F}}^{\prime }(\widehat{\mathbf{F}}-\mathbf{F}\mathbf{H})|{|}_{\text{max}}=O_P(1+\sqrt{n/p})$;

(iii) $||\mathbf{U}(\widehat{\mathbf{F}}-\mathbf{F}\mathbf{H})|{|}_{\text{max}}=O_P((1+n/p)\sqrt{\log \hspace{0.17em}p}+n||\mathbf{\Sigma }|{|}_1/p)$;

(iv) $||\mathbf{H}{\mathbf{H}}^{\prime }-\mathbf{I}|{|}_{\text{max}}=O_P(1/n+1/p)$.

Combining the above results with Lemma B.1, we have

$$\widehat{\mathbf{U}}-\mathbf{U}=-\frac{1}{n}\mathbf{U}\mathbf{F}{\mathbf{F}}^{\prime }+\mathbf{\Pi },$$

where $||\mathbf{\Pi }|{|}_{\text{max}}=O_P(\sqrt{\log \hspace{0.17em}n\log \hspace{0.17em}p}(1/\sqrt{p}+1/n)+\sqrt{\log \hspace{0.17em}n}||\mathbf{\Sigma }|{|}_1/p)$ and additionally

$$\widehat{\mathbf{U}}{\widehat{\mathbf{U}}}^{\prime }-\mathbf{U}{\mathbf{U}}^{\prime }=-\frac{1}{n}\mathbf{U}\mathbf{F}{\mathbf{F}}^{\prime }{\mathbf{U}}^{\prime }+\Delta ,$$

where $||\Delta |{|}_{\text{max}}=O_P((1+n/P)\log \hspace{0.17em}p+n^2||\mathbf{\Sigma }|{|}_1^2/p^2)$. Thus we complete the proof for Theorem 3.1. We are left to check Lemma C.1, which is done in the following three subsections.

C.1. Convergence of factors $\widehat{\mathbf{F}}$

Recall $\mathbf{H}={(np)}^{-1}{\mathbf{\Lambda }}^{\prime }\mathbf{\Lambda }{\mathbf{F}}^{\prime }\widehat{\mathbf{F}}{\mathbf{K}}^{-1}$. Substituting $\mathbf{X}=\mathbf{\Lambda }{\mathbf{F}}^{\prime }+\mathbf{U}$, we have,

$$\begin{array}{l}\widehat{\mathbf{F}}-\mathbf{F}\mathbf{H}=(\sum _{i=1}^3{\mathbf{E}}_i){\mathbf{K}}^{-1},\\ {\mathbf{{\rm E}}}_1=\frac{1}{np}\mathbf{F}{\mathbf{\Lambda }}^{\prime }\mathbf{U}\widehat{\mathbf{F}},\hspace{0.17em}{\mathbf{{\rm E}}}_2=\frac{1}{np}{\mathbf{U}}^{\prime }\mathbf{\Lambda }{\mathbf{F}}^{\prime }\widehat{\mathbf{F}},\hspace{0.17em}{\mathbf{{\rm E}}}_3=\frac{1}{np}{\mathbf{U}}^{\prime }\mathbf{U}\widehat{\mathbf{F}}.\end{array}$$ (C.1)

To bound $||\widehat{\mathbf{F}}-\mathbf{F}\mathbf{H}|{|}_{\text{max}}$, note that there is a constant C > 0, so that

$$\left|\right|\widehat{\mathbf{F}}-\mathbf{F}\mathbf{H}|{|}_{\text{max}}\le C|\left|{\mathbf{K}}^{-1}\right|{|}_2\sum _{i=1}^3\left|\right|{\mathbf{E}}_i|{|}_{\text{max}}.$$

Hence we need to bound $||{\mathbf{E}}_i|{|}_{\text{max}}\hspace{0.17em}\text{for}\hspace{0.17em}i=1,2,3$ since $||{\mathbf{K}}^{-1}|{|}_2=O_P(1)$. The following lemma gives the stochastic bounds for each individual term.

Lemma C.2. (i) ${\Vert {\mathbf{E}}_1\Vert }_F=O_P(\sqrt{n/p})={\Vert {\mathbf{E}}_2\Vert }_F$, ${\Vert {\mathbf{E}}_3\Vert }_F=O_P(1/\sqrt{n}+1/\sqrt{p}+\sqrt{n}/p).$

(ii) ${\Vert {\mathbf{E}}_1\Vert }_{\text{max}}=O_P(\sqrt{\log n/p})={\Vert {\mathbf{E}}_2\Vert }_{\text{max}}$,${\Vert {\mathbf{E}}_3\Vert }_{\text{max}}=O_P(1/\sqrt{p}+\sqrt{\log \hspace{0.17em}n}/n).$

Proof. (i) Obviously ${\Vert {\mathbf{E}}_1\Vert }_F\le p^{-1}{\Vert {\mathbf{\Lambda }}^{\prime }\mathbf{U}\Vert }_F=O_P(\sqrt{n/p})$ according to Lemma F.1. ${\Vert {\mathbf{E}}_2\Vert }_F$ attains the same rate. In addition, ${\Vert {\mathbf{E}}_3\Vert }_F\le n^{-1/2}{p}^{-1}{\Vert {\mathbf{U}}^{\prime }\mathbf{U}\Vert }_F=O_P(1+\sqrt{n/p})$ again according to Lemma F.1. So combining the three terms, we have ${\Vert \widehat{\mathbf{F}}-\mathbf{F}\mathbf{H}\Vert }_F=O_P(1+\sqrt{n/p}).$ We now refine the bound for ${\Vert {\mathbf{E}}_3\Vert }_{F\cdot }{\Vert {\mathbf{E}}_3\Vert }_F\le {(np)}^{-1}({\Vert {\mathbf{U}}^{\prime }\mathbf{U}\mathbf{F}\Vert }_F{\Vert \mathbf{H}\Vert }_F+{\Vert {\mathbf{U}}^{\prime }\mathbf{U}\Vert }_F{\Vert \widehat{\mathbf{F}}-\mathbf{F}\mathbf{H}\Vert }_F)=O_P(1/\sqrt{n}+1/\sqrt{p}+\sqrt{n}/p).$ Then the refined rate of ${\Vert \widehat{\mathbf{F}}-\mathbf{F}\mathbf{H}\Vert }_F$ is $O_P(\sqrt{n/p}+1/\sqrt{n}).$

(ii) Since ${\Vert {\mathbf{\Lambda }}^{\prime }\mathbf{U}\widehat{\mathbf{F}}\Vert }_F=O_P(n\sqrt{p})$ by Lemma F.1,

$${\Vert {\mathbf{E}}_1\Vert }_{\text{max}}=O_P({(np)}^{-1}{\Vert \mathbf{F}\Vert }_{\text{max}}{\Vert {\mathbf{\Lambda }}^{\prime }\mathbf{U}\widehat{\mathbf{F}}\Vert }_F)=O_P(\sqrt{\log n/p}).$$

${\Vert {\mathbf{E}}_2\Vert }_{\text{max}}$ is bounded by $p^{-1}{\Vert {\mathbf{U}}^{\prime }\Lambda \Vert }_{\text{max}}=O_P(\sqrt{\log n/p})$ while ${\Vert {\mathbf{E}}_3\Vert }_{\text{max}}$ is bounded by

$$O_P({(np)}^{-1}({\Vert {\mathbf{U}}^{\prime }\mathbf{U}\mathbf{F}\Vert }_{\text{max}}+\sqrt{n}{\Vert {\mathbf{U}}^{\prime }\mathbf{U}\Vert }_{\text{max}}{\Vert \widehat{\mathbf{F}}-\mathbf{F}\mathbf{H}\Vert }_F)),$$

which based on results of Lemma F.2 and (i) is $O_P(1/\sqrt{p}+\sqrt{\log \hspace{0.17em}n}/n).$ □

The final rate of convergence for ${\Vert \widehat{\mathbf{F}}-\mathbf{F}\mathbf{H}\Vert }_{\text{max}}$ and ${\Vert \widehat{\mathbf{F}}-\mathbf{F}\mathbf{H}\Vert }_F$ are summarized as follows.

Proposition C.1.

$${\Vert \widehat{\mathbf{F}}-\mathbf{F}\mathbf{H}\Vert }_{\text{max}}=O_P(\sqrt{\frac{\log \hspace{0.17em}n}{p}}+\frac{\sqrt{\log \hspace{0.17em}n}}{n})\hspace{0.17em}and\hspace{0.17em}{\Vert \widehat{\mathbf{F}}-\mathbf{F}\mathbf{H}\Vert }_F=O_P(\sqrt{\frac{n}{p}}+\frac{1}{\sqrt{n}}).$$ (C.2)

Proof. The results follow from Lemmas C.2. □

C.2. Rates of ${\Vert {\mathbf{F}}^{\prime }(\widehat{\mathbf{F}}-\mathbf{F}\mathbf{H})\Vert }_{\text{max}}$ and ${\Vert \mathbf{H}{\mathbf{H}}^{\prime }-\mathbf{I}\Vert }_{\text{max}}$

Note first that the two matrices under consideration is both K by K, so we do not lose rates bounding them by their Frobenius norm.

Let us find out rate for ${\Vert {\mathbf{F}}^{\prime }(\widehat{\mathbf{F}}-\mathbf{F}\mathbf{H})\Vert }_F$. Basically we need to bound ${\Vert {\mathbf{F}}^{\prime }{\mathbf{E}}_i\Vert }_F$ for i = 1, 2, 3. Firstly

$${\Vert {\mathbf{F}}^{\prime }{\mathbf{E}}_1\Vert }_F=p^{-1}{\Vert {\mathbf{\Lambda }}^{\prime }\mathbf{U}\widehat{\mathbf{F}}\Vert }_F\le p^{-1}({\Vert {\mathbf{\Lambda }}^{\prime }\mathbf{U}\mathbf{F}\Vert }_F{\Vert \mathbf{H}\Vert }_F+\hspace{0.17em}\hspace{0.17em}{\Vert {\mathbf{\Lambda }}^{\prime }\mathbf{U}\Vert }_F{\Vert \widehat{\mathbf{F}}-\mathbf{F}\mathbf{H}\Vert }_F).$$

Since ${\Vert {\mathbf{\Lambda }}^{\prime }\mathbf{U}\mathbf{F}\Vert }_F=O_P(\sqrt{np})$ and ${\Vert {\mathbf{\Lambda }}^{\prime }\mathbf{U}\Vert }_F=O_P(\sqrt{np})$ by Lemma F.1, we have ${\Vert {\mathbf{F}}^{\prime }{\mathbf{E}}_1\Vert }_F=O_P(\sqrt{n/p}+n/p).$ Secondly,

$${\Vert {\mathbf{F}}^{\prime }{\mathbf{E}}_2\Vert }_F\le p^{-1}{\Vert {\mathbf{F}}^{\prime }{\mathbf{U}}^{\prime }\mathbf{\Lambda }\Vert }_F=O_P(\sqrt{n/p}).$$

Finally,

$${\Vert {\mathbf{F}}^{\prime }{\mathbf{E}}_3\Vert }_F=O_P(\frac{1}{np}{\Vert \mathbf{U}\mathbf{F}\Vert }_F^2+\frac{1}{np}{\Vert {\mathbf{F}}^{\prime }{\mathbf{U}}^{\prime }\mathbf{U}\Vert }_F{\Vert \widehat{\mathbf{F}}-\mathbf{F}\mathbf{H}\Vert }_F)=O_P(1+\sqrt{n}/p).$$

So combining three terms we have ${\Vert {\mathbf{F}}^{\prime }(\widehat{\mathbf{F}}-\mathbf{F}\mathbf{H})\Vert }_{\text{max}}\le {\Vert {\mathbf{F}}^{\prime }(\widehat{\mathbf{F}}-\mathbf{F}\mathbf{H})\Vert }_F=O_P(1+\sqrt{n/p}).$

Now we bound ${\Vert \mathbf{H}{\mathbf{H}}^{\prime }-\mathbf{I}\Vert }_F$. Since ${\mathbf{H}}^{\prime }\mathbf{H}=n^{-1}{(\mathbf{F}\mathbf{H}-\widehat{\mathbf{F}})}^{\prime }\mathbf{F}\mathbf{H}+n^{-1}{\widehat{\mathbf{F}}}^{\prime }(\mathbf{F}\mathbf{H}-\widehat{\mathbf{F}})+\mathbf{I}$, we have

$${\Vert {\mathbf{H}}^{\prime }\mathbf{H}-\mathbf{I}\Vert }_F=O_P(\frac{1}{n}{\Vert {\mathbf{F}}^{\prime }(\widehat{\mathbf{F}}-\mathbf{F}\mathbf{H})\Vert }_F+\frac{1}{n}{\Vert \widehat{\mathbf{F}}-\mathbf{F}\mathbf{H}\Vert }_F^2)=O_P(\frac{1}{n}+\frac{1}{p}).$$

Therefore ${\Vert \mathbf{H}{\mathbf{H}}^{\prime }-\mathbf{I}\Vert }_F$ has the same rate since ${\Vert \mathbf{H}{\mathbf{H}}^{\prime }-\mathbf{I}\Vert }_F\le {\Vert \mathbf{H}\Vert }_F{\Vert {\mathbf{H}}^{\prime }\mathbf{H}-\mathbf{I}\Vert }_F{\Vert {\mathbf{H}}^{-1}\Vert }_F$. So ${\Vert \mathbf{H}{\mathbf{H}}^{\prime }-\mathbf{I}\Vert }_{\text{max}}=O_P(1/n+1/p).$

C.3. Rate of ${\Vert \mathbf{U}(\widehat{\mathbf{F}}-\mathbf{F}\mathbf{H})\Vert }_{\text{max}}$

In order to study rate of ${\Vert \mathbf{U}(\widehat{\mathbf{F}}-\mathbf{F}\mathbf{H})\Vert }_{\text{max}}$,we essentially need to bound ${\Vert \mathbf{U}{\mathbf{E}}_i\Vert }_{\text{max}}$ for i = 1, 2, 3. We handle each term separately.

$$\begin{array}{l}{\Vert \mathbf{U}{\mathbf{E}}_1\Vert }_{\text{max}}=O_P(\frac{1}{np}{\Vert \mathbf{U}\mathbf{F}\Vert }_{\text{max}}{\Vert {\mathbf{\Lambda }}^{\prime }\mathbf{U}\widehat{\mathbf{F}}\Vert }_F)=O_P(\frac{1}{n}{\Vert \mathbf{U}\mathbf{F}\Vert }_{\text{max}}{\Vert {\mathbf{F}}^{\prime }{\mathbf{E}}_1\Vert }_F)\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}=O_P(\sqrt{\frac{\log \hspace{0.17em}p}{p}}+\frac{\sqrt{n\log \hspace{0.17em}p}}{p}).\end{array}$$

By Lemma F.5, ${\Vert \mathbf{U}{\mathbf{U}}^{\prime }\mathbf{\Lambda }\Vert }_{\text{max}}=O_P(\sqrt{np\log \hspace{0.17em}p}+n{\Vert \sum \Vert }_1).$ Therefore,

$${\Vert \mathbf{U}{\mathbf{E}}_2\Vert }_{\text{max}}=O_P(\frac{1}{p}{\Vert \mathbf{U}{\mathbf{U}}^{\prime }\mathbf{\Lambda }\Vert }_{\text{max}})=O_P(\frac{n{\Vert \sum \Vert }_1}{p}+\sqrt{\frac{n\log \hspace{0.17em}p}{p}}).$$

From bounding ${\Vert {\mathbf{E}}_3\Vert }_F$, the last term has rate

$$\begin{array}{l}{\Vert \mathbf{U}{\mathbf{E}}_3\Vert }_{\text{max}}=\frac{1}{np}{\Vert \mathbf{U}{\mathbf{U}}^{\prime }\mathbf{U}\widehat{\mathbf{F}}\Vert }_{\text{max}}\le \frac{1}{\sqrt{np}}{\Vert \mathbf{U}\Vert }_{\text{max}}{\Vert {\mathbf{U}}^{\prime }\mathbf{U}\widehat{\mathbf{F}}\Vert }_F\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}=O_P((1+n/p)\sqrt{\log \hspace{0.17em}p}).\end{array}$$

So combining three terms, we conclude ${\Vert \mathbf{U}(\widehat{\mathbf{F}}-\mathbf{F}\mathbf{H})\Vert }_{\text{max}}=O_P((1+n/p)\sqrt{\log \hspace{0.17em}p}+n{\Vert \sum \Vert }_1/p).$

Appendix D: Proof of Theorem 3.2

Recall that by the definition of $\tilde{\mathbf{F}}$, we have

$$\frac{1}{np}{\mathbf{X}}^{\prime }\mathbf{P}\mathbf{X}\tilde{\mathbf{F}}=\tilde{\mathbf{F}}\mathbf{K},$$

where K is a K × K diagonal matrix with the first K largest eigenvalues of ${(np)}^{-1}{\mathbf{X}}^{\prime }\mathbf{P}\mathbf{X}$ in descending order as its diagonal elements. Define the K by K matrix H as in [18]:

$$\mathbf{H}=\frac{1}{np}{\mathbf{B}}^{\prime }\Phi {(\mathbf{W})}^{\prime }\Phi (\mathbf{W})\mathbf{B}{\mathbf{F}}^{\prime }\tilde{\mathbf{F}}{\mathbf{K}}^{-1}.$$

It has been shown that $\Vert \mathbf{K}\Vert$, $\Vert {\mathbf{K}}^{-1}\Vert$ and $\Vert \mathbf{H}\Vert$, $\Vert {\mathbf{H}}^{-1}\Vert$ are all O_P(1). Here we remind that though H and K are different from those in regime 1 defined in the previous section, they play essentially the same roles (thus with same notations).

The following lemma provides all the rates of convergences that are needed for downstream analysis.

Lemma D.1. Choose $J={(p\min \left\{n,p,{\nu }_p^{-1}\right\})}^{1/k}$ and assume $J^2{\varphi }_{\text{max}}^2\log (nJ)=O(p)$ where ${\varphi }_{\text{max}}={\text{max}}_{\nu \le J}{\sup }_{x\in X}{\varphi }_{\nu }(x).$ Under Assumptions 2.1, 2.3, 2.4 and 3.1, we have ${\Vert \mathbf{\Lambda }\Vert }_{\text{max}}=O_P(J{\varphi }_{\text{max}}+\sqrt{\log \hspace{0.17em}p})$ and

(i) ${\Vert \tilde{\mathbf{F}}-\mathbf{F}\mathbf{H}\Vert }_F=O_P(\sqrt{n/p})$ and ${\Vert \tilde{\mathbf{F}}-\mathbf{F}\mathbf{H}\Vert }_{\text{max}}=O_P(\sqrt{\log \hspace{0.17em}n/p});$

(ii) ${\Vert {\mathbf{F}}^{\prime }(\tilde{\mathbf{F}}-\mathbf{F}\mathbf{H})\Vert }_{\text{max}}=O_P(\sqrt{n/p}+n/p+n\sqrt{{\nu }_p/p});$

(iii) ${\Vert \mathbf{U}(\tilde{\mathbf{F}}-\mathbf{F}\mathbf{H})\Vert }_{\text{max}}=O_P(\sqrt{n\log p/p}+nJ{\varphi }_{\text{max}}{\Vert \sum \Vert }_1/p);$

(iv) ${\Vert \mathbf{H}{\mathbf{H}}^{\prime }-\mathbf{I}\Vert }_{\text{max}}=O_P(1/p+1/\sqrt{pn}+\sqrt{{\nu }_p/p}).$

Combining the above lemma with Lemma B.1, we obtain

$$\tilde{\mathbf{U}}-\mathbf{U}=-\frac{1}{n}\mathbf{U}\mathbf{F}{\mathbf{F}}^{\prime }+\mathbf{\Pi },$$

where ${\Vert \mathbf{\Pi }\Vert }_{\text{max}}=O_P(\sqrt{\log \hspace{0.17em}n/p}(J{\varphi }_{\text{max}}+\sqrt{\log \hspace{0.17em}p})+J{\varphi }_{\text{max}}{\Vert \mathbf{\Sigma }\Vert }_1\sqrt{\log n/p})$ and

$$\tilde{\mathbf{U}}{\tilde{\mathbf{U}}}^{\prime }-\mathbf{U}{\mathbf{U}}^{\prime }=-\frac{1}{n}\mathbf{U}\mathbf{F}{\mathbf{F}}^{\prime }{\mathbf{U}}^{\prime }+\mathbf{\Delta },$$

where ${\Vert \mathbf{\Delta }\Vert }_{\text{max}}=O_P(n\sqrt{{\nu }_p/p}(J^2{\varphi }_{\text{max}}^2+\log \hspace{0.17em}p)+nJ{\varphi }_{\text{max}}{\Vert \mathbf{\Sigma }\Vert }_1(J{\varphi }_{\text{max}}+\sqrt{\log \hspace{0.17em}p})/p+n^2{J}^2{\varphi }_{\text{max}}^2{\Vert \mathbf{\Sigma }\Vert }_1^2/p^2)$ if there exists C s.t. ν_p > C/n. We choose to keep ${\Vert \mathbf{\Sigma }\Vert }_1$ terms here although it makes a long presentation of the rate.

Thus we complete the proof for Theorem 3.2. We are left to check Lemma D.1, which is done in the following three subsections.

D.1. Convergence of factors $\tilde{\mathbf{F}}$

Recall $\mathbf{H}={(np)}^{-1}{\mathbf{B}}^{\prime }\Phi {(\mathbf{W})}^{\prime }\Phi (\mathbf{W})\mathbf{B}{\mathbf{F}}^{\prime }\tilde{\mathbf{F}}{\mathbf{K}}^{-1}$. Substituting $\mathbf{X}=\Phi (\mathbf{W})\mathbf{B}{\mathbf{F}}^{\prime }+\mathbf{R}(\mathbf{W}){\mathbf{F}}^{\prime }+\mathbf{\Gamma }{\mathbf{F}}^{\prime }+\mathbf{U}$, we have,

$$\tilde{\mathbf{F}}-\mathbf{F}\mathbf{H}=(\sum _{i=1}^{15}{\mathbf{A}}_j){\mathbf{K}}^{-1}$$ (D.1)

where A_i,i ≤ 3 has nothing to do with R(W) and Γ:

$${\mathbf{A}}_1=\frac{1}{np}\mathbf{F}{\mathbf{B}}^{\prime }\Phi {(\mathbf{W})}^{\prime }\mathbf{U}\tilde{\mathbf{F}},\hspace{0.17em}{\mathbf{A}}_2=\frac{1}{np}{\mathbf{U}}^{\prime }\Phi (\mathbf{W})\mathbf{B}{\mathbf{F}}^{\prime }\tilde{\mathbf{F}},\hspace{0.17em}{\mathbf{A}}_3=\frac{1}{np}{\mathbf{U}}^{\prime }\mathbf{P}\mathbf{U}\tilde{\mathbf{F}};$$

A_i, 3 ≤ i ≤ 8 takes care of terms involving R(W):

$$\begin{array}{l}{\mathbf{A}}_4=\frac{1}{np}\mathbf{F}{\mathbf{B}}^{\prime }\Phi {(\mathbf{W})}^{\prime }\mathbf{R}(\mathbf{W}){\mathbf{F}}^{\prime }\tilde{\mathbf{F}},\hspace{0.17em}{\mathbf{A}}_5=\frac{1}{np}\mathbf{F}\mathbf{R}{\left(\mathbf{W}\right)}^{\prime }\Phi (\mathbf{W})\mathbf{B}{\mathbf{F}}^{\prime }\tilde{\mathbf{F}},\\ {\mathbf{A}}_6=\frac{1}{np}\mathbf{F}\mathbf{R}{(\mathbf{W})}^{\prime }\mathbf{P}\mathbf{R}(\mathbf{W}){\mathbf{F}}^{\prime }\tilde{\mathbf{F}},\hspace{0.17em}{\mathbf{A}}_{\text{7}}\text{=}\frac{\text{1}}{np}\mathbf{F}\mathbf{R}\text{(}\mathbf{W}{)}^{\prime }\mathbf{P}\mathbf{U}\tilde{\mathbf{F}}\text{,}\\ {\mathbf{A}}_8=\frac{1}{np}{\mathbf{U}}^{\prime }\mathbf{P}\mathbf{R}(\mathbf{W}){\mathbf{F}}^{\prime }\tilde{\mathbf{F}};\end{array}$$

the remaining are terms involving Γ:

$$\begin{array}{l}{\mathbf{A}}_9=\frac{1}{np}\mathbf{F}{\mathbf{B}}^{\prime }\Phi {(\mathbf{W})}^{\prime }\mathbf{\Gamma }{\mathbf{F}}^{\prime }\tilde{\mathbf{F}},\hspace{0.17em}{\mathbf{A}}_{10}\text{=}\frac{\text{1}}{np}\mathbf{F}{\mathbf{\Gamma }}^{\prime }\mathbf{\Phi }(\mathbf{W})\mathbf{B}{\mathbf{F}}^{\prime }\tilde{\mathbf{F}}\text{,}\\ {\mathbf{A}}_{11}=\frac{1}{np}\mathbf{F}{\mathbf{\Gamma }}^{\prime }\mathbf{P}\mathbf{\Gamma }{\mathbf{F}}^{\prime }\tilde{\mathbf{F}},\hspace{0.17em}{\mathbf{A}}_{12}\text{=}\frac{\text{1}}{np}\mathbf{F}{\mathbf{\Gamma }}^{\prime }\mathbf{P}\mathbf{U}\tilde{\mathbf{F}}\text{,}\\ {\mathbf{A}}_{13}=\frac{1}{np}{\mathbf{U}}^{\prime }\mathbf{P}\mathbf{\Gamma }{\mathbf{F}}^{\prime }\tilde{\mathbf{F}},\hspace{0.17em}{\mathbf{A}}_{14}\text{=}\frac{\text{1}}{np}\mathbf{F}{\mathbf{R}}^{\prime }\mathbf{P}\mathbf{\Gamma }{\mathbf{F}}^{\prime }\tilde{\mathbf{F}}\text{,}\hspace{0.17em}{\mathbf{A}}_{15}\text{=}\frac{\text{1}}{np}\mathbf{F}{\mathbf{\Gamma }}^{\prime }\mathbf{P}\mathbf{R}{\mathbf{F}}^{\prime }\tilde{\mathbf{F}}.\end{array}$$

To bound ${\Vert \tilde{\mathbf{F}}-\mathbf{F}\mathbf{H}\Vert }_{\text{max}}$, as in Theorem C.1 we only need to bound ${\Vert {\mathbf{A}}_i\Vert }_{\text{max}}$ for i = 1,…,15 since again we have ${\Vert {\mathbf{K}}^{-1}\Vert }_2=O_P(1).$ The following lemma gives the rate for each term.

Lemma D.2. (i) ${\Vert {\mathbf{A}}_1\Vert }_{\text{max}}=O_P(\sqrt{\log n/p})={\Vert {\mathbf{A}}_2\Vert }_{\text{max}}$,

(ii) ${\Vert {\mathbf{A}}_3\Vert }_{\text{max}}=O_P(J{\varphi }_{\text{max}}\sqrt{\log (nJ)}/p)$,

(iii) ${\Vert {\mathbf{A}}_4\Vert }_{\text{max}}=O_P(J^{-k/2}\sqrt{\log \hspace{0.17em}n})={\Vert {\mathbf{A}}_5\Vert }_{\text{max}}$ and ${\Vert {\mathbf{A}}_9\Vert }_{\text{max}}=O_P(\sqrt{{\nu }_p\log n/p})={\Vert {\mathbf{A}}_{10}\Vert }_{\text{max}}$,

(iv) ${\Vert {\mathbf{A}}_6\Vert }_{\text{max}}=O_P(J^{-k}\sqrt{\log \hspace{0.17em}n})$ and ${\Vert {\mathbf{A}}_{11}\Vert }_{\text{max}}=O_P(J{\nu }_p\sqrt{\log \hspace{0.17em}n}/p)$,

(v) ${\Vert {\mathbf{A}}_7\Vert }_{\text{max}}=O_P({\varphi }_{\text{max}}\sqrt{p^{-1}{J}^{1-k}\log (nJ)\log \hspace{0.17em}n})={\Vert {\mathbf{A}}_8\Vert }_{\text{max}}$ and ${\Vert {\mathbf{A}}_{12}\Vert }_{\text{max}}=O_P(J{\varphi }_{\text{max}}\sqrt{{\nu }_p\log (nJ)\log n/p})={\Vert {\mathbf{A}}_{13}\Vert }_{\text{max}}$,

(vi) ${\Vert {\mathbf{A}}_{14}\Vert }_{\text{max}}=O_P(\sqrt{p^{-1}{J}^{1-k}{\nu }_p\log \hspace{0.17em}n})={\Vert {\mathbf{A}}_{15}\Vert }_{\text{max}}.$

Proof. (i) Because ${\Vert \mathbf{F}\Vert }_{\text{max}}=O_P(\sqrt{\log \hspace{0.17em}n})$, ${\Vert \tilde{\mathbf{F}}\Vert }_F=O_P(\sqrt{n}).$ By Lemma F.3 and F.4, ${\Vert {\mathbf{U}}^{\prime }\Phi (\mathbf{W})\mathbf{B}\Vert }_F=O_P(\sqrt{pn})$ and ${\Vert {\mathbf{U}}^{\prime }\Phi (\mathbf{W})\mathbf{B}\Vert }_{\text{max}}=O_P(\sqrt{p\log \hspace{0.17em}n}).$

Hence

$$\begin{array}{l}{\Vert {\mathbf{A}}_1\Vert }_{\text{max}}\le \frac{\sqrt{K}}{np}{\Vert \mathbf{F}\Vert }_{\text{max}}{\Vert {\mathbf{B}}^{\prime }\Phi {(\mathbf{W})}^{\prime }\mathbf{U}\Vert }_F{\Vert \tilde{\mathbf{F}}\Vert }_F=O_P(\sqrt{\log \hspace{0.17em}n/p}),\\ {\Vert {\mathbf{A}}_2\Vert }_{\text{max}}\le \frac{\sqrt{K}}{np}{\Vert {\mathbf{U}}^{\prime }\Phi (\mathbf{W})\mathbf{B}\Vert }_{\text{max}}{\Vert \mathbf{F}\Vert }_F{\Vert \tilde{\mathbf{F}}\Vert }_F=O_P(\sqrt{\log \hspace{0.17em}n/p}).\end{array}$$

(ii) We have ${\mathbf{A}}_3=\frac{1}{np}{\mathbf{U}}^{\prime }\Phi (\mathbf{W}){(\Phi {(\mathbf{W})}^{\prime }\Phi (\mathbf{W}))}^{-1}\Phi {(\mathbf{W})}^{\prime }\mathbf{U}\tilde{\mathbf{F}}.$ By Lemma F.3 and F.4, ${\Vert {\mathbf{U}}^{\prime }\Phi (\mathbf{W})\Vert }_F=O_P(\sqrt{npJ})$ and ${\Vert {\mathbf{U}}^{\prime }\Phi (\mathbf{W})\Vert }_{\text{max}}=O_P({\varphi }_{\text{max}}\sqrt{p\log (nJ)}).$ By Assumption 3.1, ${\Vert {(\Phi {(\mathbf{W})}^{\prime }\Phi (\mathbf{W}))}^{-1}\Vert }_2=O_P(p^{-1}).$ Note the fact that for matrix ${\mathbf{A}}_{m\times n}$, ${\mathbf{B}}_{n\times n}$, ${\mathbf{C}}_{n\times r}$,${\Vert \mathbf{A}\mathbf{B}\mathbf{C}\Vert }_{\text{max}}={\text{max}}_{i\le m,k\le r}|{\mathbf{a}}_i^{\prime }\mathbf{B}{\mathbf{c}}_k|\le \sqrt{n}{\Vert \mathbf{A}\Vert }_{\text{max}}{\Vert \mathbf{B}\Vert }_2{\Vert \mathbf{C}\Vert }_F$. So

$$\begin{array}{l}{\Vert {\mathbf{A}}_3\Vert }_{\text{max}}\le \frac{\sqrt{Jd}}{np}{\Vert {\mathbf{U}}^{\prime }\Phi (\mathbf{W})\Vert }_{\text{max}}{\Vert {(\Phi {(\mathbf{W})}^{\prime }\Phi (\mathbf{W}))}^{-1}\Vert }_2{\Vert \Phi {(\mathbf{W})}^{\prime }\mathbf{U}\Vert }_F{\Vert \tilde{\mathbf{F}}\Vert }_F\\ =O_P(J{\varphi }_{\text{max}}\sqrt{\log (nJ)}/p).\end{array}$$

(iii) Note that ${\Vert \Phi (\mathbf{W})\mathbf{B}\Vert }_2\le {\Vert \mathbf{G}(\mathbf{W})\Vert }_2+{\Vert \mathbf{R}(\mathbf{W})\Vert }_2=O_P(\sqrt{p})$, and ${\Vert \mathbf{R}(\mathbf{W})\Vert }_{\text{max}}=O_P(J^{-k/2}).$ Hence we have ${\Vert {\mathbf{B}}^{\prime }\Phi {(\mathbf{W})}^{\prime }\mathbf{R}(\mathbf{W})\Vert }_{\text{max}}\le {\Vert {\mathbf{B}}^{\prime }\Phi {(\mathbf{W})}^{\prime }\Vert }_1{\Vert \mathbf{R}(\mathbf{W})\Vert }_{\text{max}}\le \sqrt{p}{\Vert {\mathbf{B}}^{\prime }\Phi {(\mathbf{W})}^{\prime }\Vert }_2{\Vert \mathbf{R}(\mathbf{W})\Vert }_{\text{max}}=O_P(p{J}^{-k/2}).$ Thus

$${\Vert {\mathbf{A}}_4\Vert }_{\text{max}}\le \frac{K^{3/2}}{np}{\Vert \mathbf{F}\Vert }_{\text{max}}{\Vert {\mathbf{B}}^{\prime }\Phi {(\mathbf{W})}^{\prime }\mathbf{R}(\mathbf{W})\Vert }_{\text{max}}{\Vert \mathbf{F}\tilde{\mathbf{F}}\Vert }_F=O_P(J^{-k/2}\sqrt{\log \hspace{0.17em}n}).$$

Similarly, ${\Vert {\mathbf{A}}_5\Vert }_{\text{max}}$ attains the same rate of convergence.

In addition, notice A₉, A₁₀ have similar representation as A₄, A₅. The only difference is to replace R by Γ. It is not hard to see ${\Vert {\mathbf{B}}^{\prime }{\Phi }^{\prime }\mathbf{\Gamma }\Vert }_{\text{max}}=O_P(\sqrt{p{\nu }_p}).$ Therefore ${\Vert {\mathbf{A}}_9\Vert }_{\text{max}}=O_P(\sqrt{{\nu }_p\log n/p})={\Vert {\mathbf{A}}_{10}\Vert }_{\text{max}}$.

(iv) Note that

$${\Vert \mathbf{P}\Vert }_2={\Vert {(\Phi {(\mathbf{W})}^{\prime }\Phi (\mathbf{W}))}^{-1/2}\Phi {(\mathbf{W})}^{\prime }\Phi (\mathbf{W}){(\Phi {(\mathbf{W})}^{\prime }\Phi (\mathbf{W}))}^{-1/2}\Vert }_2=1$$

and ${\Vert \mathbf{R}{(\mathbf{W})}^{\prime }\mathbf{P}\mathbf{R}(\mathbf{W})\Vert }_{\text{max}}\le p{\Vert \mathbf{R}(\mathbf{W})\Vert }_{\text{max}}^2{\Vert \mathbf{P}\Vert }_2=O_P(p{J}^{-\kappa }).$ Hence

$${\Vert {\mathbf{A}}_6\Vert }_{\text{max}}\le \frac{K}{np}{\Vert \mathbf{F}\Vert }_{\text{max}}{\Vert \mathbf{R}{(\mathbf{W})}^{\prime }\mathbf{P}\mathbf{R}(\mathbf{W})\Vert }_{\text{max}}{\Vert \mathbf{F}\tilde{\mathbf{F}}\Vert }_F=O_P(J^{-\kappa }\sqrt{\log \hspace{0.17em}n}).$$

A₁₁ has similar representation as A₆. Since

$${\Vert {\mathbf{\Gamma }}^{\prime }\mathbf{P}\mathbf{\Gamma }\Vert }_{\text{max}}\le {\Vert {\Phi }^{\prime }\mathbf{\Gamma }\Vert }_F^2{\Vert {({\Phi }^{\prime }\Phi )}^{-1}\Vert }_2=O_P(J{\nu }_p),$$

we have ${\Vert {\mathbf{A}}_{11}\Vert }_{\text{max}}=O_P(J{\nu }_p\sqrt{\log \hspace{0.17em}n}/p).$

(v) According to Lemma F.4, ${\Vert {\mathbf{U}}^{\prime }\Phi (\mathbf{W})\Vert }_{\text{max}}=O_P({\varphi }_{\text{max}}\sqrt{p\log (nJ)}).$ Thus

$$\begin{array}{l}{\Vert {\mathbf{A}}_7\Vert }_{\text{max}}\le \frac{K}{\sqrt{np}}{\Vert \mathbf{F}\Vert }_{\text{max}}{\Vert \tilde{\mathbf{F}}\Vert }_F{\Vert {\mathbf{R}}^{\prime }\Phi {({\Phi }^{\prime }\Phi )}^{-1}{\Phi }^{\prime }\mathbf{U}\Vert }_{\text{max}}\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{0.17em}\le O_P(p^{-1}\sqrt{J\log \hspace{0.17em}n}){\Vert {\mathbf{R}}^{\prime }\Phi \Vert }_F{\Vert {({\Phi }^{\prime }\Phi )}^{-1}\Vert }_2{\Vert {\Phi }^{\prime }\mathbf{U}\Vert }_{\text{max}}\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{0.17em}=O_P({\varphi }_{\text{max}}\sqrt{\frac{J\log (nJ)\log \hspace{0.17em}n}{p{J}^{\kappa }}}),\end{array}$$

since ${\Vert {\mathbf{R}}^{\prime }\Phi \Vert }_F\le {\Vert \mathbf{R}\Vert }_F{\Vert \Phi \Vert }_2=O_P(p{J}^{-k/2}).$ The rate of convergence for A₈ can be bounded in the same way. So do A₁₂ and A₁₃. Given that ${\Vert {\mathbf{\Gamma }}^{\prime }\Phi \Vert }_F=O_P(pJ{\nu }_p),$ we have ${\Vert {\mathbf{A}}_{12}\Vert }_{\text{max}}=O_P(J{\varphi }_{\text{max}}\sqrt{{\nu }_p\log (nJ)\log n/p})={\Vert {\mathbf{A}}_{13}\Vert }_{\text{max}}$.

(vi) Obviously, ${\Vert {\mathbf{A}}_{14}\Vert }_{\text{max}}=O_P(p^{-1}\sqrt{\log \hspace{0.17em}n}{\Vert {\mathbf{R}}^{\prime }\mathbf{P}\mathbf{\Gamma }\Vert }_{\text{max}})$ and $||{\mathbf{R}}^{\prime }\mathbf{P}\mathbf{\Gamma }|{|}_{\text{max}}\le ||{\mathbf{R}}^{\prime }\Phi |{|}_F||{({\Phi }^{\prime }\Phi )}^{-1}||{\Vert {\Phi }^{\prime }\mathbf{\Gamma }\Vert }_F$. We conclude ${\Vert {\mathbf{A}}_{14}\Vert }_{\text{max}}=O_P(\sqrt{p^{-1}{J}^{1-k}{\nu }_p\log \hspace{0.17em}n})$. Same bound holds for A₁₅. □

The final rate of convergence for ${\Vert \tilde{\mathbf{F}}-\mathbf{F}\mathbf{H}\Vert }_{\text{max}}$ and ${\Vert \tilde{\mathbf{F}}-\mathbf{F}\mathbf{H}\Vert }_F$ are summarized as follows.

Proposition D.1. Choose $J\hspace{0.17em}=\hspace{0.17em}{\left(p\min \left(n,p,{\nu }_p^{-1}\right)\right)}^{1/k}$ and assume $J^2{\varphi }_{\max }^2\log \left(nJ\right)=O\left(p\right)$ and ν_p = O(1),

$${\Vert \tilde{\mathbf{F}}-\mathbf{F}\mathbf{H}\Vert }_{\max }=O_P\left(\sqrt{\frac{\log \hspace{0.17em}n}{p}}\right)\hspace{0.17em}and\hspace{0.17em}{\Vert \tilde{\mathbf{F}}-\mathbf{F}\mathbf{H}\Vert }_F=O_P\left(\sqrt{\frac{n}{p}}\right).$$ (D.2)

Proof. The max norm result follows from Lemmas D.2 and (D.1), while the Frobenius norm result has been shown in [18]. □

D.2. Rates of ${\Vert {\mathbf{F}}^{\prime }(\tilde{\mathbf{F}}-\mathbf{F}\mathbf{H})\Vert }_{\text{max}}$ and ${\Vert \mathbf{H}{\mathbf{H}}^{\prime }-\mathbf{I}\Vert }_{\text{max}}$

Note first that the two matrices under consideration is both K by K, so we do not lose rates bounding them by their Frobenius norm.

It has been proved in [18] that ${\Vert {\mathbf{F}}^{\prime }(\tilde{\mathbf{F}}-\mathbf{F}\mathbf{H})\Vert }_F=O_P(\sqrt{n/p}+n/p+n\sqrt{{\nu }_p/p}+n{J}^{-k/2})$. By the choice of J, the last term vanishes. So

$${\Vert {\mathbf{F}}^{\prime }(\tilde{\mathbf{F}}-\mathbf{F}\mathbf{H})\Vert }_{\text{max}}\le {\Vert {\mathbf{F}}^{\prime }(\tilde{\mathbf{F}}-\mathbf{F}\mathbf{H})\Vert }_F=O_P(\sqrt{n/p}+n/p+n\sqrt{{\nu }_p/p}).$$

[18] also showed that ${\Vert {\mathbf{H}}^{\prime }\mathbf{H}-\mathbf{I}\Vert }_F=O_P(1/p+1/\sqrt{pn}+J^{-\kappa /2}+\sqrt{{\nu }_p/p})$. Since $\Vert \mathbf{H}\Vert$ and $\Vert {\mathbf{H}}^{-1}\Vert$ are both $O_P(1)$, we easily show ${\Vert \mathbf{H}{\mathbf{H}}^{\prime }-\mathbf{I}\Vert }_{\text{max}}\le {\Vert \mathbf{H}{\mathbf{H}}^{\prime }-\mathbf{I}\Vert }_F\le \Vert \mathbf{H}\Vert {\Vert {\mathbf{H}}^{\prime }\mathbf{H}-\mathbf{I}\Vert }_F\Vert {\mathbf{H}}^{-1}\Vert =O_P(1/p+1/\sqrt{pn}+\sqrt{{\nu }_p/p})$ since $J^{\kappa }\ge p/{\nu }_p.$

D.3. Rate of ${\Vert \mathbf{U}(\tilde{\mathbf{F}}-\mathbf{F}\mathbf{H})\Vert }_{\mathbf{m}ax}$

By (D.1), in order to bound ${\Vert \mathbf{U}(\tilde{\mathbf{F}}-\mathbf{F}\mathbf{H})\Vert }_{\text{max}}$ we essentially need to bound ${\Vert \mathbf{U}{\mathbf{A}}_i\Vert }_{\text{max}}$ for $i\hspace{0.17em}\hspace{0.17em}=\hspace{0.17em}\hspace{0.17em}1\hspace{0.17em},\dots ,\hspace{0.17em}15.$ We do not bother going into the details of each term again as in Lemma D.2. However, we point out the difference here. All A_i are separated into two types: the ones starting with F and the ones starting with U.

If a term A_i starts with F, say A_i = FQ, in Lemma D.2, we bound ${\Vert {\mathbf{A}}_i\Vert }_{\text{max}}$ in using $\sqrt{K}{\Vert \mathbf{F}\Vert }_{\text{max}}{\Vert \mathbf{Q}\Vert }_F$. Now we use bound ${\Vert \mathbf{U}{\mathbf{A}}_i\Vert }_{\text{max}}\le \sqrt{K}{\Vert \mathbf{U}\mathbf{F}\Vert }_{\text{max}}{\Vert \mathbf{Q}\Vert }_F$ so that we obtain all related rates by just changing rate ${\Vert \mathbf{F}\Vert }_{\text{max}}=O_P(\sqrt{\log \hspace{0.17em}n})$ to ${\Vert \mathbf{\text{UF}}\Vert }_{\text{max}}=O_P(\sqrt{n\log \hspace{0.17em}p})$.

Terms starting with U includes A_i, i = 2,3,8,13. In Lemma D.2, we bound ${\Vert {\mathbf{A}}_i\Vert }_{\text{max}}$, i = 3,8,13 using ${\Vert {\mathbf{U}}^{\prime }\Phi \Vert }_{\text{max}}$ while we bound ${\Vert {\mathbf{A}}_2\Vert }_{\text{max}}$ using ${\Vert {\mathbf{U}}^{\prime }\Phi \mathbf{B}\Vert }_{\text{max}}$. Correspondingly now we need to control ${\Vert \mathbf{U}{\mathbf{U}}^{\prime }\Phi \Vert }_{\text{max}}$ and ${\Vert \mathbf{U}{\mathbf{U}}^{\prime }\Phi \mathbf{B}\Vert }_{\text{max}}$ separately to update the rates. The derivation is relegated to Lemma F.5. We have ${\Vert \mathbf{U}{\mathbf{U}}^{\prime }\Phi (\mathbf{W})\Vert }_{\text{max}}=O_P({\varphi }_{\text{max}}(\sqrt{np\log \hspace{0.17em}p}+n{\Vert \mathbf{\Sigma }\Vert }_1))$ and ${\Vert {\mathbf{\text{UU}}}^{\prime }\Phi \left(\mathbf{\text{W}}\right)\mathbf{B}\Vert }_{\text{max}}=O_P(\sqrt{np\log \hspace{0.17em}p}+nJ{\varphi }_{\text{max}}{\Vert \mathbf{\Sigma }\Vert }_1)$.

So we replace the corresponding terms in Lemma D.2. It is not hard to see the dominating term is ${\Vert \mathbf{U}{\mathbf{A}}_2\Vert }_{\text{max}}=O_P(\sqrt{n\log \hspace{0.17em}p/p}+nJ{\varphi }_{\text{max}}{\Vert \mathbf{\Sigma }\Vert }_1/p)$. Therefore, ${\Vert \mathbf{U}(\tilde{\mathbf{F}}-\mathbf{F}\mathbf{H})\Vert }_{\text{max}}$ has the same rate.

Appendix E: Proof of Theorem 4.1

Proof. Denote the oracle empirical covariance matrix as

$${\mathbf{\Sigma }}_N=\frac{1}{N}\sum _{i=1}^m{\mathbf{U}}^i{\mathbf{U}}^{i^{\prime }}.$$

As in [9] the upper bound on $\Vert \widehat{\mathbf{\Omega }}-\mathbf{\Omega }\Vert$ is obtained by proving

$${\Vert (\widehat{\mathbf{\Sigma }}-{\mathbf{\Sigma }}_N)\mathbf{\Omega }\Vert }_{\text{max}}=O_p({\tau }_{m,N,p})\hspace{0.17em}\text{and}\hspace{0.17em}{\Vert ({\mathbf{\Sigma }}_N-\mathbf{\Sigma })\mathbf{\Omega }\Vert }_{\text{max}}=O_p({\tau }_{m,N,p}).$$ (E.1)

Once the two bounds are established, we proceed by observing

$${\Vert {\mathbf{I}}_p-\widehat{\mathbf{\Sigma }}\mathbf{\Omega }\Vert }_{\text{max}}={\Vert (\widehat{\mathbf{\Sigma }}-\mathbf{\Sigma })\mathbf{\Omega }\Vert }_{\text{max}}=O_p({\tau }_{m,N,p}),$$

and then it readily follows that if $\lambda \asymp {\tau }_{m,N,p}$,

$$\begin{array}{l}{\Vert \widehat{\mathbf{\Omega }}-\mathbf{\Omega }\Vert }_{\text{max}}\le {\Vert \mathbf{\Omega }({\mathbf{I}}_p-\widehat{\mathbf{\Sigma }}\widehat{\mathbf{\Omega }})\Vert }_{\text{max}}+{\Vert {({\mathbf{I}}_p-\widehat{\mathbf{\Sigma }}\mathbf{\Omega })}^{\prime }\widehat{\mathbf{\Omega }}\Vert }_{\text{max}}\\ \le {\Vert \mathbf{\Omega }\Vert }_1{\Vert {\mathbf{I}}_p-\widehat{\mathbf{\Sigma }}\widehat{\mathbf{\Omega }}\Vert }_{\text{max}}+{\Vert {\mathbf{I}}_p-\widehat{\mathbf{\Sigma }}\mathbf{\Omega }\Vert }_{\text{max}}{\Vert \widehat{\mathbf{\Omega }}\Vert }_1\le \lambda {\Vert \mathbf{\Omega }\Vert }_1+\tau {\Vert \mathbf{\Omega }\Vert }_1\\ =O_p({\tau }_{m,N,p}),\end{array}$$

where the first term of the last inequality uses the constraint of (4.4) while the optimality condition of (4.4) is applied to bound ${\Vert \widehat{\mathbf{\Omega }}\Vert }_1$ by ${\Vert \mathbf{\Omega }\Vert }_1$. So it remains to find ${\tau }_{m,N,p}$ in (E.1). Since $\mathbf{\Omega }\in \mathcal{F}(s,C_0)$,${\Vert \mathbf{\Omega }\Vert }_1\le C_0$, so we just need to bound ${\Vert \widehat{\mathbf{\Sigma }}-{\mathbf{\Sigma }}_N\Vert }_{\text{max}}$ and ${\Vert {\mathbf{\Sigma }}_N-\mathbf{\Sigma }\Vert }_{\text{max}}$. Obviously,

$${\Vert {\mathbf{\Sigma }}_N-\mathbf{\Sigma }\Vert }_{\text{max}}=O_p(\sqrt{\frac{\log \hspace{0.17em}p}{N}}).$$

We have shown in (4.3) that $\widehat{\mathbf{\Sigma }}$ given by (4.2) attains the rate ${\Vert \widehat{\mathbf{\Sigma }}-{\mathbf{\Sigma }}_N\Vert }_{\text{max}}=O_P(a_{m,N,p})$. Thus ${\tau }_{m,N,p}=\sqrt{\log p/N}+a_{m,N,p}$. Similar proof as in [9] can also reach error bounds under ${\Vert \hspace{0.17em}\cdot \hspace{0.17em}\Vert }_1$ and ${\Vert \hspace{0.17em}\cdot \hspace{0.17em}\Vert }_2$, which we omit. The proof is now complete. □

Appendix F: Technical lemmas

Lemma F.1. (i) ${\Vert {\mathbf{\Lambda }}^{\prime }\mathbf{U}\Vert }_F^2=O_P(np)$,

(ii) ${\Vert {\mathbf{U}}^{\prime }\mathbf{U}\Vert }_F^2=O_p(n{p}^{{}^2}+p{n}^2)$,

(iii) ${\Vert {\mathbf{U}}^{\prime }\mathbf{U}\mathbf{F}\Vert }_F^2=O_P(n{p}^2+p{n}^2).$

Proof. We simply apply Markov inequality to get the rates.

$$\mathbb{E}{\Vert {\mathbf{\Lambda }}^{\prime }\mathbf{U}\Vert }_F^2=\mathbb{E}\left[\text{tr}({\mathbf{\Lambda }}^{\prime }\mathbf{U}{\mathbf{U}}^{\prime }\mathbf{\Lambda })\right]=n\cdot \text{tr}({\mathbf{\Lambda }}^{\prime }\mathbf{\Sigma }\mathbf{\Lambda })\le n\Vert \mathbf{\Sigma }\Vert \cdot \text{tr}({\mathbf{\Lambda }}^{\prime }\mathbf{\Lambda })=O(np).$$

$$\begin{array}{l}\mathbb{E}{\Vert {\text{U}}^{\prime }\text{U}\Vert }_F^2=\mathbb{E}\left[\sum _{t=1}^n\sum _{t^{\prime }=1}^n{(\sum _{j=1}^p{u}_{jt}{u}_{j{t}^{\prime }})}^2\right]\\ =\sum _{j_1,j_2=1}^p\left(\sum _{t=1}^n\mathbb{E}\left[u_{j_{1}t}^2{u}_{j_{2}t}^2\right]+\sum _{1\le t\ne t_1\le n}{\sigma }_{j_1{j}_2}^2\right)\\ =O_P(n{p}^2+p{n}^2),\end{array}$$

since ${\sum }_{j_1,j_2}{\sigma }_{j_1{j}_2}^2=\text{tr}({\mathbf{\Sigma }}^2)\le \Vert \mathbf{\Sigma }\Vert \text{tr}(\text{Σ})=O(p).$

$$\begin{array}{l}\mathbb{E}{\Vert {\mathbf{U}}^{\prime }\mathbf{U}\mathbf{F}\Vert }_F^2=\mathbb{E}\left[{\sum _{t=1}^n\sum _{k=1}^K(\sum _{t^{\prime }=1}^n\sum _{j=1}^p{u}_{jt}{u}_{j{t}^{\prime }}{f}_{t^{\prime }k})}^2\right]\\ =\sum _{k=1}^K\sum _{j_1,j_2=1}^p\left(\sum _{t=1}^n\mathbb{E}\left[u_{j_{1}t}^2{u}_{j_{2}t}^2\right]f_{tk}^2+\sum _{1\le t\ne t_1\le n}{\sigma }_{j_1{j}_2}^2{f}_{t_{1}k}^2\right)\\ =O_P(n{p}^2+p{n}^2).\end{array}$$

□

Lemma F.2. (i) ${\Vert {\mathbf{\Lambda }}^{\prime }\mathbf{U}\Vert }_{\text{max}}\hspace{0.17em}=\hspace{0.17em}{O}_P(\sqrt{p\hspace{0.17em}\text{log}\hspace{0.17em}n})$.

(ii) ${\Vert {\mathbf{U}}^{\prime }\mathbf{U}\Vert }_{\text{max}}\hspace{0.17em}=\hspace{0.17em}{O}_P(p)$,

(iii) ${\Vert {\mathbf{U}}^{\prime }\mathbf{U}\mathbf{F}\Vert }_{\text{max}}\hspace{0.17em}=\hspace{0.17em}{O}_P(\sqrt{np\hspace{0.17em}\text{log}\hspace{0.17em}n}+p\sqrt{\text{log}\hspace{0.17em}n}).$

Proof. (i) ${\Vert {\mathbf{\Lambda }}^{\prime }\mathbf{U}\Vert }_{\text{max}}\hspace{0.17em}=\hspace{0.17em}{\text{max}}_{t,k}|{\mathbf{u}}_t^{\prime }{\lambda }_k|$ where λ_k is the k^th column of Λ. Since ${\mathbf{u}}_t^{\prime }{\lambda }_k$ is mean zero sub-Gaussian with variance proxy ${\lambda }_k^{\prime }\mathbf{\Sigma }{\lambda }_k\hspace{0.17em}\le \hspace{0.17em}\Vert \mathbf{\Sigma }\Vert {\Vert {\lambda }_k\Vert }^2\hspace{0.17em}=\hspace{0.17em}O(p)$, we have ${\Vert {\mathbf{\Lambda }}^{\prime }\mathbf{U}\Vert }_{\text{max}}\hspace{0.17em}=\hspace{0.17em}{O}_p(\sqrt{p\hspace{0.17em}\text{log}\hspace{0.17em}n})$.

(ii) ${\Vert {\mathbf{U}}^{\prime }\mathbf{U}\Vert }_{\text{max}}\hspace{0.17em}=\hspace{0.17em}{\text{max}}_{t,t^{\prime }}|{\mathbf{u}}_t^{\prime }{\mathbf{u}}_{t^{\prime }}|\hspace{0.17em}\le \hspace{0.17em}{\text{max}}_{t\ne t^{\prime }}|{\mathbf{u}}_t^{\prime }{\mathbf{u}}_{t^{\prime }}|\hspace{0.17em}+\hspace{0.17em}{\text{max}}_t|{\mathbf{u}}_t^{\prime }{\mathbf{u}}_t|$. We need tobound each term separately. The second term is bounded by the upper tail bound of Hanson-Wright inequality for sub-Gaussian vector [24, 41] i.e.

$$\mathbb{P}({\Vert {\mathbf{u}}_t\Vert }^2\hspace{0.17em}>\hspace{0.17em}\text{tr}(\mathbf{\Sigma })\hspace{0.17em}+\hspace{0.17em}2\sqrt{\text{tr}(\mathbf{\Sigma })s}\hspace{0.17em}+\hspace{0.17em}2\Vert \mathbf{\Sigma }\Vert s)\hspace{0.17em}\le \hspace{0.17em}{e}^{-s}\hspace{0.17em}.$$

Choose s = log n and apply union bound, we have ${\text{max}}_t|{\mathbf{u}}_t^{\prime }{\mathbf{u}}_t|\hspace{0.17em}=\hspace{0.17em}{O}_p(\text{tr}(\mathbf{\Sigma })\hspace{0.17em}+\hspace{0.17em}2\sqrt{\text{tr}(\mathbf{\Sigma })s})\hspace{0.17em}=\hspace{0.17em}{O}_p(p\hspace{0.17em}+\hspace{0.17em}\sqrt{p\hspace{0.17em}\text{log}\hspace{0.17em}n})\hspace{0.17em}=\hspace{0.17em}{O}_p(p)$. Then we deal with the first term. By Chernoff bound,

$$\mathbb{P}(\underset{t\ne t^{\prime }}{\text{max}}|{\mathbf{u}}_t^{\prime }{\mathbf{u}}_{t^{\prime }}|\hspace{0.17em}>\hspace{0.17em}s)\hspace{0.17em}\le \hspace{0.17em}2n^2{e}^{-s\theta }\mathbb{E}\left[\text{exp}(\theta {\mathbf{u}}_t^{\prime }{\mathbf{u}}_{t^{\prime }})\right],$$

where $\mathbb{E}\left[\text{exp}(\theta {\mathbf{u}}_t^{\prime }{\mathbf{u}}_{t^{\prime }})\right]\hspace{0.17em}=\hspace{0.17em}E\left[\text{exp}({\theta }^2{\mathbf{u}}_t^{\prime }\mathbf{\Sigma }{\mathbf{u}}_t/2)\right]\hspace{0.17em}\le \hspace{0.17em}E\left[\text{exp}(C{\theta }^2{\Vert {\mathbf{u}}_t\Vert }^2)\right]$. [24] showed that

$$\mathbb{E}\left[\text{exp}(\eta {\Vert {\mathbf{u}}_t\Vert }^2)\right]\hspace{0.17em}\le \hspace{0.17em}\text{exp}\hspace{0.17em}(\text{tr}(\mathbf{\Sigma })\eta \hspace{0.17em}+\hspace{0.17em}\frac{\text{tr}({\mathbf{\Sigma }}^2){\eta }^2}{1\hspace{0.17em}-\hspace{0.17em}2\Vert \mathbf{\Sigma }\Vert \eta })$$

For $\eta \hspace{0.17em}<\hspace{0.17em}1/(4\Vert \mathbf{\Sigma }\Vert )\hspace{0.17em}\le \hspace{0.17em}\text{tr}(\mathbf{\Sigma })/(4\text{tr}({\mathbf{\Sigma }}^2))$, the right hand side is less than exp(3tr(Σ)η/2) ≤ exp(Cpη). Choose η = Cθ², we have

$$\mathbb{P}(\underset{t\ne t^{\prime }}{\text{max}}|{\mathbf{u}}_t^{\prime }{\mathbf{u}}_{t^{\prime }}|\hspace{0.17em}>\hspace{0.17em}s)\hspace{0.17em}\le \hspace{0.17em}2n^2\hspace{0.17em}\text{exp}(-s\theta \hspace{0.17em}+\hspace{0.17em}C{\theta }^{2}p).$$

We minimize the right hand side and choose θ = s/(2Cp), it is easy to check $\eta \hspace{0.17em}<\hspace{0.17em}1/(4\Vert \mathbf{\Sigma }\Vert )$ and see that ${\text{max}}_{t\ne t^{\prime }}\hspace{0.17em}|{\mathbf{u}}_t^{\prime }{\mathbf{u}}_{t^{\prime }}|\hspace{0.17em}=\hspace{0.17em}{O}_p(\sqrt{p\hspace{0.17em}\text{log}\hspace{0.17em}n})$. So we conclude that ${\Vert {\mathbf{U}}^{\prime }\mathbf{U}\Vert }_{\text{max}}\hspace{0.17em}=\hspace{0.17em}{O}_p(p)$.

(iii) Let ${\overline{\mathbf{f}}}_k$ be the k^th column of F. ${\Vert {\mathbf{U}}^{\prime }\mathbf{U}\mathbf{F}\Vert }_{\text{max}}\hspace{0.17em}=\hspace{0.17em}{\text{max}}_{t,k}|{\mathbf{u}}_t^{\prime }\mathbf{U}{\overline{\mathbf{f}}}_k|\hspace{0.17em}\le \hspace{0.17em}{\text{max}}_{t,k}|{\mathbf{u}}_t^{\prime }{\mathbf{U}}_{(-t)}{\overline{\mathbf{f}}}_{k(-t)}|\hspace{0.17em}+\hspace{0.17em}{\text{max}}_{t,k}\hspace{0.17em}|{\mathbf{u}}_t^{\prime }{\mathbf{u}}_t{f}_{tk}|$ where ${\mathbf{U}}_{(-t)},\hspace{0.17em}{\overline{\mathbf{f}}}_k(-t)$ are U and ${\overline{\mathbf{f}}}_k$ canceling the t^th column and element respectively. From (ii) we know the second term is of order $O_p(p\hspace{0.17em}{\text{max}}_{tk}|f_{tk}|)\hspace{0.17em}=\hspace{0.17em}{O}_p(p\sqrt{\text{log}\hspace{0.17em}n})$. Define $\mathbf{\xi }\hspace{0.17em}=\hspace{0.17em}{\mathbf{U}}_{(-t)}{\overline{\mathbf{f}}}_{k(-t)}\hspace{0.17em}\sim$ subGaussian $(\mathbf{0},\hspace{0.17em}\mathbf{\Sigma }{\Vert {\overline{\mathbf{f}}}_{k(-t)}\Vert }^2)$, which is independent with u_t. Thus

$$\mathbb{P}(\underset{t,k}{\text{max}}|{\mathbf{u}}_t^{\prime }\mathbf{\xi }|\hspace{0.17em}>\hspace{0.17em}s)\hspace{0.17em}\le \hspace{0.17em}2nK{e}^{-s\theta }\mathbb{E}\left[\text{exp}(\theta {\mathbf{u}}_t^{\prime }\mathbf{\xi })\right],$$

where $\mathbb{E}\left[\text{exp}(\theta {\mathbf{u}}_t^{\prime }\mathbf{\xi })\right]\hspace{0.17em}\le \hspace{0.17em}\mathbb{E}\left[\text{exp}({\theta }^2{\mathbf{u}}_t^{\prime }\mathbf{\Sigma }{\mathbf{u}}_t{\Vert {\overline{\mathbf{f}}}_{k(-t)}\Vert }^2/2)\right]\hspace{0.17em}\le \hspace{0.17em}\mathbb{E}\left[\text{exp}(C{\theta }^{2}n{\Vert {\mathbf{u}}_t\Vert }^2)\right]$. Similar to (ii), we choose η = Cθ²n here. It is not hard to see ${\text{max}}_{t,k}|{\mathbf{u}}_t^{\prime }\mathbf{\xi }|\hspace{0.17em}=\hspace{0.17em}{O}_p(\sqrt{np\hspace{0.17em}\text{log}\hspace{0.17em}n})$. Thus ${\Vert {\mathbf{U}}^{\prime }\mathbf{U}\mathbf{F}\Vert }_{\text{max}}\hspace{0.17em}=\hspace{0.17em}{O}_p(\sqrt{np\hspace{0.17em}\text{log}\hspace{0.17em}n}\hspace{0.17em}+\hspace{0.17em}p\sqrt{\text{log}\hspace{0.17em}n})$. □

Lemma F.3.(i) ${\Vert {\mathbf{F}}^{\prime }{\mathbf{U}}^{\prime }\Vert }_F^2\hspace{0.17em}=\hspace{0.17em}{O}_p(np)$.

(ii) ${\Vert {\mathbf{U}}^{\prime }\Phi (\mathbf{W})\Vert }_F^2\hspace{0.17em}=\hspace{0.17em}{O}_p(npJ),\hspace{0.17em}{\Vert {\mathbf{U}}^{\prime }\Phi (\mathbf{W})\mathbf{B}\Vert }_F^2\hspace{0.17em}=\hspace{0.17em}{O}_p(np)$.

(iii) ${\Vert \Phi {(\mathbf{W})}^{\prime }\mathbf{U}\mathbf{F}\Vert }_F^2\hspace{0.17em}=\hspace{0.17em}{O}_p(npJ),\hspace{0.17em}{\Vert {\mathbf{B}}^{\prime }\Phi {(\mathbf{W})}^{\prime }\mathbf{U}\mathbf{F}\Vert }_F^2\hspace{0.17em}=\hspace{0.17em}{O}_p(np)$.

Proof. This results can be found in the paper of Fan, Liao and Wang (2014). But the conditions they used are a little bit different from our conditions. In particular, we allow no time (sample) dependence and only require bounded ${\Vert \mathbf{\Sigma }\Vert }_2$ instead of ${\Vert \mathbf{\Sigma }\Vert }_1$. By Markov inequality, it is sufficient to show the expected value of each term attains the corresponding rate of convergence.

$$\mathbb{E}{\Vert {\mathbf{F}}^{\prime }{\mathbf{U}}^{\prime }\Vert }_F^2\hspace{0.17em}=\hspace{0.17em}\mathbb{E}\left[\text{tr}({\mathbf{F}}^{\prime }\mathbb{E}\left[{\mathbf{U}}^{\prime }\mathbf{U}\right]\mathbf{F})\right]\hspace{0.17em}=\hspace{0.17em}\mathbb{E}\left[\text{tr}({\mathbf{F}}^{\prime }\text{tr}(\mathbf{\Sigma })\mathbf{F})\right]\hspace{0.17em}=\hspace{0.17em}n\hspace{0.17em}\cdot \hspace{0.17em}\text{tr}(\mathbf{\Sigma })\hspace{0.17em}=\hspace{0.17em}O(np).$$

$$\begin{array}{l}\mathbb{E}{\Vert {\mathbf{U}}^{\prime }\Phi (\mathbf{W})\Vert }_F^2\hspace{0.17em}=\hspace{0.17em}\mathbb{E}\left[\text{tr}({\Phi }^{\prime }\mathbb{E}\left[\mathbf{U}{\mathbf{U}}^{\prime }|\mathbf{W}\right]\Phi )\right]\hspace{0.17em}=\hspace{0.17em}n\cdot \mathbb{E}\left[\text{tr}({\Phi }^{\prime }\mathbf{\Sigma }\Phi )\right]\hspace{0.17em}\le \hspace{0.17em}nJd\hspace{0.17em}\cdot \hspace{0.17em}\mathbb{E}\left[{\Vert {\Phi }^{\prime }\mathbf{\Sigma }\Phi \Vert }_2\right]\\ \le \hspace{0.17em}nJd{C}_0\mathbb{E}\left[{\Vert {\Phi }^{\prime }\Phi \Vert }_2\right]\hspace{0.17em}=\hspace{0.17em}O(npJ).\end{array}$$

$\mathbb{E}{\Vert \Phi {(\mathbf{W})}^{\prime }\mathbf{U}\mathbf{F}\Vert }_F^2=\mathbb{E}\left[\text{tr}({\Phi }^{\prime }\mathbb{E}\left[\mathbf{U}\mathbf{F}{\mathbf{F}}^{\prime }{\mathbf{U}}^{\prime }|\mathbf{W}\right]\Phi )\right]=\mathbb{E}\left[\text{tr}(\mathbf{F}{\mathbf{F}}^{\prime })\text{tr}({\Phi }^{\prime }\mathbf{\Sigma }\Phi )\right]=O(npJ).\mathbb{E}{\Vert {\mathbf{U}}^{\prime }\Phi (\mathbf{W})\mathbf{B}\Vert }_F^2$ and ${\Vert {\mathbf{B}}^{\prime }\Phi {(\mathbf{W})}^{\prime }\mathbf{U}\mathbf{F}\Vert }_F^2$ are both O(np) following the same proof as above. Thus the proof is complete. □

Lemma F.4. (i) ${\Vert {\mathbf{F}}^{\prime }{\mathbf{U}}^{\prime }\Vert }_{\text{max}}\hspace{0.17em}=\hspace{0.17em}{O}_P(\sqrt{n\hspace{0.17em}\text{log}\hspace{0.17em}p})$

(ii) ${\Vert {\mathbf{U}}^{\prime }\Phi (\mathbf{W})\Vert }_{\text{max}}\hspace{0.17em}=\hspace{0.17em}{O}_P({\varphi }_{\text{max}}\sqrt{p\hspace{0.17em}\text{log}(nJ)}),\hspace{0.17em}{\Vert {\mathbf{U}}^{\prime }\Phi (\mathbf{W})\mathbf{B}\Vert }_{\text{max}}\hspace{0.17em}=\hspace{0.17em}{O}_P(\sqrt{p\hspace{0.17em}\text{log}\hspace{0.17em}n})$.

(iii) ${\Vert \Phi {(\mathbf{W})}^{\prime }\mathbf{U}\mathbf{F}\Vert }_{\text{max}}\hspace{0.17em}=\hspace{0.17em}{O}_P({\varphi }_{\text{max}}\sqrt{np\hspace{0.17em}\text{log}\hspace{0.17em}J}),\hspace{0.17em}{\Vert {\mathbf{B}}^{\prime }\Phi {(\mathbf{W})}^{\prime }\mathbf{U}\mathbf{F}\Vert }_{\text{max}}\hspace{0.17em}=\hspace{0.17em}{O}_P(\sqrt{np})$.

Proof. (i) It is not hard to see ${\Vert {\mathbf{F}}^{\prime }{\mathbf{U}}^{\prime }\Vert }_{\text{max}}\hspace{0.17em}=\hspace{0.17em}{\text{max}}_{k\le K,j\le p}|{\sum }_{t=1}^n{f}_{tk}{u}_{jt}|\hspace{0.17em}=\hspace{0.17em}{O}_p(\sqrt{n\hspace{0.17em}\text{log}\hspace{0.17em}p})$. The detailed proof by Chernoff bound is given in the following. By union bound and Chernoff bound, we have

$$\mathbb{P}(\underset{k\le K,i\le p}{\text{max}}|\sum _{t=1}^n{f}_{tk}{u}_{jt}|\hspace{0.17em}>\hspace{0.17em}t)\hspace{0.17em}\le \hspace{0.17em}2pK{e}^{-t\theta }\hspace{0.17em}\cdot \hspace{0.17em}\mathbb{E}\left[e^{\theta {\sum }_{t=1}^n{f}_{tk}{u}_{jt}}\right].$$

The expectation is calculated by fist conditioning on F,

$$E\left[e^{\theta {\sum }_{t=1}^n{f}_{tk}{u}_{jt}}\right]=\mathbb{E}\left[\mathbb{E}\left[e^{\theta {\sum }_{t=1}^n{f}_{tk}{u}_{jt}}|\mathbf{F}\right]\right]\le \mathbb{E}\left[e^{{\theta }^2{\sum }_{t=1}^n{f}_{tk}^2{\sigma }_{jj}/2}\right]\le e^{\frac{1}{2}n{C}_0{\theta }^2},$$

where the second equality uses the sub-Gaussianity of u_jt and the last inequality is from $n^{-1}{\mathbf{F}}^{\prime }\mathbf{F}\hspace{0.17em}=\hspace{0.17em}\mathbf{I}$ and ${\Vert \mathbf{\Sigma }\Vert }_2\hspace{0.17em}\le \hspace{0.17em}{C}_0$. Therefore, choosing $\theta \hspace{0.17em}=\hspace{0.17em}\frac{t}{n{C}_0}$, we have

$$\mathbb{P}(\underset{k\le K,j\le p}{\text{max}}|\sum _{t=1}^n{f}_{tk}{u}_{jt}|\hspace{0.17em}>\hspace{0.17em}t)\le 2pK{e}^{-t\theta }{e}^{\frac{C_0}{2}n{\theta }^2}\hspace{0.17em}=\hspace{0.17em}2pK{e}^{-\frac{t^2}{2C_{0}n}}.$$

Thus ${\Vert {\mathbf{F}}^{\prime }{\mathbf{U}}^{\prime }\Vert }_{\text{max}}\hspace{0.17em}=\hspace{0.17em}{O}_p(\sqrt{n\hspace{0.17em}\text{log}\hspace{0.17em}p})$.

(ii) ${\Vert {\mathbf{U}}^{\prime }\Phi (\mathbf{W})\Vert }_{\text{max}}\hspace{0.17em}=\hspace{0.17em}{\text{max}}_{\nu ,l,t}\hspace{0.17em}|{\sum }_{j=1}^p{u}_{jt}{\varphi }_{\nu }(W_{jl})|\hspace{0.17em}=\hspace{0.17em}{\text{max}}_{\nu ,l,t}|{\overline{\varphi }}_{\nu l}^{\prime }{\mathbf{u}}_t|$, where ${\overline{\varphi }}_{\nu l}\hspace{0.17em}=\hspace{0.17em}{({\varphi }_{\nu }({\mathbf{W}}_{1l}),\dots ,{\varphi }_{\nu }({\mathbf{W}}_{pl}))}^{\prime }$. Consider the tail probability condition on W:

$$\begin{array}{l}\mathbb{P}\left(\underset{\nu \le J,l\le d,k\le n}{\text{max}}|{\overline{\varphi }}_{\nu l}^{\prime }{\mathbf{u}}_k|\hspace{0.17em}>\hspace{0.17em}t|\mathbf{W}\right)\hspace{0.17em}\le \hspace{0.17em}2Jdn\hspace{0.17em}\cdot \hspace{0.17em}{e}^{-t\theta }\mathbb{E}\left[e^{\theta {\overline{\varphi }}_{\nu l}^{\prime }{\mathbf{u}}_k}|\mathbf{W}\right]\\ \le 2Jdn\hspace{0.17em}\cdot \hspace{0.17em}\text{exp}\left\{-t\theta \hspace{0.17em}+\hspace{0.17em}\frac{1}{2}{\theta }^2{\overline{\varphi }}_{\nu l}^{\prime }\mathbf{\Sigma }{\overline{\varphi }}_{\nu l}\right\}.\end{array}$$

The right hand side can be further bounded by

$$2Jdn\cdot \text{exp}(-t\theta +\frac{1}{2}{\theta }^2{C}_0{\Vert {\overline{\varphi }}_{\nu l}\Vert }^2)\le 2Jdn\cdot \text{exp}(-t\theta +\frac{1}{2}p{C}_0{\theta }^2{\varphi }_{\text{max}}^2).$$

Choose θ to minimize the upper bound and take expectation with respect to W, we obtain

$$\mathbb{P}(\underset{\nu \le J,l\le d,k\le n}{\text{max}}|{\overline{\varphi }}_{\nu l}^{\prime }{\mathbf{u}}_k|>t)\le 2Jdn\cdot \text{exp}\left\{-\frac{t^2}{2p{C}_0{\varphi }_{\text{max}}^2}\right\}.$$

Finally choose t ≍ ${\varphi }_{\text{max}}\sqrt{p\hspace{0.17em}\text{log}(nJ)}$, the tail probability is arbitrarily small with a proper constant. So ${\Vert {\mathbf{U}}^{\prime }\Phi (\mathbf{W})\Vert }_{\text{max}}\hspace{0.17em}=\hspace{0.17em}{O}_p({\varphi }_{\text{max}}\sqrt{p\hspace{0.17em}\text{log}(nJ)})$. The second part of the results follows similarly. Note ${\Vert {\mathbf{U}}^{\prime }\Phi (\mathbf{W})\mathbf{B}\Vert }_{\text{max}}\hspace{0.17em}\le \hspace{0.17em}{\Vert {\mathbf{U}}^{\prime }\mathbf{G}(\mathbf{W})\Vert }_{\text{max}}\hspace{0.17em}+\hspace{0.17em}{\Vert {\mathbf{U}}^{\prime }R(\mathbf{W})\Vert }_{\text{max}}$ and the first term dominates. So the same derivation gives

$$\mathbb{P}({\Vert {\mathbf{U}}^{\prime }\mathbf{G}(\mathbf{W})\Vert }_{\text{max}}>t)\le 2Kn\cdot \text{exp}\left\{-\frac{t^2}{2C_0{\Vert {\overline{g}}_k\Vert }^2}\right\},$$

where ${\overline{g}}_k\hspace{0.17em}=\hspace{0.17em}(g_k({\mathbf{W}}_1),\dots ,g_k({\mathbf{W}}_p)).{\Vert {\overline{g}}_k\Vert }^2\hspace{0.17em}=\hspace{0.17em}{O}_p(p)$ since it is assumed eigenvalues of $p^{-1}\mathbf{G}{(\mathbf{W})}^{\prime }\mathbf{G}(\mathbf{W})$ is bounded almost surely. Hence, ${\Vert {\mathbf{U}}^{\prime }\Phi (\mathbf{W})\mathbf{B}\Vert }_{\text{max}}\hspace{0.17em}=\hspace{0.17em}{O}_p(\sqrt{p\hspace{0.17em}\text{log}\hspace{0.17em}n})$.

(iii) ${\Vert \Phi {(\mathbf{W})}^{\prime }\mathbf{U}\mathbf{F}\Vert }_{\text{max}}\hspace{0.17em}=\hspace{0.17em}{\text{max}}_{\nu \le J,l\le d,k\le K}|{\sum }_{j=1}^p{\sum }_{i=1}^n{\varphi }_{\nu }(W_{jl})u_{ji}{f}_{ik}|$. Using Chernoff bound again, we get

$$\mathbb{P}(\underset{\nu \le J,l\le d,k\le K}{\text{max}}|\sum _{j=1}^p\sum _{i=1}^n{\varphi }_{\nu }(W_{jl})u_{ji}{f}_{ik}|>t)\le 2JdK\cdot e^{-t\theta }.\mathbb{E}\left[e^{\theta {\sum }_{t=1}^n{f}_{tk}{\overline{\varphi }}_{\nu l}^{\prime }{\mathbf{u}}_t}\right].$$

Since ${\sum }_{t=1}^n{f}_{tk}{\overline{\varphi }}_{\nu l}^{\prime }{\mathbf{u}}_t|\mathbf{F}\text{~sub-Gaussian}(0,{\sum }_{t=1}^n{f}_{tk}^2{\overline{\varphi }}_{\nu l}^{\prime }\mathbf{\Sigma }{\overline{\varphi }}_{\nu l})=\text{sub-Gaussian}(0,n{\overline{\varphi }}_{\nu l}^{\prime }\mathbf{\Sigma }{\overline{\varphi }}_{\nu l})$, the right hand side is easy to bound by first conditioning on F.

$$\mathbb{E}\left[e^{\theta {\sum }_{t=1}^n{f}_{tk}{\overline{\varphi }}_{\nu l}^{\prime }{\mathbf{u}}_t}\right]\le \mathbb{E}\left[\exp \left(\frac{1}{2}n{\theta }^2{\overline{\varphi }}_{\nu l}^{\prime }\mathbf{\Sigma }{\overline{\varphi }}_{\nu l}\right)\right]\le E\left[\exp \left(\frac{1}{2}np{C}_0{\varphi }_{\text{max}}^2{\theta }^2\right)\right].$$

Therefore, choosing $\theta =\frac{t}{np{C}_0{\varphi }_{\text{max}}^2}$, we have

$$\begin{array}{l}\mathbb{P}(\left|\right|\Phi {(\mathbf{W})}^{\prime }\mathbf{U}\mathbf{F}|{|}_{\text{max}}>t)\le 2JdK.\exp \left\{-t\theta +\frac{1}{2}np{C}_0{\varphi }_{\text{max}}^2{\theta }^2\right\}\\ =2JdK\exp \left\{-\frac{t^2}{2np{C}_0{\varphi }_{\text{max}}^2}\right\}.\end{array}$$

So we conclude $||\Phi (\mathbf{W}{)}^{\prime }\mathbf{U}\mathbf{F}|{|}_{\text{max}}=O_p({\varphi }_{\text{max}}\sqrt{np\log \hspace{0.17em}J})$. By similar derivation as in (ii), we also have $||{\mathbf{B}}^{\prime }\Phi {(\mathbf{W})}^{\prime }\mathbf{U}\mathbf{F}|{|}_{\text{max}}$ and $||\mathbf{G}{(\mathbf{W})}^{\prime }\mathbf{U}\mathbf{F}|{|}_{\text{max}}$ are both of order $O_P(\sqrt{np})$. □

Lemma F.5. (i) $||\mathbf{U}{\mathbf{U}}^{\prime }\mathbf{\Lambda }|{|}_{\text{max}}=O_P(\sqrt{np\log \hspace{0.17em}p}+n||\mathbf{\Sigma }|{|}_1)$,

(ii) $||\mathbf{U}{\mathbf{U}}^{\prime }\Phi (\mathbf{W})|{|}_{\text{max}}=O_P({\varphi }_{\text{max}}(\sqrt{np\log \hspace{0.17em}p}+n||\mathbf{\Sigma }|{|}_1))$ and $||\mathbf{U}{\mathbf{U}}^{\prime }\Phi (\mathbf{W})\mathbf{B}|{|}_{\text{max}}=O_P(\sqrt{np\log \hspace{0.17em}p}+nJ{\varphi }_{\text{max}}||\mathbf{\Sigma }|{|}_1)$.

Proof. (i) $||\mathbf{U}{\mathbf{U}}^{\prime }\mathbf{\Lambda }|{|}_{\text{max}}\le {\text{max}}_{j,k}|{\sum }_{t=1}^n{u}_{jt}{\mathbf{u}}_t^{\prime }{\mathbf{\lambda }}_k-n{\sum }_{j^{\prime }=1}^p{\sigma }_{j{j}^{\prime }}{\text{λ}}_{j^{\prime }k}|+n\hspace{0.17em}{\text{max}}_{j,k}{\sum }_{j^{\prime }=1}^p|{\sigma }_{j{j}^{\prime }}||{\text{λ}}_{j^{\prime }k}|$. The second term is $O(n||\mathbf{\Sigma }|{|}_1)$. So it suffices to focus on the first term. Let $\mathbf{\Sigma }=\mathbf{A}{\mathbf{A}}^{\prime }$ and ${\mathbf{u}}_t=\mathbf{A}{\mathbf{v}}_t$ so that Var(v_t) = I. Write ${\mathbf{A}}^{\prime }=({\mathbf{a}}_1,\dots ,{\mathbf{a}}_p)$, so we have $u_{jt}={\mathbf{a}}_j^{\prime }{\mathbf{v}}_t$. Also denote ${\mathbf{d}}_k={\mathbf{A}}^{\prime }{\mathbf{\lambda }}_k$. Thus $u_{jt}{\mathbf{u}}_t^{\prime }{\mathbf{\lambda }}_k={\mathbf{a}}_j^{\prime }{\mathbf{v}}_t{\mathbf{v}}_t^{\prime }{\mathbf{d}}_k$ and ${\sum }_{j^{\prime }=1}^p{\sigma }_{j{j}^{\prime }}{\text{λ}}_{j^{\prime }k}={\mathbf{a}}_j^{\prime }{\mathbf{d}}_k$.

$$\begin{array}{l}\mathbb{P}(\underset{j,k}{\text{max}}|\sum _{t=1}^n({\mathbf{a}}_j^{\prime }{\mathbf{v}}_t{\mathbf{v}}_t^{\prime }{\mathbf{d}}_k-{\mathbf{a}}_j^{\prime }{\mathbf{d}}_k)|>s)\\ \le pK\mathbb{P}(|\sum _{t=1}^n({\tilde{\mathbf{a}}}_j^{\prime }{\mathbf{v}}_t{\mathbf{v}}_t^{\prime }{\tilde{\mathbf{d}}}_k-{\tilde{\mathbf{a}}}_j^{\prime }{\tilde{\mathbf{d}}}_k)|>\frac{s}{{\text{max}}_{j,k}\Vert {\mathbf{a}}_j\Vert \Vert {\mathbf{d}}_k\Vert }),\end{array}$$ (F.1)

where ${\tilde{\mathbf{a}}}_j$ and ${\tilde{\mathbf{d}}}_k$ are two unit vectors of dimension p. We will bound the right hand side with arbitrary unit vectors ${\tilde{\mathbf{a}}}_j$ and ${\tilde{\mathbf{d}}}_k$.

$$\begin{array}{l}\mathbb{P}\left(\left|\sum _{t=1}^n{\tilde{\mathbf{a}}}_j^{\prime }{\mathbf{v}}_t{\mathbf{v}}_t^{\prime }{\tilde{\mathbf{d}}}_k-n{\tilde{\mathbf{a}}}_j^{\prime }{\tilde{\mathbf{d}}}_k\right|>s\right)\\ \le \mathbb{P}\left(\left|\sum _{t=1}^n{({({\tilde{\mathbf{a}}}_j+{\tilde{\mathbf{d}}}_k)}^{\prime }{\mathbf{v}}_t)}^2-n||{\tilde{\mathbf{a}}}_j+{\tilde{\mathbf{d}}}_k|{|}^2\right|>2s\right)\\ +\mathbb{P}\left(\left|\sum _{t=1}^n{({({\tilde{\mathbf{a}}}_j-{\tilde{\mathbf{d}}}_k)}^{\prime }{\mathbf{v}}_t)}^2-n||{\tilde{\mathbf{a}}}_j-{\tilde{\mathbf{d}}}_k|{|}^2\right|>2s\right).\end{array}$$

Note that ${({\tilde{\mathbf{a}}}_j+{\tilde{\mathbf{d}}}_k)}^{\prime }{\mathbf{v}}_t~\text{subGaussian(0,||}{\tilde{\mathbf{a}}}_j+{\tilde{\mathbf{d}}}_k|{|}^2)$ and $||{\tilde{\mathbf{a}}}_j+{\tilde{\mathbf{d}}}_k|{|}^2\le 4$. By Bernstein inequality, we have for constant C > 0,

$$\mathbb{P}\left(\right|\sum _{t=1}^n({\tilde{\mathbf{a}}}_j^{\prime }{\mathbf{v}}_t{\mathbf{v}}_t^{\prime }{\tilde{\mathbf{d}}}_k-{\tilde{\mathbf{a}}}_j^{\prime }{\tilde{\mathbf{d}}}_k)|>s)\le 2\exp (-C\min (s^2/n,s)).$$

Choose $s=C\sqrt{n\log \hspace{0.17em}p}\hspace{0.17em}{\text{max}}_{jk}\Vert {\mathbf{a}}_j\Vert \Vert {\mathbf{d}}_k\Vert$ in (F.1), we can easily show that the exception probability is small as long as C is large enough. Therefore, noting ${\text{max}}_{jk}\Vert {\mathbf{a}}_j\Vert \Vert {\mathbf{d}}_k\Vert \le C\hspace{0.17em}{\text{max}}_k||{\mathbf{\lambda }}_k||$,${\text{max}}_{j,k}|{\sum }_{t=1}^n{u}_{jt}{\mathbf{u}}_t^{\prime }{\mathbf{\lambda }}_k-n{\sum }_{j^{\prime }=1}^p{\sigma }_{j{j}^{\prime }}{\text{λ}}_{j^{\prime },k}|=O_P(\sqrt{n\log \hspace{0.17em}p}\hspace{0.17em}{\text{max}}_k||{\mathbf{\lambda }}_k||)=O_P(\sqrt{np\log \hspace{0.17em}p})$. Finally $||\mathbf{U}{\mathbf{U}}^{\prime }\mathbf{\Lambda }|{|}_{\text{max}}=O_P(\sqrt{np\log \hspace{0.17em}p}+n||\mathbf{\Sigma }|{|}_1)$.

(ii) The rates of $||\mathbf{U}{\mathbf{U}}^{\prime }\Phi (\mathbf{W})|{|}_{\text{max}}$ and $|\mathbf{U}{\mathbf{U}}^{\prime }\Phi (\mathbf{W})\mathbf{B}|{|}_{\text{max}}$ can be similarly derived as (i). Denote ${\mathbf{\Phi }}_{\nu l}={({\varphi }_{\nu }(W_{1l}),\dots ,{\varphi }_{\nu }(W_{pl}))}^{\prime }$, so

$$\begin{gathered} \begin{array}{l}\left|\right|\mathbf{U}{\mathbf{U}}^{\prime }\Phi (\mathbf{W})|{|}_{\text{max}}\le \underset{j,\nu ,l}{\text{max}}|\sum _{t=1}^n{u}_{jt}{\mathbf{u}}_t^{\prime }{\mathbf{\Phi }}_{\nu l}-n\sum _{j^{\prime }=1}^p{\sigma }_{j{j}^{\prime }}{\varphi }_{\nu }(W_{j^{\prime }l})| \\ \hspace{1em}\hspace{1em}+n\underset{j,\nu ,l}{\text{max}}\sum _{j^{\prime }=1}^p|{\sigma }_{j{j}^{\prime }}||{\varphi }_{\nu }(W_{j^{\prime }l})|\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}=O_P(\sqrt{n\log \hspace{0.17em}p}\underset{\nu ,l}{\text{max}}\Vert {\mathbf{\Phi }}_{\nu l}\Vert +n{\varphi }_{\text{max}}{\Vert \mathbf{\Sigma }\Vert }_1)\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}=O_P({\varphi }_{\text{max}}(\sqrt{np\log \hspace{0.17em}p}+n{\Vert \mathbf{\Sigma }\Vert }_1)).\end{array} \end{gathered}$$

Denote the k^th column of Φ(W)B by (ΦB)_k, we have

$$\begin{gathered} \begin{array}{l}\left|\right|\mathbf{U}{\mathbf{U}}^{\prime }\Phi (\mathbf{W})\mathbf{B}|{|}_{\text{max}}\le \underset{j,k}{\text{max}}|\sum _{t=1}^n{u}_{jt}{\mathbf{u}}_t^{\prime }{(\mathbf{\Phi }B)}_k-n\sum _{j^{\prime }=1}^p{\sigma }_{j{j}^{\prime }}{(\mathbf{\Phi }B)}_{j^{\prime }k}| \\ \hspace{1em}\hspace{1em}+n\underset{j,k}{\text{max}}\sum _{j^{\prime }=1}^p|{\sigma }_{j{j}^{\prime }}||{(\mathbf{\Phi }B)}_{j^{\prime }k}|\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{0.17em}=O_P(\sqrt{n\log \hspace{0.17em}p}\underset{k}{\text{max}}\Vert {(\mathbf{\Phi }B)}_k\Vert +nJ{\varphi }_{\text{max}}{\Vert \mathbf{\Sigma }\Vert }_1)\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{0.17em}=O_P(\sqrt{np\log \hspace{0.17em}p}+nJ{\varphi }_{\text{max}}{\Vert \mathbf{\Sigma }\Vert }_1),\end{array} \end{gathered}$$

where we use max ${\text{max}}_k\Vert {(\mathbf{\Phi }\mathbf{B})}_k\Vert \le {\Vert \mathbf{\Phi }\mathbf{B}\Vert }_F=O_P(\sqrt{p})$. □

Appendix G: More details on synthetic data analysis

G.1. Model calibration and data generation

We calibrate (estimate) the 264 by 264 covariance matrix $\widehat{\mathbf{\Sigma }}$ of u_t by our proposed method to the data in the healthy group. Plugging it as input in CLIME solver delivers a sparse precision matrix Ω, which will be taken as truth in the simulation. Note that after regularization in CLIME, Ω⁻¹ is not the same as $\widehat{\mathbf{\Sigma }}$, and we set the true covariance Σ = Ω⁻¹. To obtain the covariance matrix used, in setting 1, we also calibrate, using the same method, a sub-model that involves only the first 100 regions. We then copy this 100 × 100 matrix multiple times to form a p × p block diagonal matrix and use it for simulations in setting 1. We describe how we calibrate these ‘true models’ and generate data from the models as follows.

1. (External covariates) For each j ≤ p, generate the external covariate W i.i.d. from the multinomial distribution with $\mathbb{P}$(W_j = s) = w_s,s ≤ 10 where ${\left\{w_s\right\}}_{s=1}^{10}$ are calibrated with the hierarchy clustering results of the real data.

2. (Calibration) For the first 15 healthy subjects, obtain estimators for F, B and Γ by PPCA, resulting in $\tilde{\mathbf{F}},\tilde{\mathbf{B}}=n^{-1}{(\Phi {(\mathbf{W})}^{\prime }\Phi (\mathbf{W}))}^{-1}\Phi {(\mathbf{W})}^{\prime }\mathbf{X}\tilde{\mathbf{F}}$ and $\tilde{\mathbf{\Gamma }}=n^{-1}(\mathbf{I}-\mathbf{P})\mathbf{X}\tilde{\mathbf{F}}$ according to [18]. Use the rows of the estimated factors to fit a stationary VAR model f_t = Af_t−1 + ∈_t, where ∈_t ∼ N(0, Σ_∈), and obtain the estimators $\tilde{\mathbf{A}}$ and ${\tilde{\mathbf{\Sigma }}}_{\in }$.

3. (Simulation) For each subject i ≤ m, pick one of the 15 calibrated models and their associated parameters from above at random and do the following.

   • (a)
     Generate ${\gamma }_{jk}^i$ (entries of Γⁱ) i.i.d. from $N(0,{\tilde{\sigma }}_{\gamma }^2)$ where ${\tilde{\sigma }}_{\gamma }^2$ is the sample variance of all entries of $\tilde{\mathbf{\Gamma }}$. For the first three settings, compute the ‘true’ loading matrix ${\mathbf{\Lambda }}^i=\Phi (\mathbf{W})\tilde{\mathbf{B}}+{\mathbf{\Gamma }}^i$. For the last setting, set Λⁱ = Γⁱ since G(W) = 0.
   • (b)
     Generate factors ${\mathbf{f}}_t^i$ from the VAR model ${\mathbf{f}}_t^i=\tilde{\mathbf{A}}{\mathbf{f}}_{t-1}^i+{\mathbf{\in }}_t$ with ${\mathbf{\in }}_t~N(0,{\tilde{\mathbf{\Sigma }}}_{\in })$ where the parameters $\tilde{\mathbf{A}}$ and ${\tilde{\mathbf{\Sigma }}}_{\in }$ are taken from the fitted values in step 2.
   • (c)
     Finally, generate the observed data ${\mathbf{X}}^i={\mathbf{\Lambda }}^i{\mathbf{F}}^{i^{\prime }}+{\mathbf{U}}^i$, where each column of Uⁱ is randomly sampled from N(0,Ω⁻¹), where Ω has been calibrated by the CLIME solver as described at beginning of the section.

G.2. More on pervasiveness

In this subsection, we discuss the pervasive assumption, which requires the spikes to grow with order p, and present numerical performance of ALPHA for different levels of c_min and c_max (defined in Assumption 2.3). The readers will have a rough idea about how the spikiness (or the constant in front of the rate) affects the performance. We particularly consider the cases when c_max is small or c_min is large. As a threshold matter, we verify that the real data is consistent with the pervasive assumption.

Denote the maximum and minimum eigenvalues of the matrix ${\mathbf{\Lambda }}^{\prime }\mathbf{\Lambda }/p$ by λ_max and λ_min respectively, and denote the maximum eigenvalue of the matrix ${\mathbf{U}}^{\prime }\mathbf{U}/p$ by ${\text{λ}}_{\text{max}}^u$. We first investigate the magnitude of λ_min, λ_max and ${\text{λ}}_{\text{max}}^u$ derived from the real data. Following exactly the same data generation procedure as in the original simulation study, we randomly generate 1,000 subjects. We find that λ_max has mean 15.352 and standard deviation 4.918, λ_min has mean 10.069 and standard deviation 5.416 and ${\text{λ}}_{\text{max}}^u$ has mean 1.317 and standard deviation 0.119. We also investigate the signal-to-noise ratio ${\lambda }_{\min }{\text{/λ}}_{\text{max}}^u$, which has mean 7.711 and standard deviation 4.230. Therefore, our real data demonstrates a spiked covariance structure while the spikes are not extremely spiky.

Then we manipulate the data generation process correspondent to two different cases. One is to multiply the original loading matrix Λ by 3, called Modified (a), while the other is to divide Λ by 3, called Modified (b). Note that in the case of Modified (b), λ_min will be 1/9 of the original λ_min and thus smaller than ${\text{λ}}_{\text{max}}^u$, so we do not see a clear eigen-gap in this case. Table 3 compares the performance of recovering the precision matrix Ω under the original and modified setting when n_i = 100.

Table 3.

Gaussian Graphical Model Analysis

	$||\widehat{\mathbf{\Omega }}-\mathbf{\Omega }|{|}_{\text{max}}$	$||\widehat{\mathbf{\Omega }}-\mathbf{\Omega }|{|}_1$	$||\widehat{\mathbf{\Omega }}-\mathbf{\Omega }|{|}_2$
Original	0.564	3.445	1.188
Modified (a)	0.524	3.052	1.066
Modified (b)	0.749	4.914	1.719

We can see from the table above that the performance of ALPHA in the case of Modified (a) is slightly better than that in the original case. Note that increasing c_min makes the heterogeneity part more spiky. Larger c_min allows PCA or PPCA to distinguish the spiky heterogeneity term more easily. In contrast, decreasing c_max makes the original spiky heterogeneity term hard to detect. We also tend to miss several heterogeneity factors while extracting them. Therefore, in Modified (b), the estimation error becomes significantly larger compared with the original case.

G.3. Sensitivity analysis on the number of factors

In this section, we study how the estimated number of factors affects the recovery of the Gaussian graphical model through simulations. The specification of the number of factors is critical to the validity of our ALPHA method, which inspires us to assess the performance of $\widehat{K}$ and $\tilde{K}$ on our simulated datasets in the first place. Recall that

$$\begin{array}{l}\widehat{K}=\arg \hspace{0.17em}{\text{max}}_{k\le K_{\text{max}}}{\text{λ}}_k({\mathbf{X}}^{\prime }\mathbf{X})/{\text{λ}}_{k+1}({\mathbf{X}}^{\prime }\mathbf{X}),\\ \tilde{K}=\arg \hspace{0.17em}{\text{max}}_{k\le K_{\text{max}}}{\text{λ}}_k({\mathbf{X}}^{\prime }\mathbf{P}\mathbf{X})/{\text{λ}}_{k+1}({\mathbf{X}}^{\prime }\mathbf{P}\mathbf{X}),\end{array}$$

where P is the projection operator defined in (3.5) in the main text. The final estimator of the number of factors, denote by Ǩ, comes from the heuristic strategy we developed for choosing between PCA or PPCA. We choose PCA if ${\text{λ}}_{\widehat{K}}({\mathbf{X}}^{\prime }\mathbf{X})/{\text{λ}}_{\widehat{K}+1}({\mathbf{X}}^{\prime }\mathbf{X})\ge {\text{λ}}_{\tilde{K}}({\mathbf{X}}^{\prime }\mathbf{P}\mathbf{X})/{\text{λ}}_{\tilde{K}+1}({\mathbf{X}}^{\prime }\mathbf{P}\mathbf{X})$ and choose PPCA vice versa. The intuition is that we favor the method that yields larger eigen-ratio between the spiked and non-spiked part of the covariance.

Analogous to the simulation study in our paper, we generate m = 1,000 people’s BOLD data based on calibrated “true” data. We investigate the accuracy of the proposed $\widehat{K}$, $\tilde{K}$ and Ǩ for two cases: (i) n_i = 20,p = 264 and (ii) n_i = 100, p = 264, presented in Table 4. As we can see from the table, when n_i is small, $\tilde{K}$ outperforms $\widehat{K}$, and when n_i is large, $\widehat{K}$ is better. Note also that our heuristic estimator Ǩ has great performance in both cases of large and small n_i.

Table 4.

Accuracy of $\widehat{K}$, $\tilde{K}$ and Ǩ

		ni = 20		ni = 100
	TotErr	OverEst	UnderEst	TotErr	OverEst	UnderEst
$\widehat{K}$	38.7%	0%	38.7%	0.7%	0%	0.7%
$\tilde{K}$	29.7%	6.8%	22.9%	4.7%	2.7%	2.0%
Ǩ	29.7%	6.8%	22.9%	3.5%	2.3%	1.2%

Given the performance of our proposed estimators of the factor number, we now artificially enlarge this estimation error and see how it affects the Gaussian graphical model analysis. Let η be a random perturbation with P(η = 0) = 1/2, P(η = 1) = 1/3 and P(η = 2) = 1/6. Define K⁺: = K + η and K⁻: = max(K−η,0), where K is the true number of factors. As the notations indicate, K⁺ overestimates the factor number while K⁻ underestimates it. Since P(η ≠ 0) = 1/2, their estimation accuracy is only 50%, worse than that of $\widehat{K}$ and $\tilde{K}$ as presented. We use K⁺ and K⁻ as the estimators of the number of factors respectively to recover the precision matrix of U and compare their performance with that of Ǩ. The results are presented in Table 5.

Table 5.

Gaussian Graphical Model Analysis

	ni = 20			ni = 100
	$||\widehat{\mathbf{\Omega }}-\mathbf{\Omega }|{|}_{\text{max}}$	$||\widehat{\mathbf{\Omega }}-\mathbf{\Omega }|{|}_1$	$||\widehat{\mathbf{\Omega }}-\mathbf{\Omega }|{|}_2$	$||\widehat{\mathbf{\Omega }}-\mathbf{\Omega }|{|}_{\text{max}}$	$||\widehat{\mathbf{\Omega }}-\mathbf{\Omega }|{|}_1$	$||\widehat{\mathbf{\Omega }}-\mathbf{\Omega }|{|}_2$
Oracle	0.687	4.131	1.311	0.335	2.018	0.695
Ko	0.873	2.824	1.351	0.536	2.006	2.017
Ǩ	1.156	8.581	2.950	0.564	3.445	1.188
K +	0.771	3.27	1.49	0.586	2.154	1.074
K −	1.618	11.384	4.062	1.84	15.133	4.941

“Oracle” above means that we directly use the generated noise U to calculate its sample covariance and plug it in CLIME to recover the precision matrix. K^o means we know the true number of pervasive factors, and use PCA or Projected-PCA (choosing the method that yields larger eigen-ratio) to adjust factors. As we can see from the table above, K⁺ is nearly as good as K^o, which means that overestimating the number of factors does not hurt the recovery accuracy. In contrast, underestimating the number factors will seriously increase the estimation error of Ω, as shown by K⁻, because the unadjusted pervasive factors heavily corrupt the covariance of U. Nevertheless, both K⁺ and K⁻ uses partial information of the true number of factors. In comparison, our procedure Ǩ, without any prior knowledge about the number of factors, have a great performance in recovering Ω.