Impact of nuclear vibrations on van der Waals and Casimir interactions at zero and finite temperature

Van der Waals interactions in atomistic systems depend strongly on temperature, vibrational effects, and dimensionality.

Abstract

Recent advances in measuring van der Waals (vdW) interactions have probed forces on molecules at nanometric separations from metal surfaces and demonstrated the importance of infrared nonlocal polarization response and temperature effects, yet predictive theories for these systems remain lacking. We present a theoretical framework for computing vdW interactions among molecular structures, accounting for geometry, short-range electronic delocalization, dissipation, and collective nuclear vibrations (phonons) at atomic scales, along with long-range electromagnetic interactions in arbitrary macroscopic environments. We primarily consider experimentally relevant low-dimensional carbon allotropes, including fullerenes, carbyne, and graphene, and find that phonons couple strongly with long-range electromagnetic fields depending on molecular dimensionality and dissipation, especially at nanometric scales, creating delocalized phonon polaritons that substantially modify infrared molecular response. These polaritons, in turn, alter vdW interaction energies between molecular and macroscopic structures, producing nonmonotonic power laws and nontrivial temperature variations at nanometric separations feasible in current experiments.

INTRODUCTION

Van der Waals (vdW) interactions play an integral role in binding and interaction energies of molecules in condensed phases (1), and their long-range many-body nature (2, 3) can modify phonons in molecular crystals to the extent of producing qualitatively different predictions of thermodynamic stability at finite temperature compared to common pairwise approximations (4, 5). However, while these treatments of many-body vdW interactions account for multiple scattering and electromagnetic (EM) screening to all orders and derive material properties from ab initio calculations, they only account for valence electrons and not phonons in the molecular response, despite the large role of the latter in interactions at finite temperature; moreover, these treatments neglect EM retardation, which becomes important at length scales where phononic contributions to molecular response also become important. These accounts of phonons have more typically arisen in continuum treatments of Casimir interactions, where polarizable objects are modeled as dipoles or continuum local dielectrics, with infrared resonances determined empirically (6–8). In the related domain of thermal radiation, vibrational resonances have been treated atomistically via mechanical Green’s function (9, 10) as well as molecular dynamics (11) methods, but these have the respective pitfalls of being limited to bulk materials or using heuristic pairwise approximations to noncovalent interactions.

Here, we develop and apply a framework for computing retarded, many-body (RMB) vdW interactions in mesoscopic systems, where molecules can be treated in an ab initio atomistic way and larger bodies can be treated via continuum electrodynamics, to include the impact of phonons and dissipation in molecular response as well as finite temperature, based on related recent developments (12). In particular, we focus on the interactions of fullerenes, carbyne wires, and graphene and hexagonal boron nitride (BN) sheets with a gold surface, which we approximate as a perfect electrically conducting plane for computational simplicity, and compare interaction energies with and without phonon contributions at zero and room temperatures to each other, as well as to predictions from dipolar and continuum treatments where appropriate. We find that phonons can substantially delocalize the molecular response, which is especially relevant when the molecule is close to the surface, in a manner strongly dependent on the molecular dimensionality, size, and dissipation properties, due to the shape-dependent coupling of those phonons with EM fields to form phonon polaritons. Moreover, in contrast to common macroscopic treatments of Casimir forces in bulk media, which find nontrivial temperature effects only at large separations of at least 1 μm (13), we find that phonon-induced nonlocality can lead to temperature-sensitive vdW interactions even at small separations. In particular, we show that “zero-dimensional” compact fullerenes exhibit strong shifts in vdW interaction free energies with temperature even in the far field compared to standard predictions for dipolar oscillators, while “one-dimensional” carbyne wires also exhibit further large quantitative and qualitative deviations, including nonmonotonic power laws, at much smaller nanometric separations. By contrast, “two-dimensional” graphene sheets have many more avenues for dissipation and stronger bonds than isolated compact molecules, leading to damping of the nonlocal response, in which case finite temperature effects, while larger than previously predicted, only become evident at larger (tens of nanometers) separations. We expect our predictions to be relevant to ongoing experiments on vdW interactions among molecules and metallic objects at nanometric scales (14).

RESULTS

Retarded many-body framework

The RMB expression for the vdW interaction free energy at temperature T among a collection of N_mol disjoint molecules in an arbitrary macroscopic environment is (12)

$$\mathcal{F}=k_{\mathrm{B}}T{\displaystyle \sum _{n=0}^{\infty }}\prime \begin{array}{c}\underbrace{\text{ln} (\text{det} ({\mathbb{T}}_{\infty }{\mathbb{T}}^{-1}))}\\ \mathrm{\Phi }(\mathrm{i}{\mathrm{\xi }}_n)\end{array}$$ (1)

whose integrand Φ(iξ), evaluated at the Matsubara frequencies ${\mathrm{\xi }}_n=\frac{2\mathrm{\pi }{k}_{\mathrm{B}}\mathit{Tn}}{\hslash }$ (with a half-weight on the n = 0 term in the sum, denoted by a prime), depends on the inverse of the scattering T operator ${\mathbb{T}}^{-1}={\sum }_l{\mathbb{V}}_l^{-1}-{\mathbb{G}}_{\text{env}}$, which encodes EM scattering to all orders among the molecules l of susceptibilities V_l mediated by the macroscopic environment whose Maxwell Green’s function is ${\mathbb{G}}_{\text{env}}$, and ${\mathbb{T}}_{\infty }^{-1}={\prod }_l{\mathbb{T}}_{l\infty }^{-1}$, which encodes the scattering properties of each molecule isolated in vacuum via ${\mathbb{T}}_{l\infty }^{-1}={\mathbb{V}}_l^{-1}-{\mathbb{G}}_0$ in terms of the vacuum Maxwell Green’s function ${\mathbb{G}}_0$; note that all of these quantities depend on iξ, but this is suppressed for notational brevity.

For the insulating and weakly metallic atomistic systems we consider, we describe the molecular susceptibilities via (15, 16)

$${\mathbb{V}}_l=-\frac{{\mathrm{\xi }}^2}{c^2}{\displaystyle \sum _{p,i,q,j}}{\mathrm{\alpha }}_{\mathit{pi},\mathit{qj}}\mid {\mathbf{f}}_{\mathit{pi}}\rangle \langle {\mathbf{f}}_{\mathit{qj}}\mid$$ (2)

in terms of localized basis functions ∣f_pi〉 representing the EM response of valence electrons via dipolar ground-state wave functions of effective polarizabilities α_pi,qj. The polarizability matrix α_pi,qj is constructed from a partitioning of the ground-state electron density of the microscopic system, computed from ab initio density functional theory (DFT) methods including short-range quantum exchange and correlation effects, into atomic fragments, which are then mapped onto a set of coupled valence electronic and nuclear oscillators for each atom (Fig. 1) (see Methods for more details). Our inclusion of nuclear oscillations contrasts with past iterations of the RMB framework, which only captured the high-frequency behavior of electronic oscillations, and leads to the emergence of collective vibrations (phonons) at infrared and lower frequencies, in turn delocalizing the susceptibility. The impact of this nonlocality on EM interactions, especially at short distances, is captured through our use of atom-centered Gaussian basis functions (3, 15)

$${\mathbf{f}}_{\mathit{pi}}(x)={\left(\sqrt{2\mathrm{\pi }}{\mathrm{\sigma }}_p\right)}^{-3}\text{exp}[-\frac{{(\mathbf{x}-{\mathbf{r}}_p)}^2}{2{\mathrm{\sigma }}_p^2}]{\mathbf{e}}_i$$ (3)

centered at the equilibrium atomic positions r_p, polarized along the Cartesian direction e_i, and normalized so that ∣ ∫ f_pi(x) d³x ∣ = 1. The isotropic widths σ_p of these basis functions are chosen at each frequency as

$${\mathrm{\sigma }}_p(i\mathrm{\xi })=\frac{1}{\sqrt{4\mathrm{\pi }}}{\left(\frac{\mid {\mathrm{\alpha }}_p(i\mathrm{\xi })\mid }{3}\right)}^{1/3}$$ (4)

such that a dipolar oscillator of isotropic polarizability α_p has the same self-interaction energy $-\frac{{\mathrm{\xi }}^2}{3c^2}{\sum }_i\langle {\mathbf{f}}_{\mathit{pi}}\mid {\mathbb{G}}_0{\mathbf{f}}_{\mathit{pi}}\rangle$ as that of a Gaussian dipole distribution in vacuum. The effective atomic polarizabilities α_p are constructed from the overall molecular polarizability matrix α_pi,qj via

$${\mathrm{\alpha }}_p(\mathrm{i\xi })=\frac{1}{3}{\displaystyle \sum _{q,j}}{\mathrm{\alpha }}_{\mathit{pj},\mathit{qj}}(\mathrm{i\xi })$$ (5)

so that they and, in turn, the Gaussian basis functions capture the spatial extent of nonlocality in the molecular response due to phonons at low frequencies.

Fig. 1. RMB model of molecular response.

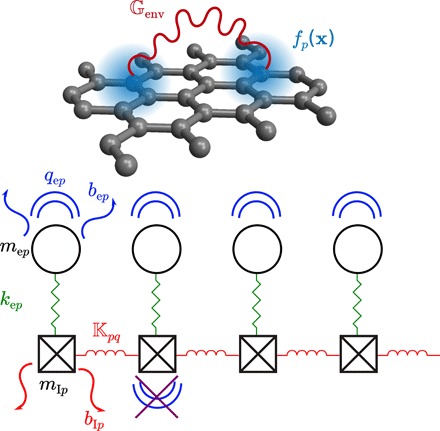
A collection of atoms with electronic polarization response modeled as Gaussian basis functions f_p(x) interact via long-range EM fields ${\mathbb{G}}_{\text{env}}$. The individual electronic response of each atom arises from the coupling of valence electronic and phononic excitations via short-range interactions, represented schematically: For every atom p, a nuclear oscillator of mass m_Ip with dissipation b_Ip is connected to nuclear oscillators of other atoms q via anisotropic spring constants ${\mathbb{K}}_{\mathit{pq}}$, and to an electronic oscillator of mass m_ep with dissipation b_ep and isotropic spring constant k_ep; only the electrons couple directly to long-range EM fields with effective charge q_ep.

We demonstrate that the combination of nonlocal response due to phonons, leading to the smearing and renormalization of divergent short-range EM interactions, and the interactions of those phonons with long-range EM fields to yield phonon polaritons strongly modifies vdW free energies at zero and room temperatures (T = 0 and 300 K, respectively), as captured in the power law dependence of the free energy on the separation of each microscopic system considered from the macroscopic gold surface, as well as the ratios of free energies between zero and room temperatures. In particular, we define the power law as follows

$$\text{Power law}=\frac{\partial \text{ln} (\mid \mathcal{F}\mid )}{\partial \text{ln}(z)}$$ (6)

While we primarily consider low-dimensional carbon allotropes, we find that these modifications depend strongly on molecular geometry and dissipation. For the cases of fullerene and carbyne, we compare the results in our RMB framework with phonons to those in the RMB framework neglecting phonons, which changes the form of the susceptibility to be local, as encoded in the polarizability matrix α_pi,qj being diagonal in the atom-centered basis; the corresponding free energy is denoted ${\mathcal{F}}_{\text{e}}$. In addition, for the case of carbyne, we compare with the Casimir-Polder (CP) approximate free energy

$${\mathcal{F}}_{\text{CP}}=-k_{\mathrm{B}}T{\displaystyle \sum _{n=0}^{\infty }}\prime \text{Tr}[{\overleftrightarrow{\mathrm{\alpha }}}^{\text{CP}}(i{\mathrm{\xi }}_n)\cdot {\overleftrightarrow{\mathrm{G}}}_{\text{sca}}(i{\mathrm{\xi }}_n,\mathbf{r},\mathbf{r})]$$ (7)

defined in terms of the scattering Green’s function ${\mathbb{G}}_{\text{sca}}={\mathbb{G}}_{\text{env}}-{\mathbb{G}}_0$ and an effective polarizability tensor ${\mathrm{\alpha }}_{\mathit{ij}}^{\mathit{CP}}={\sum }_{p,q}\langle {\mathbf{f}}_{\mathit{pi}}\mid {\mathbb{T}}_{l\infty }{\mathbf{f}}_{\mathit{qj}}\rangle$ contracting the molecule to a point dipole such that it includes long-range interactions among molecular degrees of freedom in vacuum to infinite order in the scattering, but only to lowest order with the surface. Last, for the case of graphene, we compare to predictions obtained from common macroscopic (continuum) models.

Zero-dimensional fullerene

We begin with the case of a zero-dimensional fullerene above the gold surface (Fig. 2). An isolated fullerene will not have the same dissipation mechanisms as a fullerene in solution (6), so we neglect the dissipation altogether; however, we constrain the center of mass of this isolated molecule by fixing the positions of two nuclei on opposite sides of the fullerene. At large z, the finite size of the fullerene is negligible, so it may be treated like a point dipole with respect to scattering from the plate. Without phonons, the susceptibility is characterized by a single frequency scale arising from the electronic response (Fig. 2A), so when the cutoff frequency c/z falls below that as z increases (Fig. 2B), the power law monotonically approaches the standard retarded dipolar limit of −4 at zero temperature (Fig. 2C). At room temperature, the power law will eventually increase to −3 only when z becomes comparable to the thermal wavelength, ℏc/(k_BT) ≈ 7.6 μm, because once the cutoff frequency c/z falls below the first Matsubara frequency 2πk_BT/ℏ, only the zero Matsubara frequency will contribute. These predictions are similar to predictions from macroscopic formulations of Casimir physics (6); namely, in the absence of phonons, the free energies at zero versus room temperatures are essentially identical for z ≤ 1 μm, like in typical macroscopic situations.

Fig. 2. Impact of phonons at large separations of a fullerene from the gold plate.

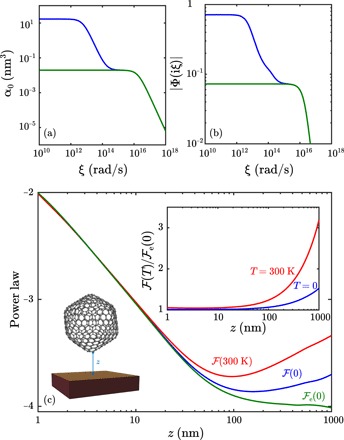
(a) Representative polarizability of an individual atomic constituent of a fullerene molecule suspended above a gold plate by a surface-surface gap z, comparing the full (including phonons) α (blue) and purely electronic α_e (green) polarizabilities. (b) RMB free energy integrand Φ(iξ) as a function of imaginary frequency ξ corresponding to $\mathcal{F}$ (blue) and $\mathcal{F}$_e (green) at a fixed z = 1 nm. (c) RMB power laws for $\mathcal{F}$(0) (blue), $\mathcal{F}$(300 K) (red), and $\mathcal{F}$_e(0) (green). Inset: Energy ratios $\mathcal{F}$(T)/$\mathcal{F}$_e for the fullerene at zero (blue) or room (red) temperature.

Matters change drastically when phonons are considered, in which case the susceptibility is characterized by two frequency scales due to the vastly different nuclear and electronic masses. Even for z ≤ 1 μm, as z increases, these frequency scales compete with the cutoff frequency c/z to produce pronounced nonmonotonic interaction power laws for both zero and room temperatures; the onset of this deviation based on temperature occurs at separations far smaller than one would expect from common macroscopic predictions. This substantial sensitivity to temperature at small z ≈ 100 nm illustrates that even for a small, compact molecule like fullerene, the interplay between phononic response and long-range EM fields can make the interaction power laws deviate substantially from typical macroscopic predictions. The increased relative importance of phononic response at large z also leads to strong deviations of the free energy ratios $\mathcal{F}$(T)/$\mathcal{F}$_e(0) from 1 for large z at both temperatures (Fig. 2C). At smaller separations, the finite size and curved spherical shape of the fullerene dominate the interaction power law. Because of the small size of the fullerene, at larger frequencies ∼ c/z, phonons neither substantially delocalize the molecular response nor strongly couple to EM fields, consistent with the fact that Gaussian widths throughout the molecule are smaller than the smallest value of z = 1 nm considered here. Hence, all three power laws converge upon each other for z ∈ [1 nm,10 nm], and the free energy ratios also converge to 1 in this limit. Note that at z ≈ 100 nm, where the power laws exhibit nonmonotonic behavior, the vertical vdW force on the fullerene by the surface is 1.38 × 10⁻¹⁸ N at room temperature with phonons, which is far smaller than currently measurable in state-of-the-art vdW or Casimir force experiments (14, 17, 18); likewise, the magnitude of the interaction free energy at that separation is less than 10⁻²⁵ J [see the Supplementary Materials for more details, which refers to (19–31)]. That said, if these forces were measurable, the force at that separation would be 15% larger than the prediction of 1.20 × 10⁻¹⁸ N for the room temperature force without phonons.

One-dimensional carbyne

We now turn to the case of a one-dimensional carbyne wire (Fig. 3). As with the fullerene, we assume dissipation to be negligible when the molecule is in isolation and constrain the nuclei at each end of the wire to remain fixed. While the qualitative behaviors of the interaction power laws ∂ ln (F)/∂ ln (z) for a wire at large z above a gold plate are similar to those of the fullerene, the elongated shape of the wire allows it to support longer-wavelength phonons, which couple much more strongly to low-frequency and infrared EM fields, leading to a richer dependence on separation and temperature even for z < 100 nm. To better understand the physics of these interactions, we compare the RMB predictions to those from the CP approximation of (7) for a 500-atom-long carbyne wire above a gold plate.

Fig. 3. Nonmonotonicity and temperature deviations due to phonon-induced nonlocal response in carbyne at short distance from the gold plate.

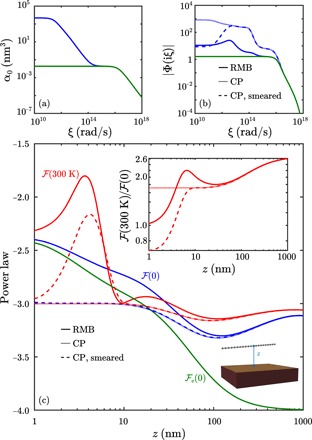
(a) Polarizability as a function of imaginary frequency for the middle atom (0) in a 500-atom-long carbyne wire, comparing α (blue) to α_e (green). (b) Imaginary frequency integrands for $\mathcal{F}$ (blue) and $\mathcal{F}$_e (green) at z = 1 nm via RMB (solid) or CP, without (fine dashed) or with (coarse dashed) artificial smearing. (c) RMB (solid) and CP, without (fine dashed) or with (coarse dashed) artificial smearing, interaction power laws of a 500-atom-long carbyne wire parallel to a gold plate, for $\mathcal{F}$(0) (blue), $\mathcal{F}$(300 K) (red), and $\mathcal{F}$_e(0) (green). Inset: Free energy ratios $\mathcal{F}$(300 K)/$\mathcal{F}$(0) as functions of z via RMB (solid) or CP, without (fine dashed) or with (coarse dashed) artificial smearing.

For a 500-atom-long carbyne wire, delocalization in the response due to phonons has the strongest effect at low frequencies, leading to static Gaussian basis function widths σ₀(ω → 0) ≈ 3.3 nm at the middle of the wire. Figure 3A plots α₀ ∼ σ₀(iξ)³ as a function of ξ, showing the existence of two characteristic frequency scales arising from the much stronger phonon-induced electronic delocalization at infrared wavelengths. In contrast, the response in the absence of phonons exhibits only a single frequency scale, and the Gaussian widths never exceed 1 Å. These enlarged Gaussian smearing widths lead to nonmonotonicity in the RMB integrand (Fig. 3B) with respect to ξ for z < σ₀(0), as the Gaussian basis functions overlap with the response of the gold plate (i.e., interactions with image basis functions in the perfectly conducting limit). This nonmonotonicity cannot be observed in the absence of phonons, as the bare susceptibility is essentially local in that case. However, as this nonmonotonicity occurs for very small ξ in the integrand, the behavior of the RMB power law at zero temperature with phonons with respect to z is less sensitive to the nonmonotonic integrand, simply approaching the power law without phonons as z decreases (Fig. 3C). By contrast, at room temperature, the RMB power law with phonons shows substantial deviations from that at zero temperature even up to z < 20 nm; essentially, the sampling of Matsubara frequencies at room temperature makes the free energy disproportionately sensitive to the response at static and infrared ξ. In addition, the sensitivity of these vdW interactions at room temperature to the response at infrared and smaller ξ leads to a free energy ratio $\mathcal{F}$(T)/$\mathcal{F}$(0) that exceeds 2 even for z < 20 nm, and that energy ratio is nonmonotonic because the zero and room temperature RMB free energy power laws with phonons cross each other. At large z, the magnitude of the RMB free energy ratio $\mathcal{F}$(300 K)/$\mathcal{F}$(0) is consistent with recent work by Maghrebi et al. (32), which shows the sensitivity of this energy ratio to geometry for continuum objects even in the absence of nonlocal response. Note that at z = 4 nm, the vertical force on the wire at room temperature is 1.11 × 10⁻¹¹ N with phonons, and as can be observed from the power laws and energy ratios, the ratio of room to zero temperature forces is approximately 1.2; in addition, the room temperature force without phonons is 8.3 × 10⁻¹² N, which is 25% smaller than the prediction with phonons. Both the forces themselves and their differences with respect to temperature should therefore be measurable and resolvable in state-of-the-art Casimir experiments (33), although it should be pointed out that long free-standing carbyne wires have not been stably fabricable, and carbyne has only been found in solution or confined to supramolecular structures like carbon nanotubes (34, 35).

To better understand these phenomena, we compare these results to those obtained by the CP approximation, where the phonon polaritonic response is contracted into a point dipolar polarizability. We find that if the response is associated with a Dirac delta basis function characteristic of an ideal point dipole, the integrand monotonically and markedly drops as ξ increases, so the resulting vdW interaction power laws for z < 20 nm are monotonic at zero and finite temperature, and the energy ratios asymptotically approach a constant larger than 1 as z → 0. However, if the response is associated with a Gaussian basis function whose width σ₀(iξ) is artificially chosen to match that used in the RMB framework, the overlap of the basis function with its reflected image for z < σ₀(0) will lead to nonmonotonic integrands, and thus nonmonotonic power laws at room temperature, although such a “smeared CP approximation” still leads to quantitative differences compared to RMB, as it neglects explicit consideration of the finite molecular size and geometry. In any case, for z > σ₀(0), the CP approximate power laws converge to each other irrespective of basis function choice, and both converge to the corresponding RMB power laws at each respective temperature at much larger z.

To conclude the discussion of carbyne, we point out that nonmonotonic power laws are not merely an artifact of the overlap of enlarged Gaussian basis functions with the gold plate but can be seen even at zero temperature for parallel carbyne wires in vacuum. In addition, we point out that the nonmonotonic behavior in the room temperature power law can be seen as a bump in the corresponding free energy in that range of separations, with the magnitude of the interaction free energy at room temperature exceeding 10⁻²⁰ J there. Further details concerning both of these points are provided in the Supplementary Materials.

Two-dimensional graphene or BN

Last, we consider two-dimensional atomically thin materials above the gold plate, starting with an infinite graphene sheet. Unlike fullerene molecules or carbyne wires, atomically thin graphene sheets can be exfoliated and suspended in vacuum (36, 37); therefore, compared to the other aforementioned carbon allotropes, there is substantially more theoretical and experimental work characterizing the mechanical and vibrational (22, 38), electronic (39), and thermal (40) properties of graphene. In the particular context of vdW interactions, several theoretical macroscopic models for the response of graphene have been used. Given this, we specifically compare our RMB predictions to those obtained from a Lifshitz formula of the Casimir interaction between a graphene and a plate, based on a tight-binding model of the electronic band structure of graphene. Such a model is consistent with the random phase approximation (RPA) (41) and includes spatial dispersion and the possibility of doping but does not consider contributions from phonons or other dissipation mechanisms. In contrast, our RMB model of graphene explicitly includes phonons, and because extended graphene has many more channels for damping of the response, we include explicit nonzero dissipation terms in the susceptibility (see Methods for more details), unlike our neglect of dissipation in fullerene and carbyne.

Casimir and vdW interactions involve sums over all frequencies (1), in which case the infrared response (including both temporal and spatial dispersion) is expected to be relevant. We therefore begin by demonstrating the differences in the graphene nonlocal susceptibility χ(iξ, k) (see Methods for more details) in our RMB framework (Fig. 4A) compared to the RPA model (Fig. 4B) in the absence of doping and at zero temperature. In the RMB model, at small ξ, and especially at small k, corresponding to nearly spatially uniform incident fields, contributions from long-wavelength acoustic phonons tend to dominate, delocalizing the electronic response over several primitive unit cells and drastically increasing ∣χ∣ to more than 100; as ∣k∣ increases, so too do the contributions of localized optical phonons, decreasing the magnitude and nonlocality of the response. It is only for ξ > 10¹⁴ rad/s that phonons no longer contribute appreciably to the response, so ∣χ∣ is essentially independent of k and its magnitude is less than 10, consistent with RPA and decaying quickly as ξ increases further. In contrast to RMB, the electronic orbitals in the RPA model are tightly bound to fixed nuclei, in which case the resulting response vanishes as k → 0 for nonzero frequency, and hence χ increases with increasing ∣k∣, in qualitative opposition to the RMB prediction. In particular, in the short-wavelength regime, χ approaches a constant asymptote $q_{\mathrm{e}}^{2}g/(32\hslash {\mathrm{ϵ}}_0{v}_{\mathrm{F}})\approx 4$ at a rate controlled by ξ, which is far smaller than the RMB prediction at low ξ. Given that the π orbitals within RPA are tightly bound to nearby nuclei, one would expect that phonons should have a substantial impact upon the valence electronic and static response of graphene. The low-frequency behavior of metals is particularly important in the context of vdW interactions, as exemplified by recent discrepancies in the response of Drude versus plasma models of gold (33).

Fig. 4. Phononic versus purely electronic response and vdW interactions in graphene.

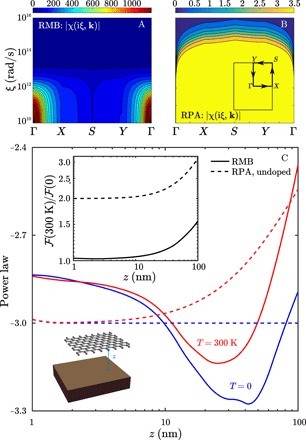
Magnitude of the Fourier space susceptibility ∣χ(iξ, k)∣ of a pristine (undoped) graphene sheet with rectangular unit cell 3.9 nm × 3.4 nm, obtained via either (A) RMB or (B) macroscopic, random-phase approximation (RPA) (41) models. (C) Power law of interaction free energy for a graphene sheet suspended above gold plate by a vacuum gap z, at zero (blue) or room (red) temperature, comparing RMB (solid) results to macroscopic RPA (dashed) predictions without doping. The inset shows the interaction free energy ratios $\mathcal{F}$(300 K)/$\mathcal{F}$(0) as a function of z.

We now compare the predictions of both RMB and RPA models for the vdW interaction free energy per unit area of graphene above a gold plate, at both zero and room temperatures. In particular, Fig. 4C shows the free energy power law and corresponding energy ratios, with respect to the gap separation z. The RPA model is analyzed in the absence of electronic doping. Our RMB predictions for the power laws are qualitatively similar to those of the fullerene in that the delocalization in the response due to phonons leads to power laws at both temperatures that are nonmonotonic, although the higher dimensionality of graphene compared to fullerene or carbyne causes the onset of nonmonotonic behavior to arise at smaller z, around 20 nm, than for the fullerene or carbyne. Likewise, as the impact of phonons is more pronounced at larger temperatures, the energy ratio starts to deviate noticeably from 1 at z, not much smaller than 20 nm. Note that, at z = 100 nm, the ratio of the vertical forces at room to zero temperatures is approximately 1.3 and the corresponding pressure at zero temperature is approximately 1 N/m², so these differences should be measurable in state-of-the-art experiments involving graphene (42, 43); in addition, the free energy per unit area exceeds 10⁻⁸ J/m² in magnitude at that separation, with more details in the Supplementary Materials. Compared to our previous predictions in carbyne systems, the assumption of much larger dissipation in graphene substantially dampens and smears the impact of long-wavelength acoustic phonons, limiting the phonon mean free path and hence the spatial extent of delocalization in our Gaussian widths σ to a much greater degree. Consequently, we observe energy ratios much closer to 1 and monotonic power laws at small separations z < 20 nm. In contrast, the RPA power law is a constant −3 at zero temperature over all z, while it increases monotonically toward −2 at finite temperatures. In addition, since this RPA model does not include phonons, there is no nonmonotonic behavior in the power laws, and the RPA power laws are consistently above −3 in the range of separations z that we consider, unlike the RMB power laws that drop below −3 for z around 20 nm. However, the RPA free energy ratio is 2, rather than 1, even at z = 1 nm, and increases monotonically to 3.2 by z = 100 nm. This is because, in the absence of doping, electrons fill the band structure exactly up to the Dirac point, so thermal fluctuations at room temperature can have a much larger relative effect on the response. In contrast, the material model entering the RMB framework for all materials we consider, including both DFT calculations and atom-centered partitioning of the density, is formulated at zero temperature, and thermal effects are only considered via the Matsubara summation. A more consistent model of atomistic response would account for the effects of finite temperature on the mechanical structure and phonon dispersion of graphene itself.

Developments before the RMB framework, particularly the many-body dispersion (MBD) framework, have shown strong agreement with experimental measurements and state-of-the-art theoretical predictions of static binding energies, equilibrium structures, and elastic moduli in single and multiple layers of graphene, BN, and other two-dimensional materials (44, 45). This suggests that the RMB framework can accurately capture the contributions of phonons and EM retardation to long-range vdW interaction forces involving large molecules and spatially extended low-dimensional materials, including two-dimensional materials, due to our ab initio consideration of both effects. However, the interplay between phonons and inherently delocalized electrons, like that observed in the semimetallic Dirac cone electronic structure in pristine graphene, may not be fully captured in the material model of single electronic oscillators associated with each atom, and this could have further effects [Dobson type C nonadditivity (46)] on the interaction power laws at nanometric and larger separations, which go beyond the regimes typically considered by the MBD framework for binding energies and structural properties. Having examined semimetallic pristine graphene, we now consider atomically thin hexagonal BN (Fig. 5), which behaves as a polar dielectric and which we expect, in the absence of other experimental evidence, may be more accurately described by the material model of single electronic and nuclear oscillators associated with each atom. Numerical difficulties preclude consideration of an infinite BN sheet with periodic boundary conditions as we did with graphene, so we use supercells of approximate dimensions 11 nm × 10 nm in each case, with atoms at two of the four opposite corners constrained, and only consider z ≤ 10 nm to mitigate sampling of finite size effects. The RMB calculations of vdW interactions show similar power laws for $\mathcal{F}$_e (without phonons) for graphene and BN in the range z ∈ [1 nm,10 nm], which suggests the need for more work to distinguish electronic structure effects between graphene and BN even at low frequency; that said, phonons dominate the response, so when their contributions are included, it is less unexpected that the similar nuclear masses, geometries, and resulting internuclear couplings K_I of the two systems lead to negligible qualitative distinctions between the two systems. In particular, at z = 2 nm, where the nonmonotonic behavior of the room temperature power law is most prominent for graphene as well as BN, the room temperature force per unit area is 2.80 × 10⁶ N/m² with phonons versus 2.57 × 10⁶ N/m² without phonons for BN, compared to 2.86 × 10⁶ N/m² with phonons versus 2.62 × 10⁶ N/m² without phonons for graphene. We emphasize the sensitivity of the RMB predictions to the confluence of material effects, dimensionality, and boundary conditions: Finite size leads not only to quantitative deviations when the separation approaches the supercell size but also to qualitative deviations as the room temperature power law for the graphene supercell exhibits nonmonotonic behavior for z < 10 nm, which is similar to the behavior of the compact carbyne wire but different from infinite pristine graphene.

Fig. 5. Graphene versus BN interaction power laws at short separations.

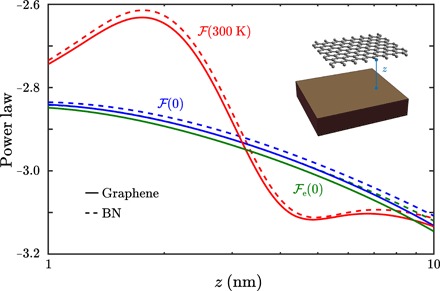
RMB power laws for the vdW interactions of parallel graphene (solid) or hexagonal BN (dashed) rectangular supercell with a gold plate, without phonons (green) or with phonons at zero (blue) or room (red) temperature.

At this initial stage, the RMB framework may do a better job handling insulating two-dimensional materials like BN or graphene with defects (whether in the form of vacancies or foreign atoms or molecules) (47) compared to semimetallic pristine graphene. That said, we expect that further development of the electronic response model used in the RMB framework will allow it to accurately model vdW interactions along the range of insulating to semimetallic low-dimensional materials as well as in electronically doped systems like graphene (which we discuss in the Supplementary Materials), which become more metallic due to the fully delocalized response of free mobile charge carriers. This ultimately requires changing the form of the susceptibility V and the corresponding basis functions, without changing the general formula for the vdW energy in terms of EM Green’s functions and scattering operators, thereby clarifying that the improvements must come from the side of material modeling rather than from modified consideration of long-range EM interactions.

DISCUSSION

We have demonstrated the strong influence of nonlocal response arising from phonons on the vdW interactions of molecular systems, particularly highlighting the dependence of these effects on molecular shape, size, temperature, and material dissipation. These effects can conspire to produce changes in the vdW interaction energy, relative to treatments that neglect phonons or finite temperature, which should be measurable with state-of-the-art experiments, particularly at nanometric separations where macroscopic treatments of Casimir forces in bulk media (13, 33) predict negligible temperature effects.

The characteristics of molecular vibrations (phonons) in our calculations were derived from covalent bond properties, so one might expect more delocalization of electronic response along the bonds than perpendicular to them. This implies that further accuracy in modeling could be achieved by using anisotropic Gaussian widths to account for this anisotropy. For example, in carbyne, the ratio of transverse to longitudinal internuclear spring coupling coefficients between nearest neighbors is 0.04, while this difference is approximately 0.35 in graphene, so the strong anisotropy in the nonlocal response should be captured in the Gaussian widths to more accurately model the material response at short separations.

In addition, a more accurate comparison between the RMB predictions and those of macroscopic models for undoped graphene requires smaller dissipation rates, which is likely to result in more temperature-sensitive energies (potentially leading to nonmonotonic behavior at small z akin to those observed in carbyne wires). However, the computational complexity of simulating large unit cells supporting more strongly delocalized phonons makes such a demonstration challenging, so we aim to address this issue in future work.

Last, we expect that compared to zero temperature, thermal fluctuations at room temperature will substantially alter the mechanical structures and phonon properties of all of the systems we have considered in this paper. We anticipate needing to incorporate such effects at the level of DFT and include the effects of changes in the atomistic geometries within the RMB framework; fleshing out these details will be the subject of future work.

METHODS

Molecular response in the retarded many-body framework

We describe the construction of the polarizability matrix α_pi,qj entering the molecular susceptibilities (2) for the insulating or weakly metallic atomistic systems that we consider. As we assume short-range correlations to be negligible between molecules, we compute the ground-state electron density of each molecule in isolation via DFT in the Born-Oppenheimer approximation; the nuclear coordinates are, in turn, varied to relax each molecular shape to its ground state, yielding ground-state densities and nuclear coordinates that incorporate short-range quantum exchange, correlation, hybridization, and electrostatic effects. We then apply Hirshfeld partitioning to the ground-state electron density due to its localization, yielding atomic fragments for the electron density that are then used with the electron densities of the corresponding isolated atoms to produce static electronic polarizabilities α_ep(0) associated with each atom p. These fragments are then mapped onto a set of coupled harmonic oscillators for each atom p in each molecule, namely, a single effective electronic oscillator of charge q_ep, mass m_ep, spring constant k_ep connecting only to the nucleus, and damping coefficient b_ep, which together describe the valence electrons, and a single nuclear oscillator of mass m_Ip, anisotropic spring constants ${\mathbb{K}}_{\mathit{pq}}$ connecting to other nuclei, and damping coefficient b_Ip, which together represent the nuclei screened by inner electrons that give rise to phonons. Our consideration of single electronic oscillators effectively represents an Unsöld approximation (48), which, in principle, could be relaxed by assigning multiple oscillators to account for many different possible electronic transitions. Within the Unsöld approximation, for the purpose of constructing the molecular response, the electronic oscillator in each atom is initially taken to be undamped (with dissipation to be added later); given α_ep(0), the electronic oscillator frequencies ω_ep are computed by fitting the oscillator dispersion to nonretarded vdW C₆ coefficients for each atom taken from a large reference of theoretical and experimental atomic and small molecular data (15, 48). From this, the effective number of electrons N_ep associated with that atom can be determined, and so can the effective charge q_ep = N_epq_e, mass m_ep = N_epm_e, and isotropic spring constant k_ep; these quantities, by virtue of deriving from α_ep(0) and ω_ep, encode the same short-range quantum and electrostatic effects present in DFT and other high-level quantum calculations (3, 15). The nuclear masses are taken from elemental data as they are four orders of magnitude larger than the electronic masses, while the internuclear spring constants ${\mathbb{K}}_{\mathit{pq}}$ are computed as the second spatial derivatives of the ground-state energy in DFT with respect to the nuclear coordinates at equilibrium.

Within the RMB framework, only the valence electronic oscillators are assumed to couple to long-range EM fields via their charges q_ep, thereby giving rise to the molecular response in the first place, but the features of the response are strongly influenced by the coupling of the electronic oscillators to their corresponding mobile nuclear oscillators via k_ep and the coupling of nuclei to each other via ${\mathbb{K}}_{\mathit{pq}}$; in particular, the screening of the nuclei by the inner electrons means that the tensors ${\mathbb{K}}_{\mathit{pq}}$ are typically only nonzero for nearest neighbors (49), and also justifies our assumption that the nuclear oscillators do not couple directly to long-range EM fields. Notably, this means that our consideration of the effects of phonons on vdW interactions requires both ${\mathbb{K}}_{\mathit{pq}}$ and k_ep to be nonzero; if k_ep were to vanish, then nuclear degrees of freedom would be fully decoupled from long-range EM fields in the RMB framework, leading to no vdW interactions. All of these quantities, except the damping coefficients b_ep and b_Ip, incorporate short-range interaction effects by virtue of being computed from ab initio DFT calculations or elemental data; in principle, the damping coefficients may also be rigorously derived by coupling these oscillator degrees of freedom to appropriate reservoirs describing the full system, whether the molecule is in vacuum, is suspended in a condensed phase, or is large enough to support a continuum of phonons that irreversibly carry energy away, but we choose simple approximate values, independent of frequency, justified by empirical considerations appropriate to each system. These quantities are collected from all molecules and respectively arranged into 3N × 3N matrices (M_e, Q_e, B_e, K_e, M_I, B_I, and K_I) that satisfy the frequency-domain equations of motion (12)

$$\begin{array}{c}\left[\begin{array}{cc}{K}_{\mathrm{e}}-i\mathrm{\omega }{B}_{\mathrm{e}}-{\mathrm{\omega }}^2{M}_{\mathrm{e}}& -K_e\\ -K_{\mathrm{e}}& K_{\mathrm{e}}+K_{\mathrm{I}}-i\mathrm{\omega }{B}_{\mathrm{I}}-{\mathrm{\omega }}^2{M}_{\mathrm{I}}\end{array}\right]\left[\begin{array}{c}{x}_{\mathrm{e}}\\ x_{\mathrm{I}}\end{array}\right]\\ =\left[\begin{array}{c}{Q}_{\mathrm{e}}{e}_{\mathrm{e}}\\ 0\end{array}\right]\end{array}$$ (8)

for the electronic and nuclear oscillator displacements (x_e, x_I) in terms of the total electric field ∣E〉 represented in the basis of electronic oscillators as a 3N-dimensional vector e_e. These equations of motion describe coupled driven dissipative harmonic oscillators, and the frequency independence and positivity of the mass, spring constant, and dissipation matrices ensure satisfaction of the Kramers-Kronig relations. Solving for the electronic oscillator dipole moment p_e = Q_ex_e = αe_e yields the electric susceptibility matrix evaluated at frequency $\mathrm{\omega }=i\mathrm{\xi }$

$$\mathrm{\alpha }=Q_{\mathrm{e}}(K_{\mathrm{e}}+\mathrm{\xi }{B}_{\mathrm{e}}+{\mathrm{\xi }}^2{M}_{\mathrm{e}}-K_{\mathrm{e}}{(K_{\mathrm{e}}+K_{\mathrm{I}}+\mathrm{\xi }{B}_{\mathrm{I}}+{\mathrm{\xi }}^2{M}_{\mathrm{I}})}^{-1}{K}_{\mathrm{e}}){}^{-1}{Q}_{\mathrm{e}}$$ (9)

entering the expansion of V above. The nuclear and electronic masses differ by four orders of magnitude, while their respective harmonic coupling strengths are comparable, leading to two frequency scales relevant to the response, with phonons dominating the static and infrared response, while valence electrons dominate at visible and ultraviolet imaginary frequencies. While our use of oscillators leads to susceptibilities that would not accurately capture intrinsic electronic delocalization in strongly metallic or electronically doped systems, our inclusion of phonons does lead to an emergent delocalization of the static and infrared molecular response, without substantially affecting the response at higher visible or ultraviolet frequencies. When we compare to results neglecting phonons, whose free energies are denoted $\mathcal{F}$_e, we use the purely electronic polarizability matrix α_e = Q_e(K_e + ξB_e + ξ²M_e)⁻¹Q_e corresponding to fixing all of the nuclear degrees of freedom, to construct the susceptibility, consistently replacing α_{pi, qj} everywhere it appears.

In our calculations, we neglect damping in fullerene and carbyne as they are compact molecules isolated in vacuum, so we set the matrices B_e = B_I = 0, although we constrain two nuclei in each of those compact molecules to reflect a physical suspension above a surface that freezes out rigid translational and rotational modes. In extended graphene, the approximation of no damping is no longer valid. In particular, the scattering of electrons from phonons produces dissipation in the infrared, leading to dissipation rates around 10¹² rad/s (50) in pure neutral graphene, but computational challenges lead us to set B_I such that b_Ip/m_Ip = 10¹³ rad/s for every atom p in graphene; this dissipation rate has been observed in measurements of DC mobility in strongly (electronically) doped graphene (51), but while our RMB framework can strictly only model undoped graphene, this high dissipation rates may be justified if the neutral graphene sample is sufficiently impure. For similar reasons, we use the same value for b_Ip/m_Ip for supercells of graphene and BN. In addition, we do not constrain any of the nuclei in infinite graphene due to the computational difficulties in freezing out the rigid translational rotational modes exactly at k = 0 without also affecting Goldstone modes at arbitrarily small ∣k∣, although we do constrain atoms at opposite corners for supercells of graphene as well as BN.

For all of our RMB calculations, we sample the integrand Φ(iξ) at 81 values of ξ logarithmically spaced between 10¹⁰ and 10¹⁸ rad/s, and interpolate to perform the integration or Matsubara summation at zero and room temperatures, respectively. Also, our consideration of graphene of infinite extent involves Bloch-periodic boundary conditions for a rectangular supercell of size 3.9 nm along x and 3.4 nm along y; this requires sampling in the irreducible Brillouin zone, which we do by sampling 250 points largely clustered near k = 0. We find that by progressively increasing the number of frequencies and Bloch wave vectors sampled to these final values, the integrands and integrated interaction energies are converged to well within 1%; this convergence criterion is also achieved when evaluating the EM Green’s functions with periodic boundary conditions by using an extension of the Ewald summation method (52) with five terms in each direction for the reciprocal space summation and up to five terms in each direction for the real space summation. To parameterize the material response functions in our RMB model, all DFTs were performed with the FHI-aims all-electron DFT code (53), using the Perdew-Burke-Ernzerhof exchange-correlation functional, “tight” basis sets and numerical thresholds, and a 4 × 4 × 4 k-point grid for the supercells of graphene and hexagonal BN. The force constants of nuclear coupling for the RMB model were obtained from finite differences of analytical nuclear gradients using a five-point formula with displacements of 5 × 10⁻⁴ nm. The two-dimensional materials were modeled using periodic boundary conditions, with the individual sheets separated by 3 nm, which makes the interactions between adjacent layers negligible in semilocal DFT.

Comparison to RPA model of graphene susceptibility

The RPA model of susceptibility in graphene considered by Sernelius (41) as well as Ramezanali et al. (54) derives from a quantum mechanical tight-binding Hamiltonian for the localized π-bonding orbitals (41, 55–57), while neglecting contributions from phonons to the material response and dissipation. This electronic Hamiltonian is also commonly approximated as having linear dispersion around the Dirac points, in which case the susceptibility is derived as the lowest-order linear response to an applied perturbative electric field, consistent with the RPA. While such a framework is typically presented at zero temperature for analytical convenience, the addition of a Fermi-Dirac distribution in the formula for the linear response allows consideration of finite temperature effects as well as doping (by varying the chemical potential) on the bare response. However, only models of doped graphene (which are independent of p- versus n-type doping for the same doping concentration) seem to explicitly consider any dissipation, as changing the doping concentration allows more dissipative mechanisms (e.g., electron-electron or electron-phonon scattering), especially when the chemical potential is far from the Dirac point or when finite temperature is directly used in the construction of the bare response. It is also common in the context of vdW interactions to simplify these expressions by neglecting spatial dispersion by taking the limit k → 0, or even temporal dispersion by using the frequency-independent conductivity $q_{\mathrm{e}}^2/(16\mathrm{\pi }\hslash {\mathrm{ϵ}}_0)$ (51). That said, we choose to preserve temporal and spatial and temporal dispersion in the RPA model of Sernelius (41) for our comparison with RMB predictions, and use the RPA model of Ramezanali et al. (54) to explicitly include finite temperature effects in the bare response (while reducing to the Sernelius model in the limit of zero temperature); Sernelius claims that finite temperature corrections to the response of graphene are small enough to be neglected, but this is based on a local model of conductivity (58), whereas Ramezanali et al. (54) derive their temperature- and doping-dependent response functions including spatial and temporal dispersion.

Recent work by Dobson et al. (59) has shown that renormalization group corrections to the response of tightly bound electrons in graphene change the Dirac cone into a cusp, so the effective Fermi velocity at long wavelength becomes infinite and the resulting effective coupling constant becomes zero in the same limit. This has the effect of pushing the power law of the vdW interaction energy between parallel undoped graphene sheets at zero temperature away from −3 and toward −4, depending on the renormalization group model used; essentially, renormalization group corrections make the electronic density of states at the lowest frequencies and longest wavelengths decay to zero faster in the limit ∣k ∣ → 0 so that it has the biggest effect on vdW interactions when phonons are ignored. However, we do not focus further on this model as a point of comparison for two reasons. The first is that while it may be possible to make a more direct comparison to this model by including renormalization group corrections to the electronic response properties computed in RMB, these corrections will primarily affect the response properties at higher frequencies; inclusion of phonons will still dominate the quasi-static response most relevant to vdW interactions, so it is not clear that substantial quantitative differences will emerge overall. The second is that these renormalization group corrections are quoted at zero temperature, and the effects of finite temperature are less obvious; as we discuss in the main text, the effects of finite temperature are clear in the RPA models of Sernelius and Ramezanali, and a shortcoming of the RMB model of atomistic response is the restriction to zero temperature given the large changes to the mechanical structure and phonon dispersion of graphene at room temperature, so addressing that shortcoming of the RMB framework will likely be much more important in the context of vdW interactions than inclusion of finite temperature renormalization group corrections that will still affect just the higher frequency electronic response.

Any of these continuum models gives a wave vector–dependent permittivity ϵ(ω, k) = 1 + χ(ω, k) defined in terms of the susceptibility χ(ω, k). The Sernelius model at zero temperature derives the susceptibility

$$\mathrm{\chi }(\mathrm{\omega },\mathbf{k})=\frac{q_{\mathrm{e}}^{2}g\mid \mathbf{k}\mid }{32\mathrm{\hslash }{\mathrm{ϵ}}_0\sqrt{v_{\mathrm{F}}^2{\mid \mathbf{k}\mid }^2-{\mathrm{\omega }}^2}}$$ (10)

without doping, or

$$\begin{array}{c}\mathrm{\chi }(\mathrm{\omega },\mathbf{k})=\frac{q_{\mathrm{e}}^2{D}_0}{2{\mathrm{ϵ}}_0\mid \mathbf{k}\mid }(1+\frac{{\mathrm{\kappa }}^2}{4\sqrt{{\mathrm{\kappa }}^2-{\mathrm{\zeta }}^2}}[\mathrm{\pi }-\mathrm{\varphi }(\mathrm{\kappa },\mathrm{\zeta })])\\ \mathrm{\varphi }(\mathrm{\kappa },\mathrm{\zeta })=\text{arcsin} ((1-\mathrm{\zeta })/\mathrm{\kappa })+\text{arcsin} ((1+\mathrm{\zeta })/\mathrm{\kappa })\\ -\frac{\mathrm{\zeta }-1}{\mathrm{\kappa }}\sqrt{1-{\left(\frac{\mathrm{\zeta }-1}{\mathrm{\kappa }}\right)}^2}+\frac{\mathrm{\zeta }+1}{\mathrm{\kappa }}\sqrt{1-{\left(\frac{\mathrm{\zeta }+1}{\mathrm{\kappa }}\right)}^2}\end{array}$$ (11)

with doping, for k in the plane. These are defined in terms of the Fermi velocity v_F = 8.73723 × 10⁵ m/s and the spin-pseudospin degeneracy g = 4, as well as the Fermi wave vector $k_{\mathrm{F}}=\sqrt{4\mathrm{\pi }\mid n\mid /g}$, Fermi energy E_F = ℏv_Fk_F, electron density of states $D_0=\frac{\sqrt{g\mid n\mid /\mathrm{\pi }}}{\hslash v_{\mathrm{F}}}$ at the Fermi level, and dimensionless variables κ = ∣ k ∣ /(2k_F) and ζ = ℏω/(2E_F). In both cases, the response functions at imaginary frequency can be derived simply by substituting ω = iξ into the definitions of χ(ω, k). The Ramezanali model extends this to finite temperature and arbitrary doping with the susceptibility

$$\begin{array}{c}\mathit{\text{Im}}(\mathrm{\chi }(\mathrm{\omega },\mathbf{k}))=-\frac{{\mathit{gq}}_{\mathrm{e}}^2\mid \mathbf{k}\mid }{8{\mathrm{\pi ϵ}}_0}\times \\ {\displaystyle \sum _{s=\pm }}(f(\mathrm{\omega },v_{\mathrm{F}}\mid \mathbf{k}\mid )(G_{+}^{(s)}(\mathrm{\omega },\mathbf{k})-G_{-}^{(s)}(\mathrm{\omega },\mathbf{k})\left)\mathrm{\theta }\right(v_{\mathrm{F}}\mid \mathbf{k}\mid -\mathrm{\omega })+\\ f(v_{\mathrm{F}}\mid \mathbf{k}\mid ,\mathrm{\omega })(H_{+}^{(s)}(\mathrm{\omega },\mathbf{k})-\frac{\mathrm{\pi }}{2}{\mathrm{\delta }}_{s,+}))\end{array}$$ (12)

from which the Kramers-Kronig relation gives $\mathrm{\chi }(i\mathrm{\xi },\mathbf{k})=\frac{2}{\mathrm{\pi }}{\int }_0^{\infty }\frac{\mathrm{\omega }\mathit{\text{Im}}(\mathrm{\chi }(\mathrm{\omega },\mathbf{k}))}{{\mathrm{\omega }}^2+{\mathrm{\xi }}^2} \mathrm{d\omega }$. This is defined in terms of the functions

$$\begin{array}{c}f(x,y)=\frac{1}{2\mathrm{\hslash }\sqrt{x^2-y^2}}\\ G_{\pm }^{(s)}(\mathrm{\omega },\mathbf{k})={\displaystyle {\int }_1^{\infty }}\frac{\sqrt{u^2-1}}{\text{exp}(\frac{\mathrm{\hslash }(v_{\mathrm{F}}\mid \mathbf{k}\mid u-\mathrm{\omega })-2s\mathrm{\mu }}{2k_{\mathrm{B}}T}+1)} \mathrm{d}u\\ H_{+}^{(s)}(\mathrm{\omega },\mathbf{k})={\displaystyle {\int }_{-1}^1}\frac{\sqrt{1-u^2}}{\text{exp}\left(\frac{\mathrm{\hslash }(\mathrm{\omega }+v_{\mathrm{F}}\mid \mathbf{k}\mid u)-2s\mathrm{\mu }}{2k_{\mathrm{B}}T}\right)+1} \mathrm{d}u\end{array}$$ (13)

which depend on the temperature directly as well as indirectly through the chemical potential μ, although we set μ = 0 in the absence of doping even at finite temperature.

We directly plot the susceptibility χ(iξ, k) from the RPA model of graphene in Fig. 4B, and compare with the Fourier transform of the RMB susceptibility in Fig. 4A, which we define as

$$\mathrm{\chi }(i\mathrm{\xi },\mathbf{k})=\frac{1}{3}{\displaystyle \sum _{p,i,q,j}}{\mathrm{\alpha }}_{\mathit{pi},\mathit{qi}}(i\mathrm{\xi })(\int {\mathrm{d}}^3\mathbf{x} {\mathbf{f}}_{\mathit{pi}}(\mathbf{x})e^{-i\mathbf{k}\dot{}\mathbf{x}})\dot{}{\mathbf{f}}_{\mathit{qj}}(0)$$ (14)

although the atomism inherent in the RMB framework means that the resulting susceptibility of graphene does not exhibit continuous translational symmetry, so there is some ambiguity regarding the choice of

$$\mathbf{x}\prime$$

in which to evaluate

$${\mathbf{f}}_{\mathit{qj}}(\mathbf{x}\prime )$$

; we choose

$$\mathbf{x}\prime =0$$

to be the center of a hexagonal honeycomb cell. The plots in Fig. 4 (A and B) sample

$$\mathbf{k}$$

along the edge of the irreducible Brillouin zone for our rectangular supercell of graphene.

EM Green’s functions

Beyond phonons leading to delocalization of the molecular susceptibility, further nonlocality in the response and resulting interactions of the atomistic systems we study arises from long-range EM couplings, encapsulated in the EM Green’s function. The vacuum EM Green’s function can be written in imaginary frequency as ${\overleftrightarrow{G}}_0(i\mathrm{\xi },\mathbf{x},\mathbf{x}\prime )=(\overleftrightarrow{I}-\frac{c^2}{{\mathrm{\xi }}^2}\nabla \otimes \nabla )\frac{e^{-\mathrm{\xi }\mid \mathbf{x}-\mathbf{x}\prime \mid /c}}{4\mathrm{\pi }\mid \mathbf{x}-\mathbf{x}\prime \mid }$, while the Green’s function in a macroscopic environment described by a collective susceptibility ${\mathbb{V}}_{\text{env}}$ solves the macroscopic Maxwell’s equation

$$[\nabla \times \nabla \times +\frac{{\mathrm{\xi }}^2}{c^2}(\mathbb{I}+{\mathbb{V}}_{\text{env}})]{\mathbb{G}}_{\text{env}}=\mathbb{I}$$ (15)

(setting ε₀ = 1). The latter can be solved using any number of state-of-the-art computational EM techniques (1, 60), but we only consider vacuum or a gold plate; in particular, we approximate the latter as a perfect conductor for computational simplicity, allowing us to exploit image theory. Note that both the vacuum and macroscopic environmental Green’s functions diverge for x = x′; however, our use of Gaussian basis functions ensures that the matrix elements $\langle {\mathbf{f}}_{\mathit{pi}}\mid \mathbb{G}{\mathbf{f}}_{\mathit{qj}}\rangle$ always converge to finite values, while the behavior as the Gaussian widths grow captures the screening of long-range EM interactions by phonons.

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/5/11/eaaw0456/DC1

Section S1. VDW interaction free energies

Section S2. VDW interactions of one versus two carbyne wires

Section S3. DFT phonon dispersions for carbyne and graphene

Section S4. RPA model of doped graphene

Section S5. VDW power laws versus dimensionality for perfect conductors

Fig. S1. vdW free energies of low-dimensional compact molecules.

Fig. S2. vdW free energies of two-dimensional materials.

Fig. S3. Nonmonotonicity and temperature deviations due to phonon-induced nonlocal response in carbyne at short distance from the gold plate.

Fig. S4. Phonon dispersions of carbyne and graphene.

Fig. S5. Graphene interaction power laws in the continuum RPA model.

Table S1. Power laws versus dimensionality for perfect conductors.