Abstract
The morphologies of cell membranes, and specifically the local curvature distributions are determined either by its intrinsic components such as lipids and membrane-associated proteins or by the adhesion forces due to membrane interactions with the cytoskeleton, extracellular matrix (ECM) and other cells in the tissue, as well as physical variables such as membrane and frame tensions. We present a computational analysis for a model of pinned membranes based on the dynamically triangulated Monte Carlo (MC) model for membranes. We show that membrane adhesion to ECM or a substrate promotes curvature generation on cell membranes, and this process depends on the excess area, or equivalently membrane tension, and the density of adhesion sites. This biophysics based model predicts adhesion induced biogenesis of microvesicles in cell membranes. For a moderate density of adhesion sites and high excess membrane area, an increase in membrane tension can result in the formation of microvesicles and tubules on the membrane. We also demonstrate the significance of intrinsically curved proteins in promoting vesiculation on pinned membranes. The results presented here are relevant to the understanding of microvesicle biogenesis and curved membrane topographies due to physical factors such as substrate stiffness and ECM interactions.
Keywords: membarane adhesion, excess area, dynamic pinning, membrane tension, dynamically triangulated Monte Carlo
1. Introduction
Lipid membranes constitute the physical boundary of cells and intracellular organelles; they govern several biophysical processes by maintaining the specific microenvironment at the cytoplasmic side and allowing communication across its interface. These membranes are characterized by complex morphological transformations that are central to cellular trafficking, migration, and growth [1, 2]. The known molecular mechanisms that generate membrane curvatures are lipid geometry and composition, presence of membrane-binding proteins, and external forces due to the interaction with cytoskeleton and membrane [3]. The shapes of lipids with different head to tail ratios can generate curved bilayers. The proteins associated with membranes (integral membrane proteins and peripheral proteins), generate curvatures through mechanisms such as insertion of helices, wedging, scaffolding, oligomerization, etc. [4]. Curvature remodeling by cytoskeleton is mainly due to the forces generated by polymerization at the growing filament end, and due to the active forces generated by motor proteins [5]. In addition to these mechanisms, membrane curvature can also be generated by an interplay between membrane tension and local adhesions. As the adhesive interfaces act as significant determinants in cell recognition and response to the cell micro-environment, both chemical and physical cues associated with adhesive signaling have gained significant attention [6].
Recent in vitro studies using cultured cells on engineered materials have demonstrated the extraordinary ability of cells to sense and respond to the rigidity, anisotropy, and topography of the ECM [6, 7, 8]. The increasingly apparent biophysical mechanisms governing this behavior depend on the contractility of the actin-myosin cytoskeletal network that links to the focal adhesion complexes and the adhesive complexes [9, 10, 11]. The adhesive complexes in the cell are formed by ligand-receptor binding and clustering at the membrane interface. The key cell adhesion proteins are integrins, cadherins, immunoglobulins, and selectins [12], and of these, the integrins constitute the major class of cell surface receptors that mediate membrane-extracellular matrix (ECM) interactions. The fast rearrangement of the adhesion machinery and cytoskeletal filaments in response to the microenvironment require localized topographical modifications of the plasma membrane. Given the high compression/stretching modulus of the membrane structural reorganization primarily proceeds through membrane bending leading to the formation of highly curved structures. These structures include highly complex cellular morphologies such as invaginations, protrusions, and bud or bleb shaped membrane structures whose sizes range from nano to micrometers in feature dimensions (e.g., diameter) [13, 14, 15, 16].
There is a growing interest in defining the roles of extracellular vesicles (EVs), which are membrane-bounded vesicles that are formed and released into the extracellular region in response to cellular stresses [17, 18]. EVs that carry bioactive molecules such as proteins and RNAs represent novel and highly effective means of intracellular communication that either function locally or over distances via the circulation, and have been implicated in different aspects of tumorigenesis and metastasis [19]. They have also been used as biomarkers for various types of cancers and have been developed as functional nanocarriers for therapeutic applications. EVs are classified into two major types, namely exosomes and microvesicles (MVs). Exosomes are 50–120 nm vesicles that are generated when the limiting membranes of endosomes invaginate into the lumen to form multivesicular bodies (MVBs). Unlike exosomes, MVs are 150–1000 nm vesicles that are generated when regions of the plasma membrane bud and shed off in the form of vesicles [17, 18]. The generation of MVs involves actomyosin contraction at the cell cortex and is dependent upon glutamine metabolism in cancer cells [17, 18]. The dependance of receptor endocytosis [20], and the formation of exosome and MVs [21], on the mechanical properties of the extracellular microenvironment such as substrate stiffness point to the adhesion-induced transformations in cell membrane morphologies [22].
From a biophysical point of view, cell membrane adhesion is abstracted as the pinning of a deformable membrane with molecular machines that bind the membrane to the substrate or ECM. The elements that define membrane shapes are membrane tension, bending rigidity, and the presence of membrane-cytoskeleton-linker-proteins [23]. The density of adhesion molecules and their mobility, clustering, binding-unbinding dynamics, are also determining factors of membrane morphology. Earlier works have used the methods of statistical physics and reaction kinetics to study membrane receptor interactions and have shown that in cell-mimetic models the adhesion domains are result of short-ranged ligand-receptor interactions and long-ranged membrane-mediated interactions due to the presence of glycocalyx and elastic stresses in membranes [24, 25, 26]. The membrane-mediated interactions in the adherent cells allow for morphological changes in membranes and aggregation of intramembrane junctions [27]. While these studies present membrane deformations as a mediator for the aggregation of adhesion machinery, other theoretical [28, 29] and experimental studies predict large scale deformations in membranes as a result of adhesion. Experiments on vesicle and confined bilayers have shown micrometer-scale deformations in membranes resulting in tubulations and spherical bud formations [30, 31]. From a modeling standpoint vesiculation mediated by curvature inducing protein and cytoskeletal forces have been investigated in previous studies [32, 33, 34, 35, 36, 37]. However, the effect of membrane pinning on emergent membrane morphology has not been studied.
In this work, we have developed a computational model for membrane adhesion that accounts for both biophysical factors of membrane anchorage and the effect of the substrate or ECM interactions in cells. The membrane tension set by the reorganization of cortical cytoskeletal mesh and other cellular processes is accounted either by initializing via a given excess area present in the membrane patch, or through an applied frame tension. The objective of our work is to explicitly model a membrane patch with adhesion complexes that can diffuse and cluster on the membrane surface to characterize the adhesion-induced membrane conformations as a function of membrane tension and adhesion strength.
2. Model and computational method
Dynamically Triangulated Monte Carlo (DTMC) method:
To model a patch of the cell membrane we use DTMC method in which membrane is described as a triangular network with Ntri triangles, constructed with Nv vertices and Nl links that connect the vertices [38]. The elastic energy of the membrane is defined by the discrete form of Canham-Helfrich Hamiltonian [39, 40], given by
| (1) |
where κ is the bending rigidity of membrane, Av is the area, Hv the mean curvature and C0 the spontaneous curvature at vertex v. Each vertex is modeled as a hardsphere of radius a0. The details of the model and MC procedure in given in supplementary information, section S1.
Membrane excess area and tension:
The characteristic deformations of the fluctuating membrane are described by a dimensionless quantity called excess area defined as Aex = (Amem − Ap)/Ap × 100% where Amem is the curvilinear area and Ap the projected area of the equilibrated membrane patch. Aex defines the allowed excess area in the membrane for its characteristic deformations and is conjugate to the tension experienced by the membrane. To obtain membrane configurations with different Aex two different methods can be employed. The first one is a constant projected area method where we keep Ap fixed and vary Amem to obtain different Aex. In the second method, we apply a constant frame tension τ to the membrane and allow the projected area Ap to fluctuate [41]. We use the constant Ap method throughout the study except in section 3.5 where we compare the results from two methods and show conformations for Aex values that are not reachable by constant Ap method. The details of the methods are given in supplementary information, section S2. The range of Aex explored here is 0 54%, which is similar to that studied in the previous work [41]. The maximum value of experimentally measured cortical tension in mammalian cells is 413.6µN/m [5] and this corresponds to Aex ~ 80% [41].
Pinning interactions:
The adhesion interaction of the membrane with the adhesion surface is accounted for through a Bell-bond potential [42, 43]. A fraction of the membrane vertices (Np), selected randomly, are assigned to have a pinning interaction with point sites on the planar surface below the membrane patch. The total energy of the membrane patch due to pinning interaction is given by:
| (2) |
where dv is the distance between the vertex v and bound point on the planar surface. The scalar field sv = 1 for vertices that adhere to the planar surface and sv = 0 for all the vertices without adhesion. The membrane pinning sites are allowed to adhere to any point on the planar surface when . ∆G is the free energy of pinning and kbell the stiffness of the pinning interaction. For the results presented here we take the interaction energy parameters that are comparable to intercellular adhesion molecule ICAM [44], given as ∆G = 19 kBT and kbell = 60 kBT/a0, unless otherwise stated. To extend our model to include other adhesion molecules, we also study the effect of a range of pinning energy parameters.
We consider two different types of adhesive interactions, static and diffusive. In both cases, we assume that the membrane pinning sites can bind at any point on the planar surface under the membrane pinning site when the distance criterion for bonding is satisfied. As the pinning site on the membrane moves, for diffusive pins, the bound point on the planar surface also diffuses on the plane, but for non-diffusive pins, the initial binding site on the planar surface stays static and does not diffuse. To model this, in the case of static pins, dv in Eqn. 2 is taken to be the 3D distance between the vertex and the pinning site and for the diffusive case, we set dv = dz where dz is the vertical distance of the pinning membrane site from the planar surface.
We simulate the binding-unbinding dynamics of the adhesion molecules through MC steps that allow for making and breaking of Bell bonds, and these moves are accepted via the Metropolis scheme. We also ensure the avoidance of the membrane with the adhering surface by restricting vertex moves that intersect the membrane plane with the planar surface. The membrane patch is equilibrated through a set of MC steps with effective total Hamiltonian:
| (3) |
Run-time parameters:
We consider a membrane patch with Nv = 2500. The vertex hard sphere radius is set to be a0 = 10 nm. For constant Ap simulations we take a membrane patch with L = 60a0 and this sets Ap = 3600 nm2. The membrane bending rigidity is taken to be 20kBT unless otherwise specified. For each pin binding or unbinding is attempted once in 100 MC steps. Membrane undulations spectra and relative energies presented here are ensemble averages of 10 runs where each window is equilibrated for 107 MC steps.
3. Results and Discussion
3.1. Influence of adhesion sites on membrane undulations and curvature
As membrane fluctuations are known to play a significant role in the early stage of cell adhesion, we first demonstrate the effect of pinning induced confinement in the height fluctuations of the membrane patch. For this analysis, we keep the range of excess area and pinning density to be small so that the fluctuation spectrum can be analyzed with the Monge-gauge approximation for the membrane patch which is only satisfied on a surface with a small slope. Fig. 1 compares the undulation spectra and conformations of the membrane patch with and without pinning. The height-height correlation of planar membrane in the Monge-gauge representation [45, 46] in the absence of any spontaneous curvature is given by . As shown in Fig. 1(a), for a membrane without adhesion interaction, the height fluctuations scales as q−2 and q−4 for lower and higher q modes respectively. The bending rigidity (κ) and the tension (σ) obtained from the spectra are given in table 1.
Figure 1.
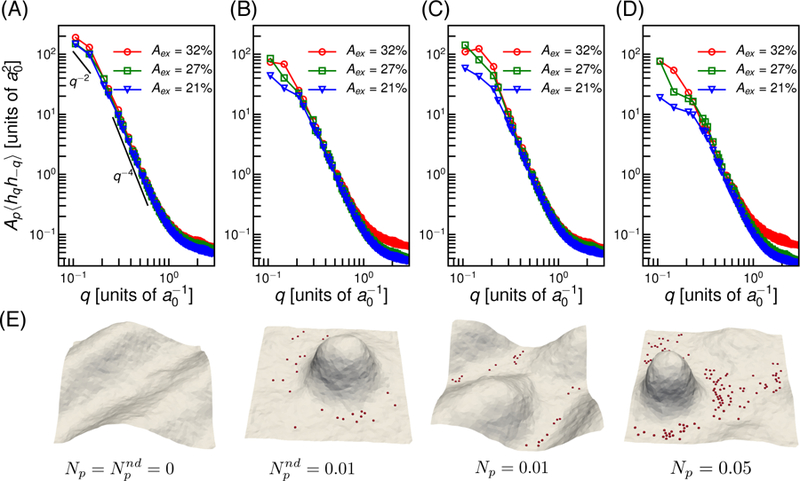
Membrane fluctuations in the absence and presence of pinning interactions. (A) Undulation spectra of the membrane patch without pinning . (B) Spectra in presence of non-diffusing pins for . (C) and (D) shows the spectra with diffusing pins, with Np = 0.01 and Np = 0.05 respectively. (E) The membrane conformations corresponding to A, B, C and D for Aex = 21%. The red spheres on the membrane shows the locations of the pinning sites.
Table 1.
Membrane bending rigidity and tension at different excess areas computed from fluctuation spectrum in units of kBT and respectively. The resultant tension at and Np = 0.01 shows the diffusing pins induce lower tension compared to the no-diffusing pins at same concentration.
| Np = 0.01 | Np = 0.05 | |||||||
|---|---|---|---|---|---|---|---|---|
| Aex(%) | κ | σ | κ | γ | κ | γ | κ | γ |
| 32 | 8.49 | 0.29 | 7.58 | 0.81 | 8.13 | 0.36 | 7.34 | 0.97 |
| 27 | 9.03 | 0.37 | 9.28 | 0.83 | 9.31 | 0.3 | 8.26 | 1.09 |
| 21 | 10.05 | 0.39 | 9.39 | 1.27 | 9.28 | 0.92 | 7.23 | 2.51 |
To understand the role of the mobility of the adhesion complexes, we consider diffusing and non-diffusing pins. The effect of non-diffusive pins are shown in Fig. 1(B) with , where represents the fraction of vertices with non-diffusive pinning sites. In comparison to Fig. 1(A), the addition of pinning sites decreased amplitudes at small q. A significant change in high q mode is observed when Aex = 32%. Fig. 1(C) represents the spectra for diffusive pinning sites, with Np = 0.01, where Np represents the fraction of vertices with diffusive pinning sites. In the case of the diffusing pins, the effect of pins is much smaller at all q modes compared to non-diffusing pins. Diffusion promotes rearrangement of pins to form clusters, and this allows the membrane modes to undulate without restriction. However, increasing the number of diffusive pins leads to the same effect as seen for non-diffusive pins with . This is shown in Fig. 1(D) for Np = 0.05.
The deviation of the undulation spectra due to pinning interaction at small q modes indicate the change in effective tension in the membrane. Table 1 reports the tension computed from fluctuation spectra for systems with and without pinning interactions. Comparing and Np = 0.01 in table 1, we observe higher tension in presence of non-diffusing pins compared to diffusing pins at the same concentration and an increase in number of pins increase effective tension.
The characteristic shapes of the membrane patch with Aex = 21% with different values of Np are shown in Fig. 1(E). In the absence of pins, membrane undulates with all allowed wavelengths. In the presence of pins, the entropic pressure pushes the membrane away from the substrate, and the shapes are dictated by elastic energy. The largest wavelengths are restricted for and Np = 0.05 and this results in out of plane protrusions. For Np = 0.01 the pins cluster such that membrane is nearly unaffected. The membrane-mediated clustering of adhesion molecules and observed deviations in the fluctuation spectra agree with previous studies [47, 48].
3.2. Membrane vesiculation due to pinning interactions
Having shown that the effect of non-diffusive pins is the same as that of diffusive pins at higher concentration, we will limit our focus to membranes with diffusive pins. When the out of plane fluctuations of the membrane are restricted by the presence of adhesion sites, the excess area is drawn into membrane protrusions that grow perpendicular to the plane of adhesion. The amplitude of each undulation mode depends on the excess area, and the number of modes that are restricted by pinning depends on the density of pinning sites. The resultant conformations depend on both Aex and Np. The membrane conformations as a function of number of diffusive pins Np and Aex are given in Fig. 2A. As seen from the top panel (Np = 0.05) pins show more clustering with an increase in Aex and the additional area in the membrane form more tube-like protrusions.
Figure 2.
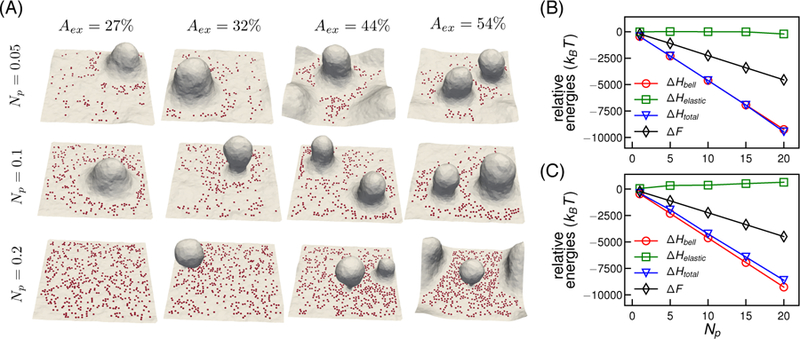
(A) Representative equilibrium conformations of the membrane patch as a function of Aex and Np. (B) and (C) Comparison of relative free energies ∆F and other internal energies of the system as a function of Np for Aex = 27% and Aex = 54% respectively. Elastic energy is denoted by ∆Helastic, pinning energy as ∆Hbell, sum of elastic and pinning energies as ∆Htotal. Error bars of the relative energies are smaller than symbol sizes.
The effect of pinning is more prominent upon an increase in the number of pins for Aex > 27%. We observe stabilization of spherical morphologies, similar to membrane buds or vesicular structures in the fused state prior to pinch off, at high pinning densities (Fig. 2A, Np = 0.2). Higher Aex leads to more natural fluctuations, which can be much easily channelized into the protrusions or vesicular membrane buds. The resulting equilibrium membrane shapes are determined by a balance between membrane bending energy and pinning energy. At high pinning densities, the high bending energy associated with the vesicular region is balanced by the local pinning energy. For low pinning density, the membrane bending energy dominates, resulting in protrusive structures rather than vesicular buds (as observed for Np = 0.05 and 0.1). At low excess areas and high pinning density, it is energetically unfavorable for the membrane to bend against the pins to generate protrusions or vesicular buds, and hence the membrane shows a relatively flat morphology, as observed for Aex = 27% and Np = 0.2 in Fig. 2A.
To understand the energetics of pinning induced biophysical changes in membranes, we perform a free-energy analysis on the membrane patch with adhesive interactions. A detailed description of the free energy method is given in supplementary information S3. The free energy analysis of the membrane states for Aex = 27% and Aex = 54% is summarized in Fig. 2B. The relative internal energies ∆Helastic, ∆Hbell and ∆Htotal are computed with respect to a system with Np = 0. The pinning energy ∆Hbell is the dominant contribution to the total energy, and it decreases as the number of pins increase. With the increase in Np, the curvature energy increases for Aex = 54% but remains nearly unchanged for Aex = 27% due to the increase in high curvature deformations on the membrane for high Aex. The sum of the internal energy contribution is related to the free energy difference as ∆F = ∆Htotal − T∆S, where ∆S is the change in entropy relative to the reference state. The difference between ∆Htotal and ∆F increases with Np indicating that the entropic loss becomes more significant with an increasing number of pins.
3.3. Effects of pinning density, strength, and membrane bending rigidity on the emergent membrane morphology
The undulations and the curvature distributions on the membrane are renormalized by the strength and number of adhesive interaction or pinning sites. The physiological values for the adhesive interaction energy for both natural and synthetic ligand-receptor systems vary from 0kBT to 30kBT. To represent the pinning interactions, we adopted a Bell bond model that considers the binding energy of adhesion complex as 19 kBT. Here we extend our study by varying binding energy of the pins for different pinning densities. The ∆G − Np phase diagram in Fig. 3(A) depicts the emergent topographies of the membrane patch. For very small values of ∆G, as seen for ∆G = 2kBT, the fluctuations in the membrane overcome the pinning interaction resulting in unbinding of adhesion molecules. Hence this region shows undulating membrane patches (~) for all values of Np. With an increase in ∆G, we first obtain membrane patch with protrusions, and at high energy values, we observe vesicular buds at moderate to high pinning densities. For intermediate values of ∆G and Np, we observe either protrusions or an undulating membrane. In addition to ∆G, the pinning stiffness kbell is also a determining factor membrane deformations. The effect of kbell is describe later in section 3.6.
Figure 3.
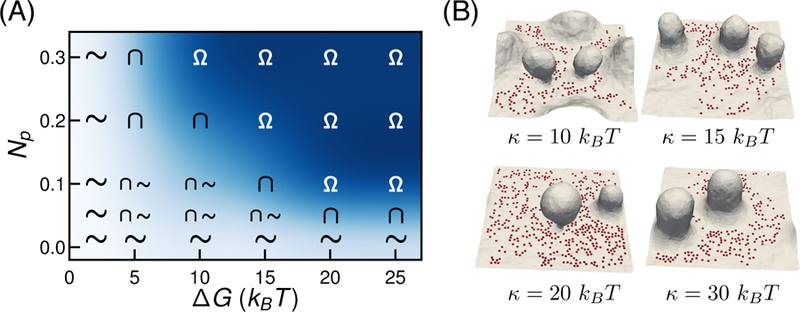
(A) ∆G − Np phase diagram for vesicle formation in the membrane patch with Aex = 44% and Np = 0.2. The symbols Ω represents the region with atleast one membrane bud with a stabilized and well defined narrow neck on the membrane, ∩ represent membrane with protrusion and ∼ is an undulating membrane. (B) Effect of κ on membrane conformations when Aex = 44% and Np = 0.2. Representative shapes of membrane patch shows lower κ results in the formation of higher number of vesicles.
The membrane parameters that affect the surface topographies are the bending rigidity κ and the membrane tension, or equivalently the excess membrane area. The effect of Aex is already described in the previous section. Here, we look at the membrane deformations with different values of κ. Given the conformations are a result of membrane relaxation and the pinning interaction, changing κ is expected to affect the vesicle formation. Fig. 3(B) shows the membrane morphologies as a function of κ when Aex = 44% and Np = 0.2. A decrease in κ implies a decrease in the energy required to bend the membrane, and as a result, less energy is required to form a vesicular bud at low κ, compared to high κ. Hence, we observe membrane with lower rigidity (κ = 10, 15kBT) stabilize a greater number of vesicular buds compared to the membrane with higher κ values. At very high bending rigidity (κ = 30kBT) the bending energy dominates over the pinning energy, and as a result, we observe protrusive structures instead of vesicular buds.
3.4. Intrinsically curved proteins promote vesiculation on pinned membranes
Curvature sensitive or generating proteins are integrally or peripherally associated parts of cell membranes, and their presence has been shown to alter membrane topography. They either generate curvature by bending the membrane or migrate to the regions of the membrane with local curvature matching their intrinsic curvature. These two mechanisms are known to drive protein localization and stabilize highly curved regions in cell membranes. In this section, we explore the effect of such proteins in the presence of pinning interactions induced deformations.
The protein concentration on the membrane is modeled by setting C0 > 0 in Eqn. 1, at selected vertices occupied by the proteins. We set the fraction of vertices with proteins to be Nprotein = 0.04 and C0 = 0.3/a0 = 0.03 nm−1. The chosen value of spontaneous curvature is comparable to the curvatures generated by proteins consisting of N-BAR domains and ENTH domains which is in a range of 0.02 to 0.07 nm−1 [49, 50]; see also [35, 33]. The equilibrium membrane conformations obtained as a function of Aex and Np are shown in Fig 4. In Fig 4 we compare the membrane topographies in presence of proteins with (Np > 0) and without (Np = 0) pinning interactions. Unlike the protein-induced deformations reported in the literature, the emergent curvilinear topographies here are a result of the pinning interactions; we note that the given density of proteins with C0 = 0.3/a0 is not sufficient to induce highly curved protrusions or vesicular buds. As shown in Fig 4, when Np > 0, the proteins, which are initially at random positions, preferentially localize to the regions of higher local curvature. Moreover, the localized proteins promote the formation of mature buds, compare Fig. 2 and Fig 4.
Figure 4.
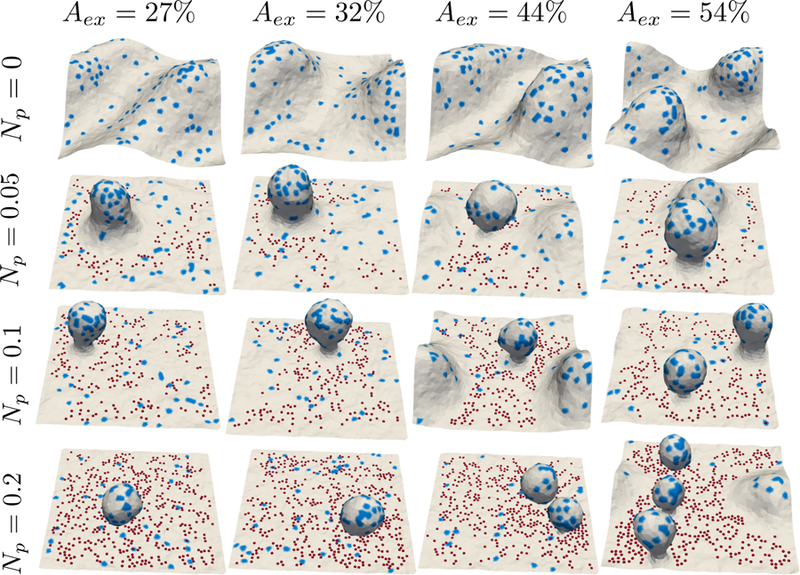
Membrane patch in the presence of intrinsically curved proteins as a function of Aex and Np; the protein fields are shown in blue. The curvature strength of the proteins is C0 = 0.3/a0 and Nprotein = 0.04.
3.5. The effect of membrane frame tension on undulation and vesiculation
So far we have studied membrane patches of given Aex holding the projected area Ap constant. In this scheme, the physiological range of membrane tensions is obtained by varying Aex. We next explicitly apply a frame tension to the membrane patch allowing the projected area Ap to be a variable. The constant frame tension method is more generic and allows us to study a range of Aex that are not accommodated by the constant Ap method. A more detailed analysis of both Ap and the frame tension method is given in ref. [41]. Here we will demonstrate the equivalence of the two methods in the presence of pinning and then proceed to investigate the conformational changes induced by adhesive interactions in membranes with very large values of the frame tension.
First, we performed fluctuation analysis as in section 1, but with a constant frame tension. The excess area of the membrane decreases with an increase in frame tension yielding an Aex = 40% for τ = 0 µN/m. To obtain Aex = 21%, 27% and 32% we applied a frame tension τ = 90.2, 53.3 and 20.5 µN/m. The membrane fluctuation spectra without and with pinning interaction using the constant frame tension method are given Fig. 5(A) and (B) respectively, and these estimates compare well with those obtained from the spectra shown in Fig. 1(A) and (C). We also show membrane conformations as a function of Aex and Np in Fig. 5(C). The formation of membrane protrusions and vesiculation observed here matches well with the constant Ap simulations shown in 2(A).
Figure 5.
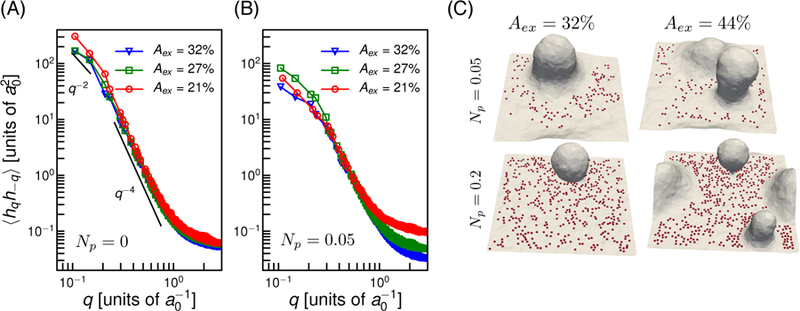
Membrane fluctuation spectrum in constant frame tension simulations. (A) Spectra without pinning interactions and (B) with pinning interaction for Np = 0.05. (C) Representative membrane conformations as a function of Aex and Np.
The constant frame tension framework allows us to simulate a membrane patch with very high excess areas (high negative tensions) that are not accessible by the constant Ap simulations. The membrane conformations in the presence of high contractile (negative) tension (τ = −600 µN/m) and high pinning density are shown in Fig. 6. Here the applied tension τ = −600 µN/m when A0 = 5539 gives Aex = 95% at equilibrium. When Np = 0.2 we observe the formation of spherical or quasi-spherical vesicles that are similar to the ones we discussed in sections(2) and (5). At high pinning densities, the membrane form tubular morphologies with smaller radii compared to the spherical ones. The formation of tubules and length of tubules depend on the number of pinning sites. Similar observations of tubular and vesicular structures have been made in theoretical studies of membranes in the presence of spontaneous curvature [51] and experimental studies of supported bilayers [52, 53].
Figure 6.
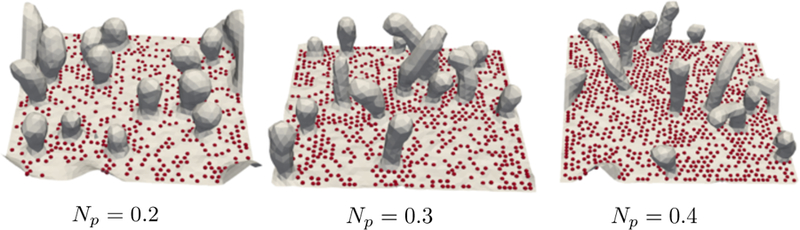
Equilibrium membrane conformations showing membrane tubulation at high frame tension and high pinning density. Surface morphologies shown at different pinning densities correspond to τ = −600 µN/m and A0 = 5539 .
3.6. Membrane topography at different pinning stiffness kbell
The pinning interactions introduced here can be either due to membrane cytoskeletal interactions or due to membrane ECM interactions. In the case of the latter, the effective stiffness kbell of the pins become dependent on the substrate stiffness. Given that the tissue stiffness can span four orders of magnitude from a few hundred Pascals for soft tissues such as brain to a few 100 kPa for stiff tissues such as the bone [54], a dependence of the emergent membrane morphologies on kbell varied over such magnitudes is of interest. The equilibrium shape of membrane patch as a function of Aex and kbell is shown in Figure 7. Decreasing kbell increases the width of pinning potential and reduces the energy required to move pinned membrane sites. Hence a change in kbell from 20kBT/a0 to 0.01kBT/a0 changes membrane topography from a vesiculated conformation ( top panel Aex = 32% and 44%) to a membrane patch undulating without restriction ( bottom panel Aex = 32% and 44%).
Figure 7.
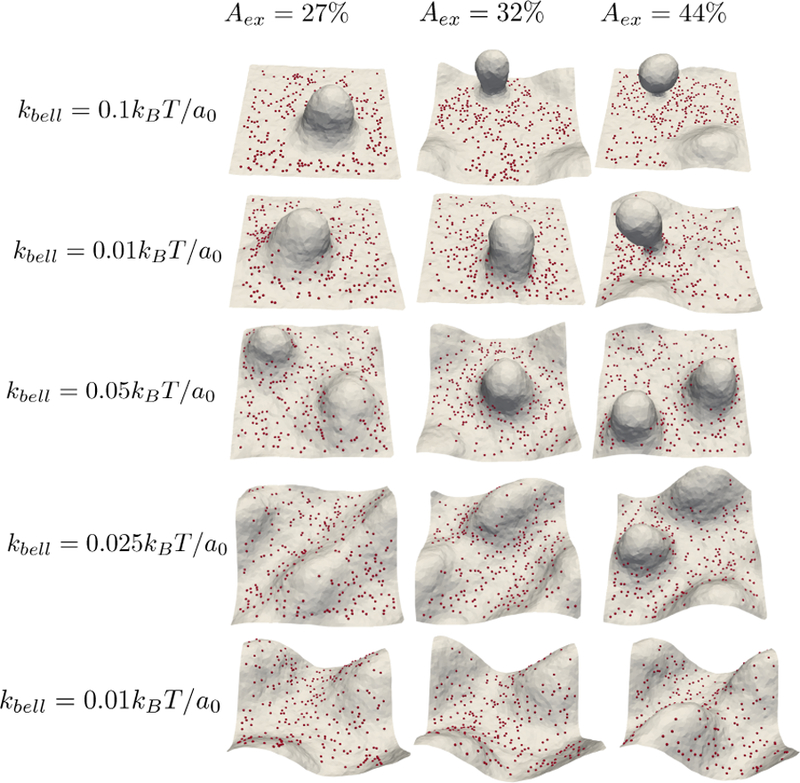
Equilibrium membrane conformations showing the effect of stiffness of adhessive complexes at different Aex values when ∆G = 19kBT, κ = 20kBT and Np = 0.1.
4. Conclusion
We have presented a computational approach to study the adhesion-induced morphologies in cell membranes of varying tension and density of adhesion molecules. To capture the elastic, thermal, and fluidity properties of a patch of the cell membrane, we utilize a well-established model for continuum elastic membranes known as dynamically triangulated MC. An extension of this model to include a given excess area or frame tension allows us to represent a membrane patch in various physiological tension conditions. In our approach, the molecular anchoring of cell membranes to a substrate or ECM is accounted via pinning interaction modeled using a Bell potential. The pinning sites mimic the diffusion and the dynamic binding-unbinding characteristics of adhesion molecules on cell membranes.
We showed the effect of pinning on membrane fluctuations and the curvature generation induced by pinning at a low pinning density. The confinement effect of pinning in restricting long-wavelength modes of the membrane patch has been previously shown [47, 48] and agree with our findings. Our results show that the formation of adhesion induced protrusions on the membrane depends on the density and diffusivity of the anchoring molecules. Significant changes in membrane topography occur at large excess areas and high pinning densities. Under these conditions, our method predicts the formation of vesicular buds from the membrane patch. We constructed a phase diagram of membrane morphologies and identified the range of adhesion strength and density that is favorable for microvesicle biogenesis. The application of very high negative tension at large densities of adhesion molecules is shown to induce tubules on the membrane. Though most studies in the literature show that morphological changes in membranes are primarily due to the presence of intrinsically curved proteins, our observations with such proteins on the membrane patch suggest that such shape changes can also occur as a result of static or dynamic adhesions either due to membrane-cytoskeletal or membrane-ECM interactions, and the proteins that preferentialy migrate to these highly curved structures can promote vesiculation.
Supplementary Material
Acknowledgments
We thank Wei Guo, Valerie Weaver, and members of the Penn PSOC for insightful discussions. The research leading to these results has received funding from the National Institutes of Health Grant U54 CA193417, U01 CA227550, and GM111942. Computational resources were provided in part by the National Partnership for Advanced Computational Infrastructure under Grant number MCB060006 from XSEDE.
References
- [1].Schmick M and Bastiaens PI 2014. Cell 156 1132–1138 ISSN 0092-8674 [DOI] [PubMed] [Google Scholar]
- [2].Huang S and Ingber DE 1999. Nature Cell Biology 1 [DOI] [PubMed] [Google Scholar]
- [3].Jarsch IK, Daste F and Gallop JL 2016. The Journal of Cell Biology 214 375–387 ISSN 0021-9525 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [4].McMahon HT and Gallop JL 2005. Nature 438 590–596 [DOI] [PubMed] [Google Scholar]
- [5].Sens P and Plastino J 2015. Journal of Physics: Condensed Matter 27 273103. [DOI] [PubMed] [Google Scholar]
- [6].Vogel V and Sheetz M 2006. Nature Reviews Molecular Cell Biology 7 265. [DOI] [PubMed] [Google Scholar]
- [7].Discher DE, Janmey P and Wang Y l 2005. Science 310 1139–1143 ISSN 0036-8075 [DOI] [PubMed] [Google Scholar]
- [8].Engler AJ, Sen S, Sweeney HL and Discher DE 2006. Cell 126 677–689 ISSN 0092-8674 [DOI] [PubMed] [Google Scholar]
- [9].Benjamin Geiger JPS and Bershadsky AD 2009. Nature Reviews Molecular Cell Biology 10 21–33 [DOI] [PubMed] [Google Scholar]
- [10].Andrew D Doyle Nicole Carvajal AJ, Matsumoto K and Yamada KM 2016. Nature Communications 6 8720. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [11].Chan CE and Odde DJ 2008. Science 322 1687–1691 ISSN 0036-8075 [DOI] [PubMed] [Google Scholar]
- [12].Harvey Lodish Arnold Berk SLZ, Matsudaira P, Baltimore D and Darnell J 2000. Molecular Cell Biology (4th edition (New York, NY: Freeman & Co; ) [Google Scholar]
- [13].Gauthier NC, Fardin MA, Roca-Cusachs P and Sheetz MP 2011. Proceedings of the National Academy of Sciences 108 14467–14472 ISSN 0027-8424 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [14].Wen PJ, Grenklo S, Arpino G, Tan X, Liao HS, Heureaux J, Peng SY, Chiang HC, Hamid E, Zhao WD, Shin W, Näreoja T, Evergren E, Jin Y, Karlsson R, Ebert SN, Jin A, Liu AP, Shupliakov O and Wu LG 2016. Nature Communications 7 12604. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [15].Kosmalska AJ, Casares L, Elosegui-Artola A, Thottacherry JJ, Moreno-Vicente R, González-Tarragó V, del Pozo MÁ, Mayor S, Arroyo M, Navajas D, Trepat X, Gauthier NC and Roca-Cusachs P 2015. Nature Communications 6 7292. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [16].Boulant S, Kural C, Zeeh JC, Ubelmann F and Kirchhausen T 2011. Nature Cell Biology 13 1124. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [17].Raposo G and Stoorvogel W 2013. The Journal of Cell Biology 200 373–383 ISSN 0021-9525 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [18].Wilson KF, Erickson JW, Antonyak MA and Cerione RA 2013. Trends in Molecular Medicine 19 74–82 ISSN 1471-4914 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [19].Becker A, Thakur BK, Weiss JM, Kim HS, Peinado H and Lyden D 2016. Cancer Cell 30 836–848 ISSN 1535-6108 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [20].Weaver VM. Unpublished.
- [21].Chen G, Huang AC, Zhang W, Zhang G, Wu M, Xu W, Yu Z, Yang J, Wang B, Sun H, Xia H, Man Q, Zhong W, Antelo LF, Wu B, Xiong X, Liu X, Guan L, Li T, Liu S, Yang R, Lu Y, Dong L, McGettigan S, Somasundaram R, Radhakrishnan R, Mills G, Lu Y, Kim J, Chen YH, Dong H, Zhao Y, Karakousis GC, Mitchell TC, Schuchter LM, Herlyn M, Wherry EJ, Xu X and Guo W 2018. Nature 560 382–386 ISSN 1476-4687 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [22].Desrochers LM, Bordeleau F, Reinhart-King CA, Cerione RA and Antonyak MA 2016. Nature Communications 7 11958 article [DOI] [PMC free article] [PubMed] [Google Scholar]
- [23].Anitei M and Hoflack B 2011. Nature Cell Biology 14 11. [DOI] [PubMed] [Google Scholar]
- [24].Sackmann E and Smith AS 2014. Soft Matter 10(11) 1644–1659 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [25].Paszek MJ, Boettiger D, Weaver VM and Hammer DA 2009. PLOS Computational Biology 5 1–16 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [26].Paszek MJ, DuFort CC, Rossier O, Bainer R, Mouw JK, Godula K, Hudak JE, Lakins JN, Wijekoon AC, Cassereau L, Rubashkin MG, Magbanua MJ, Thorn KS, Davidson MW, Rugo HS, Park JW, Hammer DA, Giannone G, Bertozzi CR and Weaver VM 2014. Nature 511 319. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [27].Schmidt D, Monzel C, Bihr T, Merkel R, Seifert U, Sengupta K and Smith A S c v 2014. Phys. Rev. X 4(2) 021023 [Google Scholar]
- [28].Sens P and Turner MS 2006. Phys. Rev. E 73(3) 031918. [DOI] [PubMed] [Google Scholar]
- [29].Sens P and Gov N 2007. Phys. Rev. Lett 98(1) 018102. [DOI] [PubMed] [Google Scholar]
- [30].Staykova M, Arroyo M, Rahimi M and Stone HA 2013. Phys. Rev. Lett 110(2) 028101. [DOI] [PubMed] [Google Scholar]
- [31].Moreno-Flores S 2016. Biochimica et Biophysica Acta (BBA)-Biomembranes 1858 793–799 ISSN 0005-2736 [DOI] [PubMed] [Google Scholar]
- [32].Liu J, Sun Y, Drubin DG and Oster GF 2009. PLOS Biology 7 1–16 URL 10.1371/journal.pbio.1000204 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [33].Tourdot RW Bradley RPRN and R R 2014. IET Syst Biol 8 198–213 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [34].Hassinger JE, Oster G, Drubin DG and Rangamani P 2017. Proceedings of the National Academy of Sciences 114 E1118–E1127 ISSN 0027-8424 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [35].Agrawal NJ, Nukpezah J and Radhakrishnan R 2010. PLOS Computational Biology 6 1–10 URL 10.1371/journal.pcbi.1000926 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [36].Zhao Y, Liu J, Yang C, Capraro B, Baumgart T, Bradley R, Ramakrishnan N, Xu X, Radhakrishnan R, Svitkina T and Guo W 2013. Developmental Cell 26 266–278 ISSN 1534-5807 URL http://www.sciencedirect.com/science/article/pii/S1534580713004152 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [37].Tourdot RW, Ramakrishnan N, Baumgart T and Radhakrishnan R 2015. Phys. Rev. E 92(4) 042715 URL https://link.aps.org/doi/10.1103/PhysRevE.92.042715 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [38].Ho JS and Baumgartner A 1989. Phys. Rev. Lett 63(12) 1324–1324 [DOI] [PubMed] [Google Scholar]
- [39].Helfrich W. Z. Naturforsch. C. 1973;28:693. doi: 10.1515/znc-1973-11-1209. [DOI] [PubMed] [Google Scholar]
- [40].Winterhalter M and Helfrich W 1988. J. Phys. Chem 92 6865–6867 [Google Scholar]
- [41].Ramakrishnan N, Sreeja KK, Roychoudhury A, Eckmann DM, Ayyaswamy PS, Baumgart T, Pucadyil T, Patil S, Weaver VM and Radhakrishnan R 2018. Physical Biology 15 026002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [42].Bell G 1978. Science 200 618–627 ISSN 0036-8075 [DOI] [PubMed] [Google Scholar]
- [43].Bell G, Dembo M and Bongrand P 1984. Biophysical Journal 45 1051–1064 ISSN 0006-3495 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [44].McKenzie M, Ha SM, Rammohan A, Radhakrishnan R and Ramakrishnan N 2018. Biophysical Journal 114 1830–1846 ISSN 0006-3495 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [45].Seifert U 1997. Advances in Physics 46 13–137 [Google Scholar]
- [46].Brown FLH. Quarterly Reviews of Biophysics. 2011;44:391432. doi: 10.1017/S0033583511000047. [DOI] [PubMed] [Google Scholar]
- [47].Fenz SF, Bihr T, Schmidt D, Merkel R, Seifert U, Sengupta K and Smith AS 2017. Nature Physics 13 906 [Google Scholar]
- [48].Marzban B and Yuan H 2017. Membranes 7 ISSN 2077-0375 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [49].Ford MGJ, Mills IG, Peter BJ, Vallis Y, Praefcke GJK, Evans PR and McMahon HT 2002. Nature 419 361–366 ISSN 1476-4687 [DOI] [PubMed] [Google Scholar]
- [50].Gallop JL, Jao CC, Kent HM, Butler PJG, Evans PR, Langen R and McMahon HT 2006. The EMBO Journal 25 2898–2910 ISSN 0261-4189 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [51].Lipowsky R 2013. Faraday Discuss 161(0) 305–331 [DOI] [PubMed] [Google Scholar]
- [52].Staykova M, Holmes DP, Read C and Stone HA 2011. Proceedings of the National Academy of Sciences 108 9084–9088 ISSN 0027-8424 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [53].Solon J, Pécréaux J, Girard P, Fauré MC, Prost J and Bassereau P 2006. Phys. Rev. Lett 97(9) 098103. [DOI] [PubMed] [Google Scholar]
- [54].Smith LR, Cho S and Discher DE 2018. Physiology 33 16–25 [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


