Quality of Daily-Life Gait: Novel Outcome for Trials that Focus on Balance, Mobility, and Falls

Abstract

Technological advances in inertial sensors allow for monitoring of daily-life gait characteristics as a proxy for fall risk. The quality of daily-life gait could serve as a valuable outcome for intervention trials, but the uptake of these measures relies on their power to detect relevant changes in fall risk. We collected daily-life gait characteristics in 163 older people (aged 77.5 ± 7.5, 107♀) over two measurement weeks that were two weeks apart. We present variance estimates of daily-life gait characteristics that are sensitive to fall risk and estimate the number of participants required to obtain sufficient statistical power for repeated comparisons. The provided data allows for power analyses for studies using daily-life gait quality as outcome. Our results show that the number of participants required (i.e., 8 to 343 depending on the anticipated effect size and between-measurements correlation) is similar to that generally used in fall prevention trials. We propose that the quality of daily-life gait is a promising outcome for intervention studies that focus on improving balance and mobility and reducing falls.

1. Introduction

Effective interventions to prevent falls in older people address balance and mobility problems through exercise interventions, medication reviews, and environmental modifications [1]. Despite a focus on balance and mobility, the default primary outcomes of such intervention trials are the rate of falls or the proportion of fallers. These outcomes require 6 to 12 months of intensive follow-up and are susceptible to definitional issues and recall biases [2,3]. Moreover, the incidence of falls does not directly equate fall risk, since exposure to random environmental events plays an important role [4,5]. Clinical tests of balance and mobility can be assessed relatively quickly and can be used as proxies for fall risk in intervention trials. However, their utility has been hampered by the requirement of in-person assessments under standardized conditions, which may not reflect an individual’s performance in daily life [6,7].

Technological advances in wearable sensors allow for the assessment of the quantity and quality of daily-life activities. Several studies have shown that characteristics of daily-life gait, assessed by a single trunk-worn sensor, are associated with fall risk among older people [8,9,10]. These gait characteristics, such as gait stability and variability, provide complementary information to commonly-used clinical tests in the prediction of falls [11]. Experimental studies further provide evidence that gait characteristics, during standardized assessments, are sensitive to relatively small balance impairments and are affected by disturbances of the sensory systems, medication, muscle fatigue, and training [12,13,14,15,16]. Effect sizes for these manipulations approximate a Cohen’s d of 3.0–5.0 for desensitization of the feet and electrical vestibular stimulation in healthy young [13,14], 0.3 for rivastigmine medication in people with Parkinson’s disease [16], 0.5–0.6 for muscle fatigue in older people [12] and 0.3–0.8 for a dance intervention in older people [15]. The difference in daily-life gait quality between older people who fall, and those who do not fall in the next 6 months, is in the order of a Cohen’s d of 0.3 (range 0.03 to 0.5) [11]. The assessment of daily-life gait characteristics may hence be valuable for intervention trials.

In order to determine whether daily-life gait characteristics are sensitive to change, such as intervention effects, large-scale clinical trials are required. Sample size calculations are essential in the design of such trials. However, the estimation of the variance components that are needed for these calculations, requires large samples of repeated measurements, which are generally not available early in a study. We analyzed trunk accelerometry data collected for [10] to provide this information to support the design of intervention trials. We estimated the variance components and performed a sample size calculation to reveal how many participants would be required in order to detect the statistically significant intervention effects on daily-life gait quality characteristics obtained from inertial sensor data in older people.

2. Materials and Methods

2.1. Participants

This study was part of a larger project investigating fall risk in older people (FARAO [8,10]). The participants were older people, who were recruited from Amsterdam (the Netherlands) and its surroundings via advertisements through general practitioners, hospitals, and residential care facilities. Inclusion criteria were: being between 65 and 99 years of age, having no major cognitive impairments (assessed as a Mini Mental State Examination score exceeding 18 out of 30 points [17]), and being able to walk at least 20 m with, or without, the help of a walking aid. The medical ethics committee of the VU medical centre approved the protocol (ID 2010/290) and all participants signed informed consent.

2.2. Measurements

The data of 163 older people (mean age 77.5, SD 7.5 years; 107♀) were analyzed for the current paper. The participants wore a trunk accelerometer (DynaPort MoveMonitor, McRoberts BV, The Netherlands) for two separate one-week periods, with a median between-assessment interval of 14 days (interquartile range 28 days, maximum 65 days). They were instructed to wear the accelerometer at all times, except during water activities, such as showering or swimming as this would damage the device. No intervention took place during the between-assessment interval. The tri-axial trunk accelerometer was placed on the back of the trunk at the level of L5 using a supplied elastic belt, and registered trunk accelerations in vertical (VT), mediolateral (ML), and anteroposterior (AP) directions with a sample frequency of 100 samples/s and range of +/-6 g.

2.3. Data Analysis

The episodes of locomotion were identified using the manufacturers algorithm. This algorithm was validated against video [18] and the detection of locomotion episodes was shown to be reliable over weeks [19]. The raw data of locomotion periods were extracted and realigned with anatomical axes, based on the accelerometer’s orientation with respect to the gravity and optimization of left-right symmetry [8,10]. Subsequently, gait quality was estimated as median values over each week of 40 characteristics, reflecting walking speed, stride frequency, regularity, intensity, symmetry, smoothness, stability, and complexity of gait [8,10]. We report on 18 gait characteristics, that were significantly associated with prospective falls [10] in our tables, and provide data for all gait characteristics in Appendix A. We calculated a single gait quality composite score, based on a weighted sum of autocorrelation at stride frequency, power at step frequency, root mean square of the accelerations and index of harmonicity, which was previously found to be an important predictor for falls [10]. The custom Matlab-code to calculate this gait quality composite score can be found here: github.com/KimvanS/EstimateGaitQualityComposite.

2.4. Statistics

Data was inspected for normality using Q-Q plots and KS tests. Most variables followed a normal distribution, except for the amplitude of the dominant frequency. However, since its difference scores did follow a normal distribution, parametric statistics are reported for all variables. We tested for structural differences between both measurement weeks, using repeated measures ANOVAs, and Pearson correlations. The repeated measures ANOVAs were subsequently used to extract the overall mean and variance components, reflecting between-subjects (i.e., among participants), within-subject (i.e., between measurement weeks), and error variability (i.e., individual differences due to sampling error). Sample size calculations, for repeated measures, were performed to determine the number of participants required to detect changes in these gait quality characteristics over measurements. The number of participants (n) was estimated following [20] as:

$$n=\frac{2\ast s_{\mathrm{S}}^2\ast \left(1-\left(r\ast \frac{s_{\mathrm{BS}}^2}{s_{\mathrm{S}}^2}\right)\right)\ast {\left(t_{n-1,1-\beta }+t_{n-1,1-\alpha /2}\right)}^2}{{\Delta }^2}$$ (1)

where $s_{\mathrm{S}}^2$ is the total variance, $s_{\mathrm{BS}}^2$ the between-subject variance, r the within-subject correlation, t_df,p the p^th-percentile of a t-distribution with df degrees of freedom, 1- β the desired level of statistical power, α the desired level of statistical significance, and Δ the effect size. Statistical power was set to 0.8 and statistical significance was set to 0.05. The numbers of participants required to detect an effect size Δ of Cohen’s d 0.3 (small), 0.5 (medium), and 0.8 (large), were estimated for all gait quality characteristics.

3. Results

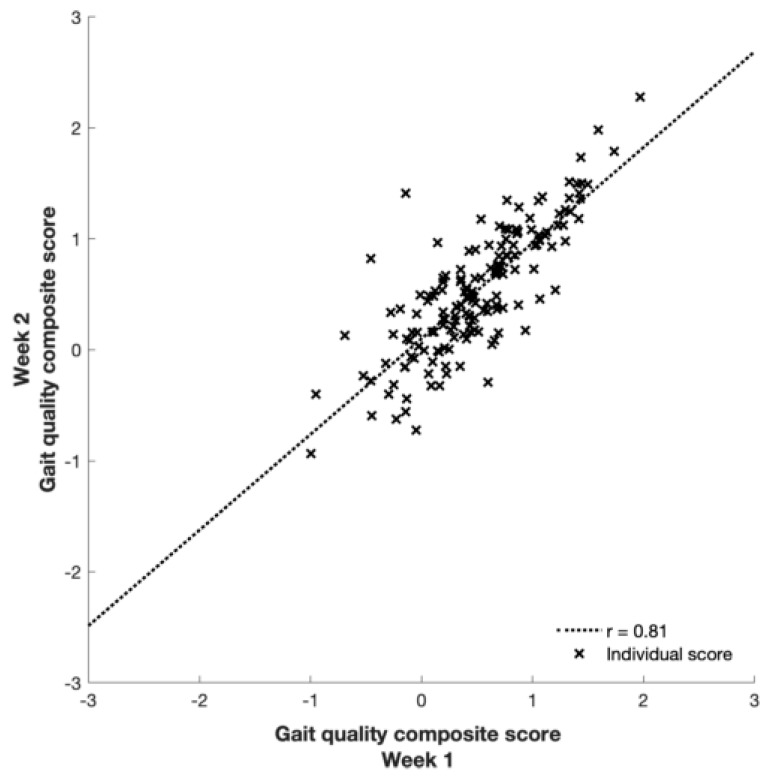
None of the gait quality characteristics differed significantly between the two measurement weeks (all p ≥ 0.11) and all were strongly correlated (r = 0.80 to 0.96; Figure 1 and Table 1). Between-subject variance was the largest variance component for all characteristics, and 3 to 26 times higher than within-subject variance. Moreover, between-subject variance components were highest for characteristics that were orientation invariant (e.g. walking speed, step length, and time), and generally higher for ML compared to AP, with VT in between (Table 1 and Table A1 for all 40 characteristics).

Figure 1.

Agreement between the gait quality composite scores of the first and second week.

Table 1.

Agreement between weeks and estimated variance components for gait characteristics associated with prospective falls in [10].

	p	r	Mean	s2BS	s2WS	s2E
Gait quality composite score	0.64	0.81	0.51369	0.54700	0.08068	0.05759
Walking speed	0.39	0.93	0.45073	0.01030	0.00027	0.00036
Stride frequency	0.51	0.95	0.82482	0.01119	0.00013	0.00030
Standard deviation VT	0.77	0.92	1.32658	0.17858	0.00061	0.00733
Standard deviation ML	0.18	0.94	1.16407	0.09332	0.00560	0.00305
Range AP	0.40	0.91	7.33318	7.13497	0.23150	0.32894
Stride autocorrelation VT	0.54	0.82	0.37464	0.01051	0.00040	0.00103
Stride autocorrelation AP	0.63	0.83	0.32881	0.00945	0.00021	0.00088
Amplitude of dominant frequency VT	0.68	0.93	0.49412	0.04264	0.00026	0.00155
Amplitude of dominant frequency ML	1.00	0.91	0.47481	0.05827	9.26 × 10−9	0.00263
Amplitude of dominant frequency AP	0.11	0.85	0.51044	0.02357	0.00501	0.00198
Width of dominant frequency AP	0.14	0.80	0.75841	0.00611	0.00167	0.00075
Index of harmonicity VT	0.19	0.96	0.62043	0.04940	0.00156	0.00092
Index of harmonicity ML	0.68	0.92	0.64420	0.06977	0.00048	0.00276
Harmonic ratio VT	0.47	0.90	1.53576	0.07348	0.00211	0.00406
Local divergence rate/stride VT	0.75	0.87	2.11436	0.13693	0.00097	0.00919
Local divergence rate/stride AP	0.58	0.86	2.19507	0.09652	0.00217	0.00707
Sample entropy ML	0.74	0.91	0.31207	0.00394	2.07 × 10−5	0.00018

Note: We tested for structural differences between both measurement weeks using a repeated measures ANOVA (p-value) and Pearson correlations (r). We subsequently report mean values (mean) and variance components between-subjects (s²_BS), within-subjects (s²_WS) and due to sampling error (s²_E).

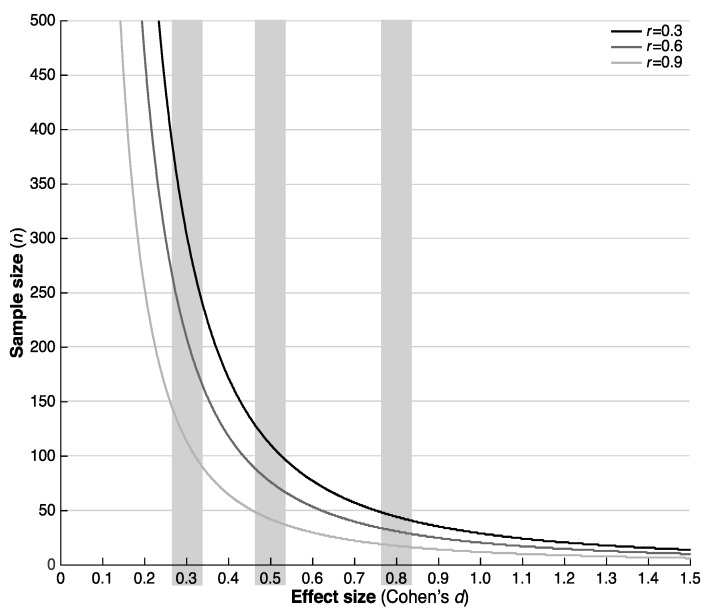
The number of participants required to detect intervention effects with sufficient statistical power ranged from 8 (large effect, r = 0.9) to 343 (small effect, r = 0.3) (Figure 2 and Table 2; see Table A2 for all characteristics).

Figure 2.

Number of participants required to detect an effect of Cohen’s d on the gait quality composite score.

Table 2.

Number of participants required to detect an effect of Cohen’s d on gait characteristics associated with prospective falls in [10].

	Small Effect			Medium Effect			Large Effect
	Cohen’s d = 0.3			Cohen’s d = 0.5			Cohen’s d = 0.8
	r = 0.3	r = 0.6	r = 0.9	r = 0.3	r = 0.6	r = 0.9	r = 0.3	r = 0.6	r = 0.9
Gait quality composite score	303	208	114	110	76	42	44	31	18
Walking speed	259	158	56	95	58	22	38	24	10
Stride frequency	254	151	49	93	56	19	37	23	9
Stride length	251	148	44	92	54	17	37	22	8
Standard deviation VT	252	151	51	92	56	19	37	23	9
Standard deviation AP	266	163	61	97	60	23	39	25	10
Range AP	262	162	62	96	60	23	39	24	10
Stride autocorrelation VT	268	173	77	98	63	29	39	26	13
Stride autocorrelation AP	263	167	71	96	61	27	39	25	12
Amplitude of dominant frequency VT	253	151	50	92	56	19	37	23	9
Amplitude of dominant frequency ML	251	151	51	92	56	19	37	23	9
Amplitude of dominant frequency AP	323	227	130	118	83	48	47	34	20
Width of dominant frequency AP	343	250	156	125	91	57	50	37	24
Index of harmonicity VT	260	157	54	95	58	21	38	24	9
Index of harmonicity ML	253	152	51	92	56	20	37	23	9
Harmonic ratio VT	262	162	63	96	60	24	39	25	11
Local divergence rate/stride VT	256	157	59	93	58	23	38	24	10
Local divergence rate/stride AP	261	164	66	95	60	25	38	25	11
Sample entropy ML	253	153	53	92	56	20	37	23	9

4. Discussion

The purpose of this paper was to report the variance components required for sample size calculations in studies focusing on characteristics of daily-life gait quality as outcome measures. This paper also aimed to determine the number of participants required to detect intervention effects in a repeated measure design with sufficient statistical power (here set at 80%). Our sample size calculations indicate that the number of participants required for a test-retest intervention design will range from 8 to 343, depending on the anticipated between-measurement correlation and effect size. These numbers seem reasonable, compared to the 200 to 500 (range 10 to 9940, median 230 [1]) participants that are generally included in fall prevention intervention studies. This approach has the additional advantage that outcomes are available directly after the intervention, and that physical activity or exposure, can be readily assessed using similar methods. Future studies are required to determine whether changes due to interventions focusing on improving balance and mobility, and reducing falls can indeed be detected with daily-life gait quality characteristics.

The high correlation between measurements, combined with the relatively small within-subject variance, suggests that participant’s daily-life gait characteristics are relatively stable, at least over weeks without an intervention. Possible changes in orientation, due to reattaching the sensor after water activities, may have increased within-subject variance, a source of variance that can be remediated by fixing a waterproof sensor directly onto the body. Changes in orientation, over days, may have contributed to the higher number of participants required for orientation-dependent characteristics, when compared to orientation-invariant characteristics. The relatively small within-subject variance is encouraging for clinical use, as it holds promise for evaluation on the individual level.

The magnitude of the between-subject variance components for gait stability and variability characteristics in this study, was larger than those reported by Toebes and colleagues for treadmill gait [20]. This could be a result of differences in experimental setup and algorithms [21] to assess these characteristics. However, it is also possible that assessments in daily life result in better differentiation between individuals. A direct comparison of the sensitivity to change of the laboratory-based and daily-life assessment of gait quality characteristics for fall risk seems warranted.

Despite the benefits of using daily-life gait characteristics as outcomes in fall prevention trials, there are barriers to their broad uptake. Although, inertial sensors are relatively cheap compared to other motion registration equipment, they generally cost ~$500–5000. Moreover, these sensors require charging and setting-up, can be logistically inconvenient and need specialist code to extract meaningful outcomes. Finally, non-wearing might render collected data useless. Nevertheless, we feel that the advantages outweigh the disadvantages and hope that this paper provides the tools and data necessary to facilitate their implementation.

This study has some limitations. The locomotion detection algorithm may have introduced some error. However, its validity and reliability are high [18,19]. Moreover, we limited this study to median values of the distribution of the daily-life gait quality characteristics while more extreme percentiles, that better reflect participants’ capacity [6,8], may show different variances. The estimated variance components will also depend on sensor characteristics, the methods of fixation and fixation location, and thus might not generalize to other settings. The strength of the correlation between measurements, used in the sample size calculations, was estimated and actual values may be lower, with longer follow-up times and individuals responding differently to interventions. The time between measurements was relatively short in this study, which warrants the assumption of little changes within individuals over time; longer follow-up periods in trials may therefore present larger within-subject variance.

5. Conclusions

We provided variance estimates to determine the number of participants required for intervention trials using daily-life gait characteristics as outcomes. The subsequent sample size estimations indicate that a substantial number of participants is required to detect the effects of interventions. However, this number is lower than that commonly used in trials with incidence of falls as the outcome. Therefore, characteristics of daily-life gait quality seems to be a promising outcome for intervention studies, focusing on balance, mobility, and falls.

Appendix A

Table A1.

Agreement between weeks and estimated variance components for all gait characteristics.

	p	r	Mean	s2BS	s2WS	s2E
Gait quality composite score	0.64	0.81	0.51369	0.54700	0.08068	0.05759
Stride autocorrelation VT	0.54	0.82	0.37464	0.01051	0.00040	0.00103
Stride autocorrelation ML	0.65	0.94	0.34724	0.02069	0.00013	0.00060
Stride autocorrelation AP	0.63	0.83	0.32881	0.00945	0.00021	0.00088
Walking speed	0.39	0.93	0.45073	0.01030	0.00027	0.00036
Step length	0.41	0.97	0.63683	0.02457	0.00022	0.00032
Stride time variability	0.74	0.85	9.36259	13.19347	0.11324	1.05325
Stride speed variability	0.87	0.95	0.04695	0.00030	2.20 × 10−7	7.90 × 10−6
Stride length variability	0.65	0.93	0.04456	0.00029	2.07 × 10−6	1.01 × 10−5
Standard deviation VT	0.77	0.92	1.32658	0.17858	0.00061	0.00733
Standard deviation ML	0.18	0.94	1.16407	0.09332	0.00560	0.00305
Standard deviation AP	0.13	0.96	1.08260	0.09554	0.00479	0.00203
Stride frequency	0.51	0.95	0.82482	0.01119	0.00013	0.00030
Percentage of power <0.7 hz VT	0.65	0.88	0.23888	0.04349	0.00059	0.00284
Percentage of power <0.7 hz ML	0.76	0.90	11.96214	96.31279	0.45914	4.98382
Percentage of power <0.7 hz AP	0.85	0.77	11.29116	29.95935	0.13423	3.85606
Index of harmonicity VT	0.19	0.96	0.62043	0.04940	0.00156	0.00092
Index of harmonicity ML	0.68	0.92	0.64420	0.06977	0.00048	0.00276
Index of harmonicity AP	0.45	0.90	0.77248	0.00890	0.00026	0.00046
Harmonic ratio VT	0.47	0.90	1.53576	0.07348	0.00211	0.00406
Harmonic ratio ML	0.23	0.92	1.33320	0.02929	0.00187	0.00129
Harmonic ratio AP	0.61	0.86	1.46828	0.05386	0.00103	0.00396
Dominant frequency VT	0.22	0.78	1.82738	0.16622	0.03063	0.02044
Dominant frequency ML	0.22	0.84	0.85494	0.13286	0.01897	0.01257
Dominant frequency AP	0.23	0.88	1.58025	0.06492	0.00598	0.00417
Amplitude of dominant frequency VT	0.68	0.93	0.49412	0.04264	0.00026	0.00155
Amplitude of dominant frequency ML	1.00	0.91	0.47481	0.05827	9.2 × 10−9	0.00263
Amplitude of dominant frequency AP	0.11	0.85	0.51044	0.02357	0.00501	0.00198
Width of dominant frequency VT	0.14	0.80	0.76624	0.02141	0.00572	0.00267
Width of dominant frequency ML	0.39	0.90	0.79147	0.01238	0.00049	0.00066
Width of dominant frequency AP	0.14	0.80	0.75841	0.00611	0.00167	0.00075
Range VT	0.60	0.89	9.56290	9.84092	0.15828	0.55808
Range ML	0.47	0.95	7.95077	10.04315	0.13792	0.26707
Range AP	0.40	0.91	7.33318	7.13497	0.23150	0.32894
Local divergence rate/stride VT	0.75	0.87	2.11436	0.13693	0.00097	0.00919
Local divergence rate/stride ML	0.21	0.92	2.16970	0.15560	0.01077	0.00689
Local divergence rate/stride AP	0.58	0.86	2.19507	0.09652	0.00217	0.00707
Sample entropy VT	0.80	0.91	0.24764	0.00271	8.33 × 10−6	0.00013
Sample entropy ML	0.74	0.91	0.31207	0.00394	2.07 × 10−5	0.00018
Sample entropy AP	0.06	0.91	0.26908	0.00359	0.00064	0.00017

Note: We tested for structural differences between both measurement weeks using a repeated measures ANOVA (p-value) and Pearson correlations (r). We subsequently report mean values (mean) and variance components between-subjects (s²_BS), within-subjects (s²_WS) and due to sampling error (s²_E).

Table A2.

Number of participants required for all gait characteristics.

	Small effect			Medium effect			Large effect
	Cohen’s d = 0.3			Cohen’s d = 0.5			Cohen’s d = 0.8
	r = 0.3	r = 0.6	r = 0.9	r = 0.3	r = 0.6	r = 0.9	r = 0.3	r = 0.6	r = 0.9
Gait quality composite	303	208	114	110	76	42	44	31	18
Walking speed	259	158	56	95	58	22	38	24	10
Stride frequency	254	151	49	93	56	19	37	23	9
Stride length	251	148	44	92	54	17	37	22	8
Standard deviation VT	252	151	51	92	56	19	37	23	9
Standard deviation ML	270	169	67	99	62	25	40	25	11
Standard deviation AP	266	163	61	97	60	23	39	25	10
Range VT	258	158	59	94	58	23	38	24	10
Range ML	254	152	50	93	56	19	37	23	9
Range AP	262	162	62	96	60	23	39	24	10
Walking speed variability	250	148	45	91	54	18	37	22	8
Stride time variability	257	160	63	94	59	24	38	24	11
Stride length variability	253	152	50	92	56	19	37	23	9
Stride autocorrelation VT	268	173	77	98	63	29	39	26	13
Stride autocorrelation ML	252	150	48	92	55	18	37	23	8
Stride autocorrelation AP	263	167	71	96	61	27	39	25	12
Amplitude of dominant frequency VT	253	151	50	92	56	19	37	23	9
Amplitude of dominant frequency ML	251	151	51	92	56	19	37	23	9
Amplitude of dominant frequency AP	323	227	130	118	83	48	47	34	20
Width of dominant frequency VT	341	248	155	124	91	57	50	37	23
Width of dominant frequency ML	265	166	66	97	61	25	39	25	11
Width of dominant frequency AP	343	250	156	125	91	57	50	37	24
Percentage of power <0.7 hz VT	258	159	61	94	59	23	38	24	10
Percentage of power <0.7 hz ML	254	154	54	93	57	21	37	23	9
Percentage of power <0.7 hz AP	260	167	74	95	61	28	38	25	12
Index of harmonicity VT	260	157	54	95	58	21	38	24	9
Index of harmonicity ML	253	152	51	92	56	20	37	23	9
Index of harmonicity AP	262	162	62	95	59	24	38	24	10
Harmonic ratio VT	262	162	63	96	60	24	39	25	11
Harmonic ratio ML	273	172	72	99	63	27	40	26	12
Harmonic ratio AP	260	163	65	95	60	25	38	25	11
Local divergence rate/stride VT	256	157	59	93	58	23	38	24	10
Local divergence rate/stride ML	274	174	73	100	64	28	40	26	12
Local divergence rate/stride AP	261	164	66	95	60	25	38	25	11
Sample entropy VT	253	152	52	92	56	20	37	23	9
Sample entropy ML	253	153	53	92	56	20	37	23	9
Sample entropy AP	310	210	110	113	77	41	45	31	17

Author Contributions

Conceptualization, K.S.v.S., M.P., S.R.L., J.H.v.D.; data collection, K.S.v.S., M.P., J.H.v.D.; data analysis, K.S.v.S.; data interpretation, K.S.v.S., M.P., S.R.L., J.H.v.D.; writing—original draft preparation, K.S.v.S.; writing—review and editing, M.P., S.R.L., J.H.v.D.; final approval, K.S.v.S., M.P., S.R.L., J.H.v.D.

Funding

This work was supported by the Dutch Organization for Scientific Research [NWO TOP NIG grant 91209021] and the Human Frontier Science program [HFSP long-term fellowship number LT001080/2017].

Conflicts of Interest

Between 06/2014 and 09/2015, K.v.S. was partially supported by a commercial grant of McRoberts BV (the Hague, the Netherlands). McRoberts B.V. had no role in the study design, data collection and analysis, decision to publish, or the preparation of the manuscript.