Humans falling in holes: adaptations in lower-limb joint mechanics in response to a rapid change in substrate height during human hopping

Abstract

In getting from here to there, we continuously negotiate complex environments and unpredictable terrain. Our ability to stay upright in the face of obstacles, such as holes in the ground, is quite remarkable. However, we understand relatively little about how humans adjust limb mechanical behaviour to recover from unexpected perturbations. In this study, we determined how the joints of the lower-limb respond to recover from a rapid, unexpected drop in substrate height during human hopping. We recorded lower-limb kinematics and kinetics while subjects performed steady-state hopping at their preferred frequency on an elevated platform (5, 10 and 20 cm). At an unknown time, we elicited an unexpected perturbation (i.e. a hole in the ground) via the rapid removal of the platform. Based on previous research in bipedal birds, we hypothesized (i) that distal joints would play an increased role in fall recovery when compared to steady-state hopping, and (ii) that patterns of joint power redistribution would be more pronounced with increases in perturbation height. Our results suggest that humans successfully recover from falling in a hole by increasing the energy absorbed predominantly in distal lower-limb joints (i.e. the ankle) across perturbation heights ranging from 5 to 10 cm. However, with increased perturbation height (20 cm) humans increase their reliance on the more proximal lower-limb joints (i.e. the knee and the hip) to absorb mechanical energy and stabilize fall recovery. Further investigations into the muscle–tendon mechanics underlying these joint-level responses will likely provide additional insights into the neuromotor control strategies used to regain the stability following unexpected perturbations and provide biological inspiration for the future design of wearable devices capable of performing within unpredictable environments.

1. Introduction

During everyday locomotion, animals often move continuously through complex and uneven environments in a safe and economical manner. For example, humans often encounter unexpected disruptions to natural gait due to curbs, holes and bumps within their environment. Yet, much of our knowledge regarding human locomotion has come from studies conducted under steady-state conditions on level surfaces. To date, we know very little about the features of human lower-limb joint biomechanics and neuromuscular control that allow for stability in the face of unpredictable terrain. To better understand this, we aimed to determine how humans coordinate the mechanics of the lower-limb joints in order to maintain upright, rhythmic hopping during rapid, unexpected changes in the height of the ground.

The physiological behaviour with which lower-limbs store and return energy during steady gait has inspired the design of passive wearable assistive devices capable of augmenting human locomotion during walking [1], running [2] and hopping [3,4]. However, our incomplete understanding regarding how the human body responds to gait conditions whereby energy must be rapidly generated or dissipated has, in part, limited our ability to improve exoskeleton performance for variable terrains. Recently developed powered assistive devices have highlighted the importance of implementing adaptive controllers that assist different lower-limb joints with specific actuation magnitudes and timings [5–7]. Although these studies present remarkable progress in the field of wearable assistive devices, the experiments were conducted on flat walking surfaces, and thus provide minimal insight into the patterns of lower-limb assistance necessary for energy dissipation tasks. The findings of the present study aim to provide fundamental insights into the mechanisms for locomotor stability during unexpected perturbations and have rich potential to inspire the future design of lower-limb wearable robotic devices including prostheses and exoskeletons capable of performing within complex and unpredictable environments.

To provide insight into how non-human animals achieve stability during unexpected perturbations, researchers have investigated how bipedal birds modify their whole body and joint-level mechanics [8,9], neuromuscular control and muscle–tendon dynamics [10,11] during drop perturbations. For example, when birds encounter a sudden and unexpected drop in substrate height, camouflaged using a tissue paper to avoid visual cues, they use whole body spring–mass dynamics as a passive stabilizing mechanism to maintain their locomotor trajectory [8]. Further research into the joint-level behaviour during these perturbations highlights that limb mechanical function in birds displays a proximo-distal gradient, whereby the proximal joints (hip and knee) maintain a similar mechanical role to level running and the distal joints (ankle and tarsometatarso-phalangeal) undergo rapid changes in kinematics and kinetics in order to stabilize their centre of mass and maintain forward and upright gait [9]. Surprisingly, when the substrate drop is visible, birds display an increased difficulty as compared to the unexpected condition and often stumble or slow down [12].

In vivo recordings of the underlying neural and mechanical behaviour of leg muscles highlight that the distal extensor muscle–tendon units exhibit rapid changes in force–length dynamics and work output for the perturbed stride and the first two recovery strides [10]. However, muscle activation increases only in the first stride following the perturbation, and not the perturbation stride itself, suggesting that neural drive and contractile dynamics may be uncoupled during the recovery to steady gait. Drop landing experiments in turkeys highlight the role of series elasticity within the muscle–tendon unit which acts as a buffer to rapidly absorb mechanical energy and protect the muscle fascicles from potentially injurious strains [11]. This series of studies provide a comprehensive understanding, spanning organizational levels (e.g. whole body, joint, nervous system, muscle–tendon unit, muscle fibre), outlining key mechanisms that bipedal animals use to maintain stability in response to sudden perturbations and thus provide a framework from which we can design human perturbation experiments.

Few studies have investigated the physiological responses to expected or unexpected changes in substrate height during walking or running in humans. These studies have shown that small (5–10 cm), unexpected decreases in ground height during walking are associated with a series of neuromechanical responses: vertical impact forces increase [13–15], step length increases to control the body's forward momentum [13] and anti-gravity muscles in the perturbed limb (ipsilateral) and flexor muscles in the opposite limb (contralateral) are co-activated [16]. When the perturbation is unexpected, camouflaged with a thin black cloth similar to the bird experimental paradigm, humans display rapid reflexive muscle activity at the perturbed ankle, delayed toe-off to maintain a stance duration similar to that of normal walking, and increased knee flexion during stance [17]. A series of walking [18] and running [15,19] studies by Müller and colleagues demonstrate that when a drop in height is visible and expected, subjects perform preparatory actions to lower their centre of mass over two to three steps prior to the perturbation, yet when the drop is camouflaged and unexpected, these compensations occur within a single step [15]. Panizzolo and colleagues [20] measured the response to unexpected bumps, rather than drops, during level walking and found that humans adapt either an ankle strategy by increasing plantarflexor muscle activity or a hip strategy by increasing quadriceps muscle activity, although neither strategy elicits changes in total lower-limb mechanical work [20]. However, these previous human studies are limited to few and relatively small perturbation heights (maximum of 10 cm) and have predominately focused on the whole body rather than joint-level responses. Thus, we are still limited in our understanding of the characteristics of lower-limb joint mechanics in response to unexpected, rapid perturbations.

In this study, we investigated how humans adjust lower-limb mechanics to negotiate unexpected vertical perturbations during hopping. Human hopping is an attractive experimental paradigm to study perturbation responses. Similar to walking and running, it is characterized by alternating stance (ground contact) and swing (flight) phases, and like running and other bouncing gaits, it has dynamics that can be explained using a simple spring–mass model [21]. Here, we aimed to (i) investigate the patterns of joint-level mechanics that humans use to maintain stability during unexpected vertical perturbations and (ii) test whether these mechanical strategies vary with the size of the perturbation, by varying the change in substrate height. To do this, we used inverse dynamics analysis to determine individual lower-limb joint moments and powers during two-legged hopping before, during and following a rapid vertical perturbation using three changes in the height of the ground (5, 10 and 20 cm). We hypothesized that when perturbed, (i) the distal lower-limb joints (e.g. ankle) would play an increased role to help stabilize the body during recovery from a perturbation as compared to normal hopping and (ii) that these patterns of joint power redistribution towards more distal lower-limb joints would be more pronounced with increases in perturbation height.

2. Methods

2.1. Experimental protocol

Data were recorded from 10 healthy individuals (mean ± s.d., six male four female; 26.7 ± 4.4 years; 1.73 ± 0.09 m; 70.1 ± 10.9 kg). Subjects provided written informed consent and all experimental protocols were approved by the Institutional Review Board of the University of North Carolina at Chapel Hill, USA. Participants were instructed to perform bilateral hopping in place on a stationary split-belt treadmill instrumented with two separate force platforms (Bertec, Columbus, OH, USA) (figure 1). While wearing a safety harness, participants hopped continuously at their preferred frequency (2.4 ± 0.02 Hz, range 2.13–2.8 Hz) while an unexpected perturbation, via manual removal of two custom-built platforms directly under the left and right lower-limbs, was elicited at a random time between the 10th and 20th hop (electronic supplementary material, video S1). Subjects were instructed to continue hopping following the perturbation event. Preferred frequency was experimentally determined. Subjects hopped at their preferred frequency, but were not instructed to reach a height target nor paced with a metronome. To test the effect of drop height, experimental trials were performed for three different platform heights (5, 10 and 20 cm) presented in a randomized order. The initial experimental condition for each subject was repeated as the final condition to test for learning effects. During each trial, we collected bilateral lower-limb joint kinematics and kinetics.

Figure 1.

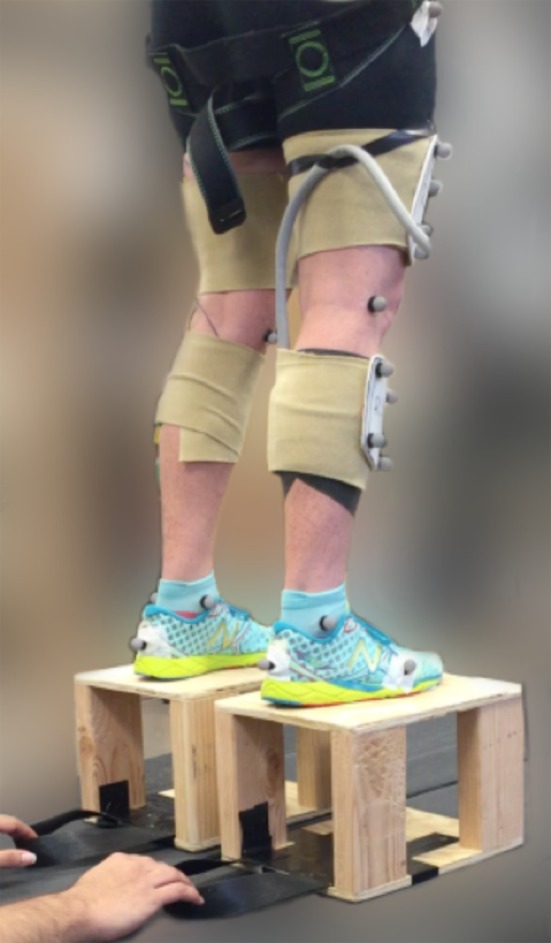
Experimental set-up for perturbation trials. Individuals hopped continuously at their preferred frequency (2.4 ± 0.02 Hz) until an unexpected perturbation was elicited via manual removal of the custom-built platforms (20 cm height shown). Lower-limb kinematics were measured using motion capture and ground reaction forces were measured using a stationary split-belt treadmill. (Online version in colour.)

2.2. Kinematics and kinetics

Lower-limb rigid body segment and pelvis kinematics were measured using an eight-camera motion capture system (120 Hz, Vicon, Oxford, UK) that captured the three-dimensional (3D) positions of 32 reflective markers. Individual markers were placed bilaterally on lower-limb bony landmarks and rigid marker clusters of four markers were secured to the right and left shanks, thighs and to the pelvis. This marker set is consistent with previous experimental protocols (e.g. [22]). A static calibration trial was collected during standing to scale a musculoskeletal model to each subject (OpenSim v. 3.3, [23,24]). A subject-specific scaled model was used together with the motion capture data in an inverse kinematics analysis to determine the time-varying joint angles for the ankle, knee and hip for each trial and subject. Briefly, this process performs a weighted least-squares fit of the model markers to the experimental 3D marker positions to determine the pose of the model at each time point, and from this, joint angles were determined.

Ground reaction forces (GRF) applied to the right and left legs during hopping were measured using an instrumented stationary split-belt treadmill (980 Hz, Bertec, Columbus, OH, USA). Participants hopped with each foot on a separate belt of the treadmill such that one 3D ground reaction force (GRF) vector could be attributed to each of the right and left lower-limbs. The raw analogue force platform data were filtered using a second-order low-pass Butterworth filter with the cut-off frequency of 35 Hz.

Next, we combined the model kinematics with measured GRF data recorded from the two force platforms on the treadmill in an inverse dynamics analysis to compute the net joint moments at the ankle, knee and hip during hopping prior to the perturbation (p⁻¹), during the perturbation (p) and following the perturbation (p^+1,+2,+3). Kinematics and kinetics were calculated for the right leg only. Hopping trials, where the platforms were not completely removed from the force plates before foot ground contact, were repeated.

2.3. Mechanical work and power calculations

We determined the mechanical work and power at each of the lower-limb joint during normal hopping, the perturbed hop and up to 10 hops following the perturbation according to the methods presented in Farris & Sawicki [25]. Briefly, we calculated instantaneous joint powers for the ankle, knee and hip over the hop cycle as the product of joint moment and joint angular velocity (the time derivative of joint angle). Joint angles were the internal angles between the proximal and distal segments with positive changes/velocities indicating extension. Positive joint moments and powers represent moments acting to extend the joint and the rate of work being done to extend the joint, respectively.

We used the trapezium method to integrate joint power data for the ankle, knee and hip with respect to time over discrete periods of positive and negative work [25]. For each hop, at each joint, all periods of positive work were summed and all periods of negative work were summed to determine the average total positive and negative work done at each of the lower-limb joints for an average hop cycle. Positive and negative mechanical work values for the ankle, knee and hip were divided by contact time to calculate average positive and negative joint mechanical powers. Next, the average positive and negative mechanical powers calculated for the ankle, knee and hip were summed and this value was taken as total average positive and negative mechanical power output of the limb. We computed each joint's contribution to the total limb average positive and negative mechanical power as a percentage of total average positive or negative power based on the ratio of individual joint power for the ankle, knee or hip to the sum of ankle, knee and hip joint powers according to the following equation:

$$J_{\text{\%}}=\frac{P_j}{P_{\mathrm{ank}}+P_{\mathrm{knee}}+P_{\mathrm{hip}}}\hspace{0.17em}\times \hspace{0.17em}100\text{\%},$$

where P_ank, P_knee, P_hip are the total ankle, knee and hip average (positive or negative) powers, respectively. J_% is the per cent contribution of an individual joint, whose joint power is P_j, to total average positive or negative limb mechanical power. Additionally, net limb work was calculated as the sum of the ankle, knee and hip net work over each hop cycle (multiplied by two, to account for the work done at the contralateral limb) and compared to the change in the potential energy of the whole body due to the vertical perturbation. All data processing following inverse dynamics was conducted using custom-written scripts in Mathematica v. 11 (Wolfram Research Inc., Champaign, Illinois, USA).

2.4. Statistical analysis

For all analyses, a within-subject design was used, including subject as random factor using the lme.R function from the nlme package [26] in R (v. 3.4.3, Vienna, Austria). To examine variation in joint angles, joint moments and joint powers between factors (hop cycle [hop]: p⁻¹, p, p⁺¹; drop [height]: 5 cm, 10 cm, 20 cm) we specified the model with lme.R function, and then used glht.R function from the multcomp package [27] to perform Tukey post hoc tests. Differences were considered significant at the p < 0.05 level. Statistical outputs from the lme.R analysis for joint angles, joint moments and joint powers are reported in electronic supplementary material, table S1, with post hoc results reported in the main text.

3. Results

3.1. Joint angles

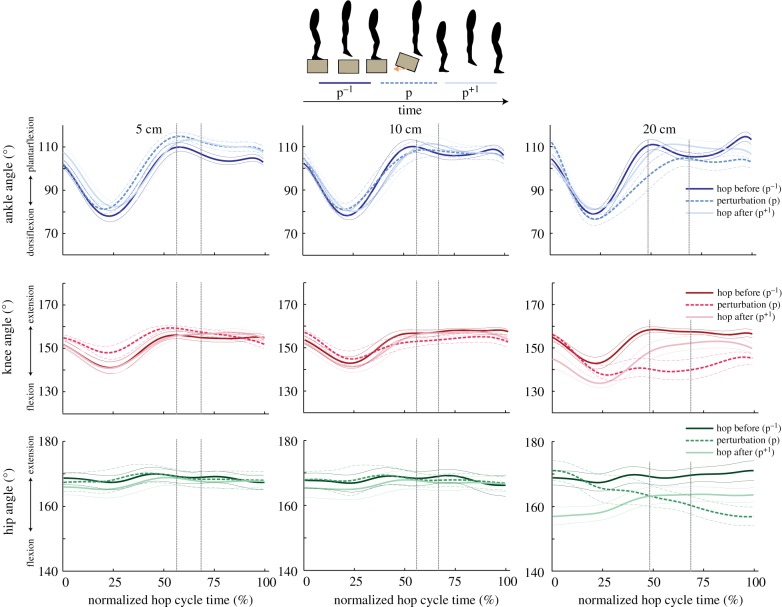
Joint angles for the ankle, knee and hip varied during the perturbation as compared to normal hopping and varied with drop height (table 1; electronic supplementary material, table S1; figure 2). Peak ankle plantarflexion, ankle dorsiflexion and knee flexion angles increased significantly with increasing drop height during the perturbation (figure 2). A comparison of lower-limb kinematics before the perturbation (p⁻¹) to the perturbation (p) showed a significant increase in peak knee flexion angle (p = 0.041), and peak hip flexion angle (p = 0.009) during the 20 cm drop height only, and a significant increase in peak ankle plantarflexion angle (p = 0.019) and peak knee flexion angle (p = 0.01) at 5 cm. Following the perturbation, the ankle approached its normal kinematic pattern within one hop for all drop heights, whereas the knee and hip joints remained in a flexed position following the 20 cm drop only (figure 2).

Table 1.

Lower-limb joint angles during perturbation recovery. Data are presented as group mean range of motion (mean minimum–mean maximum) for the ankle, knee and hip angles for hop before the perturbation (p⁻¹), the perturbation (p) and the hop directly following the perturbation (p⁺¹) for the three perturbation heights: 5 cm, 10 cm and 20 cm.

	ankle ROM (deg.)			knee ROM (deg.)			hip ROM (deg.)
	p−1	p	p+1	p−1	p	p+1	p−1	p	p+1
5 cm	79–110	82–116	82–114	142–161	148–163	142–161	162–171	165–172	164–170
10 cm	80–111	82–109	81–112	142–162	142–162	141–161	162–171	163–172	164–170
20 cm	79–111	76–105	82–111	141–161	126–160	133–156	166–172	155–172	156–166

Figure 2.

Group mean (thick lines) ± s.e. (thin lines) for the ankle (top row), knee (middle row) and hip (bottom row) joint angles for 5 cm (left panel), 10 cm (middle panel) and 20 cm (right panel) perturbation heights. Data are shown for the hop before the perturbation (p⁻¹; dark lines), the perturbation (p; dashed lines) and the hop directly following the perturbation (p⁺¹; light lines) and are time-normalized to each hop cycle. Vertical lines represent the range of normalized ground take-off times across hop cycles. (Online version in colour.)

3.2. Joint moments

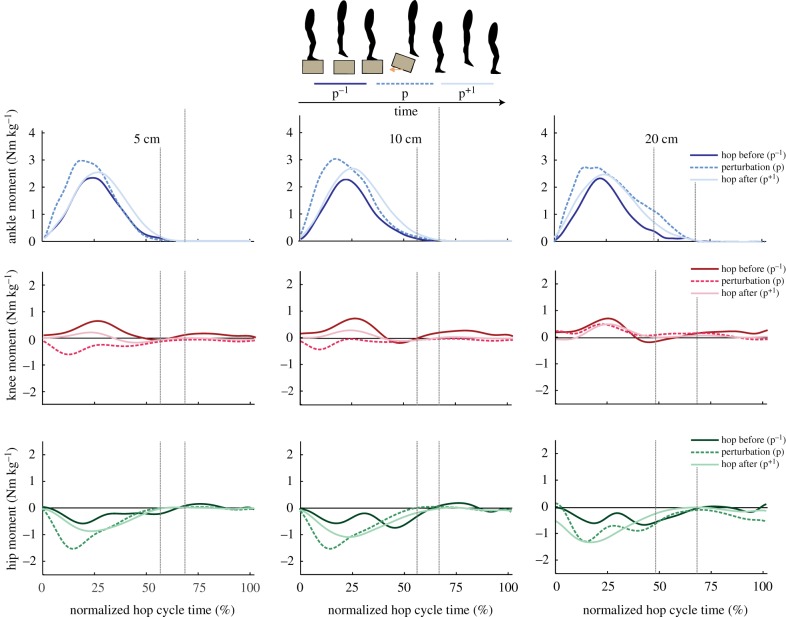
When comparing joint mechanics before the perturbation (p⁻¹) to the perturbation (p), there was a significant increase in peak ankle plantarflexion (positive) moment at all three drop heights and a significant increase in peak hip flexion (negative) moment for all three drop heights. However, there were no significant changes in peak or average ankle, knee or hip moment when comparing across the three perturbation heights (electronic supplementary material, table S1; figure 3). Kinematics and kinetics remained unchanged between the same height condition tested as both the first and the final hopping trial, suggesting minimal learning effects throughout the duration of our experimental protocol.

Figure 3.

Group mean ankle (top row), knee (middle row) and hip (bottom row) joint moments for 5 cm (left panel), 10 cm (middle panel) and 20 cm (right panel) perturbation heights. Data are shown for the hop before the perturbation (p⁻¹; dark lines), the perturbation (p; dashed lines) and the hop directly following the perturbation (p⁺¹; light lines) normalized to body mass and time-normalized to each hop cycle. Vertical lines represent the range of normalized ground take-off times across hop cycles. (Online version in colour.)

3.3. Joint powers

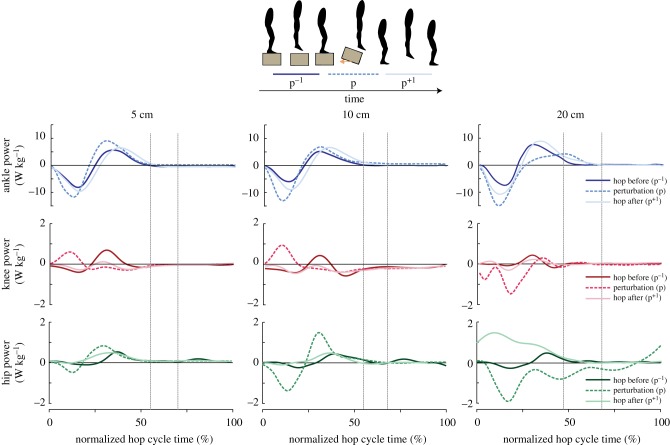
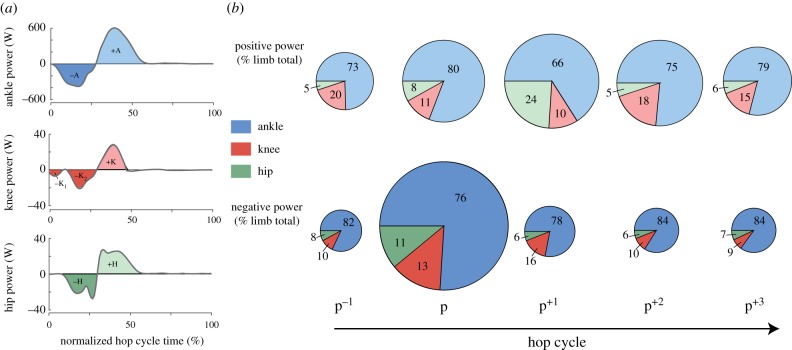
Our results indicate changes in instantaneous joint mechanical powers for the ankle, knee and hip during the perturbation (figure 4). Specifically, there was a significant increase in peak negative ankle, peak negative knee and peak negative hip power during the 20 cm perturbation as compared to normal hopping with smaller effects on peak negative joint power at the lower drop heights (5 and 10 cm) (figure 4). There were no significant differences in lower-limb joint mechanical powers between drop heights for the hop before the perturbation (p⁻¹).

Figure 4.

Group mean instantaneous ankle (top row), knee (middle row) and hip (bottom row) joint powers for 5 cm (left panel), 10 cm (middle panel) and 20 cm (right panel) perturbation heights. Data are shown for the hop before the perturbation (p⁻¹; dark lines), the perturbation (p; dashed lines) and the hop directly following the perturbation (p⁺¹; light lines) normalized to body mass and time-normalized to each hop cycle. Vertical lines represent the range of normalized ground take-off times across hop cycles. (Online version in colour.)

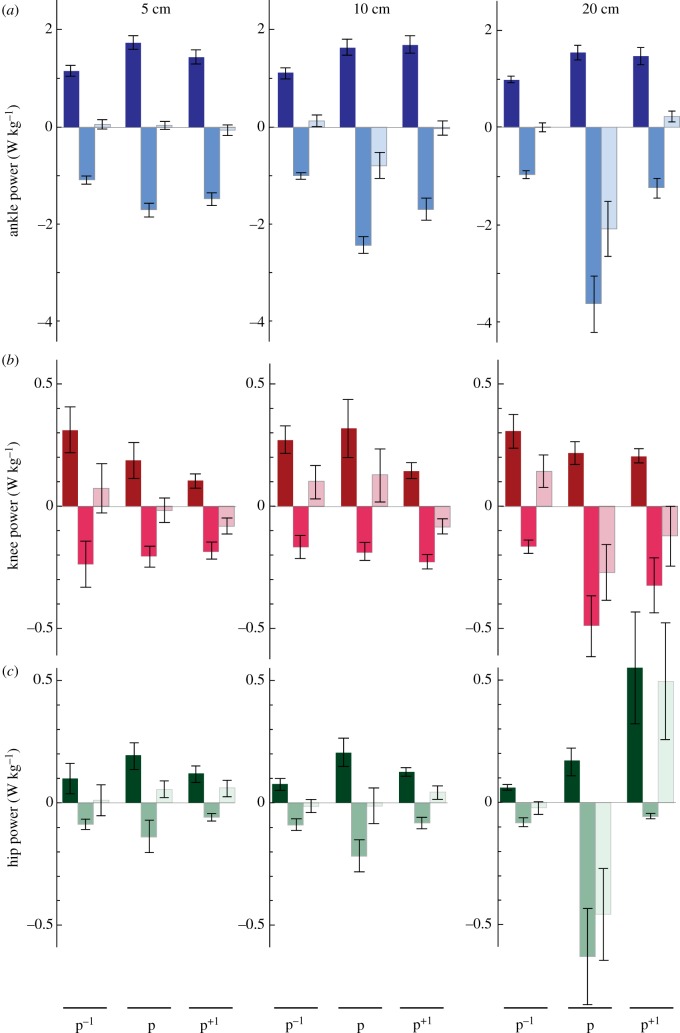
Independent comparisons of positive, negative and net joint powers highlight the mechanical adjustments that occurred at the ankle, knee and hip in response to a rapid perturbation in the height of the ground (figure 5; electronic supplementary material, table S1). We found a significant increase in positive ankle power during the perturbation (p) as compared to normal hopping (p⁻¹) that was independent of drop height, suggesting that positive ankle power increased similarly at all drop heights. Additionally, there was an increase in negative ankle power from p⁻¹ to p, with a significant effect of drop height and the interaction between hop and height, such that larger drop heights were associated with greater increases in negative ankle power (5 cm: p < 0.001; 10 cm: p < 0.001; 20 cm: p = 0.003). As a result, net ankle power significantly decreased during the perturbation and with drop height, with a significant interaction between the two, such that only the greater drop heights were associated with the increases in net ankle power (10 cm: p = 0.006; 20 cm: p = 0.008). For the knee, there was a significant increase in negative knee power from hop p⁻¹ to p and a significant interaction between hop and height, such that only the 20 cm drop height was associated with an increase in negative knee power (p = 0.044). There was a significant decrease in net knee power from hop p⁻¹ to p (with no change in positive knee power). At the hip, we found an increase in positive hip power and an increase in negative hip power from hop p⁻¹ to p, which were both independent of drop height. Additionally, we found a significant decrease in net hip power with increasing drop height (figure 5). Additionally, we found an increase in average negative ankle and negative knee power and an increase in positive hip power between p⁻¹ and p⁺¹ (figure 5), suggesting that recovery does not occur within a single cycle.

Figure 5.

Perturbation responses vary with drop height. Group mean average positive power (darker), negative power and net power (lighter) (W kg⁻¹) ± s.e. produced at the ankle (a), knee (b) and hip (c) for hop before the perturbation (p⁻¹), the perturbation (p) and the hop directly following the perturbation (p⁺¹). Data are shown for three perturbation heights: 5 cm (left panel); 10 cm (middle panel); 20 cm (right panel) and normalized to body mass. (Online version in colour.)

During normal, steady-state hopping (p⁻¹), perturbed hopping (p) and the recovery hops (p⁺¹, p⁺², p⁺³), the ankle joint mechanical power provided the largest contribution to both average positive (66–80%) and average negative (76–85%) limb mechanical power, with the knee and hip joints providing less of both the positive (knee: 10–20%, hip: 5–24%) and negative (knee: 9–16%, hip: 6–11%) contribution (figure 6b). Both total limb negative mechanical power and total limb positive power increased during the perturbation compared to normal hopping (as indicated by the diameter of the pie graph; figure 6b). The percentage contribution of the lower-limb joints to the total average negative and positive lower-limb power varied between normal, steady hopping (p⁻¹) and the perturbation (p) (figure 6b). During the perturbation, the knee significantly increased its negative contribution to total limb mechanical power (p = 0.02), whereas the ankle decreased its negative contribution (p = 0.002) (figure 6b). A comparison of each of the joints' relative contributions to total limb mechanical power between steady hopping (p⁻¹) and the initial recovery hop (p⁺¹) indicated no differences in the distribution of lower-limb joint negative powers, but a significant increase in the contribution of positive hip power (p < 0.001) and decrease in the contribution of positive ankle power (p < 0.001) (figure 6b). There were no significant differences in the relative contributions of ankle, knee or hip joint mechanical powers when comparing the second (p⁺²) or the third (p⁺³) recovery hops to a normal steady hop cycle (p⁻¹).

Figure 6.

The relative contribution of the ankle, knee and hip joints to total lower-limb power varies during perturbation recovery from a 20 cm drop in substrate height. (a) Ankle, knee, and hip power for a representative hop cycle. Lighter areas indicate periods when the joint is doing positive work and darker areas indicate when the joint is doing negative work. Individual periods of positive and negative work are labelled as +A, −A, +K, −K, +H, −H for the ankle, knee, and hip, respectively. Positive and negative work done at each joint per hop cycle was calculated as the sum of the positive or the negative work values. (b) Pie charts display the average percentage of total average positive power (top) and total average negative power (bottom) contributed by the ankle, knee, and hip joints at 20 cm. The diameter of each pie indicates the total positive or negative power relative to the other conditions. (Online version in colour.)

3.4. Time course of energy dissipation

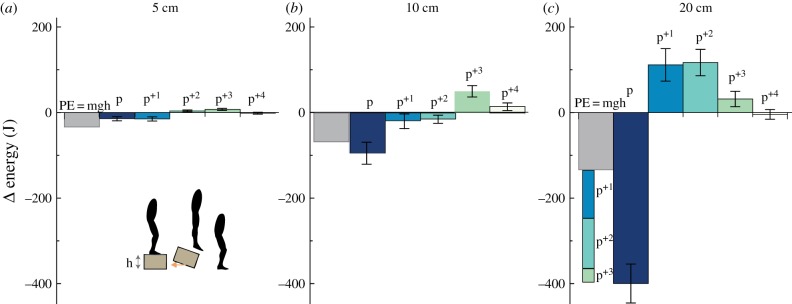
The magnitude of energy dissipated per hop, as assessed by comparing the net limb work per hop to the change in potential energy due to the vertical perturbation, suggests that the lower-limb overcompensates by dissipating more mechanical energy than necessary upon the initial ‘fall’ (p) from the 20 cm drop (figure 7c), and to a lesser extent from the 5 and 10 cm drop (figure 7a,b). At 20 cm, on average, −399.7 ± 45.5 J of energy, which represents three times (200% more) the change in potential energy due to the vertical perturbation (133 J), was dissipated upon the initial perturbation hop cycle, p (as negative joint work), and then subsequently recovered in the three following hop cycles (p⁺¹; 111.4 ± 37.9 J, p⁺²; 116.9 ± 30.8 J, p⁺³; 31.7 ± 17.9 J) (figure 7c). By the fourth cycle p⁺⁴, net zero energy hopping behaviour is recovered.

Figure 7.

Assessing the rate of energy dissipation over hop cycles. Average (±s.e.) net limb work (energy) during continuous hop cycles (p, p⁺¹, p⁺², p⁺³, p⁺⁴) for the 5 cm (a), 10 cm (b) and 20 cm (c) drop heights compared to the change in the potential energy (PE) due to the drop height (h). Net limb energy (J) was calculated as the sum of the ankle, knee and hip net powers multiplied by the cycle duration for each hop cycle. The average change in PE (grey bar) was calculated for each subject as the product of subject mass (m), gravity (g) and drop height (h). (Online version in colour.)

4. Discussion

In this study, we aimed to quantify the joint-level strategies that humans use to dissipate energy and stay upright during a rapid unexpected perturbation in the height of the ground (i.e. a fall into a hole). From studies on non-human animals (e.g. bipedal birds), we know that stability is achieved using a control strategy whereby the proximal joints (hip and knee) maintain a similar mechanical function to steady-state locomotion, but the distal joints (ankle) undergo rapid changes in joint mechanics [9]. Our results suggest that humans adopt a similar strategy to birds and successfully recover from falling in a hole by increasing the energy absorbed in only distal lower-limb joints (i.e. the ankle) across perturbation heights ranging from 5 to 20 cm. However, with increased perturbation height (20 cm) humans increase their reliance on the more proximal lower-limb joints (i.e. the knee and the hip) to absorb mechanical energy and stabilize fall recovery. Interestingly, we found that at drop heights greater than 5 cm, the lower-limb overcompensated and dissipated more mechanical energy than was necessary due to the change in vertical height, and thus required additional positive work to be performed in subsequent hops in order to regain steady-state locomotor behaviour.

Humans are able to recover from small, unexpected perturbations with minimal changes in joint mechanics. Here, we found that both 5 and 10 cm drop heights were associated with marginal alterations in lower-limb joint angles and joint moments. Previous studies have examined the effects of expected and unexpected changes in surface height between 5 and 10 cm during walking and running [13,16,18–20,17]. Similar to our results, Shinya and colleagues found that successful perturbation recovery is associated with small increases in knee flexion angle. They suggest that this may be a useful strategy for withdrawing the perturbed leg and allowing toe clearance to step out of the hole [17]. Others have proposed that humans will commonly flex their knees to negotiate obstacles during walking [28]. Again, our results are similar to those displayed during human walking over a 5 or 10 cm unexpected drop in surface height [18]. Müller and co-workers found that when subjects stepped into an unexpected hole, they increased their initial ground reaction force and increased their knee flexion angle, but found no change in these responses between 5 and 10 cm drops. It should be noted that direct comparisons between these previous studies [15,18,19] and ours are challenging. These previous experiments allowed for subjects to conduct trials with the change in surface height first visible, followed by camouflaged and the authors note anticipatory kinematic and kinetic adaptations during the unexpected perturbations that were facilitated by the subjects having prior experience with the perturbation and knowledge of its location within the trackway.

The ankle plantarflexors are characterized by short pennate muscle fibres and a long elastic tendon. This design allows for the behaviour of muscle fibres to be uncoupled from joint motion (e.g. [29]). For example, during human walking, a catapult-like mechanism at the ankle allows elastic strain energy to be slowly stored in the Achilles tendon during stance (while the plantarflexor muscle fibres remain near isometric) and then rapidly released in late-stance to enable forward propulsion [29]. Experiments in turkey drop landings highlight that the tendon plays an additional role in energy dissipation [30]. Specifically, it alters the time course of muscle lengthening and effectively attenuates the rate of energy dissipation by muscle fascicles [30]. These authors suggest that this power-attenuating behaviour allows the tendon to serve a protective mechanism by reducing the risk of muscle fascicle damage during active lengthening. In this study, it is possible that at the lower perturbation heights, energy dissipation occurred at the level of the muscle–tendon unit (e.g. co-activation) and thus would not be evident at the joint level. Future studies using dynamic imaging techniques to measure in vivo muscle–tendon behaviour during rapid perturbation tasks are necessary to examine this possibility.

In contrast to the lower drop heights, perturbation recovery from a drop height of 20 cm, which represents approximately 30% of leg length, was associated with substantial adjustments to lower-limb mechanics. Until now, experimental data during unexpected perturbations from drops greater than 15% leg length (10 cm in humans) are available only in bipedal birds. It appears that humans and birds both maintain stability during forward running via rapid changes in kinematics, joint moments and joint work in the distal limb joints when negotiating unexpected drops in terrain [9,12]. However, unlike birds which seem to be capable of adjusting limb mechanics within one step (the perturbation) to recover, humans dissipate excess energy and require 2–3 hops to recover steady-state behaviour. Although, it is challenging to make direct comparisons between these studies because the animal work does not typically report perturbation responses following p⁺¹. Unperturbed hopping is an ankle-dominated locomotor task with 50–80% of the positive mechanical power generated by the ankle muscle–tendon units [31]. The increased reliance on proximal joints to initially absorb energy (negative power) and later generate mechanical energy (positive power) may suggest a motor control strategy that aims to minimize musculoskeletal stresses in the ankle plantarflexors by allowing the larger muscles, which cross the hip and knee joints, to increase their mechanical contribution. In fact, minimizing muscle stress has been proposed as a physiologically reasonable criterion when solving the redundancy problem in muscle force predictions during locomotion [32] and is commonly used as a performance criterion in musculoskeletal simulations [23]. Additionally, experimental data from turkey drop landings suggest a more local stress minimization strategy whereby upon initial ground contact, the ankle plantarflexors activate to shorten, and then slowly lengthen following peak force [11]. This active muscle–tendon contribution, whereby the series elastic structures undergo substantial lengthening to absorb energy, has been suggested as a strategy to reduce the risk of high strain fascicle damage, which has been shown to be particularly damaging at lengths greater than 1.25 l₀ [33]. It is likely that humans adopt a combination of both strategies, whereby they (i) re-direct joint mechanical power, work and force to the larger proximal muscles and (ii) use an active muscle–tendon strategy in the ankle plantarflexors to reduce the risk of muscle injury that can result from rapid and forceful muscle fascicle lengthening.

During cyclical locomotor tasks, like walking, there is an optimally tuned neuromechanical interaction whereby muscles are activated at discrete times in the muscle–tendon unit's length change cycle [34]. Previous work has shown that adjusting muscle onset timing, a seemingly simple neural control strategy, can shift a muscle–tendon unit from producing energy to absorbing energy [35]. This is important as it allows the function of individual muscle–tendon units to be tuned to the locomotor demands of the task. It is likely that unexpected perturbations to cyclical tasks, via changes in substrate height, result in an automatic adjustment (phase shift) in muscle activation relative to muscle–tendon unit length change. Specifically, a perturbation that acts to increase the time to ground contact (e.g. a hole) effectively delays the onset of muscle–tendon lengthening relative to the onset of feedforward-timed muscle activation. As a result, muscle activation occurs relatively earlier in the muscle–tendon unit length change cycle. Earlier onset of muscle activation is associated with muscles generating increasing amounts of negative work [35]. This ‘automatic phase shift’ may enable the muscle–tendon unit to absorb more energy than during steady cycles, leading to more effective dissipation. It is possible that this mechanism, an emergent property of a feedforward dominant motor control strategy, yields generalized robustness to ground height perturbations; however, experiments involving simultaneous muscle activation and muscle–tendon length change measurements are needed to provide further insight.

Despite the impressive ability for biologically inspired devices to emulate the biological behaviour of lower-limb muscle–tendon units during bouncing [36] and walking gaits [1], designing exoskeletons and prostheses capable of rapidly responding to unexpected perturbations remains an open challenge [37,38]. The results of this study have rich potential to help guide the design of wearable devices (e.g. prostheses and exoskeletons) capable of augmenting human locomotion during unexpected perturbations, like falling in a hole. For example, our results suggest that when designing a lower-limb exoskeleton with actuated ankle, knee and hip joints capable of performing in variable terrains, engineers may need to consider control strategies that account for (i) changes in the relative contributions of proximo-to-distal joint powers (timing and magnitude) and (ii) (over)compensatory energy dissipation to aid in fall recovery.

Indeed, we show that to successfully recover from an unexpected perturbation and avoid a fall, humans absorb more energy (at the joint-level) than is expected due to the change in vertical height (figure 7). It is possible that this is a safety prioritization strategy [39], whereby individuals are willing to dissipate excess energy to stabilize their centre of mass trajectory and avoid a forward stumble in exchange for spending extra energy later in order to regain steady, vertical hopping. These results are consistent with jump landing responses whereby humans absorb nearly 40% more energy than necessary in the form of negative work in order to avoid the potential pain and discomfort associated with high ground impacts [40]. Furthermore, when instructed to land softly, humans perform 76% more negative work than required, highlighting the influence of subjectivity on preferred locomotor strategies [41]. In this case, exoskeletons that are nominally designed to deliver net positive work over a gait cycle, may counterintuitively enable more stable gait by compensating for the excess energy dissipated by the individual. But, an entirely passive ‘springy’ exoskeleton, which cannot dissipate nor generate energy, could act to reduce the over-compensatory behaviour given that humans reduce muscle activations and joint powers during steady gait in passive exoskeletons [1,4]. In this case, when faced with a perturbation, lower-limb muscles would be less active in the first place, perform less negative work during the perturbed step and enable recovery in fewer steps. Future work, using simulations and robotic testbeds informed with experimental data (e.g. [42]), will allow a better understanding of how robust these balance recovery mechanisms are across a range of perturbation conditions. In particular, simple models and simulations (e.g. [43,44]) ought to prove useful for exploring the relatively large performance landscape, which is challenging to elicit in human experimental studies.

There are limitations to the experimental protocol and joint-level analysis techniques implemented in this study. First, joint mechanics were estimated using inverse dynamics. This technique is limited given that the calculated joint moments and powers are the net result of synergistic and antagonistic muscles acting at each joint. Walking studies suggest that co-contraction of antagonist muscles can result in estimated joint work that slightly underestimates (7%) actual muscle–tendon positive work [45]. In vivo studies of individual muscle fascicle and tendinous tissue behaviour during perturbations similar to those studied here will help to confirm or refute joint-level results and help reveal the muscle-level strategies underpinning perturbation recovery. Second, within our inverse dynamics analysis we did not account for the mechanical contribution of the foot, which has recently been shown to play an energy dissipation role during running [46]. Future studies into the role of the foot during energy dissipation tasks, such as falling in a hole, will further our understanding of balance recovery strategies. Third, we refer to the task as an unexpected perturbation, and although subjects were blinded to the perturbation timing during the experiments, there may have been minimal auditory cues caused by the sliding of the wooden platforms along the force plates, confounding our claim that perturbations were truly ‘unexpected’. Finally, we must note that more common locomotor tasks (e.g. walking and running) where the centre of mass moves forward are associated with more complex kinematics and mechanics than hopping and thus care should be taken in extrapolating these joint-level findings to such tasks. For example, Daley and colleagues [9,12] show that leg retraction can also help dissipate energy to maintain stability while running over an unexpected drop in terrain height [9,12]. Additionally, Van Dieen et al. [13] highlight the importance of controlling angular momentum immediately following landing from both expected and unexpected stepping down, which is not captured in our hopping paradigm.

In this study, we used a joint-level analysis to determine how humans recover steady, vertical hopping gait following falling in a hole. When we elicited rapid, unexpected perturbations in ground height, we found a change in the relative contributions of the ankle, knee and hip joint to total lower-limb mechanical power. In particular, there was an increased reliance on the distal ankle joint to absorb energy at drop heights less than or equal to 10 cm whereas the proximal knee and hip joints increased their contribution to energy absorption only at the greatest perturbation height (20 cm, which represents approximately 30% leg length). Additionally, we found that more energy was dissipated (at the joint-level) than was expected due to the change in vertical height, suggesting that subjects take a conservative strategy that prioritizes safety, by overcompensating, to guarantee the maintenance of stability and avoid falling. Future investigations into the in vivo muscle–tendon dynamics underpinning these joint-level responses will likely provide insight into the neuromotor control strategies (e.g. feedforward versus feedback) used to recover from unexpected perturbations and provide biological inspiration for future designs of wearable robotic devices (e.g. exoskeleton and prostheses) capable of handling discrete changes in terrain associated with ‘real-world’ environments.

Data accessibility

Subject average kinetic and kinetic data (N = 10) for each of the experimental conditions (drop height = 5, 10 and 20 cm) presented here can be downloaded at: http://pwp.gatech.edu/hpl/archival-data-from-publications/.

Authors' contributions

T.J.M.D., L.K.P. and G.S.S. conceived of the study and designed the experimental protocol; T.J.M.D. and L.K.P. carried out the experiments; T.J.M.D. analysed the data and drafted the manuscript; T.J.M.D., L.K.P. and G.S.S. edited the manuscript. All authors gave final approval for publication.

Competing interests

We declare we have no competing interests.

Funding

This research was partially supported by U.S. Army Natick Soldier Research, Development and Engineering Center (W911QY18C0140) to G.S.S.