Probabilistic TFCE: a generalised combination of cluster size and voxel intensity to increase statistical power

Abstract

The threshold-free cluster enhancement (TFCE) approach integrates cluster information into voxelwise statistical inference to enhance detectability of neuroimaging signal. Despite the significantly increased sensitivity, the application of TFCE is limited by several factors: (i) generalisation to data structures, like brain network connectivity data is not trivial, (ii) TFCE values are in an arbitrary unit, therefore, P-values can only be obtained by a computationally demanding permutation-test.

Here, we introduce a probabilistic approach for TFCE (pTFCE), that gives a simple general framework for topology-based belief boosting.

The core of pTFCE is a conditional probability, calculated based on Bayes’ rule, from the probability of voxel intensity and the threshold-wise likelihood function of the measured cluster size. In this paper, we provide an estimation of these distributions based on Gaussian Random Field theory. The conditional probabilities are then aggregated across cluster-forming thresholds by a novel incremental aggregation method. pTFCE is validated on simulated and real fMRI data.

The results suggest that pTFCE is more robust to various ground truth shapes and provides a stricter control over cluster “leaking” than TFCE and, in many realistic cases, further improves its sensitivity.

Correction for multiple comparison can be trivially performed on the enhanced P-values, without the need for permutation testing, thus pTFCE is well-suitable for the improvement of statistical inference in any neuroimaging workflow.

Implementation of pTFCE is available at https://spisakt.github.io/pTFCE.

Introduction

Voxel-wise univariate statistical inference on neuroimaging signals is problematic due to the large number of simultaneously performed statistical comparisons and the unknown, complex dependency between tests. While correcting inferences for a brain-wide search is essential (Bennett et al., 2011; Vul et al., 2009), the attempt to diminish Type I errors rendered most of the statistical thresholding approaches overly conservative (Nichols and Hayasaka, 2003). This might result in increased Type II errors (i.e. missing true effects)(Lohmann et al., 2017) and publication biases (Lieberman and Cunningham, 2009) e.g. toward studying large rather than small effects.

Since the signal of interest is usually spatially more or less extended (that is, clustered), sensitivity can be significantly boosted by relating the size of the activation cluster to the (empirical or theoretical) distribution of random clusters in an image of given smoothness (Forman et al., 1995; Friston et al., 1994b). This approach is called cluster-wise inference. It captures the spatial nature of the signals, and thus suffers from less multiplicity than voxel-wise inference. However, it is not always more sensitive, and its power depends on the spatial scale of the signal relative to the noise smoothness. For instance focal, intense signals will be better detected by voxel-wise inference (Nichols, 2012). Another serious pitfall when using cluster-level inference is to over-simplistically interpret it at the voxel-wise level: spatial specificity in this case is low and the number of false positive voxels is increased, especially when the significant clusters are large or the applied cluster-forming thresholds are low (Woo et al., 2014). In this paper, we will refer to this phenomenon as “cluster leaking” and discuss it in detail. Moreover, the dependence of results on the (initial cluster-forming) hard-threshold is, on its own, problematic, since finding an optimal threshold is not trivial and might even lead to another multiple comparison problem, if simultaneously testing many different thresholds.

An improved way of making use of spatial neighbourhood information in order to boost belief in extended areas of neuroimaging signals is the threshold-free cluster enhancement (TFCE) approach (Smith and Nichols, 2009). In contrast to simple cluster-based inference, TFCE does not need a predefined cluster-forming hard-threshold. Instead, it calculates the product of some powers of the spatial extent of clusters and the corresponding image height threshold and aggregates this quantity across multiple thresholds. The exponents of these powers are free parameters, but in practice they are fixed to values justified by theory and empirical results.

The use of the TFCE method is limited by two factors. The first is that TFCE transforms statistical images into an arbitrary value domain, which is then subject of permutation-testing to obtain P-values. Therefore, it cannot be applied with parametric statistical approaches and a computationally intensive statistical resampling step is always needed. Second, although fixing the free parameters of TFCE provide robust results for three-dimensional images (Salimi-Khorshidi et al., 2011; Smith and Nichols, 2009), generalization of the method for other data structures (e.g. brain connectivity networks) is not trivial (Vinokur et al., 2015) and using suboptimal parameters might be even “statistically dangerous”, that is, might result in an elevated number of false positives and false negatives or non-nominal FWER-rates (Smith and Nichols, 2009).

Here, we introduce a method, which is similar to TFCE in its basic concept, but overcomes some of these limitations by giving a general, extendable probabilistic framework for integrating cluster- and voxel-wise inference. The introduced framework allows for converting P-values directly to enhanced P-values and, in several cases, significantly improves the accuracy and the robustness of topology-based belief boosting. The generalisability of the introduced core method lies in the freedom of choice in defining what a cluster is in various data structures. In the present study we apply the cluster concept of Gaussian Random Filed theory which downgrades the generalisation property of our core formulation to 3D images, but gives a fast implementation of the approach with clear links to the current analysis practice in neuroimaging.

Theory

Typical neuroimaging data (and most other datasets with multiplicity), given its inherent spatial autocorrelation, is massively multicollinear. This property of the data does not allow for exploiting the localising performance of the typical voxel-wise statistical inference which handles the results of mass-univariate analyses largely as independent observations. In such datasets, making use of multicollinearity information in order to boost belief in correlated clusters of signals during statistical inference can retain part of the sensitivity that has been lost due to the massive multiplicity. For neuroimages, incorporating information about the clustering properties of image data can be considered as optimising the “localisation performance – sensitivity” trade-off by throwing out only that “part” of localisation capacity which was “unutilised” due to image smoothness.

Such an approach, in practice, can be realised as an integration of the original voxel-level P-value (resulting from the mass-univariate voxel-wise analysis) with the probability of the cluster it is part of. The resulting single “enhanced” P-value should exhibit the following properties:

Enhancement property: Enhancing sensitivity if data is spatially structured (clustered): the original P-value is enhanced so that it incorporates the information about the spatial topology of the environment of the voxel. Practically speaking, the method enhances the P-value, if it is part of a cluster-like structure (large enough to be unlikely to emerge when the null hypothesis is true).

Control property: Controlling for false positives and multiplicity: the enhancement of P-values does not result in an undesirable accumulation of false positive voxels (e.g. due to “cluster leaking”), so that the use of various statistical thresholding and multiplicity correction methods (like family-wise error rate, FWER) remain approximately valid at the voxel-wise level.

In this section, we introduce a mathematical formulation of a novel candidate for such an enhancement approach. Our basic concept is similar to that known as threshold free cluster enhancement (Smith and Nichols, 2009). Both methods are based on a threshold-wise aggregation of a quantity, which realises a combination of spatial neighbourhood information and intensity in the image at a given threshold. In the next section, these two methods, together with the case of no enhancement, are evaluated and compared in terms of sensitivity on simulated and real datasets (Enhancement property). On the same data, we demonstrate that the methods provide an adequate control over false positive voxels (Control property, “cluster leaking”). Moreover, our approach directly outputs P-values (without permutation test), and we show that it is valid to correct these enhanced p-values for FWER based purely on the original unenhanced data (Control property, multiplicity). This implies that, with our method, thresholds corrected for the FWER in the original data (e.g. via parametric, GRF-based maximum height thresholding) remain directly applicable on the cluster enhanced data.

1.1. TFCE

The widely-used TFCE approach enhances areas of signal that exhibit some spatial contiguity without relying on hard-threshold-based clustering (Smith and Nichols, 2009). The image is thresholded at h, and, for the voxel at position x, the single contiguous cluster containing x is used to define the score for that height h. The height threshold h is incrementally raised from a minimum value h₀ up to the height v_x (the signal intensity in voxel x, typically a Z-score), and each voxel's TFCE score is given by the sum of the scores of all “supporting sections” underneath it. Precisely, the TFCE output at voxel x is:

$$\mathit{\text{TFCE}}(x)={\displaystyle \underset{h=h_0}{\overset{v_x}{\int }}{c}_x{(h)}^E{h}^{H}dh},$$ Eq. 1

where h₀ will typically be zero (but see (Habib et al., 2017) for details), c_x(h) is the size of the cluster containing x at threshold h and E and H are empirically set to 0.5 and 2, respectively. The cluster-enhanced output image can be turned into P-values (either uncorrected or fully corrected for multiple comparisons across space) via permutation testing. The values of parameters E and H were chosen so that the method gives good results over a wide range of signal and noise characteristics and, accordingly, can be pre-fixed in many cases. However, they have to be chosen differently for (largely two-dimensional) skeletonized data, like in the tract-based spatial statistics (Smith et al., 2006) approach (E=1, H=2, with 26-connectivity), and, interestingly, optimal parameter values become strongly dependent on effect topology and effect magnitude in the case of graphs (e.g. structural or functional brain connectivity data) (Vinokur et al., 2015).

1.2. pTFCE

Although TFCE is based on raw measures of image “height” and cluster extent, it is straightforward to hypothesise a close relationship to corresponding cluster occurrence probabilities (that is, the probability of the cluster extent, given the cluster forming threshold, as also used in cluster-level inference). In fact, in Appendix C of (Smith and Nichols, 2009) it is clarified that with a specific pair of exponent parameters (H=2 and E=2/3) h^Hc_x(h)^E is approximately proportional to the −log P-values of clusters found with different thresholds. This concept could directly link TFCE to cluster probability and allow for easy generalization, independent of data dimensionality and topology. However, as demonstrated by (Woo et al., 2014), the number of false positive voxels within an otherwise significant cluster is unknown and their proportion largely increases, if the cluster forming threshold is decreased. This leads to the phenomenon of “leaking” of positive observations into areas of background (if results are interpreted at the voxel-level). Therefore, one could expect that simply integrating the cluster occurrence probabilities and using traditional voxel-wise thresholding approaches might also integrate “cluster leaking” and, therefore, might easily lead to an accumulation of false positive voxels. In fact, this was confirmed by our preliminary analysis, where we computed the (negative logarithm of the) geometric mean of cluster occurrence probabilities across multiple thresholds: ${\mathit{\text{TFCE}}}_{\mathit{\text{Pclust}}}(x)={\displaystyle {\int }_{h=h_0}^{v_x}-\mathit{\text{log}}P\left(C>c_x\left(h\right)\right)}dh/N_h,$ where N_h is the number of thresholds (See Supplementary Figure 1 for results).

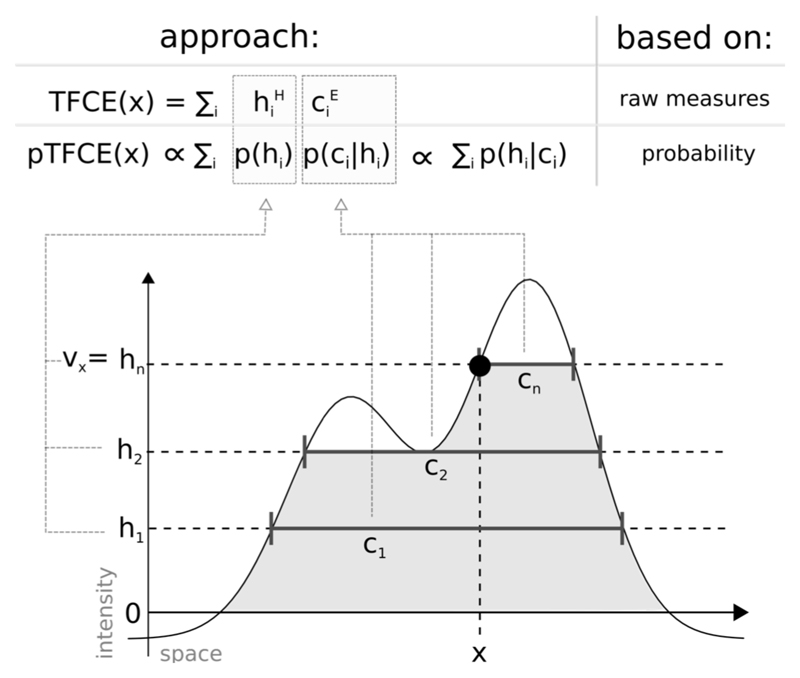
To ensure a truly parameter-free, generalized cluster enhancement, and at the same time, reduce the issue of “cluster leaking”, here we introduce a method, called probabilistic TFCE (pTFCE). Instead of raw measures or probabilities of clusters, pTFCE aggregates the conditional probability of a voxel having an intensity greater or equal to the applied threshold, given the size of the corresponding cluster. By doing so, pTFCE projects the cluster-level neighbourhood information into the voxel-space and allows for voxel-level interpretation (which is not possible by conventional cluster-level inference). For an illustration of the proposed method and its relation to TFCE, see Figure 1.

Figure 1. Illustration of the relation between the TFCE and the pTFCE approach.

Both approaches are based on the integration of cluster-forming height threshold (h₁, h₂, …, h_n) and the supporting section or cluster size (c₁, c₂, …, c_n) at that given height. The difference is that, while TFCE combines raw measures of height and cluster size to an arbitrary unit, pTFCE realises the integration by constructing the conditional probability p(h|c) based on Bayes’ rule, thereby providing a natural adjustment for various signal topologies. Aggregating this probability across height thresholds provides enhanced P-values directly, without the need of permutation testing.

Core formula of pTFCE

In the following, let us focus on a single voxel x and, if not relevant, in the given context, neglect the x subscript in the notations. Accordingly, let V be the random variable modelling voxel intensity at an arbitrary voxel, and p(v) denote the corresponding probability density function (PDF). For clarity, let us use p(h) instead of p(v), if we denote a suprathreshold voxel in a binary image thresholded at h. As conventionally, let P(V≥v) and P(V≥h) denote the probabilities for a given unthresholded or thresholded voxel value, respectively. Furthermore, let p(c|h) denote the PDF of cluster size c, given that the image was thresholded at h. Next, let us, for a moment, consider that we were blinded on the actually applied threshold value h_i and are only informed on the measured cluster size c_i=c(h_i). In that case, by using p(c_i|h) as a likelihood function, the PDF for h, given c_i can be expressed using Bayes’ theorem:

$$p(h|c_i)=\frac{p(c_i,|h)p(h)}{{{\displaystyle \int }}_{-\infty }^{\infty }p(c_i,|\xi )p(\xi )d\xi }$$ Eq. 2

The probability of V≥h_i at the applied threshold h_i, given the measured cluster size c_i is then simply:

$$\text{P}\left(\text{V}\ge h_i|c_i\right)=\{\begin{array}{lll}\underset{h=h_i}{\overset{\infty }{\int }}\hfill & p(h|c_i)dh\hfill & ,\mathit{\text{if}}v\ge h_i\hfill \\ \hfill & 1\hfill & ,\mathit{\text{otherwise}}\hfill \end{array},$$ Eq. 3

where v is the voxel value (Z-score) in the voxel of interest and the v<h_i branch simply covers the case of subthreshold voxels.

Here we propose, that a proper aggregation of the P(V≥h_i|c_i) probabilities over a h_i series of thresholds (0≤ h_i <v, i=1, …, n), would satisfy our Enhancement property and Control property and provide an appropriate way for integrating cluster information with voxel intensity. An illustration of the “internal workings” of the proposed method can be seen in Figure 2 (parts A and B).

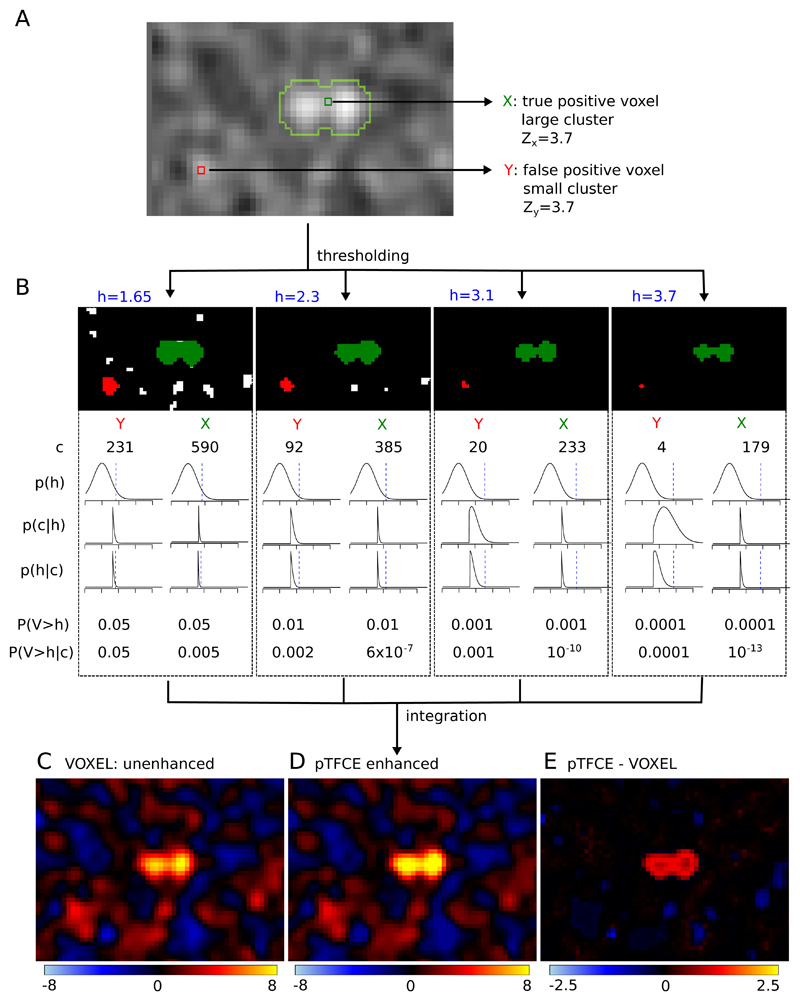
Figure 2. The “internal workings” of the pTFCE approach in a simulation case.

Two voxels in a simulated image (signal 01 with SNR=1 and smoothing FWHM=1.5, see Evaluation Methods) with equal Z-score were chosen. One of them is part of a true signal artificially added to the smoothed noise image (denoted as X and with green colour), the other is random noise (Y, red). In part (A), the location of the selected voxels on the image is shown and the true positive areas are outlined with light green contour. Part (B) shows thresholded versions of the image (thresholds: h=1.65, 2.3, 3.1, 3.7, thresholds denoted by blue colour). The green and red clusters belong to voxels X and Y, respectively. For both clusters, the size of the cluster (c), the PDF of p(h) and the likelihood p(c|h) are plotted against Z-score thresholds on a range of [-2, 6]. Multiplying these and dividing by a normalizing constant gives the posterior p(h|c). Unenhanced (P(V>h)) and pTFCE-enhanced (P(V>h|c)) P-values are calculated for both voxels at each cluster forming threshold. While enhanced P-values are only slightly different from the original unenhanced P-values for the random noise voxel Y, they exhibit a remarkable difference in the case of the true positive voxel X. In the pTFCE approach, these probabilities belonging to various thresholds are aggregated by an equidistant incremental logarithmic probability pooling approach (See section “Probability aggregation across thresholds” and Figure 3 for a geometric representation). Subtracting the unenhanced image (C) from the pTFCE enhanced image (D) reveals a remarkable intensity enhancement in the area of true signal.

Probability aggregation across thresholds

The introduced conditional probability applies for the value of the actual cluster-forming threshold instead of the value of the actual voxel. (As also suggested by the notation: P(V≥h_i|c_i) instead of P(V≥v|c_i)). That means that, when summarizing across thresholds, the aggregated probability should be computed from an “incremental series” of probabilities (each of them corresponding a cluster forming threshold), rather than a pool of beliefs about the same event. Therefore, to aggregate the P(V≥h_i|c_i) probability over all h_i thresholds, the common probability pooling methods (Genest and Zidek, 1986; Stone, 1961), e.g., logarithmic pooling, are not suitable.

To overcome this, in the following, we give a solution for this scenario, hitherto referred to as equidistant incremental logarithmic probability aggregation. Our aim can be formalized as finding an aggregation function Q(.), which exhibits the following properties:

• (i)
  Q(.) is interpreted on the sum of a series of negative log-probabilities P_i, which are equidistantly distributed in the logarithmic domain, and returns the negative logarithm of the aggregated probability $\overline{P}$ (With the sum of logarithms, we implement a multiplicative model, see Appendix B and C of (Smith and Nichols, 2009)).

  $$\begin{array}{c}Q:{\displaystyle {\sum }_i-\mathit{\text{log}}\left(P_i\right)}\to -\mathit{\text{log}}\left(\overline{P}\right),\\ \text{i}=1,2,\dots ,\text{n};\forall i:\mathit{\text{log}}\left(P_i\right)-\text{log}\left(P_{i+1}\right)=\mathit{\text{constant}}\end{array}$$ Eq. 4
• (ii)
  for the sum of a series of unenhanced –log P-values, P₁=1 and P_n=P(V≥v)), Q(.) gives back the negative logarithm of P_n, that is, the original voxel probability:

  $$Q\left({\displaystyle {\sum }_i-\mathit{\text{log}}\left(P_i\right)}\right)=Q\left({\displaystyle {\sum }_i-\mathit{\text{log}}\left(P(V\ge h_i)\right)}\right)=-\mathit{\text{log}}\left(P_n\right)\cong -\mathit{\text{log}}\left(P\left(V\ge v\right)\right)$$ Eq. 5
• (iii)Q(.) is monotonically increasing, in the sense that it ensures monotonicity about local maxima in the image.

Let us note, that our assumption about the constant increment in log probabilities in property (i) is not obligatory for an appropriate aggregation method, but, as detailed below, by allowing a mathematical analogy to the equation of triangular numbers, it simplifies the construction of a proper aggregation method. Furthermore, the uniform sampling of the log(P) space is a natural way to address a greater accuracy at small p-values, which are typically of interest.

In the followings, we introduce a Q function, which fulfils properties i-iii. Moreover, below we present how the value Q(.) returns with the series of enhanced –log P-values as input (instead of the original unenhanced ones, like in property ii) can be considered as the negative logarithm of the pooled probability of interest:

$$Q\left({\displaystyle {\sum }_i-\mathit{\text{log}}(P{(V\ge h_i|c_i)}_x)}\right)≔pTFCE(x)$$ Eq. 6

As a starting point, let us consider the problem of finding the sum of the first n non-negative integer numbers, which is $S_n={\displaystyle {\sum }_{k=0}^{n}k}=\frac{n(n+1)}{2}$ (giving the so-called triangular numbers). It is easy to generalize this, instead of non-negative integers, to equidistantly distributed positive real numbers from 0 to nΔ_k and by an increment of Δ_k:

$$S_{{\Delta }_k,n{\Delta }_k}={\displaystyle {\sum }_{k=0}^{n}k{\Delta }_k=\frac{n{\Delta }_k\left(n+1\right)}{2}}=\frac{n{\Delta }_k\left(\frac{n{\Delta }_k}{{\Delta }_k}+1\right)}{2}$$ Eq. 7

If we use the notation w=nΔ_k and denote S_Δk,nΔk as simply S, we can write Eq. 7 as:

$$0=\frac{1}{2{\Delta }_k}{w}^2+\frac{1}{2}w+S$$ Eq. 8

Solving Eq. 8 for w and taking the positive root gives:

$$w_{+}=\frac{\sqrt{{\Delta }_k\left(8\text{S}+{\Delta }_k\right)}-{\Delta }_k}{2}:=Q\left(\text{S}\right)$$ Eq. 9

In the context of our pTFCE approach, let S(x) denote the sum of the −log P(V≥h_i |c) enhanced log-probabilities in voxel position x, so that the h_i thresholds change incrementally in the negative logarithmic domain (to ensure a constant Δ_k):

$$pTFCE\left(x\right)=\text{Q}\left(\text{S}\left(x\right)\right)=\frac{\sqrt{{\Delta }_k\left(8\text{S}\left(\text{x}\right)+{\Delta }_k\right)}-{\Delta }_k}{2},$$

where

$$\text{S}\left(\text{x}\right)={\displaystyle \sum _{i=0}^{N_h}-\text{log}\left(\text{P}\left(\text{V}\ge h_i|c_i\right)\right)}invoxelpositionx$$

and

$$\forall \text{i},0\ge \text{i}>N_h:\text{log}\left(P\left(V\ge h_{i+1}\right)\right)-\text{log}\left(P\left(V\ge h_i\right)\right)={\Delta }_k$$ Eq. 10

The proposed Q(S(x)) probability pooling for pTFCE clearly satisfies (i), (ii), (iii) of the above conditions. Let us note, that the formulation of the introduced probability aggregation method forces the starting -logP threshold to be zero (P₁=1) and, importantly, the number of thresholds and the maximal threshold does only affect the accuracy of the approximation as we normalise for Δ_k and the enhanced –log P-values are zero for subthreshold voxel.

The rationale of the proposed equidistant incremental logarithmic probability aggregation method can be understood as searching for the probability corresponding to a v′ voxel value for which the threshold-wise unenhanced sum of negative log probabilities would be the same as the real enhanced sum corresponding to the observed voxel value v.

Another, analogous and even more straightforward way to think about the method is that it links the series of enhanced probabilities produced by a “strongly clustered” voxel to another hypothetical series of probabilities produced by a higher intensity voxel, but with “average” clustering (relative to smoothness), where therefore enhancement has no effect at all; and uses this higher intensity as the pooled (and enhanced) intensity value.

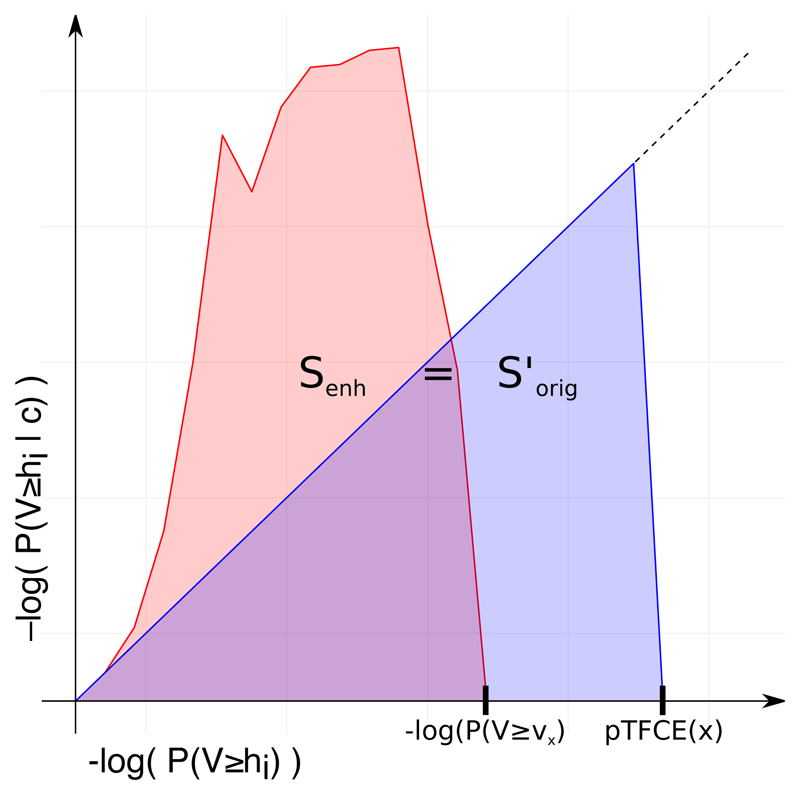
It can be also intuitive to consider a geometric meaning of the method as demonstrated on Figure 3. Computing the pooled log probability pTFCE(x) of voxel x by the Q function is equal to finding the hypothetical voxel value, for which the sum of the unenhanced (original) incremental log probability series (S_{Δk, v’} according to Eq. 7, denoted as S’_orig and the blue area on the figure) is equal to the sum of the pTFCE enhanced log probability series belonging to the actual (observed) voxel intensity v (denoted as S’_orig and the red area on the figure).

Figure 3. Geometric representation of the proposed equidistant incremental logarithmic probability pooling approach.

The proposed equidistant incremental logarithmic probability aggregation method links the series of enhanced probabilities produced by a “strongly clustered” voxel (red area, S_enh) to another hypothetical series of probabilities produced by a higher intensity voxel, but with “average” clustering (blue area, S’_orig), where therefore enhancement has no effect at all; and uses this higher intensity as the pooled (and enhanced) intensity value.

Let us note that, up to this point, our formulation of the pTFCE approach does not contain any detail about the data structure and it can be easily generalized to various features of the data beside clustering. In the next section, we link the introduced formulation to the typical volumetric data structure in neuroimaging by estimating the appropriate PDFs based on Gaussian Random Field Theory.

Estimating the likelihood function

We see at least two obvious ways for determining or approximating the probability density functions p(h) and p(c|h) in order to construct the P(V≥h), P(C≥c|h) and P(V≥h|c) probabilities: for n-dimensional images, the PDFs in question can be approximated based on Gaussian Random Field (GRF) theory, and in general, empirical estimation of the PDFs can be given by statistical resampling or permutation test. Since GRF theory (Bardeen et al., 1986; Nosko, 1969) is extensively used in statistical analysis of medical images (Friston et al., 1996; Nichols, 2012; Worsley et al., 2004), in the present work, we choose to investigate the use of GRF Theory to give an approximation of the PDFs and use simulations with a known ground truth to justify the validity of the approximation. Let us note however, that the use of GRF theory makes our approach specific to 3D images and implicitly introduces several assumptions not involved in the above discussed general formulation. While the GRF-based approach is well suited to establish the links of pTFCE to the existing practice in the field of neuroimaging, more general formulations (like the use of permutation-based empirical distributions) are subject of further investigation in order to fully exploit the generalisable formulation of the core pTFCE approach.

Determining p(h) for a given threshold h (or p(v) if v is the voxel value) for Gaussianised Z-score images is straightforward: it is simply the PDF of the normal distribution with zero mean and unit variance:

$$p\left(h\right)=\varphi \left(h\right)$$

and

$$P\left(V\ge h\right)=1-\Phi \left(h\right),$$ Eq. 11

where Φ (uppercase) is the cumulative distribution function and ϕ (lowercase) is the probability density function of the standard Gaussian. Note that, according to Eq. 11, we define the input image for pTFCE as an image of Z-scores, nevertheless, it is easy to convert any other statistical parametric images (like T- or P-values) to Z-scores.

For inference on clusters, we first utilize GRF theory to find the mean cluster size under the null at a given threshold, the distribution of cluster size about that mean and also, the P-value for a given cluster size.

Let N be the total supra-threshold volume (equivalently, the sum of all of the cluster sizes); let L be number of clusters observed. Assuming a large search region relative to the smoothness, and thus independence of number of clusters and cluster size, the mean cluster size under the null is

E[C] = E[N]/E[L]. Here, the numerator is easily obtained: E[N] = V P(V ≥ h), and specifically for a Gaussian image: E[N] = V (1 − Φ(h)), where Φ(.) is the CDF of a Gaussian and V is the total number of voxels (Friston et al., 1996).

The expected number of clusters is E[L] approximated by the expected Euler Characteristic (Worsley et al., 1996). The Euler Characteristic (EC) of a D-dimensional random field thresholded at h is written χ_h, and is the number of clusters minus the number of holes (D≥2) plus the number of handles (D≥3). For sufficiently high h the probability of a hole or handle is small, and so the EC offers a good approximation of the number of clusters. Worsley's general results (Worsley et al., 1996) give a closed-form expression for E[χ_h] as a sum of D terms: $E\left[{\chi }_h\right]={\displaystyle {\sum }_{d=0}^D{R}_d}{\rho }_d(h),$ where Rd is the RESEL count and ρ_d is the EC density. The RESEL count is a length, area or volume, depending on d, and it is the product of the spatial measure and a roughness measure |Λ|^1/2, where Λ is the d × d variance-covariance matrix of the partial derivatives of the data. Usually, only the d = D term is appreciable, so for the 3D case we have $\left[{\chi }_h\right]=R_3\left(h^2-1\right)e^{-\raisebox{1ex}{$h^2$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}{\left(2\pi \right)}^{-\raisebox{1ex}{$4$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\cdot$ Thus, the expected cluster size for a 3D Gaussian (Z-score) image with cluster-forming threshold h is:

$$E\left[c_h\right]=\frac{V\left(1-\Phi \left(h\right)\right)}{V{\left|\Lambda \right|}^{\frac{1}{2}}\left(h^2-1\right)e^{-\frac{h^2}{2}}{\left(2\pi \right)}^{-2}}=\frac{V\left(1-\Phi \left(h\right)\right)}{R_D\left(h^2-1\right)e^{-\frac{h^2}{2}}{\left(2\pi \right)}^{-2}}$$ Eq. 12

Finally, using the result that cluster size to the 2/D power follows an exponential distribution (Nosko, 1969), with

$${\lambda }_h={\left(\frac{E\left[c\right]}{Г\left(\frac{D}{2}+1\right)}\right)}^{-\frac{2}{D}},$$ Eq. 13

the PDF of the cluster size at threshold h is:

$$p(c|h)=\frac{2{\lambda }_h{e}^{-{\lambda }_h{c}^{\raisebox{1ex}{$2$}\!\left/ \!\raisebox{-1ex}{$3$}\right.}}}{3c^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$3$}\right.}},$$

and

$$P\left(C>c|h\right)=c^{\raisebox{1ex}{$2$}\!\left/ \!\raisebox{-1ex}{$3$}\right.}{e}^{-\lambda c^{\raisebox{1ex}{$2$}\!\left/ \!\raisebox{-1ex}{$3$}\right.}},$$ Eq. 14

where λ is the rate of the exponential distribution and Γ(·) is the gamma function.

There are several implicit assumptions in the Gaussian Random Filed approach (Friston et al., 1996), and, importantly, GRF theory-based estimates become inaccurate or even undefined at low thresholds. Therefore, for the GRF-based implementation of pTFCE, here we propose that for any thresholds h smaller than a specific value h_GRF, the enhanced probability P(H>h | c) is to be approximated simply by the unenhanced P(H>h). Moreover, in Eq. 2, p(c|h) should be truncated by setting it to 0 when h< h_GRF. Let us note, that this also truncates the resulting p(h|c) distribution on the left side, thus slightly increases the enhanced probability P(V ≥ h |c), meaning that with this approximation, the cluster enhancement is expected to be conservative. That also means that, while this approximation might mean a loss in sensitivity, we can still expect our pTFCE approach to perform well in terms of our Control property (that is, it remains controllable e.g., for family wise error). Investigation of the effect of h_GRF for using GRF theory revealed that the pTFCE is robust to the choice of this value (see Supplementary Figure 5). Therefore, we fixed this value at h_GRF=1.3 (default parameter in the software implementations, as well), and tested the validity of this approximation in simulations with known ground truth and on real data.

Evaluation Methods

1.3. Simulated data

To assess the statistical validity of our methods, simulated data comprising seven 3D test image shapes (the same as in (Smith and Nichols, 2009)) were used to compare the pure voxel-level (a.k.a. unenhanced, hereinafter denoted simply as “VOXEL” method), the TFCE and the proposed pTFCE methods against each other, with ROC evaluations giving objective combined measures of specificity and sensitivity. Additionally, we tested whether the P-values output by the pTFCE method are valid for correction for multiple comparisons, by correcting based on the P-value distribution of the unenhanced voxel-based approach (See ROC methodology). This method we denote as pTFCE_VOX, to emphasize that is uses the thresholds computed for the VOXEL method and to distinguish it from the variant with the randomisation-based threshold (denoted simply as pTFCE).

1.3.1. Test signal shapes

In our simulations, we used the same seven 3D test signal shapes as in (Smith and Nichols, 2009). These are shown on Error! Reference source not found.A. These ground truth images cover a wide range of signal types, including small blobs, touching blobs and extended areas of activation. Each test signal has a background value of 0 and a peak height of 1. We then scaled the signal by a factor or 0.5, 1, 2 or 3 and added unsmoothed Gaussian white noise of standard deviation 1, to give a range of peak signal-to-noise (SNR) values: 0.5, 1, 2 and 3.

We evaluated also the effect of different Gaussian smoothing kernels, with full-width-at-half-maximum (FWHM) values of 1, 1.5, 2, 3 voxels applied. After smoothing, the data was scaled so as to keep the noise standard deviation equal to 1, so that the images were still analogous to T/Z images. For the TFCE method, we used the standard parameter values E=½, H=2.

1.3.2. ROC methodology

An ROC (receiver-operator characteristic) curve, given a signal+noise image and the known ground truth, plots true positive rate (TPR) against false positive rate (FPR), as one varies a threshold applied to binarise the image. An ideal algorithm gives perfect true positive rate at zero false positive rate, i.e., the perfect ROC curve jumps immediately up to TPR=1 (y-axis) for FPR=0 (x-axis) and stays at 1 for all values of FPR. Hence a commonly-used single summary measure of the whole ROC curve is the AUC (area under curve); the higher the AUC, the better. To ease interpreting our results in relation to those in (Smith and Nichols, 2009), we use an analogous ROC methodology: we use AUC values for alternative free-response receiver-operator characteristic (AFROC) (Bunch et al., 1977; Chakraborty and Winter, 1990).

Alternative free-response ROC

AFROC analysis plots the proportion of true positive tests (among all possible positive tests) on the y-axis and the probability of any false positive detections anywhere in the image on the x-axis (that is, the family-wise error rate, or FWER). Here we calculate FWER for the AFROC curves by counting the number of images with one or more false positive voxels among 1000 smoothed noise-only images. As neuroimaging analyses typically seek to control the FWER, we used this method to test the Enhancement property of different spatial enhancement/thresholding methods. For AFROC analysis, we define true positives based on the smoothed ground truth images.

Since ROC analysis is predominantly a binary concept, we threshold and binarise the smoothed ground truth images at 0.1/SNR. This ensures, that voxels, in which a significant amount of signal was introduced by smoothing, count as true positive observation, if detected by any of the methods.

The above approach of calculating AFROC, by estimating FWER from processed pure-noise data, avoids the need to determine what is “real” background in the signal+noise data after passing through a given algorithm (Smith and Nichols, 2009). It is exactly what we want in the standard scenario of null-hypothesis testing which aims to explicitly control the FPR in the presence of no true signal; it tests sensitivity when the specificity is being controlled globally (that is among studies and not over voxels), in the way that we generally require in practice. This method of calculating FWER ignores the FP voxels in the signal+noise images that are spatially close to the true signal (as distinct from “real” FP voxels in the noise-only data), and in doing so does not weight, for example, against the smearing of estimated signal into neighbouring voxels due to smoothing.

“Negative” alternative free-response ROC

Since FWER for AFROC is calculated from the noise-only images, aside from the effect of smoothing, AFROC is insensitive to “cluster leaking”, as well. This might be an undesirable property since “leaking” will possibly merge small blobs of activity with neighbouring random local maxima and present them as large clusters with lots of false positive voxels (Woo et al., 2014). Therefore, while AFROC is suitable for measuring signal detectability, to control for the voxel-level spatial specificity of the methods, here we introduce the “negative AFROC” method.

In the negative AFROC (short: nAFROC) analysis, we test our Control property for “cluster leaking”, by thresholding the smoothed ground truth images also at 0.001/SNR and then binarising and inverting it to define a region where the amount of signal can be neglected. Applying our AFROC method with this region as ground truth, we create ROC curves for the FPR, plotted against the FWER. An appropriate cluster enhancement algorithm should keep the area under the negative AFROC curve very close to zero, to minimise voxel-level Type I errors.

Correcting for multiple comparisons on enhanced probability values

As the introduced pTFCE enhancement method directly outputs probability values, we also tested whether these enhanced probability values can indeed be interpreted in the range of the original, unenhanced probability values (Control property: multiplicity) that is, thresholds corrected for multiple comparisons on the original, unenhanced data are directly applicable to the pTFCE enhanced data, as well. We did this by using the unenhanced noise-only images to calculate the FWER thresholds for the AFROC and negative AFROC curves. The rationale behind this analysis is that if thresholds computed from, and interpretable on unenhanced data are valid on pTFCE-enhanced probability values, as well (that is, they always guarantee a smaller or equal FWER), then a freedom in the choice of the correction method is granted, as long as it is valid on the original statistical image. In practice this would mean that no special correction methods for enhanced images (like permutation test-based maximum height correction) are needed and any threshold will give an equal (or close) FWER for the enhanced image than for the unenhanced.

We denote this analysis case, as pTFCE_vox, the subscript standing for VOXEL and referring to the way corrections for multiple comparisons were based on the P-values of the (unenhanced) voxel-level.

1.3.3. Simulation details

To summarize, our simulation and ROC analysis consisted of the following steps:

1. Generate the raw ground truth 3D image (“signal”).

2. Generate 1000 random Gaussian noise images (mean zero, unit variance) that, when added to the signal, give a specified SNR in the resulting 1000 signal+noise images. We applied exactly the same noise realizations as in (Smith and Nichols, 2009) and generated signal+noise images for SNRs 0.5, 1, 2 and 3.

3. Pass all noise-only and signal+noise images through a smoothing stage (with FWHMs 1, 1.5, 2 and 3) and afterwards, through the algorithm being tested: VOXEL (=no enhancement), TFCE, pTFCE, pTFCE_vox (=pTFCE at this stage).

4. Pass also the ground-truth image through the smoothing stage, normalise its intensity to max=1, and threshold it at 0.1/SNR and binarise, to define a ROI of true positive observations. The rationale behind smoothing the ground truth image is, that “de-smoothing” should not be the responsibility of any statistical inference method. Similarly, when smoothing is applied in a real data scenario, we can only expect to detect the smoothed version of the underlying activation pattern (which is also a strong argument against using excessive smoothing). Accordingly, areas of false positive observations are also defined based on the smoothed ground truth image, by thresholding it at 0.001/SNR, and then binarising and inverting it.

5. Compute the traditional ROC curves for the processed signal+noise images and for the ground truth mask thresholded at 0.1/SNR.

6. Compute AFROC and negative AFROC curves: threshold the appropriately processed noise-only and signal+noise images for the methods voxel, TFCE and pTFCE and pTFCE_vox at the full range of possible threshold values. FWER, TPR and FPR at each threshold are computed as follows:

• FWER: For each threshold level, count the number of processed noise-only images which contain any supra-threshold voxels. This count (divided by 1000) gives the family-wise FPR for this threshold level (i.e., achieves full correction for multiple comparisons across space). For pTFCE_vox, FWER is computed based on the unenhanced noise-only images (same as for the “voxel” method).

• TPR: For each threshold level, use each of the 1000 processed signal+noise images, along with the ground truth mask thresholded at 0.1/SNR, to obtain an estimate of the TPR. We use the raw voxel-wise TPR (fraction of non-background signal voxels correctly reported), averaged over the 1000 signal+noise images (we also record the IQR of the TPR across the 1000 images, as a measure of the stability of the various algorithms being tested).

• FPR: For each threshold level, use each of the 1000 processed signal+noise images, and use the “negative” ground truth mask (thresholded at 0.01/SNR, binarised and inverted) to obtain an estimate of the FPR. The raw voxel-wise FPR is then averaged across the 1000 images (again, we record the IQR, as well).

• 6.Take the resulting ROC, AFROC and negative AFROC curves, and, using only the x-range of 0 to 0.05, calculate the AUC values (AUC ROC, AUC AFROC, AUC negative AFROC, respectively). Normalise AUC by 0.05.

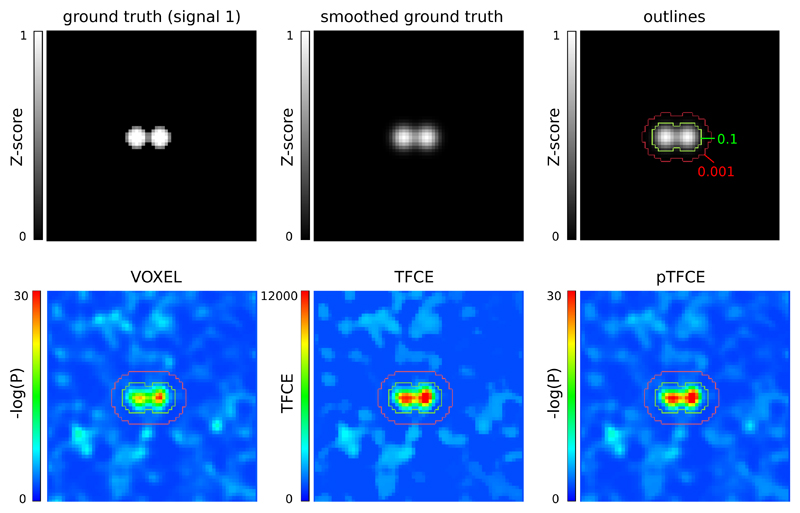
For an example of ground truth smoothing and the ROIs used for the ROC methodology along with demonstrative results of the tested approaches, see Figure 4.

Figure 4. Representative images of the simulation and ROC ROIs for the investigated approaches.

In the upper row, the unsmoothed and the smoothed (FWHM=1.5) versions of signal 2, and the outlines corresponding to the ROC (inside vs. outside the 0.1 contour), AFROC (inside the 0.1 contour) and negative AFROC (outside the 0.001 contour) analysis. In the lower row, results of the VOXEL, TFCE and pTFCE methods with the same noise realisation (noise 0001) are visualized with the contours as overlay.

For estimating smoothness of the signal+noise images, for generating signal+noise images and for AFROC analysis, we used FSL (Jenkinson et al., 2012; Smith et al., 2004). (We performed a “traditional” ROC analysis, as well, see Supplementary Figure 2 and Supplementary Table 1) The pTFCE algorithm was implemented in R, using the packages “mmad” (Clayden, 2014) (used for a fast labelling of connected components in thresholded images) and “oro.nifti” (Whitcher et al., 2011) (to manipulate nifty images). Calculation of pTFCE was performed with a fixed number of log(P)-thresholds (n=100), ranging from 0 to the negative logarithm global image maximum $-\mathit{\text{log}}(\underset{x}{\text{max}}{v}_x),$ and distributed equidistantly. Although this results in different deltas for various images, theory suggests that this affects only the accuracy of the probability aggregation and our supplementary analysis (Supplementary Figure 3) confirmed that the proposed equidistant incremental logarithmic probability aggregation method is robust above a reasonable number (n≥100) of thresholds and magnitude of delta values. Overflow problems were handled in most of the cases in the same way as in the FSL source code (Jenkinson et al., 2012; Smith et al., 2004). Results were plotted with the oro.nifti and the ggplot2 (Wickham, 2016) packages of R. We compare the AUC values at identical parameter settings. Moreover, since it is a common practice to optimise neuroimaging pipelines in terms of smoothing to achieve maximal sensitivity, and optimization often implicitly takes into account the typical signal-to-noise level of the experimental design (through the inherent properties of the data used to optimise the workflow), for each method, each test signal and each SNR, we chose an optimal smoothing based on the best AUC values of the AFROC curves and compared methods with their optimal settings.

1.4. Testing on real data

Since real neuroimaging data differs in many properties from the simplistic Gaussian model used in the simulation, we use various fMRI datasets for the purposes of (1) evaluating the improvement in sensitivity by investigating the dependence of results on sample size, (2) investigating whether pTFCE maintains nominal family-wise error rates when corrected for multiple comparison, given that the null hypothesis is true; and (3) illustrate the effect of pTFCE with enhancing the activation map reflecting the pain matrix which is well known and complex enough to capture the advantages of our method. Due to the large computational cost of the current implementation of pTFCE, in the real-data scenarios, we did not apply the permutation-based FWER thresholds for pTFCE, only the pTFCE_vox method (maximum-height thresholding based on GRF-theory) was tested.

1.4.1. Demonstration of the increased statistical power on real data

For both the demonstration of increased statistical power and the evaluation of family-wise error rates, we obtained data from the UCLA Consortium for Neuropsychiatric Phenomics LA5c Study (CNP) (Gorgolewski et al., 2017; Poldrack et al., 2016) as shared via the OpenNeuro database (accession number: ds000030, https://openfmri.org/dataset/ds000030/). Processed 1^st-level activation maps (contrast of parameter estimates, a.k.a “cope” images, as provided with the dataset) of N=119 healthy participants from the “switch-noswitch” contrast (cope39) of the task switching paradigm were obtained and fed into FSL “randomise” (number of permutations: 5000) to create a group-mean activation map. This activation map was then thresholded at an FWER-corrected p<0.05 threshold and considered as “ground truth” for further analysis. As a next step, a total of 900 activation maps were computed from random subgroups of the healthy population with sample sizes N=5, 10, 20, 30, 40, 50, 60, 80 and 100 and with 100 random sampling per sample size (900 randomise runs in total). Corrected (FWER, p<0.05) voxel-level and TFCE images and T-score maps were obtained. The latter ones were converted to Z-score maps, fed into the pTFCE algorithm and thresholded based on GRF theory, with a corrected threshold of p<0.05 (implementing the pTFCE_vox approach). True positive rate was defined as the proportion of “ground truth” voxels found by the thresholded activation maps of the subsamples. Mean, 0.025% and 0.975% percentiles of this true positive rate were obtained for each of the investigated methods (VOXEL, TFCE and pTFCE_vox) and plotted against the sample sizes.

1.4.2. Evaluation of family-wise error rates on real data

Evaluation of family-wise error rates in the case of a true null hypothesis was performed on the same dataset as the demonstration of statistical power (CNP study, OpenNeuro database, ds000030). The true null hypothesis (no group difference) was approximated by comparing 1^st-level activation maps (contrast of parameter estimates, a.k.a “cope” images, as provided with the dataset) of two random samples (N=20 per group) from the group of healthy participants from the “switch-noswitch” contrast (cope39) of the task switching paradigm. One thousand of these random control-to-control comparisons was performed with FSL “randomise” (number of permutations: 5000). Corrected (FWER, p<0.05) p-value images of the voxel-level and TFCE methods and simple voxel-wise T-score maps were obtained. The latter were converted to Z-score map, fed into the pTFCE algorithm and thresholded based on GRF theory, with a corrected threshold of p>0.05 (implementing the pTFCE_vox approach). Family-wise error rate for each method was than estimated by the ratio of images with any non-zero value across the 1000 random comparisons, for each method.

1.4.3. Illustration of the cluster enhancement effect

For the illustration of the cluster enhancement effect, we used data published as part of (Bingel et al., 2011). This study investigated how divergent expectancies alter the analgesic efficacy of a potent opioid in healthy volunteers by using fMRI. We aimed to evaluate enhancement approaches on the published group-mean map of brain activation to painful stimulation, activating the pain matrix (Figure 3. of the paper).

For TFCE, we fed the appropriate spatially standardized subject-level SPM contrast images into randomise and estimated TFCE-enhanced, FWER-corrected p-values for the group mean activation (number of permutations: N=10000). For pTFCE, we simply obtained the corresponding second-level spmT image (see (Bingel et al., 2011) for details) and converted it to Z-score, based on the degrees of freedom (dof=63). We estimated the smoothness of the map with the “smoothest” command-line tool of FSL. The Z-score map and the smoothness estimate was then fed into the pTFCE algorithm which computed the enhanced map (outputting negative log P-values). The working resolution of the data in standard space was 2×2×2 mm for both TFCE and pTFCE. For visualization, the original and the enhanced negative log P-value maps were thresholded at 13.61, the –log(P) threshold determined by the FWER correction (P<0.05) in the original study. The FWER correction for TFCE was based on the permutation test.

Results

1.5. Implementation details

The pTFCE algorithm is available as an R package called “pTFCE”, and also as an SPM (Friston et al., 1994a) Toolbox with the same name. These packages, together with a fast C++ and FSL-based implementation and nipype interfaces (Gorgolewski et al., 2011) are also available at https://spisakt.github.io/pTFCE.

1.6. Simulation results

The full AFROC curves (See Error! Reference source not found.C for some representative curves) reveal that our AUC results are not dependent on the applied x-axis threshold (FWER P<0.05), since all curves have a smooth rise in the 0-0.05 interval and differences between approaches are constant at nearly all FWER thresholds. Therefore, AUC values provide valid description of these curves in the following sections.

1.6.1. Comparing enhancement methods with optimal parameter settings

It is common practice to optimise neuroimaging pipelines in terms of smoothing to achieve maximal sensitivity. Moreover, optimization often implicitly considers the typical signal-to-noise level of the experimental design. Therefore, besides comparing all tested methods with identical parameter settings (section 1.6.2), for each method, each test signal and each SNR, we chose an optimal smoothing, based on the best AUC values of the AFROC curves. Results for SNR=1 and 2 are plotted in Figure 5.

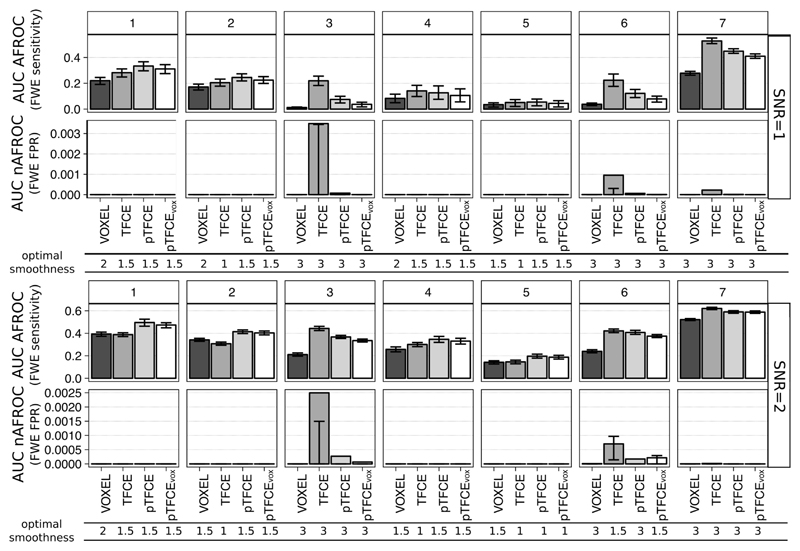
Figure 5. AUC values of the AFROC (representing FWER-level sensitivity) and negative AFROC (representing 1-FWER-level specificity) curves for all methods, ground truth shapes, SNRs, with the optimal smoothing.

Barplots represent the mean across 1000 simulation runs, and whiskers represent the inter-quartile range.

The mean(±sd) optimal smoothing FWHM across all test signal shapes and SNR values was 2.29(±0.65), 1.86(±0.84), 2.02(±0.78) and 1.96(±0.76) voxels for VOXEL, TFCE, pTFCE and pTFCE_vox, respectively. Although pooling across test signal shapes obviously does not necessary provide summary statistics that are representative for real experimental settings, these results still strongly suggest that the cluster enhancement methods generally require less smoothing. Not surprisingly, in the case of spatially extended test signal shapes (signals 3, 6 and 7) a greater smoothing was preferred by all methods. In the case of the other, spatially more restricted signal shapes (signals 1, 2, 4 and 5) an optimal smoothing of 1 or 1.5 was found. TFCE preferred in several instances an even smaller smoothing than pTFCE and pTFCE_vox.

In general, when pooled over all ground truth images and all SNRs, pooled mean(±sd) for the mean AUC of AFROC curves with optimal smoothing were 0.102(±0.16), 0.141(±0.2), 0.142(±0.2) and 0.134(±0.2) for VOXEL, TFCE, pTFCE and pTFCE_vox, respectively, clearly underpinning the improvement in sensitivity in the case of cluster enhancement methods. Moreover, with optimal smoothing, pTFCE and pTFCE_vox outperformed the unenhanced inference for all SNR values and ground truth shapes. TFCE did not manage to improve sensitivity in case of test signals 1, 2 and 5 with large SNR values. Summarising the inter-quartile ranges suggests that pTFCE and pTFCE_vox (mean IQRs 0.018, 0.02) might be somewhat more robust than TFCE (0.022), but the unenhanced inference displayed the strongest stability (0.013).

When comparing the FWER-controlled sensitivity of cluster enhancement methods against each other, we found that pTFCE and pTFCE_vox outperforms TFCE in almost all cases with spatially more restricted test signals (signal 1, 2, 4 and 5). This difference is present already at SNR=1, but becomes more expressed with greater SNR. In contrast to pTFCE and pTFCE_vox, TFCE preferred ground truth images with spatially extended signal. With these ground truth images, it produced remarkably greater AUC values in AFROC analysis than pTFCE. However, we observed an increased number of probably “cluster leaking”-related false positives in these cases. Notably, a modest increase of false positives was experienced also in case of pTFCE and pTFCE_vox, but AUC values of nAFROC curves were significantly lower than for TFCE (second row in each panel of Figure 5). For the aforementioned spatially restricted test signals, all cluster enhancement methods give very strict control over cluster-leaking and corresponding false positives, as shown by the nAFROC curves and corresponding AUC values.

The AUC values of pTFCE_vox are systematically slightly below the mean AUC values of pTFCE, but, relative to the other methods, are not very much lower. This suggests that correcting enhanced pTFCE P-values for multiple comparisons gives valid results even if it is based on the distribution of the unenhanced P-values (“VOXEL” noise images instead of “pTFCE noise images”).

1.6.2. Comparing enhancement methods with identical parameter settings

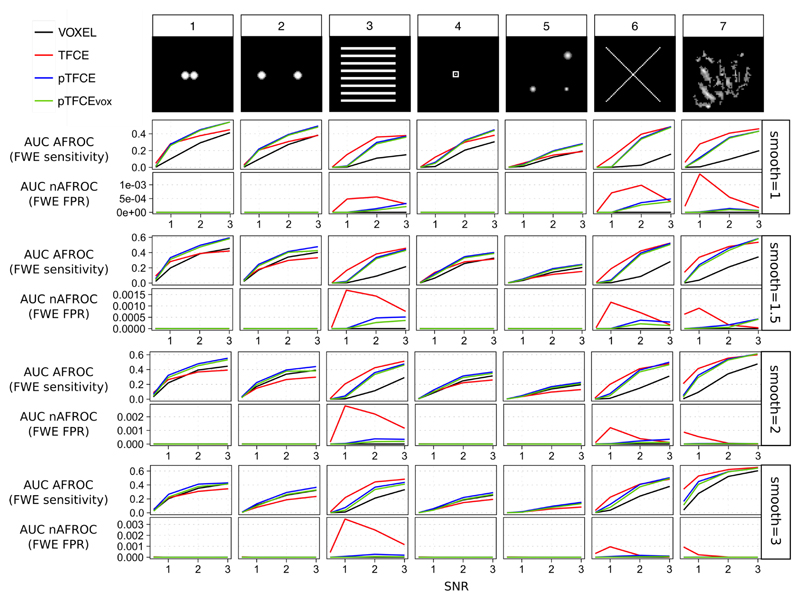
Another possible concept for contrasting the tested approaches is to investigate their performance with identical parameter settings, instead of using the optimized smoothing values for each. Separate comparison of the tested approaches with each parameter-setting showed, in general, very similar results to those revealed with optimized smoothing.

In these comparisons, as well, cluster enhancement methods tended to be superior to the unenhanced voxel-level inference (Figure 6, AUC AFROC: upper row for each smoothing value), although again, in a few cases (typically for high SNRs with test signals 1, 2 and 5) TFCE yielded lower mean AUC values than unenhanced voxel-level thresholding with the same simulation parameters. On the other hand, pTFCE robustly outperformed the unenhanced thresholding in all of the simulation parameter settings. The same is true for pTFCE_vox suggesting that thresholding the pTFCE enhanced image with thresholds originally interpreted on the unenhanced image also results in an enhanced sensitivity.

Figure 6. Mean AUC values of the AFROC (representing FWER-level sensitivity) and negative AFROC (representing 1-FWER-level specificity) curves for all methods, ground truth shapes, SNRs and smoothing kernels.

The mean area under the negative AFROC curve is, for most of the parameter settings, relatively close to zero, meaning an appropriate control for false positives and “cluster leaking”. However, in case of the cluster enhancement methods (TFCE, pTFCE and pTFCE_vox), false positives (defined by our nAFROC analysis, very conservatively, as regions where the noise is at least 1000 times greater than signal) slightly accumulate by ground truth images with extended area of signal (signals 3, 6 and 9, upper row of each smoothing parameter panel on Figure 6).

When comparing cluster enhancement methods against each other, we found a very similar pattern to that with optimized smoothing: pTFCE and pTFCE_vox tended to slightly outperform TFCE in terms of FWER-controlled sensitivity in almost all cases with spatially more restricted test signals (signals 1, 2, 4 and 5). In these cases, all cluster enhancement methods give a very strict control over cluster-leaking and corresponding false positives. On the contrary, TFCE tends to outperform pTFCE and pTFCE_vox in simulations with spatially extended ground truth (signals 3, 6 and 7) and low SNRs; however, it does it at the price of decreased specificity, as suggested by the mean AUC of negative AFROC curves in these cases (second rows on each smoothing panel on Figure 6). All in all, in most of the cases pTFCE and pTFCE_vox seems to provide a similar or stricter control over cluster leaking than TFCE.

Importantly, low AUC values for the negative AFROC curves of the pTFCE_vox method imply that thresholding the pTFCE enhanced image with thresholds originally interpreted on the unenhanced image gives an appropriate control for FWER.

1.7. Real data evaluation

1.7.1. Demonstration of increased statistical power

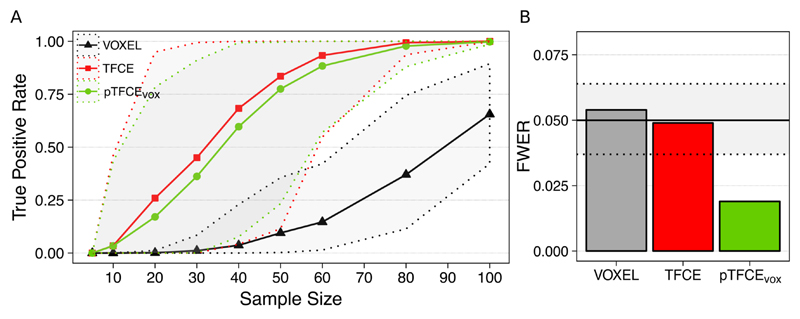
Our real-data analysis demonstrates that both enhancement methods (TFCE and pTFCE_vox) result in a substantial increase of detected “true positive” voxels (see Methods for our assumption on true positives). For the investigated dataset (Figure 7A), the increase in statistical power introduced by the cluster enhancement methods allows for detecting about half of the “true activation” on average at a sample size of about N=35, as opposed to the sample size of about N=90 needed for the unenhanced statistical inference for the same average performance. Moreover, in 95% of the cases the true positive rate of 0.5 was already reached by the enhancement methods at a sample size 60. On the other hand, for the same sample size of N=20, the enhanced statistical inference might already detect 25% of the “true” activation while without enhancement no voxels at all were detected in most of the random samples. While the average true positive rate for pTFCE is slightly lower than that of TFCE, across the random samples of sizes 30-60, pTFCE yielded a narrower confidence interval and therefore a more pronounced separation (more robust improvement) from the unenhanced analysis.

Figure 7. Performance of pTFCE on the “taskswitch” paradigm of the NCP dataset (Gorgolewski et al., 2017; Poldrack et al., 2016).

(A) Counting the voxels of the full-sample (N=119) group-level FWER-corrected, unenhanced activation map also found by the investigated methods in various subsamples and plotting the mean (solid lines) and the 95% confidence intervals (dotted lines) as a function of sample sizes provides an estimate of the improvement in statistical power. (B) Family-wise error rates (FWER) of the investigated methods. Methods VOXEL and TFCE were thresholded using permutation test while pTFCE was thresholded at the same threshold as VOXEL, resulting in the pTFCE_vox approach. Dotted lines denote the 95% confidence interval for FWER for the 1000 repetitions.

1.7.2. Evaluation of family-wise error rate

Family-wise error rates in our real-data scenario with a true-null hypothesis were found to be in the nominal range for the VOXEL and TFCE methods (0.054 and 0.049, respectively) and, in accordance to the simulation results, below the nominal range (0.02) for pTFCE_vox.

1.7.3. Demonstration of enhancing an activation map with pTFCE

Applying TFCE and pTFCE on real data resulted in an enhanced detection of pain-related activation in both cases. The total number of FWER-corrected suprathreshold voxels approximately doubled for both approaches (from 23665 voxels to 46722 for TFCE and to 50063 for pTFCE). The newly detected areas, besides border regions of the unenhanced activation pattern, involve also completely new activation maxima (See Error! Reference source not found. and Supplementary Table 2 and 3). New local maxima emerge in the thalamus, brainstem, amygdala, caudate nuclei, pallidum, middle cingulate cortex, middle frontal gyrus, postcentral gyrus, planum temporale and superior parietal lobule.

Besides the striking similarity of the TFCE and the pTFCE map, several activations, among others, in the cerebellum and the brainstem (and additionally, some border regions) were only detected by pTFCE. In contrast, some blobs in white matter were detected only by TFCE. Notably, due to the required permutation test, processing time of TFCE is longer than that of pTFCE by more than an order magnitude.

Discussion

In this paper, we have formulated and comprehensively evaluated a novel, generalized approach which unifies the advantages of cluster- and voxel-wise statistical inference. Since the basic concepts of our method are similar to those of the threshold-free cluster enhancement approach (TFCE) (Smith and Nichols, 2009), we refer to our method as probabilistic TFCE or pTFCE.

In a pure theoretical sense, as we start to use spatial neighbourhood information to boost neuroimaging signals we should inherently start to lose spatial localization accuracy. However, the inherent smoothness of typical neuroimaging data (even without artificial smoothing) does not allow for taking advantage of the high localising performance of the simple voxel-wise inference. On the other hand, incorporating image smoothness (or clustering) information into the statistical inference might also be considered as optimising the “localisation performance – sensitivity” trade-off by throwing out only localisation capacity which is “unutilised” (due to smoothness). Both TFCE and pTFCE take advantage of this property of neuroimages.

As opposed to the simple cluster-wise inference, both TFCE and pTFCE generate a voxel-wise output image and maintains information about spatial detail within extended areas of signal. For example, local maxima in the pTFCE output image can easily be identified, and separated from each other if a “cluster” contains more than one maximum. These local maxima locations will be identical to those in the original statistical image. This means that, similarly to TFCE, pTFCE provides rich and interpretable output, retaining much more spatial information than traditional cluster-based approaches.

Our evaluation on simulated and real data underpins former results (Smith and Nichols, 2009) and clearly justifies that incorporating spatial topological information when testing voxel-level differences in neurological images provides a significant improvement in sensitivity over the simple, unenhanced voxel-level inference (Error! Reference source not found.B, C). While the mathematical background of pTFCE is significantly different from that of TFCE, importantly, pTFCE results are highly similar to those of TFCE (Error! Reference source not found.B), suggesting that the spatial localisation performances of the two methods are similar.

Our analysis with optimized values of smoothing reveals that pTFCE prefers smoothing extents similar to TFCE, and typically smaller than the unenhanced inference. This can be considered as a desirable property, because an extensive artificial smoothing changes the area of activation and the positions of local maxima on the image, possibly leading to false conclusions.

The results also suggest that, in terms of family-wise sensitivity, pTFCE is always superior to the uncorrected inference. Moreover, in doing so, pTFCE is more stable than TFCE, given the few cases of the latter producing lower AUC values than the unenhanced inference (typically at high SNRs with test signals 1 and 2; see Figure 6). The rationale behind these results might be that TFCE, with E=0.5, H=2, is possibly better optimised for more extended signal shapes (where it performs very well), while pTFCE might implement a more objective enhancement, unbiased regarding of the shape and extent of the true signal. TFCE tends to produce higher AUC values than pTFCE for spatially extended test signals, mainly at low signal-to-noise ratios. However, these cases were successively paired with an elevated number of positive observations within background regions as revealed by our “negative AFROC” analysis.

Here we argue that this undesirable property is most probably the result of “cluster leaking”: when, typically, low-threshold clusters containing many false positive voxels are integrated during enhancement so that areas of no signal became enhanced enough to be detected even with FWER-level correction. Let us note however, that TFCE, with E=0.5, H=2, possibly implements a trade-off by allowing for some more FPs but, at the same time, capturing the extended low-signal boundary regions, as well, thereby being closer to what we could intuitively feel “true” for a big cluster. Nevertheless, in terms of this issue, pTFCE seems to be more “pragmatic”, by maintaining an acceptable low-level of “leaked” false positives even with morphologically complex and spatially extended ground truth signals. In other words, the spatial localisation performance of pTFCE seems to be somewhat superior to that of TFCE in case of large-extent signal shapes.

Combining the results of analysis with optimal and identical parameter-sets suggest that the above discussed differences are not a consequence of suboptimal parameter settings for any of the methods, but general differences in their overall performance. Therefore, we encourage the use of pTFCE in any case, as an alternative to TFCE.

Importantly, our results also indicate that, when thresholding the pTFCE-enhanced image at FWER corrected values completely based on the original unenhanced image, the thresholded image still provides improved sensitivity, and gives a strict control for FWER, as well, comparable to that within the original image. (see pTFCE_vox on Error! Reference source not found., Figure 5 and Figure 6). Therefore, in contrast to TFCE, pTFCE does not require a permutation test, because the threshold values obtained for the unenhanced image can be directly applied on the enhanced image. This property renders pTFCE suitable for a wide range of studies, for instance with study designs where permutation tests are not possible or not preferred.

We took advantage of this property when demonstrating pTFCE on real data. Our results demonstrate that both TFCE and pTFCE result in a significant increase in statistical power (Figure 7A), allowing for detecting the same activations at a lower sample size or more true positive voxels at the same sample size as compared to the unenhanced statistical inference. While the tested pTFCE_vox approach (that is using the GRF-theory based maximum-height threshold of the unenhanced values) seems to perform slightly inferior to TFCE, it also seems to maintain narrower confidence intervals across the random samples and therefore a more robust improvement over the unenhanced VOXEL approach. While it was not investigated in this study on real data, analysis of simulated data suggests that correcting pTFCE for multiple comparisons with a permutation-based approach (that is using pTFCE instead of pTFCE_vox) would further improve sensitivity, and depending on the spatial topology of the true signal, might even outperform TFCE.

Analysis of family-wise error rates (Figure 7B) also suggest, that pTFCE_vox gives an overly strict control of FWER. Based on our simulations, correcting pTFCE for multiple comparisons with a permutation-based approach might yield a more liberal thresholding and result in nominal FWER values. This aspect, together with a detailed evaluation of the effect of inhomogeneous spatial autocorrelation on pTFCE is subject to further investigation.

Demonstrating the effect of enhancement approaches on an activation map (capturing response to painful stimuli) reveals that both TFCE and pTFCE makes several extra activations detectable. Some of these activation areas include completely new local maxima, meaning that the enhanced activation map is not only a simply “boosted” version of the original image, with stronger activation borders, but indeed, new activations are brought over the level of significance. The majority of the newly detected activation maxima are considered to be part of the pain matrix, thus naturally fit into the results of (Bingel et al., 2011). With the applied methods, pTFCE (pTFCE_vox) discovers slightly more new voxels than TFCE and those seem to be in more relevant locations (cerebellum, brainstem) than those specific for TFCE only (white matter). While analysis of the real-data example also demonstrates that it is valid to threshold pTFCE images with values set up for the unenhanced image, our simulation results still suggest, that, when it comes to correction for multiple comparisons, permutation based maximum height thresholding using the empirical distribution of the enhanced data gives a slightly better sensitivity. Nevertheless, the improvement over TFCE in the most realistic simulation cases is present at the pTFCE_vox approach (that is, without the need for permutation test), as well. This improved sensitivity, together with the marginal processing time (compared to permutation-test required for TFCE) renders pTFCE beneficial and easily applicable with any neuroimaging workflow.

Limitations

An obvious limitation of our study is that in the simulations we applied a stationary Gaussian noise model, without any inhomogeneous spatial autocorrelation. Although, in that aspect, we did not capture some relevant properties of real neuroimaging data, this is more than a reasonable simplification: it is a standard first approximation of modelling neuroimaging data and as such, a necessary first step in evaluating pTFCE. Therefore, the presented work should be considered as a basis for further investigations aiming at the evaluation and adjustment of the pTFCE approach for autocorrelation and nonstationarities in the data. Nevertheless, since pTFCE implements a concept similar to TFCE, we could expect a similar robustness (Salimi-Khorshidi et al., 2011) to these characteristics of real datasets. Indeed, our initial analysis (Figure 7B) revealed that, despite the assumption of homogenous spatial autocorrelation in the GRF-based estimation of probabilities, pTFCE_vox still gives a very strict control of FWER on real data. Furthermore, the GRF theory based implementation of TFCE can trivially be extended to consider local properties of smoothness, analogous to (Salimi-Khorshidi et al., 2011), or alternatively, permutation-based nonparametric estimation of the cluster-size distributions can be also used, yielding a “brute force” solution to the issues of spatial inhomogeneity of image smoothness in real data.

Although, when introducing the theoretical background, we clarified that GRF theory is only one way to estimate the necessary distributions for pTFCE, the main aim of this paper was to establish and validate the links of pTFCE to existing, “de facto” standards in neuroimaging analysis, and accordingly focused on the GRF-based solution. Exploring the novel possibilities provided by non-GRF based pTFCE solutions (e.g. cluster enhancement on graphs), together with the comprehensive evaluation of the effect of spatial inhomogeneities, will be the topic of upcoming research.

Conclusion

Here, we have proposed a novel approach for the integration of information about autocorrelation into mass-univariate statistical analysis. Our solution, called pTFCE, can be considered as an improvement and generalisation of the widely used threshold-free cluster enhancement (TFCE) approach. While the theory behind pTFCE allows for generalising the approach for various data structures, in this paper we have focused on a Gaussian Random Field-based implementation in order to establish clear links to the standard volumetric analysis methodology in neuroimaging.

In our evaluation, we found that pTFCE is more robust to various ground truth shapes and provides a stricter control over cluster “leaking” than TFCE and, in some realistic cases, further improves its sensitivity. The fact that, as opposed to TFCE, pTFCE directly outputs (enhanced) P-values, makes it well-suitable for the improvement of statistical inference in any neuroimaging workflow.

Importantly, the presented GRF-based likelihood function in the Bayesian formulation of pTFCE can easily be exchanged, thus pTFCE is easy to adapt for data structures other than images (e.g. skeletons, surfaces or graphs), and carries the potential to deploy the concept of topology-based enhancement of statistical inference on a wider range of applications than ever before.

Various software implementations and documentation of the pTFCE approach are available at https://spisakt.github.io/pTFCE.

Abbreviations

TFCE

threshold-free cluster enhancement

FWER

family-wise error rate

PDF

probability density function

GRF

Gaussian random field

TPR, FPR

true positive rate, false positive rate

ROC

receiver-operator characteristic

AFROC

alternative free-response ROC

AUC

area under the curve

FWHM

full width at half maximum