In Silico Analysis of an Exercise-Safe Artificial Pancreas With Multistage Model Predictive Control and Insulin Safety System

Abstract

Background:

Maintaining glycemic equilibrium can be challenging for people living with type 1 diabetes (T1D) as many factors (eg, length, type, duration, insulin on board, stress, and training) will impact the metabolic changes triggered by physical activity potentially leading to both hypoglycemia and hyperglycemia. Therefore, and despite the noted health benefits, many individuals with T1D do not exercise as much as their healthy peers. While technology advances have improved glucose control during and immediately after exercise, it remains one of the key limitations of artificial pancreas (AP) systems, largely because stopping insulin at the onset of exercise may not be enough to prevent impending, exercise-induced hypoglycemia.

Methods:

A hybrid AP algorithm with subject-specific exercise behavior recognition and anticipatory action is designed to prevent hypoglycemic events during and after moderate-intensity exercise. Our approach relies on a number of key innovations, namely, an activity informed premeal bolus calculator, personalized exercise pattern recognition, and a multistage model predictive control (MS-MPC) strategy that can transition between reactive and anticipatory modes. This AP design was evaluated on 100 in silico subjects from the most up-to-date FDA-accepted UVA/Padova metabolic simulator, emulating an outpatient clinical trial setting. Results with a baseline controller, a regular MPC (rMPC), are also included for comparison purposes.

Results:

In silico experiments reveal that the proposed MS-MPC strategy markedly reduces the number of exercise-related hypoglycemic events (8 vs 68).

Conclusion:

An anticipatory mode for insulin administration of a monohormonal AP controller reduces the occurrence of hypoglycemia during moderate-intensity exercise.

Introduction

Type 1 diabetes (T1D) is an autoimmune condition resulting in absolute insulin deficiency and a life-long need for exogenous insulin.¹ Glycemic control in T1D remains a challenge, despite the availability of modern insulin analogs,² and advanced technology such as insulin pumps, continuous glucose monitoring (CGM)³ and artificial pancreas (AP) systems that automatically titrate insulin doses.⁴

Artificial pancreas systems have become a focus of significant research and industrial development.^4,5 During the past decade, studies have advanced from short-term, inpatient investigations using algorithm-driven manual control⁶ to long-term clinical trials in free-living conditions.⁷ Most AP studies show a significant reduction in glucose variability, particularly overnight, and lower risk of hypoglycemia. In September 2016, the US Food and Drug Administration (FDA) approved the first hybrid, closed-loop control system, the Medtronic 670G. This AP is capable of automatically adjusting the insulin basal rate, but still faces many issues, such as time spent in closed loop (72%-75%),^8,9 low time-in-range (~65%) in comparison to other proposed systems, and its hybrid design: user input for major disturbances like meals and exercise.^8,10

In spite of significant effort from the scientific community, meals and exercise remain the most challenging hurdles to overcome before a fully automated AP can be developed. Physical activity is particularly challenging to account for, as its effects on glucose are based on intensity, duration, and patient-specific physiology.^11,12 For example, moderate-intensity exercise is known to cause a decrease in glucose levels as opposed to high-intensity and anaerobic exercise which may cause an increase in glucose levels, and hence, an increased insulin requirement.¹² The current treatment guides suggest basal insulin reduction for pump users and/or carbohydrate supplementation prior to moderate exercise.¹³ A recent study showed that in order to prevent exercise-related hypoglycemia, basal insulin needs to be reduced ~90 to 120 minutes before activity began.^12,14 However, these approaches should be taken cautiously, since carbohydrate overconsumption and aggressive reduction of basal insulin levels may also lead to hyperglycemia during and after exercise.¹⁵

Studies addressing different AP designs to improve glycemic control during and after exercise bouts are increasingly prevalent in the literature.^16-23 In these studies, the incorporation of additional sensors (eg, HR and accelerometry) for exercise detection and the use of different control strategies were assessed during moderate-intensity exercise (eg, one-hour brisk walk, bicycling, and soccer).

The proposed multistage model predictive controller (MS-MPC) differs from the previous exercise-oriented AP designs through three major improvements: (i) the incorporation of subject-specific exercise behavior into the controller design which can be updated periodically, (ii) anticipatory and reactive modes that compensate for expected and ongoing exercise, and (iii) an adaptive detuning strategy that modulates the controller’s aggressiveness before and after a meal. Additionally, the controller leverages the Unified Safety System (USS Virginia), a safety supervision module to limit basal injections based on the perceived risk for hypoglycemia.²⁴ The safety and performance of the MS-MPC and a regular MPC (baseline controller—rMPC) are evaluated on 100 in silico subjects from the most up-to-date FDA-accepted UVA/Padova simulator in a specific outpatient clinical trial design, including intra- and interpatient variations. Here, the primary outcome is the comparison between the number of hypoglycemic treatments.

Methods

Prediction Model

In this work, both the baseline rMPC and the proposed MS-MPC make predictions using a personalized version of the Subcutaneous Oral Glucose Minimal Model (SOGMM).²⁵ Model equations are as follows:

$$\stackrel{.}{G}\left(t\right)=-\left[S_{\mathrm{g}}+X\left(t\right)\right]G\left(t\right)+S_{\mathrm{g}}{G}_{\mathrm{b}}+\frac{k_{\mathrm{abs}}f}{V_{\mathrm{g}}\mathrm{BW}}{Q}_2\left(t\right)+w\left(t\right)$$ (1)

$$\stackrel{.}{X}\left(t\right)=-p_{2}X\left(t\right)+p_2{S}_{\mathrm{I}}\left[\frac{I_{\mathrm{p}}\left(t\right)}{V_{\mathrm{I}}\mathrm{BW}}-I_{\mathrm{b}}\right]$$ (2)

$${\stackrel{.}{Q}}_1\left(t\right)=-k_{\mathrm{\tau }}{Q}_1\left(t\right)+m\left(t\right)$$ (3)

$${\stackrel{.}{Q}}_2\left(t\right)=-k_{\mathrm{abs}}{Q}_2\left(t\right)+k_{\mathrm{\tau }}{Q}_1\left(t\right)$$ (4)

$${\stackrel{.}{I}}_{\mathrm{sc}1}\left(t\right)=-k_d{I}_{\mathrm{sc}1}\left(t\right)+u\left(t\right)$$ (5)

$${\stackrel{.}{I}}_{\mathrm{sc}2}\left(t\right)=-k_d{I}_{\mathrm{sc}2}\left(t\right)+k_d{I}_{\mathrm{sc}1}\left(t\right)$$ (6)

$${\stackrel{.}{I}}_{\mathrm{p}}\left(t\right)=-k_{\mathrm{cl}}{I}_{\mathrm{p}}\left(t\right)+k_{\mathrm{d}}{I}_{\mathrm{sc}2}\left(t\right)$$ (7)

where $G$ is the plasma glucose concentration output (mg/dL), X is the proportion of insulin in the remote compartment (L/min), $Q_1$ and $Q_2$ are the glucose masses in the stomach and the gut (mg), respectively, $I_{\mathrm{sc}1}$ and $I_{\mathrm{sc}2}$ are the amounts of nonmonomeric and monomeric insulin in the subcutaneous space (mU), respectively, $I_{\mathrm{p}}$ is the amount of plasma insulin (mU), $w$ represents the effect of exercise on blood glucose levels (mg/dL/min), $m$ is the input rate of mixed-meal carbohydrate absorption (mg/min), and $u$ is the exogenous insulin input (mU/min). Parameters of model equations (1-7) are described in Table 1. As observed, some can be fixed using a priori information, eg, $\mathrm{BW}$ is easily measured, $f$ is set to 0.9,²⁶ $G_{\mathrm{b}}$ can be estimated from the patient’s most recent glycated hemoglobin²⁵

Table 1.

Model Parameters of the Subcutaneous Oral Glucose Minimal Model.

Symbol	Meaning	Units
S g	Fractional glucose effectiveness	L/min
V g	Distribution volume of glucose	kg/dL
k abs	Rate constant—oral glucose consumption	L/min
kτ	Time constant related with oral glucose absorption	L/min
p 2	Rate constant of the remote insulin compartment	L/min
f	Fraction of intestinal absorption	-
V I	Distribution volume of insulin	L/kg
k cl	Rate constant of subcutaneous insulin transport	L/min
kd	Rate constant of subcutaneous insulin transport	L/min
S I	Insulin sensitivity	L/min/mU/L
BW	Body weight	kg
G b	Basal glucose concentration	mg/dL
I b	Basal insulin concentration	mU/L

$$G_{\mathrm{b}}=28.7.\mathrm{HbA}1\mathrm{c}-46.7$$ (8)

and $I_{\mathrm{b}}$ can be computed from the basal infusion rate $u=u_{\mathrm{b}}$ as

$$I_{\mathrm{b}}=\frac{u_{\mathrm{b}}}{\mathrm{BW}{k}_{\mathrm{cl}}{V}_{\mathrm{I}}}$$ (9)

In this work, synthetic glucose measurements for model identification were generated from the FDA-accepted UVA/Padova simulator.^27,28 To this end, for each of the 100 in silico adults, 10 days of data collection considering intrapatient and interday variability were simulated with three meals per day. Since in the simulator each subject is equipped with a particular G_b, Equation (8) was not used in this in silico study.

A subset of parameters was selected, $\mathrm{\theta }=\left\{S_{\mathrm{g}},S_{\mathrm{I}},V_{\mathrm{I}},k_d\right\}$, based on the previous work by the authors.²⁹ An example of the identification results is depicted in Figure 1. The performance of each model after identification was assessed by means of the root mean square error (RMSE) criterion:

Figure 1.

Example of identification results for one of the in silico adults. The solid blue line represents the daily glucose profile generated using the UVA/Padova simulator and the dashed blue line is the glucose predicted by the identified model. The orange line indicates the insulin boluses and basal pattern.

$$\mathrm{RMSE}=\frac{\Vert \widehat{y}-y\Vert }{\sqrt{N}}$$ (10)

where ‖.‖ indicates the two-norm, and $N$, $y$, and $\widehat{y}$ are the number of data points, the CGM measurements, and model output, respectively. In this case, N was set to 288 as daily profiles with a sampling time of five minutes were identified. Average RMSE results considering all 1000 model identifications (10 identifications per each of the 100 virtual subjects) is $14.5\pm 6.6$ mg/dL. Identified parameters for the population, ie, value (std), are given in Table 2. In order to define the prediction model used by the MPC controllers, mean values of the 10 sets of daily parameters related to each virtual subject were finally considered.

Table 2.

Average Estimates from In Silico Data for the Selected Parameters of the Subcutaneous Oral Glucose Minimal Model.

Parameter	Mean (SD)	Units
S g	$0.0265\left(0.0092\right)$	L/min
V I	$0.0442\left(0.0250\right)$	L/kg
kd	$0.1460\left(0.0980\right)$	L/min
S I	$1.6784\times {10}^{-4}\left(1.4305\times {10}^{-4}\right)$	L/min/mU/L

Hybrid Multistage AP With Exercise Behavior Recognition

Multistage model predictive control was introduced by Lucia et al^30,31 as a way to make the MPC strategy robust for cases where the prediction model is uncertain but less conservative than classic approaches. This approach assumes a tree of semi-independent disturbance realizations which are only related in the initial condition by means of the so-called non-anticipativity constraint. Such a formulation makes it possible to include further insight of what may happen in the future. In this sense, future control actions can be adapted according to hypothetical future realizations of the uncertainty.

In our case, we assume the effect of moderate-intensity exercise bouts on glucose dynamics as the main source of uncertainty in the prediction model. Since the user is not expected to exercise at the exact same time or for the same duration, different exercise realizations arise. Instead of optimizing the insulin infusion for a given exercise condition, a specific number of $N_{\mathrm{en}}$ of disturbance realizations are considered. Although a higher $N_{\mathrm{en}}$ may lead to better disturbance characterization, a high number of considered disturbances may pose a large computational burden. Because this control scheme will be embedded on a smartphone in future clinical trials, an appropriate tradeoff between performance and low $N_{\mathrm{en}}$ must be a design consideration.³¹ In the following sections, we explain the main components of our control system.

Subject-Specific Exercise Behavior

Exercise input $w$

The UVA/Padova simulator is equipped with an exercise model that describes widely acknowledged short- and long-term exercise-related alterations in insulin-independent glucose uptake (U_ii), endogenous glucose production (EGP), and insulin sensitivity (S_I).^12,32-35 While the increase in U_ii was modeled as a pulse-wise signal that is only active during exercise,¹² changes in S_I and EGP were defined to increase during exercise and slowly decay to their baselines in hours following. Data from four randomized cross-over clinical studies (NCT01418703, NCT01390259, 2009-A00421-56, and 2010-A00538-31) were considered for model tuning to statistically describe the immediate increase observed in all U_ii, EGP, and S_I. On the other hand, the glucose clamp procedure described in McMahon et al³⁶ was simulated to represent the long-term effect of exercise on glycemia and adjust the time constants associated with the posterior decays in S_I and EGP. For each in silico adult of the simulator, the glucose infusion rates (GIRs) needed to maintain the glucose level at its basal value during a 45-minute bout of moderate exercise and in the hours following was commanded by a discrete proportional-derivative controller. The biphasic behavior of GIR detected in McMahon et al³⁶ was successfully recreated by adjusting the decay of both S_I and EGP after exercise, and accommodating the increase in S_I that occurs several hours later and then decays slowly to its baseline.

To consider this effect in the MPC predictions, SOGMM was augmented by including the additional input $w$. To this end, the mean GIR for a 45-minute bout of moderate exercise across all subjects ($\overline{\mathrm{GIR}})$ was computed, and the following discrete-time linear time-invariant (LTI) system with a sampling time $t_{\mathrm{s}}=5$ minutes was identified using the adaptive subspace Gauss-Newton search (91.9% fitting):

$$\begin{array}{c}E\left(z\right)=E_f\left(z\right)+E_s\left(z\right)=\frac{b_{11}z+b_{12}}{z^2+a_{11}z}\\ +\frac{b_{21}{z}^2+b_{22}z+b_{23}}{z^3+a_{21}{z}^2+a_{22}z+a_{23}}{z}^{-75}\end{array}$$ (11)

The identified parameters are $b_{11}=0.7153$, $b_{12}=0.0004$, $b_{21}=0.1457\times {10}^{-3}$, $b_{22}=0.5580\times {10}^{-3}$, $b_{23}=0.1336\times {10}^{-3}$ $a_{11}=-0.8440$, $a_{21}=-2.8317$, $a_{22}=2.6729$, and a₂₃= −0.8410. Note that $E\left(z\right)$ is defined as the combination of two transfer functions, $E_f\left(z\right)$ and $E_s\left(z\right)$, that describe the immediate glucose requirement associated with exercise as well as the delayed glucose uptake associated with the physical activity, respectively. In this way, given a $d$-minute exercise signal, ${\mathrm{\pi }}_{d,k}$ is defined as follows:

$${\mathrm{\pi }}_{d,k}=\{\begin{array}{cc}1& \mathrm{if}{t}_k\in \left[t_{\mathrm{ex}},t_{\mathrm{ex}}+d\right]\\ 0& \mathrm{otherwise}\end{array}$$ (12)

with $t_{\mathrm{ex}}$ the exercise start time. Assuming linearity, the disturbance signal $w_{d,k}$(mg/dL/min) can be found through the discrete convolution of ${\mathrm{\pi }}_{d,k}$ and the impulse response, $h_k$ (mg/kg/min), of $E\left(z\right)$:

$$w_{d,k}=-\sum _{n=-\infty }^{\infty }{\mathrm{\pi }}_{d,k}{h}_{k-n}/V_g$$ (13)

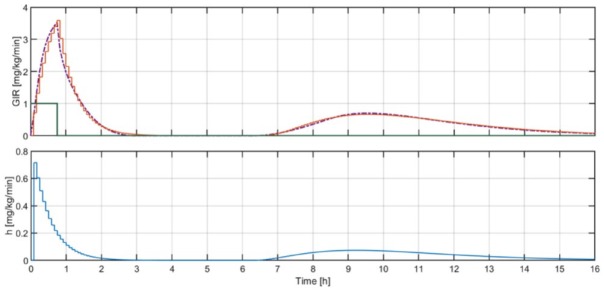
where $V_{\mathrm{g}}$ is the distribution volume of glucose (dL/kg). Results of this procedure are depicted in Figure 2. Since no individualization of $w$ is performed in this work, $V_g$ was fixed to 1.6 dL/kg as reported in Patek et al.²⁵

Figure 2.

Above: Mean $\mathrm{GIR}$ across all subjects, $\overline{\mathrm{GIR}}$, (purple) obtained with the UVA/Padova simulator vs the response of $E\left(z\right)$ (orange) when it is excited with ${\mathrm{\pi }}_{k,45}$ (green). Below: Impulse response of $E\left(z\right)$, $h_k$.

Extracting subject-specific exercise behavior

To represent data that would be collected leading up to a clinical admission, we simulated 30 days for each of the in silico subjects involved in our protocol. On one-half the 30 simulated days, the subjects exercised for about 45 minutes in between 4 and 7 pm, under moderate-intensity exercise training. The exercise bout was represented with a rectangular signal, ${\mathrm{\pi }}_{d,k}$, equal to 1 during exercise and corresponding to the length of the activity. This was then convolved with the response of the previously described LTI system, $h_k$, representing the dynamics of glucose uptake related to moderate-intensity exercise. Exercise disturbance signals were calculated for each day of data collection through the aforementioned process.

A total of 24-hour exercise-related disturbance signals were then clustered into five distinct groups (to meet the tradeoff of number of parallel controllers and performance) using the k-medoids algorithm with a squared Euclidean distance measure. Although not described here in full due to space constraints, the decision to choose five clusters was based on an experiment where approximately 30 days of exercise data from different patients were clustered using different cluster sizes. The average silhouette score was calculated from each of these configurations and five clusters provided the highest silhouette score on average for the subjects in the training data. The clustered signals were then averaged across each sampling period to create a 24-hour profile trace for each grouping. The proportion of days of the month that fell into each cluster was considered its relative probability for each subject

$$\mathrm{Pr}\left(i\right)=\frac{n_i}{{\sum }_{j=1}^c{n}_j}$$ (14)

where $\mathrm{Pr}\left(i\right)$ is the probability of cluster $i$, $n_i$ is the number of days in cluster $i$, and $c$ is the number of total clusters (in this case 5).

Figure 3 shows an example clustering for an in silico subject. For simplicity in this particular implementation, five profiles for each subject were generated. Two profiles had average traces equal to 0 ($\mathrm{Pr}\left(i\right)=0.2$) and the other three represented the glucose uptake from exercise bouts performed randomly between 4 and 7 pm.

Figure 3.

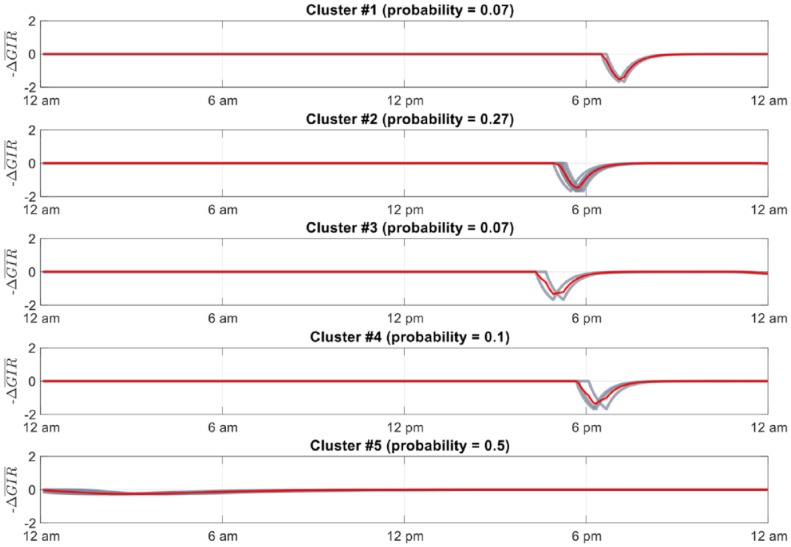
Clustered glucose uptake signals for 30 days of a representative subject’s exercise data. Red lines show profile (average) trace. Black lines show each trace represented in the cluster. Probability of each cluster occurring shown above each respective subplot.

Multistage Model Predictive Control

The core of the AP system is represented by the MS-MPC whose mathematical problem is defined as follows:

$$\underset{{\tilde{u}}_k^i,{\tilde{\mathrm{\nu }}}_k^i}{\min }{\mathrm{\varphi }}^{\mathrm{ms}}$$ (15)

$$\mathrm{s}.\mathrm{t}.x_{k+j+1|k}^i=A{x}_{k+j|k}^i+B_{\mathrm{I}}{u}_{k+j|k}^i+B_{\mathrm{w}}{w}_{k+j|k}^i$$ (16)

$$y_k^i=C{x}_k^i$$ (17)

$$u_{\min }\le u_{k+j|k}^i\le u_{\max },\forall i=1,\dots ,N_{\mathrm{en}}$$ (18)

$$\mathrm{\Delta }{u}_{\min }\le \mathrm{\Delta }{u}_{k+j|k}^i\le \mathrm{\Delta }{u}_{\max },\forall i=1,\dots ,N_{\mathrm{en}}$$ (19)

$$y_{\min }-y_{k+j}^i\le {\mathrm{\eta }}_{k+j}^i$$ (20)

$${\mathrm{\eta }}_{k+j}^i\ge 0$$ (21)

$$u_k^i=u_k^l\mathrm{with}i\ne l$$ (22)

where ${\tilde{u}}_k^i={\left[\begin{array}{cccc}{u}_k& u_{k+1}& \cdots & u_{k+N_{\mathrm{c}}-1}\end{array}\right]}^i$ and ${\tilde{\mathrm{\eta }}}_k^i={\mathrm{\eta }}_k{\mathrm{\eta }}_{k+1}\dots {\mathrm{\eta }}_{{k+}_{N_{p-1}}}$ are, respectively, the control policy and the policy of slack variables related to the soft constraint (20) optimized at the $i$th MPC with control and prediction horizons $N_{\mathrm{c}}$ and $N_{\mathrm{p}}$, respectively, and $i=1,2,\dots ,N_{\mathrm{en}}$. Bearing the above in mind, our AP should solve the mathematical problem (15)-(22) at every sampling time. As a result, we obtain $N_{\mathrm{en}}$ control policies ${\tilde{u}}_k^i$ $\left(i=1,\dots ,N_{\mathrm{en}}\right)$, but only $u_k$, which is common in all the problems as per constraint (22), is sent to the insulin pump for actual infusion, following the receding horizon principle from MPC.

In the above formulation, Equation (16) corresponds to the linear state-space representation of the $i$th prediction model with $x_k^i\in {\mathrm{ℝ}}^n$ being the system state, $u_k^i\in {\mathrm{ℝ}}^m$ the control policy, and $w_k^i\in {\mathrm{ℝ}}^d$ a specific realization of the effect of exercise on glucose dynamics, with $n=7,m=1,$ and $d=1$ in our case. The quadruplet $\left(A,B_{\mathrm{I}},B_{\mathrm{w}},\mathrm{and}C\right)$ are found after discretizing $\left(t_{\mathrm{s}}=5\mathrm{minutes}\right)$ the matrices of the continuous-time linear approximation of Equations (1) to (7) defined by

$$\begin{array}{l}{A}_{\mathrm{c}}={\frac{\partial g}{\partial x}|}_{\begin{array}{c}x=x_{\mathrm{ss}}\\ u=u_{\mathrm{ss}}\end{array}},B_{\mathrm{I},\mathrm{c}}={\frac{\partial g}{\partial u}|}_{\begin{array}{c}x=x_{\mathrm{ss}}\\ u=u_{\mathrm{ss}}\end{array}},B_{\mathrm{w},\mathrm{c}}={\left[\begin{array}{cccc}1& 0& \cdots & 0\end{array}\right]}^{\mathrm{T}},\\ C_{\mathrm{c}}=\left[\begin{array}{cccc}1& 0& \cdots & 0\end{array}\right]\end{array}$$ (23)

where $x_{\mathrm{ss}}$ denotes the steady state found by solving the system (1) to (7), considering $x_1=y_{\mathrm{sp}}=120\mathrm{mg}/\mathrm{dL}$, $u=u_{\mathrm{ss}}=u_{\mathrm{b}}$ and $w=0$, with $u_{\mathrm{b}}$ being the subject-specific basal infusion. Note that model (16) does not account for the meal for prediction purposes since this disturbance is assumed to be mostly covered by the premeal bolus. Moreover, the model prediction for every scenario is the same except for the disturbance realization; Equation (17) is the output equation at the $i$th scenario; Equations (18) and (19) ensure both insulin infusion and the difference between two consecutive insulin infusions along the control horizon to be in the intervals $\left[u_{\min },u_{\max }\right]$ and $\left[\mathrm{\Delta }{u}_{\min },\mathrm{\Delta }{u}_{\max }\right]$, respectively; Equations (20) and (21) are together a soft constraint over the output’s lower bound; Equation (22) is the nonanticipativity constraint and prevents the controller to take actions on hypothetical noncausal scenarios. The cost function for this optimization problem is defined as

$${\mathrm{\varphi }}^{\mathrm{ms}}=\frac{1}{2}\sum _{i=1}^{N_{\mathrm{en}}}\mathrm{Pr}\left(i\right).\left[\begin{array}{l}{\Vert y_{k+j+1|k}^i-r_{k+j+1|k}^i\Vert }_Q\\ +{\mathrm{\kappa }}_1\Vert {\mathrm{\eta }}_{k+j+1|k}^i\Vert +{\mathrm{\lambda }}_1\Vert \mathrm{\Delta }{u}_{k+j|k}^i\Vert \end{array}\right]$$ (24)

where ${\Vert .\Vert }_W$ denotes the weighted norm of vector, $\mathrm{Pr}\left(i\right)$ denotes the probability of occurrence of scenario $i=1,\dots ,N_{\mathrm{en}}$ ${\mathrm{\lambda }}_1$ and ${\mathrm{\kappa }}_1$ are scalar weights, and $Q$ is a matrix weighting the confidence on model predictions. The term ${\mathrm{\kappa }}_1\Vert {\mathrm{\eta }}_{k+j+1|k}^i\Vert$ is a cost to prevent the controller to take actions leading to low glucose levels. In this design, we use a modified version of the asymmetric, time-varying, exponential reference signal.³⁷ The equation describing the time-varying reference is given by

$$r_{k+j+1|k}=\{\begin{array}{rr}\hfill \left(y_k-y_{\mathrm{sp}}\right).{\mathrm{e}}^{-\left(t_{k+j+1}-t_k\right)/{\mathrm{\tau }}_{\mathrm{r}}^{+}},& \hfill y_k\ge y_{\mathrm{sp}}\\ \hfill 0,& \hfill y_k\le y_{\mathrm{sp}}\end{array}$$ (25)

with $j\in \left[1,\dots ,N_{\mathrm{p}}\right]$, ${\mathrm{\tau }}_{\mathrm{r}}^{+}$ the time constant modulating the reference decay toward the set point, and $t_k$ the discrete time.

Each model prediction uses ${\widehat{x}}_{k|k}$, the estimate of $x_k$, as the initial condition computed by means of a hybrid implementation of the Kalman filter.^38,39 Our implementation includes an observable and nonobservable (open-loop) submodels.

In order to improve the AP’s safety, we propose a detuning strategy for $Q$ described as follows. As seen in the cost function (24), $Q$ weights the difference of the model prediction with respect to the evolution of the controller’s reference. Since our controller is not fully automated and requires meal announcements, a detuning strategy of $Q$ is implemented to avoid a possible overreaction to meal-induced glycemic excursions, which may cause postprandial hypoglycemia. Such a detuning strategy depends on the insulin on board ($\mathrm{IOB}$) estimate relative to its basal value as follows:

$$Q\left(\mathrm{IOB}\right)=\{\begin{array}{cc}{Q}_0& \mathrm{if}\mathrm{IOB}<0\\ m.\mathrm{IOB}+Q_0& \mathrm{if}\mathrm{IOB}\in \left[0,\mathrm{TDI}/\mathrm{\alpha }\right]\\ Q_0/\mathrm{\beta }& \mathrm{if}\mathrm{IOB}>\mathrm{TDI}/\mathrm{\alpha }\end{array}$$ (26)

with $m=\frac{\mathrm{\alpha }.\left(1-\mathrm{\beta }\right).Q_0}{\mathrm{\beta }.\mathrm{TDI}}$, where $\mathrm{TDI}$ denotes the subject-specific total daily insulin requirement, $Q_0$ is the default value of $Q$ at the basal $\mathrm{IOB}$, and $\mathrm{\alpha }$ and $\mathrm{\beta }$ are tuning parameters. The higher $\mathrm{\alpha }$ and $\mathrm{\beta }$, the less responsive the controller is at mealtimes. In this work, $Q_0$, $\mathrm{\alpha }$, and $\mathrm{\beta }$ were set to 10, 20, and 1000, respectively.

By default, the AP operates in anticipative mode and progressively reduces the insulin infusion during times where there is a high probability of exercise. If exercise is detected, the system transitions to reactive mode, meaning that instead of having $N_{\mathrm{en}}$ parallel controllers with corresponding disturbance realizations, the controller relies on a single controller acting under the assumption that exercise is being performed. This allows the controller to adjust to a specific exercise bout and mitigates hypoglycemia in cases where exercise is not expected. In the clinical trial, exercise detection is based on HR and step count signals retrieved in real-time from an activity tracker (Sony SmartBand2, Tokyo). This detection system is not discussed here due to space limitations.

Exercise-Informed Premeal Bolus

An exercise-informed premeal bolus calculator was developed to adjust the patient’s insulin bolus based on the anticipated increase in glucose uptake during the hours following exercise. In section C, we explain the generation of the signal $w_{d,k}$, which is the anticipated change in the glucose uptake over time following a performed exercise lasting $d$-min. From this signal, we obtain ∆${\mathrm{GU}}_{\mathrm{DIA}}$ the additional glucose uptake that is anticipated to occur during the time that the meal bolus will be active (ie, duration of insulin action—DIA). ∆${\mathrm{GU}}_{\mathrm{DIA}}$ is calculated as the corresponding area under the ∆$\mathrm{GIR}$ curve and translated into grams as follows:

$$\mathrm{\Delta }{\mathrm{GU}}_{\mathrm{DIA}}=-\sum _{k=t}^{t+\mathrm{DIA}}\frac{w_{d,k}{V}_g\mathrm{BW}}{1000}$$ (27)

Mealtime insulin is computed based on the carbohydrate intake, $\mathrm{BG}$ value at the time of the meal, $\mathrm{IOB}$, and ∆${\mathrm{GU}}_{\mathrm{DIA}}$ The exercise informed bolus is obtained by correcting the standard bolus to account for the anticipated change in the glucose uptake resulting from the exercise performed prior to the bolus as follows:

$$\begin{array}{c}{\mathrm{EX}}_{\mathrm{B},k}=\frac{{\mathrm{CHO}\mathrm{Intake}}_k}{\mathrm{CR}}+\frac{{\mathrm{BG}}_k-{\mathrm{BG}}_{\mathrm{target}}}{\mathrm{CF}}\\ -{\mathrm{IOB}}_k-\frac{\mathrm{\Delta }{\mathrm{GU}}_{\mathrm{DIA}}}{\mathrm{CR}}\end{array}$$ (28)

where ${\mathrm{CHO}\mathrm{Intake}}_k$ is the amount of ingested carbohydrates at time $k$, ${\mathrm{BG}}_{\mathrm{target}}=y_{\mathrm{sp}}$, $\mathrm{CR}$ and $\mathrm{CF}$ are the subject’s current carbohydrate ratio and correction factors, respectively, $\mathrm{BG}$ is the sensor reading at the time of the meal, and $\mathrm{IOB}$ is the current insulin on board from basal and correction insulin injections. We obtain the $\mathrm{BG}$ correction component of the bolus by dividing ∆ by $\mathrm{CR}$ and subtract it from the total bolus calculated.

Unlike the basal insulin controller actions, no anticipatory action is taken in meal bolus calculations. Bolus adjustments are made only based on the disturbance signal from the previously observed exercise. In the specific clinical trial design that this manuscript features, a mealtime bolus is administered at the end of the first increased glucose uptake phase, and therefore, no significant meal bolus reduction is applied.

Numerical Simulations

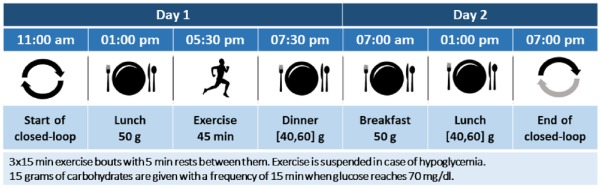
The presented results were obtained using the most up-to-date version of the FDA accepted UVA/Padova simulator.²⁷ All 100 virtual adults were used for this evaluation. Dawn phenomena and intra- and interday insulin sensitivity variations were included in the experimental setup. Simulation protocol was designed to mimic the 36-hour in vivo clinical trial where the feasibility of the proposed control strategy will be tested (see Figure 4).

Figure 4.

Timeline of the in silico protocol.

Closed-loop simulations started at 11.00 am. At each five-minute interval, the proposed control strategy computed a new basal insulin dose and transmitted it to the insulin pump. Following the principles of hybrid closed-loop control, a manual meal bolus was administered at mealtimes using a patient-specific premeal bolus calculator. Here, it is worth mentioning that although each in silico subject has a basal insulin profile that changes throughout the day, a single nominal basal rate was used for each subject. Since the proposed control strategy works as a basal modulator and it will be operating over a basal insulin rate that does not minimize glucose oscillations caused by insulin sensitivity and dawn phenomena, this should increase the amount of basal rate changes that the controller must make.

On day 1, the subjects received a lunch and dinner at 1:00 and 7:30 pm containing 50 and 50±10 g of CHO, respectively. At around 5:30 pm, they underwent a 45-minute long moderate exercise challenge. On day 2, the subjects received two meals while they were under observation at 7:00 am (50 g) and 1:00 pm (50±10 g). The simulation was concluded at 7:00 pm before dinner.

Results

The above protocol was used as a testbed to assess the safety and efficacy of the MS-MPC strategy in preventing hypoglycemic events and regulating glucose levels. The performance and safety of the proposed controller is compared to a baseline controller, the rMPC, published elsewhere.⁴⁰ The tuning parameters for both controllers are presented in Table 3.

Table 3.

Tuning Parameters for the Regular Model Predictive Control and Multistage Model Predictive Control.

Parameter	rMPC	MS-MPC	Parameter	rMPC	MS-MPC
$N_{\mathrm{en}}$	N.A.	5	${\mathrm{\tau }}_{\mathrm{r}}^{+}$	25 min	25 min
$N_{\mathrm{p}}$	24	24	$u_{\min }$	$-u_{\mathrm{b}}$	$-u_{\mathrm{b}}$
$N_{\mathrm{c}}$	18	18	∆$u_{\max }$	50	50
${\mathrm{\lambda }}_1$	$1750/u_{\mathrm{b}}$	$1750/u_{\mathrm{b}}$	$y_{\min }$	70	70
${\mathrm{\kappa }}_1$	100	100

Abbreviations: r-MPC, regular model predictive control; MS-MPC, multistage model predictive control.

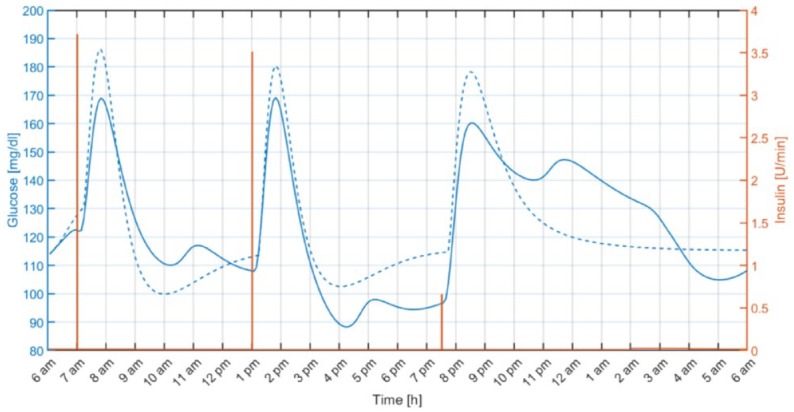
Figure 5 shows an individual closed-loop response under both MS-MPC and rMPC. As illustrated, the anticipatory response of the MS-MPC avoids the hypoglycemic event during exercise by progressively reducing the insulin infusion rate when exercise is likely to happen. Note that although the rMPC reacts to the effect of exercise on the glucose level by almost switching off the insulin pump, that action is still futile,⁴¹ and the subject required a hypo treatment.

Figure 5.

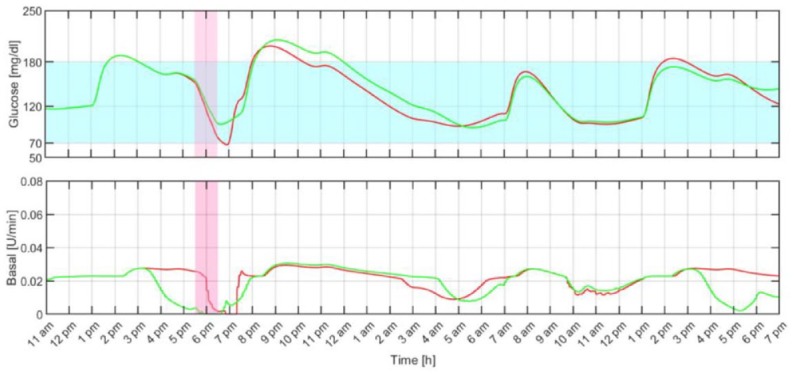
Individual closed-loop response with the proposed multistage model predictive control (green) and regular model predictive control (red). The filled light blue and pink regions represent the 70 to 180 mg/dL range and the exercise period, respectively.

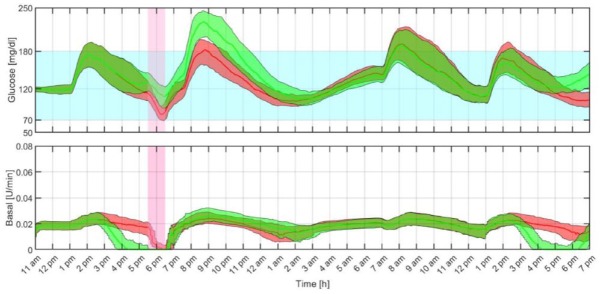
The average closed-loop responses obtained with both the proposed MS-MPC and rMPC are compared in Figure 6 and the average results are summarized in Table 4. Safety and effectiveness endpoints based on consensus outcome metrics for glucose controllers’ performances⁴² are computed for the duration of the in silico protocol. Time within the target range of 70 to 180 mg/dL exceeds 80%, and the primary safety parameter, the low blood glucose index (LBGI), indicates minimal risk of hypoglycemia (LBGI < 1.1).⁴³ As expected, the MS-MPC demonstrates better performance for hypoglycemia protection during and after exercise than the rMPC with less time spent in hypoglycemia. In this regard, 58 subjects received at least one hypo treatment during the exercise period and 10 subjects received two under rMPC, while only eight received the treatment when using the MS-MPC. In addition, exercise was suspended 44 times with the rMPC and four with the MS-MPC. Differences between the number of exercise suspensions and hypo treatments are because, in some cases, rescue carbs were administered at the end of the exercise period. It is worth remarking that although higher average glucose concentration is obtained with the MS-MPC controller, the high blood glucose index (HBGI) still indicates low risk of hyperglycemia (HBGI < 4.5).⁴³ In the future, however, mechanisms to transition the underinsulinization state to a state of normal infusion rate will be explored to avoid postprandial glycemic excursions.

Figure 6.

Closed-loop responses for all the in silico adults with the proposed multistage model predictive control (green) and regular model predictive control (red). The thick lines are the median values, and the boundaries of the filled areas are the 25th and 75th percentiles. The filled light blue and pink regions represent the 70 to 180 mg/dL range and the exercise period, respectively.

Table 4.

Average Closed-loop Results for all the In Silico Adults With the Multistage Model Predictive Control and Regular Model Predictive Control Strategies.

	MS-MPC			rMPC
	Mean	Median	IQR	Mean	Median	IQR
Overall
Average blood glucose (mg/dL)	144.7	142.5	16.6	136.6	135.3	19.0
Max blood glucose (mg/dL)	239.9	235.5	42.3	206.4	205.5	50.1
Min blood glucose (mg/dL)	80.7	82.4	22.0	68.2	65.8	13.6
% time > 250 mg/dL	1.66	0.00	2.34	0.52	0.00	0.00
% time > 180 mg/dL	18.56	16.10	15.71	13.66	11.69	20.26
% time in [70-180] mg/dL	81.16	83.90	16.49	85.56	87.92	20.26
% time in [70-140] mg/dL	54.62	54.55	21.56	60.38	58.70	22.99
% time < 70 mg/dL	0.28	0.00	0.52	0.77	0.78	1.04
% time < 54 mg/dL	0.00	0.00	0.00	0.00	0.00	0.00
LBGI	0.19	0.18	0.20	0.36	0.35	0.21
HBGI	3.90	3.44	2.84	2.94	2.68	2.63
Total daily insulin (U/d)	36.0	34.0	10.8	37.4	35.0	11.6
# hypo treats during exercise		8			68
Exercise
Average blood glucose (mg/dL)	119.7	117.8	27.7	96.3	92.5	18.6
Max blood glucose (mg/dL)	137.0	131.8	29.8	122.3	115.0	27.5
Min blood glucose (mg/dL)	104.5	105.0	29.8	72.9	67.7	21.6
% time > 250 mg/dL	0.00	0.00	0.00	0.00	0.00	0.00
% time > 180 mg/dL	2.6	0.0	0.0	0.5	0.0	0.0
% time in [70-180] mg/dL	96.2	100	0.0	86.7	84.6	23.1
% time in [70-140] mg/dL	80.5	100	30.8	81.5	76.9	30.8
% time < 70 mg/dL	1.2	0.0	0.0	12.8	15.4	23.1
% time < 54 mg/dL	0.0	0.0	0.0	0.8	0.0	0.0

Abbreviations: r-MPC, regular model predictive control; MS-MPC, multistage model predictive control.

# hypo treats during exercise indicates the number of hypo treatments (15 g CHO, fast absorption) given to the entire in silico cohort during the exercise period.

Discussion

Meaningful studies and position papers have shown the importance of manipulating insulin infusion proactively to prevent hypoglycemic events during and after moderate-intensity exercise.^11-13 In this contribution, we have demonstrated promising mechanisms to (i) gather user-specific exercise behavior, (ii) provide this useful insight to a predictive controller able to reduce insulin infusion in a prospective way, and (iii) transition between anticipative and reactive modes according to the certainty on the occurrence of exercise. The main objective of this AP strategy is to reduce the risk of hypoglycemia during and after exercise. In this regard, in silico results suggest that the proposed closed-loop system decreases both the time in hypoglycemia and the number of hypo treatments, without increasing the risk of hyperglycemia beyond safe levels. Hypo treatments were included in these simulations to recreate the future in vivo evaluation of this AP strategy, where the safety of the participant is our main priority. The performance of the MS-MPC in preventing exercise-related hypoglycemia against the rMPC is highlighted when hypo treatments are removed from the simulations (% time < 70 mg/dL during exercise [median (interquartile range, IQR)]: MS-MPC, 0.0 (0.0)%; rMPC, 15.4 (38.5)%).

Despite benefits, as illustrated in Figure 6, higher glucose peaks are detected after the meal that follows when exercise is likely to occur. This is mainly due to the underinsulinization state reached to avoid the hypoglycemia during exercise. We acknowledge that this is a limitation of the proposed system. A possible solution is to allow the controller to respond more aggressively and/or progressively transition to a normal insulin state before meal consumption. In that case, postprandial glucose excursions will be further mitigated, but this comes at the expense of increasing the risk of late hypoglycemia due to the delayed glucose uptake associated with exercise and the sustained duration of action of the current insulin analogs. Insulins with faster-on and -off pharmacodynamics would be beneficial in this scenario where anticipatory reduction of insulin levels is necessary and later increase in the risk of hypoglycemia is expected. Finally, it is worth considering that in these simulations we are assigning to each subject three exercise-related signatures randomly distributed between 4 and 7 pm and equally probable. Therefore, the controller has to perform a pump-suspension for almost the complete time window. If more specific probabilities are assigned to each signature, then the glucose rebound after exercise will be attenuated.

Conclusion

This contribution proposes a novel (hybrid) AP system based on MS-MPC for hypoglycemia prevention during and after moderate-intensity exercise bouts. To test the safety and reliability of our AP system, we created an in silico replica of an upcoming outpatient clinical trial in our FDA-accepted UVA/Padova metabolic simulator including both inter- and intrapatient variability. Results demonstrated that our controller is safe and effective in preventing exercise-related hypoglycemia in the proposed scenario.