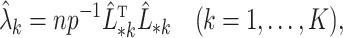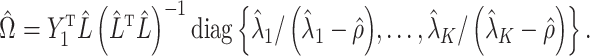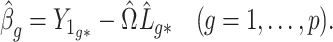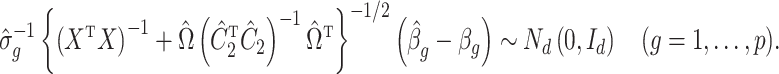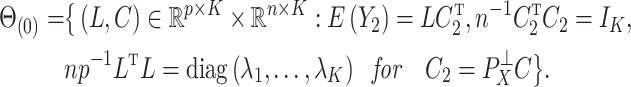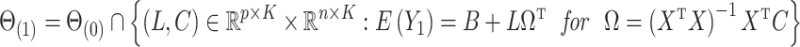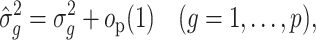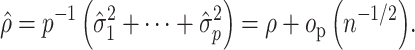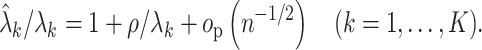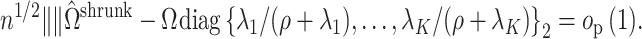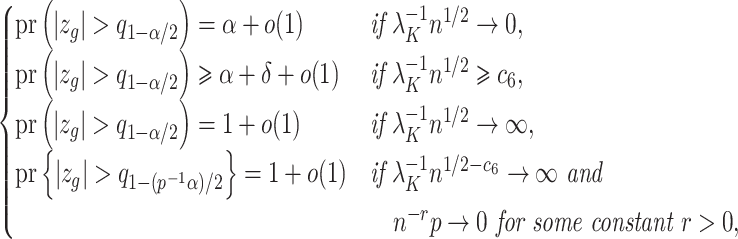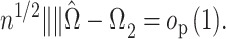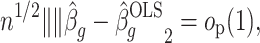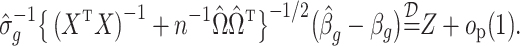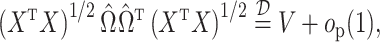Summary
An important phenomenon in high-throughput biological data is the presence of unobserved covariates that can have a significant impact on the measured response. When these covariates are also correlated with the covariate of interest, ignoring or improperly estimating them can lead to inaccurate estimates of and spurious inference on the corresponding coefficients of interest in a multivariate linear model. We first prove that existing methods to account for these unobserved covariates often inflate Type I error for the null hypothesis that a given coefficient of interest is zero. We then provide alternative estimators for the coefficients of interest that correct the inflation, and prove that our estimators are asymptotically equivalent to the ordinary least squares estimators obtained when every covariate is observed. Lastly, we use previously published DNA methylation data to show that our method can more accurately estimate the direct effect of asthma on DNA methylation levels compared to existing methods, the latter of which likely fail to recover and account for latent cell type heterogeneity.
Keywords: Batch effect, Cell type heterogeneity, Confounding, High-dimensional factor analysis, Unobserved covariates, Unwanted variation
1. Introduction
High-throughput genetic, DNA methylation, metabolomic and proteomic data are often influenced by unobserved covariates that are difficult or impossible to record (Johnson et al., 2007; Leek et al., 2010; Houseman et al., 2012). Suppose we observe data  , where the number of genomic units,
, where the number of genomic units,  , is on the order of or larger than the sample size,
, is on the order of or larger than the sample size,  . For example, in most DNA methylation data, the number of studied methylation sites,
. For example, in most DNA methylation data, the number of studied methylation sites,  , is between
, is between 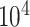 and
and 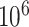 and
and 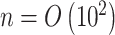 . Assume the true model for
. Assume the true model for 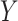 is
is
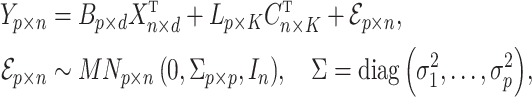 |
(1) |
where 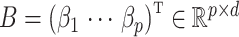 ,
, 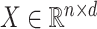 contains the covariates of interest and
contains the covariates of interest and 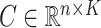 contains the
contains the 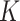 unobserved covariates. Our goal is to estimate and perform inference on the coefficients of interest,
unobserved covariates. Our goal is to estimate and perform inference on the coefficients of interest, 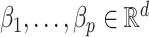 .
.
Under model (1), the naive ordinary least squares estimate of 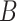 ,
,
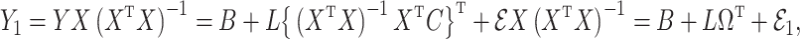 |
is biased by 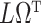 , where
, where 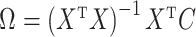 is the ordinary least squares coefficient estimate for the regression of
is the ordinary least squares coefficient estimate for the regression of 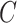 on to
on to  . The bias induced by
. The bias induced by 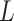 and
and 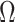 is often consequential in biological data. For example, in DNA methylation studies where disease status is the covariate of interest, DNA methylation
is often consequential in biological data. For example, in DNA methylation studies where disease status is the covariate of interest, DNA methylation 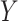 depends on the latent cellular heterogeneity of the
depends on the latent cellular heterogeneity of the 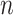 samples (Jaffe & Irizarry, 2014), and cellular heterogeneity often depends on disease status
samples (Jaffe & Irizarry, 2014), and cellular heterogeneity often depends on disease status 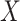 (Fahy, 2002; Stein et al., 2016). Ignoring unobserved covariates
(Fahy, 2002; Stein et al., 2016). Ignoring unobserved covariates 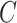 when analysing these types of data can therefore drastically affect the interpretation of results.
when analysing these types of data can therefore drastically affect the interpretation of results.
There have been a number of methods proposed to estimate and correct for the latent factors 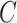 in model (1) (Leek & Storey, 2008; Gagnon-Bartsch & Speed, 2012; Sun et al., 2012; Gagnon-Bartsch et al., 2013; Houseman et al., 2014; Lee et al., 2017). While these methods perform well on selected datasets, they either do not have the requisite theory to justify downstream inference on
in model (1) (Leek & Storey, 2008; Gagnon-Bartsch & Speed, 2012; Sun et al., 2012; Gagnon-Bartsch et al., 2013; Houseman et al., 2014; Lee et al., 2017). While these methods perform well on selected datasets, they either do not have the requisite theory to justify downstream inference on 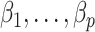 (Leek & Storey, 2008; Sun et al., 2012; Houseman et al., 2014; Lee et al., 2017) or they require the practitioner to have prior knowledge regarding which coefficients
(Leek & Storey, 2008; Sun et al., 2012; Houseman et al., 2014; Lee et al., 2017) or they require the practitioner to have prior knowledge regarding which coefficients 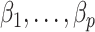 are zero (Gagnon-Bartsch & Speed, 2012; Gagnon-Bartsch et al., 2013).
are zero (Gagnon-Bartsch & Speed, 2012; Gagnon-Bartsch et al., 2013).
Recently, Fan & Han (2017) and Wang et al. (2017) proposed methods that first compute 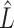 , an estimate of
, an estimate of 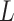 , from
, from 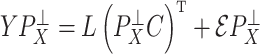 , where
, where 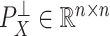 is the orthogonal projection matrix on to the orthogonal complement of
is the orthogonal projection matrix on to the orthogonal complement of 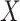 . They then estimate
. They then estimate 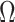 by regressing
by regressing 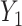 on to
on to 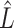 , and finally estimate
, and finally estimate 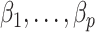 by subtracting the estimated bias
by subtracting the estimated bias 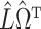 from
from 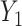 . The advantage of this estimation paradigm is obvious: it decouples the estimation of
. The advantage of this estimation paradigm is obvious: it decouples the estimation of 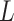 and
and 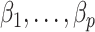 without requiring the practitioner to have prior knowledge regarding which coefficients
without requiring the practitioner to have prior knowledge regarding which coefficients 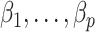 are zero. These articles are quite remarkable because, when their assumptions hold, the authors prove that they can perform inference on
are zero. These articles are quite remarkable because, when their assumptions hold, the authors prove that they can perform inference on 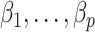 that is as accurate as when
that is as accurate as when  is known. However, it has been observed that these methods tend to inflate test statistics and cause anticonservative inference in both simulated and real data (van Iterson et al., 2017).
is known. However, it has been observed that these methods tend to inflate test statistics and cause anticonservative inference in both simulated and real data (van Iterson et al., 2017).
One source of the discrepancy between theory and practice is that the aforementioned articles assume that all 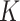 of the nonzero eigenvalues of
of the nonzero eigenvalues of 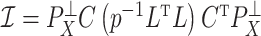 are on the order of the number of samples,
are on the order of the number of samples, 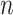 , and are overtly larger than the average residual variance
, and are overtly larger than the average residual variance 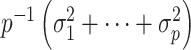 . If these assumptions were valid, there would be an unambiguous gap between the
. If these assumptions were valid, there would be an unambiguous gap between the 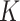 th and
th and 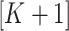 th eigenvalues of
th eigenvalues of 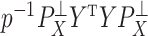 . However, this rarely occurs in practice (Cangelosi & Goriely, 2007; Owen & Wang, 2016; Wang et al., 2017). When these eigenvalue assumptions are violated, we show that previous methods’ techniques to estimate
. However, this rarely occurs in practice (Cangelosi & Goriely, 2007; Owen & Wang, 2016; Wang et al., 2017). When these eigenvalue assumptions are violated, we show that previous methods’ techniques to estimate 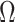 from the regression of
from the regression of 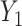 onto
onto 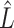 are sensitive to the error in the estimated design matrix
are sensitive to the error in the estimated design matrix 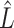 , which causes inaccurate estimates of
, which causes inaccurate estimates of 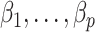 . In practice, some of the nonzero eigenvalues of
. In practice, some of the nonzero eigenvalues of 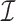 will not be large if the sample size is not sufficiently large, if some of the
will not be large if the sample size is not sufficiently large, if some of the 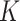 latent covariates do not influence the response of every genomic unit, or if some of the latent covariates are correlated with the covariate of interest
latent covariates do not influence the response of every genomic unit, or if some of the latent covariates are correlated with the covariate of interest 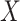 , since this will dampen
, since this will dampen 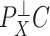 . The latter is common in DNA methylation data because unobserved cellular heterogeneity is often correlated with
. The latter is common in DNA methylation data because unobserved cellular heterogeneity is often correlated with 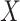 (Jaffe & Irizarry, 2014).
(Jaffe & Irizarry, 2014).
The purpose of this article is to fill the described gap in the literature by studying the unobserved covariate problem when some or all of the 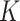 nonzero eigenvalues of
nonzero eigenvalues of 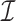 are not exceedingly large. We prove that when the eigenvalues fall below a certain threshold, then for fixed
are not exceedingly large. We prove that when the eigenvalues fall below a certain threshold, then for fixed 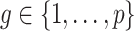 , previous methods have a propensity to inflate Type I error when testing the null hypothesis
, previous methods have a propensity to inflate Type I error when testing the null hypothesis 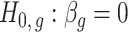 , and even tend to falsely reject
, and even tend to falsely reject 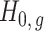 when using the conservative Bonferroni correction. We then provide alternative estimators for
when using the conservative Bonferroni correction. We then provide alternative estimators for 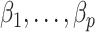 and prove that when
and prove that when 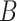 is suitably sparse, our estimators are asymptotically equivalent to the ordinary least squares estimators obtained using the design matrix
is suitably sparse, our estimators are asymptotically equivalent to the ordinary least squares estimators obtained using the design matrix 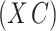 , regardless of the size of the eigenvalues of
, regardless of the size of the eigenvalues of 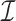 . We lastly use simulated data and real DNA methylation data from Nicodemus-Johnson et al. (2016) to show that latent covariates with ostensibly small effects can be detrimental to inference if not properly accounted for, and that our method can better account for latent covariates than the leading competitors.
. We lastly use simulated data and real DNA methylation data from Nicodemus-Johnson et al. (2016) to show that latent covariates with ostensibly small effects can be detrimental to inference if not properly accounted for, and that our method can better account for latent covariates than the leading competitors.
2. The model, our estimation procedure and intuition
2.1. Notation
For any integer 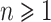 , we define
, we define 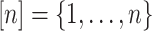 . For any matrix
. For any matrix 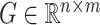 , we define
, we define 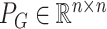 and
and 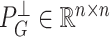 to be the orthogonal projection matrices that project vectors on to the image of
to be the orthogonal projection matrices that project vectors on to the image of 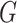 and the orthogonal complement of
and the orthogonal complement of 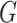 , respectively, and
, respectively, and 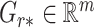 ,
, 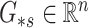 and
and 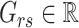 to be the
to be the 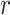 th row,
th row, 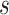 th column and
th column and 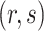 element of
element of 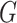 . Lastly, we define
. Lastly, we define 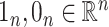 to be the vectors of all ones and all zeros and use the notation
to be the vectors of all ones and all zeros and use the notation 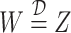 if the random variables, or matrices,
if the random variables, or matrices, 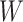 and
and 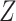 have the same distribution.
have the same distribution.
2.2. A model for the data
Let 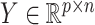 be the observed data, where
be the observed data, where 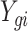 is an observation at genomic unit
is an observation at genomic unit 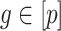 in sample
in sample 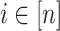 . Let
. Let 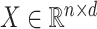 be an observed, full rank matrix containing the covariates of interest and define
be an observed, full rank matrix containing the covariates of interest and define 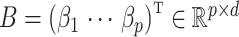 to be their corresponding coefficients across all
to be their corresponding coefficients across all 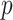 genomic units. We also define an additional covariate matrix
genomic units. We also define an additional covariate matrix 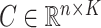 and let
and let 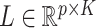 be its corresponding coefficient. We assume that
be its corresponding coefficient. We assume that 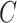 is unobserved, but
is unobserved, but 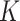 is known. Evidently,
is known. Evidently, 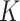 is rarely known in true data applications. While we acknowledge that estimating
is rarely known in true data applications. While we acknowledge that estimating 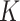 is a challenging problem, there is a large body of work devoted to estimating it (Leek & Storey, 2008; Onatski, 2010; Gagnon-Bartsch & Speed, 2012; Owen & Wang, 2016; McKennan & Nicolae, 2018). We discuss how different values of
is a challenging problem, there is a large body of work devoted to estimating it (Leek & Storey, 2008; Onatski, 2010; Gagnon-Bartsch & Speed, 2012; Owen & Wang, 2016; McKennan & Nicolae, 2018). We discuss how different values of 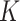 affect our downstream estimates in § 4. We assume (1) is the true model for
affect our downstream estimates in § 4. We assume (1) is the true model for 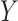 , and we define
, and we define
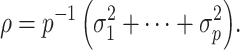 |
(2) |
We also define
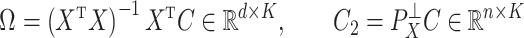 |
(3) |
to be the ordinary least squares coefficient estimates and residuals from the regression of 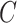 on to
on to 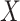 , respectively. We have not assumed an explicit relationship between
, respectively. We have not assumed an explicit relationship between 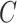 and
and 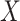 , because one can always decompose
, because one can always decompose 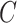 as
as
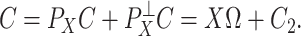 |
A more general model for 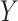 would be
would be 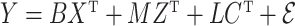 , where
, where 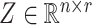 contains observed nuisance covariates, like the intercept or technical covariates, whose coefficients
contains observed nuisance covariates, like the intercept or technical covariates, whose coefficients 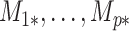 are not of interest. We can get back to model (1) by multiplying
are not of interest. We can get back to model (1) by multiplying 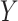 on the right by a matrix whose columns form an orthonormal basis for the null space of
on the right by a matrix whose columns form an orthonormal basis for the null space of 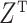 . Therefore, we work exclusively with model (1) and assume any observed nuisance factors have already been rotated out, as they would be in ordinary least squares.
. Therefore, we work exclusively with model (1) and assume any observed nuisance factors have already been rotated out, as they would be in ordinary least squares.
2.3. Estimating 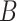 when
when 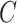 is unobserved
is unobserved
We break 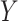 into two independent pieces using a technique proposed in Sun et al. (2012):
into two independent pieces using a technique proposed in Sun et al. (2012):
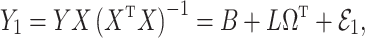 |
(4) |
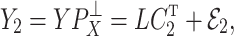 |
(5) |
where 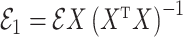 and
and 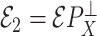 are independent because
are independent because 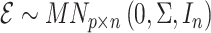 and
and 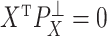 . The matrix
. The matrix 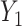 is the ordinary least squares estimate of
is the ordinary least squares estimate of 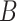 that ignores
that ignores 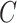 , and the rows of
, and the rows of 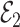 lie on an (
lie on an ( )-dimensional linear subspace of
)-dimensional linear subspace of 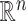 . We now describe how to use
. We now describe how to use 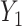 and
and 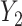 to derive the ordinary least squares estimates of
to derive the ordinary least squares estimates of 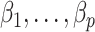 when
when 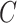 is observed. This will provide a template for estimating
is observed. This will provide a template for estimating 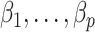 when
when 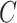 is unobserved.
is unobserved.
Algorithm 1
(Ordinary least squares when
is observed) Let
,
,
and
be given. Our goal is to use ordinary least squares to estimate and perform inference on
, the rows of
.
. Use
to estimate
and
as
where
is the
th row of
.
(b) Set
.
to be
where
(6) and
are the
th rows of
and
, respectively.
It is straightforward to derive the asymptotic properties of the estimators defined in Algorithm 1. In Step (a), 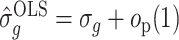 as
as 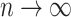 and
and 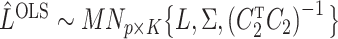 . Since
. Since 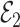 is independent of
is independent of 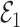 , both of these estimates are independent of
, both of these estimates are independent of 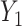 . This implies that the asymptotic distribution of
. This implies that the asymptotic distribution of 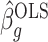 is
is
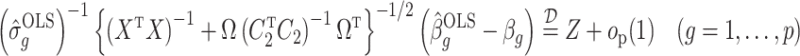 |
as 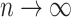 , where
, where 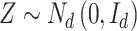 .
.
A property of the ordinary least squares estimate 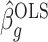 is
is
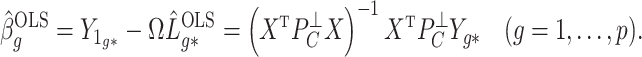 |
That is, 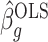 depends only on the column space
depends only on the column space 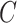 , meaning we may replace
, meaning we may replace 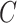 with
with 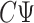 as input in Algorithm 1 for any invertible matrix
as input in Algorithm 1 for any invertible matrix 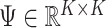 . In particular, we may choose
. In particular, we may choose 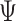 so that
so that 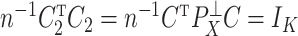 . This parametrization of
. This parametrization of 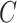 , and therefore
, and therefore 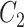 , is convenient because it suggests that a reasonable estimate of
, is convenient because it suggests that a reasonable estimate of 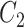 when
when  is unobserved is a scalar multiple of the first
is unobserved is a scalar multiple of the first 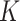 right singular vectors of
right singular vectors of 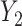 . Using this intuition, we now present our method to estimate and perform inference on
. Using this intuition, we now present our method to estimate and perform inference on 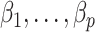 when
when 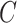 is unobserved. This is described in Algorithm 2, which mimics the three steps of Algorithm 1.
is unobserved. This is described in Algorithm 2, which mimics the three steps of Algorithm 1.
Algorithm 2
(Estimation and inference when
is unobserved). Let
,
,
and
be given. Our goal is to estimate and perform inference on
, the rows of
.
be the singular value decomposition of
where
and
. Define
, where
is the
th column of
. Estimate
and
as
(7)
(8) and
where
(9) is the
th column of
. Estimate
as
(10) as
(11) Just like the estimates
and
,
and
defined in (7) and (8) are independent of
. To perform inference on
, we assume
2.4. Intuition regarding Step (b) of Algorithm 2
The estimates of 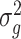 (
(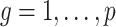 ) and
) and 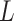 in Step (a) of Algorithm 2 are similar to those used in Sun et al. (2012), Gagnon-Bartsch et al. (2013), Lee et al. (2017) and Wang et al. (2017). However, the estimate of
in Step (a) of Algorithm 2 are similar to those used in Sun et al. (2012), Gagnon-Bartsch et al. (2013), Lee et al. (2017) and Wang et al. (2017). However, the estimate of 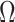 in Step (b) is different from those used in previous methods. Recall from (4) that
in Step (b) is different from those used in previous methods. Recall from (4) that 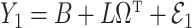 . If
. If 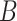 is sufficiently sparse, Sun et al. (2012), Gagnon-Bartsch et al. (2013), Lee et al. (2017) and Wang et al. (2017) propose using variations of the following estimator to recover
is sufficiently sparse, Sun et al. (2012), Gagnon-Bartsch et al. (2013), Lee et al. (2017) and Wang et al. (2017) propose using variations of the following estimator to recover 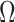 :
:
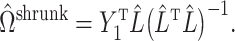 |
(12) |
That is, they ignore the uncertainty in 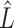 when regressing
when regressing 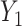 on to
on to 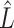 . To see why this is imprudent, let
. To see why this is imprudent, let 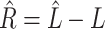 be the residual and suppose for the sake of argument that
be the residual and suppose for the sake of argument that 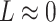 . Then the regression coefficients from the regression
. Then the regression coefficients from the regression 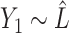 should be very close to 0, since
should be very close to 0, since 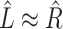 is independent of
is independent of 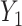 . In other words, existing estimates of
. In other words, existing estimates of 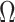 are shrunk towards 0. We quantify the shrinkage exactly in § 3.3 and use that result to derive an inflation term,
are shrunk towards 0. We quantify the shrinkage exactly in § 3.3 and use that result to derive an inflation term, 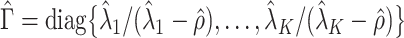 . We then use
. We then use 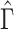 to inflate the shrunken estimate
to inflate the shrunken estimate 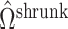 , which allows us to better estimate
, which allows us to better estimate 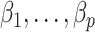 in Step (c) of Algorithm 2.
in Step (c) of Algorithm 2.
The importance of the inflation term 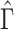 in (10) is related to how informative the data are for
in (10) is related to how informative the data are for 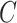 . The estimate
. The estimate 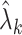 (
(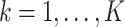 ) defined in (9) is the
) defined in (9) is the 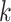 th largest eigenvalue of
th largest eigenvalue of 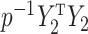 , and can therefore be viewed as an estimate of
, and can therefore be viewed as an estimate of 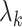 , the
, the 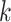 th largest eigenvalue of
th largest eigenvalue of 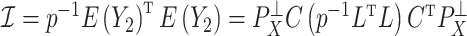 . The eigenvalue
. The eigenvalue 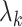 is also the
is also the 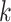 th largest eigenvalue of
th largest eigenvalue of 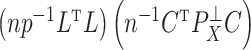 . When
. When 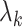 is sufficiently large for all
is sufficiently large for all 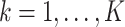 , we say that the data are strongly informative for the latent factors
, we say that the data are strongly informative for the latent factors 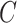 . Under this regime,
. Under this regime, 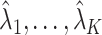 will tend to dominate
will tend to dominate 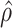 , an estimate of the constant
, an estimate of the constant 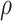 defined in (2), meaning
defined in (2), meaning 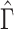 will be negligible. In this case it suffices to use
will be negligible. In this case it suffices to use 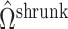 or other previously proposed estimates of
or other previously proposed estimates of 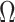 in place of
in place of 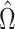 in (11). On the other hand, we say the data are only moderately informative for
in (11). On the other hand, we say the data are only moderately informative for 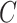 if one or more of
if one or more of 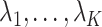 is not large. This can occur if the sample size
is not large. This can occur if the sample size 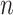 is not large enough, if some of the columns of
is not large enough, if some of the columns of 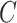 do not affect the expression or methylation of all
do not affect the expression or methylation of all 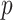 genomic units, or if
genomic units, or if 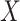 is correlated with the columns of
is correlated with the columns of  , since this will dampen
, since this will dampen 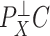 . In these cases,
. In these cases, 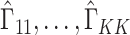 will be moderate to large. In fact, we prove in § 3.3 and show with simulation and a real data example in § 4 that existing methods that ignore the shrinkage in their estimates of
will be moderate to large. In fact, we prove in § 3.3 and show with simulation and a real data example in § 4 that existing methods that ignore the shrinkage in their estimates of 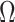 are not amenable to inference. We define the informativeness of the data for
are not amenable to inference. We define the informativeness of the data for 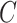 precisely in Definition 1 in § 3.3.
precisely in Definition 1 in § 3.3.
3. Theoretical results
3.1. Assumptions
In all of our assumptions and theoretical results, we assume model (1) holds, 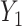 and
and 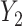 are as defined in (4) and (5), and
are as defined in (4) and (5), and 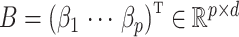 .
.
Assumption 1.
(a) Let
be an observed, nonrandom matrix such that
.
(b) Let
be an unobserved, nonrandom matrix with
nonzero singular values, where
is a known constant.
(c) For some constant
,
for all
.
Under (a) and (b), 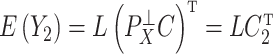 ,
, 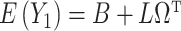 and
and 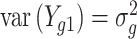 (
(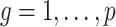 ) are identifiable. The choice to treat
) are identifiable. The choice to treat 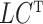 as nonrandom is to illustrate that ignoring this term tends to bias estimates of
as nonrandom is to illustrate that ignoring this term tends to bias estimates of 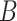 . However, all of our results in § § 3.2–3.4 can be extended to the case when
. However, all of our results in § § 3.2–3.4 can be extended to the case when 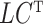 is a random variable using results from the Supplementary Material. Item (c) is a standard assumption in the high-dimensional factor analysis literature (Bai & Li, 2012; Wang et al., 2017). We next place assumptions on
is a random variable using results from the Supplementary Material. Item (c) is a standard assumption in the high-dimensional factor analysis literature (Bai & Li, 2012; Wang et al., 2017). We next place assumptions on 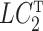 .
.
Assumption 2.
Let
and
be a constant and let:
(a)
for all
;
(b)
has
nonzero eigenvalues
such that
and
for all
, where
;
(c)
be a nondecreasing function of
such that
and
as
.
The quantity 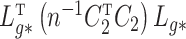 is identifiable because
is identifiable because 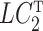 is identifiable, and (a) is equivalent to
is identifiable, and (a) is equivalent to 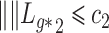 for all
for all 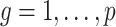 if
if 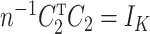 . We comment on this further after we state Proposition 1 below. The assumptions on
. We comment on this further after we state Proposition 1 below. The assumptions on 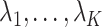 in (b) are weaker than those considered in previous work that provide inferential guarantees, which focused on the case when
in (b) are weaker than those considered in previous work that provide inferential guarantees, which focused on the case when 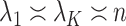 (Bai & Li, 2012; Fan & Han, 2017; Wang et al., 2017). Lee et al. (2017) do allow
(Bai & Li, 2012; Fan & Han, 2017; Wang et al., 2017). Lee et al. (2017) do allow 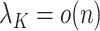 , provided
, provided 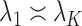 and
and 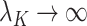 as
as 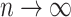 . However, they only prove the consistency of their estimates of
. However, they only prove the consistency of their estimates of 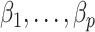 . In fact, we show in § 3.3 that inference with their method, as well as other existing methods, is fallacious if
. In fact, we show in § 3.3 that inference with their method, as well as other existing methods, is fallacious if 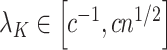 for some
for some 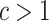 . The assumptions on
. The assumptions on 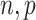 in (c) are the same as those used by Wang et al. (2017), who only consider the case
in (c) are the same as those used by Wang et al. (2017), who only consider the case 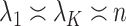 . We next place assumptions on the parameters of
. We next place assumptions on the parameters of 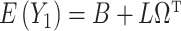 .
.
Assumption 3.
Let
be a constant.
(a) Let
for all
as
.
(b) Let
for all
and
.
(c) Let
be any matrix such that
for some
. Then for
and
,
.
Item (a) is the same sparsity as assumed in Wang et al. (2017). Item (c) is justifiable because we prove that 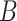 and
and 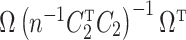 are identifiable under Assumptions 1, 2 and 3(a) in Proposition 1 below, and Proposition S1 in § S2.1 of the Supplementary Material.
are identifiable under Assumptions 1, 2 and 3(a) in Proposition 1 below, and Proposition S1 in § S2.1 of the Supplementary Material.
In DNA methylation data with 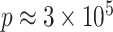 –
–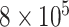 ,
, 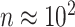 and in the previously unexplored regime
and in the previously unexplored regime 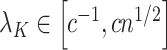 , Assumption 3(a) restricts the number of genomic units with nonzero coefficient of interest to be on the order of hundreds to thousands, which is common in many studies (Liu et al., 2018; Morales et al., 2016; Yang et al., 2017; Zhang et al., 2018). We also show through simulations that we can egregiously violate Assumption 3(a) and still perform accurate inference on
, Assumption 3(a) restricts the number of genomic units with nonzero coefficient of interest to be on the order of hundreds to thousands, which is common in many studies (Liu et al., 2018; Morales et al., 2016; Yang et al., 2017; Zhang et al., 2018). We also show through simulations that we can egregiously violate Assumption 3(a) and still perform accurate inference on 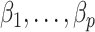 . We now state a proposition regarding the identifiability of
. We now state a proposition regarding the identifiability of 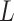 and
and 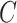 .
.
Proposition 1.
Let
, suppose Assumptions 1 and 2 hold and define the parameter space
(13) Then
is nonempty and if
, then
and
for some
. If Assumptions 1, 2 and 3(a) hold, then there exists a constant
such that
is identifiable and
(14) is nonempty for all
. Further, if
, then
and
for some
for all
.
The condition that 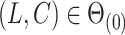 is a classic constraint to identify the components of factor models (Bai & Li, 2012). If
is a classic constraint to identify the components of factor models (Bai & Li, 2012). If 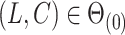 , Assumption 2(a) becomes
, Assumption 2(a) becomes 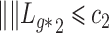 for all
for all 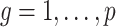 , and if
, and if 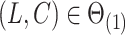 ,
, 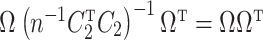 . While we prove it is unnecessary to assume a particular parametrization of
. While we prove it is unnecessary to assume a particular parametrization of 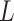 and
and 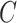 to estimate and perform inference on
to estimate and perform inference on 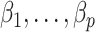 using Algorithm 2, we use the parameter spaces
using Algorithm 2, we use the parameter spaces 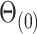 and
and 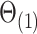 in the statements of theoretical results regarding the accuracy of estimates of
in the statements of theoretical results regarding the accuracy of estimates of 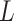 and
and 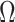 , respectively, in § § 3.2– 3.4.
, respectively, in § § 3.2– 3.4.
3.2. Asymptotic properties of the estimates from Step (a) of Algorithm 2
We start by illustrating the asymptotic properties of 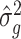 (
(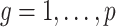 ) and
) and 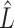 defined in (7) and (8).
defined in (7) and (8).
Lemma 1.
Suppose Assumptions 1 and 2 hold and
. Then, for
defined in (2),
(15)
(16)
Lemma 2.
Suppose Assumptions 1 and 2 hold and
. Then, for
defined in (9),
(17) Let
and
be as defined in
13
and Step (a) of Algorithm 2, respectively. If we also assume that
and the K diagonal elements of
are nonnegative, then, for
,
(18)
Remark 1.
The identifiability constraints, that
and
has nonnegative diagonal elements, are equivalent to the IC3 constraint used in Bai & Li (2012) to identify the components of factor models.
Remark 2.
When
is observed and
, (17) and (18) hold for the ordinary least squares estimator
defined in Step (a) of Algorithm 1.
Lemmas 1 and 2 show that 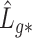 and
and 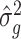 have the same asymptotic properties as
have the same asymptotic properties as 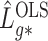 and
and 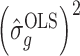 , the ordinary least squares estimates of
, the ordinary least squares estimates of 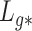 and
and 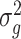 defined in Algorithm 1. However, (17) states that the estimates of
defined in Algorithm 1. However, (17) states that the estimates of 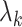 are biased by
are biased by 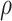 , which we show below is the primary reason why previously proposed methods often return inflated test statistics.
, which we show below is the primary reason why previously proposed methods often return inflated test statistics.
3.1. Previous estimates of 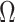 in Step (b) of Algorithm 2 inflate test statistics
in Step (b) of Algorithm 2 inflate test statistics
Existing methods that use the estimation paradigm outlined in Algorithm 2 ignore the uncertainty in 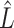 , and use variations of
, and use variations of 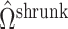 to estimate
to estimate 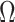 . We show in Proposition 2 and Corollary 1 below that these methods tend to underestimate
. We show in Proposition 2 and Corollary 1 below that these methods tend to underestimate 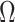 , which can lead to spurious inference on
, which can lead to spurious inference on 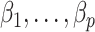 .
.
Proposition 2.
Suppose Assumptions 1, 2 and 3 hold with
,
and
, where
was defined in (14). In addition, suppose the diagonal elements of
are nonnegative and
for some constant
. If we estimate
as
defined in (12), then
(19)
Corollary 1.
Fix some
and let
be a small constant. In addition to the assumptions of Proposition 2, suppose
and the following hold:
(i) We replace
with
in (11) and estimate
as
.
(ii) There exists some constant
such that,
, where
is the
th element of
.
Define
to be the
th z-score and let
be any significance level. Then for
, the
quantile of the standard normal distribution, there exists a constant
such that, as
,
where
is the Bonferroni threshold at a level
.
Remark 3.
Gagnon-Bartsch et al. (2013) used
to estimate
, but Lee et al. (2017) and Wang et al. (2017) used slightly different estimators. We prove analogous versions of Proposition 2 and Corollary 1 for the estimators used by Lee et al. (2017) and Wang et al. (2017) in the Supplementary Material.
Remark 4.
The assumption that
made in Proposition 2 and Corollary 1 requires the eigenvalues be on the same order of magnitude. It is a standard assumption made by previous authors who use versions of Algorithm 2 to estimate
(Lee et al., 2017; Wang et al., 2017). In Remark 6, after the statement of Theorem 2, we discuss how to extend it to allow
to diverge.
When Condition (ii) in the statement of Corollary 1 does not hold, it implies that the bias 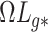 in
in 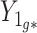 is minor, or the largest components of
is minor, or the largest components of 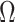 load on to the columns of
load on to the columns of 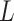 corresponding to the largest eigenvalues
corresponding to the largest eigenvalues 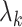 , which are the components least affected by the shrinkage in Proposition 2. The shrinkage in
, which are the components least affected by the shrinkage in Proposition 2. The shrinkage in 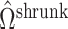 will have less of an impact on inference in these cases. If
will have less of an impact on inference in these cases. If 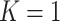 , Condition (ii) can be replaced with
, Condition (ii) can be replaced with 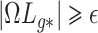 for some constant
for some constant 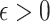 .
.
The results of Proposition 2 and Corollary 1 show that ignoring the uncertainty in 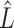 when estimating
when estimating 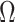 can lead to inflated test statistics and Type I errors if
can lead to inflated test statistics and Type I errors if 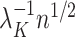 is not small enough, even if one uses the conservative Bonferroni threshold. We therefore define the informativeness of the data for
is not small enough, even if one uses the conservative Bonferroni threshold. We therefore define the informativeness of the data for 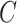 in terms of the magnitude of
in terms of the magnitude of 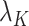 in relation to
in relation to 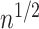 .
.
Definition 1
(Informativeness of the data for
). The data
are strongly informative for
if
as
, and moderately informative for
if there exists a constant
such that
for all
.
Corollary 1 shows that existing methods risk performing anticonservative inference when the data are only moderately informative for 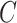 . We next show that our shrinkage-corrected estimate of
. We next show that our shrinkage-corrected estimate of 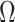 in (10) begets estimates of
in (10) begets estimates of 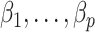 that are asymptotically equivalent to the corresponding ordinary least squares estimates obtained when
that are asymptotically equivalent to the corresponding ordinary least squares estimates obtained when 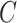 is known, even when the data are only moderately informative for
is known, even when the data are only moderately informative for 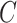 .
.
3.4. Estimates of 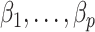 from Algorithms 1 and 2 are asymptotically equivalent
from Algorithms 1 and 2 are asymptotically equivalent
We first prove that our shrinkage-corrected estimate of 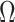 ,
,  , corrects the aforementioned shrinkage present in existing methods’ estimates of
, corrects the aforementioned shrinkage present in existing methods’ estimates of 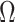 .
.
Lemma 3.
Suppose Assumptions 1, 2 and 3 hold and
. Further, assume the diagonal entries of
are nonnegative and
, where
was defined in the statement of Proposition 2. If
is defined as in (10) and
, then
(20)
We use this result to prove that inference with 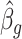 (
(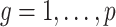 ) is asymptotically equivalent to the ordinary least squares estimator obtained when
) is asymptotically equivalent to the ordinary least squares estimator obtained when 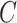 is known.
is known.
Theorem 1.
Let
and suppose Assumptions 1, 2 and 3 hold with
and
. Then inference with
is asymptotically equivalent to inference with
in the following sense:
(21)
(22) The estimates
,
and
are defined in (6), (10) and (11), and
.
In some real experimental data, the largest eigenvalue 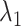 may be substantially larger than the smallest eigenvalue
may be substantially larger than the smallest eigenvalue 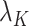 . We therefore extend Theorem 1 to relax the assumption that the
. We therefore extend Theorem 1 to relax the assumption that the 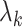 are the same order of magnitude in the following theorem.
are the same order of magnitude in the following theorem.
Theorem 2.
Let
, suppose Assumptions 1, 2 and 3 hold and assume
. Define
to be the
th left singular vector of
(
). If
for some constant
for all
, then (21) and (22) hold.
Remark 5.
Under Assumptions 1 and 2,
is identifiable for all
. If Assumptions 1 and 2 hold and
,
for all
.
Remark 6.
Proposition 2 and Corollary 1 can be extended to accommodate data where
diverges by replacing the condition that
with
for all
.
The condition on 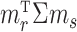 (
(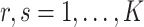 ) is quite general, as it can be shown to hold in probability when
) is quite general, as it can be shown to hold in probability when 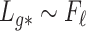 and
and 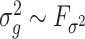 (
(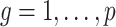 ) for any distributions
) for any distributions 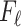 and
and 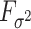 with compact support, such that
with compact support, such that  has eigenvalues bounded away from 0 with high probability. We refer the reader to the Supplementary Material for more detail.
has eigenvalues bounded away from 0 with high probability. We refer the reader to the Supplementary Material for more detail.
3.5. Inference on the relationship between 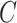 and
and 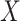
One may be interested in understanding the origin of 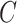 . For example, if components of
. For example, if components of 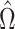 were large, it would be informative to know if this were due to random experimental variation, or if some of the columns of
were large, it would be informative to know if this were due to random experimental variation, or if some of the columns of 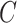 truly depended on
truly depended on 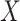 . To incorporate this type of inference, we state the following theorem that allows
. To incorporate this type of inference, we state the following theorem that allows 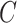 , and therefore
, and therefore 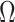 , to be treated as a random variable.
, to be treated as a random variable.
Theorem 3.
Let
be a constant. In addition to Assumptions 11, 11 and 3(b), suppose the following hold:
(i)
and
is a nonrandom matrix such that
, where
is known;
(ii) let
. Then
and
for all
,
for all
and
for all
;
(iii)
is a nondecreasing function of
such that
,
as
and
for all
;
(iv)
, where
is nonrandom and
has independent and identically distributed rows
that are independent of
such that
,
and
for all
and
.
Let
be the standard Wishart distribution in
dimensions with
degrees of freedom. If the null hypothesis
is true and
, then
where
is defined in (10) and
. If
,
.
Remark 7.
Under the definition of
in (iv),
and
.
4. Simulations and data analysis
4.1. Simulation study
In this section we use simulations to compare the performance of our shrinkage-corrected method defined by Algorithm 2 with that of methods proposed in Leek & Storey (2008), Gagnon-Bartsch & Speed (2012), Gagnon-Bartsch et al. (2013), Lee et al. (2017) and Wang et al. (2017), as well as the ordinary least squares estimator when 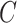 is known and when it is ignored. We do not include results from Fan & Han (2017) or Houseman et al. (2014), because these methods perform similarly to those proposed in Lee et al. (2017) and Wang et al. (2017). In all of our simulations, we set
is known and when it is ignored. We do not include results from Fan & Han (2017) or Houseman et al. (2014), because these methods perform similarly to those proposed in Lee et al. (2017) and Wang et al. (2017). In all of our simulations, we set 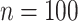 ,
, 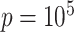 and
and 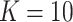 to mimic DNA methylation data where
to mimic DNA methylation data where 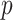 ranges from
ranges from 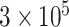 to
to 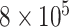 , although our results are nearly identical for
, although our results are nearly identical for 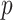 on the order of gene expression data (
on the order of gene expression data (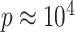 ). We set
). We set 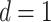 and assigned 50 samples to the treatment group and the rest to the control group so that
and assigned 50 samples to the treatment group and the rest to the control group so that 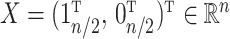 . We then set the eigenvalues
. We then set the eigenvalues 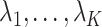 so that
so that 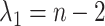 ,
, 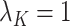 and, for the others,
and, for the others,
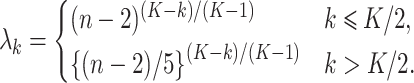 |
For a predefined value of 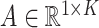 we simulated
we simulated 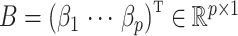 ,
, 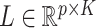 ,
, 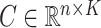 ,
, 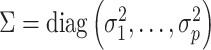 and
and 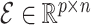 according to
according to
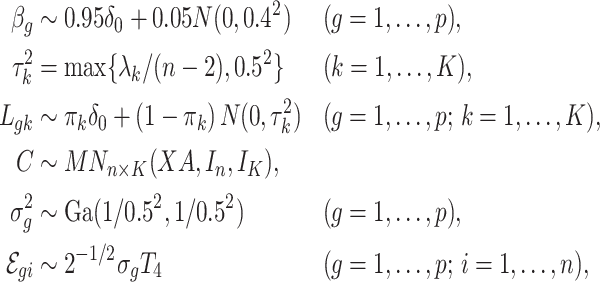 |
(23) |
where 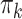 was chosen so that
was chosen so that 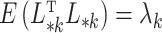 and
and 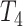 is the
is the 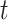 -distribution with four degrees of freedom. We then set the observed data to be
-distribution with four degrees of freedom. We then set the observed data to be 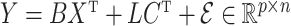 . Although our theory from § 3 assumes the residuals
. Although our theory from § 3 assumes the residuals 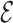 are normally distributed, we simulated
are normally distributed, we simulated 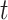 -distributed data to mimic real data with heavy tails. The values used for
-distributed data to mimic real data with heavy tails. The values used for 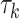 and
and 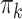 (
(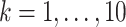 ) are given in Table 1. We show additional simulation results where we simulate
) are given in Table 1. We show additional simulation results where we simulate 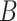 according
according 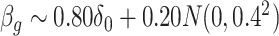 in the Supplementary Material.
in the Supplementary Material.
Table 1.
The 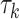 and
and 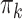 values
values 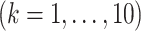 used to simulate
used to simulate 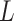
Factor no. (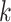 ) ) |
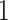
|
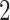
|
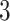
|
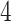
|
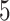
|
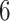
|
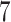
|
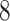
|
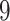
|
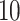
|
|---|---|---|---|---|---|---|---|---|---|---|
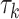
|
1 | 0.78 | 0.60 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 |
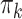
|
0 | 0 | 0 | 0.13 | 0.48 | 0.85 | 0.89 | 0.92 | 0.94 | 0.96 |
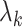
|
98.0 | 58.9 | 35.4 | 21.3 | 12.8 | 3.8 | 2.7 | 1.9 | 1.4 | 1.0 |
We set the parameter 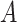 used to simulate
used to simulate 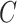 , where
, where 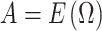 in (23), to be one of two values:
in (23), to be one of two values:
 |
with the scalar 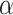 chosen so that
chosen so that 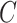 explained 30% of the variability in group status
explained 30% of the variability in group status 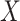 , on average. The choice of 30% was not arbitrary, as we estimated that over 30% of the variance in group status was explained by
, on average. The choice of 30% was not arbitrary, as we estimated that over 30% of the variance in group status was explained by 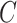 in our data application in § 4.2.
in our data application in § 4.2.
As simulated, the eigenvalues 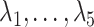 are large enough that the shrinkage terms
are large enough that the shrinkage terms 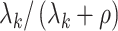 (
(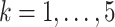 ) from (19) in Proposition 2 are negligible. This implies that when
) from (19) in Proposition 2 are negligible. This implies that when 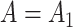 ,
, 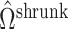 will likely be a suitable estimate of
will likely be a suitable estimate of 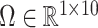 , since
, since 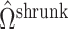 will correctly estimate the largest and most important components of
will correctly estimate the largest and most important components of 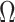 ,
, 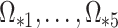 . The anticonservative nature of
. The anticonservative nature of 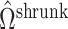 implied by Corollary 1 does not apply when
implied by Corollary 1 does not apply when 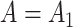 because Condition (ii) Corollary 1 will generally not hold. We would therefore expect our shrinkage-corrected method defined by Algorithm 2 to perform similarly to previous methods that ignore the shrinkage in their estimates of
because Condition (ii) Corollary 1 will generally not hold. We would therefore expect our shrinkage-corrected method defined by Algorithm 2 to perform similarly to previous methods that ignore the shrinkage in their estimates of 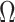 in this simulation scenario. However, when
in this simulation scenario. However, when 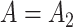 ,
, 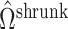 will not recover the largest and most consequential components of
will not recover the largest and most consequential components of 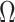 ,
, 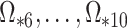 , because of the substantial shrinkage caused by the relatively small eigenvalues
, because of the substantial shrinkage caused by the relatively small eigenvalues 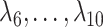 . In this case, Corollary 1 and Remark 6 suggest that ignoring the shrinkage will lead to anticonservative inference on
. In this case, Corollary 1 and Remark 6 suggest that ignoring the shrinkage will lead to anticonservative inference on 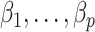 , whereas Theorems 1 and 2 imply that our shrinkage-corrected method will be asymptotically equivalent to ordinary least squares when
, whereas Theorems 1 and 2 imply that our shrinkage-corrected method will be asymptotically equivalent to ordinary least squares when 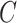 is observed.
is observed.
We simulated 100 datasets with 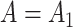 and another 100 with
and another 100 with 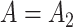 . We found that we could perform the best inference on
. We found that we could perform the best inference on 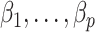 with each method by performing ordinary least squares with the design matrix
with each method by performing ordinary least squares with the design matrix 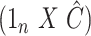 , where
, where 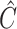 was
was 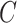 if
if 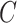 was known, or was estimated with any one of the six methods described above. Our shrinkage-corrected estimate of
was known, or was estimated with any one of the six methods described above. Our shrinkage-corrected estimate of 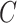 was
was 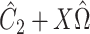 , where
, where 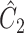 was defined in Step (a) of Algorithm 2. We describe how the other five methods estimate
was defined in Step (a) of Algorithm 2. We describe how the other five methods estimate 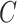 below. We compared the ordinary least squares
below. We compared the ordinary least squares 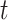 -statistics from all the methods to a
-statistics from all the methods to a 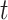 -distribution with
-distribution with 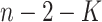 degrees of freedom to compute
degrees of freedom to compute 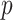 -values for the null hypotheses
-values for the null hypotheses 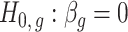 (
(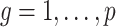 ). We then judged the performance of each method by comparing their true false discovery proportion at a nominal 20% false discovery rate, estimated using
). We then judged the performance of each method by comparing their true false discovery proportion at a nominal 20% false discovery rate, estimated using 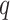 -values (Storey, 2001), because this is the inference method popular among biologists.
-values (Storey, 2001), because this is the inference method popular among biologists.
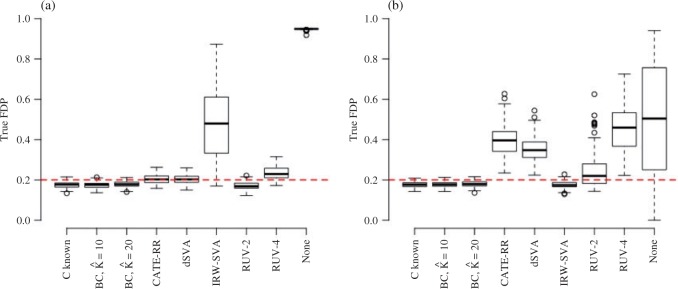
Figure 1 provides the simulation results. We see that our shrinkage-corrected method is able to control the false discovery rate both when 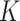 is known to be 10 and when we drastically overestimate it to be 20. Further, our method’s power to detect units with nonzero
is known to be 10 and when we drastically overestimate it to be 20. Further, our method’s power to detect units with nonzero 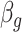 at this nominal 20% false discovery rate threshold was 13.6% when
at this nominal 20% false discovery rate threshold was 13.6% when 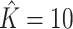 and 12.8% when
and 12.8% when 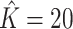 , which is compared to 13.6% when
, which is compared to 13.6% when 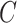 was known. The power of all three methods was the same for both values of
was known. The power of all three methods was the same for both values of 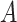 . This is exactly what one would expect from Theorems 1 and 2, which prove that inference with our shrinkage-corrected estimator is asymptotically equivalent to that with ordinary least squares when
. This is exactly what one would expect from Theorems 1 and 2, which prove that inference with our shrinkage-corrected estimator is asymptotically equivalent to that with ordinary least squares when 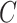 is known. This equivalence was also manifested when we overtly violated Assumption 3(a) and simulated
is known. This equivalence was also manifested when we overtly violated Assumption 3(a) and simulated 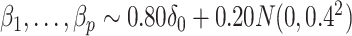 ; see the Supplementary material for more detail.
; see the Supplementary material for more detail.
Fig. 1.
The false discovery proportion, FDP, for each method at a 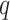 -value threshold of 0.2 in simulations when (a)
-value threshold of 0.2 in simulations when (a) 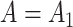 and (b)
and (b) 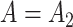 . BC is our shrinkage-corrected method defined in Algorithm 2 and
. BC is our shrinkage-corrected method defined in Algorithm 2 and 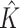 is the number of factors used to estimate
is the number of factors used to estimate 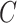 . CATE-RR, dSVA, IRW-SVA, RUV-2 and RUV-4 are the methods proposed in Leek & Storey (2008), Gagnon-Bartsch & Speed (2012), Gagnon-Bartsch et al. (2013), Lee et al. (2017) and Wang et al. (2017), respectively. These five methods were all applied with
. CATE-RR, dSVA, IRW-SVA, RUV-2 and RUV-4 are the methods proposed in Leek & Storey (2008), Gagnon-Bartsch & Speed (2012), Gagnon-Bartsch et al. (2013), Lee et al. (2017) and Wang et al. (2017), respectively. These five methods were all applied with 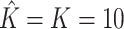 . Inference with None was performed using the design matrix
. Inference with None was performed using the design matrix 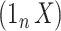 .
.
It is also informative to study the performance of the other five methods, as this can be important to practitioners deciding which method to apply to their data.
The methods of Wang et al. (2017), CATE-RR, and Lee et al. (2017), dSVA, estimate 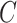 as
as 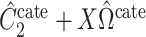 and
and 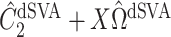 , respectively, where their estimates of
, respectively, where their estimates of 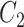 ,
, 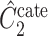 and
and 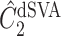 , are nearly identical to
, are nearly identical to 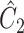 as defined in Step (a) of Algorithm 2. However, their estimates of
as defined in Step (a) of Algorithm 2. However, their estimates of 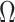 ,
, 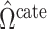 and
and 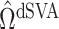 , ignore the shrinkage described in Proposition 2. We would therefore expect them to introduce more Type I errors when
, ignore the shrinkage described in Proposition 2. We would therefore expect them to introduce more Type I errors when 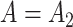 . Both CATE-RR and dSVA’s false discovery proportion estimates were closer to nominal values when
. Both CATE-RR and dSVA’s false discovery proportion estimates were closer to nominal values when 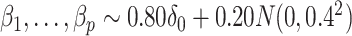 , since any rejection region was likely to have more genomic units with nonzero coefficients of interest.
, since any rejection region was likely to have more genomic units with nonzero coefficients of interest.
The method of Leek & Storey (2008), IRW-SVA, estimates  by performing a factor analysis on
by performing a factor analysis on 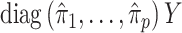 , where
, where 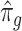 is an estimate of
is an estimate of 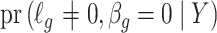 (
(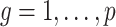 ), by iteratively estimating
), by iteratively estimating 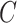 and
and 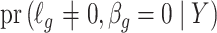 . Since the first iteration assumes
. Since the first iteration assumes 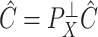 ,
,  tends to be small if the marginal correlation between
tends to be small if the marginal correlation between 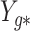 and
and 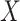 is large, which occurs if
is large, which occurs if 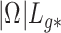 is large. Therefore, the latent factors that influence
is large. Therefore, the latent factors that influence 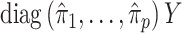 will be different than those of
will be different than those of 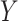 if the latent factors with the largest effects are also correlated with
if the latent factors with the largest effects are also correlated with 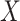 . This explains why IRW-SVA performs poorly when
. This explains why IRW-SVA performs poorly when 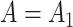 . Unfortunately, there is no theory that states when IRW-SVA is expected to accurately recover
. Unfortunately, there is no theory that states when IRW-SVA is expected to accurately recover 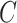 .
.
Both RUV-2 (Gagnon-Bartsch & Speed, 2012) and RUV-4 (Gagnon-Bartsch et al., 2013) assume the practitioner has prior knowledge of a subset 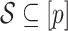 of control genomic units where
of control genomic units where 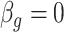 for all
for all 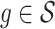 . We selected
. We selected 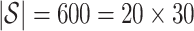 control units uniformly at random from the set of all genomic units with
control units uniformly at random from the set of all genomic units with 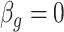 across all simulations, because simulations in Wang et al. (2017) use 30 control units when
across all simulations, because simulations in Wang et al. (2017) use 30 control units when 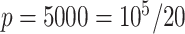 . RUV-2 estimates
. RUV-2 estimates 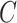 via factor analysis using only data from genomic units in
via factor analysis using only data from genomic units in 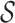 , whereas RUV-4 first estimates
, whereas RUV-4 first estimates 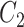 and
and 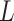 as
as 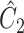 and
and 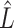 defined in Step (a) of Algorithm 2, and then estimates
defined in Step (a) of Algorithm 2, and then estimates 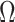 as
as 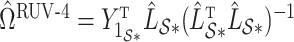 . Here,
. Here, 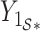 and
and 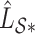 are the submatrices of
are the submatrices of 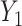 and
and 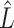 restricted to the rows in
restricted to the rows in 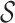 . The RUV-4 estimate of
. The RUV-4 estimate of 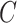 is then
is then 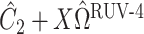 . The obvious caveat for RUV-2 and RUV-4 is that the practitioner must have a list of units whose coefficients of interest are zero and whose expression or methylation carries the latent factor signature, i.e., the first
. The obvious caveat for RUV-2 and RUV-4 is that the practitioner must have a list of units whose coefficients of interest are zero and whose expression or methylation carries the latent factor signature, i.e., the first  eigenvalues of
eigenvalues of 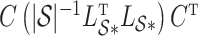 must be suitably large. For example, the large variability in RUV-2’s false discovery proportion when
must be suitably large. For example, the large variability in RUV-2’s false discovery proportion when 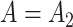 is because the
is because the 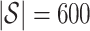 control units were not sufficient to capture the latent factor signature in many simulations.
control units were not sufficient to capture the latent factor signature in many simulations.
4.2. Data application
In order to demonstrate the importance of using our shrinkage-corrected estimator, we applied our method to reanalyse data from Nicodemus-Johnson et al. (2016), which studied the correlation between adult asthma and DNA methylation in lung epithelial cells. The authors collected endobronchial brushings from 74 adult patients with a current doctor’s diagnosis of asthma and 41 healthy adults, and quantified their DNA methylation at 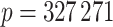 methylation sites, also referred to as CpGs, using the Infinium Human Methylation 450K Bead Chip (Dedeurwaerder et al., 2011). Nicodemus-Johnson et al. (2016) then used ordinary least squares to regress the methylation at each of the
methylation sites, also referred to as CpGs, using the Infinium Human Methylation 450K Bead Chip (Dedeurwaerder et al., 2011). Nicodemus-Johnson et al. (2016) then used ordinary least squares to regress the methylation at each of the 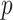 sites on to the mean model subspace that included asthma status, age, ethnicity, sex and smoking status to estimate the effect due to asthma,
sites on to the mean model subspace that included asthma status, age, ethnicity, sex and smoking status to estimate the effect due to asthma, 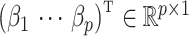 . They found 40 892 CpGs that were differentially methylated between asthmatics and healthy patients at a nominal false discovery rate of 5%.
. They found 40 892 CpGs that were differentially methylated between asthmatics and healthy patients at a nominal false discovery rate of 5%.
We investigated whether or not the strong association between DNA methylation and asthma status was in part due to unobserved covariates. In particular, lung cell composition may differ between asthmatics and nonasthmatics, with asthmatic patients generally having a greater proportion of airway goblet cells that excrete mucus (Rogers, 2002; Bai & Knight, 2005). We therefore reanalysed these data to account for latent covariates with our shrinkage-corrected method defined by Algorithm 2, and compared the results to those obtained using the methods proposed in Leek & Storey (2008), Lee et al. (2017) and Wang et al. (2017). We could not apply the methods proposed in Gagnon-Bartsch & Speed (2012) and Gagnon-Bartsch et al. (2013) because we did not have access to control CpGs. We first used bi-crossvalidation (Owen & Wang, 2016) to estimate that there were 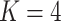 latent factors in these data, and subsequently estimated
latent factors in these data, and subsequently estimated 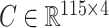 using the four different methods. We then computed
using the four different methods. We then computed 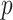 -values for the null hypotheses
-values for the null hypotheses  (
(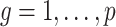 ) using ordinary least squares with the design matrix
) using ordinary least squares with the design matrix 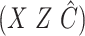 , where
, where 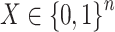 was asthma status and
was asthma status and 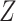 contained the observed nuisance covariates age, ethnicity, sex and smoking status. The total number of asthma-related CpGs returned by each method as a function of
contained the observed nuisance covariates age, ethnicity, sex and smoking status. The total number of asthma-related CpGs returned by each method as a function of 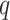 -value cut-offs (Storey et al., 2015), as well as the uncorrected and shrinkage-corrected estimates of
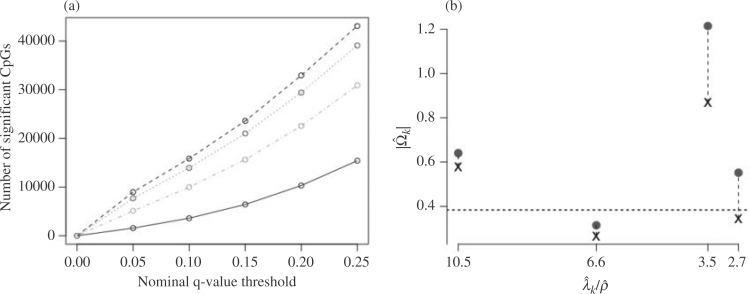
-value cut-offs (Storey et al., 2015), as well as the uncorrected and shrinkage-corrected estimates of 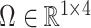 , are given in Fig. 2. At a
, are given in Fig. 2. At a 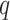 -value threshold of 20%, our method identifies 10 324 asthma-related CpGs, while the methods proposed in Leek & Storey (2008), Lee et al. (2017) and Wang et al. (2017) ostensibly identify 32 952, 29 415 and 22 545 asthma-related CpGs, respectively. These numbers changed only slightly when we let
-value threshold of 20%, our method identifies 10 324 asthma-related CpGs, while the methods proposed in Leek & Storey (2008), Lee et al. (2017) and Wang et al. (2017) ostensibly identify 32 952, 29 415 and 22 545 asthma-related CpGs, respectively. These numbers changed only slightly when we let 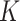 be as high as 7.
be as high as 7.
Fig. 2.
Results from our analysis of lung DNA methylation data from Nicodemus-Johnson et al. (2016). (a) The number of asthma-related CpGs at a given 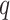 -value cut-off using our shrinkage-corrected estimator (solid line), as well as the estimators proposed in Lee et al. (2017) (dot-dashed line), Wang et al. (2017) (dotted line) and Leek & Storey (2008) (dashed line). (b) The
-value cut-off using our shrinkage-corrected estimator (solid line), as well as the estimators proposed in Lee et al. (2017) (dot-dashed line), Wang et al. (2017) (dotted line) and Leek & Storey (2008) (dashed line). (b) The  components of
components of  (
(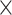 ) and
) and 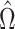 (
( ) as a function of
) as a function of  . The dashed line is the 0.95 quantile of the
. The dashed line is the 0.95 quantile of the 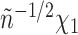 distribution, where
distribution, where 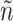 is defined such that
is defined such that 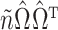 converges to a chi-squared random variable with
converges to a chi-squared random variable with 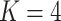 degrees of freedom under the null hypothesis from Theorem 3.
degrees of freedom under the null hypothesis from Theorem 3.
We estimated that approximately 36% of the variance in asthma status was explained by 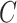 , which, using Theorem 3, corresponds to a
, which, using Theorem 3, corresponds to a 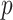 -value for the null hypothesis
-value for the null hypothesis 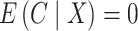 of
of 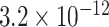 . Moreover, assuming
. Moreover, assuming 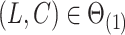 , the largest component of
, the largest component of 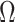 appeared to load on to the third column of
appeared to load on to the third column of 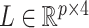 , where
, where 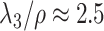 . Since this was much smaller than
. Since this was much smaller than 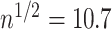 and we estimated
and we estimated 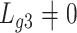 at over 40% of the studied CpGs
at over 40% of the studied CpGs 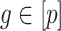 , Proposition 2, Corollary 1 and simulations connote that the methods proposed in Lee et al. (2017) and Wang et al. (2017) are likely underestimating the fraction of CpGs with
, Proposition 2, Corollary 1 and simulations connote that the methods proposed in Lee et al. (2017) and Wang et al. (2017) are likely underestimating the fraction of CpGs with 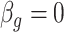 at any nominal
at any nominal 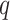 -value threshold. It is likely the case that
-value threshold. It is likely the case that 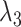 , the third largest eigenvalue of
, the third largest eigenvalue of 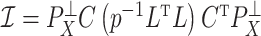 , was small even though the third factor explained a significant portion of the variability in methylation levels because its strong correlation with asthma status dampened
, was small even though the third factor explained a significant portion of the variability in methylation levels because its strong correlation with asthma status dampened 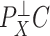 .
.
We next sought to determine if differences in lung cell composition between asthmatic and healthy patients were responsible for some of the correlation between asthma status and the latent factors, since understanding the origin of the latent covariates could help practitioners determine which method is most appropriate for their data. To do so, we fit a topic model with 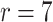 topics on the same individual’s gene expression data, which has been shown to cluster bulk RNA-seq samples by tissue and cell type (Taddy, 2012; Dey et al., 2017). We then used the
topics on the same individual’s gene expression data, which has been shown to cluster bulk RNA-seq samples by tissue and cell type (Taddy, 2012; Dey et al., 2017). We then used the 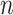 -dimensional factor whose corresponding loading was the largest on the MUC5AC gene as a proxy for the proportion of goblet cells in each sample, as MUC5AC is a unique identifier for goblet cells (Zuhdi Alimam et al., 2000). Just as one would expect, asthmatics tended to have a higher proportion of estimated goblet cells than healthy controls, and we rejected the null hypothesis that asthmatics and healthy controls had the same mean estimated goblet cell proportion at the significance level of
-dimensional factor whose corresponding loading was the largest on the MUC5AC gene as a proxy for the proportion of goblet cells in each sample, as MUC5AC is a unique identifier for goblet cells (Zuhdi Alimam et al., 2000). Just as one would expect, asthmatics tended to have a higher proportion of estimated goblet cells than healthy controls, and we rejected the null hypothesis that asthmatics and healthy controls had the same mean estimated goblet cell proportion at the significance level of 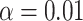 . This indicates that cell composition is presumably driving much of the observed correlation between methylation levels and asthma status in Nicodemus-Johnson et al. (2016), as well as the results from the reanalysis with the methods proposed in Lee et al. (2017) and Wang et al. (2017).
. This indicates that cell composition is presumably driving much of the observed correlation between methylation levels and asthma status in Nicodemus-Johnson et al. (2016), as well as the results from the reanalysis with the methods proposed in Lee et al. (2017) and Wang et al. (2017).
These conclusions also help to explain why the method proposed in Leek & Storey (2008) is likely underestimating the number of false discoveries. We estimated that 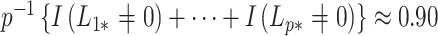 in these data, which is precisely what one would expect if cellular heterogeneity were among the unobserved factors, since changes in methylation help drive cellular differentiation. And since we have already shown that
in these data, which is precisely what one would expect if cellular heterogeneity were among the unobserved factors, since changes in methylation help drive cellular differentiation. And since we have already shown that 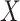 is correlated with
is correlated with 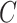 , the method proposed in Leek & Storey (2008) would not be expected to control the false discovery rate, as the simulations in § 4.1 showed exactly this when
, the method proposed in Leek & Storey (2008) would not be expected to control the false discovery rate, as the simulations in § 4.1 showed exactly this when 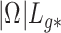 was large for many genomic units
was large for many genomic units 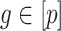 .
.
5. Discussion
The prevalence of unobserved covariates in high-throughput omic data has precipitated the development of methods that account for unobserved factors 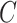 in downstream inference. While these methods perform well when the data are strongly informative for
in downstream inference. While these methods perform well when the data are strongly informative for 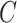 , they are not amenable to inference when the data are only moderately informative for
, they are not amenable to inference when the data are only moderately informative for 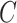 . On the other hand, we prove that inference using estimates from our shrinkage-corrected method in Algorithm 2 is asymptotically equivalent to ordinary least squares when
. On the other hand, we prove that inference using estimates from our shrinkage-corrected method in Algorithm 2 is asymptotically equivalent to ordinary least squares when 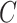 is observed.
is observed.
Our method is not a cure-all for inference with unobserved covariates. For example, Assumption 3(a) restricts the number of units with nonzero main effect in DNA methylation data to be on the order of hundreds to thousands when the data are only moderately informative 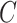 . Even though simulations show we can potentially relax this number substantially to tens or even hundreds of thousands in practice, it begs the question as to whether or not practitioners should spend time and money to measure nuisance variables like cellular heterogeneity, or estimate them directly from the data. If the practitioner is concerned that
. Even though simulations show we can potentially relax this number substantially to tens or even hundreds of thousands in practice, it begs the question as to whether or not practitioners should spend time and money to measure nuisance variables like cellular heterogeneity, or estimate them directly from the data. If the practitioner is concerned that 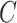 is correlated with
is correlated with 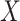 , but has reason to believe
, but has reason to believe 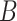 is sparse, our theory suggests the effort should be spent collecting more samples. However, if
is sparse, our theory suggests the effort should be spent collecting more samples. However, if 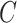 is correlated with
is correlated with 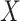 and
and 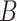 is dense, it may be worthwhile to attempt to measure some of the latent factors with other technologies. We are currently working with the authors of Nicodemus-Johnson et al. (2016) to use external sources of information to potentially better account for cellular heterogeneity in their data.
is dense, it may be worthwhile to attempt to measure some of the latent factors with other technologies. We are currently working with the authors of Nicodemus-Johnson et al. (2016) to use external sources of information to potentially better account for cellular heterogeneity in their data.
Supplementary Material
Acknowledgement
We thank Carole Ober and Michelle Stein for comments that have substantially improved this manuscript. The research was supported in part by the National Institutes of Health.
Supplementary material
Supplementary material available at Biometrika online includes additional simulation results and proofs of all the propositions, lemmas and theorems presented in this paper. An  package implementing our method, together with instructions and code to reproduce the simulations from § 4.1, are available from https://github.com/chrismckennan/BCconf.
package implementing our method, together with instructions and code to reproduce the simulations from § 4.1, are available from https://github.com/chrismckennan/BCconf.
References
- Bai, J. & Li, K. (2012). Statistical analysis of factor models of high dimension. Ann. Statist. 40, 436–65. [Google Scholar]
- Bai, T. R. & Knight, D. A. (2005). Structural changes in the airways in asthma: observations and consequences. Clin. Sci. 108, 463–77. [DOI] [PubMed] [Google Scholar]
- Cangelosi, R. & Goriely, A. (2007). Component retention in principal component analysis with application to cDNA microarray data. Biol. Direct 2, 2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dedeurwaerder, S., Defrance, M., Calonne, E., Denis, H., Sotiriou, C. & Fuks, F. (2011). Evaluation of the Infinium Methylation 450K technology. Epigenomics 3, 771–84. [DOI] [PubMed] [Google Scholar]
- Dey, K. K., Hsiao, C. J. & Stephens, M. (2017). Visualizing the structure of RNA-seq expression data using grade of membership models. PLOS Genetics 13, e1006599. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fahy, J. V. (2002). Goblet cell and mucin gene abnormalities in asthma. Chest 122, 320S–26S. [DOI] [PubMed] [Google Scholar]
- Fan, J. & Han, X. (2017). Estimation of the false discovery proportion with unknown dependence. J. R. Statist. Soc. B 79, 1143–64. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gagnon-Bartsch, J. A., Jacob, L. & Speed, T. P. (2013). Removing unwanted variation from high dimensional data with negative controls. Tech. rep. 820, UC Berkeley. [Google Scholar]
- Gagnon-Bartsch, J. A. & Speed, T. P. (2012). Using control genes to correct for unwanted variation in microarray data. Biostatistics 13, 539–52. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Houseman, E. A., Accomando, W. P., Koestler, D. C., Christensen, B. C., Marsit, C. J., Nelson, H. H., Wiencke, J. K. & Kelsey, K. T. (2012). DNA methylation arrays as surrogate measures of cell mixture distribution. BMC Bioinformatics 13, 86. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Houseman, E. A., Molitor, J. & Marsit, C. J. (2014). Reference-free cell mixture adjustments in analysis of DNA methylation data. Bioinformatics 30, 1431–9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jaffe, A. E. & Irizarry, R. A. (2014). Accounting for cellular heterogeneity is critical in epigenome-wide association studies. Genome Biol. 15, R31. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Johnson, W. E., Li, C. & Rabinovic, A. (2007). Adjusting batch effects in microarray expression data using empirical Bayes methods. Biostatistics 8, 118–27. [DOI] [PubMed] [Google Scholar]
- Lee, S., Sun, W., Wright, F. A. & Zou, F. (2017). An improved and explicit surrogate variable analysis procedure by coefficient adjustment. Biometrika 104, 303–16. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Leek, J. T., Scharpf, R. B., Bravo, H. C., Simcha, D., Langmead, B., Johnson, W. E., Geman, D., Baggerly, K. & Irizarry, R. A. (2010). Tackling the widespread and critical impact of batch effects in high-throughput data. Nature Rev. Genet. 11, 733–9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Leek, J. T. & Storey, J. D. (2008). A general framework for multiple testing dependence. Proc. Nat. Acad. Sci. 105, 18718–23. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu, C., Marioni, R. E., Hedman, Å. K., Pfeiffer, L., Tsai, P. C., Reynolds, L. M., Just, A. C., Duan, Q., Boer, C. G., Tanaka, T., et al. (2018). A DNA methylation biomarker of alcohol consumption. Molec. Psychiatry 23, 422–33. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McKennan, C. & Nicolae, D. (2018). Estimating and accounting for unobserved covariates in high dimensional correlated data. arXiv:1808.05895v1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Morales, E., Vilahur, N., Salas, L. A., Motta, V., Fernandez, M. F., Murcia, M., Llop, S., Tardon, A., Fernandez-Tardon, G., Santa-Marina, L., et al. (2016). Genome-wide DNA methylation study in human placenta identifies novel loci associated with maternal smoking during pregnancy. Int. J. Epidemiol. 45, 1644–55. [DOI] [PubMed] [Google Scholar]
- Nicodemus-Johnson, J., Myers, R. A., Sakabe, N. J., Sobreira, D. R., Hogarth, D. K., Naureckas, E. T., Sperling, A. I., Solway, J., White, S. R., Nobrega, M. A., et al. (2016). DNA methylation in lung cells is associated with asthma endotypes and genetic risk. JCI Insight 1, e90151. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Onatski, A. (2010). Determining the number of factors from empirical distribution of eigenvalues. Rev. Econom. Statist. 92, 1004–16. [Google Scholar]
- Owen, A. B. & Wang, J. (2016). Bi-cross-validation for factor analysis. Statist. Sci. 31, 119–39. [Google Scholar]
- Rogers, D. F. (2002). Airway goblet cell hyperplasia in asthma: Hypersecretory and anti-inflammatory? Clin. Experim. Allergy 32, 1124–7. [DOI] [PubMed] [Google Scholar]
- Stein, M. M., Hrusch, C. L., Gozdz, J., Igartua, C., Pivniouk, V., Murray, S. E., Ledford, J. G., Marques Dos Santos, M., Anderson, R. L., Metwali, N., et al. (2016). Innate immunity and asthma risk in Amish and Hutterite farm children. New Engl. J. Med. 375, 411–21. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Storey, J. D. (2001). A direct approach to false discovery rates. J. R. Statist. Soc. B 63, 479–98. [Google Scholar]
- Storey, J. D., Bass, A. J., Dabney, A. & Robinson, D. (2015). qvalue: Q-value Estimation for False Discovery Rate Control. R package version 2.10.0. http://github.com/jdstorey/qvalue [last accessed 14June2019]. [Google Scholar]
- Sun, Y., Zhang, N. R. & Owen, A. B. (2012). Multiple hypothesis testing adjusted for latent variables, with an application to the AGEMAP gene expression data. Ann. Appl. Statist. 6, 1664–88. [Google Scholar]
- Taddy, M. (2012). On estimation and selection for topic models. Proc. Mach. Learn. Res. 22, 1184–93. [Google Scholar]
- van Iterson, M., van Zwet, E. W. & Heijmans, B. T. (2017). Controlling bias and inflation in epigenome- and transcriptome-wide association studies using the empirical null distribution. Genome Biol. 18, 19. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang, J., Zhao, Q., Hastie, T. & Owen, A. B. (2017). Confounder adjustment in multiple hypothesis testing. Ann. Statist. 45, 1863–94. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang, I. V., Pedersen, B. S., Liu, A. H., O’Connor, G. T., Pillai, D., Kattan, M., Misiak, R. T., Gruchalla, R., Szefler, S. J., Khurana Hershey, G. K., et al. (2017). The nasal methylome and childhood atopic asthma. J. Allergy Clin. Immunol. 139, 1478–88. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang, X., Biagini Myers, J. M., Burleson, J., Ulm, A., Bryan, K. S., Chen, X., Weirauch, M. T., Baker, T. A., Butsch Kovacic, M. S. & Ji, H. (2018). Nasal DNA methylation is associated with childhood asthma. Epigenomics 10, 629–41. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zuhdi Alimam, M., Piazza, F. M., Selby, D. M., Letwin, N., Huang, L. & Rose, M. C. (2000). Muc-5/5ac mucin messenger RNA and protein expression is a marker of goblet cell metaplasia in murine airways. Am. J. Respir. Cell Molec. Biol. 22, 253–60. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.