Estimating the Genome-wide Mutation Rate with Three-Way Identity by Descent

Abstract

The two primary methods for estimating the genome-wide mutation rate have been counting de novo mutations in parent-offspring trios and comparing sequence data between closely related species. With parent-offspring trio analysis it is difficult to control for genotype error, and resolution is limited because each trio provides information from only two meioses. Inter-species comparison is difficult to calibrate due to uncertainty in the number of meioses separating species, and it can be biased by selection and by changing mutation rates over time. An alternative class of approaches for estimating mutation rates that avoids these limitations is based on identity by descent (IBD) segments that arise from common ancestry within the past few thousand years. Existing IBD-based methods are limited to highly inbred samples, or lack robustness to genotype error and error in the estimated demographic history. We present an IBD-based method that uses sharing of IBD segments among sets of three individuals to estimate the mutation rate. Our method is applicable to accurately phased genotype data, such as parent-offspring trio data phased using Mendelian rules of inheritance. Unlike standard parent-offspring analysis, our method utilizes distant relationships and is robust to genotype error. We apply our method to data from 1,307 European-ancestry individuals in the Framingham Heart Study sequenced by the NHLBI TOPMed project. We obtain an estimate of 1.29 × 10⁻⁸ mutations per base pair per meiosis with a 95% confidence interval of [1.02 × 10⁻⁸, 1.56 × 10⁻⁸].

Introduction

Mutation adds new genetic variation to populations. This genetic variation is crucial for evolution, and it affects the amount of information available for many common genetic analyses such as genotype imputation, estimation of relatedness, and estimation of ancestral origins. Accurate estimation of the genome-wide mutation rate is important for inferring key demographic parameters such as the timing of population splits.¹ Genome-wide mutation rate estimates are also helpful for understanding the evolution of mutation rate.² Despite its importance, measuring mutation rates has been difficult. The direct approach to mutation rate estimation involves sequencing nuclear families and counting de novo mutations in the offspring. However, there are only a small number of de novo mutations per offspring (typically 40–120 genome-wide in humans)³ and it is difficult to distinguish true mutations from genotype errors and somatic mutations.⁴ The choice of filters to remove variants with higher rates of genotype error and the assessment of false positive and false negative rates is somewhat arbitrary, which makes it possible for researchers to unintentionally choose filters and methods for assessing error rates that produce an estimate of mutation rate that is close to previously published estimates. Indeed, a recent review found that pedigree-based estimates of mutation rate appear underdispersed, suggesting a lack of independence across studies.⁴

An alternative approach to estimating mutation rates that is less susceptible to genotype error and that uses mutation across large numbers of meiosis is based on the comparison of the human genome with the genomes of closely related species, calibrated by the fossil evidence for the dates of splits between species. The estimates from these inter-species comparisons can be biased by selection, incorrect estimate of average generation length, uncertainty in dating the fossil record, and changes in mutation rates over time. Genome-wide mutation rate estimates from family-based studies are approximately half as high as estimates from inter-species comparisons, suggesting that inter-species estimates are inflated.¹

An alternative approach to mutation rate estimation uses identity by descent (IBD) segments. An IBD segment is a shared portion of a chromosome inherited intact (except for small regions of gene conversion) by two individuals from a common ancestor. The inherited segment will have an identical sequence of alleles in both individuals, except at positions that have mutated since the common ancestor or that were affected by gene conversion. The length of an IBD segment provides information on the number of meioses linking the two haplotypes through their common ancestor, while mismatches in the haplotype sequences provide information regarding the total number of mutations from those meioses. The use of IBD segments to estimate mutation rates has the potential to combine the best features of inter-species and parent-offspring comparisons. Large samples of distantly related individuals can be assayed, leading to assessment of mutations from a large number of meioses. Since IBD looks back thousands rather than millions of years, there is no danger of confounding the mutation rate in modern humans with that in ancestral human groups and closely related species.

Recently, Palamara et al. proposed an IBD-based method for estimating mutation rates from accurately phased whole-genome sequence data, such as that obtained from parent-offspring trios.⁵ Whereas ordinary trio-based analyses use only meioses within trios, Palamara et al.’s approach uses meioses from IBD between pairs of trio offspring, and thus it draws on many more meiosis than methods that count only de novo mutations. Palamara et al.’s method accounts for the effect of genotype error on mutation counts through a regression of the apparent number of mutations in an IBD segment on the estimated time to most common ancestor (TMRCA) of the IBD segment, since the rate of genotype errors is not influenced by the TMRCA, but the number of mutations increases proportionally with the TMRCA. However, genotype error can also affect other key aspects of IBD-based mutation rate estimation in addition to mutation counts, such as the estimation of IBD segment lengths and the estimation of the population’s demographic history. The latter two aspects are critical for estimating the TMRCAs of the IBD segments. Palamara et al.’s study considered the effect of genotype error on mutation counts, but not its effect on mis-estimation of IBD segment lengths or incorrectly inferred demographic history. In this study, we find that Palamara et al.’s method can give biased estimates of mutation rate, with the amount of bias depending on the level of genotype error and whether the true or inferred demographic history is used.

Another IBD-based approach uses heterozygous genotypes within segments of autozygosity in individuals from populations with high parental relatedness.^{6, 7} Advantages of this method over a general IBD-based method is that it is easier to accurately infer long segments of autozgyosity than short segments of IBD, and no estimation of demographic history is needed because one needs only to estimate the degree of parental relatedness of each individual. A limitation is that it is applicable only to populations for which consanguineous marriages are common. Another approach that utilizes autozygosity rather than between-individual IBD is based on comparing local heterozygosity with estimated TMRCAs along the genome for the two haplotypes in an outbred individual.⁸ This latter method incorporates mutations resulting from meioses far back in human history, much further back than IBD-based approaches, and thus requires a very high-resolution recombination map for accurate estimation. Another disadvantage of this method is that it is computationally demanding, and thus it can be applied only to a very small number of individuals, which leads to low precision.

We present a likelihood-based method for estimating genome-wide average mutation rates from sets of three individuals who share a single haplotype identical by descent. We count rare variants shared by two of the three individuals. This avoids the use of singleton variants which have higher genotype error rates,^{9, 10} and it requires that two genotype errors are needed to create any false apparent mutation. The third individual who is IBD with the first two and does not carry the rare alleles provides information on the age of the mutations through the length of IBD sharing between this individual and the other two. We incorporate the distribution of the length of IBD segments, the probability of time to coalescence, the mutation rate, and genotype error into a likelihood function which we maximize to estimate the mutation rate. Our method is applicable to accurately phased sequence data, such as that obtained from parent-offspring data.

Material and Methods

Coalescence Probabilities for Three Haplotypes

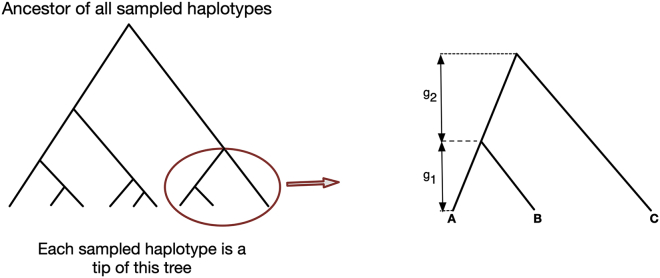
Our calculations are based on the Wright-Fisher model, which has discrete generations.¹¹ In a coalescent tree for three haplotypes (Figure 1), there are two coalescence events: the first coalescence, between haplotypes A and B, occurred g₁ generations before present, and the second coalescence, between C and the common ancestor of A and B, occurred g₁ + g₂ generations ago. We write N[g] for the diploid effective size g generations in the past. The probability that two present-day haplotypes coalesce at generation g, given that they haven’t coalesced more recently, is the probability that they both are assigned the same ancestor out of the 2N[g] ancestral haplotypes existing in generation g. This probability is 1/(2N[g]). Thus the probability that the two haplotype don’t coalesce is 1 − 1/(2N[g]). Similarly, the probability that no pair of haplotypes among three present-day haplotypes coalesce at generation g, given that none of these haplotypes have coalesced more recently, is the product of the probability that the second haplotype is assigned an ancestor that is different from the first haplotype’s ancestor, and the probability that the third haplotype is assigned an ancestor that is different from the other two ancestors, which is (1 − 1/(2N[g]))(1 − 2/(2N[g])). Thus, the probability of no coalescences in generations 1 to g₁ − 1 is

$$\prod _{g=1}^{g_1-1}\left(1-\frac{1}{2N\left[g\right]}\right)\left(1-\frac{2}{2N\left[g\right]}\right).$$

Figure 1.

An Example of the Coalescent Tree that Links Three Haplotypes

In this example, A, B, and C are the IBD haplotypes that form a set of three-way IBD. Haplotypes A and B coalesce g₁ generations before the present, while C and the common ancestor of A and B coalesce g₁ + g₂ generations before the present. The true tree is unknown, and this figure demonstrates one possible tree linking the three haplotypes.

Using similar reasoning, the probability of a coalescence between a given pair of haplotypes (A and B) but no coalescence with the third haplotype (C) at generation g₁, given no coalescences more recently, is (1 − 1/(2N[g₁]))(1/(2N[g₁])). The probability of no coalescence between C and the common ancestor of A and B between generations (g₁ + 1) and (g₁ + g₂ − 1) is ${\prod }_{g=g_1+1}^{g_1+g_2-1}\left(1-1/\left(2N\left[g\right]\right)\right)$. The probability of coalescence between C and the common ancestor of A and B at generation g₁ + g₂, given that this coalescence has not occurred more recently, is 1/(2N[g₁ + g₂]). Thus, the overall probability of this coalescent tree (which we refer to as “tree3” since it is a tree for three haplotypes) is

$$P\left(\mathrm{tree}3\right)=\left\{\prod _{g=1}^{g_1-1}\left(1-\frac{1}{2N\left[g\right]}\right)\left(1-\frac{2}{2N\left[g\right]}\right)\right\}\frac{1}{2N\left[g_1\right]}\left(1-\frac{1}{2N\left[g_1\right]}\right)\left\{\prod _{g=g_1+1}^{g_1+g_2-1}\left(1-\frac{1}{2N\left[g\right]}\right)\right\}\frac{1}{2N\left[g_1+g_2\right]}.$$

Probability Distribution of IBD Lengths Given the Coalescent Tree

A genetic map is used to convert physical base pair positions to genetic positions in Morgans (one Morgan equals one hundred centiMorgans). By definition, the recombination rate is 1 per Morgan per meiosis at any point in the genome. We also assume that recombinations occur as a Poisson process.¹²

Let g be the number of generations to the most recent common ancestor of two haplotypes at a given randomly chosen genomic position. If we look on one side of the given position, the length of the IBD segment on that side is exponentially distributed with rate 2g per Morgan since any recombination occurring in either of the lineages would end the IBD segment. Therefore, if we look both upstream and downstream of the chosen site, the distribution of the length of an IBD segment is the sum of two independent exponential distributions each with rate 2g per Morgan; that is, the length has a gamma distribution with shape 2 and rate 2g per Morgan. We next extend this result to three-way IBD sharing.

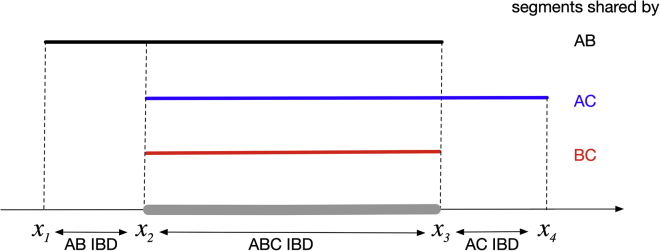
When three haplotypes are jointly identical by descent at a given point in the genome, the lengths of IBD sharing around that position can vary. We consider not only the three-way region over which all three haplotypes are identical by descent, but also the larger region over which any two of the three haplotypes are identical by descent, because the pairwise IBD segment lengths provide information about the coalescent tree (the ordering of the coalescence events and the coalescence times) in the three-way IBD region. For example, looking to the left of the given position, haplotype C may cease to be IBD with haplotypes A and B at some position, and then at some more distant position A and B also cease to be IBD (Figure 2). In Figure 2, x₁, x₂, x₃, x₄, are the positions of changes in IBD status measured in Morgans. In this example, the IBD segment shared by haplotypes A and B starts at x₁ and ends at x₃; the IBD segment shared by A and C starts at x₂ and ends at x₄; and x₂ to x₃ is the region shared jointly by A, B, and C. Then if the coalescent tree corresponding to the segment of three-way IBD sharing is that shown in Figure 1, the length of the IBD segment shared jointly by A, B, and C has a gamma distribution with shape 2 and rate 3g₁ + 2g₂ per Morgan, because the total number of meioses in the coalescent tree is 3g₁ + 2g₂, and a recombination on any one of those meioses will end the joint IBD segment. When the first recombination occurs to end the three-way IBD at the right end (at position x₃), the probability that B is lost rather than A or C is g₁/(3g₁ + 2g₂), and in this case the length of the pairwise IBD segment shared by A and C to the right of x₃ is exponentially distributed with rate 2g₁ + 2g₂ per Morgan. Similarly, when the first recombination occurs to end the three-way IBD at the left end (at position x₂), the probability that C is lost rather than A or B is (g₁ + 2g₂)/(3g₁ + 2g₂), and in this case the length of the IBD segment shared by A and B to the left of x₂ is exponentially distributed with rate 2g₁ per Morgan. In this way, we can calculate the probability of the IBD lengths (which we refer to as “IBD3” since they summarize the three-way IBD sharing for three haplotypes) for any possible coalescent tree. Table S1 gives the probabilities P(IBD3|tree3) for each possible configuration of IBD segments.

Figure 2.

An Example of Three-Way IBD

This figure illustrates one possible IBD sharing configuration among three haplotypes denoted A, B, and C. The IBD segment shared by A and B starts at x₁, ends at x₃, and is colored black. The IBD segment shared by A and C starts at x₂, ends at x₄, and is colored blue. The IBD segment shared by B and C starts at x₂, ends at x₃, and is colored red. The gray region from x₂ to x₃ is the IBD region shared jointly by A, B, and C.

Probability Distribution of Mutation Counts Given the Coalescent Tree

Given a mutation rate $\mu$ per base pair per meiosis, and assuming the infinite sites model,¹³ the number of mutations accumulated within a genome region of length l base pairs over g meioses has a Poisson distribution with mean $lg\mu$. If the coalescent tree is that shown in Figure 1, in which haplotypes A and B coalesce first, before coalescing with C, with g₂ being the number of meioses from the common ancestor of A and B to the common ancestor of all three haplotypes, then the number of mutations shared by haplotypes A and B but not C across a region of l base pairs within the three-way IBD sharing region is distributed as Poisson($l{g}_2\mu$). Some apparent mutations in this region may actually be the result of genotype error. We assume that the rate $\mathit{ϵ}$ of errors of this type (i.e., a miscalled allele in a specific two of three haplotypes) is constant and does not depend on the coalescence times. Thus, across a region of l base pairs, the number of errors of this type is Poisson with rate $l\mathit{ϵ}$. In consequence, the number of apparent mutations shared by A and B but not C (real mutations and errors) across the region is Poisson with rate $l\left(g_2\mu +\mathit{ϵ}\right)$. In contrast, considering two of three haplotypes that are not the first coalescing pair, such as haplotypes A and C for this coalescent tree, any apparent mutations shared by these two haplotypes but not the third will be genotype errors rather than real mutations because they are inconsistent with the coalescent tree (the probability of recurrent mutation is negligible and is ignored under the infinite sites model). Thus, the number of such apparent mutations between any two haplotypes that do not coalesce first is modeled as Poisson with rate $l\mathit{ϵ}$.

For a given labeling of the three IBD haplotypes, let “mut3” denote the vector (n_AB, n_AC, n_BC) containing the number of apparent mutations shared by haplotypes A and B but not C (n_AB), by haplotypes A and C but not B (n_AC), and by haplotypes B and C but not A (n_BC) across the region in which all three haplotypes are IBD. An apparent mutation is an allele that is shared by two of the three haplotypes and has frequency less than the maximum allele frequency threshold. The maximum allele frequency threshold is chosen to be large enough so that all true mutations will be included in the counts and is never set to a value above 0.5. Thus, if two of the three haplotypes share the major allele, this will not contribute to the apparent mutation count.

Let $P_{\mu ,\mathit{ϵ}}\left(\mathrm{mut}3|\mathrm{tree}3,\mathrm{IBD}3\right)$ denote the probability of the vector of apparent mutations given the coalescent tree and the IBD endpoints if the mutation rate is $\mu$ and the error rate is $\mathit{ϵ}$. Note that after conditioning on $\mathrm{tree}3$, the distribution of the number of mutations depends on the IBD endpoints only through the base pair length $l$of the three-way IBD region on which the apparent mutations are counted. If tree3 is the coalescent tree shown in Figure 1, then

$$P_{\mu ,\mathit{ϵ}}\left(\mathrm{mut}3|\mathrm{tree}3,\mathrm{IBD}3\right)=\frac{\exp \left(-l\left(g_2\mu +\mathit{ϵ}\right)\right){\left[l\left(g_2\mu +\mathit{ϵ}\right)\right]}^{n_{AB}}}{n_{AB}!}\frac{\exp \left(-l\mathit{ϵ}\right){\left[l\mathit{ϵ}\right]}^{n_{AC}}}{n_{AC}!}\frac{\exp \left(-l\mathit{ϵ}\right){\left[l\mathit{ϵ}\right]}^{n_{BC}}}{n_{BC}!}.$$

Gene conversion can also introduce variants that are carried by two of the three haplotypes. While we do not incorporate gene conversion directly into our likelihood, we account for its effects with a post-processing regression step that is described in the section on correction for gene conversion.

The Mutation-Rate Likelihood

The sections above present the components needed to obtain the overall mutation-rate likelihood. Here we combine these components to give the overall likelihood for one set of three-way IBD for three haplotypes around a given position in the genome. The data provide multiple such sets of three-way IBD, and we multiply the likelihoods for each such set. Such sets of three IBD haplotypes are not fully independent, because IBD often occurs in clusters of more than three haplotypes, and we analyze each subset of three haplotypes from such a cluster. Thus, the overall likelihood obtained by multiplication is a composite likelihood.

For each set of three IBD haplotypes that we observe in the data, with IBD lengths recorded in IBD3 and apparent mutation counts recorded in mut3, the likelihood of the mutation rate and error rate given the data can be obtained using the law of total probability as

$$L\left(\mu ,\mathit{ϵ}\right)=P_{\mu ,\mathit{ϵ}}\left(\mathrm{IBD}3,\mathrm{mut}3\right)=\sum _{\mathrm{tree}3}{P}_{\mu ,\mathit{ϵ}}\left(\mathrm{IBD}3,\mathrm{mut}3,\mathrm{tree}3\right)=\sum _{\mathrm{tree}3}{P}_{\mu ,\mathit{ϵ}}\left(\mathrm{mut}3|\mathrm{tree}3,\mathrm{IBD}3)P(\mathrm{IBD}3|\mathrm{tree}3\right)P\left(\mathrm{tree}3\right)$$

The sum over possible coalescent trees, tree3, includes an infinite number of possible trees, but only those with low to moderate coalescent times are consistent with the long IBD segments that we use. In practice we restrict the sum to positive integer coalescent times g₁ ≤ 300 and g₂ ≤ 300, as these limits proved to be sufficient in our simulation studies and data analyses, and we sum over the three possible orderings of the coalescent events.

With a large number of such sets of three IBD haplotypes, we can estimate the mutation rate with precision. We numerically maximize the composite likelihood by performing a grid search (Figure S1). To reduce the computing time required for performing a grid search, we use adaptive grids. We first obtain estimates for the mutation rate and the error rate from a coarse search grid. We then refine the estimates by applying a finer search grid to a targeted area based on the confidence interval of the initial estimates.

We use bootstrap resampling to assess the precision of the estimated mutation rate. We resample chromosomes with replacement and obtain a maximum likelihood estimate from the sampled chromosomes in each bootstrap sample. The 95% confidence interval is determined from the 2.5th and 97.5th percentiles of 10,000 bootstrap estimates.

IBD Detection and Mutation Ascertainment

We used Refined IBD¹⁴ in BEAGLE v.4.1 to detect pairwise IBD segments from phased genotypes using only diallelic SNPs with minor allele frequency 10% or higher, with a minimum LOD score threshold of 3 and a minimum length threshold of 1 cM. The minor allele frequency threshold reduces computation time compared to using more variants and ensures that recent mutations that could contribute to the mutation rate estimation are not used in the IBD detection. We used a minimum length threshold of 1 cM because most IBD segments with a LOD score of 3 or higher have length greater than 1 cM, and because using a smaller threshold would increase computation time. Refined IBD uses a haplotype-based method to detect IBD segments. Consequently, genotype errors and haplotype phase errors can result in gaps in the estimated IBD segments and underestimation of the length of IBD segments. We filled gaps between two detected IBD segments for the same pair of haplotypes when the gap between the IBD segments had a length less than 0.5 cM and the gap contained at most two positions at which the genotypes for the two individuals were inconsistent with IBD (Figure S2). This gap-filling step has been shown to make IBD length estimation robust to genotype errors.¹⁵ Our data are phased using parent-offspring trio relationships; hence phasing is highly accurate. After the gap-filling step, we impose a 3 cM minimum length threshold on the pairwise IBD segments. We then find overlapping IBD segments shared by sets of three individuals. In the three-way IBD regions (e.g., region ABC from x₂ to x₃ in Figure 2), we should have detected IBD between all three pairs of the three individuals (e.g., AB, AC, and BC in Figure 2). If one of the three IBD segments was not detected (for example if we found AB and AC but not BC), we do not include the three-way IBD segment in the analysis. Because the detected IBD is based on haplotype identity-by-state, the endpoints are necessarily consistent between the three pairwise IBD segments (e.g., AC and BC have the same reported left endpoint x₂ in Figure 2).

When counting possible mutations, we trim 0.5 cM from each end of the region in which we detect three-way IBD sharing. The reason for this trimming is that the observed identity by state often extends somewhat beyond the true IBD region.^{5, 14} The number of apparent mutations is the number of rare variants shared by two of the three individuals in this trimmed region. We then adjust the base pair length, $l$, of shared region in the calculation of $P_{\mu ,\mathit{ϵ}}\left(\mathrm{mut}3|\mathrm{tree}3,\mathrm{IBD}3\right)$ accordingly.

For analyses with IBDMUT,⁵ we inferred IBD segments using GERMLINE.¹⁶ We ran GERMLINE with the “-haploid” flag allowing the maximum number of mismatching markers (“-err_hom” flag) to be 1 or 2 (2 for the Framingham Heart Study analysis, to match the Genomes of the Netherlands analysis in Palamara et al.⁵).

Effective Population Size Estimation

We used IBDNe¹⁷ to infer the effective population size. The input to the IBDNe program was the set of pairwise gap-filled IBD segments with a minimum length of 2 cM. For effective population size estimation on the Framingham Heart Study data, we used the whole dataset of 4,166 individuals. We identified 13,211 pairs of closely related individuals as those with total length of detected IBD segments exceeding 5% of the genome length, and we removed IBD segments corresponding to such pairs from the IBDNe analysis. The estimated recent effective population size for the Framingham Heart Study data is shown in Figure S3.

Correction for Gene Conversion

Gene conversion copies variants from one haplotype onto another. Gene conversion can create the appearance of mutation events in the three-way IBD, because a gene conversion event occurring between the common ancestor of the two most-recently coalescing haplotypes and their common ancestor with the third haplotype may introduce a variant that is shared by the two most-recently coalescing haplotypes but not by the third haplotype. The rate of gene-conversion variants in a set of three IBD haplotypes is proportional to the number of generations, g₂, between the more recent coalescence time and the less recent coalescence time (Figure 1), as is the number of mutation variants. A major difference between gene-conversion variants and mutation variants is that mutation variants tend to be rare, while gene-conversion variants tend to be common. The probability that an allele is changed via gene conversion is proportional to the heterozygosity of the variant in the population, at the time of the gene conversion, because the recipient allele is only changed if the donor allele (the ancestral individual’s other allele) is different from it. Common variants have higher heterozygosity and hence are more likely to be changed via gene conversion.

We thus use only the less-common variants when counting mutations, applying a maximum allele frequency filter. However, gene conversion affects low-frequency variants to some extent (albeit less than the effect on high-frequency variants), and one cannot set the allele frequency threshold too low or one risks removing some actual mutations. Hence, we apply a modified version of the regression adjustment developed by Palamara et al.⁵

Consider an allele frequency threshold, f. Only alleles with frequency below this threshold will be included in the apparent mutation counts. If f is sufficiently large, then all mutations occurring on the branch from the most recent common ancestor of all three IBD haplotypes to the most recent common ancestor of the two most recently related IBD haplotypes will have frequency less than f and will be included in the mutation count. If the length of this branch is g₂ generations, then the expected number of such mutations contributing to the overall mutation count across a region of length $l$ basepairs is $l{g}_2\mu$, as previously described. During the g₂ meioses occurring on this branch, the expected number of basepairs involved in a gene conversion event is $l{g}_2\theta$, where $\theta$ is the rate of gene conversion initiation (per bp per generation) multiplied by the mean gene conversion tract length (in bp). Let h_f denote the rate of heterozygosity (per bp), excluding variants with minor allele frequency greater than f. The probability that a given base is changed and that the change is to an allele with frequency less than f, conditional on the base being involved in a gene conversion event, is the probability that the position was heterozygous in the individual in which the gene conversion took place and that the heterozygous genotype had the minor allele on the donor haplotype, which is h_f/2. Thus the expected contribution to the mutation rate count from gene conversion is $l{g}_2\theta h_f/2$, the total expected mutation rate count is $l{g}_2\left(\mu +\theta h_f/2\right)+l\mathit{ϵ}$, and the nominal mutation rate estimated by our method is ${\mu }_f^{\ast }=\mu +\theta h_f/2$. Thus if we apply the method with different values of f (and corresponding different values of h_f), we can regress the estimated nominal mutation rate estimates ${\hat{\mu }}_f^{\ast }$ against estimated frequency-bounded heterozygosity ${\hat{h}}_f$ to obtain an estimate of the mutation rate $\mu$ in the intercept of the regression.

In the above, we implicitly assumed that the frequency-bounded heterozygosities, h_f, are fixed across time and geography. Although this assumption may appear doubtful, in fact autosomal heterozygosities are almost identical across populations in Europe,¹⁸ for example, even including Finland which has experienced a recent population bottleneck. Thus, for relatively homogeneous (single continental-level ancestry) populations, the assumption of stable heterozyosities gives a reasonable approximation.

For a given allele frequency threshold f, the estimated heterozygosity is

$${\hat{h}}_f=\sum _{i}2p_i\left(1-p_i\right)1_{\left\{p_i<f\right\}}/L$$

where the sum is over all variants (indexed by i) in a genome of total length L basepairs. The minor allele frequency of each such variant is p_i and $1_{\left\{p_i<f\right\}}$ is the indicator function that takes value 1 if the minor allele frequency is less than f and 0 otherwise. Here we use the expected heterozygosity based on allele frequency and assuming Hardy-Weinberg equilibrium, whereas we could instead use observed heterozygosity; we find that the two approaches give almost equal estimates in the simulated data and Framingham Heart Study data (data not shown).

To perform the regression, we use only allele frequency thresholds that are large enough to minimize the possibility of excluding some true mutations. We thus use frequency thresholds between 0.1 and 0.5 in the regression (following Palamara et al.⁵). We choose to use an upper bound of 0.5 to maximize the amount of data in the regression, and we use a lower bound of 0.1 which is high enough to ensure that no true mutations are excluded, yet not so high as to exclude much data from the regression. We also analyzed the data using lower bounds of 0.05 and 0.2 to ensure that the results were robust to this choice. For each frequency threshold, f, we estimate the mutation rate ${\hat{\mu }}_f^{\ast }$, considering as potential mutations only variants with frequency below the threshold. We estimate heterozygosity ${\hat{h}}_f$ across all variants in the data with frequency below the threshold. We then perform the regression, with the y axis (mutation rate) intercept providing a gene-conversion-adjusted estimate of mutation rate.

Data Simulation

We evaluated the performance of the proposed method on simulated data with known haplotype phase. For all simulated datasets, the simulated genome size was 30 chromosomes of 100 Mb each, with a mutation rate of 1.30 × 10⁻⁸ per base pair per meiosis and a constant recombination rate of 1.0 × 10⁻⁸ per base pair per meiosis. We used ARGON,¹⁹ a discrete-time Wright-Fisher process simulator, to simulate data under three different demographic scenarios: a population with exponentially growing population size and increases in growth rate over time (the “super-exponential” model), a homogeneous population with constant population size (the “homogenous” model), and an admixed population with exponentially growing population size (the “admixture” model). We also used MaCS,²⁰ a Markovian coalescent simulator, to simulate data with gene conversion under a “European-American” demographic history.

In the “super-exponential” scenario, we simulated genome-wide data for 10,000 diploid individuals with a demographic model that matches the heterozygosity, magnitude of linkage disequilibrium, and rate of IBD observed in the UK10K sequence data.²¹ The demographic model has an initial population size of 24,000 in the distant past, with an out-of-Africa reduction to 3,000 occurring 5,000 generations ago. The population begins to grow 1.4% per generation 300 generations ago. The growth rate increases to 6% and 25% at 60 and 10 generations ago, respectively. The final effective population size is around 21 million.

In the “homogeneous” scenario, we simulated 2,000 homogeneous diploid individuals with a constant effective population size of 10,000 diploid individuals.

In the “admixture” scenario, we simulated 400 admixed diploid individuals with non-constant effective population size and population structure. The population size was 15,000 until 1,000 generations ago, at which time a population split occurred, resulting in two subpopulations with sizes of 10,000 and 5,000. The two subpopulations merged together (admixed) 20 generations ago and then grew at a rate of 1.44% per generation to a current size of 20,000.

The “European-American” model uses the demographic history that we inferred using IBDNe from samples in Framingham Heart Study (Figure S3) for generations 1–300, with a population size of 24,000 prior to 5,000 generations ago and a reduction to 6,930 occurring 5,000 generations ago. We simulated 2,000 diploid individuals under this scenario. The simulation included gene conversion, with a gene-conversion initiation rate of 1.0 × 10⁻⁸ per base pair per meiosis and mean conversion tract length of 100 bp.²²

We created two versions of the simulated data, each with a different type of genotype error. The first type of genotype error includes both false positive errors (major allele miscalled as minor) and false negative errors (minor allele miscalled as major). For diallelic SNPs with minor allele frequency p, we give each allele a probability $\min \left(\delta ,2p\right)$ of being changed to the other allelic form (major to minor or vice versa), with the error rate $\delta$ taking values of 0.01%, 0.05%, and 0.1% for the homogeneous and admixture models. As the computation time is high for the super-exponential model due to the large sample size, we only added an error rate of 0.02% for this model. We refer to this first error scheme as “unbiased” error because the rate of error doesn’t depend on whether the true allele is the major or minor allele. For rare variants, most of the added errors under this scheme are false positive errors, because there are relatively few minor alleles that could be changed to the major allele. We also wanted to further investigate the effect of false negative error, which may be more prevalent for rare variants. Thus we created a second set of data in which we added only false negative error. For variants with m minor allele copies present in the dataset, we give each copy probability ${0.5}^m$ of being changed to the major allele. We refer to this second error scheme as “false-negative” error. For both types of genotype error, the errors are added prior to IBD detection; therefore, the presence of genotype errors can affect IBD detection, subsequent inference of demographic history with IBDNe, and mutation ascertainment.

Results

Simulation Study

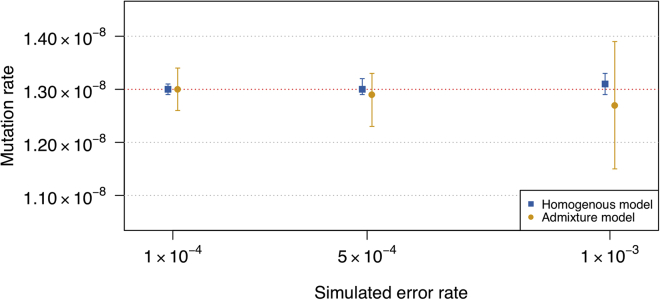
Under the super-exponential scenario with a genotype error rate of 0.02%, we obtained a mutation rate estimate of 1.29 × 10⁻⁸ per base pair per meiosis with a 95% confidence interval of [1.281 × 10⁻⁸, 1.301 × 10⁻⁸] (the simulated mutation rate is 1.3 × 10⁻⁸). We also obtained accurate estimates of mutation rate under the homogeneous and admixture simulation scenarios (Figure 3). Accuracy is maintained even with the highest rate of genotype error considered (0.1%), but at high rates of genotype error, fewer segments of IBD are detected and hence confidence intervals are wider.

Figure 3.

Estimated Mutation Rates under Different Rates of Genotype Error

The simulated mutation rate is 1.30 × 10⁻⁸ per base pair per meiosis and is indicated with the red dotted line. Point estimates (shapes) and 95% confidence intervals (bars) are shown. The maximum allele frequency threshold for the variants used for the mutation rate estimation is 3.75%. Two different simulation models, the homogeneous model (blue squares) and the admixed model (yellow circles) are assessed at error rates of 1 × 10⁻⁴, 5 × 10⁻⁴, and 1 × 10⁻³. Errors are simulated using the “unbiased” genotype error scheme (described in Material and Methods).

We also applied IBDMUT, the pairwise IBD method of Palamara et al.,⁵ to the dataset simulated under the super-exponential scenario. In the IBDMUT analysis, we used IBD segments estimated by GERMLINE¹⁶ with one or two allowed mismatching sites and we used the same estimated demographic history as we used for our method, obtained using IBDNe. Since IBDMUT requires more than 250 gigabytes of memory to process the full simulated dataset, we analyzed a subset of 2,000 individuals. We observe biased estimates of mutation rate whether allowing for one or two mismatches, whether using the true or estimated demographic history, and whether or not the data include genotype errors (Figure S4). Up to 8% relative bias is observed.

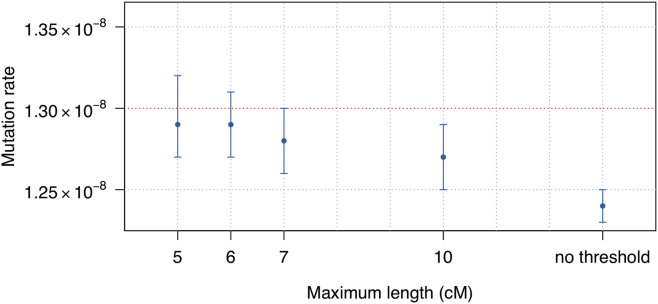
We investigated the impact on our method of false negative errors, in which copies of the minor allele are miscalled as the major allele, by adding genotype errors according to our “false-negative” genotype error scheme to the homogeneous simulated dataset. In this setting, variants with lower allele frequency are more susceptible to false negative error. These rare variants are usually carried by long IBD segments since they generally arose recently. Hence three-way IBD that involves very long pairwise IBD segments has the most potential to be affected by false negative error. To control the downward bias caused by false negative error, we thus restricted the analysis to IBD segments with length below some threshold. Reducing the maximum length threshold reduces the number of IBD segments that can be used, thus increasing the variance of the estimation. We found that a threshold of 6 cM provides good control of potential downward bias due to false negative errors while not overly increasing the variance of estimation (Figure 4).

Figure 4.

Estimated Mutation Rates under False Negative Genotype Errors

Data were simulated under the “homogeneous” model, and errors were added using the “false-negative” genotype error scheme (described in Material and Methods). The simulated mutation rate is 1.30 × 10⁻⁸ per base pair per meiosis and is indicated with the red dotted line. We set different thresholds on the maximum length of IBD segments (x axis) to control the impact of false negative errors. The maximum allele frequency threshold for the variants used for the mutation rate estimation is 3.75%. Point estimates (dots) and 95% confidence intervals (bars) are shown.

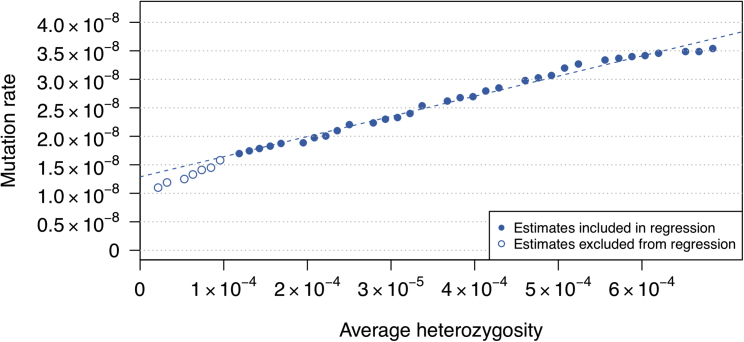
In the data simulated with gene conversion under the European-American scenario, we find that the estimated mutation rate continues to increase with increasing maximum frequency of the alleles included in the analysis (Figure 5), as expected under gene conversion. In contrast, under the same simulation scenario but without gene conversion events, we observe that the estimates of mutation rate remain the same for maximum allele frequencies above 2.5%. To correct for the impact of gene conversion events, we performed a regression on heterozygosity (see Material and Methods; Figure 5) and obtained a mutation rate estimate of 1.34 × 10⁻⁸ per base pair per meiosis with a 95% confidence interval of [1.30 × 10⁻⁸, 1.38 × 10⁻⁸] (the simulated mutation rate is 1.3 × 10⁻⁸). When we adjusted the lower bound on the range of allele frequency thresholds used in the regression (from 0.1), we obtained similar results: 1.33 × 10⁻⁸ [1.30 × 10⁻⁸, 1.37 × 10⁻⁸] for a lower bound of 0.05 and 1.35 × 10⁻⁸ [1.30 × 10⁻⁸, 1.39 × 10⁻⁸] for a lower bound of 0.2.

Figure 5.

Estimated mutation rates in simulated data with gene conversion, as a function of the average heterozygosity of included variants.

Data were simulated under the “European-American” model with gene conversion (see Material and Methods). The blue dashed line is the fitted regression line; the y axis intercept of this line gives an overall estimate of mutation rate that is adjusted for the effects of gene conversion. Points corresponding to maximum allele frequency thresholds of 0.1–0.5 are included in the regression (filled points on the plot), as lower thresholds may exclude some true mutations (open points on the plot). For each maximum allele frequency threshold, the average heterozygosity was calculated (x axis) and the mutation rate estimate was obtained (y axis). The simulated mutation rate is 1.3 × 10⁻⁸ and is shown with the horizontal red dashed line.

TOPMed Framingham Heart Study Data

The Framingham Heart Study data from the NHLBI TOPMed Project that we analyzed consist of high-coverage sequence data on 4,166 subjects with European ancestry (dbGaP: phs000974.v2.p2). We restricted all our analyses to diallelic SNPs passing quality control filters, and we used the Rutgers genetic map.²³ We identified 697 mother-father-offspring trios and performed trio-based phasing using BEAGLE v.4.0.²⁴ Trio-based phasing has high accuracy for both common and rare variants because Mendelian inheritance constraints determine the haplotype phase in the parents and offspring at most positions.

There were 1,362 unique parents from the 697 trios. By using trio parents rather than offspring for the analysis, we double the sample size, and the phasing is well determined except at those small number of points of crossing-over in the meioses from trio parents to trio offspring. We ran principal component analysis (PCA) on these parents. In order to account for relatedness in the PCA, we removed 194 individuals who were closely related to others in the sample (total length of detected IBD segments exceeding 40 cM on chromosome 22) when computing the principal components, and then determined PC scores of the excluded samples by projecting them onto the principal component axes. We found two distinct clusters on the second principal component (PC2 > 0.05 and PC2 ≤ 0.05; Figure S5), and we inferred the demographic history of each cluster separately using IBDNe. We found that the cluster with PC2 > 0.05 experienced a recent severe population bottleneck around 30 generations ago (Figure S6), which is consistent the demographic history of the Ashkenazi Jewish population.²⁵ Although our method is robust to population structure (Figure 3), we conservatively removed the 55 samples with PC2 > 0.05 from the mutation rate analysis. We also present results without the exclusion.

As for the analysis of simulated data, we used Refined IBD¹⁴ in BEAGLE v.4.1 to detect pairwise IBD segments from the phased genotypes using only diallelic SNPs with minor allele frequency 10% or higher. After filling short gaps between segments (Material and Methods), we removed segments with length less than 3 cM or larger than 6 cM. Our simulation study (reported above) showed that removal of segments larger than 6 cM reduces the potential impact of false negative errors.

We excluded regions with extremely high levels of IBD from the analyses. We find that these regions are mainly in areas of the genome with low marker density, such as around centromeres. In such regions, the IBD detection method tends to overestimate the IBD segment lengths, because identity by state extending beyond the end of the IBD segment may cover a large genetic distance. To perform this exclusion, we calculated the level of three-way IBD along the genome in windows of 500 base pairs and removed any three-way IBD that overlapped windows for which the three-way IBD level exceeded the 99th percentile. Regions that were outside the limits of the genetic map were also removed from the analysis. In addition, some regions of the genome did not contribute to the estimation because they contained no three-way IBD. After removing all these regions, the remaining data covered 2.01 gigabases across the autosomes. Many of the excluded regions are near the centromeres and telomeres due to poor data quality or low variant density in those areas (Figure S7).

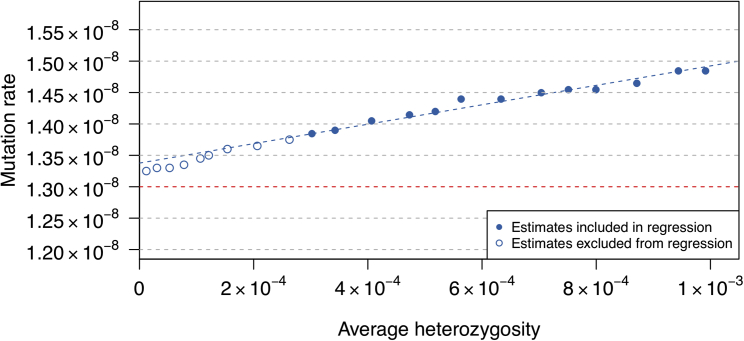
We ran analyses with a range of maximum allele frequencies (Figure S8). The estimates increase as the maximum allele frequency increases, as expected with gene conversion. We thus applied regression on heterozygosity to correct for gene conversion (see Material and Methods). Our corrected estimate is 1.29 × 10⁻⁸ with 95% confidence interval [1.02 × 10⁻⁸, 1.56 × 10⁻⁸] (Figure 6). For comparison, when we don’t exclude the individuals who were outliers (PC2 > 0.05) on the principal components analysis, the estimate is 1.21 × 10⁻⁸ with 95% CI [1.00 × 10⁻⁸, 1.45 × 10⁻⁸]. When we apply the exclusions but change the lower bound on the maximum allele frequency, the estimates are 1.24 × 10⁻⁸ [1.02 × 10⁻⁸, 1.46 × 10⁻⁸] for a lower bound of 0.05 and 1.36 × 10⁻⁸ [0.98 × 10⁻⁸, 1.73 × 10⁻⁸] for a lower bound of 0.2.

Figure 6.

Estimated Mutation Rates from the Framingham Heart Study Data as a Function of the Average Heterozygosity of Included Variants

The dashed line represents the fitted regression line; the y axis intercept of this line gives an overall estimate of mutation rate that is adjusted for the effects of gene conversion. Points corresponding to maximum allele frequency thresholds of 0.1–0.5 are included in the regression (filled points on the plot), as lower thresholds may exclude some true mutations (open points on the plot). For each maximum allele frequency threshold, the average heterozygosity was calculated (x axis) and the mutation rate estimate was obtained (y axis).

We also applied IBDMUT⁵ to these data. We used the same estimated demographic history as for our method (see Material and Methods and Figure S3), and we used IBD segments estimated by GERMLINE.¹⁶ Regions with extremely high levels of pairwise IBD sharing were excluded from the analysis. We removed any segments that overlapped regions in which the pairwise IBD level exceeded the 99th percentile. We further removed segments with length less than 3 cM or larger than 6 cM from the analysis. The mutation rate estimate was 1.31 × 10⁻⁸ with 95% confidence interval [1.20 × 10⁻⁸, 1.42 × 10⁻⁸]. In this case, IBDMUT’s estimate is consistent with our estimate, although our simulations show that this will not always be the case. IBDMUT has a narrower confidence interval because IBDMUT makes use of more meioses. Our method uses the meioses only between the coalescence of the first two haplotypes and their coalescence with the third haplotype in each set of three IBD haplotypes, while IBDMUT uses all the meioses for each pair of IBD haplotypes, including more recent meioses.

Discussion

In this paper, we have presented a method for estimating mutation rates based on IBD segments shared among sets of three individuals, and we provide an estimate of mutation rate for individuals of European descent from the Framingham Heart Study. Our analysis includes only single-nucleotide substitutions; indels and other structural variants are excluded from the analysis. The data underlying our analysis cover 2.01 gigabases of the autosomes. Our estimate is 1.29 × 10⁻⁸ per base pair per meiosis with 95% confidence interval [1.02 × 10⁻⁸, 1.56 × 10⁻⁸]. Software for our method (METIBD3) is freely available (see Web Resources).

Our estimate is consistent with previous pedigree-based estimates of mutation rate that range from 0.97 × 10⁻⁸ to 1.36 × 10⁻⁸ per base pair per meiosis.^{3, 4, 7, 9, 26, 27, 28, 29, 30, 31} A major and difficult to quantify source of uncertainty in pedigree-based estimates is the choice of quality control filters to reduce the impact of genotype error. Overly stringent filtering will depress the mutation rate estimate.⁴ In contrast, our method accounts for genotype error by modeling it, allowing for much reduced dependence on filtering. Pedigree-based methods are also affected by somatic mutation, unless three generations of individuals are genotyped.⁴ Our method is robust to somatic mutations, because such mutations will be carried by only one of the three IBD individuals that we consider, and thus will not be counted.

The estimated mutation rate from our three-way IBD method applied to data from the Framingham Heart Study is significantly lower than that estimated by Palamara et al. with their pairwise-IBD-based method applied to data from the Genome of the Netherlands study, which was 1.66 ± 0.04 × 10⁻⁸.⁵ The Genomes of the Netherlands data analyzed by Palamara et al. have lower average sequence read depth, and thus are likely to have a higher rate of error, which could bias the results.

Our mutation rate estimate is consistent with estimates from two other IBD-based methods: An estimate of 1.61 ± 0.26 × 10⁻⁸ (confidence interval here given as estimate ±2× standard error, rather than estimate ± standard error given in the original publication) based on segments of ancient autozygosity in eight European and Asian individuals,⁸ and an estimate of 1.45 ± 0.05 × 10⁻⁸ based on segments of recent autozygosity in British-Pakistani individuals.⁶

Our approach uses IBD segments detected with the haplotype-based Refined IBD algorithm applied to phased data from parent-offspring trios. Unlike pedigree-based mutation rate estimation, our method uses cross-family IBD to identify mutations arising over a much larger number of meiosis. The difficulty of distinguishing genotype error from true mutations is handled through statistical modeling and is also reduced by requiring that the variants be seen in at least two of three identical-by-descent individuals. While the a priori rate of error for a very low frequency variant may be relatively high, evidence for a long IBD segment shared by the two individuals carrying the variant greatly increases the chance that the allele calls for that variant are accurate in those individuals.

When estimating mutation rate, the most serious type of genotype error is false positive error in which a major allele is called as the minor allele. These errors significantly increase the apparent mutation rate if not appropriately accounted for. Our method has strong control of these false positive errors through our error rate modeling. In addition, false negative errors, in which a minor allele is called as the major allele, can also have an effect, somewhat reducing the apparent mutation rate. Genotype error rates are highest for rare and singleton variants because variant callers use databases of common SNPs to calibrate their results.³² With our method, singleton variants are ignored. Furthermore, the lowest frequency non-singleton variants, such as variants with only two or three copies in a large dataset, are very recent and have a relatively greater impact on mutation counts for the longest IBD segments which represent very recent common ancestry. Thus, we are able to significantly reduce the impact of false negative errors by excluding the very longest IBD segments.

Another potential source of error is gene conversion, which inserts existing alleles from one haplotype onto another haplotype. Such alleles can then differ between IBD haplotypes, which mimics the signal of mutation. However, most of the alleles inserted due to gene conversion are common alleles with high heterozygosity, while recent mutations are low in frequency. Thus, applying regression on heterozygosity corrects for gene conversion.⁵

Our method is based on mutations that occurred since common ancestors living at most several hundred generations ago, which is more recent than continental-level population split times. Thus, there is potential to distinguish differences in mutation rates between populations, which may be due to differing environmental exposures or average parental ages.^{3, 6} With larger sample sizes in future studies, there is also the potential to obtain mutation rate estimates for particular genomic regions or other subsets of the genome, in contrast to the genome-wide estimation that we performed here. At present our method requires accurately phased rare variants, which restricts the applicability of the method to data that include families. If our method were to be extended to account for phasing uncertainty, it would be applicable to analysis of larger datasets of unrelated individuals, which would increase the precision of the estimates.

Declaration of Interests

The authors declare no competing interests.

Published: October 3, 2019

Web Resources

• Beagle 4.0, https://faculty.washington.edu/browning/beagle/b4_0.html

• Beagle 4.1, https://faculty.washington.edu/browning/beagle/b4_1.html

• dbGaP, https://www.ncbi.nlm.nih.gov/gap

• IBDNe, http://faculty.washington.edu/browning/ibdne.html

• METIBD3 (Mutation rate estimation through three-way IBD), https://github.com/tianxiaowen/mutation_phased/

• Refined IBD, http://faculty.washington.edu/browning/refined-ibd.html