EcSeg: Semantic Segmentation of Metaphase Images Containing Extrachromosomal DNA

Summary

Oncogene amplification is one of the most common drivers of genetic events in cancer, potently promoting tumor development, growth, and progression. The recent discovery that oncogene amplification commonly occurs on extrachromosomal DNA, driving intratumoral genetic heterogeneity and high copy number owing to its non-chromosomal mechanism of inheritance, raises important questions about how the subnuclear location of amplified oncogenes mediates tumor pathogenesis. Next-generation sequencing is powerful but does not provide spatial resolution for amplified oncogenes, and new approaches are needed for accurately quantifying oncogenes located on ecDNA. Here, we introduce ecSeg, an image analysis tool that integrates conventional microscopy with deep neural networks to accurately resolve ecDNA and oncogene amplification at the single cell level.

Graphical Abstract

Highlights

• •We identify extrachromosomal DNA (ecDNA) in metaphase spreads using deep learning
• •ecSeg integrates DAPI with FISH probes to provide oncogene amplification location
• •High intra-tumoral heterogeneity of ecDNA drives cancer pathogenesis

Genomics; Bioinformatics; Automation in Bioinformatics

Introduction

Despite the well-recognized importance of oncogene amplification in cancer pathogenesis (Davoli et al., 2017), the underlying mechanisms remain incompletely understood. How do amplified oncogenes reach such a high copy number in many tumors while still showing considerable cell-to-cell variability? Numerous mechanisms, including tandem duplications (Menghi et al., 2018), breakage fusion breakage cycles (Kitada and Yamasaki, 2008), aneuploidies (Davoli et al., 2017) chromothripsis (Ly and Cleveland, 2017), and neochromosome formation (Garsed et al., 2014) events have been implicated in oncogene amplification, but the recent discovery that extrachromosomal (ecDNA) oncogene amplification is common across a wide variety of tumor types (Turner et al., 2017, Verhaak et al., 2019) has raised new interest in understanding where amplified oncogenes actually reside within the genome of tumor cells.

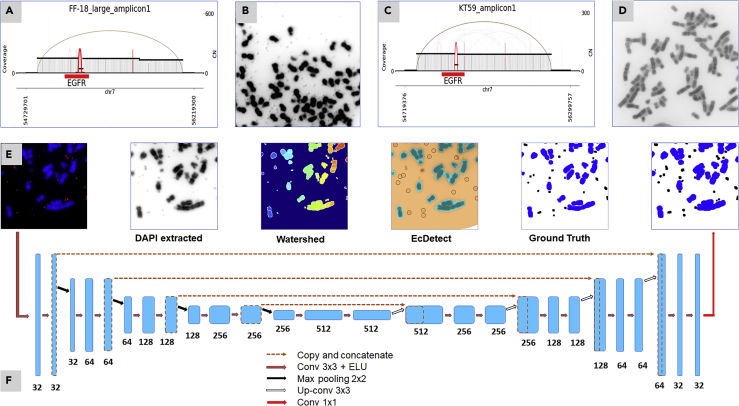
In fact, ecDNA have long been found to occur in cancer cells studied in metaphase (Cox et al., 1965), referred to as double minutes, but the difficulty in linking these observations with modern cancer genomics led to a massive underestimation of their prevalence (Verhaak et al., 2019). In part, the challenge has been made more difficult by the fact that the 3D structure of DNA in an intact nucleus does not permit unambiguous localization of a particular gene, especially when there are many copies of that gene. Recently, sequence-based methods (Deshpande et al., 2019) have been developed to reconstruct the fine structure of focal amplifications, including ecDNA. However, ecDNA are known to reintegrate into and egress out of chromosomes based on cellular environment (Nathanson et al., 2014) while maintaining their structural features. For example, focal amplifications containing epidermal growth factor receptor (EGFR) have identical structures but can be extrachromosomal or integrated into non-native locations within chromosomes (Figures 1A–1D). Therefore, sequence-based reconstructions have limited power in revealing the spatial location of focal amplifications.

Figure 1.

Detecting ecDNA in DAPI-Stained Images

(A and B) Copy number amplification of EGFR in a glioblastoma cell line due to extrachromosomal DNA (ecDNA) formation.

(C and D) Copy number amplification of EGFR in a glioblastoma cell line with no ecDNA. Note that the sequence-based reconstruction does not distinguish between ecDNA (A) and homogeneously stained regions (C).

(E) Identification of ecDNA in DAPI-stained images of cells in metaphase. Although a FISH signal for EGFR is also shown, only the DAPI signals are used for calling ecDNA using the Watershed method, ecDetect, manually annotated ground truth, and ecSeg.

(F) A neural network architecture for semantic segmentation of the pixel into ecDNA, chromosomes, nuclei, and background, as described in Transparent Methods.

The use of fluorescence in situ hybridization (FISH) probes to study amplified oncogenes in interphase nuclei often reveals a pattern of many FISH probe-positive spots, but with limited ability to discriminate between their chromosomal and extrachromosomal location. During metaphase, the compact alignment of chromosomes enables unambiguous localization of specific genes within the genome and ecDNA can be detected using FISH probes. Moreover, the cell-to-cell variability in terms of ecDNA content and number poses additional challenges.

To accurately quantify ecDNA in cells, we investigated DAPI stained images of cells in metaphase, when chromosomal structures are condensed and separated from ecDNA. However, the large class imbalance in cellular features (Figure 2A), inherently high noise ratio in metaphase images, small size, and paucity of morphological features in ecDNA (particularly in comparison with chromosomes), present challenges to identifying and segmenting ecDNA. Moreover, we observed large variance in prevalence, relative pixel intensity, size, and presence of other partially burst nuclei across samples. It is difficult for traditional image processing algorithms with hand-crafted features to automatically account for the high level of contextual information and different sources of variation between cell types and images within a cell type.

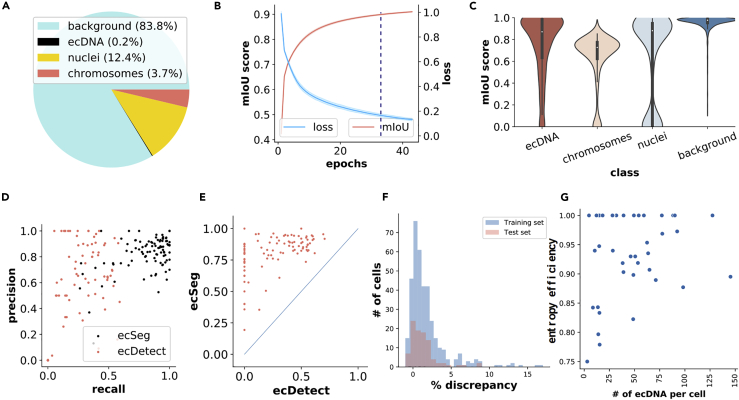
Figure 2.

ecSeg Performance and Applications

(A) Pie chart showing class imbalance.

(B) Loss and mIoU on validation data as a function of training epochs. Only the loss function is used for training.

(C) mIoU score distributions for ecDNA, chromosomes, nuclei, and background on test data.

(D) Precision versus Recall for ecDetect and ecSeg on test data. Each point represents a complete image.

(E) F1 score comparison between ecSeg and ecDetect on test data. Notably, the ecDetect F1 scores rarely exceed 0.5 because of low recall, whereas ecSeg F1 scores are generally above 0.75.

(F) Distribution of Discrepancy in ecDNA counts ([ecSeg count - ground truth counts]/ground truth counts) shows a slight over-estimate for ecSeg, with 90% of the calls being within 5%.

(G) Entropy efficiency for 40 cell lines.

For these reasons, computational tools for identifying ecDNA in DAPI-stained images are limited. Figure 1E shows a patch from a DAPI-stained image of a cell in metaphase. An off-the-shelf method, Watershed (Beucher and Lantuejoul, 1979) detected only 14 of 25 ecDNA. An earlier tool, ecDetect (Turner et al., 2017), used image processing methods, including thresholding and morphological operations, to detect and quantify ecDNA. The tool was optimized for precision and had low recall. For example, when applied to a cropped image from a metaphase PC3 cell line (Figure 1E), ecDetect detected only 16 of 25 ecDNA. Moreover, although the tool performs accurate segmentation of intact nuclei and chromosomes, it does not automatically differentiate between the two classes and requires further post-processing. Therefore, ecDetect cannot identify FISH-stained homogeneously staining regions. Additionally, ecDetect often requires a manual step to demarcate the regions containing metaphase chromosomes. We address these issues in our method.

Deep neural networks, specifically convolutional neural networks, have consistently outperformed traditional image processing algorithms on biological datasets (Hamilton, 2018). By using a large number of learnable parameters, they can recognize complex underlying patterns in large datasets (Krizhevsky et al., 2012). In contrast to image classification tasks, fully convolutional networks were constructed to perform pixel-wise classification (Long et al., 2015). Pixel-wise classifications allows for images to be semantically segmented, i.e., acquire class labels while retaining their spatial organization. However, ecDNA are small and irregularly shaped and can be confused with other proximal objects. Thus, resolving local details at a fine spatial resolution, as well as reasoning about categorical information based on global context, is necessary to successfully segment ecDNA. These dual goals can be achieved using U-nets (Ronneberger et al., 2015), a variant of FCNs, which gradually up-sample features and use skip connections to recover spatial resolution. U-nets have become widely recognized as the common choice of architecture in the medical image community for their superior performance on a number of imaging challenges (Litjens et al., 2017).

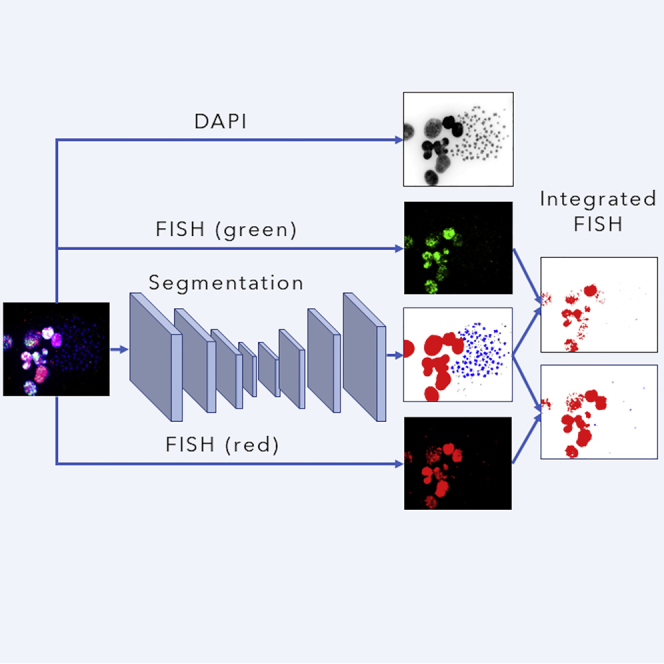
In this research, we developed ecSeg, a U-net-based platform (Figure 1F) for automatically classifying DAPI signal, identifying and quantifying ecDNA, and incorporating FISH data to clarify the location of oncogene amplification on ecDNA and chromosomes. It accepts DAPI and FISH-stained metaphase images and classifies each image pixel into one of the following classes: Cytoplasm, Nucleus, Chromosome, and ecDNA (Figure 1E, right panel). Subsequently, it computes connected components of ecDNA pixels (Transparent Methods) to demarcate and count ecDNA. When FISH probes are present, it quantifies their spatial location in a separate post-processing step and correlates those locations with ecDNA and chromosomes.

Results

Network Training Procedure

To train ecSeg, we developed and made available a unique dataset containing ground truth labeling of nuclei, chromosomes, and ecDNA, starting from 483 unlabeled images of dimensions 1040 × 1392 from Turner et al. (2017). The ground truth labeling was created by multiple scientists involved in independent annotation (Transparent Methods). Owing to the difficulty of annotating 18.9K ecDNA across 483 images, a decision was made early on to use a coarsely annotated dataset that allowed for the possibility of a few missed and/or false ecDNA calls. For the training and testing of learning frameworks, we generated 5,949 image patches (256 × 256 each) that were cropped from the larger images. We randomly split these patches into training (4,760 patches) and test (1,189 patches) datasets. Importantly, to have higher fidelity while testing the network, we further annotated the test data to reduce false ecDNA calls. The test data was a “holdout” set that was used only for final quantification of the model and had no direct effect on the training itself.

In training the network, we used a weighted loss function comprising the binary cross entropy and Dice coefficient to correct for the severe class imbalance. We also modified the architecture and adjusted hyper-parameters to account for the small size and lack of discriminating features on ecDNA (Transparent Methods). To optimize the model, various iterations of the architecture and hyper-parameters were trained using the training data on 8 GeForce GTX 1080 Ti GPUs (Transparent Methods). We also tested with different network architectures such as U-net with multi-scale context aggregation using dilated convolution (Yu and Koltun, 2015), pre-trained weights from VGG16 (Simonyan and Zisserman, 2014) trained on ImageNet, and the base U-net. The performance was optimized on a network with 32 filters in the first layer and doubling the number of filters in each layer, input image sizes of 256 × 256, and an L2 regularization parameter of 0.0001. For the optimal model, we found that the loss converged after 33 epochs (Figure 2B). As the loss function did not provide an intuitive explanation of performance, we additionally used a “mean Intersection over Union” (mIoU) score (Transparent Methods) to measure the fraction of true calls. The mIoU score showed similar convergence behavior on the training data (Figure 2B).

Test Set Segmentation Accuracy

On the test data (1,189 patches) ecSeg displayed good performance for each of the classes with mIoU scores of 0.75 for ecDNA, 0.68 for chromosomes, 0.78 for nuclei, and 0.97 for background (Figure 2C). Notably, 50% of the patches had an ecDNA mIoU score of at least 0.871 and 25% had a score of 0.938. The relatively worse performance for chromosomes was partially due to images in which the chromosomes are tightly clustered, making it difficult to differentiate them from intact nuclei (Figure S1).

Although we used a pixel-based image segmentation approach, the primary goal of ecSeg is to detect and count ecDNA in entire images. For example, an incorrect pixel classification adjacent to a correctly annotated ecDNA pixel does not change the fact that the ecDNA was detected. Therefore, ecSeg also post-processes the output by computing connected components of adjacent pixels with the same class label (Transparent Methods). We defined true-positive or TP (respectively, false-positive or FP) predictions as an ecDNA connected component whose centroid was within (respectively, outside) a pixel-distance threshold α (=5) of a manual annotation (see Transparent Methods). Similarly, we defined a false-negative (FN) call as a manual annotation with no ecSeg prediction within 5 pixels. On the test patches, the mean precision (TP/TP + FP) and recall (TP/TP + FN) were measured as 85% and 86%, respectively.

Comparison of Segmentation Methods

To compare against ecDetect predictions, we combined the predictions of all patches for an image. We plotted the precision versus recall performance of ecSeg for each image, along with the ecDetect predictions (Figure 2D, Table S2). At the image level, the mean precision and recall values were 82% each, in contrast with 59% and 23% achieved by ecDetect, which rarely achieved recall above 50%, and had a worse F1 (combined) score than ecSeg for each image (Figure 2E). The ecSeg performance varied across cell lines (Table S3). Thus COLO205, where the ecDNA are notably larger in the nine images (Figure S2) had worse performance (75% precision, 64% recall) compared with CA718 (84%, 90%). Moreover, in at least some cases, ecSeg predictions that did not match the manual annotation were in fact true calls as verified by external annotators who were not involved in the original annotation process. Similarly, a small number of manual annotations not called by ecSeg were truly not ecDNA (Figures S3 and S4). Including the totality of 483 training and test images, the number of ecDNA called by ecSeg were within 5% of the manual annotation calls in 88% of the images, validating the applicability of ecSeg in providing an accurate estimate of ecDNA abundance (Figure 2F).

ecDNA Heterogeneity

The ecDNA model of focal amplification (Deshpande et al., 2019, Verhaak et al., 2019) suggests that ecDNA segregate randomly into daughter cells, driving and maintaining intra-tumoral genetic heterogeneity of ecDNA counts. For a sample with n metaphase images, let n_i denote the number of samples with exactly i ecDNA counts. The Shannon Entropy, measured using

$${\mathcal{H}}_n=\sum _{i:n_i>0}-\frac{n_i}{n}{\text{log}}_2\frac{n_i}{n},$$

showed large variation across different cell lines (Table S4). Noting that the entropy value depends on the number n of sampled cells (images), we also plotted the normalized entropy-efficiency value (${\mathcal{H}}_n/{\text{log}}_{2}n$) for 40 cell lines. Interestingly, most (21 of 29) cell lines whose ecDNA copy numbers exceeded 10 per cell had an entropy efficiency above 90% (Figure 2G, Table S4), suggesting an important role for ecDNA in maintaining copy number heterogeneity.

Modeling the Effect of Environmental Changes (Drug Treatment) on ecDNA

Activated oncogenes on ecDNA can provide a selective advantage to cells with higher ecDNA counts, leading to rapid proliferation of those cells and focal amplification (Turner et al., 2017). However, environmental changes that restrict metabolite availability may impose a selective disadvantage on ecDNA-containing cells. Indeed, a previous report had shown a dramatic decrease of ecDNA in a glioblastoma cell line when targeted with the anti-EGFR drug Erlotinib (Eb), followed by a rapid increase in ecDNA upon withdrawal of drug treatment (Nathanson et al., 2014). To test the effect of drugs and other environmental factors in modulating ecDNA counts, we used ecSeg to quantify ecDNA counts in cells before Eb treatment and followed up 2 and 4 weeks after treatment.

To quantify the effect of drug treatment, we extended earlier work that modeled these selective forces using a Galton-Watson branching process (Bozic et al., 2010, Turner et al., 2017) (Transparent Methods), where each cell containing k ecDNA either replicates with probability b_k, or dies (probability d_k = 1 − b_k), to create the next generation. Positive selection was modeled by setting $b_k-d_k\propto f_{m,\alpha }\left(k\right)$, where

$$f_{m,\alpha }\left(k\right)=\{\begin{array}{cc}\frac{k}{M_s}& (0\le k\le M_s),\\ \frac{1}{1+e^{\alpha \left(k-m\right)}}& \left(M_s<k<M_a\right).\end{array}$$ (Equation 1)

is positive, increasing for small values of k and decreasing logistically to 0 for larger values of k (Figure 3A, black line). To this model, we added the effect of a drug targeting the protein product of the oncogene by using f_k that logistically decreases to a negative value for increasing k (Figure 3A, blue line and Transparent Methods).

$$f_{r,\alpha }\left(k\right)=-\frac{e^{\alpha \left(k-r\right)}}{1+e^{\alpha \left(k-r\right)}}.$$ (Equation 2)

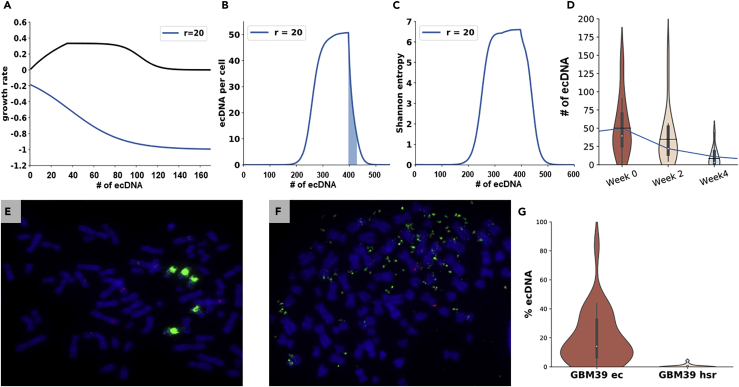
Figure 3.

ecSeg Applications

(A) The black line shows the growth rate b_k − d_k for ecDNA-driven amplification (parameters α = 0.1, m = 100), which rises initially and slowly decreases to 0. The effect of a drug on growth rate (blue line)is modeled using a negative selection function $f_{r,\alpha }\left(k\right)$ for parameters α = 0.04, r = 20.

(B and C) (B) Simulated changes in the mean copy number and Shannon entropy (C) as a function of time, when the drug is applied at day 400 with α = 0.04, r = 20.

(D) Reduction of ecDNA counts in glioblastoma cell line GBM39 upon Erlotinib treatment. Black lines inside the violin plots show sample means, whereas white circles and box plots show the median and the middle 50th percentile. The blue line shows mean values of the simulation from (B) (shaded region). The mean, median counts per cell were (50,26) at week 0, (38,14) at week 2, and (10,1) at week 4, consistent with the theoretical model.

(E and F) (E) A glioblastoma cell line with EGFR proto-oncogene (stained using green FISH signal) found in homologously stained regions (HSR) (F) A glioblastoma cell line with EGFR found on ecDNA.

(G) Percentage of FISH signal on ecDNA in the ec and hsr cell lines.

Different choices of the decay parameters r, α all predicted a sharp decrease in ecDNA per cell, and a decrease in heterogeneity (Figure S5), but show very different rates of decrease in ecDNA.

On the experimental data, ecDNA counts, estimated by ecSeg, reduced dramatically from a mean of 50 per cell (median 26) at week 0 to 38 (median 14) at 2 weeks and 10 (median 1) at 4 weeks (Figures 3B and 3C, Table S5). The entropy efficiency of the cells changed from 0.98 at week 0 to 0.73 at week 4. The results closely matched simulations for r = 20, α = 0.04. Although the theoretical models are admittedly simplistic, they showcase the power of ecSeg in inferring model parameters and providing quantitative comparisons of drugs used to target ecDNA.

Oncogene Amplification on Homologously Stained Regions and ecDNA

The tumor cell can respond rapidly to a changing environment by dynamically modulating RNA expression through ecDNA formation as well as reintegration of ecDNA as homologously stained regions (HSRs) (Nathanson et al., 2014). This is shown in the example of two glioblastoma cell lines where EGFR amplifications occur either as ecDNA (“ec” cell line) or as HSR (“hsr” cell line, Figures 3E and 3F). To quantify this phenomenon, we used an EGFR FISH probe and ecSeg analysis to locate EGFR (Transparent Methods) in the two cell lines. The median fraction of FISH signal explained by ecDNA was 0% in the hsr cell line but rose to 14% in the ec cell line (Figure 3G). In contrast, 71% (respectively, 15%) of the FISH signal was found on chromosomes in the hsr (respectively, ec) cell line. The results document the ability of ecSeg to provide insight into potentially important biological processes. Specifically, they suggest that ecDNA-driven amplifications, which are inherently capable of rapidly changing tumor copy number, can be “stabilized” by reintegrating into chromosomes, validating the prescient concept that ecDNA-based amplification (aka double minutes) is “unstable,” whereas chromosomal amplification on HSRs is stable (Haber and Schimke, 1981).

Discussion

The finding that ecDNA-based oncogene amplification is common in cancer raises some challenges for our current topological maps of cancer genes, including the fact that oncogene location within the nucleus could greatly impact tumor aggressiveness, as well as through non-chromosomal mechanisms of ecDNA inheritance. Nevertheless, it is difficult with existing genomic tools to quantify the extrachromosomal origin of copy number amplification. ecSeg provides a new tool for the research community to quantify ecDNA-based amplification at the single cell level.

FISH-based methods have been used to probe for oncogenes involved in tumor development, to identify cellular location of other proteins, including those involved in DNA repair, and for foci scoring (Verhaak et al., 2019, Nathanson et al., 2014). ecSeg can be used to determine the sub-cellular location of these proteins, helping to differentiate between intra-chromosomal and extrachromosomal repair mechanisms.

Genomic tools have been invaluable for precise measurements of copy number amplification, but bulk sequencing does not reveal the cell-to-cell variability in the copy number counts. Tools for quantifying copy number heterogeneity are very limited as single-cell genomic analyses of copy number variation are often confounded by PCR-mediated artifacts. Automated cytogenetic analysis allows for an automated measurement of heterogeneity and understanding of its consequence. The ecDNA model of oncogene amplification suggests that ecDNA segregate independently into daughter cells and selection helps modulate a rapid change in copy number. An identical mechanism allows cells to rapidly reduce copy numbers under negative selection from a drug. ecSeg allows for the measurement of the rate of change and helps quantify the positive or negative selection strength. In summary, ecSeg can provide new insight into how cell-to-cell variability with respect to specific oncogenes contributes to tumor growth, progression, and drug resistance.

Limitations of the Study

We note that the network was trained on data from established cell lines, and the abundance and physical characteristics of ecDNA could be different in primary cancers, thus requiring additional fine-tuning. Most of the metaphase spreads were generated in a single laboratory. Differences in metaphase spread preparation could change the resolution of the input data.

Currently, the ecSeg method is trained only to analyze up to two FISH probes and will need to be updated to handle multiple probes.

Methods

All methods can be found in the accompanying Transparent Methods supplemental file.

Published: November 22, 2019