Assessment of Protein Model Structure Accuracy Estimation in CASP13: Challenges in the Era of Deep Learning

Abstract

Scoring model structures is an essential component of protein structure prediction that can affect the prediction accuracy tremendously. Users of protein structure prediction results also need to score models to select the best models for their application studies. In CASP, model accuracy estimation methods have been tested in a blind fashion by providing models submitted by the tertiary structure prediction servers for scoring. In CASP13, model accuracy estimation results were evaluated in terms of both global and local structure accuracy. Global structure accuracy estimation was evaluated by the quality of the models selected by the global structure scores and by the absolute estimates of the global scores. Residue-wise, local structure accuracy estimations were evaluated by three different measures. A new measure introduced in CASP13 evaluates the ability to predict inaccurately modeled regions that may be improved by refinement. An intensive comparative analysis on CASP13 and the previous CASPs revealed that the tertiary structure models generated by the CASP13 servers show very distinct features. Higher consensus towards models of higher global accuracy appeared even for free modeling targets, and many models of high global accuracy were not well optimized at the atomic level. This is related to the new technology in CASP13, deep learning for tertiary contact prediction. The tertiary model structures generated by deep learning pose a new challenge for EMA method developers. Model accuracy estimation itself is also an area where deep learning can potentially have an impact, although current EMA methods have not fully explored that direction.

INTRODUCTION

Estimating accuracy of a protein model structure is an essential component of protein structure prediction. Selecting models for biomedical applications also require accuracy estimation. Estimation of model accuracy (EMA), or previously called model quality assessment, has been operated as one of the prediction categories in the community-wide blind prediction experiment CASP (Critical Assessment of techniques for protein Structure Prediction)^1–6.

Protein structure prediction methods need to score model structures in various stages of prediction, for example, during model generation or model selection. A scoring function may also serve as an objective function for local or global optimization. In any cases, the scoring components of protein structure prediction methods may be separated out and tested independently. The CASP prediction center has been providing such a platform for evaluating EMA methods using the protein model structures submitted by the tertiary structure (TS) prediction servers.

Advanced EMA methods are expected to advance protein structure prediction by being incorporated as parts of prediction methods. EMA methods have been used as components of meta-servers in the TS human prediction category by scoring TS server models. However, such meta-servers do not have scientific or practical value because they rely heavily on the models generated only in the CASP setting. In several latest rounds of CASP, an interesting community-wide collaboration emerged (WeFold), where methods from different prediction groups were combined for model generation, EMA, and structure refinement^7,8. However, more intricate combinations of EMA with other structure prediction components beyond simple scoring of pre-generated models have yet to come.

Assessing EMA methods is a difficult problem requiring decision on assessment measures and group ranking methods. First, it is not clear what model accuracy measure might provide the best quality estimate. Fortunately, different measures tend to show strong correlation as models become more accurate. Different measures emphasize different aspects of model accuracy as models become less accurate. Second, the native structure, which is the reference of model accuracy, is unknown at the time of prediction and determined by its physical stability relative to all other possible states. This means that accuracy of a model structure is in principle not a property of a single model. Overall, we followed the general practice of CASP⁶. Two model accuracy measures, GDT-TS⁹ for global fold accuracy and LDDT¹⁰ for local environment accuracy, were adopted after testing several available measures¹¹. We also introduced a new analysis, in which the ability of accuracy estimators to detect stretches of inaccurately modeled residues was evaluated. Accurate detection of inaccurate regions is expected to be extremely helpful for improving model structures by refinement. For group ranking, target-averaged Z-scores were employed to account for differences in target difficulty.

Assessing the progress of EMA methods over CASPs is also difficult because the protein targets and the TS prediction methods are all different in different CASPs. In CASP13, the set of models generated by TS servers showed a very distinct property from those generated in previous CASPs. This is related to the models of high global quality generated by using the contact (or distance) information extracted from related sequences by deep learning. This poses a new challenge for EMA methods which have been trained on the previous CASP TS models and methods.

A scoring function used in physics-based protein structure prediction attempts to estimate the depth of the valley represented by a given structure in the energy landscape. However, accuracy estimation assesses the distance of a given structure from the unknown native structure. Big data for the true depth in the energy landscape is hard to obtain. Big data for the true distance from the native state may be generated by using tertiary structure prediction methods and the known native structures. Deep learning may also impact the field of EMA in the near future.

ASSESSMENT METHODS

Overview of the EMA experiment performed in CASP13

In CASP13, tertiary structure (TS) predictions for 80 protein sequences (excluding 10 sequences which were cancelled by the prediction center) submitted by TS servers were collected and released for estimation of model accuracy. Tertiary structure models were released in two stages, just as in the previous CASPs^4–6. In the first stage, 20 server models spanning the whole range of model accuracy were selected by the Davis-EMA consensus method⁴ and released for each protein target. In the second stage, the top 150 server models per target were released except for targets T0951 (149 models) and T0999 (143 models) for which fewer than 150 server models were submitted altogether. In both stages, model accuracy predictors were asked to predict the global accuracy of each model as a single score between 0 (inaccurate) and 1 (accurate) and the local accuracy of each residue as a distance error in Angstroms. The model accuracy prediction results of the first stage were used only to compare with those of the second stage for the purpose of checking whether a prediction method is a ‘single-model’ method that by definition estimates model accuracy using only the model itself or a ‘consensus’ method that uses other TS models to generate an accuracy score. This distinction is necessary because performances of consensus methods can be CASP-specific, while those of single-model methods are expected to be CASP-independent.

In CASP13, 51 and 29 groups submitted estimations of global and local accuracy, respectively. Among them, two groups who did not submit predictions for more than half of the targets were not considered in the assessment. Only the second-stage predictions were subject to detailed analysis and ranking. Group rankings were obtained in terms of target-averaged Z-scores, as in other CASP analyses. Z-score of each group was computed in the background of the results of all groups for each target using the mean and variance calculated by neglecting the samples with initial Z-score < −2, and Z-score < −2 was treated as −2.

Methods for assessing global structure accuracy estimation

It is not possible to invent a single model accuracy measure to describe various different aspects of structure models. Model accuracy measures used in previous CASP assessments include GDT-TS⁹, LDDT¹⁰, CAD^12,13, and SphereGrinder¹⁴. In this assessment, GDT-TS and LDDT were chosen as evaluation metrics for measuring global fold accuracy and local environment accuracy, respectively. Both GDT-TS and LDDT scores were scaled to the range between 0 and 100. Examples of the cases in which the two scores, GDT-TS and LDDT, reveal different aspects of model structure accuracy are presented in Supplementary Text. A total of 79 targets were considered for the assessment of global accuracy predictions, excluding the target T0980s2 which forms an inter-wound oligomer with no secondary structure.

Two different kinds of analyses were conducted in the assessment of global accuracy prediction. First, accuracy estimations submitted by each group for given models of each target were used to rank the models, and the top model was selected. The quality of the top model by the predicted score and that of the best model measured by GDT-TS (and LDDT) with the knowledge of the experimental structure were compared, and the absolute difference of the two is defined as ‘top 1 GDT-TS loss’ (and ‘top 1 LDDT loss’). For this analysis, only the targets with at least one “reasonable” model, which is defined to have a score of > 40, were considered, resulting in 65 and 76 targets for GDT-TS and LDDT, respectively. Second, the absolute value of the predicted score was assessed by taking the difference between the predicted score and an accuracy measure (GDT-TS or LDDT) for all models. All 79 targets were used in this analysis.

Methods for assessing local structure accuracy estimation

Assessment of local accuracy estimation was performed at the level of evaluation units (EUs)¹⁵. Five EUs, T0960-D1, T0960-D4, T0963-D1, T0963-D4, and T0980s2-D1, for which hydrophobic core is absent within the monomer structure and oligomeric contacts seem to be critical for structure formation, were excluded. Considering only model structures with GDT-TS > 40 we ended up in analyzing 9,288 models from 108 EUs.

Three kinds of analyses, ASE, AUC, and ULR, were conducted. ASE and AUC analyses were carried out in the same way as in the previous CASP⁶. ASE measures an average residue-wise S-score error by $\text{ASE}=\left(1-\frac{1}{N}\sum _{i=1}^N\left|S(e_i)-S(d_i)\right|\right)\times 100$, where S-score error $\left|S(e_i)-S(d_i)\right|$ for the ith residue is calculated with the predicted (e_i) and the actual (d_i) distance errors of the ith Cα atom of a given model after evaluation-unit superposition of the model to the experimental structure by LGA⁹, S-function is $S(d)=1/\left[1+(d/d_0{)}^2\right]$ with d₀ = 5 Å, and N is the number of residues in the evaluation unit (EU).

AUC and ULR are two different ways to assess how well the predicted local accuracy score distinguishes accurately modeled residues from inaccurately modeled ones in each model, where residues in a model whose Cα distance within 3.8 Å from the experimental structure after superposition are defined accurately modeled. AUC measures the area under the ROC curve which plots the true positive rate against the false positive rate in the prediction of accurate/inaccurate residues, varying the cut-off score for distinguishing accurate/inaccurate residues.

ULR (unreliable local region) analysis assesses the ability to detect the stretches of inaccurately modeled residues. A ULR is defined as a region consisting of three or more sequential model residues deviating by more than 3.8 Å from the corresponding target residues upon their optimal superposition. Two ULRs separated by a single residue are merged into a single ULR. After assigning ULRs, their accuracy and coverage are calculated. ULRs predicted within 2 residues from the boundaries of the actual ULRs are considered to be accurately predicted. For each accuracy prediction group, the $\text{F}1=2\frac{\text{accuracy}\times \text{coverage}}{\text{accuracy}+\text{coverage}}$ score is calculated by adjusting the cut-off score and the sign of the score to maximize the target-averaged F1 score, because some groups did not submit local accuracy scores as predicted distance deviations.

ASSESSMENT RESULTS AND DISCUSSION

Classification of EMA methods to single-model and consensus methods

Accuracy of each model structure may be predicted based on the given single model or in the background of an ensemble of other models. Accuracy of a model structure is a property relative to the native structure, so an ideal accuracy estimation method may need a background of structures that can point towards the native structure. Many accuracy estimation methods in CASP use model structures generated by CASP TS servers as well as internally generated model structures. Traditionally, methods that use other TS server models tend to show high performance in CASP when compared to single-model methods⁶. However, the diversity and the quantity of the CASP TS server models are simply not available in non-CASP situations, so performance of consensus methods would not be transferable to real-life tasks. In distinction from previous CASP assessments, methods that employ additional model structures generated in-house but do not depend on CASP TS server models (formerly quasi-single methods) are also classified here as single-model methods because such methods also use single models as input.

Another issue regarding consensus methods is that the consensus methods end up exploiting the fact that many CASP tertiary structure prediction methods tend to generate similar models, especially when higher-accuracy predictions are possible. This is because TS servers from different research groups have evolved together over time with CASPs, sharing many prediction components and concepts, for example, template search method based on hidden-Markov models¹⁶ and contact prediction method based on co-evolutionary analysis¹⁷. It is therefore very difficult to assess whether high performance of CASP consensus model accuracy estimation methods over the single-model methods are due to the community-wide consensus effect in TS methods or not. An interesting phenomenon has been observed in this CASP regarding this issue, and it will be discussed at the end of the Results and Discussion section.

Accuracy estimation methods were classified to single-model methods and consensus methods based on the difference of the first and the second stage accuracy estimation results on the same model structures (see Methods). Among the 49 methods evaluated, 33 methods were designated as single-model methods and 16 as consensus. Details on the method classification can be found in Supplementary Figure S1. Throughout the figures in the paper, single-model methods are color-coded in green and consensus methods in black.

Assessment results of global accuracy estimation

Ranking in top 1 loss:

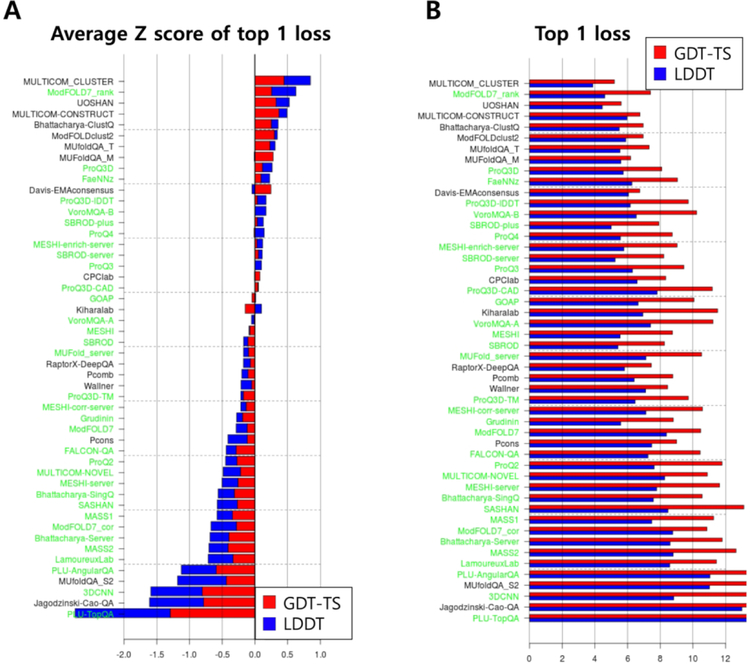
CASP13 ranking of EMA methods in global accuracy estimation in terms of top 1 loss is presented in Figure 1. The ranking is based on the sum of average Z-score of top 1 GDT-TS loss and average Z-score of top 1 LDDT loss. The Z-scores were averaged over the 65 and 76 targets for which at least one model had GDT-TS > 40 and LDDT > 40, respectively. The best consensus method according to this ranking is ‘MULTICOM_CLUSTER’, and the best single-model methods are ‘ModFOLD7_rank’, ‘ProQ3D’, and ‘FaeNNz’. Overall, Z-score of top 1 GDT-TS loss and that of top 1 LDDT loss are somewhat correlated. A statistical analysis of the performance differences among top groups is provided in Supplementary Figure S1.

Figure 1.

Ranking of the methods in global accuracy estimation in terms of top 1 loss. (A) Sum of average Z-score of top 1 GDT-TS loss and that of top 1 LDDT loss used to rank the methods is shown for each group, single-model methods in green and consensus methods in black. (B) Average values of top 1 GDT-TS/LDDT loss are shown. Scores for GDT-TS are shown in red, and those for LDDT in blue.

It is notable that single-model methods (green names) tend to do relatively better in LDDT (blue bars) than in GDT-TS (red bars), when compared to consensus methods(black). This means that single-model methods can select models of high LDDT scores better than models of high GDT-TS. This may be because GDT-TS depends more on the global character of the native structure, which in turn depends on the whole conformational space, making it difficult to estimate by training on single models. ‘ModFOLD7_rank’, a single-model method that was previously classified as quasi-single method²⁰, shows the largest Z-score of top 1 GDT-TS loss among single-model methods which is comparable to top consensus methods.

‘Davis-EMAconsensus’, a reference consensus method, shows very high performance in the top 1 GDT-TS loss. ‘Davis-EMAconsensus’ estimates model accuracy purely based on consensus, by scoring the ith model by an average GDT-TS to all other models in the pool as ${\text{score}}_i={\langle N_{\text{res},\text{model}}/N_{\text{res},\text{target}}{(\text{GDT-TS})}_{i,\text{model}}\rangle }_{\text{model}}$⁴. Z-score of top 1 GDT-TS loss for ‘Davis-EMAconsensus’ is even higher than that of the best single-model method in this category, ‘ModFOLD7_rank’. ‘GOAP,’ a distance- and orientation-dependent statistical potential²¹, was also examined as a reference single-model method, and performed above average in this CASP.

Average values of top 1 loss for GDT-TS and LDDT are shown in Figure 1B. Average top 1 GDT-TS loss and average top 1 LDDT loss are 5.2 and 3.9, respectively, for the best consensus method ‘MULTICOM_CLUSTER’, and 7.5 and 4.6, respectively, for the best single-model method ‘ModFOLD7_rank’. A single-model method ‘SBROD-plus’ and other variants of the ‘SBROD’ family of methods show very low (good) top 1 loss values, comparable to the top single-model methods, but their Z-scores are also low (bad) because predictions for some targets were not submitted and Z-scores of −2 were assigned for those targets.

Among the 65 (and 76) targets considered above for the top 1 GDT-TS (and LDDT) loss analysis, 10 (and 18) are composed of multiple EUs. Since relative orientation between evaluation units is not usually well predicted by TS servers, analysis of top 1 GDT-TS (and LDDT) loss was performed again with only the 55 (and 58) single-EU targets for which the relative EU orientation is not an issue. The overall ranking, especially for the top groups, did not change much, as can be seen from Supplementary Figure S2.

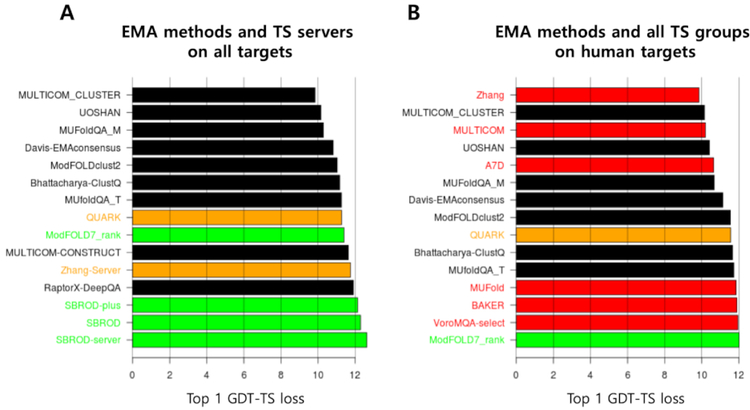
Performance of EMA methods as meta servers in top 1 GDT-TS loss:

In this section we examine performance of EMA methods as meta-servers (i.e., model selectors) in tertiary structure prediction Average top 1 GDT-TS loss of such meta-servers is shown in Figure 2A together with TS servers on all targets and in Figure 2B in comparison with all TS methods on human targets. The results are similar to those in the previous CASP in the sense that the best EMA methods perform better than the best TS servers, but not better than the best TS human method.

Figure 2.

Performance of EMA methods in average top 1 GDT-TS loss when EMA methods are used to select models from TS servers. (A) Comparison with TS servers on all targets and (B) comparison with all TS groups on human targets. Single-model EMA methods are colored in green, consensus EMA methods in black, TS servers in orange, and TS human groups in red.

Comparison of the meta-servers with TS servers is not fair because TS servers did not use other TS server models. There is no scientific or practical value of the meta-servers as competitors of TS human methods, as discussed earlier in the Introduction. Such comparisons were made here only for the purpose of checking the status of the current EMA relative to the TS methods and to the EMA methods of the previous CASPs.

The difference in top 1 GDT-TS loss between the top TS human method and the best EMA method is very small (~3%), implying that the current top tertiary prediction human groups added some, but not great values beyond consensus. It is notable that a pure consensus method ‘Davis-EMAconsensus’ is placed very high in this comparison, making us to suspect a high level of consensus among model structures in this CASP.

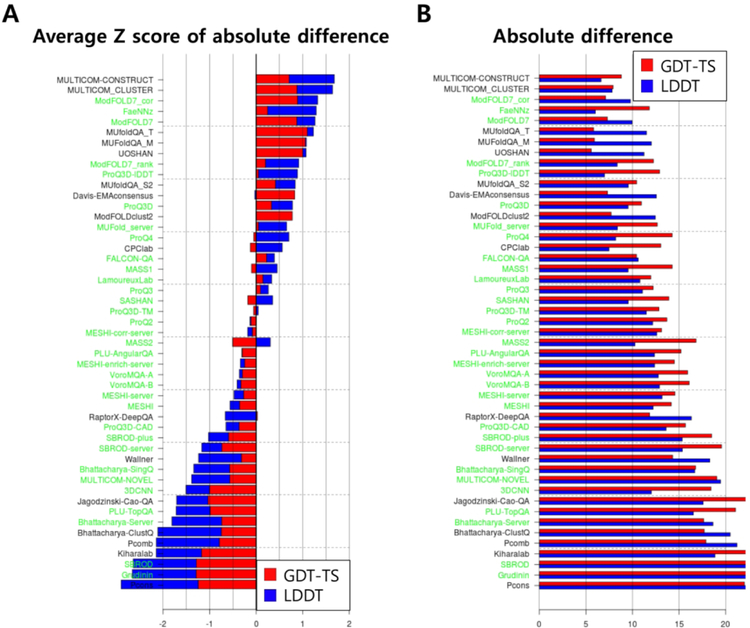
Ranking in absolute accuracy estimation:

CASP13 ranking of EMA methods in global accuracy estimation in terms of absolute score value is presented in Figure 3. This ranking is based on the sum of average Z-score of GDT-TS differences and average Z-score of LDDT differences, as shown in Figure 3A. The Z-scores were averaged over all 79 targets. According to this ranking, the best consensus method is ‘MULTICOM_CONSTRUCT’ and the best single-model method is ‘ModFOLD7_corr’. These methods are from the same groups that ranked the best in the top 1 loss analysis. The best absolute GDT-TS estimation was obtained by the consensus method ‘UOSHAN’ with the average GDT-TS difference of about 5.7 and the best LDDT estimation was achieved by the single-model method ‘FaeNNz’ with the average LDDT difference of 6.1 (Figure 3B). A statistical analysis of the performance differences among top groups is provided in Supplementary Figure S2.

Figure 3.

Ranking of the methods in global accuracy estimation in absolute accuracy estimation. (A) Sum of average Z-score of GDT-TS error and that of LDDT error used to rank the methods is shown for each group, single-model methods in green and consensus methods in black. (B) Average values of the absolute GDT-TS/LDDT error are shown. Scores for GDT-TS are shown in red, and those for LDDT in blue.

Assessment results of local accuracy estimation

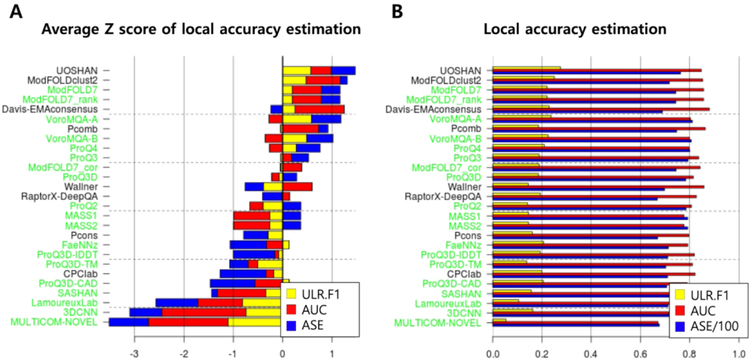
Ranking in local accuracy estimation:

CASP13 ranking of EMA methods in local accuracy estimation is presented in Figure 4. The ranking is based on the sum of average Z-scores of ASE, AUC, and ULR scores, as shown in Figure 4A. The Z-scores were averaged over the 108 evaluation units. According to this ranking, the best consensus method is ‘UOSHAN’, and the best single-model methods are ‘ModFOLD7’, ‘ModFOLD7_rank’, and ‘VoroMQA_A’. The three assessment measures ASE, AUC, and ULR do not show high correlation. In particular, the method that shows the best average Z-score of AUC, ‘Davis-EMAconsensus’, shows a negative average Z-score of ASE, and the method that shows the best average Z-score of ULR, ‘VoroMQA_A’, shows a negative average Z-score of AUC. Some methods predict local scores like LDDT or CAD instead of distance errors, and those methods perform poorly in the ASE measure because the 0 to 1 range of such scores results in in a predicted S-score of approximately 1 for all residues, while the reference S-score usually comes close to 1 only on a small subset of residues. A statistical analysis of the performance differences among top groups is provided in Supplementary Figures S3–S5 for each of the three local accuracy measures.

Figure 4.

Ranking of the methods in local accuracy estimation. (A) Sum of average Z-scores for ULR (yellow), AUC (red), and ASE (blue) used to rank the methods is shown for each group, single-model methods in green and consensus methods in black. (B) Average values of the individual measures are shown.

Prediction of inaccurately modeled regions:

ULR analysis has been introduced newly in this CASP for the assessment of local accuracy scores. The best average ULR F1 scores are 0.28 and 0.24 for the consensus method ‘UOSHAN’ and the single-model method ‘VoroMQA_A’, respectively. This means that inaccurately modeled regions (ULRs) in a model structure may be detected with accuracy and coverage of about 25% with current QA methods.

Inaccurately modeled loops and termini are typical ULRs, and mis-oriented secondary structure segments or secondary structure segments extended from loops are also assigned as ULRs, as illustrated in Supplementary Figure S3. ULRs occur due to the differences between the target and evolutionarily related proteins whose information is used for structure prediction. Template-based modeling uses structure information of related proteins in PDB, and template-free method may use contact information derived from related sequences. Therefore, ULRs may be relevant to functional specificity of the target protein, and thus important to model accurately by further refinement for functional studies or other applications. The average and median ULR lengths are 11.1 and 7, respectively, and the average number of ULRs per evaluation unit is 4.7 for the CASP13 models considered here. Such regions may be subject to model structure refinement if identified correctly. Accuracy of ULR prediction may be emphasized more than coverage at this point because the possibility of improving the initial model is not very high with current refinement methods.

Global accuracy estimation using local accuracy estimation:

An average of residue-wise local accuracy score was used as a global accuracy score for each evaluation unit, and the top 1 loss analysis was performed, as presented in Supplementary Figure S4. The global accuracy score generated in this way performed worse than the best methods presented in Figure 1 both in terms of the top 1 GDT-TS loss and the top 1 LDDT loss.

Progress over the previous CASPs

Progress of individual methods:

It is very difficult to assess progress in EMA methods over CASPs objectively because of the differences in the prediction targets and changes in the TS server methods that generate models. According to three top EMA participants of CASP13 (developers of ‘MULTICOM’, ‘ProQ’, and ‘ModFOLD’ series), their new versions of EMA methods showed better performance than their previous versions that participated in CASP12, when the previous versions were tested on the same CASP13 EMA targets²⁰.

Spuriously high performance of a pure consensus method ‘Davis-EMAconsensus’:

In addition to the progress made by individual groups, an analysis for the whole community has to be conducted. We therefore decided to adopt the approach of comparing the performance of the best methods with that of a reference method, as in the previous CASPs⁶. In CASP13, ‘Davis-EMAconsensus’, which was also used as a reference method in CASP12 to compare with the previous CASPs, performed significantly better than before. In CASP13, ‘Davis-EMAconsensus’ ranks higher than ‘ProQ3’ which was one of the best methods in CASP12 and was also tested in CASP13, as can be seen from the top 1 GDT-TS loss in Figure 1.

A detailed analysis revealed that the pure consensus method ‘Davis-EMAconsensus’ won over the single model method ‘ProQ3’ for a much higher fraction of “FM targets” in CASP13 (8 out of 11 FM targets) than in CASP 12 (only 1 out of 5 in CASP12). This implies that there was higher consensus among CASP13 TS models compared to CASP12 for FM targets. The fraction of FM targets selected for EMA experiment also increased because higher-accuracy models were generated for FM targets in CASP13 [ref: CASP13 FM assessment article]. The number of targets for which GDT-TS of the best model > 40, a criterion for EMA target, was 11 out of 15 single-EU FM targets in CASP13, compared to 5 out of 13 in CASP12. Higher consensus among top-quality CASP13 TS server models compared to CASP12 for all targets was also confirmed by the average pairwise GDT-TS for top 10 GDT-TS models, which increased from 40 in CASP12 to 59 in CASP13.

Progress in CASP EMA methods relative to reference methods:

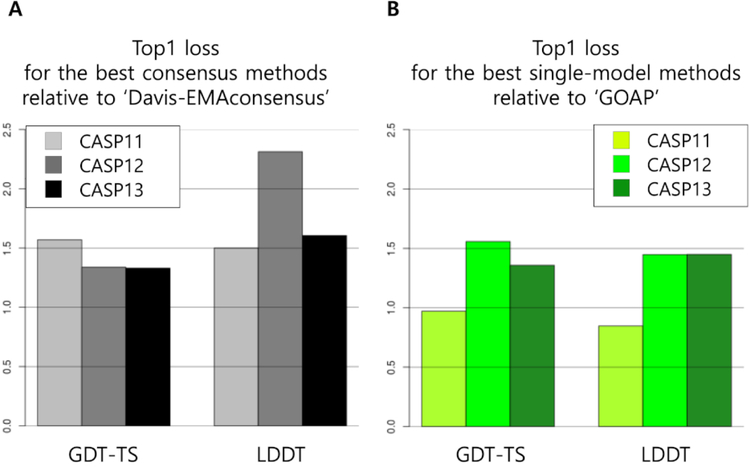
Performances in terms of top 1 GDT-TS/LDDT loss for the best methods relative to the reference methods in CASP11, 12, and 13 are presented in Figure 5A and 5B for consensus and single-model methods, respectively. A statistical potential ‘GOAP’²¹, was introduced as a reference method for single-model methods to exclude the effect of consensus. The best methods in Figure 5 in terms of GDT-TS and those in LDDT can be different.

Figure 5.

Performance comparison of EMA methods relative to the reference methods over the last three CASPs. (A) Ratio of top 1 loss of ‘Davis-EMAconsensus’ to that of the best consensus EMA method and (B) Ratio of top 1 loss of ‘GOAP’ to that of the best single-model method.

Figure 5A shows that the best consensus methods performed better than the reference consensus method ‘Davis-EMAconsensus’ with the ratio of top 1 loss > 1.0 in all CASPs in both GDT-TS and LDDT. However, the relative performance did not improve from CASP12 to CASP13. In particular, there is a sudden drop in the relative performance in top 1 LDDT loss from CASP12 to CASP13. This is due to the spuriously high performance of ‘Davis-EMAconsensus’, as discussed above.

According to Figure 5B, the best single-model methods performed worse than ‘GOAP’ in CASP11, but progressed to perform better in CASP12 and 13. However, relative performance of the best single-model methods in terms of top 1 GDT-TS decreased from CASP12 to CASP13, and that of top 1 LDDT remained the same. Since the absolute values of top 1 GDT-TS loss became large in CASP13 compared to CASP12 for both the best single-model method (5.0 to 7.5) and ‘GOAP’ (7.8 to 10.2), their relative performance in terms of ratio decreased significantly (1.56 to 1.36) although their performance in absolute difference decreased only slightly (2.8 to 2.7). Absolute values of top 1 LDDT loss for the best single-model methods also became large (3.0 to 4.6) in CASP13 compared to CASP12, although their ratio relative to ‘GOAP’ remained the same.

Reason for no progress relative to the reference methods:

Figure 5 shows no progress in relative performance of the best EMA methods to the reference methods. Relative performance of the best consensus method to ‘Davis-EMAconsensus’ did not improve because ‘Davis-EMAconsensus’ performed so well. ‘Davis-EMAconsensus’ performed particularly well on FM targets. The best consensus method in CASP13 (‘MULTICOM_CLUSTER’) also did significantly better than the best consensus method in CASP12 (‘MESHI_CON_SERVER’) on FM targets. This may be attributed to the fact that advent of more effective contact prediction methods for FM targets resulted in more high-quality models [ref: CASP13 FM server predictors’ articles].

Analysis on the performance of single-model methods relative to the reference method was more difficult because different methods showed very different behavior on different classes of targets. For example, ‘ModFOLD7_rank’, the best single-model method in CASP13 previously classified as a quasi-single method, showed slightly improved performance on FM targets and highly decreased performance on FM/TBM targets, while ‘GOAP’, the reference method, and ‘ProQ3’, one of the best single-model methods in CASP12, showed highly decreased performance on both FM and FM/TBM targets (See Supplementary Figure S5). The best single-model method in CASP12 (‘SVMQA’) did not participate in CASP13, making the analysis more difficult. Based on the fact that the individual groups showed progresses from CASP12 to CASP13 when tested on the same CASP13 targets²⁰, the decreased relative performance of the single-model methods to the reference may be attributed to the changed nature of the models generated by the CASP13 TS servers.

One clue is that many models of higher GDT-TS for CASP13 FM targets tend to have poor MolProbity score²² that measures physical reality and stereochemical correctness in the atomic level. Such models of poor MolProbity score tend not to be estimated highly by single-model methods that are strict on stereochemistry. This can be seen from Supplementary Table S6. While ‘Davis-EMAconsensus’ selected models of poor MolProbity score but higher GDT-TS, ‘GOAP’ selected models of better MolProbity score but lower GDT-TS, as shown in the table. A single-model method ‘ProQ3’ selected models of poor MolProbity score in a few cases because the method improves stereochemistry of models by sidechain sampling and energy minimization before accuracy estimation²³.

CONCLUSION

An increased number of model accuracy estimation methods, 51, participated in CASP13 compared to 42 in CASP12. The CASP13 experiment of EMA was run in the same way as in CASP12. However, very different features were discovered in CASP13 TS server models. First, CASP13 EMA had more FM targets for which high-quality models were generated by CASP13 TS servers. Second, there was higher consensus among high-quality models on average than ever before. This is due to the significant progress made in the TS prediction methods, including deep learning methods for extracting 3D contact information from 1D sequences of related proteins [ref: CASP13 FM server predictors’ articles]. Third, many model structures generated by using contact information were not well optimized at atomic-level structure [ref: CASP13 FM server predictors’ articles].

Such features of the models resulted in spuriously high performance of a pure consensus method compared to single-model methods. Single-model EMA methods showed progresses when compared to the previous versions individually on the same CASP13 targets²⁰, but performance relative to a reference method did not improve. This may be again due to the changed nature of the models generated in CASP13 by the new TS methods because the EMA methods were trained on the previous CASP models and methods.

The deep learning methods for tertiary structure prediction [ref: CASP13 TS assessment paper] seemingly affected the nature of the TS models presented for accuracy estimation. How accuracy estimation methods would deal with this new situation is left as an important challenge for EMA method developers. How deep learning methods themselves can affect future EMA method development is also an interesting point of view because effective deep learning requires relevant big data, and such big data may be generated with current technology.