Abstract
The intrinsically limited spatial resolution of PET confounds image quantitation. This paper presents an image deblurring and super-resolution framework for PET using anatomical guidance provided by high-resolution MR images. The framework relies on image-domain post-processing of already-reconstructed PET images by means of spatially-variant deconvolution stabilized by an MR-based joint entropy penalty function. The method is validated through simulation studies based on the BrainWeb digital phantom, experimental studies based on the Hoffman phantom, and clinical neuroimaging studies pertaining to aging and Alzheimer’s disease. The developed technique was compared with direct deconvolution and deconvolution stabilized by a quadratic difference penalty, a total variation penalty, and a Bowsher penalty. The BrainWeb simulation study showed improved image quality and quantitative accuracy measured by contrast-to-noise ratio, structural similarity index, root-mean-square error, and peak signal-to-noise ratio generated by this technique. The Hoffman phantom study indicated noticeable improvement in the structural similarity index (relative to the MR image) and gray-to-white contrast-to-noise ratio. Finally, clinical amyloid and tau imaging studies for Alzheimer’s disease showed lowering of the coefficient of variation in several key brain regions associated with two target pathologies.
Keywords: deblurring, super-resolution, joint entropy, PET, MR, partial volume correction
I. Introduction
POSITRON emission tomography (PET) is an in vivo medical imaging technique that enables visualization of the distribution of radiotracers that bind to specific molecular targets with functional or physiological significance [1]–[3]. The spatial resolution of PET is intrinsically very limited, thereby hindering its potential as a quantitative imaging tool, particularly for applications involving localized or constricted imaging targets. PET imaging systems capture coincidences of emitted pairs of photons traveling approximately collinearly in opposite directions following positron-electron annihilation events. A number of physical factors, some related to the imaging system hardware, limit PET resolution. These include the non-collinearity of the emitted photon pairs, intercrystal scatter, crystal penetration, and non-zero positron range of PET radionuclides [4]–[6]. Furthermore, it is fairly commonplace to use smoothing penalties during image reconstruction or to apply smoothing filters post-reconstruction for lowering the noise levels in the final images. This image-domain smoothing further compounds the resolution challenge [7]. Attempts to alleviate this challenge have led to the development of sophisticated edge-preserving penalties [8]–[10] or the incorporation of image-domain or sinogram-domain point spread functions (PSFs) in the PET image reconstruction framework [11]–[13]. Some techniques incorporate anatomical information from a segmented magnetic resonance (MR) image to guide the reconstruction process [14]–[19]. In contrast to these reconstruction methods, this paper aims to improve PET quantitation by means of a post-reconstruction processing technique that is applicable to existing images. Post-processing approaches have wider adoptability because they obviate the need for raw data. Furthermore, their relative simplicity resulting from the decoupling of the deblurring and reconstruction problems makes their adoption in a clinical setting easier than that for reconstruction-based tools.
In neurological contexts, quantitation based on PET usually entails the computation of a mean activity measure, such as standardized uptake value ratio (SUVR) or binding potential, over different regions-of-interest (ROIs). The combined effect of image blurring and spatial sampling for image digitization (the latter referred to as tissue fractioning) leads to the socalled partial volume effect, which manifests in PET images as spillover of estimated activity across different ROIs [20]. PET resolution recovery is key to the development of accurate image-based biomarkers based on ROI measures for Alzheimer’s disease and other neurological disorders [21]–[23]. From an image processing perspective, the combination of deblurring and upsampling to improve resolution and reduce tissue fractioning respectively is a super-resolution imaging problem [24]. In this paper, we present a super-resolution imaging framework for PET that incorporates anatomical information to assist and stabilize the deconvolution procedure required for deblurring.
While a range of iterative deconvolution techniques exist in literature, including those with additive or multiplicative updates like the Richardson-Lucy [25], [26] and Van Cittert [27] algorithms, standalone deconvolution is an ill-posed problem characterized by poor convergence and noise amplification. A variety of strategies have been employed to control noise, including early termination, edge-preserving penalty functions such as total variation [28], [29], and topology based regularization [30]. In [31], an MR-guided filtering strategy was demonstrated to be effective both as an edge-preserving post-filtering tool and as a deblurring tool. In [29], the PET image was modeled as a Markov random field with Gibbs interactions terms weighted by MR-derived edge information. Some correction techniques use wavelet or other transform domains for extracting anatomical information [32]. Additionally, a broad array of methods exist that attempt to correct for partial volume effects using a geometric transfer matrix (GTM) derived from anatomical parcellations [20], [33]–[37]. These methods assume (i) an approximate PSF that is stationary across the scanner bore and (ii) accurate segmentation of an anatomical image, which is often challenging. Here, we present an anatomically-guided PET image deblurring framework inspired by the success of information-theoretic priors in reconstruction [38], [39]. Unlike GTM-based methods, this technique does not require prior segmentation of the anatomical image. We offered a proof of concept for this idea in our earlier paper on this topic [40]. In this paper, we validate the idea using realistic simulation and phantom datasets and apply it to tau and amyloid imaging datasets from neuroimaging studies on Alzheimer’s disease. The details of estimation and optimization are presented in section II. Section III provides details on the simulation setup, experimental data acquisition, and validation. Section IV outlines the results obtained using this approach in comparison with other techniques. A discussion and a summary of this method are presented in sections V and VI respectively.
II. Theory
A. Blurring and Downsampling Model
PET images exhibit spatially-variant resolution depending on the radial and axial coordinates inside the cylindrical scanner bore. The PSF for PET can be modeled in either the sinogram (detector) domain or the image (voxel) domain. While modeling the PSF within the reconstruction framework, the choice between these two alternatives is guided by whether the primary contributor to blurring is the detector hardware (a sinogram-domain effect) or the positron range of the radioisotope (an image-domain effect). Post-reconstruction deblurring techniques, however, must exclusively rely on image-domain blur modeling. Here we model the blur using a series of image-based PSFs measured at multiple radial and axial locations in the scanner bore [12], [41], [42]. At all in-between locations, the blur model is determined as a linear combination of the PSF models at the nearest points of measurement, assuming radial and axial symmetry. As will be described in section III, to avoid an inverse crime, the simulation dataset for validation in this paper is generated using a sinogram-domain PSF while the correction is performed using an image-domain PSF model. Because the PSF depends on a number of factors, including the radioisotope choice and the scanner properties, we focused both simulation and experimental studies in this paper on a single radioisotope and scanner combination. The Siemens ECAT EXACT HR+ scanner was chosen due to its widespread use, and the 18F radioisotope was chosen as it is one of the preferred radionuclides for PET imaging studies.
Our framework utilizes a low-resolution 3D PET image which is scanner-generated and has n voxels and a high-resolution MR image with N voxels (N > n) to generate a super-resolution PET image with N voxels (same as the number of voxels in the scanner-generated high-resolution MR image). The PET image blurring and downsampling operation can be modeled using a system matrix , such that [43]:
| (1) |
Here is a block Toeplitz matrix representing the kth PSF, is a downsampling matrix, and K is the total number of PSFs. Linear combinations of the individual blur models are created using a series of diagonal matrices containing interpolation weights, such that:
| (2) |
where is the identity matrix. For an unknown high-resolution PET image vectorized as and a scanner-reconstructed low-resolution PET image , the least squares cost function for data fidelity is:
| (3) |
Multiplication by the forward model matrix (Ax) and its transpose (AT b) can be efficiently computed as linear combinations of 3D fast Fourier transform (FFT) outputs.
B. Joint Entropy Penalty
Most clinical and preclinical PET scanners come equipped with anatomical imaging capabilities, in the form of computed tomography (CT) or MR imaging, to complement the functional information in PET with structural information. We denote the unknown PET image as a vector , where N is the number of voxels in the image. Dividing the intensity range of the image into M equal-sized intensity bins, we create an intensity histogram vector from x, where ui is the number of voxels in the ith intensity bin. We denote the MR image as a vector and the corresponding intensity histogram based on M equal-sized intensity bins as . The joint entropy (JE) penalty function can be computed from the joint probability density function (pdf) in the intensity spaces of the two images as follows:
| (4) |
Here δu and δv are the widths of the discrete intensity bins and p(ui, Vj) is the ijth element of the joint pdf computed on the regularly spaced intensity grid. We approximately calculate the joint pdf using a Parzen window technique:
| (5) |
where is a 1D Gaussian kernel. Assuming σu >> δu and σv >> δv, the pdf can be obtained through a 2D convolution operation, which can be efficiently computed using the FFT:
| (6) |
Here represents the 2D convolution kernel, and is computed through bilinear interpolation of the joint histogram using the triangle function:
| (7) |
C. Iterative Optimization
The target image is the solution to the following constrained optimization problem:
| (8) |
To determine the optimal image, we adopt a gradient-based optimization strategy based on an iterative update:
| (9) |
where dk is the search direction at the kth iteration and αk is a scalar step size, which is typically computed using a backtracking line search. A number of gradient-based approaches can be employed to determine the descent direction dk. In Newton’s method, for example, the inverse of the Hessian is used as a preconditioner which modifies the negative gradient to compute the descent direction:
| (10) |
Here H(xk) is the Hessian matrix (comprised of second derivative terms) and gk is the gradient computed at the kth iteration. The quasi-Newton family of methods avoids the expensive computation of the Hessian matrix and its inverse using first-order approximations. The descent direction is based on a preconditioned negative gradient derived from an inverse Hessian approximation (denoted Lk):
| (11) |
To efficiently solve the constrained optimization problem in (8), we use a quasi-Newton type preconditioner based on the Limited-Memory Broyden-Fletcher-Goldfarb-Shanno (L-BFGS) method. A variant of this approach known as L-BFGS-B that combines L-BFGS updates with a gradient-projection strategy to impose box or bound constraints was utilized to ensure that the solution is restricted to the non-negative orthant. In the L-BFGS-B implementation, Lk is computed from first order-derivatives alone and is iteratively updated as follows:
| (12) |
where , s = xk+1 − xk, and t = gk+1 − gk.
D. Gradient Computation
The gradient at the kth iteration is computed as a weighted sum of the cost and penalty gradients:
| (13) |
1). Data-Fidelity Cost:
The gradient for the data-fidelity cost function is given by:
| (14) |
2). JE Penalty:
The gradient for the JE penalty can be computed from partial derivatives of the joint probability density function as follows:
| (15) |
where dp(ui, vj)/dxk can be approximately but efficiently computed by 2D FFT-based convolution:
| (16) |
III. Methods
A. Overview
In the following, we describe a simulation study using the BrainWeb digital phantom and the 18F-fluorodeoxyglucose (18F-FDG) radiotracer, an experimental phantom study using the Hoffman phantom and the 18F-FDG radiotracer, and two clinical neuroimaging studies for Alzheimer’s disease, one based on 18F-florbetapir (also known as 18F-AV-45), which targets amyloid plaques, and another based on 18F-flortaucipir (also known as 18F-AV-1451), which targets tau tangles. Amyloid plaques and tau tangles are two types of misfolded proteins that are pathological hallmarks of Alzheimer’s disease. All studies were based on the Siemens ECAT EXACT HR+ scanner. All low-resolution PET images have 2.54 mm × 2.54 mm × 2.43 mm voxels with a 128×128×63 grid size consistent with the HR+ output. All super-resolved PET images have 1 mm × 1 mm × 1 mm voxels with a 256×256×256 grid size consistent with the anatomical MR images used in this work. All PET images were reconstructed using the ordered subsets expectation maximization (OSEM) algorithm (6 iterations, 16 subsets) followed by 3D Gaussian filtering with 6 mm full width at half maximum (FWHM).
B. Simulation Setup
1). PSF Generation:
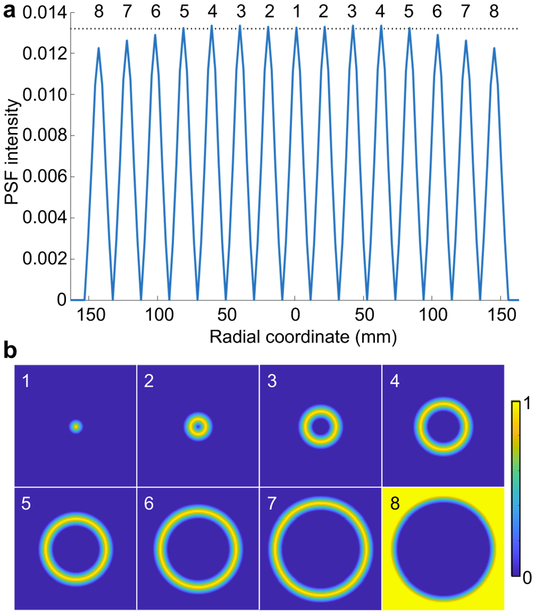
For 18F radiotracers, the positron range is negligible, and therefore the sinogram blurring model is reasonably accurate. A 1D radially-varying blur kernel has been demonstrated to be realistic via Monte Carlo simulations [12], [13]. All simulation data in the projection (sinogram) space were therefore subjected to a 1D radial blur. Axial variation in the blur kernel was not modeled in the simulation but has been incorporated into the PSF model for the phantom and clinical data subsequently described. Eight image-domain 3D PSFs corresponding to different radial locations were computed by reconstructing unit point sources at each location. These eight sampled PSFs, all fitted to Gaussian kernels, were used in the forward model in (1) for spatially-variant deblurring. The fitted PSFs at different radial locations (forming Hk) and the corresponding distribution of interpolation weights (forming Dk) in the transverse image plane are visualized in Fig. 1(a) and (b) respectively.
Fig. 1.
(a) Gaussian PSFs measured and fitted in the image domain from a simulated radially-varying sinogram-domain blur. The PSFs were sampled at eight radial locations starting at the center of the scanner bore and going outward. A dotted line has been included for reference. (b) Transverse slices showing the radially-varying linear interpolation weights (corresponding to the eight labeled PSFs). The weights at a given location are non-zero only for the two nearest PSFs.
2). Data Generation:
To validate the deblurring framework, we performed realistic simulations using the 3D BrainWeb digital phantom (http://brainweb.bic.mni.mcgill.ca/brainweb/). A T1-weighted MR image with 1 mm3 isotropic resolution was used from the BrainWeb database, and its corresponding segmented label volume with gray matter, white matter, blood pool, and cerebrospinal fluid ROIs was used to simulate a PET “ground truth” image. Dynamic PET time activity curves were simulated with ROI kinetic parameters as listed in Table I for gray matter (GM) and white matter (WM) tissue types. The dynamic frames were summed to generate a “ground-truth” static PET image arising from a 1 hour long 18F-FDG scan with a mean gray-to-white intensity ratio of 1.43. The geometric model of the HR+ scanner with sinogram-domain blurring was used to generate sinogram data. Noisy data were generated using Poisson noise realizations of the projected sinograms, a noise model widely accepted in the PET imaging community [44], The Poisson deviates were generated with a mean of 108 counts for the full scan duration of 3640 s.
TABLE I.
Simulated kinetic parameters for different ROIs in the brain
| ROI | Blood fraction |
K1 (ml min−1 g−1) |
k2 (min−1) |
k3 (min−1) |
k4 (min−1) |
|---|---|---|---|---|---|
| GM | 0.0446 | 0.1104 | 0.1910 | 0.1024 | 0.0094 |
| WM | 0.0270 | 0.0622 | 0.1248 | 0.0700 | 0.0097 |
C. Experimental Setup
1). PSF Measurement:
To estimate the true PSF, we placed 0.5 mm diameter point sources filled with 18F-FDG at different radial and axial positions inside the scanner bore, 56.2 cm in diameter and 15.5 cm in length. PSFs were sampled at eight radial locations and two axial locations (total 16 PSFs). The reconstructed PSF images were fitted with Gaussian kernels. The FWHM of the fitted PSFs had ranges of 6.03-7.21 mm and 6.63-7.89 mm in the radial and axial directions respectively. Interpolation weights for the experimental datasets were determined by means of bilinear interpolation over an irregular grid consisting of the quadrilaterals formed by the nearest radial and axial PSF sampling locations from a given point.
2). Phantom Scan:
The Hoffman brain phantom filled with 18F-FDG was scanned on the HR+ scanner for 15 min when the phantom activity was 27 MBq. A T2-weighted MR image of the phantom was separately acquired and rigidly coregistered with the PET image using FSL (https://fsl.fmrib.ox.ac.uk/) [45], [46].
3). Amyloid Scan:
The amyloid imaging data used in this paper were derived from the Alzheimer’s Disease Neuroimaging Initiative (ADNI) http://adni.loni.usc.edu, a public repository containing images and clinical data from 2000+ human datasets. An 81 year old male subject underwent a 10 mCi bolus injection of 18F-florbetapir followed by a 50 min scan on the HR+ in accordance with the ADNI-GO protocol. T1-weighted magnetization-prepared rapid gradientecho (MPRAGE) MR images were obtained and co-registered with the PET images using the FreeSurfer neuroimaging data processing suite (https://surfer.nmr.mgh.harvard.edu) [47], FreeSurfer was also used to parcellate the MR volume for ROI analysis.
4). Tau Scan:
The tau imaging data used in this paper were acquired at Massachusetts General Hospital (MGH). All procedures were performed after written informed consent and with approval from the MGH Institutional Review Board obtained satisfying appropriate protocol requirements. PET data were acquired for 90 min after a 10 mCi bolus injection of 18F-flortaucipir. MR image acquisition was performed on a 3T Tim Trio (Siemens). As with the amyloid study, the MR image was co-registered with the PET image using FreeSurfer. FreeSurfer was also used to parcellate the MR volume for ROI analysis.
D. Reference Approaches and Evaluation Metrics
We compare the results of deconvolution using a spatially-variant PSF with no penalty/prior (SVPSF), a quadratic penalty (QP) based on nearest neighbor differences, an anisotropic total variation (TV) penalty, and a Bowsher penalty (BP). These penalty functions are defined as follows:
| (17) |
| (18) |
| (19) |
where Δk, (k = 1, 2, or 3) are finite difference operators along the three Cartesian coordinate directions, ‘o’ denotes the Hadamard product, and the weights, wk, for the BP term are computed from the anatomical image y using a tuning parameter σb as follows [48]–[50]:
| (20) |
The evaluation metrics used here are defined below. We use the notation μx and σx for the mean and standard deviation respectively of an image x and and for the same statistics computed over an ROI . The true and estimated images are denoted x and respectively.
1). Contrast-to-Noise Ratio (CNR):
The CNR for a given ROI and a reference ROI is defined as:
| (21) |
2). Structural Similarity Index (SSIM):
The SSIM is a well-accepted measure of perceived image quality and is defined as:
| (22) |
Here c1 and c2 are parameters stabilizing the division.
3). Root-Mean-Square Error (RMSE):
The RMSE is computed as:
| (23) |
4). Peak Signal-to-Noise Ratio (PSNR):
The PSNR is the ratio of the maximum signal power to noise power and is defined as:
| (24) |
5). Coefficient of Variation (CV):
The CV for a given ROI is defined as:
| (25) |
For the simulation study, where the ground truth is known, we compute all the aforementioned metrics. For the phantom experiment where the ground truth is unknown, we only compute the CNR and MR-based SSIM. For the clinical datasets, we compute means of specific ROIs relevant to each pathology. The ROI mean SUVRs are useful as image-based biomarkers in diagnostics and therapeutics, including clinical trials for drug discovery. For localized ROIs, the CV measures of biomarkers are critical, especially while using image processing pipelines that tend to amplify noise. Accordingly, CV values for important ROIs are used to compare different methods for the clinical data.
IV. Results
A. Simulation Study
1). Parameter Selection and Initialization:
To select regularization parameters (weights of the penalty functions in the combined cost) for the BrainWeb digital phantom study, the QP, TV, BP, and JE regularization parameters were swept over a range of values. As a rule of thumb, a typical test value of the regularization parameter was set based on the ratio of the norms of the data-fitting and penalty gradients to: , where is an upsampled version of the blurry image b generated via trilinear interpolation, p is swept over a range of values {…, 4, 2, 1, 1/2, 1/4, … } with . Fig. 2 shows plots of gray-to-white CNR, SSIM, RMSE, and PSNR for the QP, TV, BP, and JE cases for different regularization parameters. The regularization parameters were selected to ensure the highest CNR as indicated by the inverted red triangles in Fig. 2. We observed that JE typically exhibits a peak in CNR and a corresponding dip in RMSE when the regularization parameter is in the optimal range. Very large values of the regularization parameter can substantially increase the RMSE and lower the CNR.
Fig. 2.
Regularization parameter selection. Plots of CNR, SSIM, RMSE, and PSNR for the QP, TV, BP, and JE techniques for different values of the regularization parameters. The regularization parameters that led to the highest CNR for each case are indicated by the inverted red triangles.
SVPSF (no penalty) suffers from the well-known instabilities of the standalone deconvolution problem. Continued iteration leads to noise amplification. The iteration number was set to a value of 20 in way of ensuring early termination. All methods were initialized by setting x0 to . QP, TV, BP, and JE were iterated till convergence. For the JE penalty, the Parzen window widths were set to σu = max(b)/q and σv = max(y)/q with q = 50, and M was set to 385.
2). Simulation Results:
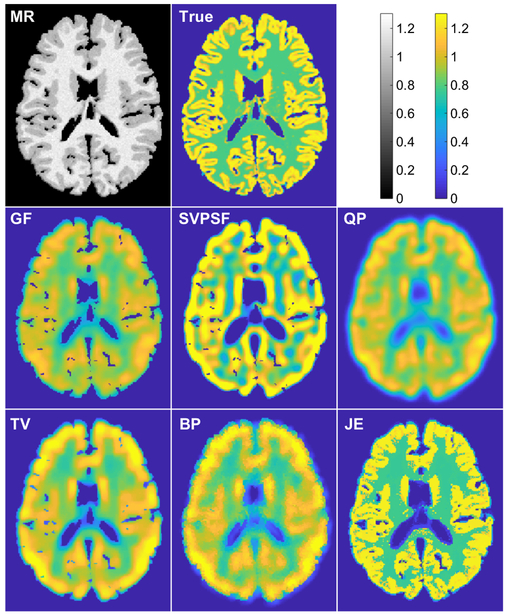
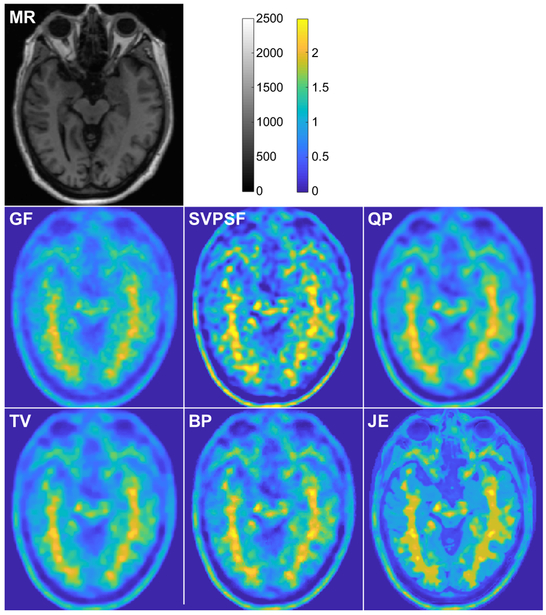
Fig. 3 shows a comparison of images obtained from the different methods. For SVPSF, the displayed image is the output of the 20th iteration. For QP, TV, BP, and JE, the displayed images correspond to the parameter values in Fig. 2 that led to maximum gray-to-white CNR for each case. Qualitatively, the JE penalty generated well-defined tissue boundaries well-conforming with the MR image. As expected, SVPSF led to noise amplification. With QP, the data-fitting cost function and smoothing penalty function are somewhat conflicted in terms of their ultimate goals but together lead to a stable solution unlike SVPSF. In comparison, TV and BP led to sharper images with better-defined edges. Table II shows the evaluation metrics for all displayed images. Among the methods compared here, JE produced the best values for all the metrics.
Fig. 3.
Simulation results. Transverse slices from the T1-MR image, true PET image, Gaussian-filtered OSEM image (GF), and deblurred images with the spatially-variant PSF but no penalty (SVPSF), quadratic penalty (QP), anisotropic total variation penalty (TV), Bowsher penalty (BP), and MR-based joint entropy penalty (JE).
TABLE II.
BrainWeb simulation study: Performance comparison
| Metric | SVPSF | QP | TV | BP | JE |
|---|---|---|---|---|---|
| CNR | 0.17 | 0.31 | 0.30 | 0.40 | 0.63 |
| SSIM | 0.90 | 0.91 | 0.91 | 0.92 | 0.94 |
| RMSE | 0.51 | 0.35 | 0.34 | 0.30 | 0.29 |
| PSNR | 17.22 | 18.92 | 18.99 | 20.23 | 20.59 |
3). Impact of the PSF Model:
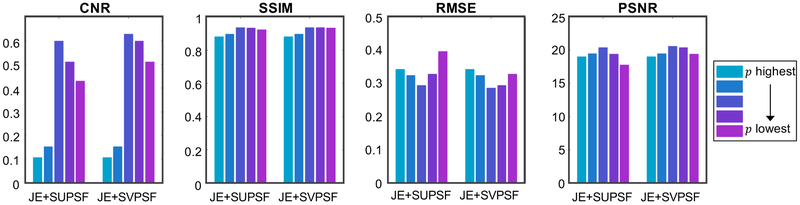
To determine the impact of the spatially-variant blurring model, we performed a comparison of this model with a spatially uniform PSF (SUPSF) model. Fig. 4 shows the evaluation metrics CNR, SSIM, RMSE, and PSNR for JE+SUPSF and JE+SVPSF. For this study, the PSF corresponding to the center of the scanner was used to create the SUPSF model. Compared to JE+SUPSF, JE+SVPSF showed a modest improvement in the best value obtained for each metric. More importantly, however, these plots show that the variation of the metrics with the regularization parameter is noticeably less drastic for SVPSF than SUPSF, indicating improved robustness of this model.
Fig. 4.
Comparison of SUPSF and SVPSF. The plots show the evaluation metrics CNR, SSIM, RMSE, and PSNR for JE+SUPSF and JE+SVPSF. SVPSF shows improvement in each metric relative to SUPSF. Also, compared to SUPSF, SVPSF demonstrated slower variation of the metrics with varying regularization parameter indicating improved robustness.
B. Experimental Studies
1). Phantom Results:
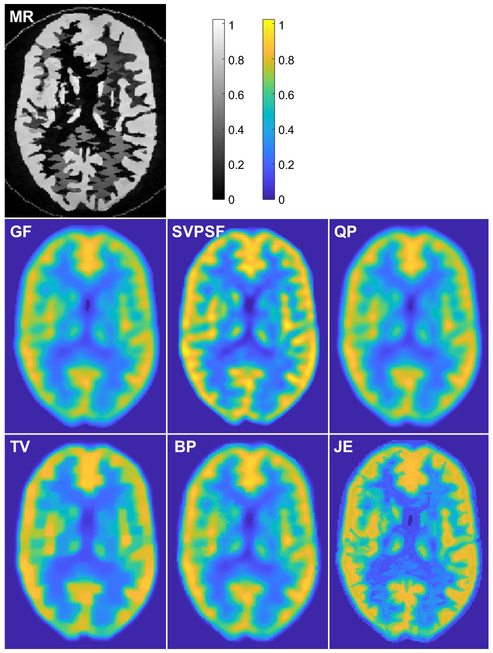
The SVPSF, QP, TV, BP, and JE deblurring techniques were applied to the Hoffman phantom dataset. Initialization of each method and JE Parzen window width selection were performed as described for the simulation study. Fig. 5 shows a comparison of images obtained from the different methods. For SVPSF, the displayed image is the output of the 20th iteration. For QP, TV, BP, and JE, the regularization parameter was set with p = 1/2, 2, 1 and 1 respectively to maximize the gray-to-white CNR for each case. JE led to well-defined boundaries matching the MR for the Hoffman phantom. TV produced a sharp image with a piecewise-constant appearance, while BP successfully incorporated some boundary information from the MR. SSIM (using the MR as a reference) and CNR are reported in Table III. JE led to higher values for both metrics relative to all other reference approaches.
Fig. 5.
Phantom experiment results. Transverse slices from the T2-MR image, Gaussian-filtered OSEM image (GF), and deblurred images with the spatially-variant PSF but no penalty (SVPSF), quadratic penalty (QP), anisotropic total variation penalty (TV), Bowsher penalty (BP), and MR-based joint entropy penalty (JE).
TABLE III.
Hoffman phantom study: Performance comparison
| Metric | SVPSF | QP | TV | BP | JE |
|---|---|---|---|---|---|
| CNR | 1.2814 | 1.1904 | 1.2245 | 1.3452 | 1.7968 |
| SSIM (MR) | 0.85 | 0.83 | 0.82 | 0.85 | 0.89 |
2). Clinical Results:
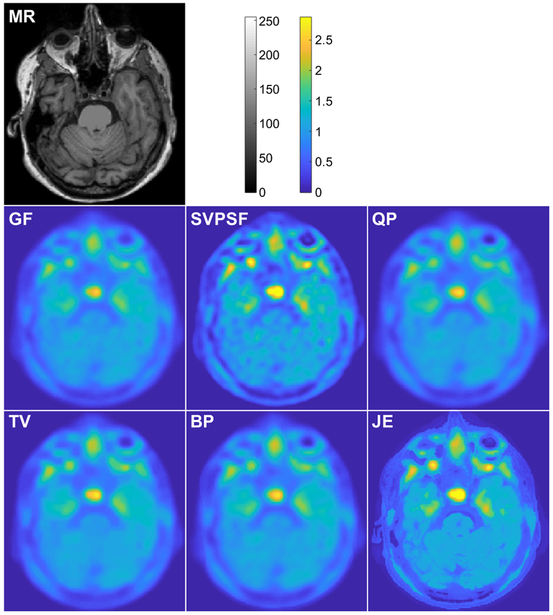
The SVPSF, QP, TV, BP, and JE deblurring techniques were applied to the amyloid and tau imaging datasets. Initialization of each method and JE Parzen window width selection were performed as described for the simulation study. Figs. 6 and 7 show comparisons of images obtained from the different methods for the amyloid and tau PET scans respectively. For SVPSF, the displayed image is the output of the 20th iteration. The regularization parameter was set heuristically so as to yield the lowest CVs in several key ROIs. Qualitatively, TV, BP, and JE produced sharper images than SVPSF and QP. As with the previous studies, JE led to well-defined boundaries matching the MRs for the clinical datasets.
Fig. 6.
Clinical results. Amyloid imaging study: Transverse slices from the T1-MR image, Gaussian-filtered OSEM image (GF), and deblurred images with the spatially-variant PSF but no penalty (SVPSF), quadratic penalty (QP), anisotropic total variation penalty (TV), Bowsher penalty (BP), and MR-based joint entropy penalty (JE).
Fig. 7.
Clinical results. Tau imaging study: Transverse slices from the T1-MR image, Gaussian-filtered OSEM image (GF), and deblurred images with the spatially-variant PSF but no penalty (SVPSF), quadratic penalty (QP), anisotropic total variation penalty (TV), Bowsher penalty (BP), and MR-based joint entropy penalty (JE).
For the amyloid study, CV values were computed for several clinically relevant ROIs for image-derived amyloid measures. Of these, the frontal-lateral-retrosplenial (FLR) area is generally used for image-based amyloid measures [51], [52], Several major sub-ROIs within the FLR were also examined, including frontal, temporal, and parietal cortices. Lastly, the striatal region was also evaluated separately as recent studies have highlighted distinct roles for cortical (FLR) amyloid and striatal amyloid measures [53], [54], The CVs for these regions are reported in Table IV. JE led to consistently lower CV values in all the ROIs relative to SVPSF, QP, TV, and BP.
TABLE IV.
Amyloid imaging study: Performance comparison
| Metric | SVPSF | QP | TV | BP | JE |
|---|---|---|---|---|---|
| CV: FLR | 0.4259 | 0.3103 | 0.2783 | 0.3270 | 0.2506 |
| CV: Frontal | 0.4876 | 0.3517 | 0.3247 | 0.3772 | 0.2704 |
| CV: Temporal | 0.4275 | 0.3217 | 0.2889 | 0.3348 | 0.2565 |
| CV: Parietal | 0.4035 | 0.2960 | 0.2859 | 0.3032 | 0.1975 |
| CV: Striatal | 0.3962 | 0.3069 | 0.2549 | 0.3217 | 0.2286 |
For the tau study, CV values were computed for a different set of clinically relevant ROIs considered critical for image-based tau measures. These include the inferior temporal cortex (ITC), middle temporal cortex (MTC), superior temporal cortex (STC), fusiform gyrus (FG), parahippocampal gyrus (PHG), and hippocampus (HC) [55], [56]. The CVs for these regions are reported in Table V. JE led to consistently lower CV values in all but one of the ROIs relative to SVPSF, QP, TV, and BP. The only exception was the hippocampus where QP had the best performance.
TABLE V.
Tau imaging study: Performance comparison
| Metric | SVPSF | QP | TV | BP | JE |
|---|---|---|---|---|---|
| CV: ITC | 0.1549 | 0.1404 | 0.1353 | 0.1377 | 0.1251 |
| CV: MTC | 0.1734 | 0.1484 | 0.1423 | 0.1459 | 0.1227 |
| CV: STC | 0.1787 | 0.1460 | 0.1421 | 0.1440 | 0.1299 |
| CV: FG | 0.1324 | 0.1042 | 0.0982 | 0.1018 | 0.0915 |
| CV: PHG | 0.1758 | 0.1458 | 0.1382 | 0.1426 | 0.1315 |
| CV: HC | 0.3311 | 0.1919 | 0.2048 | 0.1937 | 0.2548 |
V. Discussion
Overall, our simulation results indicate that JE leads to noticeable improvements in CNR, SSIM, RMSE, and PSNR compared to SVPSF (no penalty), QP, TV, and BP techniques. JE’s performance, however, may be quite sensitive to the choice of the regularization parameter. Very large values of the regularization parameter can substantially increase the RMSE and lower the CNR and sometimes introduce visual artifacts. One concern while incorporating cross-modality information with JE is the potential for crosstalk introduced by structural discrepancies between the PET and its anatomical counterpart. For example, MR features could sometimes be incorrectly introduced into PET images, or PET features could incorrectly be suppressed due to not being represented in the MR images. A related concern about JE is the potential imperfect mapping of edges in certain scenarios. For example, edges in the MR image may be over- or underrepresented in the JE-based PET image. The JE penalty, as defined here, is based on the similarity of image intensity distributions and does not contain spatial neighborhood information for the PET and MR image voxels. Crosstalk and imperfect edge mapping are known issues with information theoretic penalty functions and have been addressed in existing literature by embedding multiscale spatial features to make the penalty more robust [39], [57]. Our future work will focus on further investigations to address/alleviate this concern.
It should be noted that any anatomically-guided correction requires accurate multimodality co-registration. For intrasubject cases, standard rigid registration tools with 6 degrees-of-freedom have been demonstrated to work well. All studies in this paper, therefore, used well-characterized rigid registration tools that are part of routine neuroimaging data processing pipelines [45]–[47]. It should also be noted that PET image resolution is not only spatially-variant but also object-dependent. The latter cannot be fully accounted for via an image-domain correction. However, to reduce overall variability, we used the same image reconstruction protocol for the simulation, phantom, and clinical studies. Finally, we would like to emphasize that the deblurring framework does not model the PET noise covariances in the data-fidelity term, because the computation of the (iteration-dependent) covariance matrices of OSEM-reconstructed PET images is a challenging task [5]. The performance of the method for low-count images may need to be separately evaluated. For dynamic PET datasets (which typically have low-count earlier image frames), a more attractive strategy than postreconstruction deblurring may be to implement a JE prior for direct reconstruction of kinetic parameters.
For deblurring of post-filtered images, the Gaussian filtering step is typically the leading contributor to the blur. In cases where the raw (unfiltered) OSEM-reconstructed image is available, an MR-guided edge-preserving filter is an attractive option over deblurring after Gaussian filtering. However, in such cases, parameter tuning for the filter will be critical because different protocols use different OSEM iteration numbers, leading to different final noise levels. It should be added that, compared to post-reconstruction processing, reconstruction-based priors tend to be more effective from a quantitative perspective. However, this requires access to raw data, correction factors, and specialized reconstruction tools and models. A key advantage of the post-processing method presented here is its direct applicability to existing datasets for which the raw data (sinograms) and unfiltered images are either unavailable or not readily available.
For the clinical amyloid and tau imaging studies, CV measures were computed for several clinically meaningful ROIs. Our results show consistent lowering of CV in all amyloid ROIs. For tau, the CV was lower in all ROIs except the hippocampus. However, despite the significant role of the hippocampus in memory consolidation, it should be noted that 18F-flortaucipir suffers from well-known off-target effects in the vicinity of this ROI making it a poor candidate for ROI-based tau quantitation with this tracer [58].
VI. Conclusion
Despite the versatility of quantitative PET imaging arising from the availability of a wide gamut of radiotracers targeting different physiologically meaningful biomolecules, its quantitative accuracy is often limited by its poor spatial resolution. We have designed and implemented an anatomically guided framework that recovers PET resolution by means of deconvolution based on spatially-variant blur kernels measured in the image domain. The ill-posed deconvolution problem is stabilized using a JE prior based on the high-resolution MR counterpart of the PET. We tested the performance of this method using a BrainWeb phantom simulation, a Hoffman phantom experiment, and clinical amyloid and tau imaging scans. The method was compared with standalone deconvolution and penalized deconvolution using QP, TV, and BP regularization and demonstrated to be promising in terms of a number of evaluation metrics, including CNR, SSIM, RMSE, PSNR, and CV. As future work, we plan to develop a modified JE penalty that incorporates multiscale spatial information and is more robust against parameter variations and potential crosstalk introduced by structural discrepancies between the two modalities. ROI-based tau quantitation is promising for new biomarker development for Alzheimer’s disease, which, in turn, is vital for enabling drug development efforts. We will, therefore, apply this technique to specific neuroimaging scenarios pertaining to Alzheimer’s disease and validate the method by deriving CV measures for a much larger cohort.
Acknowledgment
This work was supported in part by the NIH grants K01AG050711 and P41EB022544.
Contributor Information
Tzu-An Song, Department of Electrical and Computer Engineering, University of Massachusetts Lowell, Lowell, MA, 01854, USA; Massachusetts General Hospital, Boston, MA, 02114, USA.
Fan Yang, Department of Electrical and Computer Engineering, University of Massachusetts Lowell, Lowell, MA, 01854, USA; Massachusetts General Hospital, Boston, MA, 02114, USA.
Samadrita Roy Chowdhury, Department of Electrical and Computer Engineering, University of Massachusetts Lowell, Lowell, MA, 01854, USA; Massachusetts General Hospital, Boston, MA, 02114, USA.
Kyungsang Kim, Massachusetts General Hospital, Boston, MA, 02114, USA..
Keith A. Johnson, Massachusetts General Hospital, Boston, MA, 02114, USA.
Georges El Fakhri, Massachusetts General Hospital, Boston, MA, 02114, USA..
Quanzheng Li, Massachusetts General Hospital, Boston, MA, 02114, USA..
Joyita Dutta, Department of Electrical and Computer Engineering, University of Massachusetts Lowell, Lowell, MA, 01854, USA; Massachusetts General Hospital, Boston, MA, 02114, USA.
References
- [1].Delbeke D, “Oncological applications of FDG PET imaging: brain tumors, colorectal cancer, lymphoma and melanoma,” J. Nucl. Med, vol. 40, no. 4, pp. 591–603, April 1999. [PubMed] [Google Scholar]
- [2].Bergmann SR, Fox KA, Rand AL, McElvany KD, Welch MJ, Markham J, and Sobel BE, “Quantification of regional myocardial blood flow in vivo with ,” Circulation, vol. 70, no. 4, pp. 724–733, October 1984. [DOI] [PubMed] [Google Scholar]
- [3].Farde L, Eriksson L, Blomquist G, and Halldin C, “Kinetic analysis of central [11C]raclopride binding to D2-dopamine receptors studied by PET–a comparison to the equilibrium analysis,” J. Cereb. Blood Flow Metab, vol. 9, no. 5, pp. 696–708, October 1989. [DOI] [PubMed] [Google Scholar]
- [4].Leahy RM and Qi J, “Statistical approaches in quantitative positron emission tomography,” Stat. Comput, vol. 10, no. 2, pp. 147–165, April 2000. [Google Scholar]
- [5].Dutta J, Ahn S, and Li Q, “Quantitative statistical methods for image quality assessment,” The ranostics, vol. 3, no. 10, pp. 741–756, October 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [6].Dutta J, Leahy RM, and Li Q, “Non-local means denoising of dynamic PET images,” PLoS ONE, vol. 8, no. 12, p. e81390, December 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [7].Qi J and Leahy RM, “Resolution and noise properties of MAP reconstruction for fully 3-D PET,” IEEE Trans. Med. Imaging, vol. 19, no. 5, pp. 493–506, May 2000. [DOI] [PubMed] [Google Scholar]
- [8].Wang G and Qi J, “Penalized likelihood PET image reconstruction using patch-based edge-preserving regularization,” IEEE Trans. Med. Imaging, vol. 31, no. 12, pp. 2194–2204, December 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [9].Kim K, Son YD, Bresler Y, Cho ZH, Ra JB, and Ye JC, “Dynamic PET reconstruction using temporal patch-based low rank penalty for ROI-based brain kinetic analysis,” Phys. Med. Biol, vol. 60, no. 5, pp. 2019–2046, March 2015. [DOI] [PubMed] [Google Scholar]
- [10].Wang G and Qi J, “Edge-preserving PET image reconstruction using trust optimization transfer,” IEEE Trans. Med. Imaging, vol. 34, no. 4, pp. 930–939, April 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [11].Reader AJ, Julyan PJ, Williams H, Hastings DL, and Zweit J, “EM algorithm system modeling by image-space techniques for PET reconstruction,” IEEE Trans. Nucl. Sci, vol. 50, no. 5, pp. 1392–1397, October 2003. [Google Scholar]
- [12].Alessio AM, Kinahan PE, and Lewellen TK, “Modeling and incorporation of system response functions in 3-D whole body PET,” IEEE Trans. Med. Imaging, vol. 25, no. 7, pp. 828–837, July 2006. [DOI] [PubMed] [Google Scholar]
- [13].Panin VY, Kehren F, Michel C, and Casey M, “Fully 3-D PET reconstruction with system matrix derived from point source measurements,” IEEE Trans. Med. Imaging, vol. 25, no. 7, pp. 907–921, July 2006. [DOI] [PubMed] [Google Scholar]
- [14].Leahy R and Yan X, “Incorporation of anatomical MR data for improved functional imaging with PET,” in Inf. Process. Med. Imaging., vol. 511 Springer, 1991, pp. 105–120. [Google Scholar]
- [15].Comtat C, Kinahan PE, Fessler JA, Beyer T, Townsend DW, Defrise M, and Michel C, “Clinically feasible reconstruction of 3D whole-body PET/CT data using blurred anatomical labels,” Phys. Med. Biol, vol. 47, no. 1, pp. 1–20, January 2002. [DOI] [PubMed] [Google Scholar]
- [16].Bowsher JE, Yuan H, Hedlund LW, Turkington TG, Akabani G, Badea A, Kurylo WC, Wheeler CT, Cofer GP, Dewhirst MW et al. , “Utilizing MRI information to estimate F18-FDG distributions in rat flank tumors,” in IEEE Nucl. Sci. Symp. Conf. Rec., vol. 4 IEEE, 2004, pp. 2488–2492. [Google Scholar]
- [17].Baete K, Nuyts J, Van Paesschen W, Suetens P, and Dupont P, “Anatomical-based FDG-PET reconstruction for the detection of hypometabolic regions in epilepsy,” IEEE Trans. Med. Imaging, vol. 23, no. 4, pp. 510–519, April 2004. [DOI] [PubMed] [Google Scholar]
- [18].Bataille F, Comtat C, Jan S, Sureau F, and Trebossen R, “Brain PET partial-volume compensation using blurred anatomical labels,” IEEE Trans. Nucl. Sci, vol. 54, no. 5, pp. 1606–1615, April 2007. [Google Scholar]
- [19].Pedemonte S, Bousse A, Hutton BF, Arridge S, and Ourselin S, “4-D generative model for PET/MRI reconstruction,” Med. Image Comput. Comput. Assist. Interv, vol. 14, no. Pt 1, pp. 581–588, 2011. [DOI] [PubMed] [Google Scholar]
- [20].Rousset OG, Ma Y, and Evans AC, “Correction for partial volume effects in PET: principle and validation,” J. Nucl. Med, vol. 39, no. 5, pp. 904–911, May 1998. [PubMed] [Google Scholar]
- [21].Su Y, Blazey TM, Snyder AZ, Raichle ME, Marcus DS, Ances BM, Bateman RJ, Cairns NJ, Aldea P, Cash L, Christensen JJ, Friedrichsen K, Hornbeck RC, Farrar AM, Owen CJ, Mayeux R, Brickman AM, Klunk W, Price JC, Thompson PM, Ghetti B, Saykin AJ, Sperling RA, Johnson KA, Schofield PR, Buckles V, Morris JC, and Benzinger TLS, “Partial volume correction in quantitative amyloid imaging,” Neuroimage, vol. 107, pp. 55–64, February 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [22].Yang J, Hu C, Guo N, Dutta J, Vaina LM, Johnson KA, Sepulcre J, Fakhri GE, and Li Q, “Partial volume correction for PET quantification and its impact on brain network in Alzheimer’s disease,” Sci. Rep, vol. 7, no. 1, p. 13035, October 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [23].Shidahara M, Thomas BA, Okamura N, Ibaraki M, Matsubara K, Oyama S, Ishikawa Y, Watanuki S, Iwata R, Furumoto S, Tashiro M, Yanai K, Gonda K, and Watabe H, “A comparison of five partial volume correction methods for Tau and Amyloid PET imaging with [18F]THK5351 and [11C]PIB,” Ann. Nucl. Med, vol. 31, no. 7, pp. 563–569, August 2017. [DOI] [PubMed] [Google Scholar]
- [24].Park SC, Park MK, and Kang MG, “Super-resolution image reconstruction: a technical overview,” IEEE Signal Process. Mag, vol. 20, no. 3, pp. 21–36, May 2003. [Google Scholar]
- [25].Richardson WH, “Bayesian-based iterative method of image restoration,” J. Opt. Soc. Am, vol. 62, no. 1, pp. 55–59, January 1972. [Google Scholar]
- [26].Lucy LB, “An iterative technique for the rectification of observed distributions,” Astron. J, vol. 79, p. 745, June 1974. [Google Scholar]
- [27].Van Cittert PH, “Zum Einfluß der Spaltbreite auf die Intensitätsverteilung in Spektrallinien II,” Z. Phys, vol. 69, no. 5–6, pp. 298–308, May 1931. [Google Scholar]
- [28].Tohka J and Reilhac A, “Deconvolution-based partial volume correction in Raclopride-PET and Monte Carlo comparison to MR-based method,” Neuroimage, vol. 39, no. 4, pp. 1570–1584, February 2008. [DOI] [PubMed] [Google Scholar]
- [29].Wang H and Fei B, “An MR image-guided, voxel-based partial volume correction method for PET images,” Med. Phys, vol. 39, no. 1, pp. 179195, January 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [30].Kirov AS, Piao JZ, and Schmidtlein CR, “Partial volume effect correction in PET using regularized iterative deconvolution with variance control based on local topology,” Phys. Med. Biol, vol. 53, no. 10, pp. 2577–2591, ”May 2008. [DOI] [PubMed] [Google Scholar]
- [31].Yan J, Lim JC, and Townsend DW, “MRI-guided brain PET image filtering and partial volume correction,” Phys. Med. Biol, vol. 60, no. 3, pp. 961–976, February 2015. [DOI] [PubMed] [Google Scholar]
- [32].Boussion N, Hatt M, Lamare F, Bizais Y, Turzo A, Cheze-Le Rest C, and Visvikis D, “A multiresolution image based approach for correction of partial volume effects in emission tomography,” Phys. Med. Biol, vol. 51, no. 7, pp. 1857–1876, April 2006. [DOI] [PubMed] [Google Scholar]
- [33].Meltzer CC, Leal JP, Mayberg HS, Wagner HN, and Frost JJ, “Correction of PET data for partial volume effects in human cerebral cortex by MR imaging,” J. Comput. Assist. Tomogr, vol. 14, no. 4, pp. 561–570, Jul-Aug 1990. [DOI] [PubMed] [Google Scholar]
- [34].Müller-Gärtner HW, Links JM, Prince JL, Bryan RN, McVeigh E, Leal JP, Davatzikos C, and Frost JJ, “Measurement of radiotracer concentration in brain gray matter using positron emission tomography: MRI-based correction for partial volume effects,” J. Cereb. Blood Flow Metab, vol. 12, no. 4, pp. 571–583, July 1992. [DOI] [PubMed] [Google Scholar]
- [35].Soret M, Bacharach SL, and Buvat I, “Partial-volume effect in PET tumor imaging,” J. Nucl. Med, vol. 48, no. 6, pp. 932–945, June 2007. [DOI] [PubMed] [Google Scholar]
- [36].Thomas BA, Erlandsson K, Modat M, Thurfjell L, Vandenberghe R, Ourselin S, and Hutton BF, “The importance of appropriate partial volume correction for PET quantification in Alzheimer’s disease,” Eur. J. Nucl. Med. Mol. Imaging, vol. 38, no. 6, pp. 1104–1119, June 2011. [DOI] [PubMed] [Google Scholar]
- [37].Bousse A, Pedemonte S, Thomas BA, Erlandsson K, Ourselin S, Arridge S, and Hutton BF, “Markov random field and Gaussian mixture for segmented MRI-based partial volume correction in PET,” Phys. Med. Biol, vol. 57, no. 20, p. 6681, 2012. [DOI] [PubMed] [Google Scholar]
- [38].Nuyts J, “The use of mutual information and joint entropy for anatomical priors in emission tomography,” in IEEE Nucl. Sci. Symp. Conf. Rec, vol. 6 IEEE, 2007, pp. 4149–4154. [Google Scholar]
- [39].Somayajula S, Panagiotou C, Rangarajan A, Li Q, Arridge SR, and Leahy RM, “PET image reconstruction using information theoretic anatomical priors,” IEEE Trans. Med. Imaging, vol. 30, no. 3, pp. 537549, March 2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [40].Dutta J, El Fakhri G, Zhu X, and Li Q, “PET point spread function modeling and image deblurring using a PET/MRI joint entropy prior,” in Proc. IEEE Int. Symp. Biomed. Imaging IEEE, 2015, pp. 1423–1426. [Google Scholar]
- [41].Cloquet C, Sureau FC, Defrise M, Van Simaeys G, Trotta N, and Goldman S, “Non-Gaussian space-variant resolution modelling for listmode reconstruction,” Phys. Med. Biol, vol. 55, no. 17, pp. 5045–5066, September 2010. [DOI] [PubMed] [Google Scholar]
- [42].Barbee DL, Flynn RT, Holden JE, Nickles RJ, and Jeraj R, “A method for partial volume correction of PET-imaged tumor heterogeneity using expectation maximization with a spatially varying point spread function,” Phys. Med. Biol, vol. 55, no. 1, pp. 221–236, January 2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [43].Nagy JG and O’Leary DP, “Restoring images degraded by spatially variant blur,” SIAM J. Sci. Comput, vol. 19, no. 4, pp. 1063–1082, July 1998. [Google Scholar]
- [44].Lange K, “Convergence of EM image reconstruction algorithms with Gibbs smoothing,” IEEE Trans. Med. Imaging, vol. 9, no. 4, pp. 439–446, December 1990. [DOI] [PubMed] [Google Scholar]
- [45].Jenkinson M and Smith S, “A global optimisation method for robust affine registration of brain images,” Med. Image Anal, vol. 5, no. 2, pp. 143–156, June 2001. [DOI] [PubMed] [Google Scholar]
- [46].Jenkinson M, Bannister P, Brady M, and Smith S, “Improved optimization for the robust and accurate linear registration and motion correction of brain images,” Neuroimage, vol. 17, no. 2, pp. 825–841, October 2002. [DOI] [PubMed] [Google Scholar]
- [47].Greve DN and Fischl B, “Accurate and robust brain image alignment using boundary-based registration,” Neuroimage, vol. 48, no. 1, pp. 6372, October 2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [48].Bousse A, Pedemonte S, Kazantsev D, Ourselin S, Arridge S, and Hutton BF, “Weighted MRI-based Bowsher priors for SPECT brain image reconstruction,” in IEEE Nucl. Sci. Symp. Conf. Rec. IEEE, 2010, pp. 3519–3522. [Google Scholar]
- [49].Kazantsev D, Bousse A, Pedemonte S, Arridge SR, Hutton BF, and Ourselin S, “Edge preserving Bowsher prior with nonlocal weighting for 3D SPECT reconstruction,” in Proc. IEEE Int. Symp. Biomed. Imaging. IEEE, 2011, pp. 1158–1161. [Google Scholar]
- [50].Lu L, Ma J, Feng Q, Chen W, and Rahmim A, “Anatomy-guided brain PET imaging incorporating a joint prior model,” Phys Med Biol, vol. 60, no. 6, pp. 2145–2166, March 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [51].Hedden T, Van Dijk KR, Becker JA, Mehta A, Sperling RA, Johnson KA, and Buckner RL, “Disruption of functional connectivity in clinically normal older adults harboring amyloid burden,” J. Neurosci, vol. 29, no. 40, pp. 12686–12694, October 2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [52].Buckley RF, Hanseeuw B, Schultz AP, Vannini P, Aghjayan SL, Properzi MJ, Jackson JD, Mormino EC, Rentz DM, Sperling RA, Johnson KA, and Amariglio RE, “Region-specific association of subjective cognitive decline with tauopathy independent of global β-amyloid burden,” JAMA Neurol, vol. 74, no. 12, pp. 1455–1463, December 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [53].Ishibashi K, Ishiwata K, Toyohara J, Murayama S, and Ishii K, “Regional analysis of striatal and cortical amyloid deposition in patients with Alzheimer’s disease,” Eur. J. Neurosci, vol. 40, no. 4, pp. 2701–2706, August 2014. [DOI] [PubMed] [Google Scholar]
- [54].Sauerbeck J, Ishii K, Hosokawa C, Kaida H, Scheiwein FT, Hanaoka K, Rominger A, Brendel M, Bartenstein P, and Murakami T, “The correlation between striatal and cortical binding ratio of 11C-PiB-PET in amyloid-uptake-positive patients,” Ann. Nucl. Med, vol. 32, no. 6, pp. 398–403, July 2018. [DOI] [PubMed] [Google Scholar]
- [55].Johnson KA, Schultz A, Betensky RA, Becker JA, Sepulcre J, Rentz D, Mormino E, Chhatwal J, Amariglio R, Papp K, Marshall G, Albers M, Mauro S, Pepin L, Alverio J, Judge K, Philiossaint M, Shoup T, Yokell D, Dickerson B, Gomez-Isla T, Hyman B, Vasdev N, and Sperling R, “Tau positron emission tomographic imaging in aging and early Alzheimer disease,” Ann. Neurol, vol. 79, no. 1, pp. 110–119, January 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [56].Jack CR, Wiste HJ, Schwarz CG, Lowe VJ, Senjem ML, Vemuri P, Weigand SD, Therneau TM, Knopman DS, Gunter JL, Jones DT, Graff-Radford J, Kantarci K, Roberts RO, Mielke MM, Machulda MM, and Petersen RC, “Longitudinal tau PET in ageing and Alzheimer’s disease,” Brain, vol. 141, no. 5, pp. 1517–1528, May 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [57].Tang J and Rahmim A, “Anatomy assisted PET image reconstruction incorporating multi-resolution joint entropy,” Phys Med Biol, vol. 60, no. 1, pp. 31–48, January 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [58].Ikonomovic MD, Abrahamson EE, Price JC, Mathis CA, and Klunk WE, “[F-18]AV-1451 positron emission tomography retention in choroid plexus: More than “off-target” binding,” Ann. Neurol, vol. 80, no. 2, pp. 307–308, August 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]