Size-optimized Ultrasmall Porous Silica Nanoparticles Depict Vasculature-based Differential Targeting in Triple Negative Breast Cancer

Abstract

Rapid sequestration and prolonged retention of intravenously injected nanoparticles by the liver and spleen (reticuloendothelial system (RES)) presents a major barrier to effective delivery to the target site and hampers clinical translation of nanomedicine. Inspired by biological macromolecular drugs, synthesis of ultrasmall (diameter ~12 −15 nm) porous silica nanoparticles (UPSNs), capable of prolonged plasma half-life, attenuated RES sequestration, and accelerated hepatobiliary clearance, is reported. The study further investigates the effect of tumor vascularization on uptake and retention of UPSNs in two mouse models of triple negative breast cancer (TNBC) with distinctly different microenvironments. A semi-mechanistic mathematical model is developed to gain mechanistic insights into the interactions between the UPSNs and the biological entities of interest, specifically the RES. Despite similar systemic pharmacokinetic (PK) profiles, UPSNs demonstrate strikingly different tumor responses in the two models. Histopathology confirmed the differences in vasculature and stromal status of the two models, and corresponding differences in the microscopic distribution of UPSNs within the tumors. The studies demonstrate the successful application of multidisciplinary and complementary approaches, based on laboratory experimentation and mathematical modeling, to concurrently design optimized nanomaterials, and investigate their complex biological interactions, in order to drive innovation and translation.

Graphical Abstract

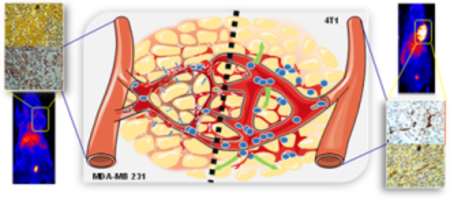
Ultrasmall porous silica nanoparticles are developed with prolonged blood circulation, enhanced tumor uptake and hepatic clearance, precisely monitored in vivo by real-time longitudinal positron emission tomography. In vivo pharmacokinetics and nano-bio interactions are studied in two models of triple negative breast cancer, complemented by semi-mechanistic mathematical modeling and high resolution microscopy.

1. Introduction

Nanoparticles (NPs) have been often termed as “magic bullets” for their ability to carry out targeted drug delivery, and the past two decades have seen an unprecedented boom in research activities in the area of nanomedicine, specifically in oncology, resulting in a tremendous volume of work published each year.[1] Unfortunately, the pace of translation has failed to keep up with the rapid pace of innovation, and only a handful of nanotechnologies have made it to the clinic or clinical trials.[2] A recently published meta-analysis concluded that less than 0.7 % of intravenously injected (i.v.) nanomedicines reach the tumor.[3] Although this is a significant improvement when compared to i.v. injected small molecule drugs, concerns about high and long-term sequestration of NPs by the reticuloendothelial system (RES), and associated potential toxicities, have posed serious barriers to the clinical translation of nanomedicines.[4, 5] Hence, ultrasmall renal clearable, and larger biodegradable NP have been proposed, each with their own advantages and disadvantages.[6, 7] For example, although rapid clearance of ultrasmall NPs (< 8 nm, the renal clearance threshold) via the renal pathway reduces toxicity concerns, it also impedes sufficient accumulation at the tumor site for effective tumor inhibition.[8] On the other hand, engineering biodegradable NPs with tailored in vivo degradation and PK profiles remains a significant technological impediment.[9] Despite advantages such as enhanced loading and co-delivery of both small and macromolecular drugs,[10] long-term and comprehensive in vivo studies documenting their tumor uptake, drug delivery, and successful hepatobiliary clearance are yet to be explored.

To address the long-standing dilemma, we took cues from macromolecular biologics such as antibodies, and designed ultrasmall porous silica nanoparticles (UPSNs), with size optimized to mimic that of antibodies. We hypothesized that this size range (hydrodynamic diameter ~10–15 nm) would be large enough to resist rapid renal clearance and accumulate selectively at the tumor site via enhanced permeability and retention (EPR) effect, but small enough to resist early sequestration by the RES, and clear via the hepatobiliary pathway within a reasonable timeframe. Introduction of porosity into the UPSNs aimed to deviate from a strictly spherical morphology, for improved hemodynamic performance, as well as to enhance the surface area for facile surface engineering.[11]

Despite significant progress, the ability to strictly and effectively manipulate the in vivo behavior of NPs remains elusive, partly due to the oversimplification of the complex biodistribution processes. Moreover, the heterogeneity in tumor microenvironment (TME) has been correlated with differential patient response to therapeutic NPs, which tend to distribute differently across tumors. Parameters such as tumor vascularization, stromal stiffness, and cellularity have been shown to influence NP extravasation and penetration into the tumors.[12] The key to selective accumulation of NPs in tumors lies in both the structural properties of NPs and tumors. Thus, it is pertinent that NPs can be rationally designed with superior pharmacokinetic (PK) properties, and that their in vivo behavior, specifically, their interactions with the TME, be investigated in detail.

The goal of this study was to understand the in vivo transport and intratumoral distribution of the UPSNs, in order to determine the influence of TME on their biological performance. We employed non-invasive, longitudinal positron emission tomography (PET) to gain insights into the macromolecular dynamic interactions of UPSNs with the biological milieu. These results were subsequently modeled using a multi-compartment, semi-mechanistic mathematical model to provide a description of UPSN disposition kinetics in vivo. Compared to empirical PK modeling approaches that solely model plasma concentration kinetics of NPs, multi-compartment, whole-body scale models are physiologically more realistic, and provide a thorough understanding of systemic distribution and clearance of NPs, including kinetics in tumor.[2] Thus, mathematical models that incorporate the relevant physiological information can more reliably predict the pharmacological effects of NPs. We found that the model presented here was able to accurately describe the plasma and tissue disposition kinetics of UPSNs. Furthermore, two widely used models of triple negative breast cancer (TNBC), 4T1 and MDA-MB 231, were chosen to evaluate passive tumor targeting of UPSNs afforded by ultrasmall size, prolonged blood circulation, and reduced non-specific RES sequestration. Results from microscopic and histopathological analyses indicated that significant disparities existed within the TME of syngeneic and xenograft TNBC models and contributed to the differences in UPSN infiltration into the tumors.

2. Results and Discussion

2.1. Synthesis and Characterization of UPSNs.

Precisely controlled PEGylated UPSNs with hydrodynamic diameters; HD: ~13.64 ± 1.99 nm; PdI: 0.13 (Figure 1D) and singular pores ~ 1.767 nm in diameter, were synthesized by condensing a rapidly hydrolyzing silica precursor, tetramethyl orthosilicate (TMOS) in the presence of hexadecyltrimethyl ammonium bromide (CTAB) structure-directing micelles and ammonium hydroxide as a catalyst.[13] PEG₅₀₀-silane, followed by 0.1 mol % N-3-[amino-(polypropylenoxy)]aminopropyltrimethoxysilane (NH₂-PPO₃₅₀-silane), was added to the reaction mixture for 24 h at 30 °C, to quench particle growth and sterically stabilize the nanoparticles. (Figure 1A) The addition of NH₂-PPO₃₅₀-silane was refined iteratively in terms of amount, time of addition and reaction duration. Substitution of 0.1 mol % PEG₅₀₀-silane by NH₂-PPO₃₅₀-silane was found to be optimal, allowing the incorporation of sufficient number of functional amine moieties for further surface engineering, without significantly affecting the reaction conditions or UPSN morphology, stability, or biological behavior. This was followed by post-synthesis heating at 80 °C for further 24 h. The final product was generated after acid extraction of the CTAB template by dialysis, and exhaustive washing with miliQ water. The purification procedures undertaken were found sufficient in removing or dispersing any undesirable micelles formed by condensation of PEG₅₀₀-silane and NH₂-PPO₃₅₀-silane, yielding homogenously sized UPSN population.

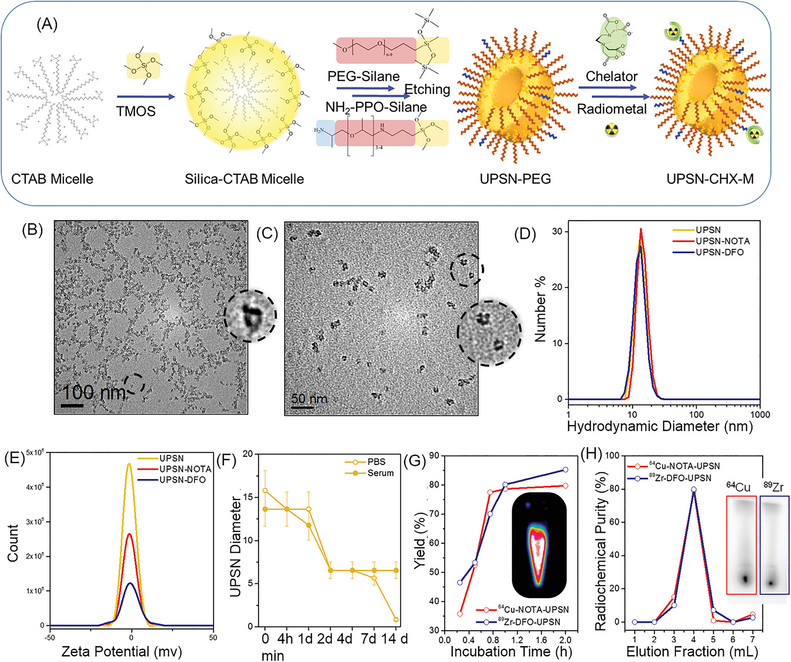
Figure 1. Synthesis and Characterization.

(A) Schematic of the synthesis strategy and surface modification of UPSNs. Rapidly hydrolyzing silica precursor TMOS is condensed on CTAB (surfactant) micelles, followed by arrest of nanoparticle growth by addition of PEG-silane (capping agent). NH₂-PPO-silane is added to impart functional amine groups for further conjugation of chelator (CHX) for radiolabeling or fluorescent dyes for in vivo studies. TEM images of (B) UPSN and (C) UPSN-CHX. Insets show a magnified image of an individual UPSN with fully-formed single pores in the center. (D) Hydrodynamic diameters and (E) zeta potential measurements of UPSN and UPSN-CHX in water/PBS. (F) Change in hydrodynamic diameters of UPSN immersed in PBS or serum, over a period of 2 weeks. (G) Radiolabeling yield and (H) radiochemical purity of ⁶⁴Cu-NOTA-UPSN and ⁸⁹Zr-DFO-UPSN. Inset in (G) depicts PET image of ⁶⁴Cu-NOTA-UPSN sample. Inset in (H) represents thin layer chromatographs (TLC) of ⁶⁴Cu-NOTA-UPSN and ⁸⁹Zr-DFO-UPSN depicting high radiochemical yield and purity with negligible migration of free isotope to the solvent front.

Nanoparticle size and size distribution were measured by transmission electron microscopy (TEM) and dynamic light scattering (DLS), revealing well-dispersed populations with narrow size distribution and absence of aggregation. (Figure 1B, D) TEM at a higher magnification revealed well-formed UPSNs with fully formed, highly uniform single pores. (Figure 1B (inset) and Supplementary figure S1A–B, outset; green box) A small percentage of UPSNs possessed half pores, forming a sac-like nanostructure, possibly due to incomplete encapsulation of CTAB micelles by silica precursor (Supplementary figure S1A–B outset; yellow box). A small population of UPSNs also depicted non-porous morphology. As expected, TEM measurements demonstrated smaller average diameters (11.06 ± 1.45, PdI: 1.002) and larger pore sizes (2.99 ± 1.02) since this technique is insensitive to hydrodynamic layer formed by PEG surface coating (Supplementary figure S1D). Importantly, as-synthesized UPSNs demonstrated prolonged long shelf-life. When formulated in miliQ water, the nanoparticles remained stable even after 6 months, confirmed by DLS measurements. Intensity, volume and number measurements indicated well-dispersed populations with narrow size distributions: 17.23 ± 0.48, 14.6 ± 0.2, and 12.82 ± 0.43, respectively, and absence of aggregation (Supplementary figure S2A). The ability to strictly control particle size within a biologically favorable range, indicates great promise for this one-pot synthesis strategy.

Near neutral surface charge of UPSNs (zeta potential: 0.77 ± 0.1 mV) measured in PBS, pH 7.4 indicated almost complete coverage of surface silanol groups with PEG and PPO chains (Figure 1E). UPSNs were further characterized by nitrogen sorption/desorption measurements. Introducing porosity into the nanosystem significantly increased the surface area, when compared to similarly sized nanoparticles, reported in literature.[14, 15] BET/BJH isotherms indicated a surface area of 156.168 m²/g, pore size ~ 1.767 nm and pore volume of 0.279 cm³/g. The increased surface area and volume could be potentially harnessed in the future for enhanced conjugation and delivery of small molecule drugs, radiotherapeutics and photosensitizers. FTIR spectra of as-synthesized UPSNs indicated a Si-O-CH₃ peak at 795 cm⁻¹, silanol (Si-O-H) peak at 945 cm⁻¹ and silica vibrations (Si-O-Si) at 1075 and 985 cm⁻¹ (Supplementary figure S2B). A large peak at 713 cm⁻¹ due to (-CH₂-)_n indicated the presence of PEG chains, while absence of peaks at 2850 and 2920 cm⁻¹ (indicative of symmetric and asymmetric stretching of C-H region in CTAB) confirmed the removal of the surfactant.

Long-term structural stability of UPSNs was tested in vitro, under physiological conditions (pH 7.4), both in PBS and mouse serum. Hydrodynamic size was monitored over a two-week period. (Figure 1F) As-synthesized UPSNs depicted a gradual dissolution in PBS, evidenced by shift in DLS histograms towards smaller sizes, day 2 onwards (Supplementary figure S2C). The disintegration process appears to be complete by day 14, as seen by the emergence of a sole peak around 1 nm in diameter, attributed to UPSN fragments or its molecular components. The dissolution or disintegration was decelerated in serum, where a shift is observed by day 4, possibly due to adsorption of serum proteins. (Supplementary figure S2D) A reduction in size to below renal clearance threshold (~8 nm) was observed over a period of 14 days (HD: ~4 – 6 nm), however, it was difficult to distinguish between the UPSN fragments and serum proteins. Of note, UPSNs demonstrated excellent colloidal stability, as seen by the absence of aggregation either in PBS or serum throughout the study period, predictive of their excellent potential as intravenously administered agents. Majority of nanomedicine formulations, although stable under normal storage conditions, tend to aggregate in complex biological fluids, such as blood, directly altering their biodistribution, and hence, efficacy and immune responses in the body.[16]

2.2. Surface engineering of UPSN and radiolabeling.

Minor tweaking of the synthetic precursors, i.e. substitution of 0.1 mol % PEG₅₀₀-silane by NH₂-PPO₃₅₀-silane conferred surface functional amine groups on UPSN, for further conjugation of radiometal chelators (CHX) and dyes, for in vivo studies. Aminated UPSN was conjugated to either deferroxamine (DFO) or 2-S-(4-Isothiocyanatobenzyl)-1,4,7-triazacyclononane-1,4,7-triacetic acid (NOTA), following previously reported amine-isothiocyanate chemistry.[17] TEM images indicated no change in morphology. (Figure 1C and Supplementary figure S1C) DLS measurements indicated uniform, well-dispersed populations for both UPSN-DFO (14.78 ± 2.78; PdI: 0.146) and UPSN-NOTA (12.76 ± 2.40; PdI: 0.19) and negligible change in surface charge. (Figure 1D–E) Subsequently, UPSN-DFO was radiolabeled with long-lived radioisotope, zirconium-89 (⁸⁹Zr; t_1/2 = 78.4 h) for long-term assessment of UPSN biodistribution, while UPSN-NOTA was labeled with short-lived copper-64 (⁶⁴Cu; t_1/2 = 12.7 h) for tumor tropism studies, following previously optimized protocols.[17, 18] As seen in Figure 1G and 1H, both ⁶⁴Cu-NOTA-UPSN and ⁸⁹Zr-DFO-UPSN demonstrated high radiochemical yields (> 85 %) within 2 h of incubation, and final products were isolated with high radiochemical purity. Serum stability studies were performed with radio-TLC, and indicated excellent fidelity of the isotope, > 62 % and 40 % intact radioactivity, 2 and 14 days post-incubation for ⁶⁴Cu-NOTA-UPSN and ⁸⁹Zr-DFO-UPSN, respectively. (Supplementary figure S3). The gradual loss of isotopes from the nanoconstructs may be attributed to both detachment from the chelator, as well as dissolution of the nanoparticles (previously shown in Supplementary figure S2).

2.3. Pharmacokinetics of ⁶⁴Cu-NOTA-UPSN and ⁸⁹Zr-DFO-UPSN.

Whole-body PET imaging was employed to gain greater information about the key components of UPSN PK, including biodistribution, stability, and clearance. ⁶⁴Cu-NOTA-UPSNs were administered systemically in healthy, non-tumor-bearing female Balb/c mice, with concurrent imaging using the following protocol: real-time dynamic PET scan up to 1 h post-injection (p.i.), followed by serial static scans at 2, 7, 18, 48 and 72 h p.i. (Supplementary figure S4A) ⁶⁴Cu-NOTA-UPSNs demonstrated prolonged systemic circulation, with 32.8 ± 0.1 %ID·g⁻¹ plasma concentration at 10 min p.i., decreasing slowly over time thereafter. (Supplementary figure S4B) A two-compartment PK model with an initial distribution phase (t_1/2,α ≈ 1.5 h) and a terminal elimination phase (t_1/2,β ≈ 16 h) best described the observed systemic concentration kinetics of ⁶⁴Cu-NOTA-UPSN; area under the curve (AUC_0−∞) was found to be 590.6 %ID·g⁻¹·h. (see Figure 4F and Methods for details) Region-of-interest (ROI) analysis of major organs indicated reasonable exposure to UPSNs and significant clearance within 72 h p.i.. These in vivo findings were confirmed via terminal PET scans followed by ex vivo gamma counting of radioactivity in major tissues. (Supplementary figure S4C)

Figure 4. In vivo ROI quantification and ex vivo biodistribution study.

(A) Tumor accumulation efficiency of ⁶⁴Cu-NOTA-UPSN in 4T1 and MDA-MB 231 tumors. Comparison of (B) Area-under-the-curve (AUC) for major organs and tumors, (C) tumor-to-blood ratio, (D) tumor-to-liver ratio, and (E) tumor-to-muscle ratios, between the two groups. (F) Plasma concentration kinetics of ⁶⁴Cu-NOTA-UPSN (red circles) and corresponding bi-exponential fit from a two-compartment PK model (blue curve) to evaluate plasma half-lives of ⁶⁴Cu-NOTA-UPSN: distribution t_1/2,α ≈ 1.5 h and elimination t_1/2,β ≈ 16 h. (G) Ex vivo biodistribution profiles of the two groups, 72 h p.i. (n = 4). *p < 0.05, **p < 0.01, ***p < 0.001, ****p < 0.0001, ns = non-significant (p > 0.05).

Moreover, ⁶⁴Cu-NOTA-UPSN demonstrated excellent ability for high-resolution sentinel lymph node mapping upon intradermal injection. Progressive delineation of the popliteal, sciatic, lumbar, renal, and pancreatic lymph nodes (LNs) was possible on longitudinal PET scans from 30 min p.i. up to 48 h p.i. (Supplementary figure S5A) ⁶⁴Cu-NOTA-UPSNs demonstrated maximum homing into the popliteal LNs with ~30 %ID·g⁻¹ at 30 min p.i. and prolonged retention with ~10 %ID·g⁻¹ still present at 48 h p.i. (Supplementary figure S5C) Ex vivo assessment with the gamma counter at the end of the 48 h time-point corroborated the results from in vivo ROI analysis. (Supplementary figure S5D) Overall, the results demonstrate that ⁶⁴Cu-NOTA-UPSNs could serve as excellent contrast agents for sensitive, precise, and prolonged delineation of sentinel lymph nodes, and hence for indicating the extent of metastatic spread of primary tumors.

To further investigate the long-term behavior, ⁸⁹Zr-DFO-UPSN was i.v. injected into healthy non-tumor-bearing Balb/c mice, and in vivo kinetics were monitored for a period of 2 weeks. Serial maximum intensity projection (MIP) images are shown in Figure 2A. Long-circulating ⁸⁹Zr-DFO-UPSN showed plasma concentration (40.1 ± 3.9 %ID·g⁻¹ at 1 h p.i.), which decreased gradually over time with an elimination half-life of ≈ 31 h, as estimated by a one-compartment PK model (see Supplementary figure S6D and Methods for details), giving an AUC_0−∞ of 1758.2 %ID·g⁻¹·h. Metabolic studies performed in parallel indicated that UPSNs cleared primarily through the hepatobiliary pathway; with 35.2 ± 5.2 %ID of UPSNs excreted in the feces by day 10. (Figure 2E and Supplementary figure S6A) DLS measurements indicated that ~8 % (by number) of UPSNs demonstrated HD below the renal threshold of ~8 nm (Figure 1D), possibly contributing to partial clearance from the renal pathway (typically faster than hepatic route). ⁸⁹Zr-DFO-UPSNs demonstrated almost complete clearance from the body with only 2.34 ± 0.15 %ID being retained 2 weeks p.i., indicated by almost background level of radioactivity on the terminal PET scan (Figure 2A,F) After an initial hepatic accumulation of 15.5 ± 2.9 %ID·g⁻¹ at 1 h p.i., ⁸⁹Zr-DFO-UPSNs cleared gradually, reducing to 5.7 ± 1.6 %ID·g⁻¹ at day 14 p.i. (Figure 2B) Similarly, accumulation of ⁸⁹Zr-DFO-UPSNs in the spleen reduced from 10.3 ± 2.7 to 7.2 ± 2.2 %ID·g⁻¹. AUCs for liver and spleen compartments were found to be 2362.95 and 2820.9 %ID·g⁻¹·h, respectively. (Supplementary Table S1) Of note, ⁸⁹Zr signal remained conspicuously absent from the bones up to almost a week p.i. and only appears marginally in the joints thereafter, indicating the superior radioastability of ⁸⁹Zr-DFO-UPSNs (non-chelated ⁸⁹Zr is an osteophile).[19] (Figure 2A–B) Release of the free isotope and its osteal accumulation could be possibly attributed to the dissolution and excretion of the UPSNs, in accordance with the observed in vitro serum stability data (Supplementary figure S3B–C). Uptake in the muscle remained low (< 1 %ID·g⁻¹) throughout the observation period. (Figure 2B)

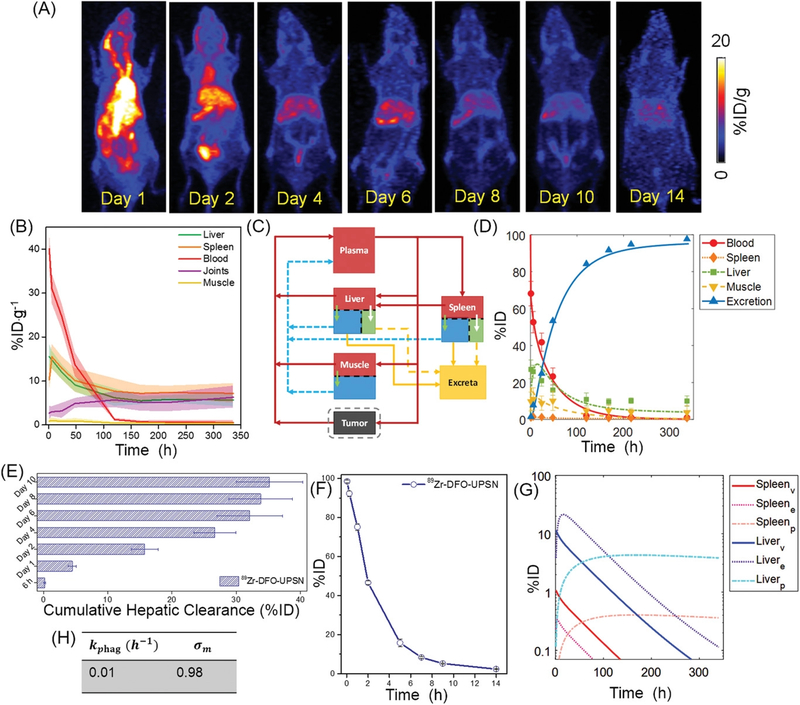
Figure 2. Long-term biodistribution of ⁸⁹Zr-DFO-UPSN.

(A) Maximum intensity projections (MIP) from longitudinal PET scanning of healthy Balb/c mice, i.v. injected with ⁸⁹Zr-DFO-UPSN. (B) Time-activity curves (TAC) for major organs obtained from in vivo region-of-interest (ROI) analysis. (C) Schematic of semi-mechanistic mathematical model as developed for UPSNs. Liver and spleen are further sub-compartmentalized into vascular (red), extravascular (blue), and phagocytic (green) compartments. Red arrows depict plasma flow; blue arrows indicate lymph flow; yellow arrows indicate excretion (solid: macrophage; dotted: hepatobiliary); and green and white arrows depict transvascular flow and phagocytic uptake, respectively. (D) TAC obtained from fitting the model to the data. (E) Cumulative hepatic clearance of ⁸⁹Zr-DFO-UPSN over a period of 2 weeks. (F) Whole body residual radioactivity (%ID) retained in the mice over two weeks. (G) Sub-compartment activity kinetics for liver and spleen as predicted by the model. (H) Phagocytic uptake rate constant (k_phag) and muscle reflection constant (σ_m) estimated from least squares regression of the model to the data. Data represents mean ± SD (n = 4).

Unlike our previous modeling approaches to study tissue disposition kinetics[20] and tumor delivery efficacy[21–25] of NPs, here we developed a multi-compartment, semi-mechanistic model, which is a reduced physiologically based pharmacokinetic (PBPK) model[26], comprising a systemic blood pool, RES (i.e. liver and spleen), muscle, and a facultative tumor compartment (applicable for tumor-bearing groups only), which represent the dominant distribution sites of the UPSNs in vivo, connected in an anatomical fashion via plasma (red arrows) and lymph (blue arrows) flow. (Figure 2C and Supplementary figure S7) In traditional PK modeling, organs are modeled as well-stirred, black-box like compartments with homogenous, time-dependent exposure to administered drugs.[20] This approximation often leads to a limited understanding of the pharmacological behavior of the administered agent, thus resulting in partial or heterogeneous responses in the clinic. This issue is especially relevant in the case of modeling the uptake of nanoformulations by the RES organs, where resident macrophages (Kupffer cells and splenic macrophages) respond differently to NPs than to small molecules. The model employed in this study incorporates mechanisms pertinent to NP-cellular interactions by compartmentalizing each organ into physiologically relevant sub-compartments (Methods and Supplementary Information S1 for details).

We began by fitting the PBPK model to the time-course PET imaging data for different ROIs (Figure 2D) and estimated the parameters (Figure 2H, Supplementary Table S7) including k_phag (0.01 h⁻¹), σ_m (0.98), and f (895), k_phag represents the time-averaged phagocytic uptake rate constant of hepatic and splenic sinusoidal macrophages, and an estimated value of 0.01 h⁻¹ suggests a timescale of 100 h for the phagocytic process, which indicates a relatively slow macrophage-driven sequestration of the UPSNs with respect to comparable particles reported in the literature [27]; σ_m is the reflection coefficient of muscle microvasculature, and a value ~1 indicates very high resistance to the transvascular extravasation of UPSNs, primarily due to the small size (~5 nm) of vessel wall pores in the muscle tissue. [28] The f parameter is a ratio of plasma to lymph flow rates (see Methods); a value of 895 indicates that the convective extravasation of UPSNs via lymph is slower than the lymph flow itself (a typical physiological value for f is ≤ 500).[29] This disparity between UPSN extravasation rate and lymph flow rate is possibly because of interactions of UPSNs with intravascular components or endothelial cells, causing reduced transvascular flow of UPSNs. Moreover, model predictions of UPSN mass kinetics from the model show strong correlation with experimental data (Pearson correlation coefficient R = 0.99; Supplementary figure S6C), thereby validating the mechanistic basis of the model.

The calibrated model was then employed to investigate the RES disposition kinetics of UPSNs as shown in Figure 2G. Model simulations of UPSN mass kinetics in the RES sub-compartments indicate the dominant role of hepatic phagocytes followed by splenic phagocytes in governing the retention of NPs in the RES. The time-activity curves (TACs) generated for various sub-compartments in liver yielded AUC_0–340h values of 505.3, 1551.9, and 1272.5 %ID·h for the vascular, extravascular, and phagocytic sub-compartments, respectively. For the spleen, the AUC_0–340h values for vascular, extravascular, and phagocytic sub-compartments were 47.4, 16.7, and 119.5 %ID·h, respectively. (Supplementary Table S2)

2.4. In vivo passive tumor targeting with ⁶⁴Cu-NOTA-UPSN.

To investigate whether the prolonged circulation and initial escape from the RES can be translated to improved accumulation at the intended tumor site, tumor disposition kinetics of UPSNs were tested in murine TNBC model. Heterogeneity in the EPR effect has been well-documented, and is known to be influenced by both vascular bed and surrounding stroma, as well as tumor type, size, and other physiological and environmental factors.[30] To explore how such heterogeneities affect the tumor-tropic transport of UPSNs, systematic in vivo studies were performed in two TNBC models, 4T1 (rapidly growing syngeneic model with pronounced microvasculature) and MDA-MB 231 (slow growing, human xenografts with diminished microvascular network). Tumors were implanted in age-matched mice and used when they reached 5–8 mm in diameter (10 days for 4T1 and 21 days for MDA-MB 231 tumors).

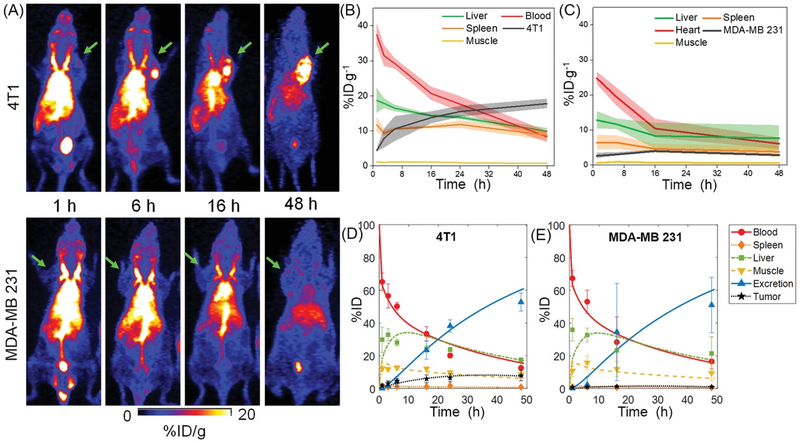
⁶⁴Cu-NOTA-UPSNs were systemically administered into tumor-bearing mice, followed by serial PET scanning up to 48 h p.i. (Figure 3A) Dominant signal from the heart for up to 16 h p.i. indicated that UPSNs were largely confined to the blood pool and cleared slowly over time. (Figure 3B–C) AUC_0–48h values of 792.08 and 536.33 %ID·g⁻¹·h were measured in 4T1 and MDA-MB 231 tumor-bearing mice, respectively. (Supplementary figure S8B and S11C) UPSNs remained in the blood pool at the end of the 48 h observation period, with 8.3 ± 1.6 and 6.1 ± 1.6 %ID·g⁻¹ in 4T1 and MDA-MB 231 groups, respectively (Figure 3B–C). RES uptake was consistent with that seen with ⁸⁹Zr-DFO-UPSN, showing an initial hepatic signal of 18.6 ±3.5 (4T1) and 12.8 ± 2.5 %ID·g⁻¹ (MDA-MB 231) at 1 h p.i. that decreased constantly to final values of 9.9 ± 0.8 and 7.6 ± 3.6 %ID·g⁻¹, respectively at 48 h p.i. (Figure 3A–C) Spleen was the second major organ of clearance, with 8.7 ± 1.4 and 3.8 ± 1.5 %ID·g⁻¹, respectively for 4T1 and MDA-MB 231 models. (Figure 3B–C). TACs for individual animals in each cohort are presented in Supplementary figure S8A and S11B and indicate uniform trends across all experimental animals.

Figure 3. Differential tumor uptake of ⁶⁴Cu-NOTA-UPSN in different TNBC models.

(A) Whole body MIP from longitudinal PET scans of 4T1 (top panel) and MDA-MB 231 (lower panel) tumor-bearing mice after i.v. injection of ⁶⁴Cu-NOTA-UPSN. Green arrows indicate the tumors. TACs obtained from in vivo ROI analysis of (B) 4T1 and (C) MDA-MB 231 tumor-bearing mice. (D, E) TACs derived from modeling of the observed data. Data represents mean ± SD (n = 4).

Owing to significant differences in their microvascular architectures and stromal composition, both 4T1 and MDA-MB 231 demonstrated different permeability and retention of ⁶⁴Cu-NOTA-UPSN. Representative MIPs (Figure 3A and Supplementary figure S11A) at earlier time-points indicated comparable tumor uptake of the UPSNs at 1 h p.i. with 4.4 ± 0.4 and 2.6 ± 0.8 %ID·g⁻¹ in the 4T1 and MDA-MB 231 groups, respectively. However, the passive accumulation of UPSNs at the 4T1 tumor site increased progressively over the next 48 h, reaching a maximum of 17.7 ± 1.4 %ID·g⁻¹ (Figure 4A), greater than any other passively-targeted nanoformulation reported to date.[3] Comparison with off-target organs (i.e., muscle and liver) indicated excellent tumor-to-background ratios and high contrast capability of ⁶⁴Cu-NOTA-UPSN (Figure 4C–E). As the UPSNs were cleared from the body over 48 h, the tumor-to-liver ratio increased exponentially (from 0.23 ± 0.07 at 1 h p.i. to 1.8 ± 0.02 at 48 h p.i.).(Figure 4D) Despite a favorable PK profile, accumulation of ⁶⁴Cu-NOTA-UPSN in the MDA-MB 231 tumors increased only marginally up to 16 h p.i. to a maximum value of 3.9 ± 0.4 %ID·g⁻¹, reducing thereafter to 2.8 ± 0.3 %ID·g⁻¹ at 48 h p.i. Comparison with off-target tissues (i.e., muscle and liver), yielded modest ratios of 6.91 ± 2.12 and 0.5 ± 0.12 at 48 h p.i. (Figure 4D–E) To eliminate the concern that this variation in tumor uptake resulted from a difference in their blood pool activities (Supplementary figure S14A), the ratio of UPSN accumulation in the two tumor types (T_4T1/T_MDA-MB231), as well as plasma (B_4T1/B_{MDA-MB 231}), was calculated at all time-points. As seen clearly in Supplementary figure S14B, B_4T1/B_{MDA-MB 231} ratio of 1.45 ± 0.01 at 1 h p.i. (when UPSNs are in circulation), yielded a corresponding T_4T1/T_MDA-MB231 ratio of 1.40 ± 0.14. However, by 48 h p.i., the T_4T1/T_MDA-MB231 ratio increases exponentially while B_4T1/B_{MDA-MB 231} ratio tends to 1, indicating that high accumulation of UPSNs in 4T1 indeed originated from tumor-specific effects.

Tumor permeability of ⁶⁴Cu-NOTA-UPSN, defined as ratio of NP uptake in tumor and in the blood, was found to be higher for 4T1 than that for MDA-MB 231 at all time-points except the initial scan at 1 h. (Figure 4D) This is consistent with the distribution half-life of ⁶⁴Cu-NOTA-UPSN (~1.5 h; Figure 4F), where the NPs begin to interact with the tumor vasculature, and extravasation is limited. With each longitudinal scan, as ⁶⁴Cu-NOTA-UPSNs reach a steady-state, the differences in vascular permeability between the two models become more pronounced, leading to significant differences in tumor accumulation and retention. Consequently, ⁶⁴Cu-NOTA-UPSN dose exposure to the two TNBC subtypes differed significantly, indicated by the AUC_0–48h for 4T1 (730.75 ± 115.56 %ID·g⁻¹·h), which was nearly 5 times higher than that for MDA-MB 231 (158.17 ± 14.71 %ID·g⁻¹·h). The results were further confirmed with ex vivo gamma counting (Figure 4G).

To further characterize the tumor microvascular transport differences between 4T1 and MDA-MB 231 tumors, we fitted the model to the PET data. (Figure 3D–E, Supplementary figure S9 and S12) The k_phag and σ_m parameter values estimated from the healthy cohort were used as constants in the tumor compartment-bearing model in order to estimate the k_in and k_out parameters, representing the inflow and outflow rate constants of ⁶⁴Cu-NOTA-UPSN in the tumor compartment. The k_in and k_out parameter values for 4T1 are greater than that for MDA-MB 231 (P value < 0.05); this suggests improved vasculature for 4T1, thereby allowing increased passage of NPs through the tumor and thus potentially enhanced retention. (Supllementary Table S3–S5). In terms of the RES tissue disposition, there was comparable accumulation of UPSNs in both tumor-bearing cohorts, indicating that the differences in tumor accumulation are not a result of the difference in RES uptake (Supplementary figure S9 and S12, Tables S2, S6). The strong correlation between model predictions and experimental data of UPSN mass kinetics further validated the findings (Supplementary figure S10 and S13). Of note, the sub-compartment kinetics of ⁶⁴Cu-NOTA-UPSN in liver and spleen obtained from tumor-bearing mice matched with the healthy mice. (Supplementary figure S15 and Table S2) The phagocytic compartments of liver and spleen were exposed to the least cumulative ⁶⁴Cu-NOTA-UPSN doses up to day 2 p.i., compared to vascular and extravascular sub-compartments, indicating an initial resistance to uptake by the resident phagocytes. (Supplementary table S2)

Overall, the selective tumor accumulation of UPSNs, coupled with rapid clearance from the body, can be harnessed in future studies for intrinsically targeted therapeutic delivery. Furthermore, the observations from our analysis show strong indications towards the promising application of radioisotope labeled UPSNs as a companion contrast agent for patient stratification, treatment planning, and non-invasive prediction of therapies relying on nanomaterials, and macromolecular biologics, as well as prediction and monitoring of vascular effects of anti-angiogenic therapies.

2.5. Histopathological investigation of tumor microenvironment in TNBC subtypes.

NP accumulation in tumors is a complex phenomenon, governed both by NP characteristics such as size, charge and surface chemistry, as well as tumor properties such as vascular density, permeability, cell density, stromal content etc.[11, 30, 31] Heterogeneity in tumor microenvironment, even within tumors of same molecular subtype, poses a barrier to delivery and hence, therapeutic efficacy of macromolecular drugs such as antibodies and NPs. PET imaging indicated obvious macroscopic differences in the tumor uptake and retention of ⁶⁴Cu-NOTA-UPSN in 4T1 and MDA-MB 231 models. To gain further insight into the intra-tumoral distribution of UPSNs at the microscopic level, systematic and comprehensive histopathological studies were performed. FITC dye-labeled UPSN (UPSN-FITC) were intravenously administered in size-matched 4T1 and MDA-MB 231 tumor-bearing mice, and tumors and RES organs were harvested 24 h p.i. Liver and spleen indicated no difference in UPSN signal among the two models. (Supplementary figure S16) Confocal microscopy of tumor specimens confirmed significant accumulation of UPSN-FITC in the periphery and penetration into the center of the 4T1 tumor. (Figure 5A and Supplementary figure S17A)

Figure 5. Ex vivo fluorescence microscopy and histopathology.

Fluorescence micrographs of UPSN-FITC accumulation (green) with respect to blood vessels (CD31: red) on the periphery and in the center of (A) 4T1, and (B) MDA-MB 231 tumors. DAPI: nucleus. (C,D) CD31 expression in the two tumor groups. Left to right: Whole tissue section, CD31 expression at the periphery (left panel) and core (middle panel) (scale bar: 100 μm). Right panel shows higher magnification images of blood vessel morphology in the highlighted section (red box) (scale bar: 50 μm). Scale bar: 50 μm.

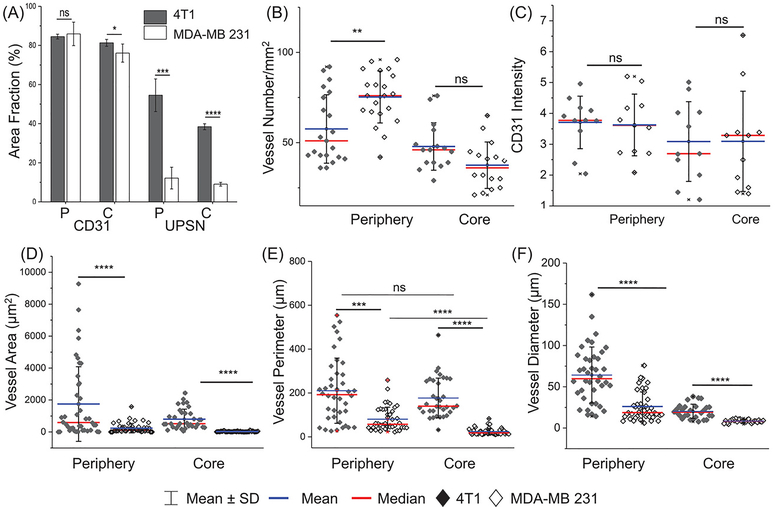
In contrast and in accordance with the PET imaging results (see Figure 3), MDA-MB 231 tumors demonstrated negligible uptake of UPSN-FITC, either on the edges or the core (Figure 5B and Supplementary figure S17B). When stained for vascular endothelial biomarker, CD31, both the TNBC models showed similar CD31 expression intensity and area coverage fraction in both the peripheral and core regions (Supplementary figure 6A,C). Most surprisingly, peripheral microvascular density (MVD; defined as number of blood vessels per mm²) was found to be higher in the MDA-MB 231 model than 4T1, although core areas showed no statistically significant difference. (Figure 6B) Despite sufficient vascularization in the periphery, UPSN-FITC uptake was severely retarded in MDA-MB 231, when compared to 4T1 (almost 5-times lower; Figure 6A). This is in sharp contrast to previously reported observations involving larger (100–200 nm) or ultrasmall small (< 6 nm) NPs, where MVD was demonstrated to play a central role in tumor uptake of NPs.[8, 32] These observations indicated that superficial parameters were insufficient to explain the intra-tumoral kinetics of UPSNs, necessitating a closer look at the differences in tissue architectures of the two models.

Figure 6. Image analysis of tumor histology.

(A) Quantification of CD31 and UPSN-FITC signal from confocal micrographs (area fraction percentage) of periphery and core of 4T1 and MDA-MB 231 tumors. Comparison of (B) vascular densities (number of blood vessels/mm²), (C) intensity of CD31 expression, (D) area of blood vessels, (E) perimeter of blood vessels, and (F) diameter ((calculated as geometric mean over 4 measurements of individual blood vessel), in the tumor periphery and core, for the two models. Each data point represents average value over one field of view. Atleast 6 fields each for tumor periphery and core were imaged per sample in both 4T1 and MDA-MB 231 groups. (n = 3) *p < 0.05, ** p < 0.01, ***p < 0.001, ****p < 0.0001, ns = non-significant (p > 0.05).

Accordingly, 4T1 syngeneic and MDA-MB 231 xenograft models were characterized for differences in vascular morphology (CD31 staining). Two zones with varying architectures could be clearly discerned in whole tissue histopathological analysis (Figure 5C–D). An outer peripheral zone in both the carcinoma models possessed relatively well-formed blood vessels (Figure 5C–D) and well-organized cell mass. (H&E staining, Supplementary figure S17 and S18) However, blood vessels in the xenografts demonstrated significantly attenuated microstructure, with smaller diameters, mean areas and perimeter measurements, when compared to faster growing syngeneic 4T1 tumors. (Figure 6D–F) Interior of MDA-MB 231 tumors demonstrated largely avascular, necrotic areas, with chaotic cellular islands, in accordance with the clinical observations in patients with aggressive tumors.[32]

Blood vessels in these islands presented distorted microstructure, collapsed or absent luminal area and spotted appearance (Figure 5D, center and right panels), although there was no statistically significant difference in the MVD when compared to 4T1 tumor cores (Figure 6B). The observations indicated that vascular morphology, and not vascular density, played a major role in determining tumor permeability to incoming UPSNs. Malformed blood vessels and rampant necrosis in tumors may result from excessive deposition of stroma, leading to tumoral solid stresses.[33] Compared to 4T1 tumors, MDA-MB 231 tumors demonstrated increased deposition of α smooth muscle actin (α-SMA)-positive stromal fibroblasts (indicative of acquisition of myofibroblast-like phenotype) and extracellular matrix protein, collagen I (col I; indicative of augmented tissue stiffness and aggressiveness). (Supplementary figure S18) Peripheral region in MDA-MB 231 tumors showed dense col I staining around tumor cells, and α-SMA staining of pericytes around the blood vessels, indicating thickening of vessel walls and reduced permeability (Supplementary figure S18–20), accounting for decreased UPSN-FITC accumulation and retention. Increased ECM rigidity has been associated with altered vascular structure and distribution, observed also in the current study. Core zones with malformed vasculature was found to be surrounded by severely desmoplastic regions, which may further limit UPSN infiltration.

3. Conclusion

In summary, we have demonstrated the synthesis of size-optimized ultrasmall porous silica nanoparticles, with improved PK, i.e. prolonged blood circulation half-life and reasonably fast systemic clearance. The design of the UPSN aims to combine the best from both macromolecular biologics, as well as inorganic ultrasmall NPs and small molecule agents. We have systematically investigated the influence of vascular architecture and stromal microenvironment on the accumulation and retention of as-designed UPSNs in two different TNBC models. Furthermore, using a mathematical model, we have attempted to obtain a mechanistic insight into the in vivo transport properties of UPSNs, in order to further our understanding of their nano-bio interactions in the body, with the ultimate goal to drive their clinical translation.

Our studies indicated that while nanomaterial engineering is important, merely reaching the tumor at high doses is not sufficient. Intratumoral complexities can hamper even the most optimized nanosystems, making the one-for-all approach insufficient for broad applications. Instead, the incorporation of multidisciplinary approaches alongside rigorous and comprehensive studies at the nano-bio interface is necessary to rationally design effective interventions.

4. Experimental Section

Synthesis of Amine-modified Ultrasmall Porous Silica Nanoparticles (UPSN-NH2):

Synthesis of ultrasmall porous silica nanoparticles (UPSN) was modified based on the methods published previously by Ma et al.[13] Briefly, 0.23 mmol of hexadecyltrimethylammonium bromide (CTAB) was added to 2 mL of distilled H₂O, followed by addition of 4.0 mM ammonia solution and further addition of 8 mL H₂O. The solution was stirred at 30 °C for 0.5 h until it turned clear. 0.43 mmol tetramethyl orthosilicate (TMOS) was added and stirred for 24 h. 0.21 mmol PEG-silane (MW: 500 Da; 5–9 ethylene glycol units) was added under vigorous stirring, followed by 0.004 mmol N-3-[(amino(polypropylenoxy)]aminopropyltrimethoxysilane (NH₂-PPO-silane; 350–400 Da, 3–4 propylenoxy units), 16 h later. The final solution was stirred at 30 °C for 4 h. The final molar ratio of TMOS: CTAB: PEG-silane: NH₂-PPO-silane was optimized to be 1: 0.5: 0.5: 0.01 for synthesis of sub-15 nm UPSN. Thereafter, the temperature was increased to 80 °C and reacted for 24 h. CTAB extraction was carried on 10 kDa dialysis membrane filters against acid: ethanol solution (DI water: ethanol: acetic acid :: 1:1: 0.007). The process was repeated thrice, for 24 h each time. The final product was dialyzed against water for several times and passed through a 0.2 μm syringe filter for further testing.

Surface modification of UPSNs.

UPSNs were surface modified with radioisotope chelators (CHX); 2-S-(4-Isothiocyanatobenzyl)-1,4,7-triazacyclononane-1,4,7-triacetic acid (p-SCN-Bn-NOTA; Macrocyclics Inc, Dallas, TX) or deferroxamine (p-SCN-Bn-DFO, Macrocyclics Inc, Dallas, TX) or fluorescent dye, fluorescein isothiocyanate (FITC) for further in vitro and in vivo studies, following procedures described previously.[17] Briefly, aqueous solution of UPSN-NH₂ was reacted with CHX-SCN or FITC-SCN in a 1:10 molar ratio. The pH of the solution was tuned to 8–9 and the reaction was carried out at room temperature with vigorous stirring for 2 h. As-synthesized UPSN-CHX or UPSN-FITC were purified on PD-10 columns (GE Healthcare) with PBS as the mobile phase to remove unreacted molecules.

Characterization of UPSNs.

As-synthesized UPSN and UPSN-CHX were characterized using transmission electron microscopy (TEM) on FEI Tecnai TF30 at an acceleration voltage of 300 kV. Images were processed and particle diameter and pore sizes were measured using ImageJ software. Hydrodynamic diameters and surface charge were measured using dynamic light scattering (DLS, Malvern Zetasizer Nano ZS). Nitrogen adsorption-desorption isotherms were measured at 77 K on a Quantachrome Nova 4000e system. The samples were freeze-dried for 48 h and surface area was determined using the BET method. Pore size distribution data was collected by the Barrett-Joyner-Halenda (BJH) method of the desorption branch of the isotherm. Fourier transmission infrared spectroscopy measurements were carried out on a Bruker Equinox 55/S FT–IR Spectrophotometer.

Synthesis of Radiolabeled

UPSNs.⁸⁹Zr-oxalate and ⁶⁴CuCl₂ were produced in an onsite cyclotron (GE PETrace) at the University of Wisconsin-Madison cyclotron facility.[17, 19] 2 nmol of UPSN-DFO was reacted with 74 MBq ⁸⁹Zr-oxalate for 2 h, in the presence of 0.1 M HEPES buffer, at pH 7–8 (adjusted using 2 M Na₂CO₃), 37 °C. ⁶⁴Cu-labeled UPSNs were similarly produced by reacting 2 nmol of UPSN-NOTA with 74 MBq of ⁶⁴CuCl_{2 in} 0.1 M sodium acetate buffer. The pH was tuned to 5.5 and reaction allowed to proceed for 1 h at 37 °C. Both ⁸⁹Zr-DFO-UPSN and ⁶⁴Cu-NOTA-UPSN were purified on PD-10 columns. Time-dependent radiochemical yields were determined via instant thin layer chromatography (radio-TLC) using 50 mM EDTA as the mobile phase. Serum stability study was carried out by incubating the radiolabeled UPSNs in 1x mouse serum over 48 h. Aliquots were drawn as regular intervals and spun at 300 kDa centrifugal filters. Radioactivity in retentate and filtrate fractions was estimated to calculate the radiochemical stability.

in vivo static and dynamic PET and ex vivo biodistribution studies.

For all in vivo PET imaging studies, scans were performed on a microPET/microCT Inveon rodent model scanner (Siemens Medical Solutions USA, Inc.). For long-term evaluation of UPSNs in vivo, healthy female Balb/c mice (n=3) were i.v. injected with 9.25 MBq of ⁸⁹Zr-DFO-UPSN, and a 60 min dynamic scan was acquired and framed into 6 frames of 10 min each, followed by serial static PET scans up to 72 h p.i.

In a separate study, tumor-bearing mice (n=4) were injected with ~ 7.4 MBq of ⁶⁴Cu-NOTA-UPSN via the tail vein and PET imaging was performed 1, 6, 24 and 48 h p.i. Image reconstruction and region-of-interest (ROI) analyses were performed on company software Inveon Research Workplace (IRW) following standard protocols, as described before.[10] All data was decay corrected and converted to activity concentration, and percentage of injected dose per gram of tissue (%ID·g⁻¹). After the final PET scans, all mice were euthanized, and their organs and tumors were harvested, wet-weighed and counted on Wizard² gamma counter (PerkinElmer). Organ radioactivity was presented as %ID·g⁻¹ after dose calibration and radioactivity decay correction.

In vivo clearance using metabolic cages.

To quantitatively evaluate the metabolic clearance profile of ⁸⁹Zr-DFO-UPSN, healthy mice (n = 3) were injected with 9.25 MBq of ⁸⁹Zr-DFO-UPSN. The mice were housed individually in metabolic cages and feces were collected at specific time-points p.i. Radioactivity in the feces were counted on Wizard² gamma counter (PerkinElmer), decay corrected and presented as percentage injected dose (%ID). The mice were PET scanned periodically to monitor the changes in whole body retention of i.v. injected ⁸⁹Zr-DFO-UPSN with time. Images were reconstructed and analyzed as described before and data is presented as %ID.

Pharmacokinetic modeling.

Empirical PK modeling[34] was employed to estimate relevant PK parameters (systemic half-life t_1/2 and AUCs) of UPSNs in healthy mice from the systemic concentration kinetics data. Based on the observations, a one-compartment PK model (Eq. (1)) was used for ⁸⁹Zr-DFO-UPSN and a two-compartment PK model (Eq. (2)) for ⁶⁴Cu-NOTA-UPSN. The following mono-exponential equation is the analytical solution of a one-compartment PK model:

$$C_b=C_0{e}^{-k\cdot t}$$ (1)

Where C_b is the concentration of NPs in systemic blood; C₀ is the systemic concentration of NPs at time t = 0; and k is the phenomenological first order elimination rate constant of UPSNs used to calculate t_1/2 = ln(2)/k.

The following bi-exponential equation is the analytical solution of a two-compartment PK model:

$$C_b=C_1{e}^{-k_1\cdot t}+C_2{e}^{-k_2\cdot t}$$ (2)

where, C₁ and C₂ are the intercepts of the back-extrapolated initial distribution phase and terminal excretion phase, respectively, with slopes k₁ and k₂ on a semi-logarithmic scale used to calculate distribution (t_1/2,α = ln(2)/k₁) and elimination(t_1/2,β = ln(2)/k₂) half-lives, respectively. Further, the trapezoidal numerical integration method was used to estimate the AUCs of the TACs. Analysis was performed in MATLAB R2018a.

Semi-mechanistic mathematical modeling.

Our mathematical model, based on simplification of currently available physiologically based pharmacokinetic (PBPK)[26], is formulated as a system of ordinary differential equations (ODEs) accounting for the transport and cellular interactions of NPs, to describe NP radioactivity kinetics (surrogate for NP mass kinetics) in the various compartments and sub-compartments. A representative system of ODEs for a general compartment i containing all the three sub-compartments (e.g., spleen and liver) is (see Supplementary figure S7):

Vascular sub-compartment

$$\frac{d{N}_{\text{v},\text{i}}}{dt}=\frac{N_{\text{P}}}{V_{\text{P}}}{Q}_{\text{i}}-\frac{N_{\text{v},\text{i}}}{V_{\text{v},\text{i}}}\left(Q_{\text{i}}-L_{\text{i}}\right)-\frac{N_{\text{v},\text{i}}}{V_{\text{v},\text{i}}}\cdot \left(1-{\sigma }_{\text{i}}\right)-N_{\text{v},\text{i}}\cdot k_{\text{phag}},N_{\text{v},\text{i}}\left(0\right)=0$$ (3)

Extravascular sub-compartment

$$\frac{d{N}_{\text{e},\text{i}}}{dt}=\frac{N_{\text{v},\text{i}}}{V_{\text{v},\text{i}}}{L}_{\text{i}}\cdot \left(1-{\sigma }_{\text{i}}\right)-\frac{N_{\text{e},\text{i}}}{V_{\text{e},\text{i}}}{L}_{\text{i}}-\frac{N_{\text{e},\text{i}}}{V_{\text{e},\text{i}}}B,N_{\text{e},\text{i}}\left(0\right)=0$$ (4)

Phagocytic sub-compartment

$$\frac{d{N}_{\text{p},\text{i}}}{dt}=N_{\text{v},\text{i}}\cdot k_{\text{phag}}-N_{\text{p},\text{i}}\cdot k_{\text{ex}},N_{\text{p},\text{i}}\left(0\right)=0$$ (5)

where, N_v,i, N_e,i, and N_p,i represent the mass of NPs in the vascular, extravascular, and phagocytic sub-compartments, respectively; N_p is the mass of NPs in the systemic blood pool (plasma compartment) and V_p is the volume of the plasma compartment; V_v,i and V_e,i represent the volume of the vascular and extravascular sub-compartments, respectively.

As represented by Equation (3), NPs entering from the plasma compartment into the vascular sub-compartment, via arterial plasma flow rate Q_i, either undergo convective transvascular extravasation to enter the extravascular space following the lymph flow rate L_i, or are phagocytized according to the phenomenological, time-averaged, first order uptake rate constant k_phag. Transvascular flow of NPs is limited by the impedance of the vessel walls, which is described as the reflection coefficient σ_i and is typically a function of NP to vessel wall pore size ratio and NP charge.[33] The remaining NPs exit the vascular space to rejoin the plasma compartment via the venous plasma flow rate Q_i − L_i. As described in Equation (4), the NPs that enter the extravascular space are either excreted via bile (only in liver and spleen), which is produced at a rate B, or exit the extravascular sub-compartment via lymph to recycle to the plasma compartment. Finally, NPs sequestered by phagocytes (Equation (5)) are eventually excreted following a phenomenological first order rate constant k_ex. The complete system of equations of the model is given in SI and was solved numerically as an initial value problem in MATLAB R2018a using the non-stiff ODE solver ‘ode45’.

Model parameterization.

Compartment and sub-compartment volumes, plasma flow rates, and excretion rates were known a priori from published literature. (Table S7)[2, 29] Due to extreme disparity in the literature, the lymph flow rates were assumed to be a fraction of plasma flow rates, $L_i=\frac{Q_i}{f}$, where f > 1, and was estimated by non-linear regression of the model to the experimental data. The other unknown parameters k_phag and σ_M were estimated by fitting the data from the healthy cohort, and the values thus obtained were used as constants for the tumor-bearing cohorts. Given that hepatic and splenic sinusoids have vessel wall fenestrations that are much larger[28] than the UPSNs being studied, we therefore fixed σ_L and σ_S (the reflection coefficients for liver and spleen) at zero for all cohorts assuming negligible resistance to transvascular flow. In the tumor bearing groups, in addition to f, the k_in and k_out parameters were estimated by non-linear regression.

Immunohistochemical (IHC) staining and immunofluorescence (IF) microscopy.

For immunohistochemical studies, 4T1 and MDA-MB 231 tumor-bearing mice were euthanized once the tumors reached 6 mm in diameter. The tumors were excised and immediately soaked in 4 % paraformaldehyde (4 % PF) at room temperature overnight with gentle shaking. Following this, the tumors were washed repeatedly in ethanol, followed by PBS, and transferred for paraffin embedding and sectioning, using standard protocols. Standard procedures were employed for hematoxylin and eosin (H&E), CD31, α-SMA and Col I staining.[35] High resolution whole tissue images were taken at 40x magnification on an EVOS™ FL Auto Imaging System. Brightfield images were taken from atleast 10 fields of view on Nikon Eclipse Ti microscope. CD31 stained sections were used to manually count the number of blood vessels in the tumor periphery and tumor center. Blood vessels with large obvious lumen and those with small or negligible lumens were used to determine vascular density. Images were analyzed on FIJI software to determine intensity, area fraction and blood vessel area. Lumen diameters were calculated as geometric mean from 4 measurements taken per blood vessel.

For fluorescence microscopy, FITC-modified UPSNs (UPSN-FITC) were i.v. injected into 4T1 and MDA-MB 231 tumor-bearing mice. Tumors, liver and spleen were excised from mice 24 h p.i., mounted in Tissue-Tek O.C.T and frozen immediately. Tissues were sectioned at a thickness of 7 μm, soaked in cold acetone for 10 min, followed by blocking with goat serum for 1 h. Human anti-mouse CD31 antibody was added and incubated at 4 °C overnight. After washing twice with PBS, goat-anti human-cy3 secondary antibody was added and incubated for 1 h. Excess antibody was washed away by PBS washing. Stained sections were mounted with DAPI containing Gold-anti-fade mounting medium. Confocal images were obtained on Nikon A1 Confocal imaging system and analyzed on Nikon Elements Analysis software.

Statistical analysis.

Data were analyzed using unpaired t-tests using Graphpad Prism 6. Statistical significance between different experimental groups was measured at two-tailed P-values *P < 0.05, ** P < 0.01, ***P < 0.001 and ****P < 0.0001. The non-linear regression (least squares fitting) of the compartmental PK models and the semi-mechanistic model to the experimental data was performed in MATLAB R2018a using the ‘Levenberg-Marquardt’ algorithm.