Abstract
Cooking is recognized as an important source of particulate pollution in indoor and outdoor environments. We conducted more than 100 individual experiments to characterize the particulate and non‐methane organic gas emissions from various cooking processes, their reaction rates, and their secondary organic aerosol yields. We used this emission data to develop a box model, for simulating the cooking emission concentrations in a typical European home and the indoor gas‐phase reactions leading to secondary organic aerosol production. Our results suggest that about half of the indoor primary organic aerosol emission rates can be explained by cooking. Emission rates of larger and unsaturated aldehydes likely are dominated by cooking while the emission rates of terpenes are negligible. We found that cooking dominates the particulate and gas‐phase air pollution in non‐smoking European households exceeding 1000 μg m−3. While frying processes are the main driver of aldehyde emissions, terpenes are mostly emitted due to the use of condiments. The secondary aerosol production is negligible with around 2 μg m−3. Our results further show that ambient cooking organic aerosol concentrations can only be explained by super‐polluters like restaurants. The model offers a comprehensive framework for identifying the main parameters controlling indoor gas‐ and particle‐phase concentrations.
Keywords: Cooking emissions, HR‐TOF‐AMS, Indoor air quality, POA, PTR‐TOF‐MS, SOA
Practical Implications.
The model can be used for regulating indoor cooking emissions.
Particle and organic gas emissions indoors are dominated by cooking processes.
Higher cooking temperatures and frying processes enhance emissions significantly.
Concentrations may be substantially reduced with a proper ventilation.
1. INTRODUCTION
In developed countries people spend on average about 16 hours per day indoor.1 Indoor air can be heavily polluted with non‐methane organic gases (NMOG)2, 3 or high particle loadings4 posing a threat to the health of the inhabitants. While some studies suggest that the indoor air quality is mainly driven by regional outdoor pollution,5 others argue that residential exposure to particle pollution far exceeds (eg, by 150%6) the exposure to particles from outdoor origins. Residential pollution exposure cannot be characterized by ambient measurements alone, and an accurate knowledge of indoor sources and loss processes is the key for assessing indoor air quality.
Cooking is already recognized as main source of indoor particulate air pollution in developed countries.4, 7 The processes used in cooking such as frying, roasting, grilling, boiling, and broiling contribute to particle emissions. The physical stirring of food has been found to lead to primary aerosol generation due to the splashing of the ingredients. The ingredient combustion during cooking can lead to direct emissions, and hot vapors in the cooking fumes from oil decomposition8 may also cool and nucleate to form more particles. Other known indoor emission sources related to residential cooking are electrical and gas stoves emitting high amounts of small particles (<10 nm)9 and nitrogen oxides.10 While many of the ingredients and cooking methods are common to various culinary techniques, particle emission rates from cooking span several orders of magnitudes,11, 12 affected by ingredients, procedures (eg, boiling vs frying vs charbroiling), and cooking temperature. Cooking has been also identified as an important outdoor source of primary organic aerosols based on aerosol mass spectrometry measurements13; however, the processes dominating these emissions remain unclear.14 Currently, there is an urgent need for a systematic assessment of the processes controlling the cooking emission rates, in order to constrain the contribution of these emissions to indoor and outdoor air quality.
In addition to particle emissions, cooking is known to generate significant amounts of vapors, comprising aldehydes from oil heating15, 16 or restaurant emissions.17 Recent studies discovered that many cooking processes may constitute an important source of NMOG indoors including potentially harmful substances like aldehydes or terpenes.18, 19, 20 Studies on sources of indoor gas‐phase air pollution so far focused mostly on cleaning detergents and air fresheners (terpenes),21 scented candles (carbonyls),22 building materials (all classes of compounds),23 or smoking.24 Also recognized as an important source of NMOG indoors is the transfer of outdoor air pollution to the indoor.25, 26 However, how gas‐phase cooking emission rates compare to those from other indoor and outdoor sources remains unclear. Besides the direct effect of NMOGs on human health,27 they are also precursors of secondary organic aerosol (SOA) through their reactions with ozone or OH radicals.28 Still not much is known about the production of SOA from most NMOG indoors. Most studies investigating SOA formation indoors focused on terpenoid reactions (mostly limonene from cleaning detergents) with ozone.29, 30, 31, 32, 33 Two recent studies trying to model the SOA formation indoors from different NMOG also concluded that SOA formation is dominated by high terpene (mostly limonene) emissions from cleaning products.34, 35 However, all of these studies neglect the high amounts of various terpenes emitted from frying food with condiments 19 as well as the high amounts of aldehydes emitted by frying processes.18, 36, 37
Cooking‐induced primary and secondary pollution is not only controlled by the cooked ingredients and cooking style or setting (fuel,38 pan,39 oil used, and cooking method40), but also depends on the air exchange rates (eg, induced by ventilation41, 42) and the oxidant precursor levels indoor and outdoor.35 Even though, several models describing indoor air pollution from different sources exist,34, 43, 44, 45, 46 none of these addresses both the particle and gas‐phase emissions from cooking, where the aforementioned parameters driving the pollutants emission, their transformation, and their losses can be systematically varied.
Here, we have developed a modeling framework for estimating the influence of cooking processes on the indoor concentration of different compound classes. Pollutant emission rates used as model input parameters are based on a set of more than 100 cooking experiments including vegetable and meat frying and vegetable boiling. These pollutants include primary organic aerosols, acrolein, short‐chain saturated carbonyls, long‐chain saturated and unsaturated carbonyls, and terpenes. Model input parameters also comprise the reaction rates of these compounds against OH radicals and ozone and their secondary organic aerosol yields determined based on 16 smog chamber experiments. The first part of the paper describes the model implementation and input parameters, while in the second part the impact of residential cooking emissions on indoor and outdoor air is discussed and the main parameters driving the emission concentrations are identified.
2. METHODS
2.1. Experimental setup
The emission factor data as well as the specific reaction rates and secondary organic yields for the different compound groups were obtained from three measurement campaigns in 2012, 2014, and 2015. The measurement setup was similar for all three campaigns and is described in detail elsewhere.18, 19 Direct emissions generated during more than 100 cooking experiments were measured. Cooking processes studied include
Olive, canola, and sunflower oil heating at different temperatures;
Meat shallow frying and charbroiling at different temperatures;
Vegetable frying;
Deep frying;
Vegetable boiling; and
Condiment use (herbs and pepper).
The emissions from selected processes were injected into a simulation chamber to study their transformation upon aging. The chamber setup for the 2014 campaign is thoroughly described in Klein et al. (2016b),19 while in 2012 the setup was similar to that described in Platt et al. (2014,2017).47, 48 After the emissions were injected and well equilibrated in the chamber, 4 sets of 10 UV lights, situated around the chamber, were switched on to induce aging. During 2014 measurements, nitrous acid (HONO), which forms OH radicals via photolysis, was introduced into the chamber at a flow rate of about 2 L min−1. This was not the case during the 2012 campaign, which resulted in significantly lower OH concentrations. The OH exposure in the chamber during both campaigns was estimated by measuring the decay of the d9‐butanol,49 introduced into the chamber through heated lines. All experiments were conducted at 50% relative humidity and a temperature of 20°C.
2.2. Instrumentation
Non‐methane organic gases were measured using a proton‐transfer time‐of‐flight mass spectrometer (PTR‐TOF‐8000, IONICON Analytik G.m.b.H.) operated in mode. This limits the measurements to NMOG with a proton affinity higher than that of water. A detailed description of the instrument can be found elsewhere.50 Operating conditions and data treatment procedures are described in Klein et al. (2016a).18
The primary and secondary organic aerosol loads were obtained from a high‐resolution time‐of‐flight aerosol mass spectrometer (HR‐TOF‐AMS, 600°C vaporizer temperature, Aerodyne Research, Inc.). The instrument was equipped with a PM2.5 lens enabling us to measure particles with a vacuum aerodynamic diameter of up to 3 μm.51 A detailed description of the instrument and data treatment procedures can be found in DeCarlo et al. (2006).52
3. MODEL FRAMEWORK
The scheme in Figure 1 illustrates the fate of cooking emitted organic gases (OG) and aerosol (POA) in the model and the variables used in the mass balances and secondary organic aerosol (SOA) production expressions. The model used is a box model; that is, the mass balance equations for each pollutant assume the indoor environment to be a single well‐mixed volume with air exchange due to infiltration. The OG concentrations in both the indoor air and the indoor surfaces are simulated in the model. The OGs are grouped into five different compound classes according to their chemical nature, reactivity against oxidants, and SOA yields. These classes include
Figure 1.
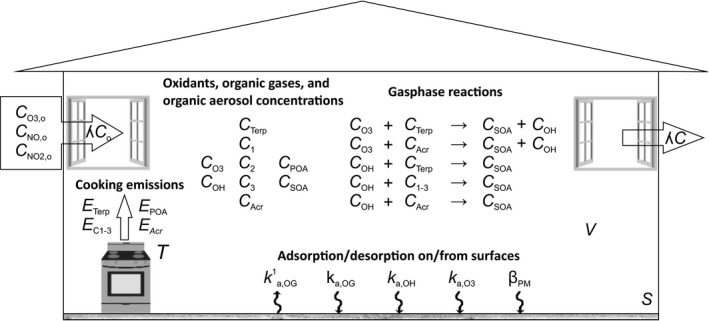
Model schematic
C1 compounds, which refer to carbonyls with less than six carbon atom backbone (mainly acetaldehyde, propylaldehyde, butylaldehyde, pentylaldehyde from meat cooking, and acetone from vegetable cooking, see Klein et al. (2016a)18);
C2 compounds, which refer to saturated carbonyls with more than five carbon atom backbone (see Klein et al. (2016a)18);
C3 compounds, which refer to unsaturated carbonyls with more than five carbon atom backbone (see Klein et al. (2016a)18);
ACR which consists only of acrolein (see Klein et al. (2016a)18);
Terpenes, which comprise p‐cymene, monoterpenes, oxygenated monoterpenes, and sesquiterpenes (see Klein et al. (2016a)18).
In addition to directly emitted POA, SOA production from the oxidation of terpenes (TerpSOA) and of the aggregate of C2, C3, and ACR (CSOA) is modeled. The sum of both fractions shall be considered as our best estimate of the total indoor SOA (totSOA) from indoor cooking processes.
The model simulates the emissions from meat frying, vegetable frying and boiling, deep frying, condiment use, and oil heating for the three different frying processes considered here. In the following, let i and j be the indices for a generic compound class emitted from a generic cooking process, respectively. The evolution of the mass concentration (in μg m−3) of a compound i, C i|g (where g denotes the gas‐phase), with time, t, may be described by the following generalized differential Equation (1):
| (1) |
where Prodi,j denotes the production rate of a compound i from a cooking process j and Lossi the loss rate of i. In the Sections 3.1 and 3.2, we present the modeling of the production and loss processes for OGs and POA, respectively. The representation of the SOA production from OG oxidation is described in Section 3.1, and the generation of input model parameters is detailed in Section 3.1. Input variables were modeled as probability distributions and used in a Monte Carlo operation such that distributions of resulting time‐dependent concentrations could be predicted and the influence of inputs on these concentrations could be quantified. Later, k shall represent a generic Monte Carlo trial.
3.1. Production rates
The production term in the model is developed to mimic as faithfully as possible the dependence of the emissions to the cooking processes and conditions applied, based on our experimental data. The processes applied to generate these data are in agreement with cooking book recommendations and our experimental data.
The time‐dependent production term (in μg m−3 s−1) of a primary compound i may be presented by Equation (2):
| (2) |
The definition and the general formulation of the different parameters in Equation (2) are expressed explicitly in the following:
V house (in m3) is the total house volume calculated as the total house floor area (A house) times the room height (h room) (from European commission report 53). A house is expressed as the product between the house area per person,54 A pers, and the number of persons per household,54 N pers. The occurrence of a given number of persons in a given space is a classic Poisson process, where N pers, which occurs independently and with a known average rate, is a discrete independent random variable following a Poisson distribution. In European households, the average N pers is 2.3 persons, leading to the following probabilities: , , , , equal to 0.1, 0.23, 0.27, 0.20, and 0.12, respectively. To avoid empty households in the model, we have considered N pers to rather follow a shifted geometric distribution, which yields similar results: , , , , equal to 0, 0.43, 0.24, 0.14, and 0.08, respectively. A pers follows a geometric distribution with a geometric mean, GM, equal to 45 m2 54 and a geometric standard deviation, GSD, equal to 1.5 (calculated based on the intercountry and intracountry variability for A pers). From these calculations, we estimate a median V house of 210 m3 (probability density function of house sizes can be seen from Figure S1), which is smaller than household volumes in the US,62 GM = 387 m3. All the input parameters can be found in Table 1.
x j is an independent random variable which takes a value of either 1 or 0, when the process j does or does not occur, respectively. For each Monte Carlo simulation k, x j is generated through a Bernoulli trial, with a predefined probability of x j = 1, , equal to p j. As the logarithm transformed outputs are examined in the Result section, we have replaced x j = 0 by x j = 10−9. The value for x oilheatingforj is set to be equal to x j, with j = vegetable frying, meat frying, or deep frying (ie, oil heating for a certain frying process only occurs if this process occurs). We have also set and equal to 0.9 and 0.1, respectively. Simulations where x j = 0 for all processes are excluded (no food cooked). For the accepted simulations (in total 1940 out of 2000), meat frying, vegetable frying, vegetable boiling, deep frying, and condiment use occur for 77, 54, 51, 5.3, and 50% of the times, consistent with the p j values we have set. This approach yields reasonable amounts of food cooked per person (Figure S2, eg, it is highly improbable that all processes occur together and that the amount of food per person exceeds a certain threshold), while still accounting for the variability in the emissions from the different processes applied.
- is a (unitless) kernel function representing the derivative of the cooking time as a function of time, such that
and(3)
Here, Δt j denotes the total time for a given cooking process j, where Δt j equals the product of the number of cooking batches, NB j, times the cooking time per batch, Γj. The number of cooking batches is set to one for all processes, except for deep frying where a batch per two persons is considered. used here takes the form of a product between two sigmoid functions, as written in Equation (5).(4) (5) Here, t j is the starting time of a cooking process j, with t j = 0s for oil heating, t j = Δt oilheating for vegetable, meat, and deep frying (as the frying only occurs after heating the oil) and t j = 600s for vegetable boiling (time required for bringing water to boil). For condiment use, the same rules as for Δt condimentuse apply to t condimentuse. τrise = 20 s and τfall = 8 s are the time constants for the beginning and the end of a cooking process j, respectively. These time constants are chosen based on an average heating rate observed during our experiments. While any other kernel could be used for the representation of the progress of a cooking process, we opted for a continuous function, such that the concentrations of the different components in time can be differentiated. Other kernel forms also tested yielded very similar results. Δt j values are largely based on our experiments and are consistent with cookbook recommendations.63 The geometric mean (geometric standard deviation) for Δt oilheating, Δt meatfrying, Δt vegetablefrying, Δt vegetableboiling, and Δt deepfrying is set to 240, 900, 1500, 1500, and 600 s (1.2, 1.4, 1.4, 1.4 and 1.2), respectively. The values for Δt condimentuse are set to be equal to either Δt meatfrying or Δt vegetablefrying (with equal probability) if both (meat and vegetable frying) occur. If only one of the two processes occurs, then Δt condimentuse takes the value of Δt j set for this process. Otherwise, Δt condimentuse is set to zero. Considering that cooking activities occur simultaneously and twice a day yields an estimated time spent on cooking per day of around 1 hour. The distribution of these estimated values is in accordance with the reported number of hours spent for cooking per household per day, ranging from 0.5 hours for households in South Korea to 1.9 hours in India.64
- ERi,j represents the emission rate of a product i from a process j. The expression of the emission rates depends on the cooking process applied. For oil heating where emissions depend on the oil surface per m2 of oil , ERi,j is
Here, (in μg m−2 s−1) denotes the emission rate of a product i from a process j per m2 of oil. The geometric mean for was set to 0.020 m2 for shallow frying (assuming only part of the pan to be covered by oil when pan frying) and 0.045 m2 for deep frying (GSD = 1.5 and 1.05). Based on our experimental results, follows an Arrhenius behavior and therefore is expressed against the oil temperature (in K), as follows:(6)
In Equation (7), (in μg m−2 s−1) and (in K) are the Arrhenius constants determined from our experimental data, reported for the different species in Table 2. The oil temperatures were assumed to follow a lognormal distribution with GM equal to 165°C and 190°C (GSD = 1.07 and 1.03), for shallow frying and deep frying, respectively, based on the average temperatures applied during our experiments. To account for emission variability, we have generated temperature‐dependent probability distributions using the prediction intervals from the error analysis of the linear regressions of the experimental data against (Table 2), according to Equation (8):(7)
Here, is the regression standard error calculated as the square root of the sum of unexplained variance normalized by the degree of freedom (dF = 26). t dist,dF is the student distribution for dF = 26, and (1/) and are the average temperature inverse and its associated sum of squared deviations, respectively.(8)
Table 1.
Input parameters used in the Monte Carlo simulations for the description of the household, loss rates, and pollutant outdoor concentrations
| GM | GSD | P10 | P25 | P50 | P75 | P90 | |
|---|---|---|---|---|---|---|---|
| N pers (#)a | — | — | 1 | 1 | 2 | 3 | 4 |
| A pers (m2)a | 45 | 1.5 | 27 | 34 | 46 | 60 | 75 |
| h room (m)a | — | — | 2.5 | 2.6 | 2.7 | 2.9 | 3.1 |
| V house (m3) | — | — | 91 | 121 | 210 | 397 | 650 |
| (m2 m−3)a | 3.4 | 1.2 | 2.7 | 3 | 3.4 | 3.9 | 4.4 |
| λ × 105 (s−1)b | 20 | 2.1 | 8 | 12 | 20 | 34 | 52 |
| β PM × 105 (s−1)b | 22 | 1.35 | 15 | 18 | 22 | 27 | 32 |
| (s−1)c | 70 | 1.5 | 40 | 53 | 71 | 91 | 114 |
| (s−1)e | 33 | 1.5 | 19 | 25 | 33 | 43 | 55 |
| J HONO × 105 (s−1)f | 5.7 | 2.48 | 1.7 | 3 | 5.8 | 10 | 18 |
| (ppb)g | 26 | 2.01 | 11 | 18 | 27 | 44 | 66 |
| C NO,out (ppb)g | 1.8 | 3.53 | 0.34 | 0.81 | 1.8 | 4.4 | 9.3 |
| (ppb)g | — | — | 0.84 | 1.8 | 4.2 | 11 | 23 |
Data are relative to European households from the European commission report on standard building specifications53 and Eurostat.54 N pers is generated using a geometric distribution with an average of 2.3 capita per household (see text for more explanations regarding the choice of the geometric distribution); h room = h min + h k, where h min is the minimum ceiling height for European living spaces = 2.4 m and h k a random variable following a lognormal distribution with GM = 0.3 and a GSD = 1.8. V house is N pers × A pers × h house.
Hodgson et al. (2004).55
Weisel et al. (2005).56
Spicer et al. (1993).59
Alvarez et al. (2013).60
EPA (2013)61 monitoring data, similar to data in Europe. C NO2,out = C NO,out × (NO2/NO)out with (NO2/NO)out being the ratio between and C NO,out generated following a lognormal distribution with GM = 2.4 and a GSD = 1.4.
Table 2.
Arrhenius input parameters determined by fitting the experimental and data against the temperature inverse, which can be used for the determination of temperature‐dependent emission rate probability distributions used in the Monte Carlo simulations. A i denotes both A S and A M, in μg m−2 s−1 and μg kg−1 s−1 for heating oil and for frying processes
| B i (K) | lnA i | SE i | |
|---|---|---|---|
| Parameters for | |||
| POA | 9183 | 24.9 | 0.6 |
| ACR | 8461 | 23.5 | 0.4 |
| C1 | 5670 | 17 | 0.5 |
| C2 | 10 352 | 28.7 | 0.4 |
| C3 | 9128 | 25.7 | 0.5 |
| Parameters for | |||
| POA | 4607 | 12.4 | 0.5 |
| ACR | 5700 | 14.5 | 0.4 |
| C1 | 2831 | 9.8 | 0.3 |
| C2 | 6114 | 16.6 | 0.4 |
| C3 | 5718 | 15 | 0.3 |
The standard error is calculated as the square root of the sum of unexplained variance normalized by the degree of freedom (dF = 26). Other parameters used include the average of the temperature inverse (0.00228 K−1) and the associated sum of squares of deviations (1.1 × 10−6K−1 and 2.0 × 10−6 K−1).
For any other cooking process, it is convenient to express ERi,j as a function of the amount of raw food cooked, as data pertinent to purchased goods are typically accessible. Accordingly, ERi,j may be written as
| (9) |
where (in kg) designates the average raw food mass per person per meal (considering two meals per day) cooked following a process j, and (in μg kg−1 s−1) the emission rate of a product i from j per one kg of food cooked.
For vegetable boiling, deep frying, and condiment use, independent values for are utilized, as indicated in Table 3. Terpenes are emitted from vegetables and from condiments, while vegetable boiling emits small amount of POA. Meanwhile, large amounts of POA and aldehydes are emitted from deep frying. For vegetable and meat frying, temperature‐dependent probability distributions were generated (here, , in , and , in K are used), using the parameters in Table 2 and similar equations as Equation (7) and Equation (8). The same temperature, , is kept for oil heating and frying. Most of the variance in the relationship between and inverse can be explained by the emission variability with the type of oil used. We note that compared to oil heating only, emission rates manifest a weaker dependence on temperature, especially for species whose emissions are enhanced in the presence of food.18 These include small aldehydes present in the meat (included in C1), acetone present in onions (included in C1), and POA emitted from the contact between food liquids and hot oil. In addition, the presence of food may change the oil surface properties (eg, total surface, temperature), which in turns varies the emission rates from oil heating.
Table 3.
data for deep frying and vegetable boiling used in the Monte Carlo simulations
| GM | GSD | P10 | P25 | P50 | P75 | P90 | |
|---|---|---|---|---|---|---|---|
| (μg kg−1 s−1) | |||||||
| POA | 7.6 | 2.25 | 2.8 | 4.3 | 7.6 | 14 | 22 |
| ACR | 4.2 | 1.29 | 3 | 3.5 | 4.2 | 5 | 5.8 |
| C1 | 5.7 | 1.21 | 4.5 | 5.1 | 5.7 | 6.5 | 7.3 |
| C2 | 17 | 1.2 | 13 | 15 | 17 | 19 | 21 |
| C3 | 34 | 1.31 | 24 | 29 | 34 | 41 | 47 |
| Terp | — | — | — | — | — | — | — |
| (μg kg−1 s−1) | |||||||
| POA | 0.0085 | 1.2 | 0.0067 | 0.0075 | 0.0085 | 0.0096 | 0.011 |
| ACR | — | — | — | — | — | — | — |
| C1 | 1.7 | 1.2 | 1.4 | 1.5 | 1.7 | 1.9 | 2.1 |
| C2 | — | — | — | — | — | — | — |
| C3 | — | — | — | — | — | — | — |
| Terp | 0.65 | 1.21 | 0.51 | 0.57 | 0.64 | 0.73 | 0.83 |
Terp are also emitted from vegetable frying and from condiment use with and = 750 μg kg−1 s−1, respectively.
Ample data on average yearly consumption per capita exist in the literature including reports for different countries and different types of food. These data will be used to determine our best estimate for values. Meat consumption data calculated using a trade balance approach would yield the carcass mass availability, which ranges between 70 and 120 kg per capita per year for developed countries.65 This estimate does not include losses in retail and food service, and thus does not represent the actual raw meat mass purchased for cooking. Losses in retail are estimated to be 5% for red meat and poultry,66 and another 5% loss can be estimated as food waste 67 (amount not cooked at all). Losses due to deboning, trimming, and cooking are not considered as our emission rates are normalized to the raw meat mass cooked (were these losses to be considered, the meat mass available per capita would be half of the carcass mass availability, based on USDA 68). Based on these estimates, we determined a geometric mean value for of 0.120 kg per capita per meal. Elmadfa (2009)69 estimates an average intake of vegetables, starchy roots, and potatoes of about 400 g per capita per day in European countries, similar to estimates for the United States (460 g, PBH foundation70). These numbers were used to generate a geometric mean value for kg. Half of the mass of vegetable cooked was considered boiled and the other fried. Geometric mean values for and are set to 1.0 × 10−2 kg and 1.2 × 10−3 kg (considering an average yearly consumption of condiments of 900 g, based on ESA71), respectively. For all processes, we varied the amounts of food used per capita within 25% (ie, GSD = 1.25). We calculate the total mass of raw food cooked per person, M food in kilogram (Figure S2), as the sum of M j from all processes, with average M food equal to 0.37 kg.
The production rates from all processes were integrated against time, which provides the total mass of a component i emitted per volume. Assuming that cooking occurs twice a day, we estimated the average amount of i emitted per time per volume, E i, which can be directly compared to scaled emission rates of the different compounds reported in the literature (see, eg, Figure 2).
Figure 2.
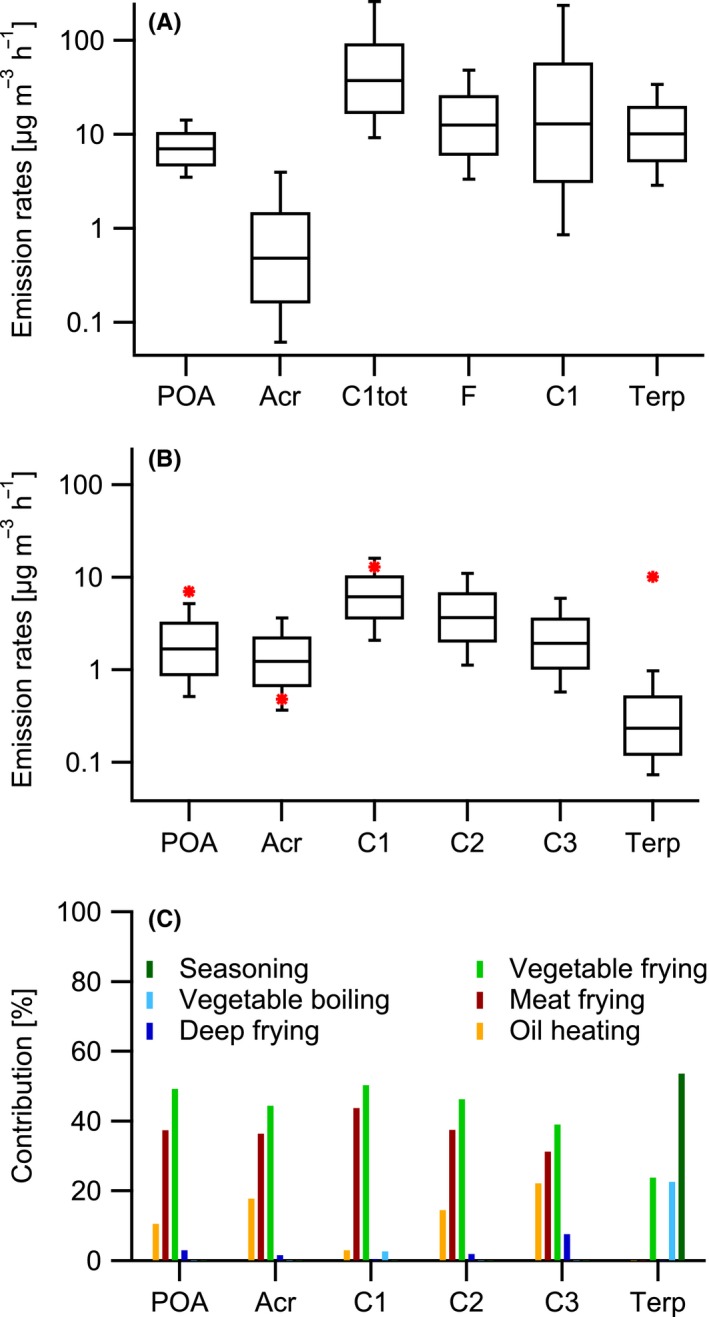
Production rates of POA and organic gases from cooking and other indoor sources. Mean values as well as 5th and 95th percentiles (whiskers) and 25th and 75th percentiles (box) are shown for modeled total indoor source emission rates from Waring (2014) 34 (A) and for modeled cooking emission rates from this study (B) as well as the contributions of the different cooking processes to the total emissions (C) of POA, acrolein (Acr), formaldehyde (F), saturated carbonyls with less than 6 carbons (C1tot) or excluding formaldehyde (C1), saturated aldehydes with more than 5 carbons (C2), unsaturated carbonyls with more than 5 carbons (C3), and terpenes (Terp). Red stars in B are median values from A
3.2. Loss rates
The loss term includes (a) transport to outdoor of gas‐ and particle‐phase components due to air exchange, (b) POA and SOA deposition, (c) OG oxidation, and (d) OG sorption onto indoor surfaces.
3.2.1. Particle losses
The loss of particles (PM, with PM = POA or SOA) can be described as follows:
| (10) |
where λ (in s−1) is the air exchange rate, due to infiltration and or open doors and windows and βPM (in s−1) the particle deposition rate (Table 1). βPM is dependent on particle size, turbulence, and the available surface in a house. These dependences are weak in the range of conditions encountered in indoor environments. First, particles in the accumulation mode (0.1–1 μm), such as those present in cooking emissions, have very similar deposition rates.72 Second, turbulence, which is typically driven by the temperature profile indoor and air velocity/exchange rate, has little to no influence on the deposition behavior. For example, particle deposition rates have been reported to vary by <20% in the range of air velocity relevant for indoor environments (0‐0.5 km h−1, Thatcher et al. (2002)72). Third, as the variation of the particle deposition rates is linear with the S/V ratio, this parameter, which varies by <20% (Table 1), is not expected to significantly affect the deposition rates. Therefore, we have opted for using an independent deposition rate coefficient (βPM), which we vary within the range encountered in indoor environments, similar to previous studies.34
3.2.2. OG losses
The loss term for an OG i is formulated in Equation (2) and the processes/parameters therein shall be successively described in the following:
| (11) |
Oxidation
We considered the oxidation of the organic gases with hydroxyl radicals and ozone. The reaction of nitrate radicals was not included as their impact on the indoor VOC conversion is expected to be one to two orders of magnitudes lower than the impact of hydroxyl radicals and ozone.35 In Equation (2), C OH and denote the hydroxyl radicals and ozone concentrations and k OH,i and are the rate constants for their reactions against OG, respectively.
Determination of OGs reaction rates: The distribution of k OH,i and values, presented in Table 4, are determined from our experimental results or taken from literature when not accessible. We consider in the following that saturated and unsaturated carbonyls react only with hydroxyl radicals, while terpenes may react with both ozone and hydroxyl radicals, given their relative reaction rates and C OH and under our conditions.
Table 4.
Lognormal parameters (GM: geometric mean and GSD: geometric standard deviation) for the reaction rates of cooking‐related organic gases against hydroxyl radicals and ozone
| GM | GSD | P10 | P25 | P50 | P75 | P90 | ||
|---|---|---|---|---|---|---|---|---|
|
| ||||||||
| ACRa | 1.8 | 1.17 | 1.5 | 1.7 | 1.9 | 2.1 | 2.3 | |
| C1a | 1.5 | 1.19 | 1.2 | 1.4 | 1.5 | 1.7 | 1.9 | |
| C2a | 2.2 | 1.23 | 1.7 | 1.9 | 2.2 | 2.5 | 2.8 | |
| C3a | 5 | 1.19 | 4 | 4.4 | 5 | 5.6 | 6.3 | |
| Terpa | 2.9 | 1.36 | 2 | 2.4 | 2.9 | 3.6 | 4.3 | |
| (molec−1 cm3 s−1) | ||||||||
| ACRd | 2.6 | 1 | — | — | — | — | — | |
| C1e | — | — | — | — | — | — | — | |
| C2e | — | — | — | — | — | — | — | |
| C3f | 6.9 | 2.61 | 1.8 | 3.4 | 7 | 13 | 23 | |
| Terpa | 250 | 1.54 | 150 | 190 | 250 | 340 | 440 | |
From this study based on the decay of these compounds against time and the estimated C OH in the chamber based on the d‐9 butanol decay (equivalent to using the relative decay technique).
From Atkinson and Arey (2003).73 Rates were weighted by the compounds’ relative abundances, and these abundances were varied through an initial, separate Monte Carlo simulation to determine the variability of these rates.
Using Terp decay rates and C OH and from this study and ratios for a mix of terpenes from Atkinson and Arey (2003),73 through a separate Monte Carlo simulation.
Considered to be inert against ozone.
Estimated using the reaction of C3 against hydroxyl radicals, k OH,C3, from this study and the relationship between k OH,C3 and reported in Colman et al. (2015)76 for α, β‐unsaturated aldehydes: ln~ln(k OH,C3) − 7.55.
For ACR, we estimate based on our chamber results a median k OH,ACR = 1.9 × 10−11 molec−1 cm3 s−1, in perfect agreement with the literature values74, 77 of k OH,ACR = 2 × 10−11molec−1 cm3 s−1. The reaction of ACR toward ozone was taken from Grosjean et al. (1993).75
C1 compounds are produced from the oxidation of higher molecular weight species, and thus, their reaction rates toward hydroxyl radicals could not be reliably determined from our chamber data. Instead, k OH,C1 values for the entire class of C1 compounds are determined using the rates of individual compounds from Atkinson and Arey (2003),73 weighted by the compounds’ relative abundances in the emissions. The latter are varied through an initial, separate Monte Carlo simulation to take into account emission variability, resulting in a k OH,C1 distribution that could be used in the model.
The reaction rates of C2 compounds against hydroxyl radicals are estimated from our chamber data to range between 1.9 × 10−11 and 2.5 × 10−11molec−1 cm3 s−1 (first and third quartiles), comparable to values reported for linear aldehydes (eg, k OH,hexanal = k OH,heptanal = 3.0 × 10−11molec−1 cm3s−1, Atkinson and Arey (2003)73 or , Bowman et al. (2003)78).
C3 compounds mainly comprise α, β‐unsaturated aldehydes with different carbon chain lengths,18 depending on the type of oil used. The reaction rates of C3 compounds against hydroxyl radicals are estimated from our chamber data to range between 4.9 × 10−11 and 5.6 × 10−11molec−1 cm3 s−1. Gao et al. (2009)79 report similar values for C6, C8, and C9 trans‐α, β‐unsaturated aldehydes, with k OH = 4 × 10−11molec−1 cm3 s−1. α, β‐unsaturated aldehydes react with ozone less efficiently than their alkene structural homologues,75 as ozone reaction with double bonds is an electrophilic addition. Colman et al. (2015)76 reported a relationship between and k OH,C3, from the study of the degradation of C7–C9 biogenic α, β‐unsaturated aldehydes: ln(k OH,C3) = 0.16 ln(k OH,C3) − 7.55. Here, we used this relationship together with k OH,C3 determined from our chamber to predict values and their distribution: Estimated values range between 3.4 × 10−18 and (first and third quartiles). These rates are relatively low compared to other indoor relevant compounds, such as terpenes.
Unlike the other compound classes, terpenes are highly reactive against ozone and therefore under our chamber conditions may react with both ozone and hydroxyl radicals. The reaction rates of identified terpenes19 against ozone and hydroxyl radicals span almost two orders of magnitude and therefore cannot be directly used in the model. In contrast, the average lifetimes of terpenes in our chamber are fairly reproducible. Therefore, in order to determine the average k OH,Terp and for the terpene mixture in the chamber, we used another separate Monte Carlo simulation to generate a probability density function of the ratio, assuming a randomly generated mixture of the most important mono‐ and sesquiterpenes identified and using reaction rates from Atkinson and Arey (2003).73 Using this ratio distribution, the calculated lifetime distributions, and the hydroxyl radicals and ozone concentrations in the chamber for these specific experiments (2.5 × 107 and 1.0 × 1012 molec cm−3, respectively, see Klein et al. (2016b)19), we determine an average k OH,Terp and of 2.9 × 10−11molec−1 cm3 s−1 (32% error) and 2.5 × 10−16molec−1 cm3 s−1 (54% error), respectively.
Determination of indoor oxidant concentrations: The prediction of C OH and would require a detailed understanding of indoor oxidant sources and sinks, which in turn entails the knowledge of outdoor reactive gases (O3, NOx, and OG), their penetration through the building envelope, their potential indoor sources, and their indoor transformation through photolysis, reactions, and deposition. Waring and Wells (2015)35 developed a Monte Carlo framework for predicting the indoor COH and , considering established and newly realized oxidant sources. A brief description of the oxidant framework and the main processes involved will follow.
In the framework of Waring and Wells (2015),35 outdoor‐to‐indoor transport is the principal indoor source of ozone, the initiator and the main driver of indoor chemistry, with a penetration coefficient >0.8.80 In the model, ozone is lost by reacting in the gas‐phase with alkenes 73 or by chemical uptake onto building materials via heterogeneous reaction with surface‐sorbed alkenes,81, 82 with an average deposition rate of 7 × 10−4 s−1 (Table 1, Spicer et al. (1993)59). As a result, indoor ozone concentrations often correlate with outdoor concentrations and are 20%‐70% of ambient values.83 Owing to their short lifetimes, outdoor‐to‐indoor transport of hydroxyl radicals is not a significant indoor source 84 and therefore is not considered in the model. An important hydroxyl radical source in the model is the aforementioned reactions between ozone and alkenes and the subsequent rearrangement and decomposition of the resulting stabilized Criegee intermediates. These reactions are traditionally considered the almost exclusive drivers of indoor hydroxyl radicals.85 However, more recently the photolysis of indoor nitrous acid (HONO) formed from combustion or NO2 hydrolysis on indoor surfaces 60 has been identified as another potentially important hydroxyl radical source indoors and therefore is included in the model. This source is especially important at high indoor actinic light fluxes in the range of 340‐405 nm and in the presence of indoor combustion sources.35 The hydroxyl radicals are lost by reaction with the OGs and NO2.
In their framework, Waring and Wells (2015)35 considered a scenario with stable indoor background concentrations of 91 OGs (from Logue et al. (2011)86), variable outdoor O3 () and NOx (C NO,out and ) concentrations, and variable indoor D‐limonene concentrations (C lim). This scenario will be considered here, while other scenarios were tested but provided similar results. By examining the effect of different model inputs on modeled indoor oxidant concentrations, Waring and Wells (2015)35 determined the most influential parameters and a relationship relating these parameters (VARl) with the natural log‐transformed outcome variables, ln(C OH) and ln():
| (12) |
| (13) |
Here, y int,OH and and RCOH,l and are the regression intercepts and coefficients for the different input variables taken from Waring and Wells (2015),35 for both OH and O3, respectively. Input variables, VARl, include , C NO,out, , C lim, λ, , , and J HONO, where is the deposition rate of NO2 and J HONO the photolysis rate of HONO. We have considered the same distributions for VAR_l as in Waring and Wells (2015)35; these are reported in Table 1. While, similar to D‐limonene, cooking emitted organic gas reaction with ozone may lead to a decrease (increase) in ozone (hydroxyl radical) concentration, this effect is not significant (<5%) and therefore not considered in the following. This effect has been assessed by adding to C lim in Equations (12) and (13), and the sum of C OG,i scaled by relative to , assuming an OH molar yield for OG i ozonolysis of 0.86, equals to that of D‐limonene ozonolysis.85
Sorption
Modeling the sorption of gases onto indoor surfaces is not straightforward. These processes heavily depend on the chemical nature and physical properties of both binding gases and adsorbing material (eg, inhomogeneity, roughness, and composition) and may involve the diffusion of the gases within the material and complex interactions and competition between these gases.87, 88 Here, we did not attempt to reproduce exactly the equilibrium of the gases at the interface through a full‐scale, computationally intensive model, while lacking observational constraints for model parameters (measurements in indoor environment where all processes except gas‐surface interactions are characterized). Instead, we have opted for a rather simplified approach, where model inputs that represent the surfaces’ sorption properties can be effectively varied, such that the sensitivity of the model outputs on the assumed parameters can be assessed. The approach is a linear absorption‐desorption model, which assumes the sorption of OGs onto building materials to follow a Langmuir process. The parameters driving the partitioning of a compound between the gas and the absorbed phase are represented in Equation (14). These include (a) the gas adsorption rate, k a,i (in mh−1), (b) the equilibrium partitioning constant, K e,i (in m), and (c) the indoor surface to volume ratio including furniture, (S/V)house (in m−1). The OG i concentration change due to adsorption is represented by k a,i * (S/V)house * C i|g, while the change due to desorption is represented by (k a,i/K e,i)*(S/V)house*C i|S, where C i|S denotes the surface‐sorbed concentration of OG i expressed as:
| (14) |
Here, we considered two main assumptions. (1) We consider the adsorption of gases on clean surfaces, which is a reasonable assumption if cooking emissions dominate the indoor concentration of the compound of interest. As it shall appear in the following, this assumption may hold for the different carbonyl species, but not for terpenes whose emissions are dominated by detergent use. (2) Based on the Langmuir theory, the adsorption onto a surface depends on the number of available sites, which means that compounds from cooking or other processes will compete for these sites. Nevertheless, under indoor conditions (high (S/V)house and K e,i, and low C i|g), the availability of these sites is not a limiting factor, and therefore, competition between the gases will not be taken into account. Based on assumptions (1) and (2), losses due to adsorption should be considered as highest estimates. The surface of indoor material available per volume is an important parameter for gas‐phase adsorption. The (S/V)house distribution (GM = 3.4, GSD = 1.2) is derived from values reported for 12 houses in California by Hodgson et al. (2004)55 and is consistent with values for furnished houses reported elsewhere (3.1 m2 m−3, Thatcher et al. (2002)72 and references therein). The equilibrium constant, K e,i, depends on both the compounds chemical properties and its affinity toward the surface. The study of these data reveals the strong dependence of ln(K e,i) on two parameters:
The compound log‐transformed vapor pressure, log(P vap,i) which for a given surface log(K e,i) increases with the decrease of log(P vap,i);
The type of surface considered where the variation of log(K e,i) for two compounds with given log(P vap,i) with the surface type exhibits an excellent correlation.
By contrast, the gas adsorption rates, k a,i, depend on the compound collision frequency and its accommodation coefficient (effective surface), which is intrinsically a function of the surface properties. Literature data support this, showing a very strong effect of the surface considered on log(k a,i) and only a little dependence on the log(P vap,i). We note that the latter might be a mathematical artifact as log(K e,i) and log(k a,i) are obtained simultaneously from fitting experimental data, which may lead to their interdependence.
These complex (real and unreal) interdependences may be effectively taken into account by considering the ensemble of log(K e,i) and log(k a,i) of the different compounds as a single vector, (with ten elements), whose distribution follows a multivariate normal distribution, generated using Equation (15).
| (15) |
Here, is the mean vector containing mean values of log(K e,i) and log(k a,i) for the different OGs and is the variance/covariance matrix presented in Table S1 in the supplement. The mean values for log(K e,i) and log(k a,i) for different compounds are based on their log(P vap,i)—see Table 5 and the relationship between average adsorption parameters against log(P vap,i) derived from values reported in An et al. (1999).90 These average parameters are as follows: (0.028, 0.017, 1.2, 3.5, 1.8) and (3.1× 10−5, 2.7× 10−5, 7.8× 10−5, 1.0× 10−4, 8.6× 10−5), which corresponds to K e,ACR, K e,C1, K e,C2, K e,C3, and K e,Terp and k a,ACR, k a,C1, k a,C2, k a,C3, and k a,Terp, respectively.
Table 5.
Lognormal distributions of the vapor pressures (Pa) of cooking‐related organic gases used in the Monte Carlo simulations
| GM | GSD | P10 | P25 | P50 | P75 | P90 | |
|---|---|---|---|---|---|---|---|
| ACR | 33 331 | 133 | — | — | — | — | — |
| C1 | 63 995 | 173 | 45 329 | 54 662 | 63 995 | 77 327 | 90 659 |
| C2 | 227 | 187 | 147 | 187 | 227 | 280 | 360 |
| C3 | 53 | 200 | 32 | 41 | 53 | 71 | 89 |
| Terp | 133 | 187 | 87 | 108 | 133 | 173 | 200 |
Data are from Lide et al. (1947),89 and ranges are determined based on the chemical speciation analysis of the different compound classes determined by the PTR‐TOF‐MS.
Based on the K e values, it can be clearly observed that compounds like long‐chain aldehydes and terpenes would tend to stay in the adsorbed phase, while short‐chain aldehydes are mostly in the gas‐phase. This is consistent with measurements in different indoor environments for a range of organic gases with a similar volatility as the cooking emissions investigated here. For example, Singer et al. (2004)91 and (2017)92 reported K e values between 1 and 3 m and between 2 and 7 m for monoterpenes and for n‐alkanes with a carbon number similar to C3 compounds, respectively. The adsorption rates (times the S/V ratio) of gaseous cooking emissions range between 0.4 and 1.2 h−1, comparable to those reported for other compounds (eg, ozone; Table 2) or determined for organic gases from measurements in simulated indoor residential environments (eg, Singer et al. (2004)91 and (2007)93).
The variance of log(K e,i) and log(k a,i) is calculated by propagating the variation of these parameters with the surface properties and their variation due to the change in their composition and therefore their log(P vap,i). We note that K e,i values vary by a factor of 2.6, while k a,i values vary by a factor of 1.7. The covariance between the parameters takes into account their similar dependence on the surface properties (ie, if surfaces in a house are highly adsorptive, then all gases would tend to be sorbed) and the interdependence between log(K e,i) and log(k a,i). The covariance values indicate that the dependence on the surface properties explains about 90% and 98% of the variability in log(K e,i) and log(k a,i), respectively, while correlation coefficients (R 2) between log(K e,i) and log(k a,i) are around 0.18.
4. SOA PRODUCTION
SOA production and loss can be described by the following expression:
| (16) |
Here, y SOA,i is the SOA yield from the oxidation of a compound i. We recognize that SOA yields depend on the activity of the oxidation products in the particle and gas‐phase. However, this dependence is minor compared to other effects (eg, oxidation, emission composition, and strength), especially within the range of concentrations encountered in our chamber and indoor. Therefore, this dependence could not be observed within our uncertainties and will not be considered in the model. Further, we note that yields depend on NOx concentrations, which were typical of ambient atmospheres (10‐20 ppb); therefore, we expect the yields determined in our chamber to be representative. From our chamber experiments, we determine an effective yield from the aggregate sum of ACR, C2, and C3 of 0.22, comparable to values reported for the oxidation of alkane compounds with a similar carbon number,94 while slightly lower values are reported for long‐chain saturated carbonyls (0.1‐0.2).95 We determine a higher effective yield for terpenes (42%),19 expected from the oxidation of a mix of mono‐ and sesquiterpenes. Single yield values, y SOA,ACR+C1+C2 = 0.22 and y SOA,Terp = 0.42 will be used to model SOA production from carbonyls and terpenes.
5. RESULTS AND DISCUSSION
5.1. Emission and loss rates
5.1.1. Cooking contribution to indoor emissions
Modeled rates of indoor cooking emissions presented in Figure 2 are estimated in μg m−3 h−1 based on total daily emissions in the entire house assuming two meals cooked per day. Rates are highly variable due to the different cooking processes involved (Figure 2B) and the amount of food cooked (Figure S2), but remain constrained within a factor of <10 (P90/P10) for all species. We compare the emission rates estimated here with those available in the literature from cooking emission studies. To estimate the importance of cooking compared to other indoor emission processes, we also compare these cooking emission rates to those compiled by Warring et al. (2014)34 representing the sum of indoor emission sources (Figure 2A).
POA emissions (GM rate 1.7 in μg m−3 h−1) are dominated by frying vegetables (49%) and meat (37%). Average POA emission factors from frying correspond to 5 mg kg−1, consistent with the range found in previous studies for frying emissions.96 For example, Schauer et al. (2002)37 reported the organic aerosol emission factors from vegetable stir frying and potato deep frying to range between 7 and 16 mg kg−1. We note that Asian‐style cooking could generate much higher particulate emissions than Western‐style cooking (100 mg kg−1)12; therefore, our results cannot be generalized to other locations. We also note that we have not observed particle emissions from heated empty pans due to desorption/nucleation of sorbed organics recently suggested as a primary source of particles from cooking processes.39 Therefore, we have not considered this additional source in our model, although such processes can still occur if pans are not cleaned well. Based on the calculations of Waring et al. (2014),34 we can infer that cooking can explain about half of the total POA emission rates indoor, including smoking.
The general picture is the same for aldehydes but with higher influence from oil heating. Acrolein GM emission rate is estimated as 0.8 μg m−3 h−1. While cooking emission rates for acrolein are higher than those estimated for overall indoor sources, they compare well to values from a study estimating cooking‐related acrolein emission rates (0.9‐1.5 μg m−3 h−1) by comparing the acrolein concentrations in a house with and without cooking events.97 C1 carbonyl emission rates are estimated to be 7.3 μg m−3 h−1, mostly generated through frying processes (vegetables: 50%, meat: 43%). Cooking can explain the average emission rates of small carbonyl indoor (neglecting formaldehyde which was not measured in our case), but the maximum values reported by Waring and coworkers are much higher. The emission rates of C2 and C3 carbonyls are estimated as 2.5 μg m−3 h−1 and 1.3 μg m−3 h−1, respectively. This corresponds to a GM emission factor for C2 compounds of 7.5 mg kg−1, a factor of 5 lower than values reported by Schauer et al. (2002)37 for stir frying of vegetables, potentially due to the different cooking style applied (cooking on a restaurant hot plate). Unfortunately, for most of the C2 or C3 carbonyls, Waring and coworkers did not calculate emission rates. However, the emission rate they reported for hexanal compares well with our estimated GM emission rate, suggesting that large saturated and unsaturated carbonyl indoors may also be dominated by cooking events. Terpenes are generated by frying and boiling vegetables (46%), and the use of seasonings (54%). A recent study reported monoterpene emission rates from several peppers used in Chinese cuisine to range between 2 and 25 μg g−1 min−1,20 comparable to the emission rates determined here (45 μg g−1 min−1 of terpenes half of which are monoterpenes). The emission rates reported for terpenes from all indoor emissions dominated by cleaning product use are about a factor of ten higher than the terpene emission rates calculated for cooking. Therefore, the emission of terpenes from cooking is overall minor compared to other indoor sources, but may play a role in confined kitchens (see below).
5.1.2. Indoor cooking contribution to outdoor emissions
The analysis above highlights that cooking dominates the emissions of most of the pollutants indoor. Here, we assess the influence of indoor cooking on outdoor air pollution. The origin of cooking organic aerosol (COA) identified during meal times in ambient air by AMS analysis has been lately challenged and the processes by which this fraction is emitted in the atmosphere remain unclear.14 The attempt of modeling cooking organic aerosols in Paris 98 and London 99 suggests that the observed concentrations are consistent with an emission rate of 80 and 320 mg person−1 day−1, respectively. These rates are significantly higher than the rates determined for indoor cooking, equal to 4.4 mg person−1 day−1 on average. Indeed, recent results indicate that cooking organic aerosol can be overestimated in ambient air compared to emission measurements by up to a factor of 4 due to the higher relative ionization efficiency (RIE) for this fraction and the use of a collection efficiency (CE) of 0.5.100 In our case, the CE/RIE factor was constrained based on scanning mobility particle sizer (SMPS) volume measurements using a density of 0.8 consistent with oil droplets obtained by comparing the aerodynamic diameter (from AMS) with the mobility diameter (SMPS). Data are consistent with a CE of ~1, if we assume the default RIE value used for organic aerosols. Despite this possible overestimation of outdoor COA, indoor cooking emissions cannot explain the observed concentration in ambient air, pointing toward the presence of other emission processes. The most likely source of outdoor COA must be related to restaurants, where emission rates are much higher than domestic emissions. For example, emission rates from meat charbroiling are around 15 g kg−1,36 three orders of magnitudes greater than those obtained here or reported for domestic cooking. The significantly higher emissions from commercial kitchens compared to domestic kitchens are also observed in the case of China,12 where COA is a prominent fraction of the aerosol in urban environments.101 This hypothesis is consistent with the observation of COA downwind of restaurants 102 and during mobile measurements in restaurant areas.103 As emissions from restaurants are about two orders of magnitude higher than top‐down estimates of cooking emission rates based on ambient measurements, it only requires <1% of food cooked in commercial kitchens to reproduce the observed ambient COA. Therefore, restaurant emissions may be considered as super‐polluters. We note that the VOC/COA ratio from these emissions is relatively low (\~1, see Schauer et al. (1999)36) compared to that found in domestic cooking emissions (\~10, this study or Schauer et al. (2002)37). Therefore, unlike for domestic cooking emissions where SOA production potential may exceed the emitted POA, for commercial cooking this would be unlikely. More studies are necessary to assess the SOA production potential of commercial kitchen emissions.
5.1.3. Loss rates
In this section, we examine the relative importance of the main processes by which the different pollutants are lost. We compare the integrated losses over 12 hours and note that some processes such as the interaction of the gases with indoor surfaces become a source of VOCs after several hours of emissions. POA is lost equally by exchange and deposition. Meanwhile, acrolein and short‐chain carbonyls (C1) are lost almost exclusively through air exchange, as their reaction toward ozone and their deposition onto indoor surfaces are negligible. The losses of the other compounds, that is, C2, C3, and Terp, by different processes are compared in Figure 3. Air exchange remains the dominant process by which all of these gases are lost (median contribution of 80%, 60%, and 56% for C2, C3, and Terp, respectively). Losses by deposition are significant, especially for unsaturated aldehydes with the lowest vapor pressures (median contribution of 34%). Our results are consistent with measurements in different indoor environments reporting that sorption does not greatly affect indoor concentrations of highly volatile species, while it appears to be a relevant indoor process for lower volatility compounds sorbed at rates close to typical residential air change rates (Singer et al. (2004)91 and (2007)93). Oxidation affects predominantly species reactive against ozone, as OH concentrations are very low. Accordingly, oxidation is only an effective loss mechanism for terpenes (median contribution of 14%). We note that we have not considered multiphase oxidation processes occurring at indoor surfaces, because of the dearth of quantitative data describing the loss rates of cooking emissions from surfaces. For compounds that are almost quantitatively adsorbed onto surfaces (eg, terpenoids104), multiphase oxidation with ozone rivals the homogeneous oxidation in the gas‐phase. Therefore, multiphase chemistry is a non‐negligible loss mechanism only for terpenes from cooking, which are reactive toward ozone and partition equally between the gas‐phase and indoor surfaces. We also note that multiphase chemistry may contribute to the transformation of the unsaturated acids and glycerides contained in the POA deposited onto indoor surfaces, which may constitute a secondary source of carbonyls. However, we note that this source is negligible compared to direct carbonyl emissions from frying (as (C1+C2+C3)/POA ~10 in the emissions). More effort should be devoted in the future to quantify the fate of cooking emissions indoor, with a particular focus on surface deposition and reactions.
Figure 3.
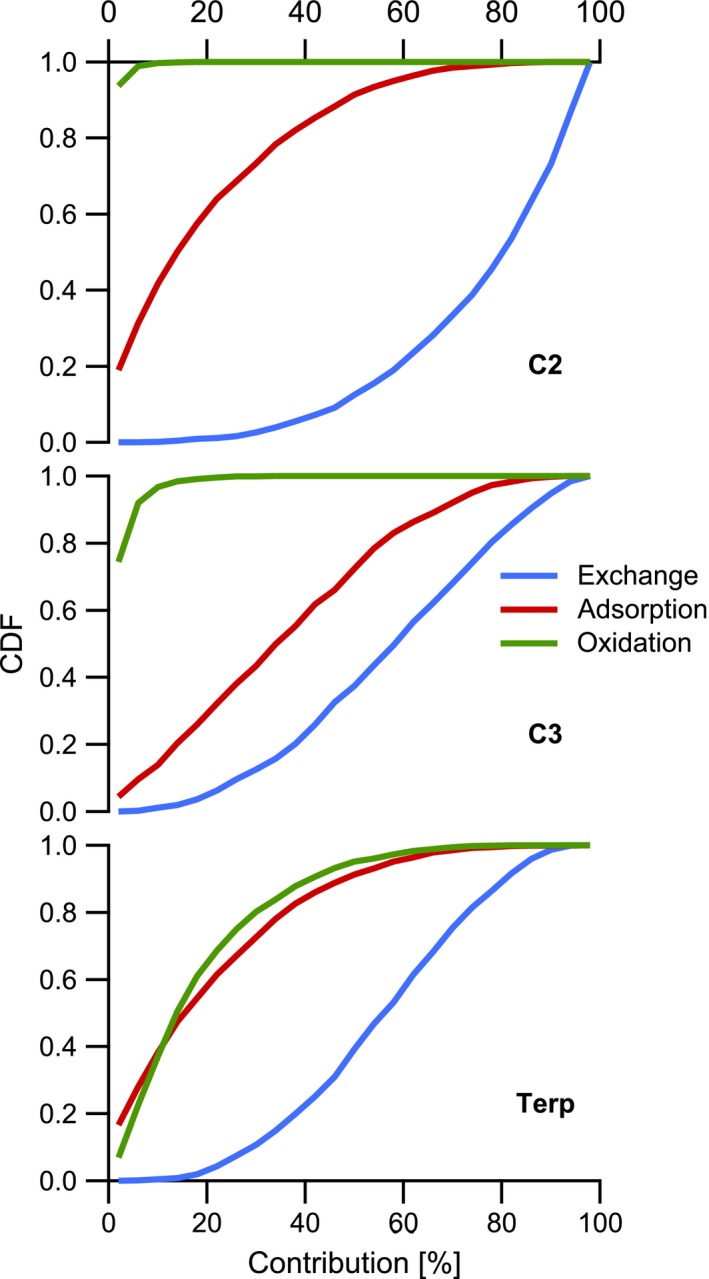
Contribution of air exchange, adsorption on surfaces, and gas‐phase oxidation to the loss of C2, C3, and terpene compounds during the first 12 hours after being emitted. CDF is the cumulative distribution function which gives the probability that the contribution of a loss mechanism is less or equal than a certain contribution
5.2. Indoor pollutant concentrations
The emissions from cooking processes can generate significant gaseous and particulate pollutant concentrations in indoor environments (Figure 4). All gaseous compounds reach their peak concentration about half an hour after the start of the cooking process. The maximum peak concentrations modeled are about 5‐600 μg m−3 for the C1 compounds (Figure 4B), while the minimum peak concentrations modeled are about 0.5‐10 μg m−3 for the terpenes (Figure 4E). The peak concentrations for acrolein, C2, and C3 are 2‐100 μg m−3, 8‐200 μg m−3, and 5‐90 μg m−3, respectively (Figure 4A,C,D). This indicates that cooking processes can generate total gaseous pollutant concentrations of up to 1000 μg m−3, spread over the whole house.
Figure 4.
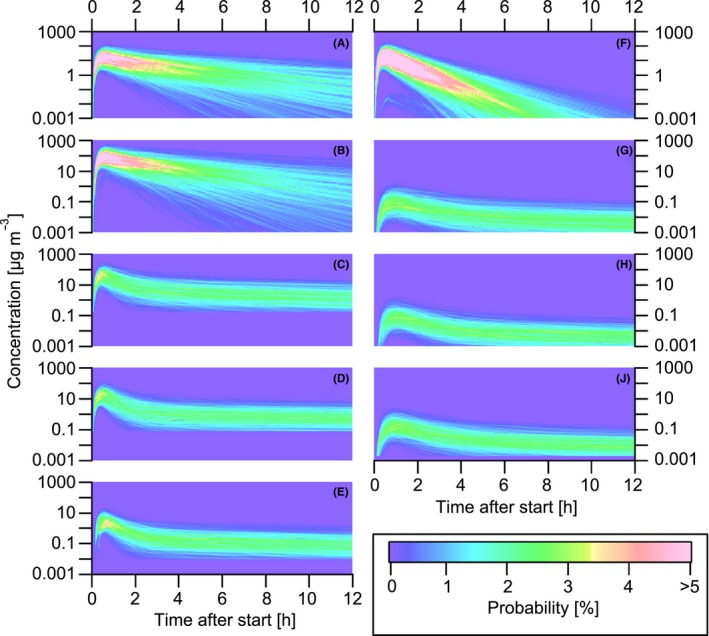
Time‐dependent probability density functions of indoor pollutant concentrations in European homes originating from Occidental style cooking processes. The left‐hand panels show the evolution of the gaseous pollutants, acrolein (A), saturated carbonyls with less than six carbons (B), saturated carbonyls with more than 5 carbons (C), unsaturated carbonyls with more than 5 carbons (D), and terpenes (E). The right‐hand panels show the evolution of the particulate species, POA (F), SOA formed from carbonyl oxidation (G), SOA formed from terpene oxidation (H), and total SOA formed (J)
The peak concentrations determined from this study compare well with aldehyde concentrations measured in a room directly after different deep frying processes.105 The average acrolein, C1, C2, and C3 concentrations resulting from the different deep frying processes are 47, 144, 71, and 41 μg m−3, respectively. While acrolein and C1 concentrations decrease constantly to background levels, the concentrations of C2, C3, and terpenes reach a plateau at about 2, 1, and 0.1 μg m−3, respectively. These plateaus are generated by desorption of the compounds from surfaces where they have been deposited before. This nicely explains the long‐term odorous contamination of the house after certain cooking procedures like cooking fish or preparing dishes with onions.
The POA reaches its peak concentration after half an hour with 5‐200 μg m−3 (Figure 4F) followed by a constant decrease to zero within 6 hours. This modeled lifetime of cooking POA is confirmed by measurements of cooking aerosol in a kitchen performed by Hussein et al. (2006)106 who reported a lifetime of 4‐6 hours. The decrease can be explained by irreversible deposition of the particles on surfaces and removal by air exchange. The modeled POA concentrations compare well with measured cooking‐related indoor concentrations from various studies conducted by Levy et al. (2002)107 (200 μg m−3), See and Balasubramanian (2006; 2008)108, 109 (66‐190 μg m−3) or Buonanno et al. (2009)110 (13‐389 μg m−3). SOA concentrations reach a maximum after about one hour with 0.05‐2 μg m−3 (Figure 4J). The maximum amount of SOA formed from the oxidation of the carbonyls and terpenes (Figure 4G,H) is comparable, with 0.03‐1 μg m−3 and 0.02‐1 μg m−3, respectively. The total SOA decreases slowly, reaching a plateau of about 0.01 μg m−3 after 6 h. This plateau is generated by the oxidation of gases which desorb from the surface they have been adsorbed on before. For the first 6 hours after cooking, POA is clearly dominating the indoor particulate concentrations while SOA formation creates a small but constant particle background. The 12‐hour average and maximum concentration distributions reveal that frying processes dominate the emissions of most gas‐ and particle‐phase species (Figure 5). As can be seen from the color code, the probability for higher concentrations of acrolein, C1, C2, C3, and POA increase almost monotonically with temperature. As expected, the use of seasonings increases the probability for higher terpene concentrations and SOA formed from terpenes compared to only frying processes. Since the carbonyl emissions are mostly dominated by frying processes, also the formation of SOA from the carbonyls is mainly explained by frying. About half of the SOA formation probability is explained by CSOA and the other half by TerpSOA. The peak of the 12‐hour average acrolein probability density function lies around 1‐10 μg m−3. This compares well with measurements from residential homes in Canada 111 or California 97 reporting acrolein concentrations of 1 and 6 μg m−3, respectively. Huang et al. (2011)112 report 17 μg m−3 of acrolein in a kitchen after cooking which compares well with our range when the concentration is normalized to the overall house. This indicates that cooking processes are the main source of acrolein in indoor environments generating high enough concentrations to possibly induce negative effects on human health.113 The C1 distribution peak lies around concentrations of 15 μg m−3; thus, cooking can only explain about one‐third to half of the concentrations of small carbonyls measured in residential houses in Europe 114 (45 μg m−3) and the United States 115 (28 μg m−3). Furthermore, cooking can explain with concentrations of 1‐10 μg m−3 more than half of the average measured concentration of larger saturated aldehydes in Finnish 114 or German 116 homes (9 μg m−3 and 16.8 μg m−3). The indoor terpene concentrations of 0.1‐1 μg m−3 generated from cooking processes are negligible compared to average concentrations measured in indoor environments in Finland 117 and Germany 116 (23 μg m−3 and 25.7 μg m−3).
Figure 5.
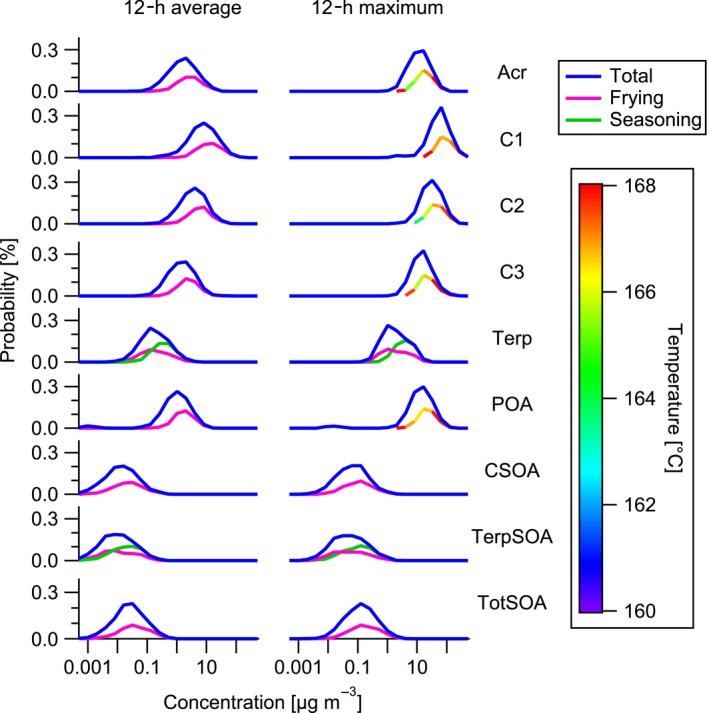
Probability density functions of 12‐h average and maximum indoor pollutant concentrations in European homes originating from frying processes, the use of seasoning, and the total of all cooking processes. The frying is color coded by the average cooking temperature if relevant for the compound emissions. The left‐hand panels show the 12‐h averages, and the right‐hand panels show the maximum concentration of acrolein (Acr), saturated carbonyls with less than six carbons (C1), saturated carbonyls with more than five carbons (C2), unsaturated carbonyls with more than five carbons (C3), terpenes (Terp), primary organic aerosol (POA), SOA formed from carbonyl oxidation (CSOA), SOA formed from terpene oxidation (TerpSOA), and total SOA formed (TotSOA)
On the other hand, maximum concentrations of terpenes in a kitchen (estimated to be 20% of the total house volume) without much air exchange with the rest of the house can reach up to 50 μg m−3. This compares well with the value reported in our previous study about indoor terpene emissions from cooking processes.19 Overall, our study shows that cooking is the most important source of gas‐phase and particle species indoor having potential deleterious effects on human health highlighting the need for efficient mechanical ventilation in kitchens. The model can be used on the one hand to predict the effect of changes in household settings (eg, hood installation), cooking habits (eg, decrease in frying), and environmental factors (eg, change in the outdoor oxidant levels) on the impact of cooking emissions on indoor air quality. On the other hand, the methodology developed here can be extended to other studies focused, for example, on assessing the impact of cooking (or other emissions) on indoor air quality in developing countries, where cooking habits and household settings are significantly different.
Supporting information
ACKNOWLEDGEMENT
This work was supported by the Swiss National Science Foundation (SNF) within the project AEROCOOK. We acknowledge Nicolas Marchand from Aix Marseille Univ, CNRS, LCE, Marseille, 13331, France, for providing parts of the particle data used for the modeling.
Klein F, Baltensperger U, Prévôt ASH, El Haddad I. Quantification of the impact of cooking processes on indoor concentrations of volatile organic species and primary and secondary organic aerosols. Indoor Air. 2019;29:926–942. 10.1111/ina.12597
Imad El Haddad and Felix Klein are contributed equally.
REFERENCES
- 1. Brasche S, Bischof W. Daily time spent indoors in german homes — baseline data for the assessment of indoor exposure of german occupants. Int J Hyg Environ Health. 2005;208:247‐253. [DOI] [PubMed] [Google Scholar]
- 2. Cometto‐Muñiz JE, Abraham MH. Compilation and analysis of types and concentrations of airborne chemicals measured in various indoor and outdoor human environments. Chemosphere. 2015;127:70‐86. [DOI] [PubMed] [Google Scholar]
- 3. Sarigiannis DA, Karakitsios SP, Gotti A, Liakos IL, Katsoyiannis A. Exposure to major volatile organic compounds and carbonyls in European indoor environments and associated health risk. Environ Int. 2011;37:743‐765. [DOI] [PubMed] [Google Scholar]
- 4. Nasir ZA, Colbeck I. Particulate pollution in different housing types in a UK suburban location. Sci Tot Environ. 2013;445–446:165‐176. [DOI] [PubMed] [Google Scholar]
- 5. Macneill M, Kearney J, Wallace L, et al. Quantifying the contribution of ambient and indoor‐generated fine particles to indoor air in residential environments. Indoor Air. 2014;24:362‐375. [DOI] [PubMed] [Google Scholar]
- 6. Bhangar S, Mullen N, Hering S, Kreisberg N, Nazaroff W. Ultrafine particle concentrations and exposures in seven residences in northern california. Indoor Air. 2011;21:132‐144. [DOI] [PubMed] [Google Scholar]
- 7. Wallace L. Indoor sources of ultrafine and accumulation mode particles: size distributions, size‐resolved concentrations, and source strengths. Aerosol Sci Technol. 2006;40:348‐360. [Google Scholar]
- 8. Nolte CG, Schauer JJ, Cass GR, Simoneit BR. Highly polar organic compounds present in meat smoke. Environ Sci Tech. 1999;33:3313‐3316. [DOI] [PubMed] [Google Scholar]
- 9. Wallace L, Wang F, Howard‐Reed C, Persily A. Contribution of gas and electric stoves to residential ultrafine particle concentrations between 2 and 64 nm: size distributions and emission and coagulation rates. Environ Sci Tech. 2008;42:8641‐8647. [DOI] [PubMed] [Google Scholar]
- 10. Dennekamp M, Howarth S, Dick C, Cherrie J, Donaldson K, Seaton A. Ultrafine particles and nitrogen oxides generated by gas and electric cooking. Occup Environ Med. 2001;58:511‐516. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11. Abdullahi KL, Delgado‐Saborit JM, Harrison RM. Emissions and indoor concentrations of particulate matter and its specific chemical components from cooking: a review. Atmos Environ. 2013;71:260‐294. [Google Scholar]
- 12. Zhao Y, Zhao B. Emissions of air pollutants from chinese cooking: a literature review. Build Simul. 2018;11:977‐995. [Google Scholar]
- 13. Mohr C, DeCarlo PF, Heringa MF, et al. Identification and quantification of organic aerosol from cooking and other sources in Barcelona using aerosol mass spectrometer data. Atmos Chem Phys. 2012;12:1649‐1665. [Google Scholar]
- 14. Dall'Osto M, Paglione M, Decesari S, et al. On the origin of ams “cooking organic aerosol” at a rural site. Environ Sci Tech. 2015;49:13964‐13972. [DOI] [PubMed] [Google Scholar]
- 15. Fullana A, Carbonell‐Barrachina nA, Sidhu S. Volatile aldehyde emissions from heated cooking oils. J Sci Food Agr. 2004;84:2015‐2021. [Google Scholar]
- 16. Katragadda HR, Fullana A, Sidhu S, Carbonell‐Barrachina AA. Emissions of volatile aldehydes from heated cooking oils. Food Chem. 2010;120:59‐65. [Google Scholar]
- 17. Alves CA, Evtyugina M, Cerqueira M, Nunes T, Duarte M, Vicente E. Volatile organic compounds emitted by the stacks of restaurants. Air Qual Atmos Health. 2015;8:401‐412. [Google Scholar]
- 18. Klein F, Platt SM, Farren NJ, et al. Characterization of gas‐phase organics using proton transfer reaction time‐of‐flight mass spectrometry: cooking emissions. Environ Sci Tech. 2016;50:1243‐1250. [DOI] [PubMed] [Google Scholar]
- 19. Klein F, Farren NJ, Bozzetti C, et al. Indoor terpene emissions from cooking with herbs and pepper and their secondary organic aerosol production potential. Sci Rep. 2016;6:36623. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20. Liu T, Liu Q, Li Z, et al. Emission of volatile organic compounds and production of secondary organic aerosol from stir‐frying spices. Sci Tot Environ. 2017;599:1614‐1621. [DOI] [PubMed] [Google Scholar]
- 21. Nazaroff WW, Weschler CJ. Cleaning products and air fresheners: exposure to primary and secondary air pollutants. Atmos Environ. 2004;38:2841‐2865. [Google Scholar]
- 22. Ahn JH, Kim KH, Kim YH, Kim BW. Characterization of hazardous and odorous volatiles emitted from scented candles before lighting and when lit. J Hazard Mater. 2015;286:242‐251. [DOI] [PubMed] [Google Scholar]
- 23. Haghighat F, Huang H, Lee CS. Modeling approaches for indoor air voc emissions from dry building materials–a review. ASHRAE Trans. 2005;111:635‐645. [Google Scholar]
- 24. National Research Council . Measuring Exposures and Assessing Health Effects Report. Washington, DC: National Academy Press; 1986. [Google Scholar]
- 25. Matysik S, Ramadan AB, Schlink U. Spatial and temporal variation of outdoor and indoor exposure of volatile organic compounds in Greater Cairo. Atmos Pollut Res. 2010;1:94‐101. [Google Scholar]
- 26. Dodson RE, Houseman EA, Levy JI, Spengler JD, Shine JP, Bennett DH. Measured and modeled personal exposures to and risks from volatile organic compounds. Environ Sci Tech. 2007;41:8498‐8505. [DOI] [PubMed] [Google Scholar]
- 27. Capello F, Gaddi AV. Clinical Handbook of Air Pollution-Related Diseases. Cham, Switzerland: Springer International Publishing; 2018. [Google Scholar]
- 28. Kroll JH, Seinfeld JH. Chemistry of secondary organic aerosol: formation and evolution of low‐volatility organics in the atmosphere. Atmos Environ. 2008;42:3593‐3624. [Google Scholar]
- 29. Sarwar G, Corsi R, Allen D, Weschler C. The significance of secondary organic aerosol formation and growth in buildings: experimental and computational evidence. Atmos Environ. 2003;37:1365‐1381. [Google Scholar]
- 30. Sarwar G, Corsi R. The effects of ozone/limonene reactions on indoor secondary organic aerosols. Atmos Environ. 2007;41:959‐973. [Google Scholar]
- 31. Coleman BK, Lunden MM, Destaillats H, Nazaroff WW. Secondary organic aerosol from ozone‐initiated reactions with terpene‐rich household products. Atmos Environ. 2008;42:8234‐8245. [Google Scholar]
- 32. Chen X, Hopke PK. A chamber study of secondary organic aerosol formation by limonene ozonolysis. Indoor Air. 2010;20:320‐328. [DOI] [PubMed] [Google Scholar]
- 33. Waring MS, Wells JR, Siegel JA. Secondary organic aerosol formation from ozone reactions with single terpenoids and terpenoid mixtures. Atmos Environ. 2011;45:4235‐4242. [Google Scholar]
- 34. Waring MS. Secondary organic aerosol in residences: predicting its fraction of fine particle mass and determinants of formation strength. Indoor Air. 2014;24:376‐389. [DOI] [PubMed] [Google Scholar]
- 35. Waring MS, Wells JR. Volatile organic compound conversion by ozone, hydroxyl radicals, and nitrate radicals in residential indoor air: magnitudes and impacts of oxidant sources. Atmos Environ. 2015;106:382‐391. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36. Schauer JJ, Kleeman MJ, Cass GR, Simoneit BRT. Measurement of emissions from air pollution sources. 1. C‐1 through C‐29 organic compounds from meat charbroiling. Environ Sci Tech. 1999;33:1566‐1577. [Google Scholar]
- 37. Schauer JJ, Kleeman MJ, Cass GR, Simoneit BRT. Measurement of emissions from air pollution sources. 4. C‐1‐C‐27 organic compounds from cooking with seed oils. Environ Sci Tech. 2002;36:567‐575. [DOI] [PubMed] [Google Scholar]
- 38. Kim KH, Pandey SK, Kabir E, Susaya J, Brown RJ. The modern paradox of unregulated cooking activities and indoor air quality. J Hazard Mat. 2011;195:1‐10. [DOI] [PubMed] [Google Scholar]
- 39. Wallace LA, Ott WR, Weschler CJ. Ultrafine particles from electric appliances and cooking pans: experiments suggesting desorption/nucleation of sorbed organics as the primary source. Indoor Air. 2015;25:536‐546. [DOI] [PubMed] [Google Scholar]
- 40. Peng CY, Lan CH, Lin PC, Kuo YC. Effects of cooking method, cooking oil, and food type on aldehyde emissions in cooking oil fumes. J Hazard Mat. 2017;324:160‐167. [DOI] [PubMed] [Google Scholar]
- 41. Lunden MM, Delp WW, Singer BC. Capture efficiency of cooking‐related fine and ultrafine particles by residential exhaust hoods. Indoor Air. 2015;25:45‐58. [DOI] [PubMed] [Google Scholar]
- 42. Singer BC, Delp WW, Price P, Apte M. Performance of installed cooking exhaust devices. Indoor Air. 2012;22:224‐234. [DOI] [PubMed] [Google Scholar]
- 43. Nazaroff WW, Cass GR. Mathematical modeling of chemically reactive pollutants in indoor air. Environ Sci Tech. 1986;20:924‐934. [DOI] [PubMed] [Google Scholar]
- 44. Sparks L, Tichenor B, Chang J, Guo Z. Gas‐phase mass transfer model for predicting volatile organic compound (voc) emission rates from indoor pollutant sources. Indoor Air. 1996;6:31‐40. [Google Scholar]
- 45. Chen F, Simon C, Lai AC. Modeling particle distribution and deposition in indoor environments with a new drift–flux model. Atmos Environ. 2006;40:357‐367. [Google Scholar]
- 46. Kraenzmer M. Modeling and continuous monitoring of indoor air pollutants for identification of sources and sinks. Environ Interact. 1999;25:541‐551. [Google Scholar]
- 47. Platt SM, El Haddad I, Pieber SM, et al. Two‐stroke scooters are a dominant source of air pollution in many cities. Nat Commun. 2014;5:3749. [DOI] [PubMed] [Google Scholar]
- 48. Platt SM, El Haddad I, Pieber SM, et al. Gasoline cars produce more carbonaceous particulate matter than modern filter‐equipped diesel cars. Sci Rep. 2017;7:4926. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49. Barmet P, Dommen J, DeCarlo PF, et al. OH clock determination by proton transfer reaction mass spectrometry at an environmental chamber. Atmos Meas Tech. 2012;5:647‐656. [Google Scholar]
- 50. Jordan A, Haidacher S, Hanel G, et al. A high resolution and high sensitivity proton‐transfer‐reaction time‐of‐flight mass spectrometer (PTR‐TOF‐MS). Int J Mass Spectrom. 2009;286:122‐128. [Google Scholar]
- 51. Williams LR, Gonzalez LA, Peck J, et al. Characterization of an aerodynamic lens for transmitting particles greater than 1 micrometer in diameter into the Aerodyne aerosol mass spectrometer. Atmos Meas Tech. 2013;6:3271‐3280. [Google Scholar]
- 52. DeCarlo PF, Kimmel JR, Trimborn A, et al. Field‐deployable, high‐resolution, time‐of‐flight aerosol mass spectrometer. Anal Chem. 2006;78:8281‐8289. [DOI] [PubMed] [Google Scholar]
- 53. European Commission . Manual of Standard Building Specifications, Report. Brussels: Office for infrastructure and logistics, 2011. [Google Scholar]
- 54. Eurostat . Household Composition, Poverty and Hardship Across Europe, Report. Luxembourg: Publications Office of the European Union, 2013. [Google Scholar]
- 55. Hodgson A, Ming K, Singer B. Quantifying Object and Material Surface Areas in Residences. Lbnl Report 56786. Report. Berkeley, CA: Lawrence Berkeley National Laboratory; 2004. [Google Scholar]
- 56. Weisel CP, Zhang J, Turpin BJ, et al. Relationships of Indoor, Outdoor, and Personal Air (RIOPA). Part I. Collection methods and descriptive analyses. Res Rep Health Eff Inst. 2005;130:1‐107. [PubMed] [Google Scholar]
- 57. Lee K, Vallarino J, Dumyahn T, Ozkaynak H, Spengler JD. Ozone decay rates in residences. J Air Waste Manag Assoc. 1999;49:1238‐1244. [DOI] [PubMed] [Google Scholar]
- 58. Morrison G, Shaughnessy R, Shu S. Setting maximum emission rates from ozone emitting consumer appliances in the United States and Canada. Atmos Environ. 2011;45:2009‐2016. [Google Scholar]
- 59. Spicer CW, Kenny DV, Ward GF, Billick IH. Transformations, lifetimes, and sources of NO2, HONO, and HNO3 in indoor environments. Air Waste. 1993;43:1479‐1485. [DOI] [PubMed] [Google Scholar]
- 60. Alvarez EG, Amedro D, Afif C, et al. Unexpectedly high indoor hydroxyl radical concentrations associated with nitrous acid. Proc Natl Acad Sci USA 2013;110:13294‐13299. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61. AQS data mart . http://www.epa.gov/ttn/airs/airsaqa/detaildata/downloadaqsdata.html, 2013. Accessed: 2016‐12‐12.
- 62. USBC . American Housing Survey. Report, Washington, DC: US Bureau of the Census, 2016. [Google Scholar]
- 63. of Como T , Parzen J, Barzini S. The Art of Cooking: The First Modern Cookery Book, 1 edition, Berkeley, CA: University of California Press, 2005. [Google Scholar]
- 64. Statista . Number of hours spent cooking per week among consumers worldwide as of June 2014, by country. https://www.statista.com/statistics/420719/time-spent-cooking-per-week-among-consumers-by-country. Accessed: 2016‐12‐12.
- 65. FAO . FAOSTAT Statistical Database: Current Worldwide Annual Meat Consumption per Capita, Livestock and Fish Primary Equivalent. Report, Rome: Food and Agriculture Organization of the United Nation, 2013. [Google Scholar]
- 66. Buzby JC, Wells HF, Axtman et al. Supermarket Loss Estimates for Fresh Fruit, Vegetables, Meat, Poultry, and Seafood and Their use in the ERS Loss‐Adjusted Food Availability Data. report. Washington, DC: United States Department of Agriculture, Economic Research Service, 2009. [Google Scholar]
- 67. Muth MK, Karns SA, Nielsen SJ, Buzby JC, Wells HF. Consumer‐Level Food Loss Estimates and Their Use in the ERS Loss‐Adjusted Food Availability Data. Washington, DC: United States Department of Agriculture, Economic Research Service; 2011. [Google Scholar]
- 68. USDA . Food Availability (per Capita) Data System. Report, Washington, DC: United States Department of Agriculture, Economic Research Service, 2016. [Google Scholar]
- 69. Elmadfa I. European Nutrition and Health Report 2009. report, Vienna: Karger Medical and Scientific Publishers, 2009. [Google Scholar]
- 70. State of the plate, 2015 study on america's consumption of fruit and vegetables, produce for better health foundation. http://www.Foundation.org, 2015. Accessed: 2016‐12‐12.
- 71. European Spice Association (ESA) . Representing the European Spice and Seasoning Industry. report, Bonn: European Spice Association, 2015. [Google Scholar]
- 72. Thatcher TL, Lai AC, Moreno‐Jackson R, Sextro RG, Nazaroff WW. Effects of room furnishings and air speed on particle deposition rates indoors. Atmos Environ. 2002;36:1811‐1819. [Google Scholar]
- 73. Atkinson R, Arey J. Atmospheric degradation of volatile organic compounds. Chem Rev. 2003;103:4605‐4638. [DOI] [PubMed] [Google Scholar]
- 74. Linstrom PJ, Mallard WG, eds. NIST Chemistry WebBook, NIST Standard Reference Database Number 69. Gaithersburg, MD: National Institute of Standards and Technology; 2016. [Google Scholar]
- 75. Grosjean D, Grosjean E, Williams EL. Rate constants for the gas‐phase reactions of ozone with unsaturated alcohols, esters, and carbonyls. Int J Chem Kinet. 1993;25:783‐794. [Google Scholar]
- 76. Colmán EG, Blanco MB, Barnes I, Teruel MA. Ozonolysis of a series of C7–C9 unsaturated biogenic aldehydes: reactivity study at atmospheric pressure. RSC Adv. 2015;5:30500‐30506. [Google Scholar]
- 77. Grosjean D. Atmospheric chemistry of toxic contaminants. 3. Unsaturated aliphatics: Acrolein, acrylonitrile, maleic anhydride. J Air Waste Manag Assoc. 1990;40:1664‐1669. [Google Scholar]
- 78. Bowman JH, Barket DJ, Shepson PB. Atmospheric chemistry of nonanal. Environ Sci Tech. 2003;37:2218‐2225. [DOI] [PubMed] [Google Scholar]
- 79. Gao T, Andino JM, Rivera CC, Márquez MF. Rate constants of the gas‐phase reactions of OH radicals with trans‐2‐hexenal, trans‐2‐octenal, and trans‐2‐nonenal. Int J Chem Kinet. 2009;41:483‐489. [Google Scholar]
- 80. Stephens B, Gall ET, Siegel JA. Measuring the penetration of ambient ozone into residential buildings. Environ Sci Tech. 2011;46:929‐936. [DOI] [PubMed] [Google Scholar]
- 81. Coleman BK, Morrison GC, Wells J. Kinetics and reaction products of ozone and surface‐bound squalene. J ASTM Int. 2008;5:1‐12. [Google Scholar]
- 82. Waring MS, Siegel JA. Indoor secondary organic aerosol formation initiated from reactions between ozone and surface‐sorbed d‐limonene. Environ Sci Tech. 2013;47:6341‐6348. [DOI] [PubMed] [Google Scholar]
- 83. Weschler CJ. Ozone in indoor environments: concentration and chemistry. Indoor Air. 2000;10:269‐288. [DOI] [PubMed] [Google Scholar]
- 84. Carslaw N. A new detailed chemical model for indoor air pollution. Atmos Environ. 2007;41:1164‐1179. [Google Scholar]
- 85. Weschler CJ, Shields HC. Production of the hydroxyl radical in indoor air. Environ Sci Tech. 1996;30:3250‐3258. [Google Scholar]
- 86. Logue J, McKone T, Sherman M, Singer B. Hazard assessment of chemical air contaminants measured in residences. Indoor Air. 2011;21:92‐109. [DOI] [PubMed] [Google Scholar]
- 87. Zhang J, Zhang J, Chen Q, Yang X. A critical review on studies of volatile organic compound (VOC) sorption by building materials. ASHRAE Transac. 2002;108:162. [Google Scholar]
- 88. Mendez M, Blond N, Blondeau P, Schoemaecker C, Hauglustaine DA. Assessment of the impact of oxidation processes on indoor air pollution using the new time‐resolved INCA‐indoor model. Atmos Environ. 2015;122:521‐530. [Google Scholar]
- 89. Lide DR CRC Handbook of Chemistry and Physics (Vol. 85). Boca Raton, FL: CRC Press; 2004. [Google Scholar]
- 90. An Y, Zhang J, Shaw C. Measurements of VOC adsorption/desorption characteristics of typical interior building materials. HVAC Res. 1999;5:297‐316. [Google Scholar]
- 91. Singer BC, Revzan KL, Hotchi T, Hodgson AT, Brown NJ. Sorption of organic gases in a furnished room. Atmos Environ. 2004;38:2483‐2494. [Google Scholar]
- 92. Singer BC, Pass RZ, Delp WW, Lorenzetti DM, Maddalena RL. Pollutant concentrations and emission rates from natural gas cooking burners without and with range hood exhaust in nine california homes. Build Environ. 2017;122:215‐229. [Google Scholar]
- 93. Singer BC, Hodgson AT, Hotchi T, et al. Sorption of organic gases in residential rooms. Atmos Environ 2007;41:3251‐3265. [Google Scholar]
- 94. Loza CL, Craven JS, Yee LD, et al. Secondary organic aerosol yields of 12‐carbon alkanes. Atmos Chem Phys. 2014;14:1423‐1439. [Google Scholar]
- 95. Chacon‐Madrid H, Donahue N. Fragmentation vs. functionalization: chemical aging and organic aerosol formation. Atmos. Chem Phys. 2011;11:10553‐10563. [DOI] [PubMed] [Google Scholar]
- 96. Hu T, Singer BC, Logue JM. Compilation of Published PM2. 5 Emission Rates for Cooking, Candles and Incense for use in Modeling of Exposures in Residences. Technical report, Berkeley, CA: Lawrence Berkeley National Lab. (LBNL); 2012. [Google Scholar]
- 97. Seaman VY, Bennett DH, Cahill TM. Origin, occurrence, and source emission rate of acrolein in residential indoor air. Environ Sci Tech. 2007;41:6940‐6946. [DOI] [PubMed] [Google Scholar]
- 98. Fountoukis C, Megaritis AG, Skyllakou K, et al. Simulating the formation of carbonaceous aerosol in a European megacity (Paris) during the MEGAPOLI summer and winter campaigns. Atmos Chem Phys. 2016;16:3727‐3741. [Google Scholar]
- 99. Ots R, Vieno M, Allan JD, et al. Model simulations of cooking organic aerosol (COA) over the UK using estimates of emissions based on measurements at two sites in London. Atmos Chem Phys. 2016;16:13773‐13789. [Google Scholar]
- 100. Reyes‐Villegas E, Bannan T, Le Breton M, et al. Online chemical characterization of food‐cooking organic aerosols: implications for source apportionment. Environ Sci Tech. 2018;52:5308‐5318. [DOI] [PubMed] [Google Scholar]
- 101. Huang RJ, Wang Y, Cao J, et al. Primary emissions versus secondary formation of fine particulate matter in the most polluted city (Shijiazhuang) in North China. Atmos Chem Phys. 2019;19:2283‐2298. [Google Scholar]
- 102. Robinson ES, Gu P, Ye Q, et al. Restaurant impacts on outdoor air quality: elevated organic aerosol mass from restaurant cooking with neighborhood‐scale plume extents. Environ Sci Tech. 2018;52:9285‐9294. [DOI] [PubMed] [Google Scholar]
- 103. Elser M, El Haddad I, Maasikmets M, et al. High contributions of vehicular emissions to ammonia in three european cities derived from mobile measurements. Atmos Environ. 2018;175:210‐220. [Google Scholar]
- 104. Shu S, Morrison GC. Surface reaction rate and probability of ozone and alpha‐terpineol on glass, polyvinyl chloride, and latex paint surfaces. Environl Sci Tech. 2011;45:4285‐4292. [DOI] [PubMed] [Google Scholar]
- 105. Seaman VY, Bennett DH, Cahill TM. Indoor acrolein emission and decay rates resulting from domestic cooking events. Atmos Environ. 2009;43:6199‐6204. [Google Scholar]
- 106. Hussein T, Glytsos T, Ondráček J, et al. Particle size characterization and emission rates during indoor activities in a house. Atmos Environ. 2006;40:4285‐4307. [Google Scholar]
- 107. Levy J, Dumyahn T, Spengler J. Particulate matter and polycyclic aromatic hydrocarbon concentrations in indoor and outdoor microenvironments in Boston, Massachusetts. J Expo Anal Environ Epid. 2002;12:104‐114. [DOI] [PubMed] [Google Scholar]
- 108. See SW, Balasubramanian R. Physical characteristics of ultrafine particles emitted from different gas cooking methods. Aerosol Air Qual Res. 2006;6:82‐92. [Google Scholar]
- 109. See S, Balasubramanian R. Chemical characteristics of fine particles emitted from different gas cooking methods. Atmos Environ. 2008;42:8852‐8862. [Google Scholar]
- 110. Buonanno G, Morawska L, Stabile L. Particle emission factors during cooking activities. Atmos Environ. 2009;43:3235‐3242. [Google Scholar]
- 111. Gilbert NL, Guay M, Miller JD, Judek S, Chan CC, Dales RE. Levels and determinants of formaldehyde, acetaldehyde, and acrolein in residential indoor air in Prince Edward Island, Canada. Environ Res. 2005;99:11‐17. [DOI] [PubMed] [Google Scholar]
- 112. Huang Y, Ho SSH, Ho KF, Lee SC, Yu JZ, Louie PKK. Characteristics and health impacts of VOCs and carbonyls associated with residential cooking activities in Hong Kong. J Hazard Mater. 2011;186:344‐351. [DOI] [PubMed] [Google Scholar]
- 113. Rey deCastro B. Acrolein and asthma attack prevalence in a representative sample of the United States adult population 2000–2009. PLoS One. 2014;9:e96926. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 114. Jurvelin JA, Edwards RD, Vartiainen M, Pasanen P, Jantunen MJ. Residential indoor, outdoor, and workplace concentrations of carbonyl compounds: relationships with personal exposure concentrations and correlation with sources. J Air Waste Manag Assoc. 2003;53:560‐573. [DOI] [PubMed] [Google Scholar]
- 115. Liu W, Zhang J, Zhang L, et al. Estimating contributions of indoor and outdoor sources to indoor carbonyl concentrations in three urban areas of the United States. Atmos Environ. 2006;40:2202‐2214. [Google Scholar]
- 116. Hippelein M. Background concentrations of individual and total volatile organic compounds in residential indoor air of Schleswig‐Holstein, Germany. J Environ Monit. 2004;6:745‐752. [DOI] [PubMed] [Google Scholar]
- 117. Edwards RD, Jurvelin J, Saarela K, Jantunen M. VOC concentrations measured in personal samples and residential indoor, outdoor and workplace microenvironments in EXPOLIS‐Helsinki, Finland. Atmos Environ. 2001;35:4531‐4543. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials


