How kinesin waits for ATP affects the nucleotide and load dependence of the stepping kinetics

Significance

Dimeric molecular motors walk on polar tracks by binding and hydrolyzing one ATP per step. Despite tremendous progress, the waiting state for ATP binding in kinesin that walks on microtubule (MT), remains controversial. One experiment suggests that in the waiting state both heads are bound to the MT, while the other shows that ATP binds to the leading head after the partner head detaches. To discriminate between these 2 scenarios, we developed a theory to calculate accurately several experimentally measurable quantities as a function of ATP concentration and resistive force. In particular, we predict that measurement of the randomness parameter could discriminate between the 2 scenarios for the waiting state of kinesin, thereby resolving this standing controversy.

Abstract

Conventional kinesin, responsible for directional transport of cellular vesicles, takes multiple nearly uniform 8.2-nm steps by consuming one ATP molecule per step as it walks toward the plus end of the microtubule (MT). Despite decades of intensive experimental and theoretical studies, there are gaps in the elucidation of key steps in the catalytic cycle of kinesin. How the motor waits for ATP to bind to the leading head is controversial. Two experiments using a similar protocol have arrived at different conclusions. One asserts that kinesin waits for ATP in a state with both the heads bound to the MT, whereas the other shows that ATP binds to the leading head after the trailing head detaches. To discriminate between the 2 scenarios, we developed a minimal model, which analytically predicts the outcomes of a number of experimental observable quantities (the distribution of run length, the distribution of velocity [$\mathit{P}\left(\mathit{v}\right)$], and the randomness parameter) as a function of an external resistive force ($\mathit{F}$) and ATP concentration ([T]). The differences in the predicted bimodality in $\mathit{P}\left(\mathit{v}\right)$ as a function of $\mathit{F}$ between the 2 models may be amenable to experimental testing. Most importantly, we predict that the $\mathit{F}$ and [T] dependence of the randomness parameters differ qualitatively depending on the waiting states. The randomness parameters as a function of $\mathit{F}$ and [T] can be quantitatively measured from stepping trajectories with very little prejudice in data analysis. Therefore, an accurate measurement of the randomness parameter and the velocity distribution as a function of load and nucleotide concentration could resolve the apparent controversy.

Kinesin-1 (Kin1) is an archetypal cellular transporter, which moves along the microtubule (MT) to shuttle cargo toward the cellular periphery. In the last quarter century, a number of spectacular experimental studies (1–5) have revealed many of the salient features of Kin1 structure and motility: 1) Kin1 is a homodimer made up of 2 ATPase and MT-binding heads. A key structural element, the neck linker (NL), undergoes an order/disorder transition during the catalytic cycle termed “NL docking.” The distal tail forms a coiled coil which is responsible for dimerization and is also involved in cargo binding (6). 2) Remarkably, the motor takes almost precisely 8.2-nm steps (5), which is commensurate with the spacing between 2 adjacent $\alpha \beta$ dimers—the building blocks of the MT filament. 3) For each diffusional encounter with the MT, Kin1 takes multiple steps before detaching, a feature termed processivity (7). 4) In the absence of resistive load ($F$), Kin1 moves nearly unidirectionally (backward steps are rare) toward the plus end of the MT (8) and predominantly along a single protofilament (9). In addition, the velocity ($v$) distribution is roughly Gaussian with a peak typically in the range (100 to 1,000) $\mathrm{n}\mathrm{m}\cdot {\mathrm{s}}^{-1}$ depending on ATP concentration (10); the mean velocity is much larger than what is found in other motors such as myosin V and dynein. As the resisting load increases, the probability that the motor takes backward steps becomes more prominent, reaching 0.5 at the stall force $F_S\approx 7\hspace{0.17em}\mathrm{p}\mathrm{N}$ (11, 12). At stall, the mean motor velocity is zero, with a velocity distribution predicted to be bimodal and distinctly non-Gaussian (13). 5) The 2 heads step by a hand-over-hand mechanism (2, 5), in which the trailing head (TH) detaches from the MT, bypasses the leading head (LH), and reattaches to the target binding site (TBS) on the MT. Although it has long been advocated that the search for the TBS occurs largely by diffusion, it is only recently this has been definitively established (14–16). The docking of the NL of the LH propels the tethered head toward the plus end of the MT, thereby minimizing the probability of taking backward steps. For this reason, NL docking is sometimes referred to as the “power stroke.” 6) The energetic cost necessary to realize this directed motion is provided by the hydrolysis of ATP, which kinesin, like other motors, consumes parsimoniously. One molecule of ATP is hydrolyzed per step (17). The binding and hydrolysis of ATP are the events associated with the NL docking (18). Based on these observations and other key experiments probing the variations of the stepping characteristics of the motor as a function of ATP concentration and applied load, several theoretical models for motors in general and the catalytic cycle of Kin1 in particular have been proposed (13, 19–24), although issues such as the mechanism of interhead communication (gating) continue to be topics of interest (25–27).

Despite these significant advances, there is a key problem related to the catalytic cycle of Kin1, which surprisingly still plagues the field: What is the waiting state of Kin1 for ATP binding? The answer to this fundamental question, which goes to one of the most important steps in the catalytic cycle of the motor, has been debated for nearly 2 decades, with contrasting pieces of evidence provided by optical trapping and single-molecule fluorescence experiments. Some studies have argued that the waiting state for ATP binding to the LH occurs when both the heads are bound (2HB) to MT (28), whereas others assert that binding occurs only after the TH has detached, placing Kin1 in a 1-head-bound (1HB) state (29, 30). The waiting state likely depends on ATP concentration. Kin1 waits with both heads bound (2HB) to MT at saturating ATP concentration whereas at low ATP concentration Kin1 might be in a 1HB state (4) before ATP binds. However, to discriminate between the 1HB and 2HB ATP waiting states, it is necessary to monitor the location of the tethered head at the time of ATP binding, which requires experiments with high temporal and spatial resolution.

The development of an experimental technique in which a large gold nanoparticle (AuNP) (between 20 and 40 nm in diameter) is attached to one of the heads has made it possible to track indirectly the position of the tethered head during the stepping process as a function of ATP concentration. By tracking the location of the AuNP, via either interferometric scattering microscopy (iSCAT) (31) or total internal-reflection dark-field microscopy (14), 2 groups have achieved a degree of temporal and spatial resolution necessary to resolve the waiting state of kinesin. From the analysis of the AuNP movement at different ATP concentrations, Mickolajczyk et al. (31) argued that the motor waits in the 2HB state when the concentration of ATP is $\ge 10\hspace{0.17em}\mathrm{\mu }\mathrm{M}$. The 2HB $\to$ 1HB transition follows ATP binding, and Kin1 spends about half of the stepping time with the tethered head parked above the bound head, which implies that the TH is displaced by about 8.2 nm from the initial binding site. In sharp contrast, Isojima et al. (14) established that ATP binds to the LH only after the TH detaches from the MT. In other words, Kin1 waits for ATP in the 1HB state. In addition, computer simulations, using coarse-grained (CG) models for motors in general (32, 33) and kinesin in particular, have provided insights into their functions. In particular, CG models that accurately reproduce several features found in experiments (15, 16, 34–36) have shown that the TH does spontaneously detach but does not walk toward the plus end of the MT until the neck linker docks to the LH, which requires ATP binding to the leading head. These findings support the 1HB conformation as the Kin1 ATP waiting state. The contradictory findings reported in refs. 14 and 31 and alluded to by Sindelar and Liu (37) leave the vexing question posed in the previous paragraph unanswered. This basic question needs to be fully answered to achieve a complete understanding of the stepping mechanism of conventional kinesin.

It is unclear whether the differing conclusions reached in the recent experimental studies (14, 31) arise because of the discrepancies in the constructs of the kinesin, the method of analysis of the trajectories, or the variations in the temporal resolution achieved in the experiments. Isojima et al. (14) used a cys-lite motor to control the location of the linkage between the motor and the AuNP. In contrast, Mickolajczyk et al. (31) used a WT Kin1, whose N terminus was extended with an Avi tag which is linked to the AuNP through a streptavidin–biotin complex. Moreover, because of the higher temporal resolution in the dark-field microscopy experiments (14), Isojima et al. (14) could discern the 1HB state by simultaneously monitoring the transverse fluctuations directly from the trajectories in a straightforward manner. On the other hand, Mickolajczyk et al. (31) relied on hidden Markov models (HMMs) to extract information from the stepping trajectories.

To discriminate between the contrasting interpretations of these experiments, it is desirable to consider quantities that are straightforward to measure and that do not require indirect techniques of data analysis. Ideally, a theoretical study capable of describing both scenarios (1HB and 2HB waiting states for ATP) should be able to identify which observable might be used to discriminate between the proposed cycles for kinesin. Here, we use a simple and accurate model for kinesin stepping and calculate analytically a number of standard measurable quantities, such as the run length ($n$) distribution, $P\left(n\right)$; velocity ($v$) distribution, $P\left(v\right)$; and the randomness parameter as a function of ATP concentration (denoted as [T] from now on) and resistive force $F$. We show that $P\left(n\right)$ is independent of [T], and $P\left(v\right)$ as a function of [T] and $F$ is qualitatively similar for both the 1HB and 2HB models but differs quantitatively, a discrepancy that is amenable to experimental test. Remarkably, we predict that the mechanical and chemical randomness parameters, which are defined from readily measurable quantities, could be used to discriminate between the 2 scenarios. In particular, we find that both the mechanical and chemical randomness parameters at different [T] and $F$ are qualitatively different for these 2 scenarios in which Kin1 waits for ATP either in the 1HB or in the 2HB state. Thus, we propose that measurements of the randomness parameters and $P\left(v\right)$ as a function of [T] and $F$ should unambiguously allow one to distinguish between the 2 very different ATP waiting states of Kin1.

Results

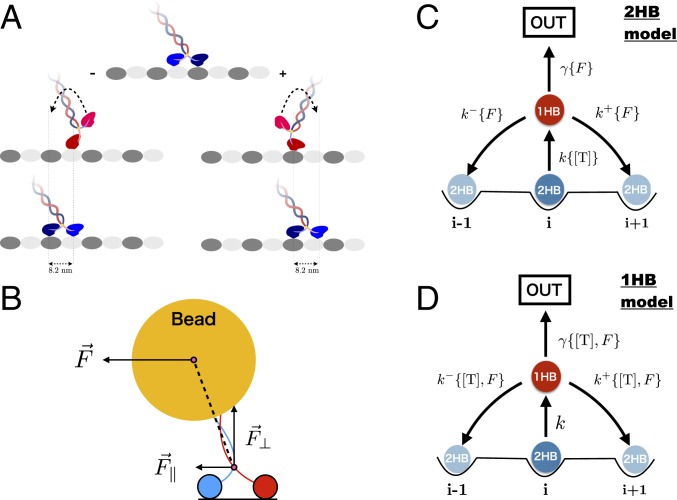
We begin by presenting some nomenclature. We refer to the scenario in which ATP binds to the LH of kinesin when both heads are attached to the MT as the “2HB model,” whereas the “1HB model” refers to the alternative sequence of events, in which the detachment of the TH of kinesin precedes the binding of ATP to the LH. To calculate $P\left(v\right)$ and $P\left(n\right)$ we created 2 versions of what is perhaps the simplest chemical kinetics model for a molecular motor (Fig. 1 C and D), one for the 2HB model and one for the 1HB model. The difference between the two lies in the dependence on ATP concentration of the kinetic rates. In the 2HB model the transition to the 1HB state occurs only after ATP binds to the leading head (Fig. 1C); therefore, the 2HB $\to$ 1HB rate accounts for the dependence on [T]. Because in the 1HB model ATP binds only after the tethered head detaches, the stepping rates, $k^{+}$ and $k^{-}$, as well as detachment rate $\gamma$ are assumed to depend on [T] (Fig. 1D).

Fig. 1.

(A) Schematic representation of a kinesin motor walking hand over hand on the MT. The tethered head detaches, undergoes diffusion, passes the LH, and reattaches to the target binding site that is roughly 16.4 nm from the starting position, resulting in a net displacement of an 8.2-nm step. In the process one ATP molecule is hydrolyzed. (B) Decomposition of the resistive force applied to the bead attached to the coiled coil of kinesin into a perpendicular ($\perp$) and parallel ($\parallel$) direction to the MT. (C) Kinetic scheme describing the ATP waiting state showing that binding to the LH occurs when both the heads are bound to the MT in the 2HB state. (D) Same as C except ATP binds when kinesin is in the 1HB state. In both the scenarios the i − 1 and i + 1 states are equivalent to i in that they correspond to both the heads bound to the track. The difference is in the state that waits for ATP. The state labeled OUT represents an absorbing state.

We use Michaelis–Menten kinetics to describe ATP binding and account for the effect of external load on the rates by adopting the Bell model (38). To distinguish between the parallel components of the vectorial load applied to the motor, which introduce the symbols $\parallel$ and $\perp$, respectively, see Fig. 1B. For the 2HB model, $k\left\{\left[\text{T}\right]\right\}=\frac{k_0\left[\text{T}\right]}{K_T+\left[\text{T}\right]}$, $k^{+}\left(F\right)=k_0^{+}{\text{e}}^{-\beta F{d}^{+}}$, $k_0^{-}\left(F\right)=k^{-}{\text{e}}^{\beta F{d}^{-}}$, and $\gamma \left(F\right)={\gamma }_0{\text{e}}^{\left|F\right|/F_d}$, where $d^{\pm }=d_{\parallel }^{\pm }{F}_{\parallel }/F$ and the load $F_d=\left(\left|F\right|k_{B}T\right)/\left(F_{\perp }{d}_{\gamma }\right)$. In the case of the 1HB model (Fig. 1D), $k$ is a constant, independent of [T] and load, $k^{+}=\frac{k_0^{+}\left[\text{T}\right]}{K_T+\left[\text{T}\right]}{\text{e}}^{-\beta F{d}^{+}}$, $k^{-}=\frac{k_0^{-}\left[\text{T}\right]}{K_T+\left[\text{T}\right]}{\text{e}}^{\beta F{d}^{-}}$, and $\gamma =\frac{{\gamma }_0\left[\text{T}\right]}{K_T+\left[\text{T}\right]}{\text{e}}^{F/F_d}$. Note that in both the scenarios we have assumed that the 2HB $\to$ 1HB transition is independent of load.

For the first step in the calculation of $P\left(v\right)$ and $P\left(n\right)$ we obtain the stationary fluxes for forward stepping, backward stepping, and detachment. The motor is viewed as a random walker starting in the 2HB state at the MT site $i$. A steady-state probability distribution of occupying the 2HB and 1HB states is enforced by replenishing the 2HB state of all of the walkers that step forward or backward (reaching $i+1$ and $i-1$, respectively) or detach (39, 40),

$$\begin{array}{cc}\hfill \frac{d{P}_{2\text{HB}}}{dt}& =-k{P}_{2\text{HB}}+\left(\gamma +k^{+}+k^{-}\right)P_{1\text{HB}}=0\hfill \\ \hfill \frac{d{P}_{1\text{HB}}}{dt}& =-\left(\gamma +k^{+}+k^{-}\right)P_{1\text{HB}}+k{P}_{2\text{HB}}=0.\hfill \end{array}$$ [1]

The normalization condition implies that $P_{2\text{HB}}+P_{1\text{HB}}=1$. The solution of Eq. 1 gives $P_{1\text{HB}}=\frac{k}{k+k^{+}+k^{-}+\gamma }$. The stationary fluxes for forward stepping ($J^{+}$), backward stepping ($J^{-}$), and detachment ($J^{\gamma }$) are computed by multiplying the steady-state probability of being in state 1HB ($P_{1\text{HB}}$) times $k^{+}$, $k^{-}$, and $\gamma$ (39, 40),

$$\begin{array}{c}\hfill J^{\pm }=\frac{k}{k_T}{k}^{\pm },J^{\gamma }=\frac{k}{k_T}\gamma ,\end{array}$$ [2]

where $k_T=k+k^{+}+k^{-}+\gamma$.

The average velocity and run length are given by $V=s\left(J^{+}-J^{-}\right)$ and $L=V/J^{\gamma }$, respectively, where $s=8.2$ nm is the kinesin step size, which we assume is a constant. It is straightforward to show that

$$\begin{array}{c}\hfill V=\frac{V_{max}\left[\text{T}\right]}{K_{\mathrm{M}}+\left[\text{T}\right]},L=\frac{\left(k^{+}-k^{-}\right)s}{\gamma },\end{array}$$ [3]

for both the 2HB and 1HB models. The maximum velocity at saturating ATP concentration for the 2HB and 1HB models is given by $V_{max}=\frac{k_0\left(k^{+}-k^{-}\right)s}{k_0+k^{+}+k^{-}+\gamma }$ and $V_{\mathrm{m}\mathrm{a}\mathrm{x}}=\left(k_0^{+}{\text{e}}^{-\beta F{d}^{+}}-k_0^{-}{\text{e}}^{\beta F{d}^{-}}\right)ks/k_T$, respectively. The concentrations at which the velocity of Kin1 is half-maximal are given by $K_{\mathrm{M}}=\frac{K_T\left(k^{+}+k^{-}+\gamma \right)}{k_0+k^{+}+k^{-}+\gamma }$ for the 2HB model (Fig. 1C) and $K_{\mathrm{M}}=K_T$ for the 1HB model (Fig. 1D).

Run Length Distribution, $\mathit{P}\left(\mathit{n}\right)$.

To solve for the run length and velocity distributions, we construct the joint probability [$P\left(m,l\right)$] that the motor takes $m$ forward steps and $l$ backward steps before detachment (see SI Appendix for details),

$$\begin{array}{c}\hfill P\left(m,l\right)=\frac{\left(m+l\right)!}{m!l!}{\left(\frac{J^{+}}{J_T}\right)}^m{\left(\frac{J^{-}}{J_T}\right)}^l\left(\frac{J^{\gamma }}{J_T}\right).\end{array}$$ [4]

In Eq. 4, $J^{+}/J_T$ ($J^{-}/J_T$) is the probability of taking a forward (backward) step starting from the 2HB state, and $J_T=J^{+}+J^{-}+J^{\gamma }$. Similarly, $J^{\gamma }/J_T$ is the probability that a motor in the 2HB state detaches. The number of all of the possible ways in which a sequence of $m$ forward and $l$ backward steps can be realized is accounted for by the binomial factor. If the run length is $n=m-l$, then $P\left(n\right)$ is given by $P\left(n\right)={\sum }_{m,l=0}^{\infty }P\left(m,l\right){\delta }_{m-l,n}$, where ${\delta }_{m-l,n}$ is the Kronecker delta function (Fig. 2). By carrying out the summation we obtain

$$\begin{array}{c}\hfill P\left(n\gtrless 0\right)={\left(\frac{2J^{\pm }}{J_T+\sqrt{J_T^2-4J^{+}{J}^{-}}}\right)}^{\left|n\right|}\frac{J^{\gamma }}{\sqrt{J_T^2-4J^{+}{J}^{-}}}.\end{array}$$ [5]

Note that the functional form of $P\left(n\gtrless 0\right)$ is independent of the model considered—it is the dependence of the fluxes on [T] and $F$ that separates the 2HB and 1HB models. We note that the expression for $P\left(n\right)$ obtained here is equivalent to the one obtained previously (13, 41), which can be derived by substituting the rates of forward step, backward step, and detachment for the corresponding fluxes defined in Eq. 2.

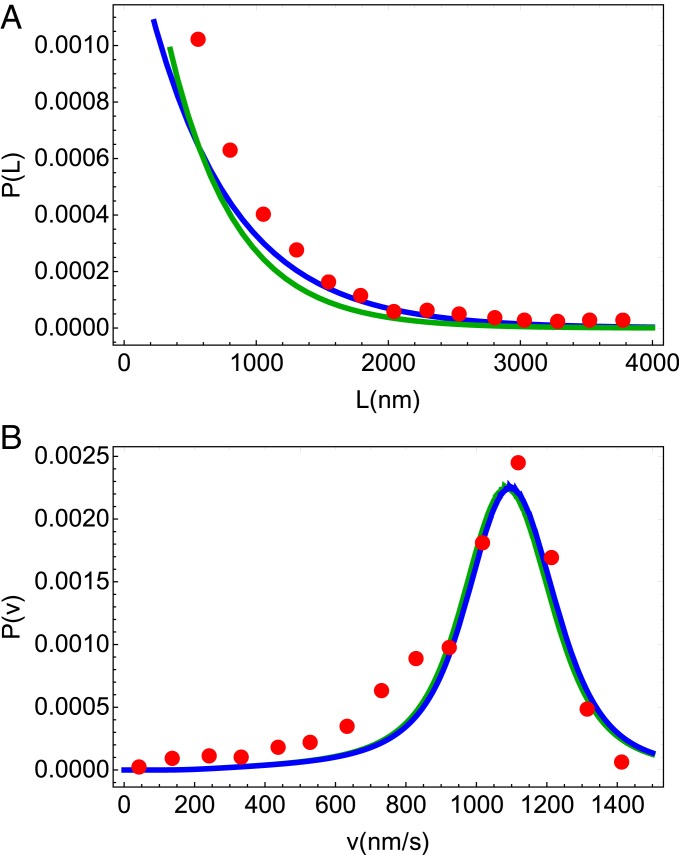
Fig. 2.

Simultaneous fits of $P\left(L\right)$ ($L=sn$ with $s$ = 8.2 nm) and $P\left(v\right)$ at zero load for Kin1 to the experimental data given in ref. 10. Red circles are from experiment and the blue and green lines are results from our theory, for the 2HB and the 1HB model, respectively. (A) Run length distribution. (B) Velocity distribution of Kin1. The comparison shows not only that the theory reproduces the measured data well but also that the overlap of the blue and green lines shows at zero load the differences in ATP waiting states are not reflected in the distributions of the run length and velocity.

Velocity Distribution, $\mathit{P}\left(\mathit{v}\right)$.

To calculate $P\left(v\right)$, we first compute $f\left(m,l,t\right)$, which is the joint probability density for detaching during a time interval from $t$ to $t+dt$ after the motor takes $m$ forward and $l$ backward steps. Let $f_{+}\left(t\right)$ be the probability density of taking a forward step between $t$ and $t+dt$, given that at $t=0$ the motor is in the 2HB state. Similarly, the probability densities for stepping backward and for detachment are denoted by $f_{-}\left(t\right)$ and $f_{\gamma }\left(t\right)$. We show in SI Appendix that $f_{+}\left(t\right)$, $f_{-}\left(t\right)$, and $f_{\gamma }\left(t\right)$ are linear combinations of 2 exponential functions with rates ${\xi }_1=k$ and ${\xi }_2=k^{+}+k^{-}+\gamma$ (see Fig. 1 for the definition of the rates). The probability density $f\left(m,l,t\right)$ is given by

$$\begin{array}{cc}\hfill & f\left(m,l,t\right)=\frac{\left(m+l\right)!}{m!l!}\hfill \\ \hfill & {\int }_0^{t}d{t}_{m+l}{\int }_0^{t_{m+l}}d{t}_{m+l-1}\dots {\int }_0^{t_3}d{t}_2{\int }_0^{t_2}d{t}_1\hfill \\ \hfill & \prod _{i=1}^m{f}_{+}\left(t_i-t_{i-1}\right)\prod _{i=m+1}^{m+l}{f}_{-}\left(t_i-t_{i-1}\right)f_{\gamma }\left(t-t_{m+l}\right).\hfill \end{array}$$ [6]

As detailed in SI Appendix, the solution of the integral equation in Eq. 6 is

$$\begin{array}{cc}\hfill f\left(m,l,t\right)& =\frac{\gamma \sqrt{\pi }}{m!l!}{e}^{-\frac{{\xi }_1+{\xi }_2}{2}t}{t}^{m+l}\frac{k^{m+l+1}{\left(k^{+}\right)}^m{\left(k^{-}\right)}^l}{{|{\xi }_2-{\xi }_1|}^{m+l+1}}\hfill \\ \hfill & \sqrt{|{\xi }_1-{\xi }_2|t}{I}_{m+l+\frac{1}{2}}\left(\frac{|{\xi }_1-{\xi }_2|}{2}t\right),\hfill \end{array}$$ [7]

where $I_{m+l+\frac{1}{2}}\left(\frac{|{\xi }_1-{\xi }_2|}{2}t\right)$ is the modified Bessel function of the first kind. The velocity distribution may be obtained by changing the variables to $v=\left(m-l\right)/t$, which gives

$$\begin{array}{cc}\hfill P\left(v>0\right)\hspace{0.17em}=\hspace{0.17em}& \sum _{\begin{array}{c}m,l\\ m>l\end{array}}^{\infty }\frac{m-l}{v^2}\frac{\gamma \sqrt{\pi }}{m!l!}{\text{e}}^{-\frac{{\xi }_1+{\xi }_2}{2}\frac{m-l}{v}}{\left(\frac{m-l}{v}\right)}^{m+l+\frac{1}{2}}\hfill \\ \hfill & \frac{k^{m+l+1}{\left(k^{+}\right)}^m{\left(k^{-}\right)}^l}{{|{\xi }_2-{\xi }_1|}^{m+l+\frac{1}{2}}}{I}_{m+l+\frac{1}{2}}\left(\frac{|{\xi }_2-{\xi }_1|}{2}\frac{m-l}{v}\right).\hfill \end{array}$$ [8]

The expression for $P\left(v<0\right)$ is presented in SI Appendix. Note that both Eqs. 7 and 8 hold if ${\xi }_1\hspace{0.17em}\ne \hspace{0.17em}{\xi }_2$. However, as we show in SI Appendix, the solution for ${\xi }_1={\xi }_2$ has the same form and can be obtained as the limit for ${\xi }_1\to {\xi }_2$ in Eq. 8. Again, the functional form for $P\left(v\right)$ is the same in the 2HB and 1HB models, which are differentiated only by the dependence on $F$ and [T] of the chemical rates.

Analyses of Experimental Data.

We first analyzed the $F=0$ experimental data for Kin1 (10, 42; see Fig. 2) to obtain the 8 parameters at zero load by fitting Eq. 5 to the run length distribution, with the constraint that the average velocity $J^{+}-J^{-}=132.8\hspace{0.17em}\mathrm{s}\mathrm{t}\mathrm{e}\mathrm{p}\mathrm{s}\hspace{0.17em}\mathrm{p}\mathrm{e}\mathrm{r}\hspace{0.17em}\mathrm{s}\mathrm{e}\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{d}$ at [T] = 1 mM (10) and the ratio of forward over backward steps $J^{+}/J^{-}=221$ at [T] = 10 $\mathrm{\mu }\mathrm{M}$ and [T] = 1 mM (42). We also used the load dependence of the average velocity at $1-\mathrm{m}\mathrm{M}$ and $10-\mathrm{\mu }\mathrm{M}$ ATP concentration in ref. 42 to obtain the parameters that depend on $F$ and [T]. Following previous studies, we set $F_d=3$ pN (13, 43) and $\left|d^{+}\right|+\left|d^{-}\right|=2.9$ nm (42). Overall we chose the fitting parameters to be $k_0$, $K_T$, $k_0^{+}$, and $d^{+}$ from the 8 parameters in our model. The best-fit parameters are listed in Tables 1 and 2 for the 2HB and the 1HB model, respectively. It is worth pointing out that $k_0^{+}$ and $k_0^{-}$ for both the 1HB and 2HB models are fairly close to each other and are in rough accord with our previous study that did not consider [T] dependence (13). Similarly, the distances to the transition state when $F\hspace{0.17em}\ne \hspace{0.17em}0$ ($d^{+}$ and $d^{-}$) for both the schemes are not too dissimilar (Tables 1 and 2).

Table 1.

Extracted parameters for the 2HB model

Parameter	Meaning of the parameter	Value
$k_0$	Bare rate of transition from 2HB to 1HB	$787.0\left({\mathrm{s}}^{-1}\right)$
$k_0^{+}$	Bare rate for forward step	$185.5\left({\mathrm{s}}^{-1}\right)$
$k_0^{-}$	Bare rate for backward step	$0.8\left({\mathrm{s}}^{-1}\right)$
${\gamma }_0$	Detachment rate at 0 load	$2.4\left({\mathrm{s}}^{-1}\right)$
$d^{+}$	Effective transition distance for forward step	$1.6\hspace{0.17em}\left(\text{nm}\right)$
$d^{-}$	Effective transition distance for backward step	$1.3\hspace{0.17em}\left(\text{nm}\right)$
$F_d$	Detachment load	$3.0\hspace{0.17em}\left(\text{pN}\right)$
$K_T$	Michaelis–Menten constant for ATP binding	$594.0\hspace{0.17em}\left(\mathrm{\mu }\text{M}\right)$

Table 2.

Extracted parameters for 1HB model

Parameter	Meaning of the parameter	Value
$k_0$	Bare rate of transition from 2HB to 1HB	$538.0\left({\mathrm{s}}^{-1}\right)$
$k_0^{+}$	Bare rate for forward step	$184\left({\mathrm{s}}^{-1}\right)$
$k_0^{-}$	Bare rate for backward step	$0.8\left({\mathrm{s}}^{-1}\right)$
${\gamma }_0$	Detachment rate at 0 load	$3.0\left({\mathrm{s}}^{-1}\right)$
$d^{+}$	Effective transition distance for forward step	$1.9\hspace{0.17em}\left(\text{nm}\right)$
$d^{-}$	Effective transition distance for backward step	$1.0\hspace{0.17em}\left(\text{nm}\right)$
$F_d$	Detachment load	$3.0\hspace{0.17em}\left(\text{pN}\right)$
$K_T$	Michaelis–Menten constant for ATP binding	$21.0\hspace{0.17em}\left(\mathrm{\mu }\text{M}\right)$

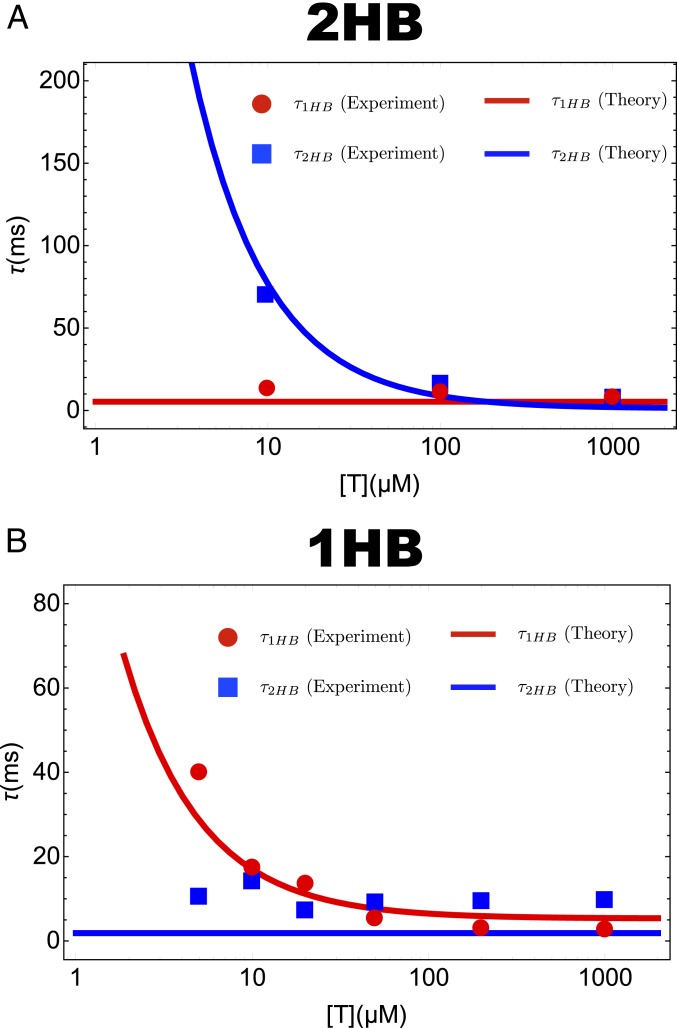
To ascertain that our kinetic schemes for the 2HB and 1HB models provide a faithful description of the data of Mickolajczyk et al. (31) and Isojima et al. (14), we compare the lifetime of the 1HB [${\tau }_{1HB}=1/\left(k^{+}+k^{-}+\gamma \right)$] and 2HB (${\tau }_{2HB}=1/k$) with the experimental measurements. As shown in Fig. 3 the agreement for both the scenarios is excellent, indicating that our theory captures the results of the experiments (14, 31) accurately. We hasten to emphasize that the data from Mickolajczyk et al. (31) and Isojima et al. (14) were not used for fitting. The agreement is a genuine emergent feature of our kinetic model, which lends credence to the additional predictions made below.

Fig. 3.

Mean dwell time for the 2HB state (${\tau }_{2HB}$) and the 1HB state (${\tau }_{1HB}$) as a function of ATP concentration at $F=0$. (A) The 2HB model (Fig. 1C). (B) The 1HB model (Fig. 1D). Red circles and blue squares are taken from the experiments by Mickolajczyk et al. (31) (A) and Isojima et al. (14) (B). Lines are the theoretical predictions for the dwell times for the 1HB state and 2HB states. Note that in A ${\tau }_{1HB}$ is [T] independent whereas in B ${\tau }_{2HB}$ does not depend on [T].

Velocity Distribution Is Bimodal When F ≠ 0.

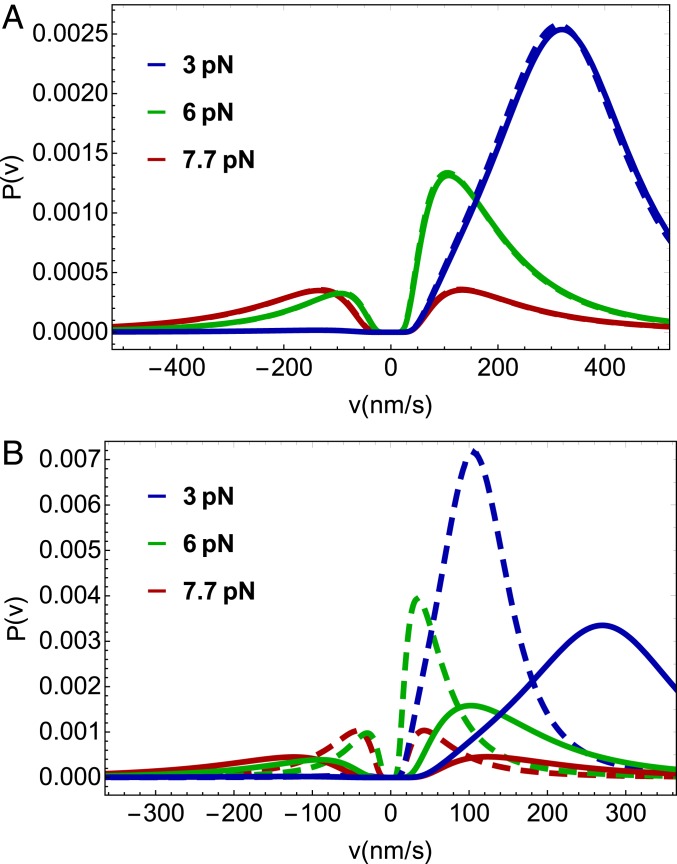
We use the analytical solutions for $P\left(n\right)$ (Eq. 5) and $P\left(v\right)$ (Eq. 8) to predict how the distributions of run length and velocity change over a broad range of load and ATP concentrations for the 2 models (Fig. 4). First, we note that the bimodality of the velocity distribution, originally predicted by Vu et al. (13), is evident at both high ($1-\mathrm{m}\mathrm{M}$) and low ($10-\mathrm{\mu }\mathrm{M}$) ATP concentrations. The peak at the negative $v$ increases as $F$ approaches $F_S$. As the ATP concentration is lowered the motor slows down and the location of the peak of the velocity distribution becomes closer to zero. Second, the $P\left(v\right)$s at all values of $F$ when [T] is 1 mM are similar in the 1HB and 2HB scenarios (Fig. 4A) and hence cannot be used to easily distinguish between them when the [T] is high. Although the shape of $P\left(v\right)$ does depend on the ATP waiting state at low [T] (Fig. 4B), which in principle is amenable to experimental test. However, the small qualitative difference may not be sufficient to discriminate between the waiting states in practice. Bimodality in $P\left(v\right)$ (13) arises because Kin1 takes nearly constant discrete steps on the MT in multiples of the step size ($s=8.2\hspace{0.17em}\mathrm{n}\mathrm{m}$). This feature is critical in the presence of load and is prominent as the stall force is approached. Mathematically, it was shown in ref. 13 that upon making a continuous approximation in the derivation of $P\left(v\right)$, which would allow us to replace discrete sums by integrals in Eq. 8 for example, the bimodality is completely washed away, and one obtains a Gaussian distribution centered at zero velocity at the stall force. Thus, it is the ability of Kin1 to take almost precisely discrete steps on the MT that results in the bimodal distribution in $P\left(v\right)$, which becomes pronounced in the presence of external resistive force.

Fig. 4.

Velocity distributions for $v\hspace{0.17em}\ne \hspace{0.17em}0$ predicted by our theory for different loads and ATP concentrations. Solid lines are for the 2HB model (Fig. 1C) and dashed lines are for the 1HB model (Fig. 1D). Colors represent different loads applied to kinesin. (A) Velocity distribution at 1 mM ATP concentration. (B) Velocity distribution for 10 $\mathrm{\mu }$M ATP concentration.

To summarize, we showed that the bimodality of $P\left(v\right)$ is robust to changes in the concentration of ATP and the model used for the ATP waiting states. This provides experimental flexibility in testing the predicted bimodality. Although the prediction of bimodal behavior as a function of [T] and $F$ is most interesting in its own right, it may be challenging to use $P\left(v\right)$ as a probe to determine the nature of the ATP waiting state in conventional kinesin.

Randomness Parameters Are Qualitatively Different in the 1HB and 2HB Waiting States for ATP.

Fluctuation analyses in molecular motors are performed using the so-called chemical and mechanical randomness parameters (11, 17, 44). The former describes the fluctuation of the enzymatic states of the motor and is given by $r_C=\left(⟨{\tau }^2⟩-{⟨\tau ⟩}^2\right)/{⟨\tau ⟩}^2$. Here, $\tau$ is the dwell time of the motor at one site and the bracket denotes the average over an ensemble of motors. The mechanical randomness parameter is given by $r_M=\underset{t\to \infty }{lim}\left(⟨n^2\left(t\right)⟩-{⟨n\left(t\right)⟩}^2\right)/⟨n\left(t\right)⟩$. It can be shown that $r_C=r_M$ and is bounded from 0 to 1 if there are no backward steps (45). However, it is possible that $r_M$ increases beyond 1 when load acts on the motor due to the presence of backward steps. We found analytical expressions for $r_C$ and $r_M$, which allowed us to compare the deviation of the 2 kinds of randomness parameter as the external load increases. We can recover $r_C$ from $r_M$ by using the relation $r_C=\left[\left(2P_{+}-1\right)r_M-4P_{+}\left(1-P_{+}\right)\right]/{\left(2P_{+}-1\right)}^2$, where $P_{+}$ is the probability of forward stepping. We denote the chemical randomness parameter calculated from the mechanical randomness parameter given above as ${\overline{r}}_C$ to differentiate it from $r_C$, which is not easy to measure experimentally (45). The relationship connecting $r_C$ and $r_M$ has been derived elsewhere (46, 47). In SI Appendix, we provide an alternate method, which connects between the chemical and mechanical randomness parameters. The chemical randomness parameter in our model is written as

$$\begin{array}{c}\hfill r_C=\frac{k^2+{\left(k^{+}+k^{-}+\gamma \right)}^2}{{\left(k+k^{+}+k^{-}+\gamma \right)}^2}.\end{array}$$ [9]

To calculate the moments needed to calculate $r_M$, we first obtain the renormalized probability distribution, $\overline{f}\left(n>0,t\right)$, for the position of the motor at time $t$ on the track,

$$\begin{array}{cc}\hfill \overline{f}\left(n,t\right)=& \frac{1}{C}\sum _{l=0}^{\infty }\frac{\gamma \sqrt{\pi }}{\left(n+2l\right)!l!}{\text{e}}^{-\frac{{\xi }_1+{\xi }_2}{2}t}{t}^{n+2l+\frac{1}{2}}\hfill \\ \hfill & \frac{k^{n+2l+1}{\left(k^{+}\right)}^{n+l}{\left(k^{-}\right)}^l}{|{\xi }_2-{\xi }_1{|}^{n+2l+\frac{1}{2}}}{I}_{n+2l+\frac{1}{2}}\left(\frac{|{\xi }_2-{\xi }_1|}{2}t\right).\hfill \end{array}$$ [10]

The normalization constant $C$, which accounts for the detachment of motors, is obtained by summing over both positive and negative values of $n$ in Eq. 10 (see SI Appendix for details). By computing the first and second moments of $\overline{f}$ for $n$ at sufficiently long times, we can obtain an expression for the mechanical randomness parameter $r_M$. Because $r_C$ in Eq. 9 depends on ATP, which occurs in different steps in the 2HB and 1HB models (Fig. 1 C and D, respectively), the variation of $r_C$ as a function of [T] could be used to assess the likelihood of the 2 models.

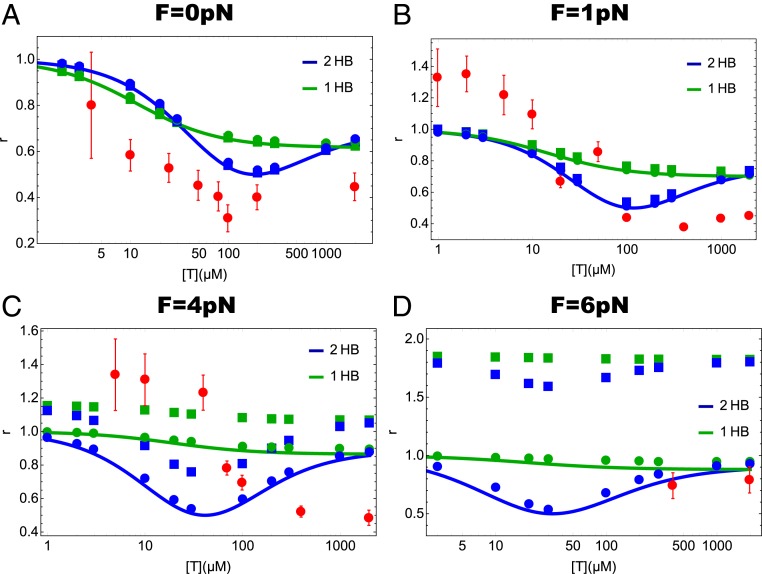
In Fig. 5 we plot the randomness parameters, $r_M$, ${\overline{r}}_C$, and $r_C$ for the kinetic schemes in Fig. 1 C and D as a function of ATP concentration at different loads. The dependence on ATP concentration of the mechanical randomness parameters for kinesin has been previously reported (11, 17, 48). We plotted the randomness parameter obtained in the experiments by Visscher et al. (11) and Verbrugge et al. (48) in Fig. 5 to assess whether the theory captures the experimental behavior. It is clear that the theory and experiments agree only qualitatively with the trends being very similar. It is known from even more complicated models that it is difficult to calculate with high accuracy the dependence of various randomness parameters on $F$ and [T] (11, 49). Because the randomness parameter measures the inverse of the number of rate-limiting states in the cycle, it is not unreasonable that our model may overestimate the randomness parameter. At higher forces our model for chemical randomness is in near-quantitative agreement ($F$ = 6 pN). In addition, we recover the trend observed in experiments ($F$ = 1 pN). At intermediate values of the forces ($F$ = 4 pN) the agreement is less accurate. Thus, we surmise that the agreement between theory and experiments is reasonable so that we can discuss the use of these parameters in deciphering the ATP waiting state of kinesin.

Fig. 5.

Theoretical prediction of the ATP concentration dependence of the 3 randomness parameters, $r_M$, $r_C$, and ${\overline{r}}_C$ at different external loads for the 2HB and 1HB models (Fig. 1 C and D, respectively). Solid squares, solid circles, and lines denote $r_M$, ${\overline{r}}_C$, and $r_C$, respectively. Red circles with error bar in A are the experimentally measured randomness parameter at $F=0$ in ref. 48. Red circles with error bar in B–D are the randomness parameters measured in ref. 11: (B) for 1.05 pN, (C) for 3.59 pN, and (D) for 5.69 pN. As explained in Discussion, the values of the randomness parameters in our schemes are always equal or greater than 0.5.

Remarkably, the dependence of the randomness parameters on [T] and $F$ is dramatically different in the 2 models for the ATP waiting states. In the 1HB model, the randomness parameters decrease monotonically. In sharp contrast, if ATP binds when both heads are engaged with the MT, we predict a nonmonotonic function of [T] with a minimum occurring at near [T] $\approx 100\hspace{0.17em}\mathrm{\mu }\mathrm{M}$. This finding suggests an alternative, and perhaps a more straightforward way, of differentiating between 2 types of waiting states for ATP. If the randomness parameters ($r_M$ and $r_C$) could be measured using the higher-resolution single-molecule experiments (14) as a function of [T] and $F$, then the timing of ATP binding to kinesin could be unambiguously determined.

It is most interesting that at all values of $F$ in the model based on the 2HB waiting state the randomness parameters have a clear minimum as the ATP concentration is changed whereas in the 1HB model the decrease is monotonic and is almost flat as $F$ increases. The difference can be appreciated by noting that in the 2HB model the rate-determining step for completing a step changes as [T] is increased from a low value. In particular, at low [T] the rate-limiting step is the 2HB $\to$ 1HB transition (Fig. 1C) whereas at high [T] the 1HB $\to$ 2HB transition is rate limiting (Fig. 1C). As a consequence of the change in the rate-determining step, there is a minimum in the values of the randomness parameter at a critical value of the ATP concentration. Let us write Eq. 9 as $r_C=\frac{1+{\left(x/k\right)}^2}{{\left(1+x/k\right)}^2}$, where $x=k^{+}+k^{-}+\gamma$. Using the parameters in Table 1 we determine that at low [T] with $F\hspace{0.17em}=\hspace{0.17em}0\hspace{0.17em}\frac{x}{k}\gg 1$, whereas at saturating ATP concentration $\frac{x}{k}\approx 0.3$ with a cross-over (location of the minimum in the randomness parameter) occurring at $\frac{x}{k}=1$. The values of [T] at which the randomness parameters are a minimum at different values of $F$ may be estimated using the values in Table 1, which is roughly in accord with the results in Fig. 5.

In sharp contrast, in the 1HB model the 1HB $\to$ 2HB is always slower than the 2HB $\to$ 1HB, a feature that is enhanced as $F$ increases. This is because the 1HB $\to$ 2HB transition is slowed down with load, whereas the 2HB $\to$ 1HB is unaffected. In other words, at all values of the ATP concentration the 1HB $\to$ 2HB transition is rate limiting with $\frac{x}{k}$ being less than unity. As a consequence, the chemical randomness parameter is nearly monotonic and is close to unity at all values of $F$, thus making $r_C$ almost independent of [T] (Fig. 5).

It might be tempting to conclude based on the randomness parameter at zero load reported in ref. 48 (Fig. 5A) that there is a small dip around $100\hspace{0.17em}\mathrm{\mu }\mathrm{M}$ as predicted theoretically using the 2HB model (Fig. 1C). Although not unambiguous, the randomness parameter with external loads measured by Visscher et al. (11) (Fig. 5 B–D) apparently shows more or less a monotonic decease with increasing [T], which agrees with the predictions of the 1HB model (Fig. 1D). We note that the experiment at zero load (Fig. 5A) was conducted using fluorescence microscopy and those at nonzero load used the optical trapping technique. Because of limited temporal resolution in prior experiments, all of the measurements of randomness parameter correspond to $r_M$, the mechanical randomness parameter. With access to temporal resolution on the order of tens of microseconds, it may be possible to directly measure the chemical randomness parameter. For a fuller understanding of the mechanochemistry of kinesin and in particular how Kin1 waits for ATP, it is desirable to explore the [T] and $F$ dependence of chemical/mechanical parameters using high-resolution stepping trajectories.

Discussion

We have introduced a simple model for stepping of conventional kinesin on the microtubule to propose single-molecule experiments, which could be used to discriminate between the waiting states for ATP binding to the leading head. We derived analytical solutions for the run length and velocity distributions and various randomness parameters as a function of ATP concentration and external resistive load. For both the 1HB and 2HB models $P\left(n\right)$ is independent of [T], which is in good agreement with experiments except at very low [T] concentrations, perhaps due to enhanced probability of spontaneous detachment (11, 48). Therefore, although $P\left(n\right)$ could be measured readily, it cannot be easily used to distinguish between the 2 distinct waiting states. The distribution of velocity, which exhibits bimodal behavior at $F\hspace{0.17em}\ne \hspace{0.17em}0$, is qualitatively similar both at high and low ATP concentrations. The velocity distribution does differ quantitatively at low ATP concentrations as $F$ is varied (Fig. 4B). The most significant finding is that that the randomness parameters, which could be measured readily, show qualitative differences as a function of $F$ and [T] between the 2HB and 1HB waiting states for ATP.

Predicted Bimodality in the Velocity Distribution Is Independent of the ATP Waiting States.

Since the mean run length does not depend significantly on the ATP concentration for Kin1 (11, 48), it follows that the mean position from which the motor detaches from the MT is roughly the same irrespective of ATP concentrations. Thus, [T] would not affect the spatial resolution needed to observe the predicted bimodality in the velocity distribution. However, since the average velocity of kinesin increases with [T], it would affect the temporal resolution needed to validate the shape in $P\left(v\right)$. We propose that it would be easier for experimentalists to observe the theoretical prediction that $P\left(v\right)$ is bimodal at lower ATP concentrations. This most interesting prediction, made a few years ago (13) without considering the [T] dependence in contrast to this study, awaits experimental tests.

Randomness Parameters Are Dramatically Different between the 2 Waiting States.

We predict that the [T] and $F$ dependence of the randomness parameters, which is an estimate of the minimum number of rate-limiting states in kinesin, holds the key in assessing the relevance of the 2 waiting states. Since the theory for both the 2HB and 1HB models considers only 2 states, the calculated randomness parameters cannot be below 0.5. Therefore, it might be tempting to conclude that our predictions may not be realizable in experiments because it has been advocated that more than 2 states might be needed to fit the experimental data (19, 20). However, we argue that the qualitative features of the [T] dependence of the randomness parameter elucidated using our theory should be observable in experiments, using the following reasoning. Because kinesin has only one ATP-dependent rate per step and the rest of the rates do not depend on ATP, just as in our model, the change of randomness parameter as a function of [T] is affected only by the step that depends on ATP concentration. On the other hand, we compressed many potentially relevant states into one internal state that is unaffected by [T]. As a consequence, we expect that when [T] becomes large, our model might overestimate the values of the randomness parameters by a factor that is proportional to the number of actual ATP-independent internal states. Indeed, if we shift our values for $r$ in Fig. 5A so that they match the experimental values at high [T], we would attain an excellent agreement with the data. The presence of force might further complicate the interplay between internal states. Kin1 might switch between the 1HB waiting state and the 2HB waiting state in an ATP-dependent manner depending on applied loads, for example. Nevertheless, the qualitative difference between the 1HB and 2HB models should be amenable to experimental verification. Therefore, we believe that accurate measurements of $r_M$ and $r_C$ using high-temporal-resolution experiments will be most useful in filling a critical missing gap in the catalytic cycle of Kin1.

Status of Experiments and Relation to Theory.

Randomness parameters have been measured previously using fluorescence microscopy (48) and optical trapping (11, 17). The experimental set up in ref. 48 did not contain cargo whereas the stepping trajectories in the optical trapping experiments were measured by monitoring the time-dependent movement of a bead attached to the coiled coil (11, 17). Both experiments from Hancock and coworkers (31) and Tomishige and coworkers (14) employ innovative experimental methods, which are different from the techniques previously used to measure the randomness parameters. These experiments also did not have cargo but a large AuNP (with diameters between 20 and 40 nm) was attached to different sites on one of the motor heads. The AuNP experiments should have sufficient temporal and spatial resolution to extract both the mechanical and chemical randomness parameters as a function of ATP concentration. The current iSCAT or experiments based on dark-field microscopy may not be able to measure the randomness parameter as a function of $F$, which would require attaching a bead (cargo) that would not interfere with the dynamics of the AuNP. Nevertheless, measurements of randomness parameters using the experimental constructs in refs. 14 and 31 as a function of [T] but with $F=0$ can be made. Such studies are needed to test our predictions (Fig. 5A), which would hopefully provide insights into the ATP waiting state of kinesin.

Mechanochemistry of the Backward Step.

In our model for the 1HB waiting state (Fig. 1D), we assumed that the rate of the backward stepping depends on [T] in the same manner as the rate for the forward step. It stands to reason that any step should consume ATP, and consequently $k^{-}$ should also depend on [T]. Indeed, it has been argued that Kin1 walks backward by a hand-over-hand mechanism by hydrolyzing ATP in much the same way as it does when moving forward (12, 42). The observation that the ratio of the probability of taking forward to backward steps as a function of $F$ at 2 ATP concentrations (1 mM and 10 $\mathrm{\mu }\mathrm{M}$) is superimposed (figure 4b in ref. 42) lends support to the supposition that $k^{-}$ should also depend on [T]. Our 2HB and 1HB models (Fig. 1 C and D, respectively), which consider ATP binding even for backward steps, lead to the prediction that both the run length and the fraction of forward step to backward step are independent of [T], as shown in the experiments (12, 42). In addition, several theoretical models have been proposed to rationalize the [T] dependence of the backward step (12, 20, 22, 23, 50, 51). Therefore, our assumption that $k^{-}$ depends on [T] seems justifiable.

However, the mechanism, especially in structural terms, of the backward step is not fully understood (12, 20, 50, 51). Therefore, it is important to entertain the possibility that $k^{-}$ has negligible dependence on [T]. Note that the magnitude of $k^{-}$ is nonnegligible only in the presence of substantial load. At very low forces one could neglect the [T] dependence of $k^{-}$. Under these conditions the mechanisms for forward and backward steps need not be the same.

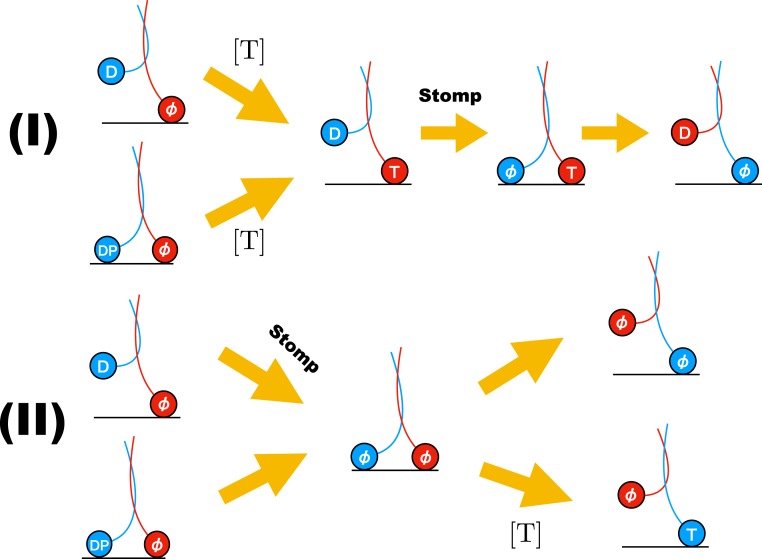
There are at least 2 possible pathways (Fig. 6) by which Kin1 could take backward steps: 1) Let us consider that ATP binds to the LH in either the 2HB state or the 1HB state and the TH detaches with bound ADP. For a backward step to occur, the TH has to release ADP and perform a “foot stomp” (return to the starting position). Although to date there is no evidence for either TH or LH foot stomping in Kin1, they have been observed in myosin V in the absence of external load (52). The probability of foot stomping could certainly increase if $F\hspace{0.17em}\ne \hspace{0.17em}0$, but is improbable in the absence of load. If stomping were to occur, then both the heads would be bound to the MT with the LH containing ATP (third step in pathway I in Fig. 6). After TH stomping, ATP should be hydrolyzed and the inorganic phosphate released from the LH, which would lead to backward stepping. This pathway results in identical [T] dependence for forward and backward steps. Consequently, the [T]-independent characteristics of Kin1, such as $P\left(n\right)$, can be explained by this scenario. 2) Let us consider another possibility for backward steps. Before ATP binds to the LH in either the 1HB state or the 2HB state, ADP is released from the TH, leading to the 2HB state with both the heads being nucleotide-free pathway II in Fig. 6. For the backward state to occur from this state, the LH should detach from the 2HB state either spontaneously or by binding ATP. The latter event, which would induce neck-linker docking and hence propel the TH forward, would tend to suppress the probability of backward steps. If the former were to occur, then it might be possible, especially if $F\hspace{0.17em}\ne \hspace{0.17em}0$, that $k^{-}$ might not depend on [T].

Fig. 6.

Plausible backward step mechanisms for kinesin. Upper panel corresponds to pathway I explained in Discussion. In this case the [T] dependence is identical to forward stepping. Lower panel is pathway II in which [T] dependence could be different from the forward stepping. T, D, DP, and $\varphi$ stand for ATP, ADP, (ADP + phosphate), and no nucleotide state, respectively. In Upper panel, after ATP binds to the leading head (shown in red), the neck linker docks. Consequently, the backward step along this pathway would be possible only at higher loads.

The theory developed based on the scheme in Fig. 1D does not account for the possibility that the backward step rate may not depend on [T]. For completeness, we created in SI Appendix a variant of the 1HB model, corresponding to scenario 2, by setting $k^{-}$ in Fig. 1D to be independent of [T]. The results in SI Appendix show that regardless of the dependence or independence of $k^{-}$ on [T] the qualitative differences in the randomness parameters as a function of $F$ and [T] between the 1HB and 2HB models remain. Thus, the theoretical predictions are robust, suggesting that high-temporal-resolution experiments that measure randomness could be used to discriminate between the 2 waiting states for ATP.

Conclusion

It has been challenging to decipher how exactly kinesin waits for ATP to bind to the leading head. Recent experiments have arrived at contradictory conclusions using similar experimental techniques. Although one cannot rule out the possibility that different kinesin constructs and the location of attachment of the gold nanoparticle used in these experiments might lead to different stepping trajectories, it is important to consider the theoretical consequences of the 2 plausible waiting states of kinesin. To discriminate between the 1HB and 2HB waiting states, we developed simple models, allowing us to calculate analytically and fairly accurately a number of measurable quantities. The theory predicts that there should be qualitative differences in the randomness parameters as a function of load and ATP concentration. Although the force dependence of the randomness parameters has been previously measured using optical trap techniques, it would be most interesting to repeat these measurements using the constructs used in the most recent experiments (14, 31). In addition, measurements of the load dependence of the randomness parameters using dark-field microscopy methods in combination with optical traps would be most illuminating to verify many of the predictions outlined here.

Materials and Methods

We created 2 stochastic kinetic models to calculate a number of quantities associated with the stepping kinetics of conventional kinesin. The sketch of the 1HB and 2HB models and the pathways leading from the resting state to the target binding states along with the rates and [T] dependence are given in Fig. 1. The model, a generalization of the one introduced previously (13) to include the important aspect of [T] dependence, can be solved exactly, thus allowing us to calculate $P\left(v\right)$ and the different randomness parameters for the 2 different scenarios for the waiting states for ATP binding (see SI Appendix for details). Despite the simplicity, we show in SI Appendix that the model does quantitatively reproduce the experimentally measured [T]-dependent force–velocity relation using physically reasonable parameters for the rates describing the 2 schemes (Fig. 1 C and D).

Note.

In a recent article (53) it has been argued that the trailing head is detached (unbound but rotationally free) but is in close proximity to the initial binding site while the leading head waits for ATP to bind. The authors also suggest that the apparent stepping trajectories could depend on the point of attachment of the gold nanoparticle.