Cortical depth profiles of luminance contrast responses in human V1 and V2 using 7 T fMRI

Abstract

Neural activity in early visual cortex is modulated by luminance contrast. Cortical depth (i.e., laminar) contrast responses have been studied in monkey early visual cortex, but not in humans. In addition to the high spatial resolution needed and the ensuing low signal‐to‐noise ratio, laminar studies in humans using fMRI are hampered by the strong venous vascular weighting of the fMRI signal. In this study, we measured luminance contrast responses in human V1 and V2 with high‐resolution fMRI at 7 T. To account for the effect of intracortical ascending veins, we applied a novel spatial deconvolution model to the fMRI depth profiles. Before spatial deconvolution, the contrast response in V1 showed a slight local maximum at mid cortical depth, whereas V2 exhibited a monotonic signal increase toward the cortical surface. After applying the deconvolution, both V1 and V2 showed a pronounced local maximum at mid cortical depth, with an additional peak in deep grey matter, especially in V1. Moreover, we found a difference in contrast sensitivity between V1 and V2, but no evidence for variations in contrast sensitivity as a function of cortical depth. These findings are in agreement with results obtained in nonhuman primates, but further research will be needed to validate the spatial deconvolution approach.

1. INTRODUCTION

The visual system is conceptualized as a hierarchical structure, in which information is conveyed from the eye, through the lateral geniculate nucleus (LGN) of the thalamus, the primary visual cortex (V1), on to extrastriate cortical areas (Felleman & Van Essen, 1991). This feedforward sweep carries incoming sensory information and is complemented by feedback mechanisms related to higher cognitive processes, such as attention. The feedback mechanisms control the flow of sensory information and modify its content according to cognition and behavioral needs (Lamme & Roelfsema, 2000).

As information is processed along the visual hierarchy, neurons become selective for increasingly complex stimulus features—that is, their preferred stimuli evolve from simple spots of light to more elaborate stimulus properties (Maunsell & Newsome, 1987). Neurons in the early stages of the visual system are particularly sensitive to luminance contrast (Albrecht, Geisler, Frazor, & Crane, 2002; Albrecht & Hamilton, 1982). For most neurons in early visual areas, the relationship between stimulus contrast and neuronal response is not linear, but can be modeled by a power function or a combination of power functions (Albrecht et al., 2002; Albrecht & Hamilton, 1982; Boynton, Demb, Glover, & Heeger, 1999; Sclar, Maunsell, & Lennie, 1990). Within the hierarchy of early visual areas, there is a gradient of contrast response properties: The responses of LGN, V1, V2, and progressively higher visual areas are successively less modulated by luminance contrast—the contrast response function becomes steeper, and the response saturates at a lower contrast (Avidan et al., 2002; Buracas & Boynton, 2007; Levitt, Kiper, & Movshon, 1994; Sclar et al., 1990).

Tootell, Hamilton, and Switkes (1995) presented drifting square wave gratings at various luminance contrasts and compared the contrast sensitivity in V1 and MT. In accordance with electrophysiological findings in monkeys (Sclar et al., 1990), fMRI contrast sensitivity in humans was found to be considerably higher in MT than in V1, but only slightly higher in V2 compared to V1. The respective fMRI data were acquired at voxel sizes of 3 × 3 × 5 to 6 mm³ or 1.6 × 1.6 × 4 mm³ (Tootell et al., 1995). Another early fMRI study (Boynton et al., 1999) used contrast‐reversing sine wave gratings at six contrast levels to study contrast response properties in early visual cortex of two human observers, at an anisotropic voxel size of 1.02 × 1.02 × 4 mm³. For contrast levels well above the perceptual threshold, the contrast discrimination function (relating the minimum detectable contrast increment to the absolute contrast of the reference stimulus) can be modelled with a power function (Legge, 1981), and, if the range of contrast levels is very broad, a combination of power functions can be used (Boynton et al., 1999). In the study by Boynton et al. (1999), the same function yielded a good fit for both the behavioral and the fMRI data for V1, V2, and V3, suggesting that contrast discrimination judgements are instantiated by neuronal processing in these areas. A significant difference in contrast sensitivity between these early visual areas was not reported (Boynton et al., 1999). Using a similar experimental design, Buracas, Fine, and Boynton (2005) presented further evidence for a link between behavioral performance on a contrast discrimination task and the fMRI response in early visual cortex. Moreover, although not explicitly stated, their data (Buracas et al., 2005) and a follow‐up study (Buracas & Boynton, 2007) support an increase of contrast sensitivity along the visual hierarchy in V1, V2, V3, and MT+. These two studies were conducted at an isotropic spatial resolution of 3 × 3 × 3 mm³. A more recent fMRI study (Yan et al., 2014) confirmed these earlier findings, and presented evidence for higher contrast sensitivity for peripheral than for central vision, at a voxel size of 2 × 2 × 2 mm³. All these fMRI studies were performed at 1.5 and 3 T. Tootell & Nasr (2017) studied response properties of extrastriate visual cortex at 7T with a voxel size of 1 × 1 × 1 mm³. In accordance with previous low‐resolution fMRI experiments and animal studies, they found differences in the contrast response between lower and higher extrastriate visual areas. In addition, they found clusters of response variation along the cortical surface, which may correspond to functional subdivisions previously only reported in macaque (Tootell & Nasr, 2017).

With the exception of Tootell and Nasr (2017), previous fMRI studies in humans averaged the signal over entire cortical areas, such as V1 and V2, thereby treating these areas as homogeneous structures and disregarding potential variability in the contrast response properties within each area. However, cortical areas are not homogeneous structures (Lund, 1988): Instead, cortical areas can be divided into cortical columns (orthogonal to the surface of the cortex) and layers (across the cortical depth, i.e., orthogonal to the columns). Most cortical areas are divided into six main layers based on microstructural features (Douglas & Martin, 2004; Fitzpatrick, Itoh, & Diamond, 1983; Kleinnijenhuis et al., 2013; Lund, 1973, 1988). Layers 3 and 4 of the primate visual cortex are further divided into sublayers (Lund, 1988). Electrophysiological (Hubel & Livingstone, 1990; Hubel & Wiesel, 1972) and tracer (Blasdel & Lund, 1983; Henderickson, Wilson, & Ogren, 1978; Rockland & Pandya, 1979; Tootell et al., 1988) studies in V1 have shown that thalamocortical projections primarily target layers 4C and 6, whereas projections from V2 to V1 terminate in layers 1, 2, and 5 (Anderson & Martin, 2009; Rockland & Pandya, 1979; Rockland & Virga, 1989). Based on this evidence, Callaway (1998) proposed a two‐stage model of information processing in V1. According to the model, thalamorecipient layer 4C constitutes the first cortical feedforward module. It projects feedforward connections to the second‐level feedforward module located in the supragranular layers. Layer 6 acts as the first‐level feedback module, receiving collaterals of the thalamic feedforward input to layer 4C as well as the output from layer 4C. In other words, this feedback module is characterized by sampling both the feedforward module's input and output (Callaway, 1998).

In recent years, high‐resolution fMRI studies at ultra‐high‐field strength (7 T and above) have demonstrated the feasibility of sampling functional signals at different cortical depth levels in humans (for recent reviews, see De Martino et al., 2017; Dumoulin, Fracasso, van der Zwaag, Siero, & Petridou, 2017; Polimeni, Renvall, Zaretskaya, & Fischl, 2017; Uludağ & Blinder, 2017). Two recurrent findings from fMRI studies investigating the cortical‐depth‐dependent responses in humans sensory cortices are (a) a signal increase toward the cortical surface and (b) an increased signal around mid‐level grey matter, which is detected in some studies but not in others.

The first finding is attributed to the fact that the laminar specificity of the fMRI signal is degraded by the properties of the vascular system, in particular when gradient‐echo (GE) fMRI sequences are used (see Uludağ & Blinder, 2017 for an overview). After having passed the capillaries and venules, blood drains through ascending veins of increasing diameter toward the cortical surface. Because GE fMRI sequences have a strong weighting toward the signal originating from veins (Uludağ, Müller‐Bierl, & Uğurbil, 2009), the reported signal increases toward the cortical surface are thought to originate from an increasingly larger contribution from draining veins (Koopmans, Barth, Orzada, & Norris, 2011; Markuerkiaga, Barth, & Norris, 2016).

The cause of the (elusive) second finding is less clear. One possible explanation suggests a neuronal origin. The thalamic input to primary visual cortex terminates mainly in layer 4 and 6 (Blasdel & Lund, 1983; Henderickson et al., 1978; Hubel & Livingstone, 1990; Hubel & Wiesel, 1972; Rockland & Pandya, 1979; Tootell et al., 1988). Thus, increased metabolic demand due to local processing of incoming signals at mid‐cortical depth may explain a peak in the amplitude of the hemodynamic response. However, an alternative explanation is offered by the differences in vascular density at different cortical depths (Uludağ & Blinder, 2017; Weber, Keller, Reichold, & Logothetis, 2008). In addition to the six cortical layers that are distinguished with respect to cytoarchitectonic features, the cortex can also be divided into four vascular layers, which are delineated based on the structure and density of blood vessels (Duvernoy, Delon, & Vannson, 1981). According to this alternative explanation, the peak fMRI signal at mid‐cortical depth may be unrelated to differences in neuronal processing across cortical layers, but an artefact of a higher vascular density at mid‐cortical depth. These two hypotheses are not mutually exclusive; that is, a peak at mid‐level grey matter could be the result of a combination of neuronal and vascular causes.

In this study, we investigated the contrast response properties of human V1 and V2 across cortical depths in an fMRI experiment at 7 T, and applied spatial deconvolution based on the simulations by Markuerkiaga et al. (2016) to account for the ascending vein effect. We employed a visual stimulus with a parametrically varied luminance contrast. The rationale of this approach is twofold: First, the processing of luminance contrast is probably the primary computational task carried out in early visual cortex. Altering the contrast of a stimulus is expected to be an effective way to reveal the profile of feedforward processing across the cortical depth in early visual cortex. Second, whereas the progression of contrast response properties has been studied along the hierarchy of visual areas in both monkeys (Albrecht & Hamilton, 1982; Tootell et al., 1988) and humans (Avidan et al., 2002; Boynton et al., 1999; Levitt et al., 1994; Sclar et al., 1990; Tootell et al., 1995), the responsiveness to contrast and the contrast sensitivity at different depths of early visual cortex has not been studied in humans so far. The only high‐resolution fMRI study on contrast responses in humans has studied variations along the cortical surface, but has not investigated response properties at different cortical depths (Tootell & Nasr, 2017).

In this study, we were able to extract cortical depth profiles of GE‐fMRI signal changes in human V1 and V2 at 7 T in response to a contrast stimulus and demonstrate that the shape of the depth profiles changes with spatial deconvolution. Only when accounting for the draining vein effect, both V1 and V2 show peak response amplitudes at mid‐grey matter, as expected for feedforward processing of visual stimuli. In addition, the contrast sensitivity was found to be different between V1 and V2 in agreement with previous studies, but constant across cortical depth, both before and after spatial deconvolution. This study demonstrates the potential of high‐resolution fMRI in humans at 7 T to investigate visual processing and perception, if vascular and MRI physics confounds are properly accounted for.

2. METHODS

2.1. Experimental design

Healthy participants (n = 11, age between 23 and 35 years, mean age 29 years, 7 females) gave informed consent before the experiment, and the study protocol was approved by the local ethics committee of the Faculty for Psychology & Neuroscience, Maastricht University. Subjects were presented visual grating stimuli at luminance contrasts of 2.5%, 6.1%, 16.3%, and 72.0% (Figure 1a). The grating stimulus had the form of an annulus, with an inner radius of 1.5° of visual angle and an outer radius of 4.0° of visual angle. Within the annulus was a square wave grating with a spatial frequency of 2.0° of visual angle. Stimuli were created with Psychopy (Peirce, 2007; Peirce, 2008) and projected on a translucent screen mounted behind the MRI head coil, via a mirror mounted at the end of the scanner bore. The projection intensity was calibrated based on luminance measurements taken with a photometer. Stimuli were presented in a block design with stimulus block durations of 11.76 s and variable rest periods in random order (20.58 s, 23.52 s, or 26.46 s). Each run began with an initial rest period with a fixed duration of 23.52 s, and ended with a rest period of one of the three possible durations. Within each stimulus block, the luminance contrast of the stimulus was constant, and the stimulus orientation was altered between 0°, 45°, 90°, and 135° in a random order. Each orientation was presented for 1.68 s, interspersed with equally long interstimulus intervals (Figure 1b). All lights in the scanner room were switched off during the experiment, and black cardboard was placed on the inside of the MRI transmit coil in order to minimize light reflection.

Figure 1.

Stimuli used in the main experiment. (a) Grating stimuli were presented at four luminance contrast levels (2.5%, 6.1%, 16.3%, and 72.0%). (b) Within each stimulus block, the luminance contrast of the stimulus was constant, but the stimulus orientation was altered in a random order

Throughout the experiment, participants were asked to fixate a central dot and to report randomly occurring changes in the dot's color by button presses to retain the subjects’ attention. These targets were presented for 300 ms, with a mean intertrial interval of 16 s (range ± 4 s). No targets occurred during the first and last 20 s of each run. The timing of the color changes was arranged such that the predicted hemodynamic responses to the grating stimulus and to the color changes have minimal correlation. First, a design vector representing the stimulus blocks and a design vector containing pseudorandomly timed target events were separately convolved with a gamma function serving as a model for the hemodynamic response. Second, the correlation between the predicted response to the stimulus blocks and to the target events was calculated. Third, if the correlation coefficient was above threshold (r > .001), a new pseudorandom design matrix of target events was created, and the procedure was repeated. This procedure was repeated until the correlation was below threshold, separately for each run. Each subject completed six functional runs, with four repetitions of each luminance contrast level per run. The total duration of a run was 588 s. In an additional run, retinotopic mapping stimuli were presented for population receptive field estimation, allowing us to delineate early visual areas V1 and V2 on the cortical surface (Dumoulin & Wandell, 2008). The stimuli used for retinotopic mapping were oriented bars at four different orientations and eight different positions per orientation. Each of the resulting 32 stimulus configurations was presented 12 times for 2.94 s in random order.

2.2. Data acquisition and preprocessing

Functional MRI data were acquired on a 7 T scanner (Siemens Medical Systems, Erlangen, Germany) and a 32‐channel phased‐array head coil (Nova Medical, Wilmington, MA, USA) using a 3D GE EPI sequence (TR = 2.94 s, TE = 26 ms, nominal resolution 0.7 mm isotropic, 52 slices, coronal oblique slice orientation; Poser, Koopmans, Witzel, Wald, & Barth, 2010). We also acquired whole‐brain structural T1 images using the MP2RAGE sequence (Marques et al., 2010) with 0.7 mm isotropic voxels, and EPI images with opposite phase encoding for distortion correction of the functional data (Andersson, Skare, & Ashburner, 2003).

Motion correction was performed using SPM 12 (Friston, Williams, Howard, Frackowiak, & Turner, 1996), and the data were distortion corrected using FSL TOPUP (Andersson et al., 2003). More specifically, data were motion corrected within runs before estimating and correcting geometric distortions individually for each run. Afterward, the distortion‐corrected images were registered to correct for across‐run head movement using SPM12's two pass procedure: images were first registered to the first image of the first run, and subsequently to the mean of all images after the first realignment. Standard statistical analyses were performed using FSL (Smith et al., 2004), fitting a general linear model (GLM) with separate predictors for the four stimulus conditions (luminance contrast levels) and a nuisance predictor for the target events of the fixation task. High‐pass temporal filtering (cutoff value 100 s) was applied to both the model and the functional time series before GLM fitting. Population receptive field mapping (Dumoulin & Wandell, 2008) was performed using publicly available python code (Marquardt, Schneider, & Gulban, 2018) and standard scientific python packages (Numpy/Scipy, Matplotlib, Cython; Behnel et al., 2011; Millman & Aivazis, 2011; Oliphant, 2007; van der Walt, Colbert, & Varoquaux, 2011).

Each of the 11 subjects completed 6 functional runs of the main experiment. One subject completed two identical sessions on separate days. Cortical depth sampling requires a high level of spatial accuracy. However, the fMRI time series sometimes contained artefacts, such as unstable geometric distortions or strong, global image intensity fluctuations. These artefacts are presumably due to subject motion or field fluctuations due to scanner instability or physiological noise. To remove low‐quality data based on a quantifiable and reproducible exclusion criterion, we calculated the spatial correlation between each functional volume and the mean EPI image of that session after the across‐runs registration. If the mean correlation coefficient of the volumes in a run was lower than 0.93, that run was excluded from further analysis. The threshold (r < .93) was chosen based on visual inspection of respective plots for all subjects (Supporting Information, Figure S1), in order to discriminate low‐ and high‐quality runs. Note that the value of 0.93 is conservative and may have led to exclusion of valid data but made sure that only high‐quality data was included in the final results. For studies with low number of subjects and/or runs, a lower threshold can be chosen. The spatial correlation exclusion criterion resulted in the exclusion of 19 runs in total from 4 out of 11 subjects (for two subjects, all six runs were excluded; for four subjects, one run was excluded; and one subject had three runs removed). One additional run was excluded because the subject had detected <75% of targets, compared to an average performance of 95% across subjects. Thus, 20 runs were excluded in total. Because of hemispheric imbalances in temporal signal‐to‐noise ratio (tSNR), we limited the cortical‐depth analysis to the left hemisphere in all subjects. (Functional data were acquired using a 3D EPI sequence with right–left phase encoding. The tSNR imbalance between hemispheres possibly is due to the asymmetric coil sensitivity profile and phase readout polarity. The asymmetry of the NOVA medical coil at 7 T is a commonly observed issue and the result of the coil's design to improve the general homogeneity and reduce the sensitivity to head size and position within the coil. Because the stimulus was symmetric about the vertical meridian, it is not expected that the results qualitatively differ for the right hemisphere. Thus, we decided to focus our analysis on the hemisphere with the higher data quality. We tested this hypothesis on a subsample of subjects, which yielded very similar results for the right and left hemispheres (data not shown).)

2.3. Segmentation and depth sampling

The anatomical MP2RAGE images were registered to the mean functional image of each subject using boundary‐based registration (Greve & Fischl, 2009; Jenkinson, Bannister, Brady, & Smith, 2002; Jenkinson & Smith, 2001), and used for grey/white matter segmentation. We obtained an initial tissue type segmentation from FSL FAST (Zhang, Brady, & Smith, 2001). These initial segmentations were manually improved using publicly available python code (Gulban & Schneider, 2016) and ITK‐SNAP (Yushkevich et al., 2006). Manual corrections of the automatic segmentations were based on the T1 image from the MP2RAGE sequence and aimed to remove mistakes in the definition of the white/grey matter boundary and at the pial surface. Particular care was taken to ensure that voxels outside the pial surface were correctly labelled as CSF. To this end, the T1 images were upsampled to a voxel size of 0.35 mm isotropic using trilinear interpolation, allowing for a more fine‐grained delineation of tissue types.

Given the maximum spatial resolution currently achievable with fMRI, it is not yet possible to sample individual cortical layers. Therefore, cortical‐depth‐specific fMRI studies need to increase the effective spatial resolution during postprocessing, by upsampling (as in this study), or by another super‐resolution approach, such as spatial GLM (Kok, Bains, van Mourik, Norris, & de Lange, 2016). (See Supporting Information for more details on spatial resolution and upsampling.) The final grey and white matter definitions were used to construct cortical depth profiles using volume‐preserving parcellation implemented in CBS‐tools (Bazin et al., 2007; Waehnert et al., 2014). CBS‐tools represents information about cortical depth in distance maps, also known as level‐set images. Based on these distance maps, the cortical grey matter was divided into 10 compartments, resulting in 11 depth‐level images delineating the borders of these equivolume compartments. The parameter estimates and z‐scores from the GLM analysis, the population receptive field estimates, and the mean EPI images were up‐sampled to the resolution of the segmentations (0.35 mm isotropic voxel size) using nearest‐neighbor interpolation, and sampled along the previously established depth‐levels using CBS‐tools (Bazin et al., 2007; Waehnert et al., 2014). The depth‐sampled data were then projected onto a surface mesh (Tosun et al., 2004), and visual areas V1 and V2 were delineated on the cortical surface based on the polar angle and eccentricity estimates from the pRF modelling using Paraview (Ahrens, Geveci, & Law, 2005; Ayachit, 2015). Note that the purpose of representing the data on a surface mesh was only to select our regions of interest (ROIs); the depth‐sampling was performed in the previous step, and cortical fMRI profiles were obtained as described below. See Figure 2 and Supporting Information, Figure S2 for a scheme of the preprocessing and analysis pipeline.

Figure 2.

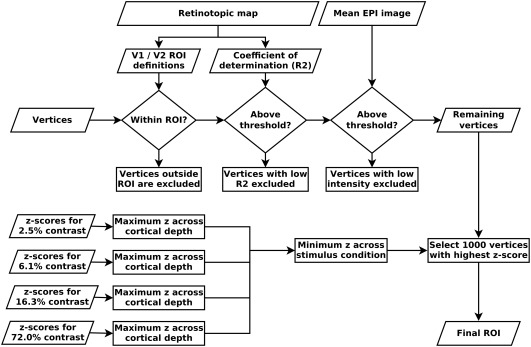
Overview of region of interest (ROI) selection. Vertices were selected based on a combination of criteria: retinotopic information, mean EPI image intensity, and z‐scores from the GLM analysis. The selection procedure attempts to select vertices with a specific response to the stimulus while minimizing subjective selection bias. This procedure was applied separately for V1 and V2. See Section 2 and Supporting Information, Figure S2 for details

2.4. ROI selection

We defined the ROIs, on which all further analyses were performed, in a sequential procedure, designed to obtain an observer‐independent, unbiased selection (Figure 2). The first step of the ROI selection procedure was the retinotopic V1 and V2 definitions: Only “columns” (i.e., grey matter segments covering all depths) that were located within V1 or V2 were selected (the procedure was carried out separately for V1 and V2). Second, “columns” with a low population receptive field model fit at any depth level were excluded (minimum R2 across cortical depth > 0.12). The purpose of this step was twofold: An unreasonably low pRF model fit indicates that the polar angle and eccentricity estimates may not be reliable, therefore calling into question the validity of the first selection criterion (i.e., V1 and V2 definitions). Furthermore, even in case of a cortical location that is certainly contained within V1 or V2 based on its anatomical location, a low pRF model fit is indicative of an unspecific visual response, which may be due to the presence of a large draining vein with a strong but unspecific signal change in response to visual stimulation. After these initial selection based on retinotopic information, the third selection criterion excluded “columns” with a very low signal intensity at any cortical depth level in the mean EPI image, to avoid sampling from veins and low intensity regions around the transverse sinus, due to slight imprecisions in the registration and/or segmentation. Specifically, we excluded all “columns” with EPI image intensity below 7,000 at any cortical depth in the mean functional image, which has a mean intensity of about 10,000 for voxels contained within the brain.

The selection criteria described so far are based on anatomical and retinotopic information, irrespective of stimulus‐induced signal changes in the main experiment. The final ROI selection was performed based on the responsiveness to the grating stimulus in the main experiment, as indicated by the GLM z‐scores contrasting each of the four stimulus conditions against rest. For each “column” that had passed all previous selection criteria, the maximum z‐score across cortical depth levels was obtained separately for each of the four stimulus conditions. The minimum of these four z‐values (one per stimulus condition) was determined, and from these the “columns” containing the maximum 1,000 z‐values were selected. By first taking the minimum z‐value across conditions, we aimed to select “columns” that are responsive to all stimulus conditions, and not only to the highest luminance contrast. Note, however, selection based on minimum or mean across conditions did not produce significant differences in the main results (data not shown). The selection was based on z‐values (and not on parameter estimates) because we expect the z‐statistic to be less sensitive to pials veins (due to the high physiological noise caused by a large vein).

The ROI selection procedure was carried out separately for V1 and V2. Selection criteria were always applied to an entire “column”—that is, either the entire “column” was included or excluded. The ROI selection described in this section, and all subsequent analysis steps were performed using standard scientific python packages (Numpy, Scipy, Matplotlib; Hunter, 2007; Millman & Aivazis, 2011; Oliphant, 2007; van der Walt et al., 2011).

2.5. Creation of cortical depth profiles

For each subject, we sampled the GLM parameter estimates corresponding to the four stimulus conditions within the final ROIs, separately for V1 and V2. The parameter estimates were then averaged within the cortical depth levels to obtain one depth profile of stimulus‐induced activation for each subject. Because the fMRI signal amplitude of the stimulus‐induced responses differed across subjects, we normalized the depth profiles of each subject before averaging across subjects. Normalization was performed by dividing each subject's depth profile by the within‐subject mean activation (given by the GLM parameter estimates) across depth levels and stimulus conditions. In this way, averaging across subjects does not bias the resulting group‐level profiles toward subjects with a strong level of activation.

2.6. Draining effect spatial deconvolution

As described above, cortical depth‐specific BOLD fMRI using GE sequences is expected to result in depth‐profiles with a signal increase toward the surface of the brain, due to the sensitivity to ascending draining veins (Koopmans et al., 2011; Zhao, Wang, & Kim, 2004; Markuerkiaga et al., 2016; see Uludağ & Blinder, 2017 for a review). That is, the fMRI signal at each cortical depth is not only influenced by the local neuronal activation but also by the draining of altered deoxyhemoglobin content and increased blood pressure from lower layers. As a result, the laminar‐resolved, measured fMRI signal (S) is the sum of local fMRI activation (LA) and nonlocal fMRI signal changes (NL) due to ascending veins (assuming similar signal intensity S0 at each layer). If we reasonably assume the flow direction from layer 6 (close to white matter) to layer 1 (close to CSF), then we can formalize this as

$$\begin{array}{l}{\text{LA}}_6={ \mathrm{S}}_6\\ {\text{LA}}_5={ \mathrm{S}}_5–w_{6\to 5}\hspace{0.17em}\times \hspace{0.17em}{\text{LA}}_6\\ {\text{LA}}_4={ \mathrm{S}}_4–w_{6\to 5}\hspace{0.17em}\times \hspace{0.17em}{\text{LA}}_6–w_{5\to 4}\hspace{0.17em}\times {\hspace{0.17em}\text{LA}}_5\end{array}$$

and so on.

In other words, to obtain the fMRI signal due to local neuronal activation, the influence of the lower layers is subtracted from the measured signal with weighting factors w _{( n +1)→ n}. In laminar fMRI experiments, the weighting factors are usually not known. It may be, in the future, possible to derive these factors from resting‐state or hypercapnia data, as suggested by Polimeni, Witzel, Fischl, Greve, and Wald (2010) and Guidi, Huber, Lampe, Gauthier, and Möller (2016), or from laminar‐specific dynamic fMRI signal models (Havlicek and Uludag, in preparation). In the current study, we used the model proposed by Markuerkiaga et al. (2016) to derive the weighting factors (from their Figure 3f, factors shown here in Table 1). In short, Markuerkiaga et al. (2016) developed a detailed microanatomical model of the vascular system of primate visual cortex, based on histological data, following the study by Boas, Jones, Devor, Huppert, and Dale (2008). They combined this vascular model with the BOLD signal model proposed by Uludağ et al. (2009), and simulated the spread of fMRI signal changes across cortical layers. The simulations by Markuerkiaga et al. (2016) provided a specific estimate of the draining effect on the fMRI signal for each cortical layer, allowing differentiating between signal changes due to a local hemodynamic response, and signal changes due to the inflow of blood and deoxygenated hemoglobin from deeper layers. The model assumptions match our experimental parameters in terms of field strength, imaging parameters, and stimulus duration (Markuerkiaga et al., 2016). To account for the different relative thickness of the cortical layers in V1 and V2, and because the model by Markuerkiaga et al. (2016) is defined at five cortical layers (layers 2 and 3 are grouped together), we resampled our depth profiles to those five layers (Markuerkiaga et al., 2016; de Sousa et al., 2010; Waehnert et al., 2014).

Figure 3.

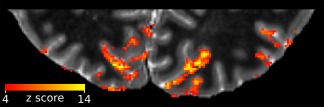
The visual grating stimulus caused strong fMRI signal changes across the visual cortex. Shown are the z‐scores for the GLM contrast of the strongest contrast stimulus (72.0% contrast) against rest, overlaid on the quantitative T1 image, for a representative subject. The T1 image has been cropped to the approximate extent of the field‐of‐view of the functional images [Color figure can be viewed at http://wileyonlinelibrary.com]

Table 1.

Weighting factors for spatial deconvolution

Depth level	1	2/3	4	5	6
1	1.00	0.41	0.59	0.20	0.26
2/3		1.00	0.59	0.20	0.26
4			1.00	0.20	0.32
5				1.00	0.32
6					1.00

Each row specifies the weighting factors w for the contribution of local fMRI activation (LA) and nonlocal fMRI signal changes (NL) to the total measured signal (S) at that depth level. For example, the measured signal S₆ is completely determined by the local activation LA₆; therefore, w _6→6 = 1.00, and ${\displaystyle \sum _{n=1}^5{w}_{\left(n\to 6\right)}}=0$. In contrast, the measured signal S₅ is the sum of the local activation LA₅ and a fraction w _6→5 = 0.32 of the nonlocal signal NL₆, that is, S₅ = 1.00 × LA₅ + 0.32 × NL₆ (weighting factors derived from Markuerkiaga et al., 2016, p. 495, figure 3f).

The spatial deconvolution has, to the best of our knowledge, not been applied in an fMRI study before, and the model parameters have not yet been empirically validated. Therefore, before proceeding with the analysis of contrast response properties in V1 and V2, we need to assess the sensitivity of the BOLD signal profile after using the deconvolution method to changes in its model parameters. Whereas it is reasonable to assume that draining veins cause a unidirectional signal spread from deeper to more superficial cortical depth levels, the exact size of this draining effect is contingent on the model assumptions made by Markuerkiaga et al. (2016). To assess how our results would change with deviations in the draining model parameters, we multiplied the weighting factors w _{( n +1)→ n} (Table 1) with two different bias sources. First, the spatial deconvolution model is based on histological data on the structure of the vascular system. The respective histological monkey data may not be representative of our sample of human subjects, resulting in a systematic overestimation or underestimation of the extent of signal spread across cortical depth levels. Another source of systematic deviation may result from a bias in the model of the BOLD signal. We modelled such an over‐ and underestimation by using weighting factors that are 30% larger and smaller than the original weighting factors at all cortical depth levels.

Second, the histological data forming the basis of the deconvolution model may be affected by random measurement error. We modeled such nonsystematic error by multiplying the weighting factors with random Gaussian noise before applying the spatial deconvolution. More specifically, each weighting factor w _{( n +1)→ n} was separately multiplied with a factor that was randomly sampled from a normal distribution with mean 1.0 and standard deviation 0.15. Thus, the average deviation of the perturbed model parameters was 15% with respect to the original model parameters. This procedure was repeated 10,000 times, each time sampling different random noise factors from the normal distribution. Because the random noise was distributed around 1.0, averaging across iterations results in mean depth profiles that are identical to the ones based on the original model parameters. The parameter of interest is therefore the spread of the resulting depth profiles.

2.7. Contrast response function

To characterize the response properties of V1 and V2 in more detail, we fitted a contrast response function to the depth profiles of stimulus induced signal changes, both before and after draining‐effect spatial deconvolution, separately for all depth levels. Because our stimuli were well above the perceptual threshold, and due to the small number of stimulus contrast levels, we fitted a simple power function, which can approximate contrast responses under the given conditions reasonably well:

$$R\left(C\right)\hspace{0.17em}=\hspace{0.17em}A\hspace{0.17em}\times \hspace{0.17em}{C}^{\mathrm{B}}$$

with C being the luminance contrast level, and A and B as free parameters (Albrecht & Hamilton, 1982). (Parameter A determines the overall response amplitude and B specifies the slope of the function.) To determine the error of the fits, the contrast response function was fitted using a bootstrapping procedure. We randomly resampled the single‐subject response profiles 10,000 times with replacement, and fitted the contrast response function to the across‐subjects average profile of each bootstrapping iteration.

Based on the fitted contrast response function, we calculated the predicted response to a 50% contrast stimulus for each bootstrapping sample (i.e., R(0.5) = A × 0.5^B). This 50% contrast response was obtained for both V1 and V2 for all cortical depth levels, both before and after spatial deconvolution. The resulting response profiles are a summary of the overall responsiveness of a region/depth level to a contrast stimulus.

Furthermore, the semisaturation contrast was derived from the fitted contrast response function of each bootstrapping sample. The semisaturation contrast is the stimulus contrast necessary to create a half‐maximum response and is used to describe the overall contrast sensitivity of neurons in the visual system (Albrecht & Hamilton, 1982; Sclar et al., 1990). Semisaturation contrast is insensitive to the overall response amplitude and relatively constant across spatial frequencies (Albrecht & Hamilton, 1982).

2.8. Peak identification

A peak identification algorithm was applied to quantify the shape of the cortical depth profiles. The depth profiles were up‐sampled to 100 points, smoothed with a Gaussian kernel with a FWHM = 5% of the cortical depth, and peaks were defined as local maxima within a neighborhood of ± 10 points. If no such local maximum was present, the global maximum across cortical depths was defined as the peak of the respective depth profile. For instance, for a profile exhibiting a monotonic increase toward the pial surface, the peak is at the most superficial cortical depth level.

A permutation test was performed to test for statistical differences in peak positions in cortical depth profiles between V1 and V2. Specifically, we compared the difference in peak position obtained from across‐subjects average depth profiles with a null distribution of the difference in peak position obtained by permuting the ROI labels (i.e., “V1” and “V2”) within subjects. The null distribution was obtained by sampling 500,000 times without replacement. This procedure was performed on depth profiles of the parameter estimates of all four stimulus conditions, before and after spatial deconvolution, and on the depth profiles of the predicted response to a 50% contrast stimulus, separately for V1 and V2.

3. RESULTS

The visual stimuli caused strong fMRI signal changes in the visual cortex (for example, see Figure 3). Not surprisingly, we observed a stronger response for higher luminance contrast levels irrespective of cortical depth (Figure 4). In the original depth‐profiles (i.e., before spatial deconvolution), the response initially increased with distance from the white matter in V1, but levelled off at mid‐cortical depth (Figure 4a). The peak positions for the four stimulus conditions, from lowest to highest contrast, were located at ∼35%, ∼30%, ∼30%, and ∼35% of cortical depth from the pial surface, respectively. (Please note that these peak positions were determined from averaged and upsampled depth profiles.) The original depth‐profiles for V2 showed a slightly more monotonic increase toward the pial surface (Figure 4c; peak position at ∼0%, ∼0%, ∼5%, and ∼0% of cortical depth from the pial surface, respectively). The difference in the distribution of peak positions between V1 and V2 was not statistically significant, after correcting for multiple comparisons, for all but the lowest stimulus contrast condition (p < .05, p > .05, p > .05, p > .05, Bonferroni corrected, for the four stimulus conditions, from lowest to highest luminance contrast).

Figure 4.

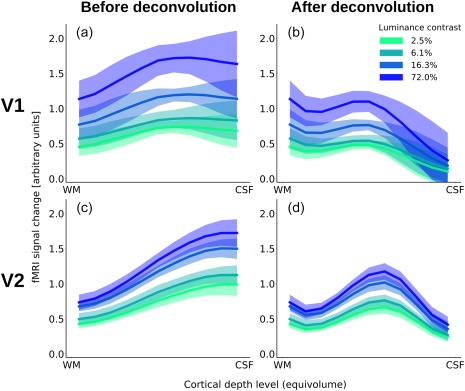
Cortical depth profiles for V1 (a and b) and V2 (c and d) before (a and c) and after (b and d) accounting for the draining effect. Shown are the mean GLM parameter estimates contrasting the response to the four different stimuli against rest, normalized, and averaged across the left hemispheres of all subjects. The shading depicts the standard deviation (across subjects) of the mean [Color figure can be viewed at http://wileyonlinelibrary.com]

The spatial deconvolution dramatically changed this picture: After accounting for the draining effect, in V1, there was a local maximum at the middle of grey matter (Figure 4b, at ∼55% of cortical depth from the pial surface in all four stimulus conditions). In addition, there was another, even slightly higher, maximum at the lowest depth in V1. The deconvolved profile for V2 also showed a pronounced peak at mid grey matter, with a slight signal decrease toward the surface (Figure 4d; peak position at ∼45% cortical depth from the pial surface for all four stimulus conditions).

Figure 5 shows the experimental fMRI response and the fitted contrast response functions exemplarily for three depth‐levels for V1 and V2 after spatial deconvolution (see Supporting Information, Figure S3 for the same data without spatial deconvolution). The fMRI responses were well approximated by a power function, and the resulting contrast response functions showed differences in shape and amplitude across areas and cortical depths. To characterize the contrast response properties in more detail, the predicted response at 50% contrast (Figure 6) and the semisaturation contrast (Figure 7) were obtained from the fitted contrast response functions.

Figure 5.

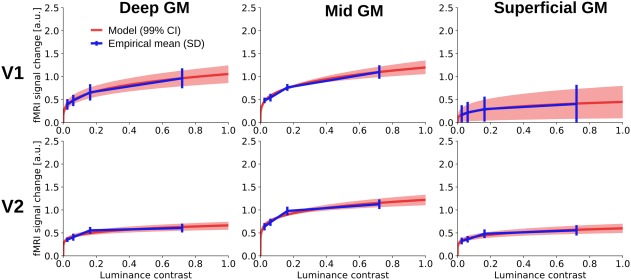
Contrast response function for V1 (upper row) and V2 (lower row) for three depth levels (left: deep grey matter; middle: mid‐grey matter; right: superficial grey matter). The blue line shows the experimental fMRI response after accounting for draining effects at the four stimulus contrast levels (2.5%, 6.1%, 16.3%, and 72.0%); the blue error bars represent the standard deviation of the mean across subjects. The red line indicates the median power function model fit across bootstrapping iterations, and the shaded region represents the corresponding 99% confidence interval. See Supporting Information, Figure S3 for the same contrast response function fitted before spatial deconvolution [Color figure can be viewed at http://wileyonlinelibrary.com]

Figure 6.

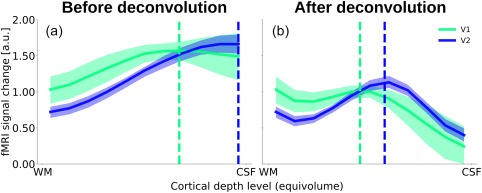
Response at 50% contrast across cortical depth, before (a) and after (b) spatial deconvolution. The solid lines indicate the median response for a stimulus with 50% luminance contrast, based on the bootstrapped contrast response function. Shaded regions indicate the 99% confidence interval of the median (percentile bootstrap). The dotted vertical lines indicate the median relative cortical depth of the peak [Color figure can be viewed at http://wileyonlinelibrary.com]

Figure 7.

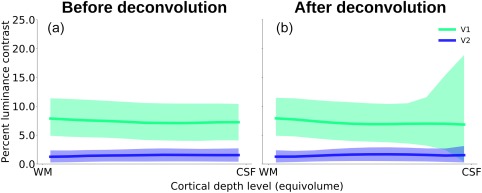
Semisaturation contrast across cortical depth in V1 and V2 (a) before and (b) after draining effect spatial deconvolution. Solid lines indicate the bootstrapped median semisaturation contrast, and the shading represents the respective 95% confidence interval. The semisaturation contrast is relatively constant across cortical depth, and is generally higher for V1 than for V2 [Color figure can be viewed at http://wileyonlinelibrary.com]

Before spatial deconvolution, the peak of the response at 50% contrast was at ∼30% of cortical depth relative to the pial surface in V1 and at ∼0% of cortical depth in V2 (Figure 6a). A permutation test revealed the difference in the distribution of peak positions between V1 and V2 to be statistically significant (p < .05). After accounting for the draining effect, the position of the mid grey matter peak in V1 was slightly deeper than in V2, at ∼55% and ∼45% of cortical depth relative to the pial surface for V1 and V2, respectively. Even though this difference in peak positions was statistically significant (p < .05), we caution against over‐interpreting this effect. The peak positions of V1 and V2 are separated by a distance of ∼10% of the cortical depth. Given the limited spatial resolution of the data, different histological layering in V1 and V2, and possibly errors in the deconvolution parameters for the removal of the draining vein effect in V1 and V2, the certainty in determining the peaks may not be sufficient to relate these differences to the spatial profiles of neuronal activity.

We did not find statistical evidence for a difference in semisaturation contrast across cortical depths (Figure 7). However, as expected, the semisaturation contrast was much higher for V1 than for V2. These results were similar before and after spatial deconvolution (parametric bootstrap linear regression, 100,000 iterations; before and after spatial deconvolution: cortical depth level, p > .05; ROI (V1/V2), p < .01). Thus, we found the V2 response to saturate at a lower contrast than the response in V1, in line with a smaller dynamic range in V2.

Figure 8 plots the results of simulated deviations of the spatial deconvolution model parameters for the strongest luminance contrast level (75% luminance contrast). Systematic over‐ and underestimation of the weighting factors are represented by the two red lines, and the effect of random error is indicated by the blue error shading. The deepest cortical depth level, close to the white matter, is not affected by perturbing the model parameters, because no deconvolution is applied there. With increasing distance from the white matter, the effect of perturbing the model parameters becomes larger, for both systematic and random error. This is not surprising, since any deviation in the weighting factors affects the deconvolution at all subsequent (i.e., more superficial) depth levels. Importantly, although the range of the distribution becomes wider toward the cortical surface, the general shape of the profiles and the presence of the local maximum in mid‐grey matter do not change.

Figure 8.

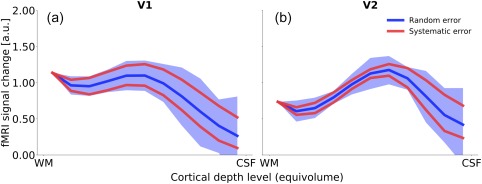
The effect of variance in the model assumptions on spatial deconvolution. We assessed the effect of two types of error: First, a systematic over‐ and underestimation of the extent of signal spread across cortical depth levels (represented by the red lines), and second, random error in the weighting factors used for spatial deconvolution (blue error shading represents the 0.5th and 99.5th percentile after applying random Gaussian noise to the deconvolution weighting factors over 10,000 iterations; see Section 2.2 for details). With increasing distance from the white matter, the spread of the distribution becomes larger, reflecting a greater effect of changes in the model parameters toward the cortical surface. However, the general shape and peak positions are not affected. For better visibility, only the data for one stimulus condition (75% luminance contrast) are shown [Color figure can be viewed at http://wileyonlinelibrary.com]

4. DISCUSSION

Along the hierarchy of visual areas, neurons’ preferred stimuli evolve from simple luminance contrasts to more complex visual features (Hochstein & Ahissar, 2002; Maunsell & Newsome, 1987; Vogels & Orban, 1996). Moreover, sensitivity to stimulus features varies between cortical layers, suggesting that cortical layers are interconnected but separate networks within the visual hierarchy (Alonso & Martinez, 1998; Gilbert, 1977; Hubel & Wiesel, 1968; Martinez & Alonso, 2003). Whereas the progression of response properties between visual areas in humans has been studied in detail (Hochstein & Ahissar, 2002), less is known about the specific role of human cortical layers in visual feature processing. To address this issue, we investigated the contrast response properties of human V1 and V2 across cortical depths in an fMRI experiment at 7 T at high spatial resolution.

4.1. Contrast response properties over cortical depth

We fitted a contrast response function (Albrecht & Hamilton, 1982) to the stimulus‐induced fMRI responses at different cortical depths, and determined the predicted response at 50% luminance contrast as a measure of the amplitude of the stimulus‐induced response, and contrast sensitivity as a measure how much this response was modulated by varying luminance contrast levels. We did not observe an effect of cortical depth on contrast sensitivity (Figure 7). Hence, our results are not indicative of a contrast sensitivity gradient between the proposed two stages of feedforward processing in the middle and superficial layers of human V1 (Callaway, 1998). Differences in contrast sensitivity between layers have been reported in monkeys (Tootell et al., 1988), and we cannot exclude the possibility that the absence of such an effect may be due to a lower sensitivity and/or specificity of depth‐dependent fMRI compared to invasive methods.

With respect to the stimulus‐induced response amplitude, our results after spatial deconvolution (see below for discussion) indicate a signal peak at mid‐grey matter in V1 and V2 (Figure 6b). While there are, to the best of our knowledge, no previous studies on the cortical depth‐dependence of contrast response properties in human visual cortex, our results can be compared with studies in monkeys: Tootell et al. (1988) measured tracer uptake across cortical layers 3–6 in macaque V1 after prolonged exposure to grating stimuli at four different luminance contrasts. We applied the same contrast response function used to fit our fMRI data to their data (Tootell et al., 1988, p. 1602, their figure 6), and found the cortical depth profiles of the normalized response amplitude in monkey V1 to be in close agreement with our data, with maxima in deep grey matter and at mid cortical depth (compare Figure 9 with Figure 6b). This result is expected for feedforward stimuli. In fact, several high‐resolution fMRI studies in animals (Chen, Wang, Gore, & Roe, 2013; Goense, Merkle, & Logothetis, 2012; Harel, Lin, Moeller, Ugurbil, & Yacoub, 2006; Jin & Kim, 2008; Kim & Kim, 2010; Lu et al., 2004; Yu et al., 2012; Yu, Qian, Chen, Dodd, & Koretsky, 2014; Zhao, Wang, Hendrich, Ugurbil, & Kim, 2006) and humans (Fracasso, Luijten, Dumoulin, & Petridou, 2017; Koopmans, Barth, & Norris, 2010; Koopmans et al., 2011) have also found a peak at intermediate depth levels in primary sensory cortex as a result of bottom–up stimulus modulation (see Uludağ & Blinder, 2017, for a review, including conflicting evidence), suggested to reflect direct thalamic input to V1, and cortico‐cortical input from V1 to V2, respectively.

Figure 9.

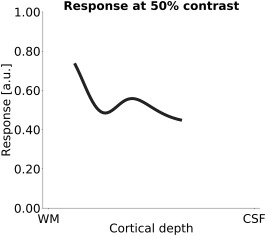
Tootell et al. (1988) measured tracer uptake across cortical layers in macaque V1 after prolonged exposure to grating stimuli at four different luminance contrasts. Shown is the predicted response at 50% luminance contrast after fitting their data with the same contrast response function that was used on our fMRI data. To facilitate the comparison with the fMRI results, Gaussian smoothing (SD = 20% of cortical depth) was applied to the histological data. Tracer uptake was reported for layers 3, 4A, 4B, 4Ca, 4Cb, 5, and 6 (Tootell et al., 1988)

In addition to the expected local response maximum at mid cortical depth, we found an elevated signal in deep grey matter in V1, presumably originating from layers 5 and/or 6. This observation was somewhat surprising, as it is commonly assumed that the response to a simple feed‐forward stimulus is characterized by a peak mainly in thalamorecipient layer IV. Several electrophysiological studies in nonhuman primates found strong postsynaptic, stimulus‐induced activity in layers 2, 3, and 4B of V1, but not in deep layers (Roberts et al., 2013; Xing, Yeh, Burns, & Shapley, 2012). Similarly, an fMRI study in rats reported evidence for a stimulus‐induced activity increase in middle layers of primary visual cortex, but not in deep layers (Bissig & Berkowitz, 2009). In contrast, some fMRI experiments measuring BOLD signal and cerebral blood volume in anaesthetised macaque monkeys observed an elevated signal in deep layers (Goense, Zappe, & Logothetis 2007, see their Figure 2B; Smirnakis et al., 2007, see their Figure 2D). Please note that most electrophysiological and fMRI studies presented drifting or flickering grating stimuli with a high temporal frequency. Self, van Kerkoerle, Goebel, and Roelfsema (2017) point out that experiments using rapidly changing visual stimuli are biasing the neuronal responses toward the feedforward modules. In contrast, stimuli at a lower temporal frequency are likely to result in different relative response strength between feedforward and feedback modules. In line with this argument, a study, in which awake Macaque monkeys were presented with a uniform luminance stimulus for 1.5 s, found a broadband response in deep grey matter that lasted throughout the stimulus presentation, in addition to an onset response at mid‐grey matter (Maier, Aura, & Leopold, 2011). Whereas the spatial properties of the stimulus used in that experiment were different to ours, the duration was very similar, and, in contrast to most invasive electrophysiological studies, the monkeys were awake. Similar to our experiment, the stimulus was not behaviorally relevant, and the monkeys’ only task was to maintain fixation. Maier et al. (2011) propose three possible causes for their observed sustained, post‐synaptic activity in deep layers: (a) direct thalamocortical sensory input from LGN, (b) indirect input from extrastriate visual cortex or from the pulvinar, or (c) intrinsic processing within V1, possibly due to recurrent activation within a cortical column. Based on the known connectivity pattern of the infragranular layers and the strengths of these connections, Maier et al. (2011) conclude that the third option, that is, intrinsic cortical connections, is the most likely cause of the observed sustained activity within the deep layers of V1. Although speculative, their results, and our finding of an elevated responsiveness in deep grey matter in V1, may be the consequence of recurrent excitation caused by the prolonged presentation of a slowly changing stimulus.

In this context, it is worth noting that layer 6 receives collaterals of the feedforward projections originating in layer 4 (Callaway, 1998; Callaway, & Wiser, 1996). Neurons in layer 6 of V1 presumably form a first‐level feedback node that modulates the responses to incoming sensory information in layer 4C of V1, and in the LGN, according to behavioral needs (Callaway, 1998; Kim, Matney, Blankenship, Hestrin, & Brown, 2014; Olsen, Bortone, Adesnik, & Scanziani, 2012; Sherman, 2005; Thomson, 2010). Similarly, layer 5 of V1 constitutes a second‐level feedback module (Adesnik & Scanziani, 2010; Callaway, 1998; Callaway & Wiser, 1996). In summary, the elevated response observed in mid grey matter in our study could be linked to the feedforward flow of transient information, whereas the peak in deep layers in V1 may be related to recurrent processing caused by the constant presence of the stimulus. Note, however, that the response peak in deep layers has only been observed under particular stimulus conditions, and may not be present for all stimulus types and/or feedforward processing of transient stimuli. Therefore, a systematic comparison between laminar fMRI responses to various stimulus parameters will be needed to validate our findings and to identify the conditions under which a high response in deep layers is evoked.

Although the relationship between electrophysiological measures of neuronal activity and the fMRI signal is not completely understood (Logothetis, 2008), the fMRI signal, particularly in primary visual cortex, is more closely related to postsynaptic activity than to spiking (Goense & Logothetis, 2008; Logothetis, Pauls, Augath, Trinath, & Oeltermann, 2001; Viswanathan & Freeman, 2007). Hence, the most obvious explanation for a local response maximum is an increased metabolic demand due to postsynaptic activity caused either by afferent signals targeting layer 4 and 6 or by local processing. Alternatively, a higher vascular density at intermediate cortical depths may cause a peak in the fMRI signal (Uludağ & Blinder, 2017). However, after applying the spatial deconvolution, we observed a peak at mid‐grey matter in both V1 and V2, but a higher local vascular density in middle layers has only been reported for V1, not for V2, in macaque monkeys (Weber et al., 2008). It is expected that human V1 and V2 exhibit a similar vascular volume distribution. Even though we cannot completely rule out the alternative, the electrophysiological evidence and relatively constant vascular volume across layers of V2 argue that the laminar fMRI signal profile after spatial deconvolution reflects the neuronal laminar profile.

4.2. Spatial deconvolution model assumptions

Our deconvolution results are contingent on the validity of the model proposed by Markuerkiaga et al. (2016). To assess the impact of deviations of the model predictions from the actual signal spread on the resulting cortical depth profiles, we modeled the effects of systematic and random error in the assumed signal spread on the resulting depth profiles (Figure 9), and found that the general shape of the profiles and the positions of local maxima remain intact despite strong perturbations of the model parameters. Therefore, our overall conclusions are relatively insensitive to the exact values of the weighting factors that represent draining of deoxygenated hemoglobin and blood volume via ascending veins toward the cortical surface. In other words, the change of the slope of the fMRI response amplitude before spatial deconvolution as a function of cortical depth is a strong indicator of the underlying neuronal laminar profile. However, this may not be true for other experimental designs resulting in more subtle neuronal changes between layers. Thus, in vivo derivation or calibration of these weighting factors or invertible generative fMRI signal models may alleviate determination of underlying neuronal laminar profiles from experimental fMRI data (Havlicek and Uludağ, in preparation).

It could be argued that the lowest cortical depth level (closest to white matter) has a particularly strong influence on the spatial deconvolution, in the sense that any measurement error at this level would affect the deconvolution at all higher depth levels. Partial volume effects at the white matter boundary may result in an underestimation of the stimulus‐induced response in deep layers, because white matter tissue is presumably not responsive to the stimulus. We have simulated the effect of an underestimation of the response amplitude at the deepest cortical depth level, and found that while a strong underestimation alters the relative amplitude of the deep grey matter and mid grey matter peaks, the presence of those peaks is not affected (see Supporting Information, Figure S4 for details).

At present, the model of signal spread between cortical depth levels developed by Markuerkiaga et al. (2016) is only defined for V1. Between‐area variability, within‐area variability, and between‐subject variability in vascular structure may therefore lead to erroneous deconvolution results. When applying the deconvolution to V2, we accounted for the different relative thickness of cortical layers, but not for differences in vascular structure (Weber et al., 2008). However, simulations using systematically and random deviations from the model parameters did lead to similar depth profiles (Figure 8). To test the generalizability of our approach, we applied the deconvolution model to cortical depth profiles from primary motor cortex (M1), recently published by Huber et al. (2017a). In that study, cortical blood volume (CBV) was measured using the VASO sequence, in addition to BOLD images acquired with a GE‐EPI sequence. As CBV changes are assumed to be located in microvasculature (see Uludağ & Blinder, 2017 for a review), the CBV spatial profile is a nonlinear proxy for the neuronal activity profile. Cortical depth profiles were obtained for activation during a sensory‐motor task. The GE‐EPI BOLD data are, similar to our results, prone to vascular signal spread due to ascending veins. Because of differences in vascular structure and cortical thickness between V1 and M1, the spatial deconvolution model is not expected to provide an optimal solution in this context. However, when applying the spatial deconvolution with model parameters optimized for V1 to the data from M1, the BOLD fMRI profile becomes more similar to the CBV profile, and thus—presumably—more similar to the “true” profile of local neuronal activity (Supporting Information, Figure S5). We take this as an indication that the optimal deconvolution parameters may not drastically differ between brain regions. Nevertheless, we recommend a sensitivity analysis of the weighting parameters to determine the dependence of the results on the exact values of the parameters.

Further research may measure cortical depth profiles of CBV or cerebral blood flow (CBF) in addition to the BOLD fMRI signal under identical stimulus conditions, and compare the cortical depth profiles of stimulus‐induced signal change after spatial deconvolution with the CBV or CBF profiles. A close match between deconvolved BOLD fMRI profiles and CBV or CBF profiles would constitute converging evidence for the validity of the deconvolution approach and/or experimentally allow for subject‐ and brain area‐specific estimation of the spatial weights.

We have applied spatial deconvolution in order to remove signal spread due to ascending veins. The resulting cortical depth profiles are expected to be “closer” to the underlying neuronal activity than before the deconvolution. However, there are most likely other (possibly nonlinear) transformations between neuronal activity and the BOLD signal, similarly as in low‐resolution fMRI studies. Thus, in an additional step, an anatomically informed transfer function that models the relationship between neuronal activity and the hemodynamic response for each depth level, including a scaling factor related to capillary and venule CBV, has to be used to quantitatively deduce the underlying spatial neuronal activation profile. Nevertheless, the main experimental observations of the current study after spatial deconvolution, namely the decrease in the BOLD signal in V1 toward CSF and the pronounced peak in the middle layers in V2, are expected to remain valid even after such scaling.

While this study focused on the fMRI response to a modulation of “bottom–up” stimulus properties, other studies have investigated the neural correlates of “top–down” perceptual processing (Kok et al., 2016; Muckli et al., 2015). Accounting for signal spread in the GE fMRI signal caused by draining veins may also benefit the deduction of other neuronal activity spatial profiles than in this study and, thus, investigations of top–down effects.

4.3. Alternative approaches

In this study, we employed a model‐based method to account for the effect of draining veins on the cortical depth profiles of the fMRI signal. Two alternative methods aim to deduce neuronal activity profiles from the fMRI signal rely on taking either (a) the difference or (b) the ratio of fMRI signal for two or more experimental conditions (Kashyap, Ivanov, Havlicek, Poser, & Uludağ, 2017). The rationale behind these methods is that any confounding vascular factors should affect different experimental conditions in the same way. The method of subtraction is used to remove nuisance signal components in fMRI studies at low spatial resolutions, as it is commonly applied in standard general linear model (GLM). However, in the case of high‐resolution fMRI, subtracting the cortical depth profile of the response to a stimulus from that of a control condition is unlikely to remove the effect of ascending veins, and/or a possible blood volume bias, on cortical depth profiles, as such vascular effects are nonlocal and result in multiplicative factors of BOLD signal sensitivity, respectively (Kashyap et al., 2017). Second, the method of division can be useful in exploring nonlinearities present in the data, most likely being neuronal in origin. That is, the division approach does not remove the ascending vein effect (but only the fMRI scaling factor proportional to baseline blood volume). Thus, it is rather an exploration tool to thoroughly characterize the properties of the data. In contrast, the method of this study explicitly takes the ascending vein bias into account, albeit with some model assumptions. It remains to be tested whether these assumptions are generalizable to other brain areas and/or physiological states. Clearly, more work is required to reliably extract neuronal laminar profiles from high‐resolution fMRI data.

Another proposed approach to deal with the spatial bias due to draining veins is to regress out time course contributions from other depth levels. Kok et al. (2016), separately for each depth level, removed the (neuronal and vascular) variance present at the other depth levels using a regression model. The goal of this regression approach is to identify each depth level's unique contribution (i.e., to identify the differential neuronal activity of each layer). The advantage of this approach is that it does not require an explicit vascular model, in contrast to the model‐based approach of the current study. However, the regression approach may inadvertently remove shared variance that is neuronal in origin, (a) if some of the neuronal signal of interest is spread over more than one depth level, and (b) because the draining vein effect leads to BOLD signal correlations between a neuronally active layer and the upstream layers. Finally, even though our approach needs spatial weights determined from a vascular model, for our specific experimental data, large deviations of these weights yield similar profiles. However, for more subtle neuronal changes in laminar profiles, this spatial deconvolution approach may not be sensitive enough, and subject‐ and brain area‐specific weights may be necessary.

4.4. Limitations and directions for future research

T2‐weighted sequences, such as GRASE (De Martino et al., 2013; Kemper, De Martino, Yacoub, & Goebel, 2015; Kemper et al., 2016), and sequences that are not based on the BOLD contrast, such as VASO (Huber et al., 2014, 2015, 2016; Huber, Uludağ, & Möller, 2017b) and ASL (Huber et al., 2017b; Pfeuffer et al., 2002; Uludağ et al., in preparation), are less affected by vascular biases and are therefore expected to yield a better estimation of local neuronal activity compared with GE sequences. However, this advantage comes at the price of a lower sensitivity and/or decreased coverage. The GE MRI sequence utilized in this study achieves good coverage and sensitivity, but for cortical‐depth‐specific studies, the problem of reduced specificity due to signal spread along the ascending draining veins needs to be addressed. The spatial deconvolution model proposed by Markuerkiaga et al. (2016) may help to remove nonlocal signal contributions from cortical depth profiles. However, to be more generally applicable, the model needs to be extended to other brain areas with a different vascular structure, and to different experimental designs and imaging sequences. In particular, in its current state, the spatial deconvolution model is only applicable to the steady‐state fMRI response to a block design. To investigate transient components of the fMRI signal, such as the initial overshoot or the poststimulus undershoot, at different cortical depths, a dynamic deconvolution model is needed. This may be achieved by a generative model of the temporal dynamics of the hemodynamic response across cortical depth (Havlicek and Uludağ, in preparation). With the help of such dynamic deconvolution models, the disadvantages of GE acquisitions for cortical‐depth‐specific fMRI research may be addressed, while retaining its good sensitivity and coverage.

4.5. Summary

We have studied the contrast response properties of human V1 and V2 using fMRI at submillimeter resolution. After accounting for signal spread due to ascending draining veins, we found the stimulus‐induced response to peak at mid cortical depths in V1 and V2, in addition to a response maximum in deep grey matter, which was more pronounced in V1. A response peak at middle depth levels is expected, as it is in agreement with electrophysiological evidence obtained in monkey V1 and V2. In contrast, a stimulus‐induced response in deep layers has been observed in some (Goense et al., 2007; Maier et al., 2011; Smirnakis et al., 2007; Tootell et al., 1988), but not all (Bissig & Berkowitz, 2009; Roberts et al., 2013; Xing et al., 2012) relevant animal studies. A systematic investigation of the stimulus conditions under which a response in deep layers is evoked will be necessary to resolve this issue.

Supporting information

Additional Supporting Information may be found online in the supporting information tab for this article.

Supporting Information

Marquardt I, Schneider M, Gulban OF, Ivanov D, Uludağ K. Cortical depth profiles of luminance contrast responses in human V1 and V2 using 7 T fMRI. Hum Brain Mapp. 2018;39:2812–2827. 10.1002/hbm.24042