Differentially categorized structural brain hubs are involved in different microstructural, functional, and cognitive characteristics and contribute to individual identification

Abstract

Very little is known regarding whether structural hubs of human brain networks that enable efficient information communication may be classified into different categories. Using three multimodal neuroimaging data sets, we construct individual structural brain networks and further identify hub regions based on eight widely used graph‐nodal metrics, followed by comprehensive characteristics and reproducibility analyses. We show the three categories of structural hubs in the brain network, namely, aggregated, distributed, and connector hubs. Spatially, these distinct categories of hubs are primarily located in the default‐mode system and additionally in the visual and limbic systems for aggregated hubs, in the frontoparietal system for distributed hubs, and in the sensorimotor and ventral attention systems for connector hubs. These categorized hubs exhibit various distinct characteristics to support their differentiated roles, involving microstructural organization, wiring costs, topological vulnerability, functional modular integration, and cognitive flexibility; moreover, these characteristics are better in the hubs than nonhubs. Finally, all three categories of hubs display high across‐session spatial similarities and act as structural fingerprints with high predictive rates (100%, 100%, and 84.2%) for individual identification. Collectively, we highlight three categories of brain hubs with differential microstructural, functional and, cognitive associations, which shed light on topological mechanisms of the human connectome.

1. INTRODUCTION

The human brain works as a complex network to support various cognitive processes through information communication and integration between interconnected regions (Bullmore and Sporns, 2009; Petersen and Sporns, 2015; Sporns, Tononi, & Kötter, 2005). Using noninvasive diffusion magnetic resonance imaging tractography approaches, researchers have reconstructed structural human brain networks at the macroscale (Gong et al., 2009; Hagmann et al., 2008). With a graph‐theoretical network analysis framework, recent studies have suggested that structural brain networks contain sets of centrally embedded and topologically important hub nodes or regions, which are generally identified using various graph measures (van den Heuvel and Sporns, 2013b). These brain hubs provide the anatomical underpinnings for the efficient transfer of information among regions (Gong et al., 2009; Hagmann et al., 2008; van den Heuvel and Sporns, 2011) and consume high wiring cost and physiological energy (Bullmore and Sporns, 2012; Collin, Sporns, Mandl, & van den Heuvel, 2014; van den Heuvel, Kahn, Goñi, & Sporns, 2012). Moreover, the abnormal topological properties of these hubs have been associated with a variety of neurological and psychiatric disorders, suggesting their vital roles to maintaining normal brain function (Crossley et al., 2014; Fornito, Zalesky, & Breakspear, 2015; Gong and He, 2015; van den Heuvel and Sporns, 2013b). Together, such recent progress has highlighted the significance of structural hubs in understanding the biological mechanisms of the brain under healthy and diseased conditions.

Notably, structural hubs in human brain networks are typically identified as the nodes with high values of certain graph‐based nodal metrics (e.g., degree centrality, closeness centrality, betweenness centrality, or participant coefficient) (Crossley et al., 2014; Gong et al., 2009; He, Chen, & Evans, 2007; Li et al., 2013; Shu et al., 2011; Zalesky et al., 2010) or combinations of several metrics (Hagmann et al., 2008; van den Heuvel et al., 2010). However, different nodal metrics are likely to capture different topological roles of nodes in brain networks. For example, for a given network node, the nodal degree centrality describes the number of connections that link to this node, the nodal betweenness centrality specifies the importance of nodes on the information flow path, and the nodal participant coefficient describes the capability that links different network modules (Borgatti and Everett, 2006; Rubinov and Sporns, 2010). Based on empirical results, although different nodal metrics detect certain common hubs (e.g., the medial parietal cortex and the precuneus) (Gong et al., 2009; Hagmann et al., 2008; van den Heuvel et al., 2010; van den Heuvel and Sporns, 2013b), there are discrepancies in spatial locations even when using the same data set in one study: for example, the inferior parietal cortex was identified as a hub using closeness centrality but not using betweenness centrality, and the superior temporal gyrus was identified as a hub using degree centrality but not closeness centrality (Hagmann et al., 2008). These different definitions from graph‐based network theory and various experimental observations raise important questions regarding whether distinct categories of structural hubs in the human brain networks exist, and if so, how these categorized hubs are spatially distributed. Specifically, previous studies have demonstrated high‐level microstructural organization (Collin et al., 2014), large wiring costs (van den Heuvel et al., 2012; Xia, Lin, Bi, & He, 2016), and functional associations (Collin et al., 2014; van den Heuvel and Sporns, 2013a) in the structural hubs. Thus, the subsequent question would be whether these distinct categorized hubs are significantly different in the above‐mentioned microstructural and functional characteristics. Answering these questions will greatly improve our understanding of the organizational principles and topological architecture of the human structural connectome.

To address these issues, we utilized diffusion MRI data (Dataset 1) to reconstruct individual structural brain networks and further estimated eight frequently used graph nodal metrics to characterize various aspects of the topological roles of each nodal region. These nodal metrics were subsequently classified into different categories based on their spatial similarity, and structural brain hubs and hub indices were identified for each category. We further investigated the underlying microstructural organization, wiring cost, functional modular integration, cognitive flexibility, and topological vulnerability of distinct category hubs. Moreover, based on a repeated scanning imaging dataset (Dataset 2), we compared the results of the classification of metrics and the spatial distribution of the hub indices between two scanning sessions to evaluate their reliability and performed an individual identification analysis to assess the individuality of the hub indices. Finally, validation analyses were conducted using different network constructions and analysis strategies as well as different diffusion imaging protocols (high angular resolution diffusion imaging, HARDI, Dataset 3).

2. MATERIALS AND METHODS

2.1. Data overview and participants

Three imaging data sets were included in this study (Table 1): a principal dataset of 146 participants with structural MRI, diffusion tensor imaging (DTI), and resting‐state functional MRI (R‐fMRI) data (Dataset 1), a test–retest dataset of 57 participants with structural MRI and DTI data (Dataset 2) and a validation dataset of 38 participants with structural MRI and HARDI data (Dataset 3). All participants were right‐handed and had no history of neurological or psychiatric disorders. Written informed consent was obtained from each participant. The study designs from Datasets 1 and 2 were approved by the Institutional Review Board of the State Key Laboratory of Cognitive Neuroscience and Learning at Beijing Normal University, and the study design for Dataset 3 was approved by the Institutional Review Board of the WU‐Minn Human Connectome Project (HCP) (Van Essen, Glasser, Dierker, Harwell, & Coalson, 2013). Table 1 shows the demographics of all participants and imaging modalities used in this study. Notably, Dataset 1 was used for the principal network analyses in this study, which involved constructing structural brain networks, identifying structural hubs and exploring miscellaneous characteristics of structural hubs (e.g., microstructural organization, wiring cost, functional associations, and topological vulnerability); Dataset 2 was used for the reliability analysis for structural network hubs and individual identification and Dataset 3 was used for the validation of the main results obtained from Dataset 1.

Table 1.

Datasets and demographics

	Dataset 1 (n = 146)	Dataset 2 (n = 57)	Dataset 3 (n = 38)
Gender (male/female)	70/76	30/27	17/21
Age (years)	19–30 (22.68 ± 2.24)	19–30 (23.05 ± 2.29)	22–35a
MRI modality	T1, DTI, R‐fMRI	T1, DTI	T1, HARDI

^aFor each subject, accurate year of age was not provided in the HCP dataset.

2.2. MRI acquisition procedures

Dataset 1: The principal data set was selected from the Connectivity‐based Brain Imaging Research Database (C‐BIRD) at Beijing Normal University. All MRI data (structural MRI, DTI and R‐fMRI) were acquired using a 3.0 T Siemens Trio Tim scanner (Siemens Medical Systems, Erlangen, Germany) with a 12‐channel phased‐array head coil in the Imaging Center for Brain Research, Beijing Normal University. The MR imaging procedures were as follows: (a) Structural MRI. T1‐weighted, sagittal 3D magnetization prepared rapid gradient echo (MP‐RAGE) sequence, repetition time (TR) = 2,530 ms, echo time (TE) = 3.39 ms, inversion time (TI) = 1,100 ms, flip angle = 7°, matrix = 256 × 256, field of view (FOV) = 256 mm × 256 mm, slice thickness = 1.33 mm, voxel size = 1 mm × 1 mm × 1.33 mm and 144 sagittal slices covering the whole brain. (b) DTI. Single‐shot twice‐refocused spin‐echo diffusion echo‐planar imaging sequence, TR = 8,000 ms, TE = 89 ms, 30 non‐linear diffusion directions with b = 1,000 s/mm² and an additional volume with b = 0 s/mm², number of excitation = 2, matrix = 128 × 128, FOV = 282 mm × 282 mm, slice thickness = 2.2 mm, voxel size = 2.2 mm × 2.2 mm × 2.2 mm, bandwidth = 1,562 Hz/pixel, and 62 transverse slices without gap covering the whole brain. (c) R‐fMRI. Echo‐planar imaging sequence (EPI), TR = 2,000 ms, TE = 30 ms, flip angle = 90°, matrix = 64 × 64, FOV = 200 mm × 200 mm, slice thickness = 3.5 mm, voxel size = 3.1 mm × 3.1 mm × 3.5 mm, 33 transverse slices with 0.7 mm gap covering the whole brain, and volume number = 200. This scan lasted for 6 min and 40 s. During the scan, the participants were instructed to rest and relax with their eyes closed and to refrain from falling asleep.

Dataset 2: The test–retest data set, which included structural MRI and DTI data, was also from the C‐BIRD. Notably, the participants in the Dataset 2 were scanned twice at an interval of approximately 6 weeks (40.94 ± 4.51 days) and had participated in the Consortium for Reliability and Reproducibility (CoRR) dataset (http://fcon_1000.projects.nitrc.org/indi/CoRR/html/bnu_1.html) (Lin et al., 2015). The scanning parameters were identical to those of Dataset 1.

Dataset 3: The validation data set, including structural MRI and HARDI data, was selected from the WU‐Minn HCP (https://db.humanconnectome.org, “unrelated 40 subjects”) (Van Essen et al., 2013). The original data set included imaging data for 40 healthy participants (Q1 and Q2 release), but two participants (subject ID: 209733 and 528446) were excluded because of structural brain abnormalities (https://www.humanconnectome.org/documentation/S500). The MRI data were acquired on an HCP's custom 3.0 T Siemens Skyra scanner using a 32‐channel head coil at Washington University. The MR imaging procedures were as follows: (a) Structural MRI. T1‐weighted, sagittal 3D MP‐RAGE sequence, TR = 2,400 ms, TE = 2.14 ms, TI = 1,000 ms, flip angle = 8°, matrix = 320 × 320, FOV = 224 mm × 224 mm, slice thickness = 0.7 mm, voxel size = 0.7 mm × 0.7 mm × 0.7 mm and 256 sagittal slices in a single slab (Glasser et al., 2013). (b) HARDI. A single‐shot 2D spin‐echo multiband EPI sequence, TR = 5,520 ms, TE = 89.5 ms, 270 diffusion directions with diffusion weighting 1,000, 2,000, or 3,000 s/mm² and 18 additional volumes with b = 0 s/mm², matrix = 144 × 168, FOV = 210 mm × 180 mm, 1.25 mm slice thickness, voxel size = 1.25 mm × 1.25 mm × 1.25 mm, and 111 transverse slices without gap covering the whole brain (Sotiropoulos et al., 2013).

2.3. Construction of individual structural brain networks

Nodes and edges are the two basic elements of a network. Here, the structural and diffusion imaging data of Dataset 1 were used to construct structural human brain networks. The relevant procedures of network construction were introduced in our previous works (Bai et al., 2012; Gong et al., 2009; Shu et al., 2011; Figure 1) and are briefly described as follows.

Figure 1.

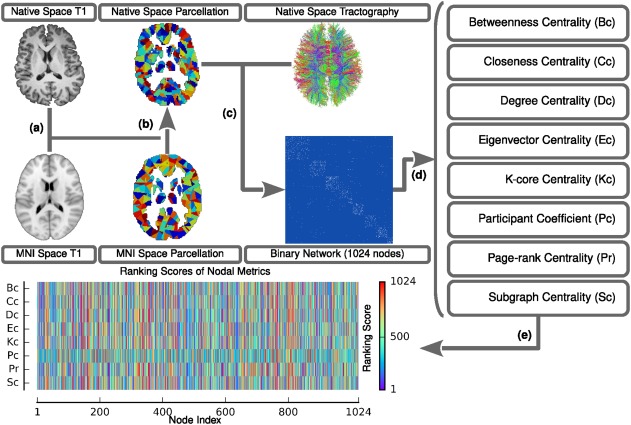
Flowchart of the network construction and graph nodal metric estimation for each participant. (a) After rigidly co‐registering to the averaged b0 image, the native space T1 image was nonlinearly transformed to the ICBM 152 T1 template in the MNI space, which resulted in a transformation matrix. (b) The inversed transformation matrix was utilized to warp the parcellation from the MNI space to the native space. (c) In terms of the parcellation and the results of the deterministic tractography in the native space, the WM network was constructed. (d) Eight nodal metrics were estimated based on the individual WM networks. (e) The metrics were ultimately converted to normalized ranking scores [Color figure can be viewed at http://wileyonlinelibrary.com]

2.3.1. Definition of network nodes

The procedure for defining network nodes was implemented by using the SPM8 package (https://www.fil.ion.ucl.ac.uk/spm/software/spm8/). Briefly, for each individual, the T1‐weighted image was initially co‐registered to the averaged b0 image in the native diffusion space using a linear transformation. The co‐registered T1‐weighted image was subsequently segmented into gray matter, white matter and cerebrospinal fluid by using a unified segmentation algorithm. The resultant images were further nonlinearly registered into the Montreal Neurological Institute space, and the transformation matrix was estimated. Finally, the inversed transformation matrix was used to warp a predefined brain parcellation with 1,024 regions of interest from the standard space to the native diffusion space. Discrete labeling values in the parcellation were preserved by the use of a nearest‐neighbor interpolation method. Notably, the brain parcellation was generated by randomly subdividing the automated anatomical labeling atlas into 1,024 cortical and subcortical regions of equal size (Zalesky et al., 2010), which enabled the capture of both major tracts and forking U‐fibers. Thus, for each individual, we obtained 1,024 brain regions, each representing a network node.

2.3.2. Definition of network edges

The procedures for defining network edges were mainly based on the whole‐brain fiber bundles, which were reconstructed using the deterministic tractography method. Briefly, each individual diffusion weighted image was first preprocessed (eddy current and motion artifact correction) and aligned to an averaged b0 image by an affine transformation using the FMRIB's Diffusion Toolbox of FSL (Version 5.0; https://www.fmrib.ox.ac.uk/fsl). The Fiber Assignment by Continuous Tracking (FACT) algorithm (Mori, Crain, Chacko, & Van Zijl, 1999) was subsequently performed to reconstruct all WM bundles in the brain using the DTIstudio package (version 3.0.3). Here, fiber tracking was computed by seeding each voxel with a fractional anisotropy value >0.2. This fiber‐tracking procedure was terminated at voxels for which the fractional anisotropy was <0.2 or if the turning angle between adjacent steps was >45°. Using this procedure, tens of thousands of streamlines were generated to etch out all major WM tracts. Two nodes were considered to be structurally connected if there were streamlines with end points located in these two regions. To this end, for each subject, we obtained a binary WM network, and subsequent analyses were conducted at an individual level, unless specifically noted.

2.4. Identification of structural brain hub categories

To identify structural hubs from the brain networks and further ascertain whether they could be classified into different categories, we utilized eight widely used graph‐based metrics to quantify nodal roles in the brain networks and performed a further hierarchical clustering analysis. These analyses were performed using the GRETNA toolkit (https://www.nitrc.org/projects/gretna/) (Wang et al., 2015), the MatlabBGL package (https://www.cs.purdue.edu/homes/dgleich/packages/matlab_bgl/), the brain connectivity toolbox (BCT, https://sites.google.com/site/bctnet), and our in‐house Matlab codes. The procedures are described in detail as follows.

2.4.1. Graph nodal metrics

We investigated eight graph‐based centrality metrics, including betweenness centrality (Bc), closeness centrality (Cc), degree centrality (Dc), eigenvector centrality (Ec), K‐core centrality (Kc), participant coefficient (Pc), page‐rank centrality (Pr), and subgraph centrality (Sc) (Figure 1 and Supporting Information, Table S1). These metrics capture different topological roles of network nodes and have been widely adopted in previous brain network studies (Fagerholm, Hellyer, Scott, Leech, & Sharp, 2015; Gong et al., 2009; Hagmann et al., 2008; He et al., 2007; Honey, Kötter, Breakspear, & Sporns, 2007; Power, Schlaggar, Lessov‐Schlaggar, & Petersen, 2013; van den Heuvel et al., 2010; Zuo et al., 2012). Notably, we performed a modularity detection for each subject and subsequently estimated the corresponding participant coefficient based on the individual modular identification. A group‐level modular identification was also used to calculate the participant coefficient for validation (for details, refer to Supporting Information, Table S1 and Figures S14 and S15). Furthermore, these nodal metrics result in different ranges of values while they are computed in a network. To compare across metrics, we transferred the original values of each metric into corresponding temporary ranking scores from 1 to 1,024. For a given metric, regarding that some nodes have the same values, we computed the mean value of their temporary ranking scores, which resulted in the final nodal ranking scores; the nodes with higher ranking scores correspond to nodes with higher topological importance in a network.

2.4.2. Spatial similarity among metrics

To investigate the similarity of spatial distributions among these eight nodal metrics, for each subject we first computed the Spearman's rank correlation ( $\mathrm{\rho }$), between every pair of metrics across nodes, resulting in an eight‐by‐eight correlation matrix. To further determine whether the spatial similarity between any pairs of metrics in the brain networks occur by chance, for each subject we compared the individual correlation matrix with those derived from 100 individual‐specific random networks that were generated using Maslov's wiring algorithm, retaining the same number of nodes, number of edges and degree distribution as the real individual brain network (Maslov and Sneppen, 2002). Then, the Z‐scores were estimated to quantify the differences between the $\mathrm{\rho }$ values of brain networks and random counterparts:

$$z_{\mathrm{a},\mathrm{b}}=\left({\mathrm{\rho }}_{\mathrm{a},\mathrm{b}}-{\mathrm{\mu }}_{\mathrm{a},\mathrm{b}}\right)/{\mathrm{\sigma }}_{\mathrm{a},\mathrm{b}},$$ (1)

where ${\mathrm{\rho }}_{\mathrm{a},\mathrm{b}}$ is the Spearman's rank correlation coefficient between metric $\mathrm{a}$ and metric $\mathrm{b}$ in the brain network, and ${\mathrm{\mu }}_{\mathrm{a},\mathrm{b}}$ and ${\mathrm{\sigma }}_{\mathrm{a},\mathrm{b}}$ are the mean and standard deviation, respectively, of Spearman's rank correlation coefficients between the two metrics in the random networks. Finally, for every pair of metrics we performed one‐sample t‐tests across individuals to determine whether these Z‐score values were significantly different from zero. Bonferroni‐corrected p < .05 was considered significant for multiple comparisons (i.e., uncorrected p < .05/28, here the 28 represents the number of comparisons among eight nodal metrics, $C_8^2$).

2.4.3. Hierarchical clustering analysis and categories of network hubs

To determine whether the eight nodal metrics can be classified into different categories, we performed the following hierarchical clustering analysis. Briefly, for each individual the metric‐by‐metric Spearman's correlation matrix was first transformed to Fisher's $z$ matrix using Fisher's $\mathrm{\rho }$‐to‐ $z$ transformation to improve normality. The Fisher's $z$ matrices were averaged across individuals and further inverse‐Fisher's z‐to‐ $\mathrm{\rho }$ transformed to generate a new group‐based correlation matrix. Then, we obtained a dissimilarity matrix by subtracting the correlation values from 1 and generated an agglomerative hierarchical clustering tree based on the single linkage algorithm using weighted average distance metric. Thus, eight nodal metrics were classified to different categories. To determine a proper category number, we employed a stability analysis procedure (Lange, Roth, Braun, & Buhmann, 2004; Yeo et al., 2011) in which a hierarchical clustering analysis was performed on the Spearman's correlation matrices that were obtained by randomly selecting 5% of all subjects 1000 times. Based on this procedure, the eight nodal metrics were classified into three categories (for details, refer to Section 2.1, Results) in which the category number was significantly stable and simultaneously ensured larger category‐assigning differences of nodal metrics than null models (for details, refer to Supporting Information, Figure S1). Finally, for each category, we identified the brain network hubs using a hub index, which was defined as the mean ranking score of metrics in this category. The nodes with the top 20% of hub index were identified as hubs, and the remaining nodes were considered nonhubs (note: two additional thresholds—15% and 25%—were used for the validation analyses). To display the distribution of each category of hubs, all hub and nonhub nodes were unfolded in the topological space using “spring model” layouts based on the “fdp” algorithm (https://www.graphviz.org).

To further clarify whether the topological profiles of each category of hubs were different from those of each nodal metric, we compared their spatial distributions. Briefly, for each subject, the top 20% nodes were initially identified as hubs from each category and each nodal metric, respectively. The overlapping percentages were subsequently calculated between any pairs of the categorized hubs and single metric defined hubs, and the percentages were averaged across individuals.

2.4.4. Distributions of structural hubs in functional brain systems

To examine whether and how different categorized structural hubs are associated with the brain's functional systems, we performed a functional network modularity analysis and further calculated the proportions of each category of structural hubs distributed in each functional system. Briefly, we first built a group‐based functional brain network at a voxel‐level using the R‐fMRI data of 146 participants from Dataset 1 and then identified functionally connected modules using a graph‐based network modularity analysis (for details, refer to Supporting Information, Methods). Seven major functional subdivisions were identified, including the default‐mode, visual, frontoparietal, sensorimotor, limbic, dorsal attention and ventral attention systems (Supporting Information, Figure S2), and this subdivision was largely compatible with previous functional brain network studies (He et al., 2009; Power et al., 2011; Yeo et al., 2011). For each category of hub, we computed their proportions that belonged to different functional systems. Finally, paired nonparametric permutation tests (N = 20,000) were performed to determine significant differences in the hub proportion among systems for each category of hubs, and among these categories of hubs for each system. Bonferroni‐corrected p < .05 was considered significant for multiple comparisons (i.e., uncorrected p < .05/84, here the 84 was the sum of the number of comparisons among systems for each category of hubs and the number of comparisons among three categories of hubs for each system, $3\times C_7^2+7\times C_3^2$).

2.5. Characterization of microstructural, functional, and cognitive associations of structural hubs

To determine whether different category structural hubs exhibited common and distinct properties, we systematically explored their microstructural organization, wiring cost, functional modular integration, cognitive flexibility, and topological vulnerability.

2.5.1. Microstructural organization and wiring cost of structural hubs

We explored the underlying microstructural organization and wiring cost of different category hubs using the four WM diffusion indices and two WM wiring cost indices, respectively. For a given network edge, we initially computed the four diffusion indices: fractional anisotropy, which reflects the degree of anisotropy of a diffusion process; axial diffusivity, which estimates the level of diffusion in the direction of the first eigenvector used to describe the level of local fiber orientation; radial diffusivity, which reflects the amount of diffusion perpendicular to the first eigenvector and specifies the level of myelination of the WM; and mean diffusivity, which assesses the total level of diffusion (Basser, 1995; Song et al., 2002). These diffusion indices were estimated by averaging the values across the WM voxels that the streamlines passed through, and they reflect the different aspects of the diffusion properties of WM tissues. Research has suggested that the diffusion indices are approximately associated with the microstructural organization of WM tracts, such as axonal membrane or myelin (Beaulieu, 2002). Then, we computed the two WM wiring cost indices: the streamline length, which captures the average length of all reconstructed streamlines in the network edge; and the streamline cost, which represents the total streamline length in the network edge (Bullmore and Sporns, 2012; Kaiser and Hilgetag, 2006; van den Heuvel et al., 2012). For a given network node, we obtained its diffusion and cost indices by computing the mean value of the edges that this node links. The diffusion and wiring cost indices were subsequently averaged across hub and nonhub nodes, respectively. Notably, for isolated nodes, we cannot estimate their WM indices; therefore, when calculating the averaged diffusion and wiring cost indices across hub and nonhub nodes, the isolated nodes were ignored. Finally, paired nonparametric permutation tests (N = 20,000) with Bonferroni‐corrected p < .05 for multiple comparisons were used to determine the significances of the statistical differences in the diffusion and wiring cost indices between hubs and non‐hubs (i.e., uncorrected p < .05/18, here the 18 was the number of the comparisons for six WM indices of three categories, $6\hspace{0.17em}\times \hspace{0.17em}3$) or among different category hubs (i.e., uncorrected p < .05/18, here, the 18 was the number of the comparisons for six WM indices among three categories of hubs, $6\times C_3^2$).

2.5.2. Functional modular integration and cognitive flexibility of structural hubs

We further investigated whether different category structural hubs play distinct roles in the functional modular integration and whether they contribute to different cognitive flexibility underlying multiple cognitive functions. Thus, we initially computed the functional participant coefficient (the participant coefficient of R‐fMRI functional network) at each voxel according to the modular architecture derived from the previously described group‐based functional brain network (for details, refer to Supporting Information, Methods). For a given type of node (i.e., hub or nonhub nodes) in the structural brain network, we computed its functional participant coefficients by averaging the participant coefficients across all voxels belonging to the corresponding nodal type. We subsequently obtained the brain map of the cognitive flexibility (Yeo et al., 2014) (https://surfer.nmr.mgh.harvard.edu/fswiki/BrainmapOntology_Yeo2015), which is defined as the number of cognitive components that activate a voxel with a probability of at least 1 × 10⁻⁵. Similarly, for a given nodal type in the structural network, we calculated its functional flexibility by averaging the cognitive component numbers of all voxels that belonged to the corresponding nodal type. Finally, we performed paired nonparametric permutation tests (N = 20,000) with Bonferroni‐corrected p < .05 to evaluate the significance levels of the differences in the functional participant coefficient or the cognitive component number between hubs and nonhubs (i.e., uncorrected p < .05/6, here the 6 was the number of the comparisons for two functional indices for three categories, $2\hspace{0.17em}\times \hspace{0.17em}3$) or among categories of hubs (i.e., uncorrected p < .05/6, here the 6 was the number of the comparisons for two functional indices among three categories of hubs, $2\times C_3^2$).

2.5.3. Topological vulnerability of structural hubs

We estimated the topological vulnerability of different categories of structural hubs using the nodal “lesion” simulation procedure as follows (Achard, Salvador, Whitcher, Suckling, & Bullmore, 2006; He et al., 2007). Briefly, for each category of hubs, we first performed targeted attacks on individual structural networks by removing the nodes one‐by‐one according to the descending order of hub indices and then measured the changes in the global efficiency and the size of the largest connected component of the networks. We also performed a random failure procedure in which brain nodes were continuously and randomly removed from individual networks 100 times and recomputed the averaged two measures of the resultant networks. Notably, to ensure that the curves from different individual networks were comparable, for each curve, we divided all the values of this curve by the value of its first point to yield the normalized curve. Then, for each individual network, we calculated the area under the top 20% curves (AUC) of both the largest component size and the global network efficiency under targeted attacks and random failures. A smaller AUC represents a faster decrease in global network performance in response to nodal removal. Finally, we evaluated the differences in the AUC of the largest component size or the global network efficiency between when under targeted attacks and when under random failure. Paired nonparametric permutation tests (N = 20,000) with Bonferroni‐corrected p < .05 was used to determine the significance of the statistical differences (i.e., uncorrected p < .05/6, here the 6 was the number of the comparisons for two topological indices of three categories, $2\hspace{0.17em}\times \hspace{0.17em}3$) or among the three categories of hubs under targeted attacks (i.e., uncorrected p < .05/6, here the 6 was the number of the comparisons for two topological indices among three categories of hubs, $2\times C_3^2$).

To determine whether the previously described miscellaneous characterizations in these categories of structural hubs were unique in the human brain networks or obtained by chance, we generated all possible combinations of nodal classifications, computed the resultant surrogated hub indices, and subsequently compared the characteristics between real categorized hub indices and surrogate ones. For details, refer to Supporting Information, Methods.

2.6. Reliability of structural brain hubs and individual identification analyses

To determine whether the classification of nodal metrics and the spatial distribution of structural brain hub indices are reliable and whether each category hub index can contribute to individual identification during repeated scans, we performed the following analyses using the imaging data of Dataset 2.

2.6.1. Reliability analysis

For each subject, we constructed two structural brain networks corresponding to two scanning sessions to classify their eight metrics into three categories and to then compute their hub indices for each category. The network construction and analysis procedures were identical to those used for Dataset 1. To evaluate the reliability of the classification of metrics and the redefinition of hubs, we determined whether the results of the classification between two scanning sessions were consistent. We further calculated the intra‐ and intersubject Spearman's correlation coefficients for each category of hub index across nodes between two scanning sessions and estimated group‐averaged hub index correlations between two sessions, to assess the reliability of the spatial distribution of hub indices at both the individual and group levels. Furthermore, we evaluated the reliability of each nodal metric by computing across‐node Spearman's correlation between two sessions. Paired t tests with Bonferroni‐corrected p < .05 were used to determine the significances of reliability differences between the categorized hub‐index and relevant nodal metrics.

2.6.2. Individual identification using structural hub indices

To explore whether the spatial patterns of different categories of hub indices contribute to individuality, we performed the following individual identification analysis. This procedure was originally proposed to identify individuals based on the brain's functional connectivity matrix (Finn et al., 2015); however, it was modified here by incorporating nodal hub indices of brain networks. Briefly, for each category of hub indices, we first selected an individual from Session 1 as a reference and then calculated the Spearman's correlation coefficient across nodes between this reference and every subject in Session 2. Then, we determined whether the reference itself retained the maximum correlation value among all individuals in Session 2; if so, we defined that the prediction succeeded, and otherwise it did not succeed. Using this procedure, we repeated this analysis for each individual from Session 1 and calculated the predictive rate for each category of hub indices. We also performed the predictive analysis from Session 2 to Session 1. Furthermore, we performed permutation tests (N = 20,000) with Bonferroni correction for multiple comparison (i.e., uncorrected p < .05/3, across three hub indices) to assess whether the intra‐ and intersubject similarities of hub indices were different.

2.7. Validation analysis

To determine whether our findings were influenced by different image preprocessing and data analysis strategies, we performed the following validation analyses. First, to estimate the effects of diffusion imaging protocols and reconstructing algorithms of fiber pathways, we constructed individual structural brain networks using HARDI data from HCP (Dataset 3) and reperformed the same analyses as Dataset 1. Second, previous studies have shown that different node definitions may affect network topological properties (Wang et al., 2009; Zalesky et al., 2010); thus, we further constructed the structural brain network using two additional parcellations: the 625‐node random parcellation, which was obtained by subdividing the anatomical transcendental boundaries of automated anatomical labeling (Tzourio‐Mazoyer et al., 2002), and a coarser 360‐node multimodal parcellation, which was parceled based on the anatomical and functional gradient information over the cortex (Glasser et al., 2016). Third, to determine whether our findings regarding the hub characteristics are independent of the hub selection threshold (top 20% in the hub indices), we added two additional thresholds, the top 15% and the top 25%, to define brain hubs. Fourth, to examine whether hub identifications were sensitive to the existence of isolated nodes in brain networks, we explored the spatial distribution of the isolated nodes by calculating the probability of isolation for each node across individuals. The nodal metrics were recalculated in the individual networks with the removal of isolated nodes and the hierarchical clustering analysis was reperformed to identify categorized hubs. Finally, to validate whether the modular identification would affect the calculation of the participant coefficient and therefore affect our main findings, we repeated our analyses performed on Dataset 1 with the participant coefficients calculated based on a group‐level modular organization. For additional details regarding the validation analyses, refer to Supporting Information, Methods.

3. RESULTS

3.1. Three categories of structural hubs in the human brain networks

3.1.1. Similarity of spatial distribution of network nodal metrics

For each subject, we constructed individual structural brain networks and generated eight nodal centrality maps (Figure 1). Visual examination indicated that several regions exhibited higher nodal centrality values (e.g., ranked in top 20%) in most of these centrality maps, which included the medial and lateral frontal and parietal regions and several subcortical regions, such as the putamen, the caudate and the thalamus (Figure 2a). Furthermore, Spearman's rank correlation analyses indicated a wide range of correlation values among these centrality maps (range: 0.38–0.93, Figure 2b), which suggests remarkably similar or different spatial distributions between specific network nodal metrics. Notably, all spatial correlations among these nodal centrality maps in the brain network were significantly (p values < .001, Bonferroni corrected) lower than those in the randomized counterparts, with the exception of the correlation between the K‐core centrality and subgraph centrality (p value = .012, uncorrected) (Figure 2c), suggesting a unique organizational architecture of brain networks.

Figure 2.

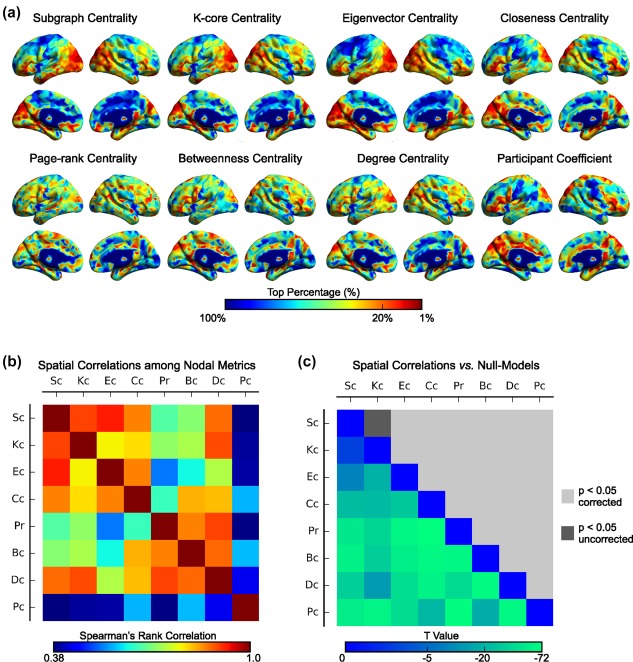
The spatial distributions of eight graph‐nodal metrics and their spatial similarities. (a) The group‐level centrality map for each graph‐nodal metric was obtained by averaging the rank maps across individuals. The color of the surface represents the top percentage for a given node in descending order of rank values. Notably, after obtaining the top percent maps, all results were smoothed for better visualization with full‐width half‐maximum (FWHM) = 2 mm. All eight smoothed group‐level top percentage of metrics were mapped to the ICBM152 brain surface template in the MNI space using BrainNet Viewer (Xia et al., 2013). (b) The Spearman's rank correlations across nodes were estimated to represent the spatial similarities among the nodal metrics. The order of metrics was arranged according to the following hierarchical clustering analysis to display the spatial similarities and dissimilarities among metrics. (c) The spatial similarities among nodal metrics were compared to a null model. The lower triangular matrix shows the t values that represent the difference in the spatial similarities among nodal metrics between those in the brain network and 100 random networks. The upper triangular matrix represents the significant level of t values [Color figure can be viewed at http://wileyonlinelibrary.com]

3.1.2. Three categories of structural brain hubs

Using the agglomerative hierarchical clustering analysis on the group‐averaged metric‐by‐metric correlation matrix, we classified the eight nodal metric maps into three categories (Figure 3a and Supporting Information, Figure S1): (a) subgraph centrality, K‐core centrality, eigenvector centrality and closeness centrality; (b) page‐rank centrality, betweenness centrality and degree centrality; and (c) participant coefficient. Within each category, the brain hubs were identified according to a hub index, and their topological and spatial positions were described (Figures 3b and 4). By visual inspection and prior knowledge from graph theory, we determined that the three categories of brain hubs showed distinct features: closely aggregated hubs, widely distributed hubs and dispersed hubs that linked structural modules, which were thus defined as aggregated hubs (A‐Hub), distributed hubs (D‐Hub), and connector hubs (C‐Hub), respectively (Figure 3b). Notably, the three categorized hubs partly overlapped with the hubs defined by single nodal metrics (the nodes with top 20% single nodal metric values). For the aggregated hub index and its relevant node metrics (subgraph centrality, K‐core centrality, eigenvector centrality, and closeness centrality), the overlapping ratios between hubs defined by single nodal metrics and hubs defined by the corresponding categorized hub indices (overlapped hub ratios) were 77.2%, 55.3%, 74.1%, and 60.2%. For the distributed hub index and its relevant node metrics (page‐rank centrality, betweenness centrality, and degree centrality), the overlapped hub ratios were 66.9%, 66.7%, and 73.9% (Table 2). Thus, the single nodal metrics cannot fully represent the properties of these categorized hubs, which suggests the necessity of hub categorization.

Figure 3.

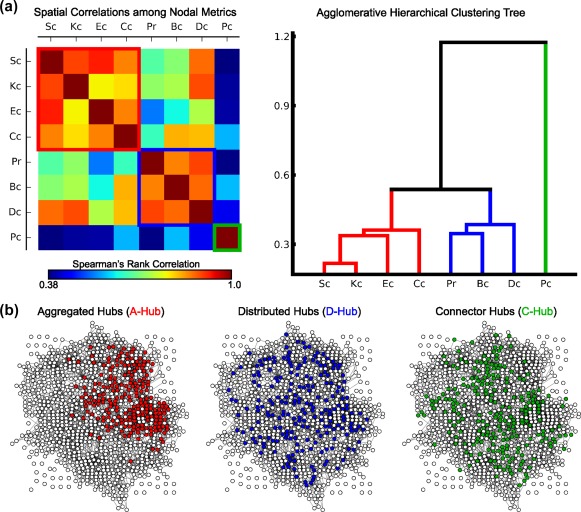
Three categories of hubs. (a) The group‐averaged map of the Spearman's correlations among the eight nodal metrics and the agglomerative hierarchical clustering tree generated from the map. The red, blue, and green solid lines show the classification results, which indicate the three categories of metrics used to identify the following aggregated hubs, distributed hubs, and connector hubs. (b) The distributions of hubs from a representative subject in the topological space. Notably, the network layouts were generated using the “fdp” algorithm in NetworkX [Color figure can be viewed at http://wileyonlinelibrary.com]

Figure 4.

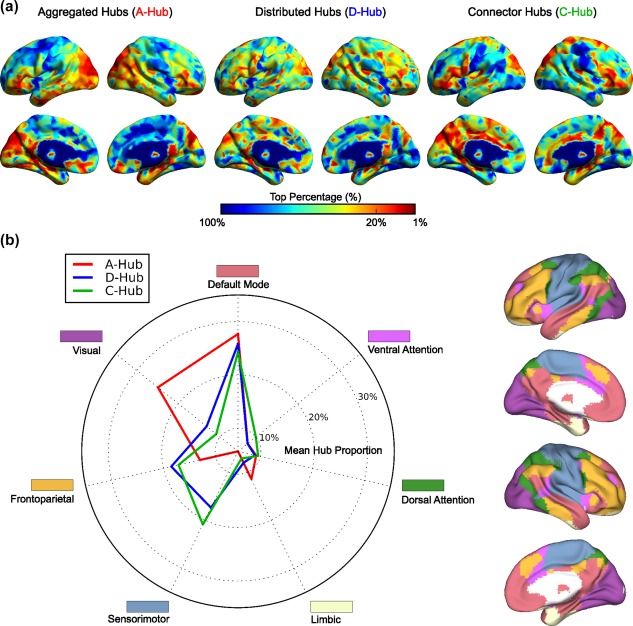
The distributions of three categories of hubs in seven functional systems. (a) The spatial distributions of group‐level hub indices mapped on a brain surface (FWHM = 2 mm). (b) The left panel describes the proportions of the three categories of hubs in seven functional systems defined by our combined R‐fMRI data. The red, blue, and green solid lines indicate aggregated, distributed and connector hubs, respectively. Each color around the radar map specifies a functional system. The right panel indicates functional systems over the brain surface, which were identified based on the group‐averaged functional network at voxel‐wise. The color index of each functional system corresponds to the color for each system of the radar map in the left panel [Color figure can be viewed at http://wileyonlinelibrary.com]

Table 2.

Detailed description of the overlapping percentages between each pair of three categorized of hubs and the hubs defined by single nodal metrics

	Sc‐Hub (%)	Kc‐Hub (%)	Ec‐Hub (%)	Cc‐Hub (%)	Pr‐Hub (%)	Bc‐Hub (%)	Dc‐Hub (%)	Pc‐Hub (%)
A‐Hub	77.2	55.3	74.1	60.2	30.4	40.0	52.4	22.2
D‐Hub	42.0	37.7	34.8	47.6	66.9	66.7	73.9	22.3
C‐Hub	18.7	22.7	19.9	29.7	17.7	28.4	21.2	100

Using a functionally defined brain parcellation (Supporting Information, Figure S2), we showed convergent and divergent spatial distributions in functional systems among the three categories of structural hubs (Figure 4); commonly identified hub nodes in all three categories were primarily located at the default‐mode system (p values < .005, Bonferroni corrected), and hub nodes were additionally identified in the visual and limbic systems for aggregated hubs, in the frontoparietal systems for distributed hubs and in the sensorimotor and ventral attention systems for connector hubs (p values < .01, Bonferroni corrected).

3.2. Miscellaneous characteristics of three categories of structural brain hubs

3.2.1. Microstructural organization and wiring cost of structural hubs

Compared with the non‐hubs, all three categories of brain hubs had significantly (p values < .001, Bonferroni corrected) larger fractional anisotropy, mean diffusivity and axial diffusivity values, smaller radial diffusivity values, longer streamline lengths and higher streamline costs, with the exception of the radial diffusivity of the connector hubs (p value = .0038, uncorrected) (Figure 5a). Among the three categories of hubs, the aggregated hubs exhibited the largest fractional anisotropy and axial diffusivity values and the longest streamline length, the distributed hubs exhibited the highest streamline cost, and the connector hubs exhibited the smallest fractional anisotropy, the smallest axial diffusivity, the largest radial diffusivity, the shortest streamline length and the lowest streamline cost (p values < .005, Bonferroni corrected, Figure 5b). These results together imply that all three categories of structural brain hubs tended to retain high‐level microstructural organization and expensive wiring costs compared to the nonhubs; however, there were significant differences in these features among the categories of hubs.

Figure 5.

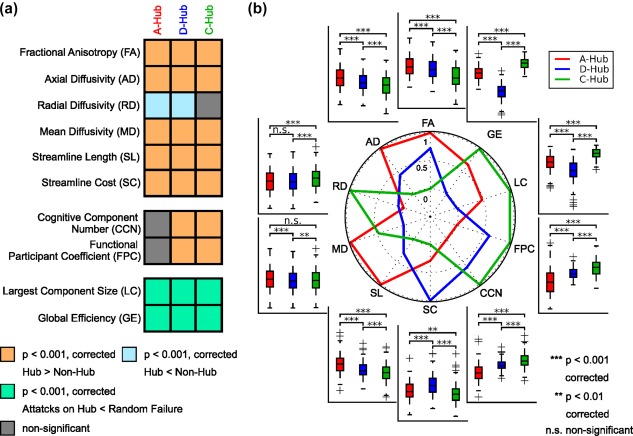
The miscellaneous characteristics of the three categories of hubs. (a) Comparisons of miscellaneous characteristics (e.g., microstructural organization, wiring cost, functional association, cognitive flexibility, and topological vulnerability) between hubs and nonhubs for each category of hubs. Bonferroni corrections were performed for each block. (b) Comparisons of these characteristics among the three categories of hubs. The radar map shows the differences in the mean characteristic indices among the three categories of hubs; for each characteristic, the mean indices of the three categories of hubs were normalized from 0 to 1, in which the minimal mean index was assigned as 0, and the maximal mean index was specified as 1. For each box plot, the bottoms and tops of the boxes indicate the first and third quartiles of the corresponding indices across individuals, the band inside the box represents the median, and the whiskers specify the 1.5 interquartile range (IQR) of the lower and upper quartiles [Color figure can be viewed at http://wileyonlinelibrary.com]

3.2.2. Functional modular integration and cognitive flexibility of structural hubs

Both the distributed hubs and the connector hubs had significantly (p values < .001, Bonferroni corrected) higher functionally defined participant coefficients and more number of cognitive components than the nonhubs; in contrast, the aggregated hubs did not have a significantly different functional participation coefficient or number of cognitive components with the nonhubs (Figure 5a). Furthermore, sorted in descending order for both the functional participant coefficient and the number of cognitive components, the hubs followed connector hubs > distributed hubs > aggregated hubs (p values < .001, Bonferroni corrected, Figure 5b). These results indicate that both distributed and connector hubs play more crucial roles in functional modular integration and contribute to greater cognitive flexibility than aggregated hubs.

3.2.3. Topological vulnerability of structural hubs

To assess the topological vulnerability of the three categories of hubs in brain networks, we performed simulation analyses in which network nodes were continuously removed in a manner of random failure or targeted attacks. As expected, the continuous attacks on all three categories of hubs had more damage on the brain network efficiency and brain network integrality than on the random failure of nodes, as indicated by the significantly lower AUC of the largest component size and global efficiency (p values < .001, Bonferroni corrected, Figures 5a and 6). Of note, targeted attacks on distributed, aggregated and connector hubs resulted in reduced network performances in a descending order when the top 20% of nodes were removed (p values < .001, Bonferroni corrected, Figures 5b and 6). Together, our results suggest that all three categories of structural hubs are critical for maintaining global communication and the topological stability of the brain networks, whereas connector hubs are the most resilient to targeted attacks compared to the other categories.

Figure 6.

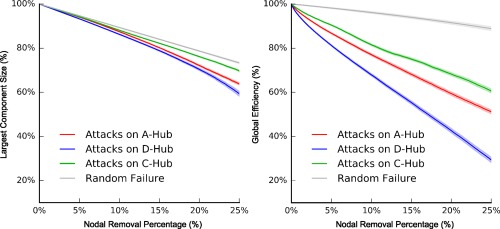
Targeted attacks on the three categories of hubs and random failure. The descending curves of the largest component size (left plot) and global efficiency (right plot) for targeted attacks of the top 25% hub indices and random failure. The red, blue, and green solid lines represent the mean curves for the targeted attacks on the aggregated, distributed, and connect hubs across individuals, respectively; the gray line represents the mean curve of random failure. The dashed areas represent the corresponding ±95% confidence intervals [Color figure can be viewed at http://wileyonlinelibrary.com]

3.2.4. Unique characteristics of three categories of hubs

We found that only a limited number of characteristics in specific surrogate combinations of nodal metrics were similar to those in the real categories of hubs (e.g., 0.71% surrogate combinations had 9 characteristics, 0.36% had 8 characteristics, 0.36% had 7 characteristics, and 2.86% had 6 characteristics). Importantly, none of the surrogate combinations of nodal metrics can produce the same characteristics results as the real categories of hubs (Supporting Information, Figure S3), which indicates the characteristics uniqueness in the three categories of structural hubs in the brain networks.

3.3. Highly reliable brain hub indices and their contributions to individual identification

3.3.1. High reliability of classification of nodal metrics and spatial distribution of hub indices

We classified eight metrics into three categories using Dataset 2 and found that the results of the metric classification from two scanning sessions were identical, suggesting that the classification of metrics and hub redefinition are highly reliable. Furthermore, the spatial distributions were similar between scanning sessions for all three category hub indices (Table 3 and Supporting Information, Figure S4), which suggests the high reliability of the spatial distribution for all three category hub indices. For each nodal metric, the spatial distributions were also highly similar between repeated scanning sessions at both individual and group levels (Table 3). Interestingly, we noticed that the aggregated hub indices defined here had significantly higher between‐session spatial similarities than the closeness centrality or K‐core centrality (p values < .001, Bonferroni corrected); moreover, the distributed hub indices had significantly higher spatial similarities than either betweenness centrality or page‐rank centrality (p values < .001, Bonferroni corrected) and lower than degree centrality (p value < .001, Bonferroni corrected).

Table 3.

Spatial similarities of three categories of hub indices and eight single nodal metrics between two repeated scanning sessions

Nodal metric name	Individual level (mean ± STD)		Group level
	Intrasubject	Intersubject
Aggregated hub index	0.767 ± 0.025	0.497 ± 0.048	0.990
Distributed hub index	0.732 ± 0.021	0.466 ± 0.027	0.988
Connector hub index	0.347 ± 0.046	0.217 ± 0.040	0.944
Subgraph centrality	0.766 ± 0.028	0.484 ± 0.054	0.990
K‐core centrality	0.693 ± 0.027	0.420 ± 0.042	0.985
Eigenvector centrality	0.774 ± 0.055	0.537 ± 0.084	0.992
Closeness centrality	0.730 ± 0.022	0.469 ± 0.036	0.987
Page‐rank centrality	0.677 ± 0.024	0.429 ± 0.028	0.984
Betweenness centrality	0.679 ± 0.023	0.433 ± 0.027	0.984
Degree centrality	0.763 ± 0.019	0.477 ± 0.030	0.989
Participant coefficient	0.347 ± 0.046	0.217 ± 0.040	0.944

Note. STD, standard deviation.

3.3.2. Hub index contributions to individual identification

We implemented individual identification for each category of hub indices. From Session 1 to Session 2, the predictive rates of subject identity reached 100%, 100%, and 89.5% for aggregated hubs, distributed hubs, and connector hubs, respectively. The similar predictive rates from Session 2 to Session 1 were 100%, 100%, and 84.2%, respectively. Notably, the intra‐subject hub index correlation coefficients were 0.767 ± 0.025 for the aggregated hub index, 0.732 ± 0.021 for the distributed hub index and 0.347 ± 0.046 for the connector hub index, respectively, which were significantly greater than the intersubject values (0.497 ± 0.048, 0.466 ± 0.027, and 0.217 ± 0.040, respectively, all p values < .001, Bonferroni corrected, Table 3 and Supporting Information, Figure S5). These findings suggest that the spatial patterns of all three category hub indices are unique across individuals and may serve as a structural fingerprint for individual identification.

3.4. Validation results

Our results were evaluated from five different aspects, which included diffusion imaging protocols and fiber reconstructing algorithms, definition of network nodes, selection of hub thresholds, consideration of isolated nodes and the modular organization for participant coefficient calculations. We determined that the results under different situations were mostly identical to the main analyses, which suggests the robustness of our findings. For more detailed results, refer to Supporting Information, Results and Figures S6–S15.

4. DISCUSSION

We defined three categories of structural brain hubs, namely aggregated, distributed, and connector hubs, with anatomically convergent and divergent spatial distributions in brain systems. Moreover, these distinct category brain hubs showed differential microstructural, functional, and cognitive associations and topological vulnerabilities. Importantly, all three categories of structural hubs retained high reliability in spatial locations and microstructural and functional characteristics across long‐term repeated scans and may act as a structural fingerprint with high predictive rates for individual identification. To our knowledge, we demonstrated for the first time three categories of structural brain hubs with different topological roles and functional significance, which highlight the organizational principles of human brain structural networks.

4.1. The classification of graph‐nodal metrics

By performing hierarchical clustering analysis, the eight commonly used nodal metrics were classified into three categories according to their spatial distributions. The first category included the subgraph centrality, K‐core centrality, eigenvector centrality and closeness centrality. Mathematically, these four metrics were designed to assess the ability of information spreading for a given node in networks: for example, the subgraph centrality of a given node captures the number of subgraphs associated with a node (Estrada and Rodriguez‐Velazquez, 2005), and it characterizes the capacity of information spreading circuits which begin from a given node and return to this node; the closeness centrality of a given node specifies the reciprocal of the averaged shortest path from this node to any other nodes in the network (Freeman, 1978), and it describes the comprehensive efficiency of information spreading from a given node to other nodes. These hubs may correspond to the “sources” or “sinks” structure that work as an input or relay station for the entire networks (Alvarez‐Hamelin, Dall'asta, Barrat, & Vespignani, 2006; Bonacich, 1972; Estrada and Rodriguez‐Velazquez, 2005; Freeman, 1978). In contrast, the second category included page‐rank centrality, betweenness centrality and degree centrality, which capture the capacities of the global and local connection integration or the position in the communication path of the networks: for example, betweenness centrality of a given node represents the number of times that this node is on the shortest path between any other two nodes in the network (Freeman, 1980), and it acts as a “bridge” between local interaction and global integration (Bullmore and Sporns, 2012). As expected, hubs of this category were evenly distributed in the networks, and work as the “router” to support information transfer at both the global and local levels (Boldi, Santini, & Vigna, 2009; Freeman, 1978; Freeman, 1980; Page, Brin, Motwani, & Winograd, 1999). Moreover, the participant coefficient quantifies the level of a node to connect with different anatomical modules, and these hubs were naturally located at the adjacent borders of the anatomical lobes, which act as a “connector” to facilitate the communication among anatomical modules underlying the functional parcellations (Guimera, Sales‐Pardo, & Amaral, 2007). Notably, the participant coefficient indicated a remarkably different spatial distribution from other seven nodal metrics, which may be because of two main reasons. First, the calculation of the participant coefficient is largely dependent on the modular organization of the network, whereas the estimations of other metrics were largely based on their connectivity patterns. Thus, the participant coefficient could be considered as a sub‐network‐level nodal metrics, which is relatively different from other nodal metrics. Second, the participant coefficient has been demonstrated to be closely associated with cognitive flexibility (Bertolero, Yeo, & D'esposito, 2015). Therefore, compared with other nodal metrics, the participant coefficient tends to be more involved in cognitive behaviors than other nodal metrics, particularly for the connector hubs. Together, each of the three categories of hub indices we identified emphasized the specifically topological centrality for a given node in the brain network.

4.2. The spatial distribution of three categories of structural hubs

The three categories of structural hubs shared common spatial distributions primarily in the default‐mode system, including the posterior cingulate cortex/precuneus, the medial prefrontal cortices and the middle temporal cortices, which is consistent with previous structural hub studies (Crossley et al., 2014; Gong et al., 2009; Hagmann et al., 2008; van den Heuvel et al., 2012, 2010; van den Heuvel and Sporns, 2013b). The default‐mode system has been proven to be a core system of the human brain network with a high cost of energy consumption (Raichle et al., 2001; Tomasi, Wang, & Volkow, 2013) and heavy regional cerebral blood flow (Liang, Zou, He, & Yang, 2013) to support highly efficient information transfer (van den Heuvel et al., 2012; Xia et al., 2016) and various cognitive processes (Buckner, Andrews‐Hanna, & Schacter, 2008; Cavanna and Trimble, 2006). Here, our results provided further evidence that the default‐mode system is the central system of structural brain networks from different topological perspectives. Intriguingly, we determined that different categories of hubs also exhibited unique distributions in several specific brain systems. For example, aggregated hubs were more located in the visual and limbic systems. The visual system is a fundamental system for capturing information from the outside environment, which lies near the bottom of the visual processing hierarchy. It provides the original signal for further processing by other functional systems, which indicates it function as a “source” structure in brain networks (Felleman and Van Essen, 1991; Maunsell and Van Essen, 1983; Yeo et al., 2011). The limbic system supports various functions, including emotion, motivation, and behavior, and by its complex anatomical connections with both the association cortex and basal ganglia, it acts as a “relay station” (Alexander, Crutcher, & DeLong, 1991; Mogenson, Jones, & Yim, 1980; Morecraft and Van Hoesen, 1998). Distributed hubs tended to be more evenly distributed in all functional systems. This even distribution characteristic may suggest their crucial roles in segregating and integrating information from separate parts of the whole‐brain networks at both the global and local levels (Bullmore and Sporns, 2009, 2012; van den Heuvel and Sporns, 2013b). Connector hubs were more significantly located in the sensorimotor and ventral attention systems than the other categories of hubs. Although the sensorimotor and ventral attention systems have their own independent functions, their anatomical locations are precisely settled on the boundaries of brain lobes (e.g., the sensorimotor system at the central sulcus and the ventral attention system in the parieto‐occipital sulcus and boundary of the cingulate/frontal cortices). Notably, the locations of the connector hubs reported in our study are consistent with a previous study (Hagmann et al., 2008). Collectively, our results demonstrated the convergence and divergence of the anatomical distributions of the three categories of hubs, which may suggest a potential topological architecture of structural networks that underlie brain functional systems.

4.3. The characteristics of the three categories of structural hubs

As expected, all three categories of hubs showed higher level of microstructural organization than non‐hubs, as indicated by the larger fractional anisotropy, mean diffusivity, and axial diffusivity values, suggesting that these hubs are associated with regular fiber architecture, greater axonal diameter, larger packing densities and higher proportions of myelinated axons in white matter (WM) tracts (Basser, 1995; Beaulieu, 2002; Collin et al., 2014). These hubs also connected with distant fiber streamlines and required greater wiring costs to build these topologically centralized hubs that facilitate communication with distant brain regions. (Collin et al., 2014; van den Heuvel et al., 2012; Xia et al., 2016). Specifically, the aggregated hubs had the highest level of microstructural organization and the longest transmission distance, which may enable them to transfer information efficiently within whole‐brain networks. The distributed hubs consumed the greatest wiring cost, which may be a result of their dispersed involvement in the integration of both global and local communication. Nevertheless, these WM traits empower all three categories of hubs to maintain fast and long‐distance communication with shorter transmission delays and larger physical consumption, which consequently facilitate synchronous information processing and increased signal transfer robustness during communication (Collin et al., 2014; Kaiser and Hilgetag, 2006; Xia et al., 2016). This phenomenon provides further experimental support for the existence of the cost‐efficient trade‐off of neural systems (Bullmore and Sporns, 2012) and suggests that the three categories of hubs are all important components in this neural circuitry formation. Moreover, all three categories of hubs, particularly the distributed hubs, had pronounced topological vulnerability as assessed by the “lesion” simulation, which suggests the core positions of all three categories of hubs in supporting the architectural organization and efficient information communication of brain structural networks (Crossley et al., 2014). Additionally, both distributed hubs and connector hubs exhibited significantly higher functionally defined participant coefficients and larger cognitive flexibility than peripheral nodes, suggesting that these two categories of structural hubs are more involved in information integration among functional modules that underlie multiple cognitive functions than aggregate hubs (Bertolero et al., 2015; He et al., 2009; Power et al., 2013; Yeo et al., 2014).

4.4. The robustness and individually uniqueness of the three categories of structural hubs

We demonstrated that the spatial distributions were significantly similar between scanning sessions for all three categories of hub indices, indicating that the existence of three categories of hubs was not induced by “artifacts” and the three categories of hub indices are useful in reflecting the organizational characteristics of structural human brain networks. More importantly, our results showed that the intrasubject individual variability of all three categories of hub indices are relatively smaller than the intersubject variability, and they may serve as the connectome fingerprints for accurate subject identification from one another (Finn et al., 2015). This finding suggests that the pattern of the three categories of hubs in the structural network is unique for each individual, which may be a crucial connectome basis for exploring the variance in individual behavior and implementing personalized medicine for neuropsychiatric illnesses (Finn et al., 2015; Li et al., 2009; van den Heuvel, Stam, Kahn, & Hulshoff Pol, 2009).

5. LIMITATIONS AND FURTHER CONSIDERATIONS

There are several issues that warrant further considerations. First, we demonstrated that our main findings are reliable under different methodological choices, including imaging protocols, fiber reconstructing algorithms, and hub selective thresholds. Nevertheless, with the growth of neuroimaging techniques, newly developed methods, such as diffusion spectrum imaging (Wedeen et al., 2008), may be taken into account in the future. Second, previous studies have suggested that finer parcellations enable the capture of both major tracts and forking U‐fibers in a structural brain network, which may thus better reflect accurate network topologies than coarser ones (Zalesky et al., 2010). In this study, we found that the anatomical overlap across different hub definitions are reproducible regardless of the resolution or generating methods of the brain parcellations (Glasser et al., 2016; Zalesky et al., 2010), which implies the stable multiple roles in contributing to the network topologies of these overlapped regions. Future studies that employ brain parcellation generated with multiple biological or cognitive information may further elucidate and clarify the roles of different brain hubs. Third, our analyses were performed based on structural brain networks constructed from diffusion MRI data, which disabled exploration in the directions of the fiber tracks, thus resulting in the inability to map information flow in the structural brain networks. Future studies that are established using more advanced imaging techniques or data from postmortem brains (Amunts et al., 2013) may provide opportunities to deepen our understanding of the directed topologies of the three categories of hubs. Fourth, we adopted WM diffusion indices to estimate the microstructural organization of the structural hubs in the current study; however, the accurate biophysical interpretation of these indices remains to be further clarified (Jones, Knösche, & Turner, 2013). Future studies that combine biophysical data from microscale cytoarchitectonics (Scholtens, Schmidt, de Reus, & van den Heuvel, 2014), myeloarchitectonics (Van Essen et al., 2012), chemoarchitectonics (Turk, Scholtens, & van den Heuvel, 2016), and the metabolic level (Collin et al., 2014; Liang et al., 2013) may better explain the association between the structural connectome and its material substrates. Moreover, in this study we used the cognitive flexibility (Yeo et al., 2014) derived from reported task activation peaks in BrainMap (Fox and Lancaster, 2002) to investigate the functional roles of hubs at the task‐involved level. As a complementary, we also adopted the functional modular integration (He et al., 2009; Power et al., 2013) based on the resting‐state data we collected to examine the functional roles of structural hubs at the resting‐state level. Both measures may be considered as general reflections of the functional importance, thus providing evidence of the functional roles of the hubs. Future studies that combine task fMRI and dMRI data are valuable to investigate the roles of different structure hubs under specific functional status. Finally, previous studies have suggested a strong nexus between brain hubs and neuropsychiatric disorders (Crossley et al., 2014), and our “lesion” simulation also demonstrated a relatively different effect on attacking different categories of structural hubs. Future studies using data that correspond to disease states are desirable to ascertain the specific associations among distinct categories of hubs and brain disorders, which would extend our insight into the pathologies of neuropsychiatric disorders, and in turn, enable a better understanding of the biological meaning of the diverse topology of different brain hubs.

DISCLOSURES

The authors have no conflict of interest to declare.

Supporting information

Additional Supporting Information may be found online in the supporting information tab for this article.

Supporting Information

Wang X, Lin Q, Xia M, He Y. Differentially categorized structural brain hubs are involved in different microstructural, functional, and cognitive characteristics and contribute to individual identification. Hum Brain Mapp. 2018;39:1647–1663. 10.1002/hbm.23941