Identifying topological motif patterns of human brain functional networks

Abstract

Recent imaging connectome studies demonstrated that the human functional brain network follows an efficient small‐world topology with cohesive functional modules and highly connected hubs. However, the functional motif patterns that represent the underlying information flow remain largely unknown. Here, we investigated motif patterns within directed human functional brain networks, which were derived from resting‐state functional magnetic resonance imaging data with controlled confounding hemodynamic latencies. We found several significantly recurring motifs within the network, including the two‐node reciprocal motif and five classes of three‐node motifs. These recurring motifs were distributed in distinct patterns to support intra‐ and inter‐module functional connectivity, which also promoted integration and segregation in network organization. Moreover, the significant participation of several functional hubs in the recurring motifs exhibited their critical role in global integration. Collectively, our findings highlight the basic architecture governing brain network organization and provide insight into the information flow mechanism underlying intrinsic brain activities. Hum Brain Mapp 38:2734–2750, 2017. © 2017 Wiley Periodicals, Inc.

INTRODUCTION

The human functional brain connectome, a comprehensive map comprising neural elements and functional connectivity, has attracted considerable interests in recent decades due to its advantage in dissecting the common rule of brain functional configurations [Biswal et al., 2010]. With the implementation of noninvasive neuroimaging techniques and graph‐theory analytical approaches, the large‐scale functional brain connectome has been studied as a network that exhibits a highly efficient small‐world architecture, functional modules and densely connected hub regions [for review, see Bullmore and Sporns, 2012; Bullmore et al., 2009; He and Evans, 2010]. Despite massive findings delineating the network topology, it is noteworthy that most studies concentrate on the undirected functional network that emerged from the interregional synchronization of brain activities. The directed functional network, which essentially characterizes the information flow in intrinsic activities [Craddock et al., 2013; Friston, 2011], has been largely overlooked.

In contrast to the undirected functional network, taking into account the direction facilitates our understanding of the driven and driving architecture in the brain as well as the ectopic foci leading to pathological conditions [Craddock et al., 2013]. Using the Granger Causality analysis (GCA) [Goebel et al., 2003; Granger, 1969], a handful of studies have attempted to investigate the directed human brain functional connectome. For instance, several functional magnetic resonance imaging (fMRI) studies reported the small‐world structure, the modular division [Liao et al., 2011; Yan and He, 2011], and more interestingly, the divergence of driven and driving hub regions in the directed human brain functional network [Wu et al., 2013; Yan and He, 2011]. However, the findings of these studies might be affected by several confounding factors. For instance, the interregional hemodynamic latency confuses the time lags caused by “real” information flow in intrinsic activity [Bandettini and Wong, 1997], and the non‐linearity of brain functional systems [Friston, 2001] may go beyond the scope of GCA. Moreover, a deeper understanding on the underlying information flow patterns supporting the driven and driving architecture, which is commonly revealed by motif patterns, has yet to be elucidated.

The network motif patterns were investigated to unravel the basic building blocks in a directed network [Milo et al., 2002; Sporns and Kötter, 2004], in which a type of motif was considered to be statistically significant if they appear much more frequently than expected in random networks. In the mammalian structural cortical networks (e.g., macaques and cats) derived from tract‐tracing data, Sporns and Kötter [2004] observed a significant class of three‐node motif, a chain of two reciprocal connections in which two nodes without direct communication are highly integrated through a third node. Subsequently, Iturria‐Medina et al. [2008] identified a closed chain of three connections as a significant motif in human brain structural networks, but it was derived from diffusion MRI data in which the directions of the connections were ignored. Moreover, because the functional coordination is shaped but not limited to the underlying structural connections [Wang et al., 2015], exploring the functional motif patterns may provide direct information about the brain's functional repertoire. Recently, by simulating the neuronal dynamical activity with the neural mass model, researchers suggested that several chain‐like motifs promoted the functional synchronizations between brain regions. Meanwhile, some other loop‐like motifs enriched the metastable functional configurations [Gollo et al., 2014, 2015; Gollo and Breakspear, 2014]. Nonetheless, the empirical evidence on the functional motifs in the human brain and their contribution for brain functional organization requires further explorations.

This study aimed to investigate functional motifs in the human brain network to unravel the underlying information flow patterns. Two fMRI datasets of 10 healthy subjects, including the breath‐holding (BH) task‐related fMRI data (T‐fMRI) and the resting‐state fMRI (R‐fMRI) data were used. The BH T‐fMRI data were used to estimate the regional hemodynamic latencies of the vascular responses, which were corrected during the preprocessing of R‐fMRI data [Chang et al., 2008; Cohen et al., 2004; Thomason et al., 2005, 2007]. The R‐fMRI data were used to reconstruct the directed functional brain networks based on the convergent cross mapping (CCM) approach that extends the coverage of GCA [Sugihara et al., 2012]. With the resultant network, the significantly recurred motifs were identified and the motif distribution patterns were elaborately analyzed in line with the modular architecture and hubs. Through these analyses, we will address the following questions: (i) which types of network motifs appear in the directed functional networks of the human brain and how are they distributed in the whole network, and (ii) how these specific network motifs topologically contribute to the brain's intrinsic activity in modular (e.g., intra‐ and inter‐module connections) and nodal (e.g., network hubs) architectures.

MATERIALS AND METHODS

Participants

The multiband functional imaging data used in this study came from a publicly released dataset from INDI (http://fcon_1000.projects.nitrc.org/indi/pro/eNKI_RS_TRT/FrontPage.html). This dataset consists of multi‐modal imaging data from 24 participants (ages: 19–60 years, 34.4 ± 12.9 years, 18 males) who underwent a deep phenotyping protocol. Recently, this dataset was used to examine the test‐retest reliability of regional functional homogeneity [Zuo et al., 2013] and functional brain hubs [Liao et al., 2013]. Notably, in the present study, the data of 14 participants were excluded from the analyses due to current/historical psychiatric disorders (n = 7), a lack of diagnostic information (n = 4), obvious brain atrophy (n = 1), excessive unknown volume in the BH T‐fMRI data (n = 1) and excessive head motion (n = 1). The remaining data from 10 participants (age: 19–48 years, 30.5 ± 10.1 years, 6 males) were used for further analysis. The demographic information of participants was illustrated in Supporting Information Table S1.

Experimental Design

For each participant, two R‐fMRI scans approximately one week apart and a BH T‐fMRI scan were acquired. During the R‐fMRI scans, participants were instructed to look at the fixation cross, but not to stare or strain their eyes. During the T‐fMRI scan obtained one day after the first R‐fMRI scan, participants were asked to perform a block‐designed BH task with seven repetitions of the blocks. In each block, participants were first instructed to breath according to the text sequentially presented on the screen, including “Rest” for 10 s, “Get ready” for 2 s, “Breath in” for 2 s, “Breath out” for 2 s, and “Deep breath and hold” for 2 s. Then participants held their breath for 18 s under the instruction of a circle decreasing in size on the screen, which indicated the remaining time for BH (Supporting Information Fig. S1). The task started at 8.4 s (i.e., the 6th volume) during the scan and lasted for 259 s.

Data Acquisition

Functional imaging data were collected on a Siemens Trio 3.0 T scanner using the multiband protocol with the following parameters: repetition time (TR) = 1,400 ms; echo time (TE) = 30 ms; flip angle 65°; numbers of slices= 64; multi‐band accelerate factor = 4; matrix = 112 × 112; field of view = 224 × 224 mm²; and voxel size = 2 × 2 × 2 mm³. The scanning protocol was the same for the R‐fMRI scans and the BH T‐fMRI scans, which lasted for 565.6 s (i.e., 404 volumes) and 260.4 s (i.e., 186 volumes), respectively. Notably, the last volume (i.e., the 404th volume for the R‐fMRI scan and the 186th volume for the T‐fMRI scan) was missing in three subjects due to malfunction in the temporary storage transfer protocol. We thus removed the last volumes of the other subjects to ensure the same scan lengths were used across all participants. As a result, for each participant, the R‐fMRI data included 403 volumes and the BH T‐fMRI data included 185 volumes.

Data Preprocessing and Analysis

Estimating hemodynamic latency using BH T‐fMRI

Previous studies have suggested that the BOLD signal reflects both the neuronal activities and vascular responses [Bandettini et al., 1992; Kwong et al., 1992; Logothetis et al., 2001; Ogawa et al., 1992], and the latter could affect the estimation of interregional neural causality [Chang et al., 2008]. In this study, we utilized a BH T‐fMRI data to estimate the individual voxel‐wise hemodynamic latency according to the procedures suggested by Chang et al. [2008]. These processes were performed using the Statistical Parametric Mapping (SPM8, http://www.fil.ion.ucl.ac.uk/spm). Briefly, the first 31 volumes of the BH task, including the 5 volumes for preparing and 26 volumes of the first task block, were first discarded due to the MRI signal equilibrium and the adaptation of subjects to the task. The remaining T‐fMRI data were preprocessed by performing the correction for head motion using imaging alignment, co‐registering to corresponding mean R‐fMRI images using linear transformation and removing linear trends using regression analysis. Second, a canonical BH regressor was defined by convolving the binary waveform of the BH task (which consisted of values of 1 during the BH period and 0s elsewhere) with a sign‐reversed canonical HRF [Chang et al., 2008; Glover, 1999]. This canonical BH regressor was theoretically an inference of the BOLD signals resulting from the BH task. We further defined a relative reference time series y(t) by averaging the time series across voxels that exhibited correlations of r > 0.25 with the canonical BH regressor [Chang et al., 2008]. This subject‐specific reference time series y(t) allowed us to identify the relative latency across voxels and simultaneously take into account the individual variations of the BH task response. Finally, the voxel‐wise hemodynamic latency was assessed in terms of time‐lag τ, which yielded the maximum correlation, R _max, between the time‐shifted time series x_i(t + τ) of voxel i and the reference time series y(t) (i.e., latency = argmax_τ (corr(x_i(t + τ), y(t))). The metric of τ was permitted at a range from −4.2 to 4.2 s at the step of one TR (i.e., 1.4 s) to cover an appropriate range of the realistic delay time [Chang et al., 2008]. We also validated our results with a different τ range (e.g., −16.8 to 16.8 s), which represented the whole length of the block in the experiment (see Validation analyses). As a result, we obtained the individual latency τ maps and the corresponding R _max maps in the whole brain for native spaces. Those voxels, which had significant R _max (q < 0.05, False Discovery Rate [FDR] corrected) with a non‐zero latency τ, were labeled for further hemodynamic latency correction in corresponding R‐fMRI data.

Data preprocessing of R‐fMRI

The R‐fMRI data were preprocessed using SPM8 and the Data Processing Assistant for Resting‐State fMRI [Yan and Zang, 2010]. Briefly, the first 14 volumes were discarded to allow for signal equilibrium and adaptation of the participants to the circumstances. The remaining data were realigned to the first volume to correct for head motion and were then spatially smoothed with a Gaussian kernel with a 4 mm full width at half‐maximum followed by removal of linear trends. Notably, data were excluded from analysis if they reached the head motion exclusion criterion (displacement > 3 mm or rotation > 3°). To correct for hemodynamic latency, we shifted the time series of those voxels with significant hemodynamic latency effects along the time axis according to their latency values (τ) estimated from previous BH T‐fMRI data for each participant. Notably, to ensure the same length of time series across all voxels, we selected the common parts (i.e., the 13th–377th time points) on the time axis of all the shifted time series for analysis. Finally, the resulting data were normalized to the Montreal Neurological Institute (MNI) space and were resampled to 3‐mm isotropic voxels. Several nuisance signals were regressed out, including six head motion parameters, cerebrospinal fluid, white matter, and global signals. The time series were not further temporally filtered because the inter‐regional causality inference uses the low‐lag orders that operate on high‐frequency deflections [Hamilton et al., 2011].

Constructing Directed Functional Brain Networks Using R‐fMRI

To construct directed functional brain networks using R‐fMRI data, we first defined the networks nodes as 160 regions of interests (ROIs) with diameters of 10 mm over the whole brain according to a functional template derived from meta‐analysis of T‐fMRI paradigms [Dosenbach et al., 2010]. Two regional parcellation templates were additionally used for validation purposes, including the anatomical automatic labeling (AAL) atlas template [Tzourio‐Mazoyer et al., 2002] and the functional 264 ROIs template [Power et al., 2011] (see Validation analyses). The mean time series of each ROI was then extracted by averaging the time series of all the voxels within the ROI. The directed functional connections among any pairs of ROIs were estimated by computing the causations of the mean time series using a novel CCM approach developed by Sugihara et al. [2012].

Comparing to the traditional causality algorithms (e.g., Granger causality approach), CCM has better applicability in the non‐separable dynamic system in which the information about a causative variable cannot be removed simply by eliminating that variable from the system. This approach better identifies weak to moderate coupling between variables [Sugihara et al., 2012]. Briefly, CCM assesses the causation by measuring the extent to which one variable could estimate the state of the other from historical records. The larger the extent is, the stronger the causality is. To measure whether the variable X (i.e., [x(t)]) is causally influencing variable Y (i.e., [y(t)]), the phase‐shifted space M_X and M_Y were reconstructed by taking the time‐lagged X and Y values as coordinates in the reconstructed space (E dimensions in total, i.e., reconstructed variables x(t) = [x(t‐T), x(t‐2T), …, x(t‐(E‐1)T)] in M_X, and y(t) = [y(t‐T), y(t‐2T), …, y(t‐(E‐1)T)] in M_Y, here T is the unit of lags). If causality exists, the value of X could be estimated from M_Y by projecting the nearest E + 1 neighbors (defined by the shortest Euclidean distances) of each point y(t) in M_Y to x(t) in M_X. In other words, there will be a convergence between X|M_Y and the real X. The dimension E of reconstruction space was preset as E = 3 here because the ratio of false neighbors [Kennel et al., 1992] was decreased to a minimum for most of the ROIs at this dimension size, and the time unit of T was chosen as one TR for the best time resolution. We also used larger E (e.g., E = 5, 7, 9, and 11) to examine whether E = 3 was sufficient to reliably provide causality measurements (see Supporting Information). Then the causality coefficient from X to Y was assessed using the correlation coefficient between the estimated time series and the real time series (i.e., X|M_Y and X), which quantified the extent of convergence. Finally, for each participant we obtained the individual causality coefficient matrix by identifying causality coefficients between any pairs of ROIs. Notably, the applicability of CCM is associated with the length of time series, as a higher predictability could be achieved by a longer time series length [Sugihara et al., 2012]. Thus, we conducted reliability analyses for CCM on different lengths of time series, using both the simulated data and the real fMRI data (see Supporting Information).

In the current study, we constructed directed functional brain networks at both the individual‐ and group‐level. To obtain the individual‐level networks, the causality coefficient matrix for each subject was transformed into a binary matrix by thresholding the coefficients with a corrected significance level q < 0.01 (FDR correction). For the group‐level analysis, the individual causality coefficient matrices were first transformed by Fisher's r‐to‐z transformation and further averaged across subjects. The averaged coefficient matrix was further thresholded into a binary matrix at a density of 18.5%, which corresponded to the average density of individual binary networks. The resultant binary causality matrix was considered to be the group‐level network. We also assessed the effects of different thresholds on our main findings (see Validation analyses). We performed all of the following network analyses on the group‐level networks and validated the main results in each of the individual‐level networks.

Network Topology Analysis

Before investigating the basic motif patterns, several network metrics were estimated to assess the topological organization of the directed functional brain networks, including the small‐world architecture, modular structure, and hubs. First, the small‐world attributes include the clustering coefficient (C _p) and the characteristic path length (L _p) [Fagiolo, 2007; Newman, 2003; Watts and Strogatz, 1998]. Their normalized versions obtained by comparing to 100 random networks that preserve the same nodes, edges, and in‐degree and out‐degree distributions as the real network [Maslov and Sneppen, 2002] (i.e., γ = C _p / $C_{\mathrm{p}}^{\text{rand}}$ and λ = L _p / $L_{\mathrm{p}}^{\text{rand}}$, respectively), were used to determine the small‐worldness (σ = γ/λ). Typically, a network will be considered small‐world only if γ ≫ 1, λ ≈ 1, and σ ≫ 1. Second, the modular structure was identified by optimizing the modularity, Q, for different partitions of the network using the algorithm derived from Leicht and Newman [2008]. The partition that corresponds to the maximum Q was regarded as the optimal modular structure. Third, hub regions of the brain network were defined according to the total‐degree (i.e., the total number of in‐coming edges and out‐going edges). Those nodes with total‐degree values of at least one standard deviation (SD) greater than the average total‐degree of the network (i.e., $k_i^{\text{total}}$ > mean( $k_i^{\text{total}}$) + std( $k_i^{\text{total}}$)) were identified as brain hubs. The detected modules and hubs were further used to investigate the participation of motif in the sub‐network and local scales. Most of the calculations were performed using the Brain Connectivity Toolbox [Rubinov and Sporns, 2010] (https://sites.google.com/site/bctnet/Home) and the visualization was performed using the BrainNet Viewer (http://www.nitrc.org/projects/bnv/) [Xia et al., 2013].

Identification and Analysis of Network Motifs

Within a network, a motif is a small local graph consisting of M nodes and a set of edges linking them [Milo et al., 2002; Sporns and Kötter, 2004]. Given a specific motif size M, the amount of motif classes was constant. For instance, when M = 2, 3, 4, and 5, there are 2, 13, 196, and 9,364 classes of motifs, respectively. In the present study, we considered the motifs for M = 2, including the unidirectional motif and the reciprocal motifs, and M = 3, including 13 classes labeled as ID 1 to 13 that were identical to the network motifs detected in the mammalian brains [Sporns and Kötter, 2004] (Fig. 1).

Figure 1.

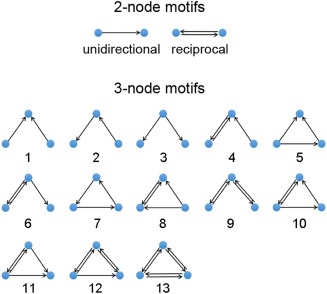
Schematic of the two‐node and three‐node motifs. The two‐node motifs include the unidirectional motif and the reciprocal motif. The three‐node motifs include 13 classes motifs labeled ID 1 to 13. [Color figure can be viewed at http://wileyonlinelibrary.com]

Network motif patterns at the overall level

Initially, we obtained the motif frequency spectrum by counting the occurrence frequency for each class of two‐node motifs and three‐node motifs within the network. Then, we compared the resulting frequency spectrum to those in 100 surrogate random networks, which conserved the same number of nodes and edges, and the same in‐degree and out‐degree distributions [Maslov and Sneppen, 2002]. Considering the class i motif, its statistical occurrence was presented by Z scores:

$$Z_i= \frac{N_i^{\mathrm{r}\mathrm{e}\mathrm{a}\mathrm{l}}- <N_i^{\mathrm{r}\mathrm{a}\mathrm{n}\mathrm{d}}>}{\mathrm{s}\mathrm{t}\mathrm{d}\left(N_i^{\mathrm{r}\mathrm{a}\mathrm{n}\mathrm{d}}\right)}$$

where $N_i^{\text{real}}$ is the occurrence frequency of motif i in real network, and < $N_i^{\text{rand}}$> and std() denote the average value and the SD of its occurrence frequencies in the 100 surrogate random networks. In the present study, the motif i was defined as statistically significant only if Z_i > 1.96 (P < 0.05). Those significant motifs represented the most basic building blocks within the directed functional brain networks. Moreover, to strictly control the effects of network density on unidirectional and reciprocal edges, stringent random surrogates were additionally used for calculating the profile of three‐node motifs. The stringent random surrogates conserved the same number of nodes and edges, and the same in‐degree and out‐degree distributions, as well as the number of unidirectional and reciprocal edges. Z scores were recalculated and motif classes with Z scores > 1.96 were considered to be statistically significant.

Moreover, for the two‐node motifs, we examined their frequency and occurrence significance at different Euclidean distance ranges to explore the wiring cost of motifs. For the three‐node motifs, to study the linkage of motif patterns between human brain and macaque cortex, we further evaluated the significant profile (SP) scores that enabled us to compare the motif frequency spectrum across networks with different sizes [Milo et al., 2004]. For each class of motifs, the SP was calculated by normalizing the Z scores as follows,

$${\mathrm{S}\mathrm{P}}_i= \frac{Z_i}{\sqrt[2]{{\sum }_{i=1}^K{Z}_i^2}}$$

where K is the total class number of three‐node motifs. Then, we calculated the Pearson correlation coefficient of SP profiles between the present network and two other prior cortical networks of the macaque cortex and macaque visual cortex, which were downloaded from https://sites.google.com/site/bctnet/datasets.

Motif analysis at the modular scale

To unravel the intra‐ and inter‐module information flow patterns, we investigated the distributions of the two‐node and three‐node motifs on the basis of previous detected modular structure. Similar to the above analyses, we first calculated the frequency spectrum of the motifs within each module as well as between each pairs of modules. Notably, for between‐module three‐node motifs, we only considered instances in which two nodes belonged to one module and the other node belonged to a different module. Then, to capture the characteristics of within‐ and between‐module frequency spectrum profile, each frequency spectrum was transformed to a probability spectrum by dividing the occurrence frequency of each motif class by the total number of all motifs' occurrences. For each motif class, the occurrence probability of within‐/between‐ module cases were compared to the probability at overall level through the one‐sample t‐test. The motif class demonstrated an increase significantly higher than the overall level (P < 0.05) was considered to contribute more to within‐ or between‐ module information coordination. Moreover, to identify significant motif class for each within‐ and between‐module case, we also estimated the Z score value for the occurrence probability of each motif class by comparing to 100 surrogate random networks, which were assigned the same modular partition as the real network. A motif class was defined as significant if the corresponding Z > 1.96 (P < 0.05).

Motif analysis at the nodal scale

We further explored how nodes participated in different classes of motifs to illustrate the major information flow patterns they were involved in. Similar to the motif frequency spectrum, we obtained the motif fingerprint of each node defined as the participation number of the node in each class of two‐node and three‐node motifs [Sporns and Kötter, 2004]. The motif fingerprint for each node was also transferred to Z scores by a comparison with 100 surrogate random networks. For each node, the motif class with Z > 1.96 (P < 0.05) was considered to be statistically significant. Moreover, we investigated if brain hubs possess the central role in network motifs. For those mostly identifying significant chain‐like motifs (ID = 4, 6, and 9), we computed the Pearson correlation coefficient between the total‐degree and the apex ratio, which was a fraction of the medium apex locations out of all instances of the motif that node participated in. A higher correlation coefficient indicated that the hub regions located in the medium apex acted as an “information transfer station.”

Validation Analyses

To examine the reproducibility of our main findings, we performed the validations following three procedures. We first validated whether the topological properties (e.g., small‐worldness) and the significantly recurring motif classes, were consistently observed in each individual network. Second, we also repeated the analysis of the group‐level whole‐brain motif patterns in the R‐fMRI data of the second session scanned approximately one week apart. Third, we assessed the effects of different preprocessing/analysis strategies. Briefly, we analyzed the small‐world architecture and identified the recurring network motifs within the whole brain in the group‐level network considering the following cases: (i) Head motion. Previous studies suggest that head motion may introduce systematic artificial differences in the R‐fMRI measurements, the influence of which cannot be eliminated by regressing out six head motion parameters [Yan et al., 2013]. Thus, prior to the step of shifting the hemodynamic latencies, we performed data scrubbing in the preprocessing steps by replacing the “bad” volumes with FD > 0.2 mm and their 1 back and 2 forward neighbors by linear interpolation [Power et al., 2014; Yan et al., 2013]. (ii) Hemodynamic latency ranges. In the main analysis, the permitted hemodynamic latency range used in the BH data analysis was set as ± 4.2 s, which might not cover the actual range for all voxels. Therefore, we alternatively chose a hemodynamic latency range of ±16.8 s that covered the whole block period in the BH task. (iii) Network density. Different densities of the network can lead to different numbers of edges and can thus affect the topological properties. We therefore constructed the group‐level network using additional density thresholds, including 10% and 25%. (iv) Node definition. Previous studies have demonstrated that different node definitions could influence the topological metrics of the functional brain networks [Fornito et al., 2010; Wang et al., 2010]. In this study, we re‐performed the motif analysis in group networks constructed from two additional parcellation templates, including the AAL atlas template of 90 cerebral ROIs [Tzourio‐Mazoyer et al., 2002] and the functional template of 264 ROIs [Power et al., 2011].

RESULTS

To unravel the network motif patterns, we first constructed the directed functional brain network based on the hemodynamic latency corrected R‐fMRI images. Then, we demonstrated the motif distributions of the resultant directed networks and the motifs' relation to the modular‐ and nodal‐scale architecture. Notably, given the compatible results between the individual‐ and group‐level networks, we mainly reported the findings from the group‐level network, with key results from the individual‐level networks included in Validation results.

Construction of Directed Functional Brain Networks

Spatial maps of hemodynamic response latency

To correct the potential latencies of vascular responses in the R‐fMRI data, the voxel‐based latency was first estimated using the BH T‐fMRI data. Under the block‐designed BH task (Supporting Information Fig. S1), we observed that the τ‐shifted BOLD signals of a large portion of brain voxels (77.3% ± 4.3%, mean ± SD across subjects) exhibited significant correlation (R _max) with the individual BH task reference time series y(t) (q < 0.05, FDR correction), which indicate that the BH task significantly modulated the cerebral blood flow in widespread brain areas during the scan. For each significant voxel, the shifted τ that corresponded to the significant R _max was regarded as the relative vascular response latency in the voxel (see Fig. 2A for the latency map of a representative subject). Notably, for each subject, we found that a large number of voxels in the whole brain exhibited non‐zero latencies (i.e., 50.7% ± 5.9%) (Fig. 2B), suggesting the necessity of hemodynamic latency correction for these voxels, which were mainly located in the precuneus, the angular gyrus, the precentral gyrus, the occipital lobe, and the cerebellum (Fig. 2C).

Figure 2.

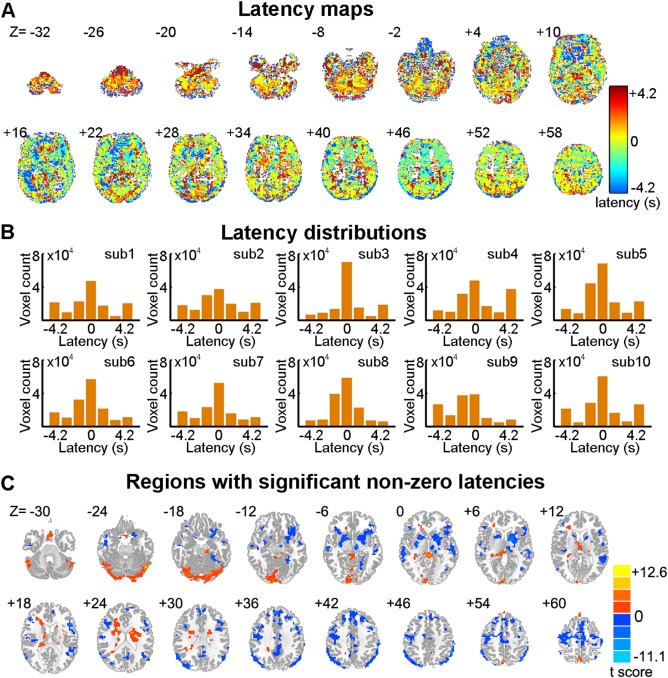
Voxel‐wise hemodynamic latency maps. (A) Voxel‐wise hemodynamic latency map of a representative participant (ID = 2475376). (B) Histograms of voxel‐wise latency values across the brain for each participant. (C) Brain regions with significant hemodynamic latency. The statistical map of latencies was obtained by performing the one‐sample t‐test on τ maps across subjects. The statistical threshold was set at P < 0.05, cluster size > 13,662 mm³, corresponding to a corrected P < 0.05 using Gaussian random field (GRF) correction. The numbers above the brain images in (A) and (C) indicate Z coordinates in the MNI space. [Color figure can be viewed at http://wileyonlinelibrary.com]

Topological properties of the directed functional brain network

The directed functional brain networks were constructed from R‐fMRI data after hemodynamic latency correction. A template comprising 160 ROIs derived from prior meta‐analyses of T‐fMRI paradigms [Dosenbach et al., 2010] was used to define nodes and the causality coefficient between any pairs of nodes were identified as functional connectivities using a novel CCM approach [Sugihara et al., 2012]. The resulting group‐level directed network exhibited small‐world architecture (σ = 1.56) with higher local clustering (γ = 1.61) and similar characteristic path lengths (λ = 1.03) compared to surrogate random networks. Meanwhile, four modules, including the sensory‐motor network (SM), visual network and cerebellum, as well as a large module containing 76 brain regions were identified in the brain network (Q = 0.34). Considering the inappropriate size, the large module was further divided into three sub‐modules, including the anterior default mode network (aDMN), the posterior default mode network (pDMN), and frontal‐parietal network (FP) by performing module detection within the module (Q = 0.19) (Fig. 3A).

Figure 3.

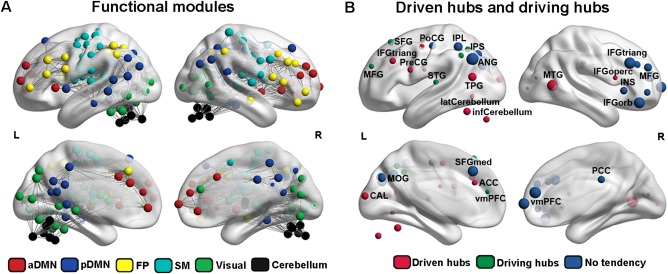
Modular architecture and functional brain hubs. (A) Six modules were identified totally, including aDMN (red), pDMN (blue), FP (yellow), SM (cyan), visual (green), and cerebellum (black). (B) Twenty‐eight functional hubs detected through the total‐degree. According to degree of in‐coming or out‐going connections, these hubs were further classified into driven hubs (red; in‐degree > out‐degree), driving hubs (green; in‐degree > out‐degree), and hubs with no tendency (blue; in‐degree = out‐degree). aDMN, anterior default mode network; pDMN, posterior default mode network; FP, frontal‐parietal network; SM, sensory motor network. [Color figure can be viewed at http://wileyonlinelibrary.com]

Several regions were identified as hubs with high total‐degree, which were mainly located in the parietal and prefrontal lobes (Fig. 3B and Supporting Information Table S2). Notably, some of these hubs participated in an imbalanced number of in‐coming and out‐going connections. For instance, hubs in the prefrontal cortex, angular gyrus, occipital lobe, and cerebellum had more in‐coming connections, whereas those in the anterior cingulate cortex and inferior parietal lobe had more out‐going connections.

Two‐Node Motif Patterns in the Brain Functional Network

Within the whole‐brain

Two classes of two‐node motifs, including the unidirectional motif and the reciprocal motif (Fig. 1), were first investigated within the whole brain. The group‐level directed network had a similar number of the two classes of two‐node motifs (i.e., 1,573 unidirectional and 1,568 reciprocal motifs). However, the reciprocal motifs appeared much more compared to motifs in the surrogate random networks (Z = 61.8), which suggested there is a significant reciprocal information transformation in the human brain. Considering the effects of spatial distance, we found distinct distributions for these two motifs. The distribution profile of the unidirectional motifs seemed to be an inverse “U,” with a large number of instances around a moderate distance (40 mm < d < 120 mm, Fig. 4A). In contrast, the number of reciprocal motifs decreased with increasing distance and was significantly larger in most ranges (10–140 mm, Z > 1.96), especially for the short distance ranges (10–40 mm, Z > 20) compared to the random networks. The proportion of unidirectional motifs obviously increased with the increasing distance. These results indicated that the brain regions typically communicate more via the reciprocal motif, especially between regions within a short distance.

Figure 4.

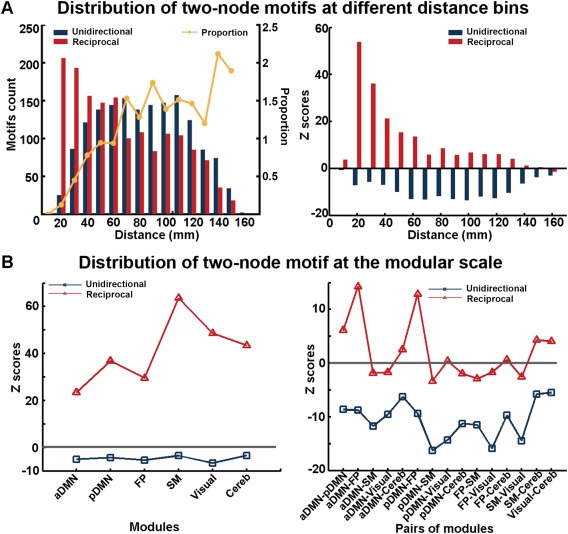
Pattern of two‐node motifs within the directed functional brain network. (A) Frequency distribution of the unidirectional motif and the reciprocal motif in different distance bins (left) and the corresponding Z score values (right). The z‐score values were obtained by a comparison with 100 random networks (right). (B) Significance for the occurrence of the two classes of two‐node motifs within each module (left) and between each pair of modules (right). The Z score values were obtained by comparing to 100 surrogate networks with the same modules. [Color figure can be viewed at http://wileyonlinelibrary.com]

Modular scale

Regarding the two‐node motif within the functional module, we found that the reciprocal motifs appeared much more often than the unidirectional motifs within each module (T _{( df = 5)} = 5.66, P < 0.01, paired t‐test across all 6 modules). Meanwhile, for each module, the number of reciprocal motifs was significantly larger than the motifs in the surrogate random networks (all Z > 1.96, P < 0.05) (Fig. 4B). In contrast, there were more unidirectional motifs than reciprocal motifs between the modules (T _{( df = 14)} = 4.57, P < 0.01, paired t‐test across all 15 possible module pairs). However, when compared to surrogate random networks, the unidirectional motif did not occur significantly, whereas a larger number of reciprocal motifs significantly occurred between the SM and the cerebellum, the visual network and the cerebellum, and among aDMN, pDMN and FP. Together, these results suggested there was a distinct contribution made by the unidirectional and reciprocal motifs in the within‐module and between‐modules communication of the human brain.

Nodal scale

We found that the network node had an unbiased tendency to involve in either the unidirectional motif or the reciprocal motif (T _{( df = 159)} = −0.10. P = 0.92, paired two‐sample t‐test across all 160 nodes). However, when compared to the surrogate random networks, all nodes were significantly more likely to participate in the reciprocal motif (all Zs > 1.96, Ps < 0.05), which indicated there was a significant occurrence of the reciprocal motif at the nodal scale.

Three‐Node Motif Patterns in the Brain Functional Network

Within the whole‐brain

We further examined distribution patterns of 13 classes of three‐node motifs, which were identical to network motifs detected in mammalian brains [Sporns and Kötter, 2004] (Fig. 1). The frequency spectrum of three‐node motifs in the directed functional brain network is shown in Figure 5A. Compared with the matched random networks (Fig. 5B), five classes of motifs were identified with significantly greater frequencies (Z > 1.96, P < 0.05), including motifs with ID = 4, 6, 9, 12, and 13 (Fig. 5C). Furthermore, different from the simple random surrogates, chain‐like motifs with bidirectional edges (ID = 4, 6, and 9) occurred more frequently in the stringent random surrogates (Fig. 5D). The loop‐like motifs with bidirectional edges (ID = 8, 10, 11, 12, and 13) were significantly more in the human brain networks as compared to these stringent random surrogates (Fig. 5E). For both random surrogates, the SP profile of the human brain functional network was significantly correlated with those of the visual cortex network (r = 0.97 and 0.90, P < 0.001) and the cerebral cortex network (r = 0.94 and 0.85, P < 0.001) in macaques, implying a similar constructive rule for the organization of the brain network during evolution (Fig. 5D,E).

Figure 5.

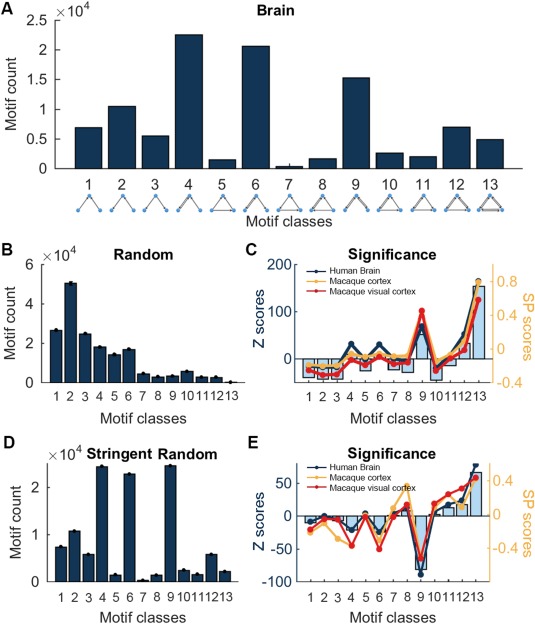
Patterns of three‐node motifs within the whole brain. (A) Frequency spectrum of 13 classes of three‐node motifs in the whole human brain. (B) Frequency spectrum of three‐node motifs in surrogate random networks conserving the same in/out degree distribution. (C) Significance of the occurrence for three‐node motifs comparing to random networks (left Y axis) and SP curves in networks from human brain (red), macaque visual cortex (blue), and macaque cortex (yellow) (right Y axis). (D) Frequency spectrum of three‐node motifs in stringent surrogate random networks conserving the same number of unidirectional/reciprocal edges. (E) Significance of the occurrence of motifs comparing to stringent surrogate random networks (left Y axis) and the corresponding SP curves for three brain networks (right Y axis). The macaque cortex networks were downloaded from https://sites.google.com/site/bctnet/datasets. [Color figure can be viewed at http://wileyonlinelibrary.com]

Modular scale

We observed that the occurrence probability spectrums of three‐node motifs within each module exhibited similar profiles, with motifs ID = 4, 6, 9, 12, and 13 appearing more often than other classes of motifs on visual inspection (Fig. 6A, left). Compared to the overall occurrence probability, the probabilities of motifs ID = 9, 12, and 13 within the modules were significantly higher (all Ts _{( df = 5 )} > 2.99, Ps < 0.02). For all six modules, the five classes of motifs ID = 4, 6, 9, 12, and 13 also appeared significantly more frequently than those in random networks (all Zs > 1.96, Ps < 0.05), in which the motif ID = 9, 12, and 13 were the most significant (all Zs > 20) (Fig. 6A, right). The results suggested there were dominant bidirectional or looping communication patterns within the functional modules. In addition, although the between‐module occurrence probability spectrums of the three‐node motifs also exhibited similar profiles by visual inspection, motifs ID = 4, 6, and 9 exhibited higher probabilities (all Ts _{( df = 14 )} > 1.95, Ps < 0.04) compared to the overall level (Fig. 6B, left). In contrast to random networks, the five classes of motifs ID = 4, 6, 9, 12, and 13 also significantly occurred in most between‐module cases (Z > 1.96, P < 0.05), with motif ID = 9 occurring at a significantly highest frequency (all Zs > 10) (Fig. 6B, right). Most of these within‐ and between‐motifs patterns remained significant occurrence when comparing to the stringent random networks, especially for ID = 9, 12, and 13 (Supporting Information Fig. S2). These results indicated the prevailing chain‐like communication configurations between functional modules.

Figure 6.

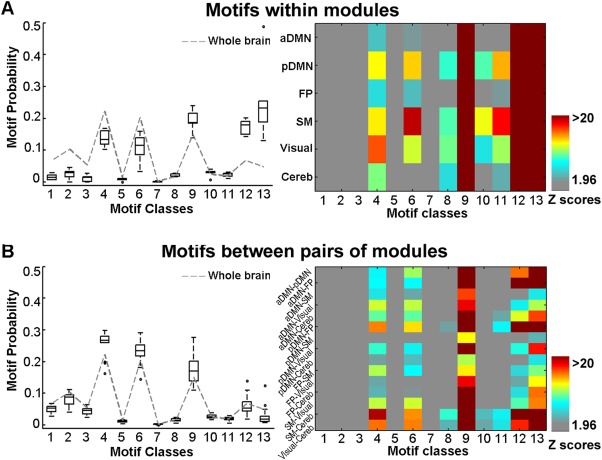
Patterns of three‐node motifs at a modular scale. (A) Occurrence probability for three‐node motifs within each module (left), and the corresponding significance of the occurrence compared to random networks (right). (B) Motif probability for three‐node motifs between each pair of modules (left), and the corresponding significance of the occurrence compared to random networks (right). In left panel of A, the box plots represent the motif probabilities across all within‐module cases, and in left panel of B, the box plots represent the motif probabilities across all between‐module cases. The central mark of each box is the median, the edges of the box are the 25th and 75th percentiles, and the whiskers extend to the most extreme data points not considered outliers. The dashed line indicates the specific profiles of the motif probability at the overall level. [Color figure can be viewed at http://wileyonlinelibrary.com]

Nodal scale

To investigate the pattern of three‐node motifs at the nodal‐scale, we derived motif fingerprint (i.e., the participation number to each motif class for a node) for each of the 160 nodes within the network. We found all motif fingerprints showed similar profiles as the frequency spectrum of three‐node motifs that were observed in the whole‐brain (all correlation coefficients rs > 0.60, Ps < 0.01). Compared to random networks, a large number of nodes had significantly higher participation numbers for motifs ID = 4, 6, 9, 12, and 13 (Z > 1.96 for 43.8%, 35.6%, 97.5%, 98.8%, and 98.8% of the nodes, respectively) (Fig. 7A). Intriguingly, we found several brain hubs in DMN, including the ventromedial prefrontal cortex (vmPFC) and the posterior cingulate cortex (PCC) as well as hubs in the visual network and cerebellum, participate in more instances of motifs ID = 4 or 6 (Fig. 7B). Given that these two chain‐like motifs contributed more to between‐module communication, it was suggested that these hubs were significantly involved in global integration. When comparing with the stringent random surrogates, motifs ID = 12 and 13 consistently remained significance, which was similar to the overall level (Supporting Information Fig. S3). Moreover, we also noticed a significantly positive correlation between the total‐degree and the medium apex ratio of chain‐like motifs ID = 4, 6, and 9 (Fig. 7C), which further indicated these hubs function as “information transfer station.”

Figure 7.

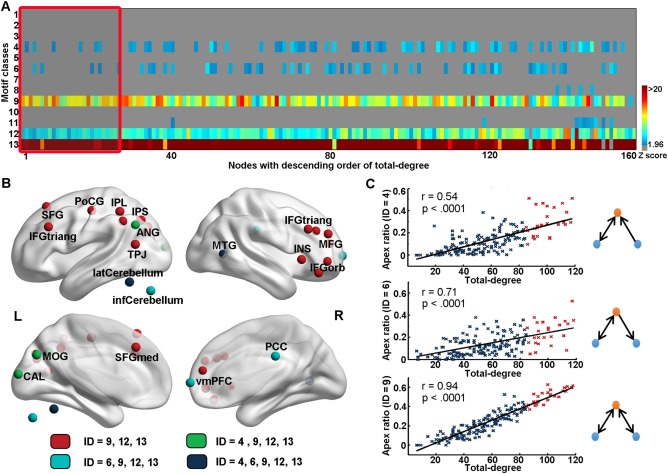
Patterns of three‐node motif at a nodal scale. (A) Significance of participation number for each node to 13 classes of three‐node motifs. The hot color indicates a higher significance. (B) Significance of participation number of hubs regions to five classes of recurring motifs within the whole brain. Red nodes: hubs that significantly participated in motifs ID = 9, 12, and 13; Green nodes: hubs that significantly participated in motifs ID = 4, 9, 12, and 13; Cyan nodes: hubs that significantly participated in motifs ID = 6, 9, 12, and 13; Blue nodes: hubs that significantly participated in motifs ID = 4, 6, 9, 12, and 13. (C) Across node relation between total‐degree and apex ratio locating in the medium of three‐node motifs ID = 4 (r = 0.54), 6 (r = 0.71), and 9 (r = 0.94). Blue nodes: non‐hubs. Red nodes: hubs. [Color figure can be viewed at http://wileyonlinelibrary.com]

Validation Results

We evaluated the reproducibility of our main findings in several ways, including individual‐level network analyses, fMRI data of the same subjects from another session, and different preprocessing/analysis strategies for network construction. As shown in Supporting Information Table S3, the directed functional brain networks constructed in all cases exhibited small‐world architectures, although their network densities differed. When compared to surrogate random networks, significantly large numbers were observed for the two‐node reciprocal motif in all cases (all Zs > 2, Ps < 0.05) and five types of three‐node motifs (i.e., ID = 4, 6, 9, 12, and 13) in most cases, except for motifs in two individual‐level networks (not significant for three‐node motifs ID = 4 or 6, Z < 0.58) and in the group‐level network constructed using the AAL template (not significant for three‐node motifs ID = 4, 6 and 12, Zs < −0.18). We also observed similar SP profiles of three‐node motifs across different cases, as shown in (Supporting Information Fig. S2). Taken together, either the two‐node motif or the three‐node motif patterns within the whole brain can be replicated in most of the validation cases (Supporting Information Table S3).

DISCUSSION

We investigated the motif patterns in the human directed functional brain networks to identify the significant functional motifs and reveal how these basic building blocks make contributions to the brain's intrinsic functional organization. The directed functional networks were constructed from the R‐fMRI data with the vascular response latency corrected. Within the network, several functional motifs were identified to be statistically significant, including the two‐node reciprocal motif and five classes of three‐node motifs labeled as ID = 4, 6, 9, 12, and 13. The SP profile of three‐node motifs suggested a high consistency in the design principle between the human brain functional networks and the large‐scale mammalian cortical networks [Milo et al., 2002; Sporns and Kötter, 2004]. Moreover, those recurring motifs were topologically distributed in distinct patterns to support not only the functional coordination at modular architecture but also the functional role of brain hubs.

Construction of Directed Functional Networks for Motif Identification

In present study, we performed motif analyses on the directed functional brain networks that were constructed from a R‐fMRI data that had the latency of vascular response corrected during data preprocessing. As addressed in prior studies, the BOLD signal is a mixture reflecting both neuronal activities and vascular responses [Bandettini et al., 1992; Kwong et al., 1992; Logothetis et al., 2001; Ogawa et al., 1992]; thus, the relative timing of neural activities reflected in BOLD signals could be influenced by the latency of the vascular response. Studies have demonstrated that large vessel effects could lead to a latency of up to 4 s compared to capillary effects, and adjacent brain areas could exhibit latency differences of up to 2 s [Miezin et al., 2000]. Consequently, the hemodynamic latency may confound the inference of interregional neural interactions, especially the causalities [Chang et al., 2008], leading to the necessity of correcting these latencies before constructing directed functional networks. To correct the latency of vascular response in R‐fMRI data, we used a BH T‐fMRI data to estimate these latencies. By modulating the cerebral blood without changes of cerebral metabolic rate of oxygen (CMRO₂) [Kastrup et al., 1999], the BH task was suggested to be a robust method for assessing the latency of vascular responses uncoupled from neural activation in all vascularized brain regions [Bandettini and Wong, 1997; Cohen et al., 2004; Thomason et al., 2005, 2007]. Notably, our findings indicated that large numbers of voxels in the brain were significantly modulated by the BH task (shown by significant R _max), and a considerable proportion of these voxels had non‐zero latency values. They also suggested the effectiveness of BH task and the necessity of latency correction before constructing brain functional networks.

After correcting the hemodynamic latency, we obtained the functional directed network using the CCM approach. Unlike the traditional Granger causality, the CCM is suitable for identifying causations in non‐separable systems, in which the information of a causative factor is embedded in the system and cannot be removed by simply eliminating that variable from the computational model [Sugihara et al., 2012]. As the brain is the most complex system in nature and the inter‐regional functional coupling might be “non‐separable,” we used CCM in the current study to obtain a more realistic evaluation of the causal effects between brain regions. In the current study, the CCM‐derived directed network exhibited a topology with small‐world architecture, well‐organized functional modules (including aDMN, pDMN, FP, SM, the visual area, and the cerebellum), and highly connected hubs, which is highly consistent with previous observations [Bullmore and Sporns, 2012; Yan and He, 2011]. These findings indicated that the CCM‐derived brain network retains typical topological properties observed in prior brain networks, meanwhile contains more intriguing information of the interregional neural causality.

Recurring Network Motifs in Human Brain

In the directed functional brain networks, the reciprocal motif is a significantly recurred two‐node motif, in which two nodes are linked by a bi‐directional connection. In functional terms, the two brain regions linked by the reciprocal motif are mutually coupled, thus they could directly regulate each other. It might be similar to its function in genes developmental transcription networks, in which the two nodes activate each other to the active “ON” state and retain stable [Alon, 2007]. Compared to the unidirectional motif, the reciprocal motif also functions more efficiently because the information can be transferred between two nodes in any direction without passing through a third one. The occurrence of this motif might be supported by the underlying white matter connectivity as this type of motif also occurs more often in mammalian cortical networks compared to corresponding random networks [Sporns and Kötter, 2004]. Notably, we also found that the reciprocal motif distributed dependent on the anatomical distance between the two regions, with a significantly large amount occurred at short‐range, compared to a small amount occurred at long‐range. This might be attributed to the large amount of low‐cost short fibers constituting the local circuitry and few high‐cost long axonal projections ensuring short mean path lengths of the whole network [Markov et al., 2011]. Thus, this distance‐dependent pattern of the reciprocal motif fully reflected the “cost‐efficiency” rule in the human brain that information is transferred efficiently at a relatively low cost [Achard and Bullmore, 2007].

We observed that five classes of three‐node motifs (i.e., ID = 4, 6, 9, 12, and 13) were significantly more likely to be embedded in human brain network compared with random networks. These five classes of motifs could be divided into two sub‐types: the chain‐like motifs (i.e., ID = 4, 6, and 9) and the loop‐like motifs (i.e., 12 and 13). Regarding the chain‐like motifs, the two ends, which are not linked directly, are integrated through the medium node. The motif ID = 9 has been first reported in studies of macaque cortex network and suggested to reflect the integration and segregation principle of the network organization [Sporns and Kötter, 2004]. Recently, the integration function has also been revealed in studies of neural mass models, where the two disconnected ends in three‐node motifs ID = 6 and 9 stably dynamically synchronized with each other [Gollo et al., 2014; Gollo and Breakspear, 2014]. Furthermore, these chain‐like motifs were also revealed to occur in a large number among the communication between functional modules, both in the current study and in the previously reported cortex network of macaques [Gollo and Breakspear, 2014; Shen et al., 2012]. The hubs regions, which play an important role in global integration, were found to more locate in the medium apex of these chain‐like motifs functioning as the “information integration center” [Harriger et al., 2012]. Densely interconnected hubs, the rich club, were suggested to form a stable synchronized core through these chain‐like motifs [Gollo et al., 2015]. All these evidences suggest that chain‐like motifs largely contribute to the information integration within the whole‐brain network.

The loop‐like motifs (i.e., ID = 12 and 13) can be derived by connecting the two ends of chain‐like motifs ID = 4, 6, and 9. Within these motifs, any two nodes within the motif can communicate directly without a third node, forming a tight loop for information processing. According to the prior study in neural mass models, the motif ID = 13 enabled metastable configurations of coexisting synchrony between each two nodes, enriching the dynamic patterns of synchronized cortical states and enhancing functional complexity [Gollo and Breakspear, 2014]. Of note, these two loop‐like motifs are largely present within each module. This finding demonstrates the high integration among functional related areas, in analogy to those in the World Wide Web hyperlink networks, in which related pages were linked by these loop‐like motifs [Milo et al., 2002, 2004]. Taking together, the loop‐like motifs may function as the key information‐processing pattern enabling local integration among functional related regions, to achieve functional specification and enrich functional states. In addition, it is noteworthy that motifs ID = 9 also largely appeared between modules, further suggesting its role in balancing the integration and segregation of the network [Sporns and Kötter, 2004].

The deploying of stringent random surrogates conserving the number of unidirectional and reciprocal connections could reduce the significance of the occurrence of the chain‐like three‐node motifs ID = 4, 6, and 9, and simultaneously increase the significance of the loop‐like three‐node motifs (e.g., ID = 8, 10, and 11). Comparing to simple random surrogates, the rewiring with controlling of the number of unidirectional/reciprocal edges tends to keep the number of chain‐like motifs and reduces the chance to close a chain‐like motif to form a loop‐like motif, because the reciprocal connections were not allowed to be disassembled into two unidirectional connections. This explained why loop‐like motifs, but not chain‐like motifs, appeared in much more amount in the human brain networks comparing to the stringent random surrogates. Moreover, these two random surrogates reflected distinct “significance”: the usage of stringent random surrogates corrects for the “carry‐over” significance from motif size M = 2, ensuring the significance was not caused by the pattern of two‐node reciprocal motifs [Milo et al., 2002]. In contrast, the usage of simple random surrogates enabled us compare the motif pattern in the human brain network to the randomly rewiring topology independent of the motif size M [Sporns and Kötter, 2004]. Nonetheless, the loop‐motif with more reciprocal connections (ID = 12 and 13) were significantly more occurred in the brain network comparing either the simple or the stringent random surrogates, suggesting their uniqueness in the architecture of the brain networks. More interestingly, different random surrogates did not alter the consistency of motif patterns among human brain and macaque brain, suggesting a stable organizational principle of brain networks during evolution.

Participation of Hubs in Functional Motifs

When considering the nodes' participation in the chain‐like motifs (i.e., ID = 4, 6, and 9), we found that hubs are more likely to occupy the medium apex location, which is consistent with the findings of previous studies in the macaque cortex network [Sporns et al., 2007], further indicating that hubs tend to act as the “transfer station.” When compared with random networks, all hubs significantly participated in motifs ID = 9, 12, and 13. Given that motifs ID = 9, 12, and 13 were largely involved in within‐module information coordination; it implied that all hubs participated in functional specification. Moreover, only hubs in vmPFC, PCC and the occipital lobe also participated in more instances of motifs ID = 6 and 4, separately. This discrepancy may reflect the specific functional roles of these brain hubs. Because the DMN appears to be more active when individuals engage in internal tasks [Buckner et al., 2008], the large participation of motif ID = 6 in the PCC and vmPFC might be related to its effect in regulating spatially distributed regions in resting state. Meanwhile, the large participation of motif ID = 4 in hubs of the visual system might indicate that regions in the primary cortex are more likely to be regulated by “higher” areas such as those in attention networks [Park and Friston, 2013]. Therefore, we suggest that the variation in participation of hubs to these motifs might support the diverse roles of functional integration within the brain.

FURTHER CONSIDERATION

First, in the current study, we used the BH task to evaluate regional hemodynamic latency to better capture causality between regions. However, executing a BH task scan in every experiment is not feasible in actual operation. Thus, it is important to develop more efficient and operation‐friendly measurement of hemodynamic responses in future studies. Second, we used CCM to estimate the directions of functional network connections. Theoretically, CCM is more suitable for estimating the causal relationship in the complex nonlinear system than other linear methods, such as Granger Causality, especially for identifying weak‐to‐moderate coupling [Sugihara et al., 2012]. However, the exact neurophysiological and biochemical substrates of the BOLD signals remain unclear. Thus, the ground truth for determining which method has better identification power is lacking. Future studies combining simultaneously electrophysiological and fMRI recording might provide essential opportunities to evaluate these causality estimation methods. Third, studies analyzing dynamics from the structural motifs in the brain provided a valuable perspective to improve the understanding of the mechanism of brain activities [Gollo et al., 2014, 2015; Gollo and Breakspear, 2014]. Findings from dynamical modeling in macaque structural networks support our results by demonstrating that chain‐like motifs boost synchronization, while loop‐like motifs enrich complexity [Gollo et al., 2014; Gollo and Breakspear, 2014]. Future modeling studies based on structural brain networks, especially the emergence of directed structural networks of the human brain, would further our understanding of the whole‐brain dynamics at the motifs level. Finally, numerous studies have demonstrated the abnormal topological properties of both the structural and functional brain networks in neuropsychiatric diseases. Probing the directed brain networks and corresponding motif alterations in the brain may provide new insights into the disease‐related changes in information‐processing modes and thus further benefit the development of potential neuroimaging biomarkers.

CONCLUSIONS

Using R‐fMRI data with the hemodynamic latency controlled, we constructed directed human functional brain networks and demonstrated two‐node and three‐node network motif patterns. Several significant motif types were identified to characterize the basic information flow modes within the network and were found to be organized in distinct patterns to support the modular and nodal network architecture underlying brain intrinsic activity. These findings provide insight into the basic information flow mechanism within the large‐scale brain functional connectome. Future studies assessing alterations of motifs patterns that corresponds to functional impairments in brain disorders would be of great interest.

Supporting information

Supporting Information