Detecting large‐scale networks in the human brain using high‐density electroencephalography

Abstract

High‐density electroencephalography (hdEEG) is an emerging brain imaging technique that can be used to investigate fast dynamics of electrical activity in the healthy and the diseased human brain. Its applications are however currently limited by a number of methodological issues, among which the difficulty in obtaining accurate source localizations. In particular, these issues have so far prevented EEG studies from reporting brain networks similar to those previously detected by functional magnetic resonance imaging (fMRI). Here, we report for the first time a robust detection of brain networks from resting state (256‐channel) hdEEG recordings. Specifically, we obtained 14 networks previously described in fMRI studies by means of realistic 12‐layer head models and exact low‐resolution brain electromagnetic tomography (eLORETA) source localization, together with independent component analysis (ICA) for functional connectivity analysis. Our analyses revealed three important methodological aspects. First, brain network reconstruction can be improved by performing source localization using the gray matter as source space, instead of the whole brain. Second, conducting EEG connectivity analyses in individual space rather than on concatenated datasets may be preferable, as it permits to incorporate realistic information on head modeling and electrode positioning. Third, the use of a wide frequency band leads to an unbiased and generally accurate reconstruction of several network maps, whereas filtering data in a narrow frequency band may enhance the detection of specific networks and penalize that of others. We hope that our methodological work will contribute to rise of hdEEG as a powerful tool for brain research. Hum Brain Mapp 38:4631–4643, 2017. © 2017 Wiley Periodicals, Inc.

INTRODUCTION

Physiological, neuropsychological and neuroimaging studies have revealed that functional specialization and integration are two distinct, yet coexisting principles of human brain organization (Friston, 2002). Specifically, although the function of an area at a given location is highly specialized, the information it processes is dependent on its precise connections with other areas in different parts of the brain (Varela et al., 2001). Large‐scale functional interactions between spatially distinct neuronal assemblies can be assessed using functional connectivity methods, which estimate statistical dependence between the dynamic activities of distinct brain areas (Friston, 2011). Functional connectivity is most often measured using functional magnetic resonance imaging (fMRI) data, which have a spatial resolution of a few millimeters and permit to construct accurate maps of large‐scale functional networks across the brain (Ganzetti and Mantini, 2013; Fox and Raichle, 2007). However, a significant drawback in the context of functional connectivity is that fMRI provides only an indirect measure of brain activity mediated by a slow hemodynamic response. Alternatively, electroencephalography (EEG) or magnetoencephalography (MEG) can be utilized to estimate large‐scale functional interactions within large‐scale brain networks. Despite a number of technical limitations, they are potentially more suited to investigating mechanisms of long‐range neuronal communication, insofar as they yield high temporal resolution and directly measure electrophysiological activity (Ganzetti and Mantini, 2013; Pfurtscheller and Lopes da Silva, 1999).

In recent years, technological advances have enabled the reliable reconstruction of ongoing activity in the brain (typically called “source space”) using MEG (Mantini et al., 2011). These developments have permitted to confirm the electrophysiological basis of fMRI‐based connectivity (Brookes et al., 2011; Hipp et al., 2012). For instance, band‐limited MEG power across distant brain regions was found to be temporally coherent during rest, and spatially organized similarly to resting state networks (RSNs) previously identified using fMRI (Brookes et al., 2011; de Pasquale et al., 2010). Moreover, MEG studies have begun to disclose important information about brain network dynamics also during task performance (de Pasquale et al., 2012; Hipp et al., 2011), suggesting that long‐range neuronal communication is characterized by rapid changes of synchronized oscillatory activity within specific brain circuits (de Pasquale et al., 2010). However, applications of MEG for large‐scale studies remain limited, mainly because MEG is not portable and has high maintenance costs.

There may be several reasons why no research group has been able to map brain networks using EEG, as previously done using fMRI (Fox and Raichle, 2007; Ganzetti and Mantini, 2013; Gillebert and Mantini, 2013) and MEG (Brookes et al., 2011; de Pasquale et al., 2010; Hipp et al., 2012). One of the main technical difficulties to obtain RSNs from EEG signals is in the need of accurate source activity reconstructions. Unlike MEG, source analysis of EEG potentials requires precise, realistic biophysical models that incorporate the exact positions of the sensors as well as the properties of head and brain anatomy (Michel et al., 2004). To build a realistic head model, accurate representation of the volume conductor of the head and precise volume conductivity of each tissue are essential (Cho et al., 2015; Fiederer et al., 2015; Haueisen et al., 1997; Ramon et al., 2006). Moreover, spatial sampling density and coverage of EEG electrodes also play a crucial role for neuronal source estimation (Slutzky et al., 2010; Song et al., 2015). High‐density EEG (hdEEG) provides both high spatial sampling density and large head coverage, which facilitates the reconstruction of brain activity in the source space. Many research groups working with EEG still make use of low‐density systems with 32 or 64 channels, whereas hdEEG systems are not widespread yet. In addition, dedicated processing tools that permit to use hdEEG for brain imaging in a manner that is analogous to MEG are currently lacking. Another issue for the detection of RSNs with EEG (also with MEG) is the so‐called “signal leakage” across brain voxels (Brookes et al., 2012; Hillebrand et al., 2012; Hipp et al., 2012). The signal leakage problem can be caused by volume conduction as well as the ill‐posed nature of the inverse solutions. While the former occurs at the sensor level, the latter is due to the fact that EEG/MEG sources are estimated in a few thousand voxels starting from a few hundred recordings. Therefore, source estimation is underspecified in nature and yields a blurred image of the true activity in the brain, where activity estimated in one voxel is in fact a weighted sum of the activities in the neighboring voxels.

Here, we propose that higher degrees of freedom needed to correctly resolve the dynamics of brain activity can be achieved through increasing the number of sensors by using hdEEG. Furthermore, MEG studies documented that the signal leakage problem is less critical when detecting RSNs with independent component analysis (ICA) than seed‐based connectivity analysis (Brookes et al., 2011). ICA performs a blind decomposition of a given number of spatio‐temporal patterns that are mixed in the data, assuming that these patterns are mutually and statistically independent in space (sICA) or time (tICA). For fMRI analyses, the use of sICA is warranted because the number of time points is typically much smaller than that of brain voxels, and this possibly leads to unreliable data decomposition by tICA (McKeown et al., 1998). However, tICA has been preferred in EEG/MEG connectivity studies (Brookes et al., 2011; Yuan et al., 2016). In the case of EEG/MEG, the use of tICA may not be problematic due to the higher temporal resolution of these techniques as compared to fMRI. No study has ever tested whether and to what extent sICA can successfully retrieve brain networks from EEG/MEG data.

In this study, we describe a complete pipeline for the detection of EEG RSNs, which exploits the advantages of high‐density as compared with low‐density EEG systems and includes state‐of‐the‐art tools for data preprocessing, realistic head model generation, source localization and ICA‐based connectivity analysis. Notably, hdEEG data can be collected simultaneously with fMRI and in combination with noninvasive brain perturbation by transcranial magnetic stimulation or transcranial direct/alternating current stimulation. Furthermore, hdEEG experiments can be easily performed not only in healthy volunteers but also in neurological and psychiatric patients. Our methodological work may therefore open up new exciting research avenues in neuroscience, and contribute to rise of hdEEG as a powerful tool for both basic and translational investigations on human brain networks.

MATERIALS AND METHODS

Data Collection

Data used in this study comprised resting‐state hdEEG signals, electrode positions and individual whole‐head anatomy MRI from nineteen healthy right‐handed subjects (age 28 ± 5.9 years, 5 males and 14 females). All participants reported normal or corrected‐to‐normal vision, had no psychiatric or neurological history, were free of psychotropic or vasoactive medication. Before undergoing the examination, they gave their written informed consent to the experimental procedures, which were approved by the local Institutional Ethics Committee of ETH Zurich.

The EEG experiment was performed in accordance with the approved guidelines, in a quiet, air‐conditioned laboratory with soft natural light. Continuous 5 min resting EEG data with eyes open were collected. To reduce eye movements and blinks, subjects were instructed to keep fixation on the center of screen during the experiment. High‐density EEG signals were recorded at 1000 Hz by the 256‐channel HydroCel Geodesic Sensor Net using silver chloride–plated carbon‐fiber electrode pellets provided by Electrical Geodesics (EGI, Eugene, OR). During recording, the EGI system used the electrode at vertex (labeled as Cz in the 10/20 international system) as physical reference. In addition, to better characterize the scalp distribution of EEG signals, all 256 sensors and three landmarks positions (nasion, left and right preauricolar) were localized prior to the EEG acquisition by using a Geodesic Photogrammetry System (GPS). In detail, GPS derives the position of each EEG electrode from multiple pictures, simultaneously captured, of all the sensors on the subject's scalp. After defining the 2D electrode positions on at least two pictures, 3D coordinates were computed by using a triangulation algorithm (Russell et al., 2005). In addition to EEG data and electrode position information, a T1‐weighted whole‐head MR image of each subject was acquired in a separate experimental session using a Philips 3T Ingenia scanner with a turbo field echo sequence. The scanning parameters were: TR = 8.25 ms, TE = 3.8 ms, 8° flip angle, 240 × 240 × 160 field of view, 1 mm isotropic resolution.

Method for EEG Network Detection

We developed a complete analysis workflow to obtain multiple subject‐specific RSNs from hdEEG recordings (Fig. 1). Four main analysis steps are involved: (1) “Data preprocessing,” to attenuate noise and artifacts that are mixed in the data; (2) “Volume conduction model creation,” to establish how brain sources (i.e., ionic currents in the gray matter) can generate specific distributions of potentials over the hdEEG sensors; (3) “Brain activity reconstruction,” to estimate ‐based on the EEG recordings and the head model‐ the distribution of active brain sources that most likely generates the potentials measured over the hdEEG sensors; (4) “Connectivity analysis,” to obtain RSN maps showing brain regions that have similar modulations of power, and are therefore thought to preferentially interact with each other.

Figure 1.

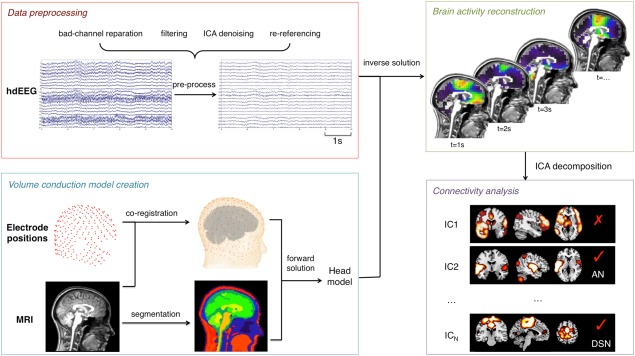
Pipeline for obtaining RSNs from hdEEG recordings. The main analysis steps include: (1) Data preprocessing, involving bad‐channel detection, filtering, ICA‐denoising, and re‐referencing; (2) Volume conduction model creation, involving electrodes co‐registration, MRI segmentation and forward modeling solution; (3) Brain activity reconstruction, to estimate the distribution of active brain sources that most likely generates the potentials measured over the hdEEG sensors; (4) Connectivity analysis, extracting ICs from the power time series of voxels and selecting the components associated with large‐scale brain network activity. [Color figure can be viewed at http://wileyonlinelibrary.com]

Data preprocessing

First of all, we detected channels with low signal quality and labeled them as “bad channels.” To this end, we used an automated procedure that combines information from two different parameters. The first parameter was the minimum Pearson correlation of the signal in a frequency band of interest (here we selected the band 1–80 Hz) against all the signals from the other channels. The second parameter was the noise variance, estimated in a frequency band in which the contribution of the EEG signal can be considered negligible (here we selected the band 200–250 Hz). We defined bad channels those for which at least one of the two channel‐specific parameters were outliers as compared to the total distribution of values. To ensure robustness of the detection, the threshold to define an outlier was set to m + 4s, where m is the average value and s is the standard deviation. The detected bad channels were interpolated by using information from the neighboring channels, as implemented in the FieldTrip toolbox (http://www.fieldtriptoolbox.org). Later, we band‐pass filtered the data in the frequency range 1–80 Hz and we applied ICA to remove of ocular and muscular artifacts (Mantini et al., 2008). A fast fixed‐point ICA (FastICA) algorithm (http://research.ics.aalto.fi/ica/fastica) using a deflation approach and hyperbolic tangent as contrast function was used to extract independent components (ICs). After ICA decomposition, the artifactual ICs were automatically classified by extracting and assessing the following parameters: (1) correlation c _p between the power of the IC with vertical electrooculogram, horizontal electrooculogram, and electromyogram (see Supporting Information Fig. S1); (2) the coefficient of determination r ² obtained by fitting the IC power spectrum with a 1/f function; (3) the kurtosis k of the IC. An IC was classified as artifactual if at least one of the above parameters was above a given threshold (Supporting Information Table S1), which was set in accordance with previous studies (de Pasquale et al., 2010; Mantini et al., 2009). Finally, following artifact rejection we re‐referenced the EEG signals using the average reference approach, which showed to be both robust and accurate when using hdEEG data (Liu et al., 2015).

Volume conduction model creation

An accurate calculation of the EEG forward solution requires the generation of realistic volume conductor model from an individual MR image and the definition of correct electrodes locations with respect to it.

Since electrode positions and MR anatomy are not in the same space, we spatially coregistered the EEG electrodes to MR space (Supporting Information Fig. S2). This procedure consisted of three distinct steps. In the first step, we estimated the positions of three anatomical landmarks (nasion, left and right preauricolar) in the MR image by projecting the corresponding predefined Montreal Neurological Institute (MNI) coordinates ([0, 85, −30], [–86, −16, −40], and [86, −16, −40]) to individual space. Then, we calculated a rigid‐body transformation to match the three landmarks in electrode space to the corresponding landmarks in MR space, and applied it to the electrode positions (Supporting Information Fig. S2A). In the second step, we aligned the electrode positions to the surface of the head extracted from individual MR image (Supporting Information Fig. S2B) using the Iterative Closest Point (ICP) registration algorithm (Besl and Mckay, 1992). In the third and last step, we ensured that each electrode was perfectly lying over the head surface by projecting it onto the surface point with the smallest Euclidean distance (Supporting Information Fig. S2C).

A realistic head model requires the definition of multiple tissue classes of the head, each characterized by a specific conductivity value. We opted for a solution involving 12 tissue classes (skin, eyes, muscle, fat, spongy bone, compact bone, cortical/subcortical gray matter, cerebellar gray matter, cortical/subcortical white matter, cerebellar white matter, cerebrospinal fluid and brain stem), which represents the current state‐of‐the‐art for studies modeling the effect of electrical stimulation on the brain (Holdefer et al., 2006; Wagner et al., 2014). This is putatively more accurate than other solutions typically used in EEG analysis, and involving five or less tissue classes (Fuchs et al., 2002; Wolters et al., 2006). Given the intrinsic difficulty in defining all 12‐tissue classes directly from the MR image (Supporting Information Fig. S3), we warped a high‐resolution head template to subject space using the normalization tool in SPM12 (http://www.fil.ion.ucl.ac.uk/spm/software/spm12). This head template was obtained from the ITIS foundation of ETH Zurich (http://www.itis.ethz.ch/virtual-population/regional-human-models/mida-model/mida-v1-0) (Iacono et al., 2015). The conductivity value associated with each tissue class was defined based on relevant literature (Haueisen et al., 1997), following recent brain stimulation studies (Holdefer et al., 2006; Supporting Information Table S2).

For the numerical approximation of the volume conduction model, we used the whole‐head finite element method (FEM) technique. FEM have been proven to be very effective for solving partial differential equations with complicated solution domain and boundary conditions (Wolters et al., 2004). A prerequisite for FEM is the generation of a mesh that represents the geometric and electric properties of the head volume conductor. A hexahedral mesh (i.e., the points of the mesh are connected to create hexahedrons) of the 12 compartments was generated directly from the warped template image. The dipoles corresponding to brain sources were placed on a regular 6‐mm grid spanning the cortical/subcortical gray matter and cerebellar gray matter. In this study, the leadfield matrix L, which contains the measured potentials corresponding to each configuration of dipole position and orientation, was calculated using the Simbio FEM method integrated in FieldTrip. Based on the reciprocity principle, the scalp electric potentials can be expressed in the following equation with leadfield matrix.

$$\mathrm{\Phi }=L·J$$ (1)

where $L\in {\mathbb{R}}^{N_{\mathrm{E}}\times \left(3N_{\mathrm{V}}\right)}$ is the leadfield matrix; $\mathrm{\Phi }\in {\mathbb{R}}^{N_{\mathrm{E}}\times 1}$ is the scalp electric potential; $J\in {\mathbb{R}}^{3N_{\mathrm{V}}\times 1}$ is the current density at the source; $N_{\mathrm{E}}$ is the number of electrodes, and $N_{\mathrm{V}}$ the number of dipole sources in the cortical/subcortical gray matter and cerebellar gray matter.

Brain activity reconstruction

We reconstructed brain activity in the source space based on the hdEEG artifact‐free recordings and the volume conduction model. To this end, we used the exact low‐resolution brain electromagnetic tomography (eLORETA) to perform source reconstruction (Pascual‐Marqui et al., 2011). The primary feature of the eLORETA algorithm is that of yielding zero localization error for dipolar sources under ideal (noise‐free) conditions. eLORETA estimates the matrix of source activity in the brain J based on the following formula:

$$J={W^{-1}·L·(L·W^{-1}{·L}^{\mathrm{T}}+\alpha H)}^{+}·\Phi$$ (2)

where the superscript + denotes the Moore‐Penrose pseudoinverse, $\alpha$ >0 is the Tikhonov regularization parameter, $W\in {\mathbb{R}}^{N_{\mathrm{V}} \times N_{\mathrm{V}}}$ is a symmetric positive definite weight matrix and $H\in {\mathbb{R}}^{N_{\mathrm{E}} \times N_{\mathrm{E}}}$ is a matrix that depends on the EEG reference. Since the EEG data were in average reference, $H=I-\frac{1}{N_{\mathrm{E}}}1$, where $I\in {\mathbb{R}}^{N_{\mathrm{E} }\times N_{\mathrm{E}}}$ is the identity matrix; $1\in {\mathbb{R}}^{N_{\mathrm{E}} \times { N}_{\mathrm{E}}}$ is a matrix with all elements equal to 1. The regularization parameter $\alpha$ was estimated based on the noise covariance matrix, ${\sum }_{\Phi }^{\mathrm{n}\mathrm{o}\mathrm{i}\mathrm{s}\mathrm{e}}$, such that ${\sum }_{\Phi }^{\mathrm{n}\mathrm{o}\mathrm{i}\mathrm{s}\mathrm{e}}=\alpha H$.

By estimating the matrix J [see Eq. (2)], we obtained the oscillation strength in each dipole with x, y, and z orientations at each temporal moment, indicated with j_x(t), j_y(t), and j_z(t) respectively. We calculated the power time series p(t) by means of the following formula:

$$p\left(t\right)=\sqrt{{\mathrm{j}}_x^2\left(t\right)+{\mathrm{j}}_y^2\left(t\right)+{\mathrm{j}}_z^2\left(t\right)}$$ (3)

One important issue to measure large‐scale connectivity is related to the presence of signal transmission delays between distant brain regions (Deco et al., 2011). To address this issue, we downsampled the power time series to 1 Hz, following an established approach that was proposed in MEG connectivity studies (Brookes et al., 2011). This downsampling permits a more accurate detection of coherent fluctuations of band‐limited power (Supporting Information Figs. S4 and S5).

Connectivity analysis

Brain network detection was performed using ICA, either in its spatial or temporal version (Calhoun et al., 2001, 2009; Smith et al., 2012), on the reconstructed power time courses. ICA yields a number of ICs, each of which consists of a spatial map and an associated time‐course. The IC spatial map reveals brain regions that have a similar response pattern, and are therefore functional connected (Brookes et al., 2011; Mantini et al., 2007). The number of ICs was estimated by using the minimum description length (MDL) criterion (Li et al., 2007). The FastICA algorithm was run 10 times using a deflation approach and hyperbolic tangent as contrast function to extract reliable ICs, as estimated by the ICASSO software package (Himberg and Hyvarinen, 2003; http://research.ics.aalto.fi/ica/icasso). EEG‐RSNs of interest were selected by using a template‐matching procedure. First, the templates were warped to individual MR space, in which the EEG‐RSNs were defined. The Pearson correlation was used to estimate the similarity in the spatial distribution of the EEG‐ICs and the template RSN maps (Supporting Information Fig. S6). The best EEG‐IC match for each template map was extracted iteratively, labeled as a specific EEG‐RSN, and removed from the pool of EEG‐ICs. Accordingly, the same IC could not be associated with two different templates.

Evaluation of Brain Network Reconstruction

We used our processing pipeline to reconstruct power envelopes of oscillatory activity in source space from each hdEEG dataset. First of all, we attempted the detection of EEG‐RSNs with tICA, following an approach suggested in previous MEG connectivity studies (Brookes et al., 2011). As such, band‐limited power envelopes were reconstructed in individual space (whole‐brain source space), transformed to common MNI space using SPM, and finally concatenated across subjects before running functional connectivity analyses by means of tICA. We then compared this approach with similar approaches in which the source space was constrained to the gray matter and/or tICA‐based connectivity was run on each single datasets and the resulting network maps were subsequently transformed to MNI space. Power envelopes were separately calculated for the following frequency bands: delta (1–4 Hz), theta (4–8 Hz), alpha (8–13 Hz), beta (13–30 Hz), and gamma (30–80 Hz). We also conducted functional connectivity analyses on power envelopes in a wide frequency range (1–80 Hz), such that the spatial pattern of the reconstructed networks would not be biased by the selection of a specific frequency band. We also examined the possibility of using sICA in alternative to tICA for the detection of EEG brain networks.

In all the analyses described above, we used fMRI‐RSN maps from one of our previous studies (Mantini et al., 2013) as templates for EEG‐RSN detection. These corresponded to: default mode network (DMN), dorsal attention network (DAN), ventral attention network (VAN), right frontoparietal network (rFPN), left frontoparietal network (lFPN), language network (LN), cingulo‐opercular network (CON), auditory network (AN), ventral somatomotor network (VSN), dorsal somatomotor network (DSN), visual foveal network (VFN), visual peripheral network (VPN), medial prefrontal network (MPN), and lateral prefrontal network (LPN), see Supporting Information Fig. S6). After the definition of EEG‐RSN maps in each subject, we derived group‐level RSN maps by using performing a voxel‐wise nonparametric permutation test by FSL (http://fsl.fmrib.ox.ac.uk/fsl/fslwiki). We used 5000 permutations for this statistical analysis, and set the significance threshold to P < 0.01 corrected for multiple comparisons by using the threshold‐free cluster enhancement (TFCE) method (Smith and Nichols, 2009).

RESULTS

First, we obtained EEG brain networks by applying tICA to alpha‐band power envelopes using a whole‐brain grid as source space and concatenated datasets, following an approach previous employed in MEG studies. We then compared the results with those obtained when using the gray matter instead of the whole brain as source space, and individual instead of concatenated datasets (Fig. 2). Reconstruction performance was evaluated for the DMN, which presents a complex spatial pattern and is therefore difficult to reconstruct. Notably, the use of a whole‐brain grid as source space resulted in blurred spatial patterns (Fig. 2A,B). Conversely, when using the gray matter as source space and performing ICA on concatenated datasets, the spatial pattern of the DMN was less widespread, but contained only the most prominent areas of the network (Fig. 2B). All the main DMN areas could instead be reconstructed by using a source space spanning the gray matter and performing ICA on non‐concatenated datasets (Fig. 2D). We therefore retained this solution for further analyses.

Figure 2.

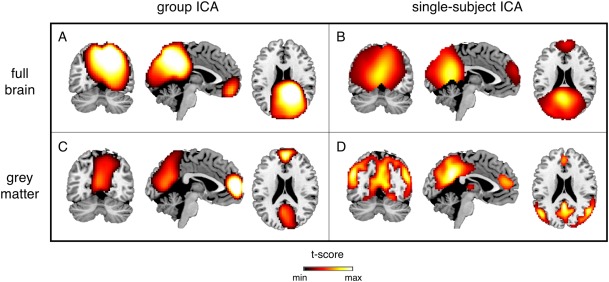
DMN maps reconstructed by tICA using alpha‐band power envelopes. A: Neuronal activity in alpha band (8–13Hz) was estimated from hdEEG data using the whole brain as source space, and brain networks were defined by tICA using concatenated datasets in MNI space. B: Brain networks were also obtained by using individual datasets (and in individual space). The resulting maps were then transformed to MNI space and subjected to group‐level statistical testing. C,D: The same analysis as in (A) and (B), respectively, was conducted with the gray matter as source space instead of the whole brain. Group‐level RSN maps (N = 19) were thresholded at P < 0.01 TFCE‐corrected. [Color figure can be viewed at http://wileyonlinelibrary.com]

Neuronal oscillations supporting functional interactions between distant brain regions are thought to be mainly in the alpha and beta bands. To test this directly on our data, we examined the performance in RSN reconstruction for different frequency bands. Notably, the DMN could be fully reconstructed using alpha‐band power envelopes, and only partially using power envelopes for delta, theta, beta, and gamma bands (Fig. 3). When we extended this analysis to other networks (see Methods), we noticed that some of these could be better reconstructed with power envelopes of other frequency bands than the alpha one. Thus, there was no frequency band that was optimal for all networks (Supporting Information Fig. S7).

Figure 3.

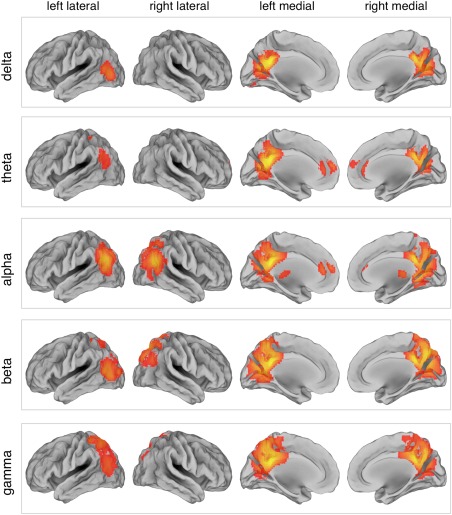
DMN maps obtained by tICA for different frequency bands. The DMN was reconstructed using power envelopes in the delta (1–4 Hz), theta (4–8 Hz), alpha (8–13 Hz), beta (13–30 Hz), and gamma (30–80 Hz) bands, respectively. Surface maps are presented in left/right lateral and medial view (N = 19, threshold P < 0.01 TFCE‐corrected). [Color figure can be viewed at http://wileyonlinelibrary.com]

We attempted RSN detection by tICA also using EEG signals in a wide frequency band (1–80 Hz). We found in this case that the spatial pattern of each EEG‐RSN clearly matched that of the corresponding fMRI‐RSN that was used as spatial template (Fig. 4). RSN detection was likewise performed using sICA, always with wide‐band EEG signals. Also in this case EEG‐RSN detection was successful for all networks under investigation (Fig. 5). The EEG‐RSN maps obtained with sICA had overall a similar spatial pattern but different features as compared to those obtained by tICA (Fig. 6). Specifically, they were less widespread, and covered 40% of the total cortical space, as compared with the 77.8% of those obtained by tICA. The spatial overlap between maps was also smaller with sICA than with tICA, and equal to 4.6 and 39.1%, respectively.

Figure 4.

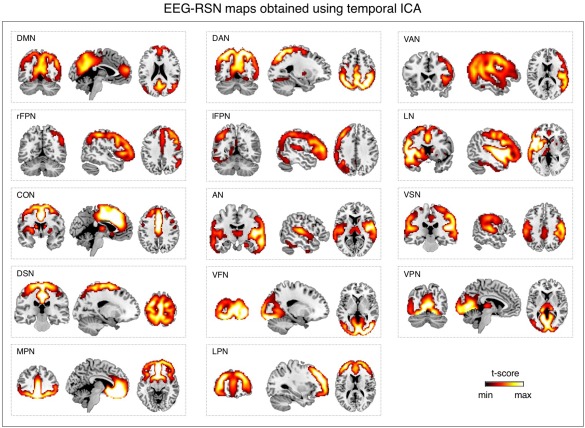
Large‐scale brain networks reconstructed using tICA from wide‐band EEG signals. EEG networks were selected and labeled on the basis of the spatial overlap with fMRI networks: DMN, DAN, VAN, rFPN, lFPN, LN, CON, AN, VSN, DSN, VFN, VPN, MPN, and LPN. Group‐level RSN maps (N = 19) were thresholded at P < 0.01 TFCE‐corrected. [Color figure can be viewed at http://wileyonlinelibrary.com]

Figure 5.

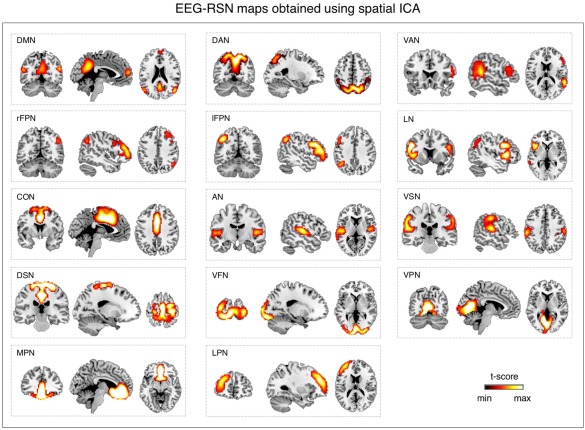
Large‐scale brain networks reconstructed using sICA from wide‐band EEG signals. EEG networks were selected and labeled on the basis of the spatial overlap with fMRI networks: DMN, DAN, VAN, rFPN, lFPN, LN, CON, AN, VSN, DSN, VFN, VPN, MPN, and LPN. Group‐level RSN maps (N = 19) were thresholded at P < 0.01 TFCE‐corrected. [Color figure can be viewed at http://wileyonlinelibrary.com]

Figure 6.

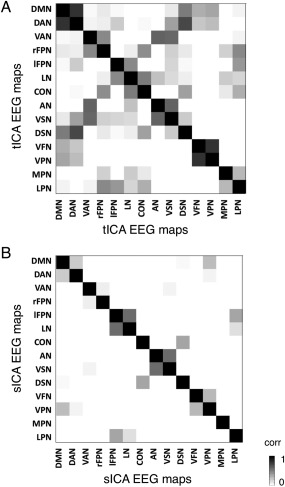
Comparison of EEG‐RSN maps reconstructed using tICA and sICA. A: Spatial correlation between EEG‐RSNs detected with tICA; B: Spatial correlation between EEG‐RSNs detected with sICA. Lower nondiagonal values indicate that the spatial patterns of the different RSNs are more distinct.

As a control analysis, we applied tICA and sICA to source‐space data defined in the whole brain (Supporting Information Fig. S8). By comparing the results of this analysis with those obtained previously (Figs. 4 and 5), we verified that source localization in the gray matter could generally enhance detection of RSNs, as previously observed for the DMN (Fig. 2). We also found that the RSN maps obtained by tICA on whole‐brain source‐space data (Supporting Information Fig. S8A), although they were relatively blurred, showed a spatial pattern more closely resembling classical RSNs than the maps obtained using sICA (Supporting Information Fig. S8B). We also tested the robustness of the RSN maps obtained using either tICA or sICA on gray‐matter source‐space data, with respect to the number of channels in the EEG montage, the head modeling approach and source localization algorithm used (Supporting Information Fig. S9). This analysis revealed a large sensitivity to any of the three aspects under examination, with one specific exception related to the tICA maps for different number of EEG channels. These were indeed largely overlapping, and their quality was only to a minor extent affected by the availability of fewer EEG channels.

DISCUSSION

The main goal of this study was the detection of large‐scale brain networks from hdEEG data, with a spatial accuracy comparable to the one that can be obtained using fMRI. This is a particularly complex task, as it requires the precise estimation of neuronal activity from recordings made over the scalp. To achieve that goal, we devised a processing pipeline that is tailored to hdEEG data and includes state‐of‐the‐art analysis techniques such as appropriate data pre‐processing, realistic head model construction, accurate source localization and ICA‐based connectivity analysis. To the best of our knowledge, only one EEG study attempted to reconstruct brain networks using tICA and failed to show maps that correspond to fMRI networks (Yuan et al., 2016). Furthermore, sICA has been extensively used for network detection from fMRI data, but never from EEG/MEG data. Notably, our study revealed that both tICA and sICA can be effectively used for the detection of EEG‐RSNs.

Source‐Space Analysis of High‐Density EEG Signals

In this study, we investigated the RSNs spatial patterns using hdEEG. Specifically, we integrated information from hdEEG data, realistic electrode positions, and structural MR images. A number of previous studies examined functional connectivity with EEG signals (Smit et al., 2008); however, connectivity analyses were kept at the sensor level due to low‐density electrode coverage. Interpretation of results from those studies is not straightforward, since EEG recordings contain a mix of neuronal activity from different brain regions. More recently, interest of the scientific community is shifting from low‐density EEG toward high‐density EEG, and from sensor space analyses toward source space analyses, thanks to technological advances and the increasing computing power of computers. Our work contributed to the development of analysis tools specifically tailored to hdEEG, providing a novel way to investigate brain activity in a noninvasive manner, and with relatively accurate spatial and temporal resolution.

Previous studies suggested that the use of a realistic head model is essential for retrieving EEG sources (Ramon et al., 2006) and for conducting connectivity analyses in the source space (Cho et al., 2015). In particular, the head model is used to find the scalp potentials that would result from hypothetical dipoles, or more generally from a current distribution inside the head. Accordingly, we paid particular attention to the construction of a realistic head model. First, we used a structural MR image for each subject, which was used to perform a detailed segmentation of head tissues. A large number of previous studies modeled the head with three compartments, that is, skull, skin and brain (Fuchs et al., 2002), or five compartments, that is, skull, skin, white matter, gray matter, and cerebrospinal fluid (Van Uitert et al., 2003). Arguing against this oversimplification, we used a finite element model (FEM) based on 12 tissues, following recent studies that modeled the effect of transcranial electrical stimulation of the brain (Holdefer et al., 2006; Wagner et al., 2014). Moreover, we used electrode positions measured just before the EEG experiment, properly aligned to the segmented MR volume, for FEM calculations. Previous work demonstrated the importance of accurate information on electrode positions for accurate EEG re‐referencing (Liu et al., 2015) and source localization (Van Hoey et al., 2000; Wang and Gotman, 2001). However, this is still neglected in a considerable part of current EEG studies.

In our pipeline, we used a realistic head model in combination with eLORETA for the reconstruction of ongoing brain activity in the source space. It should be considered that there is no general consensus about the best EEG source localization method and one should select the method that delivers the best compromise depending on the questions of the study and the data at hand (Michel et al., 2004). Unlike the classical L2 minimum norm estimate (Dale et al., 2000; Lin et al., 2006), eLORETA does not suffer from depth bias (Pascual‐Marqui et al., 2011). This is an important feature, considering that several crucial nodes in RSNs span deeper brain regions. Furthermore, eLORETA is designed to be minimally affected by the volume conduction error in the EEG (Pascual‐Marqui et al., 2011). Whereas resting state MEG studies frequently used beamformers for source localization (Baker et al., 2014; Brookes et al., 2011), the suitability of the method for EEG is not established yet. In addition, many MEG studies performed the reconstruction of neuronal activity by using a whole‐brain grid for as solution space for source localization (Brookes et al., 2011; Hipp et al., 2012; Marzetti et al., 2013). Our results suggested that having a source space that is confined to the gray matter, instead of spanning the whole brain, can improve the reconstruction of brain activity, and therefore of brain networks from hdEEG data (Fig. 2D). Notably, a gray matter constraint to the solution space can be justified from a biophysical point of view, as pyramidal neurons in the gray matter are the principal EEG generators (Schaul, 1998). Given the ill‐posedness of the source localization problem, using all the voxels in the brain as potentially active sources makes it more difficult for any source localization method to identify the correct distribution of neural activity that explains the measured EEG potentials.

Network Detection by ICA of Power Envelopes

We detected RSNs using ICA rather than alternative methods based on seed‐based connectivity (Brookes et al., 2012; de Pasquale et al., 2010, 2012). ICA is a data‐driven technique that can produce multiple RSNs by only imposing the constraint of either spatial or temporal independence between RSNs (sICA and tICA, respectively). sICA has been largely employed for the detection of RSNs with fMRI data, in which the number of time points is always much smaller than the number of voxels. In the case of EEG/MEG connectivity studies, tICA has been preferred to sICA since it is possibly better suited to capture the nonlinear and nonstationary nature of neurophysiological signals (Brookes et al., 2011; Yuan et al., 2016). Previous MEG connectivity studies used tICA on band‐limited power envelopes, primarily focusing on alpha and beta bands (Brookes et al., 2011). Our connectivity analyses of alpha but also beta power envelopes permitted the robust detection of many, but not all RSNs under investigation (Fig. 3 and Supporting Information Fig. S7). Interestingly, we could enhance RSN detection by using wideband (1–80 Hz) signals (Figs. 4 and 5). Based on this finding, we argue that the narrow band‐pass filtering may not be strictly needed for connectivity analyses. Each brain network is characterized by a combination of different neuronal oscillations (Mantini et al., 2007), and the selection of a frequency band may therefore favor the detection of specific networks against others.

Overall, our study reveals that both tICA and sICA can be successfully applied for the detection of RSNs from hdEEG data. However, specific differences between RSN maps obtained by tICA and sICA exist. In particular, RSNs with more widespread, sometimes overlapping regions can be observed with tICA, whereas RSNs reconstructed by sICA show more selective spatial patterns and cover more limited portions of the cortical space (Figs. 4 and 5). Our study has the particular merit of showing RSNs that were previously reported only using fMRI but not MEG/EEG, such as VAN, AN, and MPN (Mantini et al., 2013). A possible explanation for an increased sensitivity in RSN detection may be the fact that we extracted EEG‐RSN maps at the single‐subject level and in individual space (Fig. 2D), rather than transforming the source‐space power time‐courses to common space and performing a single ICA on concatenated time‐courses from all subjects (Fig. 2B). The primary reason for our choice is methodological, as this approach permits to better incorporate information on head modeling and electrode positioning (Marino et al., 2016) in source activity reconstructions. However, it should also be considered that the extraction of RSNs at the single subject level may be important for clinical applications, and in particular for the study of stroke, multiple sclerosis, Alzheimer's disease and all other conditions in which brain plasticity (Johnston, 2004) may occur.

Study Limitations and Caveats

The pipeline for the analysis of hdEEG data includes several analysis steps. The successful detection of EEG‐RSNs indirectly confirms that each of these steps yielded satisfactory results. From a methodological point of view, an important advancement was the creation of a realistic head model with 12 distinct compartments, which permits to better account for potential spatial distortions in the flow of currents from sources to sensors. It should be noted, however, that our head model did not consider tissue anisotropy. Considering anisotropy may lead to even more accurate results, in particular for subcortical regions (Cho et al., 2015; Wolters et al., 2006). In addition, we used conductivity values derived from the literature. A possible improvement may come from the in‐vivo estimation of head tissue conductivity, for which techniques are being developed (Akalin Acar et al., 2016; Lew et al., 2009) and may be available in the future. Another potential limitation of the present study pertains to the use of ICA for network detection. Specifically, the number of ICs extracted from the EEG power timecourses was performed using the MDL approach, in line with previous fMRI‐RSN studies (Li et al., 2007). Of note, we did not examine how the use of different IC numbers impacts on the quality of the detected RSNs. Future studies are warranted to evaluate if EEG‐RSN detection can be further improved by using alternative approaches to estimate the number of ICs.

CONCLUSION

In this study, we successfully detected large‐scale brain networks using hdEEG data, based on a robust methodology for artifact reduction, head modeling and source localization. The development of such methodology may have broader impact on the field of brain imaging and neuroscience. We posit that hdEEG can be a powerful tool for investigating temporal and spectral signatures of long‐range functional connectivity in health and disease. Notably, the characterization of functional connectivity dynamics using fMRI is problematic, given the relatively low temporal resolution of the technique. In contrast, EEG permits examining network reconfiguration at very fast time scale (Baker et al., 2014; Van de Ville et al., 2010). Moreover, the combination of hdEEG with simultaneous fMRI can unravel the direct relationship between functional connectivity measured through electrophysiological and hemodynamic techniques (Mantini et al., 2007). Finally, analyses of functional connectivity based on hdEEG data may be relevant in a clinical context. In particular, the use of functional connectivity measures from hdEEG has the potential to provide novel and more sensitive biomarkers to improve diagnostics.

Competing Financial Interests

The authors declare no competing financial interests.

Supporting information

Supporting Information