Profilometry: A new statistical framework for the characterization of white matter pathways, with application to multiple sclerosis

Abstract

Aims: describe a new “profilometry” framework for the multimetric analysis of white matter tracts, and demonstrate its application to multiple sclerosis (MS) with radial diffusivity (RD) and myelin water fraction (MWF). Methods: A cohort of 15 normal controls (NC) and 141 MS patients were imaged with T1, T2 FLAIR, T2 relaxometry and diffusion MRI (dMRI) sequences. T1 and T2 FLAIR allowed for the identification of patients having lesion(s) on the tracts studied, with a special focus on the forceps minor. T2 relaxometry provided MWF maps, while dMRI data yielded RD maps and the tractography required to compute MWF and RD tract profiles. The statistical framework combined a multivariate analysis of covariance (MANCOVA) and a linear discriminant analysis (LDA) both accounting for age and gender, with multiple comparison corrections. Results: In the single‐case case study the profilometry visualization showed a clear departure of MWF and RD from the NC normative data at the lesion location(s). Group comparison from MANCOVA demonstrated significant differences at lesion locations, and a significant age effect in several tracts. The follow‐up LDA analysis suggested MWF better discriminates groups than RD. Discussion and conclusion: While progress has been made in both tract‐profiling and metrics for white matter characterization, no single framework for a joint analysis of multimodality tract profiles accounting for age and gender is known to exist. The profilometry analysis and visualization appears to be a promising method to compare groups using a single score from MANCOVA while assessing the contribution of each metric with LDA. Hum Brain Mapp 37:989–1004, 2016. © 2015 Wiley Periodicals, Inc.

Abbreviations

AD

Axial diffusivity

BPF

Bound pool fraction

CSF

Cerebro‐spinal fluid

dMRI

Diffusion magnetic resonance imaging

DT

Diffusion tensor

FA

Fractional anisotropy;

FOV

Field of view

FSPGR

Fast spoiled gradient recalled echo

MANCOVA

Multivariate analysis of covariance

MD

Mean diffusivity

MS

Multiple sclerosis

NC

Normal controls

QMT

Quantitative magnetization transfer

RD

Radial diffusivity

ROI

Region of interest

SEM

Standard Error in the Mean

ST

Single tensor

STD

Standard deviation

INTRODUCTION

In‐vivo imaging of the white matter pathways has greatly improved since the development of diffusion magnetic resonance imaging (dMRI) [Basser et al., 1994; Le Bihan and Johansen‐Berg, 2012] which allowed two main breakthroughs. First was the characterization of the underlying fiber microstructure with metrics derived from the diffusion of water molecules, as modeled for example by the diffusion tensor (DT) [Basser, 1995]. Second was the virtual dissection of white matter fibers with a technique called tractography [Lazar, 2010; Mori et al., 1999].

Despite the unique ability of diffusion imaging to provide information allowing the reconstruction of white matter tracts, the metrics usually extracted from the DT, namely fractional anisotropy (FA) and mean (MD), axial (AD) and radial diffusivity (RD), tend to lack specificity to characterize the underlying microstructure. None of them have proven to be a specific imaging biomarker of myelin [Beaulieu, 2002; Paus, 2010; Wang et al., 2011; Yablonskiy and Sukstanskii, 2010], although RD is suggested as the closest marker of demyelination (Song et al., 2002). Other modalities aim at better quantifying myelin, and have been shown to be correlated with myelin content [Laule et al., 2006]. These include quantitative magnetization transfer (QMT) imaging [Cercignani et al., 2005; Sled et al., 2004], which assumes the decrease in signal due to the proton bound pool fraction (BPF) to come essentially from myelin, and T2 relaxometry, which can estimate the fraction of the signal due to water trapped in between the myelin layers (myelin water fraction: MWF) [MacKay et al., 1994; Raj et al., 2014].

The methods for reconstructing tracts and quantifying diffusion have both been used independently, with for example virtual dissection applied to neurosurgery (Clark et al., 2003; Fernandez‐Miranda et al., 2012; Kamada et al., 2005; Nimsky et al., 2005; Powell et al., 2008) and diffusion metrics used to detect infarcts in stroke patients (Fung et al., 2011; Lutsep et al., 1997; Redgrave et al., 2007; Weber et al., 2000; Wessels et al., 2006), and in conjunction when looking at specific tract changes with age [Clayden et al., 2012; Davis et al., 2009; Dayan et al., 2015; Eluvathingal et al.,2007; Hasan et al., 2010; Lebel and Beaulieu, 2011] or disease (amyotrophic lateral sclerosis [Aoki et al., 2005], Alzheimer's disease [Taoka et al., 2006], multiple sclerosis (MS) [Lin et al., 2007]; stroke [Møller et al., 2007]; Parkinson's disease [Nilsson et al., 2007]). When these two aspects are combined, diffusion metrics are typically averaged over the tracts of interest. However the analysis of these metrics along the tracts, so‐called “tract profiles” [Jones et al., 2005; Corouge et al., 2006; Maddah et al., 2008], has been shown to provide a wealth of additional information. For instance, analysis along tracts allows for detection of tract changes which would be lost in tract‐averaged metrics [Goodlett et al., 2009; O'Donnell et al., 2009].

Limited research has been carried out that combines tractography reconstructions, and metrics derived from modalities other than dMRI. Of notable exception are the studies of [Bells et al., 2011] and [De Santis et al., 2014] who coined the term “tractometry” for this endeavour. These studies compared MWF and QMT to dMRI metrics, and notably demonstrated that only FA correlated with MWF except in areas with tract dispersion and curvature. However, the analyses were not based on location along tracts, rather they were reported on a voxel by voxel basis [Bells et al., 2011], or averages within region of interest (ROI) [De Santis et al., 2014]. Similarly Stikov et al. [2011] gave unique insight into the relationship between FA and BPF in a set of white matter tracts but, again, they limited their analysis to tract‐averaged values. Finally, most multi‐metric analyses do not perform a joint analysis of the multiple metrics but rather investigate each metric separately.

The aim of this work is threefold. First, to describe a framework called “profilometry” which allows the joint analysis of multiple metrics—non exclusively derived from dMRI—calculated along tracts reconstructed from individual subject tractography, with a particular emphasis on the novel statistical approach of this framework. This new statistical procedure accounts for multimetric data and notably corrects for multiple comparisons along the tract while allowing for covariates such as age and gender. Second, to demonstrate the use of this profilometry framework with dMRI and MWF metrics in both a MS cohort and in single MS patients. This is of special interest considering the localized nature of MS lesions and the MWF metric which can be obtained in the time typically available in clinical settings [Nguyen et al., 2012]. Third, to provide a novel start‐to‐finish open‐source pipeline implementing profilometry, ready to use for clinical investigations. It relies on the flexible NiPype project [Gorgolewski et al., 2011] to perform the entire analysis, offering alternatives at most processing steps, from the raw data preprocessing to the generation of high‐level group statistics based on the joint analysis of multi‐modality metrics.

METHODS

Subjects

The study took place at Weill Cornell Medicine, New York, USA. This work was granted ethical approval by the local ethics committee.

Fifteen normal controls (NC) without any known medical condition took part in the study. Informed consent was obtained in all subjects before their participation. The cohort included 6 males and 9 females with mean age ± STD of 36.3 ± 13.3 years.

One‐hundred and forty‐one patients with MS, including clinically isolated syndrome, relapsing‐remitting, secondary progressive and primary progressive diagnoses were selected from our database. All patients with clinically isolated syndrome included in the analysis met the imaging criteria for MS as per [Polman et al., 2011]. These patients lacked dissemination in time (with an additional relapse or additional lesion). All patients with a clinical MRI sequence that included the T2prep 3D spiral sequence and a dMRI sequence were included in the analysis. The cohort included 48 males and 93 females with mean age ± STD of 42.1 ± 10.7 years.

Imaging

Each participant underwent a single dMRI acquisition on a 3T GE Excite scanner using 33 isotropically distributed diffusion‐encoding directions at b = 1000 s/mm² and one at b = 0 s/mm², acquired as 60 2.5 mm‐thick interleaved slices, with no gap between slices. The 128 × 128 acquisition matrix was zero‐filled during reconstruction to 256 × 256 with a field of view (FOV) of 240 mm. The T1 sequence was an axial 3D inversion recovery fast spoiled gradient recalled echo (FSPGR). The resulting T1 weighted images (TE = 1.5 ms, TR = 6.3 ms, TI = 400 ms, flip angle of 15°) had a 240 mm FOV and 140 1.2 mm contiguous partitions associated to a 256x256 matrix. The T2 relaxometry sequence was a whole‐brain T2prep 3D spiral as previously described by [Nguyen et al., 2012] and included the following parameters: axial FOV = 24 cm; matrix size = 192x192 (interpolated to 256x256); slice thickness = 5 mm; number of slices = 32; sequence TR (time between subsequent T2prep pulses) = 2.5 seconds; spiral TR = 8.1 milliseconds (ms); spiral TE = 0.5 ms; flip angle = 10°; readout bandwidth = ±125 kHz; number of spiral leaves per segment = 64; 15 nominal T2prep times = 0, 5 ms, 10‐40 ms (10 ms step), 60‐140 ms (20 ms step), 180‐300 ms (40 ms step); scan time = 10 min. A modified BIR‐4 adiabatic pulse [De Graaf and Nicolay, 1998; Jenista et al., 2013] was used in the T2prep module to improve T2 weighting accuracy against increased B0 and B1 field inhomogeneities at 3T.

T1 and dMRI Preprocessing

All processing was carried out within a custom pipeline based on the NiPype framework [Gorgolewski et al., 2011] which provides abstract interfaces to the most common neuroimaging tools. T1 images were segmented into GM, WM and CSF tissue maps with SPM New Segment toolbox to create a brain mask (Fig. 1). This toolbox relies on the registration of T1 images to MNI space, and the associated T1 to MNI transform was saved to be used in subsequent processing steps (“Lesions Analysis” section). dMRI volumes were corrected for eddy currents and small head movements by registration of the diffusion‐weighted volumes to the first non‐diffusion weighted volume via an affine transformation as implemented in FSL FLIRT [Jenkinson et al., 2002] (Fig. 1). Skull‐stripping was applied with the FSL BET command‐line tool. Due to the limited number of diffusion gradient directions, and to demonstrate the validity of the pipeline with commonly available clinical data, the simple single tensor (ST) model was used within the Camino toolbox [Cook et al., 2006] to estimate the main fiber(s) direction in each voxel. The ST model also provided the FA and RD metrics, commonly used in myelin investigations based on dMRI data. FA thresholds used as stopping criterion in tractography correspond to low anisotropy and usually range from 0.15 to 0.25 [see for example Kunimatsu et al., 2004 and Taoka et al., 2009]. For this reason the seed region for tractography included only voxels with FA values greater than 0.25. Tract reconstruction and profiling were performed as described in the tract profiling section.

Lesions Analysis

Freesurfer was used with the custom brain mask created previously to segment T1 images into GM and WM tissue maps, which were visually checked and manually edited for misclassification due to WM T1‐hypointensities associated with lesions. To create the WM hyperintensity lesion masks, the T2 FLAIR images were also segmented in different tissue classes and masked with the T1 WM mask previously calculated (and linearly registered to T2 FLAIR with a T1 → T2 FLAIR transform). The resulting WM lesion masks were overlaid on the T2 FLAIR images and manually edited, after which a trained neurologist gave a final approval.

The resulting lesion masks were warped to the MNI template in two steps. First, the inverse of the T1→ T2 FLAIR transform was applied to the lesion mask, which was thus linearly coregistered to the subject's T1. Second, the T1 to MNI transform obtained at the tissue classification stage was applied to the lesion masks (Fig. 1). A patient having a lesion on a particular tract was defined as belonging to the group “LesGroup” associated with that tract. Patients having lesions in one of the preselected tracts described in “Tract Profiling” section, according to the tracts definition in the MNI JHU white matter tractography atlas, were then allocated in turn to the appropriate “LesGroup” groups. Note that a single patient can have lesions on multiple tracts and therefore belong to several “LesGroup” groups.

MWF and Lesion Masks Processing

A multi‐voxel spatial regularization approach, that can obtain usable myelin maps from noisy but fast acquisitions [Kumar et al., 2012], was performed to analyze multiexponential T2 decay data. The size and stability of the challenging minimization problem has been greatly reduced by the “Spatially constrained multi‐Gaussian” algorithm, which employs a non‐linear model to recognize three distinct relaxation pools in the brain [Raj et al., 2014]:

• a myelin water pool modeled by a Gaussian distribution with height ${\alpha }_1$

• an intra‐ and extra‐cellular water pool modeled by a Gaussian distribution with height ${\alpha }_2$

• a cerebro‐spinal fluid (CSF) pool modeled by a delta function with height $h_{CSF}$

The parameters ${\alpha }_1$, ${\alpha }_2$ and $h_{CSF}$ are estimated during the constrained optimization and the MWF value in each voxel was computed as the ratio of the myelin water signal height to the total signal height:

$$MWF=\frac{{\alpha }_1}{{\alpha }_1+{\alpha }_2+h_{CSF}}$$ (1)

The resulting MWF maps were warped to dMRI space with a three‐step registration. First, the 1st echo of the T2 relaxometry sequence was linearly coregistered to the subject's T1 (T2‐to‐T1 linear transform). This transform was applied to the MWF maps to get them into T1 space. Second, the subject's skull‐stripped FA volume was affine‐transformed to the skull‐stripped subject's T1 with FSL FLIRT [Jenkinson et al., 2002] followed by a non‐linear registration performed with FSL FNIRT [Andersson et al., 2008] (FA‐to‐T1 non‐linear transform). Third, the FA‐to‐T1 non‐linear transform was inverted and applied to the T1‐space MWF maps (Fig. 1). To avoid unnecessary interpolation, all the transformations were concatenated using the “‐ premat” option of the FSL applywarp toolbox.

Figure 1.

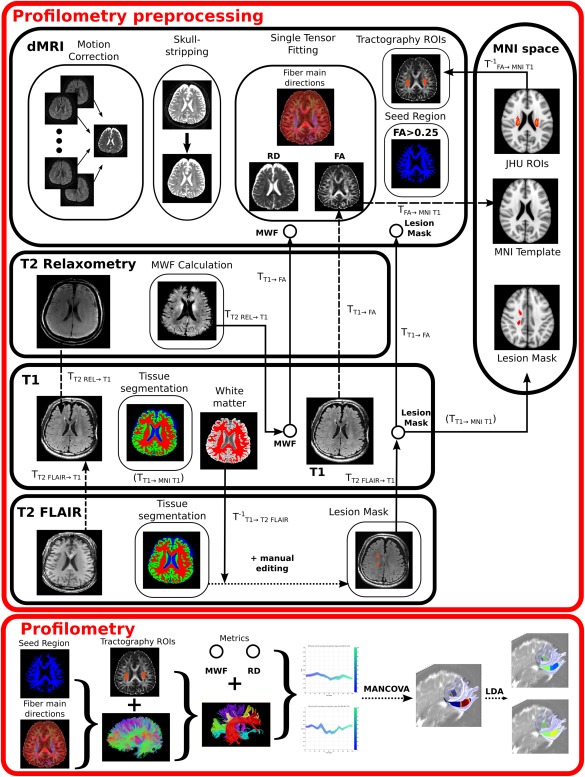
Pipeline framework required for profilometry analysis. Profilometry preprocessing involved several steps. For dMRI it includes motion‐correction, skull‐stripping, tensor fitting (notably to compute FA and RD metrics), seed region creation [voxels having FA > 0.25)] and tractography ROIs creation in native space from MNI space ROIs. For T2 Relaxometry it mainly involves the calculation of the MWF map and its registration to dMRI native space. The lesion masks were created from both T1 and T2 FLAIR as detailed in the manuscript and illustrated here. Finally the “profilometry proper” included tractography and tract parcellation, as according to the preprocessed data, and feeding the resulting tract metric profiles into the statistical procedure composed of the MANCOVA and LDA analyses. Transformations calculated from one space to another are indicated in dashed lines. The use of these transformations (or their inversed) is represented in solid lines. Please note that the T1 → MNI T1 transform was obtained from the T1 tissue segmentation step, and thus indicated as such in the diagram.

A similar procedure was applied to warp the lesion masks to dMRI space. Trilinear interpolation resulted in non‐binary lesion masks in FA space, accounting for volume deformation.

Tract Profiling

Tract reconstructions were obtained from deterministic tractography implemented in Camino, with a relatively low FA threshold of 0.1 as stopping criterion. This allowed tracts to reach grey matter regions and pass through lesioned areas, both of which having low FA (Supporting Information Fig. S1). The tract profiles were computed with the help of the AFQ toolbox as described in [Yeatman et al., 2012] and illustrated in Figure 1.

Briefly:

• Tracts were parcellated in subject dMRI space according to a predefined set of “waypoint” ROIs associated with each tract [Wakana et al., 2007], i.e., a set of ROIs streamlines have to go through to be considered as belonging to a particular tract. For example for the forceps minor, these ROIs were created in the mid‐sagittal plane, by first selecting the coronal slice in between the frontal pole and the anterior tip of the genu of the corpus callosum. Then the entire frontal lobe of the left hemisphere in that slice was defined as the first ROI and the same region in the right hemisphere as the second ROI [Wakana et al., 2007]. The forceps minor bundle is then obtained by selecting streamlines intersecting both these ROIs.

• Tract profiles were obtained by resampling the tracts between the two waypoint ROIs into 100 equally space nodes. Only tracts within a certain distance from their respective bundle core were selected [Wakana et al., 2007]. The bundle core was defined as the mean of each fibers coordinates at each node [Yeatman et al., 2012].

• The metric of interest was computed as a weighted average of each tract according to its distance from the bundle core [Yeatman et al., 2012].

• Custom code was written for profilometry visualization (i.e., the 3D tract profiles and their associated 2D projections).

To balance conciseness with thoroughness, we selected a subset of tracts relevant to our MS population. We chose to focus on the forceps minor while also including the thalamic radiation, cortico‐spinal tracts, and inferior (ILF) and superior (SLF) longitudinal fasciculi within the right hemisphere (exploratory analysis suggested that tract profiles were similar between hemispheres). The tract profiles of the RD and MWF volumes were computed along these tracts. A lesion profile was also calculated for each MS patient according to the associated lesion mask. As mentioned in “MWF and Lesion Masks Processing” section the lesion mask values in dMRI space are continuous rather than binary due to the applied deformation field. Then by considering the lesion mask volume as any other metric volume and applying the series of steps just described, lesion mask tract profile could be obtained.

Profilometry and Statistics

Profilometry—the multimetric analysis of tract profiles—results for normative data are displayed via a 3D plot having RD, MWF and tract position as axes, as well as 2D projections along each of the 3 axes (RD vs. MWF, RD vs. tract position, MWF vs. tract position).

Single‐subject profilometry was investigated on one MS patient with chronic lesions (as assessed from the MRI findings reporting no new/enhancing lesions in the previous 4 years) provided by a researcher blind to the analysis experiment. The patient profile was visually compared to the control profile displayed with mean and 95% confidence interval based on the estimated standard deviation (STD).

Group comparison according to the profilometry framework was performed using a statistical model allowing for the joint analysis of all metrics concurrently while accounting for age and gender. Multivariate analysis of covariance (MANCOVA) was used with MWF and RD as dependent variables, group (LesGroup/NC) as an independent variable, age and gender as covariates and Pillai's trace as summary statistics. Pillai's trace is the sum on the variates generated by MANCOVA of the proportion of explained variance. It is therefore similar to $R^2$ and can be related to this statistical measure for interpretation. Importantly, permutation based multiple comparison correction [Nichols and Holmes, 2002] was implemented to account for both the serial correlation and the multiple MANCOVA analyses performed at each node along the tract profiles. Ten‐thousand random samples were drawn, to estimate the corrected P‐value threshold for significance testing. This multiple‐correction procedure was run for each of the dependent variables, so that to provide three corrected P‐value thresholds associated to group membership, age and gender. For each tract, group differences were visualized on a tube‐like structure representing the tract skeleton, using the AFQ toolbox [Yeatman et al., 2012]. Only significant differences between groups were shown. To investigate the usefulness of including spatial information in the previous MANCOVA analysis, we conducted a similar analysis on the same metrics but averaged over whole tracts. To ensure that no significant tract volume differences existed between LesGroup and NC groups, an analysis of covariance was performed, with group as dependent variable and tract volume, age and gender as independent variables. This was done for each tract analyzed and thus corrected for multiple comparison.

To estimate which dependent variable best discriminated between groups at a tract node level—when a significant group‐difference was found—a linear discriminant analysis (LDA) was performed. The group was the dependent and RD and MWF values the independent variables respectively. RD and MWF were standardized according to the NC data, and corrected for age and gender effects. The latter step was performed by fitting two ANCOVA models in NC, one with MWF and the other with RD as dependent variable—with age and gender as independent variables—at each node. The estimated regression coefficients were then used to correct for normal age and gender effects in both the control and patient data population, by applying the LDA on the corrected MWF and RD values, similarly to [Asafu‐Adjei et al., 2013]. Age and gender adjustments were only performed when a significant age or/and gender effect was found, as assessed by the previous MANCOVA analysis. Due to the standardization, the weights of the metrics in the LDA linear combination could then be interpreted as the different metrics discriminating power.

RESULTS

Profilometry Normative Data Visualization

The extension brought upon by profilometry on standard diffusion imaging and tractography analyses is illustrated in Figure 2. When tract profiles are projected along the axis of tract nodes, one obtains a plot similar to traditional ROI‐based measures. When combining the tract profiles of two different metrics, a new 3D view allows the observation of the co‐variation of both metrics. Projection of the 3D plot along a metric axis creates readily understood 2D tract profiles. A novel view is provided by projecting the 3D representation along the tract nodes axis. In this view, the location along the tract is indicated by the color gradient, and the curve becomes a 2D visualization of both the tract geometry and the selected metrics co‐variation.

Figure 2.

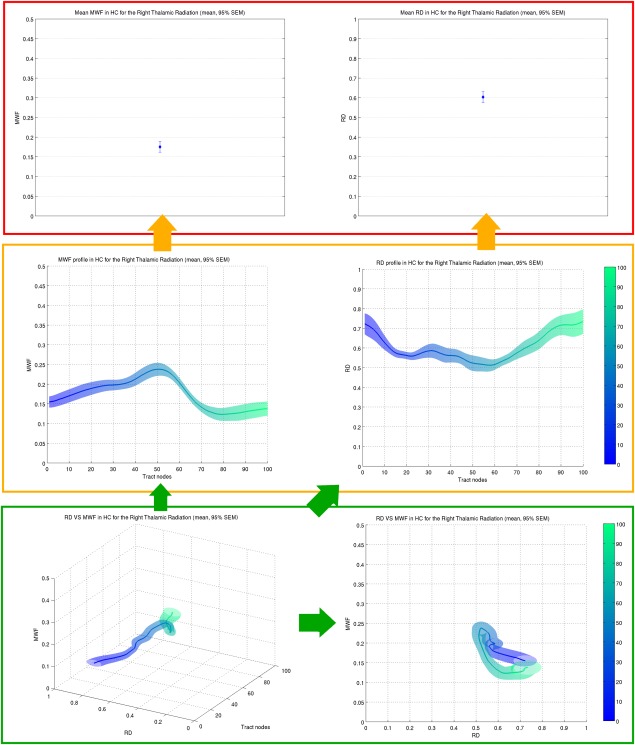
Profilometry visualization. (Top) Conventional mean metrics (MWF and RD) measured within a ROI, created from tractography of the right thalamic radiation. (Middle) Tract profiles representing each metric (MWF and RD) as it varies along the tract. The mean metrics in the top row can be obtained by collapsing the values across the tract position (tract nodes). (Bottom) 3D profilometry can be seen as a further generalized visualization (left), with projections in the {metric ‐ tract node} plane providing the tract profiles (cf. Middle), and the projection in the {metric ‐ metric} plane ({MWF‐RD}) a novel 2D tract characterization (right). Note that the same y‐axis limits have been chosen in all plots. The color scale ranging from blue to green represents the distance along the tract from node 0 (blue) to node 100 (green) as indicated by the color bars on the right of the middle and bottom rows.

Profilometry visualization of RD and MWF values in NC along the right SLF, ILF, and thalamic radiation are shown in Figure 3. Visualization of the forceps minor and right cortico‐spinal tracts are provided in the supplementary material section (Supporting Information Fig. S2).

Figure 3.

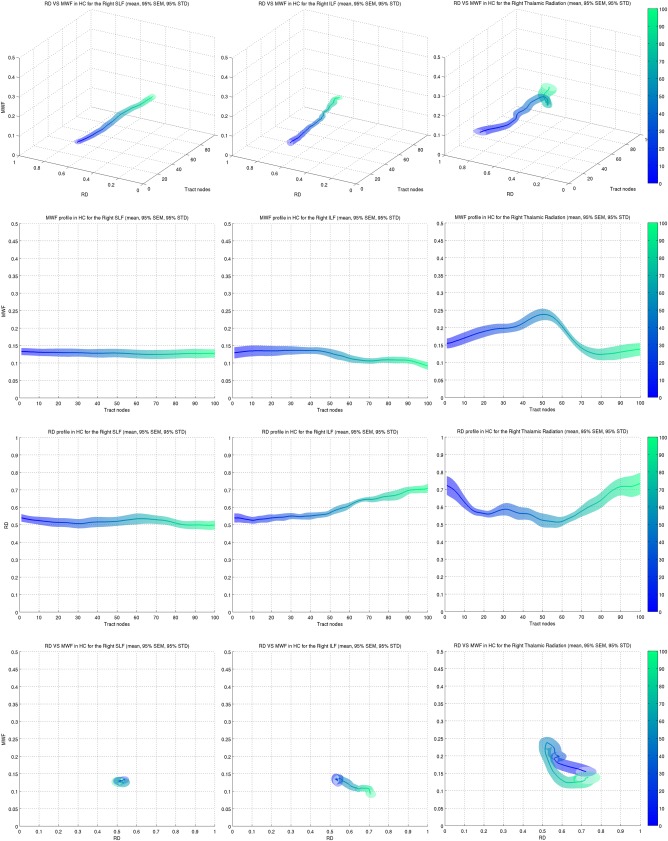
RD and MWF profilometry of the right SLF (left column), ILF (middle column) and thalamic radiation (right column). (1st row) 3D profilometry plots illustrated the changes of one metric with respect to the other along the tract. (2nd row) MWF tract profiles corresponding to the projection of the 3D plot in the {MWF ‐ tract node} plane. (3rd row) RD tract profiles. (4th row) MWF changes as a function of RD, collapsed across tract nodes. This plot can play the role of a “tract signature” and summarizes the general shape of each metric tract profile in a single plot. The color scale ranging from blue to green represents the distance along the tract from node 0 (blue) to node 100 (green) as indicated by the color bars on the right of the plots.

The top row of Figure 3 illustrates the variation of both metrics along the tract where position is represented by color ranging from blue (start) to green (end). The surrounding surface corresponding to the ±95% confidence intervals in the standard error of the mean (SEM). The subsequent two rows are the projection of the 3D profilometry visualization in the {MWF, tract position} and {RD, tract position} planes. Finally the last row shows the variation of MWF with RD. Since the tract position is encoded as color, the RD‐MWF plot in the last row can be seen as a condensed representation of the 3D plots of the first row. A demonstration of their use is discussed later on. MWF tended to exhibit a flat profile in most tracts with the exception of the thalamic radiation, which had higher values in the center portion of the tract (second row). RD varied widely in most tracts with the exception of the SLF where the profile was flat (third row). RD in the ILF exhibited a constant increase, while its profile in the thalamic radiation was somewhat an inverse to MWF. These properties could be seen in the RD‐MWF plots (bottom row) where:

• a “dot” profile (left) indicates a constant profiles of each metric

• a “line” profile (middle) indicates a constant profile of one of the metric with a relative constant decrease or increase in the profile of the other metric

• an “alternative shape” profile (right) represents a more complex variation of both metrics

Single‐Subject Profilometry

In the single‐case study, tracts affected by lesions demonstrated a change in tract profile around the location of the lesion. The RD‐MWF profilometry visualization of a lesion on the right SLF is shown on Figure 4. It can be seen that the tract profile of RD (top–middle) and MWF (top–right) extend beyond the 95% confidence interval (based on STD) around the location of the lesion (top – left). This can be seen directly on the 3D profilometry view (bottom – middle) and its 2D projection along the tract node axis (bottom – right).

Figure 4.

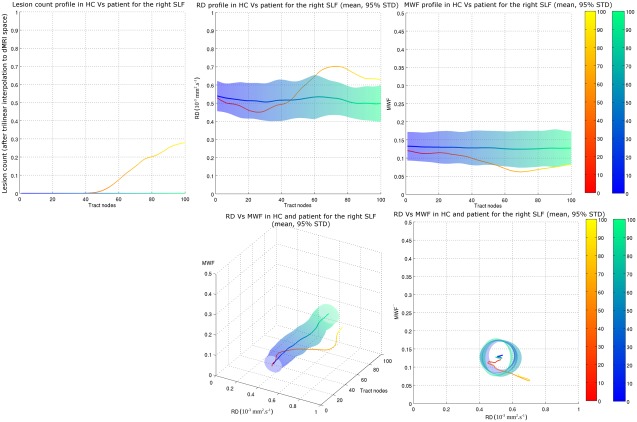
Single‐subject profilometry component visualization for a patient with a lesion in the right SLF. (Top) Tract profiles of lesion count (accounting for spatial deformation when registering the lesion mask to dMRI space), RD and MWF, on the left, middle and right respectively (Bottom) 3D profilometry view and associated 2D projection in the {MWF‐RD} plane. The deviation of the patient data from the normative data is clearly visible in the latter plot. Blue surface indicates 95% confidence interval in the NC mean, based on STD. The color scale ranging from blue to green and from red to yellow represents the distance along the tract from node 0 (blue for NC, red for patient) to node 100 (green for NC, yellow for patient) as indicated by the color bars on the right of the plots.

Profilometry Group Comparison

No significant tract volume differences were found between LesGroup and NC groups. Significant group differences identified by the MANCOVA model are shown for the Forceps Minor in Figure 5. Only significant P‐values are shown.

Figure 5.

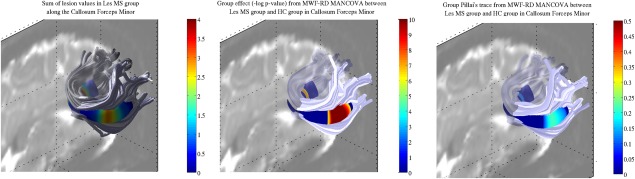
Profilometry group comparison for the forceps minor. (Left) Sum of lesions within LesGroup. (Middle) Significant group differences after multiple comparison correction. (Right) Group Pillai's trace in significant nodes.

Lesions were markedly concentrated around two areas on each side of the mid‐sagital plane (Fig. 5 left). The MANCOVA model combining MWF and RD demonstrated significant differences in the LesGroup compared to NC in the location of lesions (Fig. 5 middle). The mean Pillai's trace within the two clusters, for the group independent variable, were 0.11 and 0.16 in the left and right hemispheres respectively (Fig. 5 right). Results for the right cortico‐spinal tracts, thalamic radiation and ILF were similar and only the right SLF group comparison did not show significant differences at the lesion location (Supporting Information, Figs. S3–S6).

A significant age effect in the MANCOVA model was demonstrated in most of the tract (Fig. 6 left). The mean Pillai's trace within the two clusters, for the age independent variable, were 0.14 and 0.13 in the left and right hemispheres respectively (Fig. 6 right). No significant gender effect was found. Age and gender effects were found in both the right thalamic radiation and SLF (Figs. S3 and S5 in Supporting Information). No significant age or gender were found in the right cortico‐spinal tracts or ILF (Supporting Information Figs. S4 and S6).

Figure 6.

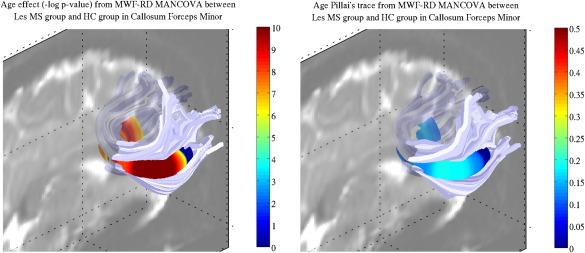
Age effect as assessed via a MANCOVA analysis with MWF and RD as dependent variables. (Left) Significant age effect. As illustrated, most nodes along the tract showed an age effect, demonstrating the importance of accounting for this variable when investigating MWF and RD metrics. (Right) Age Pillai's trace corresponding to the significant nodes. The value of Pillai's trace suggested age explained a non‐negligible part of the MWF and RD variance.

The associated profilometry component visualization, with SEM visible for healthy controls, is shown in Figure 7. As in the forceps minor, MWF and RD were shown to present significant differences between LesGroup and NC at the location of lesions and beyond in other tracts, MWF exhibiting both sensitivity and specificity to lesion locations.

Figure 7.

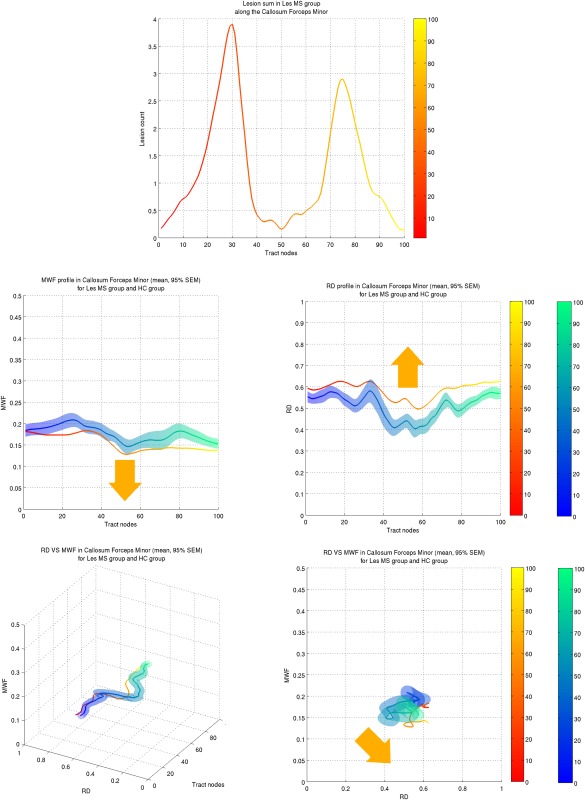
Profilometry component visualization for the forceps minor. (Top) Sum of lesions (accounting for spatial deformation when registering the lesion mask to dMRI space) along the forceps minor. Two main clusters can be seen. (Middle) Tract profiles of MWF and RD, on the left and right respectively. Data for the NC and MS LesGroup are shown in blue and red shades respectively. The orange arrow illustrates the general direction of change for the MS LesGroup: MWF tends to decrease and RD to increase. (Bottom) 3D profilometry view and associated 2D projection in the {MWF‐RD} plane. In the latter plot the shift in MWF and RD values, when comparing the MS LesGroup to NC, is at an angle corresponding to both a decrease in MWF and increase in RD. Again each metric tract profiles, and how they differ between groups, can be summarized in a single plot with this projection. The color scale ranging from blue to green and from red to yellow represents the distance along the tract from node 0 (blue for NC, red for patients) to node 100 (green for NC, yellow for patients) as indicated by the color bars on the right of the plots.

When conducting the MANCOVA analysis over metrics averaged over whole tracts, the group differences found previously in the right cortico‐spinal tracts and thalamic radiation were no longer significant.

Linear Discriminant Analysis

The results of the LDA applied to the LesGroup and NC groups after standardizing MWF and RD values are shown for the forceps minor on Figure 8. The linear combination coefficients associated with MWF were larger than those associated with RD. Similar results were found for the other tracts (Supporting Information Fig. S7).

Figure 8.

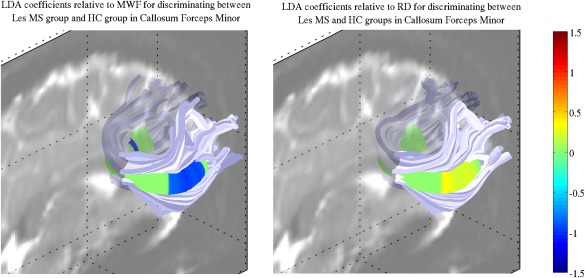
Visualization of the coefficients of MWF and RD in the linear combination best discriminating the LesGroup and HC groups, as assessed by LDA, for the forceps minor. (Left) Coefficients of MWF at each node. (Right) Coefficients of RD at each node. Note that both MWF and RD have been standardized and adjusted for age and gender as according to NC values.

DISCUSSION

Profilometry Applied to MS single‐Case Study

Although no formal statistical test has been designed in the current framework for single‐case study, it can be seen from the 95% confidence range in the mean normative data (based on STD) that single patient values outside this range could be indicative of pathology, as shown by the associated lesion location (Fig. 4). In this respect we believe that in the case of dual metric profilometry, the 2D projection in the {metric ‐ metric} plane could be used to identify deviations from normal metric values. Despite the relatively small number of NC used, we still observed anticipated lesion‐related imaging changes in a single subject basis. Increasing the number of NC to enable even more sensitive analysis will be the focus of future work.

Future studies based on profilometry could also benefit from normative data of scanner‐ and sequence‐independent metric derived from large scale initiatives.

Profilometry Applied to MS Groups Comparison

RD‐MWF profilometry applied to the forceps minor demonstrated significant group differences nearby patient lesion locations (Figs. 5 and 7). The LDA analysis provided higher coefficients for MWF, suggesting that changes in MWF were more strongly related to disease, thereby supporting the use of MWF as a biomarker of myelin insult.

RD is purported to measure both inflammation and myelin configuration while MWF is ideally assumed to only relate to myelin. By combining RD and MWF more sensitivity can then be expected in the differences detected when microstructural changes result in abnormalities in both MWF and RD. These changes are then more likely to contribute to overall significant differences since they affect all dependent variables (MWF and RD) in the MANCOVA analysis. In this work we chose for the single‐case analysis to analyze chronic lesions not affected by inflammation. However, a follow‐up study investigating the combination of MWF with a diffusion metric sensitive to inflammation could prove particularly suitable in characterizing newly detected MS lesions associated with inflammation.

For MS, the profilometry approach to group comparison would not be suited to a small cohort of patients as lesions would be unlikely to be distributed in similar locations across patients. This framework is indeed most efficient when detecting white matter changes expected to be spatially consistent across subjects. We demonstrated that it could still be useful when this condition is not met, such as in MS, when the cohort is of suitable size.

We envision that profilometry could be particularly useful in MS to understand the distribution of lesions among various tracts to describe the relationship of lesions to neurodegeneration. For example Henry et al. (2009) suggested that the higher lesion density they observed in thalamo‐cortical tracts (compared to the remaining white matter) could explain the thalamic atrophy observed early in the disease. Furthermore, Kuceyeski et al. (2015) demonstrated significant correlations between atrophy in subcortical regions (including the thalamus) and abnormalities in connecting white matter in MS, as well as a link between subtle cognitive disability and lesions in white matter connecting to the visual system. In a similar fashion, profilometry could help clarify the relationship between lesions and clinical disability (ambulation and cognitive dysfunction). In addition, through this framework, we can begin to explore differences between tracts among MS patients with regard to both propensity for lesions [lesions have been suggested to have a predilection notably for the optic nerves, brainstem and cerebellum, see e.g., Popescu et al., 2011, and Sobel and Moore, 2008], and the extent of myelin injury and potential recovery. Indeed, it has been pointed out that the location of lesions influence the amount of remyelination [Goldschmidt, 2009]. Lastly, we would like to highlight, neuromyelitis optica, a demyelinating disease which classically affects the optic nerve and spinal cord only [Pittock and Lucchinetti, 2015]. However, with the development of the aquaporin‐4 antibody, a spectrum of the disease is now appreciated and brain lesions are commonly found, yet still poorly understood [Pittock and Lucchinetti, 2015]. The profilometry framework could be particularly useful to characterize the fibers susceptible to damage within the spectrum of the disease and provide insight into clinical the significance of brain involvement.

Statistical Analysis

There are several reasons for choosing the joint analysis approach of MANCOVA, as compared to several univariate ANCOVAs. First, separate ANCOVAs ignore the relationship between the multiple metrics, as opposed to MANCOVA which uses the variance‐covariance between variables. Second, separate ANCOVAs inflate the family‐wise error rate. Third, and more importantly, MANCOVA can detect group differences according to a combination of variables, compared to ANCOVAs restriction to a single variable. As such, MANCOVA may detect group differences when separate ANCOVAs could not. Finally, MANCOVA provides a single test outcome, which simplifies group comparisons. If insight into the relative contribution of the different metrics is desired, then the follow‐up LDA analysis can be performed.

LDA of standardized variables allows interpretation of the discriminating power of each metric according to its weight in the linear combination best discriminating the two groups. This is useful when several metrics detect group differences, and when insight in the origin of the differences is needed. It can also be used to assess the discriminating power of each metric studied, as in this work where LDA suggested MWF contributed more than RD when differentiating between NC and MS patients having lesions in the forceps minor. In this work we only examined the discriminating aspect of LDA which can also be used for classification. The linear combinations best discriminating groups at each node can indeed be used to classify additional data. This will be the focus of future research.

Both MANCOVA and LDA were chosen because they allow for covariates. Indeed, white matter microstructural metrics have been shown to largely depend on age [Lebel et al., 2008; Westlye et al., 2010] and also possibly on gender [Lebel and Beaulieu, 2011]. This was also demonstrated in the results found for the forceps minor (Fig. 6). Therefore it appears crucial to account for age and gender in any statistical analysis aimed at comparing white matter microstructural properties between groups, as in the work by [Asafu‐Adjei et al., 2013].

Profilometry Framework and Novel Contributions

The possibility of examining diffusion metric changes along tracts reconstructed with tractography in individual subjects was introduced around 10 years ago [Fillard et al., 2003; Jones et al., 2005; Corouge et al., 2006], however none of these studies presented a framework for group comparison. One of the first to do so beyond visual assessment was [Lin et al., 2007] who investigated the CST, and which, despite its novelty, did not correct for the multiple comparisons at each tract node. Multiple comparison correction was implemented in [O'Donnell et al., 2009], [Colby et al., 2012] and [Yeatman et al., 2012]. However only the latter relied on automated tractography in each subject. [Goodlett et al., 2009] and [Zhu et al., 2011] introduced novel multimetric joint analysis, with only the latter accounting for covariates, and both restricted to atlas‐based tractography and dMRI metrics. While research has been carried out to combine dMRI and non‐dMRI metrics [Bells et al., 2011; Stikov et al., 2011; De Santis et al., 2014], none have combined them in tract profiles for group comparison. The main novelty of the work described in this paper is to present a statistical framework based on the joint multimetric analysis of tract profiles, relying on MANCOVA and LDA. This framework also corrects for multiple comparison and controls for covariates, a crucial feature for clinical studies of white matter microstructure where measured characteristics are often shown to be significantly dependent on age and, at times, gender. The associated visualization, composed of 3D tract profiles and their metric‐metric 2D projections, provides useful and succinct visual clues of both normative data and patient data (Figs. 3, 4, and 7).

In general, different metrics can be expected to vary in sensitivity according to particular microstructural changes; therefore, multiple metrics are optimal to characterize the underlying process. A possible caveat in the profilometry analysis can be a loss in sensitivity when including non‐informative metrics. However, in practice researchers are assumed to have made a thoughtful choice in the metrics to be used in the profilometry framework when adapting to their research hypotheses. The usefulness of the spatial information embed in the framework was demonstrated in our study with the MANCOVA analysis on the metrics averaged over whole tracts. A loss of sensitivity was shown in that case, as group differences previously found with profilometry of the right cortico‐spinal tracts and right thalamic radiation became no longer significant.

Profilometry Pipeline

While multiple tools currently exist to perform diffusion imaging analysis, from diffusion metric calculation to fiber directions estimation and tractography, limited software are available to perform both tractography in individual subjects and tract profiles analysis. While [Colby et al., 2012] described an open‐source Matlab toolbox to conduct the tract profile analysis with a linear mixed‐effects statistical model, it did not include tractography. [Yeatman et al., 2012] presented another open‐source Matlab toolbox both performing tractography and tract profile analyses. However none of these two articles presented the ability to perform the joint multimetric analysis we describe in this paper, which will be available for download at http://dx.doi.org/10.5281/zenodo.35090. The presented methodology can not only combine tract profile analyses in a single statistical model but can also take into account covariates such as age and gender which are of particular importance in most clinical investigations. Furthermore, restriction to the Matlab platform made it difficult for these packages to extend to other tools and therefore limit their use. We developed the profilometry framework within NiPype (http://nipy.sourceforge.net/nipype) which offers abstract interfaces to all the most common existing neuroimaging tools. This means that ROIs can be transformed from MNI space to subject space with deformations computed by either SPM or AFNI, the diffusion metric can be calculated with FSL, while tractography can be easily performed from fiber directions estimated in Camino or MRTrix. The profilometry open‐source package has been designed with this flexibility in mind. The existing software deemed most optimal has been chosen at each step, but additional choices will be offered as the pipeline develops.

Supporting information

Supporting Information Figure S1

Supporting Information Figure S2

Supporting Information Figure S3

Supporting Information Figure S4

Supporting Information Figure S5

Supporting Information Figure S6

Supporting Information Figure S7