Comparing within‐subject classification and regularization methods in fMRI for large and small sample sizes

Abstract

In recent years, a variety of multivariate classifier models have been applied to fMRI, with different modeling assumptions. When classifying high‐dimensional fMRI data, we must also regularize to improve model stability, and the interactions between classifier and regularization techniques are still being investigated. Classifiers are usually compared on large, multisubject fMRI datasets. However, it is unclear how classifier/regularizer models perform for within‐subject analyses, as a function of signal strength and sample size. We compare four standard classifiers: Linear and Quadratic Discriminants, Logistic Regression and Support Vector Machines. Classification was performed on data in the linear kernel (covariance) feature space, and classifiers are tuned with four commonly‐used regularizers: Principal Component and Independent Component Analysis, and penalization of kernel features using L ₁ and L ₂ norms. We evaluated prediction accuracy (P) and spatial reproducibility (R) of all classifier/regularizer combinations on single‐subject analyses, over a range of three different block task contrasts and sample sizes for a BOLD fMRI experiment. We show that the classifier model has a small impact on signal detection, compared to the choice of regularizer. PCA maximizes reproducibility and global SNR, whereas L _p‐norms tend to maximize prediction. ICA produces low reproducibility, and prediction accuracy is classifier‐dependent. However, trade‐offs in (P,R) depend partly on the optimization criterion, and PCA‐based models are able to explore the widest range of (P,R) values. These trends are consistent across task contrasts and data sizes (training samples range from 6 to 96 scans). In addition, the trends in classifier performance are consistent for ROI‐based classifier analyses. Hum Brain Mapp 35:4499–4517, 2014. © 2014 Wiley Periodicals, Inc.

INTRODUCTION

Blood‐oxygenation level dependent functional MRI (BOLD fMRI) is an imaging technique that is sensitive to the changes in blood oxygenation that accompany neuronal activity. This is used to localize stimulus‐evoked changes in brain activity, and make predictions about brain regions implicated in experimental stimuli, in order to characterize the relationship between brain function and behavior. However, fMRI is characterized by a weak, complex BOLD response, and significant noise confounds. Furthermore, identifying discriminative brain regions in whole‐brain analysis is an ill‐conditioned problem, with far more variables (brain voxels) than observations (time points). There is therefore a need for sophisticated analysis models, to reliably and accurately measure the predictors of brain‐state.

Multivariate classification and brain mapping techniques have long been applied to functional neuroimaging data [e.g. Hansen et al., 1999; Haxby et al., 2001; Kustra and Strother, 2001; Morch et al., 1997; Tegeler et al., 1999], and have become increasingly popular in fMRI in recent years, due to their sensitivity to spatially distributed, functionally connected brain networks. They have proven invaluable in numerous studies of sensory, motor and cognitive neuroscience [Berman et al., 2013; Broderson et al., 2012; Carlson et al., 2003; Davatzikos et al., 2005; LaConte et al., 2005; Mitchell et al., 2008; Raizada et al., 2010; Shaw et al., 2003; Shinkareva et al., 2007], neurofeedback and brain‐computer interface [LaConte et al., 2005; Sitaram et al., 2010; Yoo et al., 2004] and predicting disease state and recovery in clinical populations [Fu et al., 2008; Menzies et al., 2007; Modinos et al., 2012; Pagani et al., 2009; Schmah et al., 2010; Wang et al., 2006; Yoon et al., 2008]. Multivariate classification is well‐suited to fMRI studies in which the activation patterns are not known a priori, and distributed brain networks are potentially recruited (e.g. novel experimental designs, complex integrative tasks, groups with different behavioral profiles, and the complex effects of disease state); these models allow researchers to simultaneously localize activated brain areas and measure their prediction (generalization) to independent test data.

Research in these domains is typically concerned with both the generalizability of multivariate classifier models, and the confidence with which we can interpret discriminant brain maps. Prediction accuracy (P) measures the generalizability of the classifier model, based on how well we can predict brain‐state for new, independent data. Conversely, reproducibility (R) measures the stability of the discriminating brain maps (or. “sensitivity maps”) across repeated analyses. That is, how confident we can be in the identified brain regions that contain discriminative information. Both P and R are important measures of model performance, and their relationship characterizes bias‐variance tradeoffs in the classifier models [Rasmussen et al., 2012; Strother et al., 2002; Yourganov et al., 2011].

However, the researcher who wishes to employ multivariate classification must choose from among a wide variety of available models, with different underlying assumptions, and without clear information on the (P, R) tradeoffs between models. For example, generative models construct a probability distribution from the data prior to classification, whereas non‐probabilistic classifiers directly estimate an optimal decision rule on the data. In addition, the classifier's decision surface may be a linear function in the feature space (a hyperplane), or a nonlinear surface. Despite the proliferation of models, there have been only a few studies on the impact of classifier choices on fMRI results, including [Hansen et al., 2001; LaConte et al., 2005; Lange et al., 1999; Misaki et al., 2010; Rasmussen et al., 2012; Schmah et al., 2010].

Multivariate classifiers for fMRI must also be regularized, which involves imposing constraints that control model complexity, to reduce over‐fitting, and optimize the generalizability of the classifier model. Part of model training is thus to determine the optimal regularization parameters. Many regularization strategies have been applied to fMRI analysis, typically by directly penalizing features of the fMRI data (e.g. L _p‐norm penalties). Other strategies include component decompositions (e.g. Principal Component and Independent Component Analysis); although they are not often thought of as regularizers, they can be defined as special cases of L _p penalization [Kustra and Strother, 2001]. Alternatively, many studies perform a feature selection step that extracts a subset of brain voxels during model training (e.g. Haxby et al., 2001; Mitchell et al., 2004; Pereira et al., 2009; Misaki et al., 2010]. However, this approach of feature selection driven by task prediction may decrease model sensitivity and generalizability [Rasmussen et al., 2012]. The effect of regularizer choice is even less explored than classifier models, despite evidence that it significantly impacts classifier performance [Churchill et al. 2012; LaConte et al., 2005; Rasmussen et al., 2012; Strother et al., 2004].

There are other, practical considerations when selecting classifiers; namely, how stable are these models as a function of signal strength and sample size? The majority of classifier‐based studies use large, multisubject experimental datasets with hundreds of scans, and conservative preprocessing strategies. This stabilizes classifiers, and minimizes the influence of noise and artifact. It is not clear how performance generalizes to within‐subject analysis and small datasets, where only a few scans may be available per stimulus type. These issues arise when analyzing brief, single‐subject datasets and measuring cognitive changes over short time scales. They are also relevant for clinical studies, in which patients may only tolerate a few minutes of scanning, and a significant portion of the dataset may be corrupted with head motion and other noise [Carter et al., 2008]. An additional consideration is the number of input voxels in the analysis. In general, classifier studies focus exclusively on either whole‐brain analysis [e.g. LaConte et al., 2005; Rasmussen et al., 2012; Schmah et al., 2010;] or focus on smaller, predefined regions of interest (ROIs) [e.g. Haxby et al., 2001; Misaki et al., 2010]. However, it is unclear if the findings of whole‐brain studies are relevant to ROI‐driven analysis, and vice versa.

In this article, we examined the performance of different classifier/regularizer choices for the analysis of individual subject datasets, using task battery data collected from young, healthy subjects. We examined four standard classifiers: Linear Discriminant (LD), Quadratic Discriminant (QD), Logistic Regression (LR), and Support Vector Machines (SVM), all of which have been previously applied to fMRI data. We also examined the impact of four different regularization methods: L ₂ and L ₁ penalties, along with two methods of subspace estimation, Principal Component Analysis (PCA) and Independent Component Analysis (ICA). All classification and model regularization was applied to data in the linear kernel space (i.e. the untransformed covariance matrix between image volumes) because in our experience, sparse regularizers applied in the voxel space tend to produce overly sparse activation maps [Rasmussen et al., 2012]. We compared model performance under a range of different task contrasts, and as a function of sample size, by sub‐sampling from within‐subject datasets. We evaluated the classifier/regularizer models using measures of (P,R) and global Signal‐to‐Noise Ratio (gSNR), estimated in the NPAIRS cross‐validation framework [Strother et al., 2002].

We also measured the relative similarity of brain activation patterns across the different classifier models, using DISTATIS, a multidimensional scaling technique that computes bootstrapped confidence estimates of pattern similarity (Abdi et al., 2009]. Finally, we tested whether the trends in classifier performance for whole‐brain analysis generalized to ROI‐based analyses. We do not address the issue here, but for data on the effects of nonlinear kernels, see Schmah et al. [2010] and Rasmussen et al. [2012].

METHODS

We begin by reviewing the different classifier models and regularization methods that are evaluated in this article. Afterwards, we describe the experimental data that is used to test the different models, along with data preprocessing steps. Finally, we discuss the resampling framework and provide details of the metrics used to evaluate model performance: prediction (P), reproducibility (R), global Signal‐to‐Noise Ratio (gSNR) and the DISTATIS measure of brain map similarity.

Classifier Models

We examined four binary classifiers that are used in fMRI analyses: Linear Discriminant (LD), Quadratic Discriminant (QD), Logistic Regression (LR), and Support Vector Machines (SVM). In fMRI analysis, classifiers are typically used to predict the behavioral task (the “class”) that was performed during acquisition of a brain image. This is achieved in a cross‐validation framework, with a labeled training set and an unlabeled test set [Pereira et al., 2009]. We acquired a set of N image volumes, containing V brain voxels, which are represented as V‐dimensional column vectors of X. For ill‐conditioned X (V >>N), we greatly reduce the number of features while preserving data dimensionality, by classifying on the NxN linear kernel $\mathbf{\Phi }={\mathit{X}}^T\mathit{X}$; this is the covariance matrix of X, if the mean is subtracted from each voxel. We emphasize that all classifier and regularizer combinations (jointly termed “models”) were applied in the linear kernel space $\mathbf{\Phi }$; this is in contrast to much of the fMRI classifier literature, which directly regularizes the voxel features of X, imposing spatial sparsity to achieve a well‐posed solution. We chose our alternate approach, as prior research has demonstrated that voxel‐space regularization tends to produce overly‐sparse representations, particularly for weaker task contrasts [Rasmussen et al., 2012] whereas the effects of linear kernels are less understood.

The input data includes $\mathbf{\Phi }$, which is treated as a column matrix $\mathbf{\Phi }=[{\mathit{\varphi }}_{{}_{}1}{,}_{}{\mathit{\varphi }}_{{}_{}2},\mathrm{...},{\mathit{\varphi }}_{{}_{}N}]$ where each ${\mathit{\varphi }}_{{}_{}n}$ is an Nx1 feature vector; it also includes class labels y = [y₁…y_N] with y_n $\in${‐1,1}, denoting scans acquired during class 1 or 2 stimuli, respectively. Each classifier uses training data to estimate a decision boundary D( ${\mathit{\varphi }}_{{}_{}n}$) between the classes, where D( ${\mathit{\varphi }}_{{}_{}n}$)<0 assigns feature vector ${\mathit{\varphi }}_{{}_{}n}$ to class 1, and D( ${\mathit{\varphi }}_{{}_{}n}$) > 0 assigns ${\mathit{\varphi }}_{{}_{}n}$ to class 2. For all models except SVMs, we assign each data vector ${\mathit{\varphi }}_{{}_{}n}$ to the class that maximizes posterior probability $p({\text{class}\hspace{0.17em}}_{}i|{\mathit{\varphi }}_n)$. The decision boundary is given by the log‐ratio of posterior probabilities:

$$D({\mathit{\varphi }}_n)=\log \frac{p({\mathit{\varphi }}_n|\text{class}\hspace{0.17em}2)p(\text{class} 2)}{p({\mathit{\varphi }}_n|\text{class}\hspace{0.17em}1)p(\text{class} 1)}$$ (1)

For current results, we have equal sample sizes in each class, and assume equal prior probabilities $p({\text{class}\hspace{0.17em}}_{}1)=p({\text{class}\hspace{0.17em}}_{}2)$. This requires that we only estimate the conditional distribution $p({\mathit{\varphi }}_n|{\text{class}\hspace{0.17em}}_{}i)$ for each class. The classifier models are defined as follows; see Table 1 for a summary of their properties.

Table 1.

Properties of the evaluated classifier models

	Decision surface	Model type	Loss function
Linear discriminant (LD)	Linear	Probabilistic	Gaussian
Quadratic discriminant (QD)	Nonlinear	Probabilistic	Gaussian
Logistic regression (LR)	Linear	Probabilistic	Logistic
Support vector machines (SVM)	Linear	Nonprobabilistic	Hinge‐loss

Quadratic and linear discriminants

These are generative classifier models, which assume that the data from each class has a multivariate Gaussian posterior distribution, with mean vector μ _i and covariance matrix Σ _i:

$$p({\mathit{\varphi }}_n|{\text{class}\hspace{0.17em}}_{}i)={\left(2\pi \right)}^{-p/2}{\left|{\mathbf{\Sigma }}_i\right|}^{-1/2}{e}^{-\frac{1}{2}{({\mathit{\varphi }}_n-{\mathit{\mu }}_i)}^T{\mathbf{\Sigma }}_i^{-1}({\mathit{\varphi }}_n-{\mathit{\mu }}_i)}$$ (2)

During model training, the maximum‐likelihood Gaussian parameters are estimated, including within‐class means m ₁ and m ₂, and covariances S ₁ and S ₂. For QD, the decision function D( ${\mathit{\varphi }}_{{}_{}n}$) of Eq. (1) is the ratio of Gaussian log‐likelihoods. This reduces to a quadratic (that is, nonlinear) function of ${\mathit{\varphi }}_{{}_{}n}$:

$$D({\mathit{\varphi }}_n)=\frac{1}{2}\log \frac{\left|{\mathit{S}}_1\right|}{\left|{\mathit{S}}_2\right|}-\frac{1}{2}\left\{{({\mathit{\varphi }}_n-{\mathit{m}}_2)}^T{\mathit{S}}_2^{-1}({\mathit{\varphi }}_n-{\mathit{m}}_2)-{({\mathit{\varphi }}_n-{\mathit{m}}_1)}^T{\mathit{S}}_1^{-1}({\mathit{\varphi }}_n-{\mathit{m}}_1)\right\}$$ (3)

The LD classifier makes the simplifying assumption that the population covariances of the two classes are equal; in place of class‐specific sample covariances S ₁ and S ₂, LD uses the pooled covariance estimate S = (S ₁+S ₂)/₂. This reduces Eq. (3) to a linear function of ${\mathit{\varphi }}_{{}_{}n}$:

$$D({\mathit{\varphi }}_n)={\left({\mathit{S}}_{}^{-1}({\mathit{m}}_2-{\mathit{m}}_1)\right)}^T{\mathit{\varphi }}_n-\frac{1}{2}{({\mathit{m}}_2+{\mathit{m}}_1)}^T{\mathit{S}}_{}^{-1}({\mathit{m}}_2-{\mathit{m}}_1)$$ (4)

This is a decision hyperplane, defined by normal vector w = S ⁻¹(m ₂ − m ₁) and a bias term b = −¹/₂(m ₂ + m ₁)^T S ⁻¹(m ₂ − m ₁), which can be expressed as

$$D({\mathit{\varphi }}_n)={\mathit{w}}^T{\mathit{\varphi }}_n+\mathit{b}$$ (5)

Note that the LD model produces the same solution as fitting a least‐squares regression onto target variables y, which minimizes the Gaussian loss function [Hastie et al., 1995]:

$$L=\frac{1}{2}{{\displaystyle \sum _n\left({\mathit{y}}_n-\mathit{w}\cdot {\mathit{\varphi }}_n-\mathit{b}\right)}}^2$$ (6)

Both QD and LD classifiers therefore assign data points to the class of highest posterior probability, under Gaussian model assumptions.

Logistic regression

This classifier maps the unbounded features of ${\mathit{\varphi }}_{{}_{}n}$ onto the range [0, 1] using the logistic sigmoid function σ{a} = 1/(1 + e^−a). This is a probabilistic model, derived by expressing the posterior probability of Class 1 as a function of the log‐odds ratio from Eq. (1):

$$p({\text{class}\hspace{0.17em}}_{}1)=\frac{1}{1+\exp \left\{-\log \frac{p({\mathit{\varphi }}_n|{\text{class}\hspace{0.17em}}_{}1)}{p({\mathit{\varphi }}_n|{\text{class}\hspace{0.17em}}_{}2)}\right\}}$$ (7)

Assuming the log‐odds decision boundary is a linear function of the features, we produce a decision hyperplane, defined by normal vector w and bias term b (as in Eq. (5)), with a nonlinear mapping function σ{D( ${\mathit{\varphi }}_{{}_{}n}$)}. This solution requires that we minimize the logistic loss function, which may be compactly expressed as:

$$L={\displaystyle \sum _n\log \left(1+\exp \left\{y_n(\mathit{w}\cdot {\mathit{\varphi }}_n-\mathit{b})\right\}\right)}$$ (8)

There is no analytic solution to minimize this function, although a number of iterative methods have been developed; we employed the Iteratively Reweighted Least Squares (IRLS) procedure (Bishop, 2006; code developed in‐house), which can be readily adapted to L ₁ (Lasso) and L ₂ (ridge regression) regularized models (applied with Matlab's Statistics toolbox (R2007b); see Model Regularization for more details).

Support vector machines

These classifiers estimate a hyperplane (defined by Eq. (7)) in which the distance from D( ${\mathit{\varphi }}_{{}_{}n}$) to the nearest data point (defined as the “margin”) is maximized. If we penalize misclassification errors using “slack variable” weights ξ_n for individual data points, this is solved for weight parameter C and slack variable parameter p by the condition:

$$\underset{\mathit{w},\mathit{\xi },\mathit{b}}{\min }\left\{\frac{1}{2}\left|\right|\mathit{w}|{|}^2+C{\displaystyle \sum _n|{\xi }_n{|}^p}\right\}$$ (9)

under the constraint

$$y_n(\mathit{w}\cdot {\mathit{\varphi }}_n-b)\ge 1-{\xi }_n{,}_{}{{}_{}}_{}{\xi }_n\ge 0$$ (10)

That is, scans must be projected onto the correct side of the decision surface, and also projected beyond the (slack variable‐adjusted) margins of this decision surface. We use a non‐standard SVM approach. Conventionally, Eq. (10) is defined for voxel‐space data (replacing ${\mathit{\varphi }}_{{}_{}n}$ with x _n) and the SVM is solved in “dual‐space” by re‐formulating it as a function of its kernel $\mathbf{\Phi }$; in standard SVM, vector w represents voxel weights (e.g. a sensitivity map; referred to as the “primal weight vector”). We instead transform the data into kernel space $\mathbf{\Phi }$, and the SVM solves for optimal weights w on the kernel features themselves. See Constructing Voxel Sensitivity Maps below for more details on how w is transformed into voxel‐space. This approach was chosen to maintain consistency with the other classifier models, which all estimate the decision boundary on the kernel‐space features. The SVM estimates w as a linear combination of input vectors:

$$\mathit{w}={\displaystyle \sum _n{\alpha }_n{y}_n{\mathit{\varphi }}_n}$$ (11)

In general, the solution admits nonzero weights α _n > 0 for a few ${\mathit{\varphi }}_{{}_{}n}$ along the margins of the hyperplane [Rasmussen et al., 2012]. These ${\mathit{\varphi }}_{{}_{}n}$ are the “support vectors” which drive discrimination; thus ${\mathit{\varphi }}_{{}_{}n}$ which are most difficult to classify have the most influence on the decision surface. The misclassification penalty is controlled by parameter C, where a small C allows the margin to include more support vectors contributing α _n > 0 to the discriminant function. SVM was the only tested classifier that has no probabilistic interpretation for D( ${\mathit{\varphi }}_{{}_{}n}$). This model was implemented using svmtrain and svmclassify functions from MatLab's Bioinformatics Toolbox R [2007b].

Constructing voxel sensitivity maps

An important part of classification is to derive a “sensitivity map” s _vox, which weights brain voxels based on their importance in constructing the decision boundary D( ${\mathit{\varphi }}_{{}_{}n}$). For all models, we used the approach defined in [Kjems et al. 2002], which estimates s _vox based on the partial derivative ${\mathit{s}}_{\text{vox}\hspace{0.17em}}=\partial D(\mathit{x})/\partial \mathit{x}$, a function of training inputs x. For LD, LR and SVM, this is given by the linear feature weighting vector w, that minimizes loss functions in Eqs. ((6), (8), and (10)), respectively [Kjems et al., 2002; LaConte et al., 2005; Rasmussen et al., 2012]. Because w is solved in the kernel feature space, we reconstruct the voxel image via the transformation s_vox = Xw. For example in LD, ${\mathit{s}}_{\text{vox}\hspace{0.17em}}=\mathit{X}\left({\mathit{S}}^{-1}({\mathit{m}}_2-{\mathit{m}}_1)\right)$, where m ₁, m ₂ and are the kernel‐space class means and S is the within‐class covariance. For QD, the voxel‐space sensitivity map is defined [see Yourganov et al., 2010, for details]:

$${\mathit{s}}_{\text{vox}\hspace{0.17em}}=\mathit{X}\left({\mathit{S}}_2^{-1}\left(\mathit{x}-{\mathit{m}}_2\right)-{\mathit{S}}_1^{-1}(\mathit{x}-{\mathit{m}}_1)\right)$$

Model Regularization

For this article, we classify on the linear kernel $\mathbf{\Phi }$ _{( N x N )}, which greatly reduces data dimensionality relative to the original X _{( V x N )} data space. However, further regularization is important, given the noisy, often collinear nature of fMRI data. In this article, we consider “regularization” as any mathematical constraint that limits classifier model complexity, in order to stabilize the decision surface. A variety of such regularization methods are available, including directly penalizing the kernel‐space features, and projecting data into a lower‐dimensional basis space. For the current article, we examined L ₁ and L ₂‐norm penalization on the features of $\mathbf{\Phi }$ (i.e. rows of the untransformed NxN covariance matrix), as well as Principal Component Analysis (PCA) and Independent Component Analysis (ICA) subspace selection methods, all of which are commonly used in the fMRI literature.

L₁ and L₂ penalization

The L _p‐norm methods constrain the decision surface by directly penalizing the kernel basis weights of $\mathbf{\Phi }$. For LD and LR models, which have linear decision boundaries defined by a projection vector w, their loss functions Eqs. (6) (LD) and (8) (LR) have an added penalty term $\frac{\lambda }{2}{\sum }_i|w_i{|}^p$, which forces the maximum‐likelihood solution of w to have a smaller norm. For example, the penalized LD loss function is:

$$L=\frac{1}{2}{{\displaystyle \sum _n\left(y_n-\mathit{w}\cdot {\mathit{\varphi }}_n\right)}}^2+\frac{\lambda }{2}{\displaystyle \sum _i|w_i{|}^p}$$ (12)

Parameter λ dictates the amount of regularization, where a larger λ increases the influence of the penalty function on our solution.

A linear model with p = 2 (known as “ridge regression”) tends to assign uniformly high/low discriminant weights w _i to groups of correlated features. For LD, it is equivalent to estimating a decision boundary on the regularized covariance S* = (S + λ I) (13), which produces an increasingly diagonal covariance structure [Kustra and Strother, 2001]. In contrast, the p = 1 penalty (known as “lasso”) tends to select only a single feature from among a correlated group of features. This is conceptually similar to step‐wise regression [Efron et al., 2004], and is of interest because it is able to define a parsimonious subset of predictors in a regression model. The L ₁ penalty produces a non‐differentiable objective function, and so its decision function D( ${\mathit{\varphi }}_{{}_{}n}$) does not have an analytic solution. The LD–L ₂ model was solved using standard ridge regression, and LD‐L ₁ was solved using a modified version of the computationally efficient LARS procedure [Efron, 2004] (code from http://www2.imm.dtu.dk/pubdb/views/publication_details.p hp?id=3897). For LR, we used the Iterative Reweighted Least‐Squares model, which regresses on a set of adjusted target variables; this model directly performs ridge/Lasso regression for each algorithm iteration (software developed in‐house).

For QD, the quadratic decision surface requires alternative methods to implement L ₁ and L ₂‐penalties. For L ₂, in an analogous extension of the LD model [Eq. (12)], we directly regularized the within‐class covariance matrices using a fixed λ value:

$${\mathit{S}}_1*={({\mathit{S}}_1+\lambda \mathit{I})}_{}{,}_{}{{}_{}}_{}{\mathit{S}}_2*=({\mathit{S}}_2+\lambda \mathit{I})$$ (13)

For L ₁ regularization, we penalized the inverse covariance matrices of Eq. (3) (i.e. precision matrices), using the “graphical lasso” model [Friedman et al., 2008] (code from http://www-stat.stanford.edu/~tibs/glasso). This technique sequentially fits an L ₁ regression to each variable 1…N of the inverse covariance matrix, treating all other variables as predictors. It gives zero weight to elements of multiple highly collinear (i.e. redundant) variables, producing a sparse inverse covariance matrix. This is a computationally efficient method of applying L ₁ regularization to the QD classifier model.

For SVM, we enforce an L _p‐norm penalty on the support vectors, via slack variable parameter p in Eq. (9). The L ₂‐constrained model is solved using quadratic programming methods; the L ₁‐constrained model is solved using the Sequential Minimization Optimization algorithm [Cristianini et al., 2000; both provided in the MatLab Bioinformatics Toolbox; R (ver. 2007b; The MathWorks, Inc., Natick, MA).

PCA and ICA decomposition

Both of these models transform the feature‐space data $\mathbf{\Phi }$ into a linear subspace of independent and/or orthogonal components, with the component basis estimated in different ways. For all classifiers, we project the data onto a subset of components, and then perform classification in the new coordinate space.

Principal Component Analysis projects $\mathbf{\Phi }$ onto a set of K orthonormal Principal Components (PCs; for K < N), where the k ^th PC explains the greatest possible data variance that is orthogonal to all preceding PCs 1…(k − 1). This is expressed as the unique decomposition of the symmetric, positive definite matrix $\mathbf{\Phi }$:

$$svd(\mathbf{\Phi })=\mathit{V}{\Lambda }^2{\mathit{V}}^T$$ (14)

V = orthonormal basis vectors, and Λ = diagonal matrix of associated singular values. The data are represented as PC‐space coordinates Q = V ^T Λ. We perform classification on a subspace of 1 to k PCs, where we vary (1 < k < K). Lower k corresponds to a smaller, more regularized classifier subspace. Strother et al. [[Link]] have demonstrated that PCA is an important regularization technique, because it provides a highly efficient feature extraction that reflects the first‐order, linear covarying network structure of the brain, as previously shown in Positron Emission Tomography studies [Kustra and Strother, 2001; Moeller and Strother, 1991; Rottenberg et al., 1987].

ICA refers to a broad class of models that linearly decompose $\mathbf{\Phi }$ into a set of statistically independent, non‐Gaussian source signals V_IC, by estimating the linear “unmixing” transformation matrix W that produces V_IC = W $\mathbf{\Phi }$. Unlike PCs, ICs are not constrained to orthonormality, and ICA models may enforce independence in the spatial or temporal domain, producing non‐orthogonal temporal or spatial components, respectively. These models do not have an analytic solution, requiring iterative estimation; they are usually estimated on an initial reduced PCA subspace, which stabilizes the solution and reduces computational burden. In principle, ICA models allow for flexible modeling of signal components, but they are limited by issues of dimensionality, and solutions tend to be unstable [Yourganov et al., 2011]. In this article, we used the FastICA package [Hyvärinen et al., 2000) (research.ics.tkk.fi/ica/fastica, ver. 2.5), which performs ICA following an initial PCA decomposition. We employed the “tanh” (hyperbolic tangent) nonlinearity measure, which produced optimal results out of the available set of constraints, and used the deflation approach to sequentially estimate the ICs. The ICA components are sensitive to the input PC dimensionality. Since it has previously been shown that theoretical estimates of the intrinsic dimensionality are suboptimal, we empirically identified the optimal subspace, by varying both the input PC subspace and number of ICs used to perform classification (see next paragraph).

On the range of regularization

For classification in a PCA subspace, we varied the subspace dimensionality of the within‐subject analyses from 1 to K _max, where K _max is the maximum non‐rank deficient dimensionality ≤N. Similarly, we varied L ₁ regularization to admit 1 − N nonzero basis weights. For ICA, we tested all values of 1 to K ICs, for each of K = 10%, 25% and 50% of K _max input PC dimensionality (with ICs ordered by variance). For L ₂ regularization, we identified the highest and lowest values of λ at which an increment produced no statistical change in the discriminant maps, and subdivided this range into K _max steps, on the log scale. This was done to ensure that the tested range was comparable to the other regularization methods.

Experimental Data

In order to evaluate the different classifier/regularizer models, we analyzed a set of experimental fMRI task contrasts. The fMRI dataset, originally presented in [Grady et al., 2010], included 19 young, healthy adults (mean age 25 ± 3 years, range 20–30, eight women), screened using a health questionnaire to exclude health issues and/or medications that might affect cognitive function and brain activity. Images were acquired with a Siemens Trio 3‐T magnet. T₂ functional images (TE/TR = 30/2,000 ms, FA = 70^o, FOV = 200 mm) were obtained using echo planar acquisition. Each image volume consisted of 28 5‐mm thick axial slices with 3.125 × 3.125 mm² pixels. T1‐weighted anatomical volumes were also obtained using SPGR (TE/TR = 2.6/2,000 ms, FOV = 256 mm, slice thickness = 1 mm). Subject brain volumes were nonlinearly co‐registered to a common anatomical template, created from a group‐average anatomical reference; this was obtained from an iterative optimization procedure that is robust to inter‐subject anatomical variability [Kovacevic et al., 2005]. Functional data were corrected for slice‐timing offsets using AFNI (http://afni.nimh.nih.gov/afni) and motion corrected using AIR (http://bishopw.loni.ucla.edu/AIR5). Additional preprocessing consisted of spatial smoothing with a FWHM=7 mm Gaussian kernel and regressing out white matter time signal, using an averaged white matter time series as a regressor for each voxel/subject separately; we also performed linear detrending to control for residual motion and scanner drift effects.

Subjects performed four task runs (total duration of 300 TR = 600 s, for each run), in which blocks of four different stimuli were presented twice in each run, interleaved with fixation blocks; for full details, see [Grady et al., 2010]. The visual stimuli consisted of bandpass filtered white noise patches with different center frequencies; for all tasks, when subjects detected a “target” they pressed 1 of 3 buttons to indicate where the stimulus appeared. The stimulus types include:

• Fixation (FX): the participant observed a dot presented on the middle of the screen.

• Reaction Time (RT): when the participant detected a target image on a screen, they pressed the corresponding button as quickly as possible.

• Delayed Match to sample (DM): test of working memory. A target stimulus was presented and then removed from the screen, followed by a 2.5 s blank‐screen delay. Three stimuli were presented and the participant pressed the button corresponding to the target.

• Attentional Cueing (AT): the participant pressed the button corresponding to the target image, following a brief directional cue.

• Perceptual Matching (PM): the participant was presented a target in the upper portion of the screen, and three stimuli on the lower portion; they pressed the button corresponding to the one of three stimuli on the lower portion that matched the target.

During each of the four experimental runs, the FX condition was presented in 8× (10 TR) blocks, producing 32 blocks in total. The other three conditions were presented in 2× (∼20 TR) blocks per run for each condition although there is some variability due to variance in stimulus timing; this produced eight blocks in total. For all analyses, we discarded the first two TRs of each block, producing 8‐TR blocks in the FX condition, and task conditions blocks that ranged from 16 to 18 TR (except a single block of 14TR in AT). In order to maintain consistency in block sizes, we therefore trimmed all task blocks to 16TR, discarding scans from the end of the block.

We examined three contrasts, ordered by increasing difficulty of classification: (1) FXvDM, (2) ATvPM, (3) PMvDM. We consider (1) to be a “strong” contrast, as we attempt to classify between relatively large changes in cognitive state, compared to the “weaker” cognitive state differences in (2) and (3). This can be confirmed by the systematically lowered prediction and gSNR in going from (1) to (3), shown in Figs 2 to 4. We selected these contrasts, in order to test whether results are consistent across different strengths of task contrast, as there is evidence that this has an impact on optimal image processing and analysis methods [Churchill et al., 2012; Rasmussen et al., 2012].

Figure 2.

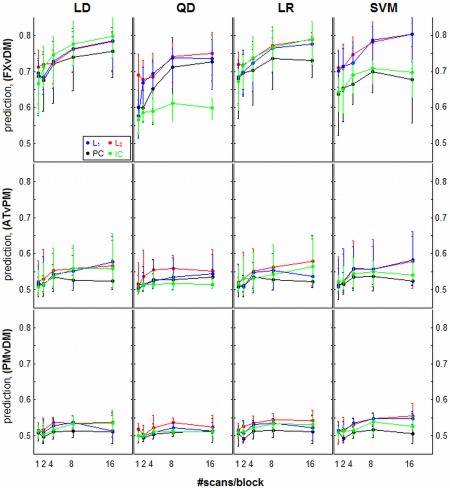
Prediction accuracy curves as a function of sample size, for different regularizer/classifier model combinations. Panels represent different classifiers of linear discriminant (LD), quadratic discriminant (QD), logistic regression (LR), and support vector machines (SVM). Each curve represents median prediction across subjects (with interquartile error bars), for a different regularization method. Results are shown for three different task contrasts, going from strongest (top row; FXvDM) to weakest (bottom row; PMvDM). [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com.]

Resampling, Performance Metrics, and Regularizer Optimization

We evaluated model performance for the single‐subject analyses, in a cross‐validation framework. The task blocks constitute our resampling units, as scans within a block are temporally correlated. The overall structure of the data consists of four task runs, with two condition blocks per run (we concatenated pairs of successive FX runs to match the 16‐TR task blocks). Given the four scanning runs, we performed fourfold cross‐validation (CV) on the data. The (two blocks) × (two conditions) from a single run were designated independent “test” data, and the remaining (six blocks) × (two conditions) were used to perform model training and validation (i.e. optimize model regularization). This procedure allowed us to maximize the independence of “test” data, relative to the training and validation stage.

We performed model training and validation in the NPAIRS split‐half cross‐validation framework [Strother et al., 2002, 2010], in which we randomly split the training and validation data into two pseudo‐independent sets of (three blocks) × (two conditions). We trained the classifier model and generated a discriminant brain map, independently for each data split. We used split‐1 data to estimate decision surface D ₁( ${\mathit{\varphi }}_{{}_{}n}$) and voxel sensitivity map s_{vox ,1}, and used split‐2 data to estimate D ₂( ${\mathit{\varphi }}_{{}_{}n}$) and s_{vox ,2}. Prediction and Reproducibility were used to quantify model performance.

Prediction (P)

P measures how well the decision surface D _i( ${\mathit{\varphi }}_{{}_{}n}$) predicts the experimental condition of data that was not used to build the decision surface. To estimate prediction, we use D₁( ${\mathit{\varphi }}_{{}_{}n}$) to assign each data‐point from split‐2 to class 1 or 2. Prediction is measured as the fraction of scans in split‐2 that are assigned to the correct class. We then use D₂( ${\mathit{\varphi }}_{{}_{}n}$) to classify split‐1 data, and take the average prediction from both splits, denoted P _valid. This provides a measure of classifier generalizability that allows us to compare probabilistic QD, LD and LR models with the non‐probabilistic SVM. We also tested an alternative prediction of Bayes' posterior probability for all models except SVM, but found no significant differences in model performance compared with classification accuracy.

Reproducibility (R)

R measures the stability of discriminating brain regions in s_{vox ,i}, across (pseudo)independent data splits. This was estimated as the Pearson correlation of the pairwise voxel values between s_{vox ,1} and s_{vox ,2}. Under Gaussian signal and noise assumptions, this R metric has the advantage of being directly related to the global Signal‐to‐Noise Ratio (gSNR) of the brain map, by the relation $g\text{SNR}\hspace{0.17em}=\sqrt{2R/(1-R)}$. We also used split‐half results to generate a reproducible Z‐scored Statistical Parametric Map (rSPMZ) of brain activation, using the bivariate scatter plot of s_{vox ,1} versus s_{vox ,2} voxel values. We project voxel values onto the first PC of the scatterplot (the signal axis) to compute reproducible signal, and normalize by the standard deviation of the second PC (noise axis), producing a Z‐scored SPM [Strother et al., 2002].

For a given analysis, we computed (P _valid, R) across the range of regularization parameter values, and used these metrics to select the optimal regularization parameter (e.g. λ for L ₁ or L ₂; subspace size k for PCA and ICA). The (P _valid, R) metrics reflect important tradeoffs in fMRI classification in a pseudo‐ROC curve [LaConte et al., 2003; Strother et al., [Link]]. In general, greater model regularization leads to decreased model prediction, and large, complex changes in reproducibility (see Fig. 1). An optimal classifier should jointly optimize P _valid and R; we chose to minimize the Euclidean distance $D=\sqrt{{(1-P_{\text{valid}\hspace{0.17em}})}^2+{(1-R)}^2}$, for which smaller D indicates better model performance. This metric has been previously implemented in model and preprocessing optimization [e.g. Churchill et al., 2012; LaConte et al., 2003; Shaw et al., 2003; Zhang et al., 2009]. Furthermore, Rasmussen et al. [2012] demonstrated that the D metric is an effective compromise between optimizing exclusively on R or P metrics: it improved the stability of brain SPMs across different classifier models, while improving detection of the less predictive nodes of the brain network that underpin motor performance. After selecting the level of regularization that minimizes D, we used the optimized model to classify data in a held‐out “test” run. This produced P _test, an independent, unbiased measure of prediction accuracy for comparison with the biased P _valid.

Figure 1.

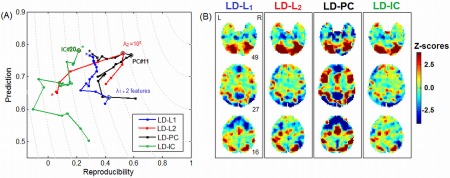
The impact of regularization choice for a representative subject in the ATvFX contrast, with the linear discriminant (LD) classifier, for a restricted range of 20 regularizer values. (A) Plots showing (P _valid = validation prediction, R = reproducibility) curves for regularization via Principal Components (PC), L ₁ and L ₂ penalties, and Independent Components (IC). Each curve traces out (P _valid, R) as a function of degree of regularization. A “*” indicates the point of weakest regularization; PC and IC with 20 components (both ordered by variance), L ₁ with nonzero weights on 20 of the linear kernel features (rows of covariance matrix $\mathbf{\Phi }$), L ₂ with λ ₂ = 10⁻⁸. The optimal point that minimizes Euclidean distance from (P _valid = 1, R = 1) is circled for each regularizer. (B) The Z‐scored subject SPM produced by each optimized regularizer. [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com.]

In this resampling framework, we designated each of the four runs the “test” dataset in sequence (i.e. fourfold CV), and we measured average P _test across the four folds. For each fold, we performed 25 training/validation resamples (of $\frac{1}{2}\left(\begin{array}{c}6\\ 3\end{array}\right)\times \frac{1}{2}\left(\begin{array}{c}6\\ 3\end{array}\right)=100$ possible ways of splitting the two task conditions) and computed median (P _valid, R) values, in order to optimize regularization. When reporting final results, we computed median P, R, gSNR and rSPMZs across the 4x25 =100 resampling splits, for each subject. Note that all figures showing prediction refer to P _test, excepting Figure 1, which demonstrates the P _valid versus R optimization tradeoff as a function of model regularization.

Model Performance and Sample Size

We analyzed each of the 19 subjects in the fourfold CV framework, for all 16 possible classifier/regularizer combinations (LD, QD, LR or SVM)x(L ₁, L ₂, PCA, or ICA). This produced median estimates of P _test, R, gSNR, and a set of 19 rSPMZs for each subject.

In order to examine the relationship between model performance and sample size, we sampled backward from the end of each task block, retaining only a subset of N _block volumes from every block. We tested a range of N _block = {1, 2, 4, 8, 16}, which gives effective training sample sizes per split, for two blocks from each of 3 runs, of {6, 12, 24, 48, 96}, which was used to build the decision surface D( ${\mathit{\varphi }}_{{}_{}n}$). For every block size N _block, we then generated all of our performance metrics, and we plot performance as a function of N _block for every classifier/regularizer model combination.

We then tested for significant trends in model performance using nonparametric testing. We used a Friedman test to identify models that are significantly different based on ranking. This was depicted using a critical‐difference diagram, with significant differences in models assessed using the Nemenyi permutation test at α = 0.05 [see Conover et al., 1999 for a review of these procedures]. These results were computed separately for each of the three different task contrasts (FXvDM, ATvPM, PMvDM). We show ranking results for a fixed N _block=16, although model rankings were generally consistent for smaller N _block values.

Additionally, we examined the relative bias of the validation prediction estimates P _valid (which are used to optimize model regularization), compared to independent unbiased test prediction P _test. We plot median P _valid and P _test for each classifier model, and test whether P _valid is significantly higher than P _test, using nonparametric paired Wilcoxon tests. A significant difference indicates a consistently biased classifier model. This was evaluated for the minimum and maximum sample size limits, of N _block=1 and N _block=16, respectively.

The Dynamic Range of Classifier Models

For the previous sections, we chose model regularization to optimize the metric D(P _valid, R) of Euclidean distance from perfect (P _valid = 1, R = 1). This provides a compromise that demonstrates how the different models perform, under equal weighting of the two metrics. However, this does not provide information on how models perform at extremes of regularization, when maximizing either P _valid or R alone. That is, what is the maximum attainable Prediction and Reproducibility for each model? We define this as the effective “dynamic range” of each model. To examine this, we optimized each classifier/regularizer model by (A) maximized P _valid, (B) minimized D(P _valid, R) and (C) maximized R, for each individual subject analysis. We then plotted median (P _test, R) values of the different models under these optimization criteria. The results are shown for a representative LD classifier model, and ATvPM task contrast, but the findings are consistent for all classifiers and contrasts. There is evidence that the brain expresses a range of different task‐related activation patterns as a function of increased regularization, ranging from the highly reproducible and spatially extensive but less predictive of the task (e.g. default‐mode networks), to the highly task‐predictive and more spatially sparse (e.g. task‐positive networks) [Rasmussen et al., 2012; Strother et al., [Link]]. We suggest that an ideal classifier model should have a wide “dynamic range”, allowing the user to tune the model to identify this spectrum of network structures.

Comparing SPM Patterns

Although prediction and reproducibility are valuable measures of model performance, they provide no information on the spatial structure of the SPM patterns themselves. In experimental data, two models can provide similar P _test and R values, and yet produce significantly different spatial patterns [Churchill et al., 2012]. To address this issue, we used the bootstrapped multidimensional scaling method of DISTATIS [Abdi et al., 2007]. This model identifies consistent trends in the within‐subject correlation of model SPMs, and does not directly compare between subject SPMs. The following steps are performed to compare 16 different classifier/regularizer models:

1. For the kth subject (1 ≤ k ≤ 19), compute the doubly‐centered 16 × 16 correlation matrix S _k, between SPMs generated by the different classifier/regularizer models.

2. Form the 19 × 19 matrix C of pairwise similarity between the S _k matrices, measured using the R_V coefficient of matrix similarity.

3. Perform PCA on matrix C. The first eigenvector gives the set of coefficient weights α_k, which indicate how similar each S _k (and thus the k _th subject) is to the strongest common S‐matrix pattern. Then compute the weighted compromise matrix ${\mathit{S}}_{+}={\sum }_k{\mathit{\alpha }}_k{\mathit{S}}_k$; this is the most common 16x16 cross‐correlation between model SPMs across subjects.

4. Perform PCA on S ₊, and project S ₊ into the new PCA basis space.

The models' rSPM(z)s are expressed as points in 15‐dimensional PCA space, typically reduced to the first two PC dimensions for visualization. The distance between any two models' points represents the Euclidean “distance” between rSPM(Z)s, with points that are closer together indicating more similar activation maps. We produced confidence estimates on the models, by Bootstrap resampling of the subject correlation matrices (1,000 iterations). The bootstrapped matrices were projected into the same PC space, and the resultant 95% confidence ellipses were drawn around the centroids.

We examined model SPMs for clustering, defined as overlap in the 95% confidence ellipses, which indicates that the model SPMs are not significantly distinguishable. This provides a representation of the relative similarity between classifier/regularizer model SPMs. We applied DISTATIS to data at N _block = 16 sample size, although trends are consistent for smaller samples.

The Effects of Voxel ROI Selection

As a final test, we examined whether results of whole‐brain analyses generalize to smaller numbers of input voxels. It is common in many fMRI studies to predefine a voxel ROI for analysis, particularly if there is an a priori hypothesis about a specific subset of brain regions. It remains unclear whether differences between classifiers are preserved when the number of input voxels (V) are much less than the number of timepoints (N). We re‐ran the analyses in Model Performance and Sample Size, for the 16 combinations of classifier/regularizer and a full sample size N _block = 16, comparing (1) whole‐brain analysis (21,535 voxels; V >> N), (2) a “liberal” ROI mask of dorsal task‐positive regions, including parietal lobes and dorsolateral prefrontal cortex (276 voxels; V ≈ N), and (3) a “conservative” ROI mask of the bilateral parietal lobes (29 voxels; V << N). These regions were chosen as areas typically implicated in overt attention and visual search, with ROIs predefined using an AAL anatomical atlas.

The analyses were run for the intermediate ATvPM contrast. We plotted median P _test, R, and gSNR as a function of the number of input voxels. We also plotted SPMs from “conservative” ROI results, to demonstrate the importance of spatial reliability, even in a relatively small subset of voxels.

RESULTS

Model Performance and Sample Size

As a demonstration of the importance of model choice, Figure 1 plots sample (P _valid, R) curves as a function of regularization, for a single representative subject (ATvFX contrast, with an LD classifier, for a maximum sample size of N _block = 16). As shown in Figure 1(A), the regularizers produce different curves in (P _valid, R) space, with different optimization points. For all models except LD‐ICA, if we trace the curve as a function of increasing regularization, we approach a point of minimum distance from (P _valid = 1,R = 1), after which overall model performance declines. Figure 1(B) further demonstrates that the resulting activation patterns may be quite different, even under a fixed classifier model. Although there are activations common to all regularizers (e.g. upper cerebellum; slice 49), there are also regions of extreme heterogeneity (e.g. superior frontal, strong signal Z‐scores for PCA and L ₁ only; slice 16).

Figure 2 plots the median prediction accuracy P _test across subjects for each classifier/regularizer model, as a function of sample size. In general, prediction distributions are overlapped, indicating relatively large inter‐subject variability in classifier performance. Only the strong FXvDM contrast shows consistent separation between different models. However, there are a few reliable trends; the significant differences are displayed as critical difference diagrams in Figure 4. Comparing regularizers, L ₁ and L ₂ maximize median prediction, and PCA generally performs worse. The effects of ICA are the most classifier‐dependent. For LD and LR, ICA is often comparable to L _p‐norm regularizers; for SVM it only weakly out‐performs PCA, and for QD it is the least predictive model. Comparing different classifiers, trends in performance depend on the chosen regularizer: for L _p‐norms, SVM > LR,LD > QD, whereas for PCA we generally observe LD > QD > LR > SVM. These trends are ambiguous for the weaker task contrasts. Interestingly, the prediction power curves do not increase monotonically with sample size, but plateau at N _block = 4 to 8 for many models. This is evidence of within‐run heterogeneity: as scans are added to the block, they increase the variability of the data distribution, making it more difficult to build a generalizable, predictive model.

Figure 4.

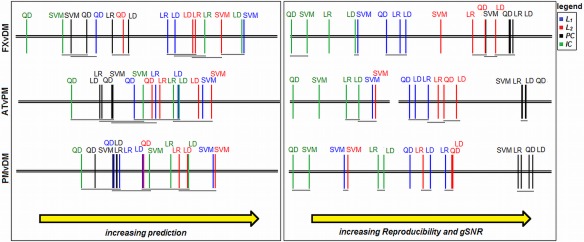
Critical difference diagrams. Each plot shows average ranking of the 16 different classifier/regularizer models for metrics of Prediction, Reproducibility and gSNR (note that Reproducibility and gSNR have the same rankings, as they are monotonically related; see Resampling, Performance Metrics, and Regularizer Optimization), computed across subjects. All rankings are significant (P < 0.01, Friedman test), and models that are not significantly different are connected by horizontal grey bars (α = 0.05, Nemenyi test). Results are shown for the maximum number of data‐points (N _block = 16), for each of the three task contrasts. [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com.]

Figure 3 plots median spatial reproducibility and gSNR for each classifier/regularizer model, as a function of sample size. We observe much stronger trends in the effect of regularizer choice compared to prediction, with non‐overlapped inter‐quartile error bars. In general, PCA > L _p > ICA, and PCA shows greater relative benefit in the weaker task contrasts. We also observe a “cross‐over” effect between L ₁ and L ₂: for weaker contrasts, L ₁ has greater reproducibility for smaller sample sizes (typically N _block < 4), but for larger sample sizes it becomes worse than L ₂. Therefore, the relative stability of the L _p‐norm regularizers is sample‐size dependent. The ICA model generally gives poor reproducibility and gSNR, and for QD and SVM classifiers, and gets worse with increased sample size, indicating that it is prone to over‐fitting these more complex decision functions. Comparing across classifiers, the choice in classifier model has a much smaller impact on reproducibility and gSNR than regularizer choice, as classifiers with the same regularization tend to have similar performance. Finally, with the exception of ICA, the reproducibility/gSNR curves increase monotonically with sample size and as a function of condition contrast, whereas a much weaker trend with contrast is observed in the prediction plots (Fig. 2). For example, SVM‐PC prediction plateaus at N _block = 4 to 8 for all contrasts, but reproducibility monotonically rises with increasing sample size, showing continued improvement in spatial SNR that may be uncoupled from prediction performance.

Figure 3.

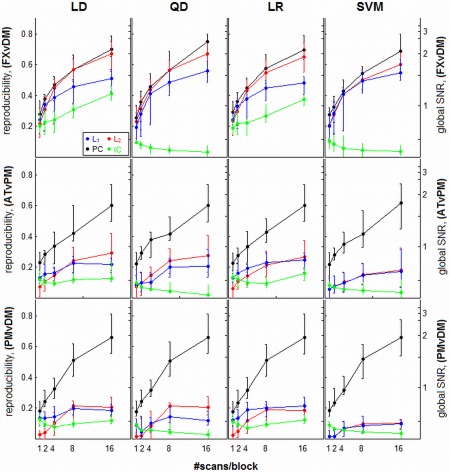
Spatial reproducibility and global signal‐to‐noise (gSNR) are both plotted as a function of sample size, for different regularizer/classifier model combinations; gSNR is a monotonic function of reproducibility. Panels represent different classifiers of linear discriminant (LD), quadratic discriminant (QD), logistic regression (LR), and support vector machines (SVM). Each curve represents median reproducibility across subjects (with interquartile error bars), for a different regularization method. Results are shown for three different task contrasts, going from strongest (top row; FXvDM) to weakest (bottom row; PMvDM). [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com.]

Figure 4 provides statistical significance tests on the relative performance of the different classifier models. For prediction P _test (left), many models are not statistically distinguishable, with increasing model overlap for weaker task contrasts. In general, models regularized with L ₁ and L ₂ perform better than PCA, and ICA is highly variable depending on classifier and task contrast. The SVM‐L ₁, SVM‐L ₂, and LD‐ICA models have consistently optimal prediction. For reproducibility and gSNR (right), a greater number of models are significantly different. PC‐based models are not significantly different, and consistently outperform all other models. L ₁ and L ₂ models offer moderate performance, and become more similar for weaker contrasts, while IC gives lowest performance. The SVM‐L ₁ and SVM‐L ₂ models are unique, as they have moderate R and gSNR for strong task contrasts, but consistently decrease in rank for weaker contrasts.

Tables 2 and 3 compare P _valid versus P _test for the 16 different models as a function of task contrast, for sample sizes of N _block = 1 and 16, respectively. At the small‐sample limit (Table 2), there is a strong contrast and regularizer‐dependent effect. For FXvDM, all models are significantly biased, for ATvPM only PC‐based models (and QD‐L ₂) are not significantly biased, and for PMvDM, no models are significantly biased. At the large‐sample limit (Table 3), there is an interaction between classifiers and task contrast. For the strongest contrast (FXvDM), LD models are consistently biased, whereas for the weakest contrast (PMvDM), SVM models are all significantly biased. However, the magnitude of upward prediction biases tends to be relatively small; in the most extreme case of FXvDM and N _block = 1, the average magnitude of (P _valid − P _test) is 0.06 ± 0.02 (mean ± standard deviation, over all subjects and models; a mean change of 8%).

Table 2.

Comparison of classifier prediction accuracy on validation data P _valid, which is used to optimize model regularization, versus independent test data P _test

	FXvDM			ATvPM			MvDM
	P valid	P test	Signif.	P valid	P test	Signif.	P valid	P test	Signif.
LD‐L1	0.77	0.68	0.01	0.56	0.51	0.07	0.50	0.51	0.50
LD‐L2	0.77	0.72	0.01	0.58	0.53	0.01	0.51	0.52	0.70
LD‐PC	0.77	0.68	0.00	0.55	0.52	0.25	0.47	0.50	0.88
LD‐IC	0.76	0.71	0.01	0.59	0.52	0.01	0.51	0.50	0.25
QD‐L1	0.72	0.67	0.00	0.57	0.51	0.01	0.51	0.50	0.20
QD‐L2	0.74	0.68	0.00	0.57	0.54	0.23	0.50	0.50	0.42
QD‐PC	0.67	0.60	0.00	0.52	0.51	0.35	0.51	0.50	0.47
QD‐IC	0.63	0.59	0.00	0.53	0.51	0.09	0.51	0.50	0.08
LR‐L1	0.77	0.70	0.00	0.57	0.51	0.05	0.49	0.51	0.72
LR‐L2	0.77	0.72	0.00	0.59	0.53	0.00	0.52	0.53	0.46
LR‐PC	0.79	0.70	0.00	0.53	0.51	0.15	0.47	0.49	0.68
LR‐IC	0.77	0.72	0.00	0.59	0.53	0.02	0.50	0.51	0.45
SVM‐L1	0.77	0.71	0.01	0.60	0.52	0.05	0.51	0.51	0.47
SVM‐L2	0.78	0.71	0.02	0.60	0.52	0.07	0.53	0.52	0.40
SVM‐PC	0.72	0.65	0.00	0.53	0.52	0.34	0.47	0.49	1.00
SVM‐IC	0.72	0.65	0.00	0.57	0.52	0.00	0.52	0.51	0.06

We plot median prediction across subject, for each classifier/regularizer model combination. The models are significantly biased if P _valid is consistently higher than P _test (significance assessed using non‐parametric paired Wilcoxon test; significant tests shaded in grey). Results are shown for the minimum sample size (N _block = 1), for the three task contrasts.

Table 3.

comparison of classifier prediction accuracy on validation data P _valid, which is used to optimize model regularization, versus independent test data P _test

	FXDM			ATvPM			PMvDM
	P valid	P test	Signif.	P valid	P test	Signif.	P valid	P test	Signif.
LD‐L1	0.77	0.73	0.02	0.55	0.52	0.17	0.53	0.51	0.34
LD‐L2	0.76	0.73	0.04	0.54	0.53	0.95	0.52	0.51	0.27
LD‐PC	0.77	0.76	0.03	0.55	0.52	0.11	0.53	0.51	0.32
LD‐IC	0.69	0.68	0.06	0.55	0.52	0.79	0.52	0.50	0.17
QD‐L1	0.79	0.79	0.39	0.60	0.58	0.18	0.55	0.54	0.29
QD‐L2	0.76	0.75	0.14	0.56	0.55	0.53	0.54	0.52	0.26
QD‐PC	0.79	0.78	0.28	0.58	0.57	0.07	0.55	0.54	0.20
QD‐IC	0.79	0.80	0.50	0.58	0.58	0.53	0.54	0.55	0.62
LR‐L1	0.79	0.78	0.11	0.57	0.54	0.14	0.54	0.52	0.27
LR‐L2	0.74	0.74	0.02	0.55	0.54	0.68	0.53	0.51	0.01
LR‐PC	0.80	0.79	0.40	0.57	0.58	0.59	0.54	0.53	0.17
LR‐IC	0.80	0.80	0.33	0.58	0.58	0.45	0.54	0.55	0.70
SVM‐L1	0.79	0.79	0.81	0.56	0.56	0.30	0.56	0.53	0.07
SVM‐L2	0.61	0.60	0.12	0.53	0.51	0.05	0.54	0.51	0.02
SVM‐PC	0.81	0.80	0.49	0.57	0.56	0.09	0.55	0.53	0.05
SVM‐IC	0.70	0.70	0.29	0.54	0.54	0.16	0.54	0.53	0.03

We plot median prediction across subject, for each classifier/regularizer model combination. The models are significantly biased if P _valid is consistently higher than P _test (significance assessed using nonparametric paired Wilcoxon test; significant tests shaded in grey). Results are shown for the maximum sample size (N_block=16), for the three task contrasts.

The Dynamic Range of Classifier Models

Figure 5 plots the median (P _test, R) values across subjects for a representative LD classifier and ATvPM task contrast, for the four different regularization methods. Results are shown for three different optimization criteria: (A) maximized P _valid, (B) minimized D(P _valid, R) and (C) maximized R. PCA regularization consistently produces the greatest range in (P _test, R) values as a function of optimization criterion. If optimized with P _valid (Fig. 5A), it is both the most predictive and reproducible model; if optimized with D(P _valid, R) (Fig. 5B), it dramatically increases reproducibility at the expense of decreased prediction; if optimized with R (Fig. 5C),we see a further small mean increase in R and decrease in P _test. In contrast, all of the other regularizers (L ₁, L ₂, and ICA) are highly consistent between the three panels of Figure 5, indicating that choice of optimization metric has little effect on model performance for these regularizers, which all have relatively low gSNR/R values. These trends were consistently observed for all task contrasts and classifier models.

Figure 5.

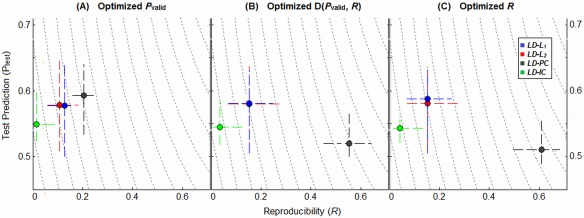
Plots illustrating the dynamic range of different regularizers in (Prediction, Reproducibility) space, for representative Linear Discriminant (LD) classifier, and the intermediate ATvFX contrast. Points represent the median (P _test, R) values for each model, with upper and lower quartile error bars. We show median performance metrics under three different optimization criteria: (A) maximized prediction P _valid, (B) minimization of the D(P _valid, R) metric which equally weights P and R (this is the metric used for all previous results), and (C) maximized reproducibility R. Results are shown for the maximum sample size (N _block = 16). [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com.]

Spatial Pattern Effects

Figure 6 shows the DISTATIS‐space plots; these are two‐dimensional representations of the relative similarity between SPMs of the 16 different models. For all task contrasts, we observe a “U‐shaped” trend. Dimension 1 (horizontal axis; axis of greatest variance) shows that the largest difference in SPMs is between PCA and ICA‐regularized models. The second dimension of effect (vertical axis) expresses a contrast between component‐regularized (PCA, ICA) versus L _p‐norm models. The primary difference between models is again driven by regularizers, and the ellipses of classifier models for a fixed regularizer are significantly overlapped. The patterns of L ₁ and L ₂‐regularized models also tend to be highly similar. The only outlier in this trend is the SVM‐L _p models, which tend to be more similar to ICA‐based models than the other classifiers.

Figure 6.

DISTATIS multidimensional scaling plot, depicting the relative similarity of different classifier/regularizer model SPMs. The ellipses denote the 95% Bootstrap confidence bounds for each model. Ellipses that are closer in DISTATIS space indicate more similar SPM patterns, and models are not significantly different if the ellipses overlap. Colors denote different regularizers: L ₁ = blue, L ₂ = red, PCA = black, ICA = green. Results are shown for the maximum sample size (N _block = 16). [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com.]

Figure 7 plots the average Z‐scored SPMs for three representative models that are most different in DISTATIS space. For a fixed LD classifier, we show SPMs for L ₁, PCA and ICA regularization. PCA consistently provides the most extensive and highest magnitude activation Z‐scores. There is a contrast‐dependent effect: the mean FXvDM patterns are relatively similar across models, although the LD‐PC model is more sensitive to decreases in mean activation for DM (increases for FX) that reflect default network‐like regions. For weaker contrasts, LD‐PC consistently produces high, spatially extensive Z‐scores, again with strong activation decreases that reflect default‐network like regions in the states of lower task engagement (AT in ATvPM; PM in PMvDM), but these activations are much weaker for other models.

Figure 7.

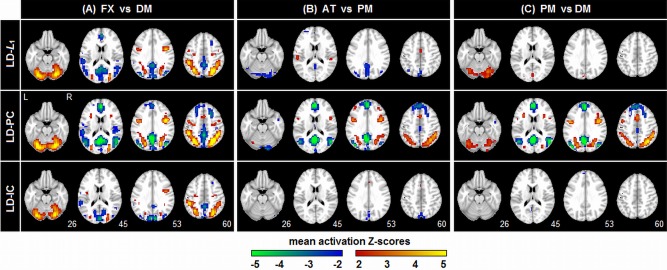
Average Z‐scored SPMs, computed across subjects, for three representative classifier/regularizer models, seen in the DISTATIS plot of Figure 6. The SPMs are plotted for each of the three different task contrasts, at the maximum sample size (N _block = 16). [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com.]

The Effects of Voxel ROI Selection

Figure 8 plots median prediction accuracy P _test (Fig. 8A) and median reproducibility (Fig. 8B) across subjects for each classifier/regularizer model, as a function number of input voxels. As the number of voxels decreases, median P _test also decreases, and the difference between classifier/regularizer choices is reduced. However, L _p‐norm regularizers still have generally higher median performance than PC and IC. In contrast, R is higher for smaller voxel ROIs, and the differences between regularizers remain consistent across ROI size, with PC > L _p > IC. Figure 8C demonstrates the importance of spatial reproducibility for ROI‐based analysis. We show sample SPMs from 3 representative subjects for a “conservative” ROI mask. The reproducible LD‐PC model produces clear regions of focal activation, with high Z‐scored reliability, showing differential lateralization across subjects. The LD‐IC model patterns are highly diffuse, with no statistical confidence (very low Z‐scores) in the pattern of BOLD activity.

Figure 8.

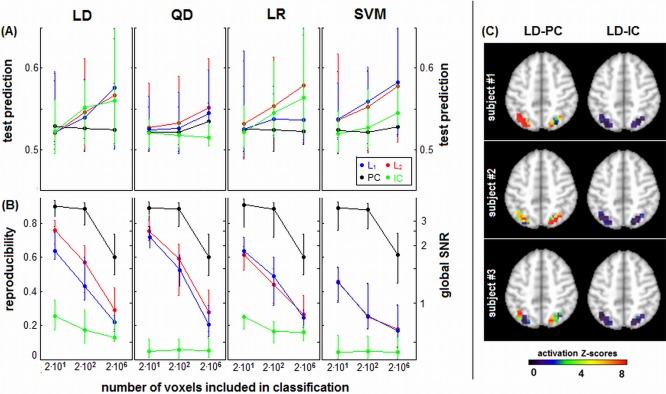
(A) Prediction accuracy and (B) spatial reproducibility curves as a function of number of voxels, for different regularizer/classifier model combinations. We compared ROI masks of 24 and 276 voxels, against whole‐brain classification (21,535 voxels). Panels represent different classifiers of linear discriminant (LD), quadratic discriminant (QD), logistic regression (LR), and support vector machines (SVM). Each curve represents median prediction across subjects (with interquartile error bars), for a different regularizer. Results are shown for the representative ATvPM contrast, and maximum sample size of N _block = 16. (C) Reproducible Z‐scored activation maps for three example subjects, showing results of classification analysis for the 29‐voxel ROI mask of the parietal lobes. Results are shown for LD‐PC and LD‐IC classifiers, which have comparable prediction accuracy but the greatest difference in spatial reproducibility. [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com.]

DISCUSSION

We compared a set of commonly‐used classification and regularization techniques, for single‐subject analyses over a range of different experimental task contrasts, with model performance quantified via metrics of prediction accuracy (P), spatial reproducibility (R), and global Signal‐to‐Noise Ratio (gSNR). For reproducibility and gSNR, the choice of classifier had a relatively small impact, whereas the regularizer choice had large effects that generalized across all tested datasets and classifier models. Conversely, prediction showed complex interactions with classifiers and regularizers, but the choice of model tended to have a smaller effect on prediction accuracy, with greater statistical overlap between models. An important finding in this article is that researchers should consider their regularizer choice at least as carefully as their choice of classifier model, when performing model selection.

Regularizer choices involve a tradeoff between spatial reproducibility versus prediction accuracy, when these metrics are given equal weight during regularization (i.e. optimizing the D metric). A PCA‐based model provides a consistently higher reproducibility and gSNR than all other regularizers, irrespective of the classifier model, but generally lower prediction accuracy. The possible advantages of PCA are demonstrated in Figure 7 where such models are better able to detect the more variable, but spatially stable, reduced activity in the states of lower relative task engagement (FX in FXvDM; AT ATvPM; PM in PMvDM), which are heavily overlapped with default network areas. In comparison, L _p‐norm regularized models had lower reproducibility and do not show default‐mode areas well for the weaker contrasts, but were more predictive. For LD and LR (linear, probabilistic models), ICA was most extreme, with the lowest model reproducibility, but relatively high prediction for LD and LR. This result was unstable for QD and SVM classifiers, where prediction was also low; this is potentially due to interactions with the complex quadratic‐ and hinge‐loss functions (respectively); regularization with ICA is most sensitive to classifier choice.

The high reproducibility of PCA is consistent with the preprocessing optimization studies of Churchill et al. [2012], which showed that LD‐PCA optimization using the D metric is more sensitive to reproducibility than prediction. This suggests that the variance‐driven PCA subspace is generally robust between data split‐halves. This strong spatial stability also generalizes down to relatively small‐sample SPMs. However, the experimental data of this study has been extensively preprocessed, including ICA‐based artifact removal, white matter and CSF regression, and temporal detrending [Grady et al., 2010]. The PCA model is sensitive to high‐variance, spatially distributed signal changes, such as motion artifact; therefore, careful preprocessing may be critical to ensure good performance when classifying on a PCA basis sensitive to signal variance [Garrett et al., 2011].

The L _p‐norm models had consistently higher prediction accuracy, across a range of task contrasts and sample sizes. The increased prediction at the expense of reproducibility is expected, as L _p‐norm analyses operate directly on the linear kernel. The kernel features are non‐orthogonal, allowing models to select the optimal predictors from among a redundant set of features, but at the expense of stability in the chosen features. For consistency with PCA/ICA, we applied L _p penalties to the linear kernel, but most other studies apply L ₁ and L ₂ penalties directly on voxel features. Interestingly, many such studies have shown that L ₁ produces excessively sparse brain maps [Carroll et al., 2009; Rasmussen et al., 2012; Ryali et al., 2010]. However, we found that L ₁ penalization on the kernel features only had worse gSNR than L ₂ for the strongest task contrast and large sample sizes. It appears that applying L ₁ to the kernel features is therefore a more stable implementation of this regularizer.

We also tested ICA, implemented in the FastICA package, and found overall poor reproducibility and gSNR for the resulting classifiers, with high prediction only for LD and LR. The poor reproducibility is not unexpected, given that (a) there is risk of model overfitting in ICA, as it estimates higher‐order statistical moments, and (b) its components tend to be unstable (e.g. performing ICA twice may not give the same subspace), often requiring additional computation methods to stabilize the subspace. Since ICA refers to a variety of different model implementations (e.g. enforcing independence on spatial vs. temporal domains, the choice of non‐Gaussianity metric, the convergence algorithm, etc.), these results are not definitive. Nonetheless, we have searched over a range of different initial PCA subspaces (retaining up to 50% of a maximum of training 96 scans), and our results are consistent with prior evaluations of FastICA in the MELODIC package, which is a sub‐optimal estimator of the signal subspace in both simulated [Yourganov et al., 2011] and experimental data [Churchill et al., 2012].

Our finding that different classifiers offer relatively similar performance for a fixed regularizer is supported in prior literature, for less extensive model comparisons. The LD and SVM classifiers on a linear kernel have comparable classification accuracy for many single‐subject analyses [Misaki et al., 2010; Ng and Abugharbieh, 2011; Schmah et al., 2010], although LaConte et al. [2005] showed that this may be a strong function of preprocessing choices. Similarly, Rasmussen et al. [2012] showed for group‐level analyses that LD, SVM, and LR on a linear kernel basis produced similar (P, R) values across a broad range of regularization values.

A number of studies also showed significant differences between classifiers, particularly linear versus nonlinear models. For example, [Misaki et al.; 2010] showed better performance for linear models in standard task analyses, and [Schmah et al., 2010] demonstrated significantly better prediction for non‐linear models for a subset of contrasts. However, these results were based on optimizing model prediction. Our results, which show non‐linear QD to be comparable to other models for most regularizers, suggest that some of the apparent differences may be due to choice in regularizer and optimization criteria, rather than the classifier itself. In the case of Schmah et al. [2010], who examined longitudinal and clinical datasets, it is also possible that there are fundamental differences in classifier performance that are simply not evident for some standard task analyses [Carter et al., 2008].

Along with classifier and regularizer choice, the criterion used to optimize regularization has a strong impact on model performance. The choice of whether to optimize R, P, or D metrics, may produce entirely different measures of model performance (Fig. 7). This has previously been observed in group analysis [Rasmussen et al., 2012], where L ₂‐regularized classifiers become increasingly similar if the D metric is chosen as the optimization criterion. We show that maximizing P _valid produces similar (P _test, R) for different regularizers, but including R as an optimization criterion increases the difference between models. Furthermore, PCA‐based regularization expresses the widest “dynamic range” of (P, R) values, indicating that it may be able to explore a greater range of brain states and potential network patterns, ranging from highly reproducible to highly predictive. Moreover, it is possible to extend PCA‐based models to explore even wider ranges of (P, R) values, using multistage PCA decompositions that exploit data heterogeneity [Strother et al., [Link]].

These findings have implications for multiple research domains where the user is performing multivariate classification, including experimental neuroscience, neurofeedback, and clinical fMRI studies. Moreover, we tested a range of different task contrast strengths, sample sizes, and both whole‐brain and ROI‐based classification, showing that the results are highly generalizable. We conclude that when researchers are choosing a classifier model, they should focus on (a) the type of regularizer and (b) the optimization criterion. For example, users who are primarily interested in classification accuracy and not underlying spatial patterns (e.g. neurofeedback with brain‐computer interfaces, many clinical biomarker studies) should either chose an L _p‐norm classifier, which has high prediction regardless of optimization criterion, or PC subspace optimized on P _valid. If the user is interested in identifying stable, coherent brain networks that may support behavioral performance without requiring optimal classification accuracy on experimental conditions (e.g. neuroscience studies of the temporal dynamics of default‐mode networks), a PC subspace optimized on D(P_valid, R) is an effective choice. Finally, in studies where both spatial localization and prediction are important (e.g. clinical neuroscience, such as some biomarker studies, pre‐surgical mapping), we suggest L _p‐norm regularization for results that are insensitive to the optimization criteria but may have a relatively low gSNR, or a carefully tuned PC‐space optimization such as available with the NPAIRS software [https://code.google.com/p/plsnpairs/) [e.g. Strother et al., [Link]].

The authors thank Dr. Cheryl Grady for providing the experimental fMRI data.