A geometric correction scheme for spatial leakage effects in MEG/EEG seed‐based functional connectivity mapping

Abstract

Spatial leakage effects are particularly confounding for seed‐based investigations of brain networks using source‐level electroencephalography (EEG) or magnetoencephalography (MEG). Various methods designed to avoid this issue have been introduced but are limited to particular assumptions about its temporal characteristics. Here, we investigate the usefulness of a model‐based geometric correction scheme (GCS) to suppress spatial leakage emanating from the seed location. We analyze its properties theoretically and then assess potential advantages and limitations with simulated and experimental MEG data (resting state and auditory‐motor task). To do so, we apply Minimum Norm Estimation (MNE) for source reconstruction and use variation of error parameters, statistical gauging of spatial leakage correction and comparison with signal orthogonalization. Results show that the GCS has a local (i.e., near the seed) effect only, in line with the geometry of MNE spatial leakage, and is able to map spatially all types of brain interactions, including linear correlations eliminated after signal orthogonalization. Furthermore, it is robust against the introduction of forward model errors. On the other hand, the GCS can be affected by local overcorrection effects and seed mislocation. These issues arise with signal orthogonalization too, although significantly less extensively, so the two approaches complement each other. The GCS thus appears to be a valuable addition to the spatial leakage correction toolkits for seed‐based FC analyses in source‐projected MEG/EEG data. Hum Brain Mapp 36:4604–4621, 2015. © 2015 Wiley Periodicals, Inc.

Abbreviations

A1

Primary auditory

CKC

Corticokinematic coherence

DICS

Dynamic Imaging of Coherent Sources

DLPFC

Dorso‐lateral prefrontal cortices

EEG

Electroencephalography

FC

Functional connectivity

GCS

Geometric correction scheme

ITG

Inferior temporal gyri

MEG

Magnetoencephalography

MNE

Minimum norm estimation

PSF

Point‐spread function

RSN

Resting‐state network

SM1

Primary sensorimotor

SM1ha

SM1 hand area

SMA

Supplementary motor area

SMG

Supramarginal gyrus

SNR

Signal‐to‐noise ratio

SSS

Signal space separation

STG

Superior temporal gyri

INTRODUCTION

A basic element of various analyses for electroencephalography (EEG) and magnetoencephalography (MEG) data is the brain electromagnetic inverse problem, i.e., the reconstruction of electric current flows from extra‐cranial electrophysiological measurements [Baillet et al., 2001; Sarvas, 1987]. A well‐known but fundamental limitation for source‐space MEG/EEG is the ill‐posed nature of this problem. In particular, a source reconstruction cannot be inferred in a unique way from extra‐cranial data only, but must be chosen among the many source configurations compatible with the observations. This selection requires the use of an inverse model, which involves adding enough prior assumptions to constraint the large set of possibilities down to one. In MEG/EEG, two widely used inversion schemes are Minimum Norm Estimates (MNE) [Dale and Sereno, 1993; Hämäläinen and Ilmoniemi, 1994] and Beamformers [Hillebrand et al., 2005; Van Veen et al., 1997]. Both approaches typically yield a spatially blurred representation of the underlying source distribution because the signals reconstructed at two different locations may be sensitive to activity in the same brain areas, in which case they must necessarily share dynamical information. This spurious co‐dependence effect of reconstructed sources bears various names in the literature and shall be henceforth referred to as “spatial leakage.”

This difficulty is particularly confounding for source‐space functional connectivity (FC) analyses. One motivation for performing MEG/EEG FC at the source level is to improve the interpretability of sensor‐space FC maps, which are substantially affected by field spreading [Schoffelen and Gross, 2009]. However, spatial leakage limits the success of this idea because the spurious connectivity patterns remaining after source projection typically dominate physiological interactions. Several dependency measures designed to be insensitive to spatial leakage have thus been introduced to investigate specific aspects of large‐scale neural communication, such as imaginary coherence [Nolte et al., 2004], the multivariate interaction measure [Marzetti et al., 2013] or the phase lag index [Hillebrand et al., 2012; Stam et al., 2007] for phase coupling, and orthogonalized envelope correlation [Brookes et al., 2012b; Hipp et al., 2012] for amplitude coupling. In the latter case, closely related but slightly different versions of signal orthogonalization procedures were actually used: a static version presuming time‐independent spatial leakage effects [Brookes et al., 2012b], a non‐stationary extension thereof [O'Neill et al., 2015] and an instantaneous version merely assuming zero phase lag effects [Hipp et al., 2012]. The common, generic idea underlying these FC indices is that spatial leakage can only induce zero‐lag linear spurious coupling, which can thus be avoided by focusing on non‐zero‐lag connectivity. One limitation, though, is that true zero‐lag linear coupling is suppressed as well, a priori leading to conservative FC estimates that might miss physiological interaction processes such as synchronization. Furthermore, this suppression leads to a mixing of phase and amplitude signals that can also bias non‐linear FC estimates such as envelope correlation [Wens, 2015]. More generally, this idea does not take into account the structure of spatial leakage, which ultimately originates from the underlying inverse model and controls the validity of the above‐mentioned assumptions.

Methods for source‐level MEG/EEG seed‐based FC analysis overcoming these limitations and applicable to any dependency measure therefore appear useful. Here, we investigate the advantages and the limitations of a geometric correction scheme (GCS) associated with a structural model of spatial leakage [Wens, 2015]. To that aim, we apply analytical and statistical tools to characterize spatial leakage correction in FC mapping and compare the GCS with signal orthogonalization, using MNE as canonical example of inverse model. Firstly, we examine the theoretical properties of a GCS‐modified inverse operator valid for any linear source reconstruction. Secondly, we assess the structural effect of the GCS on noisy point‐spread functions (PSFs) as a function of distance from the seed, signal‐to‐noise ratio (SNR) and lead field errors. Lastly, we explore the induced effect of spatial leakage corrections on FC mapping per se using simulated and experimental MEG data. We consider the primary sensorimotor (SM1) and auditory (A1) resting‐state networks (RSNs) well described in terms of envelope FC [Brookes et al., 2011,2012a,2012b; de Pasquale et al., 2010, 2012; Hall et al., 2013; Hipp et al., 2012; Luckhoo et al., 2012b; Wens et al., 2014a, 2014b], as well as a network involved in an auditorily‐cued motor task. The latter case is based on Dynamic Imaging of Coherent Sources (DICS) [Gross et al., 2001], which illustrates an example where the zero‐lag spatial leakage assumption is broken.

THEORY

Preliminaries

Figure 1 illustrates the GCS under consideration. In this section, we introduce a linear projection encapsulating this spatial leakage correction and derive some properties, including new mathematical justification. Relevant information about other spatial leakage corrections and MNE is also reviewed. Matrix notations suitable for discrete sampling of time and brain volume are used throughout, so the key formulas can be applied directly in computational implementations.

Figure 1.

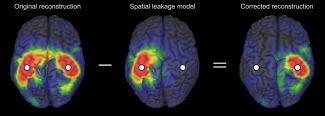
Illustration of the GCS. The reconstruction (left) of a bi‐focal source configuration localized at the SM1 cortices (white dots) is shown together with the geometric model of spatial leakage contribution from the left SM1 cortex (middle). The corrected reconstruction is obtained by subtraction (right).

Our starting point is the MEG/EEG forward model

$$\mu \hspace{0.17em}=\hspace{0.17em}\mathit{L}\psi \hspace{0.17em}+\hspace{0.17em}\varepsilon .$$

The $M\times T$ matrix $\mu$ represents $M$ sensors time series containing $T$ time samples. The model is characterized by a time‐independent, real‐valued $M\times DN$ lead field matrix L, which allows prediction of the observations generated by a known source configuration. The latter is approximated by a discrete set of $N$ sources ( $N\gg M$), each being parameterized by the $D$ components of their dipole moment. Their time series are encoded into the $DN\times T$ matrix $\psi$. Finally, the $M\times T$ matrix $\varepsilon$ denotes the prediction error, which is often modeled based on expected properties of measurement noise.

An inverse model determines a unique source matrix $\widehat{\psi }$ from given data $\mu$. We shall focus here on linear estimators of the form

$$\widehat{\psi }=\mathit{W}\mu ,$$

where the time‐independent $DN\times M$ source projection matrix $\mathit{W}$ defines the inverse operator. This class of inverse models, for which $\mathit{W}$ may be real or complex‐valued, contains stationary MNE and Beamformers as special examples.

Formally, spatial leakage effects are associated with the analytical properties of the lead field and inverse operators, which put fundamental limits to the spatial resolution of reconstructions and concomitantly introduce sources correlations (or coherencies) reflecting this geometric structure rather than dynamical information [Wens, 2015]. Spatial leakage is expected to be linear for the type of inverse models under consideration, and its geometry can be modeled. For simplicity, we shall focus on the case of one‐dimensional sources. This typically occurs upon projection of each $D\times T$ matrix block ${\psi }_s$ of $\psi$ (corresponding to a source location indexed by $s$, with $1\le s\le N$) onto directions $n_s$ (unit $D\times 1$ vector) determined by anatomical or functional constraints. In practice, this projection involves the replacements

$$D\leftarrow 1, L_s\leftarrow L_s{n}_s, W_s\leftarrow n_s^{\mathrm{T}}{W}_s,$$

where $L_s$ and $W_s$ respectively denote the matrix blocks of $\mathit{L}$ and $\mathit{W}$ corresponding to source location $s$.

In the $D=1$ case, the geometry of spatial leakage emanating from a given seed location $s_0$ can be modeled as the source configuration [Wens, 2015]

$$\frac{\mathit{W}{L}_{s_0}{\widehat{\psi }}_{s_0}}{W_{s_0}{L}_{s_0}}.$$

The $N\times T$ numerator is proportional to the PSF of the seed, $\mathit{W}{L}_{s_0}$, which corresponds to the reconstruction of a source configuration concentrated at the seed $s_0$ via forward modeling in the noiseless limit ( $\varepsilon =0$) and source projection, and indeed describes the topography of spatial leakage from that seed. The time‐dependent ( $1\times T$) normalization factor ${\widehat{\psi }}_{s_0}/\left(W_{s_0}{L}_{s_0}\right)$ is an estimate of true seed activity in the absence of measurement noise. The strict validity of this estimate, and thus of the above model, requires that the seed reconstruction ${\widehat{\psi }}_{s_0}$ does not depend on true activity originating from elsewhere. This entails the model assumption that true seed activity is sufficiently isolated from other active regions $s\ne s_0$ so that no spatial leakage effectively takes place from $s$ to $s_0$ [Wens, 2015].

Geometric Correction Scheme

The GCS for spatial leakage effects emanating from the seed $s_0$ simply consists in subtracting the spatial leakage geometry model from the reconstruction, as illustrated in Figure 1. In the present context of linear inverse modeling, the resulting corrected source configuration ${\varphi }^{\text{GCS}}$ can be expressed compactly in terms of a modified inverse operator ${\mathit{W}}^{\text{GCS}}$, i.e.,

$${\varphi }^{\text{GCS}}={\mathit{W}}^{\text{GCS}}\mu$$

with

$${\mathit{W}}^{\text{GCS}}=\mathit{W}-\frac{\mathit{W}{L}_{s_0}{W}_{s_0}}{W_{s_0}{L}_{s_0}}=\mathit{W}\left({\mathbf{1}}_M-\frac{L_{s_0}{W}_{s_0}}{W_{s_0}{L}_{s_0}}\right),$$

where ${\mathbf{1}}_M$ denotes the $M\times M$ identity matrix. This is the fundamental formula of the GCS under consideration. Corrected seed‐based FC maps are obtained by estimating FC between the uncorrected seed ( ${\widehat{\psi }}_{s_0}$) and the corrected targets ( ${\varphi }_s^{\text{GCS}}$).

Let us now describe some analytical properties of this modified inverse operator. Except for the first one, they hold independently of the underlying model assumption.

1. Phase lag of spatial leakage

   Considering a complex‐valued inverse operator $\mathit{W}$ (e.g., DICS), the corrective term in the definition of ${\mathit{W}}^{\text{GCS}}$ estimates the phase lag induced by spatial leakage from seed $s_0$ to source $s$ as the phase of the complex number $W_s{L}_{s_0}/W_{s_0}{L}_{s_0}$. For a real‐valued $\mathit{W}$, this estimate vanishes and the zero‐lag assumption thus holds.

2. Preservation of spatial properties

   The modified inverse operator ${\mathit{W}}^{\text{GCS}}$ shares the spatial properties of the original one $\mathit{W}$, such as its source blurring. Indeed, source modeling using the GCS actually coincides with original source modeling preceded by a projection $\mu \to (1_M‐L_{s_0}{W}_{s_0}/W_{s_0}{L}_{s_0})\mu$ on sensors data.

3. Depth bias independence

   A particular case of (ii) is that the original and the modified inverse operators exhibit the same depth bias, to which the GCS is thus insensitive. Indeed, a spatially inhomogeneous renormalization $W_s\to W_s/{\lambda }_s$ eliminating the depth bias ${\lambda }_s$ for source $s$ induces the same rescaling $W_s^{\text{GCS}}\to W_s^{\text{GCS}}/{\lambda }_s$ since the sensor‐space projector is invariant.

4. Local elimination of seed activity

   The role of the sensor‐space projection is to suppress the contribution of the seed $s_0$ to the reconstruction. This elimination is embodied by the identity $W_{s_0}^{\text{GCS}}=0$, which shows that corrected reconstructions always vanish at the seed location ( ${\varphi }_{s_0}^{\text{GCS}}=0$). The remaining source blurring then also imposes non‐trivial correction for neighboring sources $s$ (see also property (vii) below).

5. Elimination of spatial leakage from the seed

   A related consequence of this projection is the suppression of spatial leakage effects emanating from $s_0$. This central property of the GCS is evidenced by the vanishing of the corrected PSF

   $${\mathit{W}}^{\text{GCS}}{L}_{s_0}=0,$$

   which indeed shows that the spurious contribution of true seed activity to the corrected reconstruction has been eliminated.

6. No modification in the absence of spatial leakage

   Another key property is that the inverse operator is effectively uncorrected wherever spatial leakage effects from $s_0$ are negligible, as it should. Indeed, the absence of such effects from $s_0$ to $s$ is characterized by $W_s{L}_{s_0}\approx 0$, from which follows $W_s^{\text{GCS}}\approx W_s$. This typically happens in regions sufficiently distant from the seed, as will be shown for MNE using simulations.

7. Local overcorrection

   Ideally, a method designed to correct for spatial leakage from $s_0$ should satisfy the property (v) but leave other PSFs unaffected. However, these constraints are generally incompatible (at least in the context of linear inverse modeling) because of lead field correlations. For the GCS, this impossibility is exemplified by the formula

   $${\mathit{W}}^{\text{GCS}}{L}_s=\mathit{W}{L}_s‐k_s\mathit{W}{L}_{s_0}, k_s=W_{s_0}{L}_s/W_{s_0}{L}_{s_0} .$$

   The PSF of source $s\ne s_0$ is thus non‐trivially modified when $k_s$ deviates from zero, which happens when the lead field columns $L_s$ and $L_{s_0}$ are sufficiently correlated. The GCS thus completely eliminates spatial leakage from $s_0$ at the expense of possible overcorrection wherever $k_s\ne 0$. In MEG/EEG, this overcorrection is expected to be essentially local because lead field correlations typically arise from the spatial smoothness of the forward model. This limitation of the GCS should thus have consequences mainly for local FC estimation and seed location errors.

Properties (v) and (vi) provide a posteriori justification of the GCS, whereas avoiding the issue of overcorrection (vii) explains the stated model assumption that only sources $s$ with negligible spatial leakage from $s$ to $s_0$ (i.e., $W_{s_0}{L}_s\approx 0$ so $k_s\approx 0$) should be active. The extent of this limitation, as well as of other implicit model assumptions (no measurement noise or lead field errors), shall be assessed using simulations.

Spatial Leakage Correction by Signal Orthogonalization

The advantages and limitations of the GCS shall also be examined by comparison with signal orthogonalization. We focus here on the two foundational versions, i.e., static [Brookes et al., 2012b] and instantaneous [Hipp et al., 2012] orthogonalizations. Mathematically, they correspond respectively to temporal and phase Gram‐Schmidt orthogonalizations of the sources and the seed time courses. In our notations,

$${\varphi }^{\text{static}}={\widehat{\psi }}_{}-\frac{\mathrm{R}\mathrm{e}\left[{\widehat{\psi }}_{}{\widehat{\psi }}_{s_0}^{\mathrm{†}}\right]}{{\left({\widehat{\psi }}_{s_0},{\widehat{\psi }}_{s_0}^{\mathrm{†}}\right)}^{}}{\widehat{\psi }}_{s_0}$$

and

$${\varphi }_t^{\text{inst}}={\widehat{\psi }}_t-\frac{\mathrm{R}\mathrm{e}\left[{\widehat{\psi }}_t{\widehat{\psi }}_{s_{0}t}^{\mathrm{*}}\right]}{{\left|{\widehat{\psi }}_{s_{0}t}\right|}^2}{\widehat{\psi }}_{s_{0}t};$$

the subscript t indicating the column corresponding to the $t$ ^th time sample ( $1\le t\le T$).

It is noteworthy that these corrections (originally developed for envelope FC) can be formally applied to phase coupling measures and actually relate closely to existing FC indices such as the phase lag index [Wens, 2015] or imaginary coherence. Rephrasing an argument given in Nolte et al. [2004], the link with imaginary coherence can be traced back to the orthogonality relation

$$\text{Re}\left[\varphi {\widehat{\psi }}_{s_0}^{†}\right]=\hspace{0.17em}0\hspace{0.17em}(\varphi ={\varphi }^{\text{static}}\hspace{0.17em}\text{or}\hspace{0.17em}{\varphi }^{\text{inst}}),$$

which indicates that the cross‐density $\varphi {\widehat{\psi }}_{s_0}^{†}$ (unnormalized coherence between the uncorrected seed and the orthogonalized source time series) is indeed imaginary.

Minimum Norm Estimation

To illustrate the theory on simulations and experimental data, we shall use MNE as a basic example of linear inverse model, for which $\mathit{W}$ reads [Dale and Sereno, 1993]

$$\mathit{W}={\mathit{L}}^{\mathrm{T}} {\left(\mathit{L}{\mathit{L}}^{\mathrm{T}}+\kappa {\mathit{C}}_{\varepsilon }\right)}^{‐1},$$

the $M\times M$ matrix ${\mathit{C}}_{\mathit{\varepsilon }}$ and scalar $\kappa >0$ respectively denoting measurement noise covariance and a regularization parameter. This expression follows from a well‐known minimization problem [Backus and Gilbert, 1970; Tarantola, 2004]. It is noteworthy that the GCS for MNE also derives from a constrained minimization explicitly implementing the key property (v), and actually reduces to a special case of the DeFleCT algorithm [Hauk and Stenroos, 2014] (see Supporting Information A.1 for details).

In practice, we shall set the regularization parameter to

$$\kappa =\frac{\text{tr}\left({\mathit{C}}_{\varepsilon }^{‐1}\mathit{L}{\mathit{L}}^{\mathrm{T}}\right)}{\text{tr}\left({\mathit{C}}_{\varepsilon }^{‐1}{\mathit{C}}_{\mu }\right)-M},$$

where ${\mathit{C}}_{\mu }$ denotes the $M\times M$ data covariance. This choice can be derived from a consistency argument within the prior assumptions of MNE (see Supporting Information A.2). To simplify subsequent analyses, the $D\leftarrow 1$ projection will be applied onto the directions $n_s$ of maximum sources variance, estimated as the principal eigenvectors of each dipole $D\times D$ covariance matrix $W_s{\mathit{C}}_{\mu }{W}_s^T$ [Wens et al., 2014a, 2014b]. When needed (e.g., for visualization of PSFs), the depth bias will be corrected using sLORETA [Pascual‐Marqui, 2002], i.e., upon normalization of each source $s$ amplitude estimate by

$${\widehat{\lambda }}_s=\sqrt{W_s\left({\kappa }^{-1}\mathit{L}{\mathit{L}}^{\mathrm{T}}+{\mathit{C}}_{\varepsilon }\right)W_s^{\mathrm{T}}} .$$

For MNE, spatial leakage is essentially controlled by the correlation structure of the lead field [Wens, 2015]. We shall use two consequences of this observation. Firstly, lead field columns spatial similarity $\left|\text{corr}\left(L_s,L_{s_0}\right)\right|$ gives a natural measure of the spurious cross‐talk strength from seed $s_0$ to source $s$, where $\text{corr}$ denotes Pearson's correlation coefficient. Secondly, spatial leakage among all $N$ sources strongly restricts the number ${\rho }_{\text{MNE}}$ of spatial degrees of freedom (DOFs) involved in MNE reconstructions ( ${\rho }_{\text{MNE}}\ll N$), which can be identified generically with

$${\rho }_{\text{MNE}}=\text{rank}\left(\mathit{W}\right)=\text{rank}\left(\mathit{L}\right)$$

in view of the above equation for $\mathit{W}$. Adapting the philosophy of Barnes et al. [2011] to the specific case of MNE, we shall use an estimate of ${\rho }_{\text{MNE}}$ to control the multiple comparisons problem involved in statistically testing source‐level maps. The GCS and signal orthogonalizations remove one DOF due to seed activity (see identities ${\varphi }_{s_0}^{\text{GCS}}={\varphi }_{s_0}^{\text{static}}={\varphi }_{s_0}^{\text{inst}}=0$). Nevertheless, since some tests considered next mix uncorrected and corrected reconstructions, we shall systematically use ${\rho }_{\text{MNE}}$ instead of ${\rho }_{\text{MNE}}‐1$, which leads to only slightly conservative statistics. In practice, the lead field rank will be evaluated by computing the spectrum of the covariance matrix $\mathit{L}{\mathit{L}}^{\mathrm{T}}$ and finding the minimum number of eigenvalues whose sum reaches 99% of total variance $\text{tr} \mathit{L}{\mathit{L}}^{\mathrm{T}}$.

MATERIALS AND METHODS

Structural Effects on Noisy Point‐Spread Functions

All simulated MEG data were generated using one subject's lead field ${\mathit{L}}^{\left(0\right)}$ for a 306‐channels whole‐scalp neuromagnetometer (Vectorview, Elekta Oy, Helsinki, Finland) taken from the RSNs data (described next). Only planar gradiometers were used ( $M=204$), as explained later.

The effect of the GCS on noisy PSFs was first investigated using simulated source configurations $\psi$ ( $DN\times 1$) consisting of a single active dipole $s$ whose moment vector ${\psi }_s$ was chosen of unit amplitude and pointing in the direction of maximum magnetic response $L_s^{\left(0\right)}{\psi }_s$ (i.e., the principal eigenvector of the $D\times D$ matrix $L_s^{\left(0\right)\mathrm{T}}{L}_s^{\left(0\right)}$). Sensor‐space data $\mu$ were then generated by forward modeling with lead field $\mathit{L}={\mathit{L}}^{\left(0\right)}$ and measurement noise $\varepsilon$ obtained by randomly picking a time sample from an artifact‐free empty room MEG recording (duration: 5 min, sampling rate: 1 kHz, band‐pass filter: 0.1–330 Hz). The latter data were preprocessed beforehand using signal space separation (SSS) to suppress external interferences [Taulu et al., 2005] and rescaled so as to fix the SNR estimate

$$\zeta =\frac{1}{M} \text{tr}\left({\mathit{C}}_{\varepsilon }^{‐1}{\mathit{C}}_{\mu }\right)$$

to a given value (see below). The noise covariance matrix ${\mathit{C}}_{\mathit{\varepsilon }}$ was derived from the empty room data and regularized by adding 10% of the mean gradiometers variance $\text{tr}{ \mathit{C}}_{\varepsilon }/M$ to its diagonal elements before inversion.

Source modeling was then performed with MNE, as outlined in the Theory section. To include lead field errors, $\mathit{L}$ was chosen as an interpolation $\left(1‐\tau \right){\mathit{L}}^{\left(0\right)}+\tau {\mathit{L}}^{\left(1\right)}$ between the true lead field ${\mathit{L}}^{\left(0\right)}$ and another lead field ${\mathit{L}}^{\left(1\right)}$ taken from the RSNs data; $\tau$ denoting the interpolation parameter (see below). The resulting reconstruction $\widehat{\psi }$ then defined the noisy PSF of source $s$ at parameters $\zeta$ and $\tau$. Likewise, the GCS‐modified PSF was computed as the corrected reconstruction ${\varphi }^{\text{GCS}}$, with the seed location $s_0$ chosen at the left SM1 hand area (SM1ha, MNI coordinates: [–42, −26, 54] mm) or the left A1 cortex ([–54, −22, 10] mm). Spatial dissimilarity ${\delta }_s\left(\zeta ,\tau \right)=1‐\text{corr}(\widehat{\psi },{\varphi }^{\text{GCS}})$ was finally used to quantify the modification of PSFs by the GCS. Possible values range between 0 (same PSFs, i.e., no effect of GCS) to 1 (uncorrelated PSFs) to 2 (anti‐correlated PSFs). This index was averaged over 5 simulation runs.

Spatial dissimilarity was assessed as a function of source location by performing the above steps for all sources $s$ with $\zeta =4$ and $\tau =0$ (reference simulation). The effect of noise parameters was subsequently explored by varying the SNR ( $\zeta =$ 1.01, 2, 4, 8 and 16) and the lead field interpolation ( $\tau$ from 0 to 1 by step 0.2), and quantitatively compared to the reference simulation ${\zeta }_{\text{ref}}=4$, ${\tau }_{\text{ref}}=0$ using the fit error

$$\frac{{\sum }_s{\left({{\delta }_s\left(\zeta ,\tau \right)-\delta }_s\left({\zeta }_{\text{ref}},{\tau }_{\text{ref}}\right)\right)}^2}{{\sum }_s{{\delta }_s\left({\zeta }_{\text{ref}},{\tau }_{\text{ref}}\right)}^2}.$$

Because of the computational load, the simulations with varying parameters were limited to a random subselection of 1000 sources, to which the sums over $s$ were restricted.

Simulated Networks

The induced effect of spatial leakage correction on FC estimation was investigated using simulated networks in the β band (12‐21 Hz). Source configurations $\psi$ ( $DN\times T$) comprised a number $K$ of active nodes (seed node $s_0$, target nodes $s_1,\dots ,s_{K‐1}$) on top of a brain background (β‐band filtered gaussian white noise, duration: 5 min, sampling rate: 200 Hz, $T=6\times {10}^4$). The simulated dipole moments consisted of β‐band filtered gaussian white noises with variance 10 times that of the background; their orientations being fixed in terms of the lead field ${\mathit{L}}^{\left(0\right)}$ as in the PSF simulation. To mimic the slow amplitude FC observed in RSNs, the Hilbert envelope of the seed node was replaced by a 0.1 Hz sinusoid [Brookes et al., 2012b] shifted and rescaled to preserve envelope positivity and signal variance. The Hilbert envelope and phase of the target nodes were then modulated to set up various coupling patterns involving slow envelope FC with (non‐orthogonal signals, phase lag $\ne \pi /2$) or without (orthogonal signals, phase lag $=\pi /2$) linear correlation. The precise algorithm is detailed in Supporting Information A.3. Forward modeling of the resulting simulated configuration was then performed using $\mathit{L}={\mathit{L}}^{\left(0\right)}$ and measurement noise $\varepsilon$ taken from the empty room MEG data [downsampling to 200 Hz, β‐band filtering, rescaling for a realistic SNR estimate $\zeta =4$ (see the RSNs data)].

Several configurations were considered. Firstly, basic binodal ( $K=2$) networks of orthogonal signals were built using a seed node placed at left SM1ha and a target node probing the rolandic sulcus at various distances, or a seed node at left A1 and a target node at right A1 (MNI coordinates: [54, −22, 10] mm, distance from seed node: 10 cm). Their coupling consisted of slow envelope FC (simulated values: 0 and 0.5) without linear correlation. Secondly, a trinodal ( $K=3$) network mimicking the auditory RSN was built using a seed node at left A1, one target node in the left supramarginal gyrus (SMG, [−47, −38, 26] mm, 2 cm) and another at right A1. Couplings with the seed node consisted of equal linear and slow envelope correlations (values: 0.5 for SMG, 0.7 for right A1). Lastly, a quadrinodal ( $K=4$) network reproducing the sensorimotor RSN was built using a seed node at left SM1ha, two target nodes along the left rolandic sulcus ([−50, −12, 42] mm and [−18, −30, −72] mm, 2.5 cm) and another at right SM1ha ([42, −26, 54] mm, 8 cm). Couplings with the seed node consisted of equal linear and slow envelope correlations (value: 0.7) for the left target nodes and pure slow envelope FC (value: 0.5, orthogonal signals) for the right target node. In each case, the simulation was run 10 times.

Seed‐based FC analyses were then performed for each simulation. The used seed ${\widehat{s}}_0$ either coincided with the seed node $s_0$ or was placed 1.5 cm away to investigate the consequences of seed mislocation. The reconstruction $\widehat{\psi }$ was obtained with MNE (no lead field interpolation) and its analytic signal was extracted using the Hilbert transform. The GCS and signal orthogonalizations were also applied to correct for spatial leakage from the seed ${\widehat{s}}_0$, resulting in analytic signals ${\varphi }_s^{\text{GCS}}$, ${\varphi }_s^{\text{static}}$ and ${\varphi }_s^{\text{inst}}$ for all target sources $s\ne {\widehat{s}}_0$. Slow envelope FC maps were finally derived between the seed (X ₀) and the target (X) time series (simulated FC: $X_0={\psi }_{s_0}$, $X={\psi }_s$; reconstructed FC: $X_0={\widehat{\psi }}_{{\widehat{s}}_0}$, $X={\widehat{\psi }}_s$, ${\varphi }_s^{\text{GCS}}$, ${\varphi }_s^{\text{static}}$ or ${\varphi }_s^{\text{inst}}$), by first down‐sampling the Hilbert envelopes $\left|X_0\right|$ and $\left|X\right|$ using sliding‐window averages (width: 1 s, step: 0.5 s) and then computing their temporal correlation [Brookes et al., 2012b; Wens et al., 2014a, 2014b].

Resting‐State Networks

This resting‐state dataset is the same as the one used in Wens et al. [2014b]. Fifteen healthy adult subjects (8 females and 7 males, mean age: 24 years, age range: 19–30 years) took part in this study after written informed consent; the study being approved by the ULB–Hôpital Erasme Ethics Committee. All participants were right‐handed as assessed by the Edinburgh Handedness Inventory [Oldfield, 1971] and had no history of neurologic or psychiatric disease. Subjects performed a resting‐state MEG session (5 min), during which they were asked to sit still and gaze at a fixation cross projected on a screen in front of them. Data were recorded (sampling rate: 1 kHz, band‐pass filter: 0.1–330 Hz) in a light‐weight magnetically shielded room (Maxshield™, Elekta Oy, Helsinki, Finland) using a 306‐channels whole‐scalp neuromagnetometer (Vectorview, Elekta Oy, Helsinki, Finland) installed at the ULB–Hôpital Erasme [for its technical characteristics, see Carrette et al., 2011; De Tiège et al., 2008]. Four head‐tracking coils monitored the subjects’ head position inside the MEG helmet. Their locations relative to anatomical fiducials, as well as at least 150 head‐surface points, were recorded prior to MEG data acquisition using an electromagnetic tracker (Fastrack, Polhemus, Colchester, VT).

Off‐line preprocessing was then applied to clean data from noise and extract the sensor‐level β‐band rhythms used to derive the SM1 and the A1 MEG RSNs. The SSS method was first applied to suppress external interferences and correct for head movements [Taulu et al., 2005]. Sensor signals were then filtered between 0.5 and 45 Hz and linearly decomposed using independent component analysis [Hyvärinen et al., 2001; Vigario et al., 2000] as implemented in the FastICA algorithm (dimension reduction to 30, non‐linearity tanh). Artifactual components corresponding to cardiac, eye movements and electronic artifacts were visually selected and projected out of data (number of rejected components per subject: mean 3.3, range 2–5). Finally, the cleaned MEG time series were filtered in the β band and their analytic signals were derived using the Hilbert transform. In subsequent analyses, data were restricted to the $M=204$ planar gradiometers [to avoid possible issues associated with SSS, see Luckhoo et al., 2012a] and gathered in a complex‐valued $M\times T$ data matrix $\mu$ ( $T\approx 3\times {10}^5$). The resulting SNR estimates were $\zeta =4.6\pm 2.5$ (mean ± standard deviation over the subjects), explaining the value used in the simulations.

Computation of subjects’ lead fields $\mathit{L}$ was based on their high‐resolution 3D‐T1 weighted MRI acquired using a 1.5 T MRI scanner (Intera, Philips, The Netherlands) and anatomically segmented using the Freesurfer software (Martinos Center for Biomedical Imaging, Massachusetts, USA). MEG and MRI coordinate systems were co‐registered using the 3 anatomical fiducial points for initial estimation and the head‐surface points for further manual refinement. A source grid was then built in each subject's MRI to approximate the current flow distribution by a discrete collection of $N$ current dipoles. To facilitate group averaging, this grid was obtained by mapping a common regular 5‐mm grid sampling the Montreal Neurological Institute (MNI) brain volume ( $N=16102$) onto each subject's brain using a non‐linear spatial deformation algorithm implemented in Statistical Parametric Mapping (SPM8, Wellcome Trust Centre for Neuroimaging, London, UK). The $D=3$ lead field $\mathit{L}$ associated to each grid was then estimated using the Boundary Element Method implemented in the MNE software suite (Martinos Center for Biomedical Imaging, MA). Two of these were used in the simulations.

Inverse modeling, spatial leakage correction (GCS and signal orthogonalizations) and slow envelope FC estimation were performed as for the network simulations. To disclose the SM1 and the A1 RSNs, seed locations $s_0$ were selected at the left SM1ha and the A1 cortex as above.

Auditory‐Motor Network

This dataset investigates the corticokinematic coherence (CKC) phenomenon [Bourguignon et al., 2011, 2012, 2013]; the hand movement being here auditorily paced. Ten healthy adult subjects (4 females and 6 males, mean age: 31 years, age range: 24–40 years) took part in this study approved by the ULB–Hôpital Erasme Ethics Committee. All were right‐handed as assessed by the Edinburgh Handedness Inventory [Oldfield, 1971], had no history of neurologic or psychiatric disease, and participated after written informed consent. Subjects performed flexion‐extensions of the right‐hand fingers during 5 one‐min periods, each separated by one minute of rest. They were asked to avoid any contact between the thumb and the other fingers to reduce tactile inputs, and to gaze at a point on the ceiling of the magnetically shielded room to avoid any visual contact with the moving hand. A movement pace of 2 Hz was imposed by using an auditory cue (440 Hz pure tone with 2 Hz amplitude modulations, 60 dB above hearing threshold). Right index finger kinematics was recorded (sampling rate: 1 kHz, low‐pass filter: 330 Hz) simultaneously to MEG signals using a 3‐axis accelerometer (Acc; ADXL335 iMEMS Accelerometer, Analog Devices, Norwood, MA).

MEG data acquisition and artifact correction in the 0.5–45 Hz band was identical to the RSNs pipeline. The euclidean norm of band‐passed (1–200 Hz) Acc signals was computed for each time sample, hence reflecting movement kinematics independently of direction. The five movement periods were concatenated and defined the MEG ( $\mu$) and the Acc ( $a$) data. As before, only gradiometers were used ( $M=204$).

A time‐frequency representation adapted to coherence analysis was obtained using the Fast Fourier Transform on overlapping sliding windows (width: 3072 ms corresponding to ∼6 movement cycles, step 615 ms). This resulted for each frequency $f$ (spectral resolution: ∼ 0.33 Hz) in complex‐valued time series $\mathrm{F}\mu \left(f\right)$ ( $M\times T$) and $\mathrm{F}a\left(f\right)$ ( $1\times T$), where $\mathrm{F}$ symbolizes the Fourier transform operation and $T$ denotes the corresponding number of time windows ( $T\approx 450$). A similar decomposition was applied to the empty room data, defining measurement noise $\mathrm{F}\varepsilon \left(f\right)$ ( $M\times T$ with $T\approx 490$). Subsequent analysis was limited to movement frequency $f_0=2 \text{Hz}$ and its first harmonic $f_1=4 \text{Hz}$, which were singled out by CKC spectra [Bourguignon et al., 2011, 2012, 2013]. Data and noise $M\times M$ cross‐density matrices were estimated at $f=f_0$ and $f=f_1$ using ${\mathit{C}}_{\mu }\left(f\right)=\mathrm{F}\mu \left(f\right)\mathrm{F}\mu {\left(f\right)}^{†}/T$ and ${\mathit{C}}_{\varepsilon }\left(f\right)=\mathrm{F}\varepsilon \left(f\right)\mathrm{F}\varepsilon {\left(f\right)}^{†}/T$. The SNR estimates at these frequencies were $\zeta =23.1\pm 16.0$ at $f=f_0$ and $\zeta =18.2\pm 9.9$ at $f=f_1$ (mean ± standard deviation over the subjects).

Inverse modeling and the GCS were then applied as above, with the only difference that covariances were replaced by cross‐densities. In this setup, the resulting MNE inverse operator $\mathit{W}=\mathit{W}\left(f\right)$ was frequency specific and complex valued, hence inducing non‐zero‐lag spatial leakage effects. Reconstructed sources Fourier time series $\mathrm{F}\widehat{\psi }\left(f\right)$ and its corrected version $\mathrm{F}{\varphi }^{\text{GCS}}\left(f\right)$ ( $N\times T$) were obtained by application of the original and the modified inverse operators on $\mathrm{F}\mu \left(f\right)$.

Cortico‐cortical coherence analysis was then performed. The seed was chosen for each frequency of interest ( $f_0$ and $f_1$) on the basis of source‐level CKC analysis [Bourguignon et al., 2012]. Coherence maps $\left|\text{coh}\left(\mathrm{F}a\left(f\right),\mathrm{F}{\widehat{\psi }}_s\left(f\right)\right)\right|$ between sources and Acc signals were first computed and averaged over subjects, $\text{coh}$ denoting the complex‐valued coherence [Halliday et al., 1995]. The seed $s_0$ was selected as the local maximum located at the SM1 cortex contralateral to hand movement. Then, cortico‐cortical coherence maps with and without GCS were obtained as the magnitude coherence $\left|\text{coh}\left(\mathrm{F}{\widehat{\psi }}_{s_0}\left(f\right),\mathrm{F}{X}_s\left(f\right)\right)\right|$ with $X=\widehat{\psi }$ (uncorrected for spatial leakage) and $X={\varphi }^{\text{GCS}}$ (corrected) for all target sources $s\ne s_0$. Despite the failure of the zero‐lag spatial leakage assumption, the imaginary coherence maps $\left|\text{Im} \text{coh}\left(\mathrm{F}{\widehat{\psi }}_{s_0}\left(f\right),\mathrm{F}{\psi }_s\left(f\right)\right)\right|$ were also computed for comparison with the GCS.

Statistical Maps

Various statistics were considered to assess the significance of FC estimates, MNE spatial leakage effects and their correction by the GCS or the signal orthogonalization. All the following tests were performed at significance level $\alpha =0.05$. The family‐wise error (FWE) was controlled using Bonferroni correction for the number ${\rho }_{\text{MNE}}$ of spatial DOFs [i.e., ${\alpha }_{\text{FWE}}=\alpha /{\rho }_{\text{MNE}}$, see Barnes et al., 2011; Brookes et al., 2012b] identified in the Theory section (simulations: ${\rho }_{\text{MNE}}=55$; resting‐state: ${\rho }_{\text{MNE}}=58\pm 5$; auditory‐motor at $f_0$ and $f_1$: ${\rho }_{\text{MNE}}=62\pm 6$; mean ± standard deviation over the subjects).

Statistical significance against the null hypothesis of zero FC was assessed for the resting‐state and the auditory‐motor networks, by constructing approximately gaussian standard $Z$‐scores as Fisher‐transformed FC divided by its null standard deviation [for Fisher's transform of imaginary coherence, see Eq. (12) in Nolte et al., 2004]. The latter was estimated non‐parametrically using 1000 surrogate datasets preserving temporal autocorrelations. For slow envelope FC, the null samples were generated by computing Fisher‐transformed seed‐based envelope correlations with Fourier‐phase surrogates [Schreiber and Schmitz, 2000] of each target slow envelope time series. For coherence, they were generated as the Fisher‐transformed seed‐based magnitude or imaginary coherence with random‐phase surrogates [Faes et al., 2004] of each target Fourier time series. To detect FC typical of the population, statistical masking was derived from a conjunction analysis. Briefly, the one‐tailed tests $Z_s>0$ with FWE correction were first performed for each subject. Then, only source locations with a fraction $\gamma$ of subjects falling in the confidence interval ${\gamma }_c\le \gamma \le 1$ were included in the mask [resting‐state: ${\gamma }_c=62\%$ for 15 subjects; auditory‐motor at $f_0$ and $f_1$: ${\gamma }_c=48\%$ for 10 subjects; see Eq. (3) in Friston et al., 1999].

For the network simulations where the true interaction pattern is known, spatial leakage effects in seed‐based FC maps were gauged by the statistical difference between simulated (ground truth) and reconstructed (uncorrected, GCS and signal orthogonalizations) FC estimates. This was assessed using two‐tailed paired $T$‐tests (samples: Fisher‐transformed slow envelope FC for the 10 simulations; number of DOFs: $\nu =9$); the resulting $T_{\nu }$‐maps being thresholded at significance level ${\alpha }_{\text{FWE}}$.

Finally, in all cases, the differential effect of the considered FC reconstructions was assessed using similar $T$‐tests (samples: Fisher‐transformed slow envelope FC or coherence for the $\nu +1$ simulations or subjects; number of DOFs: $\nu =9$ for simulated and auditory‐motor networks, $\nu =14$ for RSNs).

RESULTS

Structural Effects on Noisy Point‐Spread Functions

We explored the effect of the GCS from two seed locations on the inverse operator using reconstructions of noisy PSFs. Results for the SM1ha seed are depicted in Figure 2. For the reference simulation, the spatial distribution of PSF dissimilarity showed that the GCS has mostly a local effect decreasing with distance from the seed (Fig. 2A, left and middle). Locations with PSF dissimilarity above 0.2 were observed up to 2 cm, where the GCS acted non‐trivially. Strong effect was found at the seed itself (Fig. 2B, left), reflecting the elimination of spatial leakage [property (v) in the Theory section]. An example of non‐trivial modification for a nearby ( $\le 2$ cm) source is also given (Fig. 2B, middle), illustrating local over‐correction [property (vii)]. Back to Figure 2A (middle), PSF dissimilarity was below 0.1 for sources farther than 4 cm (and in particular, in the hemisphere contralateral to the seed) where no effect of the GCS was observed, as exemplified in Figure 2B (right). This demonstrated the absence of effective long‐range modifications of the inverse operator and the locality of overcorrection [properties (vi) and (vii)]. An increasing relation between PSF dissimilarity and lead field similarity was also observed (Fig. 2A, right). This confirmed that the GCS has negligible effect for small spatial leakage [property (vi)] and gets more important for stronger spatial leakage.

Figure 2.

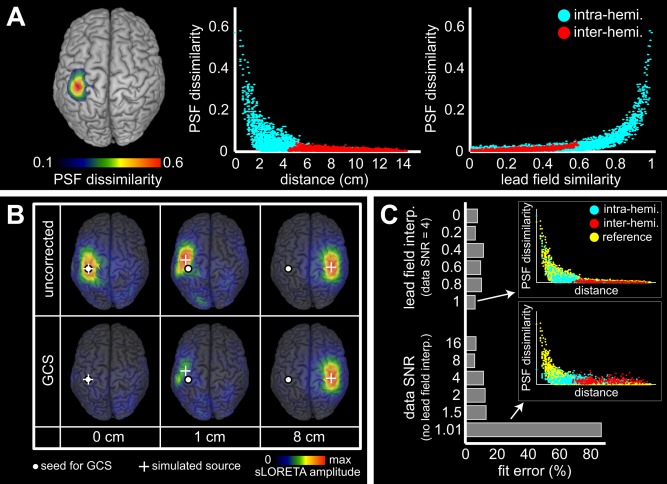
Effect of the GCS from the left SM1ha on noisy PSFs. (A) Spatial distribution of PSF dissimilarity for the reference simulation (SNR $\zeta =4$, no lead field error). It is represented as a cortical map (left) and plotted against distance (middle) or lead field similarity (right) between the seed and the simulated node. Blue and red points respectively denote sources in the left and the right hemispheres. (B) Example PSFs before (top) and after (bottom) geometric correction taken from the reference simulation with simulated node (white cross) placed along the rolandic sulcus at 0, 1 and 8 cm from the seed (white dot). Maps were normalized using sLORETA for visualization. C: Effect of parameters variation on PSF dissimilarity, as assessed by the fit error to the reference simulation. Inserts show two examples with explicit comparison to the reference simulation (yellow points).

Since the model on which the GCS is based ignores both measurement noise and lead field inaccuracies, we investigated the robustness of this method by varying the SNR and the lead field interpolation. Figure 2C shows the fit error estimating the alteration of the PSF dissimilarity distribution by these parameters, compared to the reference simulation. No effect induced by reasonable SNR or lead field interpolation (Fig. 2C, top insert) could be disclosed. The fit error only increased for very poor SNR, in which case PSFs were dominated by noise and the action of the GCS was therefore mild and random (Fig. 2C, bottom insert).

Results for the A1 seed were similar, despite its deeper location within the sylvian sulcus and henceforth lesser MEG signal SNR (see Supporting Information B.1).

Simulated Binodal Networks (Orthogonal Signals)

The effect of the GCS on FC per se was investigated and compared to signal orthogonalization using simulated networks. We began with binodal networks of orthogonal signals (coupled via slow envelope correlation) to assess the basic performance of the GCS and its limitations due to local overcorrection, which on the basis of the structural effects was expected to arise for nodes distance below 2 cm. Figure 3 illustrates the reduction of seed‐based spatial leakage FC by the GCS for various configurations. In all cases, the uncorrected maps (Fig. 3, left) were dominated by local spatial leakage FC around the seed ( $T_9$‐maps maximum $>100$), which was significantly decreased after correction (Fig. 3, middle and right). Accordingly, the effect of the GCS on spatial leakage FC prevailed around the seed, although mild (i.e., close to significance threshold) long‐range differences were also observed (Fig. 3, right). For sufficiently remote nodes with and without seed mislocation (Fig. 3A,D), the disconnected significant region was left qualitatively unaffected [as expected by locality of spatial leakage from the seed, see property (vi) and Fig. 2B, right] and its maximum FC co‐localized with the right target node. Of notice, its spurious surrounding pattern represents a “secondary” spatial leakage effect [see, e.g., Palva and Palva, 2012] combining the true simulated coupling with spatial leakage from the target node, which is indeed not corrected by the GCS. For closer nodes whose PSFs overlapped (distance $<2$ cm, see Fig. 2A,B, middle), the GCS corrected spatial leakage imperfectly [overcorrection effect, property (vii)] and resulted in spurious local FC patterns. At distance 1 cm (Fig. 3B), this spurious pattern was mild and maximum FC actually co‐localized with the target node, whereas at 0.5 cm (Fig. 3C) this spurious pattern was dominant. Likewise, seed mislocation generated dominating spurious FC around the seed (Fig. 3D; see also Supporting Information B.2 for the mislocation effects associated with the deeper A1 seed).

Figure 3.

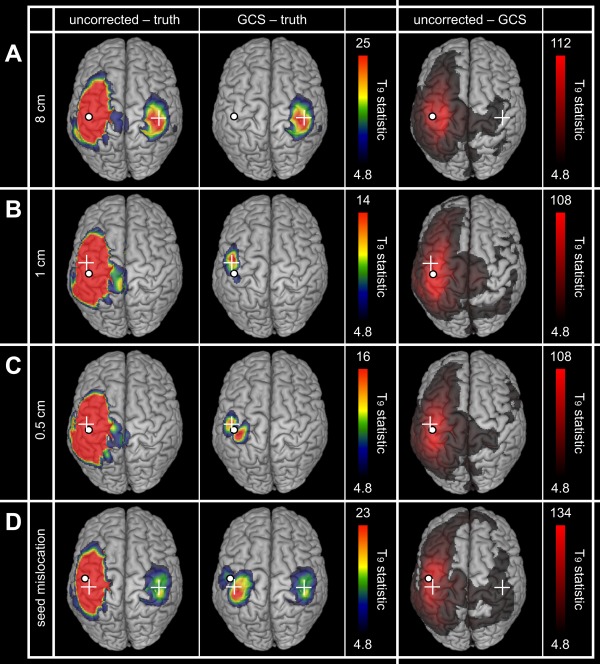
Geometric correction for simulated binodal networks (orthogonal signals). The statistical maps assess spatial leakage FC for uncorrected (left) and corrected (middle) slow envelope FC estimations as well as the differential effect of the GCS (right). Network nodes are indicated by the white dot and cross (A–C) or two white crosses (D). In all cases, the white dot shows the seed location used for FC mapping and geometric correction. Statistical thresholding was applied at FWE‐corrected significance level 0.05, while upper scales were set to the maximum of the GCS−truth (left and middle) or uncorrected−GCS (right) maps.

To check how spatial leakage correction behaves in the presence of active nodes uncoupled to the seed, binodal simulations without FC were also considered. Results are illustrated in Supporting Information B.3. Briefly, the pure spatial leakage effect observed in uncorrected maps was completely eliminated after geometric correction without seed mislocation, including for very close nodes. With seed mislocation, the same spurious local FC pattern than in Figure 3D was obtained.

Qualitatively similar observations applied to signal orthogonalization (as expected since the simulated signals conformed to the underlying orthogonality assumptions), although slightly significant differences were observed whenever overcorrection or seed mislocation effects took place. The above‐mentioned local spurious FC patterns were decreased compared to the GCS, indicating that signal orthogonalization is less affected by overcorrection issues, but it is noteworthy that they were still present. Details are given in Supporting Information B.4.

Simulated Multinodal Networks

We then considered more complex setups involving both close and distant nodes and including non‐orthogonal signals (so as to reveal ability to map linear FC). Figure 4 shows results for the sensorimotor and the auditory simulations. All spatial leakage corrections eliminated the local patterns dominating the uncorrected maps (Fig. 4, left, $T_9$‐maps maximum $>100$) and located the coupling with the orthogonal target node (Fig. 4, top). The GCS was also able to pinpoint all non‐orthogonal target nodes, whereas static orthogonalization was blind to them (as expected from the absence of simulated linear coupling). Instantaneous orthogonalization could also disclose the remote non‐orthogonal target node (Fig. 4, bottom right). The direct comparison of spatial leakage corrections is relegated to Supporting Information B.5.

Figure 4.

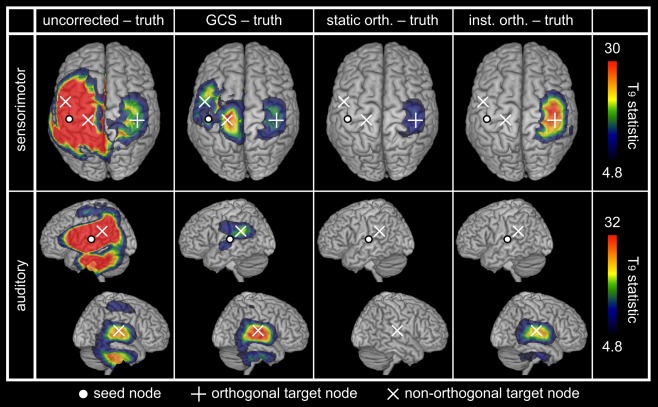
Spatial leakage correction for simulated multinodal networks. The statistical maps assess spatial leakage FC for uncorrected and corrected (GCS, static and instantaneous orthogonalizations) slow envelope FC estimations. Network nodes are indicated by white dots (seed node, also used for FC mapping and spatial leakage correction) and crosses (target nodes; +: orthogonal, ×: non‐orthogonal). Statistical thresholding was applied at FWE‐corrected significance level 0.05, while upper scales were set to the maximum of the GCS−truth maps.

Resting‐State Networks

Figure 5A shows the statistical FC maps representing the SM1 and the A1 RSNs. The uncorrected maps (Fig. 5A, left) presented the expected connectivity between left and right primary cortices but were dominated by intra‐hemispheric correlations around the seed ( $Z$‐maps maximum $>110$). The three correction methods decreased $Z$‐scores around the seed but significant local patterns persisted, either along the rolandic sulcus for the SM1 RSN or at the SMG for the A1 RSN. Corrected topographies were similar but with smaller Z‐scores after instantaneous orthogonalization (Fig. 5A, right), for which the inter‐hemispheric A1 FC was not significant.

Figure 5.

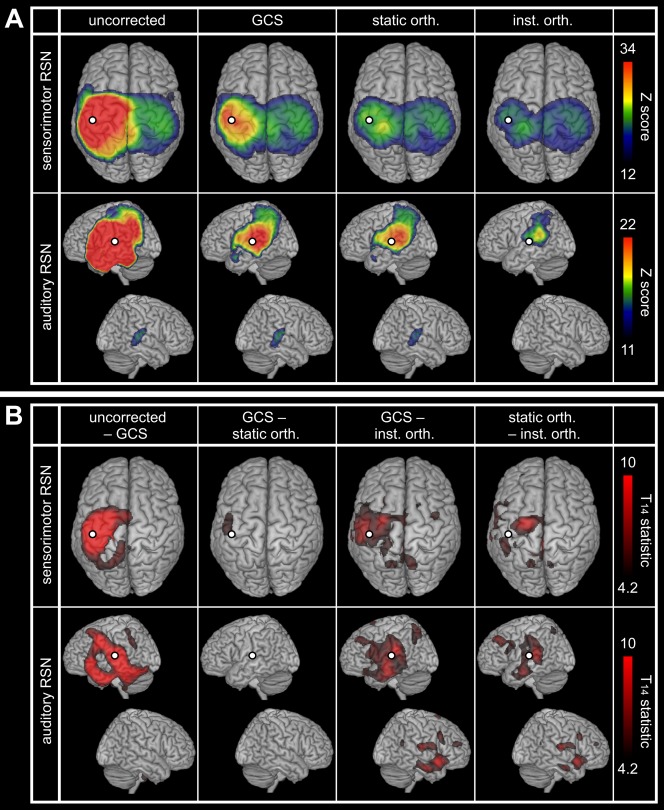
Spatial leakage correction for RSNs. (A) Statistical mapping of significant SM1 (top) and A1 (down) slow envelope FC at rest without correction for spatial leakage, with the GCS, as well as with static and instantaneous orthogonalizations. The presented values of Z‐scores were group averaged and the upper scales were based on the GCS maps maximum. Statistical masking was derived from a conjunction analysis and lower scales were set to the within‐mask minimum. (B) Differential effects of spatial leakage corrections. Statistical thresholding was applied at FWE‐corrected significance level 0.05, and upper scales were set to the maximum of GCS−inst. orth. maps. In all cases, the white dot indicates the seed used for FC mapping and spatial leakage correction.

Statistical comparisons of the different spatial leakage corrections (Fig. 5B) confirmed that the GCS decreased FC locally [Fig. 5B, left; see also property (vi)]. They did not disclose extensive differences between the GCS and static orthogonalization for these resting‐state data, but revealed non‐homogeneous FC underestimation by instantaneous orthogonalization.

Auditory‐Motor Network

The seeds MNI coordinates obtained from source‐level CKC analysis were [−27.5, −9.5, 58.5] mm (left primary motor (M1) cortex) at $f_0=2 \text{Hz}$ and [−38.5, −33.5, 47.5] mm (left primary somatosensory (S1) cortex) at $f_1=4 \text{Hz}$. Figure 6 shows the resulting statistical maps for seed‐based coherence, both uncorrected for spatial leakage and corrected with the GCS, as well as for imaginary coherence. Again, high levels of FC around the seed dominated the uncorrected maps (Fig. 6, left, $Z$‐maps maximum $>210$) and were decreased after correction (Fig. 6, middle and right). Despite preeminent spatial leakage effect, various local maxima away from the seed could be disclosed visually in the uncorrected map at $f_0$ and appeared qualitatively preserved after geometric correction (Fig. 6, top left and middle). Coherent areas overlapped the dorso‐lateral prefrontal cortices (DLPFC) bilaterally, the supplementary motor area (SMA)/medial premotor cortex, the right SM1 cortex, the posterior parietal cortex (PPC, Brodmann areas 5 and 7), the superior (STG) and inferior (ITG) temporal gyri bilaterally, and the cerebellum with predominance over the right cerebellar hemisphere. At $f_1$, spatial leakage effects spread more extensively, and the only local maxima identified before correction were left DLPFC, left ITG and right preeminent cerebellum (Fig. 6, bottom left). After applying the GCS, the right SMA, left premotor/M1 cortex, right medial SM1 cortex and left PPC were also emphasized (Fig. 6, bottom middle).

Figure 6.

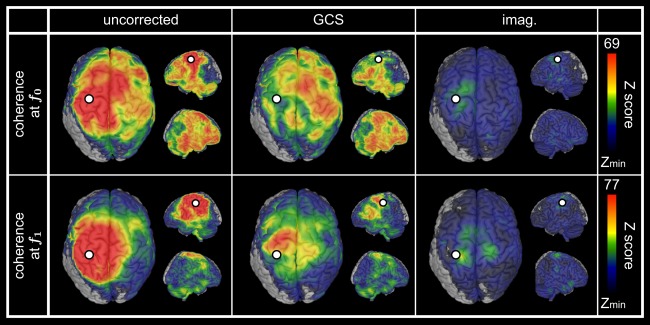
Spatial leakage correction for auditory‐motor network. Statistical mapping of significant task‐based cortico‐cortical coherence at f ₀ (top) and f ₁ (bottom) using uncorrected coherence (left), geometrically corrected coherence (GCS, middle) as well as imaginary coherence (imag. right). The presented values of Z‐scores were group averaged and the upper scales were based on the GCS maps maximum. Statistical masking was derived from a conjunction analysis, and lower scales were set to the within‐mask minimum [Z _min = 20 (f ₀) or 15 (f ₁) for uncorrected and GCS; Z _min = 9 for imag. (f ₀ and f ₁)]. In all cases, the white dot indicates the seed used for FC mapping and spatial leakage correction.

The values and topographies of $Z$‐maps appeared different for imaginary coherence (Fig. 6, right), as expected since the zero‐lag spatial leakage assumption is broken. However, statistical comparison of correction methods did not disclose extensive significant differences (see Supporting Information B.6).

DISCUSSION

Geometric Correction of Spatial Leakage

This article considers a GCS allowing elimination of spurious couplings induced by spatial leakage from a fixed location and investigates its usefulness for MEG/EEG seed‐based FC analyses.

The starting point of this approach is the observation that spatial leakage emerges from the structure of inverse operators rather than brain state dynamics. The GCS indeed relies on seed‐based spatial leakage geometry modeled as a suitably normalized PSF at the seed location. This application of PSFs shares common features with previous works [Hauk and Stenroos, 2014; Liu et al., 2002; Schoffelen and Gross, 2011]. In particular, the point‐spread metric ${\left|W_s{L}_{s_0}\right|}^2/{\left|W_{s_0}{L}_{s_0}\right|}^2$ used by Liu et al. (2002) to assess the spatial leakage from source $s_0$ to source $s$ is closely related to our model, including the same normalization denominator. We also noted the link between the GCS and the DeFleCT algorithm [Hauk and Stenroos, 2014], which builds inverse operators using constraints allowing some control over source‐level cross‐talk. For seed‐based FC analysis, it is natural to impose the single constraint of vanishing PSF at the seed location, in which case DeFleCT and the GCS applied to MNE actually coincide (Supporting Information A.1). The present work adds to this literature in two ways. From the theoretical perspective, we derived the GCS from an explicit model of spatial leakage [Wens, 2015] and focused on an assumption‐free analysis of its properties. From the applied perspective, we investigated its performance for seed‐based FC analysis by combining network simulations, experimental MEG data and statistical mapping. Critically, this proof‐of‐principle was limited to MNE, so this part can be viewed as an application of DeFleCT to FC estimation. We expect the GCS to be applicable to other linear source estimators as well, but this still requires formal confirmation since, e.g., Beamformers exhibit more complex, data‐dependent PSF shapes [Brookes et al., 2012b].

Our analyses highlighted some advantages and limitations of the GCS. One asset of the geometric approach is that it does not make dynamical assumptions about brain interactions, to the contrary of signal orthogonalization (as further discussed below). This allows mapping all types of coupling (linear or non‐linear, zero‐lag or non‐zero‐lag), including for non‐zero‐lag spatial leakage. Furthermore, the topography of PSFs being relatively focal for MNE, the GCS does not affect long‐range FC estimation, as should be in the absence of spatial leakage effects. These two points could be predicted from theoretical considerations and confirmed by simulations. Likewise, on experimental data, the GCS disclosed the inter‐hemispheric coupling typical of bilateral RSNs [Brookes et al., 2011, 2012b; Hipp et al., 2012; Wens et al., 2014a, 2014b] as well as coherencies observed in the auditory‐motor network [Bourguignon et al., 2012, 2013; Jerbi et al., 2007; Pollok et al., 2004] [including temporal areas in this auditorily‐paced paradigm, see Pollok et al., 2005], with the expected preservation of long‐range FC.

On the other hand, the model assumptions of the GCS set some limitations and we explored its robustness against their violation. The first hypothesis is the absence of statistical or systematic errors in forward modeling, i.e., zero measurement noise and exact lead field estimation. However, simulations suggested that the GCS is resilient against the introduction of such errors except for unreasonably small SNR ( $\zeta =1.01$, i.e., true data variance roughly 1% of noise variance), in which case spatial leakage and FC estimation get drowned in noise anyway. Of notice, the effect of lead field inaccuracies (modeled here using inter‐subjects interpolation) was mild and indeed similar to that of reasonable measurement noise (SNR $\zeta \ge 1.5$, i.e., true data variance roughly 50% or more of noise variance). The second hypothesis is the local isolation of the seed, which is not guaranteed in experimental data and leads to local overcorrection issues. This is the main drawback of a geometric correction and can lead to significant but spurious FC around the seed, as we illustrated using simulations including seed and target nodes with overlapping PSFs (i.e., within about 2 cm from the seed). The last limitation is that of seed mislocation, since the GCS assumes that the seed coincides with a true network node. In general, seed selection is a fundamental step for seed‐based FC mapping, independently of spatial leakage itself. Simulations with 1.5 cm error in seed placement again indicated the emergence of spurious local FC. Local overcorrection and seed mislocation thus warrant some caution when interpreting short‐range corrected FC such as the persisting intra‐hemispheric RSN couplings (notwithstanding the physiological meaningfulness of the rolandic sulcus for SM1 RSN and SMG for A1 RSN). Importantly, these issues are unavoidable for any spatial leakage correction based on seed activity elimination and were indeed also observed for signal orthogonalization, albeit less extensively.

Comparison to Signal Orthogonalization

Our comparative analyses with signal orthogonalization also highlighted the differences and the complementarity of the two correction approaches. Signal orthogonalization, being based on a linear regression from the seed time course, makes the dynamical assumptions that sources are gaussian [Brookes et al., 2014] and temporally or phase orthogonal to the seed [Brookes et al., 2012b; Hipp et al., 2012]. Its main drawback with respect to the GCS is that it cannot disambiguate spatial leakage effects from true linear interactions. Two different issues can arise. First, zero‐lag FC gets eliminated independently of its physiological relevance, even when spatial leakage is absent. This represents an overcorrection effect distinct from that of the GCS and was illustrated in our simulations including linear correlations, for which static orthogonalization missed FC between non‐orthogonal nodes whereas instantaneous orthogonalization could still disclose those far enough from the seed. This is because our simulation algorithm generated linear correlation via non‐zero phase lag, see Supporting Information A.3. For nearby nodes, spatial leakage set this phase approximately to zero, making them effectively orthogonal and thus invisible to instantaneous orthogonalization. Second, spatial leakage can be only partially corrected or not at all for non‐zero‐lag spatial leakage (e.g., when using DICS). Imaginary coherence, which we used for the auditory‐motor data, suffers the same flaw because of its close relation with signal orthogonalization. In the context of DICS, the phase‐lag optimization (rather than orthogonalization) by Drakesmith et al. [2013] represents a signal‐based alternative that would be interesting to compare with the GCS.

On the other hand, the two approaches are expected to converge when the temporal characteristics of spatial leakage are rightly identified and in the absence of non‐orthogonal interactions. This was confirmed using simulated networks of orthogonal nodes. However, signal orthogonalization proved more resilient against local overcorrection and seed mislocation, which represents its main advantage over the GCS. This is because of stronger FC suppression around the seed, although, critically, the associated spurious patterns remained significant. For RSNs, no significant differences were disclosed between the GCS and the static orthogonalization, indicating that no genuine linear correlation is sustained over sufficiently long periods between left and right primary cortices in the resting state.

Instantaneous orthogonalization underestimated RSN FC (see, e.g., the missing inter‐hemispheric A1 coupling) because the static nature of spatial leakage in MNE was not taken into account. Indeed, the non‐stationarity of its linear regression [Hipp et al., 2012] leads to the elimination of transient linear correlations, which are bound to emerge from physiological or random fluctuations [notwithstanding subtler effects described in Wens, 2015].

Further Limitations and Possible Extensions

This work was limited to the scope of stationary source reconstruction and FC estimation. In theory, the underestimation bias of instantaneous orthogonalization may be more drastic for dynamic analyses, i.e., investigations of non‐stationary fluctuations in brain interactions via, e.g., sliding windowed FC estimation [Brookes et al., 2014; de Pasquale et al., 2010, 2012; O'Neill et al., 2015]. On the other hand, methodological developments consider non‐stationary linear inverse models, e.g., based on instantaneous inverse operators $\mathit{W}\left(t\right)$ [e.g., Beamformer spatial filters derived from a time‐varying estimation ${\mathit{C}}_{\mathrm{\mu }}\left(t\right)$ of data covariance, see Baker et al., 2014; Woolrich et al., 2013], in which case non‐stationary signal orthogonalization [Hipp et al., 2012; O'Neill et al., 2015] becomes more justified than the static version. Importantly, the GCS generalizes straightforwardly to time‐dependent forward and inverse operators [Wens, 2015]. Extending this article to dynamic analyses is an interesting topic for future works.

Another limitation of the GCS and the signal orthogonalization is that they specifically eliminate spatial leakage from the seed location only. Persisting “secondary” spatial leakage induced from the target nodes [Palva and Palva, 2012] is at the basis of the local overcorrection issue for short‐range FC (discussed above) as well as the FC blur around targets (illustrated in our simulations for long‐range FC). The situation could be improved using multivariate generalizations correcting spatial leakage from multiple sources, such as the multivariate signal orthogonalization of Colclough et al. [2015]. However, it remains an open question to know if (and how) useful multivariate GCS can be designed in the presence of lead field correlations among sources of interest, since they make the multiple constraints of vanishing PSFs incompatible with each other (as reviewed in the Theory section; see also Hauk and Stenroos [2014], for an illustration of how correction goes wrong). A related comment is that seed‐based correction leads to asymmetric FC estimates. This is not a problem for seed‐based FC mapping considered here, since the seed location is singled out anyway, but should be avoided for connectomes (all‐to‐all FC) analyses. Authors have either applied a posteriori symmetrization by averaging FC indices in both directions [Hipp et al., 2012] or designed intrinsically symmetric techniques [Colclough et al., 2015]. Investigating how symmetrization of the GCS would perform for connectomes studies provides avenue for future works.

A last limitation to mention is that we only considered linear inverse models, which typically yield spatially smooth reconstructions with extensive blurring issues, implying the necessity of spatial leakage correction. An alternative strategy would be to use spatially sparse reconstructions. The most basic approaches based on $L_1$ regularization priors [Uutela et al., 1999] typically yield temporally discontinuous source estimates, making them not suitable for FC analysis. More advanced methods have been developed to generate spatially sparse and temporally continuous reconstructions, e.g., temporal projections of $L_1$‐norm estimates [Huang et al., 2006, 2014], empirical Bayesian inference [Friston et al., 2008; Wipf and Nagarajan, 2009; Wipf et al., 2010], mixed‐norm regularization [Gramfort et al., 2013; Ou et al., 2009] or subspace pursuit algorithms [Babadi et al., 2014]. By design, these approaches should limit spatial leakage effects and may thus be promising, although they have not yet been evaluated for MEG/EEG FC analyses. These inverse models being typically non‐linear, neither the GCS nor the signal orthogonalization can be strictly applied to them. (See nevertheless Wens [2015], for possible non‐linear extensions of the GCS.) However, it is noteworthy that the spatial sparsity constraint is not always suitable, e.g., when averaging procedures (over time for stationary analyses of ongoing activity, or over subjects for group‐level analyses) are involved. In such cases, spatially blurred reconstructions are relevant to smooth out sources before averaging, and spatial leakage correction therefore remains an important element of FC analyses.

CONCLUSIONS

In conclusion, this article considers the problem of spatial leakage in source‐space MEG/EEG seed‐based FC analyses and investigates the usefulness of a GCS (applied to MNE) for networks mapping. This model‐based approach is theoretically principled, robust against the introduction of forward model errors, and able to map all kinds of brain couplings. Although its ability to pinpoint local interactions is limited, the comparative analyses showed that it nicely complements signal orthogonalization methods. The GCS thus appears to be a valuable addition to spatial leakage correction toolkits.

Supporting information

Supporting Information