Abstract
Schizophrenia is characterized by heterogeneous pathophysiology. Using multiscale entropy (MSE) analysis, which enables capturing complex dynamics of time series, we characterized MSE patterns of blood‐oxygen‐level‐dependent (BOLD) signals across different time scales and determined whether BOLD activity in patients with schizophrenia exhibits increased complexity (increased entropy in all time scales), decreased complexity toward regularity (decreased entropy in all time scales), or decreased complexity toward uncorrelated randomness (high entropy in short time scales followed by decayed entropy as the time scale increases). We recruited 105 patients with schizophrenia with an age of onset between 18 and 35 years and 210 age‐ and sex‐matched healthy volunteers. Results showed that MSE of BOLD signals in patients with schizophrenia exhibited two routes of decreased BOLD complexity toward either regular or random patterns. Reduced BOLD complexity toward regular patterns was observed in the cerebellum and temporal, middle, and superior frontal regions, and reduced BOLD complexity toward randomness was observed extensively in the inferior frontal, occipital, and postcentral cortices as well as in the insula and middle cingulum. Furthermore, we determined that the two types of complexity change were associated differently with psychopathology; specifically, the regular type of BOLD complexity change was associated with positive symptoms of schizophrenia, whereas the randomness type of BOLD complexity was associated with negative symptoms of the illness. These results collectively suggested that resting‐state dynamics in schizophrenia exhibit two routes of pathologic change toward regular or random patterns, which contribute to the differences in syndrome domains of psychosis in patients with schizophrenia. Hum Brain Mapp 36:2174–2186, 2015. © 2015 Wiley Periodicals, Inc.
Keywords: schizophrenia, complexity, multiscale entropy, randomness, regularity
INTRODUCTION
The unpredictable nature of behavioral patterns in schizophrenia and other mental illnesses has implicated the use of chaos and complexity theories to understand the complex behaviors of patients with psychiatric disorders [Breakspear, 2006; Ehlers, 1995; Paulus and Braff, 2003; Tschacher et al., 1997]. From a systemic perspective, complexity reflects the ability of the brain to adapt to a constantly changing environment. Such adaptation is often impaired in schizophrenia and other mental illnesses, leading to abnormal behavioral patterns and impaired cognitive and psychosocial functions [Bassett and Gazzaniga, 2011]. Therefore, studies of complexity in brain activities may provide insights into how behavioral patterns of schizophrenia are linked to the pathophysiology of brain functions. Because of advances in brain activity monitoring and quantitative measures of system dynamics, schizophrenia research has increasingly focused on the complexity analysis of neurophysiologic signals acquired from schizophrenic patients [Bassett and Gazzaniga, 2011; Bullmore and Sporns, 2009; Keshavan et al., 2004; Kotini and Anninos, 2002; Lee et al., 2001; Meunier et al., 2009; Takahashi et al., 2010] (for reviews see [Fernandez et al., 2013; Takahashi, 2013]). In this context, complexity theory may provide a useful clinical tool for the psychiatric evaluation of symptom severity and predicting treatment outcomes.
The altered brain complexity in schizophrenia has been studied using electroencephalography [Keshavan et al., 2004; Koukkou et al., 1993; Li et al., 2008; Raghavendra et al., 2009; Takahashi et al., 2010], magnetoencephalography [Fernandez et al., 2011], and structural imaging of gyri folding [Narr et al., 2004]. The analysis of the complexity of blood‐oxygen‐level‐dependent (BOLD) signals obtained from resting‐state functional magnetic resonance imaging (fMRI) has attracted considerable interest. Previous studies have indicated that the nonlinear properties of resting‐state brain function can serve as a marker for aging and mental illness [Meunier et al., 2009], as implicated in Alzheimer's disease [Liu et al., 2013; Maxim et al., 2005], attention‐deficit hyperactivity disorder [Anderson et al., 2006; Sokunbi et al., 2013], autism [Lai et al., 2011], and aging [McIntosh et al., in press; Smith et al., 2014; Yang et al., 2013a, 2014a]. Although BOLD signals were considered hemodynamic responses rather than direct measures of neuronal activity in a previous study [Fox and Raichle, 2007], these data provide evidence that altered nonlinear, time‐varying properties of BOLD signals are influenced by the disease state and may provide a novel neuroimaging approach for investigating brain dysfunction associated with aging and mental illness. Several studies have investigated the complexity of brain activity in schizophrenia using resting‐state fMRI [Bassett et al., 2012; Sokunbi et al., 2014]. The wavelet entropy used by Bassett et al. [2012] was insufficient for assessing the difference in the complexity of regional BOLD activity between patients with schizophrenia and healthy subjects. Sokunbi et al. [2014] showed that schizophrenia had increased randomness of BOLD activity by analyzing single‐scale sample entropy and the Hurst exponent, leading to the questionable conclusion that brain complexity was increased in patients with schizophrenia.
We and others had recently applied the multiscale entropy (MSE) method [Costa et al., 2002] to assess the complexity of BOLD signals in healthy aging cohorts [Yang et al., 2013b, 2014a] and in different brain areas of white matter and ventricular space [McDonough and Nashiro, 2014; Smith et al., 2014]. The MSE method provides a profile of entropy across multiple time scales and, thus, enables extracting a signature of complexity from physiologic signals not included in traditional methods based on the mean or variance and conventional entropy methods used to measure entropy in a single time scale [Chialvo, 2002; Costa et al., 2005]. With MSE analysis, a healthy physiologic process is typically represented by a complex fluctuation with consistent entropy values over different time scales, and reduced complexity in pathologic processes can exhibit either increased regularity (i.e., decreased entropy in all time scales) or increased randomness (i.e., high entropy in short time scales followed by rapid decay in entropy as the length of time scales increases). In contrast to the single‐scale entropy method, which is simply a measure of regularity [Lake et al., 2002; Pincus and Goldberger, 1994; Richman and Moorman, 2000], a MSE profile enables differentiating true complexity from uncorrelated randomness, which does not contain meaningful information and cannot be regarded as a complex state [Goldberger et al., 2002a,b]. Therefore, increased regularity and randomness at the extreme of the dynamic process represent the reduced complexity that can be observed in various medical conditions, such as heart rate variability in congestive heart failure and atrial fibrillation [Goldberger et al., 2002b].
According to our previous review [Yang and Tsai, 2013], this generic loss of complexity scheme has not been tested in a large cohort of patients with mental illness using functional brain imaging. Such an investigation may reveal crucial information regarding whether brain processes in patients with mental illness exhibit increased complexity or reduced complexity toward regularity or uncorrelated randomness compared with those in healthy people. We hypothesized that schizophrenia is associated with the loss of multiple‐time‐scale complexity (either toward regularity or uncorrelated randomness), and investigated the entropy profiles of resting‐state fMRI signals across time scales in patients with schizophrenia, and determined the relationship between the complexity of resting‐state brain activity and relevant psychopathologic assessments.
MATERIALS AND METHODS
Study Participants
The study cohort consisted of 315 Han Chinese participants who were recruited from the Department of Psychiatry at Taipei Veterans General Hospital, Taiwan. The patient group consisted of 105 patients with schizophrenia (45 men, 60 women; mean age: 42.8 ± 9.4 years), among which 91 (86.6%) patients were referred from outpatient clinics and 14 (13.3%) patients were from the inpatient unit. To increase the homogeneity of the schizophrenic group, we enrolled patients with an age of onset between 18 and 35 years and an age at fMRI scanning between 20 and 60 years. All schizophrenic patients were evaluated by a board‐certificated psychiatrist and diagnosed according to the diagnostic criteria of the Diagnostic and Statistical Manual of Mental Disorders, Fourth Edition. Diagnoses of schizophrenia were validated using the Mini‐International Neuropsychiatric Interview [Sheehan et al., 1998]. The Positive and Negative Syndrome Scale (PANSS) was used to evaluate psychotic symptoms [Kay et al., 1987]. Chlorpromazine (CPZ) equivalent dosages were computed according to American Psychiatric Association guidelines.
The comparison group consisted of 210 healthy volunteers (89 men, 121 women; mean age: 42.9 ± 11.3 years) who were recruited from a healthy aging cohort and matched according to age and sex at a 2:1 control‐to‐patient ratio [Yang et al., 2013b, 2014a]. Healthy subjects were evaluated by a trained research assistant using the Mini‐International Neuropsychiatric Interview to exclude the presence of psychiatric disorders [Sheehan et al., 1998]. The comparison participants had no personal or family history (first‐degree relatives) of psychiatric disorders. Exclusion criteria for the participants were severe medical illness, cognitive impairment (a Mini Mental State Examination Score lower than 24), borderline personality disorder, a history of head trauma or neurological disease, and a lifetime history of substance abuse disorder. The study was conducted in accordance with the Declaration of Helsinki and was approved by the Institutional Review Board of Taipei Veterans General Hospital. Demographic and clinical data on the participants are presented in Table 1.
Table 1.
Demographics and clinical characteristics
| Schizophrenia (n = 105) | Healthy Control (n = 210) | |||||
|---|---|---|---|---|---|---|
| Variables | Mean | SD | Mean | SD | t or χ2 | P |
| Age at scan (years) | 42.8 | 9.4 | 42.9 | 11.3 | .08 | .94 |
| Gender, female | 60 | 57.1% | 121 | 57.6% | .01 | .92 |
| Handedness, right | 101 | 96.2% | 204 | 97.1% | .01 | .92 |
| Age of illness onset (years) | 25.4 | 5.0 | ||||
| Illness duration (years) | 17.4 | 9.4 | ||||
| PANSS total | 38.3 | 9.2 | ||||
| PANSS positive | 9.6 | 3.2 | ||||
| PANSS negative | 9.4 | 5.2 | ||||
| PANSS general | 20.3 | 3.9 | ||||
| CPZ equivalents | 491.3 | 390.1 | ||||
Categorical data are given as number (%)
PANSS, Positive and Negative Syndrome Scale; CPZ, Chlorpromazine equivalent dosage
fMRI Scanning and Image Processing
fMRI scanning was performed at National Yang‐Ming University using a 3.0T Siemens MRI scanner (Siemens, Erlangen, Germany) equipped with a 12‐channel head coil. All fMRI experiments were performed in the morning. The scanning protocol was consistent with that described in our prior reports [Yang et al., 2013b, 2014a]. T2*‐weighted images with BOLD contrast were measured using a 43‐slice gradient echo‐planar imaging (EPI) sequence with a repetition time (TR) of 2,500 ms, an echo time (TE) of 27 ms, a field of view (FoV) of 200 mm, a flip angle of 77°, a matrix size of 64 × 64, and a voxel size of 3.44 × 3.44 × 3.40 mm. In each run, 200 EPI volume images were acquired along the AC–PC plane. High‐resolution structural 192‐slice T1 images were acquired using a 3D magnetization‐prepared rapid gradient echo sequence with a TR of 2,530 ms, a TE of 3.5 ms, a TI of 1,100 ms, a FOV of 256 mm, and a flip angle of 7°. The duration of the fMRI scanning procedure was approximately 15 min for each participant.
The resting‐state fMRI images were preprocessed using Data Processing Assistant for Resting‐State fMRI toolbox [Chao‐Gan and Yu‐Feng, 2010] implemented in Matlab (MathWorks, Natick, MA). The preprocessing included slice‐timing corrected, realigned, and normalized to the standard stereotaxic space of the Montreal Neurological Institute (MNI) EPI template and resampled to a 3‐mm3 voxel. The covariates of the BOLD time series were regressed out before complexity analysis was performed, including the time courses of six head motions and their derivatives and cerebrospinal fluids. No global signal regression was performed to avoid introducing distortion into the time series data [Anderson et al., 2011; Murphy et al., 2009]. Physiological noise was minimized using band‐pass temporal filtering (0.01–0.08 Hz). The voxels representing white matter and cerebrospinal fluids were excluded from the analysis using a gray matter mask, which was defined using a cohort‐specific gray matter mask (N = 315) thresholding for partial volume estimates at 0.25. All participants exhibited a maximum displacement of less than 1.5 mm at each axis and an angular motion of less than 1.5° for each plane. The first five data points (12.5 s) in each BOLD time series were discarded because of the instability of initial MRI scanning; thus, 195 data points on each time series were used in analyses.
Analysis of the MSE of BOLD Signals
A conceptual illustration of MSE is provided in Figure 1. A conventional entropy method involves measuring irregularity and assigning a higher value when the irregularity of a given signal is increased. However, because conventional entropy is measured in the shortest time scale, the measured irregularity can represent either true complexity or merely uncorrelated randomness. Therefore, increased irregularity does not imply increased complexity [Goldberger, 1996; Goldberger et al., 2002b]. An ideal complexity measure assigns a high value to signals with a long‐range correlation and other nonlinear properties (e.g., 1/f noise) and assigns a low value to signals with either regularity or uncorrelated randomness.
Figure 1.
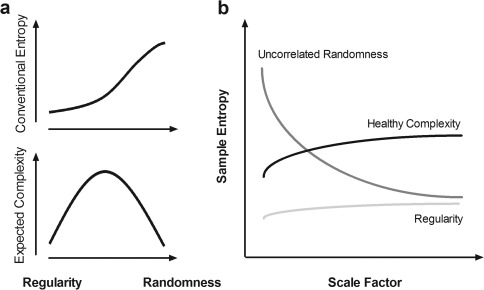
Conceptual difference between randomness and complexity. (a) Conventional entropy is a measure of irregularity based on the single shortest time scale and involves assigning a higher entropy value to uncorrelated randomness, which is often observed in pathologic disease and presumed to convey less information than 1/f noise [Goldberger et al., 2002a,b]. The relationship between the expected complexity measure and randomness is inverse U‐shaped; regularity and uncorrelated randomness are associated with reduced complexity, whereas meaningful complexity is in between [Buzsaki and Draguhn, 2004; Goldberger et al., 2002b]. (b) Multiscale entropy [Costa et al., 2002] captures the concept that complex dynamics typically arise from multiple time scales; a generic approach to measuring global complexity involves considering multiple time scales in a given physical system [Fogedby, 1992; Zang, 1991]. In this context, uncorrelated randomness (dark gray line) has high entropy in the shortest time scale, but its entropy decays as the scale factor on a coarse time scale increases. By contrast, healthy complexity (black line) maintains entropy across all time scales, and regularity (light gray line) represents low entropy in all scale factors.
According to the theory that complex dynamics arise from multiple time scales and that a generic approach for measuring global complexity must consider multiple time scales in a given physical system [Fogedby, 1992; Zang, 1991], MSE analysis [Costa et al., 2002, 2005] was developed to estimate sample entropy in multiple time scales using a coarse‐graining procedure. Sample entropy is used in MSE analysis because it provides greater consistency and is less dependent on a given signal length compared with other entropy methods [Richman and Moorman, 2000]. MSE calculation can be summarized in the following three steps: (a) constructing coarse‐grained time series according to different scale factors; (b) quantifying the sample entropy of each coarse‐grained time series; and (c) examining the sample entropy profile over a range of scales. According to this method, the length of each coarse‐grained time series is equal to the length of the original time series divided by the scale factor. For Scale 1, the time series is merely the original time series.
Sample entropy is defined by the negative natural logarithm of the conditional probability that a dataset of length N, having repeated itself within a tolerance of r (similarity factor) for m points (pattern length), will also repeat itself for m + 1 points without allowing self‐matches [Richman and Moorman, 2000]. We have previously used the parameters for MSE calculation from relatively short BOLD signals using the parameters m = 1 and r = 0.35 and scale factors up to 5 [Yang et al., 2013a, 2014a].
For a complexity analysis at the voxelwise level, the MSE of the BOLD signal was computed for all gray matter voxels to create a whole‐brain MSE parametric map for subsequent group analysis. In addition, each BOLD time series was normalized for the zero mean and unit standard deviation before MSE analysis. Instead of averaging entropy across all scale factors as a proxy of the complexity index [Lu et al., 2012; Norris et al., 2009; Yang et al., 2013b, 2014a], we followed the patterns of three types of complexity change proposed by Costa et al. [2002 and 2005] to classify the MSE profiles of BOLD signals in each gray matter voxel.
Using the MSE of BOLD signals from healthy subjects as the reference, we investigated whether the MSE of BOLD signals from patients with schizophrenia showed increased complexity (i.e., increased entropy in all scales), reduced complexity toward regularity (i.e., decreased entropy in all scales), or reduced complexity toward randomness (i.e., increased entropy in short scales followed by rapid decay in entropy as the scale factors increase). The random type of MSE profile represented a unique property of uncorrelated randomness that cannot be captured by simply averaging the entropy of all scale factors; therefore, the slope of entropy decay was used as an indicator of complexity change in the random type of complexity changes.
Statistical Analysis
Statistical analysis of the MSE parametric imaging data was conducted using the MATLAB . Regional between‐group differences in the whole‐brain MSE mapping of each time scale were examined using the general linear model (GLM). Because age, sex, and handedness were well matched in the patient and control groups, we assessed the main effect of schizophrenia on MSE complexity without introducing covariates to the GLM. To assess the association between the type of MSE complexity change and the psychopatholgy, we regressed the clinical variables (age of onset, duration of illness, CPZ dosage, and PANSS scores) with the mean MSE value of all scale factors at the voxelwise level for increased MSE complexity or the regularity type of MSE complexity changes. For the randomness type of MSE complexity change, we regressed the clinical variables with the slope of entropy decay across all scale factors. For all voxelwise analyses, significant brain clusters with peak coordinates in the MNI space were reported only if the P value corrected for multiple comparisons using the familywise error (FWE) rate was lower than 0.05 at the cluster level.
RESULTS
Between‐Group Comparison of MSE Profiles in Different Time Scales
Figure 2 shows the regional between‐group differences in the MSE of BOLD signals among all scale factors at the voxelwise level. Observing MSE profiles (i.e., patterns of between‐group entropy differences in a scale of 1–5) showed that, in schizophrenic patients, BOLD signals in the occipital, inferior frontal, and postcentral cortices exhibited a pattern of increased entropy in Scales 1 and 2, followed by decreased entropy in Scales 3–5, compared with the BOLD entropy of healthy subjects. However, entropy in the temporal cortex was reduced in all scale factors in schizophrenic patients. These observations suggested that schizophrenia exhibits two patterns of scale‐related entropy change in different brain regions.
Figure 2.
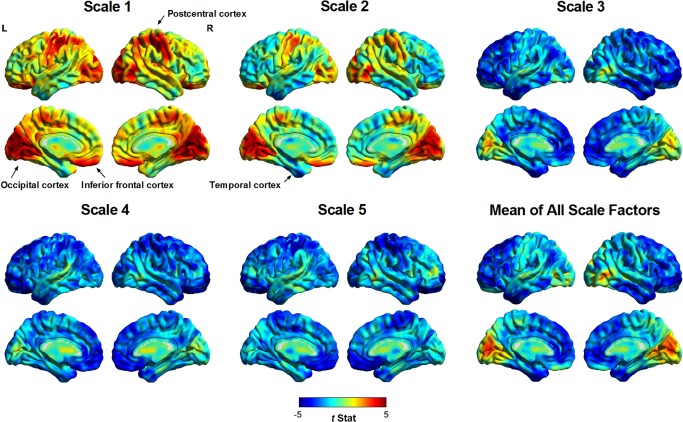
Regional differences in the MSE complexity of resting‐state BOLD activity in all scale factors between patients with schizophrenia and healthy subjects. A positive t value (warm color spectrum) represents a higher MSE value in patients with schizophrenia than in healthy subjects, and vice versa for results shown with negative t values (cool color spectrum). Visual inspection suggested two patterns of pathologic change in patients with schizophrenia. The occipital, postcentral, and inferior frontal cortices of patients with schizophrenia exhibited increased entropy (randomness) in short time scales (Scales 1 and 2) and reduced entropy (regularity) in coarse time scales (Scales 3–5) compared with those of healthy volunteers. By contrast, the inferior temporal cortex exhibited reduced entropy (regularity) across all scale factors. These two patterns of entropy change were consistent with a shift in BOLD dynamics toward randomness and regularity, respectively.
Quantification of Different Types of Complexity Change According to MSE Profile
Figure 3 shows MSE profiles extracted from the inferior temporal cortex and inferior frontal cortex. The MSE profile in the inferior temporal cortex (Fig. 3a) showed that patients with schizophrenia exhibited a reduction in entropy in all scale factors compared with healthy controls, suggesting that a regular type of complexity changes occurred in this brain region. However, the MSE profile in the inferior frontal cortex (Fig. 3b) showed that, relative to the controls, the patients with schizophrenia exhibited increased entropy in short scales, followed by decreased complexity as the scale factor increased, suggesting a pattern of complexity changes toward randomness. This randomness pattern is distinguishable from the increased physiologic complexity that is expected to occur when entropy increases in all scale factors. The regular type of complexity change was quantified according to the average sample entropy across all scale factors, whereas the random type of complexity change was assessed using the slope of entropy decay. The effect size for the difference in complexity metrics between schizophrenia and healthy subjects was 0.47 for inferior temporal cortex and 0.45 for inferior frontal cortex.
Figure 3.
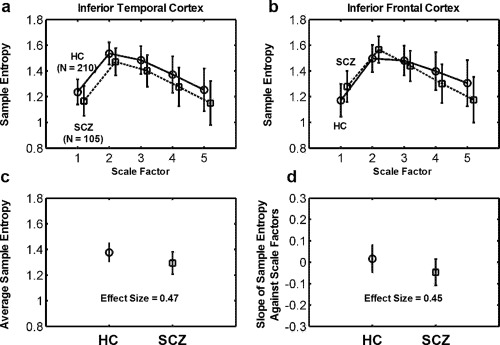
Two types of complexity change according to the MSE complexity profile of BOLD signals (scale factor vs. mean ± SD of sample entropy) extracted from (a) the inferior temporal cortex and (b) the inferior frontal cortex. The MSE complexity profile of (a) the inferior temporal cortex showed lower BOLD sample entropy in patients with schizophrenia (SCZ) than in healthy comparison (HC) subjects in all scale factors (P FWE < 0.05). By contrast, the MSE complexity profile of (b) the inferior frontal cortex showed higher BOLD entropy in SCZ than in HC in Scale 1, and the entropy values in SCZ exhibited a crossover with the MSE profile of HC. SCZ exhibited a lower BOLD entropy than HC in Scales 4 and 5 (P FWE were < 0.05 in Scales 1, 4, and 5). We defined two quantitative measures for assessing these two types of complexity change toward (a) regularity and (b) randomness. (c) For the regularity type of complexity change, we used the average sample entropy as an index to assess the extent of increased regularity of BOLD signals in SCZ. (d) For the randomness type of complexity change, we used the slope of the sample entropy against scale factors 1–5 to assess the extent of increased randomness of BOLD signals in SCZ.
Figure 4 shows that most brain regions exhibited a random pattern of BOLD complexity changes, whereas few brain regions showed decreased complexity toward regular patterns. Table 2 details the significant brain regions for each type of complexity change. No brain region in patients with schizophrenia exhibited significantly increased complexity compared with the brain regions of healthy subjects. Schizophrenic patients showed decreased complexity toward regular patterns in the left inferior temporal (peak t = −5.62), right inferior temporal (t = −5.52), right middle frontal (t = −5.73), left middle frontal (t = −4.74), left superior frontal (t = −4.47), and left supplementary motor cortices (t = −3.39) as well as the anterior lobe (t = −3.99) and posterior lobe of the cerebellum (t = −6.10). Conversely, decreased complexity toward randomness was observed in patients with schizophrenia in clusters of the inferior frontal (t = −6.35), postcentral (t = −5.23), and occipital cortices (t = −6.57) as well as the right insula (t = −4.18) and left middle cingulum (t = −4.48).
Figure 4.
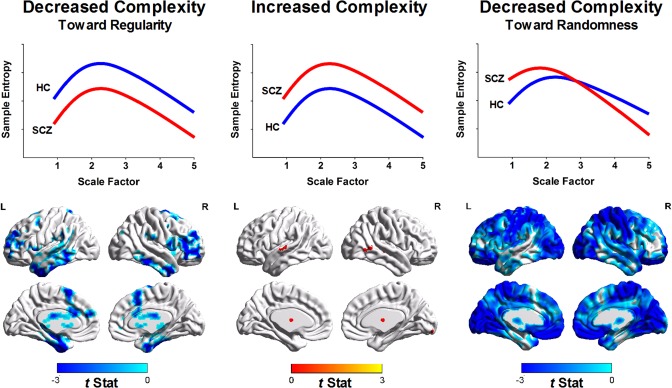
Quantification of complexity changes in patients with schizophrenia (SCZ) relative to healthy controls (HC) according to MSE profiles. (Left) Brain regions with the regularity type of complexity changes of BOLD signals (i.e., decreased sample entropy over all scale factors in SCZ relative to HC). (Middle) Brain regions with increased complexity of BOLD signals (i.e., increased sample entropy over all scale factors in SCZ relative to HC). Color shown in brain mapping represents raw t‐statistics of difference of MSE profile between SCZ and HC. No significant brain cluster was observed in this type of complexity change after correction for multiple comparisons. (Right) Brain regions with the randomness type of complexity change (i.e., increased sample entropy in short time scales followed by decay of sample entropy as the scale factor increases).
Table 2.
Regions showing significant changes in the MSE complexity profiles of BOLD signals from patients with schizophrenia
| MNI coordinates (mm) | ||||||
|---|---|---|---|---|---|---|
| Brain regiona | BA | x | y | z | Volume (mm3)b | Peak t |
| Increased complexity | ||||||
| None | ||||||
| Decreased complexity toward regularity | ||||||
| L inferior temporal gyrus | 20/21 | −39 | 0 | −42 | 19,710 | −5.62 |
| R inferior temporal gyrus | 20/21 | 36 | 6 | −39 | 13,743 | −5.52 |
| R middle frontal gyrus | 10 | 30 | 63 | −3 | 10,206 | −5.73 |
| L middle frontal gyrus | 10 | −33 | 63 | 3 | 2,268 | −4.74 |
| L superior forntal gyrus | 10/9 | −27 | 54 | 33 | 864 | −4.47 |
| R superior frotnal gyrus | 10/9 | 18 | 54 | 33 | 1,539 | −4.84 |
| L supplementary motor area | 3 | 12 | 57 | 1,026 | −3.99 | |
| R/L cerebellum posterior lobe | −33 | −75 | 45 | 39,744 | −6.10 | |
| L cerebellum anterior lobe | −27 | −57 | −30 | 1,674 | −3.99 | |
| Decreased complexity toward randomness | ||||||
| L/R inferior frontal gyrus | 11/47 | −18 | 30 | −27 | 48,600 | −6.35 |
| L/R occipital lobe | 18/19 | 18 | −84 | 30 | 98,955 | −5.23 |
| R insula | 39 | −27 | 18 | 2,727 | −4.18 | |
| L/R postcentral gyrus | 6/3 | −48 | −21 | 60 | 95,175 | −6.57 |
| L middle cingulum | 24 | −12 | −9 | 42 | 1,755 | −4.48 |
All brain clusters had P value < 0.05 corrected for multiple comparisons using familywise error methods.
L, left; R, right; BA, Brodmann area
Volume was computed from cluster size (3 × 3 × 3 mm voxel).
Correlation of the Type of Complexity Change with Psychopathology
Table 3 summarizes the correlation between the regular type of complexity change and psychopathology. The results showed that the PANSS positive syndrome score was negatively correlated with MSE complexity in the right fusiform gyrus (correlation coefficient r at peak voxel = −0.40) and the left fusiform and temporal pole of the middle temporal region (r = −0.35), whereas the PANSS negative syndrome score was negatively correlated with MSE complexity in the left posterior lobe of the cerebellum (r = −0.53).
Table 3.
Regions showing a significant correlation between clinical variables and the regular type of complexity change in patients with schizophrenia
| MNI coordinates (mm) | ||||||
|---|---|---|---|---|---|---|
| Brain regiona | BA | x | y | z | Volume (mm3)b | Peak t |
| PANSS positive syndrome | ||||||
| R fusiform gyrus | 20 | 24 | −12 | −42 | 1,647 | −4.43 |
| L fusiform gyrus and temporal pole of middle temporal gyrus | 38 | −15 | −3 | −42 | 1,458 | −3.85 |
| PANSS negative syndrome | ||||||
| L cerebelum posterior lobe | −42 | −69 | −30 | 1,782 | −6.42 | |
All brain clusters had P value < 0.05 corrected for multiple comparisons using familywise error methods.
L, left; R, right; BA, Brodmann area
Volume was computed from cluster size (3 × 3 × 3 mm voxel).
Table 4 summarizes the correlation between the randomness type of complexity change and psychopathology. Age of onset was correlated positively with the slope of MSE change in the left medial orbitofrontal gyrus (r = 0.61). The duration of illness was correlated negatively with the slope of MSE change in the right lingual gyrus (r = −0.50) and right postcentral gyrus (r = −0.44). The PANSS negative syndrome score was correlated negatively with the slope of MSE change in the left orbitofrontal gyrus (r = −0.43), left middle occipital gyrus (r = −0.44), right cuneus and part of the superior occipital gyrus (r = −0.52), left cuneus and part of the superior occipital gyrus (r = −0.46), left postcentral gyrus and superior parietal gyrus (r = −0.46), and right postcentral gyrus (r = 0.46). The CPZ dosage, PANSS score in general psychopathology, and total PANSS score were not associated with any type of complexity change. All brain clusters reported in the results had FWE‐corrected P values lower than 0.05.
Table 4.
Regions showing a significant correlation between clinical variables and the randomness type of complexity change in schizophrenia
| MNI coordinates (mm) | ||||||
|---|---|---|---|---|---|---|
| Brain regiona | BA | x | y | z | Volume (mm3)b | Peak t |
| Age of onset | ||||||
| L medial orbitofrontal gyrus | 11 | 3 | 39 | −12 | 2,025 | 7.84 |
| Duration of illness | ||||||
| R lingual gyrus | 18 | 9 | −67 | 0 | 918 | −5.79 |
| R postcentral gyrus | 40 | 48 | −36 | 56 | 999 | −4.97 |
| PANSS negative syndrome | ||||||
| L orbitalfrontal gyrus | 11 | 6 | 54 | −24 | 3,753 | −4.85 |
| L middle occipital gyrus | 18 | −27 | −96 | 6 | 864 | −4.99 |
| R cuneus and superior occipital gyrus | 19 | 15 | −93 | 33 | 1,242 | −6.23 |
| L cuneus and superior occipital gyrus | 19 | −15 | −93 | 33 | 1,026 | −5.25 |
| L postcentral gyrus and superior parietal gyrus | 2 | −36 | −51 | 63 | 1,134 | −5.24 |
| R postcentral gyrus | 3 | 42 | −36 | 66 | 1,188 | −5.27 |
All brain clusters had P value < 0.05 corrected for multiple comparisons using familywise error methods.
L, left; R, right; BA, Brodmann area
Volume was computed from cluster size (3 × 3 × 3 mm voxel).
DISCUSSION
The current analyses show that patients with schizophrenia exhibit a reduced resting‐state fMRI complexity compared with healthy subjects. Furthermore, in contrast to conventional entropy analysis, in which single‐time‐scale regularity is measured, the MSE profiles in different time scales reveal two routes of decreased BOLD complexity toward either a regular or random pattern. Reduced BOLD complexity toward the regular pattern is observed in the cerebellum and temporal, middle, and superior frontal regions, and reduced BOLD complexity toward the random process is observed extensively in the inferior frontal, occipital, and postcentral cortices as well as in the insula and middle cingulum. We determine that these two types of complexity change are associated with psychopathology and clinical variables differently. Collectively, these results suggest that resting‐state dynamics in patients with schizophrenia exhibit two patterns of pathologic change toward regular or random patterns, and these patterns may contribute to the differences in the syndrome domains of psychosis in schizophrenia.
Implication of Different Types of Complexity Change in the Pathophysiology of Schizophrenia
MSE profile analysis introduces the notion that the neither the extremes of complete regularity nor complete randomness are complex [Costa et al., 2005]. However, the alteration of system complexity toward regularity or randomness represents two distinct physical or biological processes. For example, heart rate fluctuation under different pathologic conditions may exhibit a loss of variability toward regularity (e.g., congestive heart failure) or the emergence of uncorrelated randomness (e.g., atrial fibrillation) [Goldberger et al., 2002a]. Likewise, our findings regarding the MSE profiles of BOLD signals toward regular or random patterns suggest that schizophrenia is characterized by two pathologic processes. This observation warrants future studies to investigate the specificity of these pathologic changes of MSE profile associated with schizophrenia and assess the difference in brain complexity with other mental illness or different brain states (e.g., sleep or psychedelic state).
Although the exact biological mechanisms contributing to these two types of complexity change were not delineated in this study, the differential associations of BOLD MSE profiles with psychopathology may provide clues. The PANSS positive syndrome score is associated with the fusiform gyrus and middle temporal gyrus, which exhibit a regular pattern of reduction in complexity; previous studies have shown that these brain regions are associated with auditory or imaginary hallucinations [Lawrie et al., 2002; Santhouse et al., 2000; Shergill et al., 2000]. One explanation, although speculative, is that the core of positive symptoms in schizophrenia is characterized by repetitive and involuntary hallucinatory experiences and fixed delusional thoughts, which manifest the lack of variability and may be linked to the loss of brain complexity toward regular patterns in the temporal and dorsal prefrontal regions (Table 2).
Conversely, the PANSS negative syndrome score is associated with a random type of reduction in complexity among brain regions, involving the orbitofrontal, occipital, and postcentral cortices (Table 4). These brain regions are related to affect and sensory processing. The duration of illness was negatively correlated with reduced complexity in the postcentral cortex. These results collectively suggest that a random type of reduction in BOLD complexity is linked to chronicity and negative symptoms of schizophrenia. Furthermore, erratic brain activity in these brain regions is consistent with the impaired sensory gating and sensory overload commonly observed in patients with schizophrenia [Bak et al., 2014; Brockhaus‐Dumke et al., 2008; Judd et al., 1992].
Other associations of psychopathology with decreased BOLD complexity are consistent with clinical presentations of schizophrenia. The negative correlation between the PANSS negative syndrome score and the regular type of reduced complexity in the cerebellum is consistent with recent findings of reduced complexity of postural sway in schizophrenia [Kent et al., 2012]. The positive correlation between age of onset and MSE complexity in the orbitofrontal region indicated that an earlier onset of illness is associated with a stronger degree of reduction in brain complexity toward randomness.
Remarks on Complexity Measures
The term complexity has been broadly used in neuroscience research. Various nonlinear methods have been applied to quantify the complexity of a neurophysiological time series in the temporal dimension, including the power–law spectra [Tagliazucchi et al., 2014; Zarahn et al., 1997], Hurst exponent [Bullmore et al., 2001; Lai et al., 2011], fractal dimension [Rubinov et al., 2009], Lyapunov exponent [Xie et al., 2008], and Lempel–Ziv complexity [Fernandez et al., 2011], as reviewed by Fernandez et al. [2013] and Takahashi [2013]. However, both increases and decreases in the complexity of brain signals have been reported in schizophrenic patients. The inconsistencies among the results of these studies may have been caused by differences in the study population, definition of the various types of complexity methods, or (most plausibly) by the simple up‐and‐down approach used to detect complexity changes in a single time scale along the continuum of regularity toward randomness, leading to the confusing conclusion that randomness is complex in certain cases. Therefore, MSE profile analysis across time scales provides crucial information on the complex dynamics of underlying processes and enables differentiating meaningful complexity from uncorrelated randomness [Chialvo, 2002; Costa et al., 2002; Takahashi et al., 2010; Yang et al., 2013c]. Such notion complements the monotonic view of entropy changes in different brain states [Carhart‐Harris et al., 2014; Tagliazucchi et al., 2014].
Furthermore, the relationship between the variability of local activity and connectivity strength in a given brain region remains underexplored. Bassett et al. [2012] showed that the complexity of a time series from an individual brain region is strongly predictive of the overall functional connectivity of the brain, and the strength of this relationship is altered in patients with schizophrenia. Recently, we reported that reduced BOLD complexity in elderly apolipoprotein E carriers exhibited a compensatory increase in functional connectivity between the posterior cingulum and frontal regions [Yang et al., 2014a]. The relationship between BOLD temporal complexity and spatial connectivity is likely nonlinear. A recent study based on Human Connectome Project data showed that BOLD complexity was negatively correlated with functional connectivity in short scales, but was positively correlated with functional connectivity in long scales [McDonough and Nashiro, 2014]. Incorporating both temporal and spatial complexity methods in future studies may facilitate elucidating the pathophysiology of schizophrenia in the context of the complex brain network.
Although the generic feature of dynamical complexity detected by the MSE method is independent of signal characteristics [Costa et al., 2005], the equivalence of MSE complexity metrics between resting‐state fMRI signals and electrophysiological time series is yet to be determined. The resting‐state fMRI signal and electrophysiological time series (such as electroencephalographic signals) certainly carry different aspects of neuronal information via distinct mechanisms. The former is based on neurovascular coupling which its hemodynamic response is in low frequency range (<0.1 Hz), whereas the latter is typically a measure of electrical activity over the scalp and is within a much higher frequency range (∼1–50 Hz). From the signal analysis point of view, the MSE calculation for these two types of signals captures dynamical information in very different time scales. Hence, we anticipate that MSE profile of BOLD signals may be equivalent of long time scale part of MSE profile of EEG signals (i.e., applying a large scale factor to EEG signals in coarse‐graining procedure).
Limitations
There are several limitations to our findings. First, although our results did not show that reduced resting‐state complexity was correlated with antipsychotic dosages, little is known about the effects of antipsychotic drugs on BOLD signals. A meta‐analysis revealed no common effect of antipsychotics on BOLD signals; however, antipsychotics with various affinities for the dopamine D2‐receptor may influence BOLD activity [Rder et al., 2013]. A future study categorizing patients with schizophrenia according to various outcomes or classes of antipsychotics may clarify this effect. Second, the extent of the scale factor used in MSE analysis was limited to the length of BOLD time series (195 data points); therefore, the MSE complexity profiles based on scales of 1–5 may have captured only a portion of the underlying dynamics, unlike long resting‐state fMRI signals such as those used in the Human Connectome Project [McDonough and Nashiro, 2014; Van Essen et al., 2013]. However, we suggest that this limitation had little effect on our data because previous MSE analyses of other physiologic signals [Costa et al., 2002, 2005] and BOLD signals in various brain regions [McDonough and Nashiro, 2014; Smith et al., 2014] suggested that randomness and meaningful complexity could be differentiated in the shortest scale factors. Third, we did not perform global signal regression to prevent distortion in BOLD signals; however, another study identified a difference in global signals between patients with schizophrenia and healthy subjects [Yang et al., 2014b]; this difference warrants further study of the effects of global signals on MSE estimates in healthy and disease populations. Finally, the relationship between the complexity of BOLD signals and their frequency components has not been established. Such study will facilitate delineating the functional relevance of BOLD complexity.
CONCLUSION
Using MSE profile analysis, we evaluate the complexity of resting‐state brain activity in patients with schizophrenia and its relationship with the psychopathology of illness. Our findings represent a novel perspective on the temporal dynamics of functional brain activity and enhance the understanding of the various pathophysiologic processes in schizophrenia. On a broader scale, analyzing the complexity of the human brain at the temporal dimension may facilitate developing clinically useful imaging biomarkers.
Conflict of interest
The authors declare no conflicts of interest.
REFERENCES
- Anderson CM, Lowen SB, Renshaw PF (2006): Emotional task‐dependent low‐frequency fluctuations and methylphenidate: Wavelet scaling analysis of 1/f‐type fluctuations in fMRI of the cerebellar vermis. J Neurosci Methods 151:52–61. [DOI] [PubMed] [Google Scholar]
- Anderson JS, Druzgal TJ, Lopez‐Larson M, Jeong EK, Desai K, Yurgelun‐Todd D (2011): Network anticorrelations, global regression, and phase‐shifted soft tissue correction. Hum Brain Mapp 32:919–934. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bak N, Rostrup E, Larsson HB, Glenthoj BY, Oranje B (2014): Concurrent functional magnetic resonance imaging and electroencephalography assessment of sensory gating in schizophrenia. Hum Brain Mapp 35:3578–3587. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bassett DS, Gazzaniga MS (2011): Understanding complexity in the human brain. Trends Cogn Sci 15:200–209. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bassett DS, Nelson BG, Mueller BA, Camchong J, Lim KO (2012): Altered resting state complexity in schizophrenia. NeuroImage 59:2196–2207. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Breakspear M. (2006): The nonlinear theory of schizophrenia. Aust N Z J Psychiatry 40:20–35. [DOI] [PubMed] [Google Scholar]
- Brockhaus‐Dumke A, Schultze‐Lutter F, Mueller R, Tendolkar I, Bechdolf A, Pukrop R, Klosterkoetter J, Ruhrmann S (2008): Sensory gating in schizophrenia: P50 and N100 gating in antipsychotic‐free subjects at risk, first‐episode, and chronic patients. Biol Psychiatry 64:376–384. [DOI] [PubMed] [Google Scholar]
- Bullmore E, Sporns O (2009): Complex brain networks: Graph theoretical analysis of structural and functional systems. Nat Rev 10:186–198. [DOI] [PubMed] [Google Scholar]
- Bullmore E, Long C, Suckling J, Fadili J, Calvert G, Zelaya F, Carpenter TA, Brammer M (2001): Colored noise and computational inference in neurophysiological (fMRI) time series analysis: Resampling methods in time and wavelet domains. Hum Brain Mapp 12:61–78. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Buzsaki G, Draguhn A (2004): Neuronal oscillations in cortical networks. Science 304:1926–1929. [DOI] [PubMed] [Google Scholar]
- Carhart‐Harris RL, Leech R, Hellyer PJ, Shanahan M, Feilding A, Tagliazucchi E, Chialvo DR, Nutt D (2014): The entropic brain: A theory of conscious states informed by neuroimaging research with psychedelic drugs. Front Hum Neurosci 8:20. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chao‐Gan Y, Yu‐Feng Z (2010): DPARSF: A MATLAB toolbox for “Pipeline” data analysis of resting‐state fMRI. Front Syst Neurosci 4:13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chialvo DR (2002): Physiology: Unhealthy surprises. Nature 419:263. [DOI] [PubMed] [Google Scholar]
- Costa M, Goldberger AL, Peng CK (2002): Multiscale entropy analysis of complex physiologic time series. Phys Rev Lett 89:068102. [DOI] [PubMed] [Google Scholar]
- Costa M, Goldberger AL, Peng CK (2005): Multiscale entropy analysis of biological signals. Phys Rev 71:021906. [DOI] [PubMed] [Google Scholar]
- Ehlers CL (1995): Chaos and complexity. Can it help us to understand mood and behavior? Arch Gen Psychiatry 52:960–964. [DOI] [PubMed] [Google Scholar]
- Fernandez A, Lopez‐Ibor MI, Turrero A, Santos JM, Moron MD, Hornero R, Gomez C, Mendez MA, Ortiz T, Lopez‐Ibor JJ (2011): Lempel‐Ziv complexity in schizophrenia: A MEG study. Clin Neurophysiol 122:2227–2235. [DOI] [PubMed] [Google Scholar]
- Fernandez A, Gomez C, Hornero R, Lopez‐Ibor JJ (2013): Complexity and schizophrenia. Prog Neuropsychopharmacol Biol Psychiatry 45:267–276. [DOI] [PubMed] [Google Scholar]
- Fogedby HC (1992): On the phase space approach to complexity. J Stat Phys 69:411–425. [Google Scholar]
- Fox MD, Raichle ME (2007): Spontaneous fluctuations in brain activity observed with functional magnetic resonance imaging. Nat Rev 8:700–711. [DOI] [PubMed] [Google Scholar]
- Goldberger AL (1996): Non‐linear dynamics for clinicians: Chaos theory, fractals, and complexity at the bedside. Lancet 347:1312–1314. [DOI] [PubMed] [Google Scholar]
- Goldberger AL, Amaral LA, Hausdorff JM, Ivanov P, Peng CK, Stanley HE (2002a): Fractal dynamics in physiology: Alterations with disease and aging. Proc Natl Acad Sci USA 99(Suppl 1):2466–2472. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goldberger AL, Peng CK, Lipsitz LA (2002b): What is physiologic complexity and how does it change with aging and disease? Neurobiol Aging 23:23–26. [DOI] [PubMed] [Google Scholar]
- Judd LL, McAdams L, Budnick B, Braff DL (1992): Sensory gating deficits in schizophrenia: New results. Am J Psychiatry 149:488–493. [DOI] [PubMed] [Google Scholar]
- Kay SR, Fiszbein A, Opler LA (1987): The positive and negative syndrome scale (PANSS) for schizophrenia. Schizophr Bull 13:261–276. [DOI] [PubMed] [Google Scholar]
- Kent JS, Hong SL, Bolbecker AR, Klaunig MJ, Forsyth JK, O'Donnell BF, Hetrick WP (2012): Motor deficits in schizophrenia quantified by nonlinear analysis of postural sway. PLoS one 7:e41808. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Keshavan MS, Cashmere JD, Miewald J, Yeragani VK (2004): Decreased nonlinear complexity and chaos during sleep in first episode schizophrenia: A preliminary report. Schizophr Res 71:263–272. [DOI] [PubMed] [Google Scholar]
- Kotini A, Anninos P (2002): Detection of non‐linearity in schizophrenic patients using magnetoencephalography. Brain Topogr 15:107–113. [DOI] [PubMed] [Google Scholar]
- Koukkou M, Lehmann D, Wackermann J, Dvorak I, Henggeler B (1993): Dimensional complexity of EEG brain mechanisms in untreated schizophrenia. Biol Psychiatry 33:397–407. [DOI] [PubMed] [Google Scholar]
- Lai MC, Lombardo MV, Chakrabarti B, Sadek SA, Pasco G, Wheelwright SJ, Bullmore ET, Baron‐Cohen S, Suckling J (2011): A shift to randomness of brain oscillations in people with autism. Biol Psychiatry 68:1092–1099. [DOI] [PubMed] [Google Scholar]
- Lake DE, Richman JS, Griffin MP, Moorman JR (2002): Sample entropy analysis of neonatal heart rate variability. Am J Physiol Regul Integr Comp Physiol 283:R789–R797. [DOI] [PubMed] [Google Scholar]
- Lawrie SM, Buechel C, Whalley HC, Frith CD, Friston KJ, Johnstone EC (2002): Reduced frontotemporal functional connectivity in schizophrenia associated with auditory hallucinations. Biol Psychiatry 51:1008–1011. [DOI] [PubMed] [Google Scholar]
- Lee YJ, Zhu YS, Xu YH, Shen MF, Zhang HX, Thakor NV (2001): Detection of non‐linearity in the EEG of schizophrenic patients. Clin Neurophysiol 112:1288–1294. [DOI] [PubMed] [Google Scholar]
- Li Y, Tong S, Liu D, Gai Y, Wang X, Wang J, Qiu Y, Zhu Y (2008): Abnormal EEG complexity in patients with schizophrenia and depression. Clin Neurophysiol 119:1232–1241. [DOI] [PubMed] [Google Scholar]
- Liu CY, Krishnan AP, Yan L, Smith RX, Kilroy E, Alger JR, Ringman JM, Wang DJ (2013): Complexity and synchronicity of resting state blood oxygenation level‐dependent (BOLD) functional MRI in normal aging and cognitive decline. J Magn Reson Imaging 38:36–45. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lu CW, Czosnyka M, Shieh JS, Smielewska A, Pickard JD, Smielewski P (2012): Complexity of intracranial pressure correlates with outcome after traumatic brain injury. Brain 135:2399–23408. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maxim V, Sendur L, Fadili J, Suckling J, Gould R, Howard R, Bullmore E (2005): Fractional Gaussian noise, functional MRI and Alzheimer's disease. NeuroImage 25:141–158. [DOI] [PubMed] [Google Scholar]
- McDonough IM, Nashiro K (2014): Network complexity as a measure of information processing across resting‐state networks: Evidence from the Human Connectome Project. Front Hum Neurosci 8:409. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McIntosh AR, Vakorin V, Kovacevic N, Wang H, A Diaconescu, AB Protzner (2014): Spatiotemporal dependency of age‐related changes in brain signal variability. Cereb Cortex 24:1806–1817. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Meunier D, Achard S, Morcom A, Bullmore E (2009): Age‐related changes in modular organization of human brain functional networks. NeuroImage 44:715–723. [DOI] [PubMed] [Google Scholar]
- Murphy K, Birn RM, Handwerker DA, Jones TB, Bandettini PA (2009): The impact of global signal regression on resting state correlations: Are anti‐correlated networks introduced? NeuroImage 44:893–905. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Narr KL, Bilder RM, Kim S, Thompson PM, Szeszko P, Robinson D, Luders E, Toga AW (2004): Abnormal gyral complexity in first‐episode schizophrenia. Biol Psychiatry 55:859–867. [DOI] [PubMed] [Google Scholar]
- Norris PR, Canter JA, Jenkins JM, Moore JH, Williams AE, Morris JA Jr (2009): Personalized medicine: Genetic variation and loss of physiologic complexity are associated with mortality in 644 trauma patients. Ann Surg 250:524–530. [DOI] [PubMed] [Google Scholar]
- Paulus MP, Braff DL (2003): Chaos and schizophrenia: Does the method fit the madness? Biol Psychiatry 53:3–11. [DOI] [PubMed] [Google Scholar]
- Pincus SM, Goldberger AL (1994): Physiological time‐series analysis: What does regularity quantify? Am J Physiol 266:H1643–H1656. [DOI] [PubMed] [Google Scholar]
- Raghavendra BS, Dutt DN, Halahalli HN, John JP (2009): Complexity analysis of EEG in patients with schizophrenia using fractal dimension. Physiol Meas 30:795–808. [DOI] [PubMed] [Google Scholar]
- Rder CH, Dieleman S, van der Veen FM, Linden D (2013): Systematic review of the influence of antipsychotics on the blood oxygenation level‐dependent signal of functional magnetic resonance imaging. Curr Med Chem 20:448–461. [DOI] [PubMed] [Google Scholar]
- Richman JS, Moorman JR (2000): Physiological time‐series analysis using approximate entropy and sample entropy. Am J Physiol 278:H2039–H2049. [DOI] [PubMed] [Google Scholar]
- Rubinov M, Sporns O, van Leeuwen C, Breakspear M (2009): Symbiotic relationship between brain structure and dynamics. BMC Neurosci 10:55. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Santhouse AM, Howard RJ, ffytche DH (2000): Visual hallucinatory syndromes and the anatomy of the visual brain. Brain 123:2055–2064. [DOI] [PubMed] [Google Scholar]
- Sheehan DV, Lecrubier Y, Sheehan KH, Amorim P, Janavs J, Weiller E, Hergueta T, Baker R, Dunbar GC (1998): The Mini‐International Neuropsychiatric Interview (M.I.N.I.): The development and validation of a structured diagnostic psychiatric interview for DSM‐IV and ICD‐10. J Clin Psychiatry 59(Suppl 20):22–33. [PubMed] [Google Scholar]
- Shergill SS, Brammer MJ, Williams SC, Murray RM, McGuire PK (2000): Mapping auditory hallucinations in schizophrenia using functional magnetic resonance imaging. Arch Gen Psychiatry 57:1033–1038. [DOI] [PubMed] [Google Scholar]
- Smith RX, Yan L, Wang DJ (2014): Multiple time scale complexity analysis of resting state FMRI. Brain Imaging Behav 8:284–291. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sokunbi MO, Fung W, Sawlani V, Choppin S, Linden DE, Thome J (2013): Resting state fMRI entropy probes complexity of brain activity in adults with ADHD. Psychiatry Res 214:341–348. [DOI] [PubMed] [Google Scholar]
- Sokunbi MO, Gradin VB, Waiter GD, Cameron GG, Ahearn TS, Murray AD, Steele DJ, Staff RT (2014): Nonlinear complexity analysis of brain FMRI signals in schizophrenia. PLoS One 9:e95146. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tagliazucchi E, Carhart‐Harris R, Leech R, Nutt D, Chialvo DR (2014): Enhanced repertoire of brain dynamical states during the psychedelic experience. Hum Brain Mapp 35:5442–5456. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Takahashi T (2013): Complexity of spontaneous brain activity in mental disorders. Prog Neuropsychopharmacol Biol Psychiatry 45:258–266. [DOI] [PubMed] [Google Scholar]
- Takahashi T, Cho RY, Mizuno T, Kikuchi M, Murata T, Takahashi K, Wada Y (2010): Antipsychotics reverse abnormal EEG complexity in drug‐naive schizophrenia: A multiscale entropy analysis. NeuroImage 51:173–182. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tschacher W, Scheier C, Hashimoto Y (1997): Dynamical analysis of schizophrenia courses. Biol Psychiatry 41:428–437. [DOI] [PubMed] [Google Scholar]
- Van Essen DC, Smith SM, Barch DM, Behrens TE, Yacoub E, Ugurbil K, Consortium WU‐MH (2013): The WU‐Minn Human Connectome Project: An overview. NeuroImage 80:62–79. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xie X, Cao Z, Weng X (2008): Spatiotemporal nonlinearity in resting‐state fMRI of the human brain. NeuroImage 40:1672–1685. [DOI] [PubMed] [Google Scholar]
- Yang AC, Tsai SJ (2013): Is mental illness complex? From behavior to brain. Prog Neuro‐Psychopharmacol Biol Psychiatry 45:253–257. [DOI] [PubMed] [Google Scholar]
- Yang AC, Huang CC, Yeh HL, Liu ME, Hong CJ, Tu PC, Chen JF, Huang NE, Peng CK, Lin CP, Tsai SJ (2013a): Complexity of spontaneous BOLD activity in default mode network is correlated to cognitive function in normal male elderly: A multiscale entropy analysis. Neurobiol Aging 34:428–438. [DOI] [PubMed] [Google Scholar]
- Yang AC, Huang CC, Yeh HL, Liu ME, Hong CJ, Tu PC, Chen JF, Huang NE, Peng CK, Lin CP, Tsai SJ (2013b): Complexity of spontaneous BOLD activity in default mode network is correlated with cognitive function in normal male elderly: A multiscale entropy analysis. Neurobiol Aging 34:428–438. [DOI] [PubMed] [Google Scholar]
- Yang AC, Wang SJ, Lai KL, Tsai CF, Yang CH, Hwang JP, Lo MT, Huang NE, Peng CK, Fuh JL (2013c): Cognitive and neuropsychiatric correlates of EEG dynamic complexity in patients with Alzheimer's disease. Prog Neuro‐Psychopharmacol Biol Psychiatry 47:52–61. [DOI] [PubMed] [Google Scholar]
- Yang AC, Huang CC, Liu ME, Liou YJ, Hong CJ, Lo MT, Huang NE, Peng CK, Lin CP, Tsai SJ (2014a): The APOE epsilon4 allele affects complexity and functional connectivity of resting brain activity in healthy adults. Hum Brain Mapp 35:3238–3248. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang GJ, Murray JD, Repovs G, Cole MW, Savic A, Glasser MF, Pittenger C, Krystal JH, Wang XJ, Pearlson GD, Glahn DC, Anticevic A (2014b): Altered global brain signal in schizophrenia. Proc Natl Acad Sci USA 111:7438–7443. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zang YC (1991): Complexity and 1/f noise. A phase space approach. J Phys I France 1:971–977. [Google Scholar]
- Zarahn E, Aguirre GK, D'Esposito M (1997): Empirical analyses of BOLD fMRI statistics. I. Spatially unsmoothed data collected under null‐hypothesis conditions. NeuroImage, 5:179–197. [DOI] [PubMed] [Google Scholar]


