Abstract
Two new directions of functional connectivity investigation are emerging to advance studies of the brain's functional organization. First, the identification of task‐related dynamics of functional connectivity has elicited a growing interest in characterizing the brain's functional reorganization due to task demands. Second, the nonstationarity of functional connectivity [i.e., functional connectivity variability (FCV)] within a single brain state has been increasingly recognized and studied. However, a combined investigation of these two avenues of research to explore the potential task‐modulation of FCV is lacking, which, nevertheless, could both improve our understanding of the potential sources of FCV and also reveal new strategies to study the neural correlates of task performance. In this study, 19 human subjects underwent four functional magnetic resonance imaging (fMRI) scans including both resting and task states to study task‐related modulation of FCV. Consistent with the hypothesis that FCV is partly underpinned by unconstrained mind wandering, FCV demonstrated significant task‐related decreases measured at the regional, network and system levels, which was greater for between‐network interactions than within‐network connections. Conversely, there remained a significant degree of residual variability during the task scans, suggesting that FCV is not specific to the resting state and likely includes an intrinsic, physiologically driven component. Finally, the degree of task‐induced decreases in FCV was significantly correlated with task performance accuracy, supporting its behavior significance. Overall, task modulation of FCV may represent an important direction for future studies, not only to provide insight into normal brain functioning but also to reveal potential biomarkers of various brain disorders. Hum Brain Mapp 36:3260–3272, 2015. © 2015 Wiley Periodicals, Inc.
Keywords: fMRI, neural interconnections, neural networks, task performance, behavior
INTRODUCTION
Recently, two new directions of investigation have emerged from the classic functional connectivity study of the resting brain [Biswal et al., 1995]. First, an increasing number of studies have begun to investigate the task‐related dynamics of functional connectivity and have elucidated intriguing patterns of functional reorganization related to task performance [Bluhm et al., 2011; Elton and Gao, 2014; Fornito et al., 2012; Gao et al., 2013]. Conversely, the presence of functional connectivity variability (FCV), even within a single brain state, has also been increasingly recognized [Allen et al., 2014; Chang and Glover, 2010; Hutchison et al., 2013a] and established as clinically relevant [Damaraju et al., 2014; Rashid et al., 2014]. Therefore, both directions represent promising extensions of traditional functional connectivity studies deserving further research. However, a combined investigation of these two elements—the potential task modulation of FCV—is currently lacking, which, nevertheless, could improve our understanding of the mechanisms of FCV and reveal new brain functional strategies for task performance.
Electrophysiological studies have long recognized the tonic and spontaneous firing patterns of neurons [Llinás and Sugimori, 1980; Perkel et al., 1967; Raman et al., 2000], providing support for intrinsic physiological sources of FCV. Indeed, FCV has been shown to persist in the absence of conscious thought [Barttfeld et al., 2015; Hutchison et al., 2013b]. Conversely, a recent direct comparison of FCV between awake resting and anesthetized states revealed a dramatic reduction of FCV during unconsciousness, suggesting FCV is at least partly related to conscious operations [Barttfeld et al., 2015]. In particular, one potential source of FCV during consciousness is the “wandering” of the mind, in which the brain consciously engages in different mental operations, to produce fluctuations in functional connectivity. Indeed, a recent study showed that FCV in the default‐mode network tracks the degree of daydreaming [Kucyi and Davis, 2014]. Following these theories, a systematic examination of task‐related changes of FCV may further elucidate its underlying sources from the other end of the consciousness spectrum. Specifically, we would expect FCV to persist during task performance given the hypothesized contribution of intrinsic fluctuations. However, we would also expect a significant decrease in FCV during task performance due to the increased functional constraint that likely limits mind wandering. Aside from an improved understanding of the underlying sources of FCV, such an investigation may also provide a novel perspective to inform how the brain responds to different functional demands.
In this study, we investigated the potential task‐related modulation of FCV by systematically examining four brain states: an initial resting state, a continuous relaxed‐paced task, a continuous rapid‐paced task, and a final resting state. FCV among 35 regions composing six major functional networks was measured at the regional, network and system levels. Effects of within‐ and between‐network connectivity on the task‐related modulation were further examined. Finally, the relationship between task‐related changes in FCV and task performance was explored. Our results confirm our hypothesis of task‐induced modulation of FCV, providing novel insight into its underlying sources and behavioral relevance.
METHODS
Subjects and Study Procedures
Nineteen healthy adults (5 females) between the ages of 27–40 were enrolled in this study. The absence of any psychiatric or neurological disorder was confirmed by self‐report. Subjects underwent four consecutive functional MRI scans, which started with a resting‐state scan (R1), was followed by two global‐local selective attention task scans (T1, T2), and finished with a second resting‐state scan (R2). The resting‐state scans were conducted with subjects relaxed with their eyes closed. The two task scans were self‐paced and involved instructions to perform at either a relaxed pace (T1) or a rapid pace (T2) and were presented in a counterbalanced order. Subjects were instructed to remain awake throughout all four scans and confirmed their compliance by self‐report at the completion of the session. The task paradigm has been described in detail elsewhere [Elton and Gao, 2014; Gao, et al., 2013]. Briefly, stimuli consisted of large letters (H or S) composed of smaller letters (H or S) providing either congruent (large S and small S; large H and small H) or incongruent (large S and small H; large H and small S) stimuli. Subjects were required to respond with a button press to indicate the identity of either the large letter or small letter according to a concurrently presented cue. It is important to note for the current analysis that the task was continuous in nature, without resting periods or fixation, such that consecutive trials were immediately presented following a response to the preceding trial. The use of a task with continuous performance was chosen to minimize the variability produced by a mixture of task‐related and resting baseline signals.
MRI Acquisition
Subjects were scanned with a Siemens Trio 3T MR scanner (Siemens Medical Inc., Erlangen, Germany). T1 images were collected using a 3D MP‐RAGE sequence with the following parameters: repetition time (TR) = 1,820 ms; echo time (TE) = 4.38 ms; inversion time = 1,100 ms; 144 slices; and voxel size = 1 × 1 × 1 mm3. Echo‐planar images were collected for the fMRI scans (TR = 2,000 ms, TE = 32 ms; 33 slices; and voxel size = 4 × 4 × 4 mm3). Each of the four fMRI scans lasted 5 min, producing 150 images per scan.
Preprocessing
The first 10 time points were dropped from each fMRI scan to allow magnetization to reach equilibrium. Images were subsequently preprocessed in SPM8 software using identical methods for each scan, which included slice timing correction, realignment to the second image, registration to the Montreal Neurological Institute (MNI) template, reslicing to 3 × 3 × 3 mm3 voxels, spatial smoothing with an 8 mm full width at half maximum Gaussian kernel and band pass filtering between 0.008 and 0.08 Hz. Regression techniques removed nuisance signals from white matter, cerebral spinal fluid (CSF), global signal and six directions of head motion. Next, data were “scrubbed” to minimize the effects of motion on functional connectivity calculations using a method described by Power and colleagues [Power et al., 2012]. This method removes volumes exceeding a global signal change threshold of 0.5% BOLD signal and a displacement threshold of 0.5 mm, in addition to the prior volume and the two subsequent volumes. No volumes required removal for R1, T1, and T2 for any subject. However, three of the subjects’ R2 scans required substantial scrubbing (60+ volumes removed), limiting the usefulness of that data. Therefore, R2 scans from these three subjects were omitted from analyses. No volumes were removed from the R2 scan for the remaining 16 subjects.
ROI Selection
Four higher‐order networks, the dorsal attention network (DA), default‐mode network (DM), salience network (SAL), and executive control network (CON), were defined from seed‐based functional connectivity. Seeds were defined as 8‐mm spheres within the bilateral intraparietal sulcus for DA (x=−27, y=−52, z=57; 24, −56, 55), the posterior cingulate cortex for DM (x=0, y=−53, z=26), the right dorsolateral prefrontal cortex for CON (x=44, y=36, z=20), right anterior insula for SAL (x=38, y=26, z=−10) based on previous publications [Elton and Gao, 2014; Seeley et al., 2007; Vincent et al., 2008]. For each subject and each scan the voxel‐wise Pearson correlation of the mean signal within the seed region was computed. Correlation maps were Fisher Z transformed. For these networks, regions‐of‐interest (ROIs) were identified as those clusters of voxels which exhibited stable functional connectivity with the seed region across all four fMRI scans based on one‐way analysis of variance (ANOVA). In other words, ROIs for each network were defined from those regions which exhibited (1) significant positive connectivity for all four fMRI scans and (2) did not exhibit significant changes across scans. Although ROIs were functionally defined, this strategy enabled the definition of ROIs that were consistent across the four scans and not biased by a particular brain state. These regions are identical to those reported in our prior study [Elton and Gao, 2014]. Two primary networks, the primary visual (V) and sensorimotor network (SM) were also investigated. Because V and SM networks do not form discrete clusters, ROIs for these networks were defined as sets of 8‐mm spheres defined a priori [Gao and Lin, 2012]. ROIs are displayed in Figure 1 and Table 1 lists the coordinates of ROI centers for each network. All coordinates are reported using Montreal Neurological Institute (MNI) template space.
Figure 1.
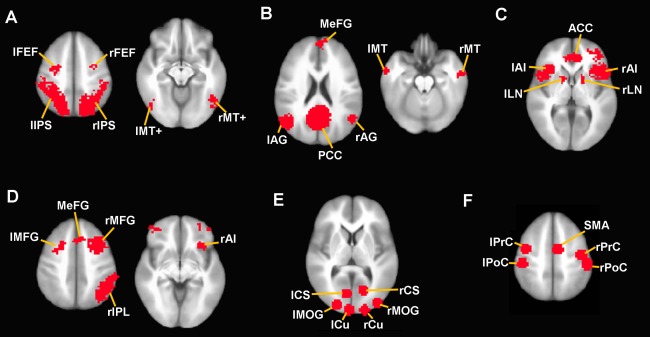
Regions‐of‐interest (ROIs) from each network. ROIs are overlaid on an anatomical image in MNI standard space for (A) DA, (B) DM, (C) SAL, (D) CON, (E) V, and (F) SM. Images are in neurological orientation (right is right). Abbreviations: ACC, anterior cingulate cortex; AG, angular gyrus; AI, anterior insula; CS, calcarine sulcus; CU, cuneus; FEF, frontal eye field; IPS, intraparietal sulcus; LN, lentiform nucleus; MeFG, medial frontal gyrus; MFG, middle frontal gyrus; MOG, middle occipital gyrus; MT, middle temporal cortex; MT+, middle temporal visual area; PCC, posterior cingulate cortex; PoC, postcentral gyrus; PrC, precentral gyrus; SMA, supplementary motor area. [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com.]
Table 1.
Regions‐of‐interest defining each network
| x | y | z | # voxels | |
|---|---|---|---|---|
| DA | ||||
| R intraparietal sulcus | 25 | −56 | 47 | 2353 |
| L intraparietal sulcus | −25 | −55 | 47 | 2280 |
| R middle temporal visual area | 38 | −67 | −12 | 525 |
| L middle temporal visual area | −40 | −74 | −6 | 244 |
| R frontal eye field | 27 | −6 | 58 | 466 |
| L frontal eye field | −25 | −7 | 58 | 447 |
| DM | ||||
| Posterior cingulate cortex | 0 | −53 | 20 | 1953 |
| Medial frontal gyrus | 1 | 50 | 16 | 1786 |
| R angular gyrus | −46 | −64 | 23 | 379 |
| L angular gyrus | 52 | −58 | 22 | 241 |
| R middle temporal gyrus | 58 | −1 | −24 | 130 |
| L middle temporal gyrus | −55 | −5 | −25 | 176 |
| SAL | ||||
| R inferior frontal gyrus/insula | 42 | 22 | −6 | 1140 |
| Anterior cingulate cortex | 2 | 30 | 28 | 647 |
| L inferior frontal gyrus/insula | −39 | 17 | −7 | 646 |
| R lentiform nucleus | 16 | 7 | 1 | 35 |
| R middle temporal gyrus | 53 | −22 | −11 | 32 |
| L lentiform nucleus | −13 | 6 | 0 | 22 |
| CON | ||||
| R middle/inferior frontal gyrus | 42 | 25 | 25 | 1385 |
| R inferior parietal lobule | 46 | −49 | 43 | 519 |
| L middle/inferior frontal gyrus | −42 | 32 | 16 | 402 |
| Medial frontal gyrus | 2 | 26 | 39 | 116 |
| L middle/superior frontal gyrus | −27 | 10 | 48 | 53 |
| R anterior insula | 32 | 23 | −5 | 46 |
| V | ||||
| R calcarine sulcus | 16 | −67 | 5 | 96 |
| L calcarine sulcus | −8 | −72 | 4 | 100 |
| R cuneus | 18 | −96 | 12 | 100 |
| L cuneus | −5 | −96 | 12 | 106 |
| R middle occipital gyrus | 37 | −85 | 13 | 106 |
| L middle occipital gyrus | −23 | −89 | 12 | 96 |
| SM | ||||
| R precentral gyrus | 42 | −13 | 53 | 106 |
| L precentral gyrus | −41 | −4 | 54 | 96 |
| R postcentral gyrus | 49 | −27 | 53 | 106 |
| L postcentral gyrus | −45 | −26 | 54 | 106 |
| Supplementary motor area | 6 | −5 | 54 | 106 |
DA, dorsal attention network; DM, default‐mode network; SAL, salience network; CON, executive control network; V, primary visual network; SM, sensorimotor network.
Sliding Window Connectivity
For each ROI, the time series was calculated as the mean signal among voxels within that region, which generated 35 time series from the 6 networks. The sliding‐windowed correlation [Allen et al., 2014; Hutchison et al., 2013a] was calculated between each pair of time series using a rectangular window with a size of 30 time points (60 s). Calculation of the sliding‐windowed correlation between two time series proceeded by first calculating the Pearson correlation in these signals considering only time points 1–30 (i.e. the size of the “window”). Next, the window was moved forward by one time point, such that the next correlation was calculated from time points 2–31 of each signal. The window was iteratively moved forward with a new correlation calculated for each iteration up to the last set of 30 time points. This procedure resulted in a sliding window time series of correlations between each pair of ROIs.
Calculation of Correlation Variability
To analyze the stability of the between‐ROI correlations over time, we calculated two independent measures of signal variability. First, for each pair of ROIs, the standard deviation of the sliding‐windowed correlation time series was calculated. A second measure of correlation variability was measured by taking the power of the mean‐centered sliding‐windowed correlation time series, which was calculated as the absolute value of the area under the curve. Supplemental analyses were performed on a third measure of variability, the coefficient of variation, which was defined as the absolute value of the mean sliding window functional connectivity divided by its standard deviation. Because the resulting values are highly skewed, a natural log transformation was applied to the data.
Statistical analyses were performed using the PROC ANOVA statement in SAS software. An omnibus test across all ROIs tested the main effects of task, within‐versus‐between network connectivity (ROIs belonging to the same network or not), as well as the interaction of task and within‐versus‐between network connectivity on each of the two measures of correlation variability using repeated‐measures ANOVA. For each network individually, within‐network effects of task on correlation variability measures were tested with two‐way ANOVAs with repeated measures over task and within‐network ROIs. For between‐network effects, the effect of task was similarly tested, but repeated measures ANOVAs tested effects over ROIs that did not belong to the same network.
Calculation of Graph Measures
Using the Brain Connectivity MATLAB toolbox [Rubinov and Sporns, 2010], we calculated system‐level measures of brain organization on both static and sliding window time series of functional connectivity. For each scan and each subject, the functional connectivity correlation matrices at each sliding window time point were calculated. Next each of these correlation matrices were used to calculate the global efficiency, mean local efficiency, and mean modularity for the graph. Graphs were not adjusted for their mean connectivity values, and thus the reported graph measures reflect both the organization and magnitude of the connections. Global efficiency is defined as the average inverse shorted path length of the entire graph. Local efficiency is a similar measure but calculated on the local neighborhood for each ROI; we then calculated the mean across all ROIs to obtain a single value of the graph's local efficiency. For efficiency measures, we used weighted, undirected graphs obtained by taking the absolute value of the 35 × 35 ROI correlation matrix. Modularity is a measure of how well ROIs cluster into discrete networks. For this measure, weighted, signed graphs were defined from the raw 35 × 35 ROI correlation matrix. We calculated the modularity based on the Louvain algorithm to provide a single value for each graph. Next, the mean, standard deviation, and power of the graph measures along the sliding window time series was calculated. The effect of task on these measures was calculated using repeated‐measures ANOVAs in SAS software.
Relationship between mean and sliding‐window connectivity
Finally, we examined the relationship between variability in sliding‐windowed correlation and the static correlation calculated over the entire time series. This analysis included data points for every connection for each subject to identify whether there is a systematic relationship between the mean and the variability of the functional connectivity. Within‐ and between‐network connections were plotted on the same graph. Based on visual inspection, the data exhibited a second order polynomial relationship but both a linear and a second order polynomial function were tested using least‐squares fit and Akaike information criterion (AIC) values were calculated to select the best model.
A similar test was conducted on graph measures, which analyzed the relationship between the mean and the variability (standard deviation and power) of the sliding windowed calculations of global efficiency, local efficiency, and modularity. Similarly, although visual inspection suggested a linear relationship, both a linear and a second order polynomial function were tested and again AIC was used to select the best model.
Effects of variability on behavior
The relationship between task‐dependent changes in variability and task performance was assessed across both task scans by partial correlation analysis, controlling for task level (T1 or T2). Task‐related variability was calculated as the mean change in variability (standard deviation or power) across all ROIs, where the change was calculated as the difference between each task scan and the average of the rest scans (i.e. T1 − (R1, R2) and T2 − (R1, R2)). For the three subjects without usable R2 data, only R1 was used to represent variability during rest. Behavioral measures included response accuracy, reaction time, and reaction time variability. Spearman's correlation coefficients were calculated due to non‐normal distributions of the behavioral variables.
RESULTS
The ROI‐wise matrix of group mean FCV across R1, T1, T2, and R2 is presented in Figure 2A,B. This figure demonstrates a general shift from high variability in the resting states to lower variability in the task states for the sliding‐windowed correlation across each pair of ROIs. For reference, the corresponding mean of the sliding window connectivity values are presented in Figure 2C. Bar graphs depicting effects of task on within‐network and between‐network FCV are presented in Figure 2. There was a significant main effect of task (based on all ROIs) on the variability of functional connectivity dynamics as measured by standard deviation (F(3, 80660)=1238.9, P<0.001) and by power (F(3, 80660)=1162.8, P<0.001). Consistent with our hypothesis, post hoc testing indicated significant differences between resting state and tasks and between the two task states (i.e., R1∼=R2 > T1 > T2). There was a significant effect of task on the standard deviation (Fig. 3A) and power (Fig. 3B) of sliding window connectivity time series for both within‐network and between‐network ROIs. Significant Bonferroni post hoc contrasts for within‐ and between‐network connections between each pair of successive brain modes are denoted with asterisks in Figure 3. However, we also detected a significant amount of residual FCV during the two task states for both within‐ and between‐network connectivity (Fig. 3). Specifically, compared with the rest scans (mean of R1 and R2), the fast‐paced task resulted in a 13.9% and 25.8% decrease in FCV, based on the standard deviation and power, respectively, indicating that less than half of FCV during rest was related to the lack of a task‐related constraint.
Figure 2.
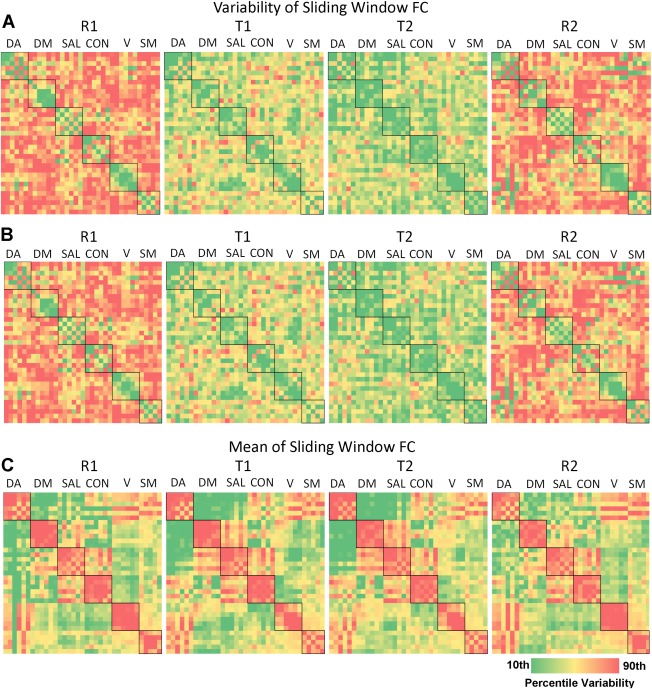
Matrices of the effect of task on regional FCV. The (A) standard deviation, (B) power, and (C) mean of sliding window connectivity time series between each set of ROIs is displayed. Within‐network connectivity is denoted with a black box. Warm colors indicate greater variability. [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com.]
Figure 3.
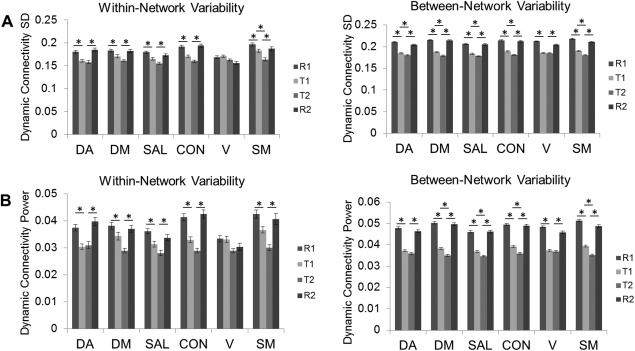
Bar plots of the effect of task on network FCV. The effect of task on the (A) standard deviation (SD) and (B) power of sliding window connectivity time series are presented for within‐network and between‐network ROIs. Error bars represent standard error of the mean. Asterisks denote significant differences between consecutive scans.
Results based on the coefficient of variation are presented in Supporting Information Figure S1. This measure largely confirmed the findings of task‐related decreases in variability as reported for standard deviation and power. However, SM and V did not conform to this pattern, and actually exhibited task‐related increases in their within‐network variability relative to mean functional connectivity. Thus, for these two primary networks, it appears that task‐related decreases in the strength of their functional connectivity outweigh the task‐related decreases in variability (Figure 2A–C), whereas this is not the case for the four higher‐order networks (i.e., DA, DM, SAL, and CON).
Additionally, there was a significant effect of within‐versus‐between network connectivity, such that within‐network ROIs demonstrated lesser variability in connectivity across all task states compared with between‐network ROIs for both standard deviation (F(1, 80660)=869.1, P<0.001) and power (F(1, 80660)=500.2, P<0.001) measurements. Finally, there was also a significant within‐versus‐between by task interaction for standard deviation (F(3, 80657)=15.6, P<0.001) and power (F(3, 80657)=16.4, P<0.001), indicating that degree of task related reductions in FCV was greater for between‐network than for within‐network ROIs. We repeated these analyses using multiple window sizes, and the results were robust against the use of shorter (30 s) or longer (90 s, 120 s) windows (Supporting Information Figures S2 and S3).
The variability of system‐level measures of brain organization demonstrated a similar pattern as reported above for the variability of functional connectivity (Fig. 4). Specifically, there was a task‐related decease in the variability of sliding‐windowed graph measures. Significance testing indicated an effect of task on the standard deviation of sliding window functional connectivity calculations of global efficiency (F(3,69)=3.00, P=0.037), local efficiency (F(3,69)=3.57, P=0.018), and modularity (F(3,69)=4.82, P=0.004) (Fig. 4A). These results were also replicated for the power of the sliding windowed calculations of local efficiency (F(3,69)=2.80, P=0.047) and modularity (F(3,69)=6.52, P<0.001), but did not meet statistical significance for global efficiency (P>0.05) (Fig. 4B). Calculations based on the mean of the sliding window calculations indicated that there was a significant task‐related decrease in the global efficiency (F(3,69)=6.63, P<0.001) and local efficiency (F(3,69)=6.04, P=0.001) and modularity (F(3,69)=7.70, P<0.001) of functional connectivity (Fig. 4C). Bonferroni post hoc tests identified significant pairwise contrasts, as indicated on Figure 4.
Figure 4.
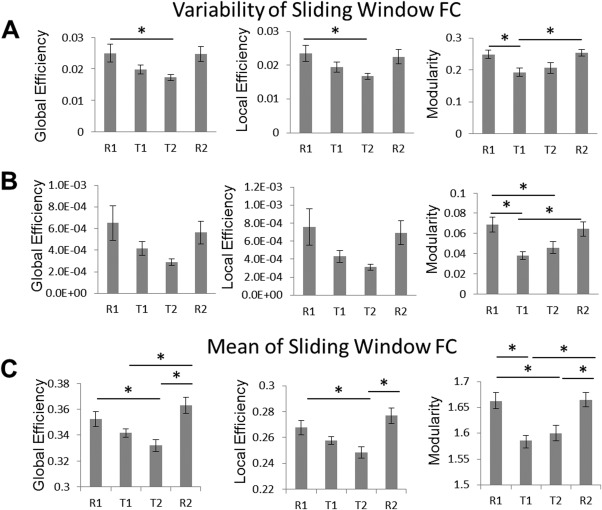
Bar plots of the effect of task on the variability of graph measures. The (A) standard deviation, (B) power, and (C) mean of graph measures measured with sliding window functional connectivity are depicted. Error bars represent standard errors of the mean. Asterisks denote significant differences between scans.
Plots of the relationship of static connectivity and connectivity variability are presented in Figure 5 and that of mean efficiency and efficiency variability are shown in Figure 6. There was a significant quadratic relationship (P<0.001, the better fit based on AIC) as assessed by model F statistic between static connectivity and connectivity variability using both standard deviation and power for each of the four scans. There was a positive linear relationship (the better fit based on AIC) between the mean and both standard deviation and power of each of the graph measures for each of the four scans, however not all of these relationships were significant (P>0.05) as shown in Figure 6. A secondary analysis, described in detail in the Supplementary Materials, considered how intersubject differences in mean connectivity are related to connectivity variability for within‐ and between‐network connections separately. Negative correlations were identified for the relationship between individual differences in mean connectivity and connectivity variability for within‐network connectivity, whereas between‐network connections demonstrated positive correlations for this relationship (Supporting Information Fig. S4). A closer inspection of these data indicates that this set of results closely mirrors the “quadratic” pattern observed in Figure 5: individuals with functional connectivity values closer to zero demonstrate greater variability whereas individuals exhibiting stronger connections (either positive or negative) exhibit lower variability.
Figure 5.
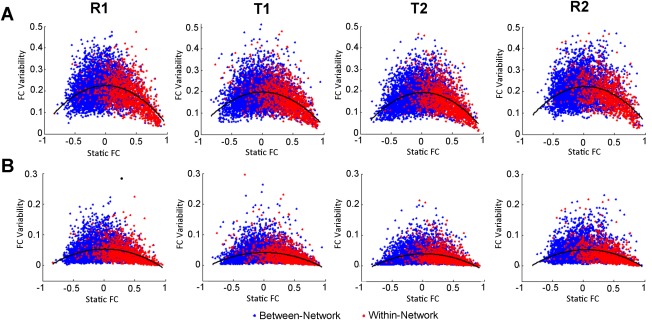
Scatter plots of the relationship of static functional connectivity and connectivity variability for all networks. Variability was measured using the (A) standard deviation (SD) and (B) power of sliding window functional connectivity. FC, functional connectivity. [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com.]
Figure 6.
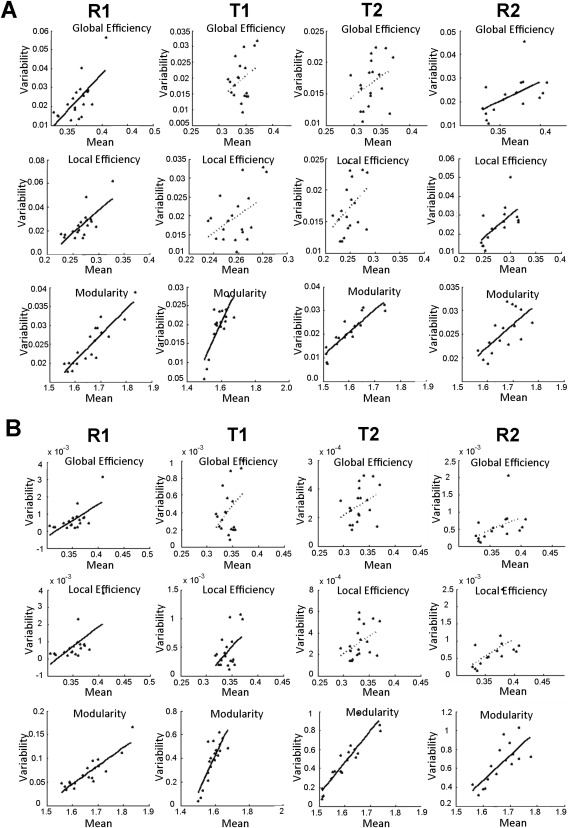
Scatter plots of the relationship between the mean and variability of graph measures. Variability was measured using the (A) standard deviation (SD) and (B) power of sliding window graph measures. Least‐squares fit lines are plotted for both significant (solid lines) and nonsignificant (dashed lines) relationships. Only the 16 subjects with usable data are plotted for R2.
Finally, there was a significant correlation between the amount of task‐induced decrease in variability and task accuracy for both standard deviation (rho=−0.40, P=0.014) and power (rho=−0.38, P=0.020), indicating that more decrease in FCV predicts higher accuracy in task performance. Relationships between task‐related changes in variability and reaction time or reaction time variability were not significant.
DISCUSSION
In this study, we examined the effects of performing an explicit task on FCV within and between six large‐scale neural networks and across the whole system. Our results revealed significantly decreased variability of regional, network, and system‐level functional connectivity measures during task performance, in addition to residual variability that persisted during the task. Furthermore, we observed significant effects of network affiliation on task‐related FCV decreases, significant relationships between static and dynamic functional connectivity measures, as well as significant effects of FCV changes on behavior. These results not only shed light on the mechanisms of FCV but also add to our understanding of the brain's task performance strategies.
Our results demonstrate that the variability of functional connectivity undergoes task‐induced decreases which are measureable at both the network and system levels. Such findings provide new insights beyond previous findings of FCV changes during anesthetized states [Barttfeld et al., 2015; Hutchison et al., 2013b]. Although both anesthesia and task performance are associated with decreased FCV compared with rest, the underlying mechanisms likely differ. Specifically, functional connectivity fluctuations during anesthesia are centered on an anatomical backbone, indicating a lapse into an anatomically defined default state [Barttfeld, et al., 2015; Liegeois, et al., 2014] due to a loss of consciousness. Conversely, because both rest and task performance are conscious states, a task‐related reduction in FCV is likely related to a stabilization of the functional connectivity pattern to a certain task‐specific functional organization (Fig. 2) [Krienen et al., 2014]. Therefore, whereas a reduction in FCV during anesthesia is driven by loss of consciousness, the reduced FCV during task performance is likely associated with increased functional constraints and demands. Theoretically, a reduction in FCV during task may serve to maintain an optimal and more stable brain organization to facilitate continuous performance of a particular task by focusing resources on task‐related neural connections [Corbetta et al., 1990]. This hypothesis is supported by the finding that task‐related reductions in FCV were associated with improved performance of task goals, as indicated by response accuracy (Fig. 7). Therefore, findings from this study complete the other end of the spectrum of FCV changes in which FCV decreases are due to task demands and support behavioral performance.
Figure 7.
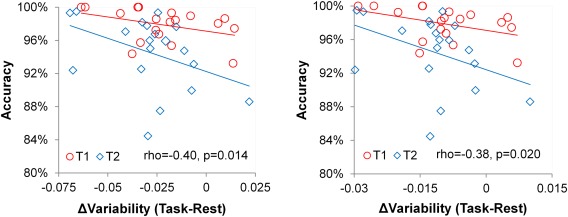
Scatter plots of the relationship between task‐related changes in variability and accuracy for (A) standard deviation and (B) power measures. Spearman partial correlation coefficients controlling for task (T1, T2) and their P‐values are provided. Separate fit lines for each task are shown for visualization purposes. [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com.]
However, despite the task‐related decreases in FCV in this study, there remained a high degree of FCV that persisted during task scans. Consistent with studies of the anesthetized state demonstrating that FCV are not simply a consequence of shifting conscious processes [Barttfeld et al., 2015; Hutchison et al., 2013b], these findings suggest that FCV is at least partly accounted for by ongoing, spontaneous neural activity that is not volitional [Hesselmann et al., 2008; Hutchison et al., 2013b]. Note, however, the remaining FCV observed during task performance in this study most likely also reflects some degree of residual mind wandering and loss of focus [Allen et al., 2014; Christoff et al., 2009; Mason et al., 2007]. Consistent with this hypothesis, the parametric decrease in FCV from rest, to the relaxed‐paced task, to the fast‐paced task, likely reflects a decrease in task‐unrelated thoughts associated with increasing task difficulty [Antrobus, 1966].
Therefore, our findings provide further support for the hypothesis that FCV during rest is partly driven by the predominance of mind wandering during this “uncontrolled” state. At rest, the brain is free to explore a number of configurations, including thought processes related to planning, self‐related thoughts, somatic awareness, and sensory processing [Binder et al., 1999; Diaz et al., 2013]. Thus the enhanced FCV may reflect the increased number of brain states explored [Tagliazucchi et al., 2014] as compared to either the performance of a task or loss of consciousness [Barttfeld et al., 2015]. Furthermore, the resting state may be particularly susceptible to a loss of vigilance relative to a focused task state, which may contribute to the observed variance in functional connections [Tagliazucchi et al., 2012]. Overall, given the significant variability decrease in addition to the residual variability during the task scans, the current data suggest that neither intrinsic biological constraints nor mind wandering fully account for the observed FCV at rest [Keilholz, 2014]. Rather, a parsimonious interpretation is that FCV reflects shifting conscious states that occur above and beyond spontaneous neural activity.
Our findings further encompassed graph theory measures, which provided a system‐level quantification of the efficiency of brain organization and demonstrated that reduced variability transcends local connections. The results revealed that the efficiency and network structure of brain organization become less variable while performing a task compared with rest. Interestingly, our results also show that the mean value of the local/global efficiency and modularity also decrease during task performance. Therefore, the whole brain efficiency and network modularity is higher during rest compared with task, despite the relatively increased variability of functional connections during this state. Consistent with this finding, the positive relationship between the mean and variability of measures of efficiency and modularity indicates that higher efficiency states undergo larger fluctuations (Fig. 6). This relationship implies that frequent brain state changes may enable greater overall efficiency [Zalesky et al., 2014]. Mechanistically, the ability to cycle through various states may enhance overall system‐level efficiency by preventing repetition‐related decreases in neural activity (i.e. due to the depletion of local resources, receptor desensitization, etc.) [Gainetdinov et al., 2004; Grill‐Spector et al., 2006]. Thus, we speculate that the brain may be the most efficient at rest when functional constraints are absent and neural connections are allowed to naturally fluctuate, whereas some efficiency is sacrificed to sustain task‐relevant organizations.
The variability of functional connectivity also decreased as a function of increasing absolute magnitude of static connectivity (Fig. 5). This finding is consistent with the report that stronger connections are associated with greater test‐retest reliability [Shehzad et al., 2009], suggesting that certain neural configurations are more stable than others. The strongest and, per the current data, the most stable connections typically occur between ROIs that are designated as belonging to a common network, consistent with the fact that stability has been a key criterion in defining neural networks [Smith et al., 2009]. This interpretation is also consistent with the finding of the current study that within‐network variability was lower across all scans and demonstrated a lesser task‐related reduction than between‐network variability. Conversely, this relationship also suggests that strong negative connections also demonstrate relatively stable connectivity. Therefore, these findings support the interpretation that neural networks primarily function as a cohesive unit across brain states and are associated with a stable set of anticorrelated regions [Fox et al., 2005]. The findings further indicate that functional connectivity fluctuations may be largely tied to connections that enable communication between networks [Zalesky et al., 2014], corroborating the finding that between‐network interactions are the most dynamic. In fact, there is some evidence that state‐dependent connectivity changes largely occur between large‐scale functional networks [Gao et al., 2013; Spreng et al., 2010; Vincent et al., 2008]. Another extended interpretation of the current results is that the lack of a static functional connectivity relationship between certain regions may be driven by the large variability in their interactions rather than the lack of meaningful interactions, per se.
The current study supports the existence of a neural signature of task engagement characterized by decreased FCV. Given the observed task effects on FCV, our results support extending FCV analyses to task fMRI data, particularly by examining task‐specific changes. Task‐related changes in FCV may exhibit unique, region‐specific profiles depending on the task being performed. Therefore, task‐based FCV analyses may provide extra information regarding brain function to complement conventional activity and connectivity measures [Price et al., 2014]. Another potential extension of task‐related FCV would be to explore FCV changes during a task to examine mechanisms of learning, adaptation, or attentional lapses. Such analyses may improve our understanding of neural functions underlying FCV during task performance and their relationship to various brain disorders and normal behaviors [Hansen et al., 2015].
Due to the unconstrained nature of the resting‐state scan, it is difficult to label the different states occurring during rest and their hypothesized relationship to mind wandering. Reverse inferences based on neural connectivity patterns [Shirer et al., 2012], EEG data [Tagliazucchi et al., 2012], or subject feedback [Christoff et al., 2009] throughout the scan may further help to characterize the sources of variability in functional connectivity. Furthermore, a direct assessment of the degree of mind wandering in each of the scans would provide a clearer link between this variable and FCV. Even though subjects claimed to remain awake during the scans, it is still possible that some variability observed during the resting state is related to subjects failing to remain alert or falling asleep [Tagliazucchi and Laufs, 2014]. Additionally, the current study considered only one continuous task performed at two different speeds. Future studies focusing on other task domains or manipulating other experimental parameters will aid in further understanding of task‐related changes in FCV. Moreover, similar analyses comparing datasets employing constrained cognitive processes in the absence of external stimuli [Krienen et al., 2014; Shirer et al., 2012] to an unconstrained resting state may provide further support for the current findings.
CONCLUSIONS
Variability in functional connectivity and system‐level organization was reduced but not eliminated by the performance of a task relative to rest. The study findings support the hypothesis that FCV is partly underpinned by the wandering of the mind, which likely occurs on top of intrinsic, physiologically driven fluctuations. The task relevance of FCV thus opens a new opportunity to probe neural functioning and explore the neural correlates of psychopathology.
Supporting information
Supporting Information
Conflict of interest: The authors declare no conflicts of interest related to this work.
REFERENCES
- Allen EA, Damaraju E, Plis SM, Erhardt EB, Eichele T, Calhoun VD (2014): Tracking Whole‐brain connectivity dynamics in the resting state. Cereb Cortex 24:663–676. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Antrobus JS (1966): Studies in the stream of consciousness: Experimental enhancement and suppression of spontaneous cognitive processes. Percept Motor Skills 23:399. [Google Scholar]
- Barttfeld, P , Uhrig, L , Sitt, J.D , Sigman, M , Jarraya, B , Dehaene, S (2015) Signature of consciousness in the dynamics of resting‐state brain activity. Proc Natl Acad Sci USA 112:887–892. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Binder JR, Frost JA, Hammeke TA, Bellgowan PSF, Rao SM, Cox RW (1999): Conceptual processing during the conscious resting state: A functional MRI study. J Cogn Neurosci 11:80–93. [DOI] [PubMed] [Google Scholar]
- Biswal B, Yetkin FZ, Haughton VM, Hyde JS (1995): Functional connectivity in the motor cortex of resting human brain using echo‐planar MRI. Magn Reson Med 34:537−541. [DOI] [PubMed] [Google Scholar]
- Bluhm RL, Clark CR, McFarlane AC, Moores KA, Shaw ME, Lanius RA (2011): Default network connectivity during a working memory task. Hum Brain Mapp 32:1029−1035. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chang C, Glover GH (2010): Time‐frequency dynamics of resting‐state brain connectivity measured with fMRI. Neuroimage 50:81–98. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Christoff K, Gordon AM, Smallwood J, Smith R, Schooler JW (2009): Experience sampling during fMRI reveals default network and executive system contributions to mind wandering. Proc Natl Acad Sci USA 106:8719–8724. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Corbetta M, Miezin FM, Dobmeyer S, Shulman GL, Petersen SE (1990): Attentional modulation of neural processing of shape, color, and velocity in humans. Science 248:1556–9. [DOI] [PubMed] [Google Scholar]
- Damaraju E, Allen EA, Belger A, Ford JM, McEwen S, Mathalon DH, Mueller BA, Pearlson GD, Potkin SG, Preda A, Turner JA, Vaidya JG, van Erp TG, Calhoun VD (2014): Dynamic functional connectivity analysis reveals transient states of dysconnectivity in schizophrenia. NeuroImage: Clin 5:298–308. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Diaz BA, Van Der Sluis S, Moens S, Benjamins JS, Migliorati F, Stoffers D, Den Braber A, Poil SS, Hardstone R, Van't Ent D, Boomsma DI, De Geus E, Mansvelder HD, Van Someren EJW, Linkenkaer‐Hansen K (2013): The amsterdam Resting‐state questionnaire reveals multiple phenotypes of resting‐state cognition. Front Hum Neurosci 7:446 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Elton A, Gao W (2014): Divergent task‐dependent functional connectivity of executive control and salience networks. Cortex 51:56–66. [DOI] [PubMed] [Google Scholar]
- Fornito A, Harrison BJ, Zalesky A, Simons JS (2012): Competitive and cooperative dynamics of large‐scale brain functional networks supporting recollection. Proc Natl Acad Sci USA 109:12788−12793. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fox MD, Snyder AZ, Vincent JL, Corbetta M, Van Essen DC, Raichle ME (2005): The human brain is intrinsically organized into dynamic, anticorrelated functional networks. Proc Natl Acad Sci USA 102:9673–9678. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gainetdinov RR, Premont RT, Bohn LM, Lefkowitz RJ, Caron MG (2004): Desensitization of G protein‐coupled receptors and neuronal functions. Annu Rev Neurosci 27:107–144. [DOI] [PubMed] [Google Scholar]
- Gao W, Lin W (2012): Frontal parietal control network regulates the anti‐correlated default and dorsal attention networks. Hum Brain Mapp 33:192–202. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gao W, Gilmore JH, Alcauter S, Lin W (2013): The dynamic reorganization of the default‐mode network during a visual classification task. Front Syst Neurosci 7:34 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grill‐Spector K, Henson R, Martin A (2006): Repetition and the brain: Neural models of stimulus‐specific effects. Trends Cogn Sci 10:14–23. [DOI] [PubMed] [Google Scholar]
- Hansen EC, Battaglia D, Spiegler A, Deco G, Jirsa VK (2015): Functional connectivity dynamics: Modeling the switching behavior of the resting state. Neuroimage 105:525−535. [DOI] [PubMed] [Google Scholar]
- Hesselmann G, Kell CA, Eger E, Kleinschmidt A (2008): Spontaneous local variations in ongoing neural activity bias perceptual decisions. Proc Natl Acad Sci USA 105:10984–10989. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hutchison RM, Womelsdorf T, Allen EA, Bandettini PA, Calhoun VD, Corbetta M, Della Penna S, Duyn JH, Glover GH, Gonzalez‐Castillo J, Handwerker DA, Keilholz S, Kiviniemi V, Leopold DA, de Pasquale F, Sporns O, Walter M, Chang C (2013a): Dynamic functional connectivity: promise, issues, and interpretations. NeuroImage 80:360–378. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hutchison RM, Womelsdorf T, Gati JS, Everling S, Menon RS (2013b): Resting‐state networks show dynamic functional connectivity in awake humans and anesthetized macaques. Hum Brain Mapp 34:2154–2177. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Keilholz SD (2014): The neural basis of time‐varying resting‐state functional connectivity. Brain Connect 4:769–779. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Krienen FM, Yeo BTT, Buckner RL (2014): Reconfigurable task‐dependent functional coupling modes cluster around a core functional architecture. Philos Trans R Soc B: Biol Sci 369:20130526 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kucyi A, Davis KD (2014): Dynamic functional connectivity of the default mode network tracks daydreaming. Neuroimage 100:471−480. [DOI] [PubMed] [Google Scholar]
- Liegeois, R , Ziegler, E , Geurts, P , Gomez, F , Bahri, M.A , Phillips, C , Soddu, A , Vanhaudenhuyse, A , Laureys, S , Sepulchre, R. (2014) Cerebral functional connectivity periodically (de) synchronizes with anatomical constraints. arXiv preprint arXiv:1409.5672. [DOI] [PubMed]
- Llinás R, Sugimori M (1980): Electrophysiological properties of in vitro purkinje cell somata in mammalian cerebellar slices. J Physiol 305:171–195. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mason MF, Norton MI, Van Horn JD, Wegner DM, Grafton ST, Macrae CN (2007): Wandering minds: the default network and stimulus‐independent thought. Science 315:393−395. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Perkel DH, Gerstein GL, Moore GP (1967): Neuronal spike trains and stochastic point processes: I. The single spike train. Biophys J 7:391–418. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Power JD, Barnes KA, Snyder AZ, Schlaggar BL, Petersen SE (2012): Spurious but systematic correlations in functional connectivity MRI networks arise from subject motion. NeuroImage 59:2142–2154. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Price T, Wee C.‐Y, Gao W, Shen D. (2014) Multiple‐network classification of childhood autism using functional connectivity dynamics In: Golland P, Hata N, Barillot C, Hornegger J, Howe R, editors. Medical Image Computing and Computer‐Assisted Intervention – MICCAI 2014. Springer International Publishing Switzerland. p 177–184. [DOI] [PubMed]
- Raman IM, Gustafson AE, Padgett D (2000): Ionic currents and spontaneous firing in neurons isolated from the cerebellar nuclei. J Neurosci 20:9004–9016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rashid B, Damaraju E, Pearlson GD, Calhoun VD (2014): Dynamic connectivity states estimated from resting fMRI identify differences among schizophrenia, bipolar disorder, and healthy control subjects. Front Hum Neurosci, 8:897 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rubinov M, Sporns O (2010): Complex network measures of brain connectivity: Uses and interpretations. NeuroImage 52:1059–1069. [DOI] [PubMed] [Google Scholar]
- Seeley WW, Menon V, Schatzberg AF, Keller J, Glover GH, Kenna H, Reiss AL, Greicius MD (2007): Dissociable intrinsic connectivity networks for salience processing and executive control. J Neurosci 27:2349−2356. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shehzad Z, Kelly AMC, Reiss PT, Gee DG, Gotimer K, Uddin LQ, Lee SH, Margulies DS, Roy AK, Biswal BB, Petkova E, Castellanos FX, Milham MP (2009): The resting brain: Unconstrained yet reliable. Cereb Cortex 19:2209–2229. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shirer WR, Ryali S, Rykhlevskaia E, Menon V, Greicius MD (2012): Decoding Subject‐driven cognitive states with Whole‐brain connectivity patterns. Cereb Cortex 22:158–165. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith SM, Fox PT, Miller KL, Glahn DC, Fox PM, Mackay CE, Filippini N, Watkins KE, Toro R, Laird AR, Beckmann CF (2009): Correspondence of the brain's functional architecture during activation and rest. Proc Natl Acad Sci USA 106:13040−13045. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Spreng RN, Stevens WD, Chamberlain JP, Gilmore AW, Schacter DL (2010): Default network activity, coupled with the frontoparietal control network, supports goal‐directed cognition. Neuroimage 53:303−317. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tagliazucchi E, Laufs H (2014): Decoding wakefulness levels from typical fMRI Resting‐state data reveals reliable drifts between wakefulness and sleep. Neuron 82:695–708. [DOI] [PubMed] [Google Scholar]
- Tagliazucchi E, Carhart‐Harris R, Leech R, Nutt D, Chialvo DR (2014): Enhanced repertoire of brain dynamical states during the psychedelic experience. Hum Brain Mapp 35:5442–5456. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tagliazucchi E, Von Wegner F, Morzelewski A, Brodbeck V, Laufs H (2012): Dynamic BOLD functional connectivity in humans and its electrophysiological correlates. Front Hum Neurosci 6:339 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vincent JL, Kahn I, Snyder AZ, Raichle ME, Buckner RL (2008): Evidence for a frontoparietal control system revealed by intrinsic functional connectivity. J Neurophysiol 100:3328–3342. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zalesky A, Fornito A, Cocchi L, Gollo LL, Breakspear M (2014): Time‐resolved resting‐state brain networks. Proc Natl Acad Sci USA 111:10341−10346. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supporting Information


