Frontal and parietal contributions to arithmetic fact retrieval: A parametric analysis of the problem‐size effect

Abstract

The goal of the present study was to investigate the neuroanatomical basis of arithmetic fact retrieval. The rationale was that areas playing a crucial role in arithmetic fact retrieval should show a systematic increase of activation with increasing retrieval effort. To achieve this goal, we utilized the problem‐size effect as this is known to be systematically related to retrieval effort. In contrast to many previous studies, we here took a parametric approach to account for the continuous increase of retrieval effort with problem size. BOLD signals were modeled with problem size as parametric regressor and negative slow waves of the EEG were categorized into six levels of problem size. The fMRI data showed that activation in the angular gyrus and ACC/SMA increased parametrically with problem size. The ERP data showed a systematic amplitude increase with increasing problem size, especially at fronto‐central electrodes. Consistent with the fMRI data, source modeling localized this effect to the ACC. While these findings support previous notions about the crucial role of the angular gyrus during fact retrieval, they also provide evidence that the medial frontal cortex is involved when single‐digit multiplications are solved. Thus, both parietal and frontal structures seem to be integral parts of a system that enables and controls arithmetic fact retrieval. Hum Brain Mapp, 2010. © 2010 Wiley‐Liss, Inc.

INTRODUCTION

Single‐digit multiplication problems are mainly solved by directly retrieving a solution from memory. It is commonly assumed that the underlying representation is a network structure in which problems and solutions are associated [for review, see Ashcraft, 1992; Domahs and Delazer, 2005; or the introduction of Verguts and Fias 2005]. While the characteristics of this network structure have been the topic of numerous behavioral and simulation studies [see e.g., Campbell, 1987; Campbell and Oliphant, 1992], the neural basis of the memory representation is still not completely understood. Several neuroimaging studies on mental calculation and number processing reported the activation of a network involving frontal and parietal structures [e.g., Gruber et al., 2001; Menon et al., 2000b; Rickard et al., 2000; Rueckert et al., 1996]. Whereas activation in the frontal cortex has been attributed mainly to working memory and attentional control demands during calculation, the activation of parietal areas seem to be directly associated with number‐related processes. Within the parietal cortex, it has been suggested that three distinct circuits mediate specific subcomponents of number processing [Dehaene et al., 2003]. The left angular gyrus has been considered responsible for arithmetic fact retrieval. However, its contribution has been questioned by some authors [e.g., Zago et al., 2001]. In the present study, we will use the so‐called problem‐size effect and its neural correlates as a tool to gain more insight into the neural basis of arithmetic fact retrieval.

Error rates and response times (RT) increase with increasing size of the operands of single‐digit arithmetic problems [see e.g., Campbell and Graham, 1985; Stazyk et al., 1982]. This problem‐size effect is well replicated in almost all studies on mental arithmetic and can be found with all four basic arithmetic operations [e.g., Ashcraft and Battaglia, 1978; Campbell and Graham, 1985; LeFevre and Morris, 1999; Seyler et al., 2003]. For multiplication problems the problem‐size effect has been ascribed mainly to the special network structure of the underlying memory representations, which makes the retrieval of larger problems' solutions less efficient.

Several explanations of the problem‐size effect have been proposed within the network account, such as problem frequency, which leads to stronger connections between operand and answer nodes for frequent problems [Ashcraft, 1987], or retrieval interference. According to the network interference model [Campbell, 1995, for an earlier version, see Campbell and Oliphant, 1992], a problem is not only associated with its correct answer, but also with incorrect answers that share features with the correct one (i.e., being a multiple of the same number, numerical size). For instance, the problem 6 × 4 not only activates the node of the correct solution 24, but also nodes representing the numbers 18, 20, 28, and 30, which are all multiples of the problem's operands. Accordingly, the retrieval process is affected by interference from incorrect solutions. Campbell further assumes that a magnitude code is activated during the retrieval process, which approximates the size of the answer. This code is specified as a logarithmic function of the number size, such that large magnitude codes activate more numbers. The problem‐size effect arises because problems with larger numbers activate more neighbors than problems with smaller numbers (i.e., because of the logarithmically compressed number line), which, in turn, results in more interference. Verguts and Fias [ 2005] stressed another aspect of the network structure, i.e., neighborhood consistency. Their “interacting‐neighbors” model assumes that retrieval efficiency depends on decade and unit consistency, i.e., whether the correct product and related incorrect answers activate the same decade or unit position. Products that are highly consistent with neighboring answers can be retrieved faster and more accurately than less consistent products. Accordingly, the problem‐size effect emerges because products of small problems tend to be more consistent with their neighboring answers regarding decades than products of large problems. For instance, the problem 6 × 4 = 24 has two decade‐consistent neighbors (5 × 4 = 20, 7 × 4 = 28) and two decade‐inconsistent neighbors (6 × 3 = 18, 6 × 5 = 30), whereas the problem 8 × 7 = 56 has only inconsistent neighbors (8 × 6 = 48, 8 × 8 = 64, 7 × 7 = 49, 9 × 7 = 63). Simulations have shown that the described network structure and the concept of neighborhood consistency can indeed explain the problem‐size effect [Verguts and Fias, 2005, for behavioral and ERP evidence see Domahs et al., 2007]. To conclude, the reported evidence shows that the problem‐size effect reflects the increasing effort of retrieving multiplication solutions from a network structure when problems become larger. Here we made use of this effect to investigate which brain areas are involved in arithmetic fact retrieval. The rational is that areas playing a crucial role in arithmetic fact retrieval should show a systematic increase of activation with increasing retrieval effort and hence with problem size.

In contrast to many previous studies we took a parametric approach. The reason is that retrieval difficulty seems to increase gradually. Systematic investigations have revealed that response times increase monotonically with problem size [e.g., Ashcraft and Battaglia, 1978; Campbell, 1994; LeFevre and Morris, 1999]. For instance, problems of the two‐operand family are solved faster than those of the three‐operand family, which, in turn, are solved faster than problems of the four‐operand family etc. (with the exception of problems of the five‐operand family, which are solved faster than predicted on the basis of their size). Despite this gradual increase, the typical way to investigate the effects of problem size is to classify the problem set (single‐digit problems) into two groups including small or easy and large or difficult problems. An often‐used cut‐off point is at a product size of 25 [see e.g., Campbell, 1999], as this leads to two groups of equal numbers of problems (when problems with 1 or 0, as well as ties, are excluded). Although a simple categorization proved to be helpful to dissociate small and large problems on behavioral and neurophysiological levels [see e.g., Jost et al., 2004, 2009; Kiefer and Dehaene, 1997; Zhou et al., 2007], it bears the risk of disregarding relevant features of numbers and arithmetic problems. As described above, not all problems of a group are equal in difficulty. It can be assumed that there is a monotonic increase of RTs with problem size even within a category, suggesting that neighborhood consistency and interference also differ for the problems within a category. Strictly speaking, a categorical analysis of problem size is not appropriate, because it disregards a substantial portion of the systematic variation in the relevant dimension “problem size” and considers this variation as measurement error, even though the variation within a category might be as large as the variation between the categories. Therefore, we reanalyzed brain signals evoked by single‐digit multiplications in a parametric way. This parametric analysis accounts for the systematic increase in problem size and should capture arithmetic fact retrieval in a more appropriate way. Theoretically, a categorical analysis of multiplication problems, i.e., contrasting problems with small and large operands, could bias the evidence for involved brain areas. Here, we analyze data of two experiments—an ERP and an fMRI study—to delineate the parametric activation increase with problem size for two independent datasets with two different methods. In addition, we validated the corresponding findings from the two datasets by means of source estimations of the parametric ERP effect.

In the present study, we are primarily interested in the involvement of parietal and frontal brain areas. These areas have been most commonly found to be activated during arithmetic processing, although results are somewhat inconsistent. In our previous fMRI study, in which participants had to (silently) produce the solution of single‐digit multiplication problems, we observed, in accordance with other studies, that simple fact retrieval activates the angular gyrus and also regions in the cerebellum and subcortical structures [see Jost et al., 2009]. According to the triple‐code model, the angular gyrus is part of a system that mediates verbal aspects of arithmetic fact retrieval [Dehaene et al., 2003]. However, inconsistent with this notion, several studies did not support an involvement of the angular gyrus [e.g., Dehaene et al., 1996; Pesenti et al., 2000]. We hope to shed more light on this issue. Regarding frontal areas, a number of studies found activations, but ascribed these to working‐memory demands and strategy selection rather than to fact retrieval per se. One reason for this interpretation is that rather complex problems had to be solved in these studies. Accordingly, frontal activations were attributed to control processes and general task difficulty [see e.g., Delazer et al., 2003; Gruber et al., 2001; Rueckert et al., 1996; Zago et al., 2001]. With the present analysis, however, we show that at least some of the activations in frontal structures seem to be closely related to the demands imposed by fact retrieval.

MATERIALS AND METHODS

Participants

For this article the datasets of two experiments, an ERP study [Jost et al., 2004] and an fMRI study [Jost et al., 2009], have been reanalyzed. Participants took part either in one or the other study. They were all right‐handed, native speakers of German, had normal or corrected‐to‐normal vision, and had no history of neurological illness. The ERP dataset consisted of 18 participants (mean age 23 years, nine female) and the fMRI dataset consisted of 16 participants (mean age 24.5 years, 10 female).

Stimuli, Task, and Procedure

In both studies participants solved single‐digit multiplications in a modified production task. Ties as well as operations with 1 were excluded. Thus, the dataset comprised 56 different multiplication problems with operands ranging from two to nine (i.e., problems ranging from 2 × 3 to 9 × 8) and 16 different problems with zero as an operand. Note that in these studies we were interested in distinct solution processes (i.e., rule application versus fact retrieval) and their neurophysiological and neuroanatomical correlates, whereas here we are interested solely in fact retrieval. Zero problems, therefore, which are assumed to be solved by rule application (e.g., n × 0 = 0), are not in the focus of the present study and were excluded from the analysis.

Multiplication problems were embedded in a chain‐calculation task: Participants were asked to silently produce the solution of the multiplication problem and use it for the next operation, i.e., a simple addition or subtraction. At the end of the sequence a final result was presented that had to be verified (e.g., “4 × 7 + 3 = 30”, for the complete sequence). The multiplication equation was presented for 500 ms and participants had sufficient time to produce the solution, i.e., 3.3 s in the ERP study and 4 s in the fMRI study. The stimulus sequence continued with the presentation of the additional operation (for 600 ms), followed by a 200‐ms blank screen and the final result [for details about stimulus presentation and timing, see Jost et al., 2004, 2009]. This procedure has the advantage that participants produce the solution without any overt response, which prevents movement artifacts that often arise when the solution has to be named. Moreover, the chain calculation guarantees that participants really produced the solution, because otherwise they could not continue with the next step.

Problems were presented interspersed with a baseline condition (about 50% of the trials) in which the operands of the multiplication problem only had to be stored. This condition was not analyzed in the present study.

ERP‐Data Acquisition and Analysis

The EEG was recorded with 61 Ag/AgCl electrodes referenced to the nose tip. The horizontal and vertical EOG was monitored with appropriate electrode pairs. The left mastoid served as ground. Impedances were kept below 7 kΩ. Signals were sampled with two 32‐channel amplifiers (SYNAMPS, NeuroScan) at 200 Hz and filtered with a band‐pass filter (DC to 40 Hz). Drift artifacts were corrected by a regression method [Hennighausen et al., 1993]. Eye blinks were detected by means of cross‐correlation with a template and corrected using linear interpolation. The EEG was segmented into epochs that covered the production phase, i.e., starting with the presentation of the multiplication problem and ending with the onset of the additional operation. A 100‐ms time epoch before the onset of the first operand was taken for baseline correction, because the operands were presented sequentially.

In the original study by Jost et al. [ 2004] negative slow waves measured in the production phase were sensitive to the difficulty of an arithmetic problem as well as to the used solution process (fact retrieval versus rule application). Negative slow waves are tonic deflections in the EEG that last for at least a couple of hundred milliseconds and have two important features: Their amplitudes increase with task‐difficulty or mental load and their topography is material‐ and task‐specific [see Rösler et al., 1997]. In our previous study, the analysis of problem size was integrated in a comparison of different problem types (assumed to be solved by distinct solution processes) and was run in a categorical way [see Jost et al., 2004]. When comparing problems with small and large operands, we observed both amplitude and topographical differences. Here, we will extend these findings on problem size by running a parametric analysis. This was achieved by extracting six levels of problem size based on the size of the product, i.e., products <13, 14–18, 20–25, 27–32, 35–45, and >45. With this categorization, the numbers of problems are similar across the levels (i.e., 8 or 10 different problems per level); commutative pairs of problems (e.g., 2 × 5 and 5 × 2) belong to the same level, as well as do problems with the same product size (e.g., 3 × 4 and 2 × 6). Only trials with correct responses were used for the averages. All in all, participants solved 392 multiplication problems (7 × 56), providing a sufficient number of trials for this kind of analysis. ERPs for each level of problem size are based on at least 33 trials (57 trials on average).

The statistics (repeated measurement ANOVAs) was done with 17 standard electrodes uniformly distributed over the scalp (i.e., FPz, F7, F3, Fz, F4, F8, T3, C3, Cz, C4, T4, T5, P3, Pz, P4, T6, and Oz) and for 200‐ms‐time windows covering the negative slow wave (i.e., starting 900 ms after the onset of the production phase).

FMRI‐Data Acquisition and Analysis

Functional imaging was performed with a 1.5 T scanner equipped with a quadrature head coil. Functional images were acquired with a T2*‐weighted EPI sequence (TR = 2 s, TE = 60 ms, flip angle = 80°). In each volume, 19 horizontal slices (5 mm slice thickness, 0.5 mm inter‐slice gap) were scanned in ascending order (FOV: 240 mm × 240 mm, acquisition matrix: 64 × 64, in‐plane resolution: 3.75 mm × 3.75 mm). Preprocessing and statistical analyses were performed with SPM2 [for details see Jost et al., 2009]. Preprocessed data were normalized to the MNI template and spatially smoothed with an isotropic gaussian kernel (FWHM = 6 mm).

The BOLD responses for multiplications with operands from two to nine were modeled with a single parametric regressor [instead of two separate dummy predictors for small and large problems as in the previous study by Jost et al., 2009] based on the product size of each problem. Zero multiplications and storage trials were modeled with two separate predictors. These three regressors marked the onset of the production phase. The second phase (containing additional operation and verification) was modeled with a single predictor. To delineate areas that show a parametric signal increase with problem size, a random‐effects analysis was computed for the main effect of the parametric regressor. Initial threshold was set to P < 0.0001 (uncorrected). Only clusters with a minimum of 15 voxels are reported.

The parametric analyses we have run here for the BOLD signal and the ERPs are different methodological approaches to capture increasing brain activation with increasing problem size. The relatively large number of trials in the EEG part allowed computing an average ERP for each of six distinct bins (levels of problem size). These six bins cover adequately the full range of problem size. At the same time the signal‐to‐noise ratio of each average ERP is large. In contrast to the ERP study, in the fMRI study participants solved only 56 different multiplication problems. This number is too small to analyze the fMRI data in the very same manner as the ERP data. Therefore, we decided to use a single parametric regressor based on product size. This optimally models the increase of the hemodynamic response and handles in an elegant way a dataset with trial frequencies that are too small for defining a larger number of bins. Thus, the methods are both optimally adapted to the specific signal types and the number of trials in the two study parts.

RESULTS

ERP Data

Figure 1 shows the ERPs during the production phase at four midline electrodes. The negative slow wave starts around 1,000 ms, following the parietal P3, and stays until the end of the production phase. Its amplitude is sensitive for problem size, with more negative potentials for large‐number than for small‐number problems. To test for this increase, we calculated ANOVAs with the factors problem size (6 levels) and electrode (17 levels) separately for 200‐ms time windows starting 900 ms after the onset of the production phase. The most pronounced effects were observed between 1,100 and 1,900 ms, with significant main effects of product size, minF(5, 85) = 3.81, P = 0.004, ε = 0.99; maxF(5, 85) = 4.16, P = 0.002, ε = 0.99 [the terms minF and maxF refer to the smallest and largest F‐values of the reported time interval; ε according to Huynh and Feldt, 1976]. Later, from 1,900 to 3,100 ms, the effects are generally smaller and in some time windows only marginally significant, minF(5, 85) = 2.22, P = 0.071, ε = 0.85; maxF(5, 85) = 2.83, P = 0.028, ε = 0.85. On the basis of this superordinate analysis, we defined the time window between 1,100 and 1,900 ms as critical time window, on which all further analyses are based. Moreover, this time window corresponds to the window of maximum effect size in our previous analysis of this dataset [Jost et al., 2004].

Figure 1.

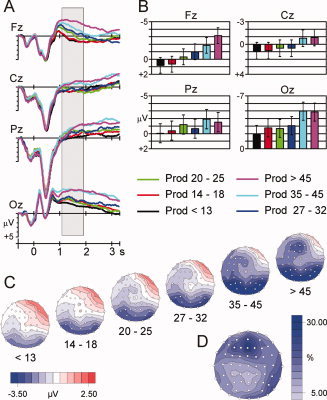
A. ERPs for the production phase at four midline electrodes. Shown are curves for six levels of problem size. The production phase starts at time point 0. Negativity is plotted upwards. B. Bar plots showing amplitude increase with problem size. The values are extracted from the time window from 1,100 to 1,900 ms (i.e., the shaded area in A), which proved to be most sensitive for problem size. A strict monotonic increase was found at electrode Fz. C. Topographic maps (derived from 61 electrodes) for the six levels of problem size in the critical time window, showing a shift of the negative maximum (blue) from posterior to frontal electrodes with increasing problem size. D. Map displaying for each electrode the percentage of variance explained by the linear trend of the variable problem size, i.e., SS_linear/SS_total. The largest percentage of explained variance was found at Fz.

The amplitude increase with problem size is widely distributed, but most pronounced over frontal sites, especially at electrode Fz. The bar graphs in Figure 1B, showing mean voltage values from the critical time window, illustrate this: The amplitude at Fz increases systematically with problem size, whereas the increase is less systematic at posterior electrodes. To substantiate this increase we ran ANOVAs and tested which trend described the main effect of problem size best. Amplitude increases with problem size should be captured by a linear trend, while polynomial trends of higher order should not reach significance. That is exactly what we found: Electrode‐wise ANOVAs disclosed that the amplitude increase followed a linear trend at all analyzed electrodes, with F(5, 85) values ranging from 6.50 (P = 0.002) to 39.37 (P < 0.001). Higher order polynomial trends were not significant.

The topographic map in Figure 1D displays the percentage of variance that is explained by the linear trend, i.e., SS_linear/SS_total. As can be seen, the contribution of the linear trend is largest at Fz. Another maximum can be seen at right temporal electrodes. This strong increase especially at frontal electrodes appears as a redistribution of the negative slow wave toward frontal sites (see the topographic maps from left to right in Fig. 1C).

FMRI Data

The analysis of the fMRI data revealed a parametric signal increase with problem size in a distributed network consisting of frontal, parietal, and subcortical areas (see Table I and Fig. 2). This pattern fits with the activations observed with the categorical analysis of problem‐size effects [Jost et al., 2009], but extends these findings, because here the increase with problem size proved to be parametric. In the parietal cortex, the left angular gyrus showed a parametric increase. The locus of this activation nicely corresponds to findings from a metaanalysis by Dehaene et al. [ 2003], in which activation for fact retrieval was localized to the angular gyrus with coordinates x = −41 (SD = 9), y = −66 (SD = 6), and z = 36 (SD = 4).

Table I.

Peak location, number of voxels, and maximum t value of activations found with the parametric analysis of the fMRI data

No.	Brain region	Peak location			Voxels	t
		x	y	z
1	Left precentral, postcentral, and inferior frontal gyrus	−36	−6	39	334	12.13
2	Left SMA, anterior and middle cingulate cortex extending to right SMA	−3	6	54	547	10.53
3	Left thalamus and basal ganglia extending to right homologues	−6	−21	−3	324	10.46
4	Left angular gyrus extending to middle and superior occipital gyrus	−45	−63	39	305	9.18
5	Right inferior frontal gyrus (orbital part) and insula	36	24	−12	52	8.50
6	Right angular gyrus extending to middle occipital gyrus	42	−57	39	33	6.73
7	Left cerebelum	−12	−84	−18	15	6.65
8	Left inferior frontal gyrus (orbital part) and insula	−30	27	−9	45	6.30

Initial threshold: P < 0.0001, uncorrected. Reported are only clusters with an extent of at least 15 voxels. Peak location indicates the coordinates in MNI space where the maximum t value of the cluster was observed. T values in bold are also significant with P < 0.05 FWE‐corrected. Labeling of activated regions is based on the AAL (automatic anatomical labeling) atlas (Tzourio‐Mazoyer et al., 2002).

Figure 2.

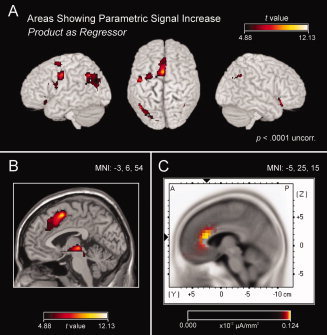
A,B. Brain areas showing a parametric signal increase with problem size. Pronounced activations were found in the left precentral, inferior frontal, and angular gyrus (see A), as well as in the anterior and middle cingulate cortex and the SMA (see B). C. Distributed source‐density maps (LORETA) for the amplitude increase observed in the slow negative wave of the ERP. The figure displays the average of five LORETA maps, i.e., maps for the amplitude increases from problem‐size levels 1 to 2, 2 to 3, 3 to 4, 4 to 5, and 5 to 6, respectively. The strongest source strength was obtained in the ACC. This pattern fits with the ACC/SMA activation observed in the fMRI data (see B).

Note, that with the present dataset differences are characterized by increasing activation [for details see the event‐related BOLD‐signal plots in Fig. 3B of Jost et al., 2009] rather than by decreasing deactivations as reported in other studies especially for the angular gyrus [see e.g., Ischebeck et al., 2006]. Accordingly, all the mentioned parametric effects represent increasing activation with increasing problem size.

The most pronounced parametric signal increase was found in the frontal cortex. There, activation in the left inferior frontal and precentral gyrus (see Fig. 2A), as well as in the medial frontal cortex (see Fig. 2B), significantly correlated with problem size. This finding strongly corresponds with the parametric increase found for the ERP data, where the frontal electrode Fz showed the most pronounced effect.

To further substantiate the corresponding findings of the two methods, we tested whether the parametric increase of EEG slow‐potential amplitudes could be the result of a parametric neural activation in those areas that have been found with fMRI. Therefore, we used the sLORETA software (standardized low resolution brain electromagnetic tomography; KEY Institute for Brain‐Mind Research, University Hospital of Psychiatry, Zurich, Switzerland) and estimated sources of the parametric slow‐wave effect. We computed five LORETA images for difference potentials representing the increase from one level of problem size to the next higher level (i.e., from level 1 to level 2, level 2 to level 3, etc.). Data points for this analysis were obtained from the critical time window (see above). To obtain a source estimation of those brain areas that are generally relevant for increases of slow‐wave amplitude with increasing problem size, we integrated the information of the five LORETA maps by averaging. The resulting map (see Fig. 2C) shows that the strongest source strength was localized to the ACC.

DISCUSSION

We analyzed ERP and fMRI data on single‐digit multiplications regarding a parametric activation increase with problem size, with the objective to determine the neural basis of arithmetic fact retrieval. Most of the previous studies investigated problem‐size effects by comparing two categories (i.e., small versus large problems) instead of treating problem size as a continuum. Detailed analyses of behavioral data, however, indicated that RT increases monotonically. Accordingly, a parametric approach is more adequate to account for the underlying network structure.

The parametric analysis of the ERP data revealed an increase of the amplitude of a negative slow wave with increasing problem size. This increase was present at almost all electrodes, but most pronounced at electrode Fz. Source localization indicated that this effect is most probably generated in the ACC. The fMRI data support this finding: A parametric increase was found in a cluster covering parts of the ACC and the SMA, though this was not the only activation. Further activations were observed in parietal, subcortical, and frontal structures. Overall, the parametric data highly correspond to the findings obtained with the categorical analysis of problem size [Jost et al., 2004, 2009], but extends these, because it shows that the activation increase found with problem size is parametric at some particular electrodes and brain areas. This finding is of interest for theories on mental calculation in general and fact retrieval in particular.

Multiplication facts are assumed to be stored in a verbal format. It has been proposed that the fact‐retrieval process is mediated by a verbal processing loop involving left‐hemispheric language areas, the thalamus, and the basal ganglia [see Dehaene and Cohen, 1995]. In recent years a central role for the verbal aspects of fact retrieval has been ascribed to the angular gyrus [see Dehaene et al., 2003], because several studies reported left angular gyrus activation for simple multiplication problems when compared with other operations or control tasks such as number comparison [see e.g., Chochon et al., 1999; Delazer et al., 2003; Gruber et al., 2001; Lee, 2000; Stanescu‐Cosson et al., 2000]. By referring to studies that found angular gyrus activation in other types of language‐mediated processes, Dehaene et al. [ 2003] suggested that the angular gyrus is part of a language system which mediates fact retrieval by phonological processing. Also in the study of Jost et al. [ 2009], the angular gyrus, together with regions in the cerebellum and subcortical structures, including the thalamus and the basal ganglia, was more activated for fact‐retrieval problems (small multiplications) than for a high‐level control condition not involving any kind of calculation. This pattern supports the notion that arithmetic fact retrieval is mediated by a cortico‐subcortical loop and that verbal processing plays a crucial role. The finding of a parametric increase in a large number of these areas including the angular gyrus suggests that the effort within the fact‐retrieval system increases systematically with problem size.

Our findings regarding the involvement of the angular gyrus in arithmetic fact retrieval are in accordance with a cortical stimulation study reporting a selective impairment of multiplication‐fact retrieval when the anterior parietal cortex (apparently close to the angular gyrus) was stimulated [Whalen et al., 1997]. Corresponding findings are also reported by Menon et al. [ 2000a]. They found decreasing activation in the angular gyrus with increasing expertise: During calculation, perfect performers showed smaller activation in the angular gyrus than less skilled performers, presumably because of their higher automaticity in retrieving arithmetic facts. Moreover, a recent study by Grabner et al. [ 2009] provided direct evidence by means of self‐reported use of fact retrieval during arithmetic problem solving that the left angular gyrus mediates the retrieval of arithmetic facts. Taken together, the evidence from our and previous studies shows that the activation in the angular gyrus varies with the involvement of search processes in associative arithmetic networks, i.e., the more intensive the search process, the stronger the angular gyrus activation. This suggests that the angular gyrus is part of a system that mediates the search in associative networks and confirms its crucial role in arithmetic fact retrieval.

Although there is wide agreement about the important role of the angular gyrus for arithmetic fact retrieval, it has to be mentioned that our findings are at variance with previous studies: While other studies reported deactivation in the angular gyrus compared to baseline [see e.g., Grabner et al., 2007; Ischebeck et al., 2006; Rickard et al., 2000] we observed activation. At this point we can only speculate about possible causes of the discrepancy. The most obvious difference between our study and others concerns the task and the design. While most other studies used variants of the verification task, we here investigated result production. Whether this could explain the divergent results needs to be clarified in future research. Moreover, there is also evidence for decreased angular gyrus activation with increasing problem size [Stanescu‐Cosson et al., 2000; Zhou et al., 2007]. At first glance, this seems to be inconsistent with the hypothesis that the angular gyrus mediates arithmetic fact retrieval and that activation increases with increasing search in the network. However, at least in the study by Stanescu‐Cosson et al., the inverse problem‐size effect for addition problems has been attributed to a change of solution mechanisms. For larger problems automatic fact retrieval plays a minor role and quantity‐based processing becomes more important. Different solution processes could also be responsible for the findings reported by Grabner et al. [ 2007]. There, the angular gyrus was more strongly activated in single‐digit problems (presumably solved by fact retrieval) than in multi‐digit problems that cannot be solved by direct retrieval.

The present data also revealed that not only regions in the parietal cortex, but also regions in the frontal cortex show a parametric signal increase, among them the left inferior frontal gyrus and a cluster covering parts of the ACC and the SMA. Activations in these areas have been repeatedly reported for arithmetic and number problems. However, in the majority of cases they have been interpreted in terms of working‐memory demands and strategy selection, because activation have been found with relatively complex tasks or multi‐digit operations [see e.g., Delazer et al., 2003; Gruber et al., 2001; Rueckert et al., 1996; Zago et al., 2001]. Although some multiplication problems may have been solved by backup strategies and the frontal‐cortex activations might reflect the associated greater load on working memory and control functions [see Jost et al., 2004, 2009], the parametric increase is nevertheless striking. The application of backup strategies when fact retrieval fails holds especially for problems with large numbers [e.g., 7, 8, and 9, see LeFevre et al., 1996]. However, as shown with the ERP data, an activation increase can be observed even within the group of small problems with products <25, suggesting that the parametric increase reflects more likely increased effort within the fact‐retrieval system than a shift to strategic processes. As the amplitude increase of the EEG data most probably stems from activation increase in the ACC, the results suggest that also the medial frontal cortex contributes to arithmetic fact retrieval.

In a large number of studies the medial frontal cortex has been found to respond to conflicts during information processing [for reviews, see e.g., Botvinick et al., 2004; Ridderinkhof et al., 2004]. Beside its engagement in overriding prepotent responses and error processing, the medial frontal cortex (ACC) signals conflict also in situations of “underdetermined responding” [see Botvinick et al., 2004], i.e., when a stimulus is associated with more than one response, such as in stem‐completion [Palmer et al., 2001] and verb generation [Barch et al., 2000; Thompson‐Schill et al., 1997]. Arithmetic fact retrieval is a similar situation: According to the network approach of arithmetic fact retrieval, a problem not only activates the correct solution, but also other associated solutions [e.g., Campbell, 1995; Verguts and Fias, 2005]. Moreover, interference by incorrect solutions increases with operand and product size [see Campbell, 1995], while neighborhood consistency decreases [Verguts and Fias, 2005]. This makes the fact‐retrieval process “underdetermined” and less efficient for larger problems. It is therefore plausible to assume that the parametric activation increase in the medial frontal cortex reflects this increasing conflict when selecting an answer among competing alternatives.

Taken together, the present study provides evidence that the angular gyrus and the ACC/SMA are integral parts of the system that mediates arithmetic fact retrieval. While the role of the angular gyrus has been discussed in previous studies [see Ansari, 2008; Dehaene et al., 2003], our findings provide evidence that also the medial frontal cortex is involved. We therefore propose that both parietal and frontal structures contribute to arithmetic fact retrieval. The use of a parametric analysis technique was critical for this conclusion. Moreover, for the fMRI data the parametric analysis revealed much stronger and more accentuated activation foci than the categorical analysis [Jost et al., 2009]. This especially holds for activation in the left inferior and angular gyrus. For the ERP data, the parametric analysis helps to understand how the shift from posterior to anterior electrodes emerges with increasing problem size, i.e., at least in part, by a steeper amplitude increase at frontal than at posterior electrodes. All in all, the present study demonstrates the usefulness and applicability of parametric methods [see also Wood et al., 2008], not only for fMRI, but also for EEG data. An open question and an issue that we did not address in the present study is whether the correct product is the best predictor of physiologically expressed problem‐size effects or whether other indices, such as the sum of the operands [cf. Stazyk et al., 1982] or the logarithm of problem size would explain more variance of brain activation data. Likewise, using neighborhood‐consistency properties [see e.g., Domahs et al., 2007; Verguts and Fias, 2005] as the regressor/item‐grouping factor could be an interesting extension of a parametric analysis. It might be promising to compare such different regressor models to delineate more precisely which predictor function best captures the activation increases of distinct brain areas. This, however, would go far beyond the scope of the present study and should be pursued with a fresh set of data and a design tailored specifically to the question of model contrasts.

Furthermore, the present study is another example of a strong correspondence of EEG slow waves and the fMRI BOLD signal in terms of parallel parametric activations and similar topographic distributions [for review, see Khader et al., 2008]. By means of this convergent multi‐method approach, we were able to gain new insight into the neural basis underlying arithmetic fact retrieval.