Functional source separation from magnetoencephalographic signals

Abstract

We propose a novel cerebral source extraction method (functional source separation, FSS) starting from extra‐cephalic magnetoencephalographic (MEG) signals in humans. It is obtained by adding a functional constraint to the cost function of a basic independent component analysis (ICA) model, defined according to the specific experiment under study, and removing the orthogonality constraint, (i.e., in a single‐unit approach, skipping decorrelation of each new component from the subspace generated by the components already found). Source activity was obtained all along processing of a simple separate sensory stimulation of thumb, little finger, and median nerve. Being the sources obtained one by one in each stage applying different criteria, the a posteriori “interesting sources selection” step is avoided. The obtained solutions were in agreement with the homuncular organization in all subjects, neurophysiologically reacting properly and with negligible residual activity. On this basis, the separated sources were interpreted as satisfactorily describing highly superimposed and interconnected neural networks devoted to cortical finger representation. The proposed procedure significantly improves the quality of the extraction with respect to a standard BSS algorithm. Moreover, it is very flexible in including different functional constraints, providing a promising tool to identify neuronal networks in very general cerebral processing. Hum Brain Mapp, 2006. © 2006 Wiley‐Liss, Inc.

INTRODUCTION

Physiological activity in the brain can be evaluated by noninvasive techniques based on measurement of the electric or magnetic field generated by electrical neuronal currents (e.g., electroencephalogram [EEG]; magnetoencephalogram [MEG]). Such neurophysiological techniques, by allowing direct investigation of neuronal pool activity when at least part of the constituent cells fire synchronously, obtain measures with the same time resolution as the cerebral processing itself. The crucial problem is to gain access to the inner neural code starting from the extracranial recorded EEG and MEG raw signals: recorded cerebral signals related to significant activity are mixed and embedded in unstructured noise and in other physiological signals nonrelevant to the desired observation. The main approach has been, after applying procedures to enhance signal‐to‐noise ratio (e.g., stimulus‐related averaging) to solve the so‐called inverse problem, i.e., to use Maxwell's equations to calculate spatial distribution of the intracerebral currents starting from the magnetic or electric field detected in a wide enough area of the scalp surface. This problem does not permit a unique solution. For this reason, it is necessary to acquire supplementary information [Del Gratta et al., 2001], i.e., to define the parameters of the forward problem, to obtain position, intensity, and direction of the modeled cerebral currents (single and multiple dipoles [Scherg and Berg, 1991], music [Mosher et al., 1992], RAP music [Mosher and Leahy, 1999], minimum norm estimates [Hämäläinen and Ilmoniemi, 1994], low‐resolution brain electromagnetic tomography (LORETA) [Pascual‐Marqui et al., 1995], and synthetic aperture magnetometry (SAM) [Vrba and Robinson, 2001]. Currently, no universally accepted criteria exist to define adequate model except in very specific cases.

In the last decade, a different approach has been introduced in the MEG/EEG community, based on exploiting statistical properties of sources composed in the observed signals: extraction of information from such signals amounts to blind separation of sources in presence of noise and interferences. To tackle such a task, blind source separation (BSS) and particularly independent component analysis [ICA; Hyvärinen et al., 2001; Cichocki and Amari, 2002] were proposed.

ICA assumes that sources are statistically mutually independent; to extract them from the recorded mixture a measure of non‐Gaussianity is maximized (e.g., kurtosis) since, by means of the Central Limit Theorem, it has been shown that a linear transformation of the data that maximizes non‐Gaussianity leads to independence as well.

Several studies have proved its effectiveness in removing artifacts and extracting relevant activations from MEG and EEG signals [Barbati et al., 2004; Ikeda and Toyama, 2000; Makeig et al., 1996; Vigario et al., 2000; for up‐to‐date reviews see Cichocki, 2004; Choi and Cichocki, 2005; James and Hesse, 2005]. BSS and ICA algorithms do not solve the inverse problem but they estimate complete source time courses for task‐related features description and provide information that could be used to estimate the source position in a successive step.

A first challenging issue in BSS neurophysiologic applications is the choice of the contrast function used to extract sources: the non‐Gaussianity assumption in the ICA model and the imposition of an orthogonality constraint between extracted components (ICs) produce source estimates that are active during short time intervals with minimal overlap. The ICA technique therefore seems to be effective for separating neuronal signals corresponding to sources that exhibit burst behavior, coming from spatially distinct compact sources. The magnetic field patterns of these ICs are close to those produced by isolated current dipoles [Makeig et al., 2004; Moran et al., 2004]. In this way, ICA achieves both temporal and spatial separation of source activity and can significantly enhance imaging accuracy [Moran et al., 2004; Zhukov et al., 2000]. ICA, however, is insensitive to the time ordering of the data points; other BSS algorithms have been claimed recently as more suitable for cerebral source separation by exploiting second‐order statistics of the source signals to decompose the recorded mixture, e.g., minimizing a set of time‐lagged cross‐correlations [Tang et al., 2004]. At present, many different BSS packages are available, implementing both high‐order ICA algorithms and second‐order BSS techniques; validation of obtained results have to be investigated case by case.

A second key point in applications is how to assign the neurophysiological and neuroanatomical meaning and interpretation to the extracted sources, because often “interesting” characteristics are not separated effectively in a single component but can remain partially mixed or split into more than one component. Usually, a post‐extraction analysis of spectral and spatial IC properties is applied to select the relevant ones, leading to the definition of clusters of “similar” components with respect to some criteria [Himberg et al., 2004; Barbati et al., 2005; Makeig et al., 2004]. The necessity of this post‐processing is the consequence of the blindness of the approach, because BSS/ICA does not take information into account other than the statistics of the data. The advantage is the generality of the assumptions that make these techniques powerful and flexible tools with respect to hypothesis‐driven procedures, which are highly dependent on the accuracy of a predefined model/template.

Sometimes, however, quite accurate information on some parameters of the signals that we want to separate is known: for this reason semi‐blind ICA algorithms have been developed recently. In Papathanassiou and Petrou [2002], the prior knowledge of the autocorrelation function of a source is used to extract it first, using a gradient optimization scheme. In Lu and Rajapakse [2005], the authors proposed a constrained optimization by means of Lagrange multipliers; this algorithm (cICA) allowed accounting for rough knowledge of the time‐course of a functional magnetic resonance imaging (fMRI) source to extract it first. Similar results were obtained in Calhoun et al. [2005] where a semi‐blind ICA approach, derived from the INFOMAX algorithm [Bell and Sejnowski, 1995], was developed.

The Bayesian approach has been presented as a comprehensive theoretical framework for including prior knowledge about sources [Knuth, 1999]; a family of denoising source separation algorithms (DSS) has been introduced recently, ranging from almost blind to highly specialized source extraction, employing additional information [Särelä and Valpola, 2005].

On this route, some of the authors have developed a semi‐blind ICA algorithm that makes it possible to introduce different functions as constraint, allowing also nondifferentiable ones. This procedure has been demonstrated effective on artificial and real fMRI data [Valente et al., 2005].

In the present work, the procedure developed by Valente et al. [2005] is exploited to extract cerebral sources including directly in the separating algorithm information about neuronal activation properties. To assess the efficiency of the approach, a very simple experiment was considered: MEG cerebral activity was recorded during separate little finger, thumb, and median nerve galvanic stimulation. To extract sources corresponding to single finger cortical representation during different activation states, a proper functional constraint was introduced within the separating algorithm and applied to data recorded during the alternated stimulation of thumb, little finger, and median nerve. A further step was then made, removing the orthogonality constraint. In fact, in the specific and restricted cortical region of interest, neural networks are highly spatially interconnected and superimposed and temporal overlap of finger sources activation could be reasonably hypothesized, particularly during nerve stimulation.

Both the proposed separating algorithm versions, defined respectively as functional component analysis (FCA, the orthogonal one) and functional source separation (FSS, the non‐orthogonal) were compared to a standard ICA algorithm [fastICA; Hyvärinen et al., 2001]. Performances were judged based on the extracted sources spatial positions and functional activation properties during the three different stimuli.

MATERIALS AND METHODS

Experimental Setup

Fifteen healthy volunteers (mean age, 31 ± 2 years, seven females and eight males) were enrolled for the study.

Somatosensory evoked fields (SEFs) were carried out in analogy with standard and widely accepted procedures [Hari et al., 1984]. In brief, measurements were performed inside a magnetically shielded room (Vacuumschmeltze GmBH), using a 28‐channel system [Foglietti et al., 1991; Tecchio et al., 1997], the active channels being distributed regularly on a spherical surface (13.5 cm of curvature radius; out of 28 channels, three channels were balancing magnetometers devoted to noise reduction) and covering a total area of about 180 cm². The noise spectral density of each magnetic sensor was 5–7 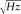at 1 Hz.

The right little finger, thumb, and median nerve at wrist were separately stimulated for three minutes by 0.2‐msec electric pulses, with an interstimulus interval of 631 msec. Intensities were set at about twice the subjective threshold of perception for fingers (via ring electrodes) and just above motor threshold, i.e., thumb twitch, for the nerve at the wrist (via surface disks). Brain magnetic fields were recorded via a single positioning on the hemisphere contralateral to the stimulated side, by centering the recording apparatus over the C3 site of the International 10–20 electroencephalographic system.

The entire MEG procedure (preparation and recording) lasted about 30 min; subjects had signed an informed consent and the experimental protocol followed the standard ethical directives of the declaration of Helsinki.

Data were filtered through a 0.16–250‐Hz bandpass and gathered at 1,000‐Hz sampling rate for offline processing, resulting for each subject in a data matrix of size 25 × 540,000 points.

ICA with Prior Information

ICA applies to blind decomposition of a set of signals X that is assumed to be obtained as a linear combination (through an unknown mixing matrix A) of statistically independent non‐Gaussian sources S:

(1)

Sources S are estimated (up to arbitrary scaling and permutation) by independent components Y as:

(2)

where the unmixing matrix W is to be estimated along with the ICs.

Of course, the decomposition problem (equation 2) has more unknowns that equations, so that the estimation relies on additional information, namely the statistical independence of sources. ICA can therefore be viewed as an optimization process that maximizes independence as described indirectly by a suitable contrast function.

Biomedical signals can often be assumed as generated through a linear mixing process as equation (1), where independent sources are supposed to model activities (of the brain in this case) that originate from separate causes. In fact, strict independence of such sources is probably in many cases unrealistic, but using such hypothesis has proved very effective in many contexts, even if a posteriori we may observe that perfect independence is never achieved.

In Valente et al. [2005], a modified ICA procedure has been proposed that explicitly uses additional information to bias the decomposition algorithm towards solutions that satisfy physiological assumptions, instead of extracting sources only based on their signal's statistical independence. The method is based on optimizing a modified contrast function:

(3)

where J can be any function normally used for ICA (in our case kurtosis), whereas H accounts for the prior information we have on sources. Parameter λ is used to weigh the two parts of the contrast function. If λ is set to zero, maximization of F leads to pure independence. The optimization is performed by simulated annealing [Kirkpatrick et al., 1983] so that function H can have any form (e.g., it does not need to be differentiable). Performance of the algorithm can be in general quite sensitive to the choice of λ, as the optimization is driven by different criteria and one of the two might prevail excessively (multiobjective optimization). For this reason, it is often useful to choose a saturating H function that is active only in an appropriate vicinity of good solutions. Such strategy actually amounts to performing constrained optimization, where H imposes a restriction to a region of search space where J is optimized freely. Further details on the implemented version of the simulated annealing optimization are given in Appendix A.

Functional Constraints

To identify neural networks devoted to individual finger central representation, the reactivity to the stimuli was taken into account. It was defined as follows: the evoked activity (EA) was computed separately for the three sensorial stimulations by averaging signal epochs centered on the corresponding stimulus (EA_L, little finger; EA_T, thumb; EA_M, median nerve).

The reactivity coefficient (R_stim) was then computed as:

(4)

with stim = T, L, M and t = 0 corresponding to the stimulus arrival. The time interval ranging from 20 to 40 msec includes the maximum activation [Allison et al., 1980; Tecchio et al., 1997] and the baseline (no response) was computed in the prestimulus time interval (−30 to −10 msec). The constraint function H_stim is then chosen as:

(5)

where

(6)

and k is a suitable parameter measuring the required minimum response. In the present application we chose k and λ heuristically, based respectively on subject data characteristics and a preliminary study on a test case. Parameter settings depend on the specific experimental set up; however, the procedure can be made automatic, as discussed in Appendix B. The shape of function ϕ is such that the constraint is inactive when response is greater than k, so as to define an admissible region where the optimization is only driven by J. Where response is smaller, if λ is large enough, H_stim dominates the search. A constrained optimization procedure therefore is obtained. To estimate the time behavior of the neural networks devoted to the two finger cortical representations during different activation states, each functional source was extracted using data along the entire recording period, alternating the two fingers and median nerve separate stimulation. Details on the parameter settings and algorithm performance are given in Appendix B.

Orthogonal (FCA) and Non‐Orthogonal (FSS) Source Extraction

To separate contributions representing individual fingers, the proposed FCA procedure was applied as follows: first, a single component was extracted using the constraint H_L and obtaining the functional component describing the time evolution of the little finger cortical representation: FC_L. After projecting residuals on the orthogonal space with respect to the extracted component, the procedure was repeated using H_T to obtain FC_T, the functional component describing the thumb source, as independent as possible with respect to the little finger source. This constraint sequence was motivated by the fact that thumb representation is physiologically larger than is the little finger one. By operating in this way, we therefore meant to favor extraction of the naturally weaker component first. Operating in reverse order, the little finger component could not be extracted satisfactorily, because the orthogonalization almost cancelled it.

Based on this experience, which shows that relevant components are not independent (and in particular not uncorrelated) in the second version of the proposed algorithm FSS, the procedure was repeated identically but the orthogonalization step was skipped, producing a non‐orthogonal functional source estimate for the thumb identification (FS_T). The little finger source FS_L is virtually identical to FC_L. In this case, the order of extraction is not significant because the procedure is applied each time to the original data. The non‐orthogonal approach has already been introduced in the BSS literature [Inki and Hyvärinen, 2002; Yeredor, 2002; Ziehe et al., 2004], both from a theoretical point of view to generalize joint diagonalization procedures to the case of a non‐orthogonal diagonalization matrix, and in applications, particularly in image modeling, to estimate overcomplete ICA bases (i.e., when the number of sources is greater than number of mixtures); in a deflationary extraction scheme, after the estimation of a component, the successive IC is searched in a space that is “quasi‐orthogonal” to the initial one. In the present work, the non‐orthogonal version of the procedure has been implemented according to considerations about the nature of the neural network under study; it is well known that finger sources are highly interconnected spatially and superimposed.

Results obtained by FCA and FSS were compared with ICs estimated by a widely used separating ICA algorithm (fastICA, freely available at http://www.cis.hut.fi/projects/ica/fastica/).

Source Localization and Activity Extraction Comparisons

As a main criterion to evaluate the goodness of extracted components in representing individual fingers, we observed their spatial position. To this aim, sources representing little finger (FC_L; FS_L) and thumb (FC_T; FS_T) were separately retroprojected, so as to obtain their field distribution, as follows:

(7)

where a_s is the estimated mixing vector (column of matrix A) for the functional source y_s (y = FS, FC, IC; s = T, L) and MEG_rec_s are the retro‐projection on the sensor channels of the estimated y_s source.

A moving equivalent current dipole (ECD) model inside a homogeneous best‐fitted sphere was used. ECD coordinates were expressed in a right‐handed Cartesian coordinate system defined based on three anatomical landmarks (x‐axis passing through the two preauricolar points directed rightward, the positive y‐axis passing through the nasion, the positive z‐axis is consequently defined). Only sources with a goodness‐of‐fit exceeding 80% were accepted. The field distribution obtained by retro‐projecting only one component is time invariant up to a scale factor; consequently, the subtending current distribution (ECD position in our case) is time‐independent. The same retro‐projection was performed also for all the fastICA estimated components. To have a benchmark for finger somatosensory source position, known markers of signal arrival in the primary sensory cortex, occurring at around 20 and 30 msec from the stimulus (M20, M30 [Allison et al., 1991; Hari and Kaukoranta, 1985; Tecchio et al., 1997]), were calculated by standard procedure of averaging original MEG channel signals and computing corresponding ECDs.

General linear models (GLM) for repeated measures were estimated to test for differences in source localization and source reactivity across subjects: as dependent variables respectively, the 3‐D coordinates vectors (x, y, z) and 3‐D reactivity vectors (R_T, R_L, R_M) were used, with the two levels Finger (thumb, little finger) as within‐subjects factor. Because FS_L and FC_L are practically identical, only FS_L has been considered in the statistical analysis.

To check for the level of residual response to the stimulation after sources extraction, we defined a “discrepancy response” index as follows:

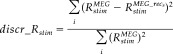(8)

where, as defined in equation (4), R_stim ^MEG is the reactivity index computed on MEG data during finger stimulation (stim = L, T) and R_stim ${}^{\text{MEG\_rec}{}_{\text{s}}}$ is the reactivity index of reconstructed MEG data with the s finger source (s = L, T) during its corresponding stimulation; the index i runs upon the four channels of minimal and maximal amplitude at M20 and M30 latencies. In fact, the dipolar field distribution generated at these peak latencies are well described by their minimum/maximum values [Tecchio et al., 2005]. Obtained indices for little finger and thumb (discr_R_L; discr_R_T) were computed and compared between the proposed FCA/FSS procedures and fastICA.

Basic ICA Model Features Comparison: Non‐Gaussianity and Basis Vectors Angles

As the proposed procedures include in the cost function physiological constraints, it is interesting to evaluate the trade‐off between non‐Gaussianity maximization and the introduced constrained optimization. For this reason, kurtosis values of the FCA, FSS sources, and the corresponding fastICA components across subjects were compared.

In this way, we could also evaluate how the functional characteristics of the estimated sources, summarized by the constraints, go with the non‐Gaussianity assumption of the basic ICA model.

Moreover, as FSS leaves out the basis vector orthogonality, the angles between FS_L and FS_T basis vectors were evaluated as an additional indication that the algorithm did not estimate several times the same components.

RESULTS AND DISCUSSION

Source Localization

Dipole coordinates (x, y, z) were computed from the retro‐projected FCA and FSS components in our 15‐subject group. We have to note that in four subjects localization of the retro‐projected FC_T was not possible (variance explained <0.8, dipole not accepted); instead, localization of the retro‐projected FS_T was acceptable for all examined subjects (Table I).

Table I.

Spatial and reactivity components characteristics

Sources	Successful cases	Explained variance	Position (mm)			Reactivity
			x	y	z	RL	RT	RM
FSS
FSL	15	0.95 ± 0.04	−33 ± 10	6 ± 12	99 ± 14	12.7 ± 4.9	7.7 ± 5.6	18.8 ± 12
FST	15	0.97 ± 0.03	−38 ± 10	10 ± 13	90 ± 10	6.3 ± 5.1	13.4 ± 4.8	18.3 ± 12.6
FCA
FCL	15	0.95 ± 0.04	−33 ± 10	5 ± 12	99 ± 13	12.7 ± 4.9	7.7 ± 5.5	18.9 ± 12
FCT	11	0.95 ± 0.05	−41 ± 10	11 ± 12	87 ± 11	1.2 ± 0.8	10.7 ± 3.1	10.0 ± 6.0
fastICA
ICL	6	0.96 ± 0.04	−36 ± 12	9 ± 23	96 ± 11	7.5 ± 5.9	4.4 ± 5.1	11.4 ± 11.3
ICT	6	0.95 ± 0.03	−41 ± 14	16 ± 43	79 ± 20	2.5 ± 3.9	6.3 ± 2.7	11.1 ± 14.2
ICT;L	9	0.93 ± 0.08	−39 ± 13	7 ± 10	97 ± 12	7.9 ± 3.7	7.3 ± 5.1	16.7 ± 16.6
MEG data
M20L	12	0.94 ± 0.06	−34 ± 9	7 ± 14	99 ± 9
M20T	15	0.96 ± 0.02	−42 ± 8	11 ± 11	91 ± 10
M30L	11	0.97 ± 0.02	−31 ± 8	4 ± 10	97 ± 9
M30T	12	0.97 ± 0.03	−33 ± 8	6 ± 13	89 ± 12

Values are mean ± SD. Successful cases, number of subjects with successful localizations (>80%); Position, coordinates of ECDs; Reactivity, sources reactivity indexes to the three stimulations R_L, R_T, R_M, pure numbers. M20_L, M20_T, M30_L, M30_T positions computed on MEG data are reported for comparison.

Factor Finger resulted significant in FS_L versus FC_T and versus FS_T (Table II), corresponding in both cases to the estimated thumb source significantly lateral, anterior, and lower with respect to the little finger source, in agreement with the well‐known homuncular finger somatotopy. The same relative positions were found with M20 and M30 ECD when stimulating thumb and little finger, respectively (Tables I, II).

Table II.

Statistical analysis on source positions and reactivity

		Subjects	Position (mm)			P	Reactivity			P
Sources			x	y	z		RL	RT	RM
FSL (FCL)	FCT	11	6 ± 12	−4 ± 14	14 ± 9	0.002	10.8 ± 4.8	−5.1 ± 3.9	5.8 ± 11.1	<0.0001
	FST	15	5 ± 13	−4 ± 14	9 ± 12	0.003	6.3 ± 4.1	−5.7 ± 3	0.4 ± 6.2	<0.0001
ICL	ICT	6	5 ± 17	−7 ± 37	18 ± 21	0.2	5 ± 4.9	−1.8 ± 7	0.3 ± 19	>0.5
ICT;L	ICT a	9;6	2 ± 7	−9 ± 14	18 ± 8	>0.1	5.3 ± 2.3	1.1 ± 2.5	5.6 ± 7.7	>0.1
	ICL a	9;6	3 ± 7	−2 ± 14	0 ± 8	>0.1	0.4 ± 2.3	2.9 ± 2.4	5.3 ± 7.7	>0.1
M20L	M20T	12	9 ± 8	−2 ± 13	9 ± 8	0.001
M30L	M30T	11	3 ± 5	0 ± 11	10 ± 8	0.03

Values are mean ± SD differences in sources ECDs coordinates and evoked activity indexes R_T, R_L and R_M. Difference in position for M20_L versus M20_T and M30_L versus M30_T are also reported. Results of GLM models evaluating contrasts between sources in position and reactivity across subjects are summarized in the corresponding P value columns (Pillai's trace within‐subject effect).

^aIndicates different groups of subjects tested in the fastICA case (ANOVA test with Bonferroni correction for multiple comparisons).

Components obtained by fastICA failed in more than half of cases (9 of 15) to separate thumb (IC_T) and little finger (IC_L) response: in those cases a unique IC was selected that responded best to both stimulations and localized with more than 80% of variance explained (IC_T;L, Table I). Testing the 6 subjects for whom thumb and little finger response was separated by fastICA, factor Finger was not significant at the standard threshold P value of 0.05. Moreover, dipole coordinates of the retro‐projected mixed source corresponding to IC_T;L with respect to IC_L and IC_T were not significantly different (using Bonferroni post‐hoc comparisons, all P values were greater than 0.05, Table II).

Due to a very poor signal to noise ratio in 3 cases, where a noise reduction preprocessing algorithm should have been applied in addition to standard average in the localization procedure, localization of M20 component was unsuccessful. On the other hand, FSS algorithm source positions were successfully determined for all 15 examined subjects, even in the cases of very noisy data. Moreover, it could be noted that FS_L and FS_T lie in‐between their respective M20 and M30 positions (Table I, Fig. 1), in agreement with the constraint time window definition (see equation 4), which includes both M20 and M30 latencies.

Figure 1.

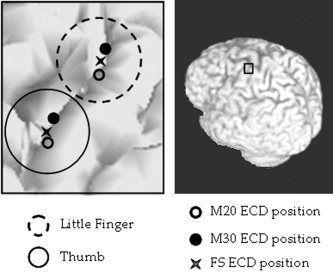
Position in one representative subject of thumb (solid circle area) and little finger (dotted circle area) sources. Positions of M20 (empty circle), M30 (filled circle) and the extracted source with the FSS procedure (star) are shown. It can be noted the in‐between position of the estimated functional source with respect to its corresponding M20 and M30 ECDs.

Activity Extraction Comparisons

Source reactivity

The activity of the source representing a finger is compared when stimulating the finger itself with respect to when the other finger or the median nerve is stimulated. To do this, the above‐defined indexes R_L, R_T and R_M describing, respectively, the responsiveness to little finger, thumb and median nerve stimulation, were all considered for each of the three estimated functional components (FS_L, FC_T, and FS_T) and for the selected fastICA ones (IC_L, IC_T, and IC_T;L, Table I).

Factor Finger resulted significant in FC_L versus FC_T in the corresponding stimulation periods, indicating a lower response of the FC_L with respect to FC_T during thumb stimulation and a higher response of the FC_L with respect to FC_T during little finger stimulation. The same behavior was observed in comparing FS_L versus FS_T (Table II, Fig. 2), as expected. A significant difference between the two methods emerged when considering the contrasts between reactivity levels in R_M versus R_T respectively for FC_T and FS_T: only in this latter a higher evoked activity to the median nerve stimulation with respect to the thumb stimulation itself was present, in agreement with the physiology of the hand innervation (paired t test, for FS_T P = 0.04; for FC_T P = 0.68). In fact, it is well known that stimulating directly a nerve, all the proprioceptive and the superficial perception fibers of innervated districts are recruited; therefore, the cerebral source representing the thumb, innervated by the median nerve, is expected to be more reactive to the stimulation of this nerve with respect to the cutaneous stimulation obtained by ring electrodes. Moreover, median nerve stimulation over the motor threshold induces a partial stimulation of the ulnar nerve (innervating the little finger) and consequently of the little finger proprioceptive and superficial perception fibers. For this reason, it is not surprising that a higher reactivity to the median nerve stimulation was also found for FS_L (R_M versus R_L; paired t test P = 0.02).

Figure 2.

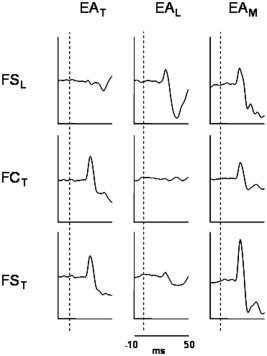
Temporal evoked activity of the extracted finger sources (little finger and thumb) by the two proposed procedures (FCA: FC_L = FS_L, FC_T; FSS: FS_L, FS_T) during the stimulation of thumb (EA_T), little finger (EA_L), and median nerve (EA_M) for one subject. To be noted the selective reactivity of each finger source to the respective finger stimulation; moreover, the FS_T reaction to the median nerve stimulation was even higher than to the stimulation of the thumb itself.

Testing the six subjects with finger sources separated by fastICA, factor Finger resulted globally not significant, with similar reactivity levels for the two sources across different stimulations. In addition, testing the mixed source IC_T;L versus IC_T and IC_L, no significant differences in reactivity were detected (Table II).

Residual response levels evaluation

The level of residual finger response to the corresponding stimulation after sources extraction (i.e., the discrepancy response indices distribution values across subjects: discr_R_L and discr_R_T, see equation [8]) was investigated. This comparison has been made in terms of relative performance between the three algorithms tested. Discrepancy reactivity was significantly lower for the FSS procedure with respect to both its orthogonal version FCA and fastICA, indicating the more satisfactory performance of the FSS procedure in extracting activity of interest; instead, no significant difference in discr_R_T mean values was found between FCA and fastICA (Table III). Low mean discrepancy reactivity values for FSS (6% of residual response for the little finger and 3% for the thumb with respect to the original averaged MEG data) indicate that the two extracted finger sources described practically all the evoked response contained in the original data matrix.

Table III.

Discrepancy response levels

Method	discr_R L	discr_R T	Contrast	P
				discr_R L	discr_R T
FCA	0.06 ± 0.07	0.22 ± 0.21	FCA vs. FSS	—	0.04
FSS	0.06 ± 0.07	0.03 ± 0.04	FCA vs. fastICA	0.004	0.3
fastICA	0.28 ± 0.27	0.32 ± 0.28	FSS vs. fastICA	0.004	0.001

Mean ± SD for the two finger discrepancy indices in the three considered algorithms are reported. Results of ANOVA test (with Bonferroni correction for multiple comparisons in the thumb case) are summarized for the corresponding contrast in the P value columns.

Basic ICA Model Features Comparison

Non‐Gaussianity

When comparing kurtosis values between FCA and FSS finger sources with respect to the fastICA ones, we found that kurtosis was significantly higher for fastICA than for FCA and FSS, and that these last two were not significantly different (FCA versus fastICA, P = 0.03; FSS versus fastICA, P = 0.01; FCA versus FSS, P = 0.8; Bonferroni‐corrected multiple comparisons). This result was not surprising, due to the introduction of the functional constraint in FCA and FSS in addition to the kurtosis maximization. An interesting finding has been obtained when comparing kurtosis values between finger sources and residual components for FCA versus fastICA. For FCA, residual components are defined as all the components extracted orthogonally to the first two, without activating the functional constraints (λ = 0). For fastICA, they are defined as the remaining ICs, having removed IC_L, IC_T and IC_T;L. From both methods the components with abnormal kurtosis values, marked as artefacts, were removed [Barbati et al., 2004]. In both cases, kurtosis values were significantly higher for the finger sources than for the residual components (FCA, P = 0.01; fastICA, P < 0.0001), indicating that higher kurtosis values are associated with functional source properties. We could not make this check between sources and noise for the FSS procedure, because without imposing the functional constraints and without the orthogonality condition, no further source extraction was feasible after the first two.

Basis vector angles

As an additional indication that FSS algorithm did not estimate several times the same components, due to the absence of the orthogonality constraint, the angles between basis vectors couples of FS_Ls and FS_T were computed across subjects. The median angle obtained (63 degrees), the interquartile range of this distribution (42–79 degrees), and the minimum at 25 degrees, indicated that the great majority of these angles were quite large, i.e., a difference in basis vectors was obtained even in absence of the orthogonality constraint.

CONCLUSIONS

In the present work, a functional source separation (FSS) technique has been introduced in the context of neurophysiologic applications using MEG recordings. Adding to a kurtosis‐based cost function physiological constraints defined on the expected temporal behavior of cerebral sources of interest, we exploited in the proposed extraction procedure information both about the source statistical distribution (time‐independent) and the temporal structure of the cerebral activity.

It has been demonstrated how addition of appropriate information to a separating algorithm and the removal of the orthogonality constraint allow distinguishing more satisfactorily activity from neural networks devoted to individual finger representation with respect to a standard ICA algorithm. In fact, the proposed procedure proved able to extract in all cases somatotopically consistent sources. Moreover, by removing the orthogonality constraint, the obtained source has been proved to express more physiologically plausible activation properties with respect to their orthogonal version and a standard ICA model. The provided sources are suitable to describe ongoing activity time courses, which allows for example trial‐by‐trial analysis, instead of describing the activations by averaging all sensor channels and only in specific instances, as usually done in the standard procedures. The obtained activation properties highlight the ability of the extracted sources in describing complex and interconnected cerebral networks. Nonetheless, the FSS procedure was characterized by minimal residual activity.

The proposed approach, consisting of a sequential estimation, with sources obtained one‐by‐one in each stage applying different criteria, is very useful also from another point of view: extracting different components with defined required properties leaves out the problematic and subjective step of a posteriori identification and classification of estimated components.

In summary, the proposed FSS approach, by adding functional constraints to standard ICA and not requiring orthogonality between extracted sources, provided solutions always correctly positioned, reacting properly neurophysiologically and with negligible residual activity. This procedure is very flexible in including different functional constraints, providing a promising tool to identify neuronal networks in very general cerebral processing.

APPENDIX A.

Simulated Annealing

Simulated annealing (SA) is a well known global optimization technique [Kirkpatrick et al., 1983] inspired to statistical mechanics. It simulates the behavior of a liquid that freezes slowly: if the process is slow enough, it will be possible to create crystals in the structure (minimum energy configuration). Starting from these principles, it is possible to optimize by SA almost any kind of contrast function, because it does not require the knowledge of its derivatives. The optimization process is based on the perturbation of a given solution, according to the concepts of temperature, statistical equilibrium and probabilistic acceptance.

Consider the problem of maximizing S(w) and choose a starting solution (state) w₁. Let S₁ = S(w₁). A new state w₂ is generated perturbing w₁ by means of a suitable rule and the value S₂ = S(w₂) is evaluated. If S₂>S₁ the new solution w₂ is accepted, while if S₁>S₂ it is accepted with probability p=min{1,exp(−(S₁−S₂)/T)}, where T is the control parameter called Temperature (according to the physical formulation). Accepting the new solution means that the system moves to the new state w₂. At large values of T, the probability p of accepting less‐optimal (lower S) solutions will be high; as the temperature decreases, the system will accept fewer such solutions. The optimization is carried out following this scheme: the system starts at a high temperature (such that most of the perturbations will be accepted anyway) and at that temperature, it generates a number of states such that the statistical equilibrium is reached.

Subsequently, the temperature is decreased according to an appropriate criterion (cooling schedule), and the procedure continues as before until a suitable stopping criterion halts the process. If the cooling schedule is slow enough (logarithmic), the algorithm is statistically guaranteed to reach a global optimum (with probability 1). Such theoretically correct cooling schedule is too slow to be applied in practice, however, so that normally a geometric schedule is applied.

SA optimization has two advantages over traditional techniques (such as gradient‐based): it does not require the use of derivatives and, if properly set, it reaches the global maximum. Although it is considerably slower if compared with those techniques, in the present application this is not a relevant drawback, because only a limited number of components have to be extracted. In fact, in this work emphasis has been placed on proving effectiveness of the constrained optimization approach, and to evaluate different options we privileged flexibility of the algorithm on the choice of constraint function over speed.

In the present application, we whitened data and for each functional constraint we started from an initial random w unmixing coefficients vector (equation [2]) and the contrast function in equation (3) was maximized by perturbing w. An optimal w_opt was found at the end of the optimization process and the corresponding source was recovered from it. We implemented a decrease rate for the temperature, such that T_t+1=T_tα, with α = 0.7. The algorithm terminated when, comparing the optimal solutions at two consecutive temperatures, the norm of the difference of the unmixing coefficients w (or of the sum, because both w and −w correspond to the same source) was under a fixed threshold (ε = 10⁻⁴). We implemented a procedure to automatically set the initial temperature T₀. Starting from a random initial temperature T_R, we kept trace of the number of accepted (A) and rejected (R) state transitions. The ratio ρ = A/(A + R) was computed after the system had reached the equilibrium, and the following criterion to set up the starting temperature T₀ was used: if ρ < 0.8, the system was not warm enough and the optimization could be not reliable, then we set T_R = 1.5T_R. If ρ > 0.9 the system was considered too warm and the optimization may take more time than needed, then T_R = 0.9T_R; if 0.8 ≤ ρ ≤ 0.9, then T₀ = T_R. In this way, the optimization does not need further temperature set up even when parameters λ and k are changed, because the optimal starting temperature is estimated according to the used dataset and the specific contrast function.

APPENDIX B.

Parameter Settings and Execution Time

In this appendix we specify how the values of parameters λ and k have been determined in the present application. Information about dimension of the data and the average execution time are given at the end of this section.

• a1A preliminary standard ICA extraction is made, setting λ = 0; it is equivalent to maximize only the independence constraint (kurtosis).
• a2Kurtosis values and R_stim (stim = T,L; as defined in equation [4]) of all extracted components are evaluated. After applying a switching system to remove artifacts (resulting for example in very extreme kurtotic components [Barbati et al., 2004]), the maximum values of kurtosis and R_stim are selected among the retained components. To set k values, the initial steps (a1) and (a2) have been performed for each subject, and corresponding maximum R_stim values obtained have been assigned as initial k values in the FCA and FSS algorithms.
• a3λ is fixed so as to make the functional constraint (λ*H_stim) approximately three orders of magnitude greater than kurtosis (J).

The result of the λ setting procedure has been observed to be quite general and suitable for all examined subjects, because the algorithm showed low sensitivity to this parameter; therefore, in our experimental setting the same value was used in all cases: λ = 1,000.

The size of the data matrices was 25 rows × 540,000 time points for each subject; the general calculator characteristics were a CPU of 3.2 GHz with 1.0 GB RAM. The average execution time over the extractions for the thumb source resulted 114 sec. and for the little finger source, 105 sec. The fastICA average execution time to extract all components was about 192 sec.