Reconstruction of extended cortical sources for EEG and MEG based on a Monte‐Carlo‐Markov‐chain estimator

Abstract

A new procedure to model extended cortical sources from EEG and MEG recordings based on a probabilistic approach is presented. The method (SPMECS) was implemented within the framework of maximum likelihood estimators. Neuronal activity generating EEG or MEG signals was characterized by the number of sources and their location and extension. Based on the noise distribution of the measured data, source configurations were associated with the according value of the likelihood function. To find the most likely source, i.e., the maximum likelihood estimator, and its level of confidence, a stochastic solver (Metropolis algorithm) was applied. The method presented supports the incorporation of virtually any constraint, e.g., based on physiological and anatomical a priori knowledge. Thus, ambiguity of the ill‐posed inverse problem was reduced considerably by confining sources to the cortical surface extracted from individual MR images. The influence of different levels and types of noise on the outcome was investigated by means of simulations. Somatosensory evoked magnetic fields analyzed by the method presented suggest that larger extended cortical areas are involved in the processing of combined finger stimulation as compared to single finger stimulation. Hum. Brain Mapping 18:100–110, 2003. © 2002 Wiley‐Liss, Inc.

INTRODUCTION

Multichannel electro‐ and magnetoencephalography (EEG and MEG) have been successfully applied to study the functional organization of the human cortex. In most of the cases, equivalent current dipole (ECD) models are considered [Baumgartner et al., 1993; Braun et al., 2000; Scherg and von Cramon, 1986]. However, information provided by these models about the spatial properties of cortical activation and their extension, which is of particular interest in considering neuronal reorganization, is rather limited and can be assessed only indirectly [Elbert et al., 1995a; Flor et al., 1995, 1997]. In order to obtain a direct estimate of the extensions of cortical sources, several approaches have been presented [Baillet and Garnero, 1997; Kincses et al., 1999; Lütkenhöner et al., 1995; Pascual‐Marqui et al., 1994; Sarvas, 1987; Schmidt et al., 1999; Wang et al., 1992]. While most of these methods yield a unique solution of the inverse problem, the ambiguity and ill‐posed character of the inverse problem results in numerous source configurations that model the recorded data similarly well. Thus, the specification of a single distinguished solution might be misleading. Statistical interference on the reliability of the source solution [Schmidt et al., 1999] might overcome this drawback.

As the bioelectromagnetic inverse problem has no unique solution, meaningful constraints have to be introduced. Ideally, these constraints should be based on a priori knowledge about the mechanisms and conditions underlying the measured activity. Since EEG and MEG activity is mainly generated by the apical dendrites of pyramidal neurons oriented predominantly perpendicular to the cortical surface [Kandel et al., 1991; Mitzdorf, 1987], confinement of any modeled activity to cortical surfaces [Dale and Sereno, 1993] is a successful strategy for reducing the ambiguity of the inverse problem. This approach can be extended by allowing only perpendicular currents. The above discussion reveals that an “ideal strategy” for modeling extended cortical sources should fulfill the following requirements: 1) it is based on a statistical approach in order to provide information about the reliability of the source solution, 2) it relies solely on theoretically or experimentally confirmed a priori knowledge, and 3) the method allows for the inclusion of any available source restriction.

In the current article, we present an approach based on a semi‐parametric model that has been developed within the framework of the maximum likelihood (ML) theory to account for the above requirements. The method (Semi‐Parametric Model for the Estimation of Extended Cortical Source, SPMECS) provides an estimator for the most likely source as well as the likelihood of suboptimal parameters. Due to the non‐linearity and complexity of the likelihood function, the ML estimator cannot be specified analytically. A Metropolis algorithm based on a Monte Carlo Markov Chain approach is an efficient way to determine the ML estimator. A major contribution of the presented method is the fact that it accounts for the structural specificity of the cortical surface by confining the modeled sources to the cortical surface. This is obtained by defining cortical patches and using geodesic distance instead of Euclidean distance in 3D space as in other approaches [Schmidt et al., 1999]. The usefulness of the method is evaluated by simulations and experimental data.

MATERIALS AND METHODS

Mathematical Basis

The recorded EEG or MEG signal at m sensors can be written as an m‐dimensional vector y with the elements:

(1)

where y_0i denotes the activity of interest at the i‐th sensor in absence of noise and ϵ_i represents the noise according to the distribution ρ_i at the respective sensor. Neural activity represented by a current distribution j(θ) generating the recorded potential or field y₀ can be described as a physical system modeled by a set of k parameters θ = {θ₁, … , θ_k}. Thus, solving the bioelectromagnetic inverse problem corresponds to estimating the parameters θ.

The maximum likelihood (ML) method is a common statistical approach. Each set of parameters is associated with a probability distribution for the realization of a measurement y [Honerkamp, 1998]:

(2)

The function L(θ) for a given sample y is named likelihood or likelihood function (LF). The ML estimator is the value of θ which maximizes the LF. Under the distribution given by the parameter , the density function is maximized at the given sample y. Assuming the noise at each sensor to be a normal distribution ρ_i ≐ N(0, σ_i), the probability of the measured data due to an arbitrary parameter set θ is [Honerkamp, 1998]:

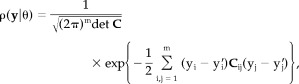(3)

where C denotes the covariance matrix with elements C _ij of the m‐dimensional noise distribution and y _i the values of the electric potential or magnetic field generated by the cortical activity at the i‐th sensor. Each y'_i is obtained by the forward solution of the bioelectromagnetic inverse problem, which according to the lead field theory can be written as [Sarvas, 1987]:

(4)

for the current distribution j(θ,r) inside the volume conductor V. F(r) denotes a vector field function (lead field).

Rather than maximizing L(θ) directly, it is often more convenient to consider its logarithm ll(θ) = log{L(θ)}, called log‐likelihood function (logLF), and to maximize this expression with respect to θ, yielding the same estimator since the logarithm is monotone. The logLF corresponding to the probability distribution (3) is given by:

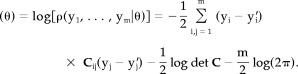(5)

Since the last two terms in equation (5) are independent of θ, maximizing ll(θ) with respect to θ corresponds to minimizing the quadratic form:

(6)

The covariance matrix C is independent of θ. To estimate for a system with m sensors, approximately m ² independent measurement points are mandatory according to the Moivre‐Laplace limit theorem. Thus, to achieve asymptotic statistics, approximately 10,000 additional trials would be necessary for 100 sensors. Since EEG and MEG experiments generally do not generate such a large number of measurement points, artificially strong correlation might be estimated. To overcome this limitation, the correlation matrix might be assumed to be diagonal, which has the additional benefit of simplifying the mathematical expression. However, for a sufficiently large number of independent baseline measurements, an estimate for the general C can be introduced into the model. Assuming uncorrelated noise, the covariance matrix C has a diagonal form with off‐diagonal elements identical to zero. Without loss of generality, the variance is assumed to be the same at each sensor. Thus, expression (6) obtains the form:

(7)

Anatomical Constraints

Assuming gray matter to be the location for all neuroelectric or neuromagnetic activity measured [Dale and Sereno, 1993], the surface between gray and white matter is extracted from MR images of the brain (CURRY software) [Fuchs et al., 1994]. Neural activity of the cortical tissue is modeled on the triangulated surface. The current in each triangle is approximated by an electrical current dipole (ECD) located at the center of gravity with a perpendicular direction to the according triangle. Its orientation depends on whether the modeled activity corresponds to activation or inhibition. The amplitude of the cortical activity is measured by ECD moment per unit area [Am/mm²].

Parameterization of the Cortical Activity

Parameters θ_i are chosen to unambiguously describe a given cortical source based on the knowledge about the anatomical and physiological constrains. As a first order approximation, the geometry of each nondisjunctive source [Pearson et al., 1999] is modeled circular. Thus, cortical activity is characterized by 3N+1 parameters: 1) the number of active cortical areas, 2) each location T, 3) each radius R, and 4) each amplitude A. The location of the source is limited to the cortical surface. Triangles pertaining to the active source satisfy the condition that the distance between their center of gravity and that of the central triangle equals not more than R. Triangles located entirely within the specified radius are weighted by their area, whereas triangles lying only partially within the circle are weighted according to the intersection.

Scanning the parameter space

In general, it is not possible to specify the ML estimator directly by solving the non‐linear equation (∂ll())/∂θ = 0 analytically. As a numerical solver, the Metropolis algorithm (MA) based on the Monte Carlo Markov Chain approach is suggested. The MA scans the space Θ^k (spanned by the k parameters θ_i) for the maximum of ll(θ) [Gelman et al., 1995]. It is based on a diffusion process within Θ^k. The logLF is evaluated at each place of this random walk of the source locations on the extracted cortical surface with concomitant random source radius R. The algorithm provides a higher scanning rate of regions of Θ^k with higher values of logLF, thereby increasing the precision of the LM estimator within the performed sample. At the same time, the diffusion process ensures the sampling of the logLF in the neighborhood of any θ ∈ Θ^k.

In our current approach, the source amplitude is not varied according to the MA. Instead, the activity of each source is calculated as the regression parameter that minimizes the mean squares of the according source activity with respect to the measured data. Also the source amplitude values are not restricted. Nevertheless, if any physiological limits are known, this information can be used as an additional physiological constraint and can be easily integrated into the algorithm.

The range of likely solutions

The scanning of the parameters of space provides a large number of modeled sources with their corresponding likelihood value. This information can be used to specify the error bounds and confidence levels of the estimated source parameters. To obtain the error bounds of the source extension, a quadratic fit was performed for the log‐likelihood values of all sources located in T̂ ₀ with different radius R. The curvature of the fitted parabola approximates the variance of the estimator of the source extension.

SIMULATIONS

Model for cortical activity

Simulated activity of one extended source located on an artificial sulcus (Fig. 1, 2) was used to validate the presented method. The artificial sulcus was composed of 1,200 triangles with an average area of 1.1 mm² each. Its shape and orientation were chosen to resemble the somatosensory cortex (see below for application). The outer and inner radius of the sulcus were 80 and 70 mm, respectively. A simulated cortical source was defined by 195 triangles within a radius of R ₀ = 10 mm around the center of gravity of triangle T ₀. Accordingly, the extended source was determined by parameter set θ₀ = {T ₀, R ₀}. Measurements y _i were obtained by superposition of the forward solutions of each triangle appertaining to the simulated activity. For the majority of EEG and MEG experiments, the number of active sources that have to be modeled can be determined by preprocessing the measured data using well‐known techniques (PCA [Baumgartner et al., 1989], ICA [Bell and Sejnowski, 1995; Makeig et al., 1996], MUSIC [Mosher et al., 1992], Multi‐ECD models [Scherg and Berg, 1991]). Consequently, we assumed the number of sources as known.

Figure 1.

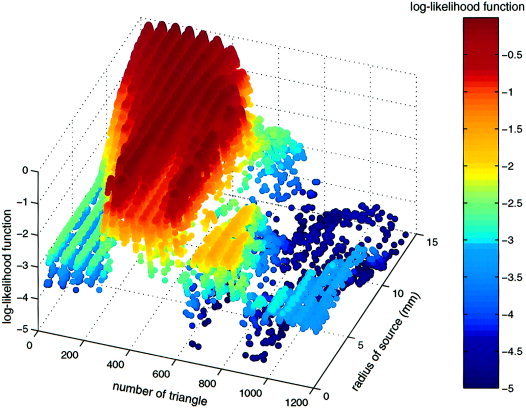
Example of sampled log‐likelihood function across location (encoded as number of center triangle) and source radius. Periodicity occurs due to triangle numbering in stripes across the surface. Note that local maxima are sampled more densely.

Figure 2.

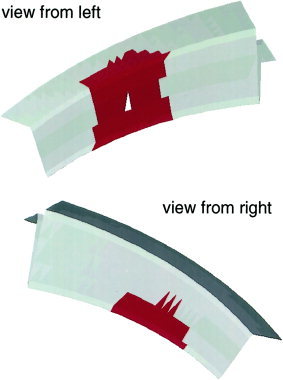
Artificial sulcus from both views with reconstructed sources without noise. The white marks the center triangle and the red area the extend of the source (R = 10 mm).

Instead of calculating the Euclidean 3D‐distance between two triangles, the distance along the cortical surface is considered. Recursively, a matrix is computed that contains the shortest path connecting each pair of triangles across vertices and centers of the other triangles. This measure accounts for the functional organization of the highly folded cerebral cortex.

The method applies to EEG as well as MEG analysis. EEG simulations were conducted for a 128‐electrodes setting covering the entire head. MEG analysis was performed for a whole‐head MEG system with 151 first order axial gradiometers (CTF Systems Inc.). A four‐layer spherical volume conductor with an outer radius of R _v = 90 mm was used. Electrical and geometrical properties were chosen as listed in Table I. The magnetic permeability of all biological tissues was assumed equal to the permeability of vacuum μ₀ = 12,566 · 10⁻⁷ N · A ⁻².

Table I.

Electrical conductivities and eccentricities of the four layers of the spherical head model used as volume conductor

Layer	Anatomical structure	Eccentricity (1/Radius)	Conductivity (1 · 10−3/Ω · m)
1	Brain Tissue	0. 8977	330.0
2	Cerebro‐spinal fluid	0. 9205	1000.0
3	Skull	0. 9659	4.2
4	Scalp	1. 0000	330.0

In order to evaluate the impact of noise on the outcome of the presented method, different noise levels of five possible error sources were investigated: non‐constant activity distributions, uncorrelated and correlated noise, erroneous localization of sensors, as well as errors regarding the volume conductor model.

Influence of activity distribution

In order to investigate the error introduced by assuming constant activation in the modeled sources, two distinct distributions were compared: In the first case, a spatially homogeneous activation was assumed. In the second case, the source was divided into three equidistant, concentric rings: activity density in the innermost region was four times higher than in the outermost region and two times higher in the middle region.

Influence of uncorrelated and correlated noise

In general, EEG and MEG recordings are superposed by uncorrelated and correlated noise that could bias solutions of the inverse problem [Braun et al., 1997]. To assess the impact of these two types of noise on the SPMECS, three different levels of uncorrelated and correlated noise were considered (1, 5, and 10%). Uncorrelated noise was simulated by adding independent normal distributed random numbers to the electrical potential and magnetic field simulated at each electrode and gradiometer, respectively. Correlated noise, mimicking spontaneous brain activity, was modeled by randomly positioned current sources with random orientations: The potential of 1,000 current dipoles with uniformly distributed orientation and position within an upper hemisphere with an eccentricity of 70 mm around the center of the head model were summed up and added to the simulated electrical potential and magnetic field, respectively. The ratio of noise and signal variance across sensors varied between 1, 5, and 10%. Ten simulations were performed for each level of uncorrelated and correlated noise.

Influence of electrode and sensor positioning error

In contrast to the MEG, electrode positions in EEG recordings must be determined one by one for each measurement and are, therefore, corrupted with a non‐systematic positioning error. In order to investigate the dependency of the SPMECS estimators to this type of distortion, two levels of erroneous electrode localization were simulated. The 128‐electrode positions were randomly misplaced around their default location by a normal distributed shift. Standard deviation of the displacement was 5 and 10 mm, respectively.

In MEG measurements, sensor positions maintain a static spatial relationship. However, the head of the examined subject is not affixed to the system. Thus, the position of the head relative to the sensors might change during measurement. Simulations were performed by randomly misplacing the sensor array around its default position. Standard deviation of the displacement was 2.5 and 5.0 mm, respectively. For MEG and EEG, each displacement level was simulated 10 times.

Influence of head model errors

In order to estimate the underlying cortical activity, the SPMECS relies on the field generated by the forward calculation of modeled active sources, which is determined using a spherical head model with four concentric layers. Table I shows the parameters considered. Erroneous specification of the head model and its parameters might influence the outcome of the SPMECS and, consequently, affect parameter estimation and source reconstruction. Simulations were limited to skull thickness because it has the smallest electrical conductivity of all four layers and, therefore, the largest smearing effect on EEG scalp potential [Gevins et al., 1991].

Influence of different source sizes

In order to estimate the influence of different source sizes on the reconstruction capabilities of the current algorithm, five sources with the same location but different radii were examined: 10.0, 7.5, 5.0, 2.5, and 1.0 mm.

Application

In order to illustrate the ML method for an experimental data set, we studied the somatosensory representation of the five left‐hand digits of a subject on the basis of MEG‐recordings. The fingers were tactilely stimulated individually and synchronously, resulting in six different stimulus conditions (d1, d2, d3, d4, d5, and d1–5). It was expected that the extended source associated with the synchronous stimulation (condition d1–d5) would cover the sources corresponding to the individual finger stimulation (conditions d1,…,d5). The somatosensory evoked magnetic fields were recorded by means of a whole‐head MEG‐system with 151 axial first‐order gradiometers (CTF Systems Inc.). The signal was sampled at a rate of 625 Hz and low‐pass filtered at 200 Hz.

During the experiment, the subject's left‐hand digits received tactile stimulation in a random order either individually or synchronously, resulting in 1,000 trials per stimulus condition (d1, d2, d3, d4, d5, and d1–d5). The averaged signal of each condition at time points between 60 and 75 msec poststimulus corresponding to maximal signal amplitude was subjected to the SPMECS. It is known that the first cortical area to be activated during tactile stimulation is SI (areas 3b and 1), whereas SII and posterior parietal cortex exhibit MEG responses only at a somewhat later interval (beyond 80–90 msec) [Elbert et al., 1995b; Hari et al., 1993]. For the considered components at 60–75 msec latency range, it is conceivable that activities originate from within SI. Whereas it is possible to allow for sources anywhere on the whole cortical sheet, additional constraints should be introduced in order to minimize the number of degrees of freedom (meaningfully reduce the parameter space Θ^k). Therefore, a region located 1 cm anterior and posterior to the central sulcus of the right hemisphere (contralateral to the stimulated side) was considered to be the region of interest for source reconstruction (Fig. 3).

Figure 3.

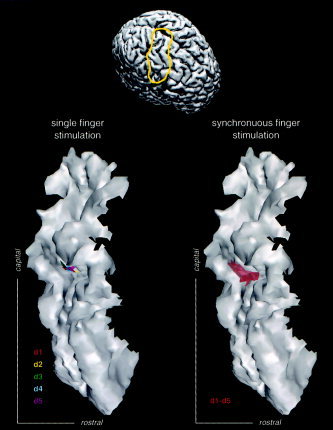
Somatosensory representation of a subjects left‐hand digits based on somatosensory magnetic field evoked by individual (condition d1, d2, d3, d4, and d5) and synchronous (condition d1–d5) stimulation of all five digits. The latter joint activity overlaps the single sources.

RESULTS

Simulations

Figure 1 displays L(θ) across source number for the simulated activity in absence of noise for 50,000 iterations. It should be noted that the Metropolis algorithm predominantly scans regions of the parameter space with higher LF values. Nevertheless, all regions are approached during the fitting procedure. The repetitive structure in the display is a result of the systematic numbering of the triangles of the analyzed sulcus.

As a measure for the accuracy of the reconstructed source the distance Δd between the central triangle of the estimated and the default source as well as the difference ΔR between their radius were chosen. The average and the maximum value of both parameters for all simulated noise and error types are presented in Tables II and III.

Table II.

EEG simulations: error estimates of source localization (Δd) and extend (ΔR) using distinct error sources

Error Source	Δd (mm)		ΔR (mm)
	Mean	Max	Mean	Max
Uncorrelated noise (level)
1%	0.7	3.0	0.0	0.0
5%	2.9	5.7	2.2	7.5
10%	4.0	5.7	3.3	7.5
Correlated noise (level)
1%	3.2	5.4	1.2	5.5
5%	5.1	8.2	2.8	9.0
10%	6.1	11.0	3.2	9.0
Activity distribution
Constant	0.0	—	0.0	—
Non‐constant	1.1	—	2.0	—
Electrode mislocalization
5.0 mm	1.3	3.0	0.0	0.0
10.0 mm	2.5	5.6	1.1	7.5

Table III.

MEG simulations: error estimates of source localization (Δd) and extend (ΔR) using distinct error sources

Error Source	Δd (mm)		ΔR (mm)
	Mean	Max	Mean	Max
Uncorrelated noise (level)
1%	0.7	3.2	0.1	0.5
5%	2.4	5.1	0.6	4.5
10%	2.5	5.1	0.6	4.5
Correlated noise (level)
1%	3.7	5.7	3.0	7.5
5%	5.0	8.2	4.0	8.0
10%	5.6	10.0	4.8	9.0
Activity distribution
Constant	0.0	—	0.0	—
Non‐constant	3.2	—	4.0	—
Head‐model center
2.5 mm	1.2	5.1	0.9	4.5
5.0 mm	1.8	5.1	1.1	6.5

The simulations for each noise and error type indicate that accuracy of the reconstructed source decreases with increasing noise level. Furthermore, the results suggest that the extension of the reconstructed source is systematically underestimated with increasing noise level.

The results for the reconstruction of the sources with different extensions are presented in Table IV. In the simulations, the source location is reconstructed correctly and the source size is generally overestimated due to the modeling of the edges. Thus, the overestimation decreases the larger the modeled source. The analysis of the confidence level of the estimated source extension showed: simulated source radius 10.0 mm; SD of source radius estimator 2.6 mm (noise level 1%), 6.0 mm (noise level 5%), and 8.4 mm (noise level 10%).

Table IV.

Predefined and estimated source areas of five different sources

Default source area (mm2)	228.2	170.5	79.7	29.1	9.3
Estimated source area (mm2)	228.2	234.7	132.3	68.4	39.4

Application

As shown by the ML method analysis, the somatosensory representation of the digits d1 to d5 are in accordance with a gradient from lateral to medial along the posterior wall of the central sulcus. The extension of the individual sources as obtained by the SPMECS analysis suggests an additive quality of the activated area (see Table V and Fig. 3).

Table V.

Source radius as estimated from neuromagnetic fields evoked by individual (d1, … , d5) and synchronous (d1–d5) tactile stimulation of the digits of the left hand

Stimulus condition	d1	d2	d3	d4	d5	d1–5
Radius (mm)	1.8	1.0	3.0	2.1	1.9	10.0

DISCUSSION

Simulations

The performed simulations demonstrate that the presented SPMECS is capable of assessing the location and size of an extended cortical source even under rather difficult circumstances, i.e., in the event of opposing activity being located at the anterior and posterior wall of an artificial sulcus, where both fractions tend to cancel each other when viewed from distant sensors.

Moreover, the adopted constant activity distribution represents an adequate approximation. However, it might lead to systematic underestimation of reconstructed sources if the analyzed activity distribution differs from constant. At the borders, smaller activity might be “overseen.”

Given the same noise level, the simulations revealed a stronger influence of correlated noise than uncorrelated noise. As measurement noise is a mixture of both types under experimental conditions, it is advisable to determine the noise covariance matrix in order to counteract their negative influence. However, as already pointed out in Methods, the number of samples necessary to guarantee a statistical independence for 128 or 151 sensors of the order of 2 · 10⁴ is, in general, not available. The simulations indicate that, on average, the source extension is underestimated with increasing noise level. Thus, to allow for comparison of source extension between different experimental conditions, an equal noise level is required.

Because erroneous localization of the sensor‐array position in MEG analysis leads to a systematic distortion of the magnetic field topography, the influence of this error is more pronounced as compared to electrode localization in EEG analysis. The latter was assumed to be non‐systematic. Due to this common problem for all source‐reconstruction methods, special attention should be paid to a stable head fixation. Additionally, tracking of the head position during the entire MEG‐measurement is recommended if technically feasible.

The simulations with respect to erroneous specification of the skull thickness revealed no bias on the ML estimator. A concomitant decrease of the ML function was accompanied by a broadening of the confidence intervals of modeled source parameters.

Application

The source analysis for the experimental data set using the ML method reveals similar extensions of the somatosensory representation of each single digit. Locations of individual sources correspond, furthermore, with the expected values. Simultaneous stimulation of all five digits (d1–d5) yields an area covering the individual finger representations. These results support the hypothesis that activation of larger skin areas results in a more extended activation at the level of the somatosensory cortex as compared to the stimulation of only parts of it.

General Discussion

The feasibility and significance of a maximum likelihood (ML) estimator for neuronal source location and extension was demonstrated through simulations and an application. The method presented in this study was developed in order to address the three requirements for an “ideal strategy” for modeling extended cortical sources presented in the introduction. A probabilistic approach was chosen in order to provide information on the source estimator‐statistics that better accounts for the ill‐posed character of the inverse problem, allowing for inference of the number of similarly appropriate solutions. In order to find the source configuration with maximum likelihood, the parameter space needs to be scanned as densely as possible, at least in ranges where parameters assume physiologically meaningful values. The implemented stochastic solver combined dense sampling in neighborhoods of high likelihood values with fast convergence [Schmidt et al., 1999].

According to requirements for an ideal source modeling approach, the SPMECS method introduces theoretically and experimentally confirmed a priori knowledge such as confining the location and the orientation of the modeled sources to the cortical surface and orthogonal to it in accordance with findings from mapping studies in primary sensory cortex [Mitzdorf, 1987]. Additionally, extended cortical sources were modeled as being contiguous in accordance with findings from mapping studies in primary sensory cortex [Pearson et al., 1999].

A constant current density was chosen as first‐order approximation since detailed information on the activity distribution across a cortical area is lacking thus far.

In order to test and present the current method, just one source was considered in our simulations. If the number of simultaneously active sources is known a priori, this information can be used as a constraint to obtain physiological meaningful solutions.

This was the case for the presented experimental application. Since magnetic activity was evoked in our experiment by unilateral tactile stimulation and peaked at a latency of about 50 msec, and since somatosensory evoked magnetic activity up to 60 msec originates solely from primary cortical regions [refer to Elbert et al., 1995b; Hari et al., 1993], the restriction to one source is justified. However, whenever the number of sources is less obviously preset, it might be derived from other considerations or experimental findings. Methods like PCA [Baumgartner et al. 1989], ICA [Bell and Sejnowski 1995; Makeig et al. 1996], MUSIC [Mosher et al. 1992], and Multi‐ECD models [Scherg and Berg 1991] can determine the number of independent topographies during a certain time interval. Alternatively, the number of sources can be considered as an additional unknown parameter and can be determined using the Metropolis algorithm or a hierarchical model.

At this point no additional assumptions have been included in the modeling. Nevertheless, further knowledge about other source features can be incorporated. If, for example, source polarity is known a priori, i.e., the flow of currents inside the pyramidal cells either points from the soma to the dendrites or vice versa, the number of possible source configurations can be further restricted by accordingly restricting its orientation.

Simulations and application of the ML method presented have demonstrated its reliability with respect to estimation of location and extension of the sources. In simulations, even in the demanding case of activation spread over opposing gyri, the source extension could be successfully identified. For somatosensory evoked fields, modeled source extensions for synchronous vs. individual finger stimulation were in good agreement with theoretical predictions.

At the same time, differences of the SPMECS method as compared with commonly used methods, i.e., minimum norm least squares (MNLS) methods [Sarvas, 1987; Wang et al., 1992, 1993], low‐resolution electromagnetic tomography (LORETA) [Pascual‐Marqui et al., 1994], Bayesian inference (BI) [Schmidt et al., 1999], and cortical patch (CP) [Kincses et al., 1999; Lütkenhöner et al., 1995] method, have to be noted. Firstly, the various methods differ with respect to the incorporated constraints on cortical activity. The activity distribution is modeled differently in the various methods. Minimum norm approaches follow the principle of parsimony by minimizing either the L2‐norm [Wang et al., 1992], the L1‐norm [Fuchs et al., 1999], or the spatial change [Pascual‐Marqui et al., 1994] of the overall underlying source current distribution. Even if the principle of parsimony is realized in various biological systems, it is not shown to be valid for summed neuronal currents. Furthermore, as a consequence of minimizing the norm of the source currents, polarity of cortical surface elements may vary from element to element, possibly resulting in patchy source polarizations. In contrast, the ML method models sources as contiguous and uniformly polarized, which is in agreement with experimental findings regarding the functional organization of the cortex [Pearson et al., 1999]. The same assumptions are made in the CP method. The latter method and the ML approach, in principal, allow for incorporation of arbitrary a priori source activity.

Secondly, coupling of activity within and between sources certainly depends on the distance between active regions. A straightforward strategy was applied in the BI method in the form introduced by Schmidt et al. [1999]: coupling between regions of activity in cortical volume elements was modeled as a function of their Euclidean 3D distance. However, the cortex of the human brain is a highly folded surface divided into numerous regions that are functionally specialized. Therefore, a spatial 3D neighborhood of cortical locations does not necessarily imply functional correlation. For example, the upper edge of the pre‐ and postcentral gyri are spatially close to each other, but are associated with motor and sensory functions, respectively. In order to account for the functional organization of the cortex resembling 2‐dimensional maps, CP and SPMECS methods consider coupling of neighboring cortical elements according to their 2D distance on an extracted cortical surface.

The SPMECS and BI method are to date the only methods modeling extended sources using a statistical approach. The BI method allows for and requires the specification of a priori knowledge, i.e., the a priori probability distribution of different activation parameters (amplitude, spatial activity correlation). However, estimated source parameters might depend strongly on the complex a priori probability distribution. Thus, under generalized conditions, it might be recommendable to exclude a bias due to inappropriate a priori information. In both the ML and BI approach, the error of the source parameters is described by confidence intervals, i.e., the parameter range in which the underlying “true” value can be found with a certain probability. In contrast, in the MNLS and the CP method, only a single solution is chosen, consequently neglecting further equally adequate solutions.

In conclusion, the SPMECS approach appears to be a promising method for estimating the extent of neural cortical sources from EEG or MEG data. In particular, under conditions where only limited information regarding source activation is available and where constraints known a priori may vary from experiment to experiment, the SPMECS method yields insight in source location, extension, and number.