Message passing on networks with loops

Significance

Message passing, a celebrated family of methods for performing calculations on networks, has led to many important results in physics, statistics, computer science, and other areas. The technique allows one to divide large network calculations into manageable pieces and hence solve them either analytically or numerically. However, the method has a substantial and widely recognized shortcoming, namely that it works poorly on networks that contain short loops. Unfortunately, most real-world networks contain many such loops, which limits the applicability of the method. In this paper we give a solution for this problem, demonstrating how message passing can be extended to any network, regardless of structure, allowing it to become a general tool for the quantitative study of network phenomena.

Abstract

Message passing is a fundamental technique for performing calculations on networks and graphs with applications in physics, computer science, statistics, and machine learning, including Bayesian inference, spin models, satisfiability, graph partitioning, network epidemiology, and the calculation of matrix eigenvalues. Despite its wide use, however, it has long been recognized that the method has a fundamental flaw: It works poorly on networks that contain short loops. Loops introduce correlations that can cause the method to give inaccurate answers or to fail completely in the worst cases. Unfortunately, most real-world networks contain many short loops, which limits the usefulness of the message-passing approach. In this paper we demonstrate how to rectify this shortcoming and create message-passing methods that work on any network. We give 2 example applications, one to the percolation properties of networks and the other to the calculation of the spectra of sparse matrices.

Networks occur in a wide range of contexts in physics, biology, computer science, engineering, statistics, the social sciences, and even arts and literature (1). Message passing (2–4), also known as belief propagation or the cavity method, is a fundamental technique for the quantitative calculation of a wide range of network properties, with applications to Bayesian inference (3), NP-hard computational problems (4, 5), statistical physics (4, 6, 7), epidemiology (8), community detection (9), and signal processing (10, 11), among many other things. Message passing can be used both as a numerical method for performing explicit computer calculations and as a tool for analytic reasoning about network properties, leading to new formal results about percolation thresholds (7), algorithm performance (9), spin glasses (12), and other topics. Many of the most powerful new results concerning networks in recent years have been derived from applications of message passing in one form or another.

Despite the central importance of the message-passing method, however, it also has a substantial and widely discussed shortcoming: It works only on trees, i.e., networks that are free of loops (4). More generously, one could say that it works to a good approximation on networks that are “locally tree-like,” meaning that they may contain long loops but no short ones, so that local neighborhoods within the network take the form of trees. However, most real-world networks that occur in practical applications of the method contain short loops, often in large numbers. When applied to such “loopy” networks, the method can give poor results and in the worst cases can fail to converge to an answer at all.

In this paper, we propose a remedy for this problem. We present a series of methods of increasing elaboration for the solution of problems on networks with loops. The first method in the series is equivalent to the standard message-passing algorithm of previous work, which gives poor results in many cases. The last one in the series gives exact results on any network with any structure, but is too complicated for practical application in most situations. In between are a range of methods that give progressively better approximations and can be highly accurate in practice, as we will show, yet are still simple enough for ready implementation. Indeed even the second member of the series—just one step better than the standard message-passing approach—already gives remarkably good results in real-world conditions. We demonstrate our approach with 2 example applications. The first one is to the solution of the bond percolation problem on an arbitrary network, including the calculation of the size of the percolating cluster and the distribution of sizes of small clusters. The second one is to the calculation of the spectra of sparse symmetric matrices, where we show that our method is able to calculate the spectra of matrices far larger than those accessible by conventional numerical means.

A number of approaches have been proposed previously for message passing on loopy networks. The most basic of these, which goes by the name of “loopy belief propagation,” is simply to apply the standard message-passing equations, ignoring the fact that they are known to be incorrect in general. While this might seem rash, it gives reasonable answers in some cases (11) and there are formal results showing that it can give bounds on the true value of a quantity in others (4, 7). Perturbation theories that treat loopy belief propagation as a zeroth-order approximation have also been considered (13). Broadly, it is found that these methods are suitable for networks that contain a subextensive number—and hence a vanishing density—of short loops, but not for networks with a nonvanishing density.

Some progress has been made for the case of networks that are composed of small subgraphs or “motifs” which are allowed to contain loops but which on a larger scale are connected in a loop-free way (14–16). For such networks one can write exact message-passing equations that operate at the higher level of the motifs and give excellent results for problems such as structural phase transitions in networks, network spectra, and the solution of spin models (6, 14–17). While effective for theoretical calculations on model networks, however, this approach is of little use in practical situations. To apply it to an arbitrary network one would first need to find a suitable decomposition of the network into motifs, and no general method for doing this is currently known or even whether such a decomposition exists.

A third approach is the method known as “generalized belief propagation,” which has some elements in common with the motif-based approach but is derived in a different manner, from approximations to the free energy (18, 19). This method, which is focused particularly on the solution of inference problems and related probabilistic calculations on networks, involves a hypergraph-like extension of traditional message passing that aims to calculate the joint distributions of 3 or more random variables at once, by contrast with the standard approach which focuses on 2-variable distributions. Generalized belief propagation was not originally intended as a method for solving problems on loopy networks but can be used in that way in certain cases. It is, however, quite involved in practice, requiring the construction of a nested set of regions and subregions within the network, leading to complex sets of equations.

In this paper we take a different approach. In the following sections we directly formulate a message-passing framework that works on real-world complex networks containing many short loops by incorporating the loops themselves directly into the message-passing equations. In traditional message-passing algorithms each node receives a message from each of its neighbors. In our approach they also receive messages from nodes they share loops with. By limiting the loops considered to a fixed maximum length, we develop a series of progressively better approximations for the solution of problems on loopy networks. The equations become more complex as loop length increases but, as we will show, the results given by the method are already impressively accurate even at shorter lengths.

Message Passing with Loops

Message-passing methods calculate some value or state on the nodes of a network by repeatedly passing information between nearby nodes until a self-consistent solution is reached. The approach we propose is characterized by a series of message-passing approximations defined as follows. In the zeroth approximation, which is equivalent to the standard message-passing method, we assume there are no loops in our network. This implies that the neighbors of a node are not connected to each other, which means they have independent states. It is this independence that makes the standard method work. In the next approximation we no longer assume that neighbors are independent. Instead, we assume that any correlation can be accounted for by direct edges between the neighbors, which is equivalent to allowing the network to contain triangles, the shortest possible kind of loop. In the next approximation after this one, we assume that neighbor correlations can accounted for by direct edges plus paths of length 2 between neighbors. Generally, in the $r$th approximation we assume that correlations between neighbors can be accounted for by paths of length $r$ and shorter.

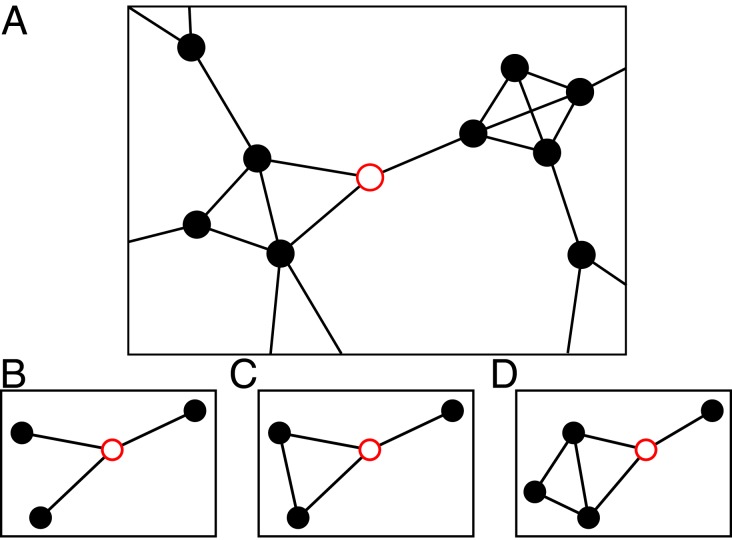
These successive approximations can be thought of as expressing the properties of nodes in terms of increasingly large neighborhoods and the edges they contain. The zeroth neighborhood $N_i^{\left(0\right)}$ of node $i$ contains $i$’s immediate neighbors and the edges connecting them to $i$, but nothing else. The first neighborhood $N_i^{\left(1\right)}$ contains $i$’s immediate neighbors and edges plus all length 1 paths between neighbors of $i$. The second neighborhood $N_i^{\left(2\right)}$ contains $i$’s neighbors and edges plus all length 1 and 2 paths between neighbors of $i$, and so forth. Fig. 1 shows an example of how these neighborhoods are constructed.

Fig. 1.

(A) A node (red open circle) and its immediate surroundings in a network. (B) In the zeroth (tree) approximation the neighborhood we consider consists of the neighbors of the focal node only. (C) In the first approximation we also include all length 1 paths between the neighbors. (D) In the second approximation we include all paths of lengths 1 and 2, and so forth.

Just as the conventional message-passing algorithm is exact on trees, our algorithms will be exact on networks with short loops. We define a primitive cycle of length $r$ starting at node $i$ to be a cycle such that at least one edge is not on a shorter cycle beginning and ending at $i$. Then our $r$th approximation is exact on networks that contain primitive cycles of length $r+2$ or less only. For networks that contain longer primitive cycles it will be an approximation, although as we will see it may be a good one.

Applications

Our approach is best demonstrated by example. In this section we derive message-passing equations on loopy networks for 2 specific applications: the calculation of cluster sizes for bond percolation and the calculation of the spectra of sparse matrices.

Percolation.

Consider the bond percolation process on an undirected network of $n$ nodes, where each edge is occupied independently with probability $p$ (20, 21). Occupied edges form connected clusters and we wish to know the distribution of the sizes of these clusters and whether there exists a giant or percolating cluster that occupies a nonvanishing fraction of the network in the limit of large network size.

Let us define the $r$th neighborhood $N_i^{\left(r\right)}$ of node $i$ as previously and then define a random variable ${\mathrm{\Gamma }}_i$ for our percolation process to be the set of nodes within $N_i^{\left(r\right)}$ that are reachable from $i$ by traversing occupied edges only. Our initial goal is to compute the probability ${\pi }_i\left(s\right)$ that node $i$ belongs to a nonpercolating cluster of size $s$. We do this in 2 stages. First, we compute the conditional probability ${\pi }_i\left(s|{\mathrm{\Gamma }}_i\right)$ of belonging to a cluster of size $s$ given the set of reachable nodes. Then we average over ${\mathrm{\Gamma }}_i$ to get the full probability ${\pi }_i\left(s\right)$.

Suppose that node $i$ belongs to a cluster of size $s$. If our network contains no primitive cycles longer than $r+2$, then the set of nodes ${\mathrm{\Gamma }}_i$ would become disconnected from one another were we to remove all edges in the neighborhood $N_i^{\left(r\right)}$—the removal of these edges removes any connections within the neighborhood and there can be no connections via paths outside the neighborhood since such a path would constitute a primitive cycle of length longer than $r+2$. Hence the sizes $s_j$ of the clusters to which the nodes in $N_i^{\left(r\right)}$ would belong after this removal must sum to $s-1$ (the $s$th and last node being provided by $i$ itself). This observation allows us to write

$${\pi }_i\left(s\mid {\mathrm{\Gamma }}_i\right)=\sum _{\left\{s_j:j\in {\mathrm{\Gamma }}_i\right\}}\left[\prod _{j\in {\mathrm{\Gamma }}_i}{\pi }_{i\leftarrow j}\left(s_j\right)\right]\delta \left(s-1,{\sum }_{j\in {\mathrm{\Gamma }}_i}{s}_j\right),$$ [1]

where ${\pi }_{i\leftarrow j}\left(s\right)$ is the probability that node $j$ is in a cluster of size $s$ once the edges in $N_i^{\left(r\right)}$ are removed.

We can now write a generating function for ${\pi }_i\left(s\mid {\mathrm{\Gamma }}_i\right)$ as follows:

$$\begin{array}{ll}\hfill H_i& \left(z\mid {\mathrm{\Gamma }}_i\right)=\sum _{s=1}^{\infty }{\pi }_i\left(s\mid {\mathrm{\Gamma }}_i\right)z^s\hfill \\ \hfill & =\sum _{s=1}^{\infty }{z}^s\left\{\sum _{\left\{s_j:j\in {\mathrm{\Gamma }}_i\right\}}\left[\prod _{j\in {\mathrm{\Gamma }}_i}{\pi }_{i\leftarrow j}\left(s_j\right)\right]\delta \left(s-1,{\sum }_{j\in {\mathrm{\Gamma }}_i}{s}_j\right)\right\}\hfill \\ \hfill & =z\prod _{j\in {\mathrm{\Gamma }}_i}\sum _{s_j=1}^{\infty }{z}^{s_j}{\pi }_{i\leftarrow j}\left(s_j\right).\hfill \end{array}$$ [2]

To calculate the full probability ${\pi }_i\left(s\right)$ we average ${\pi }_i\left(s\mid {\mathrm{\Gamma }}_i\right)$ over sets ${\mathrm{\Gamma }}_i$ to get ${\pi }_i\left(s\right)={⟨{\pi }_i\left(s\mid {\mathrm{\Gamma }}_i\right)⟩}_{{\mathrm{\Gamma }}_i}$, with the average weighted according to the sum of the probabilities of all edge configurations that correspond to a particular ${\mathrm{\Gamma }}_i$. The probability of any individual edge configuration is simply $p^k{\left(1-p\right)}^{m-k}$, where $p$ is the edge occupation probability as previously, $m$ is the number of network edges in the neighborhood $N_i^{\left(r\right)}$, and $k$ is the number that are occupied. Performing the same average on Eq. 2 gives us

$$H_i\left(z\right)=\sum _{s=1}^{\infty }{\pi }_i\left(s\right)z^s=z{G}_i\left({\mathbf{H}}_{i\leftarrow }\left(z\right)\right),$$ [3]

where $G_i\left(\mathbf{y}\right)={⟨{\prod }_{j\in N_i^{\left(r\right)}}{y}_j^{w_{ij}}⟩}_{{\mathrm{\Gamma }}_i}$ is a generating function for the random variable $w_{ij}$, which takes the value 1 if $j\in {\mathrm{\Gamma }}_i$ and 0 otherwise, and ${\mathbf{H}}_{i\leftarrow }\left(z\right)$ is the vector with elements $H_{i\leftarrow j}\left(z\right)$ for nodes $j$ in $N_i^{\left(r\right)}$.

To complete the calculation we need to evaluate $H_{i\leftarrow j}\left(z\right)$, whose computation follows the same logic as for $H_i\left(z\right)$, the only difference being that in considering the neighborhood of node $j$ we must remove the entire neighborhood of $i$ first, as described above. Doing this leads to

$$H_{i\leftarrow j}\left(z\right)=z{G}_{i\leftarrow j}\left({\mathbf{H}}_{j\leftarrow }\left(z\right)\right),$$ [4]

where $G_{i\leftarrow j}\left(\mathbf{y}\right)$ is the equivalent of $G_i\left(\mathbf{y}\right)$ when $N_i^{\left(r\right)}$ is removed. (A detailed derivation of Eq. 4 is given in SI Appendix, Derivation of the Message-Passing Equations.) If we can solve this equation self-consistently for ${\mathbf{H}}_{j\leftarrow }\left(z\right)$, we can substitute the solution into Eq. 3 to compute the full cluster size-generating function. The message-passing method involves solving Eq. 4 by simple iteration: We choose suitable starting values, for instance at random, and iterate the equations to convergence.

From the cluster size-generating function we can calculate a range of quantities of interest. For example, the probability that node $i$ belongs to a small cluster (of any size) is $H_i\left(1\right)={\sum }_s{\pi }_i\left(s\right)$. If it does not belong to a small cluster, then necessarily it belongs to the percolating cluster and hence the expected fraction $S$ of the network taken up by the percolating cluster is

$$S=1-\frac{1}{n}\sum _i{H}_i\left(1\right).$$ [5]

Similarly, the average value of $s_i$ is

$$\begin{array}{ll}\hfill ⟨s_i⟩& =\sum _{s=1}^{\infty }s{\pi }_i\left(s\right)=H_i^{\prime }\left(1\right)\hfill \\ \hfill & =H_i\left(1\right)+\sum _{j\in N_i^{\left(r\right)}}{H}_{i\leftarrow j}^{\prime }\left(1\right){\partial }_j{G}_i\left({\mathbf{H}}_{i\leftarrow }\right),\hfill \end{array}$$ [6]

where $H\prime$ is the derivative of $H$ and ${\partial }_j{G}_i$ is the partial derivative of $G_i$ with respect to its $j$th argument. $H_{i\leftarrow j}^{\prime }\left(1\right)$ can be found by differentiating Eq. 4 and setting $z=1$ to give the self-consistent equation

$$H_{i\leftarrow j}^{\prime }\left(1\right)=H_{i\leftarrow j}\left(1\right)+\sum _{k\in N_{j\backslash i}^{\left(r\right)}}{H}_{j\leftarrow k}^{\prime }\left(1\right){\partial }_k{G}_{i\leftarrow j}\left({\mathbf{H}}_{j\leftarrow }\right),$$ [7]

where $N_{j\backslash i}^{\left(r\right)}$ denotes the neighborhood $N_j^{\left(r\right)}$ with $N_i^{\left(r\right)}$ removed.

While these equations are straightforward in principle, implementing them in practice presents some additional challenges. Computing the generating functions $G_i\left(\mathbf{y}\right)$ and $G_{i\leftarrow j}\left(\mathbf{y}\right)$ can be demanding, since it requires us to perform an average over the occupancy configurations of all edges within the neighborhoods $N_i^{\left(r\right)}$ and $N_{j\backslash i}^{\left(r\right)}$, and the number of configurations increases exponentially with neighborhood size. For small neighborhoods, such as those found on low-dimensional lattices, it is feasible to average exhaustively, but for many complex networks this is not possible. In such cases we instead approximate the average by Monte Carlo sampling of configurations—see SI Appendix, Monte Carlo Algorithm for G_i(y) for details. A nice feature of the Monte Carlo procedure is that the samples need be taken only once for the entire calculation and can then be reused on successive iterations of the message-passing process.

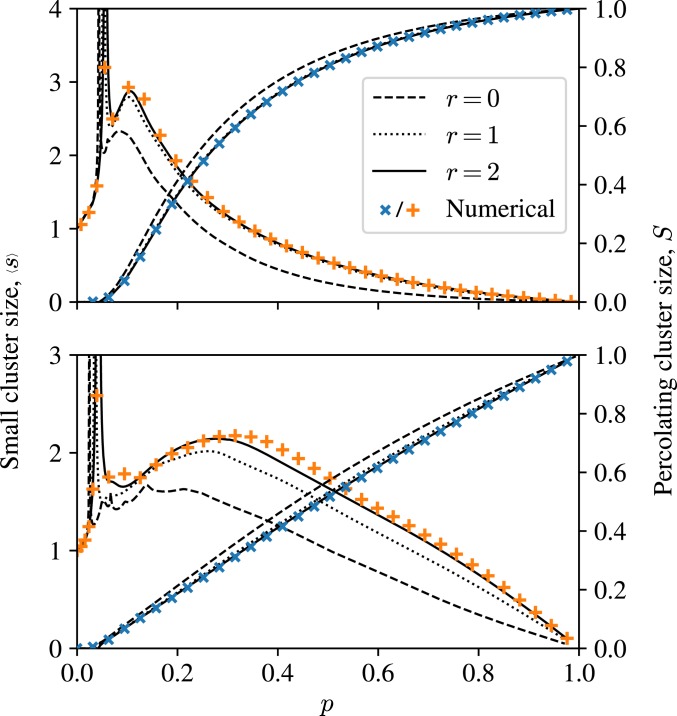
In practice the method gives excellent results. We show example applications to 2 real-world networks in Fig. 2, the first one a social network of coauthorship relations between scientists in the field of condensed-matter physics (22) and the second one a network of trust relations between users of the pretty good privacy (PGP) encryption software (23). Both networks have a high density of short loops. For each network Fig. 2 shows, as a function of $p$, several different estimates of both the average size $⟨s⟩$ of a small cluster and the size $S$ of the percolating cluster as a fraction of $n$. First we show an estimate made using standard message passing (Fig. 2, dashed line)—the $r=0$ approximation in our nomenclature—which ignores loops and is expected to give poor results. Second, we show the next 2 approximations in our series, those for $r=1$ and $r=2$ (Fig. 2, dotted and solid lines, respectively), with $G_i\left(\mathbf{y}\right)$ and $G_{i\leftarrow j}\left(\mathbf{y}\right)$ estimated by Monte Carlo sampling as described above. We use only 8 samples for each node $i$ but the results are nonetheless impressively accurate. Third, we show for comparison a direct numerical estimate of the quantities in question made by conventional simulation of the percolation process.

Fig. 2.

Percolating cluster size ($\times$ symbols) and average cluster size (+ symbols) for 2 real-world networks. (Top) The largest component of a coauthorship network of 13,861 scientists (22). (Bottom) A network of 10,680 users of the PGP encryption software (23).

For both networks we see the same pattern. The traditional message-passing method fares poorly, as expected, giving estimates that are substantially in disagreement with the simulation results, particularly for the calculations of average cluster size. The $r=1$ approximation, on the other hand, does significantly better and the $r=2$ approximation does better still, agreeing closely with the numerical results for all measures on both networks. In these examples at least, it appears that the $r=2$ method gives accurate results for bond percolation, where standard message passing fails.

The message-passing algorithm is relatively fast. For $r\le 1$ each node receives a message from each neighbor on each iteration, and so on a network with mean degree $c$ there are $cn$ messages passed per iteration. For $r\ge 2$ the number of messages depends on the network structure. On trees the number of messages remains unchanged at $cn$ as $r$ increases but on networks with loops it grows and for large numbers of loops it can grow exponentially. In the common sparse case where the size of the neighborhoods does not grow with $n$, however, the number of messages is linear in $n$ for fixed $r$ and hence so is the running time for each iteration. It is not known in general how many iterations are needed for message-passing methods to reach convergence, but elementary heuristic arguments suggest the number should be on the order of the diameter of the network, which is typically $\mathrm{O}\left(\log n\right)$. Thus we expect overall running time to be $\mathrm{O}\left(n\log n\right)$ for sparse networks at fixed $r$.

This makes the algorithm quite efficient, although direct numerical simulations of percolation run comparably fast, so the message-passing approach does not offer a speed advantage over traditional approaches. However, the 2 approaches are calculating different things. Traditional simulations of percolation perform a calculation for one particular realization of bond occupancies. If we want average values over many realizations, we must perform the average explicitly, repeating the whole simulation for each realization. The message-passing approach, on the other hand, computes the average over realizations in a single calculation and no repetition is necessary, making it potentially the faster method in some situations.

In the next section we demonstrate another example application of our method, to the calculation of the spectrum of a sparse matrix, where traditional and message-passing calculations differ substantially in their running time, the message-passing approach being much faster, making calculations possible for large systems whose spectra cannot be computed in any reasonable amount of time by traditional means.

Matrix Spectra.

For our second example application we show how the message-passing method can be used to compute the eigenvalue spectrum of a sparse symmetric matrix. Any $n\times n$ symmetric matrix can be thought of as an undirected weighted network on $n$ nodes and we can use this equivalence to apply the message-passing method to such matrices.

The spectral density of a symmetric matrix $\mathbf{A}$ is the quantity

$$\rho \left(x\right)=\frac{1}{n}\sum _{k=1}^n\delta \left(x-{\lambda }_k\right),$$ [8]

where ${\lambda }_k$ is the $k$th eigenvalue of $\mathbf{A}$, and $\delta \left(x\right)$ is the Dirac delta function. Following standard arguments (24), we can show that the spectral density is equal to the imaginary part of the complex function

$$\begin{array}{ll}\hfill \rho \left(z\right)& =-\frac{1}{n\pi }\sum _{k=1}^n\frac{1}{z-{\lambda }_k}=-\frac{1}{n\pi }Tr{\left(z\mathbf{I}-\mathbf{A}\right)}^{-1}\hfill \\ \hfill & =-\frac{1}{n\pi z}\sum _{i=1}^n\sum _{s=0}^{\infty }\frac{X_i^s}{z^s},\hfill \end{array}$$ [9]

where $X_i^s={\left[{\mathbf{A}}^s\right]}_{ii}$ is the $i$th diagonal element of ${\mathbf{A}}^s$, and $z=x+i\eta$ and we take the limit as $\eta \to 0$ from above. The imaginary part $\eta$ acts as a resolution parameter that broadens the delta-function peaks in Eq. 8 by an amount roughly equal to its value.

The quantities $X_i^s={\left[{\mathbf{A}}^s\right]}_{ii}$ can be related to sums over closed walks in the equivalent network. If we consider the “weight” of a walk to be the product of the matrix elements on the edges it traverses, then $X_i^s$ is the sum of the weights of all closed walks of length $s$ that start and end at node $i$.

A closed walk from $i$ need not visit $i$ only at its start and end, however. It can return to $i$ any number of times over the course of the walk. The simplest case, where it returns just once at the end of the walk, we call an excursion. A more general closed walk that returns to node $i$ exactly $m$ times can be thought of as a succession of $m$ excursions. Such a walk will have length $s$ if those $m$ excursions have lengths $s_1\dots s_m$ with ${\sum }_{u=1}^m{s}_u=s$.

With this in mind, let $Y_i^s$ be the sum of the weights of all excursions of length $s$ that start and end at node $i$. Then the sum $X_i^s$ over closed walks of length $s$ can be written in terms of $Y_i^s$ as

$$X_i^s=\sum _{m=0}^{\infty }\left[\sum _{s_1=1}^{\infty }\dots \sum _{s_m=1}^{\infty }\delta \left(s,{\sum }_{u=1}^m{s}_u\right)\prod _{u=1}^m{Y}_i^{s_u}\right].$$ [10]

Using this result, and defining the function

$$H_i\left(z\right)=\sum _{s=1}^{\infty }\frac{Y_i^s}{z^{s-1}},$$ [11]

we find after some algebra that

$$\rho \left(z\right)=-\frac{1}{n\pi }\sum _{i=1}^n\frac{1}{z-H_i\left(z\right)}.$$ [12]

(See SI Appendix, Derivation of the Message-Passing Equations for a detailed derivation.) Thus, if we can calculate $H_i\left(z\right)$, then we can calculate $\rho \left(z\right)$. This we do as follows.

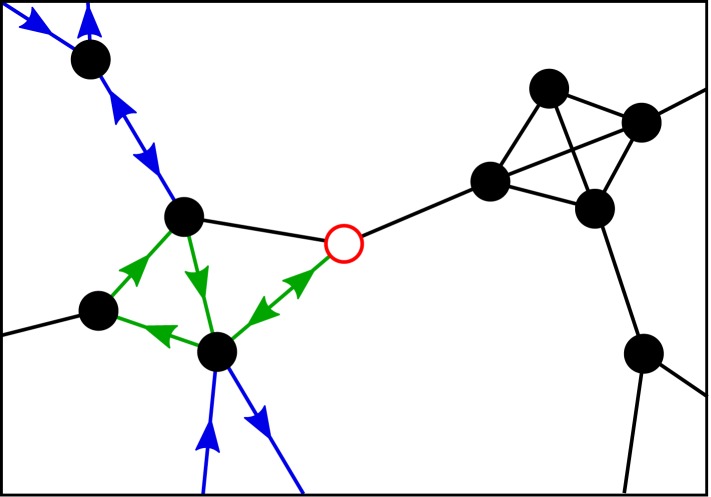
Consider the neighborhood $N_i^{\left(r\right)}$ around $i$. If there are no primitive cycles of length longer than $r+2$ in our network, then all cycles starting at $i$ are already included within the neighborhood, which means that any excursion from $i$ takes the form of an excursion $w$ within the neighborhood plus some number of additional closed walks outside the neighborhood each of which starts at one of the nodes in $w$ and returns some time later to the same node (Fig. 3). The additional walks must necessarily return to the same node they started at since if they did not, they would complete a cycle outside the neighborhood, of which by hypothesis there are none.

Fig. 3.

An example excursion from the central node (red open circle). The excursion is equivalent to an excursion inside the neighborhood, shown with green arrows, plus closed walks to regions outside of the neighborhood, shown in blue.

Let the length of the excursion $w$ be $l+1$, meaning that it visits $l$ nodes $j_1\dots j_l$ (not necessarily distinct) within the neighborhood other than the starting node $i$, and let $s_j$ be the length of the external closed walk (if any) that starts at node $j$ or zero if there is no such walk. The total length of the complete excursion from $i$ will then be $l+1+{\sum }_{j\in w}{s}_j$ and the sum of the weights of all excursions of length $s$ with $w$ as their foundation will be

$$\left|w\right|\sum _{\left\{s_j:j\in w\right\}}\delta \left(s,l+1+\sum _{j\in w}{s}_j\right)\prod _{j\in w}{X}_{i\leftarrow j}^{s_j},$$ [13]

where $\left|w\right|$ is the weight of $w$ itself and $X_{i\leftarrow j}^s$ is the sum of weights of length-$s$ walks from node $j$ if the neighborhood $N_i^{\left(r\right)}$ is removed from the network. By a similar argument to the one that led to Eq. 10, we can express $X_{i\leftarrow j}^s$ in terms of the sum $Y_{i\leftarrow j}^s$ of excursions from $j$; thus

$$X_{i\leftarrow j}^s=\sum _{m=0}^{\infty }\left[\sum _{s_1=1}^{\infty }\dots \sum _{s_m=1}^{\infty }\delta \left(s,{\sum }_{u=1}^m{s}_u\right)\prod _{u=1}^m{Y}_{i\leftarrow j}^{s_u}\right].$$ [14]

And the quantity $Y_i^s$ appearing in Eq. 11 can be calculated by summing Eq. 13 first over the set of excursions of length $l+1$ in the neighborhood of $i$ and then over $l$. This allows us to write Eq. 11 as

$$H_i\left(z\right)=\sum _{w\in W_i}\left|w\right|\prod _{j\in w}\frac{1}{z-H_{i\leftarrow j}\left(z\right)},$$ [15]

where $W_i$ is the complete set of excursions of all lengths in the neighborhood of $i$ and we have defined

$$H_{i\leftarrow j}\left(z\right)=\sum _{s=1}^{\infty }\frac{Y_{i\leftarrow j}^s}{z^{s-1}}.$$ [16]

Following an analogous line of argument for this function we can show similarly that

$$H_{i\leftarrow j}\left(z\right)=\sum _{w\in W_{j\backslash i}}\left|w\right|\prod _{k\in w}\frac{1}{z-H_{j\leftarrow k}\left(z\right)}.$$ [17]

Eq. 17 defines our message-passing equations for the spectral density. By iterating these equations to convergence from suitable starting values we can solve for the values of the messages $H_{i\leftarrow j}\left(z\right)$ and then substitute into Eqs. 12 and 15 to get the spectral density itself.

As with our percolation example, the utility of this approach relies on our having an efficient method for evaluating the sum in Eq. 17. Fortunately there is such a method, as follows. Let ${\mathbf{v}}_{i\leftarrow j}$ be the vector with elements $v_{i\leftarrow j,k}=A_{jk}$ if nodes $j$ and $k$ are directly connected in $N_{j\backslash i}^{\left(r\right)}$ and 0 otherwise. Further, let ${\mathbf{A}}^{i\leftarrow j}$ be the matrix of the neighborhood of $j$ with the neighborhood of $i$ removed, such that

$$A_{kl}^{i\leftarrow j}=\left\{\begin{array}{cc}{A}_{kl}\hfill & \hspace{1em}\text{for}\hspace{0.17em}k,l\ne j\hspace{0.17em}\text{and edge}\left(k,l\right)\in N_{j\backslash i}^{\left(r\right)},\hfill \\ 0\hfill & \hspace{1em}\text{otherwise},\hfill \end{array}\right.$$ [18]

and let ${\mathbf{D}}^{i\leftarrow j}\left(z\right)$ be the diagonal matrix with entries $D_{kk}^{i\leftarrow j}=z-H_{j\leftarrow k}\left(z\right)$. As shown in SI Appendix, Derivation of the Message-Passing Equations, Eq. 17 can then be written

$$H_{i\leftarrow j}\left(z\right)=A_{jj}+{\mathbf{v}}_{i\leftarrow j}^T{\left({\mathbf{D}}^{i\leftarrow j}-{\mathbf{A}}^{i\leftarrow j}\right)}^{-1}{\mathbf{v}}_{i\leftarrow j}.$$ [19]

Since the matrices in this equation are the size of the neighborhood, each message update requires us to invert only a small matrix, which gives us a linear-time algorithm for each iteration of the message-passing equations and an overall running time of $\mathrm{O}\left(n\log n\right)$ for sparse networks with fixed neighborhood sizes or for the equivalent sparse matrices.

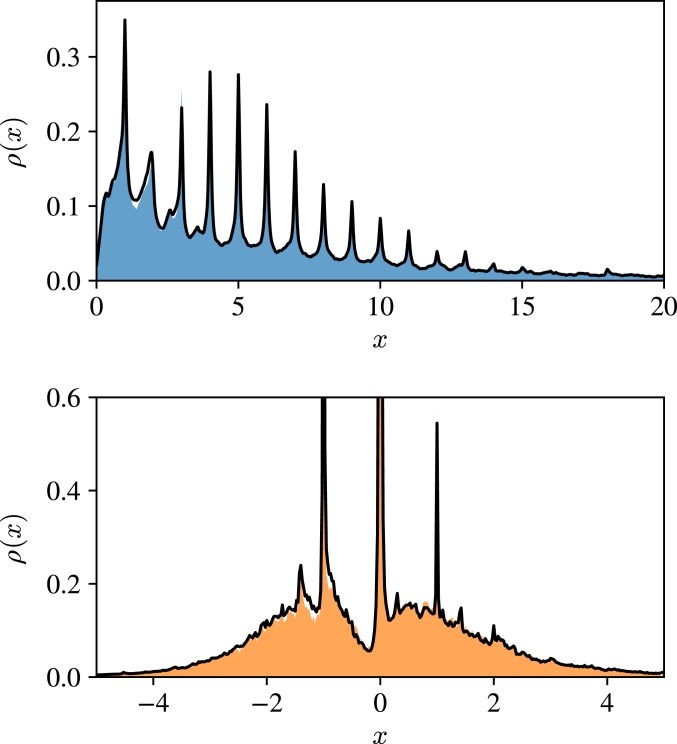
As an example of this method, we show in Fig. 4 spectra for the same 2 real-world networks that we used in Fig. 2. To demonstrate the flexibility of the method we calculate different spectra in the 2 cases: For the coauthorship network we calculate the spectrum of the graph Laplacian; for the PGP network we calculate the spectrum of the adjacency matrix. For each network the black curve in Fig. 4 shows the spectral density calculated using the message-passing method with $r=1$. We also calculate the full set of eigenvalues of each network directly using traditional numerical methods and substitute the results into Eq. 9 to compute the spectral density, shown as the shaded areas in Fig. 4. As we can see, the agreement between the 2 methods is excellent for both networks. There are a few regions where small differences are visible but in general they agree closely. Extending the calculation to the next ($r=2$) approximation gives a modest further improvement in the results.

Fig. 4.

Matrix spectra for the same 2 networks that were used in Fig. 2. (Top) The spectrum of the graph Laplacian of the coauthorship network. (Bottom) The spectrum of the adjacency matrix of the PGP network. The shaded areas show the spectral density calculated by direct numerical diagonalization. The black lines show the $r=1$ message-passing approximation. The broadening parameter $\eta$ was set to 0.05 (Top) and 0.01 (Bottom).

The $\mathrm{O}\left(n\log n\right)$ running time of the message-passing algorithm significantly outstrips that of traditional numerical diagonalization. Complete spectra are normally calculated using the QR algorithm, which runs in time $\mathrm{O}\left(n^3\right)$ and is consequently much slower as system size becomes large. The Lanczos algorithm is faster, but typically gives only a few leading eigenvalues and not a complete spectrum—it takes time $\mathrm{O}\left(rn\right)$ to compute $r$ eigenvalues of a sparse matrix. The kernel polynomial method (25) is capable of computing complete spectra for sparse matrices, but requires Monte Carlo evaluation of the traces of large matrix powers, which has slow convergence and is always only approximate, even in cases where our method gives exact results.

This opens up the possibility of using our approach to calculate the spectral density of networks and matrices significantly larger than those that can be tackled by traditional means. As an example, we have used the message-passing method to compute the spectral density of one network with 317,080 nodes. This is significantly larger than the largest systems that can be diagonalized using the QR algorithm, which on current (nonparallel) commodity hardware is limited to a few tens of thousands of nodes in practical running times.

Conclusions

In this paper we have described a class of message-passing methods for performing calculations on networks that contain short loops, a situation in which traditional message passing often gives poor results or may fail to converge entirely. We derive message-passing equations that account for the effects of loops up to a fixed length that we choose, so that calculations are exact on networks with no loops longer than this. In practice we achieve excellent results on real-world networks by accounting for loops up to length 3 or 4 only, even if longer loops are present.

We have demonstrated our approach with 2 example applications, one to the calculation of bond percolation properties of networks and the other to the calculation of the spectra of sparse matrices. In the first case we develop message-passing equations for the size of the percolating cluster and the average size of small clusters and find that these give good results, even on networks with an extremely high density of short loops. For the calculation of matrix spectra, we develop a message-passing algorithm for the spectral density that gives results in good agreement with traditional numerical diagonalization but in much shorter running times. Where traditional methods are limited to matrices with at most a few tens of thousands of rows and columns, our method can be applied to cases with hundreds of thousands at least.

There are a number of possible directions for future work on this topic. Chief among them is the application of the method to other classes of problems, such as epidemiological calculations, graph coloring, or spin models (SI Appendix, Other applications, for a brief discussion). Many extensions of the calculations in this paper are also possible, including the incorporation of longer primitive cycles in the message-passing equations, development of more efficient algorithms for very large systems, and applications to individual examples of interest such as the computation of spectra for very large graphs. Finally, while our example applications are to real-world networks, the same methods could in principle be applied to model networks and in particular to ensembles of random graphs, which opens up the possibility of additional analytic results about such models. These possibilities, however, we leave for future research.

Data Availability Statement.

All data discussed in this paper are available to readers.