Effects of ignoring clustered data structure in confirmatory factor analysis of ordered polytomous items: a simulation study based on PANSS

Abstract

Statistical theory indicates that hierarchical clustering by interviewers or raters needs to be considered to avoid incorrect inferences when performing any analyses including regression, factor analysis (FA) or item response theory (IRT) modelling of binary or ordinal data. We use simulated Positive and Negative Syndrome Scale (PANSS) data to show the consequences (in terms of bias, variance and mean square error) of using an analysis ignoring clustering on confirmatory factor analysis (CFA) estimates. Our investigation includes the performance of different estimators, such as maximum likelihood, weighted least squares and Markov Chain Monte Carlo (MCMC). Our simulation results suggest that ignoring clustering may lead to serious bias of the estimated factor loadings, item thresholds, and corresponding standard errors in CFAs for ordinal item response data typical of that commonly encountered in psychiatric research. In addition, fit indices tend to show a poor fit for the hypothesized structural model. MCMC estimation may be more robust against clustering than maximum likelihood and weighted least squares approaches but further investigation of these issues is warranted in future simulation studies of other datasets. Copyright © 2015 John Wiley & Sons, Ltd.

Introduction

The assessment tools used in many disciplines including psychiatric and psychopathology research are often administered by interviewers or raters rather than being completed by patients. Typically in psychiatric research, a single rater might assess multiple patients. Such complex data structures are encountered, for example, when examining relationships between self‐reported and clinician rated measures, when screening instruments are validated against assessments of psychopathology, or when researching topics such as the factorial validity of psychosis symptoms. Different types of nesting are possible, however, such as when multiple raters are involved in the assessment of a single patient.

The rater is usually either a clinician who provides the treatment or a researcher who rates patients to obtain information that can contribute to the evaluation of a symptomatology in terms of severity estimates. One example of such a situation is the use of the Positive and Negative Syndrome Scale (PANSS) for the assessment of severity of symptoms of schizophrenia (Kay et al., 1987). Although clinical raters in studies typically reported in psychiatry are thoroughly trained to achieve the most accurate and valid ratings possible, their ratings may still depend on their experience, subjective perception of the symptoms and syndrome under investigation or other personal judgements. Even if high inter‐rater reliability is established, part of the variability between patients can still be attributed to differences between raters. This situation leads to some degree of correlation among measurements on patients who are assessed by the same rater, such that the ones evaluated by the same rater appear to be more similar to each other than they are to other patients. Traditional factor analytic methods are grounded on the assumption that the data being analysed originate from independent and identically distributed observations (Bentler and Chou, 1987; Hox, 1993). This crucial assumption is obviously violated in the case of clustered data, and the results of confirmatory factor analysis (CFA) or related item response models may then be subject to bias.

Statistical developments have attempted to address spurious correlations between individuals within a cluster. Hierarchical modelling approaches have been developed for this purpose. Such techniques are also known as multilevel or hierarchical modelling. Although originally developed for a variety of regression models (De Leeuw and Kreft, 1986; Gelman and Hill, 2007), these techniques quickly became popular in latent variable applications, including factor analysis (FA) and item response theory (IRT) (Fox, 2005; Goldstein and Browne, 2005). If the data contain information on which rater assessed each patient, these methods provide a potentially effective and statistically well‐justified approach to account for inter‐correlation effects and, thereby, accurately describing the latent structure of the data.

Regrettably, missing identification of the cluster to which each individual belongs (i.e. not knowing exactly which patient was rated by which rater) is a problem that is often encountered with empirical datasets in psychiatric research. Such identification may be missing because the study is not designed to collect this information, for reasons of confidentiality, or simply because this information is lost. In such situations, the classic analytic approach for covariance structure modelling usually employs traditional (single‐level) FA. The consequences of this strategy in CFA have been studied using a Monte Carlo design (Julian, 2001). The results show that when the variables exhibit minimal levels of intra‐class correlation (less than 0.05), the chi‐square fit statistic, the parameter estimates, and the estimated standard errors are relatively unbiased. As the level of intra‐class correlation increases, bias is seen in all of these quantities. In addition, the effect of ignoring the multilevel data structure on the estimation quality becomes more severe as the group/member ratio decreases. Further, Julian (2001) reported slight overestimation of the majority of parameters in factor analytic models.

Another study targeting the importance of multilevel analysis in structural equation modelling was published by Muthén and Satorra (1995). They found that the standard errors of conventional analysis are underestimated as soon as positive intra‐class correlation coefficients (ICCs) are observed and clustering is ignored. In addition, the chi‐square statistic is inflated. However, the bias of estimated model parameter was found to be negligible for ICCs lower than 0.10.

The aim of the present study is to provide more insight into these features for psychiatric researchers who are aware of multilevel modelling as a topic, but have not been exposed to examples from within the field of mental health research using hierarchical factor models. We aim to show the consequences of ignoring patient clustering (within raters) in a psychiatric assessment using factor analytic methods applied to simulated data. The data is simulated according to the well‐known and validated structure of the PANSS as an illustrative case‐example and the impact of clustering on parameter estimates is considered for a typical setting in which patients are nested within rater and each patient is assessed by only a single rater (researcher or clinician).

Multilevel structural equation modelling

Multilevel modelling (Goldstein, 2011) is a class of analytical methods that has been developed to address issues related to clustering. Its name conveys that different levels are considered – individuals/patients are at the lower (within) level, and raters or services are considered as units at the higher (between) level.

There are three developmental perspectives that have defined multilevel structural equation models: the Reticular Action Model (RAM, McArdle and McDonald, 1984; McDonald, 1994); the Linear Structural Relationships (LISREL) model (Jöreskog, 1970; Jöreskog and Sörbom, 1989); the model of Muthén (Muthén, 1984, 1989) and a range of software implementations e.g. Mplus (Muthén and Muthén, 1998–2013), glamm in Stata (Rabe‐Hesketh et al., 2004), WinBUGS (Lunn et al., 2000) and others. The main aim of all developmental lines of multilevel structural equation models is to separate between‐level and within‐level variability within a framework of covariance matrices, i.e. to separate between‐level and within‐level covariance matrices. This approach allows for simultaneous estimation of covariance relations at both levels.

The general modelling framework used in this article is based on the one developed by Muthén (1984). The multilevel considerations of this general covariance structure model have been described in a series of publications (Muthén, 1989, 1991, 1994) and implemented in the Mplus software. Muthén (1991) specified the following separate factor analytic models for between‐ and within‐level covariance matrices:

$${\mathrm{\Sigma }}_B={\mathrm{\Lambda }}_B{\mathrm{\Psi }}_B\mathrm{\Lambda }{\prime }_B+{\mathrm{\Theta }}_B$$ (1)

and

$${\mathrm{\Sigma }}_W={\mathrm{\Lambda }}_W{\mathrm{\Psi }}_W\mathrm{\Lambda }{\prime }_W+{\mathrm{\Theta }}_W\text{,}$$ (2)

where Σ represents an observed covariance matrix, Λ is a matrix of factor loadings, Θ is a factor covariance matrix, Θ is a covariance matrix of uniquenesses with variances of measurement errors on the diagonal, and the subscripts B and W refer to the between‐ and within‐level covariances, respectively. Each formula represents the factor structure at the corresponding level. Within‐level factor structure and estimated parameters have the same interpretation as in traditional CFA. The between‐level factor structure explains the variation of the intercepts of the within‐level observed variables. The latent factors on between‐level may therefore refer to lenient/strict clinicians’ symptom ratings.

Several issues arise when data are ordinal rather than continuous. In a two‐level factor model for ordinal variables, for example, a threshold model that relates a set of continuous latent variables to the observed ordinal counterparts must also be defined (Grilli and Rampichini, 2007). Since the means and standard deviations of the continuous latent variables underlying the categorical items are not identifiable, a standard normal distribution constraint can be imposed on each latent continuous variable underlying observed categorical item and used to freely estimate all item thresholds.

Methods

The Positive and Negative Syndrome Scale (PANSS)

Our goal was to build a clinically relevant simulation study that would relate to measure that is well‐researched and widely known to the psychiatric community. The PANSS (Kay et al., 1987) was chosen because it is used to assess the individual differences between patients in terms of symptom presence and their severity, in the dimensional assessment of schizophrenia. PANSS consists of 30 items measured on ordered categorical response scales ranging from one (symptom absence) to seven (greatest severity of the corresponding symptom) and showed satisfactory inter‐rater reliability (Lindstrom et al., 1994; Peralta and Cuesta, 1994) as well as good validity and modest to good internal consistency (Kay et al., 1988; Peralta and Cuesta, 1994). The meta‐analytic study of more than 30 previously published factorial structures of PANSS (Stochl et al., 2014) showed that most existing studies have reported a five‐factor structure, usually containing positive, negative, anxiety/depression/preoccupation, cognitive/disorganization/dysphoric and activation/excitement factors. The same study reported the moderate superiority of the five‐factor model structure proposed by White et al. (1997) among other solutions. This solution offered an interesting and strong rationale for our data generation, and was also sufficiently complex as an exemplar.

Population model and data simulation

To accomplish the aim of this study we set up a Monte Carlo simulation. Data were simulated according to a five‐factor CFA model at within‐level (Figure 1) as introduced earlier. Based on the results of our review (Stochl et al., 2014), we set all factor loadings (i.e. all elements of vector Λ_W from Equation 2) to 0.7 and all factor correlations (i.e. all off‐diagonal elements of matrix Ψ_W) to 0.4. The item thresholds for the seven‐point ordinal categorical data were set to 0, 0.5, 1, 1.5, 2 and 2.5 for all items to determine the transition points between the observed rating categories in each item. Such setting introduces similar positive skewness of item responses to that found in typical PANSS datasets. These threshold values are in z‐scores and therefore correspond to proportions of a standard normal distribution in between corresponding thresholds (i.e. 50% of the people would obtain rating 0, 19.1% score 1, etc.).

Figure 1.

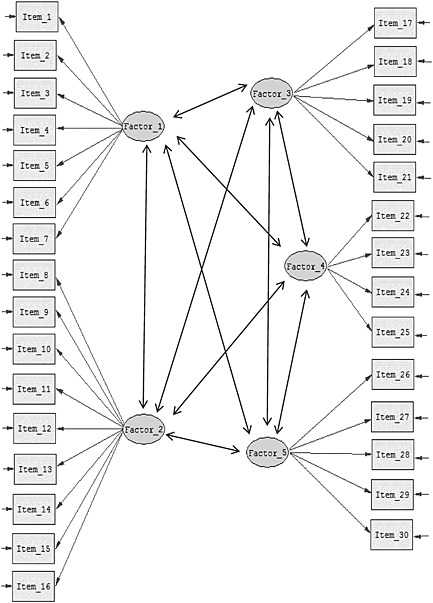
The path diagram of the population model used for data simulation.

The population model in Figure 1 corresponds to the within‐level structure of the simulated clustered data. The between‐level structure is deliberately ignored in this study [only corresponding variance (ICC, see later) between raters are specified on the between‐level represented by the diagonal elements of Θ_B from Equation 1]. This simplification is expected to be of minor importance in practice as the interest of the researcher often centres on the within‐level factor structure (Grilli and Rampichini, 2007).

The rationale and modelling design for the simulation were inspired by a real PANSS dataset (Stochl et al., 2014). Therefore the number of raters (i.e. between‐level units) was fixed to 70 in all simulated datasets. This is above the recommended number of between‐level units for a proper multilevel approach to covariance structure modelling, although maybe quite high as compared to some recommendations in methodological papers in psychiatry (Rouquette and Falissard, 2011). To eliminate any effects of the number of patients nested within raters (cluster size), the distribution of cluster sizes was constant in all simulated datasets (20 clusters of size 5, 20 clusters of size 10, 20 clusters of size 20 and 10 clusters of size 30). The mean cluster size was 14.3.

The following three explanatory variables (Boomsma et al., 2012) were manipulated in our Monte Carlo design:

1. ICC: Data were generated for 11 different levels of between‐level variability. These levels corresponded to ICCs ranging from 0.001 to 0.390: these are typical of the range of ICCs reported in the research literature. For each level, R = 100 datasets were generated (that is, 1100 datasets in total). The sample size in each simulated dataset was fixed at N = 1000 to reflect a reasonable sample size encountered in psychiatric literature for moderate sized factor analytic investigations of psychopathology data.

2. Estimator: Given previously reported differences in robustness of estimators to features such as the non‐normality of the data (Olsson et al., 2000), we hypothesize that different estimators may exhibit different performance with respect to ignoring clustering. In Mplus, the software chosen for our study, three estimators are available for CFA modelling of ordinal items when the between‐level variability is ignored: (1) weighted least squares mean and variance adjusted (WLSMV); (2) full information maximum likelihood (FIML); (3) Markov Chain Monte Carlo (MCMC) methods. Given the computational demand of FIML and MCMC estimators in multilevel modelling (the estimation in our 1100 dataset would take many months with current processor speed), we have not studied performance of different estimators when the clustering of data is acknowledged. We therefore show the results for WLSMV only.

3. Clustering: We present the results for two situations. In the first, the data were analysed without considering the multilevel structure (denoted as “clustering ignored”). In the second, the data were analysed using a multilevel approach and the rater identification for each patient was available (“clustering acknowledged”). In both cases, sample covariances were analysed and covariance structure models (multifactor CFAs) were estimated. All factor loading coefficients are presented as standardized parameter estimates.

Analysis of simulated data

In all cells of the design (3 estimators × 2 clustering × 11 ICCs), the simulated data were analysed with a CFA with an ordinal/polytomous item measurement model approach. A polychoric correlation matrix is therefore analysed instead of regular covariance or correlation matrix typically used when items are of continuous level of measurement. This approach accounts for the observed skewness in the polytomous (ordinal rating scale) data. The factor loadings, factor correlations, item thresholds and selection of fit indices [chi‐square, CFI (comparative fit index) and RMSEA (root mean square error of approximation) ] are reported. It is important to emphasize that the model was specified correctly in the analysis to study only the effects of the explanatory variables (i.e. estimator, clustering and ICC) on the factor analytic estimates. Thus the estimated model for all datasets matches the population model used for the data simulation.

Performance criteria

To evaluate the simulations we adopt conventional criteria to assess bias. The accuracy of the parameter estimates (factor loadings, factor correlations and item thresholds) is quantified by the relative bias:

$$\text{relative bias}=\frac{E\left(\widehat{\theta }\right)-\theta }{\theta }\text{,}$$

where $\widehat{\theta }$ stands for the sample estimate of the population parameter θ. For the purposes of this study, the acceptable relative bias is proposed to be at the level of 0.05 (that is 5%). Note, that relative bias for the threshold with θ = 0 (threshold one) is mathematically not defined and therefore relative bias of this particular threshold is not included in the results.

The accuracy of the standard error of the parameter estimate is assessed by analysing the relative bias of the estimate, where the population value is the standard deviation of the corresponding model parameter over R = 100 replications. In addition, we report the observed coverage of the 95% confidence interval (for FIML and WLSMV) or 95% interval credibility (for MCMC). This quantity reflects the proportion (percentage) of times when the 95% confidence/credibility interval of the parameter estimate contains the population value of the corresponding estimate.

Performance of estimators is assessed in terms of the mean square error (MSE) of the estimates, defined as:

$$MS{E}_{est}=Var\left(\widehat{\theta }\right)+{\left(E\left(\widehat{\theta }\right)-\theta \right)}^2\text{,}$$

where lower MSE values indicate better performance. MSE represents a way to simultaneously quantify the variance of the estimator as well as the difference between values implied by an estimator and the true values of the quantity being estimated. MSE can be used for comparative purposes; estimators with smaller MSE are preferred.

For fit indices, the mean values over R = 100 replications are compared to cutoff values recommended by Browne and Cudeck (1992): 0.05 for RMSEA and 0.95 for CFI. The 95% confidence intervals for fit indices are computed as:

$$\overline{x}\pm 1.96\left(\frac{1}{R}{\displaystyle \sum _1^R{\left(x-\overline{x}\right)}^2}\right)\text{,}$$

where x represents corresponding fit index.

Software used for simulation and analysis

For both simulation and analysis Mplus (Muthén and Muthén, 1998–2013) version 6.11 was used. A single seed value (0) was used for generation of all datasets. The R library MplusAutomation (Hallquist, 2012) was used for generating MPlus syntax and automating all estimation routines. An example of Mplus input and corresponding R script file syntax can be found as Supporting Information.

Results

Relative bias of parameter estimates

Figure 2 shows the relative bias of factor loadings, factor correlations and item thresholds (respective means over R = 100) when a correct multilevel approach is used for the analysis and when the clustering is ignored. Since the relative bias of the five thresholds (without threshold at θ = 0) would overlap if displayed, we present only a single figure which represents the pattern of bias for all thresholds.

Figure 2.

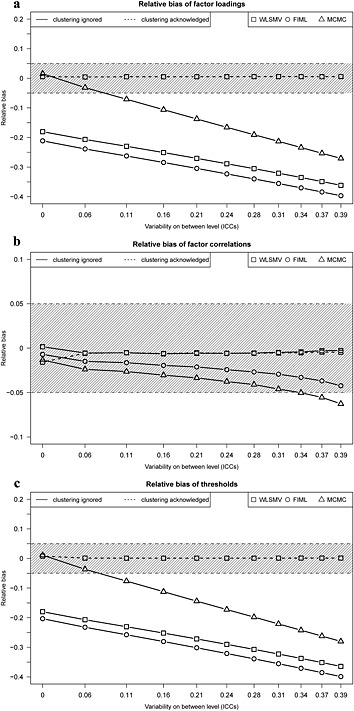
Relative bias of (a) factor loadings, (b) factor correlations, and (c) thresholds (all thresholds overlapped within estimator) for WLSMV, FIML and MCMC estimators when clustering is ignored and for WLSMV when clustering is acknowledged (N = 1000, R = 100). The grey areas represent the region of acceptable bias.

When clustering is acknowledged, all parameters appear to be recovered correctly (i.e. within acceptable range) regardless of the amount of between‐level variability.

As described, results from three estimators were available when clustering was ignored. The results suggest that WLSMV and FIML perform similarly poorly at recovering factor loadings and thresholds when clustering is ignored. The loadings and thresholds are underestimated even for low ICCs, and the bias is larger for higher ICC values. The MCMC estimator recovered the factor loadings and thresholds better than WLSMV and FIML for low ICC values but the loadings become unacceptably underestimated for ICCs ≥ 0.10. The bias gradients (slopes of bias with respect to ICC) of all of the estimators are comparable.

The point estimates of the factor correlations are almost unaffected, regardless of the estimator used. MCMC performs slightly worse; factor correlations tend to be underestimated, though only slightly and the bias becomes, according to our criteria, unacceptably large only for high ICCs (≥0.35).

Figure 3 shows that standard errors of the parameter estimates are also affected. Even if clustering is acknowledged, standard errors of factor loadings and correlations (but not thresholds) are unacceptably underestimated for all ICCs. This bias is particularly large for ICCs very close to zero, which, for the most part, reflects the large variability of estimates rather than true underestimation. This variability is caused by estimation difficulties or non‐convergence when the multilevel approach is used for almost non‐existing random effects in the model (T. Asparouhov, personal communication, 2012). Indeed, only 64 out of 100 replications succesfully converged for ICC set to 0.001.

Figure 3.

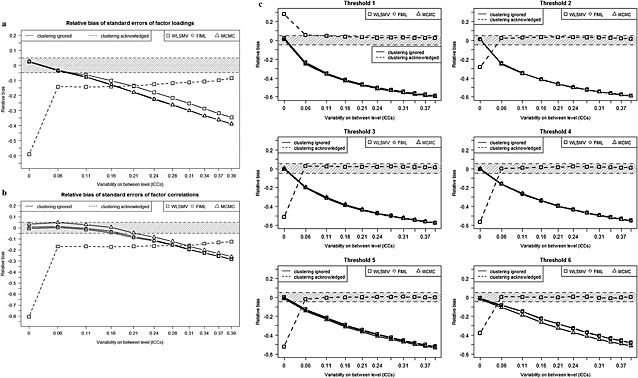
Relative bias of standard errors of (a) factor loadings, (b) factor correlations, and (c) thresholds for WLSMV, FIML and MCMC estimators when clustering is ignored and for WLSMV when clustering is acknowledged [N = 1000, R = 100 (R = 64 for ICC = 0.001)]. The grey areas represent the region of acceptable bias.

When clustering is ignored, the standard errors of the model parameters are underestimated regardless of the estimation method. The bias becomes worse with increasing degrees of between‐level variance, and becomes unacceptable (>0.05) for ICCs larger than 0.02 (for thresholds), 0.10 (for loadings), and 0.20 (for factor correlations), respectively. It is noteworthy that although the MCMC estimator recovers item thresholds closer to their true values, the underestimation of standard errors for high ICC values remains comparable to that of WLSMV and FIML.

The coverage rates of confidence intervals presented in Table 1 represent the percentage of times that the confidence (for FIML and WLSMV) or credibility interval (for MCMC) of the $\widehat{\theta }$ covers θ. When clustering is acknowledged, such probabilities are over 90% for factor loadings and all thresholds, and only slightly lower for factor correlations. If clustering is not taken into account, the coverage rates are smaller for higher ICC values regardless of the estimator. Coverage rates for factor correlations are similar for all estimators. For factor loadings, coverage rates of WLSMV and FIML are very small regardless of ICC value and MCMC shows reasonable coverage rate only for small ICC values. For the WLSMV and FIML, the higher the threshold's true value, the less likely it is that the confidence interval of the threshold point estimate will cover the true value. This might be a consequence of response distribution across the item categories (non‐symmetric) introduced in our simulated data, which leads to less information available for the response categories at the extreme end (these categories are rarely endorsed). This effect is not observed for MCMC.

Table 1.

Coverage rates (in %) for 95% confidence/credibility interval (CI)

Clustering	Estimator	Intra‐class correlation coefficient
		0.00	0.06	0.11	0.16	0.21	0.24	0.28	0.31	0.34	0.37	0.39
Loadings
Acknowledged	WLSMV	93.21	90.3	90.5	90.2	91.3	91.3	91.5	91.9	91.9	92.6	92.2
Ignored	WLSMV	4.7	2.2	1.3	0.8	0.7	0.5	0.6	0.5	0.5	0.4	0.5
Ignored	FIML	0.8	0.4	0.2	0.2	0.1	0.1	0.2	0.2	0.2	0.3	0.3
Ignored	MCMC2	94.9	92.0	83.2	71.9	60.6	51.2	43.4	37.3	33.0	29.0	26.8
Correlations
Acknowledged	WLSMV	87.21	88.4	88.2	88.6	88.9	89.3	89.5	89.5	90.5	91.3	91.4
Ignored	WLSMV	94.4	95.5	94.5	93.8	92.3	90.9	89.0	87.9	85.9	84.1	83.4
Ignored	FIML	94.7	95.0	94.5	93.2	92.0	89.7	88.3	87.2	85.6	84.9	82.6
Ignored	MCMC2	95.7	95.9	94.7	94.5	93.0	91.6	89.3	88.1	86.6	85.7	83.3
Threshold 1
Acknowledged	WLSMV	97.31	95.3	94.9	94.6	95.1	95.0	95.1	95.4	95.1	95.1	94.9
Ignored	WLSMV	95.5	87.2	79.9	75.4	71.4	67.7	65.6	63.3	61.2	59.8	58.8
Ignored	FIML	94.9	86.1	79.3	74.4	70.2	66.9	64.7	62.4	60.3	59.4	57.9
Ignored	MCMC2	94.6	85.5	78.8	74.4	70.1	66.3	63.8	61.9	60.1	59.0	57.9
Threshold 2
Acknowledged	WLSMV	97.51	95.1	95.1	95.2	94.9	95.2	95.0	95.0	95.0	94.8	94.9
Ignored	WLSMV	41.7	32.7	28.3	25.0	22.5	20.0	18.6	17.2	16.1	15.1	14.0
Ignored	FIML	15.0	14.6	12.9	11.8	10.7	9.9	8.9	8.4	7.9	7.4	7.0
Ignored	MCMC2	94.4	83.6	73.9	64.0	56.2	49.7	44.3	39.6	36.1	33.2	30.9
Threshold 3
Acknowledged	WLSMV	96.71	95.3	95.4	95.1	95.2	95.2	94.8	95.3	94.8	94.9	94.5
Ignored	WLSMV	2.3	1.8	1.4	1.2	1.1	0.9	0.7	0.6	0.6	0.4	0.4
Ignored	FIML	0.1	0.3	0.4	0.3	0.3	0.3	0.2	0.3	0.2	0.2	0.2
Ignored	MCMC2	94.3	82.7	63.5	46.2	33.3	25.2	18.4	14.6	11.1	8.8	7.0
Threshold 4
Acknowledged	WLSMV	96.51	94.3	94.7	94.8	94.9	95.1	94.8	95.0	94.8	94.6	94.5
Ignored	WLSMV	0.1	0.2	0.2	0.1	0.1	0.1	0.0	0.0	0.0	0.0	0.0
Ignored	FIML	0.0	0.1	0.1	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0
Ignored	MCMC2	94.5	79.7	55.0	33.9	19.7	12.2	7.6	5.0	3.3	2.4	1.9
Threshold 5
Acknowledged	WLSMV	95.71	94.3	94.4	95.0	94.5	95.2	95.2	94.8	94.4	94.0	93.8
Ignored	WLSMV	0.2	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0
Ignored	FIML	0.5	0.1	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0
Ignored	MCMC2	93.9	80.8	52.1	28.3	15.7	8.3	4.5	3.0	1.8	1.4	0.8
Threshold 6
Acknowledged	WLSMV	96.21	95.1	94.8	94.8	94.8	94.9	94.9	94.6	94.0	93.9	93.7
Ignored	WLSMV	2.0	0.5	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0
Ignored	FIML	8.9	3.3	1.4	0.5	0.3	0.1	0.0	0.0	0.0	0.0	0.0
Ignored	MCMC2	93.6	84.3	57.9	31.7	17.5	9.6	5.3	2.9	1.7	1.0	0.6

¹ Based on converged outputs (R = 64).

² Based on 95% credibility interval.

Mean square error (MSE)

Figure 4 depicts MSEs of the WLSMV, FIML and MCMC for factor loadings, correlations and thresholds. In general, the smallest MSEs are observed when clustering is correctly acknowledged (and WLSMV is used as an estimator) except for ICC values very close to zero. In this case, MSE is large, which reflects the difficulties of a multilevel approach to recover parameters for data with nearly non‐existing random effects.

Figure 4.

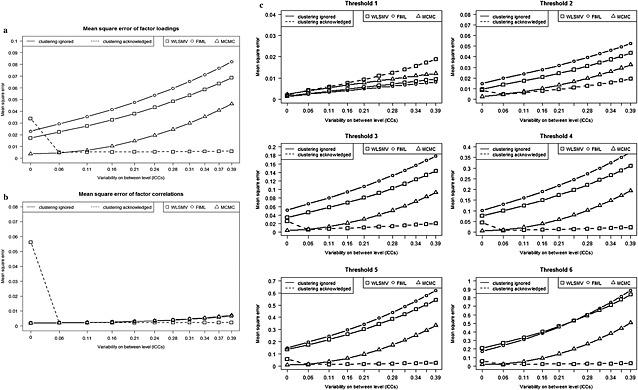
The mean square error for (a) factor loadings, (b) factor correlations, and (c) thresholds for WLSMV, FIML and MCMC estimators when clustering is ignored and for WLSMV when clustering is acknowledged [N = 1000, R = 100 (R = 64 for ICC = 0.001)].

When clustering is ignored, MCMC estimates of factor loadings and thresholds are more robust (though still inadequate) compared to WLSMV and FIML. Regarding the estimation of factor correlations, the performance of all estimators is comparable.

Fit indices (WLSMV estimator)

When clustering is acknowledged, the chi‐square statistic seems to be working as expected; that is, the population model is not rejected (see Figure 5). However, the chi‐square statistic is seriously underestimated for ICCs close to zero as a consequence of the “almost non‐existent” random effects and related estimation problems (T. Asparouhov, personal communication, 2012). Therefore, making decisions on model fit based on this statistic using a multilevel approach for data that do not have a hierarchical structure cannot be recommended (at least not when using Mplus software and WLSMV estimator). Further, the chi‐square statistic decreases for increasing ICC values and tends to be underestimated for extreme (but, in practice, unlikely) ICCs.

Figure 5.

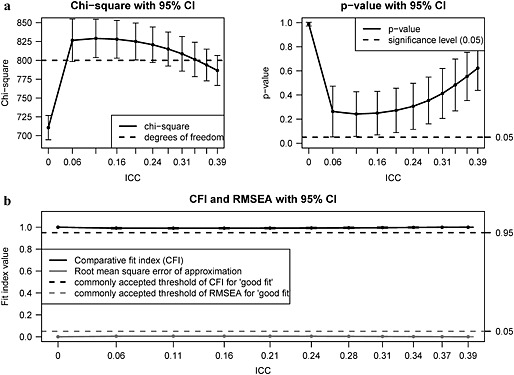
The CFA chi‐square (a) and fit indices (b) (means over R = 100 replications per ICC level) when clustering is acknowledged [WLSMV, N = 1000, R = 100 (R = 64 for ICC = 0.001)].

If the hierarchical structure is taken into account, the RMSEA and CFI work well regardless of amount of between‐level variability. The RMSEA is below the recommended cutoff value of good fit (i.e. < 0.05), and the CFI also indicates a good fit to the data (>0.95) for all values of the ICC.

Figure 6 shows the results for the scenario in which the hierarchical structure is not considered. In this case, the chi‐square statistic is inflated. The point estimate of the corresponding p‐values drops below 0.05 for ICC ≈ 0.11, and the confidence intervals suggest that the model would be rejected based on the corresponding p‐value if the hierarchical structure of the data is ignored for ICCs greater than 0.16.

Figure 6.

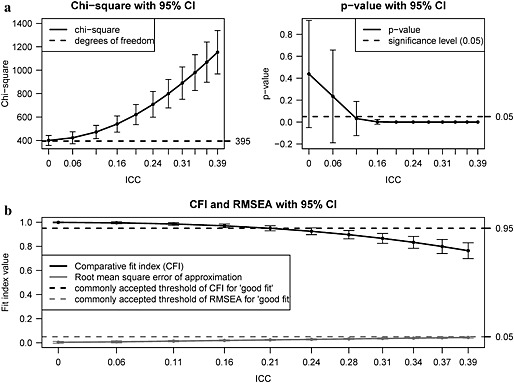
The CFA chi‐square (a), CFI and RMSEA (b) when clustering is ignored (WLSMV, N = 1000, R = 100).

A similar pattern and sensitivity to hierarchical structure can be seen for CFI (Figure 6). For ICCs higher than 0.2, CFI drops below the recommended cutoff value and therefore suggest unsatisfactory model fit. The RMSEA seems to be robust to different levels of between‐level variance. Although this fit statistic shows slightly increased values with increasing ICCs, it stays below the recommended cutoff value for all of the between‐level variability values tested.

Discussion

This study aimed to show the consequences of ignoring patient clustering in datasets on factor analytic estimates. The data were simulated based on a real‐life data set and review (Stochl et al., 2014) according to a five‐factor model of the PANSS (White et al., 1997) and analysed using CFA under two scenarios: (i) when the information on clustering is ignored; (ii) when all of the clustering information is available and taken into account. Our results provide evidence for bias in factor analytic estimates when patients are nested within raters and even only low cluster effects (ICC ≥ 0.10) are ignored. We show this using a range of different estimators and propose that MCMC may be more robust against clustering effects. We also provide evidence which should discourage researchers from applying multilevel structural equation modelling to data where there are almost non‐existent random effects.

The Monte Carlo study showed that when rater information is available for each patient and the multilevel approach is adopted, factor analytic estimates using WLSMV are unbiased, regardless of the ICC value. Additionally, the fit indices show acceptable model fit for all ICC values. Without considering clustering in the data, factor loadings, item thresholds, and their corresponding standard errors are seriously underestimated, and bias increases with larger ICC values. However, the factor correlations are almost unbiased, even for large ICCs. Bias in factor loadings and thresholds might have serious consequences, for example, in investigations of measurement invariance or differential item functioning studies for instruments such as PANSS.

When clustering is ignored, our results showed less bias for MCMC estimator compared to WLSMV and FIML, although the slope of the bias with respect to ICC and underestimation of standard errors is similar for each of these estimators. The MCMC estimates are relatively unbiased for ICCs smaller than 0.10. The goodness‐of‐fit indices tended to show a poorer fit for the analyses where clustering is ignored, especially for large ICCs which could lead to the rejection of a structurally correct model. The most robust fit index seems to be the RMSEA, possibly since the index assesses approximate model fit (Browne and Cudeck, 1992).

In a previous study employing multilevel analysis and similar Monte Carlo methodology, Julian (2001) reported that for very low levels of intra‐class correlation, the chi‐square statistic, the parameters, and their standard error estimators are relatively unbiased, but as the level of intra‐class correlation increases, all of them are biased. Those results are consistent with the findings presented here. However, we find an important difference in the direction of the reported bias. Our Monte Carlo study results revealed low factor analytic estimates when the clustering information was ignored. By contrast, Julian (2001) reported modest overestimation of factor loading estimates, factor variances and covariances. The overestimation became more serious for larger ICCs and was found to be independent of the model used for the data simulation. These different outcomes might be explained by the fact that Julian's study modelled between‐level structure, whereas ours did not. Yet another explanation might be related to the differences in software used for conducting the simulation and subsequent analysis (EQS and LISREL respectively in Julian's study). This raises the question whether amount and direction of the bias might depend on the features of individual software. We acknowledge that we relied on one analytic framework for data generation and analysis. While this might limit the remit of this study, we think that the basic framework (McDonald, 1999; Muthén, 1984) is general enough to be seen as a representative for current software applications. It should however be noted that freely available software will be of great interest to applied researchers. These options will certainly need to be considered as new packages become distributed in future [e.g. R packages lavaan, (Rosseel, 2012), OpenMx (Boker et al., 2011), and sem (Fox et al., 2014)].

Another study reporting on the consequences of ignoring a multilevel data structure was published by Muthén and Satorra (1995). They found the same pattern of bias: standard errors of conventional analysis are underestimated and the chi‐square statistic is inflated as soon as positive ICCs are observed. Unlike our results, this study found negligible bias of the parameter estimates. The difference might be due to limited range of ICCs (≤0.20) in comparison to our study.

From an applied point of view, our results can partly explain the extraordinary heterogeneity in the results of previous factor analytic studies of the PANSS. Indeed, the majority of the published studies have not considered that the PANSS is administered by clinical raters and have not applied a multilevel approach for analysis (Stochl et al., 2014). Previous results might therefore have been prone to bias, the size of which might depend on individual study characteristics.

Some limitations of our results must be outlined. First, the simulation is intentionally based on a relatively simple multilevel data structure. Each individual is completely nested (i.e. each patient is assessed by single rater), and only two levels were considered. Second, we have not considered any between‐level latent structural aspects of the model (a factor structure for between‐level variation). In practice, hierarchical structures are often much more complicated. Third, the simulation of the data was tailored to the situation often observed in psychiatric practice (non‐symmetric/skewed data, distribution of cluster sizes, PANSS model). Therefore, the external validity of this simulation is limited.

Despite the limitations of this study, we have provided evidence of potential bias in the results for key parameter estimates when FA of categorical data (i.e. item response modelling) is used for data analysis and the clustering of patients is ignored. In the light of these findings we recommend that greater attention be given to application of multilevel psychometric models and discourage researchers from ignoring random effects when performing CFA in psychiatric studies.

Declaration of interest statement

The authors have no competing interests.

Supporting information

Supporting info item

Supporting info item

Stochl, J. , Jones, P. B. , Perez, J. , Khandaker, G. M. , Böhnke, J. R. , and Croudace, T. J. (2016) Effects of ignoring clustered data structure in confirmatory factor analysis of ordered polytomous items: a simulation study based on PANSS. Int. J. Methods Psychiatr. Res., 25: 205–219. doi: 10.1002/mpr.1474.