The use of multilayer network analysis in animal behaviour

Abstract

Network analysis has driven key developments in research on animal behaviour by providing quantitative methods to study the social structures of animal groups and populations. A recent formalism, known as multilayer network analysis, has advanced the study of multifaceted networked systems in many disciplines. It offers novel ways to study and quantify animal behaviour through connected ‘layers’ of interactions. In this article, we review common questions in animal behaviour that can be studied using a multilayer approach, and we link these questions to specific analyses. We outline the types of behavioural data and questions that may be suitable to study using multilayer network analysis. We detail several multilayer methods, which can provide new insights into questions about animal sociality at individual, group, population and evolutionary levels of organization. We give examples for how to implement multilayer methods to demonstrate how taking a multilayer approach can alter inferences about social structure and the positions of individuals within such a structure. Finally, we discuss caveats to undertaking multilayer network analysis in the study of animal social networks, and we call attention to methodological challenges for the application of these approaches. Our aim is to instigate the study of new questions about animal sociality using the new toolbox of multilayer network analysis.

‘MULTIDIMENSIONALITY’ OF ANIMAL SOCIAL BEHAVIOUR

Sociality is widespread in animals, and it has a pervasive impact on behavioural, evolutionary and ecological processes, such as social learning and disease spread (Allen, Weinrich, Hoppitt, & Rendell, 2013; Aplin et al., 2014; Silk, Alberts, & Altmann, 2003; White, Forester, & Craft, 2017). The structure and dynamics of animal societies emerge from interactions between and among individuals (Hinde, 1976; Krause, Croft, & James, 2007; Pinter-Wollman et al., 2014). These interactions are typically ‘multidimensional’, as they occur across different social contexts (e.g. affiliation, agonistic and feeding), connect different types of individuals (e.g. male—male, female—female or male—female interactions) and/or vary spatially and temporally. Considering such multidimensionality is crucial for thoroughly understanding the structure of animal social systems (Barrett, Henzi, & Lusseau, 2012).

Network approaches for studying the social behaviour of animals have been instrumental in quantifying how sociality influences ecological and evolutionary processes (Krause et al., 2007; Krause, James, Franks, & Croft, 2015; Kurvers, Krause, Croft, Wilson, & Wolf, 2014; Pinter-Wollman et al., 2014; Sih, Hanser, & McHugh, 2009; Sueur, Jacobs, Amblard, Petit, & King, 2011; Webber & Vander Wal, 2018; Wey, Blumstein, Shen, & Jordán, 2008). In animal social networks, nodes (also called ‘vertices’) typically represent individual animals; and edges (also called ‘links’ or ‘ties’) often represent pairwise interactions (e.g. behaviours, such as grooming, in which two individuals engage) or associations (e.g. spatiotemporal proximity or shared group memberships) between these individuals. Such a network representation is a simplified depiction of a much more intricate, multifaceted system, A social system can include different types of interactions, with different biological meanings (e.g. cooperative or competitive), which standard network approaches often do not take into account, or they do so by analysing networks of different edge types separately (Gazda, Iyer, Killingback, Connor, & Brault, 2015b), Typical approaches ignore interdependencies that may exist between different types of interactions and between different subsystems (Barrett et al., 2012; Beisner, Jin, Fushing, & McCowan, 2015). Furthermore, networks are often studied as snapshots or aggregations of processes that change over time, but dynamics can play a major role in animal behaviour (Blonder, Wey, Dornhaus, James, & Sih, 2012; Farine, 2018; Wey et al., 2008; Wilson et al., 2014). As we highlighted recently (Silk, Finn, Porter, & Pinter-Wollman, 2018), advances in multilayer network analysis provide opportunities to analyse the multifaceted nature of animal behaviour, to ask questions about links between social dynamics across biological scales, and to provide new views on broad ecological and evolutionary processes. In this paper, we introduce the new mathematical formalism of multilayer network analysis to researchers in animal behaviour. This formalism provides a common vocabulary to describe, compare and contrast multilayer network methodologies. Our goal is to review research areas and questions in animal behaviour that are amenable to multilayer network analysis, and we link specific analyses to these questions (see Table 1). We describe different types of multilayer networks and detail how they can encode animal data. We also review several questions and hypotheses, across social scales, that multilayer network analysis can help investigate. We summarize key questions and provide a guide to available methods and software for multilayer network analysis in Table 1. We present examples to illustrate our ideas, and we consider some of the requirements and caveats of multilayer network analysis as a tool to study animal social behaviour. We also discuss several directions for future work.

Table 1.

A nonexhaustive selection of multilayer network approaches for studying questions in behavioural ecology

Research aim	Level (I/G/P/E)	Examples of questions	Multilayer approach	Description	Software package	References
Identify important or influential nodes or edges	I/G	(1) How will a group be affected if certain individuals are removed?	Eigenvector versatility	Multilayer extension of eigenvector centrality; in it, an individual’s importance depends on its connections within and across layers and on the connections of its neighbours	MuxViz (R) (De Domenico, Porter et al„ 2015)	De Domenico, Solé-Ribalta et al. (2015)
		(2) Is social influence determined by Interactions in more than one situation?
		(3) Which relationships are most critical for group cohesion (when applying measures to edges)?
		(4) How stable Is an individual’s importance over time?
		(5) Which individuals link the most Individuals in a group within or across social situations and/or over time?	Betweenness versatility	Multilayer extension of geodesic betweenness centrality; it measures how often shortest paths (including both intralayer and interlayer edges) between each pair of nodes traverse a given node	MuxViz	De Domenico, Sold-Ribalca et al, (2015)
		(6) How important is an individual for group cohesion?
		(7) Does the role of an individual in its social group carry over across social situations?	Multidegree	A vector of the intralayer degrees of each individual across all layers	Pymnet (Python) (Kivelä. n.d.)	Menichatti, Remondini, Panzarasa, Mondragón, & Bianconi (2014)
Quantify network properties at different scales	G/P/E	(1) What are the coherent groups in a network of animals?	Multi slice modularity maximization. Multilayer InfoMap	Identifies communities of individuals in which the same individuals In different layers can be assigned to different communities	MuxViz; GenLouvain (https://github.com/GenLouvain/GenLouvain (Jeub, Bazzi, Jutla, & Mucha (n.d.)); in MATLAB, MathWorks, Natick, MA, U.S.A.)	Mucha et al, (2010)
		(2) Which individuals preferentially interact with each other in different or multiple contexts?
		(3) What are the social communities, core-periphery structures, or other large-scale structures in different types of social situations?	Stochastic block models	Statistical models of arbitrary block structures in networks	Graph-tool (Python)	Peixoto (2015)
		(4) Are there consistent, ‘typical’ types of Interaction patterns across social situations?	Motifs	Interaction patterns between multiple Individuals (e.g. node pairs or triples), within and/or across layers, that appear more often than in a specified null model	MuxViz	Battiston, Nicosia, Chavez, & Latora, 2017; Wernicke & Rasche, 2006
		(5) How similar are the interaction patterns in different social situations?	Global overlap	Number of pairs of nodes that are connected by edges in multiple layers	MuxViz; Multinet R package (Magnani & Dubik, 2018)	Bianconi (2013)
		(6) How often do interactions between Individuals co-occur in multiple situations?
Model statistical properties of a network	G/P/E	(1) Are interaction patterns Influenced by group size?	Randomization for multilayer networks	Construction of randomized ensembles of synthetic multilayer networks for comparison	Pymnet	Kivelä et al., 2014, Section 4.3
		(2) Are relationships or interactions in one social situation related to relationships or interactions in a different social situation?	Exponential random graph model (ERGM)	An extension of ERGMs to multilayer networks	MPNET (Java-based) for two-layer multilayer networks	Heaney, 2014; Wang, Robins, Pattison, & Lazega, 2013
		(3) Are relationships at one time point related to those at a different time point?
		(4) How do network relationships in one social situation or at one point In time affect subsequent relationships In other situations or at other times?	Markov models of coevolving multiplex networks	Models of the probability of an edge existing in a layer at one time as a function of an edge existing between the same pair of nodes in any layer In the previous time	MultiplexMarkovChain (https://github.com/vkrmsv/MultiplexMarkovChain; in Python)	Fisher et al., 2017; Vijayaraghavan, NoSi, Maoz, & D’Souza, 2015
			Stochastic actor- oriented models for multiple networks	Statistical models of what influences the creation and termination of edges over time. The version that we consider can model the coevolution of two networks (or two layers) as a result of their Influence on each other	Code (in R) is available at https://www.stats.ox.ac.uk/~snijders/siena/siena_scripts.htm
Modelling disease or information transmission	I/G/P	(1) What are the roles of different types of social interactions or individual in information or disease transmission?	Compartmental models on networks	Classic epidemiological models that assume that individuals exist in one of several states, with probabilistic transitions between states. For example, SIR models have susceptible infected, and recovered (or removed) states; and SI and SIS models have only susceptible and infected states. These models are sometimes amenable to mathematical analysis, but stochastic simulations are often more accessible	EpiModel (R package) (for temporal network) (Jenness, Goodreau, & Morris, 2018)	Kiss et al., 2017; Pastor-Satorras, Castellano, Van Mieghem, & Vespignani, 2015; Porter & Gleeson, 2016
		(2) Do different types of transmission interact with each other?
		(a) Can the spread of information mitigate the spread of a disease?
		(b) Can the spread of one infection enhance or reduce the spread of a second infection?
		(3) What influence disease transmission in multispecies communities?

What Are Multilayer Networks?

Multilayer networks are assemblages of distinct network ‘layers’ that are connected (and hence coupled) to each other via interlayer edges (Boccaletti et al., 2014; Kivelä et al., 2014). A multilayer network can include more than one ‘stack’ of layers, and each such facet of layering is called an ‘aspect’. For instance, one aspect of a multilayer network can encode temporal dynamics and another aspect can represent types of social interactions (Fig. 1, Supplementary Material 1).

Figure 1.

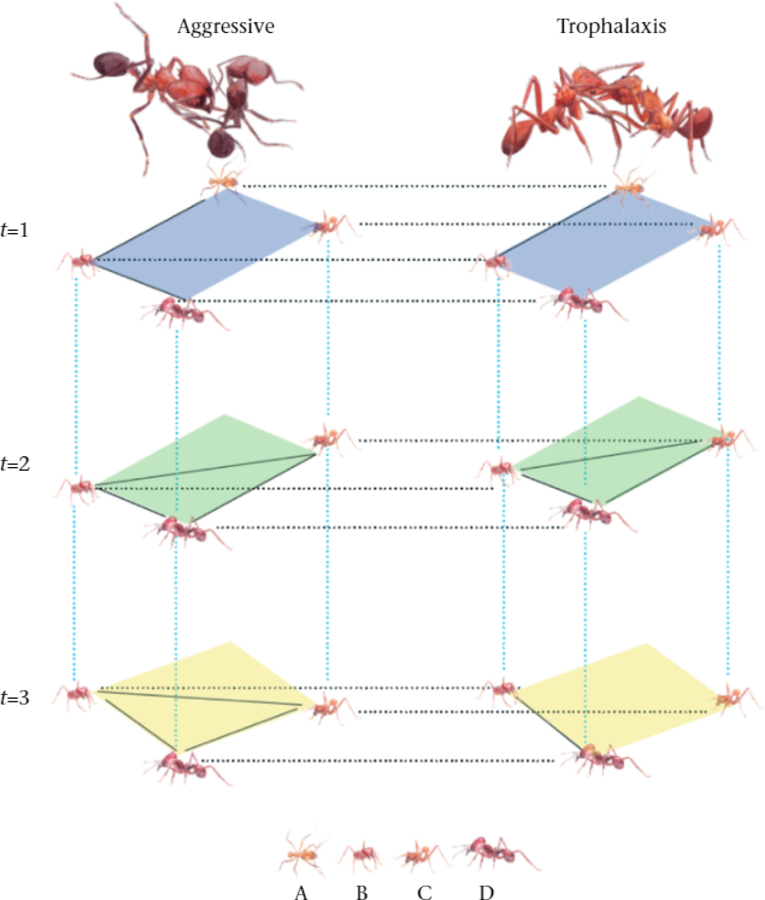
A hypothetical multilayer network. Four ants interact at different time points and in two different ways. Each diamond represents a layer. The stack of three layers on the left represents aggressive interactions, and the slack of three layers on the right represents trophalactic interactions. Each colour represents a different lime point (blue is t=1. green is t=2, and yellow is t=3). Solid lines represent intralayer (i.e. within-layer) interactions, dotted blue lines represent interlayer (i.e. across-layer) edges in the temporal aspect, and dotted black lines represent interlayer edges in the behavioural aspect. Each interlayer edge connects replicates of the same individual across different layers. See Supplementary Material 1 for further discussion and for a presentation of the mathematical formalism of multilayer networks

The recent formalism of multilayer networks has opened up new ways to study multifaceted networked systems (Boccaletti et al., 2014; Kivelä et al., 2014). The application of multilayer networks to questions in animal behaviour is still in its infancy, but multilayer network analysis has facilitated substantial advances over monolayer (i.e. single-layer) network analysis in many other fields (Aleta & Moreno, 2019; Kivelä et al., 2014). For example, multilayer network approaches have made it possible to identify important nodes that are not considered central in a monolayer network (De Domenico, Solé-Ribalta, Omodei, Gómez, & Arenas, 2015). Multilayer approaches applied to studying information spread on Twitter (where, e.g. one can use different layers to represent ‘tweets’, ‘retweets’ and ‘mentions’) have uncovered information spreaders who have a disproportionate impact on social groups but were overlooked in prior monolayer investigations (Al-Garadi, Varathan, Ravana, Ahmed, & Chang, 2016). Multilayer modelling of transportation systems has improved investigations of congestion and efficiency of transportation. For example, each layer may be a different airline (Cardillo et al., 2013) or a different form of transportation in a city (Chodrow, al-Awwad, Jiang, & González, 2016; Gallotti & Barthelemy, 2015; Strano, Shai, Dobson, & Barthelemy, 2015). Modelling dynamical processes on multilayer networks can result in qualitatively different outcomes compared to modelling dynamics on aggregate representations of networks (for a discussion of aggregating networks, see Supplementary Material 2) or on snapshots of networks (De Domenico, Granell, Porter, & Arenas, 2016). For instance, the dynamics of disease and information spread can be coupled in a multilayer framework to reveal how different social processes can impact the onset of epidemics (Wang, Andrews, Wu, Wang, & Bauch, 2015). Historically, the usage of ‘multiplexity’ dates back many decades (Mitchell, 1969), and the new mathematical formalism (De Domenico et al., 2013; Kivelä et al., 2014; Newman, 2018c; Porter, 2018) has produced a unified framework that makes it possible to consolidate analysis and terminology. For reviews of previous multilayer network studies and applications in other fields, see Aleta and Moreno (2019), Boccaletti et al. (2014), D’Agostino and Scala (2014), Kivelä et al. (2014) and Pilosof, Porter, Pascual, and Kéfi (2017).

Types of Multilayer Networks

The mathematical framework of multilayer networks was developed recently to create a unified formalism to study such networks (De Domenico et al., 2013; Kivelä et al., 2014; Mucha, Richardson, Macon, Porter, & Onnela, 2010; Porter, 2018). One can use this multilayer network framework, which we follow in this paper and detail in Supplementary Material 1, to represent a variety of network types and situations. In contrast to monolayer networks, which are traditional in network analysis and which consist of only a single network ‘layer’. multilayer networks can include many different types of data that are commonly collected in studies of animal behaviour. For example, types of social interactions, spatial locations (with connections between them) and different measures of genetic relatedness can all constitute layers in a multilayer network. Node attributes can include behavioural or physical phenotypes, sex, age, personality, and more. Edge attributes, such as their weight or direction, can encode interaction frequencies, distances between locations, dominance, and so on. Commonly studied types of multilayer networks that can accommodate such data include the following.

1. Multiplex networks (i.e. edge-coloured networks) are multilayer networks in which interlayer edges connect nodes to themselves on different layers (Fig. 1, Supplementary Material 1). It is often assumed, for convenience, that all layers consist of the same set of nodes, but this is not necessary.

   1. In multirelational networks, each layer represents a different type of interaction. For example, a network of aggressive interactions can be connected with a network of affiliative interactions through interlayer edges that link individuals to themselves if they appear in both layers (Fig. 1, horizontal dotted black lines).
   2. In temporal networks, each layer encodes the same type of interactions during different time points or over different time windows. In the most common multiplex representation of a temporal network, consecutive layers are connected to each other through interlayer edges that link individuals to themselves at different times (Fig. 1, vertical dotted blue lines).
2. In interconnected networks (i.e. node-coloured networks), the nodes in different layers do not necessarily represent the same entities, and interlayer edges can exist between different types of nodes. See our discussion of the mathematical formalism and an example figure in Supplementary Material 1.

   1. Networks of networks consist of subsystems, which themselves are networks that are linked to each other through interlayer edges between the subsystems’ nodes. For example, one can model intergroup interactions in a population-level network of interactions between social groups, which are themselves networks.
   2. In intercontextual networks, one can construe each layer as representing a different type of node. For example, interactions between males can be in one layer, interactions between females can be in a second layer, and intersex interactions are interlayer edges. See Fig. 1 in Silk, Weber et al. (2018) and Fig. 1 in Silk et al. (2018).
   3. Spatial networks, which we define here as networks of locations, can be linked with social networks of animals that move between these locations (Pilosof et al, 2017; Silk et al, 2018). Our use of the term ‘spatial networks’ refers to networks that are embedded in space, rather than networks that are influenced by a latent space (Barthelemy, 2018).

Throughout this paper, we use the term ‘multilayer networks’ to refer to any of the variants above, unless we specify that a method applies to only one or a subset of specific network types. For a review of other types of multilayer networks, see Kivelä et al. (2014).

NOVEL INSIGHTS INTO ANIMAL SOCIALITY: FROM INDIVIDUALS TO POPULATIONS

We propose that a multilayer network approach can advance the study of animal behaviour and expand the types of questions that one can investigate. Specifically, we discuss how a multilayer framework can enhance understanding of (1) an individual’s role (or roles) in a social network, (2) group-level structure and dynamics, (3) population structure and (4) evolutionary models of the emergence of sociality.

An Individual’s Role(s) in Society

Traditionally, the use of network analysis to examine the impact of individuals on their society has focused on the social positions of particular individuals using various centrality measures (such as degree, eigenvector centrality, betweenness centrality, and others; see Pinter-Wollman et al., 2014; Wasserman & Faust, 1994; Wey et al., 2008; Williams & Lusseau, 2006). It is common to construe individuals with disproportionally large centrality values as influential or important to a network in some way (but see Rosenthal, Twomey, Hartnett, Wu, & Couzin, 2015 for a different trend). The biological meaning of ‘importance’ and corresponding centrality measures differ among types of networks and is both system-dependent and question-specific. Consequently, one has to be careful to avoid misinterpreting the results of centrality calculations. Centrality measures have been used to examine which individuals have the most influence on a group in relation to age, sex or personality (Sih et al., 2009; Wilson, Krause, Dingemanse, & Krause, 2013) and to study the fitness consequences of holding an influential position (Pinter-Wollman et al., 2014). A multilayer approach can advance understanding of roles that individuals play in a population or a social group, and it can potentially identify central individuals who may be overlooked when using monolayer approaches on ‘multidimensional’ data.

An individual’s role in a social group is not restricted to its behaviour in just one social or ecological situation. A multilayer approach creates an opportunity to consolidate analyses of a variety of social situations and simultaneously examine the importances of individuals across and within situations. Many centrality measures have been developed for multilayer networks, and different ones encompass different biological interpretations. For instance, eigenvector ‘versatility’ (see Supplementary Material 1 for its mathematical definition) is one way to quantify the overall importance of individuals across and within layers, because this measure takes into account multiple layers to identify individuals who increase group cohesion in multiple layers and bridge social situations (De Domenico, Solé-Ribalta et al., 2015). In a multirelational network, an individual can have small degree (i.e. degree centrality) in each layer, where each layer represents a different social situation, but it may participate in many social situations, thereby potentially producing a larger impact on social dynamics than individuals with large degrees in just one or a few social situations. One can also account for the inter-relatedness of behaviours in different layers in a multilayer network when combining interlayer centralities, if appropriate for the study system (De Domenico, Solé-Ribalta et al., 2015). For example, it is not possible for two individuals to engage in grooming interactions without also being in proximity. By accounting for inter-relatedness between proximity and grooming when calculating multilayer centralities and versatilities, it may be possible to consider grooming interactions as explicitly constrained by proximity interactions and thereby incorporate potentially important nuances.

The appropriateness of a versatility measure differs across biological questions, just as distinct centrality measures on a monolayer network have different interpretations (Wasserman & Faust, 1994; Wey et al., 2008). Versatility measures that have been developed include shortest-path betweenness versatility, hub/authority versatility, Katz versatility and PageRank versatility (De Domenico, Solé-Ribalta et al., 2015). Experimental removal of versatile nodes, similar to the removal of central nodes in monolayer networks (Barrett et al., 2012; Firth et al., 2017; Flack, Girvan, de Waal, & Krakauer, 2006; Pruitt & Pinter-Wollman, 2015; Sumana & Sona, 2013), has the potential to uncover the effects of the removed nodes on group actions, group stability, and their impact on the social positions of other individuals. However, which versatility measure gives the most useful information about an individual’s importance may depend on the level of participation of an individual in the different types of behaviours that are encoded in a multilayer network. Furthermore, if layers have drastically dissimilar densities, one layer can easily dominate a versatility measure. For other nuances and caveats, see our discussion below in Considerations When Using Multilayer Network Analysis. In addition to calculating node versatility, one can examine versatility of edges to yield interesting insights into the importance of relationships with respect to group stability and cohesion. Such an approach can help reveal whether interlayer interactions are comparably important, more important, or less important than intralayer interactions for group cohesion. Examining edge versatility can also illuminate which interactions between particular individuals (within or across layers) have the largest impact on group activity and/or stability; and it may be helpful for conservation efforts, such as the identification of social groups that are vulnerable to fragmentation (Snijders, Blumstein, Stanley, & Franks, 2017).

A multilayer approach can help elucidate the relative importances of different individuals in various social or ecological situations. For example, a node’s ‘multidegree’ is a vector of the intralayer degrees (each calculated as on a monolayer network) of an individual in each layer. Differences in how the degrees of individuals are distributed across layers help indicate which individuals have influence over others in the different layers. For example, if each layer represents a different situation, individuals whose intralayer degree peaks in one situation may be more influential in that context than individuals whose intralayer degree is small in that situation but peaks in another one. Because multidegree does not account for interlayer connections, quantitatively comparing it with versatility or other multilayer centralities, which account explicitly for interlayer edges (Kivelä et al., 2014), can help elucidate the importance of interlayer edges and thereby highlight interdependencies between biological situations. Such behavioural interdependencies can help quantify the amount of behavioural carryover across situations (i.e. ‘behavioural syndromes’; Sih, Bell, & Johnson, 2004) if, for example, measures that account for interlayer edges explain observed data better than measures that do not take into account such interdependencies.

As a final example, one can use a multilayer approach to examine temporal changes in an individual’s role (or roles) in a group. A multilayer network in which one aspect represents time and another aspect represents situation (Fig. 1) can reveal when individuals gain or lose central roles and whether roles are lost simultaneously in all situations or if changes in one situation precede changes in another. Comparing monolayer (e.g. time-aggregated) measures and multilayer measures has the potential to uncover the importance of temporal changes in an animal’s fitness.

Roles of individuals in a group: baboon versatility in a multiplex affiliation network

To demonstrate the potential insights from employing multilayer network analysis to examine the roles of individuals in a social group using multiple interaction types, we analysed published affiliative interactions from a baboon (Papio cynocephalus) group of 26 individuals (Franz, Altmann, & Alberts, 2015a, 2015b) (Fig. 2). One can quantify affiliative relationships in primates in multiple ways, including grooming. body contact and proximity (Barrett & Henzi, 2002; Jack, 2003; Kasper & Voelkl, 2009; Pasquaretta et al., 2014). To characterize affiliative relationships, combinations of these behaviours have been investigated separately (Jack, 2003; Perry, Manson, Muniz, Gros-Louis, & Vigilant, 2008), pooled together (Kasper & Voelkl, 2009), or used interchangeably (Pasquaretta et al., 2014). These interaction types are often correlated with each other, but their networks typically do not coincide completely (Barrett & Henzi, 2002; Brent, MacLarnon, Platt, & Semple, 2013).

Figure 2.

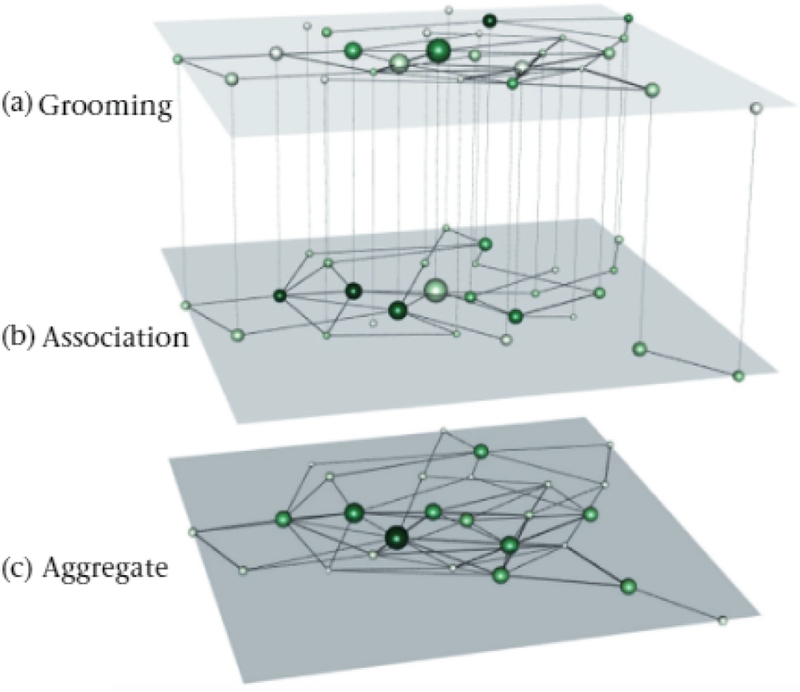
Social networks of a baboon group based oil (a) grooming interactions, (b) proximity-based association relations and (c) an aggregate or both interaction types. We created die network visualization using MuxViz (De Domenico, Porter. & Arenas, 2015). To construct a multilayer network, we joined die grooming and association monolayer networks as two layers in a multiplex network by connecting nodes that represent die same individual using interlayer edges. The sizes of the nodes are based on multilayer PageRank versatility (with larger nodes indicating larger versatilities). We colour die nodes based on monolayer PageRank centrality (with darker shades or green indicating larger values). A given individual in these two layers has die same size, but it can have different colours in the two layers. In the aggregate layer, we determine both the node sizes and their colours from PageRank centrality values in the aggregate network. We position the nodes in the same spatial location in die two layers and the aggregate network. The data (Franz el al., 2015a) are from Franz et al. (2015b).

We analyse the baboon social data in four ways: (1) as a weighted grooming network with only grooming interactions (Fig. 2a), (2) as a weighted association network with only proximity-based associations (Fig. 2b), (3) as an aggregate monolayer network that we obtained by summing the weights of grooming and association interactions of the node pairs (Fig. 2c; see Supplementary Material 2 for more details on aggregating networks) and (4) as a multiplex network with two layers (one for grooming and one for associations). We then calculated measures of centrality (for the monolayer networks in (1)–(3)) and versatility (for the multilayer network (4)) using MuxViz (De Domenico, Porter, & Arenas, 2015). We ranked individuals according to their PageRank centralities and versatilities (De Domenico, Solé-Ribalta et al., 2015), which quantify the importance of an individual in a network recursively based on being adjacent to important neighbours (Fig. 3).

Figure 3.

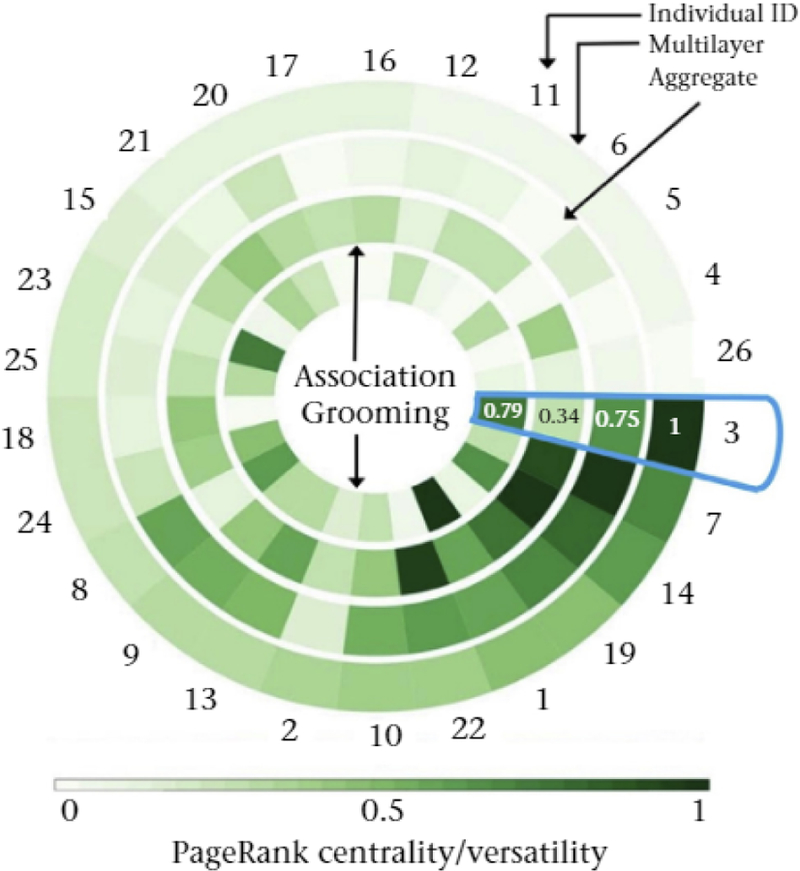
A circular heat map illustrates variation among individuals in PageRank centralities and versatilities. Darker colours indicate larger values of PageRank centralities and versatilities. A given angular wedge in the rings indicates the values for one individual, whose identity (ID) we list outside the ring. The rings are PageRank centrality values from the monolayer grooming network (innermost ring), association network (second ring), aggregate network in which we sum the grooming and association ties (third ring) and PageRank versatility Tor the multiplex network (outermost ring). Using a blue outline, we highlight individual 3. who we discuss in the main text. We indicate the PageRank centrality and versatility values of individual 3 on the rings. We created this visualization using MuxViz (De Domenico, Porter et al., 2015). The data (Franz et al., 2013a) are From Franz et al. (2015b).

The most versatile baboon in the multilayer network (individual 3 in Fig. 3) is the fourth-most central individual in the aggregated network, the second-most central individual in the grooming network and the 16th-most central individual in the association network (Fig. 3). These differences in results using the multilayer, aggregated and independent networks of the same data highlight the need to (1) carefully select which behaviours to encode in networks and (2) interpret the ensuing results based on the questions of interest (Carter, DeChurch, Braun, & Contractor, 2015; Krause, James, Franks, & Croft, 2015). When social relationships depend on multiple interaction types, it is helpful to use a multilayer network framework to reliably capture an individual’s social roles (see Table 1 for more questions and tools), because monolayer calculations may yield different results and centrality in one layer can differ substantially from versatility in an entire multilayer network (Fig. 3).

Multilayer Structures in Animal Groups

Animal social groups are emergent structures that arise from local interactions (Sumpter, 2010), making network analysis an effective approach for examining group-level behaviour. Networks provide useful representations of dominance hierarchies (Hobson, Avery, & Wright, 2013) and allow investigations of information transmission efficiency (Pasquaretta et al., 2014), group stability (Baird & Whitehead, 2000; McCowan et al., 2011), species comparisons (Pasquaretta et al., 2014; Rubenstein, Sundaresan, Fischhoff, Tantipathananandh, & Berger-Wolf, 2015) and collective behaviour (Rosenthal et al., 2015; Westley, Berdahl, Torney, & Biro, 2018). However, given that animals interact with each other in many different—and potentially interdependent—ways, a multilayer approach may help accurately capture a group’s structure and/or dynamics. In one recent example, Smith-Aguilar, Aureli, Busia, Schaffner, and Ramos-Fernández (2018) studied a six-layer multiplex network of spider monkeys, with layers based on types of interactions. In this section, we detail how multilayer methodologies can advance the study of group stability, group composition and collective movement.

One can analyse changes in group stability and composition using various multilayer calculations or by examining changes in relationships across network layers (Beisner & McCowan, 2015). For instance, Barrett et al. (2012) examined changes in a baboon group following the loss of group members by calculating a measure from information theory called ‘joint entropy’ on a multiplex network—with grooming, proximity and aggression layers—both before and after a known perturbation. A decrease in joint entropy following individual deaths corresponded to individuals interacting in a more constrained and therefore more predictable manner. Using a different approach, Beisner et al. (2015) investigated co-occurrences of directed aggression and status-signalling interactions between individuals in macaque behavioural networks. In their analysis, they employed a null model that incorporates constraints that encode interdependences between behaviour types. For example, perhaps there is an increased likelihood that animal B signals to animal A if animal A aggresses animal B. Incorporating such constraints was more effective at reproducing the joint probabilities (which they inferred from observations) of interactions in empirical data in stable macaque groups than in groups that were unstable and eventually collapsed (Chan, Fushing, Beisner, & McCowan, 2013). These findings illustrate how interdependencies between aggression and status-signalling network layers may be important for maintaining social stability in captive macaque groups. A potential implication of these findings is that analysing status signalling and aggression may be helpful for predicting social stability. Another approach that may be useful for uncovering temporal structures in multilayer networks is an extension of stochastic actor-oriented models (SAOMs) (Snijders, 2017). One can use SAOMs to examine traits and processes that influence changes in network ties over time, including in animal social networks (Fisher, Ilany, Silk, & Tregenza, 2017; Hunt et al., 2018; Ilany. Booms, & Holekamp, 2015). SAOMs can use unweighted or weighted edges, with some restrictions in how weights are incorporated (Snijders, 2017). A multiple-network extension to an SAOM enables modelling of the co-dynamics of two sets of edges, while incorporating influences of other individual or network-based traits. Such an approach has the potential to provide interesting insights into how changes in one layer may cascade into changes in other layers. It also provides a useful method to quantify links between group-level structural changes and temporal dynamics of individual centralities.

Multilayer analysis of animal groups can go beyond monolayer network analysis when highlighting a group’s composition and substructures. For example, one measure of interdependence, the proportion of shortest paths between node pairs that span more than one layer (Morris & Barthelemy, 2012; Nicosia, Bianconi, Latora, & Barthelemy, 2013), can help describe a group’s interaction structure. In social insect colonies, layers can represent different tasks. As time progresses and individuals switch tasks, an individual can appear in more than one layer. The amount of overlap among layers (see Supplementary Material 1, Similarity of Layers: Example Measures for examples of overlap measures) can indicate the level of task specialization and whether or not there are task-generalist individuals (Pinter-Wollman, Hubler, Holley, Franks, & Dornhaus, 2012). Consequently, the above interdependence measure may be useful as a way to quantify division of labour (Beshers & Fewell, 2001), because having a small proportion of shortest paths that traverse multiple layers may be an indication of pronounced division of labour. Such a new measure may reveal ways in which workers are allocated to tasks that are different from those that have been inferred by using other measures of division of labour. Comparing different types of measures may uncover new insights into the mechanisms that underlie division of labour.

Animal groups are often organized into substructures called ‘communities’ (Fortunato & Hric, 2016; Potter, Onnela, & Mucha, 2009; Shizuka et al., 2014; Wolf, Mawdsley, Trillmich, & James, 2007), which are sets of individuals who interact with each other more often (in absolute amount and/or as a rate) than they do with other individuals. Finding communities can aid in predicting how a group may split, which can be insightful for managing captive populations when it is necessary to remove individuals (Sueur, Jacobs et al., 2011). Community-detection algorithms distinguish sets of individuals who are connected more densely within a community than with individuals in other communities in a network. One example of a multilayer community-detection algorithm is maximization of ‘multislice modularity’ (Mucha et al., 2010), which can account for different behaviours and/or time windows. A recent review includes a discussion of how multilayer modularity maximization can inform ecological questions, such as the ecological effects of interdependencies between herbivory and parasitism (Pilosof et al., 2017). In animal groups, individuals can be part of more than one community, depending on the types of interactions under consideration. For example, an individual may groom with one group of animals but fight with a different group. Because maximizing multislice modularity does not constrain an individual’s membership to a single community, it can yield communities of different functions with overlapping membership. It can also be used to examine changes in community structure over time. Additionally, sex, age and kinship are known to influence patterns of subgrouping in primates (Sueur, Jacobs et al., 2011), so investigating group structure while considering several of these characteristics at once can reveal influences of subgrouping (such as nepotism) that may not be clear when using monolayer clustering approaches. See Aleta and Moreno (2019) for references to various methods for studying multilayer community structure.

Collective motion is another central focus in studies of animal groups (Berdahl, Biro, Westley, & Torney, 2018; Sumpter, 2010). Coordinated group movements emerge from group members following individual-based, local rules (e.g. in fish schools and bird flocks; Couzin, Krause, James, Ruxton, & Franks, 2002; Sumpter, 2010). Recent studies of collective motion have employed network analysis to examine relationships of individuals beyond the ones with their immediate neighbours. For instance, one can incorporate connections between individuals who are in line of sight of each other (Rosenthal et al., 2015) or with whom there is a social relationship in other contexts (Bode, Wood, & Franks, 2011; Farine et al., 2016). One can also combine multiple sensory modes into a multilayer network to analyse an individual’s movement decisions. Expanding the study of collective motion to incorporate multiple sensory modalities (e.g. sight, odour, vibrations, and so on) and social relationships (e.g. affiliative, agonistic, and so on) can benefit from a multilayer network approach, which may uncover synergies among sensory modes, social relationships and environmental constraints.

Multilayer groupings: dolphin communities emerge from multirelational interactions

To demonstrate the utility of multilayer network analysis for uncovering group dynamics, we analysed the social associations of 102 bottlenose dolphins (Tursiops truncatus) that were observed by Gazda et al. (2015b). They recorded dolphin associations during travel, socialization and feeding. They identified different communities when analysing the interactions as three independent networks and compared the results with an aggregated network, in which they treated all types of interactions equally (regardless of whether they occurred when animals were travelling, socializing or foraging). However, analysing these networks separately or as one aggregated network ignores interdependencies that may exist between the different behaviours (Kivelä et al., 2014). Therefore, we employed multiplex community detection, using the multilayer InfoMap method (De Domenico, Lancichinetti et al., 2015), to examine how interdependencies between layers influence which communities occur when the data are encoded as a multiplex network. We use multiplex community detection to assign each replicate of an individual (there is one for each layer in which an individual appears; Supplementary Material 1) to a community. Therefore, an individual can be assigned to one or several communities, where the maximum number corresponds to the number of layers in which the individual is present. The community assignments depend on how individuals are connected with each other in a multilayer network and on interactions between layers, which arise in this case from a parameter in the multilayer InfoMap method (see Supplementary Material 2 for details). The coupling between layers thus arises both from interlayer edges and their weights (Supplementary Material 1) and from a parameter in the community-detection method (Supplementary Material 2). With no coupling, the layers are distinct and communities cannot span more than one layer; for progressively larger coupling, communities span multiple layers increasingly often. For details on our parameter choices for community detection with the multilayer InfoMap method, see Supplementary Material 2.

To be consistent with Gazda et al. (2015b), our multiplex network (Fig. 4) includes only individuals who were seen at least three times, and we weight the edges using the half-weight index (HWI) of association strength (Cairns & Schwager, 1987). Our community-detection computation yielded 12 communities. The largest community (Fig. 4, dark blue) consists of individuals from all three association layers, and several smaller communities consist of only foraging individuals, only travelling individuals, and both foraging and travelling individuals. For details on the specific implementation of the InfoMap method, see Supplementary Material 2.

Figure 4.

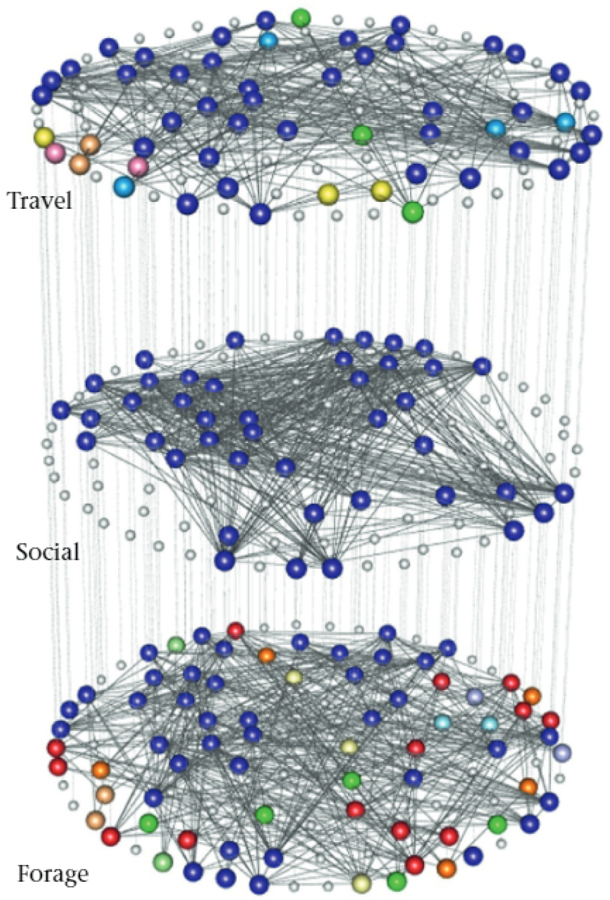
Multiplex network or dolphin proximity-based associations during (1) travelling. (2) socializing and (3) foraging. There are 102 distinct individuals, and each layer layer a node for each individual. Individuals who were never seen interacting in a specific layer (behavioural context) are the small white nodes. Individuals who interacted in at least one layer are die large nodes, which we colour based on their community assignment from multilayer InfoMap (De Domenico, Lancichinetti el at, 2015). We created the network visualization with MuxViz (De Domenico, Porter el at, 2015). The data (Gazda, Iyer, Killingback, Connor, & Branll, 2015a) are from Gazda el al. (2015b).

In their investigation, Gazda et al. (2015b) revealed contextually-dependent association patterns, as indicated by different numbers of communities in the foraging (17), travel (8) and social (4) networks. Notably, when examining the three behavioural situations as a multiplex network, we found similar trends in the numbers of communities across behavioural situations: foraging individuals were in nine communities, travelling individuals were in six communities, and individuals who interact socially were in only one community. Thus, our analysis strengthens the finding that dolphins forage in more numerous, smaller groups and socialize in fewer, larger groups. Different methods for community detection yield different communities of nodes (Fortunato & Hric, 2016); therefore, it is not surprizing that we detected a different number of communities in the monolayer networks than the number in Gazda et al. (2015b). We used InfoMap, which has been implemented for both monolayer and multilayer networks. By contrast, Gazda et al. (2015b) used a community-detection approach that has been implemented only for monolayer networks, Additionally, because we found one markedly large community that spans all layers, we note that it may also be useful to explore core—periphery structure in this network (Csermely, London, Wu, & Uzzi, 2013; Rombach, Porter, Fowler, &, Mucha, 2017).

We also analysed each layer independently and an aggregate of all layers using monolayer InfoMap (Rosvall & Bergstrom, 2007), which is implemented in MuxViz. Multiplex community detection produces somewhat different community assignments from monolayer community detection (Fig. 5). With a multiplex network, one can identify and label an individual’s membership in a community that spans one or several layers (Fig. 5a). However, in monolayer community detection, one examines individuals independently in different layers, thereby assigning their replicates in different layers to different communities (Fig. 5b). Therefore, which individuals are grouped into communities can vary substantially. See Table 1 for more questions and tools in multilayer community detection in animal behaviour. As this example illustrates, depending on the research aims, the form of the data and knowledge of the study system, one or both of monolayer and multilayer investigations may provide valuable insights into the structure of a social system of interest.

Figure 5.

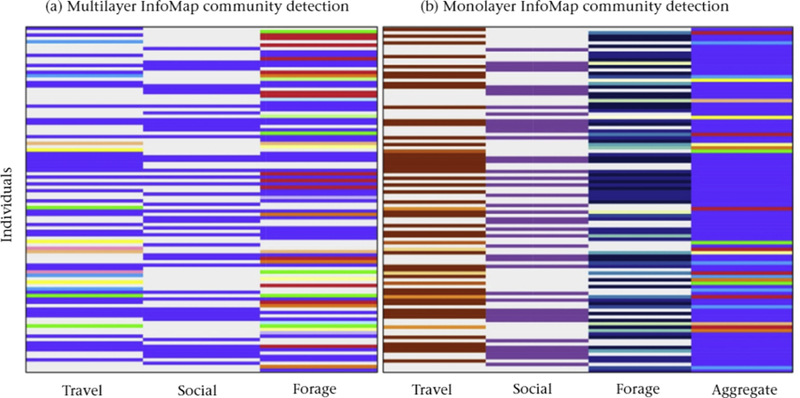
Community structures or individuals from (a) multilayer InfoMap community detection and (b) monolayer InfoMap community detection. Each row represents an individual dolphin, and each column represents a behavioural situation. In the multiplex community detection (a), communities can span all three columns of behaviours, and individuals who are the same colour in one or more columns belong to the same community. Community colours are the same as those in Fig. 4. Note that an individual who appears in all three layers can be assigned to the same community in all three situations (and therefore have the same colour in all three columns). An individual can also be part of three different communities and it then has different colours in each layer. It can also be assigned twice to one community and once to another, In monolayer InfoMap (b), each behavioural situation (as well as the aggregate monolayer network in the last column) yields a separate set or communities, so we use a different colour palette in each column. Individuals in the same column and the same colour are assigned to the same community. In both panels, white represents individuals who were not observed in the associated behavioural situation.

Multilayer Processes at a Population Level

Network analysis has been fundamental in advancing understanding of social processes over a wide range of spatial scales and across multiple social groups (Silk, Croft, Tregenza, & Bearhop, 2014; Sueur, King et al., 2011). A multilayer approach is convenient for combining spatial and social networks (e.g. in a recent study of international human migration; Danchev & Porter, 2018), and it may contribute to improved understanding of fission—fusion dynamics, transmission processes and dispersal. It also provides an integrative framework to merge social data from multiple species and extend understanding of the drivers that underlie social dynamics of multispecies communities (Farine, Garroway, & Sheldon, 2012; Sridhar, Beauchamp, & Shanker, 2009).

Many animals possess complicated fission—fusion social dynamics, in which groups join one another or split into smaller social units (Couzin & Laidre, 2009; Silk et al., 2014; Sueur, King et al., 2011). It can be insightful to study such populations as networks of networks. Additionally, recent advances in quantifying temporal dynamics of networks have shed some light on fission—fusion social structures (Rubenstein et al., 2015). A multilayer approach applied to association data (collected at times that make it reasonable to treat group membership as independent across observations) can assist in detecting events and temporal scales of social transitions in fission—fusion societies. For example, if each layer in a multiplex network represents the social associations of animals at a certain time, a multiplex community-detection algorithm can uncover temporally cohesive groups, similar to the detection of temporal patterns of correlations between various financial assets (Bazzi et al., 2016). Further development of community detection and other clustering methods for general multilayer networks (e.g. stochastic block models; Peixoto, 2014, 2015) and methods based on random walks (De Domenico, Lancichinetti et al., 2015; Jeub, Balachandran, Porter, Mucha, & Mahoney, 2015; Jeub, Mahoney, Mucha, & Porter, 2017) may provide insights into the social and ecological processes that contribute to the temporal stability of social relationships in fission—fusion societies.

Ecological environments and connections between different locations have fundamental impacts on social dynamics (Barocas, Golden, Harrington, McDonald, & Ben-David, 2016; Firth & Sheldon, 2016; Leu, Farine, Wey, Sih, & Bull, 2016; Spiegel, Leu, Sih, & Bull, 2016). A multilayer network representation can explicitly link spatial and social processes in one framework (Pilosof et al., 2017). One approach is to use interconnected networks of social interactions and spatial locations to combine layers that represent social networks with layers for animal movement and habitat connectivity. Data on social interactions can also have multiple layers, with different layers representing interactions in different locations or habitats. For example, in bison. Bison bison, it was observed that group formation is more likely in open-meadow habitats than in forests (Fortin et al., 2009). The same study also noted that larger groups are more likely than smaller groups to occur in meadow habitats. Multilayer network approaches, such as examining distributions of multilayer diagnostics, may be helpful for detecting fundamental differences in social relationships between habitats.

Important dynamical processes in animal societies, such as information and disease transmission, are intertwined with social network structures (Allen et al., 2013; Aplin et al., 2014; Aplin, Farine, Morand-Ferron, & Sheldon, 2012; Hirsch, Reynolds, Gehrt, & Craft, 2016; Weber et al., 2013). Research on networks has revealed that considering multilayer network structures can produce very different spreading dynamics than those detected when collapsing (e.g. by aggregating) multiple networks into one monolayer network (De Domenico et al., 2016). Multilayer approaches can uncover different impacts on transmission from different types of social interactions (Craft, 2015; White et al., 2017) or link the transmission of multiple types of information or disease across the same network. Compartmental models of disease spreading, which describe transitions of individuals between infected and other states (e.g. susceptible—infected (SI) models, susceptible—infected—recovered (SIR) models, and others; Kiss, Miller, & Simon, 2017) have been used to model transmission through multilayer networks (Aleta & Moreno, 2019; De Domenico et al., 2016; Kivelä et al., 2014). For example, several studies have incorporated a multilayer network structure into an SIR model for disease spreading coupled with information spreading about the disease, with the two spreading processes occurring on different network layers (Wang et al., 2015). This approach suggests that taking into account the spread of information about a disease can reduce the expected outbreak size, especially in strongly modular networks and when infection rates are low (Funk, Gilad, Watkins, & Jansen, 2009), Given the growing evidence for coupled infection and behaviour dynamics in animals (Croft, Edenbrow et al., 2011; Lopes, Block, & König, 2016; Poirotte et al., 2017), using multilayer network analysis to help understand interactions between information and disease spread is likely to be informative in studies of contagions in animals. Analogous arguments apply to the study of acquisition of social information, where learning one behaviour can influence the likelihood of social learning of other behaviours. For example, extending models of information spreading (Aleta & Moreno, 2019; De Domenico et al., 2016; Kivelä et al., 2014) to two-aspect multilayer networks that include one layering aspect to represent different types of social interactions and another aspect to represent different time periods (Fig. 1) may provide valuable insights into how social dynamics influence cultural transmissions in a population.

The study of dispersal can also benefit from utilizing a multilayer framework. Networks have been used to uncover the role of spatial (Reichert, Fletcher, Cattau, &. Kitchens, 2016) and social (Blumstein, Wey, & Tang, 2009) connectivity in dispersal decisions. One can use a two-aspect multilayer approach to integrate spatial layers that encode habitat connectivity, or movements of individuals, with social layers that encode intragroup and intergroup social relationships. For example, integrating a multilayer framework with existing multistate models of dispersal (such as the ones in Borg et al., 2017; Polansky, Kilian, & Wittemyer, 2015) can make it possible to relate the likelihood of transitioning between dispersive and sedentary states to the positions of individuals in a multilayer sociospatial network. Such integration of spatial and social contexts may provide new insights both into the relative roles of social and ecological environments in driving dispersal decisions and into the subsequent effects of dispersal on population structure.

Interspecific interactions as a multilayer network

Network approaches have been useful for studying the social dynamics of mixed-species assemblages (Farine et al., 2012). For example, in mixed-species groups of passerine birds, network analysis was used to show that social learning occurs both within and between species (Farine, Aplin, Sheldon, & Hoppitt, 2015b). Mixed-species assemblages have an inherent multilayer structure. Most simply, one can represent a mixed-species community as a node-coloured network in which each layer represents a different species (Fig. 6). To incorporate additional useful information in a mixed-species multilayer network, one can represent the type of behavioural interaction as an additional aspect of the network. For example, one aspect can encode competitive interactions and another can encode noncompetitive interactions.

Figure 6.

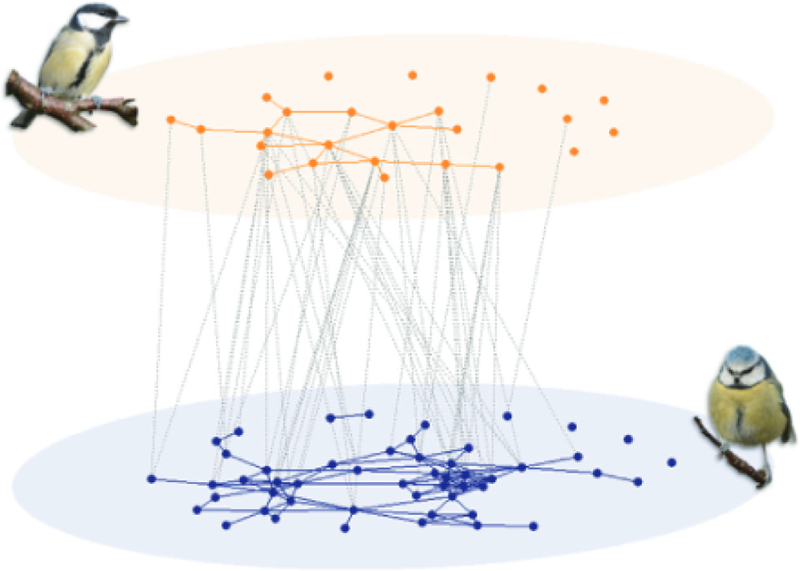
A multilayer network of mixed-species interactions between blue tits Cyanistes caeruleus (bottom layer: blue nodes), and great tits, Parus major (top layer; orange nodes), in Wytham Woods, UK. (in the Cammoor–Stimpsons area) using data from Farine, Aplin. Sheldon, and Hoppitt (2015a, 2015b). Each node represents an individual bird. Blue and orange edges connect individuals within layers (i.e. intraspecific associations), and grey edges connect individuals across layers (i.e. interspecific associations). To aid clarity, we only show edges with a simple ratio index (Cairns &. Schwager 1987; Ginsberg & Young. 1992) of 0.03 or larger. Photographs by Keith Silk.

Considering multilayer measures, such as multidegree or versatility, may provide new insights into the role (s) of particular species or individuals in information sharing in mixed-species groups. Furthermore, multilayer community detection has the potential to provide new insights into the structure of fission—fusion social systems that involve multiple species. The original study (Farine et al., 2015b) that generated the networks that we used in Fig. 6 investigated information transmission in both intraspecies and interspecies social networks (i.e. constituent interaction types of an interconnected network). The authors of the original study concluded that both networks help predict the spread of information, but that the likelihood of acquiring foraging information was higher through intraspecific associations than through interspecific associations, thereby providing a better understanding of information transmission in mixed-species communities than would be possible using monolayer network analysis. This highlights the potential of taking explicitly multilayer approaches to better understand how information can spread within and between species in mixed-species groups.

Evolutionary Models

Understanding the evolution of sociality is a central focus in evolutionary biology (Krause & Ruxton, 2002). Research approaches include agent-based simulations, game-theoretic models, comparative studies, and others. Evolutionary models have been expanded to incorporate interactions between agents, resulting in different evolutionary processes than those in models without interactions (Nowak, Tarnita, & Antal, 2010). However, social behaviours evolve and persist in conjunction with other behaviours and with ecological changes. Therefore, incorporating multiple types of interactions—social, physiological, and with an environment—as part of a multilayer framework can provide novel insights about the pressures on fitness and evolutionary processes. For example, incorporating interactions between molecules at the cellular level, organs at the organismal level, individuals at the group level and groups at the population level into a network of networks can facilitate multilevel analysis of social evolution. In the following paragraphs, we discuss how the expansion of evolutionary modelling approaches to include multilayer network analysis may enhance the study of (1) evolution of social phenomena (such as cooperation) and (2) covariation in behavioural structures across species.

Incorporating ideas from network theory into evolutionary models has made it possible to account for long-term relationships, nonrandom interactions and infrequent interactions (Lieberman, Hauert, & Nowak, 2005). These considerations can alter the outcomes of game-theoretic models of social evolution and facilitate the emergence or persistence of interactions, such as cooperation, by enabling assortativity of cooperative individuals (Aktipis, 2004, 2006; Allen et al., 2017; Croft, Edenbrow, & Darden, 2015; Fletcher & Doebeli, 2009; Nowak et al., 2010; Rand, Arbesman, & Christakis, 2011). Given the effects that group structure can have on the selection and stability of cooperative strategies, multilayer structures can significantly alter the dynamics (both outcomes and transient behaviour) of evolutionary games. Indeed, it has been demonstrated, using a multilayer network in which agents play games on multiple interconnected layers, that cooperation can persist under conditions in which it would not in a monolayer network (Gómez-Gardeñes, Reinares, Arenas, & Floría, 2012; Wang, Szolnoki, & Perc, 2012; Wang, Wang, Szolnoki, & Perc, 2015). Furthermore, the level of interdependence, in the form of coupling payoffs between layers or by strategy transfer across layers, can influence the persistence of cooperation (Wang, Szolnoki, & Perc, 2013; Xia, Miao, Wang, & Ding, 2014). Therefore, in comparison to monolayer network analysis, using a multilayer network approach can improve the realism of models by better reflecting the ‘multidimensional’ nature of sociality and allowing a larger space of possible evolutionary strategies and outcomes. Certain behaviours that may not be evolutionarily stable when considering only one realm of social interactions may be able to evolve and/or persist when considering a multilayer structure of an agent’s possible interactions. For example, expanding game-theoretic models to include multiple types of coupled interactions may facilitate the inclusion of both competition and mutualism, as well as both intraspecific and interspecific interactions.

Comparative approaches offer another powerful method to examine the evolution of different social systems across similar species (Thierry, 2004; West-Eberhard, 1969). In socially complex species, such comparisons can benefit greatly from a multilayer approach. For instance, the macaque genus consists of over 20 species that exhibit a variety of social structures, each with covarying behavioural traits, such as those related to connectivity and/or individual behaviours (Balasubramaniam et al., 2012, 2017; Sueur, Petit et al., 2011; Thierry, 2004). A multilayer network analysis of such covarying interactions—e.g. with layers as connectivity types or time periods—may offer an effective way to reveal differences in social structure. For example, using matrix-correlation methods to measure similarities between layers in a multilayer network offers a way to compare how behaviours covary across different species using a multiple regression quadratic assignment procedure (MRQAP) (Croft, Madden, Franks, & James, 2011). For multilayer networks, global overlap (Bianconi, 2013) and global interclustering coefficient (Parshani, Rozenblat, letri, Ducruet, & Havlin, 2010) are two measures that can quantify the overlap in edges between two layers. See Supplementary Material 1 for a brief discussion of layer similarity measures. One can, for instance, use global overlap between an affiliative network and a kinship network to examine the extent to which nepotism plays a role in social structure across species (Thierry, 2004). In such an analysis, it may also be useful to account for spatial dependencies.

Researchers continue to develop new approaches for measuring heterogeneous structures in multilayer networks (Aleta & Moreno, 2019; Kivelä et al., 2014) that can aid in testing specific evolutionary hypotheses. For example, the ‘social brain hypothesis’ (Dunbar, 1998) posits that the evolution of cognition is driven by sociality, which is cognitively challenging. Recently, there have been several propositions for how to define sociality to test the social brain hypothesis; all of these include the idea that relationships between animals arise from different types of interactions (Bergman & Beehner, 2015; Fischer, Farnworth, Sennhenn-Reulen, & Hammerschmidt, 2017). Multilayer network analysis can aid in developing objective measures of social structures that include the nuances of the various proposed definitions. Another evolutionary hypothesis, the ‘covariation hypothesis’ (Thierry, 2004), posits that changes in a single trait or behaviour can lead to changes in global social organization. Simulations of agent-based models (ABMs) on multilayer networks can test this hypothesis by exploring how different behavioural parameters along with coupling between layers influence group-level structure (Hemelrijk, 2002). For example, an ABM of macaque societies (called ‘Groofi world’) linked grooming and fighting behaviour through a single trait (termed ‘anxiety’) (Hemelrijk & Puga-Gonzalez, 2012; Puga-Gonzalez, Hildenbrandt, & Hemelrijk, 2009). This model has an implicitly multilayer network structure, as it includes multiple interaction ‘layers’ that are coupled by a parameter. By incorporating such structure, the model illustrated that patterns of reciprocation and exchange (Hemelrijk & Puga-Gonzalez, 2012) and aggressive interventions (Puga-Gonzalez, Cooper, & Hemelrijk, 2016) can emerge from the presence of a few interconnected interaction types along with spatial positions.

CONSIDERATIONS WHEN USING MULTILAYER NETWORK ANALYSIS

We have outlined many opportunities for multilayer network approaches to be useful for the study of animal behaviour. However, the application of multilayer network analysis to animal behaviour data is in its infancy, with many exciting directions for future work. Multilayer network analysis may not always be appropriate for a given study, and there are several important considerations about both the applicability of the tools and the types of data on which to use them. Most importantly, practical implementation of these new tools will vary across study systems, and it will differ based on the questions asked. Therefore, researchers should not blindly implement these new techniques; instead, as with any other approach, they should be driven by their research questions and ensure that the tools and data are appropriate for answering those questions.

When and How to Use Multilayer Network Analysis

Multilayer network analysis adds complexity to the representation, analysis and interpretation of data. Therefore, it should be applied only when incorporating a system’s multifaceted nature can contribute to answering a research question, without adding needless complexity to data interpretation. Different types of social relationships may differ in the ‘units’ of their measurement, and it can be challenging to interpret a multilayer network analysis of such integrated data. For example, if one layer represents genetic relatedness and another represents a social interaction, a multilayer similarity measure can reveal one or more relationships between these layers, but a versatility measure that uses both layers may be impractical or confusing to interpret, because they encode different types of connectivity data (i.e. relatedness and behaviour). In a similar vein, intralayer and interlayer edges can have entirely different meanings from each other, and it can thus be difficult to interpret the results of considering them jointly (Kivelä et ah, 2014; Supplementary Material 1).

Therefore, while the strength of using a multilayer network formalism is that it includes more information about interactions than a monolayer network, it is imperative to consider carefully which interactions to include in each layer, based on the study question. It is also important to be careful about which calculations are most appropriate for the different layers in a multilayer network, based on the functions of those layers, especially when they represent different behaviours.

Data Requirements

Just as in monolayer network analysis (or in any study that samples a population), a key challenge is collecting sufficient and/or appropriately sampled data that provide a realistic depiction of the study system (Newman, 2018a, 2018b; Whitehead, 2008). Breaking data into multiple layers can result in sparse layers that do not provide an appropriate sample of the relationships in each layer. Furthermore, if data sampling or sparsity varies across different layers or if the frequency of behaviours differs drastically, one layer may disproportionally dominate the outcome of a multilayer calculation. To avoid domination of one data type, one can threshold the associations, normalize edge weights, adjust interlayer edge weights (Supplementary Material 1) or aggregate layers (Supplementary Material 2) that include redundant information (De Domenico, Nicosia, Arenas, & Latora, 2015).

It is also important to compare computations on a multilayer network to those on suitable randomizations (Kivelä et al., 2014). Just as in monolayer network analysis (Farine, 2017; Fosdick, Larremore, Nishimura, & Ugander, 2018; Newman, 2018c), it is vital to tailor the use of null models in multilayer networks in a context-specific and question-specific way. For example, some network features may arise from external factors or hold for a large set of networks (e.g. all networks with the same intralayer degree distributions), rather than arising as distinctive attributes of a focal system.

Practical Availability and Further Development of Multilayer Methodology

In practice, there are many ways for researchers in animal behaviour to implement multilayer network analysis. Existing software packages for examining multilayer networks include MuxViz (De Domenico, Porter et al., 2015), Pymnet (Kivelä) and the R package Multinet (Magnani & Dubik, 2018). In Table 1, we summarize available tools for implementing various measures. Multilayer network analysis is a rapidly growing field of research in network science, and new measures and tools continue to emerge rapidly. Because this is a new, developing field of research, many monolayer network methods have not yet been generalized for multilayer networks; and many of the existing generalizations have not yet been implemented in publicly available code. Additionally, many multilayer approaches have been published predominantly as proofs of concept in theoretically oriented research or have been implemented only for multiplex networks, but not for other multilayer network structures (such as interconnected networks). Furthermore, multilayer networks with multiple aspects (e.g. time and behaviour type) have rarely been analysed in practice, and the potential utility of incorporating multiple aspects to investigate questions about social behaviour may propel the development of tools to do so. The ongoing development of user-friendly software and modules is increasing the accessibility and practical usability of multilayer network analysis. Multilayer network analysis is very promising, but there is also a lot more work to do, as detailed above. Interdisciplinary collaborations between applied mathematicians, computer scientists, social scientists, behavioural ecologists, and others will be crucial for moving this exciting new field forward.

CONCLUSIONS

In this article, we have discussed multilayer network analysis and outlined potential avenues for using it to provide insights into social behaviour in animals. Multilayer networks provide a useful framework for considering many extensions of animal social network analysis. For example, they make it possible to incorporate temporal and spatial processes alongside multiple types of behavioural interactions in an integrated way. We have highlighted examples in which multilayer methods have been used previously to study animal behaviour, illustrated them with several case studies, proposed ideas for future work in this area and provided practical guidance on some suitable available methodologies and software (Table 1). Using multilayer network analysis offers significant potential for uncovering eco-evolutionary dynamics of animal social behaviour. Multilayer approaches provide new tools to advance research on the evolution of sociality, group and population dynamics, and the roles of individuals in interconnected social and ecological systems. The incorporation of multilayer methods into studies of animal behaviour will facilitate efforts to improve understanding of what links social dynamics across behaviours and contexts, and it provides an explicit framework to link social behaviour with broader ecological and evolutionary processes (Silk et al., 2018).