Comparison of models for analyzing two-group, cross-sectional data with a Gaussian outcome subject to a detection limit

Abstract

A potential difficulty in the analysis of biomarker data occurs when data are subject to a detection limit. This detection limit is often defined as the point at which the true values cannot be measured reliably. Multiple, regression-type models designed to analyze such data exist. Studies have compared the bias among such models, but few have compared their statistical power. This simulation study provides a comparison of approaches for analyzing two-group, cross-sectional data with a Gaussian-distributed outcome by exploring statistical power and effect size confidence interval coverage of four models able to be implemented in standard software. We found using a Tobit model fit by maximum likelihood provides the best power and coverage. An example using HIV-1 RNA data is used to illustrate the inferential differences in these models.

1. Introduction

Biomarkers play an important role in the identification, surveillance and treatment of various disorders.¹ Such measurements can be a challenge to analyze because often biomarker outcomes have non-normal distributions and possess truncated distributions.² The “censored” data contained in the truncated part of the distribution occur because of limitations of technology to measure the amount of biomarker present in a sample and can result in a sizable amount of data below the detection limit. For instance, Human Immunodeficiency Virus Type 1 (HIV-1) Ribonucleic Acid (RNA) data are subject to a lower assay detection limit. HIV-1 RNA levels are associated with transmission, where lower values greatly reduce the probability.³ Estimates of the percentage of Human Immunodeficiency Virus (HIV) patients in care who have a nondetectable viral load vary; a recent estimate is 29%,⁴ but some samples may have much larger censoring rates (e.g., 74%⁵) possibly due to the use of older, less-sensitive assays or greater rates of effective treatment or adherence.

We refer to the minimum detectable concentration of a biomarker as the “detection limit”. This is the value at which samples have a detectable value that cannot be reliably quantified at the low end of the distribution. Others may split this limit into two components: a limit of detection and a limit of quantification.⁶ A biomarker may also have a maximum concentration at which samples cannot be reliably quantified, sometimes described as the “limit of linearity”.⁷ For this study, we considered a single detection limit referred to as d. In some cases d may differ across observations, such as when different assays are used in the same dataset. For instance, in HIV-1 RNA data, Chen et al.⁸ describe a situation where some observations were collected with the Amplicor Standard assay (d=400 copies/mL) and others with the Ultrasensitive assay (d=50 copies/mL). For simplification, we considered d to be the same for each observation. In this situation, measurements above d are deemed to be measured reliably. Conversely, those measurements below d, the non-detectable values or non-detects, are only known to be within the range [0, d). Although we focus on biomarkers, other data are commonly subject to a detection limit, such as environmental and occupational exposure^{9, 10} or pharmacokinetics¹¹ data.

Multivariable statistical modeling techniques have been developed or adapted to analyze data specifically for outcomes with non-detectable values. One model treats the distribution of the biomarker outcome as a mixture of two distributions: a Bernoulli distribution (to model whether or not the observation lies above or below the detection limit) and a continuous distribution. These models have been adapted for use with biomarkers^12–14 and environmental exposures.¹⁵ Extensions of this approach have been made to a Bayesian framework¹⁶ and to repeated measures data.¹⁷ Another model is to treat the censored observations as coming from the conditional density of the non-detectable values given the censored observations. This model was proposed by Tobin¹⁸ using least-squares and Amemiya¹⁹ provided the theoretical groundwork for finding maximum likelihood estimators (MLEs) using this approach. Recent theoretical research using this framework has focused on models for longitudinal data fit either by the EM algorithm^20–22 or by directly maximizing a likelihood.^{23, 24} These models treat all observations as coming from the same distribution, but the likelihood function consists of the probability density function (pdf) for detectable values and the cumulative density function (cdf) evaluated at d for observations below d.

Despite the availability of these models to model data with a detection limit and available resources to assist in their implementation,^{10, 25} investigators frequently choose other models. A popular approach has been to insert a single value for all observations at or below d, such as d or $\frac{d}{2}$. These simple imputation models have been shown to give biased point and standard error estimates.^{10, 20, 23, 24, 26, 27} Deleting all observations below d is likely to bias estimates and inferences^{11, 28} when data are not missing completely at random.²⁹ Another common approach in HIV/AIDS research is to dichotomize the distribution of HIV-1 RNA concentration at d or some higher concentration and use this as an outcome.^30–34 Dichotomizing has also been identified as a trend across all medical research.³⁵ Although creating a binary outcome from a continuous variable results in less power^{36, 37} and may produce wider confidence intervals,³⁸ some authors provide justification for dichotomizing continuous variables.^{39, 40} For example, a logistic regression model may be preferred as the question of interest may be to reduce (or raise) an outcome below (or above) some clinically relevant level.

Many studies have compared biases or coverage rates between models that deal with data subject to a detection limit,^{6, 9, 10, 13, 16, 20, 23, 26, 41–43} but few have explored the power of these models. Those that studied power focused on the ability to find a statistically significance association between mean exposure and a regulatory limit^{10, 15, 44} or between treatment groups.^{6, 10, 45} Of these, only Jin et al.¹⁰ systematically varied the rate at which data fall below the detection limit. However, Jin et al.¹⁰ focused on longitudinal data and did not consider the logistic regression or Bernoulli-Gaussian mixture model approaches.

This study addresses this lack of research on the influence of the censoring rate on the statistical power and confidence interval coverage of regression-type models designed to analyze multiple predictors on an outcome with a detection limit. The motivation behind this study is HIV-1 RNA, which appear to have an underlying Gaussian distribution in multiple different HIV-1 RNA reservoirs including plasma,^46–50 seminal,⁴⁸ cervicovaginal,⁵¹ nasal,⁵¹ rectal,⁵² breast milk,⁵³ and cerebrospinal,⁴⁶ though in some instances these are heavily truncated by the detection limit. Therefore, our outcome is generated from a Gaussian distribution. Our focus is on power to detect a mean difference in two treatment groups, which we assessed by performing simulations. Power is defined as the ability to detect a significant effect when a true effect exists and confidence interval coverage as the rate at which the true parameter is included in the simulation confidence interval. We compare linear regression after replacing censored values by the detection limit d or half the detection limit $\frac{d}{2}$, logistic regression where the outcome is above or below the detection limit, a mixture of a Gaussian pdf and cdf,^{18, 19} a Bernoulli-Gaussian mixture model,¹² a Bernoulli-Gaussian mixture using the long-term survivor likelihood,¹³ and the Buckley-James estimator,⁵⁴ a nonparametric regression model. Although the hypothesis of interest may dictate logistic regression as the appropriate model, we view this question as if the study purpose is to find a statistically significant association between an outcome with a limit of detection and a binary explanatory variable. To our knowledge, this study is the first to compare this group of models while varying the censoring rate across a range as wide as 0.1 to 0.9. Comparing the confidence interval coverage with the power should allow us to make more comprehensive recommendations on which models perform best with cross-sectional data for our simulation parameters. The methods section provides greater detail on these models and describes the simulation parameters. The simulation results are presented and evaluated in the results and discussion sections, respectively.

2. Methods

2.1. Statistical Models

Consider data from $i=1,\dots ,N$ participants in a cross-sectional study. As in the previous section, let d denote the limit of detection. For subject i, y_i is the outcome subject to d. The variable x_i records each participant’s group status; hence either x_i = 0 or x_i = 1. The parameter τ is the true difference between the two groups. Combined with the intercept, is each participant i’s 1 × 2 row of the design matrix and $\mathbf{\tau }$ is a 2 × 1 vector of fixed effects consisting of the intercept τ₀ and the treatment difference τ.

2.1.1. Single-value imputation

In the single-value imputation model, $y_i^{\ast }$ is defined as

$$y_i^{\ast }=\{\begin{array}{c}\frac{d}{2},\hspace{1em}\text{if}\hspace{0.17em}{y}_i<d\\ y_i,\hspace{1em}\text{if}\hspace{0.17em}{y}_i\ge d\end{array},$$

or as

$$y_i^{\ast }=\{\begin{array}{c}d,\hspace{1em}\text{if}\hspace{0.17em}{y}_i<d\\ y_i,\hspace{1em}\text{if}\hspace{0.17em}{y}_i\ge d\end{array}.$$

(In this study, the former is referred to as the “half-LOD” models and the latter as the “at-LOD” model.) Then $y_i^{\ast }$ is used in a linear regression model with the likelihood

$$L_1\left(\mathbf{\tau },\sigma \right)=\prod _{i=1}^N\frac{1}{\sigma \sqrt{2\pi }}\hspace{0.17em}{e}^{\left[-\frac{1}{{2\sigma }^2}{\left(y_i^{\ast }-X_i\mathbf{\tau }\right)}^2\right]}.$$

The residuals from L₁(τ,σ) are assumed to follow the Gaussian distribution N(0,σ²) and be independent. Estimation is via maximum likelihood. We considered both cases in these simulations, i.e., where half the limit of detection is used (the half-LOD) or the limit itself (the at-LOD) as the imputed value. Additionally, it should be noted that, if transformations are performed, the imputed single-value should also be transformed.

2.1.2. Logistic Regression

The second model uses the outcome u_i defined as

$$u_i=\{\begin{array}{c}0,\hspace{1em}\text{if}\hspace{0.17em}{y}_i<d\\ 1,\hspace{1em}\text{if}\hspace{0.17em}{y}_i\ge d\end{array}$$

and then fits a standard logistic regression model with the likelihood function

$$L_2\left(\tau \right)=\prod _{i=1}^N{p}_i^{\left(u_i\right)}{\left[1-p_i\right]}^{\left(1-u_i\right)},$$

where

$$p_i=\frac{e^{Xi\mathbf{\beta }}}{1+e^{Xi\mathbf{\beta }}},$$

with $\mathbf{\beta }=\left\{{\beta }_0,\beta \right\}$. When β > 0 this indicates a greater log odds of possessing a detectable value. Logistic regression models are unstable with small numbers of events (or non-events) per variable (EPV). There exists some disagreement on when this instability begins.⁵⁵ Hence, in an attempt to avoid reporting unstable and potentially biased results but still estimate power, we used an exact logistic regression procedure⁵⁶ when there were 10 EPV or less. The rate of exact method use is noted in the results section.

2.1.3. Tobin-Amemiya

For the third model, the likelihood becomes a mixture distribution between the Gaussian pdf and cdf (henceforth, we will refer to this as the Tobin-Amemiya model). Using the same u_i as in the previous model, the likelihood function can be defined as

$$L_3\left(\mathbf{\tau },\text{σ}\right)=\prod _{i=1}^N{\left[f\left(y_i|\mathbf{\tau },\sigma \right)\right]}^{\left(u_i\right)}{\left[\Phi \left(d|\mathbf{\tau },\sigma \right)\right]}^{\left(1-u_i\right)},$$

where f is the Gaussian pdf (see L₁) and Φ the Gaussian cdf

$$\Phi \left(d|\mathbf{\tau },\sigma \right)={\int }_{-\infty }^{d}f\left(t|\mathbf{\tau },\sigma \right)dt.$$

Observations above the detection limit contribute to the likelihood via the pdf using the detectable value. Values below the detection limit use the cdf evaluated at d. Theoretical justification and properties are expanded upon elsewhere^{18, 19} This model was fit via PROC NLMIXED in SAS software.²⁵

2.1.4. Bernoulli-Gaussian Mixture

For the Bernoulli-Gaussian mixture model, a Bernoulli likelihood is substituted in place of the Gaussian cdf. To estimate the success probability parameter in the Bernoulli likelihood, a logistic regression model is used. Additionally, the Gaussian pdf is multiplied by the probability the observation is detectable, defined by p_i from the logistic regression model. X_i is subject i’s row in the design matrix for both components, β are the fixed effects for the logistic regression, and τ are the fixed effects for the Gaussian component. The likelihood is then

$$L_4\left(\mathbf{\beta },\mathbf{\tau },\sigma \right)=\prod _{i=1}^N{\left[p_{i}f\left(y_i|\mathbf{\tau },\sigma \right)\right]}^{\left(u_i\right)}{\left[1-p_i\right]}^{\left(1-u_i\right)}.$$

As with the Tobin-Amemiya models, these models were fit in PROC NLMIXED with code similar to Thiébaut and Jacqmin-Gadda.²⁵

2.1.5. Long-Term Survivor Likelihood

Also, we performed simulations with the following likelihood function:¹³

$$L_5\left(\mathbf{\beta },\mathbf{\tau },\sigma \right)={\prod _{i=1}^N\left[\frac{p_{i}f\left(y_i|\mathbf{\tau },\sigma \right)}{\sigma }\right]}^{\left(u_i\right)}{\left[1-p_i+p_i\Phi \left(d|\mathbf{\tau },\sigma \right)\right]}^{\left(1-u_i\right)}.$$

Originally this likelihood was proposed in a survival analysis to consider “long-term” survivors.⁵⁷ In our situation, the “long-term” survivors term is considered to be a proportion of non-detectable observations which are in truth detectable. The probability of observation i being detectable (p_i) is defined in the same way as in the Bernoulli-Gaussian likelihood in L₄.

2.1.6. Buckley-James Estimator

Finally, we included a non-parametric regression model for censored data, the Buckley-James estimator.⁵⁴ Full details of the Buckley-James estimator can be found elsewhere.^{54, 58} In short, if $\overline{X}$ is the mean of X , the Buckley-James estimator is an iterative procedure which starts by taking the linear regression estimating equation for τ₀

$$\sum _{i=1}^N\left(x_i-\overline{X}\right)\left(y_i-X_i^{\prime }\mathbf{\tau }\right)=0,$$ (1)

and substitutes $\text{E}\left(y_i|d,u_i\right)-x_i^{\prime }\mathbf{\tau }$ for $y_i-X_i^{\prime }\mathbf{\tau }$. This does not have a closed-form expression but can be approximated by using the Kaplan-Meier estimate of the distribution of the residuals based on $\left\{\left(\min \left\{y_i-\mathbf{\tau },d-\mathbf{\tau }\right\},u_i\right):i\le N\right\}$. This new estimate, ${\widehat{y}}_i$, is then substituted into equation (1) for $y_i-X_i^{\prime }\mathbf{\tau }$ and the Buckley-James estimator is the solution to this equation.

We fit the Buckley-James estimator by calling the bj function in the rms package⁵⁹ from PROC IML. This uses Buckley and James’⁵⁴ variance formula that Lai and Ying⁵⁸ noted has potential shortcomings.

2.2. Simulation Methods

Our primary goal with these simulations was to assess the probability a test statistic is below a level-of-significance threshold given certain parameters, i.e., to find the statistical power. Hence, our main outcome in this study is whether or not the null hypothesis of no association can be rejected; in other words, is p < 0.05. This is recorded and the number of instances over 10,000 simulations is used to determine the estimate of the power. For all models except the Bernoulli-Gaussian and long-term survivor mixture models, this is determined by the p value associated with the test of the τ parameter. Since both mixture models test the effect of group membership in both the Bernoulli and Gaussian components, we used a likelihood ratio test with two degrees of freedom that compared the model with both treatment effects to the model with neither. Thus, to measure power, we summed the number of simulations where the null hypothesis of τ = 0 was rejected and divided that by the total number of simulations which converged and contained stable estimates.

We also wished to measure the 95% confidence interval coverage of these models. In order to measure all effects similarly, we based the coverage on effect sizes. For effects derived from a logistic likelihood function, we converted odds ratios to effect sizes by using Chinn’s⁶⁰ conversion, where

$$\text{effect}\hspace{0.17em}\text{size}\hspace{0.17em}\text{=}\hspace{0.17em}\frac{\text{ln}\left(\text{odds}\hspace{0.17em}\text{ratio}\right)}{\pi /\sqrt{3}}.$$

For simulated values, the upper and lower confidence limits of the odds ratio were computed and then converted to effect sizes by the formula above. For Gaussian effects, the estimated treatment difference was divided by the estimated standard error to compute an effect size (or Cohen’s d⁶¹). (The expected standard errors of the true effect size were calculated from the expression ${\left(\sqrt{2/N}\right)}^{-1}$.) The upper and lower confidence 95% limits of the effect size were calculated. Then, for both types, if the true effect size fell within the upper and lower confidence limits of the simulated effect size, the simulation was said to “cover” the true effect size. We then counted the number of simulations where the 95% confidence interval contained the true effect size and divided by 10,000 to find the coverage rate.

Finally, we explored the bias in the estimated point estimates, standard errors of the difference of means, and effect sizes. Bias was computed by subtracting the median value from all simulations from the true effect. These results are included in the supplementary file (Figures S1–S3).

We chose to vary the difference between the groups (τ) and the percentage of censored observations in these simulations. Values of τ considered were 0.00, −0.25, −0.50, −0.75, and −1.00 since an intervention would be expected to reduce the mean HIV-1 RNA. Zero treatment difference produces an estimate of the type I error rate. All simulations used σ = 1. Thus, the simulations with τ = −0.25, where τ is on the log₁0 scale, correspond to a difference in means a quarter as large as the standard deviation (or, in terms of HIV-1 RNA, a decrease from 1000 to 562.3 copies/mL), τ = −0.50 half as large (or from 1000 to 316.2 copies/mL), and so forth. These parameters were selected for ease of interpretation since the effect sizes equal the treatment effects.

For each parameter set, we chose to have a target power rate of 0.80, meaning that the true power rate is constant across all τ > 0 and censoring rates. Sample sizes for each value of τ > 0 and rate of censoring were determined using Lachenbruch’s⁶² formula. When τ = 0, the expected power is the type I error rate of 0.05 and the sample size was set at 300. We calculated the median R² of each simulated data set prior to censoring to demonstrate the fit of the model with fully observed data. Additionally, we performed simulations with a fixed sample size of 50 for all τ and censoring rates.

Rates of censoring (c) from 0.1 to 0.9 by increments of 0.2 were simulated. To control the rate directly, the limit of detection (d) was determined by finding the appropriate percentile of the simulated Gaussian distribution, then the distribution was shifted in order to make d = 1. This was done to standardize the range of integration for the Gaussian cdf in each simulation. All values below d were deemed to be censored. This approach was used because studies have observed that quantifiable HIV RNA data have an approximately Gaussian or log-Gaussian distribution (e.g.,^{46, 46, 47, 47–53}).

We excluded models which did not converge or contained unstable estimates, namely those models that failed to reach convergence, possessed a non-positive-definite Hessian matrix, or had any parameter with a large standard error (defined as five or greater). For the Tobin-Amemiya and Bernoulli-Gaussian models, results from the linear regression with half the limit of detection and the logistic regression were used as start values, respectively.

Simulated data were generated from an equation for each treatment group. The treatment group is simulated using the equation $y_i=\mathbf{\tau }+e_i$ with $e_i\sim N\left(0,\sigma \right)$ Data for the control group is simulated with $y_i=e_i$. These two groups are then combined for analysis. τ can also be thought of as Cohen’s d.⁶¹

Simulations were performed in SAS software, version 9.2⁶³ using the MVN macro⁶⁴ and in R version 2.15.2.⁶⁵ Figures were created using the ggplot2 package.⁶⁶

3. Results

For brevity, the true difference in means between the outcome of the two groups will be reported as the parameter τ. For the simple linear regression models without accounting for censoring as τ increases, smaller sample sizes are needed to achieve 80% power and a higher proportion of variability (R²) is accounted for in the simple linear model (Table 1).

Table 1:

Summary of simulation parameters; all parameter sets use an error standard deviation of one with 10,000 simulations.

Mean difference between groups (τ)	Percentage censored	N per Arma	R2: Median (IQR)b
0.00	10	300	0.0008 (0.0002, 0.0022)
0.00	30	300	0.00 (0.00, 0.00)
0.00	50	300	0.00 (0.00, 0.00)
0.00	70	300	0.00 (0.00, 0.00)
0.00	90	300	0.00 (0.00, 0.00)
−0.25	10	250	0.02 (0.01, 0.02)
−0.25	30	244	0.02 (0.01, 0.02)
−0.25	50	274	0.02 (0.01, 0.02)
−0.25	70	357	0.02 (0.01, 0.02)
−0.25	90	717	0.02 (0.01, 0.02)
−0.50	10	64	0.06 (0.04, 0.09)
−0.50	30	62	0.06 (0.04, 0.09)
−0.50	50	70	0.06 (0.04, 0.09)
−0.50	70	93	0.06 (0.04, 0.08)
−0.50	90	195	0.06 (0.04, 0.08)
−0.75	10	30	0.13 (0.08, 0.18)
−0.75	30	29	0.13 (0.08, 0.19)
−0.75	50	33	0.13 (0.08, 0.18)
−0.75	70	44	0.13 (0.09, 0.17)
−0.75	90	100	0.13 (0.10, 0.15)
−1.00	10	17	0.21 (0.14, 0.30)
−1.00	30	17	0.21 (0.14, 0.30)
−1.00	50	20	0.21 (0.14, 0.29)
−1.00	70	27	0.21 (0.15, 0.27)
−1.00	90	68	0.20 (0.17, 0.24)

^aSample sizes for each value of τ > 0 and rate of censoring were determined using Lachenbruch’s⁶² formula. When τ = 0, the expected power is the type I error rate of 0.05 and the sample size was set at 300.

^bR² calculated by using simulated data prior to censoring with standard R² formula of simple linear regression.

The highest number of simulations which failed to converge was observed for treatment effects further from zero and c = {0.1, 0.9} (Table 2). The Bernoulli-Gaussian model failed to converge the most and reached a low of around 40% convergence with τ = −1 and c = 0.1. For logistic regression models, exact logistic regression was needed in all simulations with c = {0.1, 0.9} and τ ≤ −0.75.

Table 2:

Number of simulations out of 10,000 that failed to satisfy convergence criteria, possessed a non-positive-definite Hessian matrix, or had a parameter with a large standard error (five or greater) for simulations using Lachenbruch’s⁶² sample size formula.

Mean difference between groups (τ)	Percentage censored	Gaussian pdf-cdf	Bernoulli-Gaussian	Long-term survivor	Buckley-James
0.00	10
0.00	30
0.00	50				46
0.00	70				84
0.00	90		1		270
−0.25	10		2
−0.25	30
−0.25	50				35
−0.25	70			1	128
−0.25	90				15
−0.50	10		138	152
−0.50	30
−0.50	50			1	546
−0.50	70			2	592
−0.50	90			27	293
−0.75	10		2167	2253
−0.75	30		9	117
−0.75	50			97	918
−0.75	70			261	1555
−0.75	90	99	99	848	929
−1.00	10		5986	6906
−1.00	30		536	1317
−1.00	50			654	1330
−1.00	70	39	39	1389	2086
−1.00	90	1257	1257	3302	2164

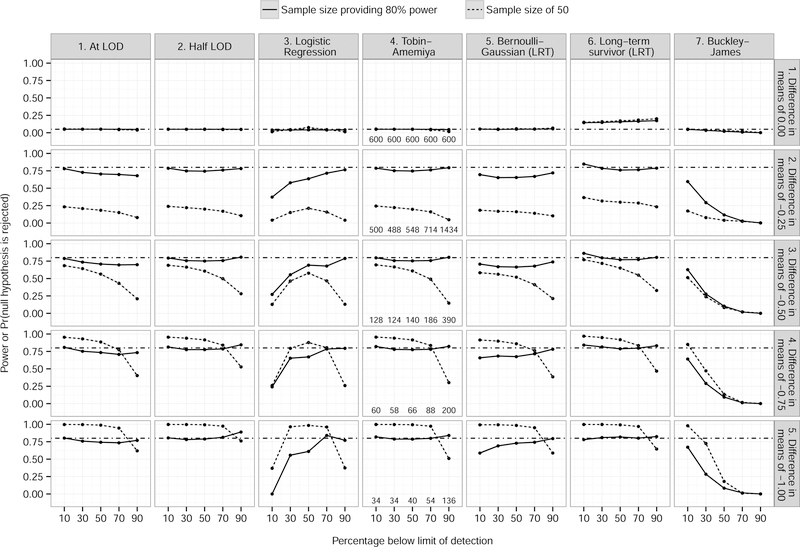
Proportions of null hypothesis rejection for τ = 0 hovered around 0.05 for all values of c for all models, except for the long-term survivor model, which was consistently around 0.15, and the Buckley-James estimator, which decreased with increasing τ (Figure 1). For τ ≤ −0.25, the patterns were similar for each model across all τ since the sample size was dependent on c. The half-LOD, Tobin-Amemiya, and long-term survivor models had power close to or slightly lower than the nominal level (0.80). Imputing a single value at the LOD had lower power as c increased. Logistic regression had substantially lower power when c ≤ 0.50. When analyzed with a Bernoulli-Gaussian model, the power was between 0.65 and 0.75 in most cases, except when c = 0.9. Finally, the Buckley-James estimator had substantially lower power, especially as c increased.

Figure 1.

Null hypothesis rejection proportion (power), broken down by method, difference between treatment and control means, and sample size providing 80% power (solid lines; sample sizes for the row are listed along the bottom of plots in the fourth column) and a fixed sample size of 50 (dashed lines), 10,000 simulations, 5% level of significance. Dot−dash lines indicate nominal power of 0.80, except when there is no difference in means (row 1) where the nominal power is equal to the type I error rate of 0.05. Grey shading denotes 95% confidence interval.

Confidence interval coverage was close to 95% for the Tobin-Amemiya model, but lower for the Gaussian component of the Bernoulli-Gaussian model, and the Gaussian component of the long-term survivor likelihood (Figure 2). Both single value imputation models (at LOD and half LOD) possessed coverage at or near 95% when c ≤ 0.7, with a precipitous drop at c = 0.9. Coverage for the Buckley-James estimator was slightly less than 95% for most values of c. Logistic regression and the Bernoulli components of the Bernoulli-Gaussian and the long-term survivor likelihood failed to achieve 95% coverage except in rare cases.

Figure 2.

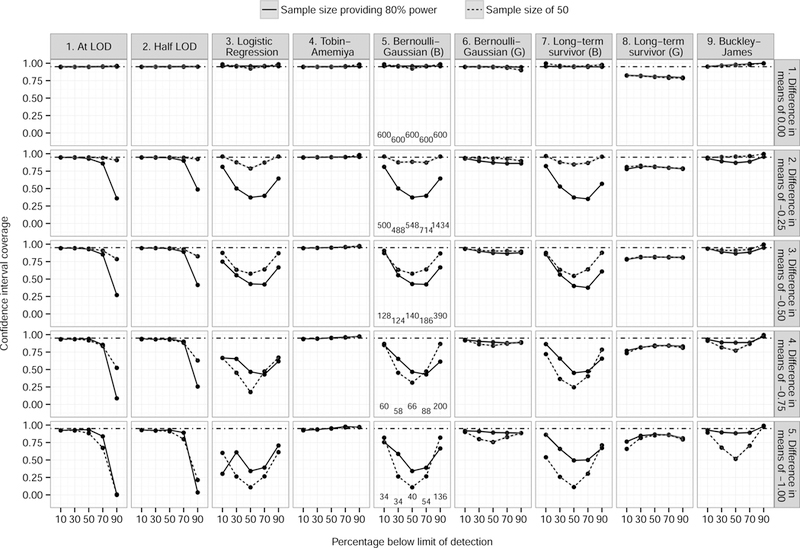
Confidence interval coverage of true effect size, broken down by method (and component if applicable), difference between treatment and control means, and sample size providing 80% power (solid lines; sample sizes for the row are listed along the bottom of plots in the fifth column) and a fixed sample size of 50 (dashed lines), 10,000 simulations, 5% level of significance. Dot−dash lines indicate expected confidence interval coverage of 0.95. Grey shading denotes 95% confidence interval. In method titles, B=Bernoulli component and G=Gaussian component.

When the sample size is fixed at 50, the differences between models are largely similar to those with sample sizes with 80% power, but those differences are not as pronounced. Especially at higher rates of censoring, the differences are almost negligible. Lines for logistic regression possessed a concave shape, which is consistent with sample size tables when the outcome rate is varied (e.g., Hsieh⁶⁷).

Results from the estimates of bias largely mirror the results shown in the power and coverage proportion (Figures S1–S3). Those models which possessed poor power or coverage did so because the point estimates are biased towards the null hypothesis. One major exception are the single value imputation models. Although the point estimates are biased towards the null hypothesis, the standard error estimates for τ < 0 are biased towards zero. This bias got progressively worse (closer to zero) as c increased.

4. Example

These data come from a project to assess the effect of raltegravir, a novel HIV medication, using data from the HIV Outpatient Study (HOPS) during the years 2007 to 2010.⁶⁸ The HOPS is a prospective, observational cohort of HIV-positive participants enrolled from nine medical facilities in the United States. In Buchacz et al.⁶⁸ the baseline dataset includes data on each patient’s medical history and current treatment at his or her initiation of raltegravir treatment or first drug regimen change post 1/1/2007. For this example, we utilize the baseline data and explore the association between participants’ HIV-1 RNA values at baseline and whether or not the patient was being prescribed raltegravir.

Our example is interesting primarily because it contradicts our simulation results. Summary statistics for patient’s log₁₀ HIV-1 RNA levels (Table 3) and parameter estimates for testing for differences between the raltegravir groups (Table 4) are presented. The null hypothesis of no association of HIV-1 RNA level with those who initiated a raltegravir-containing regimen is rejected by the imputing a single value at the LOD, Bernoulli-Gaussian, long-term survivor, and Buckley-James models and not in the half-LOD and Tobin-Amemiya models. Ironically, our simulations showed the Tobin-Amemiya model to have greater power when testing for group differences. The difference in inference in the latter two models appears to be because the root mean squared error (RMSE) is larger. Also of note, both the Bernoulli-Gaussian and long-term survivor models possess Gaussian point estimates that were more than twice as large as the single value imputation models and the Tobin-Amemiya model. Potentially, this can be explained by the fact that the Gaussian treatment effect estimate is based on the detectable data in the binomial-Gaussian model. Hence, the significance test comparing the raltegravir and non-raltegravir groups assesses whether there is a difference between the distributions of the detectable values. In contrast, the Tobin-Amemiya model incorporates all the data, not just the detectable values, to test for a difference. This is also true for the summary statistics of the log₁₀ HIV-1 RNA distributions by group. The non-raltegravir group has a higher mean and median when considering only the detectable values. With all participants, however, there the differences are much smaller between these groups (using both imputation models).

Table 3:

Summary statistics for log base 10 HIV-1 RNA by raltegravir use in the HIV Outpatient Study (HOPS).

Group	N	Mean (SE)	Median (IQR)
Detectable values only
Non-raltegravir Raltegravir	4221 3322	4.03 (0.05) 3.68 (0.07)	4.34 (1.64) 3.73 (2.25)
All data, half the limit of detection imputed for nondetects
Non-raltegravir Raltegravir	896 692	2.35 (0.06) 2.21 (0.06)	0.85 (3.43) 0.85 (2.80)
All data, zero imputed for nondetects
Non-raltegravir Raltegravir	896 692	2.80 (0.05) 2.65 (0.05)	1.70 (2.58) 1.70 (1.95)

Table 4:

Model estimates for log base 10 HIV-1 RNA, baseline data of raltegravir study, the HIV Outpatient Study (HOPS). Root mean squared error (RMSE) is an estimate of the σ parameter in each likelihood function.

Parameter	Estimate or odds ratio (95% CI)	p value
At-LOD imputation
Gaussian RMSE	−0.15 (−0.28, −0.01) 1.37	0.03
Half-LOD imputation
Gaussian RMSE	−0.14 (−0.31, 0.03) 1.72	0.11
Logistic Regression
Logistic	1.04 (0.85, 1.26)	0.73
Tobin-Amemiya
Gaussian RMSE	−0.16 (−0.44, 0.11) 2.49	0.25
Bernoulli-Gaussian
Logistic Gaussian LRT RMSE	1.04 (0.85, 1.26) −0.35 (−0.52, −0.18)   1.20	0.73 < 0.0001 0.0004
Long-term survivor
Logistic Gaussian LRT RMSE	1.05 (0.86, 1.29) −0.37 (−0.49, −0.24)   0.86	0.62 < 0.0001 < 0.0001
Buckley-James
Gaussian RMSE	−0.28 (−0.45, −0.10) 1.20	0.002

5. Discussion

As shown in our example the model chosen can have an impact on whether the null hypothesis of no treatment effect is rejected. The simulation results of these models indicate, for sample sizes with 80% power and across all censoring rates, the Tobin-Amemiya model produced an equivalent or better combination of power and effect size confidence interval coverage as compared to the other models simulated. When considering the bias in point and standard error estimates (Figures S1–S3 in the supplementary file), the Tobin-Amemiya model outperformed all other models. This conclusion concurs with the cross-sectional simulations in Jin et al.¹⁰ and, despite analyzing longitudinal data, the crossover trial simulations of Karon et al.⁶ These results have some similarities to Beal,¹¹ though are more supportive of using the Tobin-Amemiya model. Beal felt as though the Gaussian cdf-pdf was preferable, but argued models which omit all points below the LOD have value. His reasoning was that the Tobin-Amemiya model may be troublesome to implement and the shortcomings of simple models may not be large, especially at small censoring rates. We agree that, when the rate is small, a model which omits observations below the LOD will perform similarly, but the implementation difficulties are minimal with currently available software. Computation problems with the Tobin-Amemiya model only arose when a small percentage of points were detectable.

The Bernoulli-Gaussian mixture model performed well, but generally had inferior power to the Tobin-Amemiya model by roughly 5–10%. At high levels of censoring, the difference between the Bernoulli-Gaussian model and the Tobin-Amemiya model decreased, but the latter was still superior. We experienced the most convergence problems with the Bernoulli-Gaussian model at both high and low levels of censoring. Hence, the concave shape of the power function may be partially due to only certain simulated datasets converging which introduced bias into the results. Even in situations with good convergence, the Bernoulli-Gaussian model produced poorer confidence interval coverage for the Gaussian effect. Our simulations suggest that this model may be fully reliable only in situations when 0.3 ≤ c ≤ 0.7.

For the long-term survivor model, rates of null hypothesis rejection hovered around 0.15 for all censoring rates, which are similar to the rates seen in Karon et al.⁶ for the same likelihood. Hence, this likelihood seems to be oversensitive and we don’t feel it can be recommended for analyzing a cross-sectional, Gaussian outcome with a detection limit.

The Buckley-James estimator exhibited good confidence interval coverage, but poor power, especially at higher rates of censoring. We are unsure why the power was so much less and further study is warranted.

Surprisingly, the power of the at-LOD and half-LOD models are not appreciably greater than other models included in these simulations. Multiple studies have shown inserting a single value below the detection limit produces biased estimates,^{10, 20, 23, 24, 26} especially standard error estimates that are too low. Hence, a priori, we felt the bias in the standard errors would drive power upward beyond 80%. Since the power was approximately 80% and the effect size confidence interval was good (except at c = 0.9), we looked at the bias of the point estimates and standard errors separately (Figures S1–S3). The bias in standard errors concurred with prior research by showing variance estimates are biased downward as the rate of censoring increases, but results suggested that the point estimates are biased strongly toward the null hypothesis. Hence, the downward bias of the standard errors was offset by the bias in the point estimates. These results are similar to those seen in analyses of longitudinal data using half-LOD substitution.¹⁰ Although these counteracting biases gave the half-LOD model similar power to other models, inferences from such a model may be unwise to use since point and variance estimates are biased. Hence, it does not appear wise to use the single value imputation models except in situations where the censoring level is low enough to make minimal difference in the results.

The same overall conclusion is true for logistic regression. Dichotomizing at the detection limit resulted in less power than most of the other models included in these simulations when c ≤ 0.7. The difference was especially marked when the rate of censoring was low. With a small proportion of data below the detection limit, logistic regression power was driven by the small sample size in the censored group while other models used much more of the available information to test for differences. As the censoring rate increased, these differences became smaller since the data become nearly binary.

At c ≥ 0.7 and τ ≤ −0.5, logistic regression provided power at or near the levels produced by other models, but at a censoring rate of 0.9, the coverage suddenly jumped. This may have been caused by the increasingly smaller absolute number of observations in the non-censored group and the necessity for all simulations required to use an exact method. Nonetheless, logistic regression did not match other models on both power and effect size confidence interval coverage.

When the sample size is fixed at 50, the differences between models are not as pronounced. The Tobin-Amemiya model again appears to be the best choice, but the differences are almost negligible, especially at higher rates of censoring. Lines for logistic regression possessed a concave shape, which is consistent with sample size tables when the outcome rate is varied (e.g., Hsieh⁶⁷).

For the fixed sample size simulations, the most striking aspect is the observed loss of power at higher rates of censoring. The loss of power can be substantial when dichotomizing a continuous outcome.³⁶ This seems reasonable; as the amount of information decreases, there is less ability to find a difference. None of these models were able to compensate for this loss of information. Data with an outcome possessing a high level of censoring will have significantly reduced power to find a difference regardless of the model. This is important to recognize for study planning as failure to account for the detection limit may leave a study underpowered. Projecting the likely rate of non-detectable values for a study outcome may be challenging, but this may be crucial to achieve a desired level of power. Although Lachenbruch’s⁶² formula does not have the same null hypothesis we used in these simulations, it performed well at producing sample sizes with the appropriate levels of power.

Any simulation study is limited by a number of conditions. The linear predictors in these simulations included an intercept and one predictor. In most settings, multiple covariates will be used in models, meaning our models may not adequately represent settings where confounding is present. In regards to the simulation construction, one may expect the decreased performance of the Bernoulli-Gaussian mixture model compared to the Tobin-Amemiya model because the data generating mechanism more closely follows the Tobin-Amemiya model. Our focus was on models to analyze log-transformed measurements of HIV-1 RNA, which typically follow a Gaussian distribution. Hence, the Tobin-Amemiya model matches these assumptions better than any of the other models used in these simulations. Data arising from another distribution, such as a point mass-Gaussian mixture, may produce different conclusions; in particular, a Tobin-Amemiya model may be sub-optimal. We also did not consider the consequences of analyzing an outcome from a non-Gaussian distribution. Another potential limitation was the choice to include the treatment parameter in both the logistic and Gaussian components of the mixture. Determination of statistical significance was made with a likelihood-ratio test. Other approaches to defining the statistical significance of the treatment parameter estimate may give different results. Finally, in many applications, more than one, independent variable will be included in a model. Some models may perform better than others with informative covariates and the differences among models observed in these simulations might not be the same with additional covariates.

Extensions of this research could look at similar models using simulated data with a different underlying distribution. For instance, data from a semicontinuous or zero-inflated distribution would match the assumptions of the Bernoulli-Gaussian model better which may result in increased performance. Hurdle models⁶⁹ may also be appropriate or models using a truncated Gaussian as the continuous distribution. As increasingly sensitive assays are developed and used, the likelihood of observing a Bernoulli-Gaussian distribution grows. Hence, a Bernoulli-Gaussian distribution may become the standard in HIV research soon. Any of these situations could be tested under a longitudinal setting as well. We were able to approximate the nominal level of power in the Tobin-Amemiya model with a published formula.⁶² Other models are available which may provide better estimates, but are more complicated to implement.^{70, 71} Covariates informative of the censoring could be added to the models to determine if a difference in performance is achieved. Finally, although we chose not to include any models which used multiple imputation (MI)⁷² to impute data below the detection limit, these models have been used in similar settings. Comparisons between several MI implementations for semicontinous data,⁷³ comparisons to mixed models,²⁷ and of a MI approach using bootstrapping^41–43 have been performed.

6. Conclusion

Compared to the other models we examined, the Tobin-Amemiya model provided power and effect size coverage at or better than other models included in this simulation study and appropriate test size. Hence, the Tobin-Amemiya appeared to be the best model for analyzing an outcome. At low and high censoring rates, these models provided poor power and may fail to converge. Researchers and analysts must be cautious when analyzing data with a high proportion of data below a detection limit. The reduction in power is great with any of the model we evaluated and little utility may exist in analyzing such data. Exact logistic regression may be advisable with high or low censoring rates and large treatment differences.