On the energy efficiency of cell migration in diverse physical environments

Significance

Cell migration requires energy, but the metabolic cost of migration has not been quantitatively explored in detail. Here, we use a 2-phase model of the cell cytoplasm to compute cell velocities and energy efficiencies during cell movement. This model predicts that actin polymerization-driven migration is very inefficient in high-hydraulic-resistance environments. Instead, cells can adopt the water-driven mechanism. Therefore, the energetics and mechanical efficiencies of cell movement are predicted to depend on the physical environment.

Abstract

In this work, we explore fundamental energy requirements during mammalian cell movement. Starting with the conservation of mass and momentum for the cell cytosol and the actin-network phase, we develop useful identities that compute dissipated energies during extensions of the cell boundary. We analyze 2 complementary mechanisms of cell movement: actin-driven and water-driven. The former mechanism occurs on 2-dimensional cell-culture substrate without appreciable external hydraulic resistance, while the latter mechanism is prominent in confined channels where external hydraulic resistance is high. By considering various forms of energy input and dissipation, we find that the water-driven cell-migration mechanism is inefficient and requires more energy. However, in environments with sufficiently high hydraulic resistance, the efficiency of actin-polymerization-driven cell migration decreases considerably, and the water-based mechanism becomes more efficient. Hence, the most efficient way for cells to move depends on the physical environment. This work can be extended to higher dimensions and has implication for understanding energetics of morphogenesis in early embryonic development and cancer-cell metastasis and provides a physical basis for understanding changing metabolic requirements for cell movement in different conditions.

Cells must consume energy to grow, migrate, divide, and maintain essential life processes in a changing environment (1). The typical power density of a mammalian cell is on the order of $10^{-15}\hspace{0.17em}\mathrm{W}/\mathrm{\mu }{\mathrm{m}}^3$ (2), but cancer cells can have a higher metabolic rate (3, 4). As a fraction of the total power consumption, it has been proposed that only a small portion of the total cell energy budget is used to power cell migration. The estimate for migration based on actin polymerization at the cell front typically requires less than 1% of the total available adenosine triphosphate (ATP) power (2). However, this estimate is based on ideal assumptions, and it is unclear how the energy requirements change for cell migration in different physical environments and under diverse mechanisms (5, 6). For example, on 2-dimensional (2D) flat surfaces, cell migration is mostly driven by actin polymerization and forces from focal adhesions (7) (actin-driven). In confined geometries, such as dense extracellular matrix or tissues, cell migration can be driven by water permeation (8) (water-driven). Indeed, B16F10 and 4T1 tumor cells invade faster when water permeability across the membrane is increased (9). The transition between actin-driven and water-driven mechanisms of cell migration depends on the hydraulic property of the external environment (10). Each mechanism of cell migration requires energy consumed by a different set of molecules and is ultimately converted to mechanical power output and dissipation (Fig. 1A).

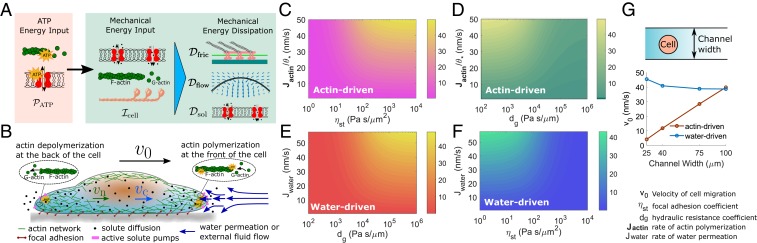
Fig. 1.

Two-phase cell-migration model and energy flow within the cell. (A) ATP energy input is eventually converted to mechanical dissipation. ${\mathcal{I}}_{\mathrm{c}\mathrm{e}\mathrm{l}\mathrm{l}}$ is the energy input during solute pumping, actin polymerization, and cytoskeletal force generation. Dissipation ${\mathcal{D}}_{\mathrm{f}\mathrm{r}\mathrm{i}\mathrm{c}}$ is from various frictional forces; ${\mathcal{D}}_{\mathrm{fl}\mathrm{o}\mathrm{w}}$ is dissipation in the passive transmembrane water flux and dissipation in the exterior fluid; and ${\mathcal{D}}_{\mathrm{s}\mathrm{o}\mathrm{l}}$ is the solute diffusive dissipation in the cytoplasm and the membrane. (B) Variables considered in our model of cell migration. $v_{\mathrm{n},\mathrm{c}}$ are the actin network and cytosol velocities, respectively. $v_0$ is the velocity of the cell. Actin polymerization and depolymerization are at the front and back of the cell, respectively. The actin network forms focal adhesion with the substrate. Solutes are transported across the cell membrane and diffuse in the cytoplasm. Water fluxes also occur across the cell membrane. (C–F) Contours of cell velocity $v_0$ (in nanometers per second) predicted from the 1D model. (C) Contour of $v_0$ as $j_{\mathrm{a}\mathrm{c}\mathrm{t}\mathrm{i}\mathrm{n}}$ and ${\eta }_{\mathrm{s}\mathrm{t}}$ vary. $d_g=0$. (D) Contour of $v_0$ as $j_{\mathrm{a}\mathrm{c}\mathrm{t}\mathrm{i}\mathrm{n}}$ and $d_g$ vary. (E) Contour of $v_0$ as $j_{\mathrm{w}\mathrm{a}\mathrm{t}\mathrm{e}\mathrm{r}}$ and $d_g$ vary. (F) Contour of $v_0$ as $j_{\mathrm{w}\mathrm{a}\mathrm{t}\mathrm{e}\mathrm{r}}$ and ${\eta }_{\mathrm{s}\mathrm{t}}$ vary. $d_g=10^2$ Pa$\cdot$s/$\mathrm{\mu }$m. In C and D, $i_{\mathrm{s}\mathrm{o}\mathrm{l}}^{\mathrm{b},\mathrm{f}}=0$. In D and E, ${\eta }_{\mathrm{s}\mathrm{t}}=10^4$ Pa$\cdot$s/$\mathrm{\mu }{\mathrm{m}}^2$. In E and F, $j_{\mathrm{w}\mathrm{a}\mathrm{t}\mathrm{e}\mathrm{r}}$ is not prescribed but calculated from the chemical potential difference of the water across the membrane. $i_{\mathrm{s}\mathrm{o}\mathrm{l}}^{\mathrm{b}}=0$, while $i_{\mathrm{s}\mathrm{o}\mathrm{l}}^{\mathrm{f}}$ varies from $6.25\times 10^{-7}$ to $6.25\times 10^{-5}$ mM$\cdot$m/s. $j_{\mathrm{a}\mathrm{c}\mathrm{t}\mathrm{i}\mathrm{n}}=0$. (G, Upper) Cells in confinement experience increased hydraulic resistance. (G, Lower) Computed cell velocities from the 2D model for a circular cell for different channel widths.

Because the cell can utilize different mechanisms to migrate, energy requirements of cell migration could be a determining factor for cells to shift between these mechanisms. Indeed, recent experiments show that cell metabolic activity depends on the density of the extracellular matrix (4). In this paper, using a theoretical framework based on energy balance, we calculate the mechanical power associated with both actin-driven and water-driven migration and compute the mechanical efficiency from each mechanism of cell migration. We will also show that cell-migration energy efficiency depends on cell shape, cell-membrane water permeability, and the geometry of the physical environment.

Results

A 2-Phase Framework Describes Cell Migration.

The cell is modeled as a 2-phase medium with an F-actin network phase and a water phase (Fig. 1B; details of the model and simulation algorithm can be found in SI Appendix). This framework is implemented in both 1-dimensional (1D) and 2D models. The 1D model is useful not only for cell migration in confined channels, but also for cell protrusions in 3-dimensional (3D) collagen matrix or any volume element of the cell in arbitrary geometry. On the other hand, the 2D model is more biophysically detailed and allows, in particular, for the exploration of flow-field and cell-shape effects on cell movement (11) or division (12).

The actin network (“n”) and the cytosol (“c”) are modeled as 2 distinct phases. Each phase has its own velocity, $v_{\mathrm{n}}$ and $v_{\mathrm{c}}$. On the cell-membrane boundary, $v_{\mathrm{n}}$ and $v_{\mathrm{c}}$ are determined by their respective fluxes, $j_{\mathrm{a}\mathrm{c}\mathrm{t}\mathrm{i}\mathrm{n}}$ and $j_{\mathrm{w}\mathrm{a}\mathrm{t}\mathrm{e}\mathrm{r}}$. $j_{\mathrm{a}\mathrm{c}\mathrm{t}\mathrm{i}\mathrm{n}}$ comes from the rate of actin (de)polymerization, and $j_{\mathrm{w}\mathrm{a}\mathrm{t}\mathrm{e}\mathrm{r}}$ comes from both hydrostatic and osmotic pressure-driven water flux across the cell membrane. The creation and destruction of the actin network at the membrane is thus explicitly modeled within a continuum framework.

The 2 phases interact with the environment in different ways. The actin-network phase is linked to the environment through focal adhesions. As a first approximation, the force transmitted from focal adhesion to the actin network is proportional but opposite to the velocity of the network, $-{\eta }_{\mathrm{s}\mathrm{t}}{v}_{\mathrm{n}}$, where ${\eta }_{\mathrm{s}\mathrm{t}}$ is the coefficient of the focal adhesion that depends on the stiffness of substrate (13, 14) and the size (15) and density (16) of adhesions. ${\eta }_{\mathrm{s}\mathrm{t}}$ is an emergent concept generic for adhesion molecules that make and break bonds under force.

The external flow field exerts a drag on the cell, and the magnitude of this hydraulic drag is dependent on the transmembrane water flux $j_{\mathrm{w}\mathrm{a}\mathrm{t}\mathrm{e}\mathrm{r}}$ (8, 10). In the 2D model, this effect is naturally accounted for by solving for the external flow field as part of the problem and enforcing force balance at the membrane (11). In 1D, we follow the approach in ref. 10 in which hydraulic resistance is given by $d_g\left(v_0-j_{\mathrm{w}\mathrm{a}\mathrm{t}\mathrm{e}\mathrm{r}}\right)$, where $v_0$ is the cell velocity and $d_g$ is the coefficient of hydraulic resistance, which depends on the geometry, viscosity, and permeability of the environment. Generally speaking, the hydraulic resistance is higher for cell migration in 1D channel and 3D collagen matrices (17) compared to migration on 2D substrates.

$j_{\mathrm{w}\mathrm{a}\mathrm{t}\mathrm{e}\mathrm{r}}$ depends on both hydrostatic and osmotic pressure differences across the cell boundary. Osmotic pressure comes from solute (or ion) mixing with the water phase (18). For simplicity, we consider a single species of electro-neutral solute with concentration $c$. The solute can diffuse in the cytosol and is also transported across the cell membrane. The membrane flux of the solute is the sum of a passive component, which follows the solute concentration gradient across the membrane, and an active component, $i_{\mathrm{s}\mathrm{o}\mathrm{l}}$, powered by ATP hydrolysis. In the model, the active component is prescribed and is considered as a parameter. A spatially asymmetric distribution of $i_{\mathrm{s}\mathrm{o}\mathrm{l}}$ on the cell membrane leads to a nonuniform distribution of $c$ within the cell and thus generates water flux across the cell membrane. We vary $i_{\mathrm{s}\mathrm{o}\mathrm{l}}$ to obtain different amounts of water flux across the cell.

Both the 1D and 2D models satisfy a free-energy identity (11, 19) (SI Appendix). To the best of our knowledge, few, if any, models of cell movement (let alone models that incorporate solute transport) satisfy this property. The energy identity gives us explicit expressions for energy expenditure, allowing us to study the energetics of cell movement.

Actin-Driven and Water-Driven Cell Migration Are 2 Complementary Mechanisms.

In the 1D model, the cell velocity is readily computed for different environmental conditions, in particular, the strength of focal adhesion, ${\eta }_{\mathrm{s}\mathrm{t}}$, and the coefficient of external hydraulic resistance, $d_g$.

In the absence of external hydraulic resistance and water flux, cell movement is driven by actin polymerization, $j_{\mathrm{a}\mathrm{c}\mathrm{t}\mathrm{i}\mathrm{n}}$. This scenario represents most cell migration on 2D substrates. The model shows that the velocity of cell migration, $v_0$, increases when the rate of actin polymerization or the strength of focal adhesion, ${\eta }_{\mathrm{s}\mathrm{t}}$, increases (Fig. 1C) and saturates at $v_0=j_{\mathrm{a}\mathrm{c}\mathrm{t}\mathrm{i}\mathrm{n}}$. In this case, focal adhesions promote faster cell migration (15). The cell slows down when the coefficient of external hydraulic resistance, $d_g$, increases (Fig. 1D). However, when there is substantial water flux, $j_{\mathrm{w}\mathrm{a}\mathrm{t}\mathrm{e}\mathrm{r}}$, across the cell membrane, without actin polymerization, the cell velocity increases with $d_g$ until the velocity saturates at $v_0=j_{\mathrm{w}\mathrm{a}\mathrm{t}\mathrm{e}\mathrm{r}}$ (Fig. 1E). In this case, increasing $d_g$ promotes cell migration, which is counterintuitive and opposite to the actin-driven case. With $j_{\mathrm{w}\mathrm{a}\mathrm{t}\mathrm{e}\mathrm{r}}$ only but without $j_{\mathrm{a}\mathrm{c}\mathrm{t}\mathrm{i}\mathrm{n}}$, however, the cell slows down with increasing ${\eta }_{\mathrm{s}\mathrm{t}}$ (Fig. 1F), showing that focal adhesion slows water-driven cell migration.

The opposing result for water- and actin-driven cell migration under varying external hydraulic resistance while actin-driven cell migration slows down is also predicted in the 2D model (Fig. 1G), where we vary the channel width to represent different hydraulic resistance: narrower channels corresponding to higher hydraulic resistance due to the higher shear stress in the external fluid passing around the cell. The predicted trend is thus a general feature of cell migration, independent of dimensionality. Moreover, the model predicts that cells are not able to achieve significant cell velocities under high external hydraulic resistance by using actin polymerization alone (Fig. 1D). Our results thus suggest that in confined spaces or dense collagen matrices, the water-driven mechanism contributes more to the cell speed than the actin-driven mechanism.

This interplay between these 2 mechanisms of cell migration can be explicitly seen in the analytic solution for $v_0$ from the 1D model,

$$v_0=\frac{{\eta }_{\mathrm{s}\mathrm{t}}}{{\theta }_{*}{\eta }_{\mathrm{s}\mathrm{t}}+2\hat{\xi }+\widehat{d_g}}{j}_{\mathrm{a}\mathrm{c}\mathrm{t}\mathrm{i}\mathrm{n}}+\frac{\widehat{d_{\mathrm{g}}}}{{\theta }_{*}{\eta }_{\mathrm{s}\mathrm{t}}+2\hat{\xi }+\widehat{d_g}}{j}_{\mathrm{w}\mathrm{a}\mathrm{t}\mathrm{e}\mathrm{r}},$$ [1]

where ${\theta }_{*}$ is the average concentration of the actin network; $\hat{\xi }$ is the scaled coefficient of membrane friction; and $\widehat{d_g}$ is the scaled coefficient of external hydraulic resistance. The cell velocity $v_0$ is a linear function in $j_{\mathrm{a}\mathrm{c}\mathrm{t}\mathrm{i}\mathrm{n}}$ and $j_{\mathrm{w}\mathrm{a}\mathrm{t}\mathrm{e}\mathrm{r}}$, with each coefficient being a nonlinear function in both ${\eta }_{\mathrm{s}\mathrm{t}}$ and $d_g$. In general, when both actin polymerization and water flux coexist, cell velocity increases compared to that under a single driving mechanism. This has also been observed experimentally (9). Each mechanism dominates at different physical regimes. The $j_{\mathrm{a}\mathrm{c}\mathrm{t}\mathrm{i}\mathrm{n}}$ term dominates when ${\eta }_{\mathrm{s}\mathrm{t}}$ is large, and the $j_{\mathrm{w}\mathrm{a}\mathrm{t}\mathrm{e}\mathrm{r}}$ term dominates when $d_g$ is large. When cells independently modulate $j_{\mathrm{a}\mathrm{c}\mathrm{t}\mathrm{i}\mathrm{n}}$ and $j_{\mathrm{w}\mathrm{a}\mathrm{t}\mathrm{e}\mathrm{r}}$ in different physical environments, they can achieve different speeds (Fig. 1 C–F).

Here, we would like to comment that experiments have shown that cell velocity is a nonmonotonic function of focal adhesion size or number (7, 15). This can arise if the actin polymerization rate is related to focal adhesion formation, i.e., more focal adhesion inhibits actin polymerization at the leading edge due to the actin monomer availability; our model would predict that the cell velocity first increases with ${\eta }_{\mathrm{s}\mathrm{t}}$ and then decreases. Other explanations are also possible. Here, we have not assumed additional complex relationships between adhesions, contraction, and polymerization and only focus on the positive contribution of focal adhesion on cell migration.

Actin Polymerization and Active Solute Pumping Consume ATP Energy.

Both actin treadmilling (20) and active solute pumping (21) are driven by energy (ATP)-consuming reactions (Fig. 1A). Here, we quantify the minimum power consumption via ATP usage for the 1D geometry. For 2D or 3D geometries, the minimum power consumption is the surface integration of the 1D result.

The effective velocity of actin polymerization at the cell front is $j_{\mathrm{a}\mathrm{c}\mathrm{t}\mathrm{i}\mathrm{n}}/{\theta }_{\mathrm{n}}^{\mathrm{f}}$, where ${\theta }_{\mathrm{n}}$ is the concentration of the actin network. The number of ATPs needed to sustain such velocity per second per F-actin filament is $n_a{j}_{\mathrm{a}\mathrm{c}\mathrm{t}\mathrm{i}\mathrm{n}}/\left({\theta }_{\mathrm{n}}^{\mathrm{f}}\delta \right)$, where $\delta$ is the length of a G-actin monomer and $n_a$ is the number of ATPs needed to complete 1 G-actin-to-F-actin cycle. The number of F-actin filaments at the cell front can be estimated from the F-actin concentration. Let $A$ be the cross-sectional area of a 1D cell and $A_F$ be the cross-sectional area of 1 F-actin filament; we then have $N_F=A{\theta }_{\mathrm{n}}^{\mathrm{f}}/A_F$, which is the number of F-actin filaments at the polymerizing front of the cell. We can write the ATP power consumed associated with actin polymerization as

$${\mathcal{P}}_{\mathrm{a}\mathrm{c}\mathrm{t}\mathrm{i}\mathrm{n}}=N_F\left[j_{\mathrm{a}\mathrm{c}\mathrm{t}\mathrm{i}\mathrm{n}}/\left({\theta }_{\mathrm{n}}^{\mathrm{f}}\delta \right)\right]G_{\mathrm{A}\mathrm{T}\mathrm{P}}{n}_a,$$ [2]

where $G_{\mathrm{A}\mathrm{T}\mathrm{P}}$ is the hydrolysis energy from 1 ATP molecule.

In active solute pumping, solute fluxes at the front and back of the cell, $i_{\mathrm{s}\mathrm{o}\mathrm{l}}^{\mathrm{f},\mathrm{b}}$, are in units of moles per meter squared per second. The ATP power associated with active solute pumping is

$${\mathcal{P}}_{\mathrm{s}\mathrm{o}\mathrm{l}}=A{N}_A{n}_c{G}_{\mathrm{A}\mathrm{T}\mathrm{P}}\left(\left|i_{\mathrm{s}\mathrm{o}\mathrm{l}}^{\mathrm{b}}\right|+\left|i_{\mathrm{s}\mathrm{o}\mathrm{l}}^{\mathrm{f}}\right|\right),$$ [3]

in which $N_A$ is Avogadro’s number and $n_c$ is the average number of ATPs needed to pump 1 solute across the cell membrane. In this work, we let $i_{\mathrm{s}\mathrm{o}\mathrm{l}}^{\mathrm{b}}=0$ and vary $i_{\mathrm{s}\mathrm{o}\mathrm{l}}^{\mathrm{f}}$ to develop the polarization of the model. The corresponding ${\mathcal{P}}_{\mathrm{s}\mathrm{o}\mathrm{l}}$ is the minimum ATP power needed to generate solute pumping that directly results in cell migration.

Using physiologically relevant parameters, we find that the water-driven mechanism requires about 4 orders higher ATP power consumption than the actin-driven mechanism (SI Appendix). The higher rate of ATP consumption can be explained by Eq. 4 derived from the 1D model,

$$\begin{array}{ll}\hfill v_0& =\left(\frac{{\eta }_{\mathrm{s}\mathrm{t}}+\eta \lambda }{K_c}\right)\frac{A_F\delta }{A{n}_a}\frac{{\mathcal{P}}_{\mathrm{a}\mathrm{c}\mathrm{t}\mathrm{i}\mathrm{n}}}{G_{\mathrm{A}\mathrm{T}\mathrm{P}}}+\left(\frac{\zeta c_r\lambda }{K_c}\right)\frac{1}{2N_A{c}_{r}A{n}_c}\frac{{\mathcal{P}}_{\mathrm{s}\mathrm{o}\mathrm{l}}}{G_{\mathrm{A}\mathrm{T}\mathrm{P}}},\hfill \\ \hfill \lambda & =\hat{\alpha }\widehat{d_g}\left[2+\hat{\alpha }\left(\widehat{d_g}+\eta {\theta }_{*}+\zeta c_r\right)\right],\hfill \\ \hfill K_c& =\left({\theta }_{*}{\eta }_{\mathrm{s}\mathrm{t}}+2\hat{\xi }\right)+\frac{2\widehat{d_g}\left(1+\hat{\alpha }\zeta c_{\mathrm{r}}\right)}{2+\hat{\alpha }\left(\widehat{d_g}+\zeta c_{\mathrm{r}}\right)},\hspace{1em}\zeta =\frac{2RT}{k_{\mathrm{s}\mathrm{o}\mathrm{l}}L},\hfill \end{array}$$ [4]

where $c_r$ is a reference solute concentration, which is taken as the external bath solute concentration; $\hat{\alpha }$ is the scaled membrane water permeability; $RT$ is the ideal gas constant times temperature; and $k_{\mathrm{s}\mathrm{o}\mathrm{l}}$ is the coefficient of passive membrane solute channels. Eq. 4 shows that ${\eta }_{\mathrm{s}\mathrm{t}}$ is the effective force coefficient acting on the actin network, while $\zeta c_r\lambda$ is the effective force coefficient acting on the solute. The effectiveness of the 2 mechanisms depends largely on the relative magnitude of these 2 numbers. For low hydraulic resistance, the effective drag on the solute is lower than that on the actin network, making actin polymerization more effective for cell migration. For high hydraulic resistance, the effective drag on the solute, $\zeta c_{\mathrm{r}}\lambda$, increases, making water-driven cell migration more effective. The overall attainable velocity decreases, however, because of the increasing frictional factor represented by $K_c$. The effectiveness of the 2 mechanisms is also strongly dependent on the value of $k_{\mathrm{s}\mathrm{o}\mathrm{l}}$, a value that the cell can control by altering its ion-channel composition; a smaller value of $k_{\mathrm{s}\mathrm{o}\mathrm{l}}$ would lead to greater efficiency for water-driven cell migration.

ATP Power Input Converts to Mechanical Dissipation.

When actin- and water-driven mechanisms work together, we can define ${\mathcal{P}}_{\mathrm{A}\mathrm{T}\mathrm{P}}={\mathcal{P}}_{\mathrm{a}\mathrm{c}\mathrm{t}\mathrm{i}\mathrm{n}}+{\mathcal{P}}_{\mathrm{s}\mathrm{o}\mathrm{l}}$ as the total ATP power input for cell migration. The energy flow from ATP to mechanical power generation by the cell and then to mechanical power dissipation is sketched in Fig. 1A. A portion of the ATP power input is converted into mechanical power generated by the cell, ${\mathcal{I}}_{\mathrm{c}\mathrm{e}\mathrm{l}\mathrm{l}}$, which includes solute pumping, actin polymerization, and cytoskeletal force generation. When the cell migrates at steady state, the energy input is ultimately dissipated through different sources: ${\mathcal{I}}_{\mathrm{c}\mathrm{e}\mathrm{l}\mathrm{l}}={\mathcal{D}}_{\mathrm{f}\mathrm{r}\mathrm{i}\mathrm{c}}+{\mathcal{D}}_{\mathrm{fl}\mathrm{o}\mathrm{w}}+{\mathcal{D}}_{\mathrm{s}\mathrm{o}\mathrm{l}}$, where ${\mathcal{D}}_{\mathrm{f}\mathrm{r}\mathrm{i}\mathrm{c}}$ originates from the various frictional forces, including the focal adhesion (the ${\eta }_{\mathrm{s}\mathrm{t}}$ term), the membrane friction, and the interfacial friction; ${\mathcal{D}}_{\mathrm{fl}\mathrm{o}\mathrm{w}}$ describes dissipation during passive transmembrane water flow and dissipation in the exterior fluid (the $d_g$ term); ${\mathcal{D}}_{\mathrm{s}\mathrm{o}\mathrm{l}}$ is the solute diffusive dissipation inside the cell and in the membrane. All 3 of the dissipation terms are positive.

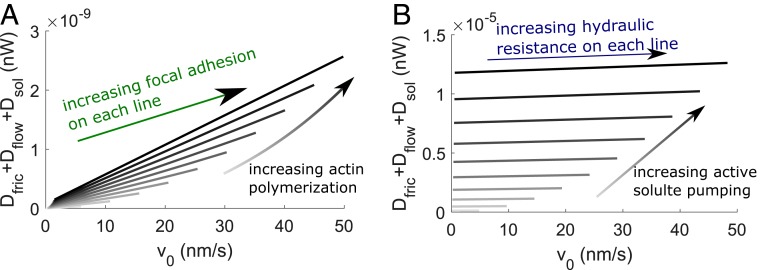
Under actin-driven cell migration (Fig. 1C), we find that the mechanical power is mainly dissipated through ${\mathcal{D}}_{\mathrm{f}\mathrm{r}\mathrm{i}\mathrm{c}}$ (SI Appendix). The total mechanical power and dissipation scales with the rate of actin polymerization and the velocity of cell migration which results from increased focal adhesion strength for a fixed rate of actin polymerization (Fig. 2A). Under water-driven cell migration (Fig. 1E), the mechanical power is mostly dissipated through the passive solute diffusion across the membrane and within the cell, ${\mathcal{D}}_{\mathrm{s}\mathrm{o}\mathrm{l}}$ (SI Appendix). The total mechanical power and dissipation increase with increasing active solute pumping, but do not vary significantly with the velocity of cell migration and thus the strength of hydraulic resistance (Fig. 2B). The power dissipation for water-driven cell migration is about 4 orders higher than that for actin-driven migration (Fig. 2 A and B). Here, we have not incorporated energetic cost of focal-adhesion formation or turnover. Since adhesion proteins are not active motors, we expect that the energetic cost of building adhesions should be similar to that of actin polymerization and should not change the order of magnitude of actin-driven mechanical-power dissipation.

Fig. 2.

Mechanical-energy dissipation during actin- and water-driven cell migration from the 1D model. (A) Total mechanical energy dissipated as a function of $v_0$ for different ${\eta }_{\mathrm{s}\mathrm{t}}$ and rates of actin polymerization. The velocity field is extracted from Fig. 1C. Darker lines represent higher rates of actin polymerization. (B) Total mechanical energy dissipated as a function of $v_0$ for different $d_g$ and rates of active solute pumping. The velocity field is extracted from Fig. 1E. Darker lines represent higher rates of active solute pumping.

We can now estimate the power conversion ratio from ATP hydrolysis to the developed mechanical power (Fig. 2), i.e., ${\mathcal{I}}_{\mathrm{c}\mathrm{e}\mathrm{l}\mathrm{l}}/{\mathcal{P}}_{\mathrm{A}\mathrm{T}\mathrm{P}}$. For both mechanisms of cell migration, the ratio is about $10^{-4}$, suggesting that only a very small portion of the power from actin polymerization and solute pumping is converted into mechanical power and dissipation. Hence, only $<$1% of the total energy of a cell is used for actin polymerization (2), and, within that portion, about 0.1‰ is dissipated through the mechanical process. This small conversion ratio between the ATP power ($\mathcal{P}$) input and mechanical dissipation ($\mathcal{I}$) is a common feature of chemically driven mechanical work under small to zero load. Most of the hydrolysis energy is used for maintaining filament network, conformational change of molecules (22), and heat dissipation.

Cell Migration and Mechanical-Power Generation.

Similar to methods used in evaluating performance of engines, we can add an opposing load force, $f_{\mathrm{e}\mathrm{x}\mathrm{t}}^{\mathrm{f}}$ (defined positive in the direction of cell migration), to the cell leading edge (Fig. 3A) (23) and compute the power associated with the force, ${\mathcal{I}}_{\mathrm{e}\mathrm{x}\mathrm{t}}=f_{\mathrm{e}\mathrm{x}\mathrm{t}}^{\mathrm{f}}{v}_0$. The minus of this power can be defined as the mechanical output of cell migration. In this case, the energy identity can be modified as ${\mathcal{I}}_{\mathrm{c}\mathrm{e}\mathrm{l}\mathrm{l}}={\mathcal{D}}_{\mathrm{f}\mathrm{r}\mathrm{i}\mathrm{c}}+{\mathcal{D}}_{\mathrm{fl}\mathrm{o}\mathrm{w}}+{\mathcal{D}}_{\mathrm{s}\mathrm{o}\mathrm{l}}+\left(-{\mathcal{I}}_{\mathrm{e}\mathrm{x}\mathrm{t}}\right)$.

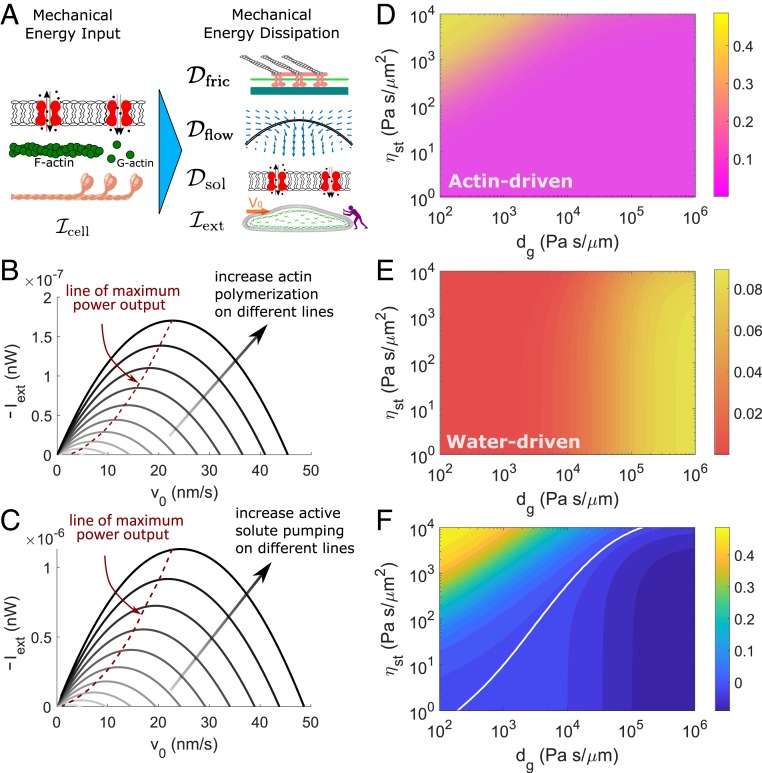
Fig. 3.

Mechanical-power output and efficiency predicted from the 1D model. (A) When the external force works against cell migration, we can take the minus of ${\mathcal{I}}_{\mathrm{e}\mathrm{x}\mathrm{t}}=f_{\mathrm{e}\mathrm{x}\mathrm{t}}^{\mathrm{f}}{v}_0$ as a power output. (B and C) Power–velocity relation. Within each line, $f_{\mathrm{e}\mathrm{x}\mathrm{t}}^{\mathrm{f}}$ increases from right to left. In B, darker lines represent higher rates of actin polymerization. ${\eta }_{\mathrm{s}\mathrm{t}}=10^4$ Pa$\cdot$s/$\mathrm{\mu }{\mathrm{m}}^2$. In C, darker lines represent higher rates of active solute pumping. $d_g=10^6$ Pa$\cdot$s/$\mathrm{\mu }$m. (D–F) Contours of the mechanical-output efficiency of migration defined by $\gamma ={\left(-{\mathcal{I}}_{\mathrm{e}\mathrm{x}\mathrm{t}}\right)}_{max}/{\mathcal{I}}_{\mathrm{c}\mathrm{e}\mathrm{l}\mathrm{l}}$. (D) Output efficiency of actin-driven cell migration ${\gamma }_{\mathrm{a}\mathrm{c}\mathrm{t}\mathrm{i}\mathrm{n}}$. (E) Output efficiency of water-driven cell migration ${\gamma }_{\mathrm{w}\mathrm{a}\mathrm{t}\mathrm{e}\mathrm{r}}$. (F) The difference of efficiency of the 2 mechanisms of migrations, ${\gamma }_{\mathrm{a}\mathrm{c}\mathrm{t}\mathrm{i}\mathrm{n}}-{\gamma }_{\mathrm{w}\mathrm{a}\mathrm{t}\mathrm{e}\mathrm{r}}$. The white line is the cross-over line showing ${\gamma }_{\mathrm{a}\mathrm{c}\mathrm{t}\mathrm{i}\mathrm{n}}-{\gamma }_{\mathrm{w}\mathrm{a}\mathrm{t}\mathrm{e}\mathrm{r}}=0$.

The cell slows down as $f_{\mathrm{e}\mathrm{x}\mathrm{t}}^{\mathrm{f}}$ increases and eventually stalls. The power–velocity relationship shows a maximum (Fig. 3 B and C) when the external force increases, similar to the power–velocity curves from mechanical engines. In the actin-driven case (Fig. 3B), when $j_{\mathrm{a}\mathrm{c}\mathrm{t}\mathrm{i}\mathrm{n}}/{\theta }_{*}=50$ nm/s, for example, the maximum power output is $-{\mathcal{I}}_{\mathrm{e}\mathrm{x}\mathrm{t}}=1.7\times 10^{-7}$ nW at $v_0=$25 nm/s, which corresponds to a force of $\sim$7 nN for a cell with cross-sectional area of 30 $\mathrm{\mu }{\mathrm{m}}^2$. This force can be understood as the maximum output force for a given rate of actin polymerization. The output force increases with increasing rates of actin polymerization (Fig. 3B). In the water-driven case, the similar trend is seen as the actin-driven cell migration, but the overall output is about 1 order higher for the same range of cell velocity. The output power increases with increasing rate of polarized active solute pumping (Fig. 3C). The maximum output force is $\sim$48 nN when $i_{\mathrm{s}\mathrm{o}\mathrm{l}}^{\mathrm{f}}=6.25\times 10^{-5}$ mol/m²$\cdot$s.

The Physical Environment Determines Output Efficiency.

Given that the mechanical-power output has a maximum, we are thus able to define the output mechanical efficiency of cell migration: $\gamma ={\left(-{\mathcal{I}}_{\mathrm{e}\mathrm{x}\mathrm{t}}\right)}_{max}/{\mathcal{I}}_{\mathrm{c}\mathrm{e}\mathrm{l}\mathrm{l}}$. Because of the linear scaling (Fig. 2), the efficiency $\gamma$ is independent of the rate of actin polymerization (active solute flux) for actin-driven (water-driven) cell migration. The output efficiency of actin-driven cell migration reaches 50% when ${\eta }_{\mathrm{s}\mathrm{t}}=10^4$ Pa$\cdot$s/$\mathrm{\mu }{\mathrm{m}}^2$ and $d_g$ is low (Fig. 3D). The efficiency decreases with decreasing focal-adhesion strength or increasing external hydraulic resistance. The output efficiency of water-driven cell migration reaches 10% when $d_g=10^6$ Pa$\cdot$s/$\mathrm{\mu }$m and decreases under lower external hydraulic resistance (Fig. 3E).

The difference in mechanical-output efficiency of 2 mechanisms of cell migration, ${\gamma }_{\mathrm{a}\mathrm{c}\mathrm{t}\mathrm{i}\mathrm{n}}-{\gamma }_{\mathrm{w}\mathrm{a}\mathrm{t}\mathrm{e}\mathrm{r}}$, shows that the efficiencies becomes equal along the white line in Fig. 3F. Although the water-driven cell migration consumes 4 orders more ATP and mechanical power than the actin-driven cell migration (Fig. 2), the mechanical-output efficiency is higher for water-driven cell migration under higher external hydraulic resistance and lower focal-adhesion strength.

Cell Mobility Depends on the Cell Shape.

When the 2-phase model is implemented for a 2D cell, we find a dependence of the cell speed on cell shape. As an example, here, cell shape is described by a parameter $a$, where $a⩾0$ describes the deviation from a circular shape (Fig. 4A). These shapes are designed to be close to the typical morphology of migrating epithelial cells (24). To minimize the effect of other physical factors, cells with different shapes have identical area and width. In the actin-driven (water-driven) case, actin polymerization (active solute influx) is perpendicular to the cell leading edge, and depolymerization (efflux) is perpendicular to the cell trailing edge. For different shape factors, the total strength of polymerization or depolymerization (influx or efflux) integrated over the cell boundary remains constant.

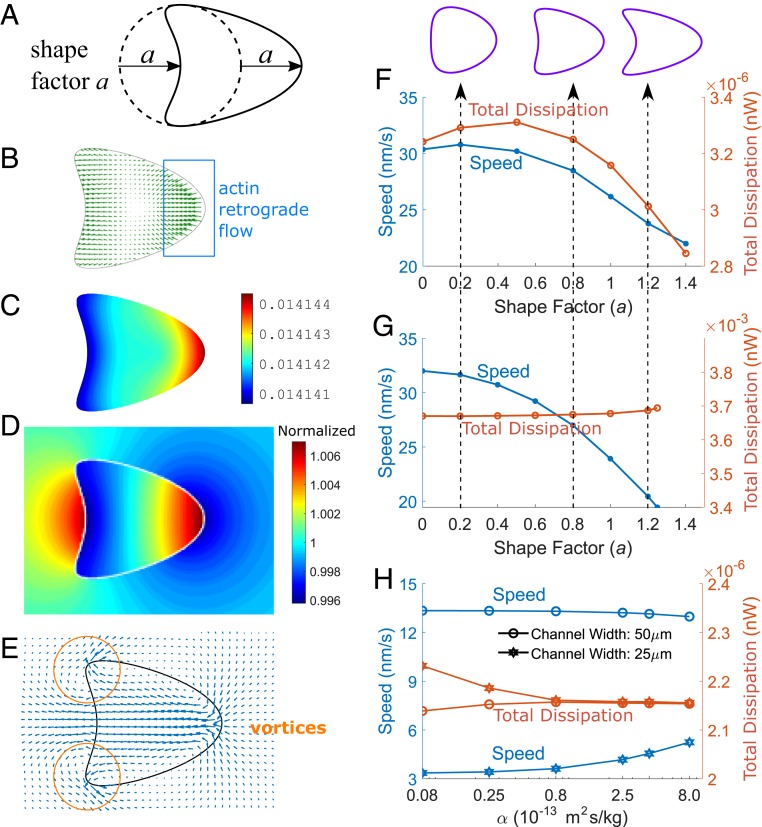
Fig. 4.

Cell-migration speed depends on the cell shape and membrane permeability. (A) Cell shapes in the 2D model parameterized by the shape factor $a$, defined as the deviation away from a circular shape. (B–E) Sample field variables from the 2D simulation where $a=0.9$. (B and C) Actin-network velocity (C) and concentration (B) in the actin-driven mechanism. (D and E) Intracellular and extracellular solution concentration (D) and fluid velocity (E) in the water-driven mechanism. (F and G) Cell speed and mechanical-energy dissipation (${\mathcal{I}}_{\mathrm{c}\mathrm{e}\mathrm{l}\mathrm{l}}$) for different cell shapes in actin-driven (F) and water-driven (G) cell migration. Shapes are defined as the initial configuration of the cell. (H) Under actin-driven without polarized active solute pumping, cell speed increases with increasing membrane permeability under high hydraulic resistance.

In actin-driven cell migration, actin retrograde flow is prominent at the leading edge of the cell (Fig. 4B), where actin polymerization is maximal and the F-actin concentration is higher (Fig. 4C). In water-driven cell migration, the solute concentration (Fig. 4D) varies both inside and outside of the cell as a result of polarized active solute pumping. The intracellular cytosol velocity and the extracellular water velocity form a continuous velocity field that transports fluid across the cell (Fig. 4E). Flow vortices in the water phase are observed, especially at the trailing edge of the cell, which is not seen in the actin-driven case.

In general, the computed cell speed reduces with increasing shape factor for both actin-driven (Fig. 4F) and water-driven (Fig. 4G) cell migration. For the actin-driven cell mechanism, 1 possibility is that when the cell shape is far from a circle, there is more actin retrograde flow in the direction perpendicular to the direction of cell velocity, and thus does not contribute to cell speed due to the reduced adhesion drag forces aligned with the direction of cell migration. The mechanical-power consumption roughly follows the cell-speed trend as the shape factor increases for actin-driven cell migration (Fig. 4F), but the total power dissipation for the water-driven cell migration remains roughly constant (Fig. 4G).

Membrane Water Permeability Increases Actin-Driven Cell-Migration Speed Under High Hydraulic Resistance.

We have shown that actin polymerization and water flux can complement each other to increase cell velocity (Eq. 1). Although water flux typically requires polarized active solute pumping, in its absence, however, cell velocity can still be enhanced in high-hydraulic-resistance environments if the membrane is permeable. This can be seen in Eq. 4 derived from the 1D model. We will consider ${\mathcal{P}}_{\mathrm{s}\mathrm{o}\mathrm{l}}=0$ to eliminate the contribution from water flux from active solute pumping. The expression in the bracket of the ${\mathcal{P}}_{\mathrm{a}\mathrm{c}\mathrm{t}\mathrm{i}\mathrm{n}}$ term suggests that as long as both $\alpha \ne 0$ and $d_g\ne 0$, actin-driven cell velocity will increase compared to the contribution from focal adhesion (${\eta }_{\mathrm{s}\mathrm{t}}$) alone. Higher $\alpha$ or $d_g$ leads to a larger velocity increase.

This trend is also seen in the 2D model. When the hydraulic resistance is low, corresponding to a 50-$\mathrm{\mu }$m channel width, increasing membrane-water permeability by 2 orders of magnitude does not change the cell speed. However, when the hydraulic resistance is high, corresponding to a 25-$\mathrm{\mu }$m channel width, increasing membrane permeability increases the cell speed by $\sim$50% (Fig. 4H). Meanwhile, cell mechanical-power consumption decreases by $\sim$3%, suggesting that higher membrane permeability and external hydraulic resistance increase the efficiency of actin-driven cell migration in these conditions. This result provides a second possible explanation as to why aquaporins can enhance in vivo cell invasion (9).

Conclusions and Discussions

During cell migration, the key physical variables are the effective strength of focal adhesion, ${\eta }_{\mathrm{s}\mathrm{t}}$, and the coefficient of external hydraulic resistance, $d_g$ (Fig. 1 C–F). For the same cell polarization, these 2 parameters generally determines the cell speed. We let ${\eta }_{\mathrm{s}\mathrm{t}}$ increase up to $10^4$ Pa$\cdot$s/$\mathrm{\mu }{\mathrm{m}}^2$. This is an estimate from the measured stress–velocity relation from traction force microscopy (25). Lower levels of cell adhesion or softer substrates will have lower ${\eta }_{\mathrm{s}\mathrm{t}}$ (13, 14). The coefficient of hydraulic resistance can be estimated from the environmental geometry, the external fluid viscosity, and the matrix permeability (17). Reported physiologically relevant matrix permeability ranges from $10^{-18}$ to $10^{-10}$ ${\mathrm{m}}^2$ (26–29); fluid dynamic viscosity ranges from 0.001 to 1 Pa$\cdot$s (30). If we assume the cell radius is 10 $\mathrm{\mu }$m, the estimated $d_g$ can range from effectively 0 to $10^6$ Pa$\cdot$s/$\mathrm{\mu }$m or higher (17). Hence, the ${\eta }_{\mathrm{s}\mathrm{t}}$ and $d_g$ we have explored (Fig. 1 C–F) cover physiologically relevant limits.

Environments that restrict extracellular fluid flow will increase hydraulic resistance. Collagen matrices, which reduce fluid permeability, also exhibit high hydraulic resistance (12). Cells like glioblastoma and neutrophils typically migrate in collagen matrices of varying permeability, and glioblastoma is known to move in an actin-independent manner (31). Our results for high-hydraulic-resistance environments is therefore applicable to cell migrating in either confined spaces or dense collagen matrices.

More details can be incorporated into future models. For example, the rate of actin polymerization may depend on the mechanical stress acting on the actin network (32), and the cell velocity shows a biphasic response on the strength of focal adhesion (25). In addition, the strength, formation, and breakdown of adhesions may depend on actomyosin contraction, which also requires ATP hydrolysis. This could increase the energy consumption of the actin-driven mechanism. In the model, we have used the concentration, ${\theta }_{\mathrm{n}}$, for the actin-network phase, instead of volume fraction. If the actual volume of the actin network were to be considered, then the G-actin monomer phase should also be included in the model to derive the energy identity. Other constraints such as the chemotactic efficiency or metabolic cost associated with cell growth and proliferation may be just as important. Inclusion of these elements into the model will enrich the range of model predictions. However, the general conclusion that the energy requirements of water-driven cell migration is several orders higher than that of actin-driven cell migration is generic and robust.

Energy difference between actin- and water-driven cell migration is dictated by the physical environment of the cell. Higher energy consumption and greater contribution from the water-driven mechanism to the cell speed is predicted for cells in confinement with high hydraulic resistance. Even if cells are able to navigate through high-hydraulic-resistance environments using a high rate of actin polymerization and strong adhesions, our model predicts that their energy efficiency is lower than the water-driven mechanism. Hence, the best strategy for cell migration depends on the environment. Our model also predicts that the output mechanical force generated by cells using the water-driven mechanism is significant, and moving cells in confined spaces may exert large forces on the surrounding tissues. In biologically relevant scenarios, cells generally move through collagen matrices with low permeability and high hydraulic resistance. For example, during cancer metastasis, cells typically squeeze through walls of blood vessels and move through somatic tissues and basement membrane, which are rich in collagen fibers. A second example is during immune response, where neutrophils migrate from the bloodstream to the infected connective tissue, which also requires neutrophils to navigate through collagen matrices. Even gastrulation during early embryonic development occurs in an environment where fluid movement is restricted. Therefore, the 2-phase mechanical framework presented here has general implications for cell motility (3, 8, 9) and provides a physical basis for understanding forces and energetics during tissue morphogenesis and cell movement.

Materials and Data Availability.

The computational code used in this work is available at GitHub: https://github.com/sxslabjhu/Cell-Migration-Energy-Code.