Recursive Feature Elimination by Sensitivity Testing

Abstract

There is great interest in methods to improve human insight into trained non-linear models. Leading approaches include producing a ranking of the most relevant features, a non-trivial task for non-linear models. We show theoretically and empirically the benefit of a novel version of recursive feature elimination (RFE) as often used with SVMs; the key idea is a simple twist on the kinds of sensitivity testing employed in computational learning theory with membership queries (e.g., [1]). With membership queries, one can check whether changing the value of a feature in an example changes the label. In the real-world, we usually cannot get answers to such queries, so our approach instead makes these queries to a trained (imperfect) non-linear model. Because SVMs are widely used in bioinformatics, our empirical results use a real-world cancer genomics problem; because ground truth is not known for this task, we discuss the potential insights provided. We also evaluate on synthetic data where ground truth is known.

I. INTRODUCTION

There is great interest in methods to improve human insight into trained non-linear models such as support vector machines (SVMs), deep neural networks, and large random forests; one existing approach is to produce a ranking of the most relevant features, a non-trivial task for non-linear models. Famous examples of this approach include Breiman’s method for ranking features in a random forest by percent increase in misclassification rate when a feature is randomly permuted [2] and Guyon’s modified version of her recursive feature elimination (RFE) approach tailored to non-linear models [3], which both ranks and performs feature selection by measuring loss in weighted sum of distances from the margin. In contrast to Guyon’s method, computational learning theory has a long history of sensitivity testing by “flipping” or changing the value of a feature, rather than deleting it, and posing a membership query to find the effect on the label of the example (e.g., [1]). In practice we do not have an oracle for such membership queries.

This paper presents an alternative algorithm to RFE, RFE by Sensitivity Testing (RFEST), that employs a trained non-linear model as an approximate oracle for such membership queries. Hence our algorithm asks how much accuracy or area under the receiver operating characteristic curve (AUC) is lost from a trained model when a variable is flipped, rather than how much is lost compared to an existing model when a variable is deleted. Where RFE deletes a variable and Breiman’s algorithm permutes a variable, this simple change to flipping the variable makes possible a positive learnability claim. We first prove a probably approximately correct (PAC)-like result showing that under certain assumptions this algorithm provides an accurate ranking; this result does not rely on any particular type of non-linear model or learning algorithm, but only on the condition that the algorithm achieves some minimum gain in accuracy over random guessing, as in weak learning. Second, we show empirically that RFEST outperforms RFE in ranking (as a surrogate for insight) the genetic features associated with breast cancer in a genome-wide association study (GWAS) data set and on multiple synthetic data sets labeled by known ground truth, a family of arguably the most challenging nonlinear target functions.

As a motivating example, genome-disease association studies (genome-wide or limited) seek genetic features associated with disease, i.e., predictive of disease. In many cases it is believed that such features may interact with one another in highly nonlinear ways to influence disease; nevertheless, for practical reasons almost all association studies use linear models and hence can find only features that individually are correlated with disease [4]. Consequently, key genetic features may be missed entirely. Because linear and non-linear SVMs have been widely used in bioinformatics applications, we will use SVMs as our learner for these empirical studies. The theoretical results show the algorithm can use any learner capable of building moderately accurate non-linear models.

II. BACKGROUND

A. Feature Ranking and Feature Selection

While feature ranking and feature selection are different problems, they are closely related and each is sometimes accomplished by the other. Recursive feature selection can rank by maintaining the order in which features are removed; feature ranking, e.g. by information gain, is often followed by removal of lower ranked features. Many feature selection algorithms utilize linear modeling approaches such as lasso-penalized logistic regression, linear SVMs, Naïve Bayes or other weighted-voting schemes among features. An alternative is to implement these same approaches after filtering features individually by information gain or by many single-variable logistic regression runs [5]. To account for interactions between features, the standard approach is to introduce interaction terms, but such terms typically are limited to pairs of features, and even then they greatly increase both run-time and risk of over-fitting.

Nonlinear SVMs have the potential to more effectively find complex interactions among features, but insight into the important interactions is hard to extract from the learned model. This paper addresses that shortcoming by presenting an alternative RFE algorithm and demonstrating that the algorithm makes it possible to identify the features that are relevant–that play a role in the learned nonlinear model, even if individually they are completely uncorrelated with the class–while removing those features that are irrelevant or redundant.

Because we do not assume we are in an active learning setting–we do not have access to an oracle for membership queries that can label feature vectors with the value of any feature altered– our key insight is to use the trained nonlinear SVM itself as such an oracle instead. While this trained model is not the target concept, we assume it is more accurate than random guessing and hence provides some information about feature relevance. In homage to earlier work on membership queries to test the sensitivity of target concepts to individual features, we call our RFE algorithm “RFE by Sensitivity Testing,” or RFEST. The remainder of the paper presents the RFEST algorithm and empirical evaluations of it, including novel and promising insights that it provides into genetic susceptibility to breast cancer.

B. SVMs, Correlation Immunity, and RFE

SVMs are known for both their strong performance and flexibility based on the chosen kernel [6]. The strength of SVMs comes from their ability to effectively learn nonlinear separators through use of the kernel trick, a mapping to a higher-dimensional feature space resulting in an ability to encode nonlinear separators in the original feature space [7].

Accordingly, it is expected that SVMs can efficiently learn correlation immune (CI) functions, which are notable nonlinear Boolean functions. A function is CI if every single-feature marginal distribution is uninformative, i.e., no feature by itself is correlated with the function value, or class, even given the entire truth table or example space. We say a function f is correlation immune of order c (or c-correlation immune) if f is statistically independent from any subset of variables with a size of at most c. A function is correlation immune if and only if every variable has zero gain (with respect to any gain measure) when computed from the input data (cf. [8]).

As a result, these functions include some of the most challenging target concepts for most classification algorithms, most noteworthy the parity functions. The most famous nonlinear separators in machine learning are exclusive-or (XOR) and exclusive-nor (XNOR), which are two-feature parity functions. These particular functions arise in practice, for example in biology (Table 1) [9]. In Table I, the interpretation of this output is that flies that will survive are either male with an active Sxl gene, or female with an inavtive Sxl gene. While a nonlinear SVM can learn this function easily given only the relevant variables (i.e. Gender Female and Sxl Active), the SVM’s accuracy will degrade dramatically as irrelevant variables are added, unless the training set is quite large (see Section IV).

TABLE I.

A TRUTH TABLE FOR DROSOPHILA (FRUITFLY) SURVIVAL BASED ON GENDER AND SXL GENE ACTIVITY.

GENDER FEMALE	SXL ACTIVE	SURVIVAL
0	0	0
0	1	1
1	0	1
1	1	0

One would expect, for example, that SVMs, with a radial basis function (RBF) kernel or polynomial kernel of degree at least two, would learn these functions with ease. Unfortunately, for the simplest case of XOR in the presence of even a modest number of irrelevant features, or variables, SVMs tend to have a difficult time learning and require a large sample size empirically. This problem is not specific to SVMs; it is also known that no algorithm based on statistical queries can PAC learn parity functions of log(n) variables [10]. We seek a method of feature selection that can remove the irrelevant variables and restore classification performance.

A widely used approach to perform such a task is RFE, an embedded-based backward selection strategy [11]. RFE constructs an SVM, ranks the features according to the constructed SVM, removes the lowest ranked feature or features (e.g., bottom ten percent), and repeats until a certain (user-specified) number of features remain. The RFE algorithm with a linear SVM simply ranks features with respect to their given coefficients (i.e. from the learned model); this approach assumes features have been normalized to have comparable ranges.

Unfortunately, for a nonlinear SVM, feature coefficients cannot be obtained; Guyon et al. [3] presented a version of RFE for use with nonlinear SVMs. We propose an alternative RFE algorithm, RFEST, and compare these algorithms on synthetic data and a real-world cancer genomics problem.

C. Breast Cancer and Single-Nucleotide Polymorphisms

The development of breast cancer is influenced by many genetic and environmental factors. We study how feature selection performs on the variations at single base pairs of the human genome, which are known as single-nucleotide polymorphisms (SNPs). In cancer, both germline SNPs (the DNA sequence with which a person is born, and which is replicated in most of the cells in her body) and somatic mutations (variants that occur in select cells during replication and can lead to cancer) are important and are widely studied. To date, germline SNPs have received more attention as they can predict a person’s future risk of breast cancer [12]. Genome Wide Association Studies (GWAS) seek to find SNPs that are associated—correlated—with risk for developing disease.

Currently, GWAS consider SNPs independently and do not take into account possible interactions between SNPs. The rationale behind this is that it is infeasible, for example, to consider all pairs of the n = 1 million SNPs that are typically measured. The main purpose of a thorough investigation of SNPs is to gain a better understanding of how these genetic variants act as biological markers. Given a set of SNPs, if we can help identify a subset of important SNPs that correlate with a particular effect in patients, then we will be able to investigate their interactions. In turn, this will help our decision processes about numerous aspects of medical care such as the following: risk of developing a certain disease, effectiveness of various drugs, and adverse reactions to specific drugs.

III. ALGORITHMS

A. RFE Algorithm

In our experiments, we compare our RFEST algorithm to the RFE method proposed by Guyon et al. [3]. Although variants of RFE have been proposed [13]–[15], the original method of Guyon et al. is still widely used in the bioinformatics community [16]–[21]. Due to the nature of the data sets used in their paper, Guyon et al. utilized a linear SVM with RFE. However, they described how their method can be carried over to handle a nonlinear SVM implementation and this is the algorithm that we use as the baseline, which we describe next.

For SVMs, the cost function that is being minimized is the following:

$$J=\frac{1}{2}{\alpha }^{\text{T}}H\alpha -{\alpha }^{\text{T}}1$$ (1)

with the following constraints:

$$0\le {\alpha }_k\le C,\sum _k{\alpha }_k{y}_k=0$$

Here, α is the vector of weights on the training instances learned by the SVM algorithm, y_k is the class value for the k^th training instance x_k, and C is a regularization parameter.

Matrix H is the kernel matrix for kernel function K and the set of training instances. Specifically, for each pair of training instances $x_c\text{and}{x}_d,H=y_c{y}_{d}K\left(x_c,x_d\right)$ [3].

To determine feature relevance, the change in cost function proposed by Guyon is the following ranking coefficient:

$$DJ(j)=\frac{1}{2}{\alpha }^{\text{T}}H\alpha -\frac{1}{2}{\alpha }^{\text{T}}H(-j)\alpha$$ (2)

where H(−j) represents a modified version of H that recomputes the matrix without the j^th feature. In turn, the feature with the smallest value for DJ(j) is removed.

Algorithm 1 RFE Algorithm

Input: data di, j, where $i\in \{1,\dots ,m\},j\in \{1,\dots ,n\}$

repeat

Train SVM, output α

Implement DJ(j) according to (2), ∀ features j

Remove the feature(s) with the smallest DJ(j)

until k features remain (k < n)

Algorithm 1 describes the RFE algorithm for the nonlinear case in more detail [22]. The benefit of using RFE over a vanilla approach (e.g. train a new SVM for each candidate feature on every iteration) allows for each iteration of the algorithm to train only one SVM model. In other words, we assume that the vector α is fixed and consider the change in the kernel as a result of removing feature j. Note that for each iteration, H(−j) must be computed for each candidate feature j. The qualitative justification behind this cost function is that a feature’s value to the learned model is measured by the change in the expected value of error when removing that candidate feature [22]. RFE iterates until k features remain, however to have a fair comparison to RFEST, the stopping criterion for RFE was set to be until the accuracy measurement AUC is less than the max AUC achieved thus far. We describe RFEST in the next section.

B. RFEST Algorithm

Our presentation of RFEST and our subsequent proof assume binary features with {−1,1} encoding. It can be extended to categorical features with a one-hot encoding, but this and possible extension to continuous features are left for future work.

Standard RFE requires recomputing the H matrix (as described in the previous section) for each feature removed and can become computationally intractable with many features. In the case where there are thousands of features, Guyon et al. [3] chose to remove half of the features at each iteration. Doing so allows for faster convergence to an idealized subset of features, but key information may be lost.

There are two main differences between RFE and RFEST. The first is that RFEST flips the binary features, rather than deleting them. Note that flipping a feature means that if its current value is −1, then it is changed to have the value 1, and vice versa.

The second difference is in the construction of the cost function. An SVM classifier can classify a dataset with the accuracy measurement AUC. In addition, for each feature j, we create a modified version of the training set by flipping feature j in each example, and then calculate the AUC of the same SVM classifier on this modified training set. We call the calculated value AUC_flipped. The ranking coefficient used by RFEST is the following:

$$R(j)=AUC-AU{C}_{flipped}$$ (3)

The interpretation of R(j) is as follows. For each j, if AUC_flipped < AUC, then the j^th feature is relevant because the model classified the instances at a lower AUC with j flipped. In contrast, if AUC_flipped ≥ AUC, then the j^th feature is irrelevant because the model classified the instances with the same or higher AUC with j flipped. Therefore, the feature corresponding to the smallest R(j) will be removed. This process does not retrain a classifier for every candidate feature to be removed and we no longer compute H(−j).

For our experiments, a nonlinear SVM with an RBF kernel was used. The reason for doing so is because the RBF kernel implicitly computes interaction terms for all subsets of input features. It has been shown that searching in exponentially growing sequences for the hyper-parameters, namely cost C and gamma γ, is a good method for identifying their respective parameter values [23]. Therefore, the best configuration for C and γ was chosen using grid search.

To determine the final subset of features, RFEST stops when the AUC at any given iteration is less than p% of the max AUC achieved thus far. This parameter controls the tradeoff between model interpretability and model efficacy. That is, a lower choice for p encourages a small number of features, whereas a larger choice encourages a better performing model. For our experiments, we set p = 95% (see Section IV). Alternatively, other heuristics can be implemented with RFEST. One approach would be to stop when AUC decreases (i.e. a hill-climbing search). Another would be to apply a simulated annealing method, where if the AUC decreases, we continue searching with a small probability. As the search continues, the probability decreases. Search methods such as simulated annealing or the approach RFEST currently uses are aimed towards avoiding a local optimum. We use our current search method since it avoids having to set additional parameters.

RFEST may suffer if the SVM model we use is overfitted to a given instance, since the model might then be sensitive to the value of every feature. For this reason, we used a ten-fold cross validation and allocated the dataset into separate training, tuning, and testing sets to produce an unbiased estimate of the efficacy of our approach. The algorithm below summarizes RFEST.

Algorithm 2 RFEST Algorithm

Input: allocated data di, j, $i\in \{1,\dots ,m\},j\in \{1,\dots ,n\}$, into separate train, tune, and test

repeat

Train SVM on train, test on tune and output AUC

Implement R(j) according to (3), ∀ features j

Remove the feature(s) with the smallest R(j)

until AUC is less than p% of the max AUC achieved

return SVM model built from train and tune and AUC from test

We next demonstrate the theoretical efficacy of using the quantity R(j) to rank features, by considering a classification problem on n binary features, where examples are labeled according to the parity of a subset of the features. We show if a nonlinear machine learning algorithm can learn a sufficiently accurate model M, then with high probability, using a polynomial-size sample to compute the R(j) values with model M will result in those values being higher for relevant features than for irrelevant features. Thus if any irrelevant features are present, the feature with the lowest R(j) value, removed by RFEST, will be irrelevant.

RFEST is a generic method. Because of the interpretation behind the ranking coefficient R(j), this allows us to use any accuracy measurement. Therefore, for simplicity and clarity of our analysis, we prove our theorem for a related measure, $\tilde{R}(j),$ which is the same as R(j) except that it is defined in terms of accuracy rather than AUC. Although we state the theorem here only for the parity function and uniformly distributed examples, we prove a more general theorem in the Supplementary Material. That theorem applies to a somewhat broader class of functions and product distributions.

Theorem III.1.

Let f be a Boolean target concept, defined on n Boolean features, which labels examples according to the parity of a fixed subset of the n features. Suppose a machine learning algorithm is used to learn a classifier M for f. Suppose further that M has true error rate $ϵ<1/2,$ with respect to the uniform distribution. Then there is a quantity t that is polynomial in $n,\ln \frac{1}{\delta },\text{and}\frac{1}{(1/2)-ϵ},$ with the following property: for all 0 < δ < 1, if the $\tilde{R}(j)$ values for all n features are computed using M and a new independent sample of size t, also drawn from the uniform distribution, then with probability at least 1 – δ, the computed $\tilde{R}(j)$ values for all the relevant features will be higher than the computed $\tilde{R}(j)$ values for the irrelevant features.

We note that Theorem III.1 does not contradict the known result that parity functions are not PAC-learnable from statistical queries because it is preconditioned on having an SVM model with accuracy better than random guessing.

IV. EXPERIMENTAL RESULTS

A. Data

We implemented RFEST and Guyon’s RFE algorithm tailored to a nonlinear SVM, and we evaluated it on two types of data. The first consists of synthetic data that takes the form of a parity function on two variables, which is a CI function of order two. Correlation immune functions of order four, five, and six were also evaluated. There are many different CI functions, so for orders four, five, and six, ten functions for each order were randomly chosen. For functions of order c, the associated target concept was defined on n features. Of those n features, c were randomly chosen and corresponded to the c variables of the CI function, and the remaining features were irrelevant. Therefore, the task of both feature selection algorithms was to find the c variables that determined the class label. Feature values for all instances were chosen from a uniform distribution and the range of the number of instances was 100 to 2000.

The second dataset presented in this paper indicates that Emca4, a genetic determinant of susceptibility to 17β-estradiol (E2)-induced mammary cancer in the rat, has been mapped to rat chromosome 7 (RNO7) [24]–[26]. Data presented herein indicate that Emca4 harbors multiple genetic determinants of mammary cancer susceptibility and tumor aggressiveness that are orthologous to breast cancer risk loci mapped to chromosome 8q24–24 in genome wide association studies (GWAS) [12], [27]–[31].

The proceeding algorithm(s) used 76 of the SNPs in the designated region that are in the Hunter GWAS data set of 1145 breast cancer cases and 1142 controls [32]. All patients that had incomplete SNP data (630 patients) were omitted from our analysis. The data was made available via dbGaP’s Cancer

Genetic Markers of Susceptibility (CGEMS) Breast Cancer GWAS.

B. Synthetic Data Results

A learning curve was created to show the average AUC for n total features, where n ∈ {20, 50, 100} (i.e. the average AUC of the ten different functions for each order, respectively). For each n, we trained datasets that contained m examples, where m ∈ {100, 200, 300,…, 2000}. In addition, a learning curve was plotted to represent the average number of features that were kept using the same number of features and examples as stated above (i.e. the average number of features retained of the ten different functions for each order, respectively). To make the comparison fair, 10% percent of the total number of features remaining at a given iteration were removed. In [3], the authors removed half of the features. However, we believe removing 10% of features at each iteration gave more accurate results since the number of features to begin with was not as large as the number in Guyon’s paper.

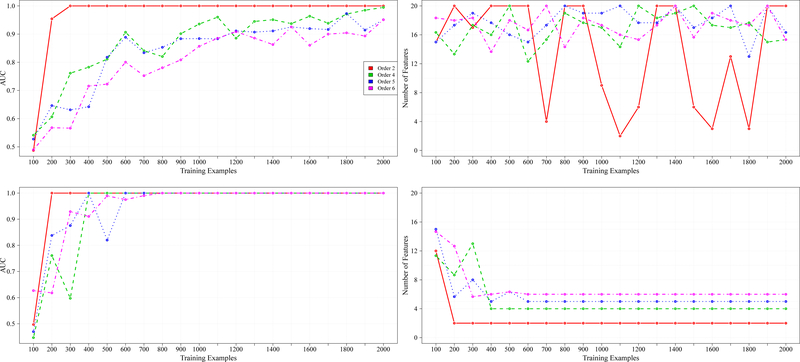
In Figure 1 we show the synthetic data results for 20 total features across the CI functions of order two, four, five, and six. The performance (in terms of AUC) of both algorithms increased as the number of training examples increased, which is to be expected. However, RFEST achieved an AUC of 1.0 at a faster rate than RFE. In fact, for orders five and six, RFE failed to attain an AUC of 1.0.

Fig. 1.

From left to right are results for 20 total features. The first column represents the AUC achieved across different training examples and the second column shows the number of features that were retained, with respect to the AUC achieved from the first column. The first row shows the results for RFE. The second row shows the results for RFEST.

The average number of features retained across the various orders was also calculated (second column of Figure 1). The goal was to output only the relevant features. For example, in the case of the parity function, we set the relevant features to be randomly chosen among the 20 features in our dataset, and the remaining features were irrelevant. For the CI function of order four, four randomly chosen features were set as the relevant variables, and the remaining features were irrelevant. The creation of the remaining CI functions followed a similar format. All feature values were chosen with respect to a uniform distribution.

Observe that in Figure 1, RFE was not able to retain the relevant features across all orders. For orders four, five, and six, the algorithm stopped prematurely, outputting nearly all of the original features. In the case of the parity function, there are several instances where the RFE algorithm outputted only a small subset of features that included the relevant variables, however, it failed to return solely those that are relevant. Unlike RFE, RFEST was able to retain solely the relevant variables for each order. For the parity function, only 200 instances were required. For orders four, five, and six, 400, 400, and 300 instances were needed to return a subset of only the relevant features, respectively. This is a significant difference.

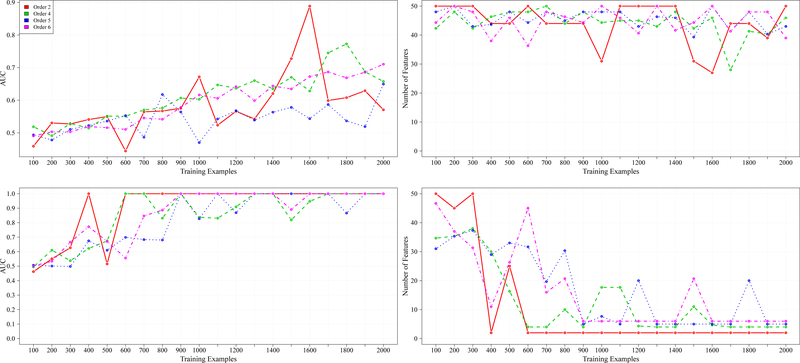
Figure 2 shows the synthetic data results for 50 total features across the CI functions of order two, four, five, and six. In a similar format to Figure 1, the first row represents the AUC achieved and features retained, respectively, for RFE. The second row represents the results for RFEST. As compared to Figure 1, there is a general decrease in AUC across all orders, as the number of irrelevant features increases. However, after a certain number of training examples, RFEST outperformed RFE. The max average AUC achieved for RFE and RFEST for all orders are represented in Table II.

Fig. 2.

From left to right are results for 50 total features. The first column represents the AUC achieved across different training examples and the second column shows the number of features that were retained, with respect to the AUC achieved from the first column. The first row shows the results for RFE.The second row shows the results for RFEST.

TABLE II.

MAX AVERAGE AUC RESULTS FOR 50 TOTAL FEATURES.

	RFE		RFEST
ORDER	AUC	TRAINING EXAMPLES	AUC	TRAINING EXAMPLES
2	0.889	1600	1.0	400
4	0.773	1800	1.0	600
5	0.649	2000	1.0	900
6	0.710	2000	1.0	900

In addition to the significant difference in performance (as shown in Table II), there is a distinct difference in the number of features returned. Across all orders and all varying training examples, RFE was not able to find the subset of relevant variables. However, RFEST was able to do so with the corresponding max average AUC’s and training examples from Table II. This observation is also shown graphically in the second column of Figure 2.

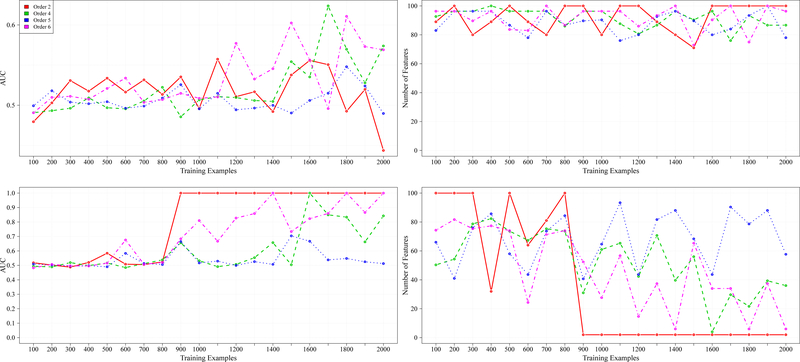
Lastly, Figure 3 shows the synthetic data results for 100 total features across the CI functions of order two, four, five, and six. Similar to the results in Figures 1 and 2, RFEST outperformed RFE in both prediction performance and the ability to retain fewer relevant features. The max average AUC results for RFE and RFEST can be found in Table III. For 100 total features, at approximately 900 training examples, there is a significant difference between the prediction performance (across CI function orders two, four, and six) for RFE and RFEST (as shown in Table III). That is, with fewer training examples, RFEST achieved higher max average AUCs compared to RFE.

Fig. 3.

From left to right are results for 100 total features. The first column represents the AUC achieved across different training examples and the second column shows the number of features that were retained, with respect to the AUC achieved from the first column. The first row shows the results for RFE.The second row shows the results for RFEST.

TABLE III.

MAX AVERAGE AUC RESULTS FOR 100 TOTAL FEATURES.

	RFE		RFEST
ORDER	AUC	TRAINING EXAMPLES	AUC	TRAINING EXAMPLES
2	0.557	1100	1.0	900
4	0.624	1700	1.0	1600
5	0.548	1800	0.704	1500
6	0.611	1800	1.0	1400

Observe that in Figure 3, as the number of training examples increased, RFEST was able to return a smaller subset of features, whereas, RFE returned more than half the number of original features. Note that RFEST demonstrated more fluctuation with 100 total features. This finding suggests that there are CI functions in which RFEST may not be the more robust method, in terms of its ability to return relevant features.

C. Germline Genomic Data for Breast Cancer Results

There is great interest in associating variations in the human genome with disease risk. Much of this work focuses on associating with any given disease the variations in SNPs. Most such work assumes the SNPs, and the variations in disease risk that they cause, are independent of one another; in general this assumption is wrong and results in lost accuracy.

We may examine variations in the germline DNA with which a person is born or variations that arise from somatic mutations in individual cells, such as in the development of cancers and which may vary widely even within the same tumor. One particular disease for which both types of variations have been studied is breast cancer. For predicting disease risk, germline genomic data is the more natural choice to use.

The data we investigate contains 76 SNPs, translating to 152 binary features, in a particular region of the human genome that is orthologous to a region of the rat genome known to modulate breast cancer risk. We use the CGEMS data set of SNP genotypes for 1145 breast cancer cases and 1142 healthy age- and gender-matched controls [32]. Applying RFEST to this data, as run in the previous section, produces a cross-validated AUC of 0.56 with only nine features, which outperforms linear SVM and nonlinear SVM cross-validated runs with the original input data (0.53 and 0.54, respectively). Likewise, RFEST outperformed RFE as RFE (as run in the previous section) returned an AUC of 0.53 with 122 features, no better than either a linear or nonlinear SVM run. We also implemented RFE with the stopping criterion stated in Algorithm 1. That is, since RFEST returned nine features, RFE also iterated until nine features remained but returned an AUC of 0.51.

While all runs were performed by eliminating 10% of features at a time, our novel algorithm is also effective (when compared to RFE) when removing 20% or even 30% of the remaining features at a time. Removing 10% of the features at a time not only resulted in an AUC of 0.56 but most notably retained only nine features. With such a small set of features, one can then exhaustively generate all pairs (and even more) of interaction terms. A linear SVM model was built with the remaining nine features and all interaction terms. In turn, the top 13 features were all pairs of SNPs rather than individual SNPs. This suggests that interactions play a major role in the effect of SNP variations in this region on breast cancer risk, as has been suspected. Studies are under way to further evaluate these nine selected SNPs.

It has been shown that incorporating, as risk factors, germline SNPs associated with breast cancer can significantly improve prediction and even mammography-based diagnosis of breast cancer, even though breast cancer is estimated to be only 30% heritable [33]. In this section we have shown that avoiding the independence assumption regarding SNPs, by using a nonlinear SVM with our novel RFE algorithm, makes it possible to associate with breast cancer risk new SNPs and their interactions, and that this association can enable more accurate breast cancer risk prediction than could be made from these SNPs without taking interactions into account.

A post-hoc analysis of these nine selected SNPs confirmed our collaborating biologist’s suspicion that interactions (rather than specific SNP values) were the most important modulator of breast cancer risk in this genomic region, and revealed which interactions were crucial to the underlying task (i.e. breast cancer diagnoses).

V. DISCUSSION & CONCLUSION

In this paper, we explored the difficulties that accompany feature selection and learning decidedly nonlinear target concepts. In addition, we discussed the challenges that are faced in using Guyon’s RFE algorithm [3]. Such a problem occurs in significantly lower AUC than the novel RFE algorithm.

We introduce a new algorithm, RFEST, for a nonlinear machine learning algorithm and demonstrate its efficacy both theoretically (refer to Theorem III.1 and Supplementary Material) and empirically (see Section IV). The RFE algorithm is an embedded-based approach but RFEST behaves like a wrapper-based approach. It uses a nonlinear SVM as a black box to determine feature relevance. In principle, with this approach one can use any machine learning algorithm to remove irrelevant or redundant features. Refer to this repository for the code implementation on a sample dataset.

RFEST differs from RFE in two important ways: it flips rather than eliminates each feature to test sensitivity and measures loss in model efficacy instead of the loss in weighted sum of distances from the margin. These differences result in substantial improvements across CI functions and a real-world breast cancer genomics problem.

Extending the feature types used by RFEST is left for future work. Lastly, if one knew that the input data contained many correlated features, then applying a filter algorithm before RFEST will aid in removing redundant features.