Tailoring Cu⁺ for Ga³⁺ Cation Exchange in Cu_2–xS and CuInS₂ Nanocrystals by Controlling the Ga Precursor Chemistry

Abstract

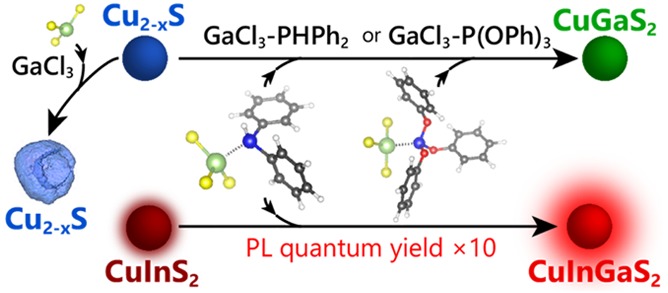
Nanoscale cation exchange (CE) has resulted in colloidal nanomaterials that are unattainable by direct synthesis methods. Aliovalent CE is complex and synthetically challenging because the exchange of an unequal number of host and guest cations is required to maintain charge balance. An approach to control aliovalent CE reactions is the use of a single reactant to both supply the guest cation and extract the host cation. Here, we study the application of GaCl₃–L complexes [L = trioctylphosphine (TOP), triphenylphosphite (TPP), diphenylphosphine (DPP)] as reactants in the exchange of Cu⁺ for Ga³⁺ in Cu_2–xS nanocrystals. We find that noncomplexed GaCl₃ etches the nanocrystals by S^2– extraction, whereas GaCl₃–TOP is unreactive. Successful exchange of Cu⁺ for Ga³⁺ is only possible when GaCl₃ is complexed with either TPP or DPP. This is attributed to the pivotal role of the Cu_2–xS–GaCl₃–L activated complex that forms at the surface of the nanocrystal at the onset of the CE reaction, which must be such that simultaneous Ga³⁺ insertion and Cu⁺ extraction can occur. This requisite is only met if GaCl₃ is bound to a phosphine ligand, with a moderate bond strength, to allow facile dissociation of the complex at the nanocrystal surface. The general validity of this mechanism is demonstrated by using GaCl₃–DPP to convert CuInS₂ into (Cu,Ga,In)S₂ nanocrystals, which increases the photoluminescence quantum yield 10-fold, while blue-shifting the photoluminescence into the NIR biological window. This highlights the general applicability of the mechanistic insights provided by our work.

Compound copper chalcogenide nanocrystals (NCs) offer a promising alternative to the widely studied CdX and PbX NCs (X = S, Se, Te), as they consist of less toxic elements and display exciting optoelectronic properties, such as photoluminescence (PL) tunability in the visible to the near-infrared (NIR) spectral window and localized surface plasmon resonances (LSPR) in the NIR.¹⁻⁴ Another advantage of these nanomaterials is the wide range of compositions that can be obtained, ranging from binary to multinary compounds with up to five different elements.¹⁻³ This makes them a versatile class of materials, offering ample opportunities for property engineering.^1−3,5 However, some morphologies and compositions are not easily accessible by direct approaches due to synthetic limitations, such as the lack of suitable precursors for multinary compounds.¹ Nanoscale cation exchange (CE) has emerged as a promising postsynthetic tool to circumvent these limitations, providing pathways to NCs and hetero-NCs with compositions, morphologies, crystal structures, and heteroarchitectures that would otherwise remain unavailable.⁵⁻⁸ The extent of the CE (ranging from doping, e.g., Ag:CdSe NCs,⁹ Zn:CsPbBr₃ NCs,¹⁰ Mn:ZnTe magic-size clusters,¹¹ to full replacement)⁵⁻⁸ and the elemental distribution profile of the product NCs (i.e., homogeneous or gradient alloys, e.g., (Cd,Zn)Se NCs,¹² or heterostructured NCs, e.g., ZnSe/CdSe,¹² PbSe/CdSe¹³ core/shell quantum dots) depends on a number of physicochemical properties, such as the miscibility of the parent and product phases and the diffusion rates of the incoming and outgoing cations within the NCs and can be tailored by adjusting reaction variables, such as reaction temperature and concentration of guest cations in solution.⁵⁻¹³

In isovalent CE, such as Zn²⁺ for Cd²⁺ exchange in ZnSe NCs¹² and Pb²⁺ for Cd²⁺ in PbX NCs,¹³⁻¹⁵ a direct place exchange reaction occurs at the surface of the template NCs, through which the outgoing host cation and the incoming guest cation swap places (i.e., the guest cation is incorporated in the NC, while the host cation forms a complex with the ligand molecule that was carrying the guest cation).¹² This is in contrast with aliovalent CE, such as Cu⁺ for In³⁺ in Cu_2–xS NCs¹⁶ or Cd²⁺ for Ag⁺ in CdSe,^5,9,17 which typically occurs through two separate chemical pathways.^5−8,16 This makes balancing the in- and outgoing diffusion rates challenging. An approach to better control aliovalent CE reactions is the use of a single precursor, which both provides the guest cation and extracts the host cation. In the case of the Cu⁺ for In³⁺ exchange, a stoichiometric InCl₃–trioctylphosphine complex has been shown to be a suitable precursor, even allowing for topotactic sequential CE (viz., Cd²⁺ for Cu⁺, followed by partial Cu⁺ for In³⁺) in large and complex anisotropic NCs such as CdSe/CdS dot-in-rod nanorods, with preservation of the size, shape, and heterostructure of the template NCs in the product CuInSe₂/CuInS₂ dot-in-rod nanorods.¹⁸ The strict control over the CE rates provided by this approach has been recently exploited to fabricate air-stable CuInSe₂ NC transistors by postdeposition sequential CE.¹⁹ Here, we extend the single precursor approach to the exchange of Cu⁺ for Ga³⁺ in Cu_2–xS and CuInS₂ NCs by using stoichiometric GaCl₃–phosphine complexes to simultaneously deliver Ga³⁺ and extract Cu⁺. Our choice is motivated by the fact that CuGaS₂ (CGS) and Cu(In,Ga)S₂ (CIGS) exhibit interesting optoelectronic properties, which make them promising materials for applications in photocatalysis,^20,21 light-emitting devices,^22,23 and photovoltaics.²⁴⁻²⁷ Moreover, studies of Cu⁺ for Ga³⁺ and In³⁺ for Ga³⁺ cation exchange are scarce.²⁸⁻³⁰ Although Ga³⁺ and In³⁺ are both trivalent cations of group IIIA metals, they have significantly different ionic radii (r_Ga³⁺ = 47 pm, r_In³⁺ = 62 pm)³¹ and Lewis acidity (η_Ga³⁺ = 17 eV, η_In³⁺ = 13 eV)³² and are thus expected to behave differently in cation exchange reactions. Our study thus offers an ideal testbed to investigate the relationship between the chemistry of the metal chloride–phosphine complexes and the outcome of cation exchange reactions in Cu chalcogenide NCs.

We investigated different GaCl₃–L Lewis acid–base adduct complexes [L = trioctylphosphine (TOP), triphenylphosphite (TPP), and diphenylphosphine DPP)] as reagents for the exchange of Cu⁺ for Ga³⁺ and found that the choice of ligand has a profound impact on the reaction outcome. Noncomplexed GaCl₃ is a strong Lewis acid that yields hollow NCs through etching by sulfide extraction, whereas the complex GaCl₃–trioctylphosphine leads to neither etching nor cation exchange. In contrast, both GaCl₃–triphenylphosphite and GaCl₃–diphenylphosphine successfully converted Cu_2–xS NCs in CuGaS₂ NCs through Cu⁺ for Ga³⁺ exchange. These different reactivities are attributed to the stability and geometry of the activated Cu_2–xS–GaCl₃–L complex that must be formed at the surface of the NCs prior to the cation exchange. Density functional theory (DFT) calculations show that, in these complexes, the Ga–P bond strength decreases with increasing electron-withdrawing nature of the side groups on the phosphine ligands (i.e., the Ga–P bond strength ε follows the trend ε_GaCl3–TOP > ε_GaCl3–DPP > ε_GaCl3–TPP). Complexing GaCl₃ with DPP or TPP lowers the activation energy barrier for the CE reaction, while kinetically favoring the Cu⁺ for Ga³⁺ place exchange over the sulfide extraction. These insights were used to successfully convert CuInS₂ NCs into Cu-poor (Cu,In,Ga)S₂ NCs through Cu⁺ for Ga³⁺ exchange, yielding NCs with vastly improved photoluminescence quantum yields with respect to the parent NCs. The findings presented in this work are thus generally applicable, resulting in nanomaterials with combinations of size, shape, composition, and crystal structure that are not directly accessible by conventional synthesis routes.

Results and Discussion

Stoichiometric InCl₃–TOP and GaCl₃–TOP as Reactants for Cation Exchange in Cu_2–xS NCs

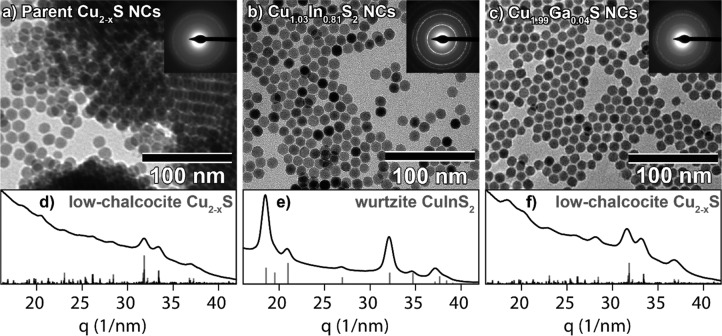
Throughout this work, low-chalcocite 12 nm Cu_2–xS (x < 0.04) bifrustum NCs are used as parent NCs to investigate the Cu⁺ for Ga³⁺ cation exchange reaction. For comparison, these NCs (Figure 1a,d) are converted into wurtzite CuInS₂ (CIS) bifrustum NCs (Figure 1b,e) by partial, self-limited Cu⁺ for In³⁺ CE at 100 °C, using a stoichiometric InCl₃–trioctylphosphine (InCl₃–TOP) Lewis acid–base adduct as precursor, as previously reported by our group.¹⁸ The transformation from low chalcocite to wurtzite is evidenced by the electron diffraction (ED) patterns (Figure 1a,b,d,e). The powder ED (PED) pattern obtained after azimuthal integration of the 2D ED pattern of the product NCs (Figure 1e) corresponds well to the reference pattern of wurtzite CIS. The shape and size of the NCs are preserved after the reaction (Supporting Information, Figure S1), confirming the topotactic nature of the Cu⁺ for In³⁺ CE reaction. Energy-dispersive X-ray spectroscopy (EDS) measurements further confirm the conversion of Cu_2–xS NCs into ternary CIS NCs (Cu/In = 1.00:0.79; Supporting Information, Figure S2). Compared to the Cu_2–xS parent NCs, the product CIS NCs no longer exhibit a LSPR absorption band in the NIR (Supporting Information, Figure S3a,b). The absorption spectrum of the CIS NCs agrees well with spectra reported in the literature.³³ In contrast, the use of the stoichiometric GaCl₃–TOP Lewis acid–base adduct as a precursor does not lead to any significant change in the composition (Cu/Ga = 1.00:0.02, Supporting Information, Figure S4), crystal structure, size, and shape of the NCs (Figure 1c,f). The absorption spectrum of NCs obtained after reaction with GaCl₃–TOP exhibits little to no LSPR band (Supporting Information, Figure S3c), which indicates the absence of excess free holes in these NCs, due to (limited) reduction at the NC surface.

Figure 1.

TEM images of (a) parent Cu_2–xS bifrustum NCs, (b) product Cu_1.03In_0.81S₂ (CIS) bifrustum NCs, after reaction with InCl₃–TOP at 100 °C, and (c) Cu_1.99Ga_0.04S nanocrystals, after reaction with GaCl₃–TOP at 100 °C. Top-right insets display the corresponding ED pattern. Bottom panels show azimuthally integrated ED (PED) patterns of (d) parent low-chalcocite Cu_2–xS nanocrystals, (e) product wurtzite CIS nanocrystals, and (f) product low-chalcocite Cu_1.99Ga_0.04S nanocrystals. Reference bars in (d,f) are calculated patterns based on the low-chalcocite Cu_2–xS crystal structure described in ref (34). Reference bars in (e) were obtained from JCPDS PDF-card 01-077-9459 for wurtzite CIS.

Reaction of Noncomplexed GaCl₃ with Cu_2–xS NCs

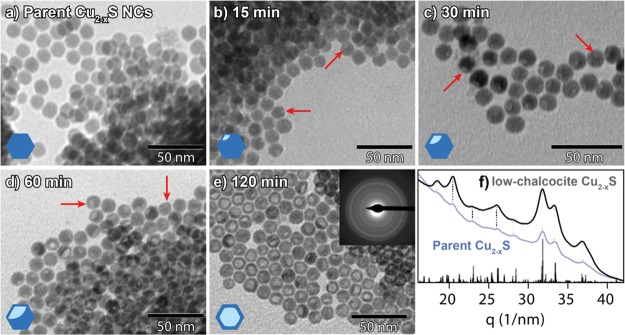
Clearly, the Cu⁺ for Ga³⁺ CE does not significantly occur when GaCl₃–TOP is used as the reactant under the same conditions that successfully lead to Cu⁺ for In³⁺ CE using InCl₃–TOP. Therefore, other Ga precursors were examined, starting with the simplest possible case: GaCl₃ dissolved in neat toluene. The reaction with GaCl₃ at the same temperature used with GaCl₃–TOP (100 °C) was found to severely deteriorate the NCs (Supporting Information, Figure S5). To minimize the degradation, the temporal evolution of this reaction was studied at a lower temperature (30 °C) (Figure 2b–e). The TEM images of the product NCs show that, despite the lower reaction temperature, a low-contrast spot appears in the NCs already after 15 min of reaction (Figure 2b, red arrows) and increases in size over time (Figure 2c–e). The PED pattern shows that the crystal structure of the NCs remains low-chalcocite Cu_2–xS, even after 120 min of reaction (Figure 2f), despite the dramatic morphological changes (Figure 2e). After 120 min of reaction, these NCs no longer exhibit an LSPR absorption band (Supporting Information, Figure S3f), presumably due to their poorly defined shape.

Figure 2.

TEM images of (a) parent Cu_2–xS NCs and (b–e) product NCs obtained after reacting the NCs shown in (a) with GaCl₃ at 30 °C for (b) 15 min, (c) 30 min, (d) 60 min, and (e) 120 min. Red arrows indicate regions of low contrast within the nanocrystals (cartoons in the lower-left corner give an impression of the observed contrast in the NCs). Top-right inset in (e) depicts an electron diffraction pattern of the corresponding sample. Panel (f) is the azimuthally integrated ED pattern depicted in (e). Reference bars in (f) are calculated patterns based on the low-chalcocite Cu_2–xS crystal structure described in ref (34). The blue curve in (f) corresponds to the PED pattern of the parent Cu_2–xS nanocrystals. Dotted lines serve as guides for the eye.

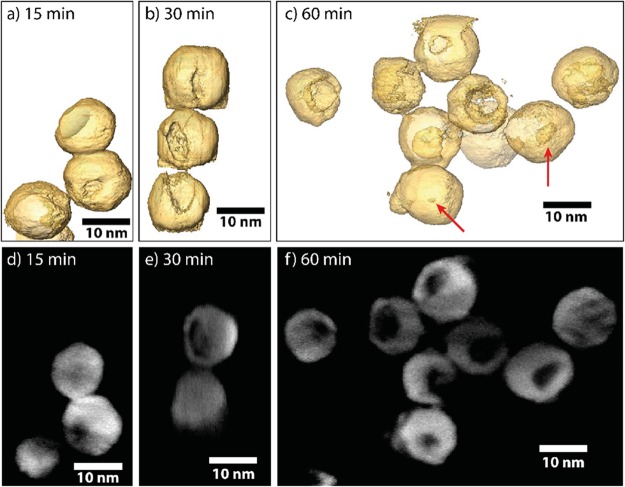
To determine the nature of the low contrast region and its position within the particles, high-angle annular dark-field scanning transmission microscopy (HAADF-STEM) tomography measurements were performed. Visualizations of the 3D reconstructed volumes of NCs after different reaction times are shown in Figure 3. Animated versions of the tomograms are also provided in the web-enhanced movies 1, 2, and 3. The tomography measurements show that, after 15 min of reaction with GaCl₃, a small cavity is present at the surface of some Cu_2–xS NCs (Figure 3a) and increases in size as the reaction progresses (Figure 3b,c). Acquired orthoslices, which were used to reconstruct the 3D morphologies, are displayed in Figure 3d–f. These measurements indicate that the brighter regions observed in TEM images coincide with cavities at the surface of the NCs. The cavities appear to form at the surface of the NCs at early reaction stages and subsequently grow inward over time. A small portion of the NCs (indicated by red arrows in Figure 3) appears to be hollow, without an obvious opening at the surface.

Figure 3.

3D characterization of tomographic visualization of the Cu_2–xS bifrustum NCs after reaction with GaCl₃ at 30 °C for (a) 15 min, (b) 30 min, and (c) 60 min. After 15 min, only a small dimple is present at the surface of the NCs. After longer reaction times, these cavities are found to be larger. Red arrows indicate hollow NCs without an apparent opening at the surface. (d–f) Orthoslices used to reconstruct the 3D morphologies presented in (a–c). Animated (rotating) versions of the models depicted in panels (a–c) are provided.

These observations bear similarities with previous reports on hollow nanoparticles, whose formation has been ascribed to the nanoscale Kirkendall effect,^35,36 which involves an imbalance between outward and inward diffusion fluxes during the chemical conversion of a NC into a different material through reaction with a reactant present in solution. The surface of the parent NC is first converted into a shell of the product material by reaction with a species present in solution, after which further conversion can only take place through solid-state diffusion of the reactant species through the NC.³⁵ In case the outward diffusion rate is faster than the inward diffusion rate, there is a net flow of material going out of the NC, leaving vacancies behind.³⁵ Condensation of these vacancies gives rise to voids that eventually collect in a central void in the NCs.³⁵ The nanoscale Kirkendall process has also been recently proposed as an explanation for the conversion of Cu_2–xS nanoplatelets into CuInS₂ nanorings through partial Cu⁺ for In³⁺ CE.³⁷ Our observations, however, are not consistent with the nanoscale Kirkendall effect, as the cavities form at the surface of the NCs and grow inward, in striking contrast with the outward growing inner voids that characterize the Kirkendall effect.

Surface erosion of the NCs and preservation of a low-chalcocite Cu_2–xS shell after the reaction with GaCl₃ indicate that a reaction other than cation exchange is taking place. In the successful Cu⁺ for In³⁺ cation exchange reaction using the InCl₃–TOP Lewis acid–base adduct complex, TOP (a soft Lewis base) acts as Cu⁺ extractor,^5,18 likely forming CuCl–TOP Lewis acid–base adduct complexes. In the present reaction using noncomplexed GaCl₃, there are no species present to directly extract Cu⁺. However, GaCl₃ is a strong Lewis acid^38,39 and therefore can extract S^2– from the NC as S^2– is a Lewis base. This extraction destabilizes the crystal lattice, as the S^2– anions form the framework of Cu_2–xS NCs, resulting in etching of the NCs and formation of cavities at the surface. The collapse of the NC framework will release Cu⁺ ions, which are likely stabilized in solution by binding to the chloride ions released from GaCl₃ after its reaction with the NC sulfides.

Although the NCs react with a strong Lewis acid, they do not dissolve completely, even after 300 min (Supporting Information, Figure S6). Interestingly, in micrographs obtained using HAADF-STEM, most particles exhibit a uniform contrast after reacting for 300 min (Supporting Information, Figure S6e). This uniform contrast indicates that the previously formed cavities are filled with new material. EDS elemental maps show that this material consists mostly of gallium. These observations suggest that Ga-containing monomers, formed upon extraction of S^2– by GaCl₃, precipitate inside the NC cavities after longer reaction times. This refilling of the cavities likely blocks further reactions on the NC surface, preventing further dissolution.

Tailoring the Ga Precursor Chemistry To Boost the Cu⁺ for Ga³⁺ Cation Exchange

We have discussed above two extreme cases of reactivity imbalance: whereas GaCl₃–TOP is too inert, hardly leading to any change in the parent Cu_2–xS NCs, noncomplexed GaCl₃ is too reactive toward the sulfide anions, thereby etching the parent NCs without any significant cation exchange. In the following, we will tailor the chemistry of the Ga precursor complex to allow successful Cu⁺ for Ga³⁺ cation exchange.

The observation that the reactivity of the GaCl₃–TOP Lewis acid–base adduct complex as a cation exchange precursor is much lower than that of the InCl₃–TOP complex is surprising, considering that the metal–phosphorus bond in GaCl₃–TOP should be weaker than that in InCl₃–TOP as Ga³⁺ is a harder Lewis acid than In³⁺ (η = 17 and 13 eV, respectively),³² whereas TOP is a soft Lewis base (η ≈ 6 eV).^5,40 This implies that other variables are more relevant in determining the Cu⁺ for Ga³⁺ cation exchange rates and prompted us to explore the influence of the nature of the phosphine ligand on the cation exchange reaction by using triphenylphosphite and diphenylphosphine as ligands for GaCl₃ (Figure 4b,c). The coordination behavior of a phosphine ligand with respect to a metal center is determined by its steric and electronic properties.^41,42 The most frequently used parameter to quantify the steric properties of phosphines is the Tolman cone angle, defined as the apex angle of a cylindrical cone with origin 2.28 Å from the center of the phosphorus atom, whose sides just touch the Van der Waals surfaces of the outermost atoms of the organic substituents.⁴¹ The three phosphine ligands used in the present work have significantly different electronic properties and total molecular volume, but their Tolman cone angles are essentially the same: 128° for both DPP and TPP and 132° for TOP.⁴¹ The value for TOP is taken to be the same as that reported by Tolman for other tertiary alkylphosphines, such as tri-n-butylphosphine, although a recent work has estimated it to be 128°.⁴⁰ Steric effects are thus not expected to play a significant role in the cation exchange reactions investigated in our work. The electronic properties of phosphines are determined by their σ-donor ability and π-acceptor strength as they bind to metals by a combination of σ-donation from the lone pair of the P atom and π-back bonding from the d orbitals of the metal into their empty P–R σ* molecular orbital (R = organic substituent).^41,42 More electronegative (i.e., electron-withdrawing) substituents on the phosphorus atom decrease the basicity and σ-donating ability of the phosphine, while increasing its π-acceptor strength.⁴⁰⁻⁴³ This effect is due to the decrease of the electronic density on the phosphorus atom and increase of the s-character of the lone electron pair.^41,42 An increase in electronegativity of the substituents on the phosphorus atom should lead to weaker bonding to the metal, as should be the case for GaCl₃–TPP and GaCl₃–DPP compared to GaCl₃–TOP.

Figure 4.

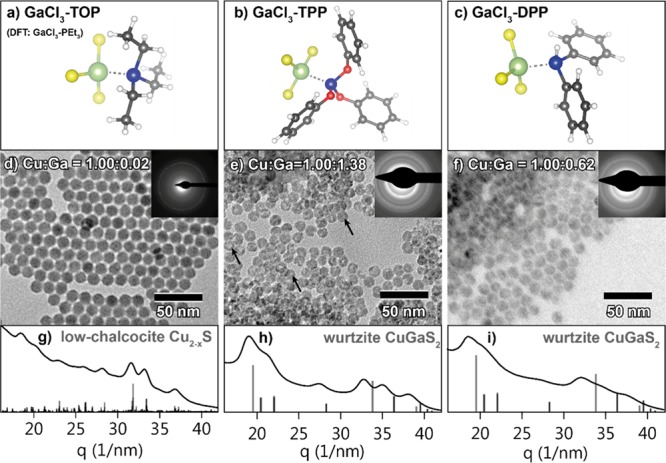
(Top row) Ground-state geometries of three GaCl₃–phosphine complexes obtained from DFT calculations (see below): (a) GaCl₃ complexed with triethylphosphine, used as model for GaCl₃ complexed with trioctylphosphine (GaCl₃–TOP), (b) GaCl₃ complexed with triphenylphosphite (GaCl₃–TPP), and (c) GaCl₃ complexed with diphenylphosphine (GaCl₃–DPP). (Middle row) TEM images of product NCs obtained after reaction of Cu_2–xS NCs with (d) GaCl₃–TOP at 100 °C, (e) GaCl₃–TPP at 100 °C, and (f) GaCl₃–DPP at 50 °C. Black arrows indicate intraparticle contrast in the NCs reacted with GaCl₃–TPP. Top-right insets show the corresponding ED patterns. Bottom row (g–i) shows the corresponding azimuthally integrated ED patterns. Reference bars in (h,i) are calculated patterns based on the wurtzite CuGaS₂ crystals structure,⁴⁴ and reference bars in (g) are based on the low-chalcocite Cu_2–xS crystal structure.³⁴

Indeed, the use of both GaCl₃–TPP and GaCl₃–DPP as reactants results in successful CE reactions even after reaction times much shorter than those used for GaCl₃–TOP (1 h instead of 12 h, at the same temperature), as clearly demonstrated by EDS analysis of the product NCs obtained after reaction with GaCl₃–TPP and GaCl₃–DPP at 100 °C, which reveals Cu/Ga ratios of 1.00:1.38 and 1.00:1.48, respectively (Supporting Information, Figures S7 and S8). The NCs that reacted with GaCl₃–TPP are partially deformed and exhibit intraparticle contrast in TEM images (Figure 4e, indicated by black arrows), similar to the NCs that reacted with GaCl₃ (see Figures 2 and 3). The NCs that reacted with GaCl₃–DPP form agglomerates (Supporting Information, Figure S9), which is likely due to displacement of the original organic capping ligands (dodecanethiol) with DPP during the CE reaction. DPP is a relatively small molecule and thus poorly suitable as a steric stabilizer. In comparison, the NCs cluster less after reaction with GaCl₃–TPP as triphenylphosphite is bulky enough to provide steric stabilization. To increase the colloidal stability of the NCs reacted with GaCl₃–DPP, oleylamine (OLAM) was added to the reaction mixture and a lower reaction temperature (50 °C) was employed, which indeed inhibited NC agglomeration (Figure 4f). However, under these milder reaction conditions, the Cu⁺ for Ga³⁺ exchange proceeds to a lesser extent, as shown by EDS analysis (Cu/Ga ratio of 1.00:0.62, Supporting Information, Figure S10). The PED pattern (Figure 4e,h) of the NCs reacted with GaCl₃–TPP corresponds to the wurtzite crystal structure, confirming that Cu⁺ for Ga³⁺ CE has indeed taken place. Interestingly, the peaks in the ED pattern are shifted to lower q values compared to those of the reference wurtzite CGS, indicating that the product CGS NCs have a larger lattice constant than the reference. This observation will be discussed in more detail below. The PED pattern (Figure 4f,i) of the NCs reacted with GaCl₃–DPP exhibits broad, poorly defined peaks, indicating that these particles have partially lost their crystallinity during the CE procedure, which precludes a definitive assignment of the crystal structure. The NCs reacted with GaCl₃–TPP and GaCl₃–DPP are both smaller than the parent Cu_2–xS NCs (diameters = 10.8 ± 1.0, 11.1 ± 1.1, and 12.3 ± 1.0 nm, respectively, Supporting Information, Figure S1). The NCs reacted with GaCl₃–TPP no longer exhibit an LSPR absorption band, whereas those reacted with GaCl₃–DPP exhibit an LSPR absorption band with a reduced intensity (Supporting Information, Figure S3d,e). In the latter NCs, Cu⁺ was exchanged for Ga³⁺ to a lesser extent; the presence of an LSPR absorption band thus indicates that these NCs remain cation-deficient, requiring excess holes for charge neutrality.

The intraparticle contrast observed in the NCs after reaction with GaCl₃–TPP was studied with HAADF-STEM and EDS elemental mapping. In micrographs obtained using HAADF-STEM, the intraparticle contrast appears similar to that observed in TEM images (compare Figure 5a to Figure 4e). In the elemental maps, the regions of low contrast coincide with regions of low signal for both cations (Figure 5, indicated by orange arrows). As the Cu and Ga distributions correlate well (Figure 5b,c), the intraparticle contrast is clearly not due to an inhomogeneous composition. Instead, it appears that the low contrast regions in HAADF-STEM and TEM images simply contain less material. Likely, surface erosion by GaCl₃ is not completely suppressed when GaCl₃–TPP is used as reactant, resulting in the formation of small cavities at the NC surface.

Figure 5.

(a) HAADF-STEM images and EDS elemental maps of (b, blue) Cu and (c, red) Ga of product NCs obtained by reacting Cu_2–xS NCs with GaCl₃–TPP at 100 °C. Orange arrows indicate regions of low contrast (HAADF-STEM) coinciding with regions of low signal (EDS maps).

Similar to the previously reported conversion of low-chalcocite Cu_2–xS into wurtzite CIS NCs by Cu⁺ for In³⁺ CE,^16,18,33 the exchange of Cu⁺ for Ga³⁺ in Cu_2–xS NCs using GaCl₃–DPP or GaCl₃–TPP as precursors is also partial and self-limited as CGS, rather than Ga₂S₃, NCs are produced. In the case of the Cu⁺ for In³⁺ CE in Cu_2–xS NCs, the topotactic, partial, and self-limited character of the exchange was attributed to the high energy barrier associated with the conversion of the hexagonal close-packed anionic sublattice of the parent low-chalcocite Cu_2–xS NCs into the face-centered cubic sublattice of the spinel structure of In₂S₃, which requires a substantial reorganization of the sulfide anions (by 58% of a S–S interatomic distance).¹⁶ In contrast, the hexagonal wurtzite structure of CuInS₂ requires only minor rearrangements of the sulfide sublattice with respect to that of the template NCs (1.4 and 6.4% contraction within and between the hexagonal S^2– layers, respectively).¹⁶ The topotactic nature of the cation exchange in Cu_2–xS NCs has been recently exploited to achieve structure-selective conversion of Cu_2–xS NC templates into ZnS, CdS, and CuInS₂, with hexagonal roxbyite Cu_1.78S and cubic digenite Cu_1.8S yielding product NCs with the wurtzite and the zinc blende structures, respectively.⁴⁵

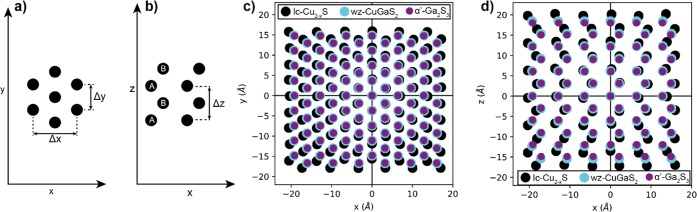
In the present case, however, the structural differences between the possible products and the template NCs are less pronounced because low-chalcocite Cu_2–xS, wurtzite CuGaS₂, and the stable form of bulk Ga₂S₃, monoclinic α′-Ga₂S₃, all have a hexagonal close-packed sulfide sublattice,^34,44,46 with hexagonally structured layers stacked in an ...ABAB... fashion (Figure 6a,b). However, we observe that, in all three dimensions, the wurtzite CuGaS₂ structure exhibits a significant lattice contraction compared to that of low-chalcocite Cu_2–xS (Figure 6c,d). These contractions are 5.6, 5.7, and 9.5% in x, y, and z, respectively. On the other hand, the anion positions of wurtzite CuGaS₂ and α′-Ga₂S₃ are very similar: transforming the former into the latter, the lattice has to contract by only 0.6, 0.5, and 2.5% in x, y, and z, respectively (the definition of x, y, and z directions in terms of crystallographic directions are provided in the caption of Figure 6). It is thus clear that, based on the bulk crystal structure parameters, the sulfide sublattice of the template low-chalcocite Cu_2–xS would have to undergo similar degrees of reconstruction, regardless of whether the cation exchange would be partial, yielding wurtzite CuGaS₂, or complete, yielding α′-Ga₂S₃. However, we note that the product wurtzite CGS NCs (with Cu/Ga ratios ranging from 1:1.48 to 1:0.62) obtained in our work exhibit a larger lattice constant than the wurtzite CuGaS₂ reference (Figure 4h,i), indicating that the degree of contraction was smaller than expected based on the bulk lattice parameters, and therefore, that the product CGS NCs are under tensile strain. This suggests that the mild reaction conditions used in our work do not allow the anion sublattice to undergo full reconstruction in order to relax the strain induced by the CE.

Figure 6.

(a,b) Hexagonal close-packed structure viewed from two different orientations: (a) characteristic arrangement into hexagonally constructed layers, defined here as the x,y-plane, and (b) characteristic ...ABAB... stacking of these hexagonal layers, defined here as the x,z-plane. (c,d) Anion positions of (black) low-chalcocite Cu_2–xS, (cyan) wurtzite CuGaS₂, and (purple) α′-Ga₂S₃ overlaid onto each other. (c) Hexagonal ordering in the x,y-plane and (d) ...ABAB... stacking in the x,z-plane. Δx, Δy, and Δz, denoted in (a,b), correspond to the lattice distances used to determine the lattice contractions mentioned in the main text. The x,y,z-directions correspond to the following crystallographic directions: (low-chalcocite Cu_2–xS) [201],[010],[001]; (wurtzite CuGaS₂) [11̅0],[110],[001]; (monoclinic α′-Ga₂S₃) [010],[100],[102]. Anion coordinates were obtained from the crystal structures of low-chalcocite Cu_2–xS,³⁴ wurtzite CuGaS₂,⁴⁴ and monoclinic α′-Ga₂S₃.⁴⁶

Recently, lattice strain was shown to play an important role in the conversion of djurleite Cu_2–xS nanorods (NRs) into Cu_2–xS/CGS hetero-NRs by partial Cu⁺ for Ga³⁺ CE.³⁰ Shim and co-workers showed that lattice strain prevented the homogeneous conversion of Cu_2–xS NRs (∼170 nm long, 20 nm diameter) into CGS NRs, resulting instead in hetero-NRs containing one or multiple wurtzite CGS domains.³⁰ The authors argued that the strain induced by the lattice mismatch between the parent djurleite Cu_2–xS phase and the product wurtzite CGS phase would make Ga³⁺ diffusion into Cu_2–xS unfavorable, thereby limiting the extent of the CE reaction and leading to wurtzite–djurleite superlattice formation as a way to minimize the resulting strain. However, we note that in the present work Cu_2–xS NCs were successfully converted into homogeneous CGS NCs, despite the tensile strain resulting from insufficient contraction to the lattice parameters of fully relaxed bulk CuGaS₂. This difference can be attributed to the fact that the NCs used here are much smaller than those used by Shim and co-workers (viz. 12 nm diameter vs ∼170 nm long, 20 nm diameter rods). The smaller volume of the template NCs used in our work favors conversion to homogeneous CGS NCs because smaller NCs can more easily accommodate lattice strain. This also offers a possible explanation for the self-limiting character of the Cu⁺ for Ga³⁺ exchange in Cu_2–xS NC templates: the α′-Ga₂S₃ structure is probably unable to accommodate as much tensile strain as wurtzite CGS, preventing full CE.

Density Functional Theory Calculations

To corroborate our assumption of weaker Ga–P bond strengths in GaCl₃–DPP and GaCl₃–TPP with respect to GaCl₃–TOP, we conducted DFT calculations at the B3LYP/6-311+G(d,p);Ga:SDD level to estimate both the ground-state geometry of the complexes and the Ga–P bond enthalpy. In the DFT calculations, we modeled TOP as triethylphosphine to avoid an extensive conformational search due to the many degrees of freedom of the long alkyl chains. We expect that only the first few CH₂ groups of TOP significantly influence the Ga–P bond, making PEt₃ an acceptable surrogate for TOP. To verify whether the outcome of these calculations is physically reasonable, we compare calculated geometries to experimental structures obtained from X-ray crystallography. We include an additional complex (GaCl₃–PPh₃), as, to the best of our knowledge, the structures of GaCl₃–DPP and GaCl₃–TPP have not been resolved experimentally. The results of the DFT calculations (Ga–P bond lengths and dissociation enthalpies) and the experimentally determined Ga–P bond lengths are shown in Table 1. The Ga–P bond lengths determined by DFT deviate from the experimental ones by only 4–5%. Moreover, the DFT results reproduce the experimental trend in Ga–P bond length from GaCl₃–PEt₃ to GaCl₃–PPh₃. Thus, although the absolute values obtained from the DFT calculations are 4–5% longer than the experimental ones, the trends in the DFT results are reliable. We observe that, with increasing electron-withdrawing nature of the side groups on the phosphine ligand, the Ga–P bond length L increases (viz., L_GaCl3–TOP < L_GaCl3–DPP < L_GaCl3–TPP). The dissociation enthalpy follows the reverse trend. These results show that, indeed, the Ga–P bonds in GaCl₃–DPP and GaCl₃–TPP are weaker than those in GaCl₃–TOP.

Table 1. DFT-Calculated (B3LYP/6-311+G(d,p);Ga:SDD) and Experimental Ga–P Bond Lengths and DFT-Calculated Dissociation Enthalpies of GaCl₃–PEt₃, GaCl₃–PPh₃, GaCl₃–DPP, and GaCl₃–TPP.

complex	Ga–P bond length (Å), calculated	Ga–P bond length (Å), experimental	dissociation enthalpy (kcal/mol), calculated
GaCl3–PEt3	2.453	2.35347	31.2
GaCl3–PPh3	2.487	2.37248	27.2
GaCl3–DPP	2.498	not available	23.0
GaCl3–TPP	2.540	not available	14.7

Mechanism for the Cu⁺ for Ga³⁺ Exchange in Cu_2–xS NCs

Nanoscale CE reactions consist of a number of linked elementary kinetic steps:^5,6,8,12 (i) extraction of the host cations from the NC surface, (ii) incorporation of guest cations at the NC surface, (iii) solid-state diffusion of the guest cations into the NC, and (iv) solid-state diffusion of the native cations to the NC surface. The thermodynamic driving force for the reaction is determined by the energy balance of the overall reaction.^5,6,8 However, the energy input or output involved in each step is important as all steps are kinetically linked and must proceed in a concerted manner. Therefore, the outcome of nanoscale CE reactions (i.e., extent of the exchange, homogeneous or heterostructured nanocrystals, etc.) is dictated by the kinetic balance between a number of competing processes taking place in solution, at the NC surface and within the NC.

Aliovalent CE reactions are inherently more complex than isovalent ones as preservation of charge balance is in this case kinetically more challenging because a different number of host and guest cations must be exchanged to keep charge neutrality (e.g., three Cu⁺ cations must be extracted to allow the incorporation of one In³⁺ or Ga³⁺ cation). Aliovalent CE involving Cu⁺ has been extensively investigated because the small charge and high solid-state diffusion rates of Cu⁺ ions make both their incorporation into and extraction from NCs facile and fast. This makes copper chalcogenide NCs attractive not only as templates for other binary, multinary, or hetero-NCs that cannot be easily obtained by direct routes (e.g., CuInS₂,^{16,28,30,33,37,45} CuInSe₂,^8,49,50 Cu₄SnS₄,^19,51 Cu_2–xSe/ZnSe,⁵² ZnS/Cu_1.8S,^28,53etc.) but also as intermediates in sequential CE reactions, making it possible to synthesize NCs and hetero-NCs that would otherwise remain inaccessible (e.g., PbS NRs from CdS NRs by Cd²⁺ for Cu⁺ followed by Cu⁺ for Pb²⁺ CE,⁵ wurtzite ZnSe/ZnS and CuInSe₂/CuInS₂ core/shell NRs from CdSe/CdS core/shell NRs^18,54). As a result of this extensive research, the thermodynamics and kinetics of aliovalent CE reactions involving Cu⁺ are reasonably well-understood and known to depend on many variables: presence of Cu-extracting ligands in solution,^5,6,8 leaving ability of the ligands bound to the incoming guest Mⁿ⁺ cation,³⁷ concentration of Cu⁺ vacancies,^52,55 valence and diffusion rate of the incoming guest Mⁿ⁺ cation,^8,28,30 crystal structure of the template Cu_2–xS NCs,^8,45 and miscibility of the parent and product phases.⁸ As we will discuss below, the results presented above unravel one more crucial parameter governing the kinetics of CE reactions: the activated complex that must form at the surface of the template NC when a direct place exchange reaction is used (i.e., when the Cu-extracting ligand is bound to the guest heterocation).

As previously demonstrated by Buhro and co-workers,³⁷ the aliovalent Cu⁺ for In³⁺ exchange in Cu_2–xS NCs is in the reaction-limited regime. The incorporation of In³⁺ is preceded by the adsorption of the InX₃ precursor on the NC surface. The displacement of the X^– ligand is proposed to occur by nucleophilic attack of lattice S^2– ions on the adsorbed InX₃ precursor.³⁷ The height of the energy barrier for this reaction is given by the leaving-group ability of the X^– ligand.³⁷ We add that when a direct place exchange reaction is promoted by using a TOP–InCl₃ complex, the energy barrier is lowered by the formation of an incipient bond between the P donor group and a Cu⁺ ion in the vicinity of the S^2– ion responsible for the nucleophilic attack on the In–Cl bond. This makes the reaction rates faster and allows for a direct place exchange between the incoming In³⁺ guest cation and one outgoing Cu⁺ cation, while facilitating extraction of two additional Cu⁺ ions as neutral CuCl units. However, the formation of such an activated complex imposes constraints on the orientation of the binding TOP–InCl₃ with respect to the surface Cu⁺ and S^2–. Nevertheless, in the case of Cu⁺ for In³⁺ CE, these constraints are not very strict because the activated complex can follow only two possible reaction pathways: CE or desorption without reaction, in which case it may bind again in the proper orientation later.

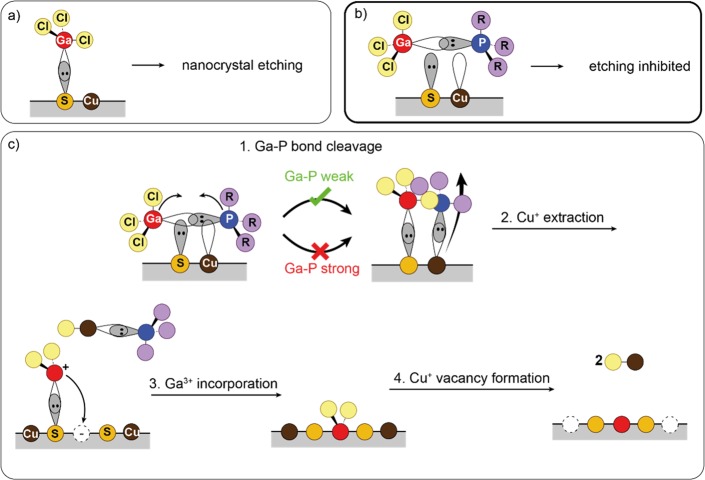
In the case of Cu⁺ for Ga³⁺ CE, the constraints imposed on the activated complex are more severe because GaCl₃ is a much stronger Lewis acid than InCl₃, therefore being capable of extracting lattice S^2– from the template Cu_2–xS NCs (Ga–S = 393 kJ/mol, In–S = 313–316 kJ/mol),⁵⁶ leading to etching rather than CE (Figure 7a), as demonstrated above (Figures 2 and 3). Complexation of GaCl₃ with TOP suppresses the NC etching but does not lead to CE. This demonstrates that the activated complex formed upon adsorption of GaCl₃–TOP on the NC surface effectively weakens the interaction between Ga and the lattice S^2– and also prevents interaction between the P donor head and the Cu⁺ ions (Figure 7b). In contrast, both GaCl₃–TPP and GaCl₃–DPP result in successful Cu⁺ for Ga³⁺ CE. All three ligands (TOP, TPP, DPP) are bound to GaCl₃ through the lone pair on the phosphorus atom and an empty sp³ orbital of gallium.^48,57,58 To extract Cu⁺, the phosphine acts as Lewis base and binds to Cu⁺ through the same lone pair. In order for the phosphine to bind to Cu⁺, while still preventing etching by attack of the Ga³⁺ to lattice S^2– ions, the activated complex at the NC surface (Figure 7c) must be such that the Cu–P bond formation and the Ga–P bond breaking occur simultaneously (Figure 7c, steps 1–3) and are followed by the immediate place exchange between Cu⁺ and Ga³⁺. We attribute the higher CE reactivities of the GaCl₃–TPP and GaCl₃–DPP to a more favorable geometry of the activated complex formed upon their adsorption on the surface of the template Cu_2–xS NCs, as well as a weaker Ga–P bond compared to GaCl₃–TOP. In GaCl₃–TPP and GaCl₃–DPP, the Ga–P bond is weaker than that in GaCl₃–TOP (see Table 1), fulfilling the conditions for a fast place exchange between Ga³⁺ and Cu⁺, while still making the competing reaction between GaCl₃ and the lattice S^2– ions less likely (Figure 7c, steps 1–3). We note that the Cu⁺ for Ga³⁺ place exchange is thermodynamically favored as it results in the formation of two new bonds that are stronger than the initial ones (viz., the Cu–P bond in the Cu–phosphine Lewis acid–base adduct, which is favored because Cu⁺ is a much softer Lewis acid than Ga³⁺, η = 6.28 and 17 eV, respectively,³² and the Ga–S bond, which has a bond strength of 393 kJ/mol while the enthalpy of formation of Cu₂S is only −79.5 kJ/mol⁵⁹). Nevertheless, some degree of etching still occurs as the NCs reacted with GaCl₃–TPP and GaCl₃–DPP are smaller than the template NCs (viz., 10.8 ± 1.0, 11.1 ± 1.1, and 12.3 ± 1.0 nm, respectively, Supporting Information, Figure S1). The observed shrinkage (12.2 and 9.76%, respectively) is too large to be attributed to a decrease in unit cell volume alone (see discussion on crystal lattice contraction above). The difference in reactivity between InCl₃–TOP and GaCl₃–TOP as CE reactants may be due to the fact that In³⁺ exhibits three-, four-, five-, and six-coordination, whereas Ga³⁺ is limited to three- and four-coordination.⁵⁷ InCl₃–TOP has thus more degrees of freedom to rearrange itself at the nanocrystal surface to form the Cu_2–xS–InCl₃–TOP activated complex, whereas GaCl₃–TOP does not, making the formation of the Cu_2–xS–GaCl₃–TOP activated complex subjected to more stringent orientational constraints and therefore less likely.

Figure 7.

Schematic depiction of the Cu⁺ for Ga³⁺ cation exchange reaction in Cu_2–xS nanocrystals. (a) Free GaCl₃ reacts as a Lewis acid, extracting S^2–, leading to etching of the nanocrystals. (b) Extraction of S^2– is inhibited when GaCl₃ is complexed with a phosphine ligand. (c) Successful cation exchange involves four steps: (i) cleavage of the Ga–P bond at the Cu_2–xS nanocrystal surface, at which point Ga–S and P–Cu bonds are made simultaneously; (ii) extraction of Cu⁺ by the phosphine; (iii) subsequent incorporation of Ga³⁺ into the nanocrystal; and (iv) reaction of remaining Cl^– with Cu⁺, extracting two additional Cu⁺ ions, completing the exchange.

As mentioned above, the steric demands of all three phosphines used in the present work are essentially the same (viz., 128° for DPP and TPP, 132° for TOP),⁴¹ and therefore, steric effects are not expected to play a significant role in the outcome of the cation exchange reactions. However, Tolman cone angles are just a first approximation as they do not take into account the effect of different M–P bond lengths, different metal centers, and the overall interaction with other ligands coordinated to the same metal center.^43,60,61 Therefore, actual cone angles obtained from X-ray structural data (the so-called solid cone angles) typically deviate from the Tolman cone angles, varying over a wide range depending on the nature of the metal center and bond length (shorter bonds result in larger cone angles).⁶⁰ For example, the solid cone angles determined for triphenylphosphine complexes range from 129 to 168°,⁶¹ whereas the Tolman cone angle of triphenylphosphine is 145°.^41,43 In the case of Ni complexes, a slightly larger solid cone angle has been reported for TPP with respect to DPP complexes (135 and 124°, respectively),⁴³ consistent with the bulkier nature of the former (containing three phenyl groups) with respect to the latter (which contains only two phenyl groups). If the impact of steric effects on the outcome of the cation exchange reactions were significant, one would expect a difference between the reactivity of the complexes using TPP and DPP as ligands, in contrast with our experimental data, which show that GaCl₃–TPP and GaCl₃–DPP have similar reactivities. This implies that the kinetics of the cation exchange reactions studied in our work are primarily dictated by the electronic properties of the phosphine ligands used, which determine the Ga–P bond strength of the resulting Lewis acid–base adduct complexes with GaCl₃ and the geometry of the activated Cu_2–xS–GaCl₃–L complex that forms at the surface of the Cu_2–xS NC at the onset of the cation exchange reaction. After the place exchange between the outgoing Cu⁺ and the incoming Ga³⁺ cations has taken place, the two chlorides still bound to the incorporated Ga³⁺ cation will react with two neighboring Cu⁺ cations, extracting them from the NC surface as neutral CuCl units, which are highly soluble in the apolar reaction medium used in our experiments (Figure 7c, step 4). This likely increases the thermodynamic driving force of the overall CE reaction both entropically and enthalpically as two more chemical species are released in solution and solvated.^5,6,8 The two Cu⁺ vacancies left will further promote the CE reaction by allowing more Cu⁺ cations to diffuse to the surface, while allowing the incorporated Ga³⁺ guest cation to diffuse inward. As previously shown for CE reactions in copper chalcogenide NCs, the CE rates increase with increasing concentration of Cu⁺ vacancies.^52,62

Cu⁺ for Ga³⁺ Exchange in Luminescent CuInS₂ NCs

To illustrate the general applicability of the findings presented above, we used GaCl₃–DPP to convert luminescent CuInS₂ (CIS) NCs into (Cu,In,Ga)S₂ (CIGS) NCs with much brighter photoluminescence (see Methods for details). The parent CIS NCs have an indium-rich composition with a Cu/In ratio of 0.68 ± 0.008:1. EDS analysis of the product NCs gives a Cu/Ga/In ratio of 0.20 ± 0.001:0.16 ± 0.001:1, indicating that Cu⁺ ions are exchanged for Ga³⁺. These cation ratios imply that the charge balance is preserved through the CE reaction, as the relative concentration of Ga ions multiplied by their charge of +3 exactly corresponds to the decrease in Cu concentration (with charge +1; 0.16 × 3 = 0.48; 0.68–0.20 = 0.48). Interestingly, the size (∼5.5 nm) and pyramidal shape of the CIS NCs are preserved in the product CIGS NCs (see Figure 8a,d), despite the removal of a significant amount of cations from the NC. Fast Fourier transform (FFT) analysis of the high-resolution TEM images allows determination of the lattice spacings, being 0.18, 0.21, and 0.34 nm before and after the reaction (i.e., they are not significantly changed by the CE reaction). However, analysis of the ED patterns shows a shift to higher q values (Figure 8e), indicating a small contraction of the unit cell. This contraction is consistent with the exchange of the relatively large Cu⁺ for the relatively small Ga³⁺ (r_Cu⁺ = 60 pm, r_Ga³⁺ = 47 pm).³¹

Figure 8.

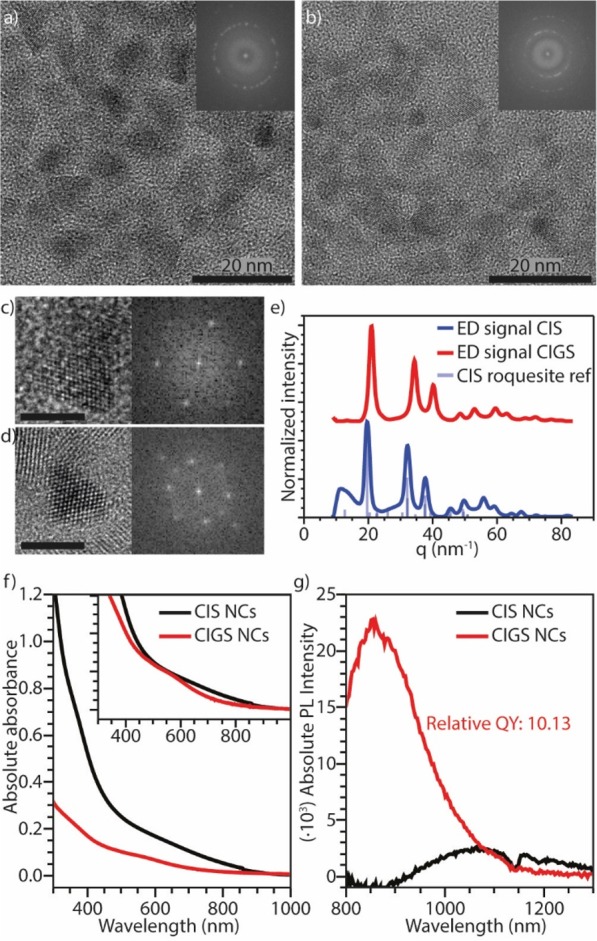
Cu⁺ for Ga³⁺ cation exchange in luminescent CIS NCs. (a) High-resolution TEM image of the parent CIS NCs. The inset shows the FFT of the image. (b) High-resolution TEM image of the product CIGS NCs after reaction; the inset shows the FFT of the image. (c,d) Enlarged TEM image of single NCs before (c) and after (d) the Ga³⁺ for Cu⁺ CE reaction, with the corresponding FFTs. Both scale bars correspond to 5 nm. (e) Azimuthally integrated ED patterns of the parent CIS NCs and product CIGS NCs, and bulk roquesite CIS X-ray diffraction reference pattern (JPCDS PDF-card 00-047-1372). (f) Absorption and (g) PL spectra of the parent CIS NCs and product CIGS NCs. The inset in (f) shows the normalized absorption spectra. The PL quantum yield of the product CIGS NCs is at least 10 times higher than that of the parent CIS NCs. The dip in the PL spectrum around 1150 nm is caused by absorption of emitted light by toluene, which was used as solvent.

The optical properties of the template CIS NCs and the product Ga-containing (CIGS) NCs are shown in Figure 8f,g. Both the absorption (Figure 8f) and photoluminescence (PL, Figure 8g) spectra show a blue shift after the CE reaction, indicating a widening of the band gap. This can be attributed to either an increase in quantum confinement due to a smaller effective CIS core size,^2,33 in case a CIS/CIGS core/shell NC is formed, or by the intrinsic increase in band gap,^63,64 in case a homogeneous CIGS alloy is formed, as the band gap of bulk CuGaS₂ is larger than that of CuInS₂ (2.50 and 1.55 eV, respectively).¹⁻³ Our results, however, do not allow a distinction between the two cases to be made. The PL quantum yield (QY) of the product CIGS NCs increases by 1 order of magnitude in comparison to that of the parent CIS NCs (Figure 8g). Such an increase in PLQY could originate from a strong enhancement of the radiative recombination rates, from elimination of nonradiative recombination pathways, or from a combination of both. Considering that similar PLQY enhancements have been previously observed upon shelling of CIS NCs with both ZnS and CdS, and attributed to passivation of nonradiative recombination centers at the surface,^1,65−67 it is likely that the higher PLQY of the CIGS NCs obtained by cation exchange is also due to improved surface passivation. It is interesting to note that PL of CIGS NCs is generally not reported,^26,68 suggesting that the exciton recombination in these materials tends to be dominated by nonradiative decay pathways, in striking contrast to the (Cu-poor) CIGS NCs prepared in our work by postsynthetic Cu⁺ for Ga³⁺ cation exchange in CIS NCs. The scarce literature on the PL of CIGS NCs makes it difficult to unambiguously identify the radiative recombination mechanism in these materials. However, their large global Stokes shift and broad PL peak suggest that, similar to CIS and other I–III–VI₂ NCs, the PL in these nanomaterials most likely originates from the radiative recombination of a delocalized conduction band electron with a hole localized at a Cu(I) ion.⁶⁹ Time-resolved spectroscopic measurements could provide additional insights into the origin of the radiative recombination in these nanomaterials but are beyond the scope of the present work. It should be noted that the PL of these Pb- and Cd-free NCs is centered in the NIR biological window.⁶⁵ This, in combination with their high PLQY, makes them promising candidates for bioimaging applications. Most importantly, the results discussed above show that the CE mechanism proposed in the present work is widely applicable.

Conclusions

Our work shows the importance of reactant chemistry in aliovalent cation exchange reactions in Cu_2–xS nanocrystals. Noncomplexed GaCl₃ reacts as Lewis acid, extracting S^2– from the nanocrystals, thereby etching them. Etching is inhibited when GaCl₃ is bound to a phosphine ligand in a GaCl₃–L complex (L = trioctylphosphine, triphenylphosphite, and diphenylphosphine). GaCl₃–TOP was found to be unreactive, whereas GaCl₃–TPP and GaCl₃–DPP lead to successful exchange of Cu⁺ for Ga³⁺, converting the parent Cu_2–xS nanocrystals into CuGaS₂ nanocrystals. This is rationalized by considering that the activated Cu_2–xS–GaCl₃–L complex that forms at the surface of the nanocrystal upon adsorption of the GaCl₃–L complex must allow for simultaneous Ga³⁺ insertion and Cu⁺ extraction, while preventing S^2– extraction. This requirement is only fulfilled by activated complexes in which the Ga–P bond is sufficiently weak. DFT calculations show that the Ga–P bond strength decreases with increasing electron-withdrawing nature of the side groups of the phosphine ligand. Our findings highlight several factors (viz., Lewis acidity, influence of ligand electronic properties on reactivity) which need be taken into account when designing cation exchange protocols. Finally, we showed that the mechanism proposed here is generally applicable by using GaCl₃–DPP to convert CuInS₂ nanocrystals into Cu-poor (Cu,Ga,In)S₂ nanocrystals with an increased photoluminescence quantum yield in the NIR spectral window.

Methods

Materials

Copper(II) sulfate pentahydrate (CuSO₄·5H₂O, 99.995%), oleic acid (OA, tech., 90%), 1-dodecanethiol (DDT, ≥98%), oleylamine (tech., 70%), gallium(III) chloride (GaCl₃, anhydrous, beads), trioctylphosphine (90%), diphenylphosphine (98%), triphenylphosphite (97%), indium(III) acetate (In(Ac)₃, 99.99%), copper(I) iodide (CuI, 98%), anhydrous methanol, anhydrous butanol, and anhydrous toluene were all purchased from Sigma-Aldrich and used as supplied, except for OA and OLAM, which were degassed prior to use.

Synthesis of Cu_2–xS Bifrustum Nanocrystals

Cu_2–xS bifrustum nanocrystals were prepared according to the method described in the literature.¹⁶ Typically, 0.203 g of CuSO₄·5H₂O, 6 mL of OA, and 7.5 mL of DDT were brought into a three-neck round-bottom flask, connected to a Schlenk line. Under constant stirring and nitrogen atmosphere, the mixture was heated to 200 °C at a rate of about 30 °C/min. After reaction for 2 h at 200 °C, the mixture was allowed to cool to approximately 110 °C, when it was quenched by injection of 5 mL of toluene. The product was precipitated by addition of a mixture of methanol and butanol as nonsolvent and isolated by centrifugation at 2500 rpm for 10 min. The supernatant was removed, and the residue was redispersed in toluene. The mass of product was estimated by weighing the empty sample vials prior to sample retrieval and after removal of the supernatant. The amount of toluene used to redisperse the particles was chosen such that a concentration of approximately 20 g/L was obtained.

Preparation of Cation Exchange Precursors

Ga– and In–phosphine precursors were prepared in a way similar to our previously reported method.¹⁸

InCl₃–TOP was prepared in a N₂-filled glovebox, by addition of 1.250 mL (2.8 mmol) of TOP to an equimolar amount (0.620 g) of InCl₃, followed by heating to 50 °C under constant stirring. The resulting turbid, white, viscous liquid was diluted by addition of 1.250 mL of toluene.

GaCl₃–TOP was prepared in a N₂-filled glovebox, by addition of 0.500 mL (1.12 mmol) TOP to an equimolar amount (0.197 g) of GaCl₃, followed by heating to 50 °C under constant stirring, yielding a transparent, orange, viscous liquid.

GaCl₃–DPP was prepared in a N₂-filled glovebox, by addition of 0.815 mL (4.683 mmol) DPP to an equimolar amount (0.8246 g) of GaCl₃, followed by heating to 50 °C under constant stirring. After a few minutes, an opaque, white, viscous liquid formed. Over the course of several hours, the liquid changed into an opaque, white, crystalline solid, which was dissolved in 10 mL of toluene at 100 °C.

GaCl₃–TPP was prepared in a N₂-filled glovebox, by addition of 1.125 mL (4.281 mmol) TPP to an equimolar amount (0.7538 g) of GaCl₃, followed by heating to 50 °C under constant stirring. After a few minutes, an opaque, white, crystalline solid formed, which was dissolved in 10 mL of toluene at 100 °C.

GaCl₃ cation exchange precursor was prepared in a N₂-filled glovebox, by making a 1 mol/L (176.08 g/L) solution of GaCl₃ in toluene, resulting in a transparent, bright green liquid. It was found that the solution degraded over time, even when stored under inert atmosphere. Degradation was indicated by a change of color from bright green to dark red. In all reactions with GaCl₃ as precursor, a fresh batch of precursor was used.

Cation Exchange in Cu_2–xS Bifrustum Nanocrystals

The cation exchange reactions were performed following the method reported in ref (18) inside a N₂-filled glovebox. The equivalent of 0.2 mmol cation exchange precursor (0.200 mL of InCl₃–TOP, 0.100 mL of GaCl₃–TOP, 0.425 mL of GaCl₃–DPP, 0.465 mL of GaCl₃–TPP, 0.200 mL of GaCl₃ solution) was placed in a vial. Toluene was added to make the total reaction volume after addition of the NC dispersion 2.700 mL (added volume: with InCl₃–TOP, 2.000 mL; with GaCl₃–TOP, 2.100 mL; with GaCl₃–DPP, 1.775 mL; with GaCl₃–TPP, 1.735 mL; with GaCl₃, 2.000 mL). The mixture of toluene and cation exchange precursor was heated to the reaction temperature (100 °C with InCl₃–TOP, GaCl₃–TOP, GaCl₃–DPP, GaCl₃–TPP and 30 °C with GaCl₃) under constant stirring at 400 rpm. Once the desired temperature was reached, 0.500 mL of parent NC dispersion (equivalent to approximately 10 mg of parent particles) was swiftly injected. The reaction was stopped (reaction time: with InCl₃–TOP, overnight; with GaCl₃–TOP, overnight; with GaCl₃–TPP, 60 min; with GaCl₃–DPP, 60 min; with GaCl₃, 15, 30, 60, 120, and 300 min) by removing the vial from the heater and quenched by the addition of methanol and butanol as nonsolvents. All samples were washed at least twice prior to analysis, by addition of methanol and butanol as nonsolvent, centrifugation and removal of the supernatant. Finally, the particles were redispersed in toluene.

Cation Exchange under Milder Reaction Conditions with GaCl₃–DPP

To prevent particle agglomeration, the reaction of Cu_2–xS nanocrystals with GaCl₃–DPP was also performed under milder reaction conditions. This reaction was performed at half the scale of the reactions discussed above, inside a N₂-filled glovebox. To this end, 0.1 mmol (0.210 mL) GaCl₃–DPP, 0.860 mL of toluene, and 0.025 mL of OLAM were placed in a vial. The mixture was heated to 50 °C, under constant stirring at 400 rpm. Once the desired temperature was reached, 0.250 mL of parent NC dispersion (equivalent to approximately 5 mg of parent particles) was swiftly injected. The reaction was stopped by removing the vial from the heater and quenched by the addition of methanol and butanol as nonsolvents. The product was washed twice prior to analysis, by addition of methanol and butanol as nonsolvent, centrifugation, and removal of the supernatant. Finally, the particles were redispersed in toluene.

Synthesis of CuInS₂ NCs

For the synthesis of luminescent CuInS₂ (CIS) NCs a protocol reported earlier by Li et al.(66) was adapted. Briefly, 297 mg of In(Ac)₃, 191 mg of CuI, and 5 mL of DDT were mixed and degassed under vacuum for 1 h at 80 °C. The reaction mixture was then heated under N₂ flow to 230 °C and allowed to react for 100 min. The reaction was stopped by removing the heating mantle. The NCs were precipitated with a methanol/butanol 1/1 mixture and, after centrifugation and decanting the supernatant, dispersed in 10 mL of toluene.

Cation Exchange in CuInS₂ NCs

CIS NCs (0.250 mL) in toluene were diluted in a vial with 1 mL of toluene and mixed with 0.1 mL of DDT (extra ligand) and 0.1 mL of GaCl₃–DPP (prepared as described above, however, not dissolved in toluene), which was melted at a heating plate with a plate temperature of 100 °C. The vial containing this mixture was placed on the heating plate with T_plate = 100 °C for 30 min, after which the vial was removed and the NCs were precipitated with a methanol/butanol 1/1 mixture and, after centrifugation and decanting the supernatant, dispersed in 0.2 mL of toluene.

Optical Spectroscopy

Samples were prepared by placing a diluted dispersion of nanocrystals in toluene in a quartz cuvette with 10 mm path length. Absorption spectra were measured using a PerkinElmer Lambda 16 UV–vis–NIR spectrometer. Photoluminescence spectra were measured on an Edinburgh Instruments FLS920 spectrofluorimeter equipped with a Hamamatsu R5509-72 PMT with a monochromator grated at 1200 nm. A 900 W Xe lamp was used as the excitation source.

Transmission Electron Microscopy

TEM images were recorded on Thermo Fisher Scientific (formerly Philips/FEI) Tecnai 10, Tecnai 12, and Tecnai 20 electron microscopes. TEM samples were prepared by drop-casting a dispersion of particles in toluene onto a copper TEM grid, with a carbon-coated polymer support film.

Energy-Dispersive X-ray Spectroscopy

EDS measurements were performed on Thermo Fisher Scientific Tecnai 20F and Talos F200X electron microscopes using Tecnai Imaging and Analysis software. Sample preparation was similar to the preparation of TEM samples. In all cases, aluminum TEM grids were used. A low-background sample holder was used. Measurements were performed on areas with >500 nanoparticles. Discussed elemental compositions are normalized to the stoichiometric sulfur contents.

Elemental Mapping

Elemental mapping was performed on a Talos F200X electron microscope equipped with a 200 kV XFEG. X-ray detection was done using four symmetrically placed SuperX-EDX detectors. Imaging was performed in high-angle annular dark-field scanning transmission electron microscopy mode, with a current of 700 pA using a Fischione Instruments HAADF detector. Obtained data were analyzed using Bruker Esprit software.

HAADF-STEM Tomography

Tilt series for HAADF-STEM tomography were acquired with a FEI Tecnai Osiris operated at 200 kV in combination with an advanced tomography holder from Fischione Instruments and the FEI XPlore3D acquisition software. Tilt series consisting of 31 HAADF-STEM images were acquired with tilt increments of 5° over a range of ±75°. Alignment of the data was carried out using the FEI Inspect3D software package. The reconstruction was performed using the simultaneous iterative reconstruction technique, with 25 iterations, implemented in Inspect3D. Amira (Visage Imaging GmbH) was used for the visualization of the reconstructed volume.

Electron Diffraction

Due to the large amount of sample required for X-ray diffraction (XRD) measurements and low signal-to-noise ratio in XRD measurements for the samples presented in this work, ED was used instead to determine the crystal structure and crystallinity of the samples. ED patterns were measured on a Tecnai 12 electron microscope with an acceleration voltage of 120 kV at a camera length of 1 m.

Data processing of ED patterns measured on Cu_2–xS NCs and the particles obtained after reaction of these parent NCs with cation exchange precursors was performed as follows: measured two-dimensional patterns were reduced to one dimension by azimuthal integration of the patterns around the center, which was manually defined for every pattern. The measured ED patterns were calibrated to a gold reference sample (Agar S106). The calibration procedure is described in detail in the Supporting Information.

Data processing of ED patterns measured on CIS NCs and the particles obtained after reaction of these parent NCs with cation exchange precursors, was performed using the Crystallographic Tool Box (CrysTBox) software,⁷⁰ which automatically performed the required steps of center localization, azimuthal integration, and calibration to a gold reference sample.

Calculated Diffraction Patterns

Diffraction patterns for the low-chalcocite Cu_2–xS and wurtzite CuGaS₂ crystal structures were calculated from the relevant crystal structures (for low-chalcocite Cu_2–xS, the crystal structure reported in ref (34); for wurtzite CGS, the crystal structure reported in ref (44)) using the Visualization for Electronic and Structural Analysis (VESTA) software program (version 3.3.9),⁷¹ using the default settings. The calculated lattice distances in real space, d, were transformed into distances in reciprocal space, q, using the equation q = 2π/d.

Comparison of the Anion Sublattices

Using the VESTA software program,⁷¹ all cations were removed from the crystal structures of low-chalcocite Cu_2–xS,³⁴ wurtzite CGS,⁴⁴ and monoclinic α′-Ga₂S₃,⁴⁶ and a supercell (consisting of multiple unit cells) was constructed. Data corresponding to a single hexagonal layer and a single ...ABAB... layer was exported for each crystal structure. The anion coordinates were translated and rotated to orient the three data sets in the same manner. In this common orientation, the x, y, and z directions correspond to the following crystallographic directions: low-chalcocite Cu_2–xS: [201],[010],[001]; wurtzite CuGaS₂: [11̅0],[110],[001]; monoclinic α′-Ga₂S₃: [010],[100],[102]. Lattice distances Δx, Δy, and Δz were measured over 5, 8, and 5 anion–anion distances in x, y, and z, respectively. Relative lattice contraction values, corresponding to a transformation of lattice A into B, are defined as 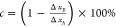(and similarly for the y and z directions).

DFT Calculations

All DFT calculations were performed using the Gaussian 09, revision D.01, software package.⁷² Geometry optimizations were performed using the B3LYP (Becke, three-parameter, Lee–Yang–Parr) functional, the relativistic Stuttgart–Dresden (SDD) pseudopotential and basis set on Ga and In and the 6-311+G(d,p) basis set on all other atoms. The structures were optimized without any symmetry restraints. Frequency analyses at the same level were performed on all calculations to verify that the obtained stationary points are in fact energy minima. Thermochemical analysis was performed using a temperature of 298.15 K. Depicted visualizations of the geometry-optimized structures were prepared using the VESTA software program.⁷¹

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acsnano.9b05337.

• NC size histograms, EDS of NCs before and after CE reaction, absorption spectra of NCs before and after CE, TEM images of NCs after reaction with GaCl₃ and GaCl₃–DPP at 100 °C, HAADF-STEM images and EDS elemental maps of Cu_2–xS NCs after reaction with GaCl₃, detailed description of PED calibration procedure (PDF)

• File showing the results of the DFT calculations (ground-state geometries and bond enthalpies for the phosphine complexes used in our work (XYZ)

Animated versions of the 3D tomographic reconstructions shown in Figure 3.

Author Present Address

^⊥ S.O.M.H.: Soft Condensed Matter/Inorganic Chemistry and Catalysis, Debye Institute for Nanomaterials Science, Utrecht University, P.O. Box 80000, 3508 TA Utrecht, The Netherlands.

Author Present Address

^¶ A.C.B.: Seaborough Research B.V., Science Park 106, 1098XG Amsterdam, The Netherlands.

Author Present Address

^# M.K.: Foseco Nederland B.V., Pantheon 30, 7521PR Enschede, The Netherlands.

Author Present Address

^▲ W.v.d.S.: Inorganic Chemistry and Catalysis, Debye Institute for Nanomaterials Science, Utrecht University, P.O. Box 80000, Universiteitsweg 99, 3584CG Utrecht, The Netherlands.

The authors declare no competing financial interest.