Abstract
Purpose
Local specific absorption rate (SAR) cannot be measured and is usually evaluated by offline numerical simulations using generic body models that of course will differ from the patient's anatomy. An additional safety margin is needed to include this intersubject variability. In this work, we present a deep learning–based method for image‐based subject‐specific local SAR assessment. We propose to train a convolutional neural network to learn a “surrogate SAR model” to map the relation between subject‐specific maps and the corresponding local SAR.
Method
Our database of 23 subject‐specific models with an 8–transmit channel body array for prostate imaging at 7 T was used to build 5750 training samples. These synthetic complex maps and local SAR distributions were used to train a conditional generative adversarial network. Extra penalization for local SAR underestimation errors was included in the loss function. In silico and in vivo validation were performed.
Results
In silico cross‐validation shows a good qualitative and quantitative match between predicted and ground‐truth local SAR distributions. The peak local SAR estimation error distribution shows a mean overestimation error of 15% with 13% probability of underestimation. The higher accuracy of the proposed method allows the use of less conservative safety factors compared with standard procedures. In vivo validation shows that the method is applicable with realistic measurement data with impressively good qualitative and quantitative agreement to simulations.
Conclusion
The proposed deep learning method allows online image‐based subject‐specific local SAR assessment. It greatly reduces the uncertainty in current state‐of‐the‐art SAR assessment methods, reducing the time in the examination protocol by almost 25%.
Keywords: convolutional neural network, deep learning, parallel transmit, specific absorption rate, subject‐specific SAR assessment, ultrahigh‐field MRI
1. INTRODUCTION
Compared with clinical systems at lower field strengths, superior SNR can be achieved with ultrahigh‐field MRI.1, 2, 3, 4, 5, 6 However, with higher magnetic field strengths, the wavelength of the RF field becomes shorter, resulting in increased signal inhomogeneity in the acquired images and higher, more inhomogeneous power deposition in the tissues.7
To achieve a greater signal homogeneity in a region of interest, parallel transmission with optimizable drive has been developed.8, 9, 10, 11, 12, 13
One of the most critical aspects that limits the application of these approaches is that they also produce a large variability of the electric fields (E‐fields) in the human body, and thereby the absorbed power in the tissue. This makes the local specific absorption rate (SAR) spatially and temporally variable with “hot spots” in various locations that are hard to predict.14, 15
During an examination, local SAR cannot be measured and is usually evaluated by numerical simulations.7, 14, 15 At this moment, it is not yet possible to perform online simulations using a subject‐specific body model. Magnetic resonance integral equation (MARIE)16 software can perform online simulations using a subject‐specific body model in a few minutes (about 5‐10 minutes). However, this is still a rather long online preparation time. Moreover, additional time to build the patient model and calculate the local SAR distribution averaged over a small sample volume is required. Therefore, the conventional, most common approach consists of performing offline electromagnetic simulations using generic body models.7, 17, 18 These simulations use numerical methods to solve the Maxwell's equations to determine the E‐field inside the model. Subsequently, the simulated E‐field and the tissue properties of the body model are used to evaluate the local SAR distribution, which is processed into Q‐matrices19, 20 and virtual observation points.21 Assuming that the investigated models are representative for the current subject, online local SAR assessment based on the actual drive scheme is performed. However, this approach does not take into account the intersubject variability.14, 22, 23 Therefore, because these models often do not well represent the features of the body under examination, this results in an inaccurate local SAR evaluation.22 Therefore, to compensate for the mismatch between simulated and real scenarios, conservative safety factors are necessary.22, 23, 24
A rigorous evaluation of subject‐specific local SAR would require the knowledge of the E‐field distribution within the subject's body and its tissue properties (electrical conductivity and mass density), all averaged over a small sample volume 10 g of tissue.25 Unfortunately, this information is not accessible during an MRI examination. An alternative to the conventional approach could be to use accessible MRI data to indirectly determine local SAR values.
The possibility of determining local SAR using mapping has been demonstrated.26 Indeed, electric and magnetic fields are related by the Maxwell's equations, and quantitative imaging of dielectric properties of tissue can be theoretically obtained from complex maps using electric properties tomography.27, 28
Undoubtedly, the complex maps still must contain relevant information. However, models derived from electromagnetic theory relating and SAR are not straightforward. All attempts so far have made by simplifying assumptions, such as assuming a negligible z‐component of the magnetic B1 field,26 which severely limits the applicability.
In this work we aim to introduce a data‐driven approach in which a convolutional neural network (CNN) is trained to learn a mapping from a complex field to a local SAR distribution without making assumptions on homogeneity of the medium or z‐components of the B1 field.
Convolutional neural networks have shown to be very powerful tools that are able to extrapolate and learn “surrogate models” to map complex relations in multidimensional data.29, 30, 31 Recently, methods based on deep learning techniques were presented for biomedical applications,32, 33, 34 and generative adversarial networks35 have achieved impressive results for the solution of image‐to‐image translation problems.36, 37, 38, 39 In this work, we present a deep learning–based method for image‐based subject‐specific local SAR assessment.40 In this data‐driven approach, a generative adversarial network is trained to learn a “surrogate SAR model,” to map the relation between subject‐specific maps and the corresponding local SAR from a large number of simulated and SAR distribution of various human pelvis models.
This method requires neither specific additional hardware, nor the execution of complex online calibration procedures. All required information is inherently included in the complex maps.
The proposed method is applied to 7T prostate imaging using a multitransmit array of 8 fractionated dipole antennas.6, 22, 41 The results demonstrate that CNNs can properly learn the relations between complex maps in nonhomogeneous media and the corresponding local SAR distributions. In particular, we show that the proposed method allows online image‐based subject‐specific local SAR assessment, which greatly diminishes the uncertainty in current state‐of‐the‐art SAR assessment procedures, allowing considerable time savings.
2. METHODS
To learn a surrogate SAR model, the proposed CNN was trained with simulated and local SAR distributions for 23 custom‐made pelvis models.22 The complex maps serve as input, and the corresponding 10‐g averaged local SAR (SAR10g) distributions serve as the ground‐truth output.
The performance of the proposed deep learning method was evaluated by in silico and in vivo validation and compared with the conventional method (use of a generic body model).
2.1. Synthetic data generation
Because local SAR cannot be measured directly, it is usually evaluated by simulations. The finite‐difference time‐domain method is used widely for solving the Maxwell's equations to determine the electromagnetic fields inside the patient, in whom subsequent postprocessing is performed to calculate the local SAR distribution.15 To build the data samples, we have used our database of 23 subject‐specific models22 with an 8–transmit channel body array for 7T prostate imaging6, 41, 42 (Figure 1A). The data of the volunteers included in our database are reported in Supporting Information Table S1. For each model and every array channel, E‐field and ‐field distributions were determined using the finite‐difference time‐domain simulations (Sim4Life; ZMT, Zürich, Switzerland). A total of 250 different and SAR10g distributions were calculated for each model using 250 different drive vectors, all with uniform amplitude (8 × 1 W input power) and random phase settings (uniformly distributed in the interval [−π, π]).
Figure 1.
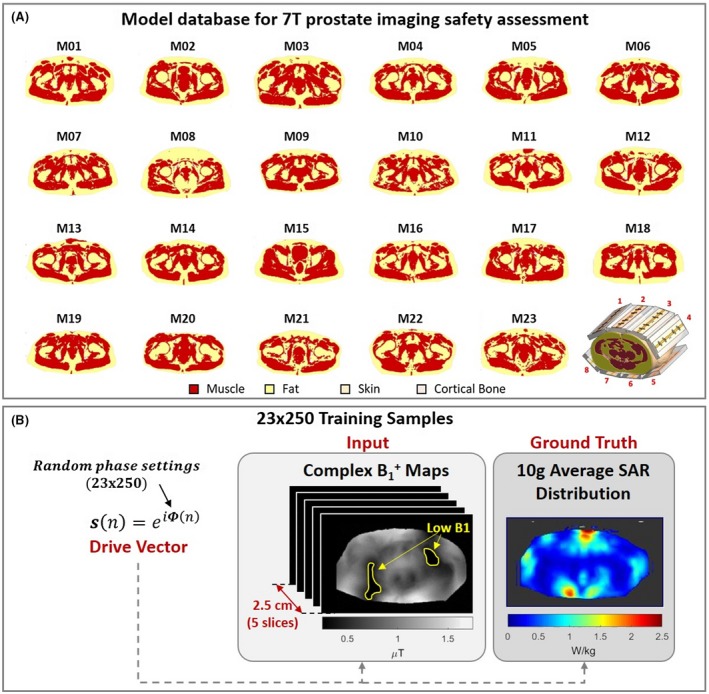
A, Twenty‐three body models (muscle, fat, skin, and cortical bone) are present in the database and the body array setup for prostate imaging at 7 T. B, Each of the 23 × 250 training samples consists of an input block of 5 complex maps and 1 ground‐truth 10‐g averaged local SAR (SAR10g) distribution. Regions of low (<0.25 µT) are excluded, as they provide inaccurate data in measured maps
For each model m (out of 23 models), and each drive setting s (out of 250 different drive vectors), the simulated maps of each channel n and the 10‐g averaged Q‐matrices (Q 10 g)19, 20 were processed to produce random maps and corresponding SAR10g distributions, as follows:
| (1) |
and
| (2) |
where r defines the spatial location, and Nch. is the number of transmit channels (Nch. = 8).
To transform the simulation data into maps similar to those that can be realistically acquired, the relative transmit phase distributions were obtained with respect to the first channel, and Gaussian noise comparable to the noise observed in the measured complex maps) was added to the real and imaginary part of the maps. Furthermore, the dual‐refocusing echo acquisition mode (DREAM)43 ‐mapping method has a limited dynamic range and presents only a good accuracy for values between 25% and 175% (stimulated echo acquisition mode [STEAM] flip angles from 10° to 70° for a nominal flip angle of 40°). Therefore, the ‐map regions outside the range (0.25 to 1.75 μT with a nominal of 1 μT) were removed, to prevent regions with inaccurate values from producing errors in local SAR predictions (Figure 1B).
2.1.1. Data sample
Because 10 g of tissue corresponds to a cube of about 2.2‐cm dimension, the input of each data sample consists of a volume of 5 adjacent, complex transverse maps with 0.5‐cm slice thickness and the corresponding ground‐truth SAR10g distribution for the center slice (Figure 1B). Each complex map was used to produce 2 images with real and imaginary parts of the maps and 1 image with the binary body mask (1: tissue, 0: air).
-
Input (3 × 5 transverse images all centered around the center slice of the volume):
-
◦
5 images with real part of the complex maps;
-
◦
5 images with imaginary part of the complex maps; and
-
◦
5 images with body mask.
-
◦
-
Ground‐truth output (1 transverse image):
-
◦
One image with SAR10g distribution for the center slice of the volume.
-
◦
2.1.2. Synthetic training set
The simulated results were processed as described to produce 23 × 250 = 5750 unique training samples. For the studied on‐body antenna setup, the location of the maximum SAR level is located exclusively in the center slice, where the antenna feed points and the target region (prostate) are located. Therefore, the training has focused only on predicting the local SAR distribution for the center slice. However, this central slice training turned out to be applicable to off‐center slices as well, as the subsequent synthetic validation study will show.
2.1.3. Synthetic validation set
For the considered array setup (8 fractionated dipoles around the pelvis, each aligned along the z‐direction),6, 41 the relation between complex maps and SAR10g should be similar for all slices, where most of the power is absorbed. Then, the SAR prediction can be extended to more than just the central slice, even although the training was performed only for the central slice.
To validate the SAR10g assessment over the entire region where the power is absorbed, for each model and for each drive vector, an additional 40 data samples (thickness = 2.5 cm) 0.5‐cm distance from one another were produced and used for validation only. As a result, we tested the SAR prediction performance for a 20‐cm region in the longitudinal direction around the prostate.
2.2. Network architecture
Based on the results of our preliminary study,40 a conditional generative adversarial network (cGAN)37 was used in this work.
2.2.1. Conditional generative adversarial networks
This network architecture houses 2 CNNs, the generator, and the discriminator. Similar to Isola et al,37 the generator is a U‐Net29 and the discriminator is a convolutional PatchGAN classifier. Several implementations of this network are available at this moment (https://phillipi.github.io/pix2pix). The only difference in our network lies in the number of channels of the first and last layers. Because the input consists of the real and imaginary part of 5 complex maps and 5 body masks, the number of channels in the first layer is 15 instead of 3. However, there is only 1 channel in the output layer, as the output consists of 1 single 2D SAR10g distribution.
2.2.2. Loss function
During the training, discriminator D and generator G compete with each other in a min‐max optimization game. The discriminator is trained to distinguish true SAR distributions from generated SAR distributions by generator images. The generator is trained to maximize the error rate of the discriminator. The standard loss function for cGAN is formulated as follows17:
| (3) |
where x represents the input data from the training set, y is the corresponding ground truth, and z is a noise vector drawn from the probability distribution pz (typically added to try to capture the full entropy of the modeled conditional distribution).35, 37
For the proposed application, the generator was trained to produce the target output SAR10g distribution from the input maps, and the discriminator was trained to discriminate the generated SAR10g distribution from the ground‐truth SAR10g distribution.
However, in the scope of SAR10g assessment, regions with high SAR10g require higher accuracy and, in particular a peak local SAR (pSAR10g) underestimation error should be avoided or at least limited as much as possible. Therefore, 2 additional terms were added to the loss function that should produce a slight overestimation, thereby reducing the pSAR10g underestimation error as follows:
| (4) |
where is the weighted L1‐norm of the difference between the ground‐truth SAR10g distribution and the generator output, with weights w proportional to the ground truth () as follows:
| (5) |
where is the loss term to penalize the pSAR10g underestimation error (Equation 6),
| (6) |
and and are the corresponding weights of the additional loss terms.
2.3. In silico validation
2.3.1. Leave‐one‐out cross‐validation
The attainable performance of the proposed method was evaluated by performing a leave‐one‐out cross‐validation. This means that, 23 separate times, the cGAN network was trained on all of the data samples from all models except for 1 model (22 × 250 = 5500 data samples). The data samples from this remaining model were used for validation.
To validate the SAR10g assessment over the entire region where the power is absorbed, and not just in the central prostate plane, the proposed method was applied to predict the SAR10g distributions in body volumes that extend 20 cm in the caudal–cranial direction.
2.3.2. Safety factor and performance evaluation
The results of all 23 validations were combined and the normalized RMS error of the predicted SAR10g distributions and pSAR10g estimation errors were evaluated.
The statistics of the pSAR10g estimation error (mean overestimation and probability of underestimation) were used to assess the performance of the proposed approach and to quantify its benefit compared with the conventional approach (i.e., using just the generic model “Duke” of the Virtual Family44 with 77 tissues [version 3.0: voxel resolution 0.5 mm × 0.5 mm × 0.5 mm]).
Because in our previous study22 no relationship was found between measurable body features (body mass index [BMI], weight, height or body cross‐sectional area) and peak local SAR with shimmed phase setting to select the appropriate model, a single model was used as a “gold standard” conventional approach.
To avoid pSAR10g underestimation errors in the conventional approach due to intersubject uncertainty, a safety factor is usually applied to the predicted pSAR10g values. The safety factor is used to increase the predicted pSAR10g level to such an extent that underestimation will not occur. Values of 1.4 to 2 have been suggested in literature.22, 23, 24 Here, based on the large data sets we have available, we define the safety factor as
| (7) |
This rules out the possibility of underestimation for all of our investigated cases.
However, the chosen definition could unbalance the comparison based on outliers in the predicted pSAR10g values with the 2 methods. Therefore, we have also evaluated a more appropriate approach to define the safety factor that is less sensitive to outliers, the so‐called upper outer fence.45 For each investigated model m and drive setting s, the safety factor was evaluated () and, using the usual upper outer fence definition over all of these safety factors, the safety factor SFUOF was defined as follows:
| (8) |
where SFUQ is the safety factor upper quartile and SFIQR is the safety factor interquartile range.
In a previous study,22 a 99.9% certain upper bound for the pSAR10g level was presented and used to define a generic safe power limit. Therefore, the performance of the proposed approach was also compared with the performance obtained by applying this generic safety limit.
2.4. In vivo MRI validation
Four healthy volunteers who were not included in our database (BMI: 21/23/24/27 kg/m2, Supporting Information Table S1) were scanned at 7 T (Achieva; Philips Healthcare, Best, Netherlands) using an 8‐channel transmit/receive fractionated dipole array combined with 16 receive loops for prostate imaging.6, 41, 42 Written informed consent was obtained according to local institutional review board regulations. For each volunteer, the following sequences were performed (FOV = 430 × 430 × 100 mm, voxel size = 2.8 × 2.8 × 5.0 mm):
map: DREAM B1 mapping (TR/TE = 4.0/0.8 ms, STEAM flip angle = 40°);
GRE dynamic: 3D incoherent gradient echo (RF spoiled) with subsequently each transmit channel active alone (TR/TE = 5.00/1.95 ms, flip angle = 1°); and
DIXON: Multislice gradient echo (TR/TE = 10.00/2.70 ms, voxel size = 1.3 × 1.3 × 5.0 mm).
For each volunteer, 2 validation tests were performed: 1 by acquiring the maps with the default phase‐shimming set (phase‐shimming set saved in the calibration file, the same for all volunteers) and another by acquiring the maps with prostate shimmed phase settings (tailored for each volunteer).
For the in vivo validation, 2 independent pipelines were implemented. One exploits the trained network to predict SAR10g distributions based on measured complex maps. The other pipeline produces a subject‐specific model similar to Meliadò et al.22 It subsequently obtains offline simulated SAR10g distributions. These simulated SAR10g distributions will be used to validate the proposed deep learning–based method for SAR10g assessment.
2.4.1. Predicted SAR distribution
To obtain the transmit phase maps relative to the first channel, the dynamic GRE images were combined as follows (Equation 9):
| (9) |
where and are the magnitude and phase images acquired with the channel n active alone. This ensures that the relative phase of each channel with respect to channel 1 is used. Subsequently, the acquired magnitude maps and the relative transmit phase maps were combined to obtain the complex maps as follows:
| (10) |
The obtained complex maps were used to produce the input data for the trained generator to infer the SAR10g distributions (Figure 2A) as follows:
| (11) |
Figure 2.
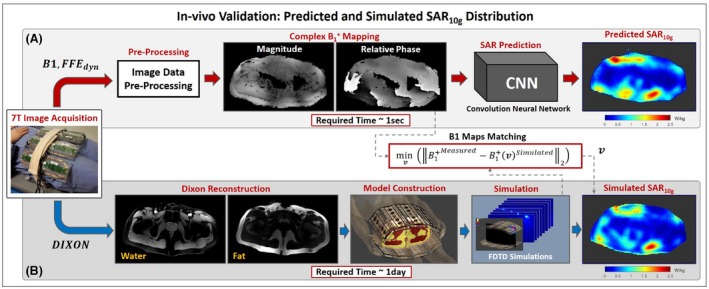
A, Pipelines to assess local SAR distribution by the trained conditional generative adversarial network network (proposed method). B, Subject‐specific model generation (muscle, fat, and skin) and offline electromagnetic field simulation (used for validation of the proposed method). Abbreviations: FDTD, finite difference time domain; FFE, fast field echo
2.4.2. Simulated SAR distribution
Following the pipeline presented in our previous study,22 the DIXON images were used to build subject‐specific 3‐tissue models (fat/muscle/skin)14, 15 of the volunteers, and electromagnetic simulations (Sim4Life; ZMT, Zürich, Switzerland) were performed.
For in vivo validation, it is not possible to have the ground‐truth SAR10g distributions. The inevitable differences between simulated and real scenarios, such as the small differences in the antenna positions, the reflected/lost power and the imperfect calibration, can make the simulated SAR10g distributions significantly different from the actual SAR10g distributions in the volunteers. However, at least the effects of the reflected/scattered and dissipated power and the imperfect calibration could be incorporated in the simulated SAR10g distribution by appropriately changing the amplitude and phase of the drive vector. The simulated SAR10g distribution was therefore tailored to be most similar to the actual SAR10g distribution by adjusting the simulated phase and amplitude settings such that agreement between simulated and measured maps was achieved. More specifically, for each validation test, the drive vector v to minimize the L2‐norm between the simulated and measured complex maps was evaluated numerically and used to calculate the reference SAR10g distribution (Figure 2B) as follows:
| (12) |
3. RESULTS
The proposed cGAN was implemented in TensorFlow46 and trained for 25 epochs (batch size 1) in about 4 hours on a GPU (Nvidia Tesla P100‐PCIe 16 GB, Santa Clara, CA).
After training, forward network evaluation takes a few milliseconds to predict a SAR10g distribution.
3.1. In silico cross‐validation
Figure 3 shows the transverse maximum intensity projection (MIP) over 41 slices of the ground truth, predicted, and error SAR10g distributions with optimized phase settings for prostate imaging for (A) the model with the highest prostate‐shimmed pSAR10g value (M01); (B) the model with the lowest prostate‐shimmed pSAR10g value (M15); (C) the model with highest BMI (28 kg/m2; M08); and (D) the model with lowest BMI (21.6 kg/m2; M22). The pSAR10g values and the normalized RMS error are reported at the top of the images. The transverse MIP of the predicted SAR10g distributions using the generic model Duke44 (BMI 22.4 kg/m2) and the corresponding error SAR10g distributions are also reported (conventional method).
Figure 3.
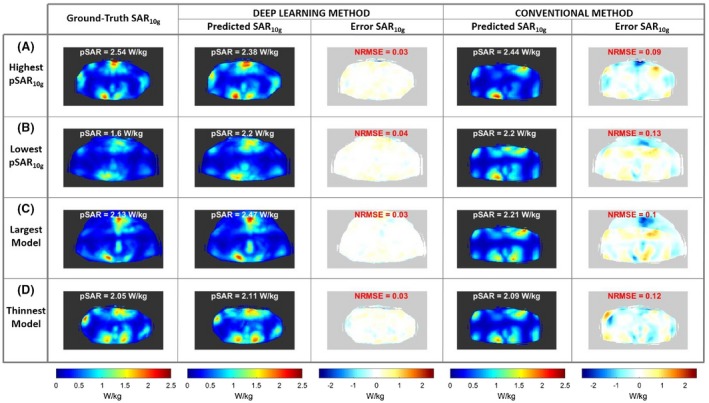
Transverse maximum intensity projection (MIP) of the ground‐truth SAR10g distributions, the predicted SAR10g distributions, and error SAR10g distributions using the deep learning method and the predicted SAR10g distributions and error SAR10g distributions using the generic model Duke (conventional method). All results are with transmit phases optimized for prostate imaging. A, Model with the highest prostate‐shimmed peak local SAR (pSAR10g) value. B, Model with the lowest prostate‐shimmed pSAR10g value. C, Largest model with body mass index (BMI) 28 kg/m2. D, Thinnest model with BMI 21.6 kg/m2. Abbreviation: NRMSE, normalized RMS error
The transverse MIP of the ground‐truth, predicted, and error SAR10g distributions for the worst pSAR10g estimation results are reported in Figure 4. Considering the proposed deep learning method, the worst pSAR10g overestimation error is 171% (predicted pSAR10g = 3.45 W/kg; ground‐truth pSAR10g = 1.27 W/kg), and it occurs for model M15 (BMI 27.4 kg/m2). The worst pSAR10g underestimation error is 28% (predicted pSAR10g = 1.62 W/kg; ground‐truth pSAR10g = 2.23 W/kg), and it occurs for model M18 (BMI 25.5 kg/m2) (Figure 4A). In contrast, using the Duke model, the worst pSAR10g overestimation error is 184% (M15) and the worst pSAR10g underestimation error is 59% (M09; BMI 22.5 kg/m2) (Figure 4B).
Figure 4.
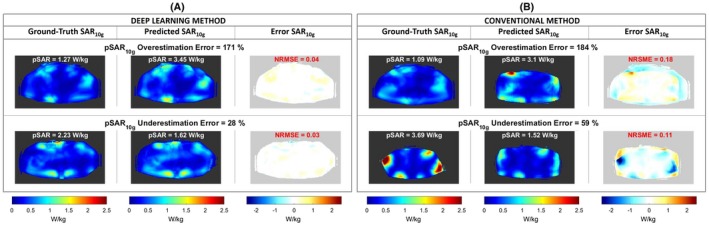
A, Transverse MIP of the ground‐truth, predicted, and error SAR10g distributions for the worst pSAR10g estimation results using the deep learning method. B, Transverse MIP of the ground‐truth, predicted, and error SAR10g distributions for the worst pSAR10g estimation results using the generic model Duke (conventional method)
A much larger image series is provided in Supporting Information Figures S1, S2, S3, and S4, where for each subject‐specific model the transverse MIP of the ground truth and predicted SAR10g distributions with phase settings for prostate imaging and for the worst pSAR10g estimation results are reported.
For the shown cases, the normalized RMS error is between 0.03 and 0.04. The normalized RMS error boxplot for each model over all considered cases is shown in Supporting Information Figure S5.
3.2. Safety factor and performance evaluation
To draw sufficiently statistical powered conclusions on the comparison of the methods (deep learning and conventional), the histograms of the pSAR10g estimation error over all data samples are reported in Figure 5. The deep learning–based pSAR10g estimation error distribution shows a mean overestimation error of 15% with 13% probability of underestimation (Figure 5A). In contrast, using the conventional method (i.e., using the virtual observation points created with the generic model Duke), the mean overestimation error is 18% and the probability of underestimation is 24% (Figure 5B).
Figure 5.
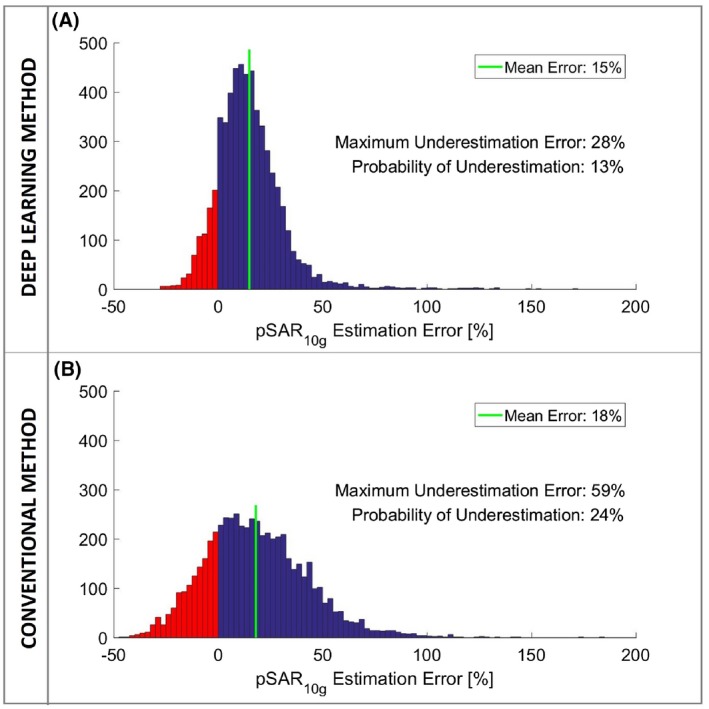
A, Histogram of the pSAR10g estimation error of the proposed deep learning method. B, Histogram of the pSAR10g estimation error of the conventional method (i.e., using the virtual observation points created with the generic model Duke)
Considering the largest pSAR10g underestimation error, the required safety factor with the proposed method is 1.38. In contrast, with the conventional method it is 2.43. The resulting safety factor for the conventional method is disproportionately large and follows from a couple of outliers. Therefore, the upper‐outer‐fence method has been used instead to arrive at more appropriate safety factors. In Figure 6A,B, the safety factor boxplots for the proposed deep learning–based method and conventional method are reported. Considering the upper outer fences, the defined safety factors are 1.36 for the proposed deep learning–based method and 1.72 for the conventional method.
Figure 6.
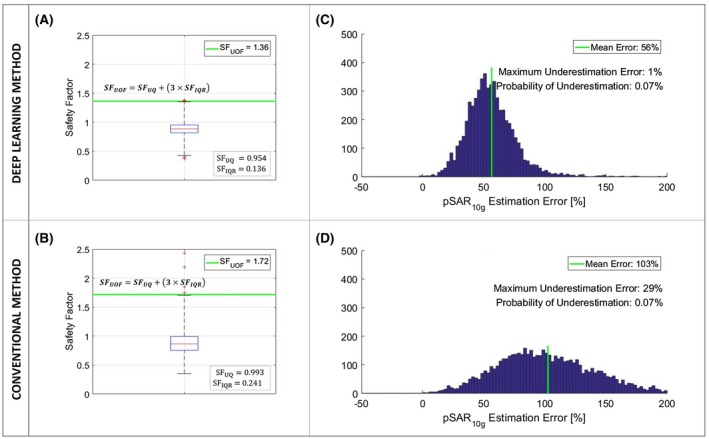
A, Boxplot of the safety factors (SFs) for the proposed deep learning method. B, Boxplot of the safety factors for the conventional method. C, Histogram of the pSAR10g estimation error of the proposed deep learning method with safety factor 1.36. D, Histogram of the pSAR10g estimation error of the conventional method with safety factor 1.72
The histogram of the pSAR10g estimation error obtained by applying the safety factor 1.36 to the predicted pSAR10g values with the deep learning method is shown in Figure 6C, whereas Figure 6D presents the histogram of the pSAR10g estimation error obtained by applying the safety factor 1.72 to the predicted pSAR10g values with the conventional method. Using the safety factors defined previously, the probability of underestimation is lower than 0.1% (0.07%) for both methods. The mean pSAR10g overestimation errors are 56% for the deep learning and 103% for the conventional method. This implies that the SAR‐limited MR sequences take 1.56 and 2.03 times, respectively, as much time as necessary. Thus, the proposed deep learning method allows on average a reduction of the scan time by 23% for SAR‐limited sequences. Note that T2‐weighted imaging is the clinical work horse for prostate imaging, and these sequences are typically SAR‐limited.
In our previous study,22 3.8 W/kg was considered a 99.9% certain upper bound for the pSAR10g values with 8 × 1 W input power and arbitrary phase settings. Using this recently defined safe upper bound, the mean pSAR10g overestimation error is 95% with 0.05% probability of pSAR10g underestimation (Figure 7).
Figure 7.
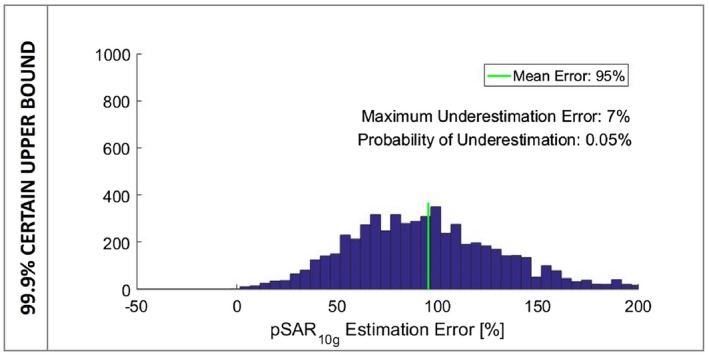
Histogram of the pSAR10g estimation error considering the 99.9% certain upper bound for the pSAR10g level (3.8 W/kg)
3.3. In vivo MRI validation
Figure 8 shows the measured and the simulated complex maps, and the predicted and simulated SAR10g distributions for each volunteer with default phase shimming set. In Figure 9 the simulated complex maps and the predicted and simulated SAR10g distributions with phase shimming set for prostate imaging are reported. All in vivo validation tests show a good qualitative and quantitative match between the predicted and simulated SAR10g distributions (error distributions are also reported in Supporting Information Figure S6). In agreement with in silico validation, before applying the safety factor, moderate pSAR10g overestimation errors are observed (between 2% and 21%). As only 4 subjects are included, only 1 pSAR10g underestimation error occurs (2%).
Figure 8.
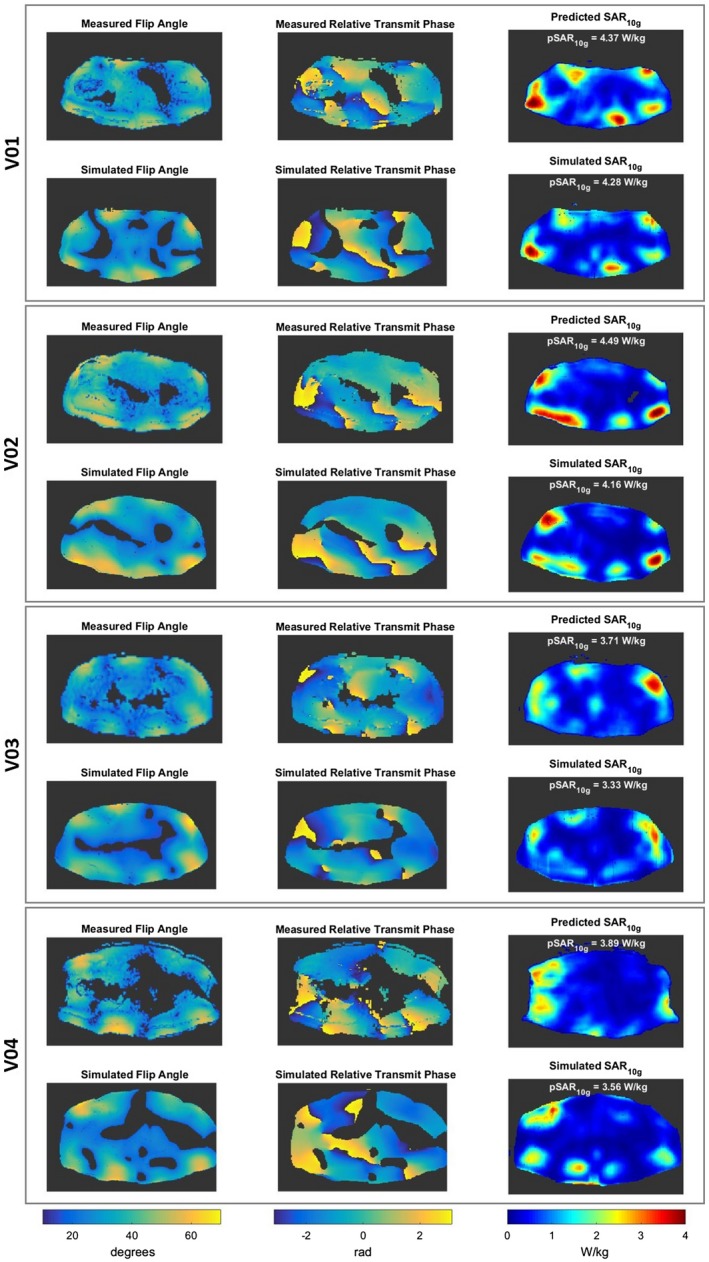
Measured and simulated flip angle maps, measured and simulated relative transmit phase maps, and predicted and simulated SAR10g distributions for each volunteer with default phase settings
Figure 9.
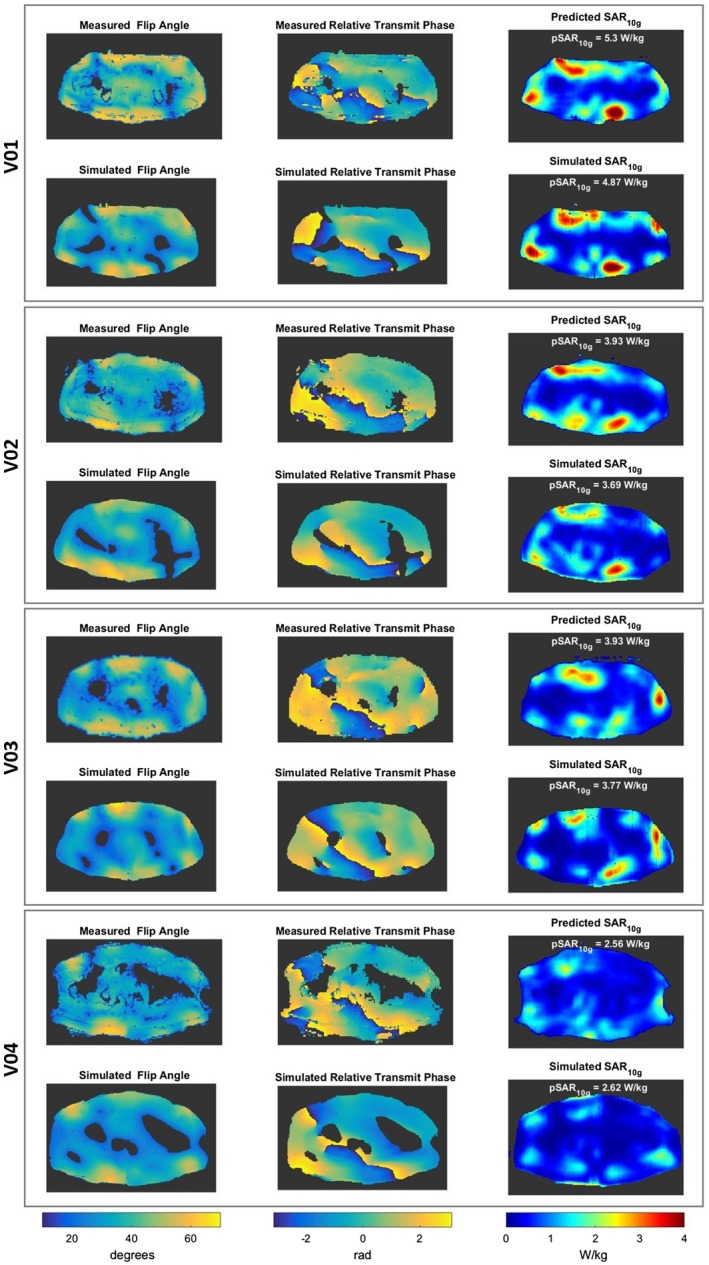
Measured and simulated flip angle maps, measured and simulated relative transmit phase maps, and predicted and simulated SAR10g distributions for each volunteer with prostate‐shimmed phase‐shimming settings
4. DISCUSSION
A new deep learning approach for subject‐specific local SAR assessment was presented. It consists of a data‐driven approach in which a CNN is trained to learn a “surrogate SAR model” to map the relation between quickly accessible MRI images (complex maps) and the corresponding local SAR distribution. The required time for the local SAR prediction with the proposed deep learning method is a few milliseconds, underlining its online local SAR assessment capability. The approach was used for SAR10g assessment of prostate imaging at 7 T with our 8‐channel fractionated dipole array, and its performance was evaluated by in silico and in vivo validation, showing a great reduction of the uncertainty compared with commonly used methods.
4.1. In silico validation and performance evaluation
In all examined cases, a very good match between the ground‐truth SAR10g distributions and the predicted SAR10g distributions were observed. The spatial SAR distribution, including most local SAR peaks, is always very well predicted for all models. Although the chosen loss function probably produces deliberate overestimation, the patterns of the predicted SAR10g distributions always match to the corresponding ground‐truth SAR10g distributions, in particular the hot spots close to the body array surface, where the near‐field effects occur. This shows that the suitability of measured alone to account for the E‐field for the considered array setup, and that CNNs can properly learn the physical relation between complex maps and SAR10g in nonhomogeneous media. Thus, the proposed deep learning method can provide a way forward to include intersubject variation in local SAR assessment.
The proposed method is also able to predict quite well the peak SAR10g values. As desired, the loss function minimization produces a little overestimation of the pSAR10g values (mean pSAR10g overestimation error of 15%). Nevertheless, some pSAR10g underestimation errors still occur, and in some cases the pSAR10g overestimation errors are greater than the acceptable threshold. Most of these pSAR10g errors are due to SAR10g peaks in very small regions near the body surface (Figure 4A).
All of these issues might be solved by using more training samples and/or a different network architecture and/or by minimizing a different loss function. Therefore, the optimization of the network and the cost function will be the subject of future work. Nevertheless, the presented results significantly exceed the performance of state‐of‐the‐art methods, allowing online subject‐specific SAR10g prediction.
It is noteworthy that some models (e.g., M03, M08, M20) present anatomical features that are unique within our database, so they were not covered by the training sets during the in silico cross‐validation. However, the prediction results for these models are comparable to the results for the well‐represented models. This could be explained if the mapping from to SAR10g requires only local information (i.e., the SAR10g at each location that is found by local information in the direct‐proximity patient size and shape are not needed for this calculation). However, based on the current data, this hypothesis cannot be verified. Potentially, patch‐based networks that work by definition on the proximal information inside the patch centered on the location of interest might generalize even better. However, this should be researched further, and the applicability of the presented method for extremely different body anatomies (e.g., obese, anorexic) cannot yet be assured.
Note that as for many existing SAR assessment methods, it is assumed that no changes occur after the local SAR distribution has been determined.
The proposed deep learning method in conjunction with the defined safety factor achieves a mean pSAR10g overestimation error of 56% with a probability of pSAR10g underestimation lower than 0.1%. If a safety factor is applied to the predicted pSAR10g with the conventional method, the resulting mean pSAR10g overestimation error is 103%, with a similar probability of underestimation. Applying the safe power limit based on the 99.9% certain upper bound for the pSAR10g level, the mean pSAR10g overestimation error is 95%, with a probability of pSAR10g underestimation lower than 0.1%. These results again confirm the large gain in SAR assessment accuracy with the presented method. Furthermore, we believe, as demonstrated by Figure 3, that a fundamental advantage of the deep learning method is that it predicts much more reliably the locations of SAR peaks compared with the conventional method that uses a generic model.
In this study, we have compared our deep learning–based SAR assessment method with a SAR prediction method using 1 generic model. Although simulations on 1 model have been used previously as a safety analysis,17, 18, 41 currently it is more common to use at least multiple models and predict peak local SAR by the maximum SAR over all models. The advantage of this method is that it will likely reduce the probability of an underestimation error; however, it will increase the mean overestimation error and therefore not likely reduce the scan time. On the other hand, the estimation error might be reduced by making use of a large database of models and have a means to select the most representative “local SAR model” for the patient being scanned. However, a preliminary study using these same 23 models has shown only very limited gains by applying such a method.22 The presented deep learning–based method does not rely on similarities between models and the patient. The expectation is that the model has truly learned the relation between the distribution and the local SAR level, based on the true patient anatomy of the patient being scanned. The library of models just acts as training data.
4.2. In vivo local SAR assessment
For the in vivo validation, offline simulated SAR10g distributions based on subject‐specific models were used as the ground truth. We tailored the simulated SAR10g distributions by driving the simulated transmit array with the drive vectors that minimized the L2‐norm between the simulated and measured complex maps. In this way, the differences due to the reflected/lost power and calibration imperfections should be compensated. However, the differences due to the inevitable small deviations in the simulated and real scenario cannot be compensated by the drive vectors. Therefore, even driving the transmit array with optimized drive vectors, the obtained simulated complex maps and SAR10g distributions may be different from the measured complex maps and the actual SAR10g distributions in the volunteers.
Nevertheless, all in vivo validation tests show a good qualitative and quantitative match between predicted and simulated SAR10g distributions. In agreement with in silico validation, moderate pSAR10g overestimation errors are observed (between 2% and 21%). Only 1 pSAR10g underestimation error occurs (2%). Note that the indicated pSAR10g levels have been obtained using a generic power limit of 2.6 W per channel that was derived from a previous statistical study.22 Using the safety factor of 1.36 as derived from the in silico cross‐validation for the deep learning–based method, the resulting predicted pSAR10g values vary between 3.5 W/kg (V04) and 7.2 W/kg (V01), which is still below the threshold of 10 W/kg. If the more accurate subject‐specific SAR10g assessment is used to increase the power limit, the resulting limits can be increased from 3.6 W (V01) to 7.5 W (V04) average power per channel. These are 39% to 187% higher than the original power restriction of 2.6 W, which illustrates the benefit of the deep learning–based method for SAR10g assessment presented in this paper.
The simulation‐based methods assume theoretical values of the dielectric properties of the tissues. However, the proposed method could potentially address differences in a given tissue's reported dielectric values, as these differences would also determine differences in the measured complex maps.
4.3. Advantages and limitations
The predicted SAR10g using the proposed image‐based method inherently includes all relevant and exam‐specific information, such as the patient anatomy, antenna position, and reflected/lost power and calibration imperfections. It does not require knowledge of the drive scheme.
All information arises from the complex maps, including only the readily accessible relative phase. This data‐driven approach exploits a priori information about the setup (which is included in the trained algorithm parameters), thus leading to a unique mapping between maps and SAR10g.
Unlike the conventional method (or any simulation‐based method), which is very sensitive to antenna (mis‐)positioning, the proposed image‐based method is robust to antenna position variations that could occur during the manual positioning (as long as they are also included in the training set).
Furthermore, the predicted SAR10g values can easily be scaled to the actual SAR10g values for sequences with similar RF waveforms and static RF shim settings. The only required information are the requested in microtesla and the duty cycle of the considered MRI sequences.
The proposed method predicts very well the spatial SAR distribution for all models in a few milliseconds. It includes intersubject variation, performs better than the commonly used method, and most likely can be applied to other coils and body regions at any field strength. However, to properly learn the intended surrogate SAR model, a specific training set is required. The relation between complex maps and SAR10g distribution is mapped only for the specific coil, body region, and field strength in the training set. It would be interesting to investigate whether such a data‐driven approach could also work for 1.5T and 3T volume transmit coils, although there will be variation in human body posture and its geometrical relation to the coil. In addition, the SAR hot spots are typically not confined to the imaging region. Quite large mapping scans may be required. The arms (when alongside the body) may not be measurable if they are too far off center. The absence of information from the arms (if these are outside the imaging region) will pose an additional challenge. Nevertheless, this application area is still worthwhile to investigate and calls for further exploratory investigations.
It is worth noting that only the x and y components of the B1 field are observable. For the considered array setup (8 fractionated dipoles around the pelvis), the z‐component of the B1 field is much less intense than the other components; thus, the SAR prediction can be extended over the entire region where the power is absorbed even though the training was performed only for the central slice (Supporting Information Figure S7).
For other coil arrays, the z‐component may not necessarily be negligible as well. Therefore, the SAR10g attributable to this component will not be negligible either. However, in this case, the relation between the z‐component and the other components and its contribution to the SAR10g is also enclosed in the training set. Note that through Gauss's law, the z‐component is related to the transverse component, so it should be a consistent relation among all of these components. It might be possible that the deep learning method will be able to learn this relation as well for the specific coil array. However, for such a coil array the training will need to be performed with a larger volume of simulated data (extending further in the +/‐ z‐direction) to include the regions where the z‐component of the B1 field is not negligible.
To calculate the SAR10g, the only required information that is nonderivable from complex maps is the tissue mass density, which has a minor influence on SAR10g level in the pelvis, where density variability is limited.
In regions with greater variability in density of tissue, such as in bone and lungs, additional tissue information types to include in the CNN input could become desirable. This could, for instance, consist of separate treating of thin cortical bones with respect to spongy bone. This would also require the recognition of these tissue types by the network. However, this should be possible as similar networks are used to predict synthetic CT based on MR images as input, such as Dixon gradient‐echo images.38 Whether this is possible for other body parts (such as the head) with many more structures, needs further investigation.
The proposed deep learning–based method could also be used to assess the SAR10g when sophisticated RF pulse design strategies are implemented.10, 19 In these cases, the complex maps for each channel have to be acquired and combined using software to produce the shimmed complex maps for each time step. Then, the SAR10g distribution for each time step can be predicted and integrated over time to assess the SAR10g for the whole designed pulse (Supporting Information Figure S8).
It is also worth noting that sophisticated RF pulse design strategies also require amplitude modulation of each channel and not only phase modulation. As shown in Supporting Information Figure S8C, for an example, spiral nonselective RF pulses designed for the model M01 (time step: 0.575 ms; ), the proposed deep learning–based method could allow local SAR assessment with amplitude modulation, even though the training was done only with phase modulation of each RF channel.
Finally, it would be worthwhile, given the current discussion, to use a thermal dose concept in RF safety monitoring to investigate whether this data‐driven approach can also be extended to predict local temperature rise or even absolute tissue temperature based on complex maps combined with surrogate thermal information of the anatomy (e.g., Dixon water/fat maps).
5. CONCLUSIONS
In this work, a deep learning–based method for subject‐specific local SAR assessment was presented. This method consists of training a CNN to learn a surrogate SAR model, to map the relation between subject‐specific complex maps and the corresponding local SAR. After training, the network takes a few milliseconds to predict the realistic and accurate local SAR distribution, providing a solution to the long‐standing challenge of estimating subject‐specific local SAR distributions.
The use of complex maps was proposed because these distributions can be acquired easily, and enclosed within them lies almost all required information for local SAR assessment. The proposed method does not require accurate calibration procedures or reflected/lost power monitoring. It does not even require knowledge of the drive scheme or the accurate position of the transmit array on the patient. All relevant information is inherently included in the complex maps.
In silico and in vivo validation was performed. A good qualitative and quantitative match between predicted and ground‐truth local SAR distributions was observed. A more narrow distribution of the peak local SAR estimation error, with a moderate mean overestimation and lower probability of underestimation, was achieved.
To avoid underestimation, multiplying the predicated peak local SAR by a safety margin is necessary. The proposed deep learning–based method in conjunction with the safety factor achieves an acceptable mean overestimation error of 56% with a probability of underestimation lower than 0.1%. This result could save almost 25% of the time in the examination protocol compared with the commonly used approach (i.e., using a generic model) or compared with our recently published result.22
CONFLICT OF INTEREST
Mr. Meliadò is an employee of Tesla Dynamic Coils.
Supporting information
FIGURE S1 Transverse MIP of the ground‐truth SAR10g distributions, the predicted SAR10g distributions, and error SAR10g distributions using the deep learning method and the predicted SAR10g distributions and error SAR10g distributions using the conventional method (generic model Duke) for the models M01‐M12. All results are with transmit phases optimized for prostate imaging. The Duke model was manually rigidly registered to the models by aligning their prostate centers
FIGURE S2 Transverse MIP of the ground‐truth SAR10g distributions, the predicted SAR10g distributions and error SAR10g distributions using the deep learning method and the predicted SAR10g distributions, and error SAR10g distributions using the conventional method (generic model Duke) for the models M13‐M23. All results are with transmit phases optimized for prostate imaging. The Duke model was manually rigidly registered to the models by aligning their prostate centers
FIGURE S3 Transverse MIP of the ground‐truth, predicted, and error SAR10g distributions for the worst pSAR10g overestimation results for each model using the deep learning method
FIGURE S4 Transverse MIP of the ground‐truth, predicted, and error SAR10g distributions for the worst pSAR10g underestimation results for each model using the deep learning method
FIGURE S5 Normalized RMS error boxplot for each model over all considered cases
FIGURE S6 Flip angle and relative transmit phase‐error distributions (between measured and simulated maps) and SAR10g error distributions (between predicted and simulated SAR10g distributions) with default and prostate‐shimmed phase‐shimming settings for each volunteer included in the in vivo validation
FIGURE S7 Ground‐truth SAR10g distributions, predicted SAR10g distributions, and error SAR10g distributions over 10 slices through the model M01 using the deep learning method with phase shimming set for prostate imaging
FIGURE S8 A, Complex maps for each channel of the model M01. B, Spiral nonselective (SPINS) RF pulses designed for the model M01 (ΔB 0(r) = 0 μT). C, Drive vector, shimmed , ground‐truth, and predicted SAR10g distributions for 1 time step (e.g., time step 0.575 ms). D, Transverse MIP of the ground‐truth and predicted SAR10g distributions with SPINS RF pulses designed for the model M01
TABLE S1 A, Data of the volunteers included in the training set. B, Data of the volunteers included for in vivo validation. C, Data of the generic body model Duke
Meliadò EF, Raaijmakers AJE, Sbrizzi A, et al. A deep learning method for image‐based subject‐specific local SAR assessment. Magn Reson Med. 2020;83:695–711. 10.1002/mrm.27948
REFERENCES
- 1. Ugurbil K, Garwood M, Ellermann J, et al. Imaging at high magnetic fields: initial experiences at 4 T. Magn Reson Q. 1993;9:259–277. [PubMed] [Google Scholar]
- 2. Collins CM, Smith MB. Calculations of B(1) distribution, SNR, and SAR for a surface coil adjacent to an anatomically‐accurate human body model. J Magn Reson. 2001;45:692–699. [DOI] [PubMed] [Google Scholar]
- 3. Vaughan JT, Garwood M, Collins CM, et al. 7T vs. 4T: RF power, homogeneity, and signal‐to‐noise comparison in head images. Magn Reson Med. 2001;46:24–30. [DOI] [PubMed] [Google Scholar]
- 4. Springer E, Dymerska B, Cardoso PL, et al. Comparison of routine brain imaging at 3 T and 7 T. Invest Radiol. 2016;51:469–482. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5. Rosenkrantz AB, Zhang B, Ben‐Eliezer N, et al. T2‐weighted prostate MRI at 7 Tesla using a simplified external transmit‐receive coil array: correlation with radical prostatectomy findings in two prostate cancer patients. J Magn Reson Imaging. 2015;41:226–232. [DOI] [PubMed] [Google Scholar]
- 6. Steensma BR, Luttje M, Voogt IJ, et al. Comparing signal‐to‐noise ratio for prostate imaging at 7T and 3T. J Magn Reson Imaging. 2019;49:1446–1455. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7. Van Den Bergen B, Van Den Berg C, Klomp D, Lagendijk J. SAR and power implications of different RF shimming strategies in the pelvis for 7T MRI. J Magn Reson Imaging. 2009;30:194–202. [DOI] [PubMed] [Google Scholar]
- 8. Van Den Bergen B, Van Den Berg CAT, Bartels LW, Lagendijk JJW. 7 T body MRI: B1 shimming with simultaneous SAR reduction. Phys Med Biol. 2007;52:5429–5441. [DOI] [PubMed] [Google Scholar]
- 9. Padormo F, Beqiri A, Hajnal JV, Malik SJ. Parallel transmission for ultrahigh‐field imaging. NMR Biomed. 2016;29:1145–1161. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10. Malik SJ, Keihaninejad S, Hammers A, Hajnal JV. Tailored excitation in 3D with spiral nonselective (SPINS) RF pulses. Magn Reson Med. 2012;67:1303–1315. [DOI] [PubMed] [Google Scholar]
- 11. Orzada S, Maderwald S, Poser BA, Bitz AK, Quick HH, Ladd ME. RF excitation using time interleaved acquisition of modes (TIAMO) to address B1 inhomogeneity in high‐field MRI. Magn Reson Med. 2010;64:327–333. [DOI] [PubMed] [Google Scholar]
- 12. Attardo EA, Isernia T, Vecchi G. Field synthesis in inhomogeneous media: joint control of polarization, uniformity and SAR in MRI B1‐field. Prog Electromagn Res. 2011;118:355–377. [Google Scholar]
- 13. Sbrizzi A, Hoogduin H, Hajnal JV, van den Berg C, Luijten PR, Malik SJ. Optimal control design of turbo spin‐echo sequences with applications to parallel‐transmit systems. Magn Reson Med. 2017;77:361–373. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14. Ipek Ö, Raaijmakers A, Lagendijk JJ, Luijten PR, Van Den Berg C. Intersubject local SAR variation for 7T prostate MR imaging with an eight‐channel single‐side adapted dipole antenna array. Magn Reson Med. 2014;71:1559–1567. [DOI] [PubMed] [Google Scholar]
- 15. Homann H, Börnert P, Eggers H, Nehrke K, Dössel O, Graesslin I. Toward individualized SAR models and in vivo validation. Magn Reson Med. 2011;66:1767–1776. [DOI] [PubMed] [Google Scholar]
- 16. Villena JF, Polimeridis AG, Eryaman Y, et al. Fast electromagnetic analysis of MRI transmit RF coils based on accelerated integral equation methods. IEEE Trans Biomed Eng. 2016;63:2250–2261. [DOI] [PubMed] [Google Scholar]
- 17. Winter L, Özerdem C, Hoffmann W, et al. Design and evaluation of a hybrid radiofrequency applicator for magnetic resonance imaging and RF induced hyperthermia: electromagnetic field simulations up to 14.0 Tesla and proof‐of‐concept at 7.0 Tesla. PLoS One. 2013;8:e61661. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18. Vaughan JT, Snyder CJ, DelaBarre LJ, et al. Whole‐body imaging at 7T: preliminary results. Magn Reson Med. 2009;61:244–248. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19. Sbrizzi A, Hoogduin H, Lagendijk JJ, Luijten PR, Sleijpen GL, Van Den Berg C. Fast design of local N‐gram‐specific absorption rate–optimized radiofrequency pulses for parallel transmit systems. Magn Reson Med. 2012;67:824–834. [DOI] [PubMed] [Google Scholar]
- 20. Graesslin I, Homann H, Biederer S, et al. A specific absorption rate prediction concept for parallel transmission MR. Magn Reson Med. 2012;68:1664–1674. [DOI] [PubMed] [Google Scholar]
- 21. Eichfelder G, Gebhardt M. Local specific absorption rate control for parallel transmission by virtual observation points. Magn Reson Med. 2011;66:1468–1476. [DOI] [PubMed] [Google Scholar]
- 22. Meliadò EF, van den Berg CAT, Luijten PR, Raaijmakers AJE. Intersubject specific absorption rate variability analysis through construction of 23 realistic body models for prostate imaging at 7T. Magn Reson Med. 2019;81:2106–2119. [DOI] [PubMed] [Google Scholar]
- 23. De Greef M, Ipek O, Raaijmakers AJE, Crezee J, Van Den Berg CAT. Specific absorption rate intersubject variability in 7T parallel transmit MRI of the head. Magn Reson Med. 2013;69:1476–1485. [DOI] [PubMed] [Google Scholar]
- 24. Le Garrec M, Gras V, Hang MF, Ferrand G, Luong M, Boulant N. Probabilistic analysis of the specific absorption rate intersubject variability safety factor in parallel transmission MRI. Magn Reson Med. 2017;78:1217–1223. [DOI] [PubMed] [Google Scholar]
- 25. IEC 60601‐2‐33 :2010. Medical electrical equipment—part 2‐33: particular requirements for the basic safety and essential performance of magnetic resonance equipment for medical diagnosis, International Standard, Edition 3.0.
- 26. Katscher U, Voigt T, Findeklee C, Vernickel P, Nehrke K, Doessel O. Determination of electric conductivity and local SAR via B1 mapping. IEEE Trans Med Imaging. 2009;28:1365–1374. [DOI] [PubMed] [Google Scholar]
- 27. Katscher U, Kim DH, Seo JK. Recent progress and future challenges in MR electric properties tomography. Comput Math Methods Med. 2013;2013:546562. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28. Katscher U, van den Berg C. Electric properties tomography: biochemical, physical and technical background, evaluation and clinical applications. NMR Biomed. 2017;30 10.1002/nbm.3729 [DOI] [PubMed] [Google Scholar]
- 29. Ronneberger O, Fischer P, Brox T. U‐Net: convolutional networks for biomedical image segmentation, medical image computing and computer‐assisted intervention. In: Proceedings of the 18th International Conference on Medical Image Computing and Computer‐Assisted Intervention, Munich, Germany, 2015. pp. 234–241. [Google Scholar]
- 30. Lecun Y, Bottou L, Bengio Y, Haffner P. Gradient‐based learning applied to document recognition. Proc IEEE. 1998;86:2278–2324. [Google Scholar]
- 31. Krizhevsky A, Sutskever I, Hinton GE. ImageNet classification with deep convolutional neural networks. Adv Neural Inf Process Syst. 2012;25:1097–1105. [Google Scholar]
- 32. Simonyan K, Zisserman A. Very deep convolutional networks for large‐scale image recognition. arXiv:1409.1556.
- 33. Han X. MR‐based synthetic CT generation using a deep convolutional neural network method. Med Phys. 2017;44:1408–1419. [DOI] [PubMed] [Google Scholar]
- 34. Schlemper J, Caballero J, Hajnal JV, Price A, Rueckert D. A deep cascade of convolutional neural networks for MR image reconstruction. arXiv:1703.00555. [DOI] [PubMed]
- 35. Goodfellow I, Pouget‐Abadie J, Mirza M, et al. Generative adversarial nets. In: Proceedings of the 28th Conference on Neural Information Processing Systems, Montréal, Canada, 2014. [Google Scholar]
- 36. Zhu J, Park T, Isola P, Efros AA. Unpaired image‐to‐image translation using cycle‐consistent adversarial networks. arXiv:1703.10593.
- 37. Isola P, Zhu J, Zhou T, Efros AA. Image‐to‐image translation with conditional adversarial networks. arXiv:1611.07004.
- 38. Maspero M, Savenije MHF, Dinkla AM, et al. Dose evaluation of fast synthetic‐CT generation using a generative adversarial network for general pelvis MR‐only radiotherapy. Phys Med Biol. 2018;63:185001–185013. [DOI] [PubMed] [Google Scholar]
- 39. Mandija S, Meliadò EF, Huttinga NRF, Luijten PR, van den Berg CAT. Opening a new window on MR‐based electrical properties tomography with deep learning. arXiv:1804.00016. [DOI] [PMC free article] [PubMed]
- 40. Meliadò EF, Raaijmakers AJE, Savenije MHF, et al. On‐line subject‐specific local SAR assessment by deep learning. In: Proceedings of the 26th Annual Meeting of ISMRM, Paris, France, 2018. p. 293. [Google Scholar]
- 41. Raaijmakers AJE, Italiaander M, Voogt IJ, et al. The fractionated dipole antenna: a new antenna for body imaging at 7 Tesla. Magn Reson Med. 2016;75:1366–1374. [DOI] [PubMed] [Google Scholar]
- 42. Steensma BR, Voogt IJ, Leiner T, et al. An 8‐channel Tx/Rx dipole array combined with 16 Rx loops for high‐resolution functional cardiac imaging at 7 T. MAGMA. 2018;31:7–18. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43. Nehrke K, Börnert P. DREAM—a novel approach for robust, ultrafast, multislice B1 mapping. Magn Reson Med. 2012;68:1517–1526. [DOI] [PubMed] [Google Scholar]
- 44. Christ A, Kainz W, Hahn EG, et al. The Virtual Family—development of surface‐based anatomical models of two adults and two children for dosimetric simulations. Phys Med Biol. 2010;55:N23–N38. [DOI] [PubMed] [Google Scholar]
- 45. Tukey JW. Exploratory Data Analysis. Boston, MA: Addison‐Wesely; 1977. [Google Scholar]
- 46. Abadi M, Agarwal A, Barham P, et al. TensorFlow: large‐scale machine learning on heterogeneous distributed systems. arXiv:1603.04467.
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
FIGURE S1 Transverse MIP of the ground‐truth SAR10g distributions, the predicted SAR10g distributions, and error SAR10g distributions using the deep learning method and the predicted SAR10g distributions and error SAR10g distributions using the conventional method (generic model Duke) for the models M01‐M12. All results are with transmit phases optimized for prostate imaging. The Duke model was manually rigidly registered to the models by aligning their prostate centers
FIGURE S2 Transverse MIP of the ground‐truth SAR10g distributions, the predicted SAR10g distributions and error SAR10g distributions using the deep learning method and the predicted SAR10g distributions, and error SAR10g distributions using the conventional method (generic model Duke) for the models M13‐M23. All results are with transmit phases optimized for prostate imaging. The Duke model was manually rigidly registered to the models by aligning their prostate centers
FIGURE S3 Transverse MIP of the ground‐truth, predicted, and error SAR10g distributions for the worst pSAR10g overestimation results for each model using the deep learning method
FIGURE S4 Transverse MIP of the ground‐truth, predicted, and error SAR10g distributions for the worst pSAR10g underestimation results for each model using the deep learning method
FIGURE S5 Normalized RMS error boxplot for each model over all considered cases
FIGURE S6 Flip angle and relative transmit phase‐error distributions (between measured and simulated maps) and SAR10g error distributions (between predicted and simulated SAR10g distributions) with default and prostate‐shimmed phase‐shimming settings for each volunteer included in the in vivo validation
FIGURE S7 Ground‐truth SAR10g distributions, predicted SAR10g distributions, and error SAR10g distributions over 10 slices through the model M01 using the deep learning method with phase shimming set for prostate imaging
FIGURE S8 A, Complex maps for each channel of the model M01. B, Spiral nonselective (SPINS) RF pulses designed for the model M01 (ΔB 0(r) = 0 μT). C, Drive vector, shimmed , ground‐truth, and predicted SAR10g distributions for 1 time step (e.g., time step 0.575 ms). D, Transverse MIP of the ground‐truth and predicted SAR10g distributions with SPINS RF pulses designed for the model M01
TABLE S1 A, Data of the volunteers included in the training set. B, Data of the volunteers included for in vivo validation. C, Data of the generic body model Duke


