The topology of vitronectin: A complementary feature for neuroblastoma risk classification based on computer‐aided detection

Abstract

Tumors are complex networks of constantly interacting elements: tumor cells, stromal cells, immune and stem cells, blood/lympathic vessels, nerve fibers and extracellular matrix components. These elements can influence their microenvironment through mechanical and physical signals to promote tumor cell growth. To get a better understanding of tumor biology, cooperation between multidisciplinary fields is needed. Diverse mathematic computations and algorithms have been designed to find prognostic targets and enhance diagnostic assessment. In this work, we use computational digital tools to study the topology of vitronectin, a glycoprotein of the extracellular matrix. Vitronectin is linked to angiogenesis and migration, two processes closely related to tumor cell spread. Here, we investigate whether the distribution of this molecule in the tumor stroma may confer mechanical properties affecting neuroblastoma aggressiveness. Combining image analysis and graph theory, we analyze different topological features that capture the organizational cues of vitronectin in histopathological images taken from human samples. We find that the Euler number and the branching of territorial vitronectin, two topological features, could allow for a more precise pretreatment risk stratification to guide treatment strategies in neuroblastoma patients. A large amount of recently synthesized VN would create migration tracks, pinpointed by both topological features, for malignant neuroblasts, so that dramatic change in the extracellular matrix would increase tumor aggressiveness and worsen patient outcomes.

Short abstract

What's new?

The tumor microenvironment has a strong influence on cancer malignancy. Here, the authors investigate whether the organization of the extracellular matrix glycoprotein vitronectin in the tumor stroma may confer mechanical properties affecting neuroblastoma aggressiveness. Combining image analysis and graph theory, they identify two topological features of vitronectin that could potentially be used to improve patient pre‐treatment risk stratification. The data also point to the creation of vitronectin migration tracks for malignant neuroblasts, so that dramatic changes in the extracellular matrix would increase tumor stiffness and aggressiveness and worsen patient outcomes.

Abbreviations

ECM

extracellular matrix

INRG

International Neuroblastoma Risk Group

MNA

MYCN amplified

NB

neuroblastoma

SCAs

segmental chromosome aberrations

VN

vitronectin

Introduction

The interplay between different fields of basic science has been revealed as an efficient way to advance in medicine. Physics and mathematics‐related terms like tensegrity, topology and tessellations (see Glossary) are now used to improve understanding of biology and biomedicine.1, 2, 3 In parallel, a robust and efficient analysis of histopathological images is required due to their increasingly accepted use. Image analysis landscape has enormous potential to improve the quality of histological image interpretation, supporting without overruling pathologists in decision‐making.4, 5 In the oncology field, a plethora of computational tools is being designed to capture medical information with the help and supervision of a variety of professionals such as pathologists, biologists or physicists.6, 7, 8 Morphometric analysis has often been used as a first approach, successfully highlighting new prognostic indicators.9, 10, 11 However, more sophisticated techniques are needed to model highly complicated diseases like cancer. In particular, computerized image analysis has proven useful to find relevant features in different types of cancer.12, 13, 14 For instance, features related to texture analysis, which is based on the intensity and colors of the images, or morphological features considering the shape of the detected elements, are broadly used. These approaches did not consider the spatial relationship between its components12, 13 or were restricted to nuclei.14 However, morphometric techniques assure the standardization of all measurements and minimize interobserver differences.15, 16 Understanding how biopsy elements are organized is important to find potential new markers for improving treatment strategies and outcome prediction.

There is an increasing emergence of network theory methods in biology.17, 18, 19, 20 In cancer, graph theory (see Glossary) is commonly used to analyze gene networks.21, 22 In the case of histopathological images, three reconstructions have recurrently been used to obtain a graph that connects the elements of the image: Delaunay triangulation, Voronoi diagram (see Glossary) and minimum spanning tree.23, 24, 25 However, these approaches did not consider the importance of the spatial context of the extracellular matrix (ECM) for patient outcomes. Likewise, small nonisomorphic induced subgraphs (graphlets, see Glossary) have been used as a means to characterize biological networks,26, 27, 28 but as yet they have not been used to topologically characterize histopathological samples regarding outcomes.

The tumor microenvironment, particularly ECM, has a strong influence on cancer malignancy.29, 30 Specifically, vitronectin (VN), a glycoprotein belonging to the ECM, is considered to promote angiogenesis and vascular permeability, aiding tumor migration.31, 32, 33 In particular in neuroblastoma (NB), a heterogeneous tumor in childhood with widely varying prognosis according to several clinical and genetic factors in the International Neuroblastoma Risk Group (INRG) classification,34 the role of VN remains incompletely defined, although our previous studies suggested a connection to tumor progression.35 Despite efforts to fully characterize the impact of the NB microenvironment on patient pretreatment risk evaluation and tumor genetic instability, it still remains unclear how ECM topology and the interplay of its elements affect patient prognosis.9, 36, 37 Our hypothesis is that tumor cells affect the organization of the different elements surrounding them, including ECM elements such as VN. Working from this, our aim is to identify independent tumor tissue parameters, like VN topology, which could help to assess the risk group of NB patients and/or tumor genetic instability.

Materials and Methods

Material

Ninety‐one primary NB tumors (at least two representative cylinders of 1 mm² from each tumor) included in eight tissue microarrays were chosen according to INRG classification parameters and/or tumor genetic instability criteria related to segmental chromosome aberrations (SCAs)34, 38 (Supplementary Table 1). Tissue microarray slices of 3 μm were stained with anti‐VN (1/100) (clone EP873Y, isotype IgG, code ab45139, Abcam), scanned at 20x with Pannoramic MIDI (3DHistech Ltd., Budapest, Hungary), and analyzed objectively with Image Pro‐Plus v.6.0 (Media Cybernetics, Inc.,Rockville, MD 20850 USA) and DensitoQuant module from Pannoramic viewer software 1.15 (3DHistech Ltd.). For each biopsy (Figs. 1 a and 1 b), we obtained three markup images (area of each image: 1 mm², see Glossary) and their morphometric data: hematoxylin stained nuclei (Fig. 1 c); territorial VN location (Fig. 1 d), strongly stained intensity; and interterritorial VN location (Fig. 1 e), represented by low and medium intensity. These biopsy results were classified as high‐risk group (≥18 months and stage M or <18 months, stage M/MS and MYCN amplified [MNA]) and non‐high‐risk group (very low, low and intermediate categories following the INRG classification) patient material (additional Table 2). Regarding tumor genetic instability criteria, results were also grouped as higher SCA patient material (genetic profiles with >3 typical SCAs plus MNA or 11q deleted or >3 gene amplifications or with hyperrearranged chromosomal segments) and lower SCA patient material (genetic profiles with numerical chromosomal aberration or ≤3 typical SCAs, excluding 11q SCA).35 Our study was approved by the Ethics Committee (reference B.0000339 29/01/2015). Participants or their family members/legal guardians provided written informed consent.

Figure 1.

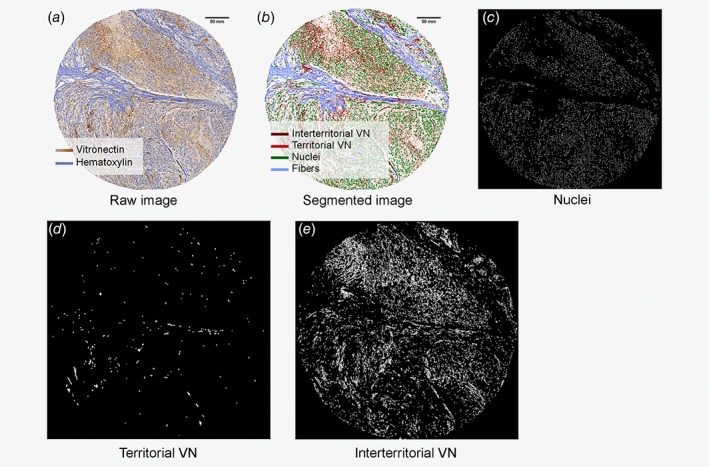
Segmentation of biopsy images from neuroblastoma (NB) patients. (a) Image of an immunohistochemical biopsy stained to detect vitronectin (VN) (brown scale). Hematoxylin is highlighted in blue, corresponding to nuclei and fibers of extracellular matrix. (b) Segmented image differentiating between territorial VN (red) and interterritorial VN (brown). The cell nuclei are also shown in the resulting image (green). (c–e) Markup images showing the segmented elements separately, but all in white: cell nuclei (c), territorial VN (d) and interterritorial VN (e). Scale bar in black, 50 mm.

Table 2.

Multivariate logistic regression. The models using the final set of features for each criterion. Each model is defined by the different coefficients (B column) of the intercept and independent variables (features). For tumor genetic instability criteria, both regular logistic regression and Firth's logistic regression are shown. SE stands for standard error. The odds ratio and confidence score are presented (exp(B) 95% CI column). In regular logistic regression, Z‐score and its associated p‐value are represented, while in Firth's logistic regression chi‐squared and its p‐value are presented

Features	B	SE	Exp (B) (95% CI)	Z‐value	Pr(>|z|)
Risk pretreatment stratification group
(Intercept)	−3.95	0.91	0.019 (0.003–0.114)	−4.36	1.32E‐05
Territorial—Euler number per node	0.65	0.26	1.92 (1.15–3.20)	2.49	0.013
Age (≥18 month)	2.66	0.61	14.36 (4.34–47.50)	4.36	1.28E‐05
Stage	−6.05E‐03	0.01	0.99 (0.97–1.02)	−0.51	0.610
MYCN (MNA)	−5.45E‐03	0.01	0.99 (0.97–1.02)	−0.50	0.620
Tumor genetic instability criteria
Regular logistic regression
(Intercept)	−23.64	2,914.00	5.45E‐11 (0–Inf)	−0.01	0.994
Territorial—mean quantity of branches per node	1.50	0.58	4.46 (1.44–13.80)	2.60	0.009
SCA	19.89	2,914.00	4.37E+08 (0–Inf)	0.01	0.995
MYCN (MNA)	22.58	3,245.00	6.43E+09 (0–Inf)	0.01	0.994
Ploidy	−2.83E‐03	1.32E‐03	1.00 (0.99–1.00)	−2.15	0.032
Firth's logistic regression
Features	B	SE	Exp (B) (95% CI)	Chi‐square	p
(Intercept)	−6.53	2.10	1.42E‐04 (4.58E‐06–4.64E‐02)	21.99	2.73E‐06
Territorial—mean quantity of branches per node	1.24	0.47	3.45 (1.42–10.96)	8.00	0.005
SCA	3.45	1.58	31.45 (3.04–4.45)	10.20	0.001
MYCN (MNA)	5.26	1.95	192.31 (9.81–4764.41)	20.04	7.56E‐06
Ploidy	−2.21E‐03	1.04E‐03	1.00 (1.00–1.00)	5.46	0.019

Topological features

To characterize our biopsies, we have extracted a set of 47 features, where 25 captured the organization of both types of VN (territorial and interterritorial), separately. First, considering the impossibility of measuring VN as if it were individual objects in our black‐and‐white markup images (Figs. 1 c–1 e), we decided to discretize the space in hexagonal regions of a fixed side of, approximately, 8.05 mm (50 pixels) (Fig. 2 and Fig. S1 b). Considering that hexagonal regions filled with VN staining represented by nodes (see Glossary), we quantified the following parameters (Table 1 a): (i) quantity of VN staining inside it (features with ID 4, 5, 16 and 17). (ii) Euler number (see Glossary): defined as the number of objects minus the number of holes within a region (7, 8, 19 and 20). (iii) Branching (see Glossary): We measured the number of crosslinks (11, 12, 23 and 24). (iv) Difference in quantity between interterritorial and territorial VN (feature with ID 25).

Figure 2.

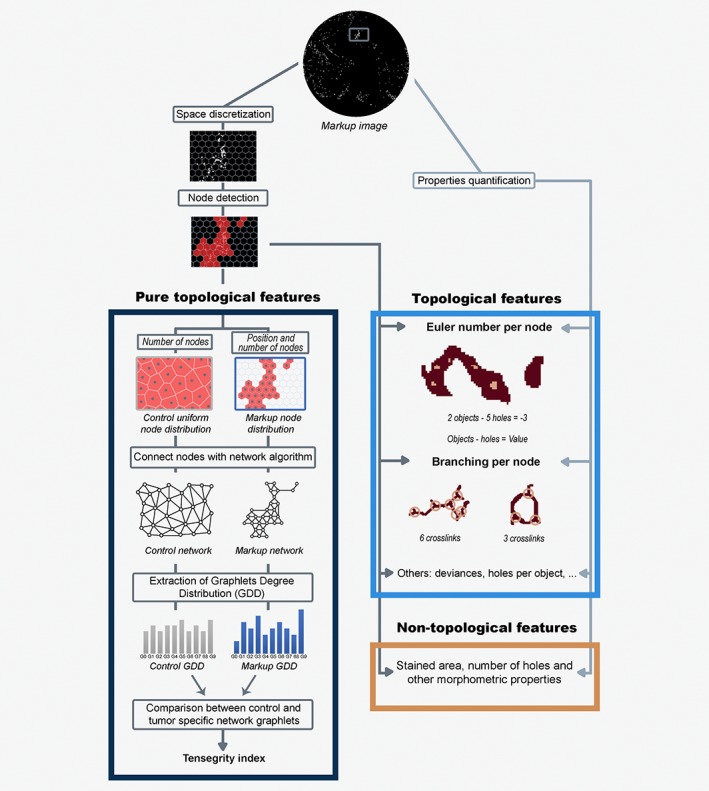
Pipeline overview of how the features are extracted. The process starts with the initial markup image, which in this example corresponds to territorial VN. A region of interest (ROI) from the initial image was selected (in dark gray) to show the space discretization and further operations. Below, the nodes (in red) are identified when a hexagon has VN inside. This information is used to obtain the pure topological features (dark blue, left side), a subset of the topological characteristics. In particular, the number of nodes is used to create the control with a uniform node distribution, while the position and number of nodes are utilized to gain the markup node distribution. Thereafter, each distribution of nodes is connected using a network algorithm (sorting, iteration or minimum spanning tree methods) and the graphlets degree distribution (GDD) is computed for both control and markup networks. To obtain the tensegrity index, the distance between the control GDD and the markup GDD is calculated. For topological characteristics (blue, right side), excluding the pure topological ones, two sources of information are used: the hexagonal grid and detected nodes (arrows in darker gray), and properties quantification performed directly on the markup image (lighter gray arrows). Two topological features are highlighted: Euler number per node, where the Euler number is calculated by subtracting the two objects (in brown) against the five holes within them (in light brown) resulting in a Euler number of minus three; and Branches per node in which the crosslinks (circles in light brown) from territorial VN shapes (in brown) were detected. Likewise, the nontopological features (orange, bottom right) use information extracted directly from the markup image and from the space discretization.

Table 1.

Statistically significant features. (a) Index of feature name and identifier used in the study, divided into topological (in white) or nontopological (gray). Topological features are the ones who capture organization, while the nontopological characteristics are morphometric measurements and other nonorganizational quantifications. (b) Results from the univariate analysis performed for tumor genetic instability criteria and high‐risk pretreatment stratification group. Only statistically significant characteristics (χ ² < 0.05) are shown. The features are ranked by their p‐values obtained on the chi‐square test, in ascending order. The selected features to be used in the next steps are underlined. The characteristics of territorial vitronectin (VN) are marked in bold (12/21 in the risk group and 15/27 in tumor genetic instability criteria). Highly statistically significant common features in tumor genetic instability criteria and risk group were marked with an asterisk. MST, minimum spanning tree; std, standard deviation

(a) Definition of features		(b) Univariate analysis
ID	Characteristics	Rank	ID	Characteristics	Chi‐square
Topological		Tumor genetic instability criteria
1	Interterritorial—sorting tensegrity index	1	20	Territorial—Euler number per node*	8.20E‐07
2	Interterritorial—iteration tensegrity index	2	24	Territorial—mean quantity of branches per node*	4.03E‐06
3	Interterritorial—MST tensegrity index	3	37	Territorial—percentage of stained area*	6.58E‐05
4	Interterritorial—std percentage of VN stained area per region	4	16	Interterritorial—std percentage of VN stained area per region	9.05E‐05
5	Interterritorial—std percentage of VN stained area per node	5	39	Total nuclei	1.27E‐04
6	Interterritorial—Euler number per VN stained area	6	29	Territorial—mean percentage of VN stained area per node	1.75E‐04
7	Interterritorial—Euler number per region	7	16	Territorial—std percentage of VN stained area per region	2.74E‐04
8	Interterritorial—Euler number per node	8	45	Territorial—ratio of strong positive pixels to total pixels	2.74E‐04
9	Interterritorial—number of holes per VN stained area	9	27	Territorial—mean percentage of VN stained area per region	3.87E‐04
10	Interterritorial—std area of holes	10	23	Territorial—mean quantity of branches per region	3.87E‐04
11	Interterritorial—mean quantity of branches per region	11	7	Territorial—Euler number per region	5.34E‐04
12	Interterritorial—mean quantity of branches per node	12	40	Percentage of hematoxylin stained nuclei area	6.11E‐04
13	Territorial—sorting tensegrity index	13	22	Territorial—std area of holes	8.44E‐04
14	Territorial—iteration tensegrity index	14	43	Interterritorial—ratio of weak positive pixels to total pixels	1.46E‐03
15	Territorial—MST tensegrity index	15	47	H‐score	0.002
16	Territorial—std percentage of VN stained area per region	16	38	Territorial—VN stained area/mm 2	0.002
17	Territorial—std percentage of VN stained area per node	17	46	Ratio of all positive pixels	0.004
18	Territorial—Euler number per VN stained area	18	31	Territorial—mean area of holes	0.005
19	Territorial—Euler number per region	19	42	Ratio of hematoxylin stained nuclei pixels to total pixels	0.006
20	Territorial—Euler number per node	20	36	Interterritorial—VN stained area/mm2	0.009
21	Territorial—number of holes per VN stained area	21	12	Interterritorial—mean quantity of branches per node	0.014
22	Territorial—std area of holes	22	34	Hematoxylin stained nuclei/mm2	0.016
23	Territorial—mean quantity of branches per region	23	2	Interterritorial—iteration tensegrity index	0.017
24	Territorial—mean quantity of branches per node	24	19	Territorial—Euler number per region	0.024
25	Std difference territorial and Interterritorial	25	21	Territorial—number of holes per VN stained area	0.030
Non‐topological		26	9	Interterritorial—number of holes per VN stained area	0.034
26	Interterritorial—mean percentage of VN stained area per region	27	6	Interterritorial—Euler number per VN stained area	0.045
27	Interterritorial—mean percentage of VN stained area per node	Risk pretreatment stratification group
28	Interterritorial—mean area of holes	1	20	Territorial—Euler number per node*	0.001
29	Territorial—mean percentage of VN stained area per region	2	24	Territorial—mean quantity of branches per node*	0.003
30	Territorial—mean percentage of VN stained area per node	3	39	Total nuclei	0.003
31	Territorial—mean area of holes	4	37	Territorial—percentage of stained area*	0.006
32	Mean difference territorial and Interterritorial	5	16	Territorial—std percentage of VN stained area per region	0.010
33	Percentage of hematoxylin stained nuclei area	6	22	Territorial—std area of holes	0.010
34	Hematoxylin stained nuclei/mm2	7	34	Hematoxylin stained nuclei/mm 2	0.010
35	Interterritorial—percentage of stained area	8	36	Interterritorial—VN stained area/mm 2	0.010
36	Interterritorial—VN stained area/mm2	9	45	Territorial—ratio of strong positive pixels to total pixels	0.010
37	Territorial—percentage of stained area	10	43	Interterritorial—ratio of weak positive pixels to total pixels	0.014
38	Territorial—VN stained area/mm2	11	17	Interterritorial—std percentage of VN stained area per node	0.016
39	Total nuclei	12	29	Territorial—mean percentage of VN stained area per region	0.019
40	Percentage of hematoxylin stained nuclei	13	23	Territorial—mean quantity of branches per region	0.019
41	Percentage of VN positive cells	14	19	Territorial—Euler number per region	0.019
42	Ratio of hematoxylin stained nuclei pixels to total pixels	15	47	H‐score	0.019
43	Interterritorial—ratio of weak positive pixels to total pixels	16	27	Territorial—std percentage of VN stained area per node	0.019
44	Interterritorial—ratio of moderate positive pixels to total pixels	17	38	Territorial—VN stained area/mm 2	0.019
45	Territorial—ratio of strong positive pixels to total pixels	18	33	Percentage of haematoxylin stained nuclei area	0.028
46	Ratio of all positive pixels	19	42	Ratio of haematoxylin stained nuclei pixels to total pixels	0.028
47	H‐score	20	30	Territorial—mean percentage of VN stained area per node	0.033
		21	46	Ratio of all positive pixels	0.033

The asterisk indicated three features that presented low values of chi‐square in both categories.

To get the final value of the features, we calculated the average of each parameter considering all the regions (features with suffix “per region,” Table 1 a) or only the nodes (suffix “per node,” Table 1 a) of the Euler number and branching, while the deviance (standard deviation [std]) of either the nodes or all the regions were computed to all the parameters. In addition, we computed a series of features that did not consider the hexagonal region (Table 1 a): the holes inside VN staining regions and the deviance of their area (features with ID 9, 10, 21 and 22). We also computed the Euler number per VN staining area of the whole image (6 and 18). All the topological features were extracted with Matlab R2014b (MathWorks).

Pure topological features

We used graph theory to obtain a subset of “pure topological” features. Briefly, to extract this set of characteristics, we collected the position and number of the hexagonal regions of our images (Fig. 2). In our network (graph), hexagonal regions filled with VN staining stand for nodes. To connect the nodes with a link (edge, see Glossary), we considered the “ordinary” (Euclidean) distance between them. We, therefore, started with all the nodes having no connections amid them. Aiming to model how the regions are distributed throughout the sample, we linked the nodes to obtain a connected network (i.e., any node can reach any node using the edges as a vehicle) using three different algorithms (iteration, sorting or minimum spanning tree, Supplementary Methods). Note that, for a given markup image, we will have three networks with the same number of nodes (one per algorithm).

Once we had the networks, which connect the regions filled with VN, we extracted the different configurations that can be achieved with a small number of nodes (graphlets26 of up to five nodes). Specifically, we used the ORCA (Orbit Counting Algorithm) computer program for graphlet identification and calculation,39 to extract the different graphlets of each network. In order to obtain the final tensegrity index (see Glossary) features, we compared, using the graphlet degree distribution distance,40 the graphlets obtained from the biopsy markup image with an in silico control, which tries to mimic a sample where the VN is equally distributed throughout the sample (represented by a homogeneous Voronoi tessellation, Supplementary Methods).

We computed the average distance between ten in silico generated controls with its tumor markup image specific network. Therefore, a tensegrity index represents how the real distribution of territorial or interterritorial VN differs from a homogeneous distribution. Finally, we obtained the six tensegrity indices (Table 1 a): three algorithms from two locations (features 1, 2, 3, 13, 14 and 15). The whole pipeline is explained in Figure 2.

Nontopological characteristics

We captured an additional set of nontopological features (Fig. 2), which involve morphometric characteristics:

1. Nuclei (Fig. 1 c). We obtained the number, area, ratio and percentage of hematoxylin stained nuclei (from non‐VN secretory cells) and the total nuclei number (from non‐secretory and VN secretory cells) from the total markups.

2. Percentage of stained area (Fig. S1 b). We quantified the VN stained areas in each delimited hexagonal area. We calculated the mean and std of the whole grid. In addition, we computed this mean and std using only the nodes. In the total markups, we also calculated VN location (percentage of stained area and number/mm²), pixel intensity ratio (ratio of positive stained pixels), positive or negative H‐score (based on a specific discriminatory threshold, ranging from 0 to 300) and number of VN secretory cells (percentage of VN positive cells).

3. Number of holes. We also identified the holes in an image.

4. Difference between interterritorial and territorial VN. We computed the average difference between interterritorial and territorial VN per region. For each hexagonal area, we operated territorial minus interterritorial.

Statistical analysis

We have adapted the pipeline shown in past studies41, 42 to obtain complementary features to refine the risk‐group assignment for NB treatment stratification and genetic instability in the present cohort. In particular, we have performed a multivariate analysis using logistic regression to collect these relevant features. See Supplementary Information for more details.

Data availability

The data set used and analyzed in the current study is available upon request.

Code availability

The code is available at: https://github.com/ComplexOrganizationOfLivingMatter/NeuroblastomeIntegration.

Results

Capturing organization from NB biopsy images

We processed and analyzed 91 histological images taken from human samples stained with anti‐VN antibody to visualize VN distribution (Figs. 1 a and 1 b, Methods). Using these images, we obtained the hematoxylin stained nuclei markup image for each biopsy (Fig. 1 c). We also distinguished two different localizations of VN according to intensity, as previously described35: strong intensity was assigned to a territorial VN, whose location is pericellular and intracellular (Fig. 1 d); and the intercellular location (peripherally to territorial matrix), which was named interterritorial VN, corresponded to low and medium intensity (Fig. 1 e). In this way, we detected the objects (VN stained areas) in the markup images, and overlapping a hexagonal grid with the related markup image, we divided the image into regions. In addition, we detected which hexagons were filled with VN objects becoming our nodes of the future graph (Figs. S1 a and S1 b, Methods). Using the information from the overlapped images and markup images, we studied the organization of the two locations of VN, by obtaining 25 features characterizing the topology of VN (Table 1 a and Fig. 2). In particular, we quantified (i) the general topology of the distribution of cells with interterritorial (features with ID 1, 2 and 3) or territorial (13, 14 and 15) VN; (ii) the variance in quantity of VN per hexagonal region (characteristics 4, 5, 16 and 17); (iii) the Euler number, which corresponds to the number of objects minus the holes (6, 7, 8, 18, 19 and 20 (Fig. S1 b); (iv) the number of holes per object (9 and 21) and the variation of the area of the holes (10 and 22); (v) branching, representing how many crosslinks are found (11, 12, 23 and 24) and (vi) the variation on the difference between interterritorial VN and territorial VN in terms of its quantity (25).

The values for the pure topological features (network characteristics 1, 2, 3, 13, 14 and 15) were obtained in three steps (Fig. 2). First, we used the superimposed images and its nodes to build a graph using different methods to connect these nodes (with edges). Specifically, we developed three different algorithms that consider the distance between the nodes: sorting, connecting all the closest distances between nodes, obtaining a highly‐linked graph (Fig. S1 c); iteration, which links the closest neighbors of the nodes emphasizing local topologies (Fig. S1 d); and minimum spanning tree, which connects all the nodes together minimizing the total edge distance, creating a minimum topological structure (Fig. S1 e). The three algorithms were designed to construct a connected graph, meaning that no nodes were isolated (Methods). Second, for each original markup image of a given VN location (Figs. 1 d and 1 e), ten control images were generated by taking the number of nodes in a biopsy (Fig. S1 b) and distributing them homogenously in the regions where it was possible to find VN (i.e., tears of the tissue were discarded) (Figs. S1 f and S1 g). The nodes of the control images were connected to obtain a corresponding control graph (Methods and Figs. S1 f and S1 g). Third, to get the final value of these features (the tensegrity indices), we calculated a descriptor of the similarity between each graph and its control (Fig. 2). To this end, we used the graphlet degree distribution distance26 (Methods). As a result, we obtained six tensegrity indices for each biopsy (three types of algorithms from two different locations of VN).

A combination of morphometric and topological features

In addition to the topological features, we captured 22 nontopological characteristics (Table 1 a), 7 of them obtained using the information from the hexagonal grid overlapped with the original markup image (Fig. 2): (i) percentage of VN (features 26, 27, 29 and 30); (ii) area of holes of the VN objects (28 and 31) and (iii) difference between territorial and interterritorial VN regarding their quantity (32). The remaining 15 morphometric features (33–47) did not consider the hexagonal grid and were acquired in a previous study.35

Altogether, we had 47 VN characteristics (Table 1 a and Supplementary Table 1): 19 came from interterritorial VN, 18 from territorial VN, 5 from both VN location, 4 from nuclei and 1 from total cells presented in their related markup images. We combined all this information to see if we could obtain a new supporting feature to enhance our two possible criteria: pretreatment risk stratification group (high‐risk vs. non‐high‐risk, 91 cases) and tumor genetic instability (higher vs. lower, 82 cases).

The pattern of VN is more homogeneous in patients with higher tumor genetic instability

As a preliminary analysis of the relation between the pure topology of the VN in the biopsy and the risk group of the patients or tumor genetic instability, we compared the distribution of our six tensegrity indices in high‐risk vs. non‐high‐risk groups and higher vs. lower tumor genetic instability. Regarding risk criteria, no feature was statistically significant between different prognoses. On the contrary, for the tumor genetic instability, both Iteration algorithms, interterritorial (lower instability: 0.22 ± 0.08; higher instability: 0.18 ± 0.10, p < 0.01) and territorial VN (lower instability: 0.26 ± 0.08, higher instability: 0.21 ± 0.09, p < 0.01), were statistically significant to divide between lower and higher genetic instability (Methods). Even though only the two mentioned results (2 out of 12) were statistically relevant, a trend was found among all the tensegrity indices: higher risk group or higher tumor genetic instability was associated with lower values in tensegrity indices, that is, differences between biopsy and controls (Fig. 3 a and Table S2). This means that using these indicators, low‐risk group and low tumor genetic instability cases were distributed more heterogeneously than low‐risk group patients and higher tumor genetic instability.

Figure 3.

The topology of territorial vitronectin (VN) is relevant to patient outcome. (a) Iteration tensegrity index values for the biopsies shown. For the same case, both VN locations are illustrated: interterritorial (top, connecting brown hexagonal areas) and territorial (bottom, connecting red hexagonal regions). (b) Region of interest (ROC) curve for the final model of risk pretreatment stratification group. (c) Territorial VN Euler number per node feature. Values are for the whole image, but the representative image is from a ROI. (d) ROC curve resulting from the model of tumor genetic instability criteria. (e) Branches per node from territorial VN. ROI taken from an image stained with territorial VN. The branches found are presented in dark orange. The skeletonized region of the marker is in light orange. Scale bar, 20 mm. Note that images from patients related to the non‐high‐risk group and lower tumor genetic instability are represented in green. Burgundy shows examples of cases belong to high‐risk group and higher tumor genetic instability. (f) Representative drawing of neuroblastoma microenvironment. Tumor with a close‐up of a stiff area: rich territorial vitronectin regions (dark brown) were associated with a desmoplastic extracellular matrix (represented by a low amount of glycosaminoglycans, crosslinked reticulin fibers, collagen I fibers and interterritorial vitronectin), tortuous blood and lymph vessels as a scaffold of tumor and stromal cells.

The territorial Euler number could enhance the prediction of poor risk group‐related prognosis

Next, considering the whole data set (47 features), we looked for variables that could improve the current tumor‐tissue predictors of patients' risk group or tumor genetic instability. For this purpose, we used a multivariate logistic regression pipeline based on the statistical analysis previously performed.41, 42 The first step of the pipeline was a univariate logistic regression analysis. This test checked whether the individual contribution of each feature was statistically significant for each criterion. Then, we retained only the features with statistical significance (p < 0.05) that could be independent factors in the study cohort (Table 1 b). Among them, the three most statistically significant in tumor genetic instability were related to territorial VN features and they also presented low chi‐square values predicting the high‐risk pretreatment stratification group. In addition, the majority of possible independent factors were characteristics of territorial VN (12/21 in high‐risk pretreatment stratification group and 15/27 in tumor genetic instability criteria, Table 1 b).

The second step of the pipeline was a multivariate logistic regression analysis, whose outputs are characteristics that should generate new insights; thus, they cannot overlap with variables that have known predictive power. Therefore, we coupled all the INRG variables, with values known to assess patient prognosis, with the top eight VN features of each criterion considered as the most statistically significant (nine features with p < 0.011 in risk group; eight characteristics with p < 3e‐04 for tumor genetic instability) by the univariate analysis (Methods and Table 1 b). Thereafter, we performed the multivariate logistic regression, which yielded a set of characteristics formed by age ≥18 months, Euler number per node from territorial VN, MYCN status (MNA) and metastatic stage (M) (Table 2), which was the best model characterizing the INRG pretreatment risk classification (nagelkerke R ²: 0.47). Using these four features, we obtained a significant model (χ ² < 0.005) with a specificity of 0.89 (non‐high‐risk group) and a sensitivity of 0.74 (high‐risk group) (Fig. 3 b). The selected independent prognostic predictor was based on the Euler number for territorial VN (Fig. 2). It stands for the number of objects in a sample minus the number of holes within those objects. Although the feature Euler number per node from territorial VN is related to the quantity of pericellular VN, it also takes into account the compactness of the territorial VN stained area including intracellular VN. Moreover, it considers the hematoxylin‐stained nuclei of active VN secretory cells with intracellular VN accumulation. In particular, we found that a greater number of objects and a lesser number of holes (a higher Euler number per node) from territorial VN was associated with the high‐risk pretreatment stratification group (p < 0.05) (Fig. 3 c).

Territorial crosslinks can assess tumor genetic instability

We repeated the second step of the pipeline to obtain the most relevant independent factors in the study cohort for tumor genetic instability. The final set was composed of the mean quantity of branches per node of territorial VN and the INRG variables: genetic profile (SCA), MYCN status (MNA) and ploidy (diploid and tetraploid) (nagelkerke R ²: 0.84), although it yielded quasi‐completion separation odd ratios, as can be seen in the standard errors of the results (Table 2). To avoid this issue, we performed a Firth's logistic regression. The output of this logistic regression was a penalized model (χ ² < 0.005) with a specificity of 0.91 and a sensitivity of 0.89 (Fig. 3 d). For tumor genetic instability, the mean quantity of branches per node of territorial VN was selected as an individual predictor in the study cohort. It considers the number of crosslinks after skeletonizing the image, taking into account only the filled hexagons (Figs. 2, 3 e and Supplementary Fig. S1b). This feature highlights the proximity of VN secretory cells with merged areas of recent VN secretion, mainly located pericellularly. We found that a higher number of branches correlated with higher tumor genetic instability. In addition, we also found a trend with the four defined levels from the genetic instability of the tumors (very low: 1.81 ± 0.8; low: 2.30 ± 1.6; medium: 2.43 ± 1.1; high: 7.05 ± 5.4; Table S1).

Discussion

In this work, we show that capturing VN organization can help improve understanding of how VN, essential to the structure of the ECM, affects or is affected by tumor progression, and thus patient prognosis. To acquire the characteristics for this purpose, we used two defined VN expression patterns that indicate the duration of time in the ECM:35 a territorial pattern indicates VN that has just been synthesized (also, intracellular) and/or was recently secreted into the surrounding matrix (pericellular); interterritorial VN has been present for a while in the intercellular space. In the same study, the optical analysis was used to determine the adequacy of further image analysis and to set the image analysis parameters. A good consistency (in terms of intensity) between the visual analysis and the digital image analysis quantification was observed using Kruskal‐Wallis test (p < 1e‐4). Our automatic image analysis approach can capture relevant information, which could be missing with traditional methods, to improve the classification of biopsy samples from NB patients. As a result, our different sets of experiments using different types of features indicate that territorial VN is relevant to evaluate the risk group of patients affected by NB and their tumor genetic instability.

The preliminary results of the pure topological features highlighted the iteration tensegrity index for both territorial and interterritorial VN with respect to tumor genetic instability (Fig. 3 a). In addition, the tensegrity index for interterritorial VN is the only relevant attribute of our novel features classifying tumor genetic instability (Table 1 b). Neither sorting nor minimum spanning tree tensegrity index appeared relevant to capture the patient's outcome. A possible reason could be the density of the resulting networks. The sorting graph (Fig. 2 and Supplementary Fig. S1c) is likely too dense, while the network of minimum spanning tree (Fig. 2 and Supplementary Fig. S1e) may be insufficiently connected for the graphlets to find differences between cases and controls. Thus, the intermediate graph of Iteration tensegrity index (Fig. 2 and Supplementary Fig. S1d), neither too dense nor too sparse, has the correct attributes to characterize the topology of the VN in these samples.

Although only one of our defined pure topological features was an independent factor in the study cohort, we found a trend in all the tensegrity indices: more homogeneous territorial and interterritorial VN patterns in node distribution emerged where patient prognosis was worse (Table S2 and Fig. 3 a). Here, rather than the direct quantity of VN, homogeneous reflects that VN is equally distributed throughout the sample: VN is spread over the tissue without restrictions in patients with poor prognosis. This is consistent with recent studies on the matter,35, 43 suggesting that VN enhanced the migratory capacity of tumor cells located in focal areas, thus associating VN with intratumor heterogeneity, tumor invasion, angiogenesis and metastasis.44 It could also be the case that endothelial cells migrate to a fibronectin and VN‐rich environment as a way to create new blood vessels in the process of neoangiogenesis.31, 33, 45, 46

We found an individual independent predictor in the study cohort for each of the criteria analyzed (pretreatment risk stratification group and tumor genetic instability). Both are topological features that can predict prognosis without overlapping with the existing known variables (age, stage, MYCN status and genetic profile). In the risk stratification group, the Euler number per node from territorial VN, which was a compendium between VN quantity and organization, came out as a remarkable feature. In our topological feature Euler number per node, we only consider the regions with information and computed the Euler number of each region separately. Therefore, a higher number of this feature, related to tumors with MNA from high‐risk patients, stage M and ≥18 months, might indicate that existing territorial VN is compacted with stretch marks in focal areas, as previously indicated. In summary, our results suggest that the topology of territorial VN would aid tumor cell migration, mechanically altering the ECM, which translates into disrupted tumor cell adhesion and easier spreading into a stiff matrix. It has been shown that the Euler number is able to characterize the aggressiveness of prostate cancer, distinguishing between tubular and cribriform growth patterns associated with lower and higher aggressive behaviors, respectively.47 These organization patterns resemble the ones we encounter in territorial VN, where a higher Euler number is related to worse prognosis (Fig. 3 c). One possibility is that the territorial VN forms cribriform‐like structures that try to surround the cancer cells with a stiff ECM, allowing migration. VN‐rich territorial regions would facilitate the disruption of ECM–cell or cell–cell interactions (Fig. 3 f). Interestingly, this pattern is similar to the fibrosis areas previously described in human lung cancer.48

For the tumor genetic instability criteria, we obtained the topological feature branches per node from territorial VN, related to the shape of VN and its number of crosslinks, as an individual independent factor. Irregular shapes (not straight), which may be surrounding the cells (Fig. 3 e, right), appeared in tumors with higher genetic instability. The displacement of malignant neuroblasts in a stiff ECM could be mediated by cycles of formation and rupture of binding glycoproteins, VN and/or fibronectin, as described in these studies in ovarian and oral squamous carcinoma tumor cells.32, 49 Likewise, VN branching could represent migration tracks with a large amount of VN, connecting integrins and fiber elements of the ECM. Furthermore, these irregular territorial VN branches would represent migrating tracks facilitating invasion by activating nuclear intracellular signaling pathways that would modify genetic and epigenetic mechanisms, increasing tumor instability in these patients (Fig. 3 f).

The digital analysis tools are increasingly numerous and powerful as a result of the growing demand for an automatic objective method that allows rapid and effective analysis (reduce inter and intraobserver variability) of the huge number of tumor samples required at a routine clinical diagnosis and research.50, 51 In particular, previous works had used textural analysis to improve the current methods of grading prostate cancer24 or malignancy detection in breast tumors,12 among others.13, 23 Although these studies achieved accurate results, the features they got did not directly unlock biological mechanisms. NB is considered a heterogeneous and complex cancer dependent on many known variables, such as age and MYCN oncogene amplification,37, 52 but there are still unknown biological factors. Thus, interpret and relate features with biology are essential to extract new insights. Likewise, most of the works using computerized image analysis rely on recognizable objects to capture the morphology or topology, such as the nuclei of the cells within the sample.14, 24, 25 In our case, VN cannot be captured as an object due to its variability in size and shape (Figs. 1 d and 1 e). We propose that these automatic methods can be enhanced with the use of mathematical tools that can capture the organization of the elements identified in the biopsies. Our approach discretizes the space to extract different topological and morphological features avoiding these two issues while obtaining statistically significant characteristics.

Overall, our conclusion is that the particular organization of territorial VN markedly changes the constitution and mechanics of the ECM by the rapid addition of new synthesized VN creating migration tracks, which may lead to more aggressive NB. However, the molecular mechanism behind these results remains unclear. In conclusion, combining topology and morphometric features seems an effective strategy to find complementary factors that could obtain a more precise pretreatment risk stratification to guide treatment strategies. We have shown that VN may play a greater role than previously assumed in prognostic assessment of human patients, in agreement with our previous work that suggested the importance of territorial VN.35 There remains a wealth of information to be captured from these biopsies. Human samples are an excellent source of information that should be thoroughly analyzed. On this sense, our topological approach requires long computational processing to obtain high‐quality and reliable markups. However, once the markup images have been validated, their topological properties can be easily extracted using our pipeline. Our mathematical approach shows a big potential in histopathological images of NB samples. In the near future, the integration of histopathological consecutive slices will be the first step to approach the 3D tumor's structure. These studies will be needed to reveal the true role of VN in NB to test whether the results of our study are consistent.

Glossary

Tensegrity: Stabilization of structures constituted by continuous elements of tension and discontinuous elements resistant to compression. Topology: How a set of elements are structured and connected in a given space. Tessellation: A surface covered by geometric components (or tiles) with no gaps and without overlapping. Graph/network: A set of elements connected between them following determined rules that represent binary relations. A graph is formed by nodes (the elements) and edges that link them. Voronoi diagram: A particular tessellation formed by convex polygons. Each convex polygon is a Voronoi cell. Every Voronoi cell emerges from a seed. All the points of a Voronoi cell are closer to its own seed that to any other seed of the surface. Graphlets: Graphs with a small number of nodes extracted from a larger network. A network can be quantitatively characterized by its graphlets composition. Markup image: A binary immunohistochemistry microscopic image in which the white regions represent detected objects, and the black ones, the background. Euler number feature: In an image where a set of objects has been identified, the Euler number is the value of the number of objects minus the number of holes inside them. Branching feature: In an image where a set of objects has been identified, the Branching is the value of the number of crosslinks that are found on the objects. Node: A representation of an object. In our case, it stands for a hexagonal area filled with vitronectin. Edge: The link between nodes. Two nodes connected by one edge are considered adjacent. Tensegrity index: Represents how different is the VN (interterritorial or territorial) organized in the biopsy compared to a homogenous distribution.

Financial support

L.M.E. is supported by the Ramón y Cajal program (PI13/01347). The work of L.M.E. and P. V.‐M. is funded by the Ministry of Economy, Industry, and Competitiveness grant BFU2016‐74975‐P cofunded by FEDER funds. P.V.‐M. and R.B.‐P. are supported by a contract by the Asociación Fundación Española contra el Cáncer. P.V.‐M. contract is also supported by Seville University (V plan propio). This work was funded by the FAECC (contract 2015, FAECC2015/006), CIBERONC (CB16/12/00484) and FIS (PI17/01558, Institute of Health Carlos III, Madrid/ERDF), NEN Association (Nico contra el cancer infantil 2017). The funders had no involvement in the research process or the preparation and submission of the article.

Supporting information

Appendix S1: Supporting Information

Supplementary Figure S1 Features derived from the markup images of a neuroblastoma (NB) biopsy. A) A segmented image representing territorial vitronectin (VN), the same as in Figure 2. Colored in light blue is a ROI that represents the region of (B). B) A cropped region from (A), where the regions with information become the nodes of the graphs in (C‐E). A single hexagonal cell from the light blue grid is selected to characterize: the percentage of stained area (left hexagon), which is the number of white pixels found on it divided by the total area of the hexagon; branching (central hexagon), after skeletonizing (light orange), crosslinks (7 in orange) are identified; and the Euler number (right hexagon), that needs to recognize the objects (2 in red) and the holes (1 in yellow). Note that a hole should be inside an object (the background of the image is not a hole). C‐E) Networks or graphs resulting from applying the algorithms in the (A) markup image: Sorting (C), Iteration (D) and Minimum Spanning Tree (E). F‐G) A Voronoi control generated using the same number of nodes as in the original case (A), covering the biopsy homogenously. Regions where the marker could not be found are in black, while in hexagonal white areas represent the uniform node distribution. Blue represents the graph computed with the algorithm Sorting (F) and Iteration (G). The control for the MST algorithm was the same as in Iteration (G).

Supplementary Table S1 Raw data of topological and non‐topological vitronectin (VN) features. Risk groups and tumor genetic instability criteria for each case are indicated. Note that tumor genetic instability criteria includes cases with no data, corresponding to atypical genetic profiles with unknown clinical implication marked as ‐. The identification (ID) list of topological and non‐topological VN features is enumerated in Table 1A.

Supplementary Table S2 Tensegrity indices per criteria and prognosis. Mean and standard deviation for each tensegrity index. In addition, results from Shapiro normality test and Mann–Whitney test. In bold, distributions that are statistically different regarding risk group or tumor genetic instability criteria. Std: standard deviation.