Honeybees use their wings for water surface locomotion

Significance

We report the honeybee’s propulsion at the air–water interface. Honeybees trapped on a water surface use their wings as hydrofoils, which means their wings generate hydrodynamic thrust. The surface wave and flow patterns generated around the bee are the first indication that the wings are used as hydrofoils. Furthermore, the water flow measured under a mechanical wing model showed that both net and oscillatory thrust contribute to their locomotion. Hydrofoiling highlights the versatility of their flapping-wing systems that are capable of generating propulsion with fluids whose densities span 3 orders of magnitude. This discovery inspires an aerial–aquatic hybrid vehicle. Moreover, the findings may have biological implications on the survival of water foragers and preflight locomotion mechanisms.

Abstract

Honeybees display a unique biolocomotion strategy at the air–water interface. When water’s adhesive force traps them on the surface, their wetted wings lose ability to generate aerodynamic thrust. However, they adequately locomote, reaching a speed up to 3 body lengths·s⁻¹. Honeybees use their wetted wings as hydrofoils for their water surface propulsion. Their locomotion imparts hydrodynamic momentum to the surrounding water in the form of asymmetric waves and a deeper water jet stream, generating ∼20-μN average thrust. The wing kinematics show that the wing’s stroke plane is skewed, and the wing supinates and pronates during its power and recovery strokes, respectively. The flow under a mechanical model wing mimicking the motion of a bee’s wing further shows that nonzero net horizontal momentum is imparted to the water, demonstrating net thrust. Moreover, a periodic acceleration and deceleration of water are observed, which provides additional forward movement by “recoil locomotion.” Their water surface locomotion by hydrofoiling is kinematically and dynamically distinct from surface skimming [J. H. Marden, M. G. Kramer, Science 266, 427–430 (1994)], water walking [J. W. M. Bush, D. L. Hu, Annu. Rev. Fluid Mech. 38, 339–369 (2006)], and drag-based propulsion [J. Voise, J. Casas, J. R. Soc. Interface 7, 343–352 (2010)]. It is postulated that the ability to self-propel on a water surface may increase the water-foraging honeybee’s survival chances when they fall on the water.

It is difficult for insects to retain the aerodynamic function of their wings when they contact a water surface. The large-amplitude wing motion required for producing thrust demands hydrophobic wing surface or enough clearance between the wing and the water to prevent wetting. Insects that satisfy 1 of these 2 conditions can perform nonflying aerodynamic locomotion on the water surface, known as surface skimming (1–3) (e.g., stoneflies, mayflies, and water lily beetles). Other insects whose wings touch the water surface and continue to be bounded, lose their ability to generate aerodynamic thrust. In this condition, it is unclear whether the insects are still capable of propelling with their wetted wings.

Water-collecting honeybees fly close to a water surface. When they fall on the water, they lose their aerodynamic ability. While their buoyant bodies provide flotation, the ventral side of the body and wings get wetted. They are not able to free their wings from the water surface, likely due to the relatively high wettability of their wings requiring large energy input for detachment (4). The contact angle (a quantitative measure of wettability) of the honeybee’s wing is 85° to 102° (5, 6) compared to 118° to 125° for the stonefly’s wing (5), which can be detached from the surface (1, 7). However, upon beating their wetted wings, honeybees display forward locomotion while producing a distinct wave and flow pattern on the water surface (Fig. 1 and Movies S1–S3). Here, we report that honeybees fallen on a water surface use their wetted wings as hydrofoils, generating positive thrust by transporting momentum to the water underneath the wing. Hydrofoiling highlights the versatility of their flapping-wing systems, which are capable of generating propulsion with fluids whose densities span 3 orders of magnitude.

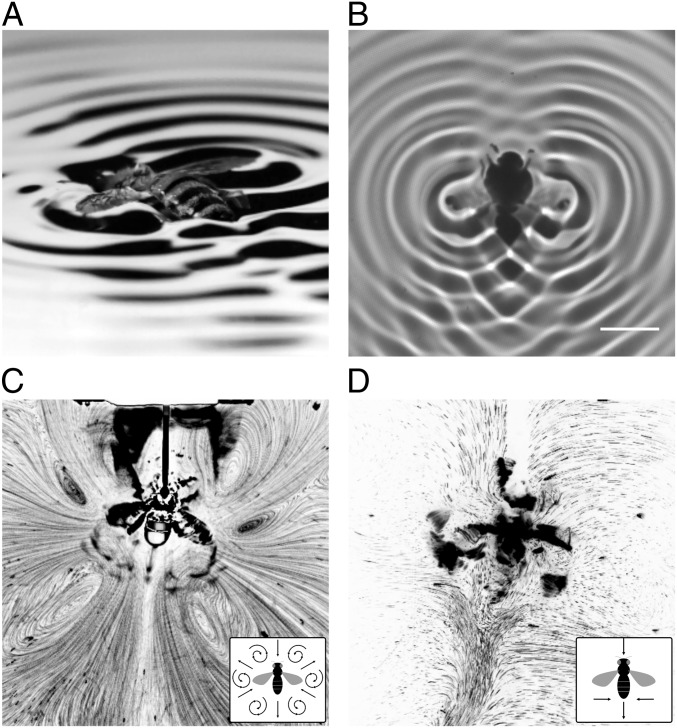
Fig. 1.

Surface wave and flow visualization. (A) Honeybee’s locomotion on a water surface. The ventral side of the wings and body are attached to the water surface (Movies S1 and S2 and SI Appendix, Fig. S1). (B) Wave pattern visualized using shadowgraph. The light and dark fringes indicate the wave crests and troughs, respectively. Wing-beat frequency, 69 Hz (Scale bar, 1 cm.) (SI Appendix, Fig. S4 and Movie S3). (C) Surface streaming flow pattern generated by a horizontally tethered bee. (D) Water flow at 2.0 mm below the water surface generated by a constrained bee. Flow directions are schematically shown in the Bottom Left corner for C and D.

Results

Our data were obtained with honeybees (Apis mellifera) collected from a garden in Pasadena, California. To simulate its accidental fall, a honeybee placed in a plastic tube (1-inch-diameter opening) was gently tapped with the opening facing the water surface. The bees were flight capable before contacting the water surface. The temperature of the water was kept above 20 °C. Note that another factor that may contribute to a honeybee’s inability to detach its wings from the water surface could be the lowered temperature of its flight muscles, which operate optimally at a temperature much higher than the experimentally set water temperature (8). The depth of the water was maintained at 2.5 to 5 cm, which is much longer than the width of their wing (∼4 mm) and the wavelength of the water wave (∼5 mm) generated by the bee. The honeybees that fell dorsal side facing up were used to collect data. The bees that fell ventral side facing up were excluded from data collection. These bees were not able to upright themselves but still showed the capability to propel.

Body Kinematics.

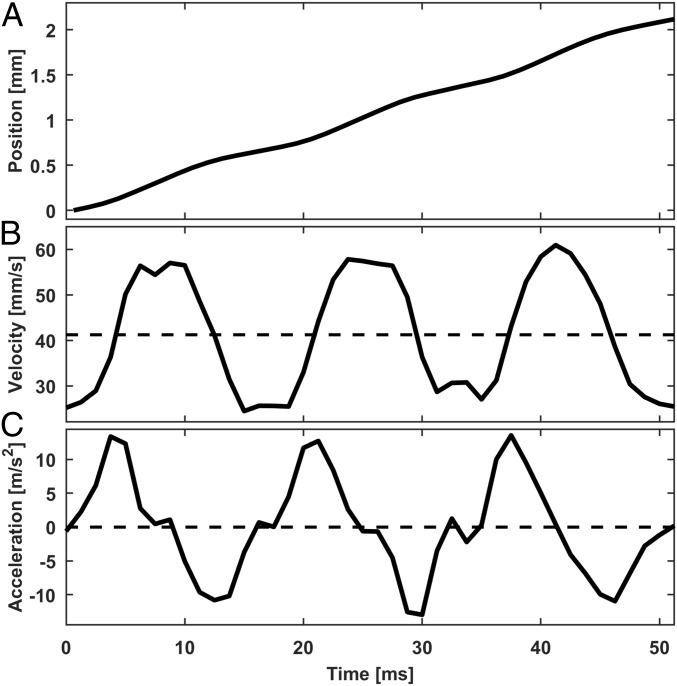
The honeybee’s wing and body kinematics were recorded with high-speed videography (500 to 1,000 frames·s⁻¹) at various camera angles on constrained and free-moving bees. In comparison to the wing kinematics during hovering flights (9) and fanning (10), the amplitude and the frequency of the wing beat at the water surface are noticeably reduced. Note that, throughout the wing motion, the ventral sides are constantly in contact with water, but the dorsal sides remain dry. The stroke amplitude on a water surface is less than 10° as opposed to 90 to 120° in air. The wings beat symmetrically and synchronously at frequencies ranging from 40 to 290 Hz (mean, 100 Hz; n = 33 bees; SD, 61 Hz). Twenty-five out of 33 bees had wing-beat frequencies less than 100 Hz (mean, 71.6 Hz; n = 25, SD, 14 Hz), substantially lower than the 200 to 250 Hz during flight (9) and ∼170 Hz during fanning (10). The stroke amplitudes tend to decrease as the wing-beat frequency increases (SI Appendix, Fig. S1). The locomotion speed and acceleration oscillate at the wing-beat frequency (Fig. 2). The time-averaged locomotion speeds were 1.4 to 4.3 cm·s⁻¹ (mean, 3.1 cm·s⁻¹; n = 18 bees; SD, 0.77 cm·s⁻¹) at steady state, corresponding to 1 to 4 body length·s⁻¹ [2 orders of magnitude slower than their free-flight speeds (11)]. Reynolds number (Re) based on the average speed is O(100). The time-averaged acceleration is approximately zero at steady state.

Fig. 2.

Honeybee’s locomotion pattern. (A) Position change with time. Wing-beat frequency, 60 Hz. (B) Forward locomotion speed. The dashed line indicates the time-averaged speed (41 mm·s⁻¹). (C) Body acceleration. The dashed line indicates the time-averaged acceleration (−0.0 m·s⁻²). Also see SI Appendix, Fig. S8 for mechanical model predicted body kinematics.

Force Generation.

For the bees to maintain locomotion speed, their wings need to exert ∼20-μN average horizontal thrust to overcome hydrodynamic drag (SI Appendix, Detailed Calculations I and Fig. S3). According to the law of momentum conservation, an equal and opposite momentum should be imparted to the surrounding fluid. If the necessary positive thrust can be traced to the negative momentum imparted to the water, then the wings are indeed used as hydrofoils rather than aerofoils. Note that, on a water surface, momentum can be carried as a surface wave and flow; therefore, we visualize using both shadowgraph and particle seeding (SI Appendix, Materials and Methods).

The wave field around the bee is bilaterally symmetric, but fore–aft asymmetric (Fig. 1B). A large-amplitude wave with an interference pattern forms at the rear of the bee, while the surface in front lacks a strong (large-amplitude) wave. The momentum contained in a propagating wave scales as a square of the wave amplitude (12); thus, the higher amplitude of the posteriorly propagating wave suggests that the bee should be pushed forward.

The surface streaming flow generated by the bee has 3 outward jets, 3 inward jets, and circulation regions between the jets (Fig. 1C). Beneath this complex surface flow pattern, a simpler flow is observed; of the 3 outward jets, only the backward flowing central jet is present in deeper water (Fig. 1D and SI Appendix, Fig. S7). This jet’s penetration of deeper layers indicates its main role as the momentum carrier. Therefore, the observed flow field is also consistent with the forward thrust production.

More quantitative calculations of wave and flow momenta are attempted with additional measurements and assumptions (SI Appendix, Detailed Calculations II). With a wave amplitude measurement, the average horizontal momentum per wing cycle contained in the surface wave was calculated as 50 μN (overestimation is discussed in SI Appendix, Detailed Calculations II). With a flow field measurement using digital particle image velocimetry (13) (DPIV), the average flow momentum per wing cycle was measured as 20 μN (SI Appendix, Materials and Methods and Fig. S7). The magnitude of the hydrodynamically imparted momentum and the thrust needed to overcome the drag are the same order of magnitude. This shows that a bee’s locomotion is sustained by imparting momentum to the water. Note that these 2 measurements are not mutually exclusive, since a traveling wave induces flow and vice versa. Previous studies on water strider locomotion have shown that localized impulsive forcing with a thin rod (i.e., leg) at the air–water interface results in 1/3 and 2/3 partitioning of the imparted momentum to waves and vortices, respectively (14). A similar study for sinusoidal motion of a thin plate is necessary for distinguishing the measured wave and flow momentum.

The net thrust generated by hydrofoiling, O(10 μN), is about 2 orders of magnitude smaller than the weight of the bee O(1,000 μN), which is also the average aerodynamic lift force produced during hovering flight (9). Interestingly, the peak thrust generated during hydrofoiling (SI Appendix, Fig. S3) and hovering are of the same order of magnitude, O(1,000 μN). The small hydrofoiling net thrust can be traced to the comparable magnitudes of positive and negative thrust.

Flow Near the Wings.

The horizontal momentum transport to water is demonstrated more directly by analysis of the interaction between the wing and the water underneath. To analyze, we first describe the general features of wing kinematics (see Fig. 4 and SI Appendix, Fig. S9), and then show the flow generated by a mechanical wing model mimicking the observed kinematics (see Fig. 5).

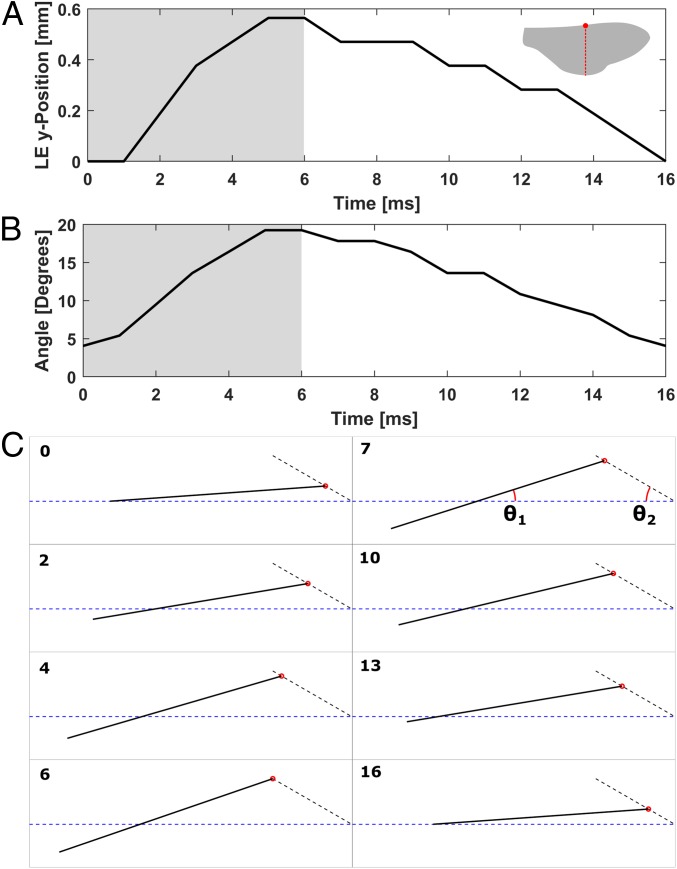
Fig. 4.

Honeybee wing kinematics. (A) Leading edge position. Wing-beat frequency, 63 Hz. Shaded regions, power stroke phase. Nonshaded region, recovery stroke phase. Left corner wing indicates the measurement location, where red circle indicates leading edge. (B) Supination and pronation angle. (C) Approximated wing motion. The wing motion was estimated with straight line. θ₁ = pronation and supination angle. θ₂ = stroke plane angle. Time stamp at the corner corresponds to time axis on A and B. The blue dashed line represents undisturbed air–water interface.

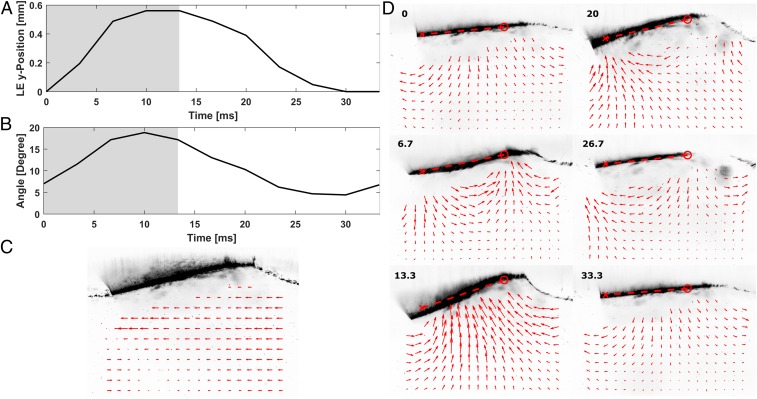
Fig. 5.

Mechanical wing kinematics and resulting flow. (A) Leading edge position. Wing-beat frequency, 30 Hz. Shaded regions, power stroke phase. Nonshaded region, recovery stroke phase. The left corner wing indicates the measurement location, where red circle indicates leading edge. (B) Supination and pronation angle. (C) Time-averaged horizontal velocity over 3 periods. (D) Velocity field under the wing. The black line above the velocity field is the cross-section of the wing. Time stamp at the corner corresponds to the time axis on A and B. See Movie S5 for a full sequence. The red “o” and “x” mark the leading and trailing edges, respectively. An angle that the red dotted line makes with a horizontal axis is the supination/pronation angle.

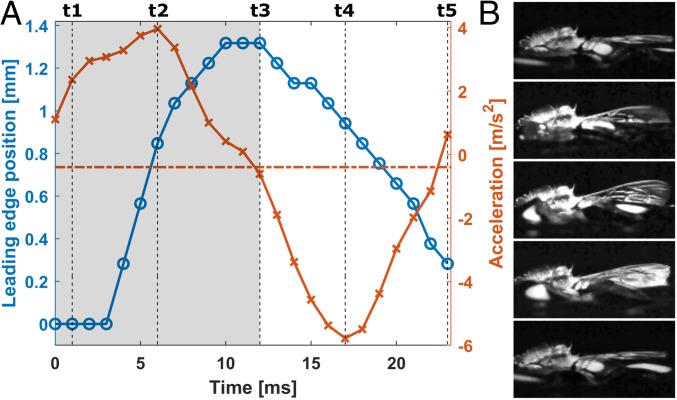
At the onset of the wing beat (Fig. 3B, t = t1; Fig. 4C, t = 0), the bee diagonally lifts the leading edges backward (Fig. 3B, t1 to t3; Fig. 4C, t = 0 ms to t = 6 ms; θ₂ = stroke plane angle ∼30°, θ₂ defined in Fig. 4C). Simultaneously, the wings supinate, and the trailing edges are pushed down (Fig. 4). The bee’s body accelerates during this phase (Figs. 3A and 4 A and B, shaded area), thus hereinafter this phase is referred to as “power stroke” phase. Following the power stroke, the bee diagonally pushes down the leading edges forward (Fig. 3B, t3 to t5; Fig. 4C, t = 7 ms to t = 16 ms). As the leading edges move down, the wings pronate, and the trailing edges move up (Fig. 4). The bee decelerates during this phase; thus, hereinafter, this phase is referred to as “recovery stroke” phase (Figs. 3A and 4 A and B, nonshaded area).

Fig. 3.

Body acceleration and wing kinematics. (A) Leading-edge vertical position and acceleration of the bee’s body. Wing-beat frequency, 44 Hz. Blue −○ line indicates the leading edge vertical position. Red −× line indicates the acceleration. Shaded regions, power stroke phase. Nonshaded region, recovery stroke phase. (B) The wing position corresponding to each time point marked on A; t1–t5, Top to Bottom.

Throughout the honeybee’s wing kinematics, the ventral side of the wing does not detach from the water surface. Thus, the described wing kinematics continually interact with the water. During the power stroke, the water underneath the wing is lifted (Movie S1). During the subsequent recovery stroke, the wing pushes down on the lifted water sending ripples around the wing. The response of the water surface to the bee’s wing motion is clearly shown in Movie S1; however, the free surface visualization alone is not enough to estimate the momentum transport. Instead, a proper calculation of the momentum exerted by the wing motion requires flow measurement.

To accomplish this, a mechanical wing model was constructed (Materials and Methods and SI Appendix, Fig. S8), and the flow directly under the mechanical wing was measured using DPIV (SI Appendix, Materials and Methods). This model was necessary to measure the flow because of the unpredictable movement of honeybees. We ensured that the mechanical wing replicates general features of the honeybee’s wing kinematics (compare Fig. 4 A and B with Fig. 5 A and B; also compare SI Appendix, Fig. S8C with SI Appendix, Fig. S8D) and the free surface response (compare Movie S1 with Movie S4). A time-resolved body motion calculated from the measured flow field (SI Appendix, Fig. S8 E–G) also resembles the body motion of the honeybee (Fig. 2 A–C). One main difference is that the mechanical wing is only passively supinated and pronated by its flexibility, whereas the bee’s wing rotation can be effected both actively and passively. The flow generated by the model wing actuated at 30 Hz is shown in Fig. 5 (Movie S5) (15).

The flow averaged over a period shows that negative horizontal momentum is imparted to the water underneath the wing (Fig. 5C). This clearly shows that the mechanical wing motion mimicking the honeybee’s wing kinematics results in nonzero horizontal thrust. In addition, a periodically oscillating momentum is observed (Fig. 5D and Movie S5). Based on the order of magnitude analysis of the different hydrodynamic forces involved, the only force that can account for this oscillation is unsteady inertial force (added mass) associated with the wing movement (SI Appendix, Detailed Calculations III). While this reactive force does not impart net thrust, it can move the body, which is known as recoil locomotion (16, 17). This unsteady force also explains the oscillatory body velocity and acceleration seen in the body kinematics of the honeybee (Fig. 2).

One question that remains is how the wing kinematics are able to generate positive thrust. From the time-varying flow field and the corresponding wing kinematics, we suggest a potential mechanism of net negative horizontal momentum generation. By the end of the power stroke, the diagonally lifting wing has accelerated water upward and backward (Fig. 5D, t = 13.3 ms). In transitioning to the recovery stroke, the wing pronates, progressively flattening its conformation (Fig. 5 B and D). The decreased wing angle would reduce the wing’s interaction with the horizontal flow during the recovery stroke, which would sustain a portion of the horizontal momentum produced by the power stroke. Hence, over a period of wing motion, the wing would impart net negative horizontal momentum to the water. As the wing resets to the initial position, the excess water momentum would be shed at the trailing edge as the surface wave and wake.

The current analysis of a bee’s hydrofoiling capability lacks certain considerations. Here, only general features of the wing kinematics are described. In the future, more detailed wing kinematics need to be studied. One feature that has not been discussed is the apparent wing bending resulting from its compliance. The interaction between a compliant wing and hydrodynamic forces would result in a transient solid–fluid wave. This wave is a dynamic phenomenon, which introduces a timescale to the well-studied quasistatic interaction between flexible sheet and hydrostatic forces (18, 19). The wave motion on the wing would be governed by the bending stiffness of the wing and the added mass of the water. If the mass of the thin elastic sheet is negligible compared to the accelerating water mass, the wave speed, c, should scale as c² ∼ k² × (bending stiffness)/(added mass), where k is the wave number. The shape of the wing deformation would correspond to the sections of the traveling solid–fluid wave form.

Moreover, we did not discuss the effect of surface tension and gravitational force. The surface tension and gravitational force are an order of magnitude smaller than the added mass force (added mass number = added mass force/steady inertial force ∼20; Weber number = steady inertial force/surface tension ∼1, Froude number = steady inertial force/gravitational force ∼3; SI Appendix, Detailed Calculations III). Although these forces are relatively small, they may be important in determining the boundary conditions at the leading and trailing edges of the wing. For instance, the shedding of surface wave and wake might be determined by the impedance mismatch at the trailing edge (the impedance of the elastic sheet region would be water density times the wave speed described above; the impedance of the water surface region would be water density times the wave speed governed by the surface tension and gravitational force). The mismatched impedance would determine how much of the propagating solid–fluid wave would be transmitted and reflected at the trailing edge.

Discussion

Comparison with Other Water Surface Locomotion.

The hydrofoiling of the honeybee is a form of biolocomotion that has not previously been characterized. Most semiaquatic insects utilize thin hydrophobic legs for their propulsion, known as water walking (20–22). Water walking relies on the surface tension rather than the inertia of water, characterized by a small Weber number << O(1). The honeybee’s hydrofoiling involves the unsteady inertial force (i.e., added mass) as the dominant hydrodynamic force. Furthermore, whereas the power stroke of the water walker strikes down on the water surface, the bee’s power stroke lifts the water surface. Thus, the 2 locomotion strategies are dynamically, kinematically, and morphologically distinct.

The locomotion of the honeybee is also different from fully submerged aquatic insects that swim near the water surface, such as the whirligig beetle (23) and the water boatman (24). Both the whirligig beetle and water boatman use drag-based propulsion with their legs, which uses asymmetric power and recovery stroke speed and propulsive area to create net thrust. The drag-based propulsion relies on steady inertial force; however, unsteady inertial force is dominant in the honeybee’s hydrofoiling.

Another interesting water surface locomotion strategy is a Marangoni propulsion displayed by some hemipterans and rove beetles (21, 22). These insects locally release a surfactant (a chemical that lowers surface tension) to create uneven surface tension around their bodies. The resulting surface tension gradient provides forward thrust. The Marangoni propulsion mechanism is different from the mechanically driven propulsion strategies mentioned above, as it is driven chemically.

Perhaps most similar to the honeybee’s hydrofoiling locomotion is a rowing locomotion of the stonefly (7). Rowing is one of the stonefly’s locomotion modes that mixes both hydrodynamic (drag-based) and aerodynamic (lift-based) propulsion. It is interesting to note that this locomotion may also utilize added mass (unsteady inertial force) as part of its propulsion. From the video provided in the referenced paper, it appears that the stonefly’s forewing supinated before detaching from the water. Presumably, this wing kinematics produce similar acceleration of the water mass underneath the lifting wing. The stonefly’s wing motion appears to be more effective for propulsion, because after wing detaches from the water surface, the wing no longer interacts with the accelerated water mass.

Compared to water surface locomotion of other insects, neither the speed nor the efficiency achieved by the honeybee’s hydrofoiling impresses. The 3 body length per s speed is much slower than the top speed of water striders, whirligig beetles, and water boatmen. Moreover, we have observed that honeybees can sustain hydrofoiling for only about 2 to 5 min. The short duration might indicate large consumption of energy or muscle fatigue, most likely as the consequence of accelerating and decelerating a fluid 1,000 times denser. Nevertheless, this duration gives honeybees a range of approximately 5 to 10 m, which may be enough to reach the shore. When bees were placed on the surface of a local pond, they were able to locomote to the shore and pull themselves out of the water. A similar observation was reported in a previous study (25). Once out of the water, they dry themselves for a short time and fly away.

Applications to Robotics.

The hydrofoiling mechanism inspires an aerial–aquatic hybrid vehicle. The honeybee’s propulsion with wetted wings show that the flapping-wing system is a viable way to generate thrust both in the air and on a water surface. As such, this mechanism could provide flapping aerial vehicles with swimming capability on water surfaces without imposing significant changes to their morphologies. For successful implementation of the hydrofoiling mechanism in a robotic system, several parameters need to be considered.

First, the scaling analysis suggests that the unsteady inertial force is important for generating thrust. The unsteady inertial force scales with amplitude and frequency of the wing motion (SI Appendix, Detailed Calculations III); thus, increasing amplitude and frequency can augment propulsion. Second, it is important for the wing’s leading edge to move diagonally, rather than vertically. This is so the wing generates a horizontal component of thrust. Third, to take advantage of a passive supination and pronation of the wing, it is important to consider the solid–fluid interaction timescale, which is governed by the suggested wave speed, c. The much weaker net force of hydrofoiling, compared to that of flight, is due to the large deceleration of body speed during the recovery stroke (Fig. 3). By timing the recovery stroke to more precisely coincide with passive pronation, a flattened wing may reduce the negative thrust generated and thus improve overall thrust production. Last, wing surface microstructures and chemistry may provide another opportunity to bypass negative thrust generation. The static and dynamic hydrophobicity of the water-walking insect’s legs (26) and the wings of the stonefly (5) are affected by hair and surface chemistry. If the hydrofoiling wing can detach from the water surface following the power stroke, the recovery stroke may be able to avoid adverse thrusting.

Biological Implications.

Hydrofoiling may also have important biological implications on the survival of water-collecting honeybees. On a hot summer day, 10 to 14% of the foraging honeybees collect water instead of nectar for hive thermoregulation (27). With increased activity near the water, foragers may fall onto a water surface more often. Although hydrofoiling with wetted wings is not as effective as flying, when becalmed on a water surface, the ability to self-propel to shore may increase the chance of survival.

More broadly, winged locomotion on a water surface could be an evolutionarily important category of biolocomotion. One of the hypotheses on the origin of insect flight is that flight evolved from the locomotion on a water surface (7), on which the weight of an organism is offset by either buoyancy or surface tension. While it is unlikely that the honeybee’s flight evolved from their water surface locomotion, the mechanism of hydrofoiling may have biomechanical resemblances to early preflight locomotion.

Materials and Methods

Mechanical Wing Model.

The mechanical model was constructed to simulate the wing kinematics of the bee (SI Appendix, Fig. S8). The model was constructed from a magnetic actuator (Plantraco Microflight) and a wing frame connected to a plastic platform. The magnetic actuator uses a magnetic field generated by the electric current flowing through copper coil to torque the lever with neodymium magnets. The wing frame was constructed by bending a steel wire with 0.38-mm diameter. The wings were constructed from a polyester film with 12.7-μm thickness. The polyester film was cut into a rectangle shape with 0.75-inch span length and 0.25-inch chord length.

The wing motion was generated by the magnetic actuator pulling on the 2 ends of the wing frame with a silk string. A function generator (HP 3314A) was used to power and control the magnetic actuator with a square wave of 50% duty cycle at varying frequencies.

Data Availability Statement.

All data discussed in the paper will be made available to readers upon request. The flow field data in Fig. 5 are available at https://data.caltech.edu/records/1292. MATLAB code developed during the current study are available from the corresponding author upon reasonable request.