Dopamine depletion alters macroscopic network dynamics in Parkinson’s disease

Using a dynamic graph theoretical approach, Shine et al. show that individuals with Parkinson’s disease demonstrate heightened network-level integration during the ‘Off’ state that is inversely correlated with motor symptom severity. Network-level integration relates to two measures of neurocognitive reserve, suggesting a protective function for ‘Off’ state integration.

Abstract

Parkinson’s disease is primarily characterized by diminished dopaminergic function; however, the impact of these impairments on large-scale brain dynamics remains unclear. It has been difficult to disentangle the direct effects of Parkinson’s disease from compensatory changes that reconfigure the functional signature of the whole brain network. To examine the causal role of dopamine depletion in network-level topology, we investigated time-varying network structure in 37 individuals with idiopathic Parkinson’s disease, both ON and OFF dopamine replacement therapy, along with 50 age-matched, healthy control subjects using resting state functional MRI. By tracking dynamic network-level topology, we found that the Parkinson’s disease OFF state was associated with greater network-level integration than in the ON state. The extent of integration in the OFF state inversely correlated with motor symptom severity, suggesting that a shift toward a more integrated network topology may be a compensatory mechanism associated with preserved motor function in the dopamine depleted OFF state. Furthermore, we were able to demonstrate that measures of both cognitive and brain reserve (i.e. premorbid intelligence and whole brain grey matter volume) had a positive relationship with the relative increase in network integration observed in the dopaminergic OFF state. This suggests that each of these factors plays an important role in promoting network integration in the dopaminergic OFF state. Our findings provide a mechanistic basis for understanding the Parkinson’s disease OFF state and provide a further conceptual link with network-level reconfiguration. Together, our results highlight the mechanisms responsible for pathological and compensatory change in Parkinson’s disease.

Introduction

Parkinson’s disease is a common neurological disorder characterized by degeneration of the dopaminergic midbrain. This pathological insult to the brainstem results in a severe dopamine depletion throughout ascending neural pathways innervating the basal ganglia, thalamus and cortex (Braak et al., 2004). The impact of such extensive dopaminergic loss on brain network dynamics remains poorly understood, partly due to the fact that dopamine depletion has been linked to both pathological and compensatory changes in brain network organization and connectivity (Bohnen and Martin, 2014; Bell et al., 2015; Poston et al., 2017).

Studies using resting state functional MRI in Parkinson’s disease consistently show alterations in functional connectivity that impact a diverse set of brain regions, including both cortico-cortical and cortico-subcortical architectures. In the dopaminergic OFF state, cortico-striatal hyperconnectivity is often observed, particularly in motor networks involving the subthalamic nucleus and primary motor cortex (Wu et al., 2010; Baudrexel et al., 2011; Kwak et al., 2012). However, alterations in interstriatal connectivity, and across a range of cortico-striatal networks, have also been shown (Helmich et al., 2010; Wu et al., 2010; Bell et al., 2015). Importantly, many of these abnormalities are normalized with dopamine replacement pharmacotherapy (Wu et al., 2010; Kwak et al., 2012), suggesting that dopamine medication may play a role in both correcting pathological activity and alleviating compensatory reorganization.

The effects of pharmacological manipulation on functional brain network architecture are often non-linear (Brezina, 2010; Marder, 2012; Tahmasian et al., 2015). For instance, increases in neural activity when OFF dopaminergic therapy may reflect the compensatory engagement of non-dopaminergic systems of the brainstem or network reorganization across the cortex and subcortex. This concept is supported by a general principal of compensation observed in ageing and neurodegeneration, wherein relatively spared circuits and networks are over-engaged to support dysfunctional nodes (Grafman, 2000). In Parkinson’s disease this effect can be observed as shifts in the topography of cortico-striatal connectivity. For example, less dopaminergically depleted striatal zones (such as the anterior putamen) may increase their coupling with cortical sensorimotor areas to overcome relatively severe posterior striatal dopamine pathology (Helmich et al., 2010; Hacker et al., 2012). Alternatively, cortico-cerebellar connections may be increasingly engaged to offset impaired cortico-striatal function (Wu and Hallett, 2013; O’Callaghan et al., 2016). When these instances of hyperconnectivity are associated with preserved behavioural function, this implies an adaptive reallocation of activity in response to focal pathological changes (Hillary and Grafman, 2017). It is also possible that in some instances, functional circuit reorganization may represent a pathological loss of network segregation or specialization (Fornito et al., 2015; Hillary and Grafman, 2017). This could conceivably occur as a ‘knock-on’ effect at the cortical network level, stemming from a fundamental loss of segregation in basal ganglia subcircuits (Nieuwhof et al., 2017), which in turn would cause an increase in correlated activity in previously segregated neural populations (Bar-Gad et al., 2003; Wilson, 2013).

Whether the changes are compensatory or pathological, the current mechanisms supporting rearrangement of large-scale cortical patterns in the dopamine-depleted state are unclear. Ultimately, the degree of compensatory versus maladaptive change may be determined by the relative balance between focused increases in connectivity and a more general loss of segregation. Importantly, this concept can be examined using network analytic approaches. Using the mathematical formalism of graph theory, network communities are taken to represent densely interconnected neural elements in which local connections are highly segregated. In contrast, network hubs integrate diverse communities, enabling channels for effective information integration (van den Heuvel and Sporns, 2013; Bertolero et al., 2017). These organizational principles are thought to balance the specialization of function with the integration of information (Park and Friston, 2013; Deco et al., 2015), and this balance gives rise to complex neural dynamics that span multiple spatiotemporal scales (Honey et al., 2012; Deco et al., 2013).

Here, we used time-resolved functional connectivity of resting state functional MRI in combination with graph theoretical analyses to determine the balance between integration and segregation in the face of dopaminergic depletion in Parkinson’s disease. To date, studies of network topology in neurological disease have largely focused on structural brain networks and time-averaged resting state functional networks, which represent an inherently ‘static’ snapshot of brain architecture (Breakspear, 2017). However, recent advances in the statistical analysis of time-varying resting state functional MRI data have demonstrated that functional brain organization is dynamic over the course of seconds to minutes (Zalesky et al., 2014; Betzel et al., 2016; Shine et al., 2016) and that fluctuating network dynamics are crucial for normal cognitive (Shine et al., 2016; Hearne et al., 2017) and motor (Bassett et al., 2011) function. Examination of time-varying functional network architecture provides an opportunity to explore the balance between segregated and integrated neural dynamics in both health and disease.

In determining the impact of dopamine depletion on dynamic network architecture in Parkinson’s disease, we further aimed to establish whether certain functional patterns in the OFF state may be linked to a compensatory mechanism. Defining compensatory activity in neurodegeneration is a non-trivial problem (Gregory et al., 2017). Brain and cognitive reserve refer to aspects of structural integrity that support increased functional resilience, and the preservation of function in the face of underlying degeneration, respectively (Fratiglioni and Wang, 2007). Importantly, these concepts can be operationalized using grey matter integrity (as a surrogate of brain reserve) and educational level or general intelligence quotient (as a surrogate of pre-morbid cognitive reserve) (Stern, 2017). These metrics can then be compared to network-level topological changes to provide an estimate of the extent to which brain organization is related to functional and structural resilience.

To examine the dynamic network architecture of the resting brain in the OFF compared with the ON dopaminergic state, we related network topology to motor function in the OFF state, and also to measures of cognitive and brain reserve. We hypothesized that removal of dopaminergic medications would lead to a relatively integrated network topology, which should also relate to a preservation of motor function in the OFF state. In addition, any compensatory pattern should be observed in the positive relationship between network topology and both cognitive and brain reserve.

Materials and methods

Participants

Thirty-seven patients were recruited from the Parkinson’s Disease Research Clinic at the Brain and Mind Centre, University of Sydney, Australia. All patients satisfied the UK Parkinson’s Disease Society Brain Bank criteria and were not demented (Martinez-Martin et al., 2011). Patients were assessed on the Hoehn and Yahr Scale and the motor section of the Unified Parkinson’s Disease Rating Scale (UPDRS-III) in the dopaminergic OFF state. The Mini-Mental State Examination (MMSE) was administered as a measure of general cognition.

Participants with Parkinson’s disease were assessed on two occasions: (i) ON their regular dopaminergic medications; and (ii) OFF following overnight withdrawal (i.e. 12–18 h) of dopaminergic medications (5.2 ± 1.4 weeks between sessions). Dopaminergic dose equivalence (DDE) scores were calculated for each patient. Specifically, 10 patients were on l-DOPA monotherapy; nine were on l-DOPA plus a dopaminergic agonist; a further eight were on l-DOPA plus adjuvant therapy (rasagaline, entacapone or a monoamine oxidase inhibitor); seven were on a combination of l-DOPA, dopaminergic agonist and adjuvant therapy; one patient was on dopaminergic agonist monotherapy, and two were on an agonist plus adjuvant therapy. No participant was taking any psychoactive medications.

Fifty healthy controls were recruited to participate in the study. Control participants were screened for a history of neurological or psychiatric disorders, and no controls were using psychoactive medications. Patients with Parkinson’s disease and healthy controls were matched for age and education. The study was approved by the local Ethics Committees and all participants provided informed consent in accordance with the Declaration of Helsinki. See Table 1 for demographic details and clinical characteristics.

Table 1.

Demographics and patient clinical characteristics

	Control	Parkinson’s disease
n	50	37
Sex, male:female	14:36	29:8
Age	65.82 (7.8)	65.05 (7.2)
Education	13.51 (2.8)	13.50 (3.0)
MMSE	29.00 (1.2)	28.59 (2.2)
BDI-II	9.41 (7.3)	10.67 (8.6)
Duration, years diagnosed	–	6.41 (4.2)
DDE, mg/day	–	808.54 (503.0)
Hoehn and Yahr stage	–	2.14 (0.8)
UPDRS III, ‘OFF’	–	32.00 (16.3)
PIGD:TD	–	30:7
NART	–	111.08 (10.3)

Values are presented as mean (standard deviation).

BDI-II = Beck Depression Inventory-II; DDE = dopaminergic dose equivalence; MMSE = Mini-Mental State Examination; PIGD = postural instability and gait dominant; TD = tremor dominant; UPDRS III = motor section of the Unified Parkinson's Disease Rating Scale. There were no significant differences in age, education, MMSE or BDI-II between the two groups, though there were differences in gender (P < 0.05).

Behavioural and neuropsychological assessment

Mood was assessed via a self-report questionnaire, the Beck Depression Inventory-II (BDI-II) (Beck et al., 1996). Patients were also administered the National Adult Reading Test (NART) (Bright et al., 2016), and their predicted pre-morbid full-scale IQ was calculated. The NART is an established measure of premorbid intelligence and serves as a surrogate of cognitive reserve, with the benefit of offering greater variance than years of education in a homogenous sample (Stern et al., 2003). These measures were assessed in the dopaminergic ON state. Results from these measures are also shown in Table 1.

Imaging acquisition

Imaging was conducted on a General Electric 3 T MRI. Whole-brain 3D T₁-weighted sequences were acquired as follows: coronal orientation, matrix 256 × 256, 200 slices, 1 × 1 mm² in-plane resolution, slice thickness 1 mm, echo time/repetition time = 2.6/5.8 ms. T₂*-weighted echo planar functional images were acquired in interleaved order with repetition time = 3 s, echo time = 32 ms, flip angle 90^°, 32 axial slices covering the whole brain, field of view = 220 mm, interslice gap = 0.4 mm, and raw voxel size = 3.9 × 3.9 × 4 mm thick. Each resting state scan lasted 7 min (140 repetition times). During the resting state scan, patients were instructed to lie awake with their eyes closed and to let their minds wander freely.

Resting state functional MRI data

Preprocessing and analyses of resting state data were conducted using SPM12 (http://www.fil.ion.ucl.ac.uk/spm/software/). Scans were first slice-time corrected to the median slice in each repetition time, then realigned to create a mean realigned image, with measures of 6 degrees of rigid head movements calculated for later use in the correction of minor head movements. For quality assurance, each trial was analysed using ArtRepair and trials with a large amount of global drift or scan-to-scan head movements >1 mm were corrected using interpolation. None of the subjects included in this study demonstrated scan-to-scan head movements >3 mm (<1 voxel breadth). Images were normalized to the Echo Planar Image template, resampled to 3 mm isotropic voxels and then subsequently smoothed using a 4 mm full-width at half-maximum isotropic Gaussian kernel.

Temporal artefacts were identified in each dataset by calculating framewise displacement (FD) from the derivatives of the six rigid-body realignment parameters estimated during standard volume realignment (Power et al., 2014), as well as the root mean square change in BOLD signal from volume to volume (DVARS). Frames associated with FD > 0.25 mm or DVARS > 2.5% were identified. However, as no participants were identified with >10% of the resting time points exceeding these values, no sessions were excluded from further analysis. However, to ensure that neither head motion nor the global signal were influencing group effects, we re-ran the analysis after: (i) scrubbing data with FD > 0.25 mm or DVARS > 2.5%; or (ii) global signal regression. Both analyses revealed similar group-level effects. No cardiorespiratory data were available, and hence, were not accounted for in our analysis.

Following artefact detection, nuisance covariates associated with the 12 linear head movement parameters (and their temporal derivatives), FD, DVARS, and anatomical masks from the CSF and deep cerebral white matter were regressed from the data using the CompCor strategy (Behzadi et al., 2007). In keeping with previous time-resolved connectivity experiments (Bassett et al., 2015), a temporal bandpass filter (0.071 < f < 0.125 Hz) was applied to the data. Finally, given the importance of head motion in functional connectivity analyses, we compared the mean and standard deviation of framewise displacement (Power et al., 2014) across the entire resting state session across the three groups (controls, Parkinson’s disease ON and Parkinson’s disease OFF).

Brain parcellation

Following preprocessing, the mean time series was extracted from 377 predefined parcels. To ensure whole brain coverage, we extracted: 333 cortical parcels (161 and 162 regions from the left and right hemispheres, respectively) using the Gordon atlas (Gordon et al., 2014); 14 subcortical regions from Harvard-Oxford subcortical atlas (bilateral thalamus, caudate, putamen, ventral striatum, globus pallidus, amygdala and hippocampus; http://fsl.fmrib.ox.ac.uk/); 28 cerebellar parcels from the SUIT atlas (Diedrichsen, 2006), and bilateral subthalamic nucleus parcels (Lambert et al., 2012) for each participant in the study. Because of the spatial resolution of our data, we were unable to adequately distinguish between the internal and external segment of the globus pallidus, and hence have included these regions, which admittedly have distinct functional capacities within the basal ganglia circuitry, as a single parcel in our analysis.

Time-resolved functional connectivity

To estimate functional connectivity between the 377 parcels, we used the multiplication of temporal derivatives (MTD) metric (Shine et al., 2015). The MTD is computed by calculating the point-wise product of temporal derivative of pairwise time series (Equation 1). The MTD is averaged by calculating the mean value over a temporal window, w. Time-resolved functional connectivity was calculated between all 377 brain regions using the MTD within a sliding temporal window of 15 time points (∼33 s), which allowed for estimates of signals amplified at ∼ 0.1 Hz (Shine et al., 2015). Individual functional connectivity matrices were then calculated within each temporal window, thus generating a weighted 3D adjacency matrix (region × region × time) for each participant.

$$MT{D}_{ijt}=\frac{1}{w}{\displaystyle \sum }_{t-\frac{w}{2}}^{t+\frac{w}{2}}\frac{\left(d{t}_{it}\times d{t}_{jt}\right)}{\left({\sigma }_{d{t}_i}\times {\sigma }_{d{t}_j}\right)}$$ (1)

For each time point, t, the MTD for the pairwise interaction between region i and j is defined according to Equation 1, where dt is the first temporal derivative of the i^th or j^th time series at time t, σ is the standard deviation of the temporal derivative time series for region i or j and w is the window length of the simple moving average. This equation can then be calculated over the course of a time series to obtain an estimate of time-resolved connectivity between pairs of regions.

Time-resolved community structure

The Louvain modularity algorithm was applied to the functional connectivity time series using the Brain Connectivity Toolbox (Rubinov and Sporns, 2010). The Louvain algorithm iteratively maximizes the modularity statistic, Q, for different community assignments until the maximum possible score of Q has been obtained (Equation 2). The modularity estimate for a given adjacency matrix quantifies the extent to which the network may be subdivided into communities with stronger within-module than between-module connections. Using this technique, time-averaged and time-resolved community structure was calculated for each participant.

$$Q_T=\frac{1}{{\mathcal{v}}^{+}}{\displaystyle \sum }_{ij}\left(w_{ij}^{+}-e_{ij}^{+}\right){\delta }_{M_i{M}_j}-\frac{1}{{\mathcal{v}}^{+}+{\mathcal{v}}^{-}}{\displaystyle \sum }_{ij}\left(w_{ij}^{-}-e_{ij}^{-}\right){\delta }_{M_i{M}_j}$$ (2)

where v is the total weight of the network (sum of all negative and positive connections), w_ij is the weighted and signed connection between regions i and j, e_ij is the strength of a connection divided by the total weight of the network, and δ_MiMj is set to 1 when regions are in the same community and 0 otherwise. The plus and minus sign symbols denote all positive and negative connections, respectively.

For each temporal window, regional community assignment was assessed 500 times and a consensus partition was identified using a fine-tuning algorithm from the Brain Connectivity Toolbox. This then afforded an estimate of both the time resolved modularity (Q_T) and cluster assignment (Ci_T) within each temporal window for each participant in the study. To define an appropriate value for the γ parameter, we iterated the Louvain algorithm across a range of values (0.5–2.5 in steps of 0.1) for 100 iterations of a single subject’s (sub1) time-averaged connectivity matrix and then estimated the similarity of the resultant partitions using mutual information. A γ parameter of 1.1 provided the most robust estimates of topology across these iterations (quantified by the minimum standard deviation across 100 iterations of the Louvain algorithm).

Cartographic profiling

Based on time-resolved community assignments, we estimated within-module connectivity by calculating the time-resolved module-degree Z-score (W_T; within module strength) for each parcel (Equation 3) (Guimerà and Nunes Amaral, 2005).

$$W_{iT}=\frac{{\kappa }_{iT}-{\mathrm{\kappa `}}_{s_{iT}}}{{\sigma }_{{\kappa }_{s_{iT}}}}$$ (3)

Module degree Z-score, W_iT, where κ_iT is the strength of the connections of region i to other regions in its module s_i at time T, ${\mathrm{\kappa `}}_{s_{iT}}$ is the average of κ over all the regions in s_i at time T, and ${\sigma }_{{\kappa }_{s_{iT}}}$ is the standard deviation of κ in s_i at time T.

To calculate between-module connectivity (B_T), we used the participation coefficient, B_T, quantifying the extent to which a region connects across all modules (i.e. between-module strength) (Equation 4).

$$B_{iT}=1-{\displaystyle \sum }_{s=1}^{n_M}{\left(\frac{{\kappa }_{isT}}{{\kappa }_{iT}}\right)}^2$$ (4)

Participation coefficient B_iT, where κ_isT is the strength of the positive connections of region i to regions in module s at time T, and κ_iT is the sum of strengths of all positive connections of region i at time T. The participation coefficient of a region is therefore close to 1 if its connections are uniformly distributed among all the modules and 0 if all of its links are within its own module.

To track fluctuations in cartography over time, for each temporal window, we computed a joint (i.e. 2D) histogram of within- and between-module connectivity measures, referred to here as a ‘cartographic profile’ (Fig. 1B). The cartographic profile is a group-level joint histogram of the B_T and W_T scores for each region, stretched out into two dimensions (x-axis: B_T; y-axis: W_T). The intensity in this graph reflects points in the topological space in which multiple regions share a similar topological signature. Interrogations of the cartographic profile (e.g. correlations against clinical symptoms) allow comparisons to be made with respect to the network as a whole, independent of whether a particular region was highly integrated or segregated. In this way, clinical symptoms (for example) can be correlated with a network-level metric of integration or segregation. The resolution of the joint histogram is user-defined and was set to 100 × 100 for our analysis—importantly, this parameter does not change the qualitative interpretation of the results. Code for this analysis is freely available at https://github.com/macshine/integration/.

Figure 1.

Network topology as a function of dopaminergic state. (A) Global mean participation coefficient (B_T) in controls (blue), Parkinson’s disease ON (green) and Parkinson’s disease OFF (red). P < 0.001. (B) Force-directed plots comparing Parkinson's disease ON and OFF dopaminergic medication. Edges represent top 1% of connections in time averaged connectivity matrix and colours of nodes reflect predefined network identity of each region. (C) Cartographic profile comparing Parkinson’s disease OFF > Parkinson’s disease ON. Subjects were more integrated (i.e. rightward shift on the B_T axis) in the OFF compared to the ON state. (D) Surface plot of regions with significantly increased participation (B_T) during OFF state. COn = cingulo-opercular network; CPar = cingulo-parietal network; DAN = dorsal attention network; FPN = frontoparietal network; FTp = fronto-temporal network; PD = Parkinson’s disease; RSp = retrosplenial network; SMh = somatomotor hand network; SMm = somatomotor mouth network; VAN = ventral attention network; Subcort = subcortical network.

Regional flexibility

The flexibility of each brain parcel was calculated by the percentage of temporal windows in which an individual region ‘switched’ between modules, normalized to the total number of modules in the data (as estimated in the previous step). Code was obtained directly from the original author (http://www.danisbassett.com/resources/). As the modular assignment was essentially arbitrary within each unique temporal window, we used a version of the Hungarian algorithm to assign regions to modules with consistent values over time.

Grey matter extraction

Grey matter extraction was performed using the FMRIB software library package FSL (http://www.fmrib.ox.ac.uk/fsl/). Scans were skull-stripped using the BET algorithm in FSL (Smith, 2002) and tissue segmentation was completed using FMRIB’s Automatic Segmentation Tool (FAST v4.0) (Zhang et al., 2001). A study-specific grey matter template was created using the maximum equal number of scans from both groups (37 from each) and registered to the Montreal Neurological Institute Standard space (MNI 152) using a non-linear b-spline representation of the registration warp field. Grey matter partial volume maps were non-linearly registered to the study template and modulated by dividing by the Jacobian of the warp field, to correct for any contraction/enlargement caused by the non-linear component of the transformation; this step corrects for total intracranial volume (ICV) so that it does not need to be included as a confounding covariate (Good et al., 2002). After normalization and modulation, the grey matter maps were smoothed with an isotropic Gaussian kernel with a sigma of 2 mm.

Whole brain grey matter volume (mm³) was then extracted for each participant. The total volume of non-zero voxels was extracted from the grey matter mask automatically generated from FAST. Using the smoothed and registered images, the mean proportion of grey matter per voxel from non-zero voxels was extracted for each subject using fslstats. Multiplying the volume within the mask by each subjects’ mean grey matter proportion inside the mask gave a measure of total grey matter volume for each person. We used whole brain grey matter volume (corrected for total ICV), a specific indicator of grey matter structural integrity, as our measure of brain reserve. For completeness, we also calculated total ICV, as it is a commonly used proxy for brain reserve. Total ICV was calculated for each individual by summing the segmented grey matter, white matter and CSF volumes obtained from the FAST procedure. We re-ran our analysis using total ICV as a measure of brain reserve to confirm that similar results were obtained using both total grey matter volume and total ICV as indicators of brain reserve.

Statistical analyses

To determine whether there were any abnormalities in functional network topology between groups, the mean cartographic profile for each Parkinson’s disease patient was compared between medication states (paired-sample t-test for each bin of the cartographic profile; FDR q ≤ 0.05) and between groups (independent-samples t-test for each bin; FDR q ≤ 0.05). Regional W_T and B_T scores were also compared across groups using independent-samples t-tests. Results were consistent when only analysing the subgroup of 30 individuals with postural instability and gait dominant-type Parkinson’s disease.

To determine the clinical relevance of functional network reconfiguration, we measured the correlation of the difference in the cartographic profile between the OFF and ON state with the severity of motor impairments in the OFF state (measured using UPDRS III) using a Spearman’s rho correlation (due to the non-parametric nature of the data).

To determine whether network level integration related to brain reserve in the individuals with Parkinson’s disease, we fit a general linear model that fit grey matter volume, predicted full-scale IQ (as estimated using normalized NART scores) and the interaction between these two measures of reserve (i.e. Grey Matter × NART) to the amount of integration present in the OFF versus ON state, while co-varying for age. Given that the interaction between Grey Matter × NART and network integration was the most effective way to test our hypothesis, we have focused our interpretation on the significant interaction term (Brambor et al., 2006). However, it is important to note that the non-significant lower order effects were in the same expected (positive) direction as the interaction term (Supplementary Fig. 1). Separate analyses were conducted at the global (i.e. cartographic profile) and regional (i.e. parcel-wise) level.

Data availability

The data that support the findings of this study are available from the corresponding author, upon reasonable request.

Results

Head motion

There were no significant differences in head movement between healthy control subjects and individuals with Parkinson’s disease in either medication state (mean framewise displacement: controls 4.9 × 10⁻⁴ ± 3.3 × 10⁻⁴, Parkinson’s disease ON: 5.7 × 10⁻⁴ ± 5.3 × 10⁻⁴; Parkinson’s disease OFF: 5.8 × 10⁻⁴ ± 5.0 × 10⁻⁴; all P > 0.200) or between dopaminergic states in the Parkinson’s disease group (P > 0.200). In addition, there was no relationship between mean framewise displacement and network integration differences across medication states (P > 0.200), nor a relationship between time-varying framewise displacement and fluctuations in network topology (P > 0.200 in both the OFF and ON states).

Relationship between network topology and dopaminergic state

In the dopaminergic OFF state, individuals with Parkinson’s disease demonstrated a more integrated functional network topology than those ON medication or healthy controls (Fig. 1A and B; P < 0.001). The magnitude of regional between-module integration was significantly higher in the OFF state (relative to the ON state) across medial and lateral frontoparietal cortical regions (Fig. 1B). These changes were diffusely mediated across multiple subsystems, including frontoparietal, cingulo-opercular, salience and dorsal attention networks (Fig. 1C and D). The majority of patients in our study (30/37) had an akinetic-rigid phenotype (tremor dominant/postural instability and gait dominant ratio ≤ 0.9), which did not allow us to formally test whether the results were related to individual differences in Parkinson’s disease syndromes.

Relationship between network topology and motor symptom severity

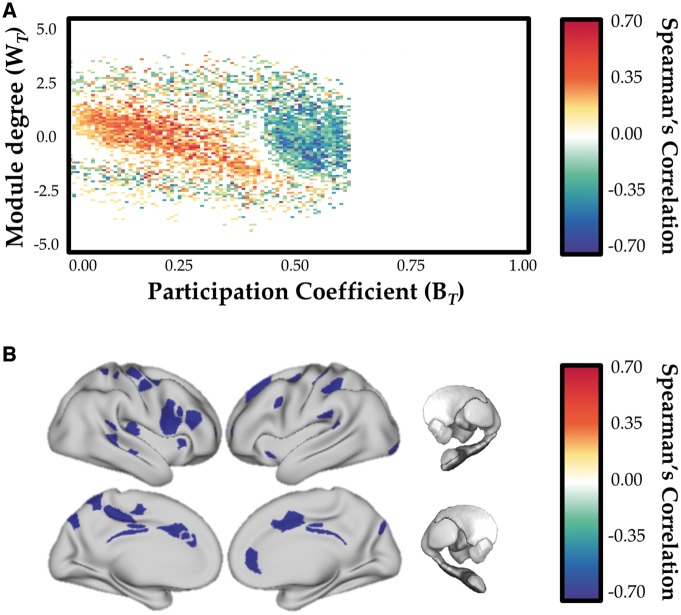
There was a significant inverse correlation between network-level integration and UPDRS III scores as measured in the OFF state (Fig. 2A) that was maximal in right dorsolateral prefrontal cortex, bilateral dorsal anterior cingulate, bilateral retrosplenial cortex and sensorimotor cortex (Fig. 2B). This is consistent with greater integration in those regions being associated with less severe motor impairment on UPDRS motor scale. In addition, we also observed a positive correlation between network level integration and disease severity (as indexed by DDE scores; r = 0.451; P = 0.003), confirming the relationship between Parkinson’s disease symptom severity and network level reconfiguration in the OFF state.

Figure 2.

Relationship between network topology and motor severity. (A) Inverse relationship between cartographic profile (Parkinson’s disease OFF > Parkinson’s disease ON) and UPDRS III (motor) severity (estimated in the dopaminergic OFF state): greater integration (i.e. rightward shift on the B_T axis) was inversely correlated with motor severity. (B) Parcels with significant inverse correlation between B_T (OFF > ON) and UPDRS III. FDR q ≤ 0.05.

Effects of dopaminergic state on regional flexibility

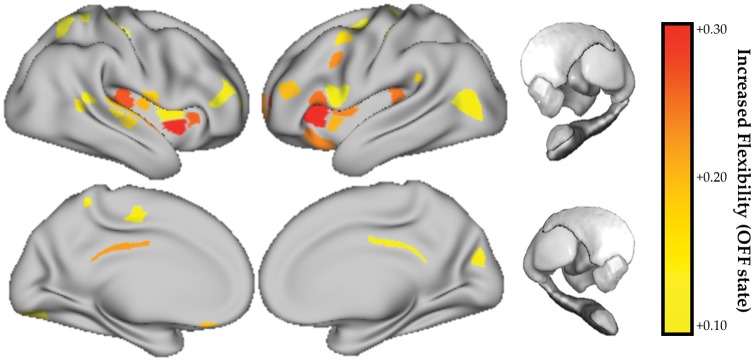
Regions were more likely to switch their modular allegiance more frequently in the dopaminergic OFF state as compared to the ON state, and to a greater extent than control subjects (P < 0.001). We observed a distributed set of insular, frontal and parietal regions that demonstrated an increase in topological flexibility and/or decreased modular stability in the resting state following dopaminergic withdrawal (Fig. 3). We did not observe a relationship between flexibility and motor severity (all P > 0.05).

Figure 3.

Topological flexibility as a function of dopaminergic state. Regions with increased topological flexibility (increased frequency of modular switching) in the OFF > ON dopaminergic state. FDR q ≤ 0.05. No regions showed a significant decrease in flexibility in the OFF state.

Relationship between network topology and brain reserve

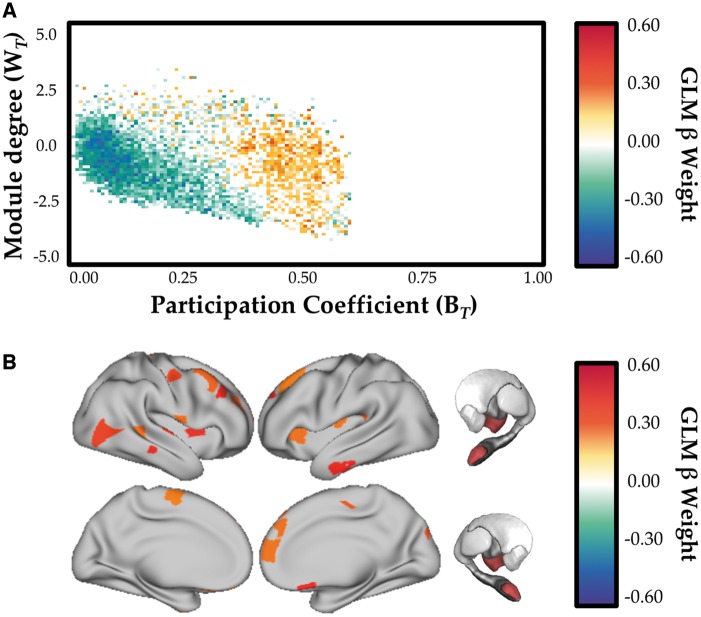
Using a linear mixed effects model specifying grey matter (Supplementary Fig. 1A), NART (Supplementary Fig. 1B) and Grey matter × NART (Fig. 4A) adjusting for age and gender as fixed covariates, we observed a positive relationship (FDR q ≤ 0.05) between network topology and the interaction between grey matter volume and NART-predicted IQ scores that was maximal in frontal cortex, insula, thalamus and amygdala (Fig. 4B; FDR q ≤ 0.05).

Figure 4.

Relationship between network topology and neurocognitive reserve. (A) Relationship between cartographic profile (Parkinson’s disease OFF > Parkinson’s disease ON) and interaction between grey matter volume and education level (NART). FDR q ≤ 0.05. Subjects with greater NART and grey matter scores were more integrated (i.e. rightward shift on the B_T axis) in the OFF compared to the ON state. (B) Regions with significant relationship between B_T (OFF > ON) and the interactions between brain (mean grey matter) and cognitive (NART) reserve, estimated using a linear mixed effects model. FDR q ≤ 0.05. GLM = general linear model.

Discussion

In this study, we demonstrated causal evidence for large-scale network reconfiguration in the OFF state in individuals with idiopathic Parkinson’s disease as compared to the dopaminergic ON state, consistent with an increase in topological integration (Fig. 1) and flexibility (Fig. 3). Within this general shift toward a more integrated state, a distributed set of regions were inversely correlated with motor symptom severity (Fig. 2), suggesting that increased integration may provide compensatory processes that offset clinical motor severity. Furthermore, we showed an association between the magnitude of integration in the OFF state and measures of grey matter volume and premorbid intelligence. This suggests that a topological shift in response to dopamine depletion is related to neurocognitive reserve (Fig. 4). Together these results show that the effect of dopamine depletion in Parkinson’s disease results in a global shift toward integration, and that this increased integration may serve some compensatory function, the extent of which may be determined by underlying cognitive and brain reserve.

Withdrawal from dopamine replacement therapy altered network topology in the medial frontal, lateral parietal and anterior temporal cortices (Fig. 1D). Importantly, these regions also exhibited an increase in topological flexibility in the OFF state, suggesting that they were not effectively ‘locked’ into an integrated state, a result that may have argued against a possible compensatory role for increased integration in the OFF state. Similar regions were inversely correlated with OFF state motor symptom severity (Fig. 2B), suggesting that regional and network-level integration may help maintain motor function in the face of dopamine depletion. It is currently unclear whether the possible compensatory benefits identified here are specific to motor impairments (as indexed by MDS-UPDRS III) or will extend into cognitive and affective domains.

The possibility that increased topological integration in the face of dopamine depletion may be associated with a compensatory function supports and extends a growing literature that highlights the importance of network level hyperconnectivity as an adaptive response to local pathological change in neurodegenerative disorders (O’Callaghan et al., 2016; Gregory et al., 2017; Hillary and Grafman, 2017). In Parkinson’s disease, this response has previously been observed and interpreted based on static measures of resting state functional MRI (Helmich et al., 2010; Wu et al., 2010; O’Callaghan et al., 2016). Here, we provide a description of the underlying dynamic processes that might support these enhanced activations; however, it is worth mentioning that the vast majority of our participants presented with akinetic-rigid Parkinson’s disease, and hence further work is required to determine if this same effect is consistent across all Parkinson’s disease phenotypes.

Prior work has highlighted a link between increased resting state functional connectivity and markers of cognitive reserve (e.g. greater years of education) in diverse cohorts, including healthy ageing, and those with mild cognitive impairment and Alzheimer’s disease (Arenaza-Urquijo et al., 2013; Franzmeier et al., 2017, 2018). However, increased functional connectivity does not necessarily lend itself to a specific mechanistic interpretation per se. Using the mathematical formalism of graph theory, our results identify a relationship between premorbid intelligence and the capacity to promote functional integration, suggesting a possible dynamic mechanism that underpins the role of cognitive reserve in compensation.

The use of overall brain volume as a measure of brain reserve in our study is somewhat underspecified. Whole-brain grey matter volume incorporates a host of factors, including neuronal count, neuronal integrity and synaptic density, which jointly determine the brain’s ability to engage compensatory activity. Despite this caveat, the structural integrity of nodes (and hence, the grey matter volume) is proposed to mediate network controllability, and therefore may explain the role of brain reserve in supporting resilience of large-scale networks in ageing and neurodegeneration (Medaglia et al., 2017). Such nodes may indeed mediate the overall flexibility of brain networks, and allow for transitions between segregated and integrated states (Pasqualetti et al., 2014). Here, we identified a relationship between brain volume and the capacity to move toward a more integrated state. This result is consistent with the proposed hypothesis that brain volume may serve as a proxy for network controllability, as it captures within it a measure of the structural integrity of nodes involved in network control (Medaglia et al., 2017).

The prospect of compensatory network-level integration in the dopamine-depleted state raises the question of the potential mechanism for this effect. One plausible hypothesis is the relative integrity of other neuromodulatory neurotransmitter systems that contribute to global brain network dynamics (Brezina, 2010). Aside from the widespread dopaminergic loss that characterizes Parkinson’s disease, the disease is also associated with neuropathological alterations within the brainstem nuclei that supply the brain with noradrenaline (Rye and DeLong, 2003), acetylcholine (Müller and Bohnen, 2013) and serotonin (Politis and Niccolini, 2015). In the OFF state, compensatory drive may be determined by the degree of relative preservation in these nuclei and the ascending projections throughout the brain.

In the context of promoting network level integration, in healthy individuals a link has been observed between the ascending noradrenergic neuromodulatory system and global functional integration (Shine et al., 2016, 2018a, b), suggesting effective functioning of this system is crucial for modulating the gain and responsiveness of ongoing neuronal processing (Shine et al., 2018a). In addition, it has been proposed that activation of the locus coeruleus noradrenergic system across the lifespan is a crucial determinant of later-life cognitive reserve (Wilson et al., 2013), potentially through brain-derived neurotrophic factor-mediated neuroplasticity (Robertson, 2013; Mather and Harley, 2016). It follows that one possible mechanism supporting compensatory increases in integration in the dopaminergic OFF state may reflect a long-term compensatory strategy, mediated at least partially by the noradrenergic locus coeruleus. The implication is that as system begins to fail, as is the case when locus coeruleus develops high levels of α-synuclein (Surmeier et al., 2017), the compensatory reserve is lost and a failure to effectively integrate the brain unmasks the clinical severity of symptoms of Parkinson’s disease.

In addition to noradrenergic function, the multi-scale nature of the brain’s neuromodulatory network (Brezina, 2010) means it is likely that other neurotransmitter systems play a crucial role in mediating adaptive brain dynamics in the face of dopaminergic cell loss. For instance, there is a well demonstrated loss of cholinergic cell bodies in the basal nucleus in Parkinson’s disease (Müller and Bohnen, 2013). Given the recent links between the global brain signal and ascending cholinergic activity (Turchi et al., 2018), it is also plausible that impairments in the cholinergic system could adversely affect the topological signature of the network, or that the relative preservation of the cholinergic system might contribute to compensatory neural dynamics. The presence of serotonergic deficits (Politis and Niccolini, 2015) further points to a complex, multi-system pathological mechanism for compensation and impairment in Parkinson’s disease.

In summary, we used a combination of time-resolved resting functional MRI, graph theoretical analysis and the manipulation of dopaminergic therapy in individuals with idiopathic Parkinson’s disease to provide evidence for alterations in network topology that related to motor severity. These topological signatures demonstrated a relationship with both brain and cognitive reserve, suggesting a possible compensatory role, which may be mediated by the relative integrity of other neuromodulatory systems. Future work that disambiguates the causal relationships between neuromodulatory systems and large-scale network dynamics in Parkinson’s disease, perhaps as a function of differing disease stage, will help to better clarify this and potentially uncover new avenues for pharmacological treatments.

Funding

J.M.S. is supported by a National Health and Medical Research Council CJ Martin Fellowship (#1072403). E.M. is supported by an NHMRC Postgraduate scholarship and the Australian and New Zealand Association of Neurologists Gwen James Dementia Fellowship. S.J.G.L. is supported by an NHMRC-ARC Dementia Fellowship (#1110414). This work was supported by funding to Forefront, a collaborative research group dedicated to the study of non-Alzheimer disease degenerative dementias, from the National Health and Medical Research Council of Australia program grant (#1037746 and #1095127). C.O. is supported by a National Health and Medical Research Council Neil Hamilton Fairley Fellowship (1091310) and by the Wellcome Trust (200181/Z/15/Z).

Competing interests

The authors report no competing interests.

Glossary

Abbreviations

ICV

intracranial volume

NART

National Adult Reading Test