DisConICA: A Software Package for Assessing Reproducibility of Brain Networks and their Discriminability across Disorders

Abstract

There is a lack of objective biomarkers to accurately identify the underlying etiology and related pathophysiology of disparate brain-based disorders that are less distinguishable clinically. Brain networks derived from resting-state functional magnetic resonance imaging (rs-fMRI) has been a popular tool for discovering candidate biomarkers. Specifically, independent component analysis (ICA) of rs-fMRI data is a powerful multivariate technique for investigating brain networks. However, ICA-derived brain networks that are not highly reproducible within heterogeneous clinical populations may exhibit mean statistical separation between groups, yet not be sufficiently discriminative at the individual-subject level. We hypothesize that functional brain networks that are most reproducible in subjects within clinical and control groups separately, but not when the two groups are merged, may possess the ability to discriminate effectively between the groups even at the individual-subject level. In this study, we present DisConICA or “Discover Confirm Independent Component Analysis”, a software package that implements the methodology in support of our hypothesis. It relies on a “discover-confirm” approach based upon the assessment of reproducibility of independent components (representing brain networks) obtained from rs-fMRI (discover phase) using the gRAICAR (generalized Ranking and Averaging Independent Component Analysis by Reproducibility) algorithm, followed by unsupervised clustering analysis of these components to evaluate their ability to discriminate between groups (confirm phase). The unique feature of our software package is its ability to seamlessly interface with other software packages such as SPM and FSL, so that all related analyses utilizing features of other software can be performed within our package, thus providing a one-stop software solution starting with raw DICOM images to the final results. We showcase our software using rs-fMRI data acquired from US Army soldiers returning from the wars in Iraq and Afghanistan who were clinically grouped into the following groups: PTSD (posttraumatic stress disorder), comorbid PCS (post-concussion syndrome) + PTSD, and matched healthy combat controls. This software package along with test data sets is available for download at https://bitbucket.org/masauburn/disconica.

INTRODUCTION

Independent Component Analysis (ICA) is a blind source separation technique that is commonly employed for extracting brain networks involving spatially distributed regions with similar/correlated temporal activity [1], especially in the baseline resting state. Consequently, it has been applied to investigate altered brain networks in various heterogeneous neurological disorders using fMRI. Von dem Hagen et al. [2] employed ICA to demonstrate that individuals with Autism Spectrum Disorders (ASD) have reduced functional connectivity within the Default Mode Network (DMN), an important resting state brain network [3]. Assaf et al. [4] studied the role of altered functional connectivity of the default mode sub-networks in ASDs using short resting fMRI scans and ICA. von Rhein et al. [5] showed that subjects with ADHD exhibit alterations in connectivity of the salience and executive control networks and associated brain regions during task performance by using ICA as a part of their methodology. Patriat et al. [6] used ICA and discovered higher inverse correlation between the whole DMN and TPN networks in pediatric posttraumatic stress disorder (PTSD). Shang et al. [7] showed using ICA and chronic earthquake-related PTSD patients that the salience network (SN), central executive network (CEN), default mode network (DMN), somato-motor network (SMN), auditory network (AN), and visual network (VN) have both an increase and a decrease in functional connectivity in PTSD. Enhanced coupling of the amygdala and the insula within the SN was observed by Thome et al. [8] in subjects with PTSD by using ICA to evaluate connectivity within SN. The effects of developing PTSD in combat personnel with mild traumatic brain injury (mTBI) exhibiting abnormal activation of distributed brain networks including the emotion network and DMN were studied by Shu et al. [9] using ICA as a part of their methodology. Cisler et al. [10] used ICA in a study involving the characterization of the relationships of assault and PTSD severity with the organization of networks that are identified in emotion processing. Many resting-state networks (RSNs) in children aged 6–10 years based upon a sample of 536 subjects are robust and discovered more frequently when ICA is applied repeatedly [11].

Another perspective we take into consideration is the general crisis of lack of reproducibility of findings reported in a given study using a different sample [11]. Often, preclinical research outcomes generate significant media attention while failing to translate into successful diagnoses or treatments [12] [13]. Although, there may be multiple potential reasons for these problems, basic scientific results frequently turn out to be irreproducible. A recent survey of more than 1500 scientists revealed that 70% had tried but failed to reproduce another scientist’s experiment, whereas 52% thought that there was a crisis of reproducibility [13]. Up to 85% of the resources were wasted while producing and reporting research relevant to clinicians and patients [14]. Major contributors to research waste have been identified as irrelevant research questions, research design and conduct, inefficient regulation and management of research, failure to provide access to full research reports, and the lack of unbiased and useable reports [15]. Sharing code written to analyze neuroimaging data improves transparency and reproducibility in neuroimaging research, as this code is necessary for interpreting and validating results, and addressing new research questions [16]. Methods, in general, need to address the issue of reproducibility of results, at least within their sample. In this paper, we not only provide a methodology that analyzes the reproducibility of independent components obtained from resting state fMRI (representing brain networks), but also implements it in a software package which is freely distributed along with this article.

We surmise that the lack of reproducibility of brain networks across heterogeneous spectrum disorders not only hinders replicability of results as mentioned above, but also the ability of potential biomarkers based on such brain networks to effectively discriminate between disease groups and healthy controls. Therefore, we hypothesize that the functional brain networks most reproducible separately within disease and healthy control groups, but not reproducible when both groups are merged, can effectively discriminate between the groups.

Recently, an algorithm was proposed for modifying traditional ICA-based characterization of the functional brain networks such that reproducibility information is taken into consideration when we choose independent components. We utilize this method, namely “generalized Ranking and Averaging Independent Component Analysis by Reproducibility” (gRAICAR, https://github.com/yangzhi-psy/gRAICAR) [17], which can provide independent components that are highly reproducible within a given group of subjects. This methodology extends a framework developed initially for single subject analysis called “Ranking and averaging independent component analysis by reproducibility - RAICAR” [18], which has been used before in various neuroimaging applications [19] [20].

Our study builds upon these previous works by introducing DisConICA or Discover Confirm Independent Component Analysis (ICA). a software package that implements a “discover-confirm” approach, wherein the “discover” phase entails estimating the reproducibility of independent components using the gRAICAR (generalized Ranking and Averaging Independent Component Analysis by Reproducibility) algorithm [17], and subsequently the “confirm” phase involves evaluating the ability of highly reproducible components thus obtained to effectively discriminate between groups of subjects or participants with heterogeneous neurological disorders. This software package implements a work flow not available previously in literature, and utilizes a system-of-systems design approach [21] that minimizes user workload. It accepts fMRI data from individual participants as input, completes pre-, para-, and post-processing of these data sets, and presents results to the user. Using results obtained from DisConICA, we can examine the reproducibility of group-level independent components, alterations in functional connectivity, and the ability of functional brain networks discovered by DisConICA to discriminate between different groups of participants in an unsupervised way. In Syed et al. [22], we used DisConICA with the ABIDE dataset and discovered that the Default Mode Network (DMN) in Autism appeared less prominent where decreased functional connectivity in default mode subnetworks contributes to core deficits observed in ASD patients. While the objective in Syed et al. [22] was to enumerate and validate the algorithmic principles underlying DisConICA using a widely used dataset (ABIDE) and known neurobiological alterations underlying Autism, the current paper is more focused on the underlying software engineering with PTSD as an illustrative example.

MATERIALS AND METHODS

This section is organized as follows. First we present a conceptual explanation of data pre-processing, main analysis and post-processing, including clustering. Next, details of the software package which implements these conceptual steps are presented. Finally, we illustrate the conceptual steps as well as the capabilities of the software package using experimental fMRI data obtained from soldiers with PTSD and mTBI.

Pre-Processing

In the first step of our pre-processing phase, we utilize a combination of Data Processing Assistant for Resting- State fMRI [22] (DPARSF, http://www.restfmri.net), which is a plug-in software based upon Statistical Parametric Mapping or SPM version 8 (http://www.fil.ion.ucl.ac.uk/spm). Resting-State fMRI Data Analysis Toolkit (REST 1.7) [23], and MATLAB. Input data in this phase can either be in DICOMor .img/ .hdr file pair format, which is converted to NIfTI-1 format images (http://nifti.nimh.nih.gov/nifti-1, .nii files) before further processing. We use DPARSF to perform realignment of 3D brain volumes relative to the initial volume using 6-parameter rigid body registration, normalization to MNI (Montreal Neurological Institute) template using nonlinear warping, spatial smoothing using a Gaussian kernel with full width at half maximum of 4 mm × 4 mm × 4 mm, de-trending using linear polynomial and temporal band-pass filtering in the frequency range of 0.01 – 0.1 Hz.

The next step of this phase picks up four dimensional NIfTI-1 format images (http://nifti.nimh.nih.gov/nifti-1,.nii files) from the previous step, and use them as input to FMRIB Software Library v5.0 [24] [25] (FSL by Analysis Group, FMRIB, Oxford, UK) to derive a set of independent components for each subject using Multivariate Exploratory Linear Optimized Decomposition into Independent Components (MELODIC) algorithm [26] [27]. Analysis tools for ICA are available within FSL for decomposing single or multiple 4D data sets into linearly independent spatial components. More information on MELODIC can be obtained at http://fsl.fmrib.ox.ac.uk/fsl/fslwiki/MELODIC. In our pre-processing, we use MELODIC analysis tool to perform standard 2D spatial ICA on each subject. In addition to one spatial map per component, this analysis also results in corresponding time course and a mixing matrix. MELODIC determines the number of components internally within FSL through a dimensionality estimation mechanism including principal component analysis technique or PCA [28]. ICA is in fact conducted using FSL MELODIC, if configured to do so. The dimensionality is estimated by MELODIC using a probability PCA approach. The number of ICs is estimated individually for each subject, and varies with subjects. It is not assumed that the numbers of ICs are identical across subjects or within a given group. The gRAICAR algorithm reveals the similarity of the spatial maps among subjects. The difference in spatial characteristics of ICs is considered as the individual difference in gRAICAR. Actually, the difference in number of ICs is also due to individual difference. We use MELODIC results for each subject in the main analysis section to determine the reproducibility of these components, and therefore, the highly reproducible ones within each group. One of the highlights of our proposed software, DisConICA is that the users do not have to deal directly with individual software packages mentioned in this phase since our software automates these tasks by seamlessly communicating with other software packages.

Main Analysis

In this section, we summarize the conceptual underpinnings of the gRAICAR algorithm. We refer our readers to the original paper by Yang et al. [17] should they need a more comprehensive review.

We can represent the pre-processed dataset from subject i (i=1,2,…,n) as a matrix A_i of dimensions α_i × β_i, with α_i representing the number of time points and β_i the number of voxels. A_i, the data matrix, can now be decomposed into c_i independent components (ICs) in the spatial domain, forming a matrix B_i of dimensions c_i × β_i, and their corresponding mixing time courses forming a matrix, C_i of dimensions c_i × α_i.

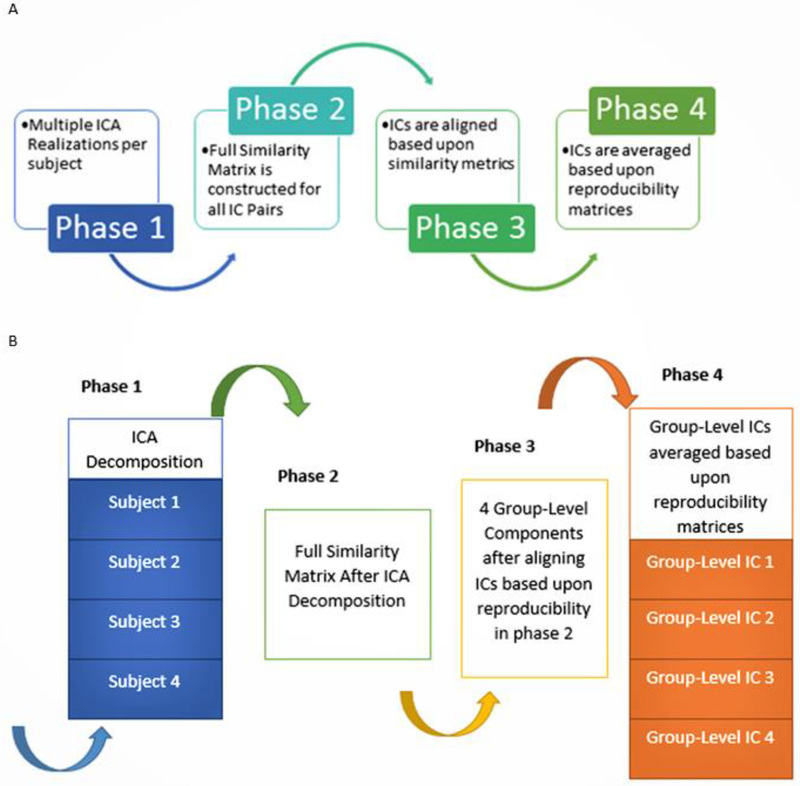
The four main processing phases in the gRAICAR algorithm have been summarized in Fig. 1. We will include a high-level overview of this algorithm referring the readers to the original work by Yang et al. [17] for a more comprehensive description. The first phase involves performing ICA decomposition k (~5000 for this study) times for each subject using random initial values leading to k × n realizations where n represents the number of subjects representing each realization as RZ_ab which refers to the ICs obtained from the b^th realization of subject a. A full similarity matrix (FSM) that has relational measures between all realizations is constructed in the second phase. Normalized mutual information or NMI quantifies the similarity between two realizations in this algorithm. Realizations that are found to be highly reproducible across subjects and ICA realizations are extracted and aligned in the third phase. Two related realizations are treated as individual-level components with the same primary group-level component or an aligned component, AC. For each aligned component, the algorithm generates a kn × kn reproducibility matrix within which NMIs between all pairs of realizations relevant to the AC are collected. The algorithm now aligns aligned components to obtain group-level component maps and examines the inter-subject consistency in the fourth phase. Fig. 1 A demonstrates the algorithm in general terms and we illustrate the specific implementation of this algorithm for an example of three subjects in Fig. 1 B, each with a set of four subject-level ICs.

Fig. 1.

A. Work flow diagram illustrating the 4 phases of gRAICAR algorithm. B. An illustration of the implementation of gRAICAR algorithm using a sample data set of 3 subjects, each with 4 subject-level ICs. Phase 1 involves multiple ICA decompositions for each subject. Phase 2 involves creating a full similarity matrix (FSM). ICs are aligned based upon similarity metrics in phase 3. In phase 4, ICs are averaged based upon reproducibility matrices.

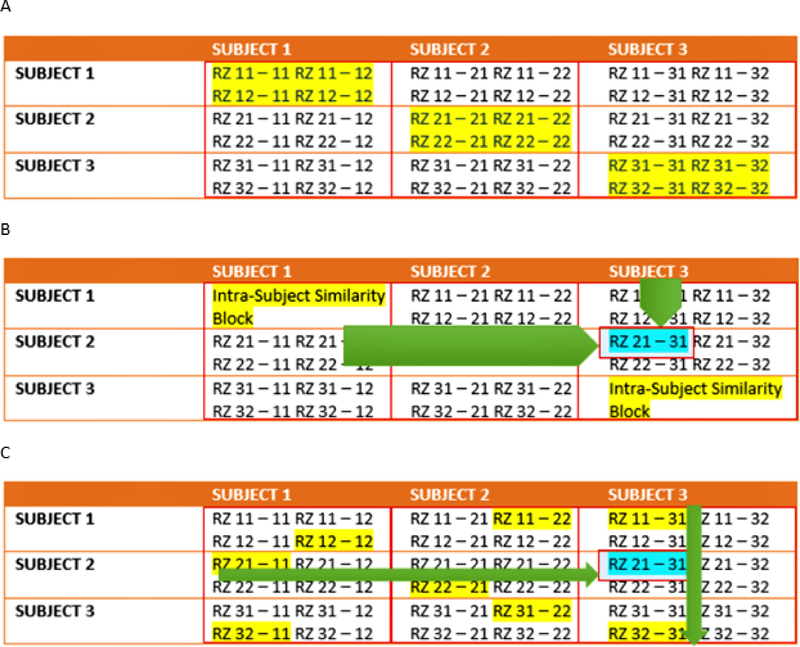
Continuing our discussion of the algorithm, we now delve into the high-level technical underpinnings of the algorithm. The full similarity matrix constructed in the second phase of the algorithm includes relational measures between all realizations. Block structure of this full similarity matrix shows subject blocks (SBLs) which in turn represent subject-wise relationships. Elements within these blocks are able to determine similarity between realizations from the same subject or pairs of realizations from different subjects depending upon the block location. In these subject blocks, there are k × k realization blocks (RBs) providing pair-wise similarity between realization components from different ICA realizations. Similarity between two realization blocks can be quantified by using normalized mutual information or NMI [29]. If two variables are identical, NMI is set to 1 and 0 if the two variables are statistically independent. This reveals higher order statistical similarity as opposed to second order similarity as defined by correlation or covariance [30]. The gRAICAR algorithm computes NMIs between each IC pair using mutual information based upon the algorithm proposed by Kraskov et al. [31]. NMIs are then standardized within an realization block, leading to standardized NMI or SNMI. Fig. 2 A shows the block structure as implemented in a full similarity matrix with 3 artificial subjects having two ICA realizations each i.e. n = 3 and k = 2.

Fig. 2.

A. Block structure of full similarity matrix (FSM) based upon an example set with 3 subjects and 2 sets of subject-level components (RZ, a set of ICs produced after two ICA decompositions). In this example, each block shows similarity between 2 pairs of RZs from the same subject or two different subjects. Also, RZ 11–31 indicates inter-subject similarity between RZ 1 of subject 1 and RZ 1 of subject 3. The first digit in 11 is an index to the subject whereas the second is an index to the RZ. Highlighted, on the diagonal blocks indicate similarity within the components of a subject or intra-subject similarity whereas off diagonal ones indicate that between the components of two different subjects. B. RZ 21–31 represents RZ 1 of subject 2 and RZ 1 of subject 3 and has been found to be the global maximum in this example. C. Determine block-wise maxima with highlighting in each block such as RZ 21–11 in row 2 and column 1. Global maximum in this figure has been highlighted in addition.

In this representation, solid lines mark subject blocks. Off the diagonal subject blocks reflect the similarity between pairs of realizations from different subjects whereas those on the diagonal reflect those from the same subject. The realization block represented as a matrix, R_ab-cd with dimensions c_a × c_c, reflects the similarity between RZ_ab and RZ_cd (a, c: 1,2,…n, b,d: 1,2,…k). In the algorithm, NMI for two realizations is now calculated as:

$$R{Z}_{ab-cd}[y,z]=NMI\left(R{Z}_y\in R{Z}_{ab},R{Z}_z\in R{Z}_{cd}\right)=\frac{H\left(R{Z}_y\right)+H\left(R{Z}_z\right)}{H\left(R{Z}_y,R{Z}_z\right)}-1$$ (1)

H(RZ_y), H(RZ_z), H(RZ_y, RZ) in (1) represent the entropies of random variables, RZ_y and RZ_z, and the mutual entropy between RZ_y and RZ_z (1 ≤ y ≤ c_a, 1 ≤ z ≤ c_c).

To obtain standardized NMI in the alignment procedure, the NMIs are further standardized using the formula:

$$R{Z}_{ab-cd}[y,z]=\frac{R{Z}_{ab-cd}[y,z]-mean\left(R{Z}_{ab-cd}[y,\ast ]\cup R{Z}_{ab-cd}[\ast ,z]\right)}{std\left(R{Z}_{ab-cd}[y,.]\cup R{Z}_{ab-cd}[.,z]\right)}$$ (2)

Where * denotes all NMI values in row y or column z of the realization block in (2). This standardized NMI or SNMI is used to compute the specificity of individual similarity values related to a given realization within the realization block. Diagonal realization blocks are generally set to zero because they represent identity matrices and are not of interest.

The gRAICAR algorithm then extracts highly reproducible realizations across subjects and ICA realizations and aligns them in its third phase of execution. To accomplish this, the algorithm searches all SNMI values within subject blocks indicating the similarity between pairs of realizations from different subjects to find a global maximum. Two realizations found to be related are considered subject-level components but with the same underlying group-level component, which we refer to as an aligned component. These realization blocks are then examined to locate the local maxima within them as this reflects possible locations of the aligned component within different ICA realizations and subjects. Rows and columns that contain these maxima are eliminated from the full similarity matrix after all realizations associated with this aligned component are located. This task is repeated until c_m = max(c _{1 ≤ i ≤ n}) aligned components have been found where c represents the number of ICs. The number of components is not the same among subjects, and hence empty matches for some subjects are allowed. A kn × kn reproducibility matrix for each aligned component is produced, thus collecting NMIs between all pairs of realizations associated with the aligned components. NMIs are then utilized to provide a more direct interpretation of similarity. In order to form its reproducibility matrix, a maximum of one realization is selected per aligned component in each ICA realization. The algorithm divides information contained within the reproducibility matrix into two metrics: inter-subject consistency and intra-subject reliability. Inter-subject consistency is defined as the mean of all NMIs within inter-subject blocks. The inter-subject consistency for a given aligned component between subjects a and c can be calculated as:

$${\propto }_{ac}=mean\left(R{Z}_{a^{\prime }-c^{\prime }}\right)=\frac{{\sum }_{b=1}^k{\sum }_{d=1}^{k}R{Z}_{ab-cd}[y(a,b),z(c,d)]}{K^2}1\le a,c\le n,a\ne c$$ (3)

Equation (3) represents the mean NMI within the inter-subject block ‘a–c’ in the reproducibility matrix, since it averages all the NMI values located at the intersection between realization b of subject a and realization d of subject c.

Fig. 2 B, a continuation of Fig.2 A, provides an example of the third phase of the gRAICAR algorithm summarizing the description presented above using the same scenario as in Fig. 2 A. The circle mark represents a global maximum, which is computed by searching all SNMIs within the off-diagonal subject blocks. Doing so provides compatibility with larger variations across subjects than within subjects. In this example, the global maximum was located at RZ_ab–cd [y, z], which represents the y-th row and the z-th column of the realization block. Two related realizations, RZ_y(a,_b) and RZ_Z(c,_d), are treated as subject-level components with the same underlying group-level component or aligned component. RZ_y(a,b) is a representation of the y-th component of the b-th realization of the a-th subject.

This identifies the aligned component in different ICA realizations and subjects. These locations have been identified in Fig. 2 C as R22–11[s, v1] and R11–31[w1, t] where v1 and w1 represent relevant realization positions in individual realization blocks indicating the largest similarity with RZ_y(a,b) and RZ_z(c,d) respectively. v1 = w1 here means [y, v1] and [w1, z] favor the same realization and the component formed as a result is considered to be related to the aligned component determined by RZ_y(a,_b) and RZ_z(c,_d). If v1 and w1 are unequal, either v1 or w1 is chosen based upon a voting mechanism to determine the proximity of one or the other to more of those realizations investigated as the v1 = w1 case.

In its fourth phase, the gRAICAR algorithm estimates aligned component maps and corresponding mixing time courses by utilizing weighted averages of their related realizations. To calculate the weighted average of therealizations, the first step is to define a subject load on inter-subject consistency reflecting the contribution or inter-subject centrality of a given subject to a given aligned component.

$${\gamma }_i=\frac{1}{n-1}{\sum }_{c=1,c\ne a}^n{\propto }_{ac},1\le \text{a}\le \text{n}$$ (4)

Equation (4) can also be described as the inter-subject centrality of a subject in a given aligned component, and is the mean of the inter-subject consistency metrics between the given subject and the rest of the subjects. In (4), ∝_ac is a reference to the inter-subject consistency metric between subjects a and c. Spatial maps and mixing time courses of an aligned component are calculated by merging this subject load on inter-subject consistency and the intra-subject reliability, as follows:

$$grpI{C}_{\tau }=\frac{{\sum }_{a=1}^n[{\beta }_a{\gamma }_a{\sum }_{b=1}^{k}R{Z}_{p(a,b,n)}]}{K{\sum }_{a=1}^n{\beta }_a{\gamma }_a},1\le \tau \le c_m$$ (5)

RZ_p(a,b,n) represents the realization or the spatial map of the IC identified in the b-th realization of the a-th subject. p sets an index on the location of the realization and can differ with different realizations and subjects. The weights vary for each aligned component, calculated by the aligned component-specific reproducibility matrix.

The algorithm now statistically detects aligned components found consistently across subjects. It explores the significance of cross-subject consistency of the resulting aligned component in two steps. It applies a nonparametric test to select the aligned component consistent across all subjects. One realization from each ICA realization in the full similarity matrix is randomly tested with replacement and the mean of inter-subject consistency metrics is calculated after a non-participating subject is artificially generated. This procedure is repeated ~500 times. The resulting means of inter-subject consistency metrics are combined to yield a null-distribution of the inter-subject consistency. The 95^th percentile, equivalent to a significance level of p = 0.05, of the null distribution provides a threshold at this point. Aligned components with mean inter-subject consistency metrics greater than the threshold value mentioned earlier are treated as common aligned components across subjects. Null distributions of the subject loads on inter-subject consistency and intra-subject reliability for each one of the aligned components mentioned earlier are produced by randomly assigning realization with replacement in the reproducibility matrix to subjects generated artificially. In the algorithm, thresholds for aforesaid metrics are determined at 95^th percentile of the equivalent null distributions, corresponding to a significance level of p = 0.05. Subjects above these two threshold levels are treated as representing the aligned component under consideration. The main tasks in the fourth phase of gRAICAR algorithm include estimating aligned component maps and corresponding time courses after weighted averaging of their related realizations, statistically detecting aligned components that are consistent across all subjects, and constructing a graph for each aligned component to characterize relationships among subjects from the standpoint of inter-subject consistency.

Post-Processing

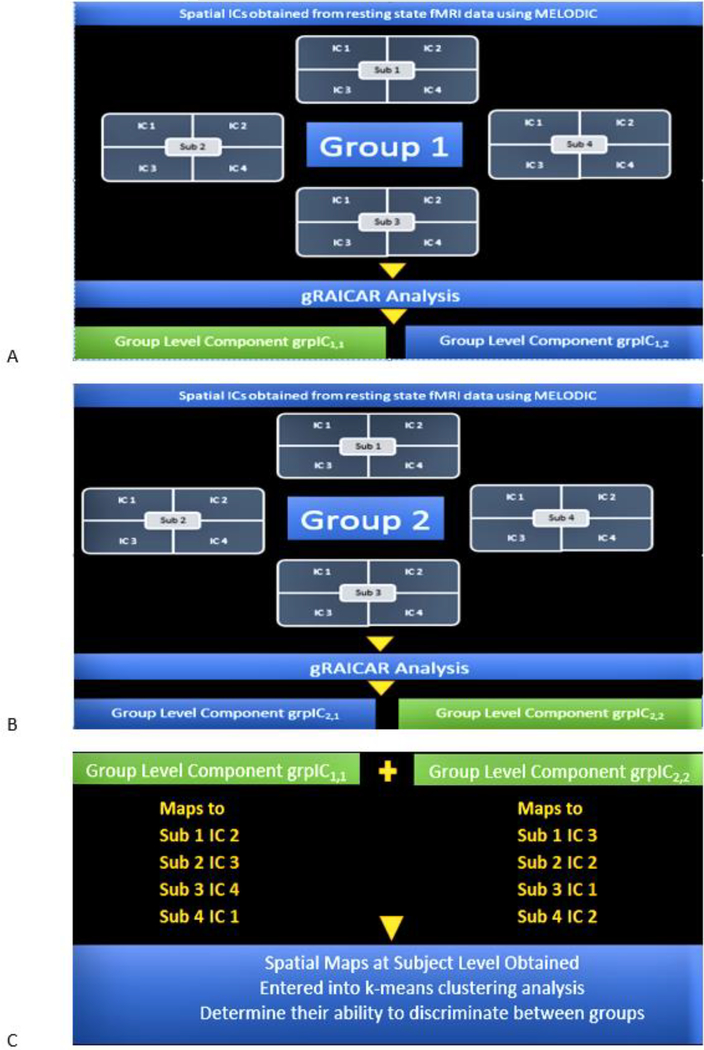
Now that we have reviewed the gRAICAR algorithm, we present our post-processing workflow including clustering analysis. To review our workflow after gRAICAR processing, we present an example case with two diagnostic groups, 4 subjects in each group and 4 IC realizations per subject. For brevity, we assume gRAICAR produces two group-level components per group, grpIC₁,₁ and grpIC₁,₂ in group 1 as shown in Fig. 3 A, as well as grpIC₂,₁ and grpIC₂,₂ in group 2, as shown in Fig. 3 B. In this example, the first digit represents group enumeration and the second digit represents group-level component index. Suppose group-level components grpIC₁,₁ and grpIC₂,₂ had the highest inter-subject consistency according to gRAICAR analysis in groups 1 and 2, respectively, as shown in equations (6) and (7).

$${\propto }_{(Sub\mathrm{1..}Sub4)}\left(grpI{C}_{1,1}\right)>{\propto }_{(Sub\mathrm{1..}Sub4)}\left(grpI{C}_{1,2}\right)$$ (6)

$${\propto }_{(Sub\mathrm{1..}Sub4)}\left(grpI{C}_{2,2}\right)>{\propto }_{(Sub\mathrm{1..}Sub4)}\left(grpI{C}_{2,2}\right)$$ (7)

We now select these two components for further processing.

Fig. 3.

A. A toy illustration of the analysis workflow. gRAICAR analysis on ICs estimated from fMRI data corresponding to Group 1 is assumed to produce group-level components grpIC_1,1 and grpIC_1,2. Let us suppose that grpIC_1,1 has highest inter-subject consistency in Group 1 and hence be selected for further processing. B. A toy illustration of the analysis workflow. gRAICAR Analysis on ICs estimated from fMRI data corresponding to Group 2 is assumed to produce group-level components grpIC_2,1 and grpIC₂,₂. Let us suppose that grpIC₂,₂ has highest inter-subject consistency in Group 2 and hence be selected for further processing. C. The spatial maps at the individual subject level corresponding to group-level components from Fig. 3 A and Fig. 3 B, i.e. the most reproducible ICs within each group, are obtained and entered into a k-means clustering analysis in order to determine their ability to discriminate between the groups.

For all subjects, we access post-MELODIC analysis results and retrieve spatial maps associated with the ICs for each subject corresponding to each selected group-level component. We then process these spatial maps in MATLAB wherein the spatial map associated with the IC index of the current subject is retrieved and singleton dimensions are removed. The resulting array is reshaped using MATLAB’s reshape function (http://www.mathworks.com/help/matlab/ref/reshape.html) thus giving us a matrix ɸ_x with dimensions p_x × q where p_x is the number of subjects in group x and q is the size of each spatial map associated with the current IC index. Suppose the size of the spatial map size for each subject in this example is 61 ɸ 73 ɸ 61. For group 1 with 4 subjects, ɸ₁ is 4 ɸ 61 ɸ 73 ɸ 61 and the same for group 2 and ɸ₂. After all subjects in both groups are processed, we combine ɸ₁ and ɸ₂ matrices from groups 1 and 2 resulting in ɸ_є, an 8 ɸ 271633 matrix representing all individual subject-level maps from all groups. We apply the k-means algorithm, utilized by several studies in the analysis of fMRI data [32] [33] [34], to ɸ_є to examine how subjects were clustered based upon their spatial maps without a priori groupings, and how this corresponds to clinically determined diagnostic clusters. We minimize the objective function, M, as follows:

$$M={\sum }_{b=1}^x{\left|{\mathrm{\varphi }}_b-C_b\right|}^2$$ (8)

ɸ_b represents combined spatial maps from all subjects in group b, C_b represents the mean of all points in group b, and x represents the number of groups in the analysis.

We set up the k-means algorithm to partition ɸ_є into two clusters since we have two example subject groups, continuing with the example we presented earlier. Cluster purity, referring to true positive rate obtained through k-means clustering analysis, provides us insight into the ability of grpIC_1,1 and grpIC₂,₂ to accurately distinguish between the two diagnostic groups. If grpIC₁,₁ and grpIC₂,₂ do not represent the same functional brain network in both groups, or the spatial correlation value between the two group-level components is less than 0.9, we take grpIC₁,₁ from group 1 and find the group-level component, grpIC₂,, in group 2 having the highest spatial correlation with it thus giving us the same functional network in group 2. The ‘.’ in grpIC₂, represents the index value of this new-found component. We then find grpIC₁,, the group-level component in group 1 with the highest spatial correlation with grpIC_2,2 in group 2, or the component representing the same network as grpIC_2,2 in group 1. We now merge (grpIC₁,₁ grpIC₂,.) and (grpIC₁,. grpIC_2,2) and examine cluster purity in both cases using the k-means algorithm. The rationale behind this second round of analysis is to examine cluster purity values if similar functional brain networks from all groups are combined. In other words, this second round of analysis provides insight into the ability of similar functional networks to distinguish between the two groups. Having determined these reproducible networks and their ability to effectively discriminate between the groups also supports furthering our “discover-confirm” approach introduced earlier in this paper. In the following section, we review the implementation of this methodology in a software package named DisConICA.

Implementation

We have designed DisConICA software to allow users to examine their fMRI data sets using the “discover-confirm” approach we have proposed using the reproducibility of independent components. It is meant to provide functionality described in our analysis workflow and resulting components with minimal effort. The main application was developed in MATLAB with wrapped subsidiary applications. We have provided two starting formats for users, DICOM or .img/ .hdr file pairs.

Prerequisites

The first version of DisConICA was developed in MATLAB environment and hence MATLAB is required to run the software. Another pre-requisite is to define the location of FSL software directory in the host system. If this has been accomplished per instructions in FSL software (FMRIB Software Library v5.0; https://fsl.fmrib.ox.ac.uk/fsl/fslwiki), the following command – “echo $FSLDIR” – should display the location of the above-mentioned directory. This gives the ability to run FSL’s ‘FEAT’ command described later in FSL analysis. Once the FSL location has been established in the environment, the user can execute DisConICA.

In order to utilize this approach, DisConICA is designed to read the following directory structure, which the user needs to create:

• Main Directory

  • Group 1

    • Sub 1

    • Sub 2

    • Sub 3

    • Sub 4

  • Group 2

    • Sub 1

    • Sub 2

    • Sub 3

    • Sub 4

In this structure, each subject directory contains DICOM or NIfTI Hdr/Img pair files. The current version of DisConICA has been limited to three diagnostic groups due to external processing constraints. This limitation is discussed later in this paper. An example structure has been discussed under gRAICAR algorithm and we continue with the same example that includes two groups – Group 1 and Group 2. Consequently, the data structure should be set up as follows:

Main Directory/Group 1/Sub 1, Sub 2, Sub 3…,

and

Main Directory/Group 2/Sub 1, Sub 2, Sub 3...

Under each subject, we may have

Sub 1/ 1.dcm,2.dcm,3.dcm,...

or

Sub 1/1. img, 1. hdr,2. img,2. hdr,...

Packaged Software

DisConICA wraps two software packages in addition to its native programming. These two packages are Data Processing Assistant for Resting-State fMRI [22] (DPARSF, http://www.restfmri.net) and fMRIB Software Library v5.0 [24] [25] (FSL by Analysis Group, FMRIB, Oxford, UK). DPARSF uses libraries from Statistical Parametric Mapping or SPM (http://www.fil.ion.ucl.ac.uk/spm) and Resting-State fMRI Data Analysis Toolkit (REST 1.7) [23]. DPARSF, SPM and REST are bundled with DisConICA software. This not only helps standardize inter-process communications, such as those to and from the DisConICA software itself, but also resolves possible software conflicts. One of the highlights of DisConICA is that users do not have to deal directly with software packages mentioned in this section as DisConICA automates pre-processing whilst minimizing user effort. DISCONICA along with test data sets is available for download at https://bitbucket.org/mas0047/disconica/downloads/.

User Interface

Minimal user effort was the philosophy behind DisConICA’s user interface design. Fig. 4 shows the user interface corresponding to the starting point of the software. It was designed to accomplish its goals through methodology proposed in our paper with minimal effort on the user’s part. Single stage user interface allows users to enter the location where the entire analysis is set to execute. This refers to the main directory as described in the prerequisites section. The user then enters repetition time (TR) and selects an input format. If the TR is not entered, the program attempts to retrieve this value from input data. There are two input format options available: DICOM and .img/ .hdr file pairs. Once the user clicks ‘Continue’, background processing takes over.

Fig. 4.

DisConICA’s user interface with options described under “User Interface” section of this paper.

Main Analysis

The software now ascertains a uniform number of input images or time points (DICOM or NIfTI) and alerts the user if any discrepancies are found, discontinuing the progress. If a uniform number of images or time points are found for each subject, the software sets the location of SPM, REST and DPARSF along with any NIfTI processing files necessary for the pre-processing phase. The program includes a separate interface to allow users to customize most DPARSF settings. Default settings are available in case customization is not needed. It communicates with DPARSF and completes the following tasks:

• Sets SPM, REST and DPARSF locations

• Disables options in these other software packages not used in our methodology

• Sets Time Points by examining files per subject

• Sets TR provided by the user

• Sets Slice Timing

• Sets Realignment

• Sets Normalization with Bounding Box [−90 −126 −72;90 90 108] and voxel size of 2×2×2

• Sets smoothing with FWHM of 4×4×4

• Sets de-trend and filter range 0.01 – 0.1 Hz

Once started, the software triggers SPM, REST and DPARSF. This processing completes steps set in the DPARSF module while the progress can be monitored through SPM and REST interfaces. Upon completion, the resulting 3D Img/Hdr pairs are saved in the following directory structure per subject:

MainDirectory/Group1/FunImgNormalizedSmoothedDetrendedFiltered/Subject1, Subject2, Subject3…

A similar structure is created for other groups. Once DPARSF steps are completed, the software finds locations as described above and collapses all 3D images per subject to a single 3D Img/ Hdr pair. This collapsed 3D Img/Hdr pair is now converted to 4D NIfTI format. The software now creates a directory per group under the main directory called ‘Melodic’ as:

MainDirectory/Group1/Melodic

4D NIfTI images created per subject are now moved to this directory. The software prepares to run the Multivariate Exploratory Linear Optimized Decomposition into Independent Components (MELODIC) algorithm [26] [27] which will decompose 4D data sets using Independent Component Analysis. More information on the MELODIC algorithm can be obtained at http://fsl.fmrib.ox.ac.uk/fsl/fslwiki/MELODIC. In order to run FSL MELODIC through DisConICA, the software first creates a design script file with the extension ‘fsf (.fsf). This file defines the following steps, some of which are set by MELODIC as defaults:

• Location of each subject’s 4D NIfTI (nii) file which is edited and adjusted by DisConICA

• High pass frequency cut off point at 100 seconds

• Linear Registration on input data using FEAT functionality before the statistical analysis with 12 degrees of freedom

• Resampling resolution which refers to the desired isotropic voxel dimension of the resampled data set to 4mm

• Variance normalize time courses so that the estimation is more influenced by voxel-wise temporal dynamics than a voxel’s mean signal

• Automatic dimensionality estimation to avoid overfitting. This is achieved by using Bayesian estimators for the model order and PCA (principal component analysis) to reduce the data prior to IC estimation

• Single-session ICA

• Threshold IC maps at 0.5. MELODIC carries out inference on the estimated maps by default using a mixture model and an alternative hypothesis testing approach. This threshold level in alternative hypothesis testing refers to a voxel that survives thresholding as soon as the probability of being in the active class – modelled by the Gamma densities – exceeds the probability of being in the background noise class.

This design file is run in the environment using the ‘FEAT’ command of FSL which reads the design script file (.fsf) and starts MELODIC IC analysis, e.g. ‘feat design.fsf’. MELODIC ICA results are stored under the ‘Melodic’ directory where new directories are created by MELODIC for each subject. In this case, the file we specifically need for gRAICAR analysis is stored under each subject’s MELODIC ICA directory created by FSL MELODIC and called ‘melodic_IC.nii.gz’. A sample location is as follows:

MainDirectory/Group1/Analysis/Melodic/Subject1.ica/filtered_func_data/melodic_IC.nii.gz

In this location, Subject1.ica is a directory based upon Subject 1’s 4D NIfTI file and holds FSL MELODIC analysis’ results.

We now prepare to run the gRAICAR algorithm. In order to do so, the software creates a directory under ‘Analysis’ called ‘gR’. All ICA directories are moved to gR directory as follows:

MainDirectory/Group1/Analysis/ gR/Subject1.ica…

The software then creates a shell script to calculate the average mask of the group based upon individual masks created by FSL and stored in each subject’s ICA directory. As mentioned earlier, users do not have to directly interact with FSL and once the script is created, it is run as an environment command from within the software. The result is a file called ‘mask.nii.gz’ stored under gR directory of the group. In addition, the software creates a list file, subjects.list, that stores the names of subject directories. This list file is used by the gRAICAR algorithm. As an example, if we had four subjects in Group 1, the gR directory would have the following structure:

MainDirectory/Group1/Analysis/gR/Subject1.ica

MainDirectory/Group1/Analysis/gR/Subject2.ica

MainDirectory/Group1/Analysis/gR/Subject3.ica

MainDirectory/Group1/Analysis/gR/Subject4.ica

MainDirectory/Group1/Analysis/gR/mask.nii.gz

MainDirectory/Group1/Analysis/gR/subjects.list

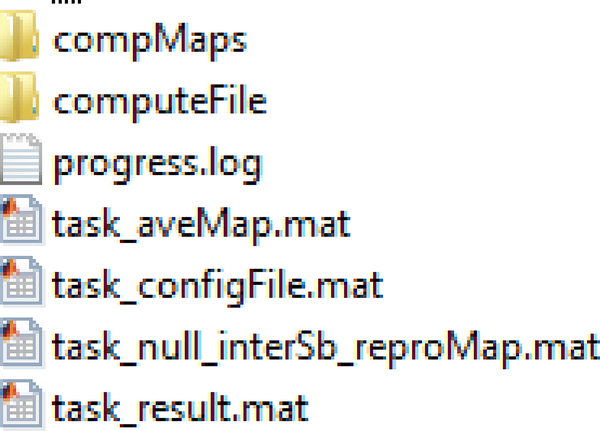
Once the preparation is complete, the software calls the gRAICAR algorithm with the location of ‘gR’ directory in addition to those of average mask and the subjects list which are also under ‘gR’. It also specifies an output directory name, gROutput, for the algorithm to store results in. Once gRAICAR processing is complete, results are stored under ‘gROutput directory for each group. If we had two groups as an example, we should now have the structure created by the gRAICAR algorithm shown in Fig. 5 for each group:

Fig. 5.

Directory structure created by the gRAICAR algorithm in MATLAB

In our example, this structure is created under the following two directories:

MainDirectory/Group1/Analysis/gR/gR_Results

MainDirectory/Group2/Analysis/gR/gR_Results

The gRAICAR algorithm is run at the group-level and ‘computeMaps’ directory holds NIfTI (.nii) files of group-level components discovered by the algorithm.

Post-Processing

Once the gRAICAR results are available, the software completes the following tasks:

1. Loads the ‘task_result.mat’ file for each group looking at the result object in this file and, specifically, the field obj.result.beta_rank_subjLoad. The lower the value of a group-level component in this field, the greater the inter-subject consistency.

2. Picks the most reproducible component.

3. For this group-level component, it looks at the ‘obj.result.foundComp’ field of the result object to determine which subject level component this group-level component maps to.

4. It then retrieves spatial maps for each subject’s IC forming the group-level component and combines them. We can call this combination x_vec.

5. Steps 1–4 are repeated for the second and third group (if we have three groups).

6. y_vec is the result of step 4 from Group 2 and the software now combines x_vec and y_vec, resulting in a combined matrix, A.

7. The software now runs k-means algorithm on A after defining the centroids as the average of x_vec and x_vec respectively. We set the number of clusters equal to the number of groups in the analysis.

8. These steps are summarized by Eq. 6 or Deshpande-Syed’s Equation for group distinction using ICA reproducibility and clustering.

9. The result of step 7 is a column vector where each row represents a subject along with the index of the cluster this subject has been assigned to. These indices help us determine cluster purity. Continuing our earlier example of two groups and 4 subjects in each group, k-means results refer to the following structure:

Group 1 Subject 1 – Cluster 1

Group 1 Subject 2 – Cluster 1

Group 1 Subject 3 – Cluster 1

Group 1 Subject 4 – Cluster 1

Group 2 Subject 1 – Cluster 2

Group 2 Subject 2 – Cluster 2

Group 2 Subject 3 – Cluster 2

Group 2 Subject 4 – Cluster 2

In this example, cluster purity is 1 as all subjects have been identified correctly.

If the most reproducible components selected per group do not represent the same network basedupon their spatial correlation values being less than 0.9, the software can take the best component from Group 1 used in k-means and calculate its covariance against all group-level components in Group 2. This step provides the group-level component in Group 2 that represents the same functional network as and, therefore, has the highest covariance with our starting component from Group 1. This step is then repeated for the best component from Group 2 that was used in k-means. Now we have the group-level component in Group 1 that has the highest covariance value with the selected component in Group 2. This additional step ensures that the best components we had selected for k-means are matched with a component within the same brain network in the opposite group. In this case, the software runs k-means after combining an initial component from Group 1 and its counterpart from Group 2 and cluster purity is examined. The step is repeated for the initial component from Group 2. In our example, we have three cluster purity values. The software, therefore, calculates x+1 cluster purity values, where x is the number of groups.

Example Application

Data Overview

Post-traumatic stress disorder (PTSD) is categorized as an anxiety disorder and develops after a traumatic event has been experienced [35]. Veterans are at a higher risk for developing PTSD as many experience traumatic events during deployment and combat. The prevalence of PTSD among veterans deployed to Iraq and Afghanistan evaluated anonymously through questionnaires was found to be 6.2 – 12.9% [36]. We used a study that included 71 male participants who were also active duty soldiers, to evaluate DisConICA. Of these 71 participants, 15 had PTSD, 30 had both PTSD and PCS (post-concussion syndrome, a chronic sequalae of mild traumatic brain injury - mTBI), and 26 combat controls. All three groups were matched in age, race and education. In addition, all participants had combat experience in Iraq (Operation Iraqi Freedom, OIF) and/or Afghanistan (Operation Enduring Freedom, OEF). In this study, PTSD Checklist-5 (PCL-5) score, clinician referral, post-concussive symptoms using the Neurobehavioral Symptom Inventory (NSI), and medical history including documentation of mTBI(s) were used when grouping the subjects [37]. Details regarding inclusion and exclusion criteria for defining the three groups can be obtained from Rangaprakash et al, 2017 [37].

Data Acquisition

A 3T Siemens MAGNETOM Verio scanner (Siemens Healthcare of Erlangen, Germany) was used for participant scanning using T2* weighted multiband echo planar imaging (MB-EPI) sequence in resting state. The participants were asked to keep their eyes open and fixated on a white cross displayed with dark background on the screen using an Avotec projection system and not think of anything specific. Scanning parameters used included a TR (repetition time) of 600ms, TE (echo time) of 30ms, FA (flip angle) at 55°, multiband factor of 2, anterior to posterior phase encoding direction, voxel size of 3×3×4 mm³ and 1000 volumes or time points. For acquiring anatomical scan using an MPRAGE (magnetization-prepared rapid gradient echo) sequence, we used a TR of 1900 ms, TE of 2.5ms, FA at 9° and voxel size of 1×1×1 mm³. Brain coverage was limited to the cerebral cortex, subcortical structures, midbrain and pons, thus excluding the cerebellum.

Technical Implementation

In order to examine our PTSD dataset, DisConICA was provided three (3) input directories representing three subject groups: PTSD, PCS+PTSD, and matched combat controls. Each subject had 1000 time points saved in the form of DICOM (.dcm) images within each directory, as described in the pre-requisites section. All software and processing settings were the same as described in the workflow, processing and implementation phases of DisConICA. During the first stage, DisConICA pre-processed these sets using DPARSF. This step created a 4D NIfTI format output file per subject. DisConICA then used these 4D NIfTI images to run independent component analysis using FSL’s MELODIC functionality. Once the ICs had been computed per subject, DisConICA used that information per subject in the gRAICAR algorithm to calculate group-level components per group. The most reproducible components were then selected as explained earlier by DisConICA, one component per group was then retrieved, combined with all selected ones in the other two groups, and k-mean clustering was performed for different combinations, ɸ_є, where є represents the permutational spatial combinations of 127 such components from the PTSD, 82 from the PCS+PTSD, and 111 from matched control groups. Resulting cluster purities were then determined for the three groups. The combination of group-level components, P^x from the PTSD group, S^x from the PCS+PTSD group, and C^x from the control group, which gave the the highest cluster purities was then examined further. We denote these as the primary group-level components. We examined the spatial correlation values of P^x with all group-level components in PCS+PTSD and control groups, those of S^x with all group-level components in PTSD and control groups, and finally those of C^x with all group-level components in the PTSD and control groups. Secondary group-level components with the highest spatial correlation with primary components were identified using the following approach.

$$\xi =\max {\sum }_{i=1}^{n_s}cov\left(\psi ,{\psi }_i\right)$$ (9)

In Eq. (9), ξ denotes the highest covariance between the primary group-level component, and the secondary group-level component, ψ_i, from the opposite group with n_s identifying the total number of components in the opposite group. Secondary group-level components thus identified are presented in Table I.

Table 1.

Notations used to refer to group-level components used in our analysis and described in the technical implementation section. This table shows the secondary components, the groups they belong to, and the primary component most significantly spatially correlated to each secondary component.

Secondary Component	Group	Primary Component
Spx	PCS+PTSD	Px
Cpx	Control	Px
Pcx	PTSD	Cx
Scx	PCS+PTSD	Cx
Psx	PTSD	Sx
Csx	Control	Sx

We then performed another set of clustering analyses, on P^x combined with S_p^x and C_p^x, on S^x combined with P_s^x and C_s^x, and finally on C_x combined with P_c^x and S_c^x. This second round of analyses determined whether the reproducible components in each group, when paired with the corresponding components with similar spatial distribution in the other groups, effectively discriminated between the groups. Finally, for components that effectively discriminated between the groups, we performed two-sample t-tests to determine whether they were stronger or weaker in the disease groups as compared to the control group.

RESULTS

We first present the most reproducible components in the PTSD, PCS+PTSD and control groups, i.e. P^x, S^x, and C^x, respectively (Figs 6–8). These group-level components, when combined and examined using k-means clustering, yielded a cluster purity value of 1 for all three clusters, one cluster per group. All three groups were identified with 100% accuracy.

Fig. 6.

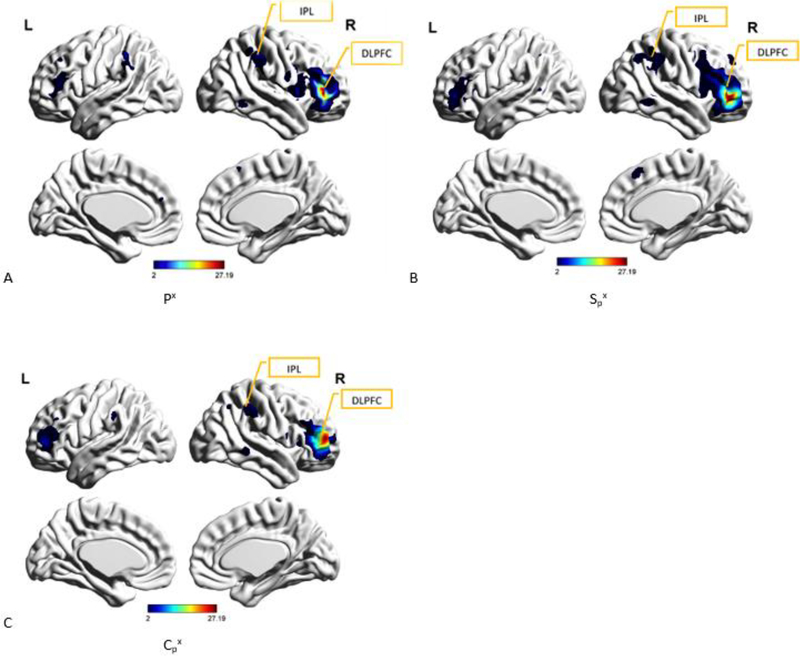
A. Spatial map of the group-level component, P^x from PTSD group, that was most reproducible within the PTSD group as well as produced the highest cluster purity when combined with S^x from PCS+PTSD group and C^x from the controls group. DLPFC (Dorsolateral prefrontal cortex) and IPL (inferior parietal lobe, also called the temporo-parietal junction or TPJ) have been identified as well. B. Spatial map of the group-level component, S_p^x from PCS+PTSD group, that was found to have the highest spatial correlation with and correspondence to P^x Fig. 6 A. DLPFC (Dorsolateral prefrontal cortex) and IPL (inferior parietal lobe) have been identified. C. Spatial map of the group-level component, C_p^x from the controls group, that was found to have the highest spatial correlation with and correspondence to P^x (Fig. 6 A). DLPFC (Dorsolateral prefrontal cortex) and IPL (inferior parietal lobe) have been identified.

Fig. 8.

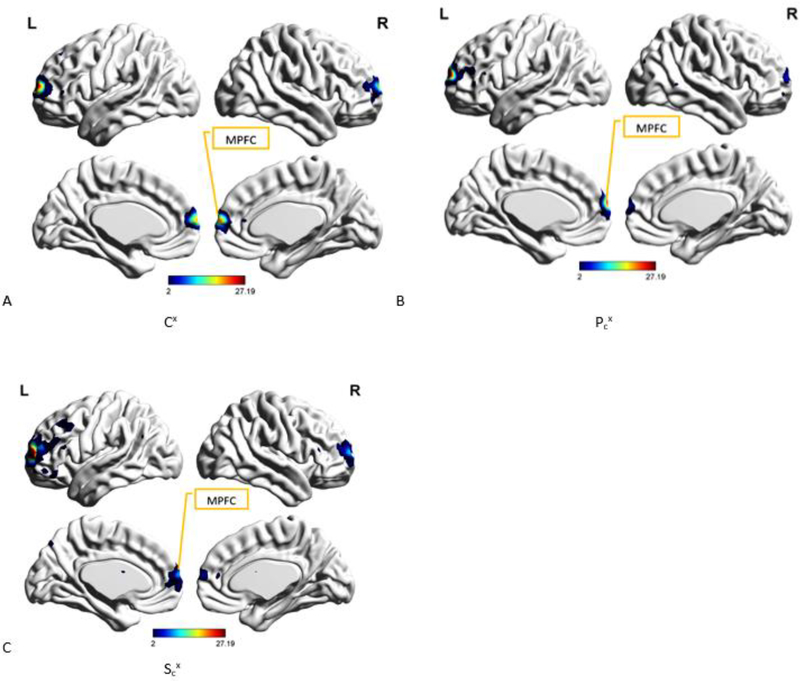
A. Spatial map of the group-level component, C^x from controls group, that was most reproducible within the control group as well as produced the highest cluster purity value when combined with P^x from PTSD group and S^x from PCS+PTSD group. MPFC (Medial prefrontal cortex) has been identified as well. B. Spatial map of the group-level component, P_c^x from PTSD group, which was found to have the highest spatial correlation with and correspondence to C^x (Fig. 8 A). MPFC (Medial prefrontal cortex) has been identified as well. C. Spatial map of the group-level component, S_c^x from PCS+PTSD group, that was found to have the highest spatial correlation with and correspondence to C^x (Fig. 8 A). MPFC (Medial prefrontal cortex) has been identified as well.

We then combined P^x with S_p^x and C_p^x and examined this combination using k-means clustering. This combination produced cluster purity values of 0.93 for PTSD group, 0.83 for PCS+PTSD group, and 0.85 for the control group. The spatial correlation coefficient value between P^x and S_p^x or ρ(P^x, S_p^x) was 0.68 (p < 0.005) while ρ(P^x, CP^x) was 0.51 (p < 0.005).

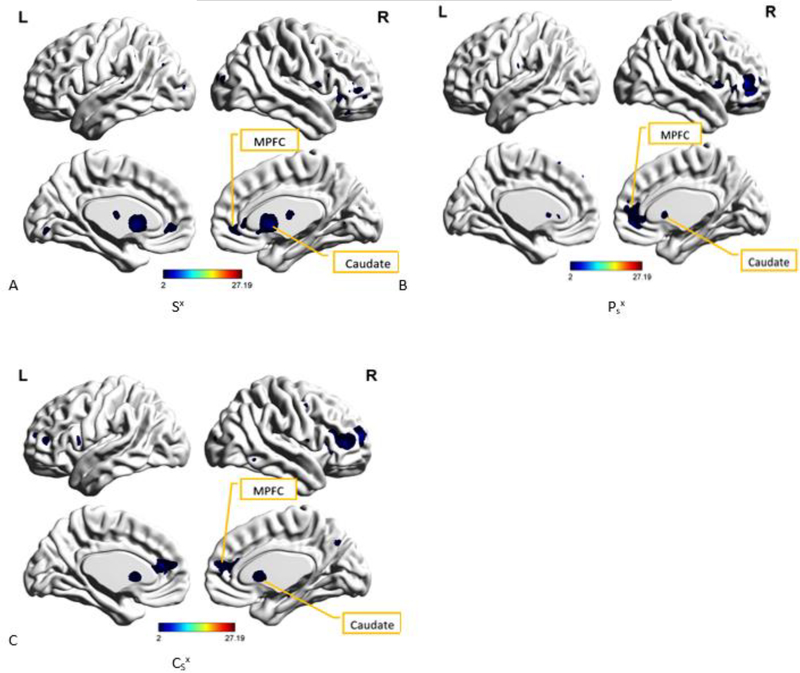
S^x was then combined with P_s^x and C_s^x and examined using k-means clustering. This combination produced cluster purity values of 1 for PTSD group, 0.97 for PCS+PTSD group, and 1 for the control group. The correlation coefficient value between S^x and P_s^x or ρ(S^x, P_s^x) was 0.55 (p < 0.005) while ρ(S^x, C_s^x) was 0.49 (p < 0.005).

Finally, we combined C^x with P_c^x and S_c^x and examined this combination using k-means clustering. This combination produced cluster purity values of 0.87 for PTSD group, 0.97 for PCS+PTSD group, and 0.92 for the control group. The correlation coefficient value between C^x and P_c^x or ρ(C^x, P_c^x) was 0.65 (p < 0.005) while ρ(C^x, S_c^x) was 0.62 (p< 0.005).

We then completed a series of two sample t-tests as described in the previous section. The goal was to examine whether there werewere significant between-group differences in the strength of the reproducible network(s) discovered in P^x, S^x, and C^x, as well as their spatial homologues. This round of tests indicated that these networks comprising medial prefrontal cortex as shown in C^x were significantly stronger in controls as compared to both PTSD (p < 0.05 unc., t = 1.67) and PCS+PTSD (p < 0.05 unc., t = 1.67) groups. Also, functional networks comprising dorsolateral prefrontal cortex and inferior parietal lobe, shown in P^x, were significantly stronger as compared to PCS+PTSD (p < 0.05, t = 1.68).

DISCUSSION

In this section, we discuss the main findings of our study. We first present the unique and beneficial features of our DisConICA software package. Next, we discuss the significance of the results we have obtained from DisConICA analysis of resting state fMRI data acquired from PTSD, PCS+PTSD and controls groups, and whether they support the hypotheses described earlier in this paper. DisConICA provides users the ability to examine the reproducibility of group-level independent components using the gRAICAR algorithm, and the ability of these group-level components to distinguish between groups using unsupervised learning algorithms such as k-means clustering. A variety of neuroimaging softwares provide the ability to view and analyze fMRI data. Functionality in existing software packages include, but are not limited to, viewing fMRI data, format conversions such as from DICOM to NIfTI, brain extraction, tissue-type segmentation, segmentation of subcortical structures, linear and nonlinear registration, voxel-wise analysis of multi-subject grey-matter density, longitudinal and cross-sectional analysis of structural changes, and structural analysis and include well respected packages such as DPARSF, SPM, FSL, Mango, AFNI, BrainNet Viewer, and Brain Voyager among others [29] [30] [31] [32] [38] [39] [40]. Taking analyses a step further are standalone packages and sub-packages of the aforementioned ones, such as Sci-kit based software, MELODIC, GIFT, and CONN, a functional connectivity toolbox, among others, that apply various multivariate functional connectivity techniques to fMRI datasets including ICA and group ICA [41] [33] [42] [43] [44].

Although there are robust fMRI analysis packages available to separately perform different steps described in our algorithm, the unique feature of our software is its ability to seamlessly interface between different packages and provide a one-stop solution. Specifically, the software incorporates ingestion, pre-, and para-processing steps from other software packages whilst including an implementation of a “discover-confirm” approach we have proposed in this study. The ability to seamlessly interface with other software packages provides pre- and para-processing functionality as well as the ability to post-process, including but not limited to, the identification of highly reproducible components in each input group, the selection and creation of a data set based upon spatial maps of highly reproducible independent components, and the application of unsupervised learning techniques, k-means clustering algorithm currently, to distinguish between input groups. Given that software packages for achieving specific, yet narrow, objectives are continuously being released and given that different packages may be better at achieving certain objectives compared to others, we feel that the approach of seamless integration and communication between different software packages is a model for future software development in neuroimaging.

We are implementing our methodology in its entirety in the DisConICA package, with no such implementations available in the literature currently. Therefore, a direct comparison with packages mentioned earlier is beyond the scope of the current report. However, we highlight how our software takes fMRI data analysis a step further. In addition to providing and automating all stages of pre-processing, it incorporates techniques to determine and analyze the reproducibility of group-level independent components using the gRAICAR algorithm [17] and k-means clustering. In DisConICA, the user simply needs to complete two tasks to setup the analysis: (i) a pre-determined directory structure where individual subject level images are arranged in group-level directories that the subjects belong to, and (ii) the availability of the required analysis environment. Other tasks are accomplished seamlessly by DisConICA in the background and user responsibilities are minimized. DisConICA completes all pre-processing steps emulating our approach and processing choices we used. It then uses a “discover-confirm” approach wherein, during the “discover” phase, it uses gRAICAR to retrieve reproducible components in each group. During the “confirm” phase, it uses unsupervised learning to determine the separation between groups based on the reproducible components in each group. During discover and confirm phases, individual subject components determined reproducibility and discriminability, respectively. The group level components are shown for interpretation purposes and did not impact the estimates of reproducibility or discriminability. This is a novel methodological framework for investigating discriminative features between diagnostic groups, as opposed to performing group-wise statistical tests or supervised classification. DisConICA then compares group-level components to find the ones that produce high cluster purities. Once a combination with one group-level component from each group that produces the highest cluster purity has been identified, group-level components with similar networks in opposite groups for each component in this combination are identified using spatial correlation. The software combines components with similar networks (i.e. spatial distributions) and determines cluster purity once more, per network, to evaluate separation between groups based upon these networks. Discriminability is assessed by using the network most reproducible within a group but not in the combined group and the spatial analog of the identified network in the other group so that the approach is not circular i.e. (i) P^x, S_p^x, C_p^x as shown in Fig. 6, (ii) S_x, P_s^x, C_s^x as shown in Fig. 7, and (iii) C_x, P_c^x, S_c^x as shown in Fig. 8.

Fig. 7.

A. Spatial map of the group-level component, S^x from PCS+PTSD group, that was most reproducible within the PCS+PTSD group as well as produced the highest cluster purity value when combined with P^x from PTSD group and C^x from the controls group. Caudate and MPFC (medial prefrontal cortex) have been identified as well. B. Spatial map of the group-level component, P_s^x from PTSD group, which was found to have the highest spatial correlation with and correspondence to S^x (Fig 7 A). Caudate and MPFC (medial prefrontal cortex) have been identified as well. C. Spatial map of the group-level component, C_s^x from the controls group, which was found to have the highest spatial correlation with and correspondence to S^x (Fig. 7 A). Caudate and MPFC (medial prefrontal cortex) have been identified as well.

gRAICAR is already a publicly available software and we use it as part of our software. Therefore, it is important to note the differences relationship between gRAICAR and DisConICA. Our software takes a user through the entire process from raw data to pre-, para- and post-processing steps including automating and integrating DPARSF, FSL MELODIC and gRAICAR. Most importantly, our software allows seamless interaction between other software packages including gRAICAR. It then builds upon results and completes clustering analysis and reporting. In cases there is enough information about a disorder, it confirms the networks between subjects and controls. Where there isn’t much information available a priori, it can lead to the discovery of networks relevant to that disorder or a research area. In short, gRAICAR is one component of our software, but it does much more, as described above.

When the tool was used to study reproducible independent components in the comparison between psychiatric populations of PTSD and PCS+PTSD along with controls, we made interesting findings. The brain regions involved in the most reproducible components in the three groups, i.e. P^x, C^x and S^x, were frontal regions including the dorsolateral prefrontal cortex (DLPFC) and medial prefrontal cortex (MPFC), the caudate and inferior parietal lobe (IPL, also recognized as the temporo-parietal junction or TPJ). These regions are generally known to be involved in executive control. Furthermore, statistical tests indicated that these networks were the strongest in controls, weaker in PTSD, and the weakest in PCS+PTSD. This observation is in agreement with the fact that brain regions involved in executive control are impaired in these disorders [45] [37] [46] [47]. PCS+PTSD appeared to be more extreme than PTSD, mirroring prior findings [37]. The functional connectivity patterns were comparable in general to previous studies [48] [49] [50]. Specifically, our findings corroborated with findings from previous studies, which implicate the prefrontal cortex (more specifically DLPFC and MPFC) [51] [52] [53] [54], lateral parietal cortex [55] [56] [57] [58], and the caudate [59] [60] [61] [62] in these disorders. Given that the DisConICA algorithm identifies reproducible components, our findings in these disorders can be utilized to further test possible diagnostic instruments and treatment interventions targeting the identified brain mechanisms.

Limitations

We now point out some technical limitations of the current version of DisConICA. This version has been developed in MATLAB 2014a and 2016, and is not standalone in its current shape and form. It also has dependencies on pre-processing software such as DPARSF v4.0, FSL v6.0, SPM v8, and REST v1.8. Even though these softwares are provided as a part of the DisConICA package, technical and performance impediments in these softwares, such as processing times, unavoidably affect the overall performance of DisConICA. The current version has been limited to the study of up to three groups, as illustrated in our example application described in this paper. This and other limitations will be reviewed in future versions and, hopefully, mitigated.

DisConICA is being designed as a comprehensive rs-fMRI analysis package which accepts data in raw formats and applies pre-, para-, and post-processing techniques to implement various algorithmic stages of our proposed approach. Due to the amount of processing involved, we have benchmarked the performance of our software using two different methods of application, interactive or non-batch (NB) and batch-mode (BM). Fig. 9. shows processing time comparison for the two data sets: the first dataset has 2 groups with 4 subjects each and 120 time points and the second dataset has 3 groups with 4 subjects each and 1000 time points. Processing stages have been presented along the y-axis. The benchmarking was completed in a Lenovo System X HPC Cluster environment where the interactive or non-batch mode processing took place on a computing node with 128GB of memory and 2 “Haswell” CPUs (10 cores/CPU). The processing time increases significantly as the number of time points or subjects increases. We believe that computational complexity could be potential limitation of the proposed software. However, we continue to explore new high performance technologies as they are introduced, in order to enhance processing times, and believe that this is less likely to be an issue in the future.

Fig. 9.

Processing time comparison (in seconds, shown on x-axis) between two data sets (the first dataset has 2 groups with 4 subjects each and 120 time points and the second dataset has 3 groups with 4 subjects each and 1000 time points) and two execution modes: interactive or non-batch (NB) and batch-mode (BM). Processing stages have been presented along the y-axis.

Storage and memory utilization are another two concerns depending upon the user’s computing environment. Since DisConICA has been designed to accept raw input data and apply all pre-, para-, and post-processing steps, the amount of memory increases significantly at run-time. During benchmarking, we noticed that a raw data set at 105 MB with 4 subjects and 120 time points increased in size to 1.4 GB whereas another raw data set with 4 subjects and 1000 time points initially at 899 MB grew to around 10 GB. This involves various phases of computation including ICA and gRAICAR analysis. A user would need to take these environmental constraints into consideration before proceeding with a larger data set. Processing may not proceed successfully if enough memory is not allocated during these stages.

Future Work

The current version of DisConICA has been written in MATLAB version 2014a but tested with the 2016 version as well. It runs on a UNIX platform (although, it can run on Windows platform with some modifications, which will be forthcoming in the future) and takes advantage of multi-processor environments for faster processing.

We would like to note some important differences between our approach and the bootstrapping analysis of stable cluster (BASC) approach proposed by Bellec et al. [65]. They perform clustering of fMRI time series themselves and the resting state networks are defined based on these clustering, while our definition of resting state networks are based on ICA. It is generally understood that the spatial independence condition of ICA may be more suitable for identifying resting state networks whereas clustering fMRI time series may be more appropriate to obtain brain parcellations. That said, we do acknowledge that the bootstrapping methodology employed by them is generalizable and it is conceivable that such a methodology may be employed to assess the stability of resting state networks discovered through ICA. Future work must attempt to assess the comparative utility of gRAICAR and BASC in assessing reproducibility of resting state networks. Future work must also attempt to evaluate the utility of our approach in various domains of application such as lifespan studies [47].