Making the Most of Clumping and Thresholding for Polygenic Scores

Abstract

Polygenic prediction has the potential to contribute to precision medicine. Clumping and thresholding (C+T) is a widely used method to derive polygenic scores. When using C+T, several p value thresholds are tested to maximize predictive ability of the derived polygenic scores. Along with this p value threshold, we propose to tune three other hyper-parameters for C+T. We implement an efficient way to derive thousands of different C+T scores corresponding to a grid over four hyper-parameters. For example, it takes a few hours to derive 123K different C+T scores for 300K individuals and 1M variants using 16 physical cores. We find that optimizing over these four hyper-parameters improves the predictive performance of C+T in both simulations and real data applications as compared to tuning only the p value threshold. A particularly large increase can be noted when predicting depression status, from an AUC of 0.557 (95% CI: [0.544–0.569]) when tuning only the p value threshold to an AUC of 0.592 (95% CI: [0.580–0.604]) when tuning all four hyper-parameters we propose for C+T. We further propose stacked clumping and thresholding (SCT), a polygenic score that results from stacking all derived C+T scores. Instead of choosing one set of hyper-parameters that maximizes prediction in some training set, SCT learns an optimal linear combination of all C+T scores by using an efficient penalized regression. We apply SCT to eight different case-control diseases in the UK biobank data and find that SCT substantially improves prediction accuracy with an average AUC increase of 0.035 over standard C+T.

Introduction

The ability to predict disease risk accurately is a principal aim of modern precision medicine. As more population-scale genetic datasets become available, polygenic risk scores (PRS) are expected to become more accurate and clinically relevant. The most commonly used method for computing polygenic scores is clumping and thresholding (C+T), also known as pruning and thresholding (P+T). The C+T polygenic score is defined as the sum of allele counts (genotypes), weighted by estimated effect sizes obtained from genome-wide association studies, where two filtering steps have been applied.1, 2, 3, 4, 5, 6 More precisely, the variants are first clumped (C) so that only variants that are weakly correlated with one another are retained. Clumping selects the most significant variant iteratively, computes correlation between this index variant and nearby variants within some genetic distance w_c, and removes all the nearby variants that are correlated with this index variant beyond a particular value, $r_c^2$. Thresholding (T) consists in removing variants with a p value larger than a chosen level of significance (p > p_T). Both steps, clumping and thresholding, represent a statistical compromise between signal and noise. The clumping step prunes redundant correlated effects caused by linkage disequilibrium (LD) between variants. However, this procedure may also remove independently predictive variants in LD. Similarly, thresholding must balance between including truly predictive variants and reducing noise in the score by excluding null effects.

When applying C+T, one has three hyper-parameters to select, namely the squared correlation threshold $r_c^2$ and the window size w_c of clumping, along with the p value threshold p_T. Usually, C+T users assign default values for clumping, such as $r_c^2$ of 0.1 (default of PRSice), 0.2 or 0.5 (default of PLINK), and w_c of 250 kb (default of PRSice and PLINK) or 500 kb, and test several values for p_T ranging from 1 to 10⁻⁸.^2,4,5,7 Moreover, to compute the PRS, the target sample genotypes are usually imputed to some degree of precision in order to match the variants of summary statistics. The inclusion of imputed variants with relatively low imputation quality is common, assuming that using more variants in the model yields better prediction. Here, we explore the validity of this approach and suggest an additional INFO_T threshold on the quality of imputation (often called the INFO score) as a fourth parameter of the C+T method.

We implement an efficient way to compute C+T scores for many different parameters (LD, window size, p value, and INFO score) in R package bigsnpr.⁸ Using a training set, one could therefore choose the best predictive C+T model among a large set of C+T models with many different parameters, and then evaluate this model in a test set. Moreover, instead of choosing one set of parameters that corresponds to the best prediction, we propose to use stacking, i.e., we learn an optimal linear combination of all computed C+T scores using an efficient penalized regression to improve prediction beyond the best prediction provided by any of these scores.⁹ We call this method SCT (stacked clumping and thresholding). Using the UK Biobank data¹⁰ and external summary statistics for simulated and real data analyses, we show that testing a larger grid of parameters consistently improves predictions as compared to using some default parameters for C+T. We also show that SCT consistently improves prediction compared to any single C+T model when sample size of the training set is large enough.

Material and Methods

Clumping and Thresholding (C+T) and Stacked C+T (SCT)

We compute C+T scores for each chromosome separately and for several parameters:

• •Threshold on imputation INFO score INFO_T within {0.3, 0.6, 0.9, 0.95}.
• •Squared correlation threshold of clumping $r_c^2$ within {0.01, 0.05, 0.1, 0.2, 0.5, 0.8, 0.95}.
• •Base size of clumping window within {50, 100, 200, 500}. The window size w_c is then computed as the base size divided by $r_c^2$. For example, for $r_c^2=0.2$, we test values of w_c within {250, 500, 1000, 2500} (in kb). This is motivated by the fact that linkage disequilibrium is inversely proportional to genetic distance between variants.¹¹
• •A sequence of 50 thresholds on p values between the least and the most significant p values, equally spaced on a log-log scale.

Thus, for individual i, chromosome k, and the four hyper-parameters INFO_T, $r_c^2$, w_c, and p_T, we compute C+T predictions

$$V_i^{\left(k\right)}\left({\text{INFO}}_T,r_c^2,w_c,p_T\right)=\sum _{\begin{array}{c}j\in S_{\text{clumping}}\left(k,{\text{INFO}}_T,r_c^2,w_c\right)\\ p_j<p_T\end{array}}{\hat{\beta }}_j\cdot G_{i,j},$$

where ${\hat{\beta }}_j$ $\left(p_j\right)$ are the effect sizes (p values) estimated from the GWAS, G_i,j is the dosage for individual i and variant j, and the set $S_{\text{clumping}}\left(k,{\text{INFO}}_T,r_c^2,w_c\right)$ corresponds to first restricting to variants of chromosome k with an INFO score ≥ INFO_T and that further result from clumping with parameters $r_c^2$ and w_c.

Overall, we compute 22 × 4 × 7 × 4 × 50 = 123,200 vectors of polygenic scores. Then, we stack all these polygenic scores (for individuals in the training set) by using these scores as explanatory variables and the phenotype as the outcome in penalized regression.⁹ In other words, we fit weights for each C+T scores using an efficient penalized logistic regression available in R package bigstatsr.¹² This results in a linear combination of C+T scores, where C+T scores are linear combinations of variants, so that we can derive a single vector of variant effect sizes to be used for prediction in the test set. We refer to this method as SCT (stacked clumping and thresholding) in the rest of the paper.

From this grid of 123,200 vectors of polygenic scores, we also derive two C+T scores for comparison. First, “stdCT” is the standard C+T score using some default parameters, i.e., with $r_c^2$ = 0.2, w_c = 500, a liberal threshold of 0.3 on imputation INFO score, and choosing the p value threshold (≥10⁻⁸) maximizing the AUC on the training set.⁴ Second, “maxCT” is the C+T score maximizing the AUC on the training set among the 5,600 (123,200/22) C+T scores corresponding to all different sets of parameters tested. Although the set used to choose optimal hyper-parameters is commonly called “validation set,” we refer to this set as “training set” here because it is also the set used for learning weights of stacking. Also note that stdCT and maxCT use the same set of parameters for all chromosomes, i.e., for one set of the four hyper-parameters, they are defined as $V^{\left(1\right)}+\cdots +V^{\left(22\right)}$. In contrast, SCT uses the whole matrix of 123,200 vectors.

Simulations

We use variants from the UK Biobank (UKBB) imputed dataset that have a minor allele frequency larger than 1% and an imputation INFO score larger than 0.3. There are almost 10M such variants, of which we randomly choose 1M in two different ways. First, we randomly sample 1M from these 10M variants, so we use variants that are mainly well imputed (Figure S1A). Second, we sample variants according to the inverse of INFO score density, so we use variants that are globally not as well imputed as before (Figure S1B).

To limit population structure and family structure, we restrict individuals to the ones identified by the UK Biobank as British with only subtle structure and exclude all second individuals in each pair reported by the UK Biobank as being related.¹⁰ This results in a total of 335,609 individuals that we split into three sets: a set of 315,609 individuals for computing summary statistics (GWAS), a set of 10,000 individuals for training hyper-parameters, and a test set of 10,000 individuals for evaluating models.

We read the UKBB BGEN files using function snp_readBGEN from package bigsnpr.⁸ For simulating phenotypes and computing summary statistics, we read UKBB data as hard calls by randomly sampling hard calls according to reported imputation probabilities. For the training and test sets, we read these probabilities as dosages (expected values). This procedure enables us to simulate phenotypes using hard calls and then to use the INFO score (imputation accuracies) reported by the UK Biobank to assess the quality of the imputed data used for the training and test sets.

We simulate binary phenotypes with a heritability h² = 0.5 using a liability threshold model (LTM) with a prevalence of 10%.¹³ We vary the number of causal variants (100, 10K, or 1M) to match a range of genetic architectures from low to high polygenicity. Liability scores are computed from a model with additive effects only: we compute the liability score of the i^th individual as $y_i={\sum }_{j\in S_{\text{causal}}}{w}_j\widetilde{G_{i,j}}+{\mathrm{\epsilon }}_i,$ where S_causal is the set of causal variants, w_j are weights generated from a Gaussian distribution $N\left(0,h^2/\left|S_{\text{causal}}\right|\right)$, G_i,j is the allele count of individual i for variant j, $\widetilde{G_{i,j}}$ corresponds to its standardized version (zero mean and unit variance), and ε follows a Gaussian distribution $N\left(\mathrm{0,1}-h^2\right)$.

We explore three additional simulation scenarios with more complex architectures. In scenario “2chr,” 100 variants of chromosome 1 and all variants of chromosome 2 are causal with half of the heritability for both chromosomes; it aims at assessing predictive performance when disease architectures are different for different chromosomes. In scenario “err,” we sample 10K random causal variants but 10% of the GWAS effects (causal or not) are reported with an opposite effect in the summary statistics; it aims at assessing whether methods are able to partially correct for errors or mere differences in effect sizes between GWAS and the target data. In scenario “HLA,” 7,105 causal variants are chosen in one long-range LD region of chromosome 6; it aims at assessing whether methods can handle strong correlation between causal variants.

To compute summary statistics, we use Cochran-Armitage additive test.¹⁴ Given that we restricted the data to have minimal population structure, this test based on contingency tables is much faster than using a logistic regression with ten principal components as covariates (a few minutes versus several hours) while providing similar effect sizes and Z-scores (Figure S2).

In simulations, we compare five methods: stdCT, maxCT, SCT (defined in Clumping and Thresholding (C+T) and Stacked C+T (SCT)), lassosum,¹⁵ and LDpred.¹⁶ Each simulation scenario is repeated 10 times and the average AUC is reported. We prefer to use AUC over Nagelkerke’s R² because AUC has a desirable property of being independent of the proportion of cases in the validation sample; one definition of AUC is the probability that the score of a randomly selected case subject is larger than the score of a randomly selected control subject.¹⁷ An alternative to AUC would be to use a better R² on the liability scale.^18,19

Real Summary Statistics

We also investigate predictive performance of C+T, SCT, lassosum, and LDpred using the UK Biobank. We first pick existing external summary statistics from published GWAS of real diseases.²⁰ We then divide the UK Biobank dataset into one training set and one test set. The training set is used to choose optimal hyper-parameters in C+T, LDpred, and lassosum, and to learn stacking weights in SCT. The test set is used to evaluate the final model. Training SCT and choosing optimal hyper-parameters for C+T (stdCT and maxCT) and lassosum use 63%–90% of the UK Biobank individuals reported in Table 1. Therefore, the training set can contain as many as 250K individuals. LDpred is excluded from this analysis due to computational infeasibility. To assess how sample size affects predictive performance of methods, we also compare these methods (including LDpred) using a much smaller training set of 500 case subjects and 2,000 control subjects only. We repeat this random split six times for each phenotype, and the average AUC is reported.

Table 1.

Summary of GWAS Data Used

Trait and GWAS Citation	UKBB Size – Training (%)	GWAS Size	GWAS #Variants
Breast cancer (BRCA)21	11,578/158,391 – 150,000 (88)	137,045/119,078	11,792,542
Rheumatoid arthritis (RA)22	5,615/226,327 – 200,000 (86)	29,880/73,758	9,739,303
Type 1 diabetes (T1D)23	771/314,547 – 200,000 (63)	5,913/8,828	8,996,866
Type 2 diabetes (T2D)24	14,176/314,547 – 250,000 (76)	26,676/132,532	12,056,346
Prostate cancer (PRCA)25	6,643/141,321 – 120,000 (81)	79,148/61,106	20,370,946
Depression (MDD)26	22,287/255,317 – 250,000 (90)	59,851/113,154	13,554,550
Coronary artery disease (CAD)27	12,263/225,927 – 200,000 (84)	60,801/123,504	9,455,778
Asthma28	43,787/261,985 – 250,000 (82)	19,954/107,715	2,001,280

Number of case and control subjects in UK Biobank (UKBB) for several disease phenotypes, along with corresponding published GWAS summary statistics. Summary statistics are chosen from GWASs that did not include individuals from UKBB. For depression, we remove UKBB individuals from the pilot release since they were included in the GWAS from which we use summary statistics.

As in simulations, we restrict individuals to the ones identified by the UK Biobank as British with only subtle structure and exclude all second individuals in each pair reported by the UK Biobank as being related.¹⁰ Table 1 summarizes the number of case and control subjects in the UKBB after this filtering and for each phenotype analyzed, as well as the number of individuals and variants used in the GWAS. For details on how we define phenotypes in the UKBB, please refer to our R code (see Reproducibility). Briefly, we use self-reported illness codes (field #20001 for cancers and #20002 otherwise) and ICD10 codes (fields #40001, #40002, #41202, and #41204 for all diseases and field #40006 specifically for cancers).

We keep all variants with a GWAS p value lower than 0.1, except for prostate cancer (0.05) and asthma (0.5). This way, we keep around 1M variants for each phenotype, deriving all C+T scores and stacking them in SCT in less than 1 day for each phenotype, even when using 300K individuals in the training set. To match variants from summary statistics with data from the UK Biobank, we first remove ambiguous alleles [A/T] and [C/G]. We then augment the summary statistics twice: first by duplicating each variant with the complementary alleles, then by duplicating variants with reverse alleles and effects. Finally, we include only variants that we match with UKBB based on the combination of chromosome, position, and the two alleles. Note that, when no or very few alleles are flipped, we disable the strand flipping option and therefore do not remove ambiguous alleles; this is the case for all phenotypes analyzed here. For example, for type 2 diabetes, there are 1,408,672 variants in summary statistics (p < 0.1), of which 215,821 are ambiguous SNPs. If we remove these ambiguous SNPs, 1,145,260 variants are matched with UKBB, of which only 38 are actually flipped. So, instead, we do not allow for flipping and do not remove ambiguous alleles, and then 1,350,844 variants are matched with UKBB.

Reproducibility

The code to reproduce the analyses and figures of this paper is available as R scripts online (see Web Resources).²⁹ To execute these scripts, you need to have access to the UK Biobank data that we are not allowed to share. An introduction to SCT is also available online (see Web Resources).

Results

Simulations

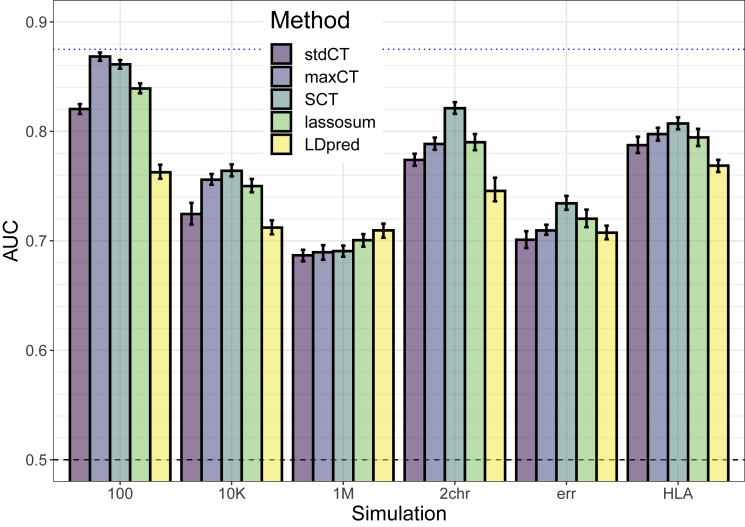
We test six different simulations scenarios. In all these scenarios, maxCT—that tests a much larger grid of hyper-parameters values for C+T on the training set—consistently provides higher AUC values on the test set as compared to stdCT that tests only several p value thresholds while using default values for the other parameters (Figure 1). The absolute improvement in AUC of maxCT over stdCT is particularly large in the cases of 100 and 10,000 causal variants, where causal effects are mostly independent of one another. In these cases, using a very stringent $r_c^2=0.01$ threshold of clumping provides higher predictive performance than using a standard default of $r_c^2=0.2$ (Figures S6A and S6B). However, $r_c^2=0.2$ provides best predictive performance when simulating 1M causal variants. Still, in this scenario, using a large window size w_c of 2,500 kb increases AUC as compared to using default values of either 250 or 500 kb (Figure S6C).

Figure 1.

Results of the Six Simulation Scenarios with Well-Imputed Variants

Scenarios are (100) 100 random causal variants; (10K) 10,000 random causal variants; (1M) all 1M variants are causal variants; (2chr) 100 variants of chromosome 1 are causal and all variants of chromosome 2, with half of the heritability for both chromosomes; (err) 10,000 random causal variants, but 10% of the GWAS effects are reported with an opposite effect; (HLA) 7,105 causal variants in a long-range LD region of chromosome 6. Mean and 95% CI of 10⁴ non-parametric bootstrap replicates of the mean AUC of 10 simulations for each scenario. The blue dotted line represents the maximum achievable AUC for these simulations (87.5% for a prevalence of 10% and an heritability of 50%; see Equation 3 of Wray et al.³⁰). See corresponding values in Table S1.

As for SCT, it provides equal or higher predictive performance than maxCT in the different simulation scenarios (Figure 1). In the first three simple scenarios simulating 100, 10K, or 1M causal variants anywhere on the genome, predictive performance of SCT are similar to maxCT. In the “2chr” scenario where there are large effects on chromosome 1, small effects on chromosome 2 and no effect on other chromosomes, mean AUC is 78.7% for maxCT and 82.2% for SCT. In the “err” scenario where we report GWAS summary statistics with 10% opposite effects (errors or mere differences), mean AUC is 70.2% for maxCT and 73.2% for SCT. In these simulations, lassosum and LDpred do not provide the best predictive performance, expect when simulating all variants as causal (1M).

Results are similar when using less well imputed variants in the simulations. Globally in these simulations, including a broad range of imputed variants with INFO score as low as 0.3 often maximizes prediction (Figures S6 and S7).

Effects resulting from SCT (Figure S5) are mostly comprised between the GWAS effects and 0. For the simulation with only 100 causal variants, resulting effects are either nearly the same as in the GWAS or near 0 (or exactly 0). When there are some correlation between causal predictors (scenarios “1M” and “HLA”) or when reporting GWAS effects with some opposite effect (“err”), some effects resulting from SCT are in the opposite direction as compared to the GWAS effects.

Real Summary Statistics

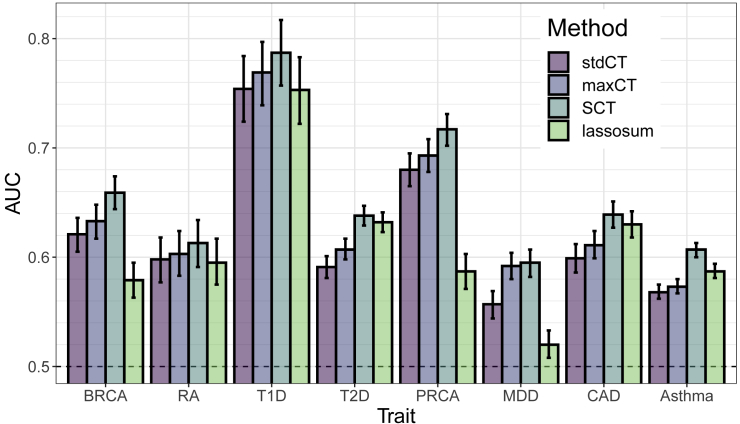
In terms of AUC, maxCT outperfoms stdCT for all eight diseases considered with a mean absolute increase of 1.3% (Figures 2 and S4). A particularly large increase can be noted when predicting depression status (MDD), from an AUC of 55.7% (95% CI: [54.4–56.9]) with stdCT to an AUC of 59.2% (95% CI: [58.0–60.4]) with maxCT. For MDD, a liberal inclusion in clumping ($r_c^2$ = 0.8) and a stringent threshold on imputation accuracy (INFO_T = 0.95) provides the best predictive performance (Figure S9f). For all eight diseases, predictions were optimized when choosing a threshold on imputation accuracy of at least 0.9, whereas optimal values for $r_c^2$ where very different depending on the architecture of diseases, with optimal selected values over the whole range of tested values for $r_c^2$ (Table 2).

Figure 2.

Results of the Real Data Applications with Large Training Size

AUC values on the test set of UKBB (mean and 95% CI from 10⁴ bootstrap samples). Training SCT and choosing optimal hyper-parameters for C+T and lassosum use 63%–90% of the individuals reported in Table 1. See corresponding values in Table S2.

Table 2.

Optimal Choices of C+T Parameters

Trait	wc	$r_c^2$	INFOT	pT
Breast cancer (BRCA)	2,500	0.2	0.95	2.2×10-4
Rheumatoid arthritis (RA)	200	0.5	0.95	7.5×10-2
Type 1 diabetes (T1D)	10K–50K	0.01	0.90	2.6×10-5
Type 2 diabetes (T2D)	625	0.8	0.95	1.1×10-2
Prostate cancer (PRCA)	10K–50K	0.01	0.90	4.2×10-6
Depression (MDD)	625	0.8	0.95	1.0×10-1
Coronary artery disease (CAD)	526	0.95	0.95	3.5×10-2
Asthma	2,500	0.2	0.90	2.2×10-4

Choice of C+T parameters is based on the maximum AUC in the training set. Hyper-parameters of C+T are the squared correlation threshold $r_c^2$ and the window size w_c of clumping, the p value threshold p_T and the threshold on the quality of imputation INFO_T. Choosing optimal hyper-parameters for C+T use 63%–90% of the individuals reported in Table 1. Resulting predictions of maxCT in the test set are reported in Figure 2.

Furthermore, when training size uses a large proportion of the UK Biobank data, SCT outperforms maxCT for all eight diseases considered with an additional mean absolute increase of AUC of 2.2%, making it 3.5% as compared to stdCT (Figure 2 and Table S2). Predictive performance improvement of SCT versus maxCT is particularly notable for coronary artery disease (2.8%), type 2 diabetes (3.1%), and asthma (3.4%).

Effects resulting from SCT have mostly the same sign as initial effects from GWAS, with few effects being largely unchanged and others having an effect that is shrunk to 0 or equals to 0, i.e., variants not included in the final model (Figure S8).

When training size is smaller (500 case subjects and 2,000 control subjects only instead of 120K–250K individuals), SCT is not as good as when training size is large, yet SCT remains a competitive method expect for depression for which maxCT performs much better than all other methods (Figure S4). Performance of C+T and lassosum, methods that use the training set for choosing optimal hyper-parameters only, as opposed to SCT that learns new weights, are little affected by using a smaller training size. However, even though lassosum can provide more accurate prediction for T2D and CAD, it can also perform very poorly for other diseases such as BRCA, PRCA, and MDD (Figures 2 and S4). LDpred performs much better than the other methods for predicting MDD, yet maxCT and SCT perform equally or better than LDpred for the seven other traits (Figure S4).

Discussion

Predictive Performance Improvement of C+T

C+T is an intuitive and easily applicable method for obtaining polygenic scores trained on GWAS summary statistics. Two popular software packages that implement C+T, namely PLINK and PRSice, have further contributed to the prevalence of C+T.^5,7,31,32 Usually, C+T scores for different p value thresholds are derived, using some default values for the other three hyper-parameters. In R package bigsnpr, we extend C+T to efficiently consider more hyper-parameters (four by default) and enable the user to define their own qualitative variant annotations to filter on. Using simulated and real data, we show that choosing optimized hyper-parameter values rather than default ones can substantially improve the performance of C+T, making C+T a very competitive method. Indeed, in our simulations (Figure 1), we found that optimizing C+T (maxCT) performed on par with more sophisticated methods such as lassosum and LDpred.

Moreover, it is possible to rerun the method using a finer grid in a particular range of these hyper-parameters. For example, it might be useful to include variants with p values larger than 0.1 for predicting rheumatoid arthritis and depression (Figures S9B and S9F). Another example would be to focus on a finer grid of large values of $r_c^2$ for coronary artery disease (Figure S9G) or to focus on a finer grid of stringent imputation thresholds only (Table 2). One can of course also optimize lassosum and LDpred, which could result in better relative performance. One limitation of LDpred is that its non-infinitesimal version is a Gibbs sampler, which can become unstable if the data do not fit the model well. In practice, this affects the robustness of LDpred and becomes more severe when applied to summary statistics with large sample sizes. Indeed, LDpred has been reported to not adequately adjust for LD structure when sample size of summary statistics is large and that using alternative methods such as PRS-CS may solve this issue.³³ Alternatively, recent work also suggests that excluding long-range LD regions when applying LDpred can improve its predictive performance.^34,35 It may therefore be possible to improve the robustness of the LDpred Gibbs sampler by handling LD and heritability estimation more carefully. When applying LDpred and lassosum, we did not explore non-standard parameter settings or extensions of LDpred.

Table 2 shows that the optimal parameters of C+T are very different depending on which trait is analyzed. For instance, T1D and PRCA have similar optimal parameters (a stringent clumping $r_c^2$ and p value threshold p_T of 10⁻⁵), while RA, T2D, MDD, and CAD perform also similarly (a lenient clumping $r_c^2$ and p value threshold). The first group captures a small set of variants with relatively large effects while the second group captures a multitude of small effects. A possible explanation is that traits of the second group are much more polygenic than in the first group. Another possible explanation is that variants associated with the second group have smaller effects that are more difficult to detect and that including more variants (possibly a lot being noise) provides higher predictive performance.

Using a large grid of C+T scores for different hyper-parameters, we show that stacking these scores instead of choosing the best one improves prediction further.⁹ Combining multiple PRSs is not a new idea,^36,37 but we push this idea to the limit by combining 123,200 polygenic scores. This makes SCT more flexible than any C+T model, but it of course also requires a larger training dataset with individual-level genotypes and phenotypes to learn the weights in stacking.

Normally, cross-validation should be used to prevent overfitting when using stacking.⁹ However, cross-validation is not necessary here since building C+T scores does not make use of the phenotype of the training set that is later used for stacking. Moreover, although it has been suggested to use positivity constraints in stacking,⁹ we allow C+T scores to have negative weights in the final model for three reasons. First, because C+T scores are overlapping in the variants they use, using some negative weights allows us to weight groups of variants that correspond to the difference of two sets of variants. Second, because of LD, variants may have different effects when learned jointly with others (Figures S5C and S5F). Third, if reported GWAS effects are heterogenous between the GWAS dataset and the validation or target dataset, then having variants with opposite effects can help to adjust the effects learned during GWAS.

Limitations of the Study

In this study, we limited the analysis to eight common diseases and disorders, as these all had substantial number of case subjects and publicly available GWAS summary statistics based on substantial sample sizes. For example, for psychiatric disease, we include only depression (MDD) because diseases such as schizophrenia and bipolar disorder have very few case subjects in the UK Biobank; dedicated datasets should be used to assess effectiveness of maxCT and SCT for such diseases. We also do not analyze many automimmune diseases because summary statistics are often outdated (2010–2011¹) and because there are usually large effects in regions of chromosome 6 with high LD, methods that use individual-level data instead of summary statistics are likely to provide better predictive models.¹² We also chose not to analyze any continuous trait such as height or BMI because there are many individual-level data available in UKBB for such phenotypes and methods directly using individual-level data are likely to provide better predictive models for predicting in UKBB than the ones using summary statistics.^12,38 Phenotypes with tiny effects such as educational attainment for which huge GWAS summary statistics are available might be an exception.³⁹

The principal aim of this work is to study and improve the widely used C+T method. The idea behind C+T is simple as it directly uses weights learned from GWASs; it further removes variants as one often does when reporting hits from GWASs, i.e., only variants that pass the genome-wide threshold (p value thresholding) and that are independent association findings (clumping) are reported. Yet, there are two other established methods based on summary statistics, LDpred and lassosum.^15,16,40 Several other promising and more complex methods such as NPS, PRS-CS, and SBayesR are currently being developed.^33,35,41 One could also consider other variants of C+T such as choosing a different set of hyper-parameters for each chromosome separately, which would be beneficial in the “2chr” simulation scenario where genetic architecture differs between chromosomes. Here, we include lassosum in the comparisons since no other method has yet shown that they provide any improvement over lassosum. In addition, we found lassosum to be easy to use. When applied to real data, lassosum yields mixed results because it achieves almost the largest AUC for some diseases (CAD, T2D) whereas it is less discriminative than standard C+T for other diseases (BRCA, MDD, PRCA) (Figure 2). This lack of robustness of lassosum may be explained by the presence of large effects in the latter diseases, which can be an issue for methods that model LD. This may also be due to the initial filtering on p value that we use for real data to keep disk usage and computation time manageable when analyzing the UK Biobank dataset. We also include LDpred in some of the comparisons as it is a widely used method. A full comparison of methods (including individual-level data methods), including binary and continuous traits with different architectures, using different sizes of summary statistics and individual-level data for training, and in possibly different populations would be of great interest, but is out of scope for this paper. Indeed, we believe that different methods may perform very differently in different settings and that understanding what method is appropriate for each case is of paramount interest if the aim is to maximize prediction accuracy to make PRS clinically useful.

Extending maxCT and SCT

The stacking step of SCT can be used for either binary or continuous phenotypes. Yet, for some diseases, it makes sense to include age in the models, using for example Cox proportional-hazards model to predict age of disease onset, with possibly censored data.⁴² Cox regression has already proven useful for increasing power in GWAS.⁴³ Currently, we support linear and logistic regressions in our efficient implementation of package bigstatsr, but not Cox regression. This is an area of future development; for now, if sample size is not too large, one could use R package glmnet to implement stacking based on Cox model.⁴⁴

One might also want to use other information such as sex or ancestry (using principal components). Indeed, it is easy to add covariates in the stacking step as (possibly unpenalized) variables in the penalized regression. Yet, adding covariates should be done with caution (see the example of CAD at the end of Supplemental Data).

Finally, note that there is an extra parameter in the SCT pipeline that makes possible for a user to define their own groups of variants. This allows to extend the grid of computed C+T scores and opens many possibilities for SCT. For example, we could derive and stack C+T scores for two (or more) different GWAS summary statistics, e.g., for different ancestries or for different phenotypes. This would effectively extend SCT as a multivariate method. We could also add other hyper-parameters to C+T, such as a threshold on the minor allele frequency (MAF). Indeed, it has been shown that imputation accuracy depends on both INFO score and MAF.⁴⁵ For MDD, we tested to add a threshold on MAF as a fifth hyper-parameter of C+T. This improved AUC of maxCT from 59.2% to 60.7% (Figure S10). For maxCT, the optimal threshold on MAF among $\left\{{10}^{-6},{10}^{-5},\dots ,{10}^{-1}\right\}$ was 0.01 (Figure S10). Note that this threshold on MAF now makes maxCT more predictive than LDpred that internally uses a MAF threshold of 0.01 by default. This raises questions about the ability of current methods to capture the effects of rare variants, and developing methods that can efficiently use both common and rare variants is a direction of future work. Note that it might be more efficient to construct one hyper-parameter combining INFO score and MAF instead of treating them as two distinct hyper-parameters; this is a direction of future work.

Conclusion

In this paper, we focused on understanding and improving the widely-used C+T method by testing a wide range of hyper-parameters values. More broadly, we believe that any implementation of statistical methods should come with an easy and effective way to choose hyper-parameters of these methods well. We believe that C+T will continue to be used for many years as it is both simple to use and intuitive. Moreover, as we show here, when C+T is optimized using a large grid of hyper-parameters, it becomes a very competitive method since it can adapt to many different disease architectures by tuning a large set of hyper-parameters.

Moreover, instead of choosing one set of hyper-parameters, we show that stacking C+T predictions improves predictive performance further, as long as training size is not too small. SCT has many advantages over any single C+T prediction: first, it can learn different architecture models for different chromosomes, it can learn a mixture of large and small effects and it can more generally adapt initial weights of the GWAS in order to maximize prediction. Moreover, SCT remains a linear model defined by a single vector of coefficients as it is a linear combination (stacking) of linear combinations (C+T scores).

Declaration of Interests

The authors declare no competing interests.

Published: November 21, 2019

Web Resources

• R scripts, https://github.com/privefl/simus-PRS/tree/master/paper3-SCT

• SCT tutorial, https://privefl.github.io/bigsnpr/articles/SCT.html

• UK Biobank, https://www.ukbiobank.ac.uk/