Skip to main content
PMC home page
ACS Omega logoLink to ACS Omega
. 2019 Nov 26;4(24):20665–20671. doi: 10.1021/acsomega.9b02851

Predicting Stability Constants for Terbium(III) Complexes with Dipicolinic Acid and 4-Substituted Dipicolinic Acid Analogues using Density Functional Theory

Hsieh Chen 1,*, Rena Shi 1, Hooisweng Ow 1
PMCID: PMC6906780  PMID: 31858052

Abstract

graphic file with name ao9b02851_0008.jpg

The relative stability constants of Tb(III) complexes exhibiting binding to a series of 4-substituted analogues of dipicolinic acid (2,6-pyridinedicarboxylic acid) (DPA) were calculated using density functional theory (DFT) with the standard thermodynamic cycle. DFT calculations showed that the strengths of the stability constants were modified by the substituents in the following (decreasing) order: −NH2 > −OH ∼ −CH2OH > −imidazole ∼ −Cl ∼ −Br ∼ −H > −F > −I, with the differences among them falling within one to two log units except for −NH2. Through population and structural analysis, we observed that the −NH2, −OH, −CH2OH, and halide substituents can donate electrons via resonance effect to the pyridine ring of DPA while inductively withdrawing electrons with different strengths, thus resulting in the different binding strengths of the 4-substituted DPAs to the Tb(III) ions. We believe that these observations possess utility not only in the ongoing development of luminescent probes for bioanalytical studies but also for more recent cross-industrial efforts to enhance reservoir surveillance capabilities using chemical tracers within the oil and gas sector.

Introduction

Since the demonstration of energy transfer from aromatic ligands to bound Tb(III) or Eu(III) results in dramatically enhanced luminescence from the bound lanthanide ions,1−4 extensive studies have been carried out on such systems. Because of the spectrally narrow and unique emission obtained from lanthanide ions and the millisecond-range excited-state lifetimes, organic donor–lanthanide acceptor complexes have been used in a wide variety of applications including biosensors,5 fluorescence immunoassays,6−8 luminescent probes for time-resolved microscopy and bioimaging,9−14 displays,15−17 and telecommunications.18,19 In recent years, the use of Tb(III)-sensitized luminescence in detecting ultralow levels of dipicolinic acid (DPA)20−28 has attracted much attention due to its relevance in microbial diagnostics29,30 and biodefense.31−34 Dipicolinic acid is a major constituent of the bacterial endospore structure,35 released from the spore upon germination; the exploitation of this naturally occurring system phenomenon lends itself toward utility as biological indicators for routine environmental monitoring, markers of sterilization efficiency,36,37 and, in the most inauspicious application, as first responder assays for Bacillus anthracis spores that have been employed as delivery vehicles in anthrax attacks.38−41 In addition, trace detection of DPA has been used in studying panspermia, defined by aeronautics and space-related life detection, and life in extreme environments.42−45

The specific motivation of this work stems from recent efforts to deploy DPA-based molecules as subsurface oil reservoir tracers.46−48 Defined as injecting tracers contained within injection fluids and monitoring for their appearance in neighboring production wells, tracer tests provide a plethora of information about reservoir heterogeneity, well-to-well communication, and fluid dynamics.49−52 This information can then be used for the optimization of improved oil recovery (waterflooding or chemical EOR).53 Our laboratory has been actively synthesizing and characterizing DPA derivatives, which altogether serve as “barcodes” that enable large-scale oil reservoir tracer campaigns including a multitude of injection and production wells47,48 (here, barcodes are referred to as uniquely identifiable molecules, which can be traced back to their specific original injection wells). To this end, it would be beneficial to develop computational methods for the prediction and prescreening of new ligand designs. Tb(III)-sensitized luminescence has been selected as the primary detection modality for DPA-based ligand tracers due to its high sensitivity. The first step of detection comprises the complexation of the ligands with the terbium (Tb3+) ions, which have conventionally been quantified by the stability constants (formation constants).54 In spite of the developments in computational methods and the vast increase in computational power over the past decades, reliable calculations of aqueous stability constants have been difficult. Absolute errors of |log K1exp – log K1calc| > 101 (with K1exp and K1calc are the experimental and calculated stability constants) have been commonplace, especially for multivalent anion ligands (due to the difficult solvation calculations of anion ligands’ diffusive electronic structures).55−57 Nevertheless, the relative errors comparing the stability constants of ligand–ion complexes with similar structures are more constrained. Using the cleverly designed thermodynamic cycles, the systematic errors within the computational protocols may be largely canceled.58−68 In this work, we attempted to calculate the relative stability constants for the complexation of terbium ions with a series of 4-substituted DPA analogues to preliminarily predict their efficiency in the Tb(III)-sensitized luminescence assays. In addition, population and structural analyses were carried out to elucidate the detailed electronic structures and the relative binding strengths of the complexes. We believe that the findings presented in this work not only inform better designs of the oil field ligand tracers but also offer meaningful insight toward the ongoing development of luminescent bioprobe applications.

Results and Discussion

Absolute Stability Constants for Nonsubstituted DPA and Tb(III) Complexes

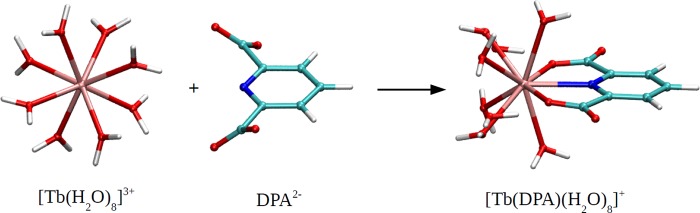
We first benchmark the different density functional theory (DFT) methods by calculating the absolute stability constants for the nonsubstituted DPA and Tb(III) complexes before transitioning to the (more robust) relative stability constant calculations for the 4-substituted DPA and Tb(III) complexes. Figure 1 shows the representative equilibrium geometries of the terbium ion with eight coordinated water molecules, [Tb(H2O)8]3+, DPA2– ligand, and their complex, [Tb(DPA)(H2O)8]+. We choose these water coordination numbers in the complexes because they have been predicted to have the most stable structures.58,69,70Table 1 summarizes the computed stability constants for the nonsubstituted DPA ligand and Tb(III) complexes (Figure 1) using DFT with different density functionals, basis sets, and solvation models. In Table 1, we also included the available experiment value.26 As shown, the computed stability constants deviated from the experiment value significantly. However, it has been identified that the prediction of “absolute” stability constants is still out of reach with current computationally efficient methods; instead, the “relative” values comparing the trends between the related structures using the same computation protocols are more trustworthy (next section)55−57,59 (It is noted that more computationally intensive methods such as explicit solvent quantum calculations may improve the predictions for absolute stability constants further;71 nevertheless, they are beyond the scope of this work). Finally, in Table 1, we observed that the selections of basis sets (6-31+G* or 6-311++G**) have the least effect on the calculated stability constants (with the calculated log K1 varied by ∼ ±1), while the selections of solvation models (COSMO or SMD) and density functionals (B3LYP or M06) have much larger effects (with the calculated log K1 varied by ∼ ±10 and ±30, respectively). Given the limitations of the current computationally efficient methods, it would be very difficult to extract more information from the absolute stability constant calculations in Table 1.

Figure 1.

Figure 1

Open in a new tab

Representative equilibrium geometries of the terbium ion with eight coordinated water molecules, [Tb(H2O)8]3+, DPA2– ligand, and their complex, [Tb(DPA)(H2O)8]+.

Table 1. Calculated and Experimental Stability Constants (log K1) for the DPA Ligand and Tb(III) Complexes.

  B3LYP
 M06
  
  COSMO SMD COSMO SMD exp26
6-31+G* 75.87 68.36 45.77 37.96 7.01
6-311++G** 74.82 66.94 45.34 37.34
Open in a new tab

Relative Complexation Free-Energy Changes and Relative Stability Constants for 4-Substituted DPA and Tb(III) Complexes

In this work, we studied eight 4-substituted analogues of DPAs (4-X-2,6-pyridinedicarboxylic acid; XDPA2– in short) with X = −F, −Cl, −Br, −I, −OH, −NH2, −CH2OH, and −imidazole. The equilibrium geometries for selected XDPA2– and [Tb(XDPA)(H2O)8]+ complexes are shown in Figure S1. These substitutes have been considered as alternative bioprobes2,4 as well as different barcodes in subsurface oil reservoir tracers. We define the relative free-energy changes in the gas phase and in aqueous solution (Figure 2A) as

graphic file with name ao9b02851_m001.jpg 1
graphic file with name ao9b02851_m002.jpg 2

with the brackets behind ΔG represent the free-energy changes of the specified complexations. There were multiple interesting observations in Figure 2A. First, the relative free-energy changes calculated in the gas phase were much higher than in solutions, with ΔΔG°g ∼ ±10 kcal/mol and ΔΔGaq ∼ ±2 kcal/mol (except for the −NH2 substitute). The reduced energy variations in solution compared to in the gas phase have been observed in prior studies (where the solvated ions included transition metals as well as rare earth elements).55,57,72 Second, the trends of ΔΔG°g and ΔΔGaq generally agree with each other (e.g., positive values for both ΔΔG°g and ΔΔGaq for the halide and imidazole substitutes (using COSMO solvation method) and negative values for both ΔΔG°g and ΔΔGaq for the NH2 substitute); however, contradictory results also exist (e.g., for OH and CH2OH substitutes where we see positive ΔΔG°g but negative ΔΔGaq). As a result, caution must be taken when correlating solution stability constants with only the gas-phase calculations.73−75 Finally, the different solvation models may give qualitatively different results (Cl, Br, and imidazole substitutes), which indicated that a consistent description of ion solvation still remains a challenge in this area.

Figure 2.

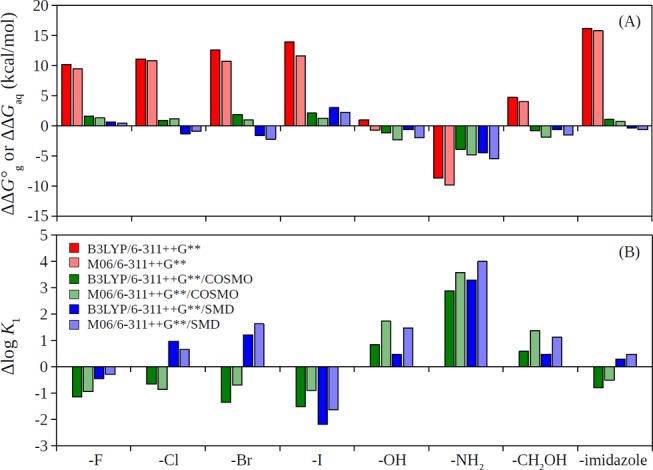
Figure 2

Open in a new tab

(A) Relative free-energy changes in the gas phase, ΔΔG°g, and in aqueous solution, ΔΔGaq and (B) relative stability constants, Δlog K1, for the 4-substituted DPA ligands complexing to Tb(III).

Figure 2B shows the relative stability constants of the different 4-substituted DPAs complexing to Tb(III), which were defined by

graphic file with name ao9b02851_m003.jpg 3

with the brackets again representing the specified complexations. Our calculations suggested that the strengths of the stability constants were modified by the substituents in the following (decreasing) order: −NH2 > −OH ∼ −CH2OH > −imidazole ∼ −Cl ∼ −Br ∼ −H > −F > −I, with the differences among them falling within one to two log units except for −NH2. We note that the calculated order was consistent with available experimental data from the literature comparing quantum yields of 4-substituted DPA and Tb(III) complexes (with order: −NH2 > −OH > −NHAc > −Cl > −H ∼ −Br),4 which partially validated our DFT calculations since the strong complexations of the ligands with the ions are the first step for strong sensitization and luminescence.

Population and Structural Analysis

To further understand the different binding strengths of the Tb(III) and XDPA2– complexes, we performed population and structural analysis for the [Tb(DPA)(H2O)8]+ and [Tb(XDPA)(H2O)8]+ complexes. Figure 3 shows the identifying labels of the key atoms within the complexes.

Figure 3.

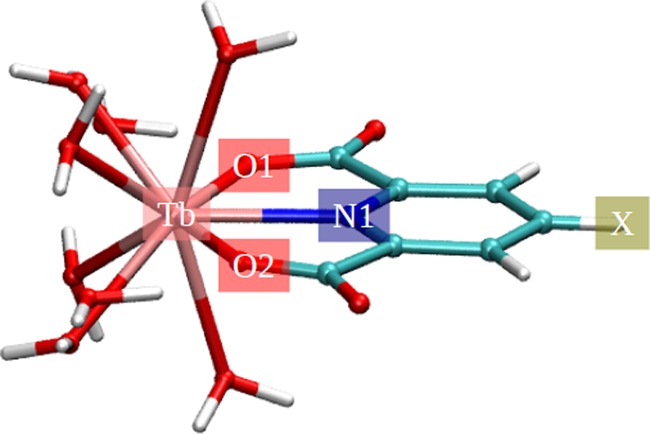
Figure 3

Open in a new tab

Identifying labels of the key atoms within the [Tb(XDPA)(H2O)8]+ complexes.

It has been understood that the substitutes on rings can donate electrons via resonance effect to the rings as well as inductively withdrawing electrons.76 The order of electron-withdrawing strengths on the X position (Figure 3): halide > −OH > −NH2 substitutes on the pyridine ring of XDPA2– result in the following order of partial charges on the N1 atom (Figure 3): halide > −OH > −NH2 substitutes, which was clearly observed from the partial charge analysis (Figures 4B and 5B). In addition, the −CH2OH and −OH substitutes were observed to have similar partial charges on N1 (Figures 4B and 5B). The order of electrostatic potential energy between Tb and N1 atoms (approximated by the product of their Mulliken charges): halide > −OH ∼ −CH2OH > −NH2 substitutes, thus, result in the order of stability constant strengths: −NH2 > −OH ∼ −CH2OH > halide substitutes (c.f. Figure 2). On the other hand, the partial charges of Tb, O1, and O2 were seem unaffected with the 4-substitution (Figures 4A,C,D and 5A,C,D).

Figure 4.

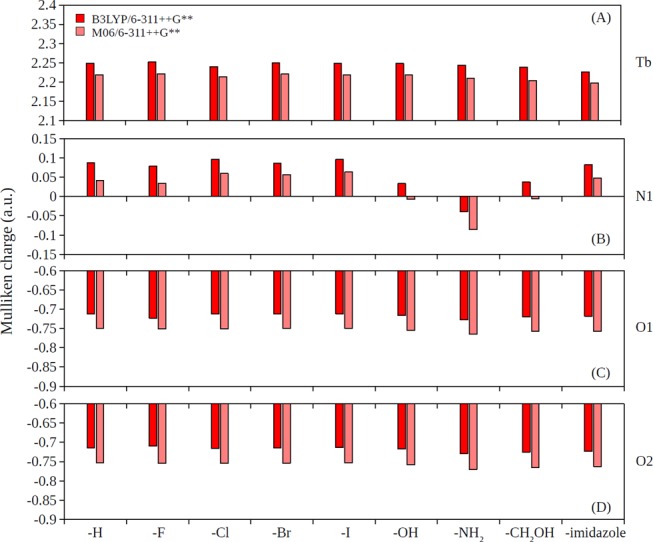
Figure 4

Open in a new tab

Partial charges predicted by the Mulliken population analysis in the gas phase for (A) Tb, (B) N1, (C) O1, and (D) O2 atoms in [Tb(XDPA)(H2O)8]+ complexes.

Figure 5.

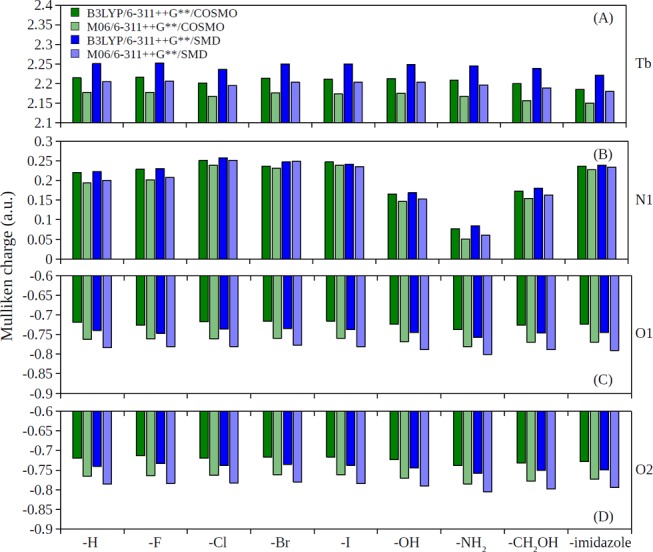
Figure 5

Open in a new tab

Partial charges predicted by the Mulliken population analysis in solution phase for (A) Tb, (B) N1, (C) O1, and (D) O2 atoms in [Tb(XDPA)(H2O)8]+ complexes.

The natural electron configuration of Tb in the complexes was analyzed by the Mulliken population analysis with 4f shell occupancy between 8.13 and 8.15 in [Tb(H2O)8]3+ complexes and between 8.15 and 8.18 in [Tb(DPA)(H2O)8]+ and [Tb(XDPA)(H2O)8]+ complexes for both the gas and solution phases. Indeed, the 0.13–0.18 electron excess on Tb inert 4f orbitals may be due to the primitive Mulliken analysis since electron donation to lanthanides occurs primarily to 5d and 6s orbitals. The natural 6s, 4f, and 5d electron configurations for Tb in different complexes are summarized in Table S4. It was observed that the 4-substitutions on DPA ligands have minimum effects on the relative electron occupations for Tb in the various complexes.

Figure 6 shows the selected interatomic distances in the [Tb(XDPA)(H2O)8]+ complexes. It was observed that Tb–N1 distances for the strongest binding X = −NH2 complex were also the shortest (about 0.03–0.04 Å shorter then X = −H or halide substitutes; Figure 6A), and the next strongest binding X = −OH and −CH2OH complexes were the next shortest (about 0.01–0.02 Å shorter then X = −H or halide substitutes; Figure 6A). On the other hand, Tb–O1 and Tb–O2 distances were seem unaffected with the 4-substitution (Figure 6B,C).

Figure 6.

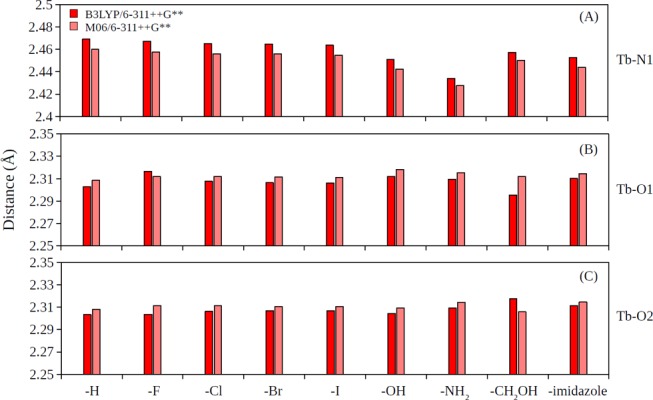
Figure 6

Open in a new tab

Interatomic distances in [Tb(XDPA)(H2O)8]+ complexes for (A) Tb–N1, (B) Tb–O1, and (C) Tb–O2 pairs.

Conclusions

In the present study, we performed DFT calculations to study the absolute and relative stability constants for the Tb(III) complexes with DPA as well as a series of 4-substituted DPA analogues. Using different basis sets, density functionals, and solvation methods, we observed that the predictions of the absolute stability constants have remained challenging, with the selections of density functionals have the largest effect. We note that the same conclusion has been pointed out by prior studies,55−57,59 and more research in this area is imminent. On the other hand, our calculations on the relative stability constants of the 4-substituted DPA ligands suggested that their binding strengths to Tb(III) were modified in the following order: −NH2 > −OH ∼ −CH2OH > −imidazole ∼ −Cl ∼ −Br ∼ −H > −F > −I, with most of the differences among them falling within one to two log units. In the context of our original motivation for selecting the ligands as oil field tracers, the results suggest that these substitutes should all be suitable for the application since the ligand–ion complexation efficiencies (as the first step for the Tb(III)-sensitization assays) are only moderately affected. Nevertheless, the predicted order of the modified stability constants remains to be experimentally verified. Last but not the least, we performed population and structural analyses on the [Tb(DPA)(H2O)8]+ and [Tb(XDPA)(H2O)8]+ complexes. We observed that the −NH2, −OH, −CH2OH, and halide substituents can donate electrons via resonance effect to the pyridine ring of DPA while inductively withdrawing electrons with different strengths resulting in different partial charges on N1 as well as different distances for Tb–N1, thus resulting in the different binding strengths.

Methods

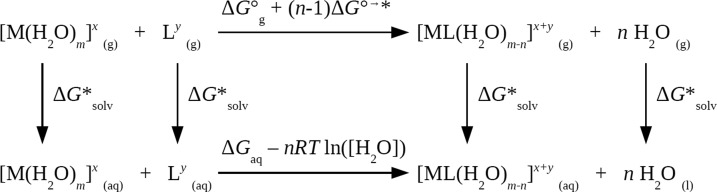
Thermodynamic Cycle for Calculating Stability Constants

In this work, we focused on the binding of DPA ligands to Tb(III) for the formation of 1:1 complexes. For the 1:1 metal/ligand complexes with equilibrium M + L ⇌ ML, the experimental stability constant K1 is related to the Gibbs free-energy change for the reaction in solution, ΔGaq, by

graphic file with name ao9b02851_m004.jpg 4

where aML, aM, and aL are the activities of the species involved in the equilibrium. First-principles methods have been developed to compute ΔGaq with the thermodynamic cycle shown in Figure 7.57,59,60 In this process, ΔG°g represent the free-energy changes of the metal and ligand bindings in the gas phase, and ΔG*solv represent the free energies of solvation for the transfer of 1 mole of solutes from the gas phase to the aqueous phase. Note that because ΔG°g were usually calculated with the standard state of an ideal gas at 1 atm whereas ΔG*solv were calculated with the standard state of 1 M, a conversion of an ideal gas from 1 atm (24.46 mol/L) to 1 M (1 mol/L) was applied with

graphic file with name ao9b02851_m005.jpg 5

Finally, with water, an additional correction, Gaql = Gaq + RT ln([H2O]), is needed if the pure solvent H2O(l) is adopted as the reference state for the solvent. Here, RT ln([H2O]) = 2.38 kcal/mol is a free-energy change associated with moving a solvent from a standard-state solution-phase concentration of 1 M to a standard state of pure liquid, 55.34 M. Note that common logarithm (log) was used to express stability constants following experimental conventions, while natural logarithm (ln) was used in the rest of the thermodynamic equations.

Figure 7.

Figure 7

Open in a new tab

Thermodynamic cycle used to calculate ΔGaq.

Computational Details

In this work, we studied [Tb(H2O)8]3+, DPA2–, XDPA2–, [Tb(DPA)(H2O)8]+, and [Tb(XDPA)(H2O)8]+ complexes with X = −F, −Cl, −Br, −I, −OH, −NH2, −CH2OH, and −imidazole. The proposed structures are shown in Figures 1 and S1. Density functional theory (DFT) calculations reported in this work were performed using the NWChem 6.8.1 program package.77 We used both B3LYP and M06 density functionals to examine the variations in the selection of different functionals.78−80 The Stuttgart relativistic small core (RSC) segmented/ECP set was used for terbium.81 The ECP on the terbium atom accounts for scalar relativistic effects by replacing 28 electrons with a relativistic pseudopotential. The 6-31+G* or 6-311++G** basis sets with diffuse functions were employed for the light atoms.82−85 All geometry optimizations and frequency calculations were performed in the gas phase. Most of the geometry optimizations and frequency calculations were performed at the B3LYP/6-311++G** and M06/6-311++G** level except for nonsubstituted DPA complexes where 6-31+G* basis set was also considered. Frequency calculations were used to verify that geometries were minima on the potential energy surface and to compute thermal corrections to enthalpies and total entropies (at T = 298.15 K), which were then combined with the total DFT energies to calculate the gas-phase free energies for individual species and their differences, ΔG°g (Figure 7).

Using the gas-phase geometries, we calculated single-point aqueous solvation free energies, ΔG*solv, with both the conductor-like screening model (COSMO)86,87 and the SMD model.88 The free-energy changes in the aqueous phase, ΔGaq, and the stability constants, log K1, can then be calculated by completing the thermodynamic cycle (Figure 7). We note that similar approaches have been used to predict the stability constants for other metal/ligand complexes including transition metals and rare earth elements with good results.56−58

The Mulliken population analysis included in the NWChem software was performed to acquire the partial charges and the natural electron configuration of the studied complexes.

Acknowledgments

We thank Aramco Research Center-Boston, Reservoir Engineering Technology team members for valuable discussions. We acknowledge ASC, IT Services for managing computational resources.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsomega.9b02851.

  • Original energy data from DFT calculations; orbital occupancy of Tb in different complexes from population analysis; equilibrium geometries of different ligands and complexes; partial charges and interatomic distances the same as in Figures 4–6 but organized as differences referenced to H (PDF)

The authors declare no competing financial interest.

Supplementary Material

ao9b02851_si_001.pdf (810KB, pdf)

References

  1. Weissman S. I. Intramolecular energy transfer the fluorescence of complexes of europium. J. Chem. Phys. 1942, 10, 214–217. 10.1063/1.1723709. [DOI] [Google Scholar]
  2. George M. R.; Golden C. A.; Grossel M. C.; Curry R. J. Modified dipicolinic acid ligands for sensitization of europium (III) luminescence. Inorg. Chem. 2006, 45, 1739–1744. 10.1021/ic051461u. [DOI] [PubMed] [Google Scholar]
  3. D’ale′o A.; Picot A.; Beeby A.; Gareth Williams J.; Le Guennic B.; Andraud C.; Maury O. Efficient sensitization of europium, ytterbium, and neodymium functionalized tris-dipicolinate lanthanide complexes through tunable charge-transfer excited states. Inorg. Chem. 2008, 47, 10258–10268. 10.1021/ic8012969. [DOI] [PubMed] [Google Scholar]
  4. Lamture J. B.; Zhou Z. H.; Kumar A. S.; Wensel T. G. Luminescence properties of terbium (III) complexes with 4-substituted dipicolinic acid analogs. Inorg. Chem. 1995, 34, 864–869. 10.1021/ic00108a017. [DOI] [Google Scholar]
  5. Pandya S.; Yu J.; Parker D. Engineering emissive europium and terbium complexes for molecular imaging and sensing. Dalton Trans. 2006, 2757–2766. 10.1039/b514637b. [DOI] [PubMed] [Google Scholar]
  6. Hemmilä I.; Webb S. Time-resolved fluorometry: an overview of the labels and core technologies for drug screening applications. Drug Discovery Today 1997, 2, 373–381. 10.1016/S1359-6446(97)01080-5. [DOI] [Google Scholar]
  7. Soini E.; Lövgren T.; Reimer C. B. Time-resolved fluorescence of lanthanide probes and applications in biotechnology. Crit. Rev. Anal. Chem. 1987, 18, 105–154. 10.1080/10408348708085565. [DOI] [Google Scholar]
  8. Charbonnière L. J.; Hildebrandt N.; Ziessel R. F.; Löhmannsröben H.-G. Lanthanides to quantum dots resonance energy transfer in time-resolved fluoro-immunoassays and luminescence microscopy. J. Am. Chem. Soc. 2006, 128, 12800–12809. 10.1021/ja062693a. [DOI] [PubMed] [Google Scholar]
  9. Marriott G.; Clegg R. M.; Arndt-Jovin D. J.; Jovin T. M. Time resolved imaging microscopy. Phosphorescence and delayed fluorescence imaging. Biophys. J. 1991, 60, 1374–1387. 10.1016/S0006-3495(91)82175-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Bünzli J.-C. G. Lanthanide luminescence for biomedical analyses and imaging. Chem. Rev. 2010, 110, 2729–2755. 10.1021/cr900362e. [DOI] [PubMed] [Google Scholar]
  11. Beeby A.; Botchway S. W.; Clarkson I. M.; Faulkner S.; Parker A. W.; Parker D.; Williams J. G. Luminescence imaging microscopy and lifetime mapping using kinetically stable lanthanide (III) complexes. J. Photochem. Photobiol., B 2000, 57, 83–89. 10.1016/S1011-1344(00)00070-1. [DOI] [PubMed] [Google Scholar]
  12. Faulkner S.; Pope S. J.; Burton-Pye B. P. Lanthanide complexes for luminescence imaging applications. Appl. Spectosc. Rev. 2005, 40, 1–31. 10.1081/ASR-200038308. [DOI] [Google Scholar]
  13. Yu J.; Parker D.; Pal R.; Poole R. A.; Cann M. J. A europium complex that selectively stains nucleoli of cells. J. Am. Chem. Soc. 2006, 128, 2294–2299. 10.1021/ja056303g. [DOI] [PubMed] [Google Scholar]
  14. Aarons R. J.; Notta J. K.; Meloni M. M.; Feng J.; Vidyasagar R.; Narvainen J.; Allan S.; Spencer N.; Kauppinen R. A.; Snaith J. S. A luminescent probe containing a tuftsin targeting vector coupled to a terbium complex. Chem. Commun. 2006, 909–911. 10.1039/b515160k. [DOI] [PubMed] [Google Scholar]
  15. Bünzli J.-C. G.; Piguet C. Taking advantage of luminescent lanthanide ions. Chem. Soc. Rev. 2005, 34, 1048–1077. 10.1039/b406082m. [DOI] [PubMed] [Google Scholar]
  16. Eliseeva S. V.; Bünzli J.-C. G. Lanthanide luminescence for functional materials and bio-sciences. Chem. Soc. Rev. 2010, 39, 189–227. 10.1039/B905604C. [DOI] [PubMed] [Google Scholar]
  17. Kido J.; Okamoto Y. Organo lanthanide metal complexes for electroluminescent materials. Chem. Rev. 2002, 102, 2357–2368. 10.1021/cr010448y. [DOI] [PubMed] [Google Scholar]
  18. Curry R.; Gillin W. Electroluminescence of organolanthanide based organic light emitting diodes. Curr. Opin. Solid State Mater. Sci. 2001, 5, 481–486. 10.1016/S1359-0286(02)00010-4. [DOI] [Google Scholar]
  19. Slooff L.; Van Blaaderen A.; Polman A.; Hebbink G.; Klink S.; Van Veggel F.; Reinhoudt D.; Hofstraat J. Rare-earth doped polymers for planar optical amplifiers. J. Appl. Phys. 2002, 91, 3955–3980. 10.1063/1.1454190. [DOI] [Google Scholar]
  20. Jenkins A. L.; Murray G. M. Ultratrace determination of selected lanthanides by luminescence enhancement. Anal. Chem. 1996, 68, 2974–2980. 10.1021/ac9603800. [DOI] [PubMed] [Google Scholar]
  21. Richardson F. S. Terbium (III) and europium (III) ions as luminescent probes and stains for biomolecular systems. Chem. Rev. 1982, 82, 541–552. 10.1021/cr00051a004. [DOI] [Google Scholar]
  22. Metcalf D. H.; Bolender J. P.; Driver M. S.; Richardson F. Chiral discrimination in electronic energy transfer between dissymmetric lanthanide (III) and cobalt (III) complexes in solution: effects of ligand size, shape, and configuration in the acceptor complexes. J. Phys. Chem. A 1993, 97, 553–564. 10.1021/j100105a006. [DOI] [Google Scholar]
  23. Pellegrino P. M.; Fell N. F.; Rosen D. L.; Gillespie J. B. Bacterial endospore detection using terbium dipicolinate photoluminescence in the presence of chemical and biological materials. Anal. Chem. 1998, 70, 1755–1760. 10.1021/ac971232s. [DOI] [PubMed] [Google Scholar]
  24. Fell N. F. Jr; Pellegrino P. M.; Gillespie J. B. Mitigating phosphate interference in bacterial endospore detection by Tb dipicolinate photoluminescence. Anal. Chim. Acta 2001, 426, 43–50. 10.1016/S0003-2670(00)01184-3. [DOI] [Google Scholar]
  25. Guilford Jones I.; Vullev V. I. Medium effects on the photophysical properties of terbium (III) complexes with pyridine-2, 6-dicarboxylate. Photochem. Photobiol. Sci. 2002, 1, 925–933. [DOI] [PubMed] [Google Scholar]
  26. Jones G.; Vullev V. I. Medium effects on the stability of terbium (III) complexes with pyridine-2, 6-dicarboxylate. J. Phys. Chem. A 2002, 106, 8213–8222. 10.1021/jp026168j. [DOI] [PubMed] [Google Scholar]
  27. Rosen D. L.; Sharpless C.; McGown L. B. Bacterial spore detection and determination by use of terbium dipicolinate photoluminescence. Anal. Chem. 1997, 69, 1082–1085. 10.1021/ac960939w. [DOI] [Google Scholar]
  28. Rosen D. L.; Niles S. Chelation number of terbium dipicolinate: effects on photoluminescence lifetime and intensity. Appl. Spectrosc. 2001, 55, 208–216. 10.1366/0003702011951524. [DOI] [Google Scholar]
  29. Gültekin A.; Ersöz A.; Sarıözlü N. Y.; Denizli A.; Say R. Nanosensors having dipicolinic acid imprinted nanoshell for Bacillus cereus spores detection. J. Nanopart. Res. 2010, 12, 2069–2079. 10.1007/s11051-009-9766-z. [DOI] [Google Scholar]
  30. Kort R.; O’brien A. C.; Van Stokkum I. H.; Oomes S. J.; Crielaard W.; Hellingwerf K. J.; Brul S. Assessment of heat resistance of bacterial spores from food product isolates by fluorescence monitoring of dipicolinic acid release. Appl. Environ. Microbiol. 2005, 71, 3556–3564. 10.1128/AEM.71.7.3556-3564.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Hindle A. A.; Hall E. H. Dipicolinic acid (DPA) assay revisited and appraised for spore detection. Analyst 1999, 124, 1599–1604. 10.1039/a906846e. [DOI] [PubMed] [Google Scholar]
  32. Cable M. L.; Kirby J. P.; Levine D. J.; Manary M. J.; Gray H. B.; Ponce A. Detection of bacterial spores with Lanthanide– Macrocycle binary complexes. J. Am. Chem. Soc. 2009, 131, 9562–9570. 10.1021/ja902291v. [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Cable M. L.; Kirby J. P.; Sorasaenee K.; Gray H. B.; Ponce A. Bacterial spore detection by [Tb3+ (macrocycle)(dipicolinate)] luminescence. J. Am. Chem. Soc. 2007, 129, 1474–1475. 10.1021/ja061831t. [DOI] [PubMed] [Google Scholar]
  34. Barnes L.; Kaneshige K.; Strong J.; Tan K.; Von Bremen H.; Mogul R. Effects of terbium chelate structure on dipicolinate ligation and the detection of Bacillus spores. J. Inorg. Biochem. 2011, 105, 1580–1588. 10.1016/j.jinorgbio.2011.08.020. [DOI] [PubMed] [Google Scholar]
  35. Lewis J. C. Determination of dipicolinic acid in bacterial spores by ultraviolet spectrometry of the calcium chelate. Anal. Biochem. 1967, 19, 327–337. 10.1016/0003-2697(67)90168-6. [DOI] [PubMed] [Google Scholar]
  36. Yang W.-W.; Ponce A. Rapid endospore viability assay of Clostridium sporogenes spores. Int. J. Food Microbiol. 2009, 133, 213–216. 10.1016/j.ijfoodmicro.2009.04.024. [DOI] [PubMed] [Google Scholar]
  37. Albert H.; Davies D.; Woodson L.; Soper C. Biological indicators for steam sterilization: characterization of a rapid biological indicator utilizing Bacillus stearothermophilus spore-associated alpha-glucosidase enzyme. J. Appl. Microbiol. 1998, 85, 865–874. 10.1046/j.1365-2672.1998.00607.x. [DOI] [PubMed] [Google Scholar]
  38. Enserink M.Biodefense Hampered by Inadequate Tests; American Association for the Advancement of Science, 2001. [DOI] [PubMed] [Google Scholar]
  39. Jernigan J. Bioterrorism-related inhalational anthrax: the first 10 cases reported in the United States. Emerging Infect. Dis. 2001, 7, 933. 10.3201/eid0706.010604. [DOI] [PMC free article] [PubMed] [Google Scholar]
  40. Sanderson W. T.; Stoddard R.; Echt A.; Piacitelli C.; Kim D.; Horan J.; Davies M.; McCleery R.; Muller P.; Schnorr T. Bacillus anthracis contamination and inhalational anthrax in a mail processing and distribution center. J. Appl. Microbiol. 2004, 96, 1048–1056. 10.1111/j.1365-2672.2004.02223.x. [DOI] [PubMed] [Google Scholar]
  41. Yung P. T.; Lester E. D.; Bearman G.; Ponce A. An automated front-end monitor for anthrax surveillance systems based on the rapid detection of airborne endospores. Biotechnol. Bioeng. 2007, 98, 864–871. 10.1002/bit.21466. [DOI] [PubMed] [Google Scholar]
  42. Yung P. T.; Shafaat H. S.; Connon S. A.; Ponce A. Quantification of viable endospores from a Greenland ice core. FEMS Microbiol. Ecol. 2007, 59, 300–306. 10.1111/j.1574-6941.2006.00218.x. [DOI] [PubMed] [Google Scholar]
  43. Shafaat H. S.; Ponce A. Applications of a rapid endospore viability assay for monitoring UV inactivation and characterizing arctic ice cores. Appl. Environ. Microbiol. 2006, 72, 6808–6814. 10.1128/AEM.00255-06. [DOI] [PMC free article] [PubMed] [Google Scholar]
  44. Nicholson W. L.; Galeano B. UV resistance of Bacillus anthracis spores revisited: validation of Bacillus subtilis spores as UV surrogates for spores of B. anthracis Sterne. Appl. Environ. Microbiol. 2003, 69, 1327–1330. 10.1128/AEM.69.2.1327-1330.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
  45. Horneck G.; Bücker H.; Reitz G. Long-term survival of bacterial spores in space. Adv. Space Res. 1994, 14, 41–45. 10.1016/0273-1177(94)90448-0. [DOI] [PubMed] [Google Scholar]
  46. Chen H.; Kmetz A. A.; Cox J. R.; Poitzsch M. E. In Impact of Irreversible Ietention on Tracer Deployments; Constraining Novel Material Deployments, SPE Abu Dhabi International Petroleum Exhibition & Conference; Society of Petroleum Engineers, 2017.
  47. Ow H.; Chang S.; Thomas G.; Shi R.; Wang W.; Chen H.; Poitzsch M. E.; Abdel-Fattah A. InFirst Deployment of a Novel Advanced Tracers System for Improved Waterflood Recovery Optimization, SPE Abu Dhabi International Petroleum Exhibition & Conference; Society of Petroleum Engineers, 2018.
  48. Thomas G.; Ow H.; Chang S.; Shi R.; Wang W.; Chen H.; Poitzsch M.; Shateeb H.; Abdel-Fattah A. In Deployment and Detection of a Novel Barcoded Advanced Tracers System for the Optimization of Improved Waterflood Recovery in Hydrocarbon Reservoirs, SPE Middle East Oil and Gas Show and Conference; Society of Petroleum Engineers, 2019.
  49. Zemel B.Tracers in the Oil Field; Elsevier, 1995; Vol. 43. [Google Scholar]
  50. Dugstad Ø.Well-to-Well Tracer Tests. In Petroleum Engineering Handbook; 2007; Vol. 5, pp 651–683. [Google Scholar]
  51. Kosynkin D.; Alaskar M. In Oil Industry First Interwell Trial of Reservoir Nanoagent Tracers, SPE Annual Technical Conference and Exhibition; Society of Petroleum Engineers, 2016.
  52. Sanni M.; Al-Abbad M.; Kokal S.; Dugstad Ø.; Hartvig S.; Huseby O. Pushing the envelope of residual oil measurement: A field case study of a new class of inter-well chemical tracers. J. Pet. Sci. Eng. 2018, 163, 538–545. 10.1016/j.petrol.2017.12.076. [DOI] [Google Scholar]
  53. Chen H.; Poitzsch M. E. In Improved Reservoir History Matching and Production Optimization with Tracer Data, SPE Annual Technical Conference and Exhibition; Society of Petroleum Engineers, 2018.
  54. Beck M. T.; Nagypal I., Complex Equilibria: Stability Constants; E. Horwood, 1989. [Google Scholar]
  55. Gutten O.; Beššeova′ I.; Ruli′šek L. Interaction of metal ions with biomolecular ligands: how accurate are calculated free energies associated with metal ion complexation?. J. Phys. Chem. A 2011, 115, 11394–11402. 10.1021/jp205442p. [DOI] [PubMed] [Google Scholar]
  56. Gutten O.; Rulisek L. Predicting the stability constants of metal-ion complexes from first principles. Inorg. Chem. 2013, 52, 10347–10355. 10.1021/ic401037x. [DOI] [PubMed] [Google Scholar]
  57. Vukovic S.; Hay B. P.; Bryantsev V. S. Predicting stability constants for uranyl complexes using density functional theory. Inorg. Chem. 2015, 54, 3995–4001. 10.1021/acs.inorgchem.5b00264. [DOI] [PubMed] [Google Scholar]
  58. Bryantsev V. S.; Hay B. P. Theoretical prediction of Am (III)/Eu (III) selectivity to aid the design of actinide-lanthanide separation agents. Dalton Trans. 2015, 44, 7935–7942. 10.1039/C4DT03275F. [DOI] [PubMed] [Google Scholar]
  59. Ivanov A. S.; Bryantsev V. S. Assessing ligand selectivity for uranium over vanadium ions to aid in the discovery of superior adsorbents for extraction of UO 2 2+ from seawater. Dalton Trans. 2016, 45, 10744–10751. 10.1039/C6DT01752E. [DOI] [PubMed] [Google Scholar]
  60. Lashley M. A.; Ivanov A. S.; Bryantsev V. S.; Dai S.; Hancock R. D. Highly preorganized ligand 1, 10-phenanthroline-2, 9-dicarboxylic acid for the selective recovery of uranium from seawater in the presence of competing vanadium species. Inorg. Chem. 2016, 55, 10818–10829. 10.1021/acs.inorgchem.6b02234. [DOI] [PubMed] [Google Scholar]
  61. Mehio N.; Ivanov A. S.; Williams N. J.; Mayes R. T.; Bryantsev V. S.; Hancock R. D.; Dai S. Quantifying the binding strength of salicylaldoxime–uranyl complexes relative to competing salicylaldoxime–transition metal ion complexes in aqueous solution: a combined experimental and computational study. Dalton Trans. 2016, 45, 9051–9064. 10.1039/C6DT00116E. [DOI] [PubMed] [Google Scholar]
  62. Radchenko V.; Mastren T.; Meyer C. A.; Ivanov A. S.; Bryantsev V. S.; Copping R.; Denton D.; Engle J. W.; Griswold J. R.; Murphy K.; et al. Radiometric evaluation of diglycolamide resins for the chromatographic separation of actinium from fission product lanthanides. Talanta 2017, 175, 318–324. 10.1016/j.talanta.2017.07.057. [DOI] [PubMed] [Google Scholar]
  63. Ivanov A. S.; Leggett C. J.; Parker B. F.; Zhang Z.; Arnold J.; Dai S.; Abney C. W.; Bryantsev V. S.; Rao L. Origin of the unusually strong and selective binding of vanadium by polyamidoximes in seawater. Nat. Commun. 2017, 8, 1560 10.1038/s41467-017-01443-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
  64. Sun Q.; Aguila B.; Perman J.; Ivanov A. S.; Bryantsev V. S.; Earl L. D.; Abney C. W.; Wojtas L.; Ma S. Bio-inspired nano-traps for uranium extraction from seawater and recovery from nuclear waste. Nat. Commun. 2018, 9, 1644 10.1038/s41467-018-04032-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
  65. Ladshaw A. P.; Ivanov A. S.; Das S.; Bryantsev V. S.; Tsouris C.; Yiacoumi S. First-Principles integrated adsorption modeling for selective capture of uranium from seawater by polyamidoxime sorbent materials. ACS Appl. Mater. Interfaces 2018, 10, 12580–12593. 10.1021/acsami.7b17031. [DOI] [PubMed] [Google Scholar]
  66. Penchoff D. A.; Peterson C. C.; Camden J. P.; Bradshaw J. A.; Auxier J. D.; Schweitzer G. K.; Jenkins D. M.; Harrison R. J.; Hall H. L. Structural Analysis of the Complexation of Uranyl, Neptunyl, Plutonyl, and Americyl with Cyclic Imide Dioximes. ACS Omega 2018, 3, 13984–13993. 10.1021/acsomega.8b02068. [DOI] [PMC free article] [PubMed] [Google Scholar]
  67. Penchoff D. A.; Peterson C. C.; Quint M. S.; Auxier J. D.; Schweitzer G. K.; Jenkins D. M.; Harrison R. J.; Hall H. L. Structural Characteristics, Population Analysis, and Binding Energies of [An (NO3)] 2+(with An = Ac to Lr). ACS Omega 2018, 3, 14127–14143. 10.1021/acsomega.8b01800. [DOI] [PMC free article] [PubMed] [Google Scholar]
  68. Peterson C. C.; Penchoff D. A.; Auxier J. D.; Hall H. L. Establishing Cost-Effective Computational Models for the Prediction of Lanthanoid Binding in [Ln (NO3)] 2 + (with Ln = La to Lu). ACS Omega 2019, 4, 1375–1385. 10.1021/acsomega.8b02403. [DOI] [PMC free article] [PubMed] [Google Scholar]
  69. Ciupka J.; Cao-Dolg X.; Wiebke J.; Dolg M. Computational study of lanthanide (III) hydration. Phys. Chem. Chem. Phys. 2010, 12, 13215–13223. 10.1039/c0cp00639d. [DOI] [PubMed] [Google Scholar]
  70. Zhang J.; Heinz N.; Dolg M. Understanding lanthanoid (III) hydration structure and kinetics by insights from energies and wave functions. Inorg. Chem. 2014, 53, 7700–7708. 10.1021/ic500991x. [DOI] [PubMed] [Google Scholar]
  71. Ryde U.; Soderhjelm P. Ligand-binding affinity estimates supported by quantum-mechanical methods. Chem. Rev. 2016, 116, 5520–5566. 10.1021/acs.chemrev.5b00630. [DOI] [PubMed] [Google Scholar]
  72. Arabieh M.; Platas-Iglesias C. A density functional theory study on the interaction of dipicolinic acid with hydrated Fe2+ cation. Comput. Theor. Chem. 2016, 1090, 134–146. 10.1016/j.comptc.2016.06.010. [DOI] [Google Scholar]
  73. Hancock R. D.; Bartolotti L. J. Prediction of formation constants of metal–ammonia complexes in aqueous solution using density functional theory calculations. Chem. Commun. 2004, 122, 534–535. 10.1039/B312518C. [DOI] [PubMed] [Google Scholar]
  74. Hancock R. D.; Bartolotti L. J. Density functional theory-based prediction of the formation constants of complexes of ammonia in aqueous solution: Indications of the role of relativistic effects in the solution chemistry of gold (I). Inorg. Chem. 2005, 44, 7175–7183. 10.1021/ic050471s. [DOI] [PubMed] [Google Scholar]
  75. Chen Y.-L.; Barlow D. J.; Kong X.-L.; Ma Y.-M.; Hider R. C. Prediction of 3-hydroxypyridin-4-one (HPO) hydroxyl p K a values. Dalton Trans. 2012, 41, 6549–6557. 10.1039/c2dt12396g. [DOI] [PubMed] [Google Scholar]
  76. Bruice P. Y., Organic Chemistry; Pearson, 2004. [Google Scholar]
  77. Valiev M.; Bylaska E. J.; Govind N.; Kowalski K.; Straatsma T. P.; Van Dam H. J.; Wang D.; Nieplocha J.; Apra E.; Windus T. L.; de Jong W. A. NWChem: a comprehensive and scalable open-source solution for large scale molecular simulations. Comput. Phys. Commun. 2010, 181, 1477–1489. 10.1016/j.cpc.2010.04.018. [DOI] [Google Scholar]
  78. Becke A. D. Density-functional thermochemistry. III. The role of exact exchange. J. Chem. Phys. 1993, 98, 5648–5652. 10.1063/1.464913. [DOI] [Google Scholar]
  79. Lee C.; Yang W.; Parr R. G. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B 1988, 37, 785. 10.1103/PhysRevB.37.785. [DOI] [PubMed] [Google Scholar]
  80. Zhao Y.; Truhlar D. G. The M06 suite of density functionals for main group thermochemistry, thermochemical kinetics, noncovalent interactions, excited states, and transition elements: two new functionals and systematic testing of four M06-class functionals and 12 other functionals. Theor. Chem. Acc. 2008, 120, 215–241. 10.1007/s00214-007-0310-x. [DOI] [Google Scholar]
  81. Dolg M.; Stoll H.; Preuss H.; Pitzer R. M. Relativistic and correlation effects for element 105 (hahnium, Ha): a comparative study of M and MO (M = Nb, Ta, Ha) using energy-adjusted ab initio pseudopotentials. J. Phys. Chem. A 1993, 97, 5852–5859. 10.1021/j100124a012. [DOI] [Google Scholar]
  82. Hehre W. J.; Ditchfield R.; Pople J. A. Self-consistent molecular orbital methods. XII. Further extensions of Gaussian-type basis sets for use in molecular orbital studies of organic molecules. J. Chem. Phys. 1972, 56, 2257–2261. 10.1063/1.1677527. [DOI] [Google Scholar]
  83. Krishnan R.; Binkley J. S.; Seeger R.; Pople J. A. Self-consistent molecular orbital methods. XX. A basis set for correlated wave functions. J. Chem. Phys. 1980, 72, 650–654. 10.1063/1.438955. [DOI] [Google Scholar]
  84. McLean A.; Chandler G. Contracted Gaussian basis sets for molecular calculations. I. Second row atoms, Z = 11–18. J. Chem. Phys. 1980, 72, 5639–5648. 10.1063/1.438980. [DOI] [Google Scholar]
  85. Curtiss L. A.; McGrath M. P.; Blaudeau J. P.; Davis N. E.; Binning R. C. Jr; Radom L. Extension of Gaussian-2 theory to molecules containing third-row atoms Ga–Kr. J. Chem. Phys. 1995, 103, 6104–6113. 10.1063/1.470438. [DOI] [Google Scholar]
  86. Klamt A.; Schüürmann G. COSMO: a new approach to dielectric screening in solvents with explicit expressions for the screening energy and its gradient. J. Chem. Soc., Perkin Trans. 2 1993, 799–805. 10.1039/P29930000799. [DOI] [Google Scholar]
  87. Klamt A.; Jonas V.; Bürger T.; Lohrenz J. C. Refinement and parametrization of COSMO-RS. J. Phys. Chem. A 1998, 102, 5074–5085. 10.1021/jp980017s. [DOI] [Google Scholar]
  88. Marenich A. V.; Cramer C. J.; Truhlar D. G. Universal solvation model based on solute electron density and on a continuum model of the solvent defined by the bulk dielectric constant and atomic surface tensions. J. Phys. Chem. B 2009, 113, 6378–6396. 10.1021/jp810292n. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

ao9b02851_si_001.pdf (810KB, pdf)

Articles from ACS Omega are provided here courtesy of American Chemical Society

RESOURCES